- 1Badan Perencanaan Pembangunan, Penelitian dan Pengembangan Provinsi Sumatera Utara, Medan, Provinsi Sumatera Utara, Indonesia
- 2Pascasarjana, Universitas Bina Bangsa Getsempena, Banda Aceh, Indonesia
- 3Pendidikan Matematika, Universitas Negeri Medan, Medan, Provinsi Sumatera Utara, Indonesia
Problem-solving skills of students are indicators of their intellectual behavior, and they determine higher-order thinking skills that students need to master. One of the approaches to improving students' mathematics problem-solving skills is understanding their learning style and personality characteristics and the influences of these two factors on problem-solving skills. The research goals are to describe students' mathematics problem-solving skills and examine the influence of gender, grade level, learning style, personality characteristics, and interaction between learning style and personality characteristics on their mathematics problem-solving skills. The study population comprised all students in five state elementary schools and five state junior high schools, with a sample size of 200 students. Statistical analysis of the data was carried out using t-tests and analysis of variance. The majority of students showed “moderate” mathematics problem-solving skills (72.77), with 60.50% falling under the “moderate” category or above. Gender and grade level had a significant influence on students' mathematics problem-solving skills. In addition, mathematics problem-solving skills were dependent on learning style and personality characteristics. Learning style, personality characteristics, and interaction between these two factors showed significant influences on students' mathematics problem-solving skills. Furthermore, the learning style “auditory-kinesthetics” and the personality characteristics “steadiness-compliance” and “dominance-influence” had significant influences on students' mathematics problem-solving skills. Moreover, “auditory-kinesthetics—steadiness-compliance” and “auditory-kinesthetics—dominance-influence” interactions showed significant influences on students' mathematics problem-solving skills.
1 Introduction
In students, problem-solving skills are indicators of their intellectual behavior and higher-order thinking skills (Ichsan et al., 2019; Akben, 2020; Nur and Kardi, 2000) and play a crucial role in inspiring innovation and creativity to achieve academic success (Rahman, 2019; Rosa and Parsusah, 2020). Using problem-solving skills, students can identify their needs and develop innovative solutions to meet these needs (Kwangmuang et al., 2021; Sumarno, 2019).
One of the approaches to improving students' mathematics problem-solving skills is understanding their learning style (Safira et al., 2024). Each individual has a unique way of learning new things, which also depends on their personality characteristics (Mulyodoro, 2017; Sunarto et al., 2011). While solving mathematics problems, each student may have a different way of thinking based on their personality characteristics (Susanti and Setianingsih, 2014; Sunarto et al., 2017; Griffin and Care, 2015).
Understanding the association between students' learning styles and personality characteristics is crucial for developing unique learning strategies that are tailormade to individuals (Khoirunisa and Hermansyah, 2024). It can also help enhance students' problem-solving skills from an early age, particularly students obtaining basic education in Indonesia who are struggling to develop these skills (Mursalin et al., 2017; Setyawati et al., 2024; Adami et al., 2017). Furthermore, understanding the association between students' learning styles and personality characteristics is crucial not only for their academic and cognitive skills but also for increasing self-confidence and learning motivation (Supriadi et al., 2024; Argaw et al., 2017; Shimizu, 2022).
2 Literature review
2.1 Problem-solving skills
The term “problem-solving skills” refers to the ability to deal with various complicated and unusual situations in flexible ways (Muhali, 2019; Adeoye and Jimoh, 2023; Lutfauziah et al., 2023), and they are complex cognitive skills (Kraft, 2019). They involve thinking about finding solutions to problems based on valid data and information and drawing appropriate conclusions (Iñiguez-Berrozpe and Boeren, 2019; Bariyyah, 2021).
Problem-solving plays a crucial role in mathematical teaching and learning (Liljedahl et al., 2016), which has been introduced to elementary school students (Suseelan et al., 2022; Riyadi et al., 2021) in Indonesia to strengthen their understanding of mathematics (Lithner, 2008). In this approach, students learn to transform problem situations into mathematical sentences and rationalize the use of mathematical concepts in various real-world problem scenarios (Verschaffel et al., 2020, 2010).
Problem-solving skills are included in the content and competency standards in the 2013 curriculum for the mathematics subject in elementary and junior high schools in Indonesia (Riyadi et al., 2021). This can help students improve and develop critical thinking, creativity, social and teamwork skills, mathematical and scientific skills, understanding of material concepts, analysis and synthesis skills, language, and logic intelligence (O'Reilly et al., 2022; Vincent-Lancrin et al., 2019).
Different studies have proposed various stages involved in problem-solving, which are as follows: (1) understanding problems, generating ideas, developing solutions, planning and taking action, and evaluating results (Martínez-Bravo et al., 2022; Mee et al., 2020); (2) identifying problems, searching for various solutions and selecting appropriate ones, and making decisions (Araiza-Alba et al., 2021; Graesser et al., 2018; Pinter and Cisar, 2018); (3) solving problems and making difficult decisions (Özreçberoglu and Çaganaga, 2018); (4) defining and determining causes and priorities of problems, and selecting and implementing solutions (Dörner and Funke, 2017); (5) identifying problems, determining and planning solutions, implementing solutions, analyzing data, making conclusions, and evaluating results (Lutfauziah et al., 2023).
In the present study, “problem-solving skills” refers to students' skills to solve mathematics problems through four stages (Polya's conceptual framework): understanding the problem, planning a solution, solving the problem, and checking and making conclusions.
In Indonesia, students' mathematics problem-solving skills are still low: among 40 students, 35% reported difficulty in reading problems, 37.5% in understanding problems, 20% in transformation, 25% in solving problems, and 67.5% in writing answers (Yuliyani et al., 2023). Of 21 elementary school students, 73% did not understand the problem; 74% did not know how to plan steps involved in problem-solving; 75% did not know how to carry out a problem-solving plan; and 78% did not know how to review problem-solving completion (Cahyadi et al.).
2.2 Learning style and its influence on mathematics problem-solving skills
“Learning style” refers to one's approach to learning and acquiring information and knowledge through various perceptions (Febrina and Hali, 2020; Argarini, 2018; El-Kufi Zair, 2021; Bhat, 2014). Learning style is classified into three types: “visual,” which emphasizes sight sharpness; “auditory,” which focuses on hearing; and “kinesthetics,” which is based on physical touch to provide or obtain certain information (Sari and Pujiastuti, 2020; Daryanto Rachmawati, 2015; Kurniawan and Hartono, 2020).
The different traits of these three learning styles are as follows (DePorter and Hernacki, 2003; Ghufron and Risnawati, 2013; Soebagyo et al., 2022): (1) an individual with the visual trait appears neat and orderly; speaks rather quickly; is not distracted by noise; has problems remembering verbal instructions; remembers what is seen from what is heard; reads quickly and diligently; and prefers music over art; (2) an individual with the auditory trait talks to themselves while working; is distracted by noise; moves lips and pronounces text while reading; enjoys reading; likes to talk, discuss, and explain things at length; is better at spelling out something loud than writing it down; and prefers oral jokes to reading comics; and (3) an individual with the kinesthetics trait speaks slowly; responds to physical attention; touches people to get attention; stands close while talking to others; is always physically oriented and moves a lot; memorizes by walking and looking around; uses many gestures; cannot sit for a long time; wants to do everything; and likes busy games.
The aforementioned characteristics were used as scientific references to develop the learning style instrument available in the application used in this study to differentiate between visual, auditory, and kinesthetics traits.
Learning style has a significant influence on students' mathematics problem-solving skills (El-Kufi Zair, 2021; Bhat, 2014; Albar and Sari, 2021). A person who recognizes his/her learning style and knows how to deal with problems will tend to be more effective in solving problems. For example, if an individual finds it easier to understand a problem through visuals, they can try sketching or diagramming to formulate a solution; similarly, an “auditory” individual can find it easier to understand problems by listening to explanations or discussions, whereas a “kinesthetics” individual is more likely to use experimental or simulation approaches.
Each student has a different learning style depending on how they receive the information, process it, and make conclusions based on the obtained information (Sari et al., 2019). If teachers understand the learning style of individual students, they can help students improve their learning, leading to good results (Febrina and Hali, 2020; Islamiah et al., 2022; Yuliana, 2022; Masamah et al., 2015).
2.3 Personality characteristics and their influence on mathematics problem-solving skills
Personality is a set of stable characteristics and tendencies that determine generality and differences in the psychological behavior of an individual (Alwisol, 2018). Personality characteristics are dynamically organized psychophysical systems within an individual so that they can adapt to the environment (Calvin Lindzey, 2008).
Dominance, influence, steadiness, and compliance (DISC) is a self-reporting test tool developed by William Moulton to understand the personality characteristics of an individual (Brose et al., 2005; Keogh et al., 2019; Bell et al., 2011). Individuals with the dominance personality characteristic like to control their environment and mobilize others in their life scope; those with the influence personality characteristic like to influence others; those with the steadiness personality characteristic remain stable and consistent; and those with the compliance personality characteristics like to get things right and be certain and do not cause problems.
The traits of the four personality characteristics are as follows (Ajmal et al., 2016; Shin, 2013): (1) dominance: these individuals tend to like giving instructions or orders; like getting things done their own way and strive for results; like new things; like to compete and be challenged; are quick; like to make decisions; do not give up easily; like to solve problems; and are result-oriented rather than process-oriented; (2) influence: these individuals are persuasive; dislike being structured; hate details and numbers; easily believe what others say; and are charismatic, optimistic, friendly, caring, overly talkative, emotional, volatile, unpredictable, confident, enthusiastic, and easily distracted; (3) steadiness: these individuals take more time to do something; think a lot before speaking; do not show much expression on the face; and are patient, steadfast, considerate, consistent, thoughtful, reliable, and casual; and (4) compliance: these individuals do right things; are stable in doing procedural things; solve problems thoroughly; focus on work; enjoy numbers and data; and are analytical, systematic, detail-oriented, precise, accurate, and organized.
The aforementioned traits were used as scientific references to develop the personality characteristic instrument available in the application used in this study to differentiate between dominance, influence, steadiness, and compliance.
As reported in previous studies, the DISC tool has shown a significant relationship with mathematics problem-solving skills (Duckworth, 2012; Rahayu, 2022; McMurran et al., 2007; Hosseinkhanzadeh et al., 2011). It has unique characteristics and is quite influential in understanding the cognitive skill processes of students (Herlinda and Aripin, 2020; Rohati, 2014; Syafmen, 2013; Kurniasari, 2012).
2.4 Research questions
RQ1: What are students' mathematics problem-solving skills?
RQ2: Does gender have an influence on students' mathematics problem-solving skills?
RQ3: Does grade level have an influence on students' mathematics problem-solving skills?
RQ4: Does learning style have an influence on students' mathematics problem-solving skills?
RQ5: Do personality characteristics have an influence on students' mathematics problem-solving skills?
RQ6: Is there any interaction between learning style and personality characteristics that has an influence on students' mathematics problem-solving skills?
The research goals are to describe students' mathematics problem-solving skills and to examine the influence of gender, grade level, learning style, personality characteristics, and interaction between learning style and personality characteristics on students' mathematics problem-solving skills.
2.5 Hypothesis
Gender, grade level, learning style, personality characteristics, and interaction between learning style and personality characteristics influence students' mathematics problem-solving skills.
3 Method
3.1 Instruments
First, the math test consisted of three problem-solving questions. These questions are challenging, cannot be easily solved using known procedures, and require correct planning. They were based on the material on fraction in which mathematical story problems were conceptualized. One of the content standards for mathematics in the Indonesian Education Curriculum System is “Numbers: Using Fractions in Problem Solving” for grade V and VI elementary school and grade VII junior high school. This indicates that fractions are always taught at all three grade levels.
Second, the learning style instrument consisted of 30 statements about visual, auditory, and kinesthetics traits, adopted from the online application in the Indonesian version1, whose results are a combination of two learning styles rather than one. We preferred the three-learning-style model over others because of the availability of the online application, so that there was no need to develop a new instrument. There were three answer options (A, B, and C) on each statement, and students responded to the statements based on their current and most appropriate condition.
Third, the personality characteristics instrument consisted of 12 statement items regarding dominance, influence, steadiness, and compliance, adopted from the online application in the Indonesian version2. There were four personality characteristics in each item to describe students' personality characteristics. Students were asked to rank each item from 1 to 4. The higher the rank they give, the less compatible their personality characteristic, and vice versa. Rank “1” indicates that the item is most compatible with their personality characteristics, and “4” indicates that the item is least compatible with their personality characteristics.
Normality, validation, and reliability tests were also carried out with α = 5%, N = 200 (the number of respondents), and n = 3 (the number of mathematics test questions). The chi-square (χ2) method was used for the normality test, Pearson product–moment correlation for the validation test, and Cronbach's alpha for the reliability test. The χ2 values of normality and reliability tests are 153.25 < χ2 table (231.83) and 0.6025 (high category). Data normality was also analyzed based on descriptive statistics, where mean = 72.767, median = 72.588, kurtosis = −1.081, and skewness = 0.388. The mean value was almost the same as the median value, and the values of kurtosis and skewness were between −2 and +2. This indicates that the data are normally distributed. Validation test results for the three mathematics test questions were rQ1 (0.450), rQ2 (0.627), and rQ3 (0.722), all of which had rxy values greater than the r-table (0.138). This indicates that the validation test has a normal distribution and is reliable and acceptable.
3.2 Sample and population
The study population comprised all students in grades V and VI in five state elementary schools, with an age range of 11–13 years, and those in grade VII in five state junior high schools, with an age range of 13–14 years. The schools were located in Meulaboh-Aceh Province and were selected from a randomly selected sample of 93 elementary school students and 107 junior high school students. Overall, 200 students were included in this study, with 90 and 110 female and male students, respectively.
3.3 Data analysis
First, the researchers calculated students' mathematics problem-solving skills scores and then converted them into values. These values were assessed based on four stages: understanding the problem, planning a solution, solving the problem, and checking and making conclusions, with the scores of 3, 3, 3, and 1, respectively. The higher the difficulty level, the higher the score, and vice versa. The total score was divided by 30 and then multiplied by 100. The resulting values were categorized as very low (0–54), low (>54–64), moderate (>64–79), high (>79–89), and very high (>89–100; Sitorus et al., 2019).
Second, the researchers counted students' answer choices in each of the three learning styles for the 30 statements, divided the resulting number by 30, and multiplied it by 100, thus obtaining the percentage of the three learning styles. It is this percentage that determines students' learning style tendencies (the two largest percentages are selected). It is possible that one individual has more than one learning style: in such cases, one learning style may be dominant or all learning styles may be equally strong. For example, a student achieved 37%, 37%, and 26% in visual (V), auditory (A), and kinesthetics (K) learning styles, so this student's learning style is VA, taking into account the two largest percentages. Based on learning style instrument results, there were 93 VA students, 67 VK students, and 40 AK students.
Third, the researchers analyzed four personality characteristics of students which the students ranked from the most to least compatible using numbers 1, 2, 3, or 4 on each item, with “1” being the most appropriate personality characteristic and “4” being the least appropriate one. The more appropriate the student's personality characteristics, the higher the score given, and vice versa. The order of the scores given from the most to the least appropriate personality characteristic was as follows: scores 4, 3, 2, and 1 for numbers “1,” “2,” “3,” and “4,” respectively.
Then, the researchers summed up students' personality characteristics scores, divided them by 48 (the maximum score for 12 items), and multiplied them by 100, thus obtaining the percentage of the four personality characteristics. It is this percentage that determines a student's personality characteristic tendencies (the two largest percentages are considered).
Based on personality characteristics instrument results, there were 45 dominance–compliance (DC) students, 45 influence–compliance (IC) students, 22 influence–steadiness (IS) students, 44 steadiness–compliance (SC) students, and 44 dominance–influence (DI) students.
Fourth, based on learning style and personality characteristics instrument results, there were nine interaction data groups between learning styles and personality characteristics: VA-DI (N (sample size) = 24 students), AK-DI (N = 20), VK-IS (N = 22), VA-SC (N = 22), VK-SC (N = 2), AK-SC (N = 20), VA-DC (N = 21), VK-DC (N = 24), and VK-IC (N = 45).
Fifth, a statistical test was carried out using the t-test to test the influences of gender and grade level on students' mathematics problem-solving skills. In addition, 95% confidence level was used, with a significance level of 5%. If the results of the t-test were higher than those of the t-table, then there was a significant influence between each of the independent and dependent variables. If t-test results were less than t-table results, then there was no influence between each of the independent and dependent variables.
Furthermore, analysis of variance (ANOVA) was conducted to test the influences of learning style, personality characteristics, and interaction between learning style and personality characteristics on students' mathematics problem-solving skills. If the results of the F-test were higher than those of the F-table, then there was a significant influence between each of the independent and dependent variables. If F-test results were less than F-table results, then there was no influence between each of the independent and dependent variables.
The researchers also conducted further tests (post-hoc tests) using t-tests if F-test results were higher than F-table results, to identify which learning style, personality characteristics, and interaction between learning style and personality characteristics have influences on students' mathematics problem-solving skills.
4 Results
4.1 Students' mathematics problem-solving skills
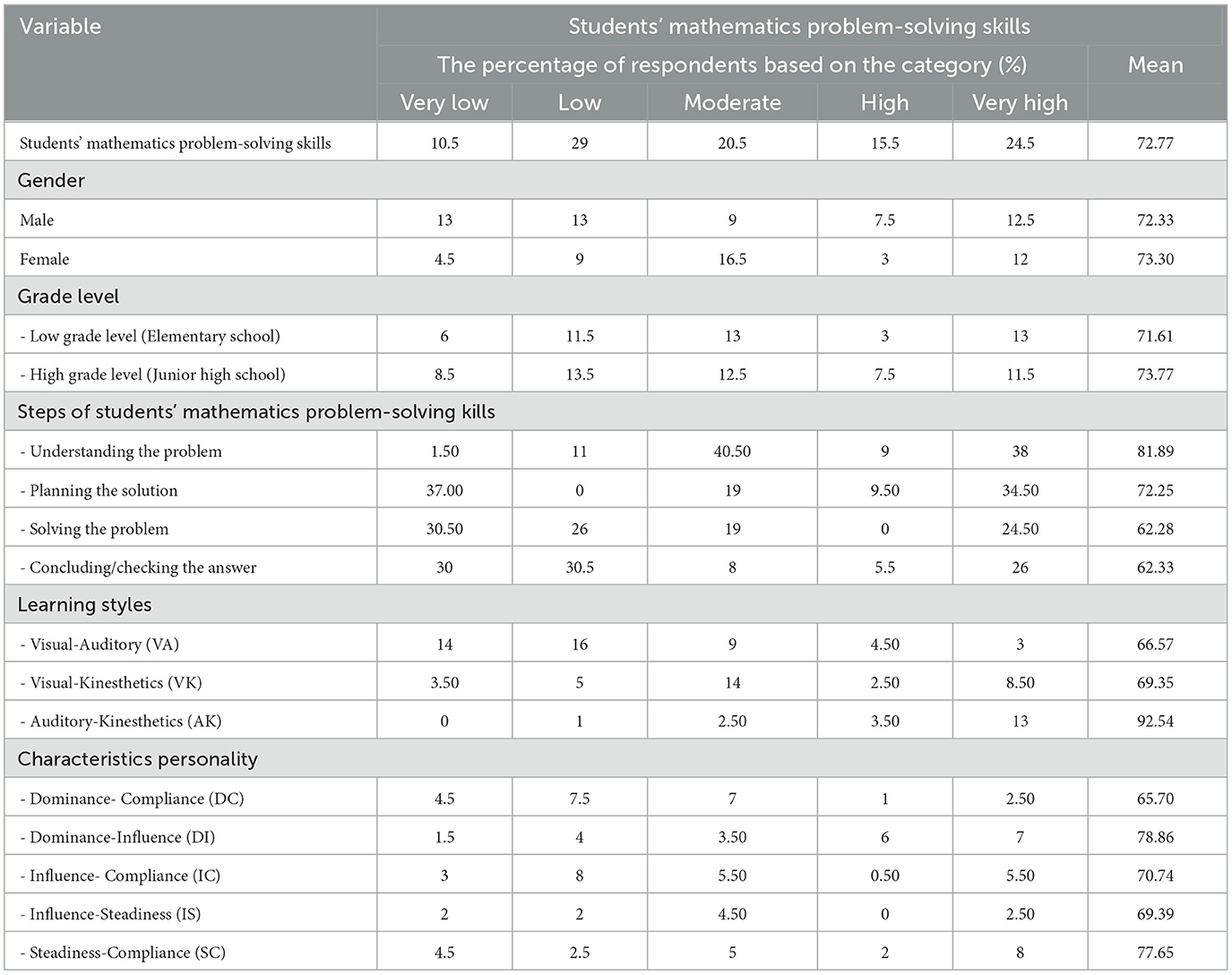
As shown in Table 1, scores < 54 (10.5%) were categorized as “very low;” scores between 54 and 64 (29%) as “low;” score between 65 and 79 (20.5%) as “moderate;” scores between 80 and 89 (15.5%) as “high;” and scores >89 (24.5%) as “very high.” The mean value of students' mathematics problem-solving skills was 72.77, falling under the “moderate” category. In total, 60.50% of students showed “moderate” mathematics problem-solving skills or above. The mean value of female students' mathematics problem-solving skills was higher than that of male students. The percentage of female and male students with “moderate” mathematics problem-solving skills or above was 31.50% and 29%, respectively. In addition, the mean value of junior high school students' mathematics problem-solving skills was higher than that of elementary school students. The percentage of junior high school and elementary school students with “moderate” mathematics problem-solving skills or above was 31.50% and 29%, respectively.
Among different stages in students' mathematics problem-solving skills, the highest mean value (81.89) was observed at the “understanding the problem” stage. The percentage of students (87.50%) with “moderate” mathematics problem-solving skills or above at the “understanding problem” stage was higher than those at the other three problem-solving stages. Furthermore, 1.50% of students had a “very low” problem understanding (score < 54); 11% had “low” problem understanding (score between 54 and 64); 40.50% had “moderate” problem understanding” (score between 65 and 79); 9% had “high” problem understanding (score between 80 and 89); and 38% had “very high” problem understanding (score >89).
Based on students' responses, 81.93% understood what was known in questions; 81.87% understood what was asked in questions; 71.31% understood what mathematical notation was appropriate to use; 70.40% understood the requirements to solve questions; 74% wrote the formula/pattern used to solve the problem; 60.33% matched what was known and what was asked in questions with the formula used; 64.28% used formulas to solve problems by multiplying, dividing, subtracting, and/or adding; and 62.33% rechecked the answers made.
Furthermore, students' mathematics problem-solving skills varied depending on their learning style: AK students belonged to the “very high” category (92.54) and VK and VA to the “moderate” category (69.35 and 66.57, respectively). The percentage of VA, VK, and AK students with “moderate” mathematics problem-solving skills or above in every learning style was 16.50%, 25%, and 19%, respectively, among the 200 respondents.
The personality characteristics of the students also influenced their mathematics problem-solving skills, with DI, SC, IC, IS, and DC students falling under the “moderate” category, with scores of 78.86, 77.65, 70.74, 69.39, and 65.70, respectively. The percentage of DC, DI, IC, IS, and SC students with “moderate” mathematics problem-solving skills or above was 10.50%, 16.50%, 11.50%, 7%, and 15%, respectively.
4.2 Influence of gender and grade level on students' mathematics problem-solving skills
As shown in Table 2, gender and grade level had no significant influence on students' mathematics problem-solving skills, with a two-tailed p-value of 0.702 and 0.390, respectively, which are higher than 0.05.
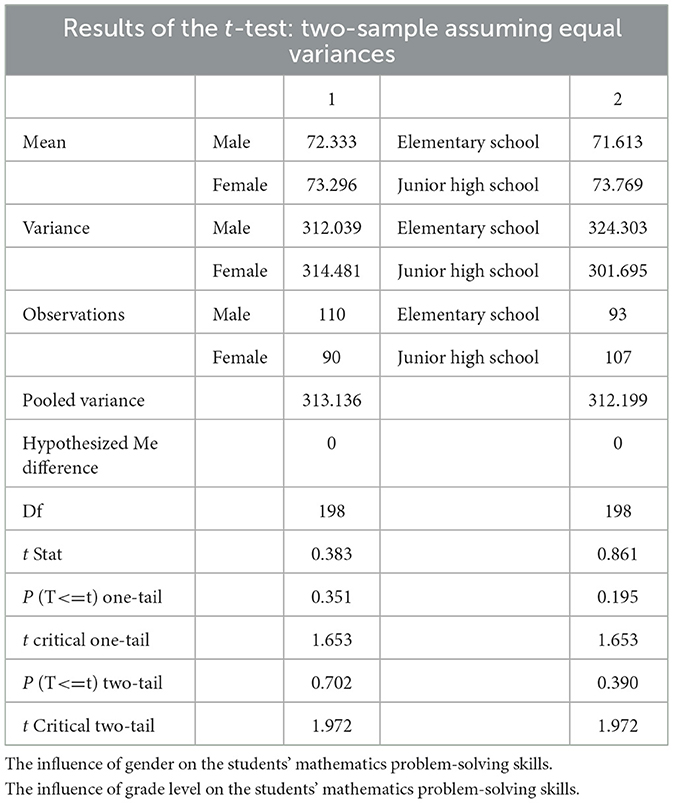
Table 2. The influence of gender and grade level on the students' mathematics problem-solving skills.
4.3 Influence of learning style, personality characteristics, and interaction between learning style and personality characteristics on students' mathematics problem-solving skills
As shown in Table 3, learning style, personality characteristics, and interaction between learning style and personality characteristics had significant influences on students' mathematics problem-solving skills, with a two-tailed p-value of 0.000, 0.001, and 0.000, respectively, which are lower than 0.05.
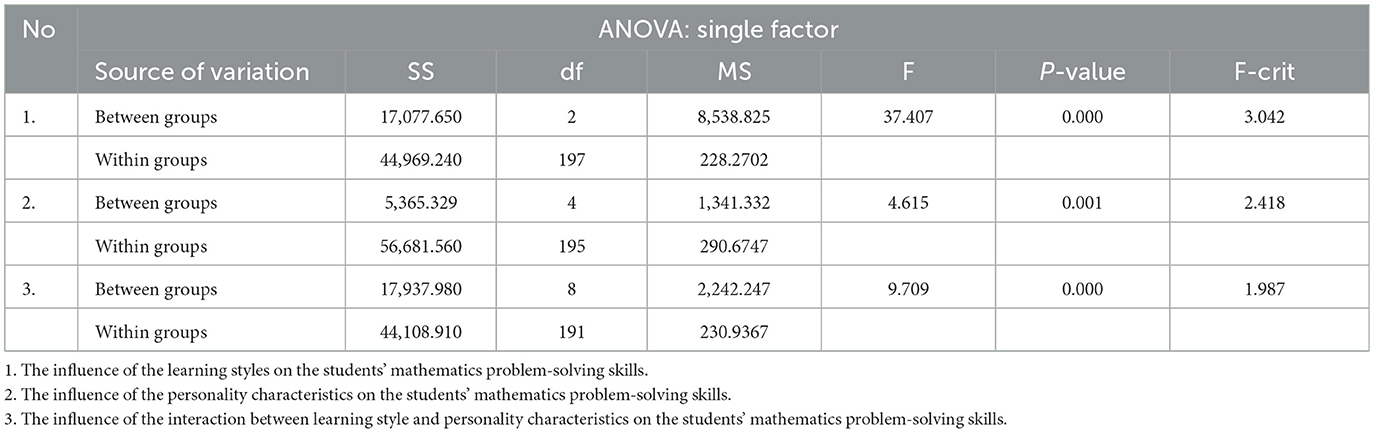
Table 3. The influence of the learning styles, personality characteristics, and the interaction between learning style and personality characteristics on the students' mathematics problem-solving skills.
As shown in Table 4, AK learning style had a significant influence on students' mathematics problem-solving skills compared with the other two learning styles (p-value of < 0.05 for both AK vs. VK and AK vs. VA).
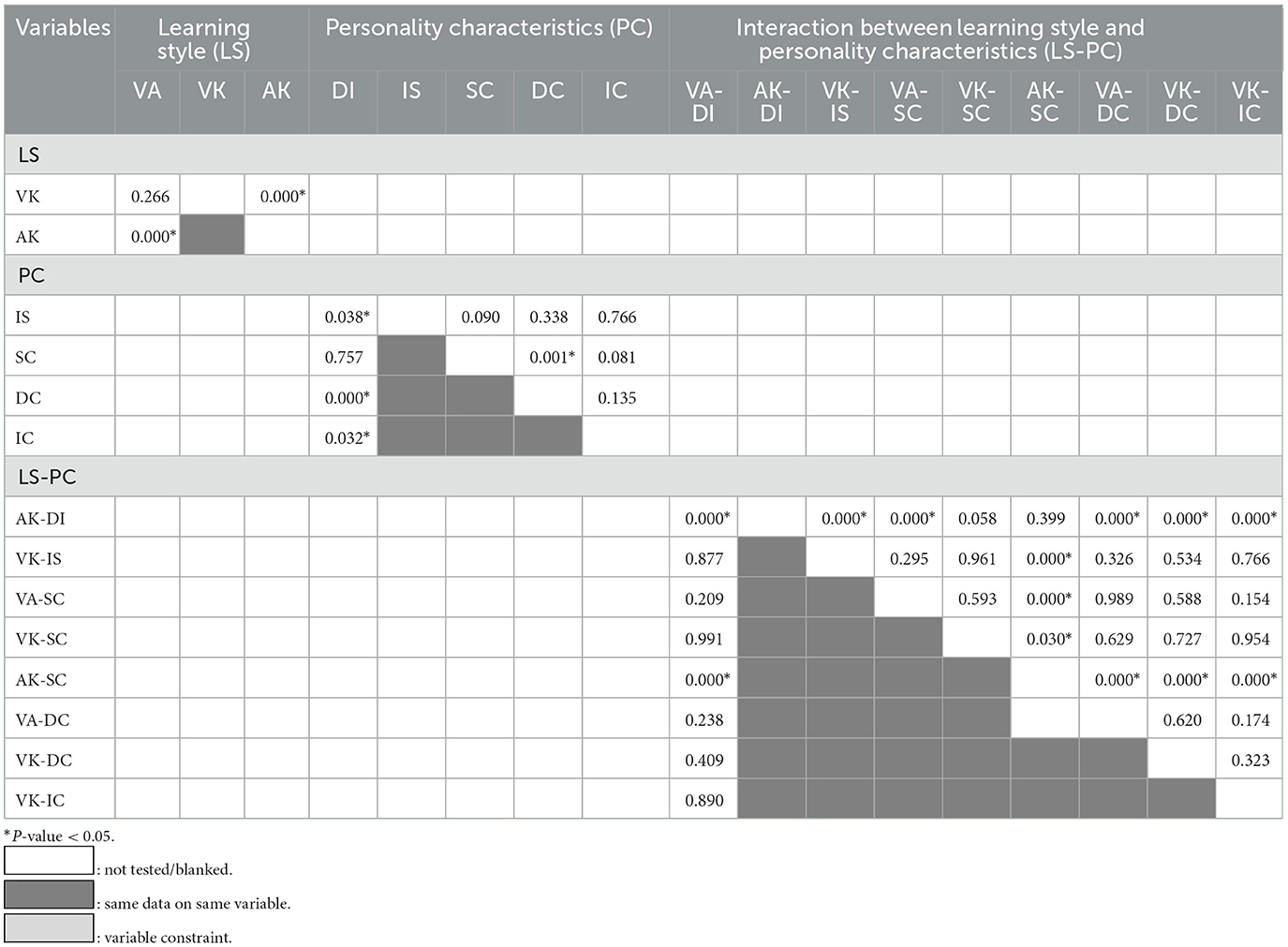
Table 4. P-value of the learning style, the personality characteristics, and the interaction between learning style and personality characteristics.
SC and DI personality characteristics showed significant influences on students' mathematics problem-solving skills with a p-value < 0.05 while comparing DI vs. IS, DI vs. DC, DI vs. IC, and SC vs. DC.
AK-SC and AK-DI interactions showed significant influences on students' mathematics problem-solving skills, with a p-value < 0.05, while comparing AK-SC interaction vs. VK-DC, VK-IC, VK-IS, VK-SC, VA-DC, VA-SC, and VA-DI; and AK-DI interaction vs. VK-DC, VK-IC, VK-IS, VA-DC, VA-SC, and VA-DI.
5 Discussion
The mean value of mathematics problem-solving skills among female students was higher than that of male students. Female students had sufficient conceptual understanding to transform mathematical questions into more operational forms, but struggled to identify appropriate concepts for problem-solving and to integrate these concepts into mathematical calculations. In contrast, male students showed superior abstraction power to solve problems compared with their female counterparts (Azizah et al., 2021). Female students in general paid attention to concrete, practical, emotional, and personal things, whereas male students focused on things that were oriented intellectually, abstractly, and objectively (Kusumawati and Nayazik, 2017).
In addition, the mean value of students' mathematics problem-solving skills was different at every problem-solving stage, with the “understanding the problem” stage showing the highest mean value, indicating that this stage often had a higher success rate than others. Students tended to find it easier to understand problems as this stage is the most basic cognitive, which only requires identifying information and does not require complicated mathematical manipulation (Riyadi et al., 2021). In contrast, the “solving the problem” stage had the lowest mean value, which indicates the challenges faced by students in associating information with mathematical solutions. Understanding a problem is the foundation of successful problem-solving, but it does not always guarantee the appropriate solution (Schoenfeld, 1985).
Besides, gender had no significant influence on students' mathematics problem-solving skills. This observation is in line with the findings of previous studies (Afianty et al., 2018; Amir, 2013; Barkatsas et al., 2019; Hyde et al., 2008). There is no consistent evidence that biological gender differences affect cognitive abilities, including mathematics problem-solving (Zhang et al., 2018). Differences in academic achievement between genders are more often attributable to variations in learning strategies than to differences in cognitive abilities, such as differentiated learning strategies, gender-equitable education, and the REACT (relating, experiencing, applying, collaborating, transferring) strategy (Nugraha et al., 2019). Differentiated learning is a strategy in which the learning needs of each student based on gender, learning styles, and personality characteristics are taken into account, so that they can learn effectively. Higher levels of student education are associated with higher levels of success in solving mathematics problems although the difference is not statistically significant. This finding is in line with Piaget's cognitive development theory (Piaget, 1972), which states that junior high school students generally reach the formal operational stage, so they are better equipped to think abstractly. Students from different education levels have not shown much different learning experiences in terms of developing problem-solving skills (Stigler and Hiebert, 1999).
Furthermore, AK learning style showed a significant influence on students' mathematics problem-solving skills, which was dependent on a combination of hearing and direct experience to understand mathematical concepts and actively build new knowledge through exploration and social discussion (Safira et al., 2024; Sari and Pujiastuti, 2020; Abouzeid et al., 2021; Widodo, 2016). Regarding multisensory learning, AK students simultaneously use different senses, namely hearing and movement, which can improve understanding (Meilina et al., 2023). Thus, AK learning style is effective in improving students' problem-solving skills and allows them to be more flexible in understanding and processing information (Pratikno and Retnowati, 2018; Dryden and Vos, 1999; Fleming and Baume, 2006).
Moreover, SC and DI personality characteristics showed significant influences on students' mathematics problem-solving skills (Rohati, 2014; Syafmen, 2013; Brandt et al., 2020; Lee and Wu, 2022). SC students show a superior, systematic, and thorough approach to solving problems (Kipman et al., 2022), which is very helpful in solving mathematics problems. They use a rule-based and logical approach and are patient in double-checking answers. DI students tend to have creativity and courage in trying different problem-solving strategies (Costa and McCrae, 2008). They have the ability to think non-linearly and innovatively, dare to take risks in exploring alternative methods, have high self-confidence in making decisions, and tend to be more proactive in seeking solutions (Kipman et al., 2022). Those who are open to experience and have a high work focus tend to be more successful in completing complex tasks (Costa and McCrae, 2008).
Finally, AK-SC and AK-DI interactions showed significant influences on students' mathematics problem-solving skills because these students had stable or innovative personalities (Abouzeid et al., 2021; Brandt et al., 2020; Lee and Wu, 2022; Stajkovic et al., 2018; Vedel, 2014; Zhang and Ziegler, 2015). Both AK-SC and AK-DI students like to think about solving problems although AK-DI students think more creatively and like newer things compared with AK-SC students, whose thinking is more procedural and systematic.
Thinking requires memory to access stored information and is a broader cognitive process. Cognitive load can increase the efficiency of information processing when learning style and personality are aligned (Sweller, 1988; Mayer and Moreno, 2003). Working memory is the ability to maintain numbers or formulas in mind while solving problems (Baddeley, 2000). Cognitive flexibility is the ability to change strategies when facing obstacles in problem-solving (Diamond, 2013). Metacognition is the ability to realize mistakes and organize more effective learning strategies (Flavell, 1979).
Cognitive flexibility, working memory, and metacognition are highly likely to be potential mediating factors in enabling children to switch strategies effectively and to be aware of their thinking processes while evaluating problem-solving strategies.
6 Conclusion
In this study, students showed “moderate” mathematics problem-solving skills, with a score of 72.77, with 60.50% of students belonging to the “moderate” category of mathematics problem-solving skills or above.
Gender and grade level had no significant influence on students' mathematics problem-solving skills, whereas learning style, personality characteristics, and interaction between learning style and personality characteristics showed significant influences.
In addition, AK learning style had a significant influence on students' mathematics problem-solving skills. Similarly, SC and DI personality characteristics had a significant influence on students' mathematics problem-solving skills. Furthermore, AK-SC and AK-DI interactions showed significant influences on students' mathematics problem-solving skills.
7 Implications and contributions of this study to the field
The findings of this study provide educators with the knowledge on experiential learning and social interaction approaches (such as discussion, concrete manipulatives, open-ended problem-solving, and direct exploration) to support students with AK and DI personality styles. Students with SC and DI personalities need to be given more complex problem-solving challenges. DC students need to be trained to be more flexible in thinking. Through personalized learning based on their learning styles and personalities, students' effectiveness in mathematics learning as a whole can be improved.
Teachers need to understand and recognize the diverse learning styles and personalities of students so that they can adjust their teaching to match various student needs. Training should be provided to teachers that focuses on helping students who have difficulty in the transition from understanding the problem to solving the problem.
By understanding students' learning styles, teachers can apply appropriate learning strategies. For example, cooperative learning, differentiated learning, and inquiry learning are suitable for students with the kinesthetics learning style, and expository learning for those with visual and auditory styles. Visual learning uses concept maps, diagrams, videos, infographics, and visual presentations, auditory learning uses vocals and music while learning, whereas kinesthetics learning uses laboratory experiments.
Depending on students' personality characteristics, teachers can adapt the following learning strategies: dominance: be more democratic, such as giving students the opportunity to choose tasks; influence: involve creative elements such as stories, games, and art projects; steadiness: design lessons with clear time allocations, structured objectives, detailed activities, and a calm rhythm; and compliance: explain the subject matter in detail and completely, if needed, using data and facts.
This study contributes to the expansion and strengthening of the existing theoretical frameworks for improving the quality and effectiveness of more personalized teaching strategies. Strengthening learning style theories through active experiential learning can improve cognitive skills. Personality plays a crucial role in education, especially in problem-solving. In addition, interaction between cognitive and affective factors helps improve the understanding of effective ways of teaching mathematics.
To understand how research findings can be implemented in the learning process, an overview of the implementation of differentiated learning based on students' learning styles and personality characteristics is presented in Table 5. As shown in the table, may be nine groups of students' learning styles and personality characteristics in one class, as in this study, more than nine groups, or < 9 groups, all of which should be accommodated by the teacher. For simplicity, only two groups (AK-SC and AK-DI) are included in the table. The learning activities are grouped into three activities, namely introduction, core, and closing activities. Differentiated learning focuses on core learning activities, namely content differentiation, process differentiation, and product differentiation, which are designed based on the traits and characteristics of AK-SC and AK-DI students, as explained in the “Literature Review” section.
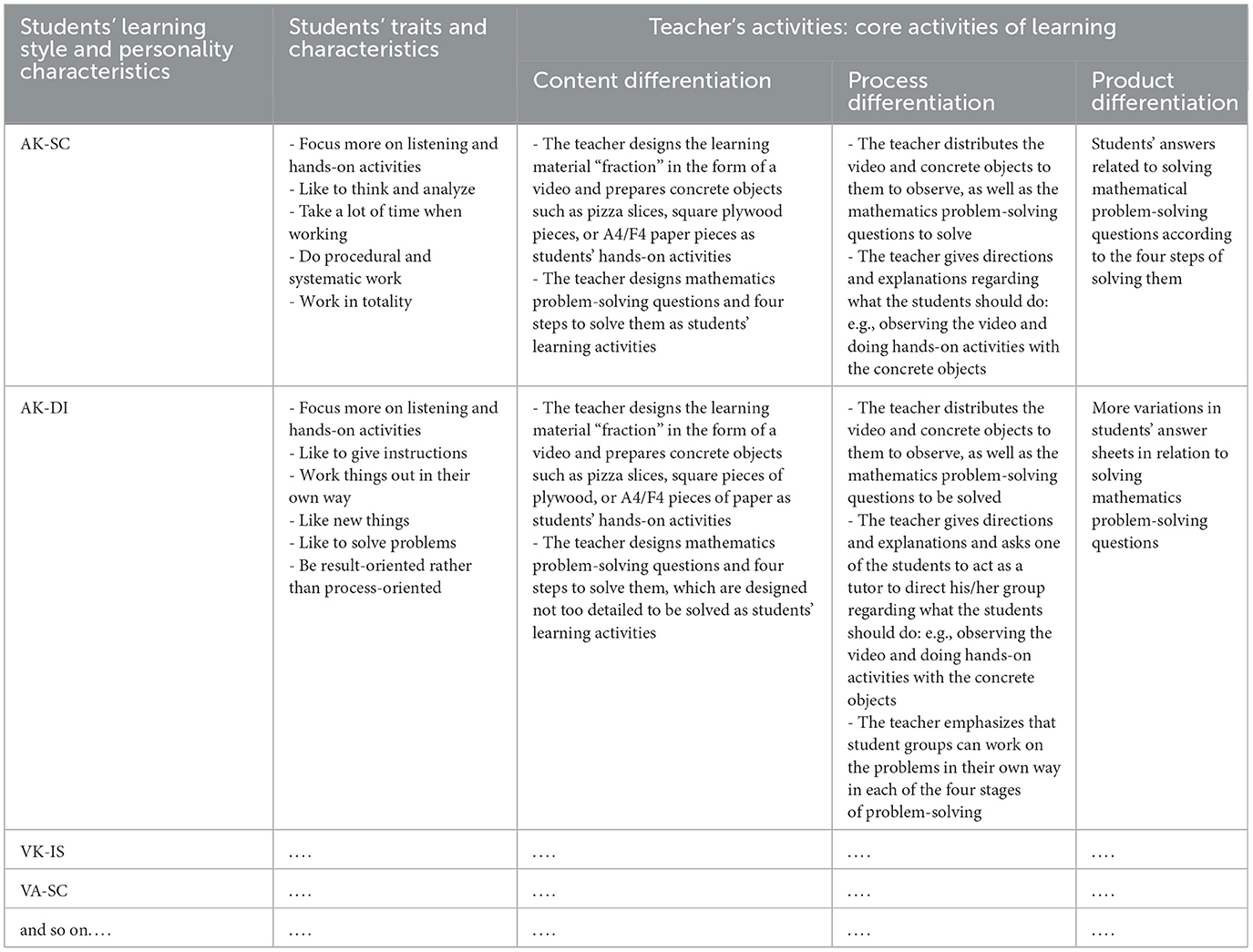
Table 5. An overview of the implementation of a differentiated learning strategy based on students' learning styles and personality characteristics for the material “fraction.”
The most prominent difference between AK-DI and AK-SC students is that the former are more creative in solving mathematics problem-solving questions than the latter, so the process of solving (process differentiation) is more interactive in group discussions among the former. In addition, the answers to the problem-solving questions are more varied among AK-DI students.
8 Limitations
This study investigated the influence of learning style and personality characteristics on problem-solving skills, and the findings may vary if dependent variables such as creativity skills, communication skills, and academic performance are included.
This study only analyzed students' mathematics problem-solving skills based on their learning styles and personality characteristics and did not investigate their mathematics problem-solving skills at each stage for all learning styles and personality characteristics. The sample included only students in primary education, and hence, the findings cannot be generalized to students in high school or university. Future studies need to include different samples such as high school or college students.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Ethics statement
The studies involving humans were approved by the Research Ethics Committee Board of State University of Medan. The team included Bornok Sinaga as the chairman, Deni Setiawan as the secretary, and Edy Surya as member. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants' legal guardians/next of kin.
Author contributions
JS: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Validation, Writing – original draft, Writing – review & editing. BS: Conceptualization, Formal analysis, Writing – original draft, Writing – review & editing. LH: Conceptualization, Investigation, Writing – original draft, Writing – review & editing. DS: Conceptualization, Formal analysis, Funding acquisition, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Gen AI was used in the creation of this manuscript.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2025.1540865/full#supplementary-material
Footnotes
1. ^https://akupintar.id/mp/tes-gaya-belajar/-/vak/instruksi-pengerjaan
2. ^https://akupintar.id/mp/tes-kepribadian/-/disc/pengerjaan-tes/0/0/0/0/0/0
References
Abouzeid, E., Fouad, S., Wasfy, N. F., Alkhadragy, R., Hefny, M., and Kamal, D. (2021). Influence of personality traits and learning styles on undergraduate medical students' academic achievement. Adv. Med. Educ. Pract. 12, 769–777. doi: 10.2147/AMEP.S314644
Adami, Z., Affan, M. H., and Hajidin. (2017). Hubungan antara gaya belajar dengan hasil belajar siswa pada kelas V SD Negeri 29 Banda Aceh. J. Ilm. Pendidik. Guru Sekol. Dasar 2, 135–140.
Adeoye, M. A., and Jimoh, H. A. (2023). Problem-solving skills among 21st-century learners toward creativity and innovation ideas. Think. Skills Creat. J. 6, 52–58. doi: 10.23887/tscj.v6i1.62708
Afianty, O., Manogu, R., and Marthaulina, M. (2018). A comparison of gender differences toward mathematics' cognitive learning outcomes in a middle school. J. Holist. Math. Educ. 1, 60–68. doi: 10.19166/johme.v1i2.804
Ajmal, A., Amin, R., and Bajwa, R. S. (2016). Personality traits as predictors of forgiveness and gratitude. Pak. J. Life Soc. Sci. 14, 91–95.
Akben, N. (2020). Effects of the problem-posing approach on students' problem-solving skills and metacognitive awareness in science education. Res. Sci. Educ. 50, 1143–1165. doi: 10.1007/s11165-018-9726-7
Albar, B. B., and Sari, I. M. (2021). “Learning technology development through podcasts for auditory learning styles,” in Proceedings of the 3rd International Conference on Educational Development and Quality Assurance (ICED-QA 2020), Advances in Social Science, Education and Humanities Research (Altantis Press), 170–174. doi: 10.2991/assehr.k.210202.030
Amir, M. Z. Z. (2013). Perspektif gender dalam pembelajaran matematika. Marwah 12, 15–31. doi: 10.24014/marwah.v12i1.511
Araiza-Alba, P., Keane, T., Chen, W. S., and Kaufman, J. (2021). Immersive virtual reality as a tool to learn problem-solving skills. Comp. Educ. 164:104121. doi: 10.1016/j.compedu.2020.104121
Argarini, D. F. (2018). Polya based problem solving analysis on vector multiplication reviewed from learning style. J. Mat. Pembel. 6, 92–99. doi: 10.33477/mp.v6i1.448
Argaw, A. S., Haile, B. B., Ayalew, B. T., and Kuma, S. G. (2017). The effect of problem-based learning (PBL) instruction on students' motivation and problem-solving skills of physics. Eurasia J. Math. Sci. Technol. Educ. 13, 857–871. doi: 10.12973/eurasia.2017.00647a
Azizah, N., and Budiyono, Siswanto. (2021). Students' conceptual understanding in terms of gender differences. J. Math. Math. Educ. 11, 41–47. doi: 10.20961/jmme.v11i1.52746
Baddeley, A. D. (2000). The episodic buffer: a new component of working memory? Trends Cogn. Sci. 4, 417–423. doi: 10.1016/S1364-6613(00)01538-2
Bariyyah, K. (2021). Problem solving skills: essential skills challenges for the 21st century graduates. J. EDUCATIO 7, 71–80. doi: 10.29210/120212843
Barkatsas, T., Law, H. Y., Seah, W. T., and Wong, N. Y. (2019). The valuing of mathematics learning in schools: a gendered perspective. Int. J. Emerg. Math. Educ. 3, 41–56. doi: 10.12928/ijeme.v3i1.11648
Bell, R. M., Fann, S. A., Morrison, J. E., and Lisk, J. R. (2011). Determining personal talents and behavioral styles of applicants to surgical training: a new look at an old problem, part I. J. Surg. Educ. 68, 534–541. doi: 10.1016/j.jsurg.2011.05.016
Bhat, M. A. (2014). The effect of learning styles on problem solving ability among high school students. Int. J. Adv. Soc. Sci. Hum. 2, 1–6.
Brandt, N. D, Lechner, C. M., Tetzner, J., and Rammstedt, B. (2020). Personality, cognitive ability, and academic performance: differential associations across school subjects and school tracks. J. Pers. 88, 249–265. doi: 10.1111/jopy.12482
Brose, L. A., Rye, M. S., Lutz-Zois, C., and Ross, S. R. (2005). Forgiveness and personality traits. Pers. Individ. Dif. 39, 35–46. doi: 10.1016/j.paid.2004.11.001
Cahyadi F. Wardana F. M. Y. Chasanah R. F. The influence of problem-solving skills towards learning outcomes in learning mathematic course at five grade of primary school. Available online at: https://callforpapers.uksw.edu/index.php/iceteach/2016/paper/view/76/81 (accessed May 12, 2024).
Calvin and Lindzey G.. (2008). Psikologi Kepribadian 3 Teori-teori Sifat dan Behavioristik. Yogyakarta: Kanisius.
Costa, P. T. Jr., and McCrae, R. R. (2008). “The revised NEO personality inventory (NEO-PI-R),” in The SAGE Handbook of Personality Theory and Assessment. Personality Measurement and Testing, eds. G. J. Boyle, G. Matthews, and D. H. Saklofske (Sage Publications, Inc.), 179–198. doi: 10.4135/9781849200479.n9
Daryanto and Rachmawati T.. (2015). Learning Theory and the Educative Learning Process. Yogyakarta: Gava Media.
Diamond, A. (2013). Executive functions. Annu. Rev. Psychol. 64, 135–168. doi: 10.1146/annurev-psych-113011-143750
Dörner, D., and Funke, J. (2017). Complex problem solving: what it is and what it is not. Front. Psychol. 8:1153. doi: 10.3389/fpsyg.2017.01153
Dryden, D., and Vos, J. (1999). The Learning Revolution: To Change the Way the World Learns. The Learning Web, 514–537.
El-Kufi and Zair M. B.. (2021). Pengaruh gaya belajar terhadap kemampuan pemecahan masalah matematika siswa kelas V Madrasah Ibtidaiyah Raudlatul Falah. Thesis. Program Studi Magister Pendidikan Guru Madrasah Ibtidaiyah, Program Pascasarjana: Universitas Islam Negeri Maulana Malik Ibrahim Malang.
Febrina, H., and Hali, F. (2020). Analysis of mathematical problem-solving ability viewed from student learning style. J. Math. Educ. 5, 70–75. doi: 10.31327/jme.v5i1.1757
Flavell, J. H. (1979). Metacognition and cognitive monitoring: A new area of cognitive-developmental inquiry. Am. Psychol. 34, 906–911. doi: 10.1037//0003-066X.34.10.906
Fleming, N. D., and Baume, D. (2006). Learning styles again: VARKing up the right tree! Educ. Dev. 7, 4–7.
Graesser, A. C., Fiore, S. M., Greiff, S., Andrews-Todd, J., Foltz, P. W., and Hesse, F. W. (2018). Advancing the science of collaborative problem solving. Psychol. Sci. Public Interest 19, 59–92. doi: 10.1177/1529100618808244
Griffin, P., and Care, E. (2015). Assessment and Teaching of 21st Century skills: Methods and Approach. Dordrecht: Springer. doi: 10.1007/978-94-017-9395-7
Herlinda, M., and Aripin, Siregar, N. (2020). Proses berpikir kritis dan kesalahan peserta didik dalam memecahkan masalah matematika ditinjau dari tipe kepribadian dominance-influence. Mathline J. Mat. Pendidik. Mat. 5, 154–171. doi: 10.31943/mathline.v5i2.161
Hosseinkhanzadeh, A. A., Niyazi, E., Mosavi, S. V., and Zahedi, M. (2011). Investigating the relationship between personality traits and problem-solving techniques in female college students with appropriate and inappropriate hijab. Procedia Soc. Behav. Sci. 15, 501–504. doi: 10.1016/j.sbspro.2011.03.130
Hyde, J. S., Lindberg, S. M., Linn, M. C., Ellis, A. B., and Williams, C. C. (2008). Gender similarities characterize math performance. Science 321, 494–495. doi: 10.1126/science.1160364
Ichsan, I. Z., Sigit, D. V., Miarsyah, M., Ali, A., Arif, W. P., and Prayitno, T. A. (2019). HOTS-AEP: higher order thinking skills from elementary to master students in environmental learning. Eur. J. Educ. Res. 8, 935–942. doi: 10.12973/eu-jer.8.4.935
Iñiguez-Berrozpe, T., and Boeren, E. (2019). Twenty-first century skills for all: Adults and problem solving in technology rich environments. Technology, Knowledge and Learning. doi: 10.1007/s10758-019-09403-y
Islamiah, M. A. U., Trapsilasiwi, D., Oktavianingtyas, E., Kurniat, D., and Murtikusuma, R. P. (2022). Analisis pemecahan masalah SPLTV berdasarkan ideal problem solving ditinjau dari gaya belajar Visual-Auditorial-Kinestetik (VAK). J. Math. Educ. Learn. 2:74. doi: 10.19184/jomeal.v2i1.25589
Keogh, T. J., Robinson, J. C., and Parnell, J. M. (2019). Assessing behavioral styles among nurse managers: implications for leading effective teams. Hosp. Top. 97:32. doi: 10.1080/00185868.2018.1563460
Khoirunisa, A., and Hermansyah, Mortini, A. V. (2024). Analysis of the eighth-grade students learning styles and personality types in learning English at State Junior High School Muhammadiyah 3 Triyoso. Esteem J. Engl. Educ. Stud. Prog. 8, 206–211. doi: 10.31851/esteem.v8i1.16060
Kipman, U., Bartholdy, S., Weiss, M., Aichhorn, W., and Schiepek, G. (2022). Personality traits and complex problem solving: personality disorders and their effects on complex problem-solving ability. Front. Psychol. 13:788402. doi: 10.3389/fpsyg.2022.788402
Kraft, M. A. (2019). Teacher effects on complex cognitive skills and social-emotional competencies. J. Hum. Resour. 54, 1–36. doi: 10.3368/jhr.54.1.0916.8265R3
Kurniasari, E. (2012). Pengambilan gaya keputusan ditinjau dari tipe kepribadian. Psikostudia 1, 60–80. doi: 10.30872/psikostudia.v1i1.2176
Kurniawan, A. P., and Hartono, S. (2020). The effect of learning style on academic achievement of prospective teachers in mathematics education. J. Math. Pedagogy 2, 26–31. doi: 10.26740/jomp.v2n1.p26-31
Kusumawati, R., and Nayazik, A. (2017). Kecemasan matematika siswa SMA berdasarkan gender. J. Medives 1, 92–99.
Kwangmuang, P., Jarutkamolpong, S., Sangboonraung, W., and Daungtod, S. (2021). The development of learning innovation to enhance higher order thinking skills for students in Thailand junior high schools. Heliyon 7:e07309. doi: 10.1016/j.heliyon.2021.e07309
Lee, P. J., and Wu, T. Y. (2022). Mining relations between personality traits and learning styles. Inf. Process. Manag. 59. doi: 10.1016/j.ipm.2022.103045
Liljedahl, P., Santos-Trigo, M., Malaspina, U., and Bruder, R. (2016). Problem Solving in Mathematics Education. ICME-13 Topical Surveys. Springer: New York. doi: 10.1007/978-3-319-40730-2_1
Lithner, J. (2008). A research framework for creative and imitative reasoning. Educ. Stud. Math. 67, 255–276. doi: 10.1007/s10649-007-9104-2
Lutfauziah, A., Handriyan, A., and Fitriyah, F. K. (2023). Assessment of problem-solving skills in the topic of environment: its validity and reliability. J. Pena Sains 10, 20–27. doi: 10.21107/jps.v10i1.14142
Martínez-Bravo, M. C., Sádaba Chalezquer, C., and Serrano-Puche, J. (2022). Dimensions of digital literacy in the 21st century competency frameworks. Sustainability 14:1867. doi: 10.3390/su14031867
Masamah, U., Sujadi, I., and Riyadi (2015). Proses berpikir reflektif siswa kelas X MAN Ngawi dalam pemecahan masalah berdasarkan langkah Krulik dan Rudnick ditinjau dari kemampuan awal matematika. J. Math. Math. Educ. 5, 38–50. doi: 10.20961/jmme.v5i1.10008
Mayer, R. E., and Moreno, R. (2003). Nine ways to reduce cognitive load in multimedia learning. Educ. Psychol. 38, 43–52. doi: 10.1207/S15326985EP3801_6
McMurran, M., Duggan, C., Christopher, G., and Huband, N. (2007). The relationships between personality disorders and social problem solving in adults. Pers. Individ. Dif. 42, 145–155. doi: 10.1016/j.paid.2006.07.002
Mee, R. W. M., Shahdan, T. S. T., Ismail, M.d.R., Abd Ghani, K., Pek, L. S., Von, W. Y., et al. (2020). Role of gamification in classroom teaching: pre-service teachers' view. Int. J. Eval. Res. Educ. 9, 684–690. doi: 10.11591/ijere.v9i3.20622
Meilina, N. P. R., Cahaya, I. M. E., and Lestari, P. I. (2023). Model pembelajaran multisensori dalam meningkatkan kemampuan membaca permulaan anak usia 5-6 tahun di TK ABCD School. JAPRA 1, 36–47. doi: 10.15575/japra.v6i1.29126
Muhali (2019). Pembelajaran inovatif abad ke-21. J. Penelit. Pengkaj. Ilmu Pendidik. E-Saintika 3, 25–50. doi: 10.36312/e-saintika.v3i2.126
Mulyodoro (2017). Kemampuan pemecahan masalah matematika siswa SMP kelas VIII berdasarkan tipe kepribadian Keirsey dalam setting PBL. Under Graduates Thesis. Universitas Negeri Semarang, 1–54. Available online at: http://lib.unnes.ac.id/32072/ (accessed May 12, 2024).
Mursalin Fauzi, and Israwati.. (2017). Kemampuan siswa dalam menyelesaikan soal matematika dalam bentuk pemecahan masalah bagi siswa kelas V SD negeri 1 pagar air aceh besar. J. Ilm. Pendidik. Guru Sekol. Dasar 2, 38–44. doi: 10.24815/primary.v2i4.4558
Nugraha, T. H., Nindiasari, H., and Syamsuri. (2019). Pengaruh strategi pembelajaran REACT terhadap kemampuan komunikasi matematis siswa SMP berdasarkan gender. Pasundan J. Res. Math. Learn. Educ. 4, 16–27. doi: 10.23969/symmetry.v4i1.1631
Nur, M., and Kardi, S. (2000). Pengajaran Langsung. Pusdat Sains dan Matematika Sekolah Program Pasca Sarjana. Surabaya: Universitas Negri Surabaya.
O'Reilly, C., Ann Devitt, A., and Hayes, N. (2022). Critical thinking in the preschool classroom - a systematic literature review. Think. Skills Creat. 46, 1–20. doi: 10.1016/j.tsc.2022.101110
Özreçberoglu, N., and Çaganaga, Ç. K. (2018). Making it count: strategies for improving problem-solving skills in mathematics for students and teachers' classroom management. Eurasia J. Math. Sci. Technol. Educ. 14, 1253–1261. doi: 10.29333/ejmste/82536
Pinter, R., and Cisar, S. M. (2018). Measuring team member performance in project-based learning. J. Appl. Technol. Educ. Sci. 8, 22−34. doi: 10.24368/jates.v8i4.56
Pratikno, H., and Retnowati, E. (2018). How Indonesian students use Polya's general problem-solving steps. Southeast Asian Math. Educ. J. 8, 39–48. doi: 10.46517/seamej.v8i1.62
Rahayu, S. (2022). Analisis kemampuan berpikir kreatif matematis siswa berdasarkan tipe kepribadian dominance, influence, steady, compliance (DISC) di kelas VII SMP Swasta Guang Ming Kota Jambi. Bachelor's Thesis. Jambi: Universitas Jambi. Available online at: https://repository.unja.ac.id/id/eprint/33819
Rahman, Md. M. (2019). 21st century skill “problem solving”: defining the concept. Asian J. Interdiscip. Res. 2, 71–81. doi: 10.34256/ajir1917
Riyadi, R., Syarifah, T. J., and Nikmaturrohmah, P. (2021). Profile of students' problem-solving skills viewed from Polya's four-steps approach and elementary school students. Eur. J. Educ. Res. 10, 1625–1638. doi: 10.12973/eu-jer.10.4.1625
Rohati (2014). Proses berpikir kritis siswa SMP tipe influence dalam memecahkan masalah matematika. Edumatica 4, 44–50. doi: 10.22437/edumatica.v4i01.1588
Rosa, A. T. R., and Parsusah, M. B. (2020). Teacher development potential (creativity and innovation) education management in engineering training, coaching and writing works through scientific knowledge intensive knowledge based on web research in the industrial revolution and society. Int. J. High. Educ. 9, 161–168. doi: 10.5430/ijhe.v9n4p161
Safira, A., Choirunnisah, Octavyanti, I. A., Apriliyani, N. D., and Wigati, N. A. (2024). Pengaruh gaya belajar terhadap kemampuan pemecahan masalah matematika siswa. Algoritma: J. Mat. Ilmu Pengetah. Alam Kebum. Angkasa 2, 249–255. doi: 10.62383/algoritma.v2i4.165
Sari, L. N. I., Sibuea, A. M., and Tanjung, S. (2019). The effect of learning models and learning styles on social science learning outcomes of Arrahman Percut students. BirLE-J. 3, 2076–2084. doi: 10.33258/birle.v3i4.1469
Sari, W. I., and Pujiastuti, H. (2020). The influence of students' learning style towards students' mathematics knowledge. Mat. Pembel. 8, 36–46. doi: 10.33477/mp.v8i1.1274
Setyawati, M., Muthi, A., Enkas, M. D., Afifah, H. R., Luklua, A. I., and Normalasari, R. (2024). Analisis kemampuan pemecahan masalah matematika siswa ditinjau dari keaktifan siswa bertanya. J. Ilm. Pendidik. Mat. Equals 7, 16–28. doi: 10.46918/equals.v7i1.2062
Shimizu, Y. (2022). Learning engagement as a moderator between self-efficacy, math anxiety, problem-solving strategy, and vector problem-solving performance. Psych 4, 816–832. doi: 10.3390/psych4040060
Sitorus, J., Anas, N., and Waruhu, E. (2019). Creative thinking ability and cognitive knowledge: Big Five personality. Res. Eval. Educ. 5, 85–94. doi: 10.21831/reid.v5i2.22848
Soebagyo, J., Umam, K., and Istikharoh, Suhendri, H. (2022). An analysis of students' mathematical problem-solving ability at class VII social arithmetic materials based on learning styles. Form. J. Ilm. Pendidik. MIPA 12, 63–74. doi: 10.30998/formatif.v12i1.10099
Stajkovic, A. D., Bandura, A., Locke, E. A., Lee, D., and Sergent, K. (2018). Test of three conceptual models of influence of the big five personality traits and self-efficacy on academic performance: a meta-analytic path-analysis. Pers. Individ. Dif. 120, 238–245. doi: 10.1016/j.paid.2017.08.014
Stigler, J. W., and Hiebert, J. (1999). The Teaching Gap: Best Ideas from the World's Teachers for Improving Education in the Classroom. New York, NY: Free Press.
Sumarno (2019). Pembelajaran kompetensi abad 21 menghadapi era society 5.0. Prosiding SEMDIKJAR. 3, 272–287.
Sunarto, M. J. D., Budayasa, I. K., and Juniati, D. (2011). ‘The thinking process profile the students of informatics system departement in solving the mathematics problem based on the personality type and gender,” in The 5th International Conference on Research and Education in Mathematics (Bandung: Respository Universitas Dinamika), 1–10.
Sunarto, M. J. D., Budayasa, I. K., and Juniati, D. (2017). Profile proses berpikir mahasiswa tipe kepribadian sensing dalam memecahkan masalah logika matematika. Cakrawala Pendidik. J. Ilm. Pendidik. 36, 299–308. doi: 10.21831/cp.v36i2.13119
Supriadi, N., Jamaluddin, Z. W., and Suherman. (2024). The role of learning anxiety and mathematical reasoning as predictor of promoting learning motivation: the mediating role of mathematical problem solving. Think. Skills Creat. 5:101497. doi: 10.1016/j.tsc.2024.101497
Susanti, R., and Setianingsih, R. (2014). Kemampuan siswa dalam menyelesaikan soal cerita materi sistem persamaan linear dua variabel ditinjau dari tipe kepribadian ekstrover-introver. MATHEdunesa: J. Ilm. Pendidik. Mat. 3, 173–180. doi: 10.26740/mathedunesa.v3n3.p%25p
Suseelan, M., Chew, C. M., and Chin, H. (2022). Research on mathematics problem solving in elementary education conducted from 1969 to 2021: a bibliometric review. Int. J. Educ. Math. Sci. Technol. 10:10031029. doi: 10.46328/ijemst.2198
Sweller, J. (1988). Cognitive load during problem solving: effects on learning. Cogn. Sci. 12, 257–285. doi: 10.1016/0364-0213(88)90023-7
Syafmen, W. (2013). Profil berfikir kritis siswa kepribadian steadiness style dalam memecahkan masalah matematika. Edumatica 3.
Vedel, A. (2014). The big five and tertiary academic performance: a systematic review and meta-analysis. Pers. Individ. Dif. 71, 66–76. doi: 10.1016/j.paid.2014.07.011
Verschaffel, L., Schukajlow, S., Star, J., and Van Dooren, W. (2020). Word problems in mathematics education: a survey. ZDM - Math. Educ. 52, 1–16. doi: 10.1007/s11858-020-01130-4
Verschaffel, L., Van Dooren, W., Greer, B., and Mukhopadhyay, S. (2010). Reconceptualising word problems as exercises in mathematical modelling. J. für Math.-Didakt. 31, 9–29. doi: 10.1007/s13138-010-0007-x
Vincent-Lancrin, S., González-Sancho, C., Bouckaert, M., de Luca, F., Fernández-Barrerra, M., Jacotin, G., et al. (2019). Fostering Students' Creativity and Critical Thinking: What it Means in School. Educational Research and Innovation. Paris: OECD Publishing. doi: 10.1787/62212c37-en
Widodo (2016). Pengembangan pembelajaran permainan adaptif berbasis perkembangan aktual bagi anak berkebutuhan khusus. J. Pendidik. Kebud. 1, 59–79. doi: 10.24832/jpnk.v1i1.227
Yuliana, M. R. (2022). Metakognisi dalam memecahkan masalah penerapan integral pada mata kuliah kalkulus ditinjau dari tipe perilaku DISC. Aksioma 11, 21–39. doi: 10.22487/aksioma.v11i1.1903
Yuliyani, P., Sariningsih, R., and Rohaeti, E. E. (2023). Analisis kesulitan kemampuan pemecahan masalah matematis siswa SMP materi persamaan garis lurus berdasarkan teori Newman. J. Pemb. Mat. Inov. 6, 1661–1670. doi: 10.22460/jpmi.v6i4.18113
Zhang, J., Dong, X., Wang, L., Zhao, L., Weng, Z., Zhang, T., et al. (2018). Gender differences in global functional connectivity during facial emotion processing: a visual MMN study. Front. Behav. Neurosci. 12:220. doi: 10.3389/fnbeh.2018.00220
Keywords: problem-solving skill, learning style, influence, personality characteristics, gender, grade level
Citation: Sitorus J, Sinaga B, Handayani L and Siagian DJM (2025) Influence of students' learning style and personality characteristics on their mathematics problem-solving skills. Front. Educ. 10:1540865. doi: 10.3389/feduc.2025.1540865
Received: 06 December 2024; Accepted: 14 April 2025;
Published: 30 April 2025.
Edited by:
Rahmah Johar, Syiah Kuala University, IndonesiaReviewed by:
Zuzana Haláková, Comenius University, SlovakiaIden Rainal Ihsan, Universitas Samudra, Indonesia
Julia Noviani, IAIN Takengon, Indonesia
Copyright © 2025 Sitorus, Sinaga, Handayani and Siagian. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jonni Sitorus, c2l0b3J1c19qb25uaUB5YWhvby5jby5pZA==
 Jonni Sitorus
Jonni Sitorus Bornok Sinaga3
Bornok Sinaga3