- 1Department of Science Education, Ahmadu Bello University, Zaria, Nigeria
- 2Department of Mathematical Sciences, University of Agder, Kristiansand, Norway
- 3Tangen Videregående Skole, Agder fylkeskommune, Norway
- 4Department of Engineering Science, University of Agder, Grimstad, Norway
- 5Department of Science, Technology and Mathematics Education, Osun State University, Osogbo, Nigeria
Background: In response to high failure rates in foundational mathematics courses, the traditional single high-stakes final examination was replaced with four digital tests, with multiple attempts, and a hand-in project.
Objectives: This study evaluates the impact of this reformed assessment strategy on a first-year calculus course for engineering students at a Norwegian university. We explored students' perceptions of the reformed assessment regarding their learning approaches, motivation, and the overall experience.
Methods: We generated the data using semi-structured interviews of purposively selected engineering students and analyzed the data using thematic analysis.
Results: The results showed that the multiple attempts on the examinations promoted consistent studying and reduced test anxiety. Additionally, students reported positive experience with collaborative learning, enhanced by peer learning and diverse perspectives during group work. Although students appreciated the flexibility of digital examinations, they noted limitations in feedback on minor errors.
Conclusion: This research highlights the effectiveness of multiple low-stakes assessments in enhancing a supportive learning environment and suggests that digital tools can improve engagement and understanding in mathematics. The findings have implications for rethinking assessment practices in STEM education and offer insights into how digital assessments can mitigate the challenges students face in foundational courses.
1 Introduction
Undergraduate students following engineering programmes require foundational mathematics courses as core elements in many degree-awarding institutions worldwide. These courses include differential calculus, integral calculus, applications of calculus, algebra and trigonometry, and linear algebra (Wilkins et al., 2021). They are crucial components of the engineering curriculum as they provide rudimentary mathematics content knowledge needed for engineering students to perform successfully in higher courses. Evidence shows that these courses are challenging for students, with negative impacts on students' attitudes toward science, technology, engineering, or mathematics (STEM) programmes (Ellis et al., 2016; Wilkins et al., 2021). In addition, several engineering students either change to non-STEM programmes or leave university education due to poor academic achievement in these courses (Ellis et al., 2016; Smith et al., 2021; Wilkins et al., 2021). The trend has consistently shown a two-digit failure rate in these courses, while Zakariya (2021) reported a 46% failure rate in a first-year calculus among engineering students in a Norwegian university. This high failure rate, among other things, prompted some research aimed at reforming the teaching and learning of these courses for engineering students (Zakariya et al., 2022). Their research focused on evaluating teaching methods, feedback delivery systems, and assessment methods and came up with interesting suggestions for mitigating the problem of poor performance among engineering students (Zakariya et al., 2022).
Zakariya et al. (2022) recommended that students' learning progress be assessed multiple times during the semester using technologies to mitigate their poor performance in the course. The argument was that multiple assessment tasks would expose students' weaknesses early enough during the semester, open opportunities for remediation, and enhance quality feedback delivery. Building on this suggestion, we restructured the assessment task from a single high-stakes final examination in the course to four tests (15% per cent each, with the opportunity to attempt each test multiple times) coupled with a 40% hand-in project submission on authentic problems. The course syllabus was split into four units, followed by an examination at the end of each unit. The end of the unit examinations took place in the system for teaching and assessment using a computer algebra kernel (STACK). STACK is an open-access computer-aided assessment system developed by Sangwin (2013) at the University of Birmingham to automate mathematics assessment and feedback delivery. According to the official website (https://stack-assessment.org/), STACK is widely and actively used for mathematics assessment and feedback delivery in 25 countries in Europe, the United States, Asia, and some parts of Africa. It is available in many European languages, in addition to English, Japanese, and Hebrew. By interacting with STACK, students can solve mathematics problems of different types and get immediate feedback at varying levels of detail. STACK is integrated with Moodle and makes use of the Maxima computer algebra system to evaluate mathematical expressions entered by students. What sets STACK apart from traditional assessment tools is its ability to automatically assess algebraic input, not just in terms of numerical correctness, but also by checking for algebraic equivalence and form. For instance, if a student enters an answer like (x+1)2, STACK can recognize that it is mathematically equivalent to x2+2x+1 or even x(x+2)+1, thanks to the capabilities of Maxima. This allows for great flexibility in accepting various valid forms of an answer that accommodate the diversity in students' problem-solving approaches.
STACK also allows for the creation of randomized questions, enabling students to practice with different versions of the same concept while receiving consistent, automated feedback. Teachers can design questions that support formative and summative assessments, with features such as partial credit, step-by-step feedback, and hints (Sangwin, 2013). This makes STACK not only a tool for testing knowledge but also for enhancing learning through guided practice. STACK has proven effective in enhancing student understanding of mathematics concepts in higher institutions (Sangwin, 2013; Sangwin and Köcher, 2016). Even though the students took the examinations online, they had to show up on campus during dedicated times for the examinations to control cheating. This change in the assessment warrants a disciplined investigation to evaluate its overall effectiveness with a particular reference to students' approaches to learning, motivation, and the affordances and constraints of taking mathematics examinations in STACK.
Thus, the purpose of the present study is twofold. First, it is to investigate the influence of multiple assessment tasks combined with multiple attempts on each test on students' approaches to learning in the course. By approaches to learning, we mean students' adopted processes and strategies used while learning mathematics content (Zakariya and Massimiliano, 2022). Evidence shows that students' approaches to learning can be deep or surface, with the former characterizing learning strategies used by students who study intending to develop a conceptual understanding of learning materials (Biggs et al., 2001; Marton and Säljö, 2005). The latter, on the other hand, characterizes learning strategies used by students who study intending to pass the course with minimal effort (Biggs et al., 2001; Marton and Säljö, 2005). Researchers (e.g., Biggs, 2012; Zakariya, 2021) argued that engineering students are expected to adopt deep approaches to learning while learning mathematics since they are being trained to solve problems that require conceptual understanding. However, previous studies (e.g., Zakariya, 2021; Zakariya et al., 2021) revealed that surface approaches to learning are prevalent among them and negatively affect their performance in first-year mathematics courses. Given the established positive relationship between approaches to learning and assessment in a course (Biggs, 2012; Maciejewski and Merchant, 2016), we focus on the effect of multiple assessment tasks on the constructs with the belief that our change in assessment will influence the adoption of deep approaches to learning mathematics among engineering students.
The second purpose of this study is to investigate students' perceptions of digital multiple assessments in the first-year calculus course. Through these perceptions, we leveraged their experience in the course to examine the influence of digital multiple assessments on their motivation to study, participation in group activities, affordances and constraints of interacting with STACK, and their overall satisfaction with the organization of the course. Further, it would be interesting to examine what emerged (affordances) as a result of students' interaction with STACK while taking multiple examinations. These include students' ability to perceive and actualise these affordances and factors (constraints) that mitigate against the actualization of the affordances. In specific terms, this study aimed to address the following questions:
1. How do digital multiple assessments (combined with multiple attempts on each test) influence engineering students' approaches to learning in a first-year calculus course?
2. What are engineering students' perceptions of digital multiple examinations (combined with multiple attempts on each test) in a first-year calculus course?
We contend that by investigating ways through which digital multiple assessments combined with multiple attempts on each test affect students' approaches to learning, we will be able to examine the effectiveness of the new method of assessment in that regard. This will offer an opportunity to ascertain whether the new method of assessment serves the purpose of influencing the adoption of deep approaches to learning mathematics among our engineering students. This finding will contribute to the international discussion on interventions that foster the adoption of deep approaches to learning. Consequently, this finding will guide university teachers, researchers, and education administrators involved in the teaching and learning of foundational mathematics courses for engineering students. Further, by examining students' perceptions of the newly introduced assessment in the first-year calculus course, we will be able to gather useful feedback toward improving future assessment methods in the course. The findings will not only be indispensable to quality assessment in our university but also reveal insightful recommendations for improving students' learning experience in foundational mathematics courses in the international context.
2 The conceptual framework
2.1 The research context
The purpose of the larger project, of which this study is a part, was to reform a first-year compulsory mathematics course for engineering students (Zakariya et al., 2022). The course is taught every autumn in Norwegian and provides 7.5 credits for students following engineering programmes in construction, computer science, electronics, renewable energy, and mechatronics. The course contents include basic differential and integral calculus, applications of calculus, Taylor polynomials with error terms and Taylor series, and complex numbers. The teaching-learning activities in the course involve lectures (physical and live streaming, twice a week, 1 h and 30 min each, and a break of 15 min) and problem-solving sessions (twice a week, 1 h and 30 min each, and a break of 15 min). The classroom instructions are mostly teacher-led, with few or no clarifying questions from the students. In previous years, the assessment tasks had been a five-hour in-class examination for all the students, regardless of the course of study, at the end of the semester in Norwegian. This single examination formed the basis for students' grades in the course. This single assessment task in the course was changed to multiple assessments in Autumn 2022, following recommendations by Zakariya et al. (2022).
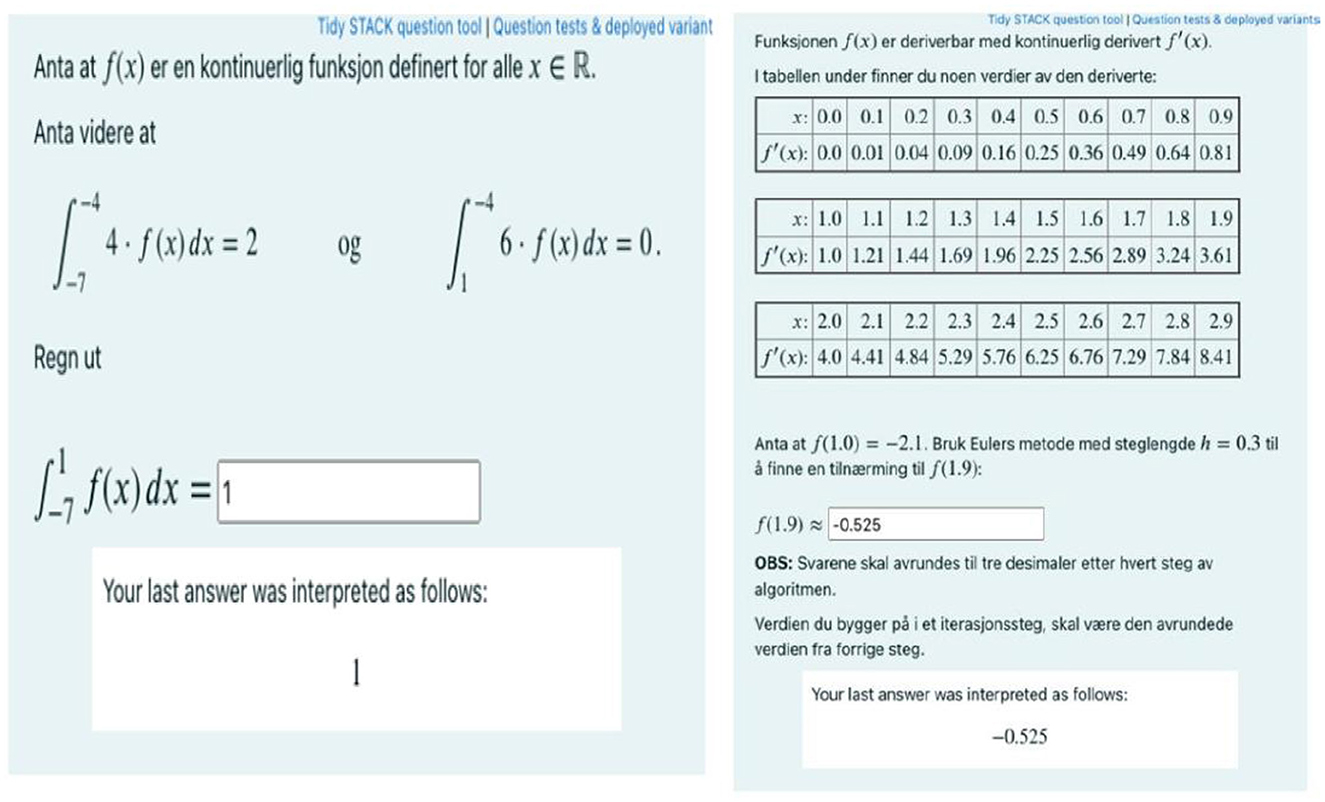
The test environment for the partial digital examinations is STACK. Throughout the semester, we dedicated test periods of two weeks where students can take the examination as many times as they wish during the period. Even though the examinations were online, the students converged in a dedicated room on campus to take the examinations under the supervision of invigilators to avoid cheating. Every mathematics task on each examination attempt is randomized so that the students get varied tasks from the same topic. Upon completion of an examination attempt, students receive immediate feedback on what tasks they have answered correctly and which tasks they have answered incorrectly, as well as feedback on how many points they have earned. If they are not satisfied, they can retake the examination, but they will get a different set of questions on the same topic. If a student retakes the examinations several times, the best test will be scored and recorded for the student for a maximum of 60 points. Figure 1 presents two sample tasks in STACK for illustrative purposes.
In addition to the four digital examinations, each student will submit their project report at the end of the semester. This submission consists of one text document written in LaTeX or another text editor on four self-selected mathematics tasks from a list of tasks provided by the lecturers. The purpose of the submission is to assess students' competence in presenting mathematics correctly according to the guidelines and producing mathematical arguments logically. This change from a single examination to multiple assessments in the course creates a prime opportunity for the present study.
2.2 Social cognitive theory
Social cognitive theory (SCT) provides the rationale, from a theoretical perspective, for investigating the effects of multiple digital assessments on students' approaches to learning and perceptions. Within this theory, an agent is someone who performs an act that is premeditated and intentionally carried out while reflecting on and regulating the execution of the act. According to Bandura (2001), “agency embodies the endowments, belief systems, self-regulatory capabilities and distributed structures and functions through which personal influence exercised, rather than residing as a discrete entity in a particular place” (p. 2). This agency can be directly enacted by an individual (personal agency), through a more able other (proxy agency), and through cultural-historical systems (collective agency) (Bandura, 2001). SCT postulates that agency is the basis of human functioning. Further, human functioning emerges from a dynamic causal relationship between three major determinants: behavioral, environmental, and personal (Bandura, 2001, 2012). Behavioral determinants are observable actions that individuals engage in, the environmental determinants, either imposed or constructed, are forces that impinge on the individual, while personal determinants include intrapersonal factors that interplay with other determinants to produce human functioning (Bandura, 2012).
As it relates to the present study, the behavioral determinants of human functioning are operationalised as students' deep approaches to learning mathematics and surface approaches to learning mathematics. These two approaches reflect observable behavioral patterns that students exhibit in response to academic tasks, aligning closely with Bandura's (2001) notion of behavioral determinants within the triadic reciprocal model of SCT. Further, the environmental determinants, in this research, are operationalised through two distinct but interconnected factors: the digital environment of multiple assessments and peer interpersonal relationships. The digital environment comprises the platforms and tools through which students engage in multiple assessments. It is essential to highlight that, as students have limited agency in choosing the digital tools employed by their institutions, this digital assessment environment can be regarded as externally imposed, an environmental determinant that shapes student behavior without their volitional input (Bandura, 2012). Conversely, students exercise agency in forming peer relationships during collaborative assessments. These interpersonal dynamics are socially constructed and can significantly mediate both motivational and cognitive outcomes, consistent with the view of SCT that environmental factors are not purely external but are also socially mediated (Schunk and DiBenedetto, 2020). The personal determinants in this study are captured by students' perceptions of digital multiple assessments and their motivation. Following Memmert et al. (2023), perception is understood as a “subjective impression of our environment or body shaped by the sensory processing of stimuli by different sensory modalities” (p. 17). This framing suggests that while environmental stimuli (e.g., digital platforms) prompt perception, the interpretation and integration of these stimuli are biologically and cognitively internal processes, thereby justifying perception as a personal determinant. We contend that motivation influences how students approach tasks, persist in the face of challenges, and ultimately perform.
Extensive research has demonstrated the critical role of these variables in mathematics and engineering education. Deep approaches to learning have been consistently linked to better conceptual understanding and long-term retention in mathematics (Cano et al., 2018; Zakariya et al., 2021). Similarly, surface approaches to learning have been associated with poor academic performance and low persistence in STEM fields (Biggs et al., 2022; Valadas et al., 2016). Environmental factors, particularly the design of digital assessment environments, have become increasingly salient. Studies have shown that digital assessments can either enhance or hinder student engagement, depending largely on the interface's usability, feedback quality, and alignment with learning outcomes (Al-Awfi et al., 2024; Zakariya et al., 2024). Personal determinants like perception and motivation also play pivotal roles in this relationship, as documented in the literature. For instance, positive perceptions of digital learning environments have been associated with greater engagement and academic success in mathematics (Al-Abdullatif and Gameil, 2021; Baluyos et al., 2023). Further, motivation significantly predicts persistence and success, especially in challenging coursework and assessment conditions among engineering students (Bayanova et al., 2023; Wang et al., 2024).
Focusing on these determinants is crucial because mathematics and engineering fields are foundational to technological innovation, yet they suffer from high attrition rates (Zakariya, 2021). Understanding how behavioral, environmental, and personal factors interact within digital assessment environments can inform interventions aimed at promoting deeper learning strategies, enhancing motivational profiles, and creating more supportive academic contexts. Given the increasing reliance on digital platforms in education, elucidating the dynamic interplay of these SCT components is not only theoretically meaningful but also practically imperative. By operationalising SCT elements explicitly, as in deep and surface approaches as behavioral determinants, the digital assessment environment and peer relationships as environmental determinants, and perception and motivation as personal determinants, this study contributes a robust framework for understanding student functioning in contemporary mathematics and engineering education. Following the tenets of SCT, it is expected that these determinants will interact dynamically to influence one another. For instance, students' engagement in digital multiple assessments could reinforce either deep or surface approaches to learning, while also shaping their perceptions of the digital environment and influencing their motivational orientation over time. Such interactions are central to understanding the complex, evolving nature of learning in digital educational contexts.
3 Methods
3.1 Design of the study
We adopt a qualitative research methodology (Bryman, 2016) following an overarching philosophy of developmental research (Goodchild, 2008; Gravemeijer, 1994) in which an observed practice is examined, and changes are proposed, implemented, and evaluated to improve the practice. The evaluation of poor performance in the first-year calculus course took place and was reported by Zakariya et al. (2022) with suggested changes in assessment tasks as a proxy to improve students' performance. Following their recommendations, the changes were implemented, and this article, in a developmental research paradigm, reports the students' perceptions of the changes in the assessment tasks as an evaluation of the intervention.
3.2 Participants
We interviewed six engineering students (three men, an average age of 21 years) who volunteered to participate in the research. In line with the recommendation by Braun and Clarke (2013), this sample size is adequate to reach saturation of opinions. These students followed a first-year calculus course, and the interviews took place toward the end of the semester. Instead of the usual single examination at the end of the semester, as in the precalculus course offered by the majority of the students, they had multiple digital tests. The students were interviewed in Norwegian on campus at an agreed time between the interviewer and the interviewees. The interviews lasted for an average of 20 min for each student.
3.3 Interview guide
Following postulations of SCT and insights from the literature, we developed an interview guide suitable for addressing the research questions. The interview guide contains 14 pre-determined questions centered around students' approaches to learning, motivation, competence development, peer-to-peer interaction, affordances and constraints of STACK, and students' overall satisfaction with the changes in assessment tasks. Some sample questions on the interview guide are: Do you think the portfolio assessment (partial tests and a written assignment) affects the way you study for the course? Do you think the portfolio assessment motivates you to study as compared to if there was only one examination in the course at the end of the semester? If yes, how? What do you think are the disadvantages of using STACK? Alternatively, what would you like to improve in using STACK for your partial tests? Being a semi-structured interview for each interviewee, there were some follow-up questions depending on the interviewee's responses to the pre-determined questions (Bryman, 2016).
3.4 Procedure for data collection
The procedure for data generation for this study started with some ethical considerations that are in line with qualitative research methodology, coupled with the Norwegian regulations on data privacy protection (Bryman, 2016). We sought and got approval for the study from the Norwegian Center for Research Data (NSD). This approval is necessary since the study involved the generation of personal data, such as participants' voices, through recorded interviews. In addition to general information about the research, the NSD required the submission of an information letter (this contains students' roles, expectations, and consent form for the research) as well as the interview guide. At the point of recruiting the participants for the study, the researchers described the purpose of the study, students' roles, expectations, and what would happen to the data generated when the study was over. We made it clear to the students that participation in the study was voluntary and that they could withhold their participation without any consequence for them. This was done orally at first, and then the NSD-approved information letters containing this same information were distributed to students for documentation. Each student was interviewed individually. During the interviews, we made six audio recordings of participants' responses to questions (one file per student) and transcribed the audio files afterwards. We clarified to the students that the recordings will be stored anonymously in a safe flash drive and used only for the research. To ensure the privacy protection of the participants, we chose to anonymize the participants' data and gave them dummy names: Jens, Adam, Lisa, Per, Oda, and Kari. We refer to these dummy names throughout the presentation of results. The research was conducted under relevant guidelines and regulations applicable to studies involving human participants (Declaration of Helsinki).
3.5 Procedure for data analysis
We critically examine and analyze the data generated from transcribed interviewees' responses using thematic analysis as propagated by Braun et al. (2019). This thematic analysis is necessary as we strive to compare interviewees' responses to our open questions and argue for cross-cutting meanings (themes) across the responses that capture perceptions of digital multiple assessments in the course. We acknowledge that there are several ways to carry out thematic analysis, even if the term is often misused and mis-conceptualized as a single qualitative analytical approach (Braun et al., 2019). We contend that themes are “a pattern of shared meaning, organized around a core concept or idea, a central organizing concept” (Braun et al., 2019, p. 845). This definition contrasts with other schools of thought (e.g., Guest et al., 2012) that conceptualize themes as a domain summary since it necessitates extracting underlying meanings in participants' responses to make a coherent argument for the situation. We adopt a reflexive approach to the analysis as we focus on contextual meanings and use our subjectivity to integrate and extract shared meanings during the coding process. Therefore, our coding process is independent of any pre-determined codebook and follows back-and-forth processes of coding, reflecting, and recoding until we obtain coherent shared meanings across the interviewee's responses (themes). To ensure the validity and reliability of our findings, we follow a stepwise process while coding the generated data. This process involved interactive coding and re-coding between the first three authors to a level of 90% agreement, and then we conducted independent coding to the end of the interview data. Finally, we arrived at four major themes that exposed underlying students' perceptions of the influence of digital multiple assessments on their approaches to learning, as well as their overall opinions on the assessment method in the calculus course. It is important to mention that the research was conducted in Norwegian, including the analysis and report and the manuscript was written in English. Thus, only the excerpts of the transcripts included in the manuscript were translated into English. The translation and back translation of the research report were conducted by the authors to ensure original meanings were maintained. The first author is a native English speaker with sufficient proficiency in Norwegian. The second and third authors are Norwegians with an advanced level of English proficiency. The fourth and fifth authors are native English speakers who have no knowledge of Norwegian but proofread the English manuscript.
4 Results
In this section, we present the results according to the emerging themes. The interview excerpts that justify the themes are presented in dialogue form to preserve the natural flow of conversation between the interviewer and the students. In each exchange, the interviewer's statements serve either as prompts for student responses or follow-up clarifications. When the interviewer appears between two student responses, it signals a transitional prompt rather than a direct reply to the preceding student. This structure is intended to reflect the interactive nature of the interviews while maintaining coherence in thematic analysis.
4.1 Theme 1: promotion of consistent studying
The participating engineering students unanimously agreed that the digital multiple assessments prompted them to learn efficiently and consistently throughout the semester. The following conversation ensued when the interviewer asked whether the new assessment methods affected the ways the students studied for the course.
Jens: Ehhhh yes, I think it makes most people work more consistently with the subject.
Interviewer: How does this affect the way you study for the course?
Jens: I usually focus on practicing a lot before each test instead of waiting longer to just, right, before an exam. So, I get to practice at regular intervals and read often.
Adam: A lot, because then I would rather study gradually throughout the year instead of maybe saving everything toward the end. And I go deeper into the subject than I would have done had it been only one examination is given in the course.
Interviewer: Deeper into the topic, what do you mean?
Adam: We kind of have four small tests there, so I am kind of going deeper into the subject there because the questions are more difficult than those who are on the exam from what I have experienced. So at least then also as I see students around studying harder now than we might have done if there is only one examination.
Lisa: I work a little more like that, what can I say, efficiently and a little better over a longer period of time. That, I work more on the topic for that period and then I learn a lot more. Also, I familiarize myself with the topic.
Lisa: Now, I enjoy it because it makes a lot more sense to have a little help in having sub-tests than the whole topics.
Oda: I probably understand the topic better, such as theorems and such. I go into that in depth.
As for motivation for study, the engineering students admitted that the multiple digital assessments motivate them to study, which they would not have done if the evaluation in the course was just once. For instance, we received the following responses to the motivation question during the interview:
Oda: Yes, I think so, as I said, you study a little more often. You study before each exam, but I do not think I am studying anything more, it is getting a little steadier and better planned.
Lisa: Yes, absolutely.
Interviewer: If so, how?
Lisa: It motivates me because it is much easier to focus on what we have in a bit rather than focusing on everything at once in the course. I feel it can be a bit of luck in a way.
Per: Yes, it does, because the focus is directed at the chapter that is for the exam at a time. And then it's much easier to stay focused on it than you have to take over a much larger subject, as in the traditional exam.
These results showed that the digital multiple assessments motivated engineering students to study more consistently and efficiently throughout the semester. Students like Jens and Adam reported that the frequent assessments encouraged regular practice and deeper engagement with the subject, rather than cramming before a final exam. Lisa and Oda mentioned that this method helped them grasp concepts better and focus their efforts over time. The structured, incremental approach fostered a deeper understanding of topics like theorems, and students felt more motivated to study gradually while adopting deep approaches to learning. We argued that students preferred these regular sub-tests, finding them beneficial for deeper learning and a better understanding of the course content. These findings resonate with SCT by illustrating how students' consistent engagement in digital multiple assessments demonstrates personal agency. Their motivation and evolving perceptions reflect the interaction of behavioral (study habits), environmental (digital assessment setup), and personal (motivation and perception) determinants (Bandura, 2012).
4.2 Theme 2: promotion of collaborative learning
All participants in the interviews were active in group work and many of them saw this as a positive thing to learn from each other. They argued that the multiple digital assessments were a driving factor in meeting and discussing exam questions and practicing together. We received some positive responses when the students were asked about the influence of the multiple digital assessments on collaborative skills. For instance, Jens, Adam, Lisa, Per, and Oda:
Jens: We have gathered every now and then and gone through some tasks on a white board that some people thought were difficult. So, we have gone through it to understand it better.
Adam: First of all, if you have come up with a solution, then someone else comes up with another solution, so it is nice to get both perspectives on how they arrive at the same answer. And then share knowledge about how to solve this task.
Lisa: We discussed so much together; we taught each other and then someone understood. So, we asked each other about so many things and if I knew the topic I would teach them then I understood it even better and remembered it much more. Besides, if I went to them and asked for help, they were also very willing to learn and wanted to teach me to understand more. So, we worked a lot in groups.
Per: What I said earlier and then there will be a much greater unity in that group. We have been very careful that we work with the physical group meetings we have had all along. And then it is very beneficial when we have someone who may be a little ahead of someone else, we are all the way to adjust the others.
Oda: Yes, if you mostly sit in a group and do it, practice for the tests and do the latex as it is now. I don't want to be alone, it's hard to be alone.
Interviewer: How does this help you study then?
Oda: It means that you can ask people who are good at something that you simply don't understand. And again, you can teach what you understand to others, which is good.
Oda shared the opinions of Per and Lisa, who argued it is good to learn from each other. She also says that it is directly related to the form of the exam, as the group gathers around more often before the examination. When asked when and why the group gathered, she answered:
Oda: Yes, we share, for instance, if someone has not received a full score, I can sit back and explain how I did it and vice versa on the first test. Then, if it was a task I didn't understand so I had to go and ask someone who had a good grasp over it. Then we discuss them.
Interviewer: Is this mostly after the exam? Have you often discussed before?
Oda: Yes, we sit before and discuss, and we always have such a test first on Monday. So then from Wednesday onwards, we dedicated ourselves to just working on the exam papers.
Interviewer: Is it more often before the exam?
Oda: It is more often before the exam, yes, it is.
Interviewer: Afterwards, then?
Oda: Afterwards, ehhh it has been a lot of math lately. But there is not very much afterwards if it has gone smoothly with everyone. But if there's someone who hasn't managed it well, and they sit next to us and work on math, then we help them.
The results showed that engineering students found group work beneficial for collaborative learning, with multiple digital assessments enhancing frequent group discussions and problem-solving. They emphasized learning from diverse perspectives, where individuals shared different approaches to the same problem, enhancing mutual understanding. Peer learning, highlighted by Jens, Adam, and Lisa, improved comprehension for both the teacher and the learner. Per and Oda noted that the group environment created a supportive space where students of varying skill levels helped each other, leading to improved academic outcomes. Group work was instrumental before exams, with students gathering to clarify doubts and share strategies, though less frequent afterwards unless challenges persisted.
4.3 Theme 3: reduction of test anxiety
The engineering students agreed that the multiple digital tests in the course helped in lowering their test anxiety. For instance, Adam pointed out when asked about his learning motivation that it was nice to have feedback along the way and that it lowered his test anxiety.
Adam: Yes, and then it's nice to get a little indication throughout the year of how you're doing. It lowered one's anxiety for the examinations. It's much easier with slightly smaller tests than the one examination.
Meanwhile, Adam ascribed the opportunity to take a test multiple times as the main reason for the reduced test anxiety when he said:
Adam: It is nice to know I can go in on the first day and maybe not be in the top shape I want and take it again the next day.
Adam: Other than exam three I took a few more times because when I went in on the first day, I was not in top shape and then there was a security in being able to take it one more time.
Adam: It is simply that if you don't feel so good one day, it doesn't ruin your grade as you know you can do better the next day.
Kari: I think it does [test anxiety], but for regular exams, it is very often that it will be intense practice right before a regular exam, but now it will be a little more distributed so that there is more practice in total. I would say it is not as intense and as stressful.
These results showed that multiple digital assessments helped reduce students' test anxiety by offering frequent feedback, smaller, more manageable tests, and the ability to retake exams. Adam appreciated the flexibility to retry when not performing at his best, which provided security and reduced pressure. Kari added that the distributed nature of digital assessments resulted in more consistent practice, lowering the intensity and stress often associated with traditional, high-stakes exams. Thus, we argue that this approach created a less stressful learning environment for students.
4.4 Theme 4: perception of STACK
The engineering students unanimously acknowledged their positive appraisal of STACK as a tool for digital assessments in mathematics. This appraisal includes a simple graphical user interface and ease of use. Per, Oda and Kari all agreed with this. For instance, when these were asked about the advantages of using STACK in assessing mathematics they replied:
Per: It is very simple in the form of an answer. So, it is very easy to use.
Kari: That program, yes. It is very simple, and it is easy to understand tasks in a way. If you understand the type of tasks, then the texts and the syntax are easy to understand.
Oda: I think it is a good way to assess mathematics knowledge.
Apart from the students' positive perceptions of STACK, they also registered some reservations about the digital tool assessment. For instance, the students mentioned that they do not have the opportunity to get feedback on where they have made mistakes. In addition to this, they also encountered some syntax errors while using STACK. However, they acknowledged these challenges are offset by the fact that they can take the tests several times and the final submission was used. These challenges are evident in the following statements of the students:
Jens: It is that I often make a small sign error in the middle of a calculation and then I get the wrong answer, even though I have done almost everything right, I don't get any points for that task.
Interviewer: Do you know where you have made the mistake?
Jens: I usually know that pretty quickly, once I get feedback, I see it.
Adam: It is a bit that a large part of the mistakes I make on exams come in the form of sign errors and those small annoying mistakes. I have the correct workings, but I have just typed the wrong plus, minus, or things like that.
Interviewer: Alternatively, what would you like to be improved about the stack for your subtests?
Adam: Considering that you can take it up to seven times, I don't think it's something I miss. The miscalculation part is in a way compensated by the fact that you can take it so many times.
These results showed that engineering students found STACK favorable for mathematics assessments. They highlighted its user-friendly interface and ease of use. Per, Oda, and Kari agreed it simplified answering and task comprehension. Despite their positive views, students noted limitations, particularly in feedback and syntax errors. Jens and Adam shared concerns about receiving no feedback on mistakes, especially for minor sign errors that impacted scores, even if most of their work was correct. However, they appreciated the flexibility of STACK. They acknowledged that allowing multiple test attempts compensated for feedback limitations in STACK.
5 Discussion
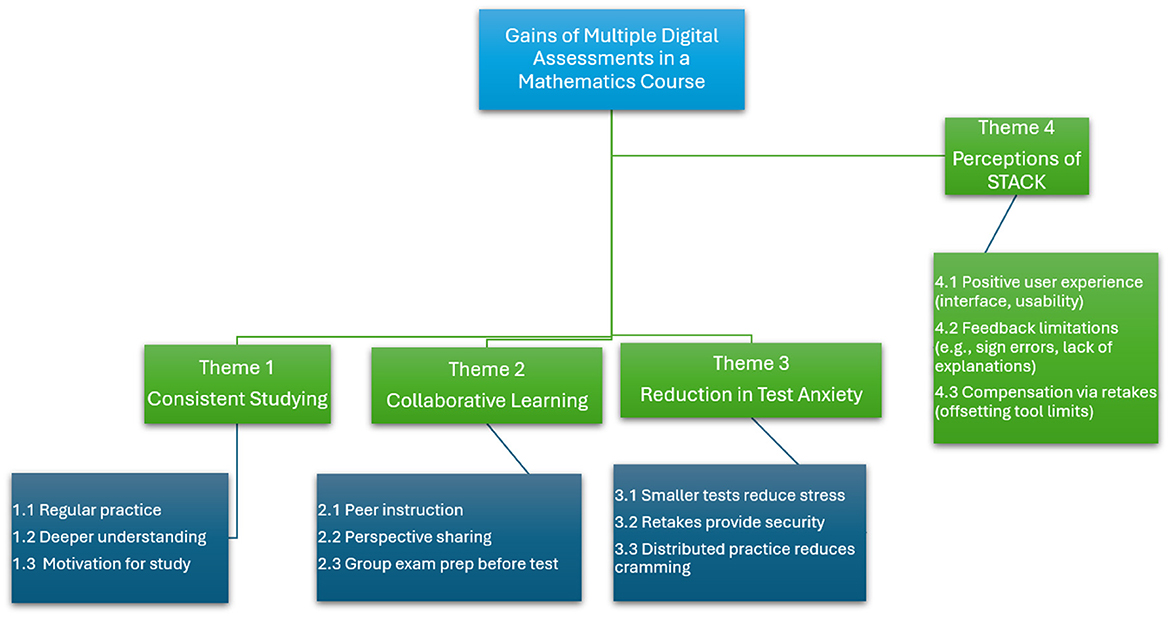
This study aimed to investigate how a shift to multiple digital assessments in a first-year calculus course is related to engineering students' approaches to learning, motivation, collaboration, and perceptions of the digital assessment environment. Drawing on SCT and some insights from the literature (Bandura, 2001, 2012), we provide rational arguments on how these assessments were ascribed to students' study behaviors and overall engagement with mathematics. We generated the research data using semi-structured interviews and analyzed them following an overarching philosophy of qualitative research methodology through thematic analysis (Braun et al., 2019). The results of this analysis revealed some interesting findings. Figure 2 shows the thematic map of these findings.
The results in Figure 2 indicated that the digital multiple examinations helped consistent studying among students, in line with the first research objective. Students emphasized that frequent assessments allowed them to study incrementally, reducing the pressure of last-minute cramming, which enhanced a stronger grasp of complex mathematical concepts. This aligns with Zakariya et al. (2022), who recommended a shift from a single summative examination to multiple assessments to encourage ongoing engagement and improved learning outcomes. This finding matches the concept of personal agency in SCT (Bandura, 2012), which could be interpreted to mean that when students have regular opportunities to engage with material, they are more likely to take ownership of their learning processes. Further, students such as Jens and Adam reported that the new assessment model motivated them to review course material regularly, echoing findings from Freeman et al. (2014), who argued that active and continuous engagement in learning is critical to internalizing complex subjects like calculus.
The results also showed that this assessment method encouraged collaborative learning among students, as they frequently worked together to discuss problems and clarify doubts. This interaction resonates with the environmental and social determinants in SCT, wherein the structured assessment environment encouraged students to build mutually supportive relationships (Bandura, 2012). Jens, Adam, and Lisa noted that peer learning played a key role in their understanding, as discussing different approaches to solving problems deepened their comprehension of the material. Research (e.g., Ginga and Zakariya, 2020; Zakariya et al., 2016) suggests that collaborative learning enhances students' problem-solving skills, as peer discussions expose students to multiple perspectives and improve their ability to articulate their understanding. Further, the digital assessment model acted as an impetus for this collaborative engagement, with students forming study groups to support each other's learning. This outcome reinforces the work by Ginga and Zakariya (2020), who identified group work as an effective pedagogical strategy, particularly in STEM education, where challenging coursework often benefits from collaborative problem-solving. By framing digital assessments as an opportunity for social learning, students exercised their agency collectively, interacting within a supportive environment that facilitated both personal and academic growth.
Another notable outcome of this study is the reduction of test anxiety among students, which aligns with the second research objective of exploring the emotional effects of digital assessments. By spreading assessments throughout the semester, students experienced less pressure associated with high-stakes, end-of-semester exams. Kari's reflection on the consistent practice afforded by multiple assessments highlights how incremental learning reduces anxiety, a finding supported by previous studies (Sotola and Crede, 2021; Trotter, 2006). The flexibility to retake the assessments further contributed to the alleviation of test anxiety, as students knew that a single poor performance would not irreparably affect their grades. Adam's appreciation of this retake option echoes findings from Roediger and Butler (2011), who noted that repeated testing opportunities can improve both learning and emotional well-being. Thus, the students enjoyed a supportive environment conducive to learning and reducing the performance pressures typically associated with summative assessments.
The results of this study showed positive students' views of the STACK assessment platform despite some concerns about its feedback limitations. The students found STACK user-friendly and appreciated its structured, accessible format, which supports previous findings on the benefits of digital platforms for learning (Zakariya et al., 2022). However, the students expressed a desire for more detailed feedback, particularly in cases where minor errors impacted scores significantly. This feedback gap aligns with (Memmert et al., 2023), who observed that timely, specific feedback is essential for student engagement, especially in a mathematics context where precision is crucial. Meanwhile, the ability to retake assessments partially compensated for the limited feedback in STACK. By allowing students to attempt different versions of tasks, STACK encouraged students to engage in self-reflective practices and refine their approaches to solving problems. The findings of this study suggest that transitioning to multiple digital assessments may be a valuable strategy for enhancing learning outcomes in mathematics and engineering courses. Educational institutions may consider adopting similar models, especially in disciplines where frequent practice is essential to mastery. However, to maximize the benefits of digital assessments, platforms like STACK should incorporate more detailed feedback mechanisms to address students' need for constructive guidance on specific errors. The emphasis on collaborative learning and the reduction of test anxiety further suggests that multiple assessments could be beneficial beyond mathematics. By structuring assessments to encourage incremental learning and peer support, educators can nurture environments where students achieve higher grades and develop critical skills in self-regulation and collaboration. Future research could explore the long-term effects of such assessment models on students' academic and professional success, potentially extending the findings of this study into broader educational contexts.
6 Conclusion
This study explores the impact of implementing a reformed assessment model in a first-year calculus course for engineering students at a Norwegian university. The shift from a single high-stakes exam to multiple digital assessments and a project submission aimed to enhance students' learning approaches, motivation, and engagement. Grounded in SCT and literature on motivation and assessment practices, the findings suggest that this approach promotes continuous engagement with the learning content and self-reflection while using surface approaches to learning. The frequent assessments allowed students to steadily engage with course material, moving away from cramming for a final examination. Moreover, the structure of smaller, incremental assessments facilitated multiple attempts and provided continuous feedback, enabling students to identify and address weaknesses early. This aligns with existing research emphasizing the benefits of formative assessment in enhancing comprehension and problem-solving skills in mathematics. A key theme in the results is the promotion of collaborative learning, as students frequently engaged in group work, which they found valuable for understanding complex topics. We contend that this collaborative learning cannot be disjointed from the introduction of hand-in projects in the course. This peer collaboration reflects the social learning aspect of SCT and contributes to a supportive environment that reduces test anxiety. By allowing retakes and immediate feedback, digital assessments reduced the pressure associated with high-stakes exams, supporting confidence-building. The positive response to STACK, the digital assessment tool, further highlights its role in improving student engagement, though students noted some issues with syntax feedback.
Despite the valuable findings of this study, several limitations should be acknowledged, which also open avenues for future research. First, the study involved a relatively small sample size, limiting the generalisability of the findings to broader populations or different educational contexts. The sample was also drawn from a single institution, potentially introducing institutional bias and limiting the transferability of insights. Additionally, the study focused exclusively on student perceptions, without triangulating these views with objective performance data or instructors' perspectives. This singular focus limits the depth of understanding regarding the pedagogical and cognitive effectiveness of STACK as an assessment tool. Moreover, while STACK is a robust platform for assessing symbolic mathematics, it presents several usability challenges. It requires substantial setup time and technical expertise, particularly in Maxima, which can be a barrier for educators without a background in computer algebra systems. Compared to more visually intuitive tools like GeoGebra or Desmos, STACK lacks dynamic graphical capabilities, which may hinder engagement, especially among students who benefit from visual learning. Its interface is less user-friendly, particularly for students unfamiliar with formal mathematical syntax or programming environments. Additionally, STACK is optimally designed for topics in algebra and calculus. It may not effectively assess broader conceptual understanding or higher-order problem-solving skills better captured through open-ended or real-world contextualized tasks. Since STACK is not as interactive as game-based tools like Kahoot or Google Forms its acceptance could be limited among the large populace of digitally savvy students in higher institution presently. Future research should consider integrating quantitative performance metrics, exploring long-term learning outcomes, and incorporating teacher experiences regarding implementation workload and feedback utility. Including complementary assessment tools could also enrich student learning by providing more holistic and formative feedback mechanisms.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving humans were approved by Norwegian Centre for Research Data (NSD). The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.
Author contributions
YZ: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Resources, Supervision, Writing – original draft, Writing – review & editing. MB: Investigation, Methodology, Writing – original draft, Writing – review & editing. TG: Formal analysis, Supervision, Writing – original draft, Writing – review & editing. RU: Methodology, Writing – original draft, Writing – review & editing. MA: Data curation, Formal analysis, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. The authors appreciate the University of Agder for paying the article processing charge of this manuscript.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Gen AI was used in the creation of this manuscript.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Al-Abdullatif, A. M., and Gameil, A. A. (2021). The effect of digital technology integration on students' academic performance through project-based learning in an e-learning environment. Int. J. Emerg. Technol. Learn.16:19421. doi: 10.3991/ijet.v16i11.19421
Al-Awfi, F., Hock, O. Y., and Seenivasagam, V. (2024). The effect of technology on student's motivation and knowledge retention: Oman's perspective. Int. J. Acad. Res. Busin. Soc. Sci. 14, 545–557. doi: 10.6007/IJARBSS/v14-i11/23528
Baluyos, G., Cabaluna, P., and Paragat, J. (2023). Students' preference in online learning environment and academic resilience in relation to their academic performance in mathematics. EduLine: J. Educ. Learn. Innovat. 3, 460–470. doi: 10.35877/454RI.eduline2038
Bandura, A. (2001). Social cognitive theory: an agentic perspective. Annu. Rev. Psychol. 52, 1–26. doi: 10.1146/annurev.psych.52.1.1
Bandura, A. (2012). On the functional properties of perceived self-efficacy revisited. J. Manage. 38, 9–44. doi: 10.1177/0149206311410606
Bayanova, A. R., Orekhovskaya, N. A., Sokolova, N. L., Shaleeva, E. F., Knyazeva, S. A., and Budkevich, R. L. (2023). Exploring the role of motivation in STEM education: a systematic review. Eurasia J. Mathem. 19:13086. doi: 10.29333/ejmste/13086
Biggs, J. B. (2012). What the student does: teaching for enhanced learning. Higher Educ. Res. Dev. 31, 39–55. doi: 10.1080/07294360.2012.642839
Biggs, J. B., Kember, D., and Leung, D. Y. P. (2001). The revised two factor study process questionnaire: R-SPQ-2F. Br. J. Educ. Psychol. 71, 133–149. doi: 10.1348/000709901158433
Biggs, J. B., Tang, C., and Kennedy, G. (2022). Teaching for Quality Learning at University (3 ed.). London: Open University Press.
Braun, V., and Clarke, V. (2013). Successful Qualitative Research a Practical Guide for Beginners. Melbourne: AGE Publication.
Braun, V., Clarke, V., Hayfield, N., and Terry, G. (2019). “Thematic analysis,” in Handbook of Research Methods in Health Social Sciences (Singapore: Springer), 843–860.
Cano, F., Martin, A. J., Ginns, P., and Berbén, A. B. G. (2018). Students' self-worth protection and approaches to learning in higher education: Predictors and consequences. Higher Educ. 76, 163–181. doi: 10.1007/s10734-017-0215-0
Ellis, J., Fosdick, B. K., and Rasmussen, C. (2016). Women 1.5 times more likely to leave STEM pipeline after calculus compared to men: Lack of mathematical confidence a potential culprit. PLoS ONE 11:e0157447. doi: 10.1371/journal.pone.0157447
Freeman, S., Eddy, S. L., McDonough, M., Smith, M. K., Okoroafor, N., Jordt, H., et al. (2014). Active learning increases student performance in science, engineering, and mathematics. Proc. Natl. Acad. Sci. USA. 111, 8410–8415. doi: 10.1073/pnas.1319030111
Ginga, U. A., and Zakariya, Y. F. (2020). Impact of a social constructivist instructional strategy on performance in algebra with a focus on secondary school students. Educ. Res. Int. 2020, 1–8. doi: 10.1155/2020/3606490
Goodchild, S. (2008). “A quest for ‘good' research: the mathematics teacher educator as practitioner researcher in a community of inquiry,” in International Handbook of Mathematics Teacher Education, eds. K. Beswick & O. Chapman (Rotterdam: Brill | Sense), 201–220.
Gravemeijer, K. (1994). Educational development and developmental research in mathematics education. J. Res. Mathem. Educ. 25, 443–471. doi: 10.2307/749485
Guest, G., MacQueen, K. M., and Namey, E. E. (2012). Applied Thematic Analysis. Thousand Oaks: Sage. doi: 10.4135/9781483384436
Maciejewski, W., and Merchant, S. (2016). Mathematical tasks, study approaches, and course grades in undergraduate mathematics: a year-by-year analysis. Int. J. Mathem. Educ. Sci. Technol. 47, 373–387. doi: 10.1080/0020739X.2015.1072881
Marton, F., and Säljö, R. (2005). “Approaches to learning,” in The Experience of Learning : Implications for Teaching and Studying in Higher Education, eds. F. Marton, D. Hounsell, and N. Entwistle (Edinburgh: University of Edinburgh, Centre for Teaching, Learning and Assessment), 39–58.
Memmert, D., Klatt, S., Mann, D., and Kreitz, C. (2023). Perception and attention. In Sport and Exercise Psychology: Theory and Application. Switzerland: Springer Nature. p. 15–40.
Roediger, H. L., and Butler, A. C. (2011). The critical role of retrieval practice in long-term retention. Trends Cogn. Sci. 15, 20–27. doi: 10.1016/j.tics.2010.09.003
Sangwin, C., and Köcher, N. (2016). Automation of mathematics examinations. Comput. Educ. 94, 215–227. doi: 10.1016/j.compedu.2015.11.014
Schunk, D. H., and DiBenedetto, M. K. (2020). Motivation and social cognitive theory. Contemp. Educ. Psychol. 60. doi: 10.1016/j.cedpsych.2019.101832
Smith, W. M., Rasmussen, C., and Tubbs, R. (2021). Introduction to the special issue: insights and lessons learned from mathematics departments in the process of change. Primus 31, 239–251. doi: 10.1080/10511970.2021.1886207
Sotola, L. K., and Crede, M. (2021). Regarding class quizzes: a meta-analytic synthesis of studies on the relationship between frequent low-stakes testing and class performance. Educ. Psychol. Rev. 33, 407–426. doi: 10.1007/s10648-020-09563-9
Trotter, E. (2006). Student perceptions of continuous summative assessment. Assessm. Eval. Higher Educ. 31, 505–521. doi: 10.1080/02602930600679506
Valadas, S. T., Almeida, L. S., and Araújo, A. M. (2016). The mediating effects of approaches to learning on the academic success of first-year college students. Scand. J. Educ. Res. 61, 721–734. doi: 10.1080/00313831.2016.1188146
Wang, X., Dai, M., and Short, K. M. (2024). One size doesn't fit all: how different types of learning motivations influence engineering undergraduate students' success outcomes. Int. J. STEM Educ. 11:1. doi: 10.1186/s40594-024-00502-6
Wilkins, J. L. M., Bowen, B. D., and Mullins, S. B. (2021). First mathematics course in college and graduating in engineering: dispelling the myth that beginning in higher-level mathematics courses is always a good thing. J. Eng. Educ. 110, 616–635. doi: 10.1002/jee.20411
Zakariya, Y. F. (2021). Undergraduate Students' Performance in Mathematics: Individual and Combined Effects of Approaches to Learning, Self-Efficacy, and Prior Mathematics Knowledge. Kristiansand: University of Agder.
Zakariya, Y. F., Danlami, K. B., and Shogbesan, Y. O. (2024). Affordances and constraints of a blended learning course: experience of pre-service teachers in an African context. Humanities and Soc. Sci. Commun. 11:1. doi: 10.1057/s41599-024-04136-5
Zakariya, Y. F., Ibrahim, M. O., and Adisa, L. O. (2016). Impacts of problem-based learning on performance and retention in mathematics among junior secondary school students in Sabon-Gari area of Kaduna state. Int. J. Innovat. Res. Multidisciplin. Field 9, 42–47.
Zakariya, Y. F., and Massimiliano, B. (2022). Short form of revised two-factor study process questionnaire: development, validation, and cross-validation in two European countries. Stud. Educ. Eval. 75. doi: 10.1016/j.stueduc.2022.101206
Zakariya, Y. F., Midttun, Ø., Nyberg, S. O. G., and Gjesteland, T. (2022). Reforming the teaching and learning of foundational mathematics courses: an investigation into the status quo of teaching, feedback delivery, and assessment in a first-year calculus course. Mathematics 10:2164. doi: 10.3390/math10132164
Keywords: approaches to learning, calculus, digital assessments, low-stakes examinations, STACK
Citation: Zakariya YF, Berg MT, Gjesteland T, Umahaba RE and Abanikannda MO (2025) From single to multiple assessments in a foundational mathematics course for engineering students: what do we gain? Front. Educ. 10:1544647. doi: 10.3389/feduc.2025.1544647
Received: 25 February 2025; Accepted: 12 May 2025;
Published: 02 June 2025.
Edited by:
Emma Burns, Macquarie University, AustraliaReviewed by:
Paul Libbrecht, IUBH University of Applied Sciences, GermanyKhanyisile Yanela Twabu, University of South Africa, South Africa
Copyright © 2025 Zakariya, Berg, Gjesteland, Umahaba and Abanikannda. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yusuf Feyisara Zakariya, eXVzdWYuemFrYXJpeWFAdWlhLm5v
 Yusuf Feyisara Zakariya
Yusuf Feyisara Zakariya Morten Tellenes Berg3
Morten Tellenes Berg3 Thomas Gjesteland
Thomas Gjesteland Ramatu Ematum Umahaba
Ramatu Ematum Umahaba