- 1School of Mathematical Sciences, Beijing Normal University, Beijing, China
- 2School of Mathematics and Big Data, Guizhou Education University, Guiyang, China
- 3School of Mathematics and Statistics, Central China Normal University, Wuhan, China
- 4Faculty of Education, Beijing Normal University, Beijing, China
- 5Collaborative Innovation Center of Assessment for Basic Education Quality, Beijing Normal University, Beijing, China
Introduction: The COVID-19 pandemic has fundamentally challenged mathematics education globally, necessitating a deeper understanding of how people utilize mathematical concepts in crisis situations. This study examines how individuals comprehend the pandemic’s inflection point, with a focus on applying mathematical concepts to real-world situations.
Methods: The research employed a mixed-methods approach, collecting data from 1,371 Chinese participants through questionnaire surveys and interviews. The study analyzed participants’ understanding of the pandemic’s inflection point and investigated the sources of their mathematical knowledge.
Results: Findings revealed that despite secondary school mathematics education and media coverage providing relevant knowledge, few participants could accurately explain the concept of an inflection point. Notably, individuals tended to rely on informal mathematical reasoning rather than formal mathematical concepts when interpreting pandemic-related data. Educational background and age significantly affect both response accuracy and the use of mathematics, while field of study only influences the latter.
Discussion: The study identifies a significant disconnect between classroom mathematics and real-world application. This gap suggests the need for educational reforms that emphasize practical applications, knowledge transfer, and out-of-school learning experiences. The findings underscore the importance of developing mathematical literacy that effectively bridges theoretical concepts with practical real-life situations, ultimately contributing to better societal understanding and decision-making during crises.
1 Introduction
Since the beginning of 2020, the COVID-19 pandemic has changed everything, bringing enormous global challenges to the mathematics education community (Bakker and Wagner, 2020). While doctors and other medical professionals were fighting the disease, people struggled to stay safe and survive the pandemic. Citizens needed to understand the situation: what the disease was, how it spread, and the consequences of not wearing masks. Researchers have noted strong links between citizenship education and mathematics education, highlighting mathematics’ sophisticated role in practical application (Geiger et al., 2023). Understanding and predicting pandemic trends helped people make decisions, adjust their behavior, comprehend government measures, and reduce anxiety during the crisis. With mathematical knowledge, citizens could better interpret trends and evaluate predictions in news reports. This enabled them to approach mathematical claims with appropriate skepticism—neither too trusting nor too rigid, but properly critical (Muğaloğlu et al., 2022).
Therefore, it is important to reflect on the responsibilities and potential contributions of mathematics education researchers in the aftermath of crisis. During the pandemic, the prevalence of data and news reports for personal health decisions highlighted how mathematics education could help people protect themselves and their communities from unknown diseases (e.g., Reiss, 2020; Muğaloğlu et al., 2022). Many researchers examined how mathematics instruction and its real-world applications influenced crisis response. For instance, Kwon et al. (2021) studied graph usage in Korean news media during the COVID-19 pandemic, providing insights to improve graph literacy education. Heyd-Metzuyanim et al. (2021) investigated how the Israeli public understood pandemic-related mathematical concepts, finding that mathematical identity strongly affected adults’ engagement with such information. Kollosche and Meyerhöfer (2021) took a critical lens to German mass media discussions on pandemic policies during the 2020 SARS-CoV-2 crisis, revealing that the public often struggled to evaluate experts’ mathematical applications critically. However, current research mainly focuses on media’s mathematical presentations (Aguilar and Castaneda, 2021), mathematical knowledge related to information (Meyer and Lima, 2023), and literacy assessment scores. These studies do not fully explore how people apply mathematics—learned both in and out of school—to understand real-world situations.
In China, many news reports used the term “inflection point” to describe the circumstance that people were facing and to give people hope in fighting the disease. For instance, the Chinese Center for Disease Control and Prevention declared that the increasing number of daily cases would peak between February 7–9, 2020, reaching the inflection point. This raises an important question about how citizens use mathematics to understand the COVID-19 pandemic’s inflection point—a reflection of people’s ability to apply mathematics to real-world problems in their daily lives. It serves as a crucial reminder for mathematics teachers and educators, highlighting the gap between what people should learn from mathematics education and what they actually use in solving real-world problems. It also emphasizes the importance of connecting mathematics with other disciplines and recognizes mathematics education’s role in lifelong learning.
As previous studies have shown (Pfannkuch et al., 2018; Verschaffel et al., 2020), applying mathematics in daily life differs from solving textbook word problems. This study, therefore, examines both “formal mathematics” and “street mathematics” to understand how citizens apply mathematical concepts in their daily lives. Specifically, we investigate how Chinese citizens use both types of mathematics to understand the concept of inflection points during the COVID-19 pandemic.
2 Theoretical consideration
2.1 Inflection point of the pandemic
The inflection point of pandemic was a critical issue worldwide (Gu et al., 2020), interpreted as a turning point in the growth trend of newly confirmed cases, which is the definition also adopted by this study. Mathematically, it is the extreme point of the curve depicting the change in the number of newly confirmed cases over time with different statistical models such as cubic, quadratic, exponential, logarithmic, power, or segmented Poisson models (Gu et al., 2020; Zhang et al., 2020).
The inflection point marks a decrease in the pandemic spread, which is a good sign, even though the number of cumulative cases continues to increase (possibly with great speed). Many mathematical concepts related to “the inflection point of the pandemic” can be used by citizens to explain and even roughly predict the pandemic prevalence trend long before the people can coexist with the virus, and to understand the effect of related public policies such as quarantine, which was one of the most important purposes of the government official media news reports.
Since many media outlets made the increasing number of daily confirmed cases accessible to citizens, individuals seemed to obtain adequate information from the media to roughly understand the trend of viral spread or critically check the prediction reported by the media in terms of the inflection point. For example, people can intuitively check if the growing curve begins to flatten, in which case they may not link the problem to the mathematics they learned at school. While formal mathematical models of viral spread, such as epidemiological models (Jia et al., 2020), may be too sophisticated for citizens to apply to real-life problems, people can draw on their secondary school mathematics to interpret pandemic trends. For example, they can use basic mathematical concepts like extreme points and slopes, which are covered in the curriculum on change and relationships.
Therefore, the mathematics that people use to understand the trend of viral spread is potentially derived from the “formal mathematics” taught in schools and the “street mathematics” obtained from living experiences outside school, such as media news reports, which interactively play an important role in equipping 21st-century citizens with the skills and knowledge they need to live in the modern world. However, there is no well-developed theoretical framework integrating formal mathematics and street mathematics to interpret people’s use of mathematics in their daily lives.
2.2 Formal mathematics
Regarding formal mathematics taught in schools, the 2022 Programme for International Student Assessment (PISA) framework (Organisation for Economic Co-operation and Development [OECD], 2021) stated that the fundamental goal of schooling systems in mathematics is to prepare their students to use mathematics in every aspect of their personal, civic, and professional lives. Specifically, PISA constructs “mathematical literacy” to embody the outcome of school systems: an individual’s capacity to reason mathematically and to formulate, employ, and interpret mathematics to solve problems in a variety of real-world contexts. It includes concepts, procedures, facts, and tools to describe, explain, and predict phenomena. It assists individuals in learning the role of mathematics in the world and in making well-founded judgments and decisions needed by constructive, engaged, and reflective citizens of the 21st century. In short, PISA deems that the acquisition of mathematics literacy can be understood as a result of school education and gives “problem-solving in real-world contexts” a prominent position in mathematics teaching and learning.
Regarding problem-solving, Lesh (2007) emphasized that it is inherently connected to concept development and the application of these concepts in real-life situations beyond school. Lesh defined Problem Solving as “the process of interpreting a situation mathematically,” noting that this process involves sorting out, integrating, modifying, revising, and refining mathematical concepts across various topics both within and beyond mathematics. As such, problem-solving can be treated as modeling activities, which are designed for students to use mathematics to make sense of real-world phenomena (Lesh et al., 2003).
When it comes to real-world contexts in mathematics teaching, realistic mathematics education (RME), as a domain-specific instruction theory, pointed out that the introduction of realistic contexts and situations helps students initiate the development of mathematical concepts, tools and procedures (Van den Heuvel-Panhuizen and Drijvers, 2014). Similar to the PISA idea, RME also attaches importance to students’ ability to use mathematics in solving real-life problems and emphasizes the role of models in bridging the gap between context-related mathematics and formal mathematics (Freudenthal, 1991).
As mentioned, the inflection point of the pandemic is explained as “the extreme point on the daily increasing confirmed cases-time function (curve)” (Gu et al., 2020). Over the years, the modern curriculum has integrated the concepts of change and its graphical representational forms (Kaput and Roschelle, 2013). Thus, the terms, phrases, and expressions provided by curricula are defined as “formal mathematics,” while all the others are defined as “street mathematics.” In China, the concepts of “change” and “variable” are formally introduced at the junior secondary stage, traditionally in grade eight. Students at the third stage (i.e., the junior secondary stage; grades seven to nine) of compulsory education are supposed to explore the change of magnitude and relationships between variables in simple contexts, model the change and relationship of variables with appropriate functions in simple contexts, and predict the change of variables based on the analysis of algebraic, tabular, and graphical representations. Though the curriculum does not touch on the concept of the extremum, it refers to the description of the change of variables and emphasizes the application of algebraic, tabular, and graphical representations in depicting change phenomena in real life. The concepts of extreme, maximum, and minimum on a continuous curve are formally introduced at the general senior secondary level, usually in grade 11. Students at this stage are supposed to experience the transition from “average rate of change” to “instantaneous rate of change,” learn the concept of a derivative and apply derivatives in studying some properties of functions to solve problems in real-life contexts, such as monotonicity, extreme value, and maximum and minimum.
In this study, a formal mathematics explanation of the inflection point as coronavirus spread can focus on the rate of change, such as “the increasing rate of newly confirmed cases decreases,” or mention a derivative properly, such as “the derivative of the number of newly confirmed cases with time,” or describe some graphic representations, such as “the number of newly confirmed cases reaches a peak/maximum.”
Moreover, it should be noted that according to the curriculum, people educated in Chinese high schools are supposed to have an adequate knowledge base and mathematics literacy regarding change and relationships to correctly understand the inflection point of the pandemic, even though the topic of health and disease control and prevention is not embodied in those materials.
2.3 Street mathematics
Notably, as time passes, people may gradually forget what they learned from school and rarely employ specific mathematical knowledge to solve real-world problems, or they might even never acquire related mathematics through formal school learning. Instead, they spontaneously apply the knowledge and methods learned from their living experience to problem-solving. This type of knowledge is referred to as “street/everyday mathematics” (Greiffenhagen and Sharrock, 2008). Street mathematics is “informal” mathematics, which contrasts with the formal kind of knowledge acquired by learners at school while supervised by a teacher (Mutemeri, 2013). For example, the techniques for solving quantitative problems developed outside of school are intertwined with everyday activities (Nunes et al., 1993). This was first discussed by Carraher et al. (1985) in the late 20th century from the perspective of developmental psychology, which led to one research line focusing on learners’ development of cognition and psychology in street mathematics. Meanwhile, another research line traces it back to the influence of cultures and politics on learners’ everyday knowledge from an ethnomathematics perspective, which is driven by the need to understand the difficulties that non-Western learners face in learning mathematics in Western schooling systems (Lave, 1988; Bishop, 1991; Knijnik, 2002; de Abreu, 2008).
Street mathematics can be quite different from the formal mathematics learned in schools. By using street mathematics knowledge, people solve real-world problems based on the concrete meaning of contexts instead of mathematical processes and modeling emphasized by mathematics literacy, in which case people use pragmatic reasoning schemas to organize relationships within the problem (Nunes et al., 1993). In addition, mathematics itself is not at the center of solving problems (Civil, 2007). Note that at times, street mathematics seems to work better than formal mathematics in solving practical problems. For instance, arithmetic in street mathematics allows people to better monitor the process of calculation and show flexibility in the paths to a solution (Rogoff, 1984; Nunes et al., 1993). Since people have different schooling experiences in mathematics in terms of the length of learning time and the breadth and depth of learned topics, street mathematics acquired outside of schools can complement what people learned at school, which can be especially advantageous for people to solve real-world problems (Nunes et al., 1993). In other words, street mathematics provides students with an opportunity to learn mathematics in real-world contexts that are meaningful to them and allows them to develop mathematical competence while solving real-life problems (Van Den Heuvel-Panhuizen, 2003).
Street mathematics studies have traditionally focused on simple mathematical models such as arithmetic (Saxe, 1982) and simple statistics (Oslington et al., 2020). However, with the development of technology and the improvement of citizens’ education, mathematics applied in daily life has become more complex and advanced. Hence, research concerning street mathematics in the modern world should advance with such changes, for example, by including the idea of functions and variables in describing the phenomena of change and relationships.
2.4 Conceptual framework
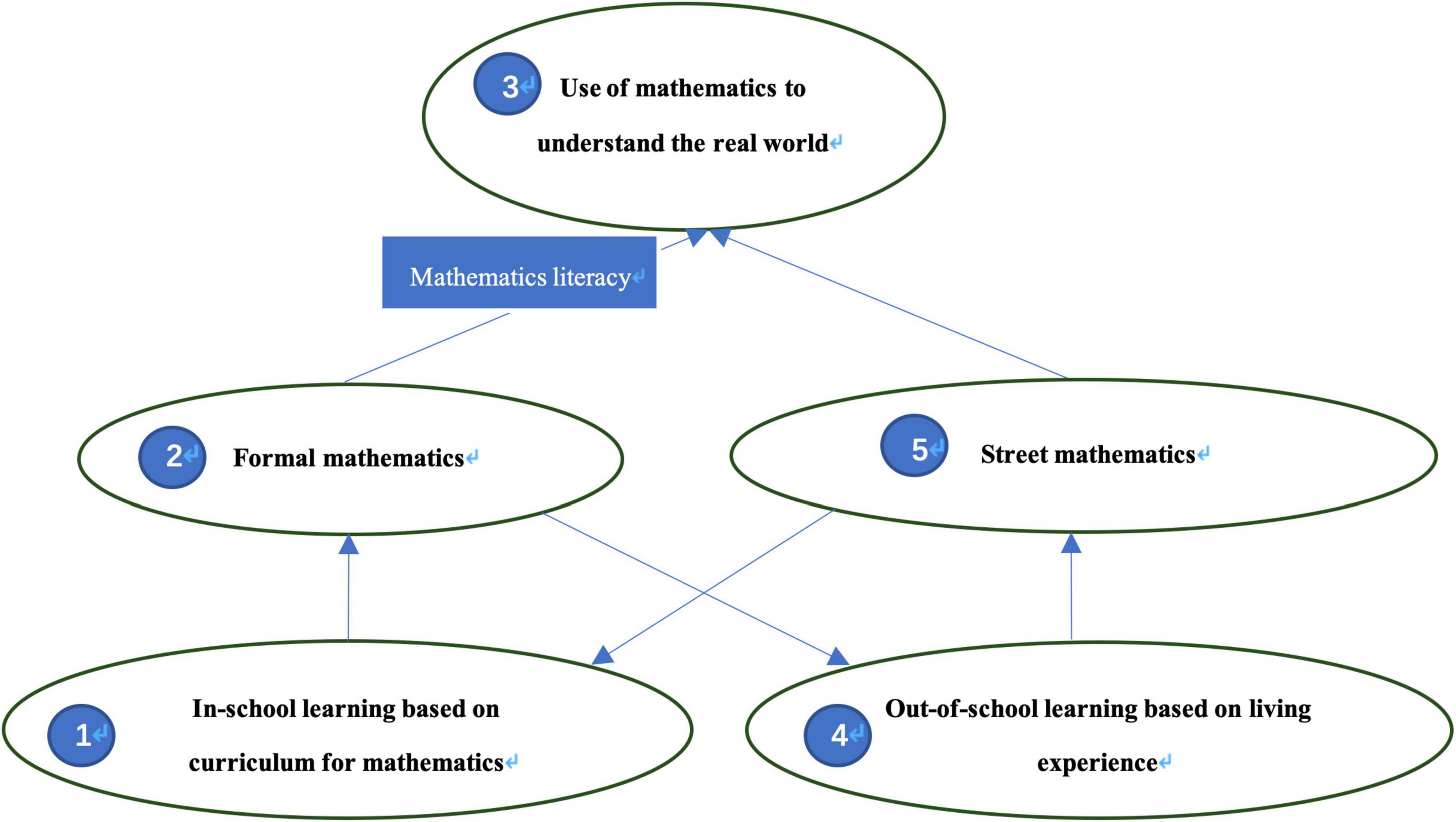
Mathematics education integrates both formal classroom instruction and informal learning experiences (de Abreu, 2008; Nemirovsky et al., 2020). Our framework (Figure 1) distinguishes between learning environments (in-school and out-of-school) and knowledge types (formal and street mathematics). While formal mathematics comes from school education, street mathematics emerges from lived experiences. These components work together, with street mathematics often enriching classroom learning through practical context.
Our study bridges formal mathematics taught in schools with real-world mathematical understanding through PISA’s mathematics literacy framework (Duchhardt et al., 2017; Organisation for Economic Co-operation and Development [OECD], 2021). This framework emphasizes the ability to formulate, employ, and interpret mathematics in real-world contexts. While formal mathematics relies on mathematical modeling, street mathematics takes a more context-driven approach to problem-solving. These represent distinct but complementary cognitive processes for addressing real-world challenges.
Moreover, the development of formal mathematics and the acquisition of street mathematics are interlaced. On one hand, formal mathematics is supposed to provide a foundation for people to develop street mathematics (usually related to advanced mathematics, such as inflection points) through informal learning (National Research Council, 2012), especially after the completion of education, shown as the route ①→②→④→⑤ in Figure 1. It seems to contradict classical theories that present informal knowledge as the foundation for scaffolding mathematical concepts. This is because advanced street mathematics, such as “the inflection point of a pandemic,” may not develop spontaneously through the accumulation of people’s living experiences (Nunes et al., 1993). It requires a foundation in formal mathematics, as Kollosche and Meyerhöfer’s study (2021) found that the public often struggled to evaluate media reports. On the other hand, street mathematics is viewed as having the potential to provide people with the experience base for formal mathematics learning in schools. For example, at the stage of primary school, street mathematics knowledge of arithmetic provides an experience base for learning multiplication in the school curriculum (Saxe, 1982), shown as the route ④→⑤→①→②. It should be noted that, during the lifelong journey of mathematics learning both in and outside school, the routes might loop, such as ①→②→④→⑤→①→② or ④→⑤→①→②→④→⑤.
3 Materials and methods
Mixed methods were applied in this study to address the research question. A questionnaire survey was conducted to explore how Chinese citizens understand the inflection of the COVID-19 pandemic. One-to-one interviews were conducted to obtain an in-depth understanding of the data collected from the questionnaire with a focus on the source from which they acquired mathematics.
3.1 Sampling
For the questionnaire survey, convenience sampling was employed to investigate citizens’ conceptual and procedural interpretations of the inflection point of the pandemic spread. We distributed an electronic questionnaire through WeChat (a popular Chinese social media app). In total, 1,371 valid questionnaires were returned, including 6 from overseas; 2 from Hong Kong, China; and the others from 24 Chinese mainland provinces. Specifically, Wuhan, Hubei, the place that became the focus of international concern as the virus began spreading, accounted for 32.2% of the responses obtained, other cities in Hubei accounted for 37.6%, and regions of China outside Hubei accounted for 30.3%. Moreover, the proportion of female participants was 68.7%, versus 31.3% for male participants.
A majority (31.8%) of the participants were aged 41 to 50 years, while the second largest group (26.5%) were between 18 and 30, followed by middle-aged participants (23.5%) and the senior group (15.6%). Regarding the education level of participants, 8.9% of the participants did not have any higher education experience, 30.9% had a college-level education, 51.4% had university-level education, and 8.8% had obtained a master’s or higher degree, which was higher than that of the average population in China.
One-to-one interviews were conducted with 12 participants after they completed the questionnaire survey, including 5 with master’s degrees and 7 with doctoral degrees. The interview data were used to complement the survey analysis, especially regarding the source of related formal or street mathematics.
3.2 Instruments
This study developed a questionnaire with six questions to collect data on citizens’ understanding of the inflection point of the pandemic. The first three questions requested demographic information, including gender, age, and educational background. The options for educational background included junior high school and below, high school or vocational high school, college, undergraduate, master’s, and doctorate levels. Question 4 requested participants to specify what majors they studied in school. Question 5 to 8 were open-ended questions.
Question 5 asked participants to explain the meaning of the “inflection point” of the pandemic (understanding from the conceptual perspective), while Question 6 asked for a description of how to find the inflection point of the pandemic (understanding from the procedural perspective). The last two questions assessed participants’ conceptual and procedural interpretations of the inflection point of the pandemic, respectively.
Furthermore, an interview protocol was developed to supplement the questionnaire: Question 1: In your opinion, what is the inflection point of the pandemic, and how did you find this inflection point, corresponding to the question 5 and 6 in questionnaire; Question 2: How did you obtain the abovementioned understanding? Did it stem from the news reports during the pandemic, your existing knowledge, or from other sources, corresponding to the question 6 and 8 in questionnaire.
3.3 Coding scheme
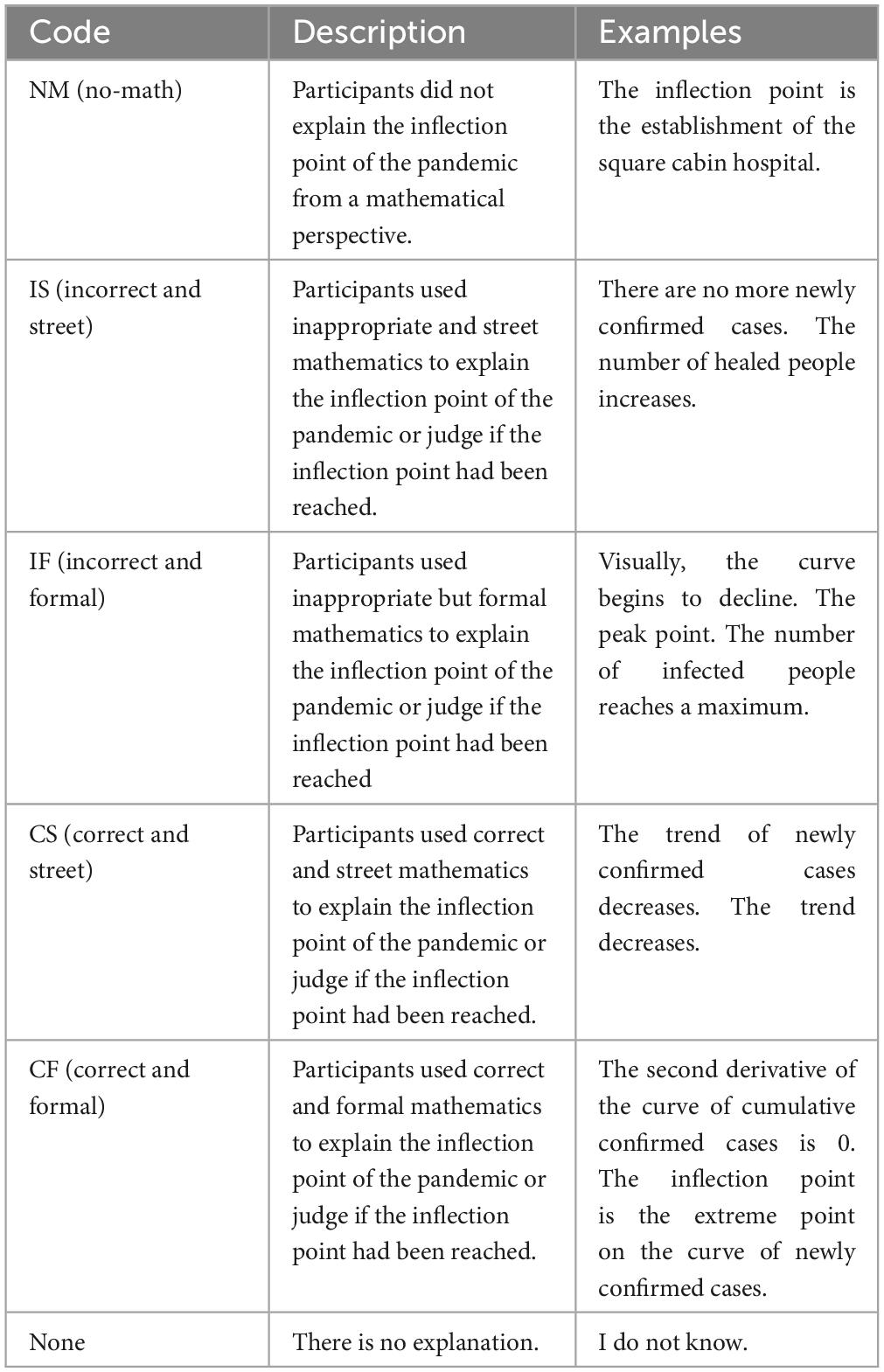
The development of our coding scheme followed a rigorous, iterative process. Initially, two researchers independently analyzed a subset of responses to identify emerging patterns and categories. They examined whether participants used correct and formal mathematics knowledge to interpret their understanding of the inflection point (either conceptually or procedurally). The coding scheme underwent three rounds of revision based on pilot coding. Each revision involved detailed discussions of discrepancies and refinement of code definitions. The final scheme was validated through expert review by two external mathematics education researchers who assessed its theoretical foundation and practical applicability (see Table 1).
3.4 Data analysis
We employed a systematic approach in which two trained coders independently coded all responses. Cohen’s kappa coefficient was used to account for chance agreement. After resolving discrepancies through consensus meetings and refining code definitions, the final round of coding achieved a 79.1% agreement rate (kappa = 0.686), indicating moderate to substantial inter-rater reliability.
The data collected from the interviews were organized according to the corresponding items in questionnaire and interpreted as supplement to provide more details regarding people’s understanding. First, we identified patterns and contradictions between the two data sources. This triangulation process revealed nuanced insights that weren’t apparent when analyzing each data source separately. Second, we developed detailed case studies for select participants where their survey responses and interview narratives provided particularly rich examples of how formal and street mathematics interact in real-world problem solving. These cases offer deeper context for understanding how individuals integrate different forms of mathematical knowledge. Finally, we created themed matrices that aligned survey responses with interview excerpts across key dimensions of the conceptual framework. This systematic integration allowed us to identify more subtle relationships between participants’ reported mathematical understanding and their actual problem-solving processes.
4 Results
4.1 A whole picture
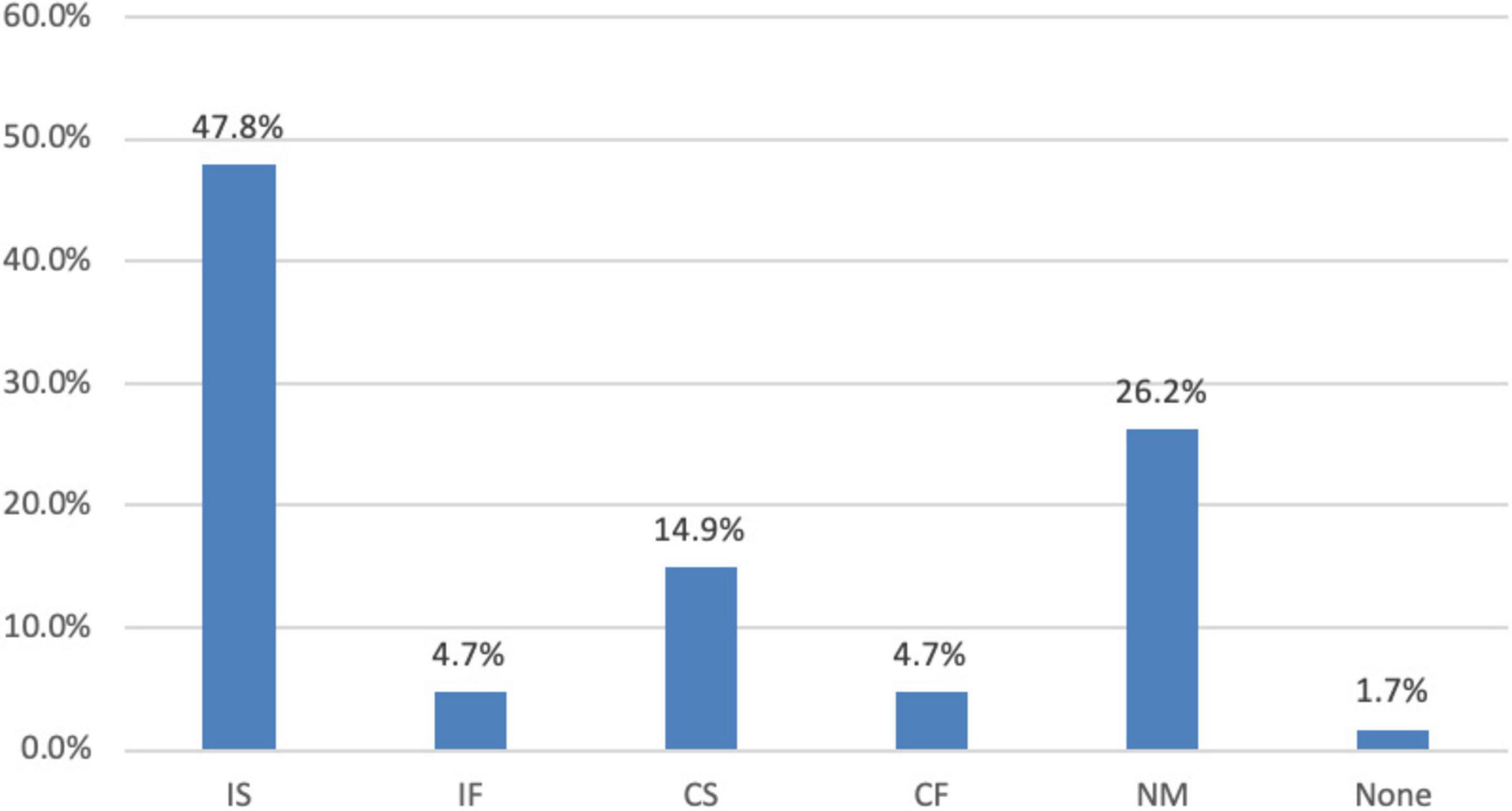
As Figure 2 shows, 47.8% of the participants used “incorrect and informal” mathematics to describe the inflection point of the pandemic, 4.7% of the participants used incorrect and formal mathematics which was the same as the category of “correct and formal,” and 26.2% did not refer to any mathematics. Only 19.6% (“CS” 14.9% + “CF” 4.7%) of the participants employed appropriate mathematics to describe their understanding of the inflection point; it is worth noting that the majority of these responses indicated informal applications of mathematics (76.0%). This is despite that Chinese students performed well in international comparative studies (Leung, 2001; Wang and Lin, 2005), and the participants in the study have a much higher level of education than the average population in China.
The majority of participants (46 out of 65) correctly used maximum points, extreme point, and statistical graphs to describe inflection points in the questionnaire survey. Another 8 participants who employed formal mathematics accurately referenced the concept of second derivatives. All of these concepts are fundamental components of the secondary school mathematics curriculum. Those are empirical evidence supporting route ①→②→③ shown in Figure 1. To be more specific, some participants interpreted the inflection point of the pandemic as “when the second derivative of the curve of cumulative confirmed cases is 0,” and “the extreme point on the curve of newly confirmed cases.” These responses first formulate the viral spread as an extreme point on the curve and then interpret results in the context of the pandemic, which reflects the process of mathematical modeling and relating the mathematics literacy of change and relationships.
Also, the majority participants (186 out of 204) correctly understood inflection point without mathematical models using the terminology “the number of newly confirmed cases decreases,” which refers to street mathematics. Hence, it was evident that people applied both formal and street mathematics to understanding the inflection point, though they tended to use more street mathematics. Among participants who used street mathematics but provided incorrect answers, descriptions such as “no growth for 14 days” appeared to mirror media reporting language. This suggests that street mathematics serves an important and practical function in addressing real-world problems in everyday life, as illustrated by route ④→⑤→③ in Figure 1.
In interviews, people indicated that their understanding of the inflection point of the pandemic was based on either their knowledge (7 out of 12 responses) or the internet and news (3 out of 12 responses), which coincides with the conceptual framework proposed by this study. Specifically, one of the subjects believed that he used his knowledge to explain the inflection point:
“the inflection point can be understood in diverse ways such as the growing rate begins to decrease or the number of confirmed cases begins to decrease, the former concerns accelerated velocity and the latter’s focus is the absolute value.”
In this interview, the key concepts “accelerated velocity” and “absolute value” are definitely taught at secondary schools, which implies a use of formal mathematics learned from schools.
Also, many participants providing “street mathematics” answers pointed out in their interviews that they learned it from the Internet and news reports, which refers to a use of street mathematics learned from living experience, supporting route ④→⑤→③ shown in Figure 1. Particularly, one of the responses seem remarkable since the interviewee hold doctoral degrees in science:
“According to the news, when new cases are fewer than recoveries, the net increase is negative.”
4.2 Correlations with demographic variables
Chi-square tests were employed to examine correlations between responses and educational background. Table 2 reveals significant differences between two educational levels (up to bachelor’s degree versus master’s degree and higher) regarding both response accuracy and use of formal mathematics. Specifically, 18.1% of respondents with up to a bachelor’s degree gave correct answers, compared to 36.7% for those with higher degrees, suggesting that people with higher educational levels were more likely to understand inflection points accurately. Similarly, 8.0% of those with up to a bachelor’s degree used formal mathematics in their answers, compared to 24.2% for those with higher degrees, indicating that people with higher educational levels are more likely to apply formal mathematics when solving real-world problems.
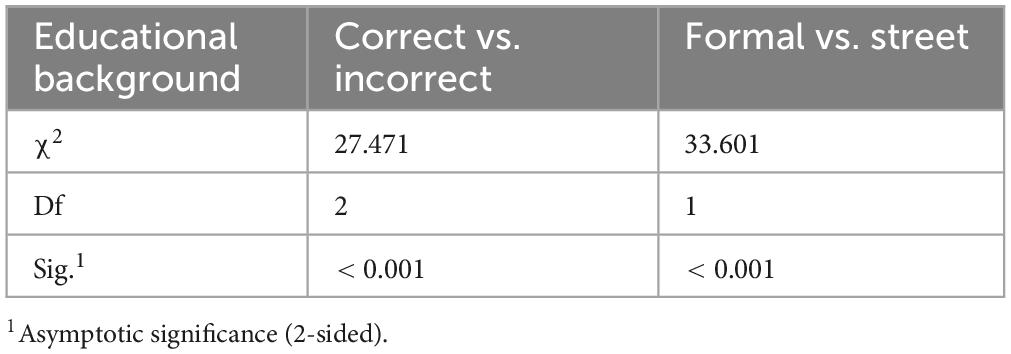
Table 2. Results of the Chi-square test of differences between “Up to bachelor’s degree” and “Master’s and higher.”
To analyze correlations with age groups, and given our sample’s above-average educational level, we selected age 30 as a threshold to examine whether accuracy and formal mathematics usage declined with time since leaving academia. Table 3 shows significant differences between age groups (up to 30 years old versus over 30 years old) regarding both response accuracy and use of formal mathematics. Specifically, 27.1% of respondents in the younger group provided correct answers, compared to 16.6% in the older group. Similarly, 15.1% of younger respondents used formal mathematics to explain inflection points, compared to 7.1% in the older group. These results indicate that both accuracy and formal mathematics usage decrease over time.
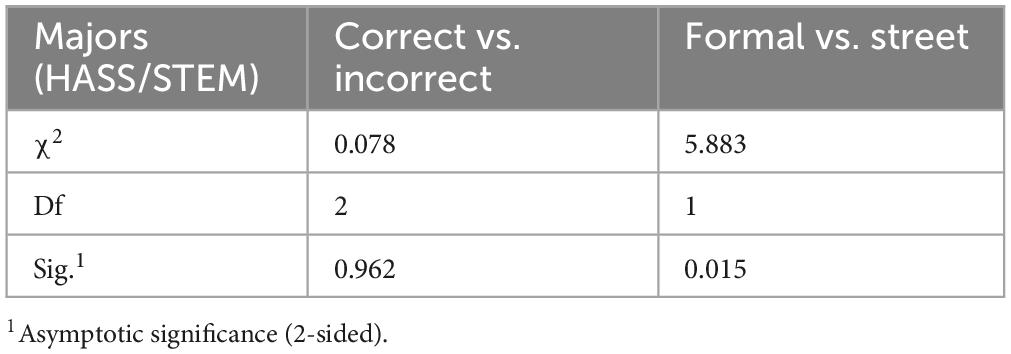
Also, Chi-square tests examined correlations between responses and academic majors. Table 4 indicates that having a mathematics degree did not lead to higher response accuracy or increased use of formal mathematics.

Table 4. Results of the Chi-square test of differences between “Major in mathematics” and “Major in others.”
Additionally, we broadened our analysis by reclassifying majors, expanding from mathematics to STEM (Science, Technology, Engineering, and Mathematics) with HASS (Humanities, Arts, and Social Sciences) as the comparison group. Chi-square tests revealed significant differences only in the use of formal mathematics (see Table 5). Specifically, 11.3% of STEM majors used formal mathematics compared to 7.4% of HASS majors, indicating that STEM graduates are more likely to apply formal mathematical approaches when solving real-world problems.
5 Discussion
5.1 How do Chinese citizens use mathematics to understand the inflection point of the COVID-19 pandemic?
This study found empirical data indicating that not many citizens precisely describe the inflection point of the pandemic and understand the situation they were facing, despite having been equipped with the knowledge and literacy provided by mathematics education in and out of school. In addition, the citizens applied two kinds of mathematics in their daily life (②→③ and ⑤→③), even though the mathematical content is complex and advanced. Notably, citizens applied more street mathematics than formal mathematics in the case of inflection point, even though our sample had a higher education level than the average citizen. There is evidence showing that the lack of context-based tasks in textbooks might be one of the reasons behind students’ difficulties in developing mathematics literacy (Wijaya et al., 2015; Li and Li, 2021). Furthermore, this study’s findings indicate that emphasizing real-world contexts in mathematics education enhances students’ mathematical literacy, ultimately enabling citizens to better understand the world through mathematics—illustrated by the typical route ①→②→③ in Figure 1. This relationship has been thoroughly examined in previous studies (Jurdak, 2006, 2016; Kohen and Orenstein, 2021). The results also suggest that the mathematics education community should rethink how (advanced) mathematics is applied in daily life. Formal mathematics might not be easy to apply in daily life, so we should strive to understand the role of street mathematics in mathematics education, which should be highlighted in future studies.
Analysis of demographic correlations revealed several key findings. Higher educational attainment strongly correlated with both improved understanding and greater use of formal mathematics. Both accuracy and formal mathematics usage declined significantly as time passed after leaving academia. This has been evidenced by large-scale assessments of adults’ mathematical literacy (Organisation for Economic Co-operation and Development [OECD], 2013, p. 120; Rammstedt, 2013). It is important to recognize that these cross-sectional studies cannot definitively establish causation between educational level, aging and observed differences, as other factors may contribute to the variations seen across age groups (Desjardins and Warnke, 2012). These variations may be influenced by cohort effects, where generational groups share common environmental experiences such as economic changes, educational reforms, or significant historical events that could help explain these observed differences. Additionally, the threshold of 30 years old is supported by an empirical study that found negative aging effects beginning around the ages of 30–40 in a wide range of countries (Desjardins and Warnke, 2012).
Notably, having a mathematics degree alone did not significantly impact either response accuracy or formal mathematics usage. When comparing STEM and HASS graduates, the only significant difference emerged in formal mathematics usage, with STEM graduates showing a higher tendency to employ formal mathematical approaches compared to HASS graduates. One plausible explanation is that STEM graduates, compared to mathematics and HASS graduates, are more likely to engage in mathematics-related work and sophisticated mathematical activities that require applying mathematics to engineering, design, and processing problems. This aligns with the “use it or lose it” hypothesis (Desjardins et al., 2005).
5.2 How does the conceptual framework help with understanding the use of mathematics in the real world?
Notably, the conceptual framework developed by this study was illustrated and interpreted by empirical data to a great extent. In our interviews, many participants mentioned that they understood the importance of the inflection point and interpreted it based on news reports and information obtained from the internet. In particular, one respondent admitted that she had forgotten her school knowledge relating to the inflection point of a pandemic, which speaks to the appeal of the utilization of street mathematics in education. In the meantime, people need to be equipped with basic knowledge to be able to distinguish accurate information from misinformation and understand the meaning of street mathematics, such as “the peak of an increasing trend” as stated by the media. Thus, formal mathematics learned in school can be the scaffolding for people to develop and make use of street mathematics, as mentioned and constructed in the conceptual framework, shown by route ②→④→⑤ in Figure 1. It was found that mainstream news provided people with the contextual meaning to understand the inflection point of the pandemic. However, many Chinese news reports employed the term “inflection point” to comfort scared people and demand certain behavior changes needed for pandemic control without any explanation of what the inflection point is, which may not adequately establish trust between the media and citizens. For example, one expert on disease control, interviewed by China Central Television news (China Central Television, 2020), mentioned that the real inflection point would come if people’s health literacy improved.
On the other hand, though most people were believed to have the relevant knowledge after completing school education (see ①→②→③ in Figure 1), only a few of them properly explained the inflection point of the pandemic using formal mathematics. The outcomes of school education in terms of solving real-world problems in daily life must be reconsidered since it might not provide the citizens with enough mathematics knowledge as the curriculum expects.
Therefore, the conceptual framework provides an opportunity for researchers and educators to rethink the link between the mathematics education effort in school and society, and depicts an initial image of how people use mathematics to understand the world and solve real-world problems. More empirical evidence is needed to develop the conceptual framework in the future, especially evidence from a psychological viewpoint (Nunes et al., 1993) and from a cognitive analysis of the role of mathematics literacy in supporting the acquisition of (advanced) street mathematics. Finally, though the results were obtained from a Chinese context, the conceptual framework can be extended to other settings since it is culture-free.
5.3 Limitations
It is worth mentioning that the sample size is relatively small in proportion to the general population and the data collected in this study were collected via convenience sampling. Many of the participants came from central China (Hubei Province), had mathematics education backgrounds, possessed higher educational levels than the general population, and worked as mathematics teachers in primary and secondary schools—factors that may limit the study’s representativeness. Thus, caution should be taken when generalizing the results and interpreting the data. Future research should consider larger and random samples to strengthen the validity of the conclusions. In addition, the empirical data only partly illustrated and verified the conceptual framework, and more comprehensive studies should be designed in the future to further explore some under-discussed routines, such as ④→⑤ in the framework.
6 Conclusion and implications
This study established a conceptual framework for examining how people use mathematics—both formal and street mathematics—to solve real-world problems in daily life, specifically in interpreting the COVID-19 infection rate’s inflection point. Empirical data was collected from 1,371 Chinese people. The results showed that few citizens could accurately describe the pandemic’s inflection point or fully understand their situation, and citizens tended to use street mathematics more than formal mathematics when interpreting the inflection point, with educational background, age, and field of study significantly influencing both accuracy and formal mathematics usage. Overall, the findings suggest that citizens did not effectively utilize either school or street mathematics, despite this knowledge being taught before tertiary education and accurate information being available through mainstream media.
The results of this study hold several implications for researchers in mathematics education. First, while we emphasize problem-solving ability and the introduction of real-life contexts into school education, there remains a gap between real-world problems and contextual questions in mathematics teaching and learning. For example, in a widely-used mathematics textbook (recently published by Beijing Normal University publishing house), only one section covers the application of derivatives in real-life contexts to reflect the curriculum standard’s connection between mathematics and reality. Of its six examples, five draw from real-life contexts including physics (power), rainfall intensity, production and profit, and volume and dimension. Physics and economics dominate these contextual examples, while other domains like health and medicine are rarely addressed. Therefore, incorporating more current and diverse contexts in mathematics textbooks and practical teaching is necessary to improve people’s mathematical problem-solving abilities across various domains. Since citizens don’t naturally apply their school-taught mathematical literacy to real-world problems, education must strengthen the connection between formal mathematics and its real-world applications.
Second, this study’s findings encourage mathematics teachers and researchers to examine street mathematics—knowledge gained through informal learning outside school—and consider how to help students apply their experience learning to real-world situations. Public outreach activities like pamphlets, community education, and media campaigns can help people better understand and use street mathematics during public crises. While arithmetic and basic statistics are established areas of street mathematics research, as noted in section “2.3 Street mathematics,” this study reveals that advanced mathematical concepts like variables and rates of change are also developed and applied beyond formal education. Future research should investigate the characteristics of street mathematics, its knowledge construction processes, and potential differences between school-taught and street mathematics in solving real-world problems. Such research would benefit from interdisciplinary collaboration across cognitive psychology, sociology, and mathematics education.
Finally, mathematics education should remind governments to take responsibility for informal learning. During the height of the pandemic three years ago, people focused on infection trends to predict when commerce would recover, and life would return to normal. However, we found no government-issued materials—whether brochures, posters, or reports, in print or digital form—to help people understand the published data and pandemic trends from a scientific perspective. Furthermore, media reports often misuse mathematical concepts. This highlighted the critical need for releasing reliable, scientific resources to help people understand key issues like infection patterns mathematically. Such instruction would not only better equip people to understand and respond to the pandemic but also demonstrate how mathematics applies to real-life situations, encouraging a more mathematical and scientific worldview.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving humans were approved by the School of Mathematical Sciences, Beijing Normal University. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.
Author contributions
YW: Conceptualization, Funding acquisition, Writing – original draft. LZ: Formal Analysis, Validation, Writing – review and editing. NL: Investigation, Validation, Writing – review and editing. CW: Validation, Writing – review and editing. LW: Methodology, Supervision, Writing – review and editing.
Funding
The authors declare that financial support was received for the research and/or publication of this article. This research is funded by “2020 Youth Projects of Beijing Office for Education Sciences Planning: A study of online learning behaviors and their influencing factors (Award No: CHCA2020101)”.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The authors declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aguilar, M. S., and Castaneda, A. (2021). What mathematical competencies does a citizen need to interpret Mexico’s official information about the COVID-19 pandemic? Educ. Stud. Math. 108, 227–248. doi: 10.1007/s10649-021-10082-9
Bakker, A., and Wagner, D. (2020). Pandemic: Lessons for today and tomorrow? Educ. Stud. Math. 104, 1–4. doi: 10.1007/s10649-020-09946-3
Bishop, A. (1991). Mathematical enculturation: A cultural perspective on mathematics education. Berlin: Springer Science & Business Media.
Carraher, T. N., Carraher, D. W., and Schliemann, A. D. (1985). Mathematics in the streets and in schools. Br. J. Dev. Psychol. 3, 21–29. doi: 10.1111/j.2044-835X.1985.tb00951.x
China Central Television (2020). The real inflection point will come if people’s health literacy improves. Bgeijing: China Central Television.
Civil, M. (2007). “Building on community knowledge: An avenue to equity in mathematics education,” in Improving access to mathematics: Diversity and equity in the classroom, eds N. Nasir and P. Cobb (New York, NY: Teachers College Press).
de Abreu, G. (2008). “From mathematics learning out-of-school to multicultural classrooms: A cultural psychology perspective,” in Handbook of international research in mathematics education, 2nd Edn, ed. L. English (Mahwah: Lawrence Erlbaum).
Desjardins, R., Murray, T. S., and Tuijnman, A. C. (2005). Learning a living: First results of the adult literacy and life skills survey. Paris: OECD.
Desjardins, R., and Warnke, A. J. (2012). Ageing and skills. a review and analysis of skill gain and skill loss over the lifespan and over time. Paris: OECD.
Duchhardt, C., Jordan, A.-K., and Ehmke, T. (2017). Adults’ use of mathematics and its influence on mathematical competence. Int. J. Sci. Math. Educ. 15, 155–174. doi: 10.1007/s10763-015-9670-1
Freudenthal, H. (1991). Revisiting mathematics education China lectures, 1st Edn. Dordrecht: Kluwer Academic Publishers, doi: 10.1007/0-306-47202-3
Geiger, V., Gal, I., and Graven, M. (2023). The connections between citizenship education and mathematics education. ZDM – Math. Educ. 55, 923–940. doi: 10.1007/s11858-023-01521-3
Greiffenhagen, C., and Sharrock, W. (2008). School mathematics and its everyday other? Revisiting Lave’s ‘Cognition in Practice.’. Educ. Stud. Math. 69, 1–21. doi: 10.1007/s10649-008-9115-7
Gu, C., Zhu, J., Sun, Y., Zhou, K., and Gu, J. (2020). The inflection point about COVID-19 may have passed. Sci. Bull. (Beijing) 65, 865–867. doi: 10.1016/j.scib.2020.02.025
Heyd-Metzuyanim, E., Sharon, A. J., and Baram-Tsabari, A. (2021). Mathematical media literacy in the COVID-19 pandemic and its relation to school mathematics education. Educ. Stud. Math. 108, 201–225. doi: 10.1007/s10649-021-10075-8
Jia, J. S., Lu, X., Yuan, Y., Xu, G., Jia, J., and Christakis, N. A. (2020). Population flow drives spatio-temporal distribution of COVID-19 in China. Nature 582, 389–394. doi: 10.1038/s41586-020-2284-y
Jurdak, M. (2016). Learning and teaching real world problem solving in school mathematics a multiple-perspective framework for crossing the boundary, 1st Edn. Cham: Springer International Publishing, doi: 10.1007/978-3-319-08204-2
Jurdak, M. E. (2006). Contrasting perspectives and performance of high school students on problem solving in real world situated, and school contexts. Educ. Stud. Math. 63, 283–301. doi: 10.1007/s10649-005-9008-y
Kaput, J. J., and Roschelle, J. (2013). “The mathematics of change and variation from a millennial perspective: New content, new context,” in The simcalc vision and contributions. advances in mathematics education, eds S. J. Hegedus and J. Roschelle (Dordrecht: Springer Netherlands), 13–26. doi: 10.1007/978-94-007-5696-0_2
Knijnik, G. (2002). Ethnomathematics: Culture and politics of knowledge in mathematics education. Learn. Math. 22, 11–14.
Kohen, Z., and Orenstein, D. (2021). Mathematical modeling of tech-related real-world problems for secondary school-level mathematics. Educ. Stud. Math. 107, 71–91. doi: 10.1007/s10649-020-10020-1
Kollosche, D., and Meyerhöfer, W. (2021). COVID-19, mathematics education, and the evaluation of expert knowledge. Educ. Stud. Math. 108, 401–417. doi: 10.1007/s10649-021-10097-2
Kwon, O. N., Han, C., Lee, C., Lee, K., Kim, K., Jo, G., et al. (2021). Graphs in the COVID-19 news: A mathematics audit of newspapers in Korea. Educ. Stud. Math. 108, 183–200. doi: 10.1007/s10649-021-10029-0
Lave, J. (1988). Cognition in practice: Mind, mathematics and culture in everyday life. Cambridge, MA: Cambridge University Press.
Lesh, R. (2007). “Problem solving and modeling,” in Second handbook of research on mathematics teaching and learning: A project of the national council of teachers of mathematics, ed. F. K. Lester (Greenwich, NC: Information Age Pub.), 763–804.
Lesh, R., Doerr, H. M., Carmona, G., and Hjalmarson, M. (2003). Beyond constructivism. Math. Think. Learn. 5, 211–233. doi: 10.1080/10986065.2003.9680000
Leung, F. K. S. (2001). In search of an East Asian identity in mathematics education. Educ. Stud. Math. 47, 35–51. doi: 10.1023/A:1017936429620
Li, J., and Li, H. (2021). The role of context in the solving of real-world problems–a historical comparison of five editions of pep junior high school mathematics textbooks. J. Math. Educ. 30, 30–34+40.
Meyer, J. F. C. A., and Lima, M. (2023). Relevant mathematical modelling efforts for understanding COVID-19 dynamics: An educational challenge. ZDM – Math. Educ. 55, 49–63. doi: 10.1007/s11858-022-01447-2
Muğaloğu, E. Z., Kaymaz, Z., Mısır, M. E., and Laçin-Şimşek, C. (2022). Exploring the role of trust in scientists to explain health-related behaviors in response to the COVID-19 pandemic. Sci. Educ. (Dordr) 31, 1281–1309. doi: 10.1007/s11191-022-00323-5
Mutemeri, J. (2013). School knowledge and everyday knowledge: Why the binary conceptualization. J. Pan. Afr. Stud. 6, 86–99.
National Research Council (2012). Education for life and work: Developing transferable knowledge and skills in the 21st century. Ottawa, ONT: National Research Council.
Nemirovsky, R., Kelton, M. L., and Civil, M. (2020). “Toward a vibrant and socially significant informal mathematics education,” in Compendium for research in mathematics education, ed. J. Cai (Beijing: National Council of Teachers of Mathematics Reston), 968–979.
Nunes, T., Schliemann, A. D., and Carraher, D. W. (1993). Street mathematics and school mathematics. Cambridge, MA: Cambridge University Press.
Organisation for Economic Co-operation and Development [OECD] (2013). Skilled for life? Key findings from the survey of adult skills. Paris: OECD.
Organisation for Economic Co-operation and Development [OECD] (2021). PISA 2021 Mathematics Framework (Draft). Paris: OECD.
Oslington, G., Mulligan, J., and Van Bergen, P. (2020). Third-graders’ predictive reasoning strategies. Educ. Stud. Math. 104, 5–24. doi: 10.1007/s10649-020-09949-0
Pfannkuch, M., Ben-Zvi, D., and Budgett, S. (2018). Innovations in statistical modeling to connect data, chance and context. ZDM 50, 1113–1123. doi: 10.1007/s11858-018-0989-2
Rammstedt, B. (2013). Grundlegende kompetenzen erwachsener im internationalen vergleich: Ergebnisse von PIAAC 2012. Germany: Waxmann.
Reiss, M. J. (2020). Science education in the light of COVID-19. Sci. Educ. (Dordr) 29, 1079–1092. doi: 10.1007/s11191-020-00143-5
Rogoff, B. (1984). Introduction: Thinking and learning in social context. Cambridge, MA: Harvard University Press.
Saxe, G. B. (1982). “Culture and the development of numerical cognition: Studies among the oksapmin of papua new guinea,” in Children’s logical and mathematical cognition: Progress in cognitive development research, ed. C. J. Brainerd (Berlin: Springer), 157–176.
Van Den Heuvel-Panhuizen, M. (2003). The didactical use of models in realistic mathematics education: An example from a longitudinal trajectory on percentage. Educ. Stud. Math. 54, 9–35. doi: 10.1023/B:EDUC.0000005212.03219.dc
Van den Heuvel-Panhuizen, M., and Drijvers, P. (2014). “Realistic mathematics education,” in Encyclopedia of mathematics education, ed. S. Lerman (Dordrecht: Springer Netherlands), 521–525. doi: 10.1007/978-94-007-4978-8_170
Verschaffel, L., Schukajlow, S., Star, J., and Van Dooren, W. (2020). Word problems in mathematics education: A survey. ZDM 52, 1–16. doi: 10.1007/s11858-020-01130-4
Wang, J., and Lin, E. (2005). Comparative studies on US and Chinese mathematics learning and the implications for standards-based mathematics teaching reform. Educ. Res. 34, 3–13. doi: 10.3102/0013189X034005
Wijaya, A., van den Heuvel-Panhuizen, M., and Doorman, M. (2015). Opportunity-to-learn context-based tasks provided by mathematics textbooks. Educ. Stud. Math. 89, 41–65. doi: 10.1007/s10649-015-9595-1
Keywords: adapting to global challenges, formal mathematics, street mathematics, use of mathematics, mathematics literacy
Citation: Wang Y, Zhang L, Li N, Wang C and Wang L (2025) How Chinese citizens understand the inflection point of COVID-19 pandemic: insight into formal mathematics and street mathematics. Front. Educ. 10:1559007. doi: 10.3389/feduc.2025.1559007
Received: 11 January 2025; Accepted: 19 May 2025;
Published: 13 June 2025.
Edited by:
Subramaniam Ramanathan, Independent Scholar, Singapore, SingaporeReviewed by:
Pilar Ester, Camilo José Cela University, SpainManwai Yuen, The Education University of Hong Kong, Hong Kong SAR, China
Copyright © 2025 Wang, Zhang, Li, Wang and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lidong Wang, d2FuZ2xpZG9uZ0BibnUuZWR1LmNu
†These authors have contributed equally to this work and share first authorship
 Yi Wang
Yi Wang Lei Zhang
Lei Zhang Na Li
Na Li Chongyang Wang4
Chongyang Wang4 Lidong Wang
Lidong Wang