A three-stage exercise-oriented problem-based learning model for double-weak students in applied undergraduate education

In the context of mass higher education, Chinese application-oriented undergraduate institutions face significant teaching challenges stemming from the increasingly diverse student population. This study focuses on a representative group of “double-weak” students—learners with weak academic foundations and limited mathematical-logical skills in high school. Empirical research reveals that the traditional Project-Based Learning (PBL) model exhibits adaptability issues, such as insufficient foundational skill support and low knowledge transfer efficiency. To address these challenges, this study proposes an innovative “Exercise-Oriented” (E-O) instructional improvement framework, establishing a “three-stage progressive spiral” PBL improvement model. The model consists of: (1) Basic Computation Reinforcement Layer, which restructures mathematical cognitive systems through structured exercises; (2) Application and Practice Transition Layer, which facilitates the targeted transfer of knowledge to practical competencies through engineering case studies; and (3) Modeling and Innovation Expansion Layer, which fosters complex problem-solving abilities through open-ended problem scenarios. A one-semester teaching experiment demonstrated that the E-O-driven approach led to a 5.75% improvement in basic computational skills, an 8.25% increase in teamwork abilities, and a 9.80% enhancement in innovative thinking compared to the control group. This research not only provides a new paradigm for the localization of PBL theory but also contributes a Chinese solution to global research on development pathways for students with weak academic foundations. The findings have significant theoretical value and practical implications for promoting educational equity and improving teaching quality.

1 Introduction

The pedagogical concept of PBL (Sinclair and Brown, 1998; Hung et al., 2008) has been widely adopted in the field of education, particularly in higher education. A comprehensive review, analyzing 66 peer-reviewed articles, explored the relationship between critical thinking and PBL in higher education, revealing how critical thinking is conceptualized within the context of PBL and highlighting its central role within this pedagogical framework (Thorndahl and Stentoft, 2020). Other studies have also examined the impact of PBL on student learning outcomes and skill development. For example, a study compared the effectiveness of PBL vs. direct instruction in improving students' mathematical problem solving skills (Pohan et al., 2020), and another implemented PBL in a financial management course to improve students' autonomous learning and higher order thinking skills (Sugeng and Suryani, 2020), both validating the pedagogical advantages of PBL through quasi-experimental methods. Currently, research that focuses on the perceptions of medical and health science students about PBL has highlighted the importance of understanding students' attitudes toward this teaching method for its effectiveness (Kibret et al., 2021). In the field of mathematics education, studies have shown that students' critical thinking skills and learning styles are closely linked under the PBL framework, underscoring the need to consider individual differences in teaching practices (Susilo, 2022). Furthermore, PBL has been shown to significantly improve students' critical thinking and interdisciplinary problem solving abilities in subjects such as physics and science (Rahman et al., 2024). These studies collectively demonstrate the significant role of PBL in enhancing student learning outcomes, skill development, interdisciplinary analysis, and problem solving skills, providing theoretical support for its widespread application in diverse educational settings.

Case-Based Learning (CBL), as one of the core instructional approaches within the PBL framework, was first introduced by McMaster University in Canada in 1969 (Neufeld and Barrows, 1974; Barrows, 1986). Since then, PBL and CBL have gained widespread attention and adoption in medical education across the United States, Europe, the United Kingdom, and other regions (Azer and Azer, 2015; McKendree, 2010). Recognized for their effectiveness in fostering clinical reasoning and practical problem-solving skills, these models became essential components of medical education. In the late 1980s, Chinese medical schools began experimenting with PBL and CBL, gradually developing localized adaptations. After decades of development, these methods have become integral to Chinese medical education, gaining recognition for their role in cultivating competent healthcare professionals (Dolmans et al., 2005; Nair et al., 2013). Numerous studies have highlighted their educational value. For instance, a Japanese study demonstrated that PBL enhances students' problem-solving and communication skills essential for addressing complex social issues (Itatani et al., 2017). Similarly, domestic research by Li et al. (2021) found that a competency-oriented approach combined with CBL not only improves students' professional knowledge and language expression abilities but also strengthens interpersonal communication and teamwork skills, making it an innovative and effective approach for medical education. Furthermore, Wang et al. (2021) emphasized the complementary strengths of these models, where PBL significantly enhances independent learning in theoretical courses, and CBL proves more effective during clinical internships, enabling students to diagnose and develop treatment plans for real-world cases. These findings underscore the necessity of integrating adaptive, student-centered, and competency-oriented teaching models that balance theoretical knowledge with practical clinical training, ultimately optimizing educational outcomes and better preparing medical students for the complex demands of modern healthcare environments.

These findings underscore the necessity of adopting flexible, student-centered, and competency-oriented teaching models that achieve a balance between theoretical knowledge and practical clinical training, thereby optimizing educational outcomes and better preparing students for the complex challenges of modern healthcare environments. Inspired by the successful application of case-based teaching in medical education, this study seeks to extend this approach to the teaching of mathematics for university students. We propose the E-O teaching model, which focuses on problem-solving in mathematics, aiming to provide theoretical support and foster innovation across various professional fields and industries.

In recent years, the massification of higher education has resulted in an increasing number of students entering universities with weak foundational knowledge, particularly in subjects such as mathematics, which are highly theoretical in nature. This shift can be attributed to the loosening of selection criteria at the secondary education level and the rising number of university enrollments. As higher education systems have expanded, the student population has become more diverse, with many students lacking the necessary preparation for higher-level academic work, especially in mathematically demanding courses. Research indicates that the rapid growth and diversification of student bodies, along with changes in institutional structures, have led to significant challenges in maintaining educational quality (Tight, 2019; Guri-Rosenblit et al., 2007). One of the major consequences is a decline in student motivation, particularly among those who enter university without adequate academic preparation (Ganah, 2012). This is especially evident in mathematics education, where the absence of solid mathematical foundations hinders students' ability to engage with complex concepts and develop essential problem-solving skills (Lake et al., 2017; Albeshree et al., 2022).

Studies have pointed out that pre-university mathematics skills are crucial for student retention and success in higher education mathematics, and a focus on these skills, rather than just targeting at-risk groups, can lead to better outcomes (Lake et al., 2017). In response to these challenges, higher education institutions are increasingly exploring and implementing innovative pedagogical strategies to address the gaps in students' mathematical competencies. For instance, interdisciplinary approaches incorporating technology and creative teaching methods have shown promise in enhancing student understanding and performance in mathematics (Albeshree et al., 2022). Furthermore, the importance of diagnostic tools for identifying students' mathematical backgrounds and providing tailored interventions has been widely acknowledged (Lake et al., 2017). With the increasing integration of data-driven tools and algorithmic modeling into instructional design, recent discussions (Chan and Lo, 2025) have emphasized the need for ongoing attention to ethical considerations such as transparency and privacy when leveraging modern educational technologies. These efforts aim to bridge the gap caused by the foundational weaknesses of many students, which is essential for improving the overall quality of mathematics education and fostering greater engagement in STEM disciplines (Pampaka et al., 2012; Anthony and Walshaw, 2008).

In the context of this study, we define PBL in mathematics education as a structured, exercise-oriented instructional approach in which students engage with progressively complex mathematical problems—ranging from basic computations to real-world applications and open-ended modeling tasks. This variant of PBL maintains the core principles of student-centered learning, problem-solving, and knowledge construction, while adapting them to the cognitive characteristics of mathematical learning through a tiered structure of guided practice.

However, the varying nature of disciplines necessitates the design of teaching approaches that are tailored to the students' foundational knowledge, disciplinary background, and intellectual reserves, oriented around thoughtfully crafted exercises. Students with weaker foundations often encounter significant challenges in mathematics courses due to inadequate learning abilities and a lack of confidence. Basic computational problems help students to master mathematical formulas and operations solidly. By integrating mathematical knowledge with their professional backgrounds, students' interest in learning and their application skills are enhanced. Designing specific applied problems that relate mathematics to the students' professional fields allows them to appreciate the practical value and disciplinary allure of mathematical knowledge. This nurtures students' innovative abilities, laying a foundation for subsequent academic studies and research. Through the creation of innovative modeling problems, students are guided to incorporate creative thinking in solving open-ended problems, deepening their understanding of mathematical concepts while gradually developing habits of independent thought and critical analysis.

2 Methods and materials

2.1 E-O driven teaching model

Drawing from both domestic and international research on PBL, it is evident that PBL significantly enhances the comprehensive and applied capabilities of students. However, due to the highly theoretical nature of mathematics, PBL requires further adjustments and optimization. Mathematics not only necessitates the drive from applied problems but also needs a focus on the development of basic computational skills, theoretical proof abilities, and rigorous logical thinking. Therefore, we propose an E-O learning strategy based on PBL, which retains the problem-orientation advantages of PBL while emphasizing differentiation on three levels: basic computational exercises to solidify core knowledge, professional background application problems to enhance knowledge transferability, and innovative modeling problems to cultivate comprehensive analytical and creative skills. The layered exercise design of E-O not only addresses the deficiencies of PBL in the discipline of mathematics but also provides students with a comprehensive skill development pathway from basics to innovation. The project centers around the core concept of E-O, systematically constructing a mathematical teaching system with three types of problem categories, aiming to comprehensively enhance the mathematical learning outcomes of undergraduates with weaker foundations. These problem types include basic computational problems, professional background application problems, and innovative modeling problems, each designed to improve the learning outcomes of students with weaker foundations. Within the project, E-O is defined as addressing students' weaknesses in mathematical foundations, professional application abilities, and innovative capacities through targeted exercises. The focus is on building three core types of problems around the E-O teaching model to tackle the primary difficulties faced by students with weak mathematical foundations. The challenge lies in the design of these three problem types, with critical difficulties.

Moreover, the three components of the E-O model—basic computation, professional application, and innovative modeling—are closely aligned with the key phases of the problem-based learning (PBL) process. The basic computational tasks support knowledge acquisition and consolidation, similar to the early stages of PBL. The professional application problems emphasize contextual transfer of knowledge, which reflects the applied practice phase in PBL. Finally, the open-ended modeling tasks promote creativity, inquiry, and collaboration, echoing the advanced PBL stages where learners engage in complex problem-solving. This layered design ensures that the E-O model meets the cognitive demands of mathematics education while remaining grounded in the essential principles of problem-based learning.

• Construction of a Basic Calculation Question Bank. This involves covering key concepts with questions on topics such as integration, matrix operations, and probability distributions. The difficulty levels are tiered to ensure that students of various learning levels can find appropriate exercises. The question bank is dynamically updated based on classroom feedback and error logs to optimize content and supplement with commonly mistaken and frequently tested points.

• Development and Effective Teaching Design of Professional Background Application Questions. Scenario design, such as analyzing temperature changes during fermentation processes using differential equations to predict optimal fermentation times; combining interest and practicality, problem designs incorporate real data or background stories, like using a brewery's production data to analyze the relationships between variables; teaching strategies, adopting a “problems first, explanation second” approach in the classroom to encourage students to start with problems and attempt to solve them independently, enhancing their ability to transfer knowledge.

• Mathematical Modeling Questions to Guide Innovative Thinking. Open-ended problem design, like creating an “optimization model for the brewing production process,” where students analyze the interactions between multiple variables and propose optimization strategies; data-driven practice, providing real data and using statistical methods to predict production efficiency for the next quarter; results presentation and sharing, where students share their modeling results through reports, presentations, or team discussions, showcasing their thought processes and solutions.

These problem types complement each other, collectively facilitating students' progress from mastering fundamental knowledge to enhancing application skills and developing innovative thinking.

2.2 Methods

The project is centered around the E-O approach, through which a tiered system of mathematical problems is constructed to address the main difficulties encountered by students with weak foundations in mathematics, aiming to comprehensively enhance their learning outcomes. The main components of the project include three parts: the design and training model for basic computation questions, the development of professional background application questions, and the design and guidance plans for innovative mathematical modeling questions.

2.2.1 Basic calculation question bank

Basic computation questions are the cornerstone of mathematical learning, with the core goal of helping students proficiently master fundamental mathematical skills to establish a solid foundation for further study. Tailored for students with weak foundations and difficulty in memorizing formulas, the design of basic computation questions focuses on hierarchical content. Questions are organized from simple to complex, ensuring students can progressively grasp the material. Moreover, to reinforce memory, the mastery of mathematical formulas requires frequent repetitive practice; hence, the project includes a systematic question bank that covers core computation problems in calculus, linear algebra, and probability theory. The project also draws on basic problem types from mathematical competitions to design slightly challenging computation questions, appropriately increasing the difficulty to enhance students' thinking abilities. Additionally, error notebooks and periodic tests are implemented as part of an error recording and feedback mechanism, assisting students in timely identifying and correcting their weaknesses.

2.2.2 Professional background application questions

Mathematics, as a universal tool, is valued for its ability to solve real-world problems. In line with professional backgrounds, particularly in applications such as brewing, a series of application questions have been designed to enhance students' interest in learning and their mathematical application skills. The problem design integrates professional scenarios, such as calculating the curve of alcohol concentration changes, analyzing temperature changes during fermentation, and predicting the relationship between yield and time. This interdisciplinary approach combines mathematics with chemistry and biology to design comprehensive problems, like using distribution models from probability theory to analyze microbial growth patterns or using linear algebra to optimize production costs. The questions emphasize practicality and interest, incorporating real data and background stories to enhance their appeal and realism. For example, students might analyze fermentation data from a brewery to assess the impact of fermentation time on alcohol yield. The project breaks down complex application questions and guides students step-by-step. Initially, students might perform simple curve-fitting tasks, then move on to optimization and decision-making based on contextual conditions, helping them gradually understand the core logic of the problems. Additionally, the project focuses on developing problem-modeling skills by guiding students to transform real-world issues into mathematical models, such as using calculus to describe processes or matrix equations for optimization, thus building a bridge between mathematics and practical application.

2.2.3 Mathematical modeling questions

Developing innovative capabilities is one of the core objectives of the project. The modeling tasks are open-ended and comprehensive, with no standard answers, requiring students to synthesize knowledge from calculus, linear algebra, and probability theory. For example, students might design an “energy efficiency optimization model for a brewery,” analyzing the relationships between multiple variables to propose optimization strategies. The project also emphasizes practical application and data analysis; innovation questions involve real data to guide students in data processing and analysis. For instance, students could be given production data from a factory to create a statistical model predicting the output for the next cycle. Furthermore, the project fosters teamwork and collaborative division of labor by organizing students into groups where they share ideas and inspire each other during discussions. Teamwork not only enhances problem-solving capabilities but also cultivates communication and collaboration skills. Additionally, the project encourages innovative thinking and the presentation of results, guiding students to develop unique approaches and solutions, and to share their findings through presentations.

Centered around the E-O approach, a tiered and diverse system of questions is constructed. The process involves specialized design, student-driven practice, teacher explanations, and reflective summarization to gradually enhance student capabilities. The specialized design covers three main types of problems: basic computational issues, professional background application problems, and innovative modeling challenges, each centered around a core issue to ensure coherence of knowledge points and a gradient of difficulty levels. For example, a calculus topic might start from basic integral calculations and progress to complex curve modeling, gradually increasing students' understanding and application skills. Students consolidate their knowledge through repeated practice of basic computation questions; delve deeper into the practical value of mathematics through professional background application problems; and expand their thinking boundaries through innovative modeling problems. Teacher explanations focus on deciphering typical problem-solving approaches and methodologies, aiming not only to aid understanding but also to guide deeper thinking about the underlying logic of problems. Reflective summaries help students consolidate knowledge, correct mistakes, and enhance problem-solving efficiency. Students organize incorrect solutions, and teachers optimize question designs through feedback mechanisms, forming a virtuous cycle. This teaching reform idea is structured into eight segments, creating a complete closed-loop research system, as illustrated in Figure 1.

Figure 1

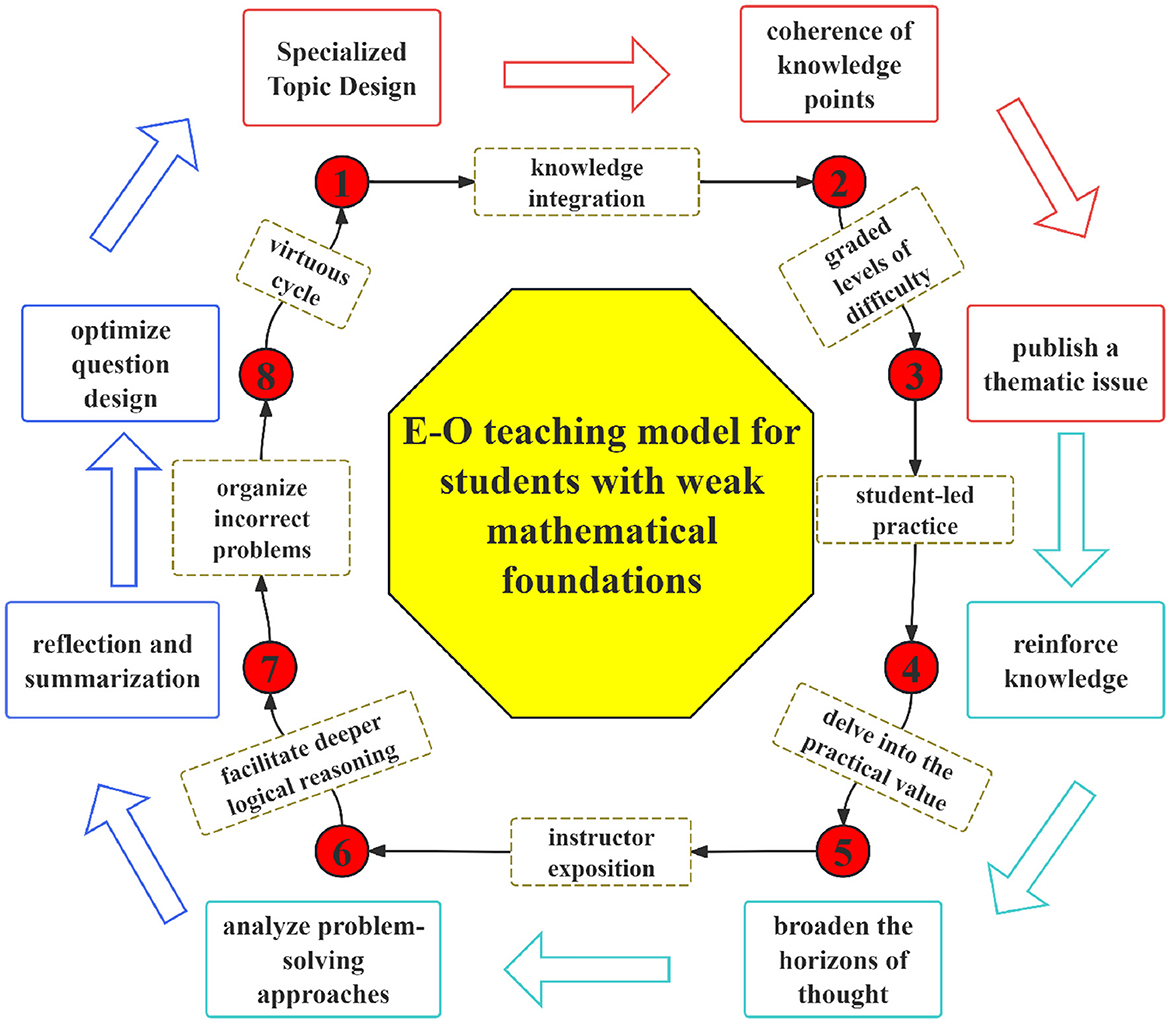
Figure 1. Closed-loop diagram for the E-O teaching model targeting students with weak mathematical foundations.

3 Example of the E-O teaching model

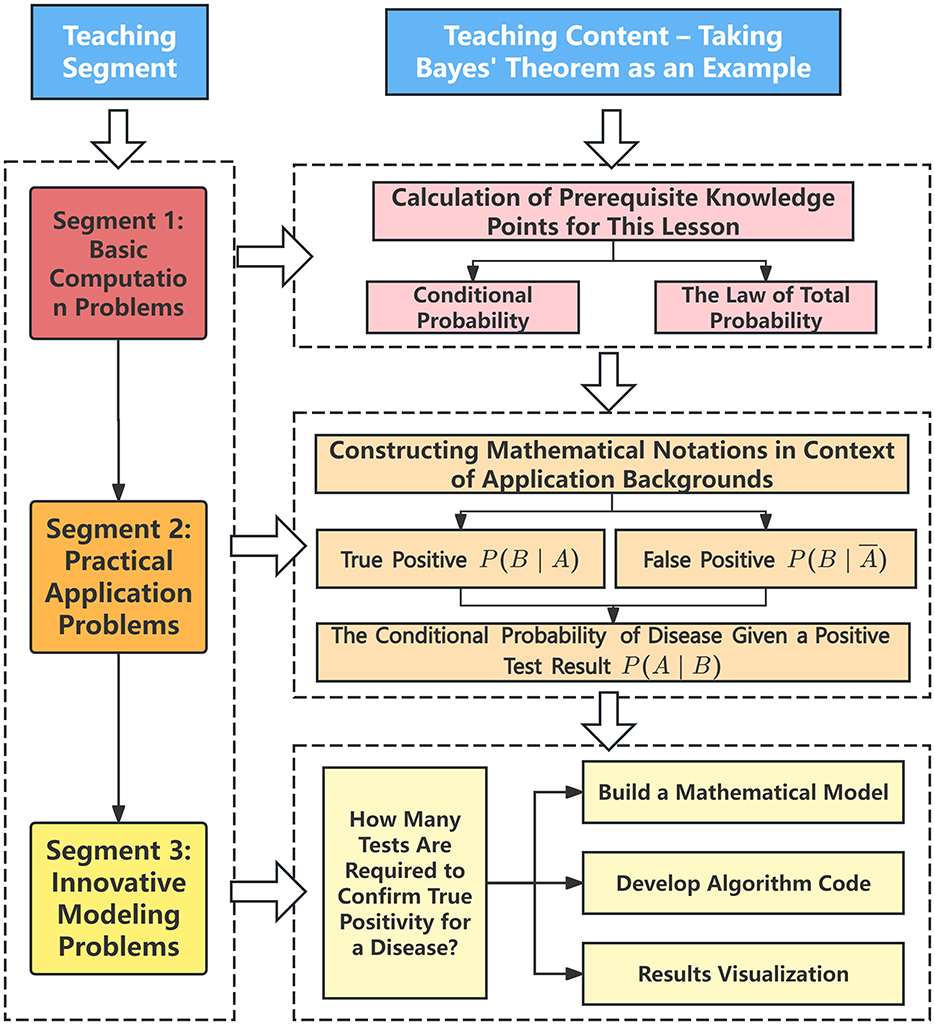
The E-O teaching model is a “problem-solving” based teaching approach. In university mathematics courses, while solving application problems is emphasized, mastering theoretical operations and memorizing formulas are equally important. Figure 2 illustrates the E-O teaching model based on the PBL concept.

Figure 2

Figure 2. Segmented teaching framework Using Bayes' Theorem as a case study.

The designed application problem is as follows:

In a certain region, a new type of flu has emerged, but the probability of contracting the disease is very low—only 0.5% (i.e., 5 out of 1,000 people are infected). A doctor uses a rapid testing method, but the test is not perfect:

Sensitivity (TPR): if the individual is infected, there is a 65% chance the test will show positive. Specificity (TNR): if the individual is not infected, there is a 50% chance the test will show negative. Suppose a person's first test result is positive.

• Problem 1: based on the first test result, what is the probability that the individual is actually infected? (Use Bayes' theorem for the calculation.)

• Problem 2: if the individual continues independent repeated tests, and each test result is positive, how many tests are required at minimum to increase the probability of infection to 99%?

The questions are published, and students begin to think about and solve them through online teaching platforms such as Learning Pass (or other network-based systems).

First segment: basic computation problems—calculation exercises on conditional probability and the law of total probability.

Second segment: Practical application problems—using the context of medical infectious diseases, students apply conditional probability and the law of total probability to calculate the probability of actual infection given a positive test result P(A∣B).

• P(A) = 0.005, The probability that an individual in this region is infected with the disease.

• P(B∣A) = 0.650, The sensitivity of the test, that is, the probability of being positive if the individual is infected.

• $P(B\mid \overline{A})=0.500$, The specificity of the test, that is, the probability of being positive if the individual is not infected.

Teacher explains Bayes' Theorem:

$\begin{array}{l}P(A\mid B)=\frac{P(AB)}{P(B)}=\frac{P(B\mid A)·P(A)}{P(A)P(B\mid A)+P(\overline{A})P(B\mid \overline{A})}=0.00649\end{array}$

Third segment: innovative modeling problems—calculate the minimum number of independent repeated tests required to raise the probability of being infected to 99%. This requires iterative computation of the probability of being infected after each test, using the previously computed probability as the new prior probability in each iteration.

The model is constructed as follows:

• Step 1: initialize the conditions.

• Step 2: calculate the probability of being infected after the first test.

• Step 3: iteratively update the probability of being infected.

• Step 4: set the termination condition (when the probability reaches 99%).

• Step 5: output the result.

Based on the steps and objectives of the model, Algorithm 1 is provided as follows.

Algorithm 1

Algorithm 1. Calculate required test count for target disease probability.

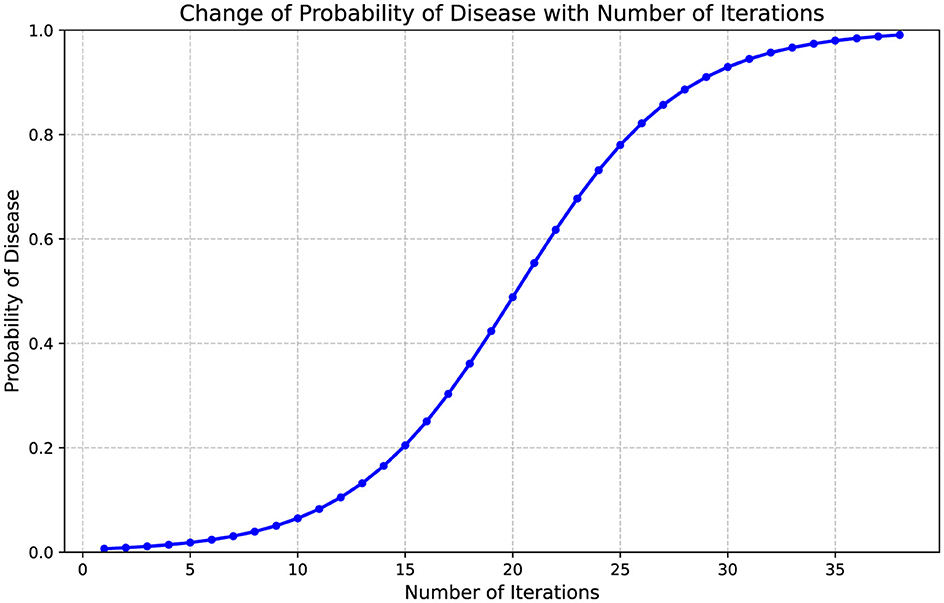
Run the code and plot the graph of iterations vs. probability of disease. Through the simulation of the model, it is determined that at least 38 iterations are required to confirm a disease probability of 99%, as shown in Figure 3.

Figure 3

Figure 3. Change of probability of disease with number of iterations.

3.1 Participants

Our study focuses on second-year undergraduate students in the field of Economic Management, specifically within the course of Probability Theory and Mathematical Statistics. Different teaching models were applied to various classes; one utilizes a traditional problem-oriented approach combined with lecture-based teaching, while the other adopts a PBL (Project-Based Learning) based E-O driven teaching model that emphasizes more class time devoted to students.

The study adopts a quasi-experimental design involving two distinct teaching groups to evaluate the effectiveness of the proposed E-O teaching model.

3.1.1 Participant groups

Experimental group: the class instructed by the first author of this paper, who implemented the E-O teaching model throughout the semester. This model emphasized interactive problem-solving sessions, competency-oriented assessments, and integrated case studies to enhance mathematical understanding and reasoning skills. Control group: the class instructed by the second author of this paper, employing traditional teaching methods that focused primarily on lecture-based instruction and independent problem-solving exercises.

3.1.2 Experimental procedure

The experiment was conducted over the course of one academic semester. Both groups were assessed using identical assessment frameworks, which included:

Formative assessments: weekly quizzes and in-class problem-solving tasks to evaluate students' computational accuracy, conceptual understanding, and engagement levels. Summative assessments: a comprehensive final examination assessing higher-order thinking skills, including logical reasoning and problem modeling.

3.1.3 Evaluation metrics

To provide a comprehensive assessment of student learning outcomes, the following metrics were adopted:

Basic computational ability: measurement of students' accuracy and efficiency in solving standard mathematical problems. Team collaboration ability: evaluation of students' performance in group activities, including communication, role distribution, and collaborative problem-solving. Innovative thinking ability: assessment of students' ability to approach novel mathematical problems and develop creative solutions.

4 Discussion

4.1 Summary of experimental outcomes

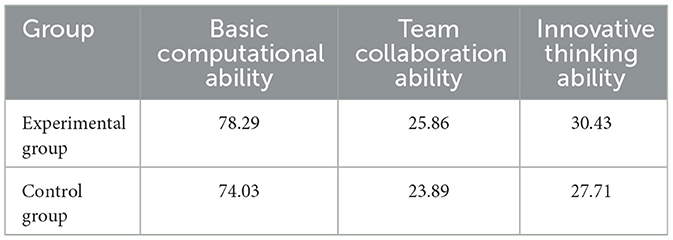
The effectiveness of the E-O teaching model was assessed by comparing students' performance across three dimensions: basic computational ability, team collaboration ability, and innovative thinking. Table 1 summarizes the comparative results between the experimental and control groups, revealing significant improvements in the experimental group across all assessment dimensions.

Table 1

Table 1. Assessment results of different abilities between the experimental and control groups.

The results demonstrate that the experimental group outperformed the control group in all assessment dimensions. The implementation of the E-O teaching model led to a 5.7% improvement in basic computational ability, an 8.2% increase in team collaboration ability, and a 9.8% enhancement in innovative thinking ability. These findings highlight the efficacy of integrating collaborative and competency-oriented teaching models in mathematics education.

4.2 Interpretation of learning gains

This study demonstrates the effectiveness of the E-O teaching model in enhancing students' mathematical competency and problem-solving skills. Through detailed analysis and comparative assessments, the following insights were drawn:

• Enhancement of basic computational skills: the frequent practice of foundational mathematical problems within a structured framework allowed students to grasp key formulas and computational methods proficiently. The tiered design of exercises, ranging from simple to complex, provided an incremental learning path that mitigated memory difficulties and operational inefficiencies. As reflected in the experimental results, the experimental group showed a significant improvement in their basic computational abilities, fostering greater learning confidence.

• Strengthening of professional application abilities: the incorporation of application-oriented problems designed around real-world professional contexts enabled students to bridge the gap between theoretical mathematics and practical problem-solving. By translating real-life problems into mathematical models and developing solutions, students enhanced their knowledge transfer capabilities. The experimental results revealed superior performance in this area compared to the control group, indicating that the E-O model is conducive to cultivating students' ability to apply mathematical knowledge to professional scenarios.

• Cultivation of innovative thinking and comprehensive abilities: the introduction of open-ended innovative modeling problems encouraged students to explore multiple solution strategies, thereby improving their logical reasoning and creativity. The experimental group's superior results in the assessment of innovative thinking ability highlight the importance of integrating such open-ended tasks in mathematics education. This approach not only enhanced students' critical thinking skills but also laid a solid foundation for future academic research and professional development.

Overall, the PBL-based E-O instructional model significantly enhances the mathematical performance of students with weak academic foundations. By implementing a tiered sequence of learning activities—ranging from repeated practice with basic computational tasks to application-based problems that foster knowledge transfer, and culminating in open-ended modeling tasks for solving real-world problems—the model effectively strengthens students' conceptual understanding, practical application skills, and overall problem-solving competence.

4.3 Implications for model scalability and adaptation

The discussion of these findings underscores the necessity for educational models that go beyond traditional instruction to foster a balance between foundational knowledge, practical application, and innovative problem-solving capabilities. Beyond its demonstrated effectiveness in instructional outcomes, the current implementation of the E-O model was designed for small-class settings, where instructors had sufficient time and capacity to provide individualized, face-to-face problem-based guidance. This structure allowed for effective exercise-driven teaching tailored to each student. However, future development of the E-O model should take into account its adaptability to other contexts, such as fully online or blended learning environments. In large-enrollment courses or resource-constrained institutions, it will be necessary to leverage online platforms and incorporate intelligent exercise-generation systems to extend the model's reach and ensure broader accessibility for diverse learners.

5 Conclusions

This study explored the application of the E-O teaching model in mathematics education and assessed its effectiveness through a comparative experimental design. The findings indicate that this model significantly enhances students' basic computational skills, professional application abilities, and innovative thinking. The tiered instructional structure effectively consolidated students' mathematical foundations and improved their problem-solving proficiency, while the integration of real-world applications bridged the gap between theoretical knowledge and practical challenges, fostering knowledge transfer abilities. Furthermore, the inclusion of open-ended problem designs stimulated creativity and logical reasoning, equipping students with essential skills for future academic and professional development.

These findings underscore the value of adopting innovative, student-centered, and competency-oriented teaching models that balance foundational knowledge, application skills, and problem-solving capabilities. Future research should investigate the adaptability of the E-O model across diverse academic disciplines and educational contexts to better address varying student needs and optimize educational outcomes. As data-driven instructional models become increasingly embedded in digital learning environments, future iterations of the E-O model may incorporate algorithmic simulations or learning analytics. Integrating ethical principles—such as data collection practices, privacy-by-design, and human-centered oversight—into its development will support the model's responsible evolution in technologically enhanced contexts.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

XH: Data curation, Methodology, Writing – original draft, Writing – review & editing. YH: Writing – review & editing. LC: Data curation, Methodology, Resources, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This project is funded by the Education Department of Guizhou Province under the Educational Teaching Research and Reform Project, Project Number: 2024C066; the Teaching Reform Project of Moutai Institute, Project Number: MTXYJG-2025018; and the Project of Reforming the Undergraduate Teaching Content and Curriculum System in Higher Education Institutions of Guizhou Province, Project Number: GZJG2024035.

Acknowledgments

We would like to express our sincere gratitude to all the participants in this study and the teachers from various departments who supported this work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Albeshree, F., Al-Manasia, M., Lemckert, C., Liu, S., and Tran, D. (2022). Mathematics teaching pedagogies to tertiary engineering and information technology students: a literature review. Int. J. Math. Educ. Sci. Technol. 53, 1609–1628. doi: 10.1080/0020739X.2020.1837399

Crossref Full Text | Google Scholar

Anthony, G., and Walshaw, M. (2008). “Characteristics of effective pedagogy for mathematics education,” in Research in Mathematics Education in Australasia 2004–2007, eds. H. Forgasz, T. Barkatsas, A. Bishop, B. Clarke, P. Sullivan, S. Keast, W. T. Seah and S. Willis (Rotterdam: Sense Publishers), 195–222.

Google Scholar

Azer, S. A., and Azer, D. (2015). Group interaction in problem-based learning tutorials: a systematic review. Eur. J. Dent. Educ. 19, 194–208. doi: 10.1111/eje.12121

PubMed Abstract | Crossref Full Text | Google Scholar

Barrows, H. S. (1986). A taxonomy of problem-based learning methods. Med. Educ. 20, 481–486. doi: 10.1111/j.1365-2923.1986.tb01386.x

PubMed Abstract | Crossref Full Text | Google Scholar

Chan, H. W. H., and Lo, N. P. K. (2025). A study on human rights impact with the advancement of artificial intelligence. J. Posthumanism 5, 1114–1153. doi: 10.63332/joph.v5i2.490

Crossref Full Text | Google Scholar

Dolmans, D. H., De Grave, W., Wolfhagen, I. H., and Van Der Vleuten, C. P. (2005). Problem-based learning: future challenges for educational practice and research. Med. Educ. 39, 732–741. doi: 10.1111/j.1365-2929.2005.02205.x

PubMed Abstract | Crossref Full Text | Google Scholar

Ganah, A. (2012). Motivating weak students: a critical discussion and reflection. Education 133, 248–258.

Google Scholar

Guri-Rosenblit, S., Sebková, H., and Teichler, U. (2007). Massification and diversity of higher education systems: interplay of complex dimensions. High. Educ. Policy 20, 373–389. doi: 10.1057/palgrave.hep.8300158

Crossref Full Text | Google Scholar

Hung, W., Jonassen, D. H., and Liu, R. (2008). “Problem-based learning,” in Handbook of Research on Educational Communications and Technology, 3rd Edn, eds. J. M. Spector, M. D. Merrill, J. J. G. van Merriënboer, and M. P. Driscoll (New York, NY: Routledge), 485–506.

Google Scholar

Itatani, T., Nagata, K., Yanagihara, K., and Tabuchi, N. (2017). Content analysis of student essays after attending a problem-based learning course: facilitating the development of critical thinking and communication skills in japanese nursing students. Healthcare 5:47. doi: 10.3390/healthcare5030047

PubMed Abstract | Crossref Full Text | Google Scholar

Kibret, S., Teshome, D., Fenta, E., Hunie, M., Taye, M. G., Fentie, Y., et al. (2021). Medical and health science students' perception towards a problem-based learning method: a case of debre tabor university. Adv. Med. Educ. Pract. 12, 781–786. doi: 10.2147/AMEP.S316905

PubMed Abstract | Crossref Full Text | Google Scholar

Lake, W., Wallin, M., Woolcott, G., Boyd, W., Foster, A., Markopoulos, C., et al. (2017). Applying an alternative mathematics pedagogy for students with weak mathematics: meta-analysis of alternative pedagogies. Int. J. Math. Educ. Sci. Technol. 48, 215–228. doi: 10.1080/0020739X.2016.1245876

Crossref Full Text | Google Scholar

Li, H., Sun, J., Zhou, Y., Ding, S., Guo, Y., Jiang, Q., et al. (2021). The utility of competency-oriented clinical laboratory teaching combined with case-based learning (CBL). Clin. Chem. Lab. Med. 59, 1784–1789. doi: 10.1515/cclm-2021-0467

PubMed Abstract | Crossref Full Text | Google Scholar

McKendree, J. (2010). Experiences of problem-based learning in the UK. Clin. Teach. 7, 262–265. doi: 10.1111/j.1743-498X.2010.00385.x

PubMed Abstract | Crossref Full Text | Google Scholar

Nair, S. P., Shah, T., Seth, S., Pandit, N., and Shah, G. (2013). Case based learning: a method for better understanding of biochemistry in medical students. J. Clin. Diagn. Res. 7:1576. doi: 10.7860/JCDR/2013/5795.3212

PubMed Abstract | Crossref Full Text | Google Scholar

Neufeld, V. R., and Barrows, H. S. (1974). The “mcmaster philosophy:” an approach to medical education. Acad. Med. 49, 1040–1050. doi: 10.1097/00001888-197411000-00004

Crossref Full Text | Google Scholar

Pampaka, M., Williams, J., Hutcheson, G., Wake, G., Black, L., Davis, P., et al. (2012). The association between mathematics pedagogy and learners' dispositions for university study. Br. Educ. Res. J. 38, 473–496. doi: 10.1080/01411926.2011.555518

PubMed Abstract | Crossref Full Text | Google Scholar

Pohan, A. M., Asmin, A., and Menanti, A. (2020). The effect of problem based learning and learning motivation of mathematical problem solving skills of class 5 students at sdn 0407 mondang. Budap. Int. Res. Crit. Linguist. Educ. J. 3, 531–539. doi: 10.33258/birle.v3i1.850

Crossref Full Text | Google Scholar

Rahman, A., Ilwandri, I., Santosa, T. A., Gunawan, R. G., Suharyat, Y., Putra, R., et al. (2024). Effectiveness of problem-based learning model in science learning: a meta-analysis study. Int. J. Educ. Lit. 3, 62–74. doi: 10.55606/ijel.v3i1.64

Crossref Full Text | Google Scholar

Sinclair, M., and Brown, G. (1998). Project-based learning. NT Learn. Curve 2:4.

Google Scholar

Sugeng, B., and Suryani, A. W. (2020). Enhancing the learning performance of passive learners in a financial management class using problem-based learning. J. Univ. Teach. Learn. Pract. 17:5. doi: 10.53761/1.17.1.5

Crossref Full Text | Google Scholar

Susilo, B. E. (2022). Students' mathematical critical thinking ability in problem-based learning viewed based on learning style. J. Elemen 8, 187–200. doi: 10.29408/jel.v8i1.4536

Crossref Full Text | Google Scholar

Thorndahl, K. L., and Stentoft, D. (2020). Thinking critically about critical thinking and problem-based learning in higher education: a scoping review. Interdiscip. J. Problem-Based Learn. 14:28773. doi: 10.14434/ijpbl.v14i1.28773

Crossref Full Text | Google Scholar

Tight, M. (2019). Mass higher education and massification. High. Educ. Policy 32, 93–108. doi: 10.1057/s41307-017-0075-3

Crossref Full Text | Google Scholar

Wang, H., Xuan, J., Liu, L., Shen, X., and Xiong, Y. (2021). Problem-based learning and case-based learning in dental education. Ann. Transl. Med. 9:1137. doi: 10.21037/atm-21-165

PubMed Abstract | Crossref Full Text | Google Scholar