Counting and subitizing skills in children with Down syndrome and autism spectrum disorder

Introduction: Previous studies have shown that the disability characteristics of Down syndrome (DS) and autism spectrum disorder (ASD) may affect the development of counting and subitizing skills.

Methods: In this study, two tasks were conducted to examine the development of counting and subitizing skills in children with intellectual disabilities, including DS and ASD, and the results were compared with the performance of typically developing (TD) children.

Results: The maximum countable number attained by children with DS was considerably lower than that of children with ASD. However, the subitizing range of children with DS was not substantially different from that of children with ASD or TD children, suggesting that the subitizing abilities of children with DS may be relatively well-developed. Although it was predicted that children with ASD would exhibit characteristic counting strategies such as frequent pointing and a smaller subitizing range, the results were not in line with the hypotheses.

Discussion: These results indicate that children with intellectual disabilities may show more specific developmental trajectories related to counting and subitizing based on disability type (DS and ASD). Moreover, children with DS may exhibit developmental variation between the two processes, as they are often able to subitize quantities consistent with their mental age yet demonstrate difficulty when counting a higher number of objects than the subitizing range.

1 Introduction

There are two ways to determine the total number of items in a collection as a cardinal value: counting and subitizing (Paliwal and Baroody, 2020), which are developmentally distinct processes (Benoit et al., 2004).

Counting is the operation in which, to specify the numerosity of any group of objects, each object in that group is paired successively with a numeral from the numeral-series (Kaufman et al., 1949). Meanwhile, the term “subitizing” was introduced into the field of psychology by Kaufmann and his colleagues (Desoete et al., 2009; Katzin et al., 2019). They defined subitizing as the process of specifying a total number of less than six objects accurately, rapidly, and confidently without counting each individual object (Kaufman et al., 1949).

Fast reaction times (RTs) and high accuracy rates thus define the process of subitizing. Meanwhile, when groups of six and above are enumerated, the process is more time-consuming, less accurate, and carried out with less confidence (Katzin et al., 2019). Therefore, there is a difference between subitizing and counting in the number that can be accurately achieved.

Historically, studies have focused on counting rather than subitizing (Starkey and McCandliss, 2021) and explored the development of children’s counting ability, primarily in how the accuracy of counting increases. For example, the smaller the number of items, the more accurately children can count that number, with even some three-year-olds being able to count two to three items correctly (Gelman and Gallistel, 1978). By the end of preschool, the percentage of correct responses to a task that asks for count a single-digit number of items reaches 96% (Le Fevre et al., 2006).

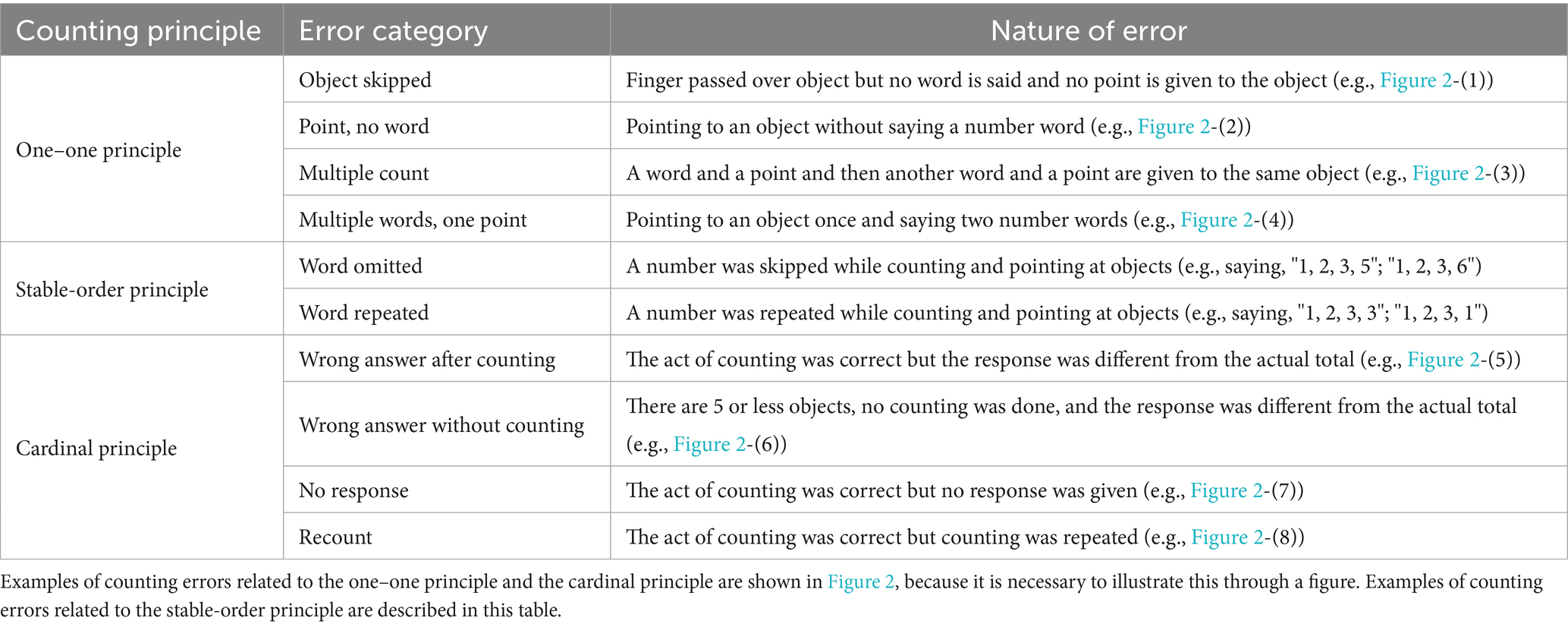
Children must understand five principles to count correctly (Gelman and Gallistel, 1978). (1) the one–one principle (every number-word assigned to each item must be one distinct number-word); (2) the stable-order principle (number tags must follow a consistent sequence); (3) the cardinal principle (the last number-word assigned to the last item must represent the total number of objects in the set); (4) the abstraction principle (any kind of object can be counted), and (5) the order-irrelevance principle (objects can be counted in any order).

The first three, known as the “how-to-count” principles, outline the fundamental rules of counting. Any procedures that violate these three fundamental counting principles cause various errors (Gelman and Gallistel, 1978). According to Fuson et al. (1988), these errors include skipping an item or counting an item twice, corresponding to the first principle. Errors in which children count using number words in the wrong order, such as saying “1, 2, 6,” correspond to the second principle (Gelman and Gallistel, 1978). Maruyama and Mutou (1997) found that violations pertaining to the third principle occur when the total number of items not being represented as a cardinal value after correct number-word assigning to each item or the act of counting was repeated, which Porter called “repeat sequence or recount” (Porter, 1999a).

The research on subitizing examines the developments in the maximum number of elements that can be subitized, or the subitizing range (Jansen et al., 2014). Studies on four-to-six-year-old children have shown that their subitizing range generally reaches three, and that they tend to count for sets of more than four items (Formoso et al., 2017; Jansen et al., 2014). It has been noted that the subitizing range expands with chronological age (CA). The longitudinal study focusing on the frequency of subitizing found that children who were in kindergarten or first grade tend to range from a skill level in which two is subitized consistently and three is subitized most of the time to a level in which four is subitized consistently (Starkey and McCandliss, 2021). By second or third grade, some children may occasionally be able to subitize five, and most children’s subitizing ranges will increase over time (Starkey and McCandliss, 2021). However, the range of numerosities that can be subitized depends on the paradigm employed, stimulus properties, input surface, individual differences, and the statistical technique used to calculate the subitizing range (Chen et al., 2022).

Both counting and subitizing are early foundations for mathematics (Jordan and Levine, 2009). For instance, children’s counting skills before formal schooling are predictive of the acquisition of basic arithmetical skills and overall mathematical performance in first grade (Aunio and Niemivirta, 2010). There is also a positive association between children’s subitizing skills in kindergarten and their abilities related to the acquisition of the “count-on” addition strategy (Wilkins et al., 2022). According to Desoete et al. (2009), this strategy is when a child counts the number of times indicated by a second addend from the first addend (i.e., 2 + 5 = (2), 3, 4, 5, 6, 7).

As research on typically developing (TD) children revealed various findings on counting and subitizing from the perspective of mathematical education, its scope was gradually expanded to children with intellectual disabilities (IDs). For example, children with mild IDs (mean CA = 14.60) performed subitizing (i.e., answering the total number of 1–4 dots correctly) faster than the TD children with the same mental age (MA) and equal to the TD children whose CA was 9–10 years (Träff et al., 2020). However, Träff et al. (2020) did not analyze the subitizing ranges. As for the counting skills of children with IDs (mean MA = 3;06), MA proved to be significantly associated with the counting accuracy rate based on the three fundamental counting principles (Porter, 1999b). The counting accuracy rate was not significantly different between children with IDs (MA = 3–6;06, CA = 6–14, mean intelligence quotient [IQ] = 51) and TD children with the same MA range (Akatsuka et al., 2002). In addition, children with IDs (CA = 7–18, mean IQ = 47) made the same kinds of counting errors as those identified in Fuson et al.’s (1988) category system for TD children (Bashash et al., 2003).

Meanwhile, some studies have examined the skills of counting and subitizing based on different types of IDs. Previous studies have shown that the disability characteristics of Down syndrome (DS) and autism spectrum disorder (ASD) may affect the development of counting and subitizing skills uniquely. For example, children with DS have been noted to accurately count a significantly smaller set of items than TD children of the same MA (Nye et al., 2001). According to Nye et al. (2001), the median of the largest set size the DS group (mean CA = 5;04, mean MA = 3;04) were able to count without parental support was two, whereas it was four for the TD group (mean CA = 3;01). Children with DS exhibited various kinds of errors related to three counting principles, including counting objects twice or skipping objects (Charitaki et al., 2015; Porter, 1999a).

Conversely, the maximum number of elements that could be subitized, or subitizing range (Jansen et al., 2014), was not significantly different between people with DS and TD children with the same non-verbal intelligence scores (Ranzato et al., 2020). According to Ranzato et al. (2020), the DS group (mean CA = 21;07) used the same enumeration processes as the TD group (mean CA = 5;02). Both groups engaged in subitizing when enumerating one to three dots.

People with ASD have been noted to display characteristic counting strategies and a decreased capacity for subitizing. Yamaguchi (2012) examined the counting skills of children with IDs, focusing on the counting strategies of students with both ASD and IDs. Students with IDs (CA = 12–15, MA = 2–7) were almost always able to accurately count 12 objects when their MA exceeded four. However, three students of the nine children who were able to accurately count to 12 also counted the small number of objects included in the subitizing range (four items) using pointing. Importantly, these three students had been diagnosed with both ASD and IDs. From the above results, Yamaguchi (2012) concluded that participants with ASD may retain developmentally earlier counting strategies (i.e., pointing) once acquired.

Most studies on the subitizing skills of people with ASD have focused on those without comorbid IDs. Gagnon et al. (2004) conducted the task that asked participants to quantify the number of items in a set as accurately and quickly as possible. The findings revealed significant differences in the slopes of their RTs for each group. The TD group showed a sharp increase in RT after numerosity 4, while the ASD group (mean CA = 15.07, IQ ≧ 90) presented a monotonous increase in RT after numerosity 3. Gagnon et al. (2004) concluded that, unlike TD participants, participants with ASD used counting processes instead of subitizing with fewer objects (around three). Similarly, O’Hearn et al. (2013) reported that children with ASD (CA = 9–12, IQ ≧ 80) exhibited a smaller subitizing range compared to TD children and may have been counting within the subitizing range (one to three objects).

The suggestion that people with ASD have a reduced subitizing range (Gagnon et al., 2004; O’Hearn et al., 2013) and that they may count small numbers of objects using pointing (Yamaguchi, 2012) are consistent with one another. It can be assumed that individuals with ASD apply counting to small numbers of objects due to their small subitizing range, which results in them using pointing.

However, the aforementioned studies focus only on counting or subitizing, not both. In other words, no integrated conclusions have been drawn regarding the influence of the specific characteristics of DS and ASD on these two processes for determining the total number of objects. Drawing integrated conclusions would lead to a multifaceted clarification of numeracy skill development in children with DS and ASD.

Incidentally, there are some aspects of the cognitive style apparent in the two disabilities that stand in stark contrast to each other. Previous studies have reported that a tendency to process stimuli globally in people with DS, in contrast to the atypical local bias in people with ASD (e.g., Porter and Coltheart, 2006; Wang et al., 2007). In addition, each disability has specific characteristics in cognition or behavior, such the poor verbal working memory in DS (Jarrold et al., 2002; Lanfranchi et al., 2004) and restricted, stereotyped behavior patterns in ASD (American Psychiatric Association, 2013). Similarly, the mechanisms for determining numerosity are different in the two processes. It is thought that subitizing is a perceptual appraisal of the whole while still noting the elements, it has a global and simultaneous aspects, whereas counting is the processing of each item individually and consecutively (Benoit et al., 2004). The underlying competence of the two processes may also be different. According to Trick (2005), the secondary task of verbally pronouncing a number-word only interferes when enumerating four to eight, but not one to three (i.e., the subitizing range). Thus, it is believed that subitizing and counting are different processes, with phonological working memory playing a larger role in counting (Trick, 2005).

Based on the results of previous studies, there is a distinct possibility that the disability characteristics of DS and ASD may impact the development of counting and subitizing skills. Poor verbal working memory and a preference for global information in DS may lead to difficulties in counting and well-developed subitizing. Unlike DS, the local processing bias and restricted, patterned behaviors in ASD may lead to difficulties with subitizing and the retained habit of pointing to count small numbers of objects. Investigating the development of counting and subitizing skills for each type of ID is significant for promoting education tailored to the difficulties and strengths of children with each disability.

Therefore, the present study conducted a cross-sectional investigation of counting and subitizing skills in children with DS and ASD. Counting and subitizing tasks were administered to children with DS and ASD and compared with the performance of TD children. Based on the existing literature, the following four hypotheses were formed:

1. Children with DS will be able to count a significantly smaller set of objects compared with TD children;

2. Children with DS will show a similar subitizing range to TD children;

3. Children with ASD will use characteristic counting strategies like pointing to count a small number of objects included in the subitizing range;

4. Children with ASD will have a smaller subitizing range than TD children.

2 Materials and methods

2.1 Participants

Children with IDs (N = 38; 21 DS, 17 ASD) were recruited through representatives of 10 organizations. Those organizations were including special schools, educational institutions, and parent associations for children with IDs in the Kanto, Chubu or Kinki region. The requirements were as follows: (a) a diagnosis of DS or ASD; (b) an IQ below 70; (c) a MA of 3–6;11; and (d) a CA of 6–12;11. The IQ range was determined based on the definition of ID (Schalock et al., 2021). The MA range was determined based on similar studies (Nye et al., 2001; Ranzato et al., 2020), and the CA range was based on the typical age range of elementary school students, during which the systematic learning of basic numeracy skills occurs. We assessed children’s disability type and CA from questionnaire for parents. IQ and MA were assessed by the intelligence test.

TD children (N = 80) were recruited through representatives of two preschools in the Kanto region with a CA of 3–6;11. They did not have a medical diagnosis for any disabilities. We assessed CA and presence of a medical diagnosis from questionnaire for parents.

Some children (1 DS, 7 TD) were excluded because they did not complete the entire assessment. Others (1 DS, 16 TD) were excluded to match for the CA in the DS and ASD group, and the MA in all groups. In total, the counting and subitizing skills of 19 children with DS (12 females, 7 males), 17 children with ASD (2 females, 15 males), and 57 TD children (27 females, 30 males) were analyzed (Table 1).

Table 1

Table 1. Participant profiles of the three groups (Down syndrome, autism spectrum disorder, typical development).

2.2 Procedures

The counting and subitizing tasks were conducted individually in rooms at the schools that cooperated with the study. The procedure of the two tasks was counterbalanced to maintain internal validity and out of the consideration that the order of task presentation may influence the results. The total duration of the two tasks was about 20 min (counting task: about 5 min, subitizing task: about 15 min).

The intelligence test was conducted for children with DS and ASD. If the intelligence test was administered with the two tasks, the entire session took about 90 min. Breaks were taken between each task and the intelligence test or during the latter as needed.

2.3 Counting task

Participants were asked to indicate the number of plastic blocks (1.5 × 1.5 × 1 cm) in eight sets, each of which were arranged in a linear array at 1-cm intervals. The number of blocks per set (2, 3, 4, 5, 6, 9, 12, 18) was determined based on similar studies (Nye et al., 2001; Yamaguchi, 2012) and the normative subitizing range, which includes sets of up to five objects (Kaufman et al., 1949). Each set was presented once, with a maximum of eight trials.

The first four trials (two to five blocks) will here be called counting trials A (CT-A), and the second four trials (6–18 blocks) will be called counting trials B (CT-B).

For CT-A, participants were asked, “How many blocks are there?” This question was phrased to avoid impacting the choice of counting strategy (i.e., pointing and saying number-words). The procedures of CT-A were counterbalanced because the procedure of the trials may affect the use of the strategies. CT-B were conducted next, starting with the smallest set size (six). During CT-B, the researcher first asked, “How many blocks are there?” After asking this question, the researcher instructed the children to “please count aloud and point to each block.” The purpose was to observe the children’s counting behaviors in detail and analyze the patterns in counting errors.

For all trials, if the participant did not represent the total number of objects in a collection as a cardinal value, the researcher asked the “how many” question only once more for each trial (Gelman, 1993). The researcher recorded the participant’s behaviors (i.e., pointing, saying number-words, and response) in writing for each trial.

In consideration of the burdens on the participant, if the child presented errors, the assignment was considered difficult to continue. In other words, if an error occurred at any point in CT-A, the task was aborted once all four trials in CT-A were completed. If an error occurred at any point in CT-B, CT-B was aborted once the trial including the error was completed. However, errors related principle (3) (Gelman and Gallistel, 1978) were excluded from the discontinuation condition for CT-A and CT-B because it did not present an issue in carrying on the task. Because CT-A were conducted on all participants (with or without errors), the range of the total number of trials was between four and eight.

2.3.1 Scoring process for the counting task

First, the maximum countable number was scored based on the largest set size that the child could count without errors (Nye et al., 2001, for a similar method of analysis). In other words, it was the maximum number of items that could be counted based on Gelman and Gallistel’s (1978) counting principles.

Two methods were used to evaluate the presence of counting errors. The first was based on all three counting principles (e.g., Bashash et al., 2003; Porter, 1999a). The second was based on only principles (1) and (2), as in Nye et al. (2001). Both methods of error assessment were adopted for this study, and the maximum countable number was scored accordingly. In other words, when the analysis was based on all three principles, the researchers assessed whether the child was able to assign one number to each item, whether the assigned numbers were in the correct order, and whether the total number of items was represented as a cardinal value. When the analysis was based on principles (1) and (2), the researchers assessed only whether a child was able to assign one number to each item and did so in the correct order, regardless of whether the total number of items was then represented as a cardinal value.

The evaluation of the presence of errors related to the counting principles was performed in order from the trial with the smallest set size (two blocks). The evaluation was terminated when an error occurred. This meant that, for example, when there was an error with the three-block set during CT-A, the results of the four- or five-block sets did not matter and the score remained two.

When scoring according to the three-principles method, the largest set size that could be counted correctly based on all three principles was used. For example, if there was no error in the two-to-six-block sets and an error in the nine-block set, the score was six based on the largest set size that could be counted accurately. Similarly, if there was no error in the 2–12-block sets and an error in the 18-block set, the score was 12. If there was an error counting the two-block set, the score was zero. This created an overall score range of 0–18.

When scoring according to the two-principles method, the score was determined by the biggest number that could be counted correctly based on principles (1) and (2). For example, if there was no error in the 2–12-block sets but an error occurred at the 15th item when counting the 18-block set, the score was 14. Meanwhile, if there were no errors during CT-A and an error in the third item of the six-block set during CT-B, the score was still five (rather than three) based on the correct counting of the five-block set during CT-A. If there was an error in the first item of the two-block set, the score was zero. This again created a score range of 0–18.

The types of counting errors were then analyzed based on the children’s errors. Other studies on the counting skills of children with IDs have classified counting errors based on various categories but lacked detailed definitions of each category (e.g., Charitaki et al., 2015; Porter, 1999a). Fuson et al.’s (1988) category system for TD children has been used in a study intended for children with IDs (Bashash et al., 2003). However, this category system has issues in that it only classifies counting errors related to principle (1). Many studies have used all three principles as an index for evaluating counting skills (e.g., Bashash et al., 2003; Porter, 1999a).

This study extended the category system from Fuson et al. (1988) to comprehensively describe the errors related to all three counting principles. Only the first error to appear during the trials was analyzed. For example, if there was an error in the three-block set during CT-A, any errors that may have occurred in the four- and five- block sets were not analyzed. Errors related to principle (1) were classified based on the category system by Fuson et al. (1988). Other errors were classified based on errors indicated in previous studies on both children with IDs and TD children (Maruyama and Mutou, 1997; Porter, 1999a; Porter, 1999b).

Finally, the maximum countable number without pointing was scored. Here, the maximum number a child could provide without pointing during CT-A was calculated to investigate the actual use of pointing for small numbers within the subitizing range.

When scoring, the presence and use of pointing strategies were assessed (i.e., whether the child pointed to all or some of the items, or the child re-counted with pointing to check their answer after making a response without pointing). In addition, it was noted whether there were any errors related to the three principles when using the pointing strategy.

The maximum countable number without pointing was scored by integrating the results of using the pointing strategy and the existence of errors. For example, if a child counted the two- or three-block sets correctly without pointing and used pointing only for the four- and five-block sets, the score was three. Similarly, if a child counted the two-to-three- and five-block sets correctly without pointing and used pointing only for the four-block set, the score was five. If pointing was used throughout CT-A, the score for this aspect was zero regardless of any errors made. This created a score range of zero to five.

2.4 Subitizing task

Participants were asked to report the number of one to eight dots on a 13.5-inch laptop screen as quickly and accurately as possible (Ranzato et al., 2020; Starkey and McCandliss, 2021). All the dots were the same size and appeared in random placements without a dice condition, symmetrical condition, or line condition (Hsin et al., 2021; Jansen et al., 2014). The children were instructed to answer by pressing the number keys on the keyboard to avoid issues caused by potential dysarthria. The response keys were numbered 1–9 (Jansen et al., 2014).

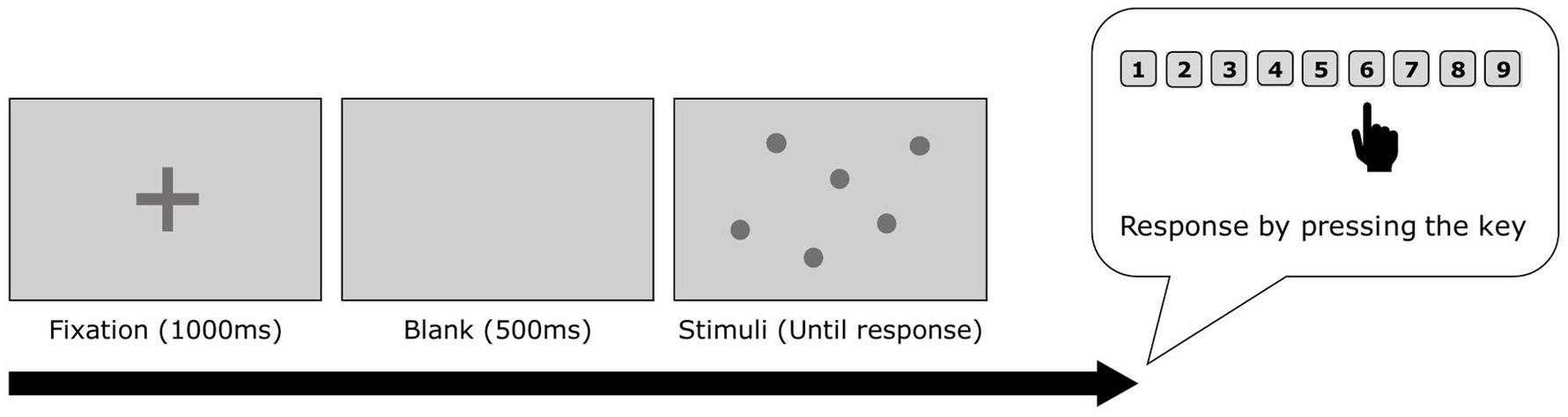
The researcher initiated each trial when the participant was fixating on the screen. Each trial began with a fixation cross for 1,000 ms, followed by a blank screen for 500 ms. Subsequently, dots appeared and remained visible until the participant pressed any of the number keys (Figure 1). To minimize visual aftereffects, both the fixation cross and the dots were dark gray, while the background was light gray (O’Hearn et al., 2013). Additionally, to reduce external visual distractions during the task and to unify different environments depending on where the task is conducted, a partition was used to cover the back of the laptop.

Figure 1

Figure 1. Stimuli and procedure of the subitizing task.

The task screen consisted of a block that randomly presented each number of dots (1–8). Thirty-two trials were conducted by repeating each block four times. RTs were recorded using SuperLab 6 (Cedrus Inc.). The researcher also made a written record of whether any counting strategies (i.e., pointing and saying number-words) were used.

2.4.1 Scoring process for the subitizing task

The subitizing range was analyzed by calculating the probabilistic span (PS) (Starkey and McCandliss, 2021) based on the accuracy of the responses and RTs. The approach using PS has demonstrated validity and usefulness in determining the subitizing capacity of young children in comparison with other metrics (Starkey and McCandliss, 2021).

According to Starkey and McCandliss (2021), most children are relatively slow counters. However, PS effectively assesses their subitizing span without being unduly influenced by counting speed development. In addition, PS can determine the percentage of trials in which subitization occurred and differentiate children who are just beginning to subitize from those who have mastered the skill.

It was here determined by the percentage of the three-to-five-dot trials that each participant subitized with the assumption that all children could subitize at least two items. For instance, if a child correctly subitized all the three-dot trials, 75% of the four-dot trials, and no five-dot trials, the child’s PS would be 3.75 (Starkey and McCandliss, 2021). The calculation process for PS is shown in Table 2.

Table 2

Table 2. Calculation process of probabilistic span.

However, as was observed during the trials, 19 children counted even sets of two dots (5 DS, 5 ASD, and 9 TD). Therefore, PS was not calculated for these children, who were assigned a score of one. PS was only calculated for children who were not observed pointing or saying number-words for sets of two dots. This created a score range of one to five.

2.5 Intelligence test

The Tanaka–Binet Intelligence Scale V (Tanaka Institute for Educational Research, 2003) was used as a measure of IQ and MA for each participant with DS or ASD. This is a standardized intelligence test and a Japanese version of the Stanford–Binet Intelligence Scale.

2.6 Data analysis

The performance of each group on the counting and subitizing tasks was analyzed to determine whether there were any significant differences in skill or strategy. The Kruskal–Wallis test of nonparametric analyses was conducted for all statistical analyses because the Shapiro–Wilk test indicated violation of the normality assumption. If significant differences were found, multiple comparisons using the Bonferroni method were made. The significance level was set at p < 0.05.

2.7 Ethics approval statement

This study obtained ethical approval from the Ethical Committee on Human Sciences at the University of Tsukuba. The children provided verbal assent. Their parents and the representatives of the relevant schools provided their written informed consent. The researchers explained that participation was voluntary, that respondents would experience no disadvantage if they did not participate, and that the privacy of participants would be protected.

3 Results

3.1 The counting task

3.1.1 Maximum countable number (three principles)

The maximum countable numbers were calculated based on the three principles. In other words, it was calculated on the condition that each item was assigned one distinct number-word according to the stable order, and the total number of items in a collection was reported as the cardinal value.

As shown in Table 3, the mean of the maximum countable number was 10.53 for the DS group (SD = 5.66), 12.35 for the ASD group (SD = 8.34), and 12.49 for the TD group (SD = 6.23). This indicates that the children with DS could generally count correctly to 11 according to the three principles, and that children with ASD and TD could generally count to 12. A Kruskal–Wallis test revealed that the maximum countable number based on the three principles was not significantly different between the three groups (H(2) = 1.37, p = 0.503).

Table 3

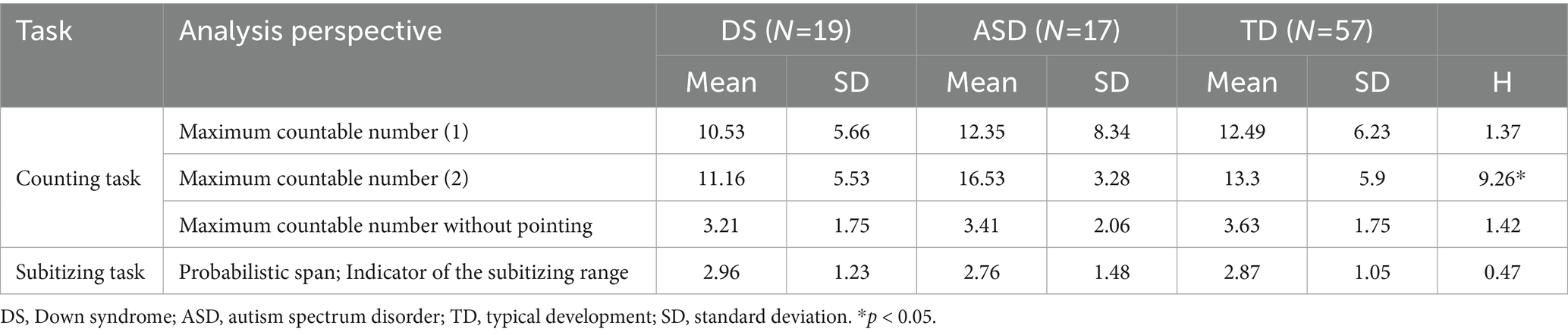
Table 3. Score of tasks in the three groups (Down syndrome, autism spectrum disorder, typical development).

3.1.2 Maximum countable number (two principles)

The maximum countable number was also calculated based only on principles (1) and (2). In other words, it was calculated only on the condition that each item was assigned one distinct number-word according to the stable order. It therefore did not matter whether the child reported a cardinal value afterward.

As shown in Table 3, the median of the mean countable number was 11.16 for the DS group (SD = 5.53), 16.53 for the ASD group (SD = 3.28), and 13.3 for the TD group (SD = 5.9). This suggests that children with DS could count correctly to 11 according to the two principles, children with ASD could count to 17, and TD children could count to 13. According to a Kruskal–Wallis test, there was a significant difference between the groups for the maximum countable number based on two principles (H(2) = 9.26, p = 0.01). Results of the Bonferroni post hoc test showed that the DS group had a statistically significantly lower score than the ASD group (p = 0.008). However, no other differences were statistically significant.

3.1.3 Types of counting errors

A total of 48 children exhibited counting errors (14 DS, 6 ASD, 28 TD). The MA range for the children with DS who made errors was 3;01–4;01 (M = 3;08, SD = 0;05), while it was 3;01–4;01 (M = 3;06, SD = 0;05) for the children with ASD. Among the TD children who made errors, the CA range was 3–5;05 (M = 4, SD = 0;08).

Upon analyzing the content of the errors made by these 48 children, 10 categories of counting errors emerged (Table 4). The errors related to principle (1) were those in which children skipped an item (i.e., objects were skipped entirely or children pointed without speaking) or counting an item twice (i.e., multiple counts or saying multiple words with one pointing action), as shown in Figure 2 (1)–(4). The errors related to principle (2) were classified as “word omitted” and “word repeated” depending on the difference in error type (Table 4). Some errors related to principle (3) occurred after counting and without counting, which indicated a discrepancy between the response and the number of items (Figure 2 [5]–[6]). The other errors related to principle (3) were “no response” or “recount” (Figure 2 [7]–[8]).

Table 4

Table 4. Categories of counting errors.

Figure 2

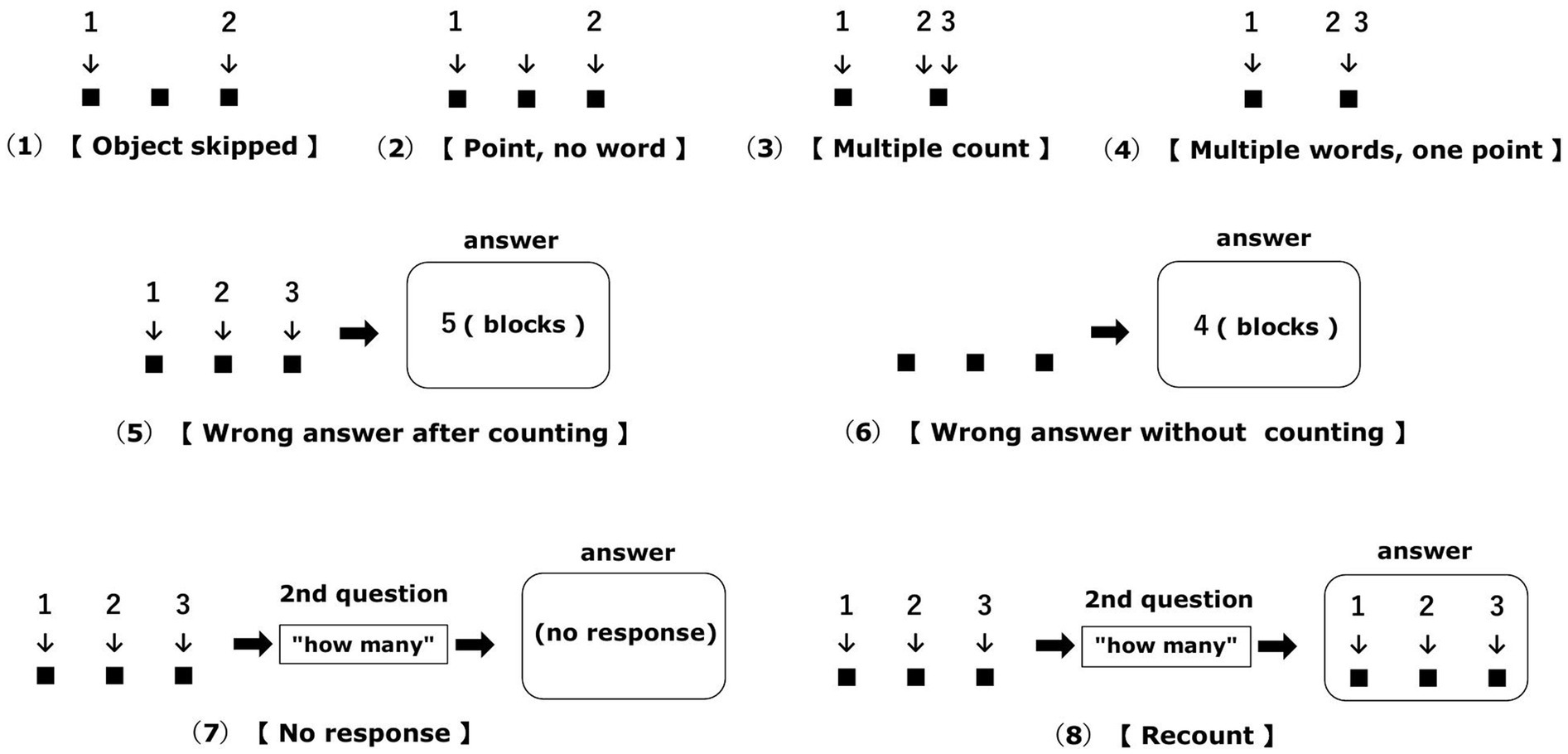
Figure 2. Examples of counting errors related to the one–one principle and the cardinal principle. Example of counting errors shown in Table 4 related to the one–one principle and the cardinal principle. The error categories indicated by [ ]. This figure was created referring to the figure in Fuson et al. (1988).

The number of errors in the groups was calculated according to the above categories (Table 5). In the DS and TD groups, a variety of errors related to the three principles were identified. However, “no response” errors did not occur in the DS group and “recount” errors did not occur in the DS and TD groups. Conversely, “no response” and “recount” errors, both related to principle (3), were both found in the ASD group. “Recount” errors also occurred only in the ASD group.

Table 5

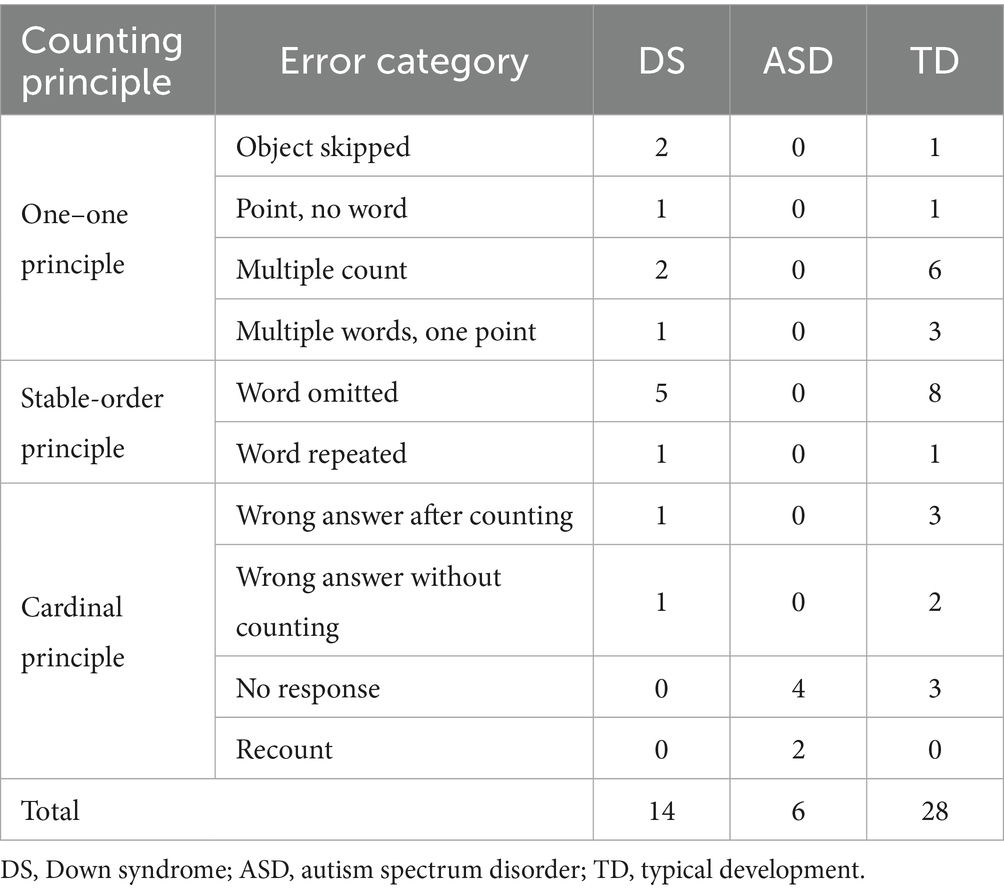
Table 5. Number of counting errors in the three groups (Down syndrome, autism spectrum disorder, typical development).

3.1.4 Maximum countable number without pointing

The maximum numbers that the children could identify without pointing are shown in Table 3. The mean was 3.21 for the DS group (SD = 1.75), 3.41 for the ASD group (SD = 2.06), and 3.63 for the TD group (SD = 1.75). This suggests that children from all three groups could identify the numerosity of items without pointing for sets of up to three or four blocks. A Kruskal–Wallis test revealed that the maximum countable number without pointing was not significantly different between the three groups (H(2) = 1.42, p = 0.491).

3.2 The subitizing task

3.2.1 Subitizing range

The PS, a measure for the subitizing range (Starkey and McCandliss, 2021), is shown in Table 3. The mean was 2.96 for the DS group (SD = 1.23), 2.76 for the ASD group (SD = 1.48), and 2.87 for the TD group (SD = 1.05). This suggests that children with DS subitized all two-dot set trials, 96% of the three-dot set trials, and none of the four-dot set trials. A similar interpretation of the PS for the ASD and TD groups suggests that children in all three groups were able to subitize two items consistently and three items most of the time. However, the children from all three groups usually counted sets of more than four items. A Kruskal–Wallis test revealed that the PS results did not demonstrate a statistically significant difference between the three groups (H(2) = 0.47, p = 0.789).

4 Discussion

4.1 Counting and subitizing in children with DS

Hypothesis (1) was that children with DS would be able to count a smaller total number of objects than TD children. However, contrary to this expectation, the maximum countable number was not significantly different between children with DS and TD.

The result was potentially because the children with DS in this study had a higher CA than in Nye et al. (2001), who noted that preschool and young elementary school-age children with DS (CA = 3;05–7) showed a lower counting performance compared to TD children. However, the children with DS in this study were all of elementary school age (CA = 6;09–12;06). Counting is one of the foundations of mathematics and is addressed by standard Japanese special school curriculum guidelines (Ministry of Education, Culture, Sports, Science and Technology, 2017). Therefore, it is possible that the learning experiences gained according to CA improved the counting performance of the children with DS in this study.

However, the maximum countable number of children with DS based on principles (1) and (2) was significantly lower than that of children with ASD. Children with DS had more difficulty counting compared to other children with IDs-controlled MA and CA. This reflects the results of Nye et al. (2001), who noted the low counting performance of children with DS.

According to an analysis of the errors, the understanding and application of the three principles presented challenges for the children with DS. However, certain errors related to principle (3) (i.e., “no response” and “recount”) were not made by these children. Here, “no response” and “recount” indicated that the total number of items was not represented as the cardinal value. Therefore, for children with DS, understanding the correct form of response (i.e., representing the total number of items as a cardinal value) may not have been the main challenge.

Previous studies have noted that children with DS were more to skip items than double count, and gender did not affect these error patterns (Charitaki et al., 2015; Porter, 1999a). However, statistical analysis has not been adequately carried out on this factor. Therefore, it is necessary to further clarify the characteristics of counting errors in children with DS using statistical analysis due to the increasing number of participants.

Hypothesis (2) was that children with DS would show a similar subitizing range to TD children. The results indicated that the subitizing range of children with DS was not significantly different from either that of TD children or children with ASD. Children with DS may have subitizing skills corresponding to MA, as shown in Ranzato et al. (2020). However, children with DS often have low counting skills (Nye et al., 2001), and the present study showed similar results. Therefore, their subitizing abilities are likely better developed than their counting abilities.

However, the results from the few studies investigating the subitizing skills of people DS are inconsistent due to the different task designs used. Sella et al. (2013) indicated low subitizing skills in children with DS based on their judgment of whether the number of two sets of dots presented successively was the same. Notably, the experimental paradigm used by Sella et al. (2013) differed from the standard dot enumeration paradigm in which participants explicitly state the number of dots presented and it thus relied heavily on the participants’ working memory abilities (Ranzato et al., 2020).

The subitizing task of this study was conducted according to the latest research and in consideration of relevant methodological problems (i.e., Ranzato et al., 2020). Consequently, the results of this study supported those of Ranzato et al. (2020). Further studies that more closely consider task design are required to further clarify the development of subitizing skills in children with DS.

Incidentally, subitizing and counting is the developmental pathway for acquiring principle (3), in which the last word used in counting represents the total number of items in a collection (Benoit et al., 2004; Paliwal and Baroody, 2020). Therefore, the results indicated a need for instruction on these skills that accounts for the specific developmental needs of children with DS (e.g., compensating for counting difficulties through subitizing). As an example, in studies of TD children, the label-first intervention (i.e., labeling a set first with total number of items and then counting) had some success in promoting the knowledge of principle (3) (Mix et al., 2012; Paliwal and Baroody, 2020). Although subitizing is often overlooked in educational practice compared with counting (Clements et al., 2019), it might be helpful to teach children with DS subitizing skills by labeling small items. Other activities that promote subitizing have been suggested, such as a child being shown a set of dots for a short interval before being asked to say, draw, or write the number (MacDonald and Wilkins, 2019).

However, the counting process is necessary for enumerating sets of items that exceed the subitizing range. This study revealed the difficulties with counting for children with DS, and the cause of this problem has not been clarified. As stated in the introduction, poor verbal working memory and poor knowledge of the number word sequence in DS (Jarrold et al., 2002; Lanfranchi et al., 2004) may be related to these difficulties. In addition, eye movements (Watson et al., 2007), the use of fingers, or the act of pointing at objects (Lafay et al., 2013) are related to counting abilities. Therefore, it would be helpful to investigate the underlying counting competencies of children with DS and identify the causes of low counting performance to address their difficulties.

4.2 Counting and subitizing in children with ASD

Hypothesis (3) was that children with ASD would use counting strategies like pointing when counting small numbers of objects included in the subitizing range. However, the maximum countable number achieved without pointing was not significantly different between the three groups (DS, ASD, TD). Yamaguchi’s (2012) hypothesis that children with ASD may retain the pointing strategy was therefore not supported.

This may have been caused by variations in the severity of ASD. As stated in the introduction, the researchers assumed that the local processing bias and restricted, patterned behaviors characteristic of ASD may lead to the use of pointing for counting with small sets. However, this study did not account for the severity of participants’ ASD, which may have varied.

In addition, the strategy of pointing at objects may be related primarily to CA. In fact, there are differences in the counting skills in students with IDs (CA = 7–18, mean IQ = 47) at different CA levels (Bashash et al., 2003). Furthermore, it has been suggested that after increasing both CA and exposure to training programs, students with IDs are demonstrated to have developed their counting strategies further, including the progressive internalization of the pointing strategy (Bashash et al., 2003). Therefore, a second survey of a lower, narrower range of participant CAs may provide more definitive conclusions to this hypothesis.

Children with ASD made only “no response” and “recount” errors related to principle (3). Therefore, children with ASD may be challenged with the understanding and application of this principle, whereas they did not find principles (1) and (2) difficult. It is possible that “no response” and “recount” errors occurred because a counting procedure was performed in imitation of adults and was not yet understood as a means of determining a total number of items (Maruyama and Mutou, 1997).

In addition, “no response” and “recount” errors may have indicated a lack of understanding of how to respond rather than difficulties with enumeration. The incorrect responses may have been due to difficulties understanding the intention of the “how many” question asked by the researcher. In fact, Gelman (1993) performed a counting task with college students and found that few bothered to repeat the last number said after counting and were puzzled by the repeated “how many” question. Considering the above results, the “no response” and “recount” errors of the ASD group may reflect the difficulties in social communication experienced by children with ASD (American Psychiatric Association, 2013), who may struggle to understand the intention behind the “how many” question and not know how to respond appropriately. Furthermore, “recount” errors, which occurred only in children with ASD, may be promoted by the repetitive behaviors characteristic of ASD (American Psychiatric Association, 2013).

The unusual characteristics of attention in ASD are likely to impact such errors. Many children with ASD have trouble disengaging from one object and shifting their attention to another (Patten and Watson, 2011). Moreover, children with ASD have difficulty paying attention to social stimuli, including human voices, compared to TD children (Kuhl et al., 2005). Therefore, children with ASD may have had difficulty diverting their attention from the blocks and paying attention to the researcher’s repeated “how many” question.

Hypothesis (4) was that children with ASD would demonstrate a smaller subitizing range than TD children. On the contrary, the subitizing range of children with ASD was not found to be significantly different from that of TD children or children with DS.

Gagnon et al. (2004) and O’Hearn et al. (2013) noted that the characteristics of ASD can include a greater ease of focus on local information than global configurations, making it more difficult for those with ASD to attend to more than one element of a scenario or problem at a time. Consequently, they may have a smaller subitizing range when faced with multiple objects (Gagnon et al., 2004; O’Hearn et al., 2013). However, there is also a possibility that people with ASD do not show a consistent local processing bias (D’Souza et al., 2016). Therefore, further research should focus on the information processing styles found among children with ASD and the relationship between those information processing styles and subitizing abilities.

As stated above, no results were found to support hypotheses (3) and (4) about children with ASD. Most previous studies on mathematics abilities and their predictors in people with ASD have used people with “high-functioning autism” (IQ > 75) or ASD-WoID (ASD without ID) as participants (Wang et al., 2023). Instead, this study based its hypotheses on a pool of children with both ASD and IDs (Yamaguchi, 2012) and a cross-sectional investigation of those without IDs (Gagnon et al., 2004; O’Hearn et al., 2013). Further studies on the characteristics of counting and subitizing among children with IDs and comorbid ASD should consider the severity of the ASD or individuals’ information processing styles.

5 Conclusion

This study examined the development of counting and subitizing skills in children with DS and ASD. The maximum countable number for children with DS, based on the one -one principle and the stable-order principle, was significantly lower than that for children with ASD. However, the subitizing range of children with DS did not significantly differ from that of children with ASD or TD children. The findings supported the hypothesis that children with DS exhibit delays in counting development, particularly with higher numbers. This suggests that their difficulties may stem more from limitations in number word knowledge than from a lack of understanding of counting principles. Although it was predicted that children with ASD demonstrate characteristic counting strategies, such as frequent pointing and a smaller subitizing range, the results did not align with the hypotheses. These findings suggest that children with IDs exhibit distinct developmental patterns in counting and subitizing, depending on the disability type. In particular, children with DS may benefit from interventions that strengthen their understanding of cardinality by fostering well-developed subitizing and addressing learning challenges associated with poor knowledge of the number word sequence and challenges with phonological working memory.

5.1 Limitations

This study had several limitations. First, the tasks used were novel, making it difficult to design tasks that were directly comparable to those in previous studies. Many studies on mathematical skills have reported inconsistencies due to variations in task design, leading to challenges in interpreting differences across studies (Chen et al., 2022; Dietrich et al., 2015). Therefore, the validity of the results should be enhanced by further research in which the identity of the issue content is assured.

For the counting task, the way of the question was differed between CT-A and CT-B. Although this aims to analyze results from multiple perspectives while reducing the burden on children as much as possible, the lack of uniformity in the implementation conditions of each trial is an issue. Therefore, the validity of the results should be enhanced by extra resurvey that guarantees the identity of the trials by narrowing the analysis perspective.

Furthermore, the Stanford–Binet Intelligence Scale used to measure intellectual functioning is standardized, but may not be sufficiently reliable. Sansone et al. (2014) demonstrated that this test does not appear to provide a valid estimate of IQ scores in individuals with IDs because of floor effects. It should be noted that this study’s findings may have been negatively impacted because IQ scores were used as a variable for selecting participants.

This study included a relatively small sample size of children with IDs (N = 36), which limited the generalizability of the findings and possibly biased the findings. Cross-sectional studies with larger samples would reinforce the results and enable the statistical analysis of counting error types according to each disability type. In addition, longitudinal studies are required to analyze changes in counting and subitizing skills in children with DS or ASD over time and better understand the developmental process.

In addition, this study took its sample based on MA and IQ but did not account for the adaptive behavior scores within the ASD and DS groups and the Autism-Spectrum Quotient within the ASD group. Therefore, future research with stricter samples that include additional measures is necessary to enhance the validity of the findings.

As stated in the introduction, previous studies have suggested that there are many variables that could influence counting or subitizing performance, such as verbal working memory or information processing style (Gagnon et al., 2004; O’Hearn et al., 2013; Trick, 2005). In addition, eye movements (Watson et al., 2007) and the use of fingers (Lafay et al., 2013) are related to these processes. However, this study did not account for those cognitive abilities or measure them. Additional measures that explain the relationship between the performance of mathematical skills and disability types are needed in future research.

Data availability statement

The datasets presented in this article are not readily available because the data will be kept in a locked locker, and after a certain period of time after the completion of the research, it will be destroyed. Requests to access the datasets should be directed to d2FrYS5rb2JheWFzaGkxMjAyQGdtYWlsLmNvbQ==.

Ethics statement

The studies involving humans were approved by The Research Ethics Committee of University of Tsukuba. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants’ legal guardians/next of kin. Written informed consent was obtained from the individual(s), and minor(s)’ legal guardian/next of kin, for the publication of any potentially identifiable images or data included in this article.

Author contributions

WK: Conceptualization, Investigation, Writing – original draft, Writing – review & editing. MaK: Investigation, Resources, Writing – review & editing. MiK: Project administration, Resources, Supervision, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Acknowledgments

The authors are grateful for the support of each participating family and the people involved in this study.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Gen AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Reference

Akatsuka, M., Ejiri, M., Matsui, H., and Koike, T. (2002). Counting performance and its developmental relation to the verbal regulation of behavior in children with intellectual disabilities. Jpn. Assoc. Spec. Educ. 40, 205–214. doi: 10.6033/tokkyou.40.205

Crossref Full Text | Google Scholar

American Psychiatric Association (2013). Diagnostic and statistical manual of mental disorders, 5th edition, (DSM-5). Washington, DC: American Psychiatric Association Publishing.

Google Scholar

Aunio, P., and Niemivirta, M. (2010). Predicting children’s mathematical performance in grade one by early numeracy. Learn. Individ. Differ. 20, 427–435. doi: 10.1016/j.lindif.2010.06.003

Crossref Full Text | Google Scholar

Bashash, L., Outhred, L., and Bochner, S. (2003). Counting skills and number concepts of students with moderate intellectual disabilities. Int. J. Disabil. Dev. Educ. 50, 325–345. doi: 10.1080/1034912032000120480

Crossref Full Text | Google Scholar

Benoit, L., Lehalle, H., and Jouen, F. (2004). Do young children acquire number words through subitizing or counting? Cogn. Dev. 19, 291–307. doi: 10.1016/j.cogdev.2004.03.005

Crossref Full Text | Google Scholar

Charitaki, G., Baralis, G., Polychronopoulou, S., Lappas, D., and Soulis, S. (2015). Common difficulties among children with down’s syndrome in acquiring basic counting skills. Br. J. Educ. Soc. Behav. Sci. 7, 121–128. doi: 10.9734/BJESBS/2015/15323

Crossref Full Text | Google Scholar

Chen, J., Paul, J. M., and Reeve, R. (2022). Manipulation of attention affects subitizing performance: a systematic review and meta-analysis. Neurosci. Biobehav. Rev. 139:104753. doi: 10.1016/j.neubiorev.2022.104753

PubMed Abstract | Crossref Full Text | Google Scholar

Clements, D. H., Sarama, J., and MacDonald, B. L. (2019). “Subitizing: the neglected quantifier” in Constructing number, research in mathematics education. eds. A. Norton and M. W. Alibali (New York: Springer, Cham), 13–45.

Google Scholar

D’Souza, D., Booth, R., Connolly, M., Happé, F., and Karmiloff-Smith, A. (2016). Rethinking the concepts of local or global processors: evidence from Williams syndrome, down syndrome, and autism spectrum disorders. Dev. Sci. 19, 452–468. doi: 10.1111/desc.12312

Crossref Full Text | Google Scholar

Desoete, A., Ceulemans, A., Roeyers, H., and Huylebroeck, A. (2009). Subitizing or counting as possible screening variables for learning disabilities in mathematics education or learning? Educ. Res. Rev. 4, 55–66. doi: 10.1016/j.edurev.2008.11.003

Crossref Full Text | Google Scholar

Dietrich, J. F., Huber, S., and Nuerk, H. C. (2015). Methodological aspects to be considered when measuring the approximate number system (ANS) – a research review. Front. Psychol. 6:295. doi: 10.3389/fpsyg.2015.00295

PubMed Abstract | Crossref Full Text | Google Scholar

Formoso, J., Barreyro, J. P., Jacubovich, S., and Injoque-Ricle, I. (2017). Possible associations between Subitizing, estimation and visuospatial working memory (VSWM) in children. Span. J. Psychol. 20, E27–E11. doi: 10.1017/sjp.2017.23

PubMed Abstract | Crossref Full Text | Google Scholar

Fuson, K. C., Briars, D. J., and Secada, W. G. (1988). “Correspondence errors in children’s counting” in Children’s counting and concepts of number. ed. K. C. Fuson (New York: Springer-Verlag), 63–91.

Google Scholar

Gagnon, L., Mottron, L., Bherer, L., and Joanette, Y. (2004). Quantification judgement in high functioning autism: superior or different? J. Autism Dev. Disord. 34, 679–689. doi: 10.1007/s10803-004-5288-9

PubMed Abstract | Crossref Full Text | Google Scholar

Gelman, R. (1993). “A rational-constructivist account of early learning about numbers and objects” in The psychology of learning and motivation, advances in research theory. ed. D. L. Medin (San Diego: Academic Press), 61–96.

Google Scholar

Gelman, R., and Gallistel, C. R. (1978). The child's understanding of number. Cambridge, Massachusetts: Harvard University Press.

Google Scholar

Hsin, C. Y., Lo, Y. H., and Tseng, P. (2021). Effect of non-canonical spatial symmetry on Subitizing. Front. Psychol. 12:562762. doi: 10.3389/fpsyg.2021.562762

PubMed Abstract | Crossref Full Text | Google Scholar

Jansen, B. R. J., Hofman, A. D., Straatemeier, M., van Bers, B. M. C. W., Raijmakers, M. E. J., and van der Maas, H. L. J. (2014). The role of pattern recognition in children’s exact enumeration of small numbers. Br. J. Dev. Psychol. 32, 178–194. doi: 10.1111/bjdp.12032

PubMed Abstract | Crossref Full Text | Google Scholar

Jarrold, C., Baddeley, A. D., and Phillips, C. E. (2002). Verbal short-term memory in down syndrome: a problem of memory, audition, or speech? J. Speech Lang. Hear. Res. 45, 531–544. doi: 10.1044/1092-4388(2002/042)

PubMed Abstract | Crossref Full Text | Google Scholar

Jordan, N. C., and Levine, S. C. (2009). Socioeconomic variation, number competence, and mathematics learning difficulties in young children. Dev. Disabil. Res. Rev. 15, 60–68. doi: 10.1002/ddrr.46

PubMed Abstract | Crossref Full Text | Google Scholar

Katzin, N., Cohen, Z. Z., and Henik, A. (2019). If it looks, sounds, or feels like subitizing, is it subitizing? A modulated definition of subitizing. Psychon. Bull. Rev. 26, 790–797. doi: 10.3758/s13423-018-1556-0

PubMed Abstract | Crossref Full Text | Google Scholar

Kaufman, E. L., Lord, M. W., Reese, T. W., and Volkmann, J. (1949). The discrimination of visual number. Am. J. Psychol. 62, 498–525. doi: 10.2307/1418556

PubMed Abstract | Crossref Full Text | Google Scholar

Kuhl, P. K., Coffey-Corina, S., Padden, D., and Dawson, G. (2005). Links between social and linguistic processing of speech in preschool children with autism: behavioral and electrophysiological measures. Dev. Sci. 8, F1–F12. doi: 10.1111/j.1467-7687.2004.00384.x

PubMed Abstract | Crossref Full Text | Google Scholar

Lafay, A., Thevenot, C., Castel, C., and Fayol, M. (2013). The role of fingers in number processing in young children. Front. Psychol. 4:488. doi: 10.3389/fpsyg.2013.00488

PubMed Abstract | Crossref Full Text | Google Scholar

Lanfranchi, S., Cornoldi, C., and Vianello, R. (2004). Verbal and visuospatial working memory deficits in children with down syndrome. Am. Assoc. Mental Retardat. 109, 456–466. doi: 10.1352/0895-8017(2004)109<456:VAVWMD>2.0.CO;2

Crossref Full Text | Google Scholar

Le Fevre, J. A., Smith-Chant, B. L., Fast, L., Skwarchuk, S. L., Sargla, E., Arnup, J. S., et al. (2006). What counts as knowing? The development of conceptual and procedural knowledge of counting from kindergarten through grade 2. J. Exp. Child Psychol. 93, 285–303. doi: 10.1016/j.jecp.2005.11.002

PubMed Abstract | Crossref Full Text | Google Scholar

MacDonald, B. L., and Wilkins, J. L. M. (2019). Subitising activity relative to units construction: a case study. Res. Math. Educ. 21, 77–95. doi: 10.1080/14794802.2019.1579667

PubMed Abstract | Crossref Full Text | Google Scholar

Maruyama, R., and Mutou, T. (1997). The features of informal mathematical knowledge in childhood. Japanese J. Develop. Psychol. 8, 98–110. doi: 10.11201/jjdp.8.98

Crossref Full Text | Google Scholar

Ministry of Education, Culture, Sports, Science and Technology (2017). The national curriculum standard for elementary and lower secondary departments of special needs education school. Tokyo, Japan: KAIRYUDO Publishing Co.,Ltd.

Google Scholar

Mix, K. S., Sandhofer, C. M., Moore, J. A., and Russell, C. (2012). Acquisition of the cardinal word principle: the role of input. Early Child Res. Q. 27, 274–283. doi: 10.1016/j.ecresq.2011.10.003

Crossref Full Text | Google Scholar

Nye, J., Fluck, M., and Buckley, S. (2001). Counting and cardinal understanding in children with down syndrome and typically developing children. Down Syndrome Res. Pract. 7, 68–78. doi: 10.3104/reports.116

PubMed Abstract | Crossref Full Text | Google Scholar

O’Hearn, K., Franconeri, S., Wright, C., Minshew, N., and Luna, B. (2013). The development of individuation in autism. J. Exp. Psychol. Hum. Percept. Perform. 39, 494–509. doi: 10.1037/a0029400

Crossref Full Text | Google Scholar

Paliwal, V., and Baroody, A. J. (2020). Cardinality principle understanding: the role of focusing on the subitizing ability. ZDM 52, 649–661. doi: 10.1007/s11858-020-01150-0

Crossref Full Text | Google Scholar

Patten, E., and Watson, L. R. (2011). Interventions targeting attention in young children with autism. Am. J. Speech-Lang. Pathol. 20, 60–69. doi: 10.1044/1058-0360(2010/09-0081)

Crossref Full Text | Google Scholar

Porter, J. (1999a). Learning to count: a difficult task? Down Syndrome Res. Pract. 6, 85–94. doi: 10.3104/reports.99

PubMed Abstract | Crossref Full Text | Google Scholar

Porter, J. (1999b). The attainments of pupils with severe learning difficulties on a simple counting and error detection task. J. Appl. Res. Intellect. Disabil. 12, 87–99. doi: 10.1111/j.1468-3148.1999.tb00068.x

Crossref Full Text | Google Scholar

Porter, M. A., and Coltheart, M. (2006). Global and local processing in Williams syndrome, autism, and down syndrome: perception, attention, and construction. Dev. Neuropsychol. 30, 771–789. doi: 10.1207/s15326942dn3003_1

Crossref Full Text | Google Scholar

Ranzato, E., Tolmie, A., and Van Herwegen, J. (2020). Perceptual subitizing and conceptual subitizing in Williams syndrome and down syndrome: insights from eye movements. Res. Dev. Disabil. 106:103746. doi: 10.1016/j.ridd.2020.103746

PubMed Abstract | Crossref Full Text | Google Scholar

Sansone, S. M., Schneider, A., Bickel, E., Berry-Kravis, E., Prescott, C., and Hessl, D. (2014). Improving IQ measurement in intellectual disabilities using true deviation from population norms. J. Neurodev. Disord. 6:16. doi: 10.1186/1866-1955-6-16

PubMed Abstract | Crossref Full Text | Google Scholar

Schalock, R. L., Luckasson, R., and Tassé, M. J. (2021). An overview of intellectual disability: definition, diagnosis, classification, and systems of supports. Am. J. Intellect. Dev. Disabil. 126, 439–442. doi: 10.1352/1944-7558-126.6.439

Crossref Full Text | Google Scholar

Sella, F., Lanfranchi, S., and Zorzi, M. (2013). Enumeration skills in down syndrome. Res. Dev. Disabil. 34, 3798–3806. doi: 10.1016/j.ridd.2013.07.038

PubMed Abstract | Crossref Full Text | Google Scholar

Starkey, G. S., and McCandliss, B. D. (2021). A probabilistic approach for quantifying children's subitizing span. J. Exp. Child Psychol. 207:105118. doi: 10.1016/j.jecp.2021.105118

PubMed Abstract | Crossref Full Text | Google Scholar

Tanaka Institute for Educational Research (2003). The Tanaka-Binet intelligence scale (V). Tokyo, Japan: Taken Publishing Inc.

Google Scholar

Träff, U., Levén, A., Östergren, R., and Schöld, D. (2020). Number magnitude processing and verbal working memory in children with mild intellectual disabilities. Dev. Neuropsychol. 45, 139–153. doi: 10.1080/87565641.2020.1744606

PubMed Abstract | Crossref Full Text | Google Scholar

Trick, L. M. (2005). The role of working memory in spatial enumeration: patterns of selective interference in subitizing and counting. Psychon. Bull. Rev. 12, 675–681. doi: 10.3758/BF03196757

PubMed Abstract | Crossref Full Text | Google Scholar

Wang, L., Liang, X., Jiang, B., Wu, Q., and Jiang, L. (2023). What ability can predict mathematics performance in typically developing preschoolers and those with autism Spectrum disorder? J. Autism Dev. Disord. 53, 2062–2077. doi: 10.1007/S10803-022-05454-W

PubMed Abstract | Crossref Full Text | Google Scholar

Wang, L., Mottron, L., Peng, D., Berthiaume, C., and Dawson, M. (2007). Local bias and local-to-global interference without global deficit: a robust finding in autism under various conditions of attention, exposure time, and visual angle. Cogn. Neuropsychol. 24, 550–574. doi: 10.1080/13546800701417096

PubMed Abstract | Crossref Full Text | Google Scholar

Watson, D. G., Maylor, E. A., and Bruce, L. A. M. (2007). The role of eye movements in subitizing and counting. J. Exp. Psychol. Hum. Percept. Perform. 33, 1389–1399. doi: 10.1037/0096-1523.33.6.1389

PubMed Abstract | Crossref Full Text | Google Scholar

Wilkins, J. L. M., MacDonald, B. L., and Norton, A. (2022). Construction of subitized units is related to the construction of arithmetic units. Educ. Stud. Math. 109, 137–154. doi: 10.1007/s10649-021-10076-7

Crossref Full Text | Google Scholar

Yamaguchi, M. (2012). The development of number concepts and strategies of equal distribution in students with intellectual disabilities. Jpn. J. Dev. Psychol. 23, 191–201. doi: 10.11201/jjdp.23.191

Crossref Full Text | Google Scholar