The language of folding: increasing spatial language and decreasing mathematics anxiety through origami

Ridgley, Lisa M.; Geary, David C.; Li, Yaoran; Myers, Perla; Ottinger, Rebecca; Silvaggio, Danielle N.; Ünal, Zehra; Popov, Vitaliy

doi:10.3389/feduc.2025.1613317

ORIGINAL RESEARCH article

Front. Educ., 17 September 2025

Sec. STEM Education

Volume 10 - 2025 | https://doi.org/10.3389/feduc.2025.1613317

The language of folding: increasing spatial language and decreasing mathematics anxiety through origami

Lisa M. Ridgley¹

David C. Geary²

Yaoran Li³

Perla Myers¹^*

Rebecca Ottinger¹

Danielle N. Silvaggio¹

Zehra Ünal²

Vitaliy Popov^4,5

¹The Jacobs Institute for Innovation in Education, University of San Diego, San Diego, CA, United States
²Department of Psychological Sciences, University of Missouri, Columbia, MO, United States
³Apple Inc., Cupertino, CA, United States
⁴University of Michigan Medical School, Department of Learning Health and Sciences, University of Michigan, Ann Arbor, MI, United States
⁵School of Information, University of Michigan, Ann Arbor, MI, United States

Although crucial for mathematical problem solving and long-term STEM achievement, visuospatial skills remain a significant challenge for many students in the United States. Therefore, it is critical to explore how spatial skill interventions can be integrated into mathematics curriculum. This research examines the effects of Project VisMO, a hands-on, origami-based curriculum and after-school program, on elementary school children's visuospatial skills, mathematical competencies, and mathematics anxiety and attitudes. An initial randomized control trial (RCT) of the online VisMO program, conducted during the COVID-19 pandemic with 179 elementary students, demonstrated promising results in enhancing spatial vocabulary and reducing mathematics anxiety. Two follow up studies of the VisMO program were conducted, featuring a 5-week and a 12-week intervention. Both studies confirmed improvements in spatial vocabulary, a reduction in math anxiety, and potential geometry gains. We discuss the need for further research on the in-person program and the importance of designing structured professional development for educators to enhance their self-efficacy and knowledge of incorporating visuospatial interventions into their teaching.

1 Introduction

Students need a strong mathematics foundation to have access to and become successful in science, technology, engineering, and mathematics (STEM) fields and make sense of STEM-related topics (National Council of Supervisors of Mathematics National Council of Teachers of Mathematics, 2018). Visuospatial skills contribute to many aspects of mathematical problem solving and are defined as the capacity to perceive, retain, retrieve, and mentally transform the static and dynamic visual information of objects and their relationships (Uttal et al., 2013; Verdine et al., 2014; Wai et al., 2009). Visuospatial ability is an important predictor of long-term achievement and attainment in STEM (e.g., Kell et al., 2013; Uttal et al., 2013; Wai et al., 2009), and visuospatial skills are needed more broadly in many STEM fields (e.g., Khine, 2017). Despite this, visuospatial ability is an area of particular struggle for many students in the United States (PISA, 2017).

1.1 Importance of spatial skills

The importance of visuospatial skills is not recognized in educational practices, and thus they remain a “major blind spot” in STEM education (National Research Council, 2006; Khine, 2017; Gagnier and Fisher, 2017). Longitudinal studies of individuals who pursue and are successful in STEM careers confirm the importance of visuospatial skills above and beyond mathematical and other competencies (Humphreys et al., 1993; Lubinski, 2010). Shea et al. (2001) found that 13-yr-old boys and girls with strong visuospatial abilities were more likely to complete STEM undergraduate degrees, independent of math and verbal competencies, than their peers with lower-visuospatial abilities. Moreover, the adolescents with strong visuospatial skills were more likely to be employed in STEM fields at 33 years of age. Later follow-ups showed that these individuals disproportionately contribute to innovation in STEM fields, as indexed by scientific publications and patents; again, independent of math and verbal competencies Kell et al., (2013). Enhancing visuospatial competencies has clear benefits in terms of long-term educational and occupational outcomes related to STEM.

Critically, these skills can be enhanced with training and practice (e.g., Wright et al., 2008). Uttal et al's (2013) meta-analysis indicated that visuospatial skills could be improved with a range of instructional methods (e.g., video games, puzzle play), and that the effects of training children (g = 0.61) were stronger than for both adolescents or adults (g = 0.44), suggesting that the investment to train children may have higher long-term returns.

In addition to independent contributions to success in STEM fields, visuospatial abilities contribute to aspects of mathematical development (e.g., Geary et al., 2023a,b; Lachance and Mazzocco, 2006; Li and Geary, 2013, 2017; Verdine et al., 2017; Zhang and Lin, 2017). State-of-the-art interventions now incorporate or simultaneously include instruction on supporting cognitive competencies (e.g., executive function) or skills (e.g., mathematics vocabulary) (Fuchs et al., 2013, 2016). The combined approach is very promising, but, at the same time, requires a deeper understanding of the cognitive processes and competencies that support mathematics learning which includes visuospatial skills. In other words, a deeper understanding on how to best incorporate visuospatial training into a mathematics curriculum is needed (Cheng and Mix, 2014; Jirout and Newcombe, 2015). The current study enhances our understanding of the relation between visuospatial abilities and mathematics development and does so through an visuospatial intervention related to spatial-related aspects of mathematics (e.g., spatial-related math vocabulary).

1.2 Why is spatial language particularly important

Though the relationships between mathematics and spatial skills are well-established (Geary et al., 2023a,b; Lachance and Mazzocco, 2006; Li and Geary, 2013, 2017; Verdine et al., 2017; Zhang and Lin, 2017), little is known about the mechanisms through which spatial skills influence mathematics performance. One factor is the influence of language skills, including spatial language, on academic achievement in general and on mathematics performance more specifically. Student knowledge of academic vocabulary predicts their performance and achievement in school beyond non-verbal cognitive ability, gender, general vocabulary, and socioeconomic status (Schuth et al., 2017; Uccelli et al., 2019; Ünal et al., 2021). These relations include mathematics-specific mathematics vocabulary and mathematics achievement (Powell et al., 2017).

Recent research reveals a significant contribution of mathematics language to students' mathematics development (e.g., Hornburg et al., 2018; Purpura and Logan, 2015; Toll and Van Luit, 2014). The former is typically defined as specialized language used to communicate and think about mathematics content (Turan and Smedt, 2022). Mathematical language comprises many subareas, including quantitative-focused, like “many” and “a few,” and spatial-focused, such as “under” and “above” (Gilligan-Lee et al., 2021). Many studies contain mathematics language measures that tap different areas simultaneously (e.g., Purpura and Logan, 2015). Even though combining different subareas is essential and provides a robust understanding of the role of mathematics language in mathematics development in general, examining each subarea is also necessary. For instance, many studies demonstrate a significant link between spatial abilities and mathematics. However, only a few studies consider the role of spatial language in the association (e.g., Gilligan-Lee et al., 2021; Ünal et al., 2023). Focusing on the spatial language aspect of mathematics vocabulary might provide unique information to address both mathematics and spatial performance difficulties.

A language to express relationships and properties of spatial concepts is crucial for developing spatial skills. Children not exposed to some form of spatial language show lower performance on tasks requiring spatial skills, even when those tasks do not require spatial vocabulary (Gentner et al., 2013). This suggests that there is a critical component of spatial language that facilitates the learning and development of spatial skills and cognition. Although spatial vocabulary is an important first step in developing spatial skills, it is not alone sufficient (Miller et al., 2016); therefore, spatial vocabulary should be integrated into more comprehensive programs and interventions.

1.3 Spatial skills interventions

Building a strong foundation in spatial skills early on sets children up for success in many areas: “diverse training strategies or programs including hands-on exploration, visual prompts, and gestural spatial training significantly foster young children's spatial skills” (Yang et al., 2020, p. 10). The benefits of these exercises extend far beyond playtime. Studies show “that spatial thinking is malleable” and that well-developed spatial skills lead to improved performance in mathematics (Gilligan et al., 2020). Strong spatial reasoning also translates to better problem-solving skills, as children learn to approach challenges from different angles to find different ways of understanding and solving problems. Yang et al.'s (2020) meta-analysis indicated that spatial training can lead to development within the Experience- Language-Pictorial-Symbolic-Application (ELPSA) framework (Lowrie et al., 2018). Furthermore, a strong grasp of spatial relationships might help to close the gender gap in some STEM fields (Sorby et al., 2018; Caiwei et al., 2023).

1.4 Role of origami

Origami is one approach for fostering spatial abilities and for developing a mathematics-specific spatial vocabulary. Origami, or “折纸”, has over one thousand years of history in China and Japan, and in other parts of the world, where parents and grandparents teach their children to fold paper after school (Franco, 1999). Origami can be conceptualized as classical or modular, where “classical” refers to paper folding in which a single piece of paper is folded to make a figure, such as a flower or bird, and “modular” refers to when small congruent units of paper are combined to form a three-dimensional figure (Beech, 2009; Tugrul and Kavici, 2002). Origami provides a low-cost, accessible, and flexible medium for children to engage in authentic spatial reasoning exercises (e.g., Lam and Pope, 2016; Tubis and Wang-Iverson, 2018).

Today, many contemporary applications of origami have been used as a rich resource in STEM around the world, including robotics, computational mathematics, and structural engineering (e.g., Lang et al., 2018). Purposeful origami is an inherently educational visuospatial task which consists of a combination of spatial rotations, 2D-to-3D transformation, visual perception, and eye-hand coordination activities (Boakes, 2009; Cakmak et al., 2014; Pearl, 2004; Taylor and Hutton, 2013).

Engaging in the art of paperfolding has a positive effect on students' spatial skills such as spatial visualization and orientation (Cakmak et al., 2014). Further, origami is just as effective as typical instruction in teaching spatial skills (Boakes, 2009). Limited studies have explored the relationships between origami and spatial and mathematical skills in general, but existing studies suggest positive impacts of origami on mathematics in general (Burte et al., 2017) and on specific mathematics skills, such as geometry (Boakes, 2009) and numerical ability (Krisztián et al., 2015). Although studies show similar outcomes between spatial skills through typical instruction and origami based instruction, origami based instruction offers a more engaging and equitable approach to teaching spatial skills, especially engaging students in difficult tasks (Cakmak et al., 2014).

Origami represents one creative way to teach math, and teaching math creatively has been shown to increase math achievement, increase positive attitudes toward math, and decrease math anxiety (Tok et al., 2015). Further, origami based instruction has improved students' attitudes and self-efficacy for spatial and math tasks (Kandil and Işiksal-Bostan, 2018), reduced stress and anxiety (Marji et al., 2023), and enhanced creative thinking and problem solving skills (Marji et al., 2023).

1.5 Reducing mathematics anxiety and improving mathematics attitudes

There are numerous barriers to spatial and mathematics learning. These barriers may be on a systemic level, such as access to early, quality mathematics instruction (James-Brabham et al., 2023), especially for some student populations (e.g., students who identify as Black) (Morgan et al., 2023). Barriers may also exist at the school level, with teachers who are unprepared to teach mathematics (Chang, 2015). At the student level, barriers could include learning challenges specifically related to mathematics or more generally. The former includes relatively poor visuospatial abilities (Geary et al., 2023b,c). The current study is focused on enhancing math-relevant spatial abilities and vocabulary and in doing so could potentially reduce mathematics anxiety, improve mathematics self-efficacy, and increase interest in learning mathematics. Improvements in these areas have the potential to further improve engagement with mathematics above and beyond gains in math-relevant spatial competencies (Shone et al., 2024; Zhang et al., 2019), whereas high self-efficacy and interest boost mathematics learning (Shone et al., 2024).

Mathematics anxiety is apprehension about engaging in mathematical activities, and is associated with lower mathematics performance (Zhang et al., 2019) even as young as second and third grade (Wu et al., 2012). Experiencing math anxiety early in mathematics learning can, in theory, impact achievement later (Gashaj et al., 2023), although cause-and-effect relations between mathematics anxiety and achievement are not well-understood. Most likely the relation is reciprocal such that early struggles with mathematics results in anxiety that in turn results in avoidance of mathematics (Geary et al., 2023c). Thus, interventions that reduce mathematics anxiety can make contributions to long-term mathematical development above and beyond specific skills taught in the intervention.

In general, being interested in learning enhances students' attention, goal setting, and level of performance (Hidi and Renninger, 2006). Interest can be initially triggered by certain tasks, settings, or projects with the ultimate goal that it moves from an external interest to a more sustained, deeper, individual interest that leads to re-engagement with the area overtime (Hidi and Renninger, 2006). This model of interest explains why early, engaging experiences that develop mathematics interest are important for later achievement (Fisher et al., 2012). Without developing interest in mathematics, students are not likely to put forth attention and effort, set goals, or engage in higher levels of learning.

Reductions in anxiety and increases in interest in mathematics should improve student self-efficacy or their beliefs about their ability to succeed in mathematics (Shone et al., 2024). Several practices have been shown to increase self-efficacy such as encouraging help-seeking (Miles and Vela, 2022) and differentiated instruction (Lai et al., 2020). From Bandura's model of self-efficacy (Bandura, 1977), students' mathematics self-efficacy can be enhanced by (a) providing opportunities that facilitate students' experiences of success (mastery experience), (b) showing students the success of others that they can relate to (vicarious experiences), (c) providing students with messages that they can do math and are good at it (social persuasion), and (d) helping students interpret physiological reactions to math as excitement rather than anxiety (physiological reaction). Thus, interventions that improve mathematical competencies and especially if they include one or more of these components should result in gains in mathematics self-efficacy.

2 Background

Project VisMO (Visuospatial skills, Mathematics, Origami) is a comprehensive, hands-on curriculum designed to develop and test the effects of an origami-based after-school program for elementary school children on their visuospatial skills, mathematical competencies, and mathematics anxiety and attitudes. The curriculum includes folding patterns, paper play activities, design journals for students to Ideate, Prototype, Reflect and Refine, inspirational material from origamists around the world who apply origami to various STEM fields, and animation videos following a young girl “Luna” and her friend “VisMO the Owl” on visuospatial adventures. The ten carefully designed progressive origami-based lessons build on each other and focus on promoting six visuospatial topics: Position and Orientation, Symmetry, Reflection, Spatial Relations, views and multiview projection (2D to 3D and 3D to 2D transformations), and rotation. Five main origami/paper play models were used for the study: (1) Introductory easy-to-fold animal models, (2) magazine box, (3) modular Sonobe units/cubes, (4) modular Tubis units, and (5) symmetrical paper cutting. Due to the need to shift to online learning during Covid-19, students were each sent a VisMO box with all of the supplies necessary to participate in the program virtually: origami paper, scissors, a ruler, markers, tape, content cards with spatial vocabulary, design journals, and stickers of VisMO and Luna.

The first two lessons use simpler models to build students' confidence and create a learning environment that embraces fun, patience, precision, and practice (Pearl, 1994). The lessons introduce origami, spatial concepts, and vocabulary through the implementation of basic origami folding steps with the standard Randlett–Yoshizawa diagramming system (Lang, 1988) for various paper manipulations (e.g., mountain/valley fold, repeat fold, turnover), and simple geometric constructions (e.g., line and angle bisector, perpendicular lines, reflection). These lessons lay the foundation for students to master spatial vocabulary, make sense of simple diagrams, and use gestures to assist in the verbal description of the sequence of folding procedures with their peers. As the lessons progress, students learn the concept of modular origami, assembling multiple identical locked units to construct larger, more intricate 2D or 3D objects. Modular origami involves the traditional folding techniques that enhance dynamic visualization and spatial understanding, and also encourages constructive play and the creative freedom of manipulating and “locking” units in various ways, potentially contributing to children's understanding of patterns, shapes, and spatial concepts (Ginsburg et al., 2001; Casey et al., 2008; Jirout and Newcombe, 2015).

The lessons are based on four research-informed approaches, which are utilized integratively in the VisMO program through “learning by doing” (Papert and Harel, 1991) and collaborative learning (Kyndt et al., 2013). The four approaches include the following:

(a) Reinforcing the use of spatial language: Creating opportunities for children to receive, understand, and apply spatial language within their learning environment plays a crucial role in developing their spatial skills (Pruden et al., 2011; Gentner et al., 2013). Constructive play, particularly when guided with diagrams, effectively encourages children to use spatial language (Ferrara et al., 2011). Instructors demonstrate and explain spatial language while introducing folding symbols and tasks. Students are encouraged to utilize the “SPORT” acronym (Shape, Position, Orientation, Relation, Transformation), developed as part of the VisMO curriculum, to practice describing their observations and folding steps to their peers using spatial language. The written instructions on the diagrams and the instructor's verbal guidance serve as models and scaffolds for the use of spatial language. This process of visualizing concepts and actively applying spatial vocabulary enhances understanding and improves memory and recall (Pearl, 2004).

(b) Strengthening the visuomotor integration skills for high fidelity visuospatial operations: The integration of vision and motor skills by interacting with physical objects helps students better direct their attention and manipulate the objects (e.g., Adolph, 2005; Piaget, 1953; Carlson et al., 2013). Students learn strategies to make careful folds and maintain the desired level of quality through attention to every stage of the folding process. Scaffolded by the instructor, students compare and evaluate the paper models made with precise folds and less precise folds, and then make adjustments or refinements.

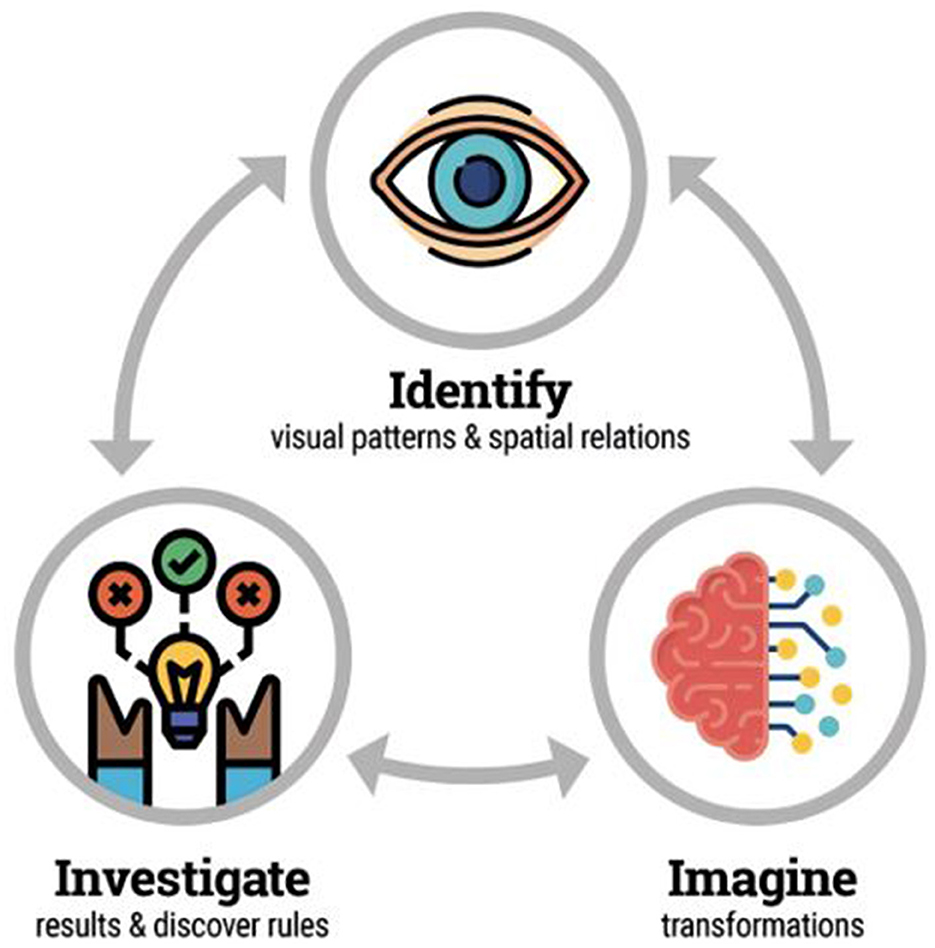
(c) Leveraging diagrams and sketching for visuospatial transformation: Diagrams are visual representations that highlight patterns, features, and landmarks and can help students navigate and process the dynamics of a transformation (Bremigan, 2005; Bobek and Tversky, 2016). Sketching is “a learner-generated external visual representation depicting any type of content, whether structure, relationship, or process, created in static two dimensions in any medium” (Ainsworth et al., 2011; National Research Council, 2012; Quillin and Thomas, 2015). In the VisMO lessons, students learn how to read folding diagrams. They practice navigating back and forth between 2-dimensional and 3-dimensional representations through a process we call the “3i process,” consisting of (1) identify, (2) imagine, and (3) investigate. Students first identify, using spatial vocabulary and the SPORT acronym, everything they notice within a diagram, usually a specific folding step. They then imagine, draw, and describe, before touching the paper, how they think their model will look after completing that step of the sequence. Finally, they investigate what actually happens when following the diagram, and unfold the paper model to examine the crease pattern and compare it to the folded model.

(d) Using gestures to scaffold visuospatial skill building: Accompanying language with appropriate gestures has been found to be an effective instructional strategy to facilitate children's learning of complex math concepts or procedures (e.g., Singer and Goldin-Meadow, 2005) and for supporting spatial reasoning and communication (e.g., Ehrlich et al., 2006; Sauter et al., 2012). Using gestures simultaneously with speech promotes students' reasoning process and enhances retention and generalizations (Wakefield et al., 2018). In the VisMO Lessons, instructors use gestures to help students visualize the folding steps and spatial concepts. For example, a class will turn hand movements into a song to remember the various orientations of an object such as “vertical, horizontal, diagonal.”

The current work explores impacts of this curriculum on students' visuospatial skills, mathematics-specific spatial language, and mathematics attitudes and anxiety. The first of three studies presents results of the initial implementation of the VisMO curriculum, which was rapidly shifted to an online format in response to the COVID-19 pandemic. Studies 2 and 3 were designed as preliminary pilot studies to explore the impacts of the curriculum delivered in-person through an informal science learning center and within an elementary school classroom. Table 1 provides an overview of consistent elements and adaptations across studies.

Table 1

Table 1. Comparing studies 1, 2, and 3.

In each study, teachers received training to implement the VisMO curriculum. For Study 1, teachers participated in a certification process that included initial learning of key concepts and observations of curriculum implementation with feedback. For Studies 2 and 3, teachers completed online modules for each lesson led by a master teacher from Study 1. Each module presented the key concepts for a lesson, modeled teaching the curriculum, and required the teachers to perform the skills themselves for feedback before curriculum implementation. The content of key concept training and first experiencing the curriculum as a learner were consistent components of the teacher training across studies to increase implementation fidelity.

3 Study 1

3.1 Research questions

The following research questions guided our exploration of the impacts of the newly developed VisMO curriculum:

RQ1: What are the immediate and sustained impacts of VisMO lessons on students' visuospatial skills and spatial vocabulary?

RQ2: What are the immediate and sustained impacts of VisMO lessons on students' attitudes toward mathematical learning and their mathematics anxiety?

RQ3: Do the benefits of VisMO lessons transfer to students' mathematical learning?

RQ4: Are there subgroup differences in the immediate or sustained impacts of VisMO lessons?

3.2 Methods

3.2.1 Participants

Students were recruited primarily from San Diego Unified School District and Los Angeles Unified School District, accompanied by a few other nearby school districts. A total of 179 students, aged 9–11 (M_age = 10.35) participated in the study. Most were primarily English speakers (n = 125; 69.8%), and nearly a quarter of them identified as primarily speaking a language other than English. Those who spoke another language most frequently reported speaking Spanish (n = 23; 48%). Other reported languages were Vietnamese (n =3), Japanese (n =2), Hindi (n =1), German (n = 1), French (n = 1), Urdu (n = 1), Chinese (n = 1), Tigrinya (n = 1), and Telugu (n = 1). Slightly more than half of participating students identified as male (n = 96; 53.6%) with 75 students identifying as female (41.9%). Two students preferred not to identify their gender.

Students were randomly assigned to two conditions; the Owl treatment group received VisMO lessons, while the Elephant control group received literacy-based social-emotional lessons. A total of 88 students were assigned to the Owl group, with 82 in the Elephant group.

3.2.2 Instruments

Students completed measures of mathematics, spatial skills, spatial vocabulary, mathematics attitudes and working memory.

3.2.3 Mathematics measures

Mathematics measures assessed arithmetic fluency, fraction arithmetic, whole number and fraction number line placement, equality problems, and geometry.

Arithmetic fluency included 24 whole-number addition (e.g., 87 + 5), subtraction (e.g., 35 – 8), and multiplication (e.g., 48 × 2) problems. The problems were presented with an answer, and the student responded Yes (correct) or No (incorrect). Half the problems were incorrect, with the answer +1 or 2 from the correct answer. Students had 2 min to solve as many problems as possible. A composite arithmetic fluency score was based on the number correct across the three operations.

Fraction fluency included 24 fractions addition (e.g., $\frac{1}{4} + \frac{1}{8} = \frac{3}{8}$ ) and fractions multiplication problems (e.g., $2 \frac{1}{2} \times \frac{1}{4} = \frac{5}{8}$ ). The problems were presented with an answer, and the student responded Yes (correct) or No (incorrect). Half the problems were incorrect, with error foils based on common fractions errors (e.g., $\frac{1}{4} + \frac{2}{4} = \frac{3}{8}$ ). A composite fractions arithmetic score was based on the number correct.

Whole number line placement included 26 items that asked students to place a whole number on a number line displaying 0–1,000. To score items, accuracy for each item was scored using the formula $(\frac{| E s t i m a t e - T a r g e t N u m b e r |}{1000}) - 1$ according to recommendations by Siegler and Booth (2004). Higher positive scores indicated better performance.

Fraction number line placement asked students to place 10 fractions on a number line displaying 0-5. Accuracy of each placement was scored using the formula $(\frac{| E s t i m a t e - T a r g e t N u m b e r |}{5}) - 1$ . Higher positive scores indicated better performance.

Equality problems assessed students' understanding of the meaning of “=” using problems in non-standard formats, such as 8 = __ + 2 – 3 (Alibali et al., 2007; McNeil et al., 2019). We used the 10-item measure developed by Scofield et al. (2021), where items are presented in a multiple-choice format (4 options). The score was the mean percent correct for the 10 items.

Geometry was assessed using items released from the National Assessment of Educational Progress (NAEP, n.d.) 4th grade assessment. After item response theory analyses conducted by our team (see Ünal et al., 2023), we used 19 of the 20 released items.

3.2.4 Spatial skills measures

Spatial skills measures included measures of visual spatial attention, mental rotation, spatial visualization, and spatial transformation.

Visual spatial attention was assessed using the Judgment of Line Angle and Position test (JLAP; Collaer et al., 2007). The task requires students to match the angle and position of a target line to one of the 15-line options in an array below the target line. There were 20 sequentially presented test items, with students selecting the item that matched the angle and position of the target. Each trial began immediately after the student's response, or at the 10-s time limit. The score was the number of correct trials.

Mental rotation was assessed with 24 items generated by the Ganis and Kievit (2015) software program. Each item presented a baseline and target figure that had been rotated between 0 and 150 degrees, where students were asked if the two figures were the same or different. The score was the number of correct responses.

Spatial visualization was assessed using the Paper Folding Task (PFT; Ekstrom et al., 1976), where students were presented with 10 items asking them to imagine how a paper square would look after being folded and hole-punched. The score was the number of correct responses.

Spatial transformation was designed by Ünal et al. (2023) to measure students' ability to identify two-dimensional representations of front, right, and top views of a figure. Students completed 16 items on the final scale, and the score was the number of correct responses.

3.2.5 Spatial vocabulary

We used Ünal et al.'s (2023) measure of elementary students' mathematics-specific spatial vocabulary. The scale includes 20 items that ask students to demonstrate their understanding of spatial terms such as recognizing parallel or horizontal lines and using simple graphs to identify adjacent objects (Figure 1). The validation of this scale showed high correlations between items (r = 0.99, p < 0.001) and high internal consistency (α = 0.81).

Figure 1

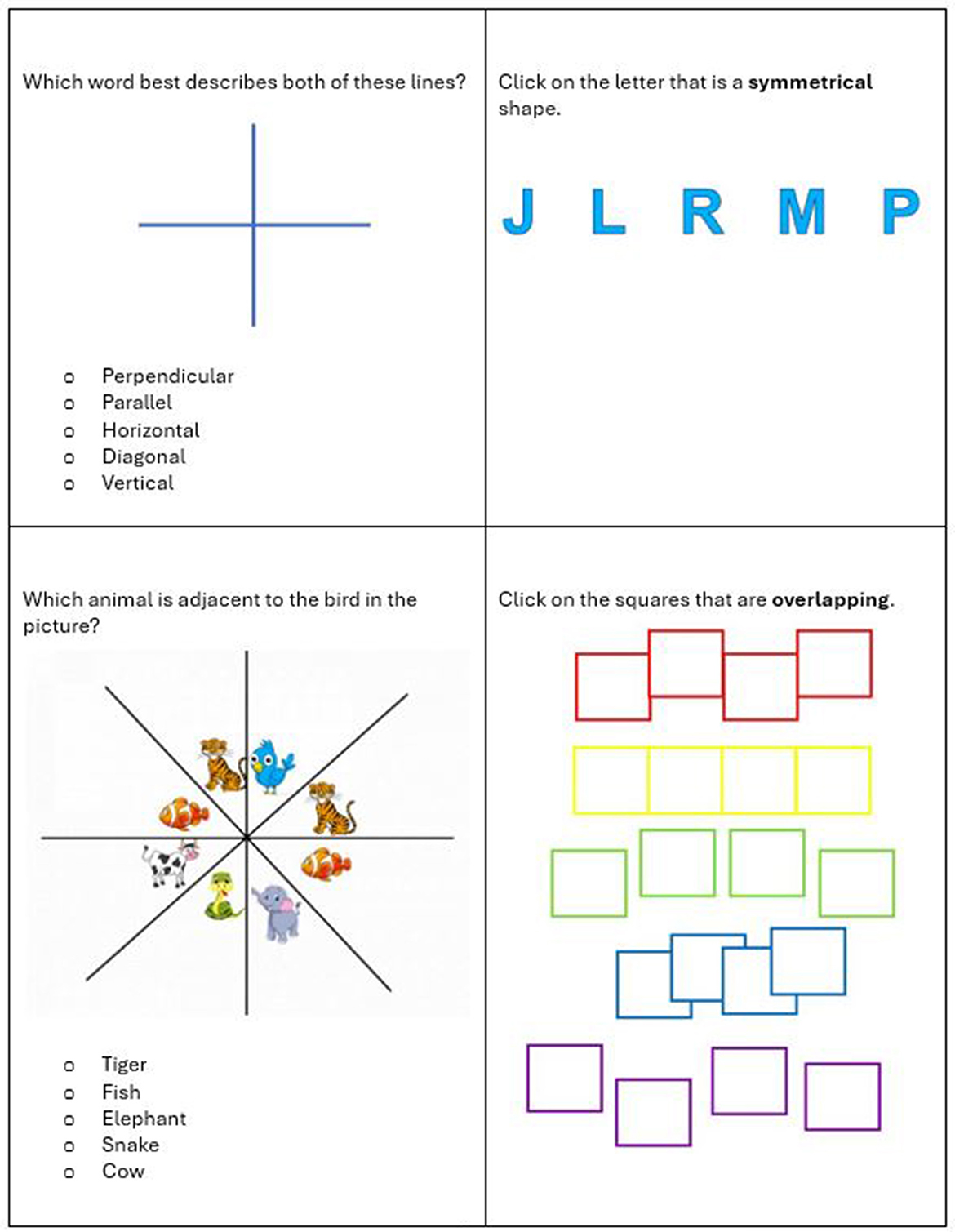
A four-panel puzzle image. Top left: A blue perpendicular cross with a multiple-choice question about line descriptions. Top right: Letters J, L, R, M, P with a prompt to identify the symmetrical letter. Bottom left: Animal icons (tiger, fish, cow, bird, snake, elephant) around a wheel, asking which is adjacent to the bird. Bottom right: Colorful stacked squares, prompting the selection of overlapping ones.

Figure 1. Sample spatial vocabulary items (Ünal et al., 2021).

3.2.6 Mathematics attitudes

3.2.6.1 Mathematics interest

The nine items were from the student attitudes assessment of the Trends in International Mathematics and Science Study (TIMSS; Martin et al., 2015). The items assessed interest in mathematics (e.g., “I learn many interesting things in mathematics,” “I like mathematics”). The items were on a 1 (Disagree a lot) to 4 (Agree a lot) scale, with negatively worded items (e.g., “Mathematics is boring”) reverse coded. The score was the mean across items.

3.2.6.2 Self-efficacy

The 9 items were from the student attitudes assessment of the TIMSS (Martin et al., 2015). The items assessed mathematics self-efficacy (e.g., “I usually do well in mathematics,” “I learn things quickly in mathematics”). The items were on a 1 (Disagree a lot) to 4 (Agree a lot) scale, with negatively worded items (e.g., “I am just not good at mathematics”) reverse coded. The score was the mean across items.

3.2.6.3 Math anxiety

Ramirez et al. 's (2013) 8-item measure was used to assess students' mathematics anxiety (e.g., “How do you feel when taking a big test in math class?”, “How do you feel when you have to solve 27 + 15?”). Students responded by clicking on one of the three options in Figure 2, and thus higher scores (1–3) reflected lower anxiety.

Figure 2

Three circular emoticons are depicted. The first emoticon shows a worried expression with wavy mouth and raised eyebrows. The second has a neutral expression with a straight line for a mouth. The third shows a slight smile with relaxed eyebrows.

Figure 2. Response options for math anxiety scale.

3.2.7 Procedure

Students in each group completed the measures described above before receiving the activities of their condition (e.g., VisMO lessons for Owl, literacy/SEL lessons for Elephant). Students completed these measures again after finishing the curriculum and a last time at a 1-year follow-up. Delivery of the VisMO lessons for both Owl and Elephant groups was done over 10 sessions, 1.5 h per session. Due to COVID-19, the curriculum was taught online using Zoom and Nearpod, an online educational tool for students to interact with the lessons. Each lesson would open with a check-in on how the students were doing that day and introduce a different visuospatial concept using an origami model and the 3i process created by the curriculum team (identify, imagine, investigate). Students would use Nearpod to go through the 3i process. This process is shown in Figure 3. For example, Identify what they saw when looking at a folding diagram; Imagine what they thought the result of performing the folding step would look like upon completion (drawing it in Nearpod); Investigate by completing the fold and comparing it to the previous drawing; and discussing the results with each other over Zoom. Teachers also used the online platform Seesaw to communicate information and share materials with parents.

Figure 3

Diagram on the left shows a cycle of “Identify,” “Imagine,” and “Investigate” for visual patterns and problem-solving.

Figure 3. The visMo 3i process: Identify, imagine investigate.

3.3 Results

Data for research questions 1, 2, and 3 were analyzed using a series of hierarchical linear models (HLM). HLM was conducted using the “nlme” package (Pinheiro et al., 2022) in R Core Team (2021). HLM was chosen to account for the nesting structure of students within different elementary schools. Students were nested within nine elementary schools, with n_{largestcluster} = 68 and n_{smallestcluster} = 6. Intraclass correlation coefficients were calculated for math and spatial outcomes to explore the impact of different schools. For spatial vocabulary, ICC = 0.13, with ICC = 0.12 for math/geometry, and 0.17 for math anxiety. These ICCs indicate that there is variance due to nesting within schools, supporting the use of HLM to answer these research questions (Finch et al., 2014). Question 4 was assessed by including subgroup membership as a Level 1 predictor. Separate HLM models were run for immediate (post-test) and sustained (follow-up) impacts with each model including treatment group, gender, language, and pre-test score as fixed level 1 predictor variables. In spatial outcome models (RQ1), working memory was also included as a predictor. Block, representing school, was included as a Level 2 predictor in all models. All variables were scaled prior to calculating models. Missing values were omitted from analyses, resulting in different sample sizes for each model fit to the data. Table 2 displays means, standard deviations, and reliability coefficients for each measure.

Table 2

Table 2. Descriptive statistics for outcome measures.

3.3.1 RQ1: What are the immediate and sustained impacts of VisMO lessons on students' visuospatial skills and spatial language?

For spatial outcomes (Table 3), Model 1 included treatment group, gender, language, and pre-test. Model 2 adds working memory covariates. Model 3 assesses sustained impacts. The results revealed an immediate impact of VisMO lessons on students' spatial vocabulary. Using AIC and BIC values, Model 2 provided a better fit to the data, and demonstrated a significant effect of group on post-test spatial vocabulary scores [β = −0.26, t(93) = −2.10, p = 0.03], with post-test scores higher for those participating in VisMO lessons compared to the control lessons.

Table 3

Table 3. Spatial outcome models.

At the same time, participating in VisMO lessons did not have an immediate or sustained effect on students' spatial visualization, visual-spatial attention, mental rotation, or spatial transformation skills.

3.3.2 RQ2: What are the immediate and sustained impacts of VisMO lessons on students' attitudes toward mathematical learning?

For math attitudes outcomes (Table 4), Model 1 assessed immediate impacts, while Model 2 assessed sustained impacts at a 1-year follow-up. VisMO lessons did not have an immediate or sustained impact on math interest, but showed an immediate impact on math self-efficacy [β = 0.28, t(95) = 2.39, p = 0.02] and math anxiety [β = 0.26, t(95) = 2.09, p = 0.04]. For math self-efficacy, students who participated in the control group showed higher levels of self-efficacy, but this was not sustained over time. For math anxiety, students who participated in the VisMO lessons showed lower math anxiety, but this was not sustained over the year.

Table 4

Table 4. Math attitudes outcomes.

3.3.3 RQ3: Do the benefits of VisMO lessons transfer to students' mathematical learning?

VisMO lessons did not show any significant immediate or sustained impacts on any of the mathematics outcomes assessed (arithmetic fluency, fraction fluency, whole number and fraction number line placement, geometry, and equality problems; Table 5).

Table 5

Table 5. Mathematics outcome models.

3.3.4 RQ4: Are there subgroup differences in the immediate or sustained impacts of VisMO lessons?

Regarding spatial skills, Model 2 indicated some significant differences in spatial transformation based on student gender [β = −0.35, t(92) = −2.56, p = 0.01] and language status [β = −0.39, t(92) = −2.26, p = 0.03], with male students and students who prefer speaking a language other than English at home showing higher transformation skills. Regarding mathematics attitudes, there were no differences in math interest, math self-efficacy, or math anxiety based on student gender or language status. Regarding mathematics skills, students who prefer to speak a language other than English at home showed higher accuracy in placing whole numbers on a number line [β = −0.35, t(92) = −2.06, p = 0.04].

4 Study 2

4.1 Background

Study 2 explored the efficacy of a 5-week in-person version of the VisMO curriculum with a diverse student population. The goal was to assess whether an in-person intervention might have higher efficacy than the online intervention.

4.2 Methods

4.2.1 Participants

Participants for this study were 75 upper elementary students (grades 3–5) who attended sessions at a non-profit science institute that serves elementary schools in the San Diego Unified School District. Students in this area are primarily those belonging to minority racial and ethnic identities (38% Latinx/Hispanic, 10% African American/Black, 9% Asian, 2% Native American, 12% identifying as multiple races, and 1% Caucasian; Retrospective Self-Change Student Survey 2020–2022). Additionally, a large proportion of this student population identifies their primary language to be other than English (Retrospective Self-Change Student Survey 2020–2022).

4.2.2 Instruments

To maximize the amount of instructional time available to students and facilitators, students completed abbreviated versions of the spatial vocabulary, mathematics anxiety, and geometry measures described in Study 1. For spatial vocabulary, students completed 6 items. For mathematics anxiety, students completed 4 items along the same facial scale presented in Figure 1. Students solving 2 geometry questions.

4.2.3 Procedure

Students completed pre-test measures before attending VisMO lessons at the science institute. Students received sessions once per week for 5 weeks. Sessions lasted approximately 1 h each and covered four visuospatial topics: Position and Orientation, Symmetry, Reflection, and Spatial Relations. Four main origami/paper play models were used: (1) Introductory easy-to-fold animal models, (2) magazine box, (3) modular Sonobe units/cubes, and (4) symmetrical paper cutting. This version of the VisMO curriculum was very similar to the online original study, the difference being that the curriculum was condensed to be more of an introduction to each of the visuospatial topics. After the last session, students completed post-test measures.

4.3 Results

Due to the within-subjects design of Study 2, findings were analyzed using dependent samples t-tests and calculating Cohen's d for each of the three outcomes: spatial vocabulary, mathematics anxiety, and geometry. Students showed significant pre-to-post-test gains in spatial vocabulary, t(48) = 2.24, p = 0.03, d = 0.32, a reduction in mathematics anxiety [t(48) = 1.09, p = 0.28, d = 0.16], and some geometry gains [t(48) = 0.42, p = 0.68, d = 0.06], Although the latter two differences were not statistically significant, the patterns suggested that an in-person intervention might be more effective than the original online intervention.

5 Study 3

5.1 Background

Given the promising results for the 5-week in-person intervention, a third study examined the impacts of a 12-week VisMO intervention delivered in a traditional classroom setting. The intervention included 10 origami sessions and two sessions for pre- and post-test assessments.

5.2 Methods

5.2.1 Participants

Classroom teachers within a large city charter school in California agreed to participate in the study. A total of 4 teachers completed 14 h of online training with a VisMO instructor, implemented curriculum, and had students complete study instruments before and after the curriculum. One teacher taught third grade, one fourth, and two taught fifth grade at the charter school. A total of 44 students from these classrooms were included in analyses. The charter school has high minority enrollment (81%), with a majority of students enrolled identifying as Hispanic/Latino. Approximately 1 out of 5 (21%) students enrolled qualifies as economically disadvantaged.

5.2.2 Instruments

Instrumentation for this study closely modeled the instruments used in Study 1. Students completed full measures of mathematics interest, mathematics self-efficacy, mathematics anxiety, spatial vocabulary, spatial visualization, spatial transformation, arithmetic fluency (whole number only), geometry, and whole and fraction number line placement. Students completed all measures online during classroom time.

5.2.3 Procedure

Students completed pre-test measures before receiving VisMO lessons in class. Students received sessions once per week over 12 weeks, during their regular geometry class time. Sessions lasted approximately 1 h each and covered four visuospatial topics: Position and Orientation, Symmetry, Reflection, and Spatial Relations. Four main origami/paper play models were used: (1) Introductory easy-to-fold animal models, (2) magazine box, (3) modular Sonobe units/cubes, and (4) symmetrical paper cutting. This version of the VisMO curriculum was very similar to the online original study, the difference being that the curriculum was condensed to be more of an introduction to each of the visuospatial topics. After the last session, students completed post-test measures.

5.3 Results

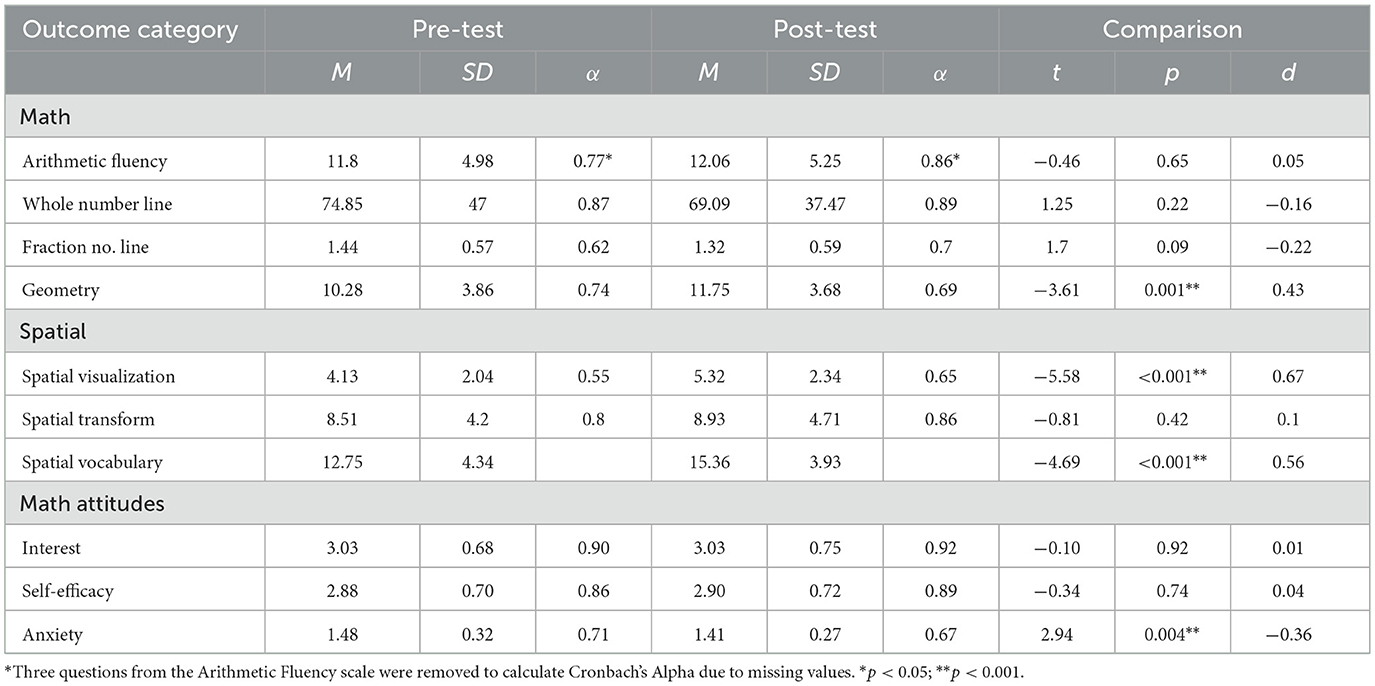
Due to the within-subjects design of Study 3, findings were analyzed using dependent samples t-tests and calculating Cohen's d for each of the outcomes (Table 6). Generally, participation in VisMO was associated with pre-to-post gains in math-specific spatial vocabulary (d = 0.56, p < 0.001) and reductions in mathematics anxiety (d = 0.36, p < 0.005). We also found gains in spatial visualization (d = 0.67, p < 0.001) and on a geometry test (d = 0.43, p < 0.001). At the same time, there were no significant gains on various arithmetic skills (ps > 0.08), suggesting the intervention did not result in a general halo effect, but rather specifically influenced spatial-related areas of mathematics and math anxiety.

Table 6

Table 6. Subscale descriptives.

6 Discussion

Children's engagement in an online version of the origami-based VisMO lessons improved their spatial vocabulary and reduced their mathematics anxiety, but did not result in immediate gains in specific mathematics skills (arithmetic fluency or number line placement of whole numbers or fractions) or improve their mathematics attitudes (interest, self-efficacy). A 1-year follow-up, however, suggested that the gains in spatial vocabulary and mathematics anxiety may fade, though only 1 out of every 3 participating students completed follow up measures and thus the fade out is uncertain. Nevertheless, smaller-scale in-person interventions suggested the online version of the intervention might have underestimated its potential benefits. In particular, the 12-week in-person intervention confirmed at least short-term gains in spatial vocabulary and reductions in mathematics anxiety, as well as potential gains in geometry, indicating that a follow-up RCT is warranted.

6.1 Treatment effects

Origami was designed as an in-person medium for teaching spatial language and skills due to the very hands-on experience of paper folding and its obvious spatial components. The need to move the VisMO lessons online, which involved adapting the paper folding instruction to a virtual classroom, may have limited the impact of the VisMO curriculum, as the original design included collaborative student-teacher and student-student interactions that could not be fully realized in an online format. Thus, once the COVID restrictions were lifted, we explored the efficacy of in-person VisMO lessons. In our first small-scale study, students received an abbreviated (due to constraints of their program) 5 week, in-person version of VisMO. As noted, the results confirmed at least short-term gains in spatial vocabulary (d = 0.32) and reductions in math anxiety (d = 0.16), and suggested potential gains in formal geometry (d = 0.06). The longer 10 week in-person intervention with full pre-test and post-test data revealed larger (relative to the 5-week intervention) gains in math-specific spatial vocabulary (d = 0.56) and reductions in mathematics anxiety (d = 0.36), suggesting intervention dosage and format (in-person vs. online) are important. In contrast to the online intervention, we also found strong gains in spatial visualization (d = 0.67) and on the geometry test (d = 0.43). The latter was larger than found for abbreviated in-person intervention, in keeping with dosage effects. At the same time, there were no significant gains on various arithmetic skills (ps > 0.08), suggesting the intervention did not result in a general halo effect for mathematics, but rather specifically influenced spatial-related areas of mathematics and math anxiety. Including more general mathematics outcomes allowed for divergent validity in showing that spatial and mathematics skills are distinct. Given this distinction, we did not expect intervention effects for arithmetic or fraction fluency. Number line performance could be related to spatial abilities, but our failure to find an effect might be because the intervention did not involve spatial manipulation of numerals or fractions. These other areas would be covered as part of their regular curriculum. The intervention itself was designed as a supplement. Overall, the gains were larger than with the online format, suggesting that in-person programs may be more effective, but more research is necessary to determine this with certainty.

6.2 Fadeout

Fadeout effects are common with educational interventions (Bailey et al., 2017) and is a field-wide issue that awaits resolution. The same pattern emerged with our online intervention. The full extent of any fadeout effects for our intervention could not be evaluated due to attrition at the 1 year follow-up. Despite continued contact with participants and small appreciation gifts throughout the study period, only 53 out of 179 (or 30%) of students returned for the follow-up assessment session. The attrition at post-test and at follow-up could have several impacts, including creating a biased sample (though attrition occurred across treatment conditions), smaller sample sizes, and lower power. Small sample sizes for most sustained impact models led to greater standard errors in estimating fixed effects and lower power likely made it difficult to make unbiased predictions about the sustained impact of VisMO lessons on spatial skills and mathematics attitudes. Future work should assess sustained impacts at a shorter follow-up period and, ideally, with a larger sample size.

6.3 Learning differences

While recruiting and assessing students, there were some learning differences that we did anticipate and included in our models. For example, each of our models included whether the student responded that they preferred to speak a language other than English at home, denoting our English Language Learner (ELL) sample. Across models, we found that the impacts of the VisMO curriculum did not differentially benefit the ELL sample as we defined them. However, we cannot discount the possibility of differences if we were to use alternative definitions of ELL such as getting language records from participating schools or asking parents whether their student is considered an ELL in their school system. Another factor that may have impacted our estimation is that we did not screen or ask parents if students had any significant learning impairments or difficulties that may have affected their ability to understand the assessment materials, VisMO lessons, or perform specific mathematics and visuospatial skills.

6.4 Teacher training

As STEM education needs are continuously evolving, professional development opportunities are important for bridging skills gaps and increasing teachers' self-efficacy for new STEM content knowledge. Although STEM professional development sessions have generally improved teachers' perceptions of STEM knowledge (Zhang et al., 2023) and their self-efficacy (Zhou et al., 2023), fewer opportunities are available for teachers to develop skills in facilitating students' exploration and for teachers to engage in that exploration for themselves. Additionally, content areas like visuospatial skills are less familiar to most teachers, reducing the likelihood that they feel confident engaging students in learning activities targeting those skills. Building this confidence is critical as some work has shown that teachers lacking self-confidence are more likely to use teaching strategies that focus on transfer of knowledge rather than those that develop critical thinking (Dilekli and Tezci, 2016), an essential skill for success in STEM.

In developing the curriculum for VisMO, we asked teachers about their experiences. Teachers shared that VisMO changed the way they thought about teaching content—thinking more as facilitators and learners themselves. For example, one teacher shared:

“My default is always to ask more questions like I think Shifting mindset as teachers of like we're not necessarily there to give students the answers, because if we were, we would just tell them and they would be able to learn it and we know that learning doesn't work that way. But shifting teachers' mindsets to think of themselves more as facilitators.”

Another teacher stated “I was like Oh, my goodness, how am I going to learn and so I was also on the same boat as them right so it's, I think, providing that space helps a lot.” Lastly, teachers felt that these experiences with unfamiliar content as a facilitator and a learner made them more mindful of other content areas: “I think it also made me more mindful of as a teacher, like the way that I teach math and geometry with VisMO it's made me like rethink how I teach my kiddos.”

Overall, future training should explore how professional development can be structured for teachers to learn skills in areas that are less familiar, like visuospatial skills, and how that experience influences their self-efficacy and teaching practice. Future training should include formal implementation fidelity checks to ensure that key aspects of the curriculum are consistently delivered across modalities and within both formal and informal learning environments.

7 Conclusions

Origami lessons delivered in multiple formats (online and in person) show positive impacts on spatial-related mathematics skills, vocabulary, and students' experience of mathematics anxiety. These promising results suggest the need for additional in person explorations to advance our understanding of the mechanisms and relationships between mathematics, origami, and anxiety - an understanding that has the potential to advance STEM engagement.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

The studies involving humans were approved by University of San Diego Institutional Review Board. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants' legal guardians/next of kin.

Author contributions

LR: Conceptualization, Writing – review & editing, Formal analysis, Methodology, Writing – original draft, Validation. DG: Data curation, Conceptualization, Writing – review & editing, Funding acquisition, Writing – original draft. YL: Funding acquisition, Writing – review & editing, Methodology, Conceptualization. PM: Supervision, Conceptualization, Data curation, Investigation, Writing – review & editing, Funding acquisition, Project administration, Writing – original draft. RO: Project administration, Writing – review & editing, Investigation. DS: Formal analysis, Validation, Writing – review & editing, Software. ZÜ: Writing – review & editing, Formal analysis. VP: Conceptualization, Writing – review & editing, Funding acquisition.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the National Science Foundation under Grant No. 1920821—Funding awarded from the National Science Foundation was used to develop the VisMO program and conduct all research activities and by the Jacobs Institute for Innovation in Education.

Conflict of interest

YL was employed by Apple Inc.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adolph, K. E. (2005). “Learning to learn in the development of action” in Action as an Organizer of Learning and Development, eds. J. J. Rieser, J. J. Lockman, and C. A. Nelson (Mahwah, NJ: Erlbaum), 91–122.

Google Scholar

Ainsworth, S., Prain, V., and Tytler, R. (2011). Drawing to learn in science. Science 333, 1096–1097. doi: 10.1126/science.1204153

PubMed Abstract | Crossref Full Text | Google Scholar

Alibali, M. W., Knuth, E. J., Hattikudur, S., McNeil, N. M., and Stephens, A. C. (2007). A longitudinal examination of middle school students' understanding of the equal sign and equivalent equations. Math. Think. Learn. 9, 221–247. doi: 10.1080/10986060701360902