- School of Mathematics, University of Birmingham, Birmingham, United Kingdom
In recent years, reducing students’ mathematics anxiety has become an objective to improve teaching quality and reduce academic stress. Mathematics anxiety is the feeling of tension or fear when students are dealing with mathematical tasks. These negative emotions may hinder students’ learning efficiency and lead to lower academic achievement. This mini-review aims to analyze the roles of teaching approaches and curriculum designs in reducing mathematics anxiety. Furthermore, this mini-review followed the PRISMA guidelines and screened 35 relevant literature sources from Google Scholar, Web of Science, and Scopus for data analysis. According to the analysis, teachers use flat teaching and the REACT model to promote students’ engagement and confidence. Specifically, REACT is an acronym for relating, experiencing, applying, cooperating, and transferring. In contrast, teachers should design application-oriented and experiential curriculums to connect mathematics with real-world contexts through practical exercises. By reading this mini-review, teachers can better understand the concept of mathematics anxiety and its impact on students’ learning. Peer researchers can also identity the limitations of the literature in this area.
1 Introduction
Mathematics anxiety is a significant factor influencing students’ academic achievement and psychological well-being (Zhang et al., 2019). Research indicated that mathematics anxiety not only reduces students’ performance in mathematics but also hinders their motivation and undermines their confidence (Živković et al., 2023). The traditional teaching approach tends to focus on knowledge transfer and standard answers, often neglecting students’ emotional needs and cognitive differences (Smith, 2023). “Dyer and Nobeoka define knowledge transfer as knowledge sharing among people which implies giving and taking of information” (Smirnova, 2014, p. 4). However, students may experience feelings of nervousness, fear, and avoidance during the learning process when teachers adopt the traditional teaching approach (Putwain and Wood, 2023). Teachers could reduce students’ mathematics anxiety by using effective methods. Such strategies include the use of appropriate instructional methods and explicit curriculum structures (Hutton, 2020).
Richardson and Suinn (1972) first introduced the concept of mathematics anxiety and developed the math anxiety scale. Subsequently, Greenwood (1984) suggested that teachers may cause anxiety by overemphasizing memorizing formulas and applying rote rules. Similarly, Vinson (2001) believed that when students’ anxiety decreases, their math ability increases. Rossnan (2006) further explained that the causes of math anxiety as students’ previous negative experiences of learning math in the classroom or at home. In addition, Frenzel et al. (2007) found that students who believe in their ability to succeed in mathematics tend to report lower levels of anxiety. Furthermore, Mutodi and Ngirande (2014) equated severe math anxiety with test anxiety and three causes including poor test-taking strategies, inadequate preparation and psychological stress.
In recent years, many studies have focused on the effects of math anxiety (Mutodi and Ngirande, 2014; Namkung et al., 2019). However, few researchers explored the effect of curriculum designs in reducing students’ mathematics anxiety (Passolunghi et al., 2020). In addition, many researchers pay insufficient attention to the implementation process of teaching (Pettigrew et al., 2013). They also lacked analysis such as teacher behaviors, classroom interaction, and student feedback (O’Hara et al., 2022; Zhang and Cao, 2022). Furthermore, small sample sizes in existing research may increase sampling bias and limit the validity of conclusions (Lin, 2018; Vasileiou et al., 2018). “Sampling bias means that the samples of a stochastic variable that are collected to determine its distribution are selected incorrectly” (Panzeri et al., 2008, p. 1).
The purpose of this study is to review the literature on math anxiety and its mitigation measures. It focuses on analyzing teacher behaviors and classroom interactions to better understand the learning process. It seeks to identify effective teaching strategies by examining the impact of various instructional methods in the mathematics classroom. Secondly, I aim to identify and evaluate curriculum design features that help reduce mathematics anxiety.
To achieve these objectives, this study is guided by the following questions: (1) What teaching approaches can teachers use to help students reduce mathematics anxiety? (2) Which curriculum designs would benefit students with mathematics anxiety?
This study has three primary contributions. First, it provides practical insights for teachers to design and refine curriculum structures to reduce students’ mathematics anxiety. Secondly, it identifies research gaps that allow scholars to better understand the limitations of current studies. Finally, students could build a sense of self-efficacy and engagement in mathematics learning. “Albert Bandura defined self-efficacy as people’s judgements of their capabilities to organize and execute courses of action required to attain designated types of performances” (Bandura, 1986, p. 94). They may ultimately improve academic performance.
The remainder of this paper is divided into three sections. Section 1 outlines the methodological approach, including data collection procedures. Section 2 offers a critical analysis of how various instructional strategies and curriculum designs influence students’ mathematics anxiety. Finally, Section 3 presents the main findings and discusses implications for future research and educational practice.
2 Method
2.1 Search strategy
The process of article selection followed the Preferred Reporting of Items for Systematic Reviews and Meta-Analyses (PRISMA) Statement (Page et al., 2021). A comprehensive search was conducted in Scopus and Web of Science on March 17, 2025, to identify peer-reviewed articles focusing on mathematics anxiety and instructional strategies. Search terms were operationalized using multiple permutations of relevant keywords, informed by previously validated search strategies. For mathematics anxiety, I referenced previous studies by Piccirilli et al. (2023) and Newstead (1998), which explore its impact on students’ mathematical performance and learning experiences. For students, I used classification by Lalayants (2012) and Rancer et al. (2013), which target education research focusing on students at different ages. For teaching approaches, I analyzed previous research by Furner and Gonzalez-DeHass (2011) and Peterson and Janicki (1979), which highlight effective strategies to help students manage mathematics anxiety. In short, employing validated search terms from prestigious journals helped the capture of appropriate citations in my searches.
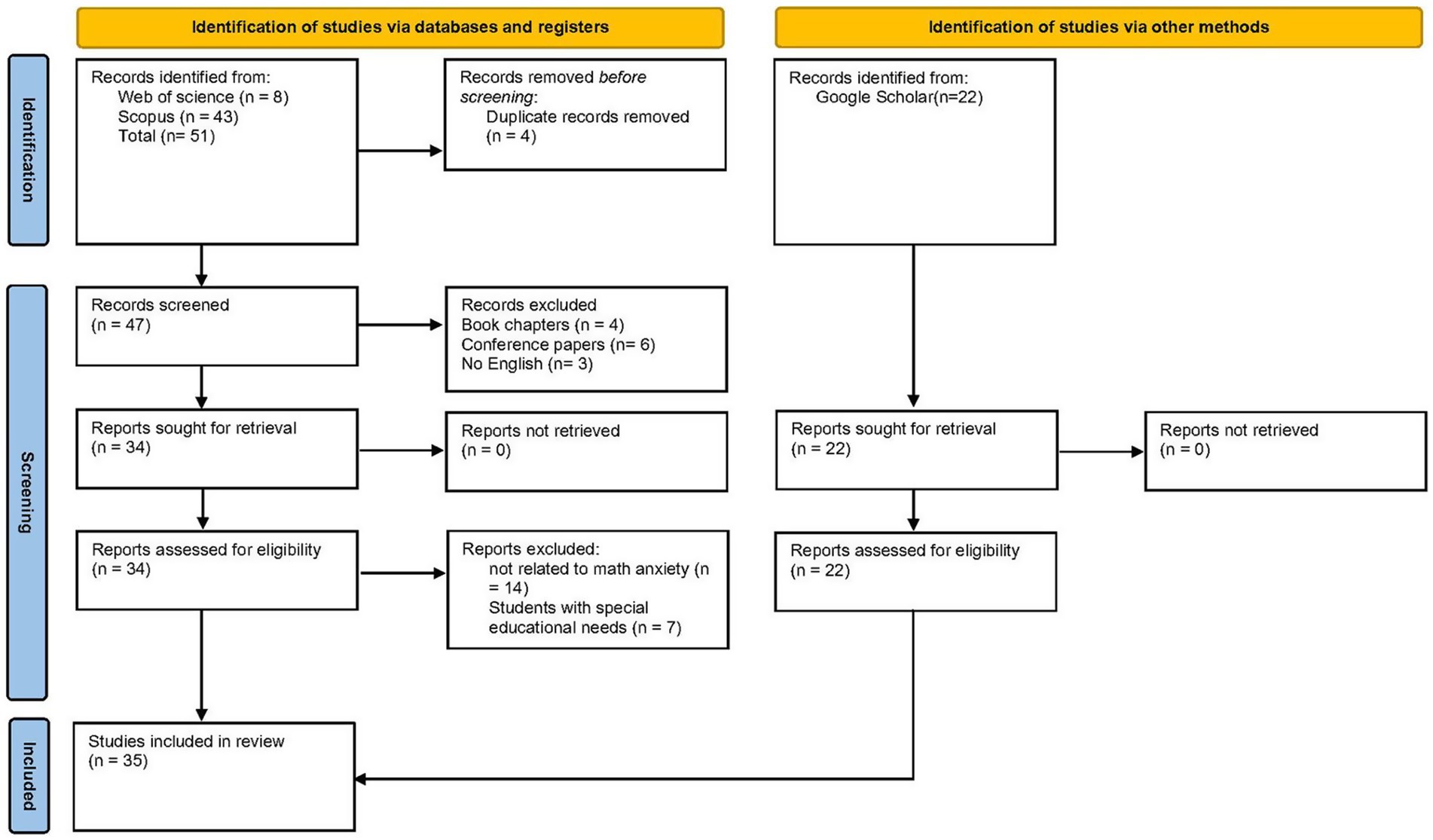
This study applied the fields title/abstract in the search. The full details are available in Figure 1. My initial search identified a total of 8 articles in Web of Science and 43 in Scopus, which were imported into Zotero reference management software. Of these 51 articles, 4 were identified as duplicates, leaving a total of 47 for screening and eligibility stages.
2.2 Inclusion and exclusion
A set of predefined inclusion and exclusion criteria was applied during the screening process. Among the 47 records initially screened, 6 were excluded for being conference papers, 4 were book chapters, and 3 were non-English publications, resulting in 34 articles retained for full-text retrieval. Full texts were successfully located for all 34 articles. During the eligibility phase, an additional 14 articles were excluded because they were not directly related to mathematics anxiety, and 7 articles were removed because the students had disabilities. To supplement the database search, 22 relevant peer-reviewed articles were also identified through Google Scholar. These articles were chosen because they include pedagogical concepts such as, constructivist ideas, Dewey’s philosophy, Bloom’s theory of cognitive goal classification, nearest development theory and knowledge transfer. This yielded a final sample of 35 articles included in the review for data analysis. Figure 2 provides a detailed overview of the inclusion and exclusion process.
3 Findings
3.1 Question 1: what teaching approaches can teachers use to help students reduce mathematics anxiety?
Many studies have shown that repeated failure in mathematics learning can lead students to withdraw from classroom participation and develop negative attitudes toward the subject (Bekdemir, 2010). This phenomenon may lead to long-term avoidance of mathematics and reduced future learning engagement (Piccirilli et al., 2023). To better support teachers in addressing these problems, the following section presents two instructional approaches to support students in re-engaging with mathematics.
3.1.1 Flat teaching design
Flat teaching design refers to an instructional approach that offers students multiple learning pathways and allows students to progress at their own pace (Hoffmann and Egri-Nagy, 2021). In traditional mathematics class, teaching contents are organized in a linear, progressive and hierarchical structure (Hoffmann and Egri-Nagy, 2021). This structure means that learning progress builds on prior knowledge, linking each new concept to foundational knowledge. However, if students do not adequately comprehend mathematical concepts, they may encounter challenges in learning following courses (Deshler et al., 2001). Therefore, students may experience learning gap anxiety (Piccirilli et al., 2023).
Learning gap anxiety indicates that if students fail to grasp foundational knowledge, then they may struggle to learn complex and abstract mathematical concepts (Furner and Gonzalez-DeHass, 2011). According to flat teaching design, I believe that teachers should incorporate multiple learning pathways into the curriculum instead of focusing on a core concept. In other words, teachers should divide the content into sub-modules, with each sub-module serving as a separate learning unit. These units can help students manage cognitive load and improve learning outcomes (Kellman et al., 2010).
Consequently, two primary educational models have been proposed. These are the multi-entry learning pathway model and dynamic knowledge mapping model (Hoffmann and Egri-Nagy, 2021). The first model provided multiple entry points into the knowledge content, enabling students to select suitable learning progressions (Hoffmann and Egri-Nagy, 2021). By following this model, teachers can divide the mathematics curriculum into distinct learning units (Kellman et al., 2010). As a result of this approach, students could choose different learning sequences according to their own learning interests. Furthermore, teacher should use this model to enhance students’ learning flexibility and stimulating initiative. For example, the function unit can be divided into multiple modules: function images, function properties, practical modelling and interdisciplinary applications (Eisenbart et al., 2017).
Dynamic knowledge mapping model focuses on interconnected and updated knowledge points (Heide and Lis, 2012). By following this model, teachers can adjust the links and order of modules based on student performance. The model structures content into three levels. The first level covers basic concepts, such as function definitions, types, domain, and range (Eisenbart et al., 2017). The second level includes formal operations, such as function transformations, inverse forms, and compositions (Bart, 1971). The third level focuses on the use of functions in problem-solving contexts, such as modelling tasks (Hall, 2014). In this model, students can select the order of modules and change learning paths based on their progress.
3.1.2 REACT teaching model
The REACT model involves five dimensions: relating, experiencing, applying, cooperating, and transferring (Putra et al., 2023). Each dimension of REACT model will be explained in the following section.
Constructivists believe that learners actively construct knowledge based on their own experiences rather than passively receiving it (Bada and Olusegun, 2015; Loyens and Gijbels, 2008). Consistent with this view, according to the first dimension ‘Relating’, it emphasizes the importance of connecting new concepts to students’ prior knowledge and experiences (Putra et al., 2023). However, research suggests that many students struggle to establish such connections, particularly in mathematics education (Sihite, 2023). This difficulty often stems from the abstract nature of mathematics, which makes it challenging for students to relate theoretical concepts to real-life questions (Sihite, 2023). To address this issue, I believe that teachers should sequence complex knowledge into stage-based learning goals. Meanwhile, instructional materials should be designed to align with students’ prior knowledge.
According to the second dimension ‘Experiencing’, it focuses on students’ hands-on involvement in practical activities to construct knowledge (Da, 2023). This principle aligns with Dewey’s philosophy of “learning by doing” which emphasizes experiential, exploratory, and reflective learning processes (Ord, 2012). In this context, students are not passive recipients of knowledge, but active participants in the construction of understanding (Ord, 2012). Therefore, teachers should foster diverse and interactive teaching models where students could experiment, reflect, and learn through firsthand experiences (Buckley and Sullivan, 2023). In this way, a supportive and low-anxiety learning environment will be fostered to encourage students’ resilience, cultivate a growth mindset, and promote meaningful learning.
In terms of “Applying”, teachers should help students to reinforce their learning by applying acquired abstract concepts to realistic scenario. This aligns with Bloom’s theory of classification of cognitive goals: remembering, understanding, applying, analyzing, evaluating and creating (Conklin, 2005). Specifically, application is learners’ ability to apply knowledge or methods to new situations (Conklin, 2005). Researchers shown that some students develop mathematics anxiety from learning applications and problems irrelevant to real life (Sitorus and Saragih, 2023). I believe that when students apply their mathematical knowledge in concrete situations, they may understand abstract concepts and improve problem-solving skills.
The fourth dimension is ‘Cooperating’. According to Mathias et al. (2024), it includes student collaboration, teacher-student interaction and home-school communication. This aligns with Vygotsky of the zone of nearest development theory. Specifically, “there are two levels of student development: one can independently complete the task; the second is the development of problem solving with the help of others” (Wu, 2025, p. 84). Furthermore, cooperative learning could reduce students’ sense of isolation, ease anxiety, and prevent excessive competition and peer pressure (Ford, 2018). In this process, students could listen to lectures, take notes and participate in discussions. Through group work activities, students should practice teamwork skills, build confidence in expressing ideas. In addition, high parental expectations may put psychological pressure on students, thereby leading to mathematics anxiety (Si et al., 2022). Consequently, I suggest that teachers should maintain positive communication with parents and create supportive learning environment.
The last dimension is “Transfer”. This means that teacher should guide students to apply their existing knowledge to new situations (Deshler et al., 2001). At this stage, students should migrate knowledge into different contexts. In educational theory, migration is categorized as near transfer and far transfer (Perkins and Salomon, 1992). Near transfer refers to migration between similar contexts. On the contrary, far transfer refers to migration between unsimilar contexts (Perkins and Salomon, 1992). Therefore, I believe that teachers should help students start with basic knowledge in similar situations and transition to high level knowledge in complex situations. In this process, students could relate and apply knowledge in realistic situations and internalize their knowledge.
By implementing the REACT model, teachers should focus on students’ psychological state and individual differences during the teaching process, reducing anxiety and improving students’ mathematics performance.
3.2 Question 2: which curriculum designs would benefit students with mathematics anxiety?
To reduce mathematics anxiety among students, teachers are required to implement curriculum innovation (Marshall et al., 2017). The following section introduces two curriculum designs and examines their role in reducing student anxiety.
3.2.1 Application-oriented curriculum
Application-oriented courses usually link abstract mathematical knowledge with college students’ majors and future careers (Oladejo et al., 2023). Research indicates that the training objectives of university education should shift from imparting knowledge toward enabling graduates to possess specific capabilities (Li et al., 2019). These capabilities must meet the demands of both enterprises and future society (Li et al., 2019). Therefore, I believe that teachers should help students develop and apply theoretical knowledge in real life.
In addition, research showed that the disconnect between course content and practice is the cause of negative learning state (Hall, 2014). Traditional mathematics courses focused on derivation and lacked links to professional contexts (Smith and Morgan, 2016). To address this issue, I believe mathematics instruction should incorporate context-specific scenarios drawn from applied fields. For example, teachers may introduce data analysis tasks related to program evaluation or client assessment in classroom activities (Lalayants, 2012). Such integration may help students understand the practical value of knowledge. In the process, students could develop statistical thinking and strengthen learning participation, and reduce anxiety associated with abstract content (Da, 2023).
Meanwhile, teachers should strengthen school-enterprise cooperation such as industrial visits and internship programs (Li et al., 2019). Industrial visits are short term visits to actual workplaces for students to study (Al-Atabi et al., 2013). Internship programs are introductory practicum for students in companies (Al-Atabi et al., 2013). These experiences can help students understand how mathematics is applied in workplace settings. Teachers should also create opportunities for students to transform theoretical knowledge into practical skills. In this way, students can apply what they have learned to real tasks and strengthen their problem-solving abilities (Smith and Morgan, 2016).
In conclusion, existing literature suggests that when teachers use application-oriented courses, they could better meet students’ professional needs and reduce their mathematics anxiety.
3.2.2 Experiential curriculum
The experiential mathematics curriculum is based on the core concept of learning by doing, which emphasizes the active participation of students in concrete situations (Da, 2023). Based on this idea, researchers and educators have proposed experiential learning as a response to persistent challenges in mathematics education, particularly mathematics anxiety (Marshall et al., 2017).
For example, some studies recommend that teachers should use contextualized curriculum design to connect mathematical concepts with practical situations and help students grasp abstract knowledge (Smith and Morgan, 2016). In this way, students could understand and apply abstract mathematical principles from familiar contexts. Secondly, teachers should incorporate hands-on learning and modelling activities (Hall, 2014). These tasks should include immediate feedback, helping students recognize the link between their actions and specific outcomes, which may enhance their sense of progress and reduce anxiety. Furthermore, teachers should promote collaborative learning by designing group-based activities that encourage students to explore mathematical problems together (Ford, 2018).
Additionally, teachers should use experiential courses to develop differentiated teaching practices. For example, teachers can diversify the content and presentation in these courses to respect students’ cognitive differences (Hoffmann and Egri-Nagy, 2021). For example, in geometry and spatial reasoning courses, teachers can introduce tools such as Geometer’s Sketchpad to guide students in constructing shapes (Liu and Kaino, 2007). From my perspective, students constructed knowledge by exploring, verifying, and interpreting mathematical ideas, rather than passively memorizing geometric theorems.
In conclusion, existing literature suggests that when teachers use experiential curriculum, they can promote students’ peer collaboration and facilitate their knowledge construction.
4 Conclusion
This article describes the definition of mathematical anxiety and explores the role of teaching approaches and curriculum designs in reducing mathematical anxiety. We find that innovative teaching methods and scientifically designed curriculum content could reduce students’ mathematical anxiety and increase their self-confidence and learning engagement. This article focuses on two aspects including teaching approaches and curriculum designs. Although student learning outcomes may vary in flat teaching model, it enables teachers to adapt content and enhance student motivation. Similarly, despite the complexity of preparation, the REACT model promotes collaboration among students and increases the application of knowledge in real-world situations. The results show that few studies simultaneously focus on teaching approaches and curriculum design.
The first limitation was that the article focused on the analysis of secondary data and existing literature. Future research should improve the variety of research approaches to combine quantitative and qualitative data. For example, researchers can use multi-dimensional quantitative criteria and in-depth interviews. The second limitation was that the data came from two databases, including Web of Science and Scopus. Future research should extend the database, such as Elsevier and SpringerLink. Meanwhile, future research also should utilize emerging tools such as big data and artificial intelligence to identify anxious students. Teachers should collect student feedback through multiple methods to optimize instructional design. Through these methods, researchers can align findings with actual teaching and address gaps in existing research.
Author contributions
YM: Writing – review & editing, Methodology, Supervision, Funding acquisition, Writing – original draft, Investigation, Validation, Conceptualization, Project administration, Formal analysis.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Acknowledgments
I am deeply grateful to Zhi Yang at Griffith University for his insightful guidance and thoughtful critiques that significantly shaped this research. I also extend my appreciation to the reviewers and editors for their valuable suggestions, and to my family for their unwavering support throughout the course of this work.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author declares that no Gen AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Al-Atabi, M., Shamel, M. M., Chung, E., Padmesh, T., and Al-Obaidi, A. (2013) The use of industrial visits to enhance learning at engineering courses. J. Eng. Sci. Technol., 8, 1–7. Available online at: https://jestec.taylors.edu.my/Special%20Issue%20on%20Engineering%20Education%20April%202013/01-07.pdf.
Bada, S. O., and Olusegun, S. (2015). Constructivism learning theory: a paradigm for teaching and learning. J. Res. Method Educ. 5, 66–70. doi: 10.9790/7388-05616670
Bart, W. M. (1971). A generalization of Piaget’s logical-mathematical model for the stage of formal operations. J. Math. Psychol. 8, 539–553. doi: 10.1016/0022-2496(71)90006-X
Bekdemir, M. (2010). The pre-service teachers’ mathematics anxiety related to depth of negative experiences in mathematics classroom while they were students. Educ. Stud. Math. 75, 311–328. doi: 10.1007/s10649-010-9260-7
Buckley, S., and Sullivan, P. (2023). Reframing anxiety and uncertainty in the mathematics classroom. Math. Educ. Res. J. 35, 157–170. doi: 10.1007/s13394-021-00393-8
Conklin, J. (2005) A taxonomy for learning, teaching, and assessing: a revision of bloom’s taxonomy of educational objectives complete edition. Educ. Horiz., 83: 154–159. Available online at: https://www.jstor.org/stable/42926529
Da, N. (2023). Realistic mathematics education and authentic learning: a combination of teaching mathematics in high schools. J. Math. Sci. Teach. 3, 1–9. doi: 10.29333/mathsciteacher/13061
Deshler, D., Schumaker, J., Bulgren, J., Lenz, K., Jantzen, J.-E., Adams, G., et al. (2001). Making learning easier: connecting new knowledge to things students already know. Teach. Except. Child. 33, 82–85. doi: 10.1177/004005990103300412
Eisenbart, B., Gericke, K., Blessing, L. T., and McAloone, T. C. (2017). A DSM-based framework for integrated function modelling: concept, application and evaluation. Res. Eng. Des. 28, 25–51. doi: 10.1007/s00163-016-0228-1
Ford, J. (2018) Blending team-based learning with standards-based grading in a calculus classroom. Math. Teach. Res. J., 10, 3–18. Available online at: https://jford.org/research/MTRJ_Submission_Fall_2018.pdf.
Frenzel, A. C., Pekrun, R., and Goetz, T. (2007). Perceived learning environment and students’ emotional experiences: a multilevel analysis of mathematics classrooms. Learn. Instr. 17, 478–493. doi: 10.1016/j.learninstruc.2007.09.001
Furner, J. M., and Gonzalez-DeHass, A. (2011). How do students’ mastery and performance goals relate to math anxiety? Eurasia J. Math. Sci. Technol. Educ. 7, 227–242. doi: 10.12973/ejmste/75209
Greenwood, J. (1984). Soundoff: my anxieties about math anxiety. Math. Teach. 77, 662–663. doi: 10.5951/MT.77.9.0662
Hall, G. (2014) Integrating real-world numeracy applications and modelling into vocational courses. Adults Learn. Math., 9, 53–67. Available online at: https://files.eric.ed.gov/fulltext/EJ1068221.pdf.
Heide, T., and Lis, L. (2012). Dynamic knowledge mapping: A visualization approach for knowledge management systems. 2012 45th Hawaii International Conference on System Sciences, 1–10. doi: 10.1109/HICSS.2012.229
Hoffmann, M., and Egri-Nagy, A. (2021). A new model of mathematics education: flat curriculum with self-contained micro topics. Philosophies 6, 1–11. doi: 10.3390/philosophies6030076
Hutton, A. (2020) The efficacy of the flipped classroom technique in undergraduate mathematics education: a review of the research Mathematics, 1–24. doi: 10.48550/arXiv.2010.11393
Kellman, P. J., Massey, C. M., and Son, J. Y. (2010). Perceptual learning modules in mathematics: enhancing students’ pattern recognition, structure extraction, and fluency. Top. Cogn. Sci. 2, 285–305. doi: 10.1111/j.1756-8765.2009.01053.x
Lalayants, M. (2012). Overcoming graduate students’ negative perceptions of statistics. J. Teach. Soc. Work. 32, 356–375. doi: 10.1080/08841233.2012.705259
Li, Y., Niu, J., Zhang, J., and Hao, R. (2019). Study of engineering-oriented teaching method in c programming course based on emerging engineering education. 2019 IEEE Frontiers in Education Conference (FIE), 1–7. doi: 10.1109/FIE43999.2019.9028516
Lin, L. (2018). Bias caused by sampling error in meta-analysis with small sample sizes. PLoS One 13, e0204056–e0204019. doi: 10.1371/journal.pone.0204056
Liu, Y., and Kaino, L. M. (2007). Geometer’s sketchpad and MSW logo in mathematics classroom instruction: a comparative analysis. J. Interdiscip. Math. 10, 715–726. doi: 10.1080/09720502.2007.10700527
Loyens, S. M., and Gijbels, D. (2008). Understanding the effects of constructivist learning environments: introducing a multi-directional approach. Instr. Sci. 36, 351–357. doi: 10.1007/s11251-008-9059-4
Marshall, E. M., Staddon, R. V., Wilson, D. A., and Mann, V. E. (2017). Addressing maths anxiety and engaging students with math within the curriculum. MSOR Connect. 15, 28–35. doi: 10.21100/msor.v15i3.555
Mathias, J., Saville, C., and Leech, S. (2024). Engaging non-mathematics students in mathematics learning through collaborative teaching. Teach. Math. Appl. 43, 67–80. doi: 10.1093/teamat/hrad003
Mutodi, P., and Ngirande, H. (2014). Exploring mathematics anxiety: mathematics students’ experiences. Mediterr. J. Soc. Sci. 5, 283–294. doi: 10.5901/mjss.2014.v5n1p283
Namkung, J. M., Peng, P., and Lin, X. (2019). The relation between mathematics anxiety and mathematics performance among school-aged students: a meta-analysis. Rev. Educ. Res. 89, 459–496. doi: 10.3102/0034654319843494
Newstead, K. (1998). Aspects of children’s mathematics anxiety. Educ. Stud. Math. 36, 53–71. doi: 10.1023/A:1003177809664
O’Hara, G., Kennedy, H., Naoufal, M., and Montreuil, T. (2022). The role of the classroom learning environment in students’ mathematics anxiety: a scoping review. Br. J. Educ. Psychol. 92, 1458–1486. doi: 10.1111/bjep.12510
Oladejo, A. I., Olateju, T. T., Okebukola, P. A., Agboluaje, T. M., Sanni, R., Shabani, J., et al. (2023). The convergence of culture, technology and context: a pathway to reducing mathophobia and improving achievement in mathematics. Sch. Sci. Math. 123, 82–96. doi: 10.1111/ssm.12573
Ord, J. (2012). John Dewey and experiential learning: developing the theory of youth work. Youth Policy, 108, 55–72. Available online at: https://www.researchgate.net/profile/Jon-Ord-2/publication/270338098_John_Dewey_and_Experiential_Learning_Developing_the_theory_of_youth_work/links/54a7c6010cf267bdb90a3779/John-Dewey-and-Experiential-Learning-Developing-the-theory-of-youth-work.pdf.url
Page, M. J., McKenzie, J. E., Bossuyt, P. M., Boutron, I., Hoffmann, T. C., Mulrow, C. D., et al. (2021). The PRISMA 2020 statement: an updated guideline for reporting systematic reviews. BMJ 372. doi: 10.1136/bmj.n71
Panzeri, S., Magri, C., and Carraro, L. (2008). Sampling bias. Scholarpedia 3, 1–2. doi: 10.4249/scholarpedia.4258
Passolunghi, M. C., De Vita, C., and Pellizzoni, S. (2020). Math anxiety and math achievement: the effects of emotional and math strategy training. Dev. Sci. 23, e12964–e12911. doi: 10.1111/desc.12964
Perkins, D. N., and Salomon, G. (1992). Transfer of learning. In T. Husén and T. N. Postlethwaite (Eds.), International encyclopedia of education (2nd ed., Vol. 2, pp. 6452–6457). Pergamon Press.
Peterson, P. L., and Janicki, T. C. (1979). Individual characteristics and children’s learning in large-group and small-group approaches. J. Educ. Psychol. 71, 677–687. doi: 10.1037/0022-0663.71.5.677
Pettigrew, J., Miller-Day, M., Shin, Y., Hecht, M. L., Krieger, J. L., and Graham, J. W. (2013). Describing teacher–student interactions: a qualitative assessment of teacher implementation of the 7th grade keep in it real substance use intervention. Am. J. Community Psychol. 51, 43–56. doi: 10.1007/s10464-012-9539-1
Piccirilli, M., Lanfaloni, G. A., Buratta, L., Ciotti, B., Lepri, A., Azzarelli, C., et al. (2023). Assessment of math anxiety as a potential tool to identify students at risk of poor acquisition of new math skills: longitudinal study of grade 9 Italian students. Front. Psychol. 14, 1–8. doi: 10.3389/fpsyg.2023.1185677
Putra, M., Rahman, A., Ilwandri, I., Suhayat, Y., Santosa, T. A., Putra, R., et al. (2023). The effect of STEM-based react model on students’ critical thinking skills: a meta-analysis study. Literacy 2, 207–217. doi: 10.46793/stream25.061p
Putwain, D. W., and Wood, P. (2023). Anxiety in the mathematics classroom: reciprocal relations with control and value, and relations with subsequent achievement. ZDM–Math. Educ. 55, 285–298. doi: 10.1007/s11858-022-01390-2
Rancer, A. S., Durbin, J. M., and Lin, Y. (2013). Teaching communication research methods: student perceptions of topic difficulty, topic understanding, and their relationship with math anxiety. Commun. Res. Rep. 30, 242–251. doi: 10.1080/08824096.2013.806259
Richardson, F. C., and Suinn, R. M. (1972). The mathematics anxiety rating scale: psychometric data. J. Couns. Psychol. 19, 551–554. doi: 10.1037/h0033456
Si, J., Guo, K., Zhao, X., Zhang, M., Li, H., Huang, B., et al. (2022). Transition of latent classes of children’s mathematics anxiety in primary school and the distinctive effects of parental educational involvement: a three-wave longitudinal study. Acta Psychol. Sin. 54, 355–370. doi: 10.3724/SP.J.1041.2022.00355
Sihite, M. S. R. (2023) Implementation of cooperative model’s jigsaw to improve mathematic ability of students. Proceedings International Conference on Education Innovation and Social Science, 2023, 119–126
Sitorus, M. S., and Saragih, M. J. (2023). Using the REACT learning model to reduce student anxiety in learning mathematics. J. Holistic Math. Educ. 7, 56–75. doi: 10.19166/johme.v7i1.6216
Smirnova, Y. (2014). Knowledge, knowledge transfer, technology transfer: a conceptualization. Int. J. Technol. Manag., 8, 1–7. Available online at: https://www.researchgate.net/publication/271326173
Smith, K. J. (2023). The social, emotional, and cognitive kinship: lessons my students taught me. Gift. Child Today 46, 25–37. doi: 10.1177/10762175221131057
Smith, C., and Morgan, C. (2016). Curricular orientations to real-world contexts in mathematics. Curric. J. 27, 24–45. doi: 10.1080/09585176.2016.1139498
Vasileiou, K., Barnett, J., Thorpe, S., and Young, T. (2018). Characterizing and justifying sample size sufficiency in interview-based studies: systematic analysis of qualitative health research over a 15-year period. BMC Med. Res. Methodol. 18, 1–18. doi: 10.1186/s12874-018-0594-7
Vinson, B. M. (2001). A comparison of preservice teachers’ mathematics anxiety before and after a methods class emphasizing manipulatives. Early Childhood Educ. J. 29, 89–94. doi: 10.1023/A:1012568711257
Wu, P. (2025). Deep participation for deep learning: relationships, dilemmas and teaching strategies. New Explor. Educ. Teach. 2, 82–85. doi: 10.70711/neet.v2i11.6073
Zhang, S., and Cao, Y. (2022). Classroom interaction in mathematics: learning of mathematics and learning to participate. Curr. Opin. Behav. Sci. 48:101234. doi: 10.1016/j.cobeha.2022.101234
Zhang, J., Zhao, N., and Kong, Q. P. (2019). The relationship between math anxiety and math performance: a meta-analytic investigation. Front. Psychol. 10, 1–15. doi: 10.3389/fpsyg.2019.01613
Keywords: mathematics anxiety, teaching approaches, curriculum design, students, teachers
Citation: Ma YF (2025) The effect of teaching approaches and curriculum designs in reducing mathematics anxiety—a literature review. Front. Educ. 10:1656419. doi: 10.3389/feduc.2025.1656419
Edited by:
Iago Portela, Universidad Isabel I de Castilla, SpainReviewed by:
Gemma Quintana, Aklan State University, PhilippinesCopyright © 2025 Ma. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yu Fei Ma, WVhNNDQxQHN0dS5zcXh5LmVkdS5jbg==
 Yu Fei Ma
Yu Fei Ma