Optimizing the home-school-society collaborative mechanism for college students' mental health: an evolutionary game theory approach

The mental well-being of college students is a critical concern that requires a collaborative effort from families, schools, and society. However, the internal mechanisms and key factors that drive effective collaboration among these three parties remain unclear, hindering the establishment of a robust support system.This study constructs a tripartite evolutionary game theory model involving families, schools, and societal institutions. The model investigates the impact of government policy support (including financial subsidies), cost-sharing arrangements, and benefit allocation mechanisms on the behavioral strategies of all stakeholders. Stability analysis and numerical simulations were employed to examine the dynamic evolution of the system.The simulation results indicate that targeted government subsidies significantly enhance the participation enthusiasm and sustained engagement of families and schools. Furthermore, the incentive intensity for social institutions is a pivotal factor in promoting their willingness to open and share resources. A stable, high-collaboration state can be achieved when families receive sufficient policy support, schools' coordination costs are covered, and the benefits for social institutions exceed their input costs. The findings confirm that an optimized incentive structure is essential for sustainable collaboration. This paper concludes by proposing concrete policy recommendations to improve the long-term home-school-society collaborative mechanism for college students' mental health, offering a valuable theoretical and practical framework for stakeholders.

1 Introduction

In recent years, the prevalence of mental health issues among college students in China has surged, reflecting the impact of social transformations and higher education reforms. The World Health Organization (2021) reports a rising annual detection rate of psychological problems, such as depression and anxiety, which compromise students' academic performance and overall wellbeing, posing challenges to national talent development and social stability (Ayiro et al., 2023). Thus, creating a supportive educational environment that promotes mental health through collaboration among families, schools, and society has become crucial.

Research increasingly emphasizes the importance of collaborative mental health education. Liu and Xiao highlight this need in primary and secondary education (Liu and Xiao, 2023), while Tang (2023) expands the concept to colleges by proposing a long-term home-school-community mechanism. Theoretical insights by Cavioni et al. (2020) emphasize the role of social and emotional learning as well as resilience building in schools. However, challenges persist, as Wang discusses unclear roles and poor coordination in his “Trinity” model for mental health education (Chu and Wei, 2024).

Innovative strategies are being explored to enhance mental health outcomes. Li advocates for positive psychology methods (Luyu, 2025), and Chen present three-dimensional education models aimed at fostering optimism and resilience (Chen et al., 2023). Nonetheless, barriers such as insufficient staffing, lack of policy support, and reliance on outdated methods hinder progress (Fengxian, 2024). These issues are exacerbated in higher education, where academic competition increases mental health stresses.

Collaborative approaches show promise in addressing these challenges. Research by Zhang et al. (2022) indicates that students' perceptions of academic value and social dynamics significantly influence their engagement. Strategies like home-school collaboration (Liu, 2025) and unified management practices (Xiaoli, 2024) highlight the effectiveness of coordinated efforts in alleviating anxiety, particularly for disadvantaged students.

Despite these advancements, a cohesive, system-level strategy integrating families, schools, and society remains essential. This study aims to optimize the Home-School-Society collaborative mechanism to improve college students' mental health by aligning stakeholders, enhancing policy support, and incorporating innovative educational models. The paper will first review pertinent literature, outline methodology, present findings, and conclude with insights and recommendations for future research and practice.

In summary, while there is growing recognition of the importance of collaborative strategies in mental health education, significant barriers still restrict effective integration among families, schools, and communities. This study aspires to address these gaps, contributing to a more supportive environment for students and improving mental health strategies within the broader social context.

1.1 Research questions

This study investigates the core challenges in constructing a collaborative home-school-community education system for university students' mental health. Specifically, it addresses the following key questions:

1. Driving mechanisms: What internal mechanisms and critical factors facilitate or hinder effective, sustainable collaboration among families, universities, and societal stakeholders? How do these parties make decisions within cooperative frameworks?

2. Cost-benefit dynamics: How can collaborative cost-sharing and benefit-distribution mechanisms be optimally designed? What level of incentive is required to motivate social institutions to openly share resources while ensuring their returns—both tangible and intangible—exceed input costs?

3. System stability conditions: Under what conditions can a stable, highly collaborative tripartite model be achieved? Key considerations include sufficient policy support for families, compensation for universities' coordination costs, and guaranteed benefits for social organizations.

4. Policy pathways: What concrete, operational policy recommendations can support the development of a sustainable, long-term collaborative mental health education mechanism?

1.2 Methodology

Figure 1 provides a schematic overview of the full research approach for this study presents a theoretical exploration aimed at modeling the underlying mechanisms of the “university-family-community” tripartite collaborative education system through formal theoretical modeling, rather than empirical validation using questionnaires or interviews.

Figure 1

Figure 1. A cyclical model of family-school partnership and resource sharing.

The research design is anchored in two foundational theoretical frameworks:

Ecological systems theory (Urie, 1979): We employ this framework to conceptualize student psychological development as emerging from interactions within microsystems (higher education institutions, families, and communities), mesosystems (linkages among these entities), and exosystems (e.g., governmental policy influences). The evolutionary game model operationalizes this structure by treating each party as an autonomous agent within the microsystem, while explicitly modeling inter-agent interactions at the mesosystem level. External factors, such as policy interventions, are incorporated as exogenous parameters that alter incentive structures, thereby influencing system evolution. This alignment ensures the model's structural coherence with real-world educational ecosystems.

Social learning theory (Albert, 1977): The behavioral dynamics of the model—specifically the replicator dynamics equation—are grounded in Social Learning Theory. Actors (universities, families, communities) are modeled as boundedly rational agents who adapt their strategies through observational learning and imitation of successful behaviors, based on perceived payoffs (fitness). This provides micromechanistic explanatory power for strategy adoption and behavioral evolution within the system.

Modeling approach: Using evolutionary game theory as our formal analytical tool, we implement a five-step modeling procedure:

(1) Delineation of the three strategic agents and their action sets;

(2) Construction of a payoff matrix reflecting costs, benefits, and risks derived from empirical literature and contextual analysis;

(3) Specification of replicator dynamics equations to capture strategic evolution over time;

(4) Identification and stability analysis of evolutionarily stable strategies (ESS);

(5) Numerical simulation of evolutionary trajectories under varying initial conditions and policy parameters.

1.3 Innovation and theoretical contribution

The adoption of evolutionary game theory constitutes a significant methodological innovation in studying collaborative education mechanisms. It enables the translation of complex social interactions into a quantifiable and dynamically simulatable framework, overcoming limitations inherent in purely qualitative approaches.

(1) From static to dynamic analysis: Unlike traditional cross-sectional studies, our model captures longitudinal dynamics and path dependencies, simulating how systems evolve from fragmentation to cooperation under specific conditions.

(2) Mechanistic insight into collaboration barriers: The model formally demonstrates how misaligned incentives—such as free-riding behaviors, institutional inertia, and weak community engagement—create social dilemmas (e.g., prisone's dilemma dynamics). This quantitative framing enables the design of incentive-compatible mechanisms to realign interests.

(3) Policy simulation for governance innovation: By enabling in silico testing of policy interventions (e.g., subsidies, accountability mechanisms, reputation systems), the approach supports evidence-based governance, allowing stakeholders to anticipate outcomes and design robust, context-sensitive strategies.

This research provides a theoretically rigorous and computationally tractable framework for addressing persistent collaboration challenges in educational ecosystems, offering both conceptual advances and practical utility for policymakers and institutional leaders.

2 Establishment of the tripartite evolutionary game model

2.1 Basic assumptions and model construction

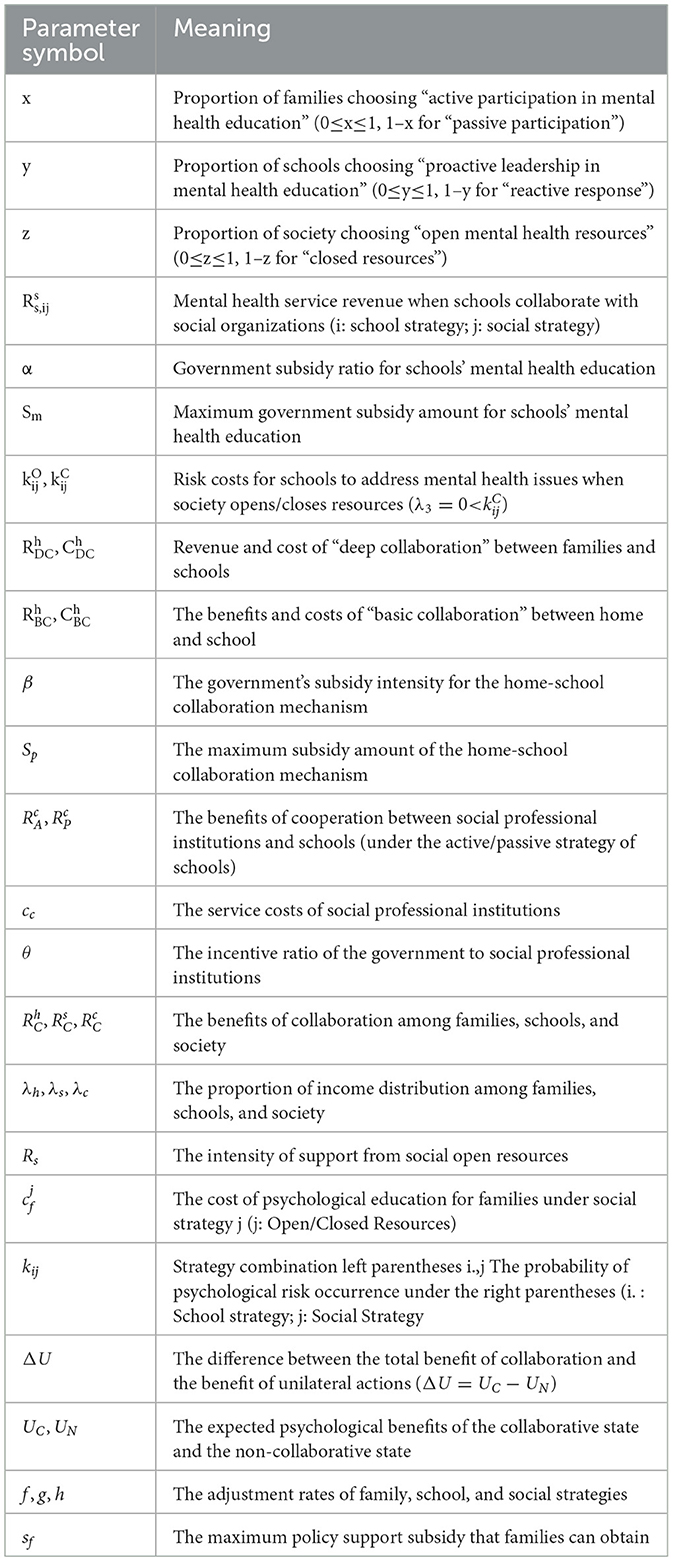
In the context of collaborative mental health education for college students, the three main participants are families, schools, and society, whose interactive behaviors form a game system. It is assumed that the strategies of families include “Active Participation” and “Passive Participation”; those of schools include “Proactive Leadership” and “Reactive Response”; and those of society include “Open Resources” and “Closed Resources.” The symbols and meanings related to the model are shown in Table 1.

Table 1

Table 1. Explanation of game-related parameters.

College students are in a critical period of psychological maturity and social transition (Koenig et al., 2025), facing multiple challenges such as academic advancement, career planning, and social adaptation. There are also some students who advocate individualism, prioritize personal interests above all else, ignore the interests of others (Williams et al., 2025), lack a sense of social responsibility, and have prominent interpersonal relationship problems (Weibull, 1997). On the other hand, although college students are adults, their mental faculties are not yet mature, and their perception of problems is often highly subjective, arbitrary, and one-sided (Gintis, 2017). Their mental health issues are more complex and latent, urgently requiring deep participation and dynamic collaboration among families, schools, and society. Research shows that young people obtaining health information through social media helps reduce stress (Sandholm, 2020). Through strategic interactions and resource integration akin to evolutionary games, a precise and systematic educational support system can be constructed to effectively promote their mental health and all-round development. Therefore, there is an urgent and necessary demand for a home-school-society collaborative education mechanism.

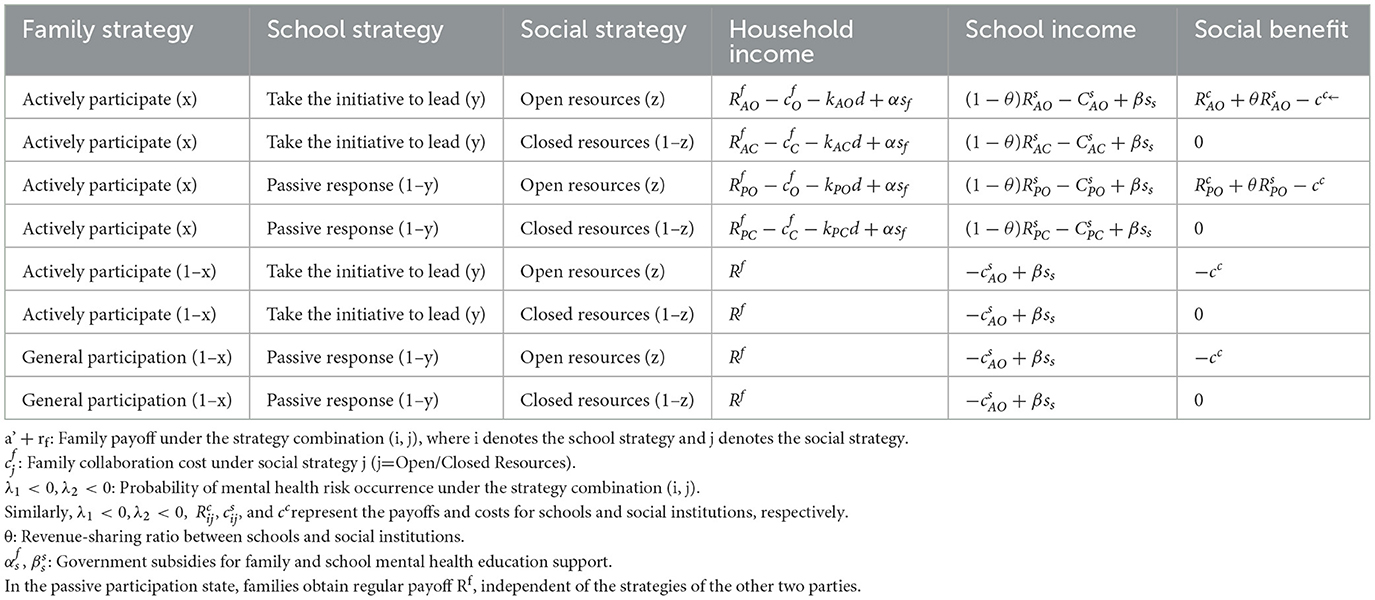
Assumption 1: The main game players in this study include families, schools, and society. Families choose the “active participation in mental health education” strategy at a proportion of x (0 ≤ x ≤ 1) and the “passive participation” strategy at (1–x); schools choose the “proactive leadership in mental health education” strategy at y (0 ≤ y ≤ 1) and the “reactive response” strategy at (1–y); society chooses the “open mental health resources” strategy at z (0 ≤ z ≤ 1) and the “closed resources” strategy at (1–z). x, y, z are functions of time, reflecting the dynamic evolution of the three parties in mental health collaboration. Their strategy choices are influenced by factors such as mental health benefits, collaboration costs, and risk aversion. Although the core analysis of this model focuses on quantifiable policy and economic variables such as fiscal subsidies (e.g, αS_m, βS_p, θR_c), cooperation costs (e.g., ${\text{C}}_{\text{DC}}^{\text{h}}$, ${\text{C}}_{\text{BC}}^{\text{h}}$, c_c, and profit distribution (λh, λs, λd), we fully recognize the important role of complex social-psychological factors such as cultural cognition (e.g., the degree of attention families pay to mental health education), social norms (e.g., the social expectation that schools play a leading role), and psychological expectations (e.g., the belief of social institutions in the long-term benefits of cooperation) in strategy selection. Although these non-quantifiable factors are difficult to be directly set as independent parameters in the model, their influence mechanisms can also be reflected indirectly in the differences of subjects' “perception” of expected profits. Specifically, the actual decision-making of subjects is not only based on the objective payoff set in the model but also driven by their subjective perceived payoff.” The perceived payoff is adjusted by the above-mentioned non-quantifiable factors and can be formally expressed as: ${\tilde{R}}_{ij}^k={\delta }_k{R}_{ij}^k+{\xi }_k,k\in \left\{f,s,c\right\}$ among them: ${\text{R}}_{\text{ij}}^{\text{k}}$ the objective payoff (e.g., family payoff ${\text{R}}_{\text{ij}}^{\text{f}}$, school payoff ${\text{R}}_{\text{ij}}^{\text{s}}$, social payoff ${\text{R}}_{\text{ij}}^{\text{c}}$) calculated based on quantifiable variables and defined in Model Tables 1, 2.

Table 2

Table 2. Payoff matrix for home-school-society tripartite game.

${\tilde{R}}_{ij}^k$ represents the perceived payoff of subject k (family f, school s, society C) under a specific strategy combination (i, j), and it is the direct basis for its strategy selection.

δ_k (Perception Adjustment Factor): It is a coefficient greater than 0, used to depict the magnification or reduction effect of non-quantifiable factors on the objective payoff.

δ_k > 1: It means that positive cultural cognition, favorable social norms, or optimistic psychological expectations magnify the subject's perception of the objective payoff (for example, families highly recognize the value of mental health and believe that the same fiscal subsidy αS_fbrings higher utility).

δ_k < 1: It means that negative cultural cognition (e.g., the concept of “valuing academic performance over psychology”), unfavorable social norms, or pessimistic psychological expectations weaken the subject's perception of the objective pay off (for example, schools believe that taking on a leading role faces excessive social pressure or reputation risks, and even if there is a subsidy βSp, its perceived net payoff is relatively low).

δ_k = 1: It means that the perceived payoff is equal to the objective payoff, and non-quantifiable factors have no adjustment effect (ideal neutral state).

ξ_k (Perception Deviation Term): It is a constant term (can be positive or negative), representing the fixed psychological utility or cost generated by non-quantifiable factors and independent of the objective payoff (for example, the improvement of the brand image brought by social institutions fulfilling social responsibilities ξc> 0, or the psychological burden brought by family participation in cooperation ξf < 0).

Assumption 2: When schools choose to collaborate with social organizations, their mental health service revenue is $R_{ij}^s$,s(iϵ{A,P}denoting proactive or reactive strategies; jupepsilon{O, C} denoting open or closed social resources) (Nou et al., 2025). Schools receive a government mental health education subsidy of αS_m, where α is the subsidy ratioand S_m is the maximum subsidy amount (Lu et al., 2021). If society opens resources (e.g., psychological counselor support), the risk cost for schools to address student mental health issues is significantly reduced, i.e., $k_{ij}^O$<$k_{ij}^C$.

Assumption 3: The revenue of the home-school collaboration mechanism is related to its service type. If “deep collaboration” (e.g., regular psychological counseling) is chosen, the revenue is $R_{CD}^h$ and the collaboration cost is $C_{DC}^h$; if “basic collaboration” (e.g., one-way information dissemination) is chosen, the revenue is $R_{BC}^h$ and the cost is $C_{BC}^h$, where β is the subsidy intensity and S_p is the maximum subsidy amount for the collaboration mechanism.

The benefits of the home-school collaboration mechanism are directly related to the selected service type and are moderated by government financial subsidies. If “deep collaboration” is chosen (e.g., regular psychological counseling, joint assessments, and follow-up interventions), the total collaborative benefits obtained by families and schools are denoted as ${\text{R}}_{\text{DC}}^{\text{h}}$. The school incurs collaboration costs of ${\text{C}}_{\text{DC}}^{\text{h}}$ but can receive a government subsidy of β·Sp to offset part of these expenses, resulting in a net cost of ${\text{C}}_{\text{DC}}^{\text{h}}$ – β·Sp for the school.

If “basic collaboration” is chosen (e.g., one-way information dissemination, one-time lectures), the total collaborative benefits obtained by families and schools are denoted as ${\text{R}}_{\text{BC}}^{\text{h}}$. The school incurs collaboration costs of ${\text{C}}_{\text{BC}}^{\text{h}}$ and typically does not receive additional subsidies.

Where: βupepsilon[0, 1]—the government's subsidy intensity (proportion) for “deep collaboration” programs; Sp—the maximum subsidy amount set by the government for such programs (a fixed amount).

Assumption 4: When social professional psychological institutions (e.g., counseling centers) collaborate with schools, if the school chooses “proactive leadership,” the institution's revenue is $R_A^c$; if the school chooses “reactive response,” the institution's revenue is $R_P^c$. The institution's service cost is c_c, and it can additionally receive a government incentive of θR_C when collaborating, where θ is the incentive ratio. The institution's willingness to collaborate depends on expected revenue and costs—the higher the incentive ratio, the stronger the collaboration tendency (Chacon et al., 2017).

Assumption 5: The total revenue of home-school-society collaboration is $R_C=R_C^h+R_C^h+R_C^c$, corresponding to the revenues of families, schools, and social institutions, respectively. The three parties distribute the revenue according to the proportion λ_h:λ_s:λ_c (e.g., the family's share is λ_h). A reasonable distribution proportion can enhance collaboration stability and avoid cooperation breakdown due to unequal distribution.

Assumption 6: Society supports home-school-society collaboration through the “open resources” strategy (e.g., providing special mental health funds) with a support intensity of Rs. Resource support can reduce family mental health education costs ($C_f^j$), school risk probabilities (k_ij), and enhance family participation enthusiasm through the incentive coefficient α. The greater the support intensity, the higher the psychological benefits of the collaboration system.

Assumption 7: The evolution of the system is driven by the difference in expected psychological benefits among the three parties. If the total collaborative benefit ΔU=U_C–U_N is higher than the benefit of unilateral actions, the system tends toward a cooperative equilibrium; otherwise, it degenerates into a low-collaboration state.

The evolution equations are described as: $dt/dx=f·x·(U_C^h-U_N^h)$, $dt/dy=g·y·(U_C^s-U_N^s)$. $dt/dz=h·z·(U_C^c-U_N^c)$, where f, g, h represent the adjustment rates of family, school, andsocial strategies, respectively, determined by marginal psychological benefits and cost.

Assumption 8: The stability of the collaboration system depends on the feedback mechanisms of the three parties and policy support. When government subsidies (α, β), family incentives (s_f), and revenue distribution (λ_h, λ_s, λ_c) are reasonable, the system tends to a stable cooperative equilibrium (e.g., equilibrium point E8 with significantly reduced psychological risks); if any party's revenue is insufficient or costs are too high (e.g., excessive family psychological burden), the system may degenerate into a low-collaboration equilibrium (e.g., E1, E3). Stability can be analyzed through the Jacobian matrix to quantify the evolutionary paths of collaborative strategies.

2.2 Construction of the game model

Based on the above assumptions, this study constructs a tripartite evolutionary game model among families, schools, and society. The mixed-strategy game matrix is shown in Table 2.

2.3 Model analysis

In this section, we will conduct a detailed analysis of the strategic evolution of families, schools, and society in the collaborative education of college students' mental health using the theory of evolutionary game with replicator dynamics, based on the aforementioned assumptions. By establishing a mathematical model, our aim is to reveal the evolutionary process and stability of the behavioral strategies of each subject, thereby providing theoretical support for effectively promoting the collaborative strategies among families, schools, and society (Perc et al., 2021).

(1) Evolution of family behavioral strategies

The behavioral strategy choices of families can be defined as a selection between “active participation” and “general participation.” Let the probability of families choosing the “active participation” strategy be xupepsilon[0,1], and its expected payoff U_f is determined by the combination of strategies of families, schools, and society. The expected payoff when families choose “active participation” is:

$\begin{array}{l}{U}_f=yz(R_{AO}^f-c_O^f-k_{AO}d+\alpha s_f)+y(1-z)(R_{AC}^f-c_C^f\\ -k_{AC}d+\alpha s_f)+(1-y)z(R_{PO}^f-c_O^f-k_{PO}d+\alpha s_f)\\ +(1-y)(1-z)(R_{PC}^f-c_C^f-k_{PC}d+\alpha s_f)\end{array}$

Among them, $R_{AC}^f$, $R_{PO}^f$, and $R_{PC}^f$ respectively represent the payoffs obtained by families under different strategy combinations, $c_O^f$ and $c_C^f$ are the collaboration costs of families, k_AO, k_AC, k_PO, and k_PC, respectively represent the probabilities of psychological risks occurring under each strategy for families, d represents the maximum possible psychological risk cost in collaboration, and αsf is the subsidy from the government to families.

When families choose the “general participation” strategy, the expected payoff is simplified to the regular payoff Rf, that is:

$\begin{array}{l}{\overline{U}}_f=x{U}_f+(1-x)R^f\end{array}$

The replicator dynamic equation for family strategies is driven by the difference in expected payoffs and can be expressed as:

$\begin{array}{l}F(x)=\frac{dx}{dt}=x(U_f-\overline{U_f})=x(1-x)(U_f-R^f)\end{array}$

This equation indicates that when the expected payoff brought by the “active participation” strategy of families is higher than the average payoff, the proportion of this strategy in the family population will increase; conversely, it will decrease.

(2) Evolution of school behavioral strategies

The behavioral strategy choices of schools can be divided into two types: “active leadership” and “passive response.” Let the probability of schools choosing the “active leadership” strategy be yupepsilon[0,1], and its expected payoff Us is:

$\begin{array}{l}{U}_f=xz((1-\theta )(R_{AO}^s-c_{AO}^s+\beta s_s)+x(1-z)((1-\theta )(R_{AC}^s\\ -c_{AC}^s+\beta s_s)+(1-x)z(-c_{AO}^s+\beta s_s)+(1-x)(1-z)(-c_{AC}^s\\ +\beta s_s)\end{array}$

Among them, $R_{AO}^s$, $R_{AC}^s,c_{PO}^s$ and $R_{PC}^s$ respectively represent the payoffs of schools under different strategy combinations, $c_{AO}^s$, $c_{AC}^s$, $c_{PO}^s$, and $c_{PC}^s$ are the collaboration costs of schools, βs_s is the subsidy from the government to schools, and θ is the profit-sharing ratio between schools and society.

The expected payoff when schools choose the “passive response” strategy is:

$\begin{array}{l}{U}_s^{\prime }=xz((1-\theta )R_{PO}^s-c_{PO}^s+\beta s_s)+x(1-z)((1-\theta )R_{PC}^s-c_{PC}^s\\ +\beta s_s)+(1-x)z(-c_{PO}^s+\beta s_s)+(1-x)(1-z)(-c_{PC}^s+\beta s_s)\end{array}$

The average expected payoff of schools is:

$\begin{array}{l}{\overline{U}}_s=y{U}_s+(1-y)U_s^{\prime }\end{array}$

The replicator dynamic equation of schools can be written as:

$\begin{array}{l}F(y)=\frac{dy}{dt}=y(1-y)(U_s-U_s^{\prime })\end{array}$

This equation indicates that when the “active leadership” strategy of schools has a higher expected payoff relative to the “passive response” strategy, schools will tend to adopt the “active leadership” strategy.

(3) Evolution of social behavioral strategies

The behavioral strategy choices of society are “open resources” and “not open resources.” Let the probability of society choosing the “open resources” strategy be zupepsilon[0,1], and its expected payoff is:

$\begin{array}{l}{U}_c=xy(R_{AO}^c+\theta R_{AO}^s-c^c)+x(1-y)(R_{PO}^c+\theta R_{PO}^s-c^c\\ -(1-x)y{c}^c-(1-x)(1-y)c^c\end{array}$

Among them, $R_{AO}^c$, $R_{PO}^c$ represent the payoffs of society under different strategy combinations, cc is the resource input cost of society, and θ is the profit-sharing ratio.

When society chooses “not open resources,” the expected payoff is zero. The replicator dynamic equation of society is:

$\begin{array}{l}F(z)=\frac{dz}{dt}=z(1-z)(U_c)\end{array}$

This equation indicates that the “open resources” strategy of society will depends relative payoff. When this strategy brings positive payoffs, society will tend to choose this strategy.

(4) System stability analysis

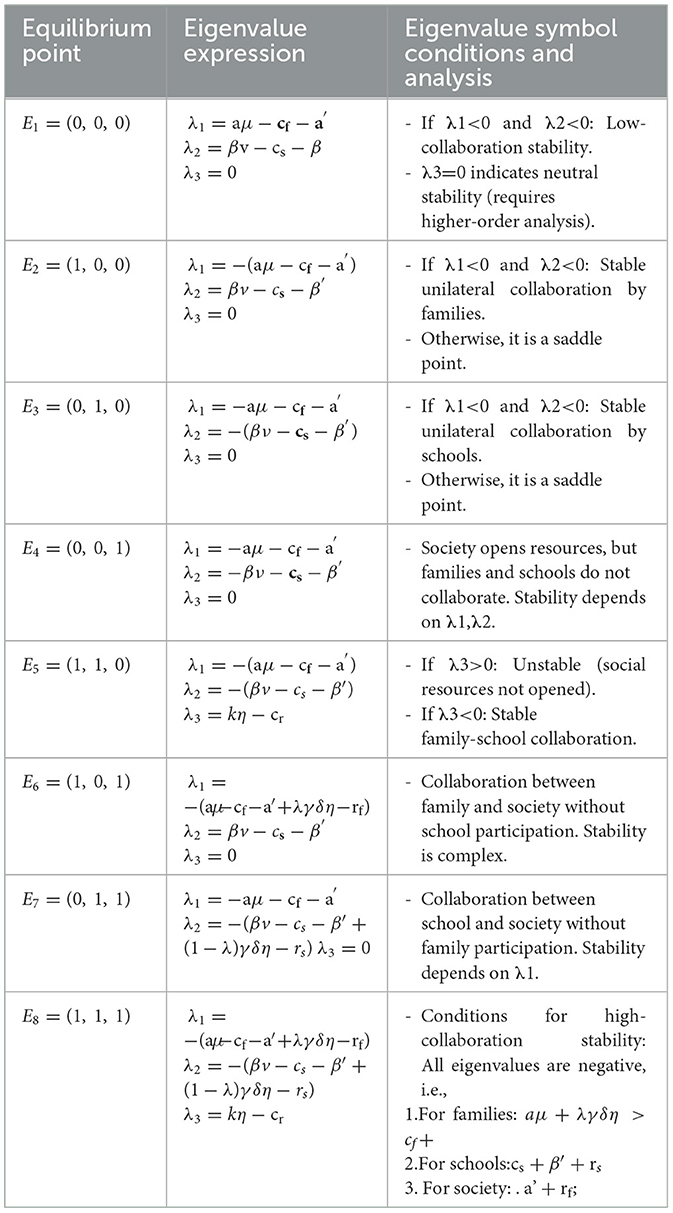
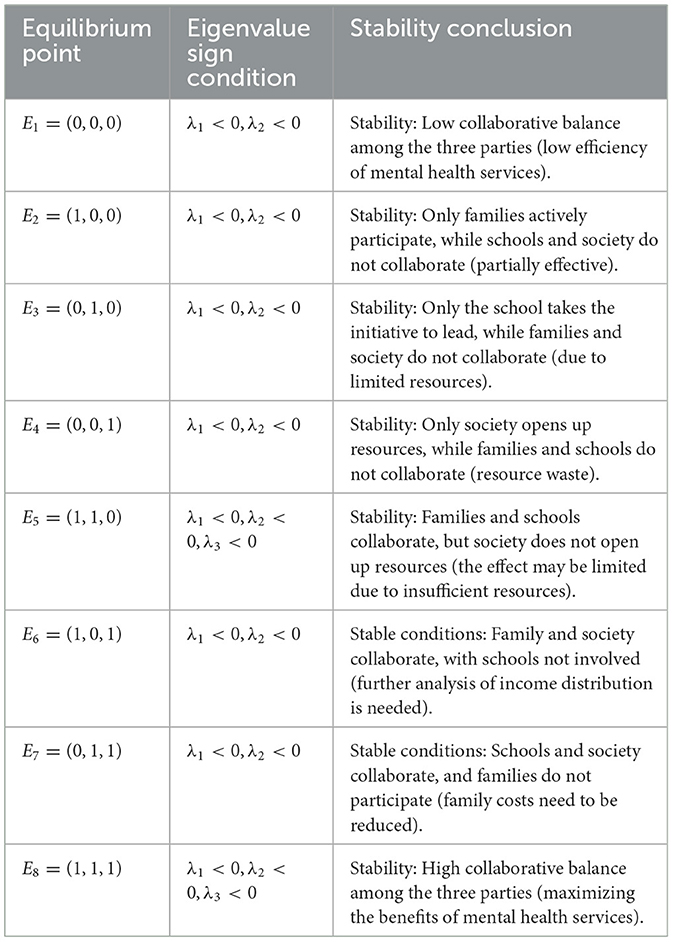
To determine the evolutionary stability of the system, we examine the equilibrium points of the replicator dynamic equations and their stability. By solving the replicator dynamic equations of each party, the evolutionary stable points are obtained as:

$\begin{array}{l}(x^{*},y^{*},z^{*})={\displaystyle (\frac{cf+{\alpha }^{\prime }-\alpha \mu }{\lambda \gamma \delta \eta -rf+(1-x^{*})cf},}\\ {\displaystyle \frac{cs+{\beta }^{\prime }-\beta v}{(1-\lambda )\gamma \delta \eta -rs+(1-y^{*})cs},...)}\end{array}$

On this basis, we use the Jacobian matrix to analyze the stability of the equilibrium points. Specifically, if the determinant “Det(J) > 0” and the trace “Tr(J) < 0” of the Jacobian matrix at a certain equilibrium point, then this point is a stable point; conversely, if the determinant is negative, it is a saddle point.

By analyzing the stability conditions, the evolutionary trends of the collaboration among families, schools, and society under different policy supports and collaboration costs can be obtained. For example, when government subsidies increase and social support strengthens, the system tends to a high-collaboration state (x*, y*, z*) = (1, 1, 1), while in the case of excessively high collaboration costs or lack of trust, the system may stabilize in a low-collaboration state.

2.4 Tripartite evolutionary stability analysis

As the core subjects of the collaborative education system for college students' mental health, the strategic choices and behavioral interactions of families, schools, and society directly influence the evolutionary direction and collaborative effectiveness of the system. Families serve as the fundamental support units for students' psychological development, schools act as the leading implementers of educational services, and society provides external guarantee for resource integration and professional services (Bronfenbrenner, 1979). Through profit sharing, cost sharing, and risk aversion, they form a dynamic game relationship, and the stability of their strategic adjustments directly determines whether the collaborative education system can achieve long-term equilibrium (World Health Organization, 2022). Therefore, this section will analyze the asymptotic stability conditions of their strategic evolution from the perspectives of families, schools, and society respectively, reveal the impact paths of different policy parameters and collaborative mechanisms on the overall stability of the system, and provide theoretical support for optimizing the collaborative education model (Smith, 1982).

Evolutionary stability analysis aims to reveal the strategic adjustment mechanisms and long-term equilibrium states of families, schools, and society in the collaborative education game. By constructing replicator dynamic equations and Jacobian matrices, this section systematically analyzes the stability conditions of each subject's strategies and their interactive effects from both the perspectives of single-subject dynamic evolution and tripartite collaboration (Organization for Economic Co-operation and Development, 2021).

(1) Asymptotic stability analysis of families

As the fundamental decision-making subject in the game, the strategic choices of families have an important impact on the stability of the system (Ostrom, 1990). This section will analyze the evolutionary stability of families under different scenarios and explore how family behaviors tend to stabilize under different policy and environmental conditions (Zhang et al., 2020).

2.5 Construction of dynamic equations

The strategic choices of families in the game are driven by payoff differences. Let the proportion of families choosing the “active participation” strategy be x(t), and their expected payoff $R_{ij}^f$ can be expressed as:

$\begin{array}{l}{\text{R}}_{ij}^f=yz(\alpha \mu +\lambda \gamma \delta \eta -c_f-r_f)+y(1-z)(\alpha \mu -c_f)\\ +(1-y)z(\alpha \mu -c_f)+(1-y)(1-z)(\alpha \mu -c_f)\end{array}$

Simplified to:

$\begin{array}{l}{\text{R}}_{ij}^f=\alpha \mu -c_f+yz\lambda \gamma \delta \eta -yz{r}_f\end{array}$

The expected payoff for families choosing “general participation” is a fixed value ${\pi }_f^P$ = α′. According to evolutionary game theory, its replicator dynamic equation is:

$\begin{array}{l}{\displaystyle F(x)=\frac{dx}{dt}=x({\text{R}}_{\text{ij}}^{\text{f}}-{\bar{\pi }}_f)=x(1-x)[\alpha \mu -c_f-{\alpha }^{\prime }}\\ {\displaystyle +yz(\lambda \gamma \delta \eta -r_f)]}\end{array}$

Among them, ${\bar{\pi }}_f=x{\mathrm{\text{R}}}_{\mathrm{\text{ij}}}^{\mathrm{\text{f}}}+(1-x){\pi }_f^P$.

In the stability judgment of the evolutionary game model, the boundary equilibrium points and interior equilibrium conditions are key analysis dimensions. For the stability judgment of family strategies, when the proportion of families choosing “active participation” x^* = 0 (i.e., complete “general participation”), if the eigenvalue γx < 0, then x* = 0 is an evolutionarily stable strategy (ESS), indicating that families generally tend not to actively participate in mental education and this state is stable; when x^* = 1 (i.e., complete “active participation”), if the eigenvalue γx < 0, then x^* = 1 is an ESS, indicating that the state of general active participation by families is sustainable. If there exists an interior equilibrium x^*upepsilon (0, 1), it must satisfy, and at this time, the stability needs to be further determined by the sign of the second derivative of the Jacobian matrix, reflecting the dynamic equilibrium state when family strategic choices are at an intermediate proportion. From a policy perspective, when the collaborative payoff satisfies λγδη > r_f and the comprehensive effect of government subsidies and family payoffs satisfies αμ > cf + α′, families are more inclined to actively participate in mental education; at the same time, increasing the intensity of social support η can reduce the family participation cost r_f, thereby enhancing the cooperation willingness of families and promoting the system to evolve toward a stable state of active participation.

(2) Asymptotic stability analysis of schools

The proportion of schools choosing the “active leadership” strategy is y(t), and their expected payoff ${\pi }_s^P$ is:

$\begin{array}{l}{\pi }_s^P=xz\left[\beta \nu +(1-\lambda )\gamma \delta \eta -c_s-r_s\right]+x(1-z)(\beta \nu -c_s)\\ +(1-x)z(\beta \nu -c_s)+(1-x)(1-z)(\beta \nu -c_s)\end{array}$

Simplified to:

$\begin{array}{l}{\pi }_s^P=\beta \nu -c_s+xz(1-\lambda )\gamma \delta \eta -xz{r}_s\end{array}$

The fixed payoff for the passive response strategy is ${\pi }_s^R$ = β′, and the replicator dynamic equation is:

$\begin{array}{l}F(y)=\frac{dy}{dt}=y(1-y){\displaystyle [\beta v-c_s-{\beta }^{\prime }+xz((1-\lambda )\gamma \delta \eta -r_s)]}\end{array}$

In the stability analysis of school strategies, the judgment of boundary equilibrium points is the core content. When the proportion of schools choosing “actively leading mental health education” y^* = 0 (i.e., complete “passive response”), its stability requires satisfying, indicating that schools generally adopt passive strategies and the state is stable; when y^* = 1 (i.e., complete “active leadership”), the stability condition requires satisfying, and at this time, the active strategy of schools becomes an evolutionarily stable strategy (ESS). The sensitivity of the interior equilibrium is reflected in that if there exists an intermediate proportion strategy y^*upepsilon (0, 1), its existence depends on the dynamic balance between collaborative payoffs and costs, that is, the strategic choice of schools between active leadership and passive response needs to achieve a balance between payoffs and costs; otherwise, the system may achieve a balance between payoffs and costs toward the boundary (World Bank, 2023). At the policy level, it is necessary to optimize the collaborative mechanism to increase the payoffs for schools to actively lead, or reduce their costs through subsidies, so as to promote the stability of school strategies toward active leadership.

(3) Asymptotic stability analysis of society

Construction of dynamic equations

The proportion of society choosing the “open resources” strategy is z(t), and its expected payoff πcO is:

$\begin{array}{l}{\text{R}}_{\text{A}}^{\text{c}}=xy(k\eta -c_r)\end{array}$

The payoff for not opening resources is always 0, and the replicator dynamic equation is:

$\begin{array}{l}F(z)=\frac{dz}{dt}=z(1-z)\left[xy(k\eta -c_r)\right]\end{array}$

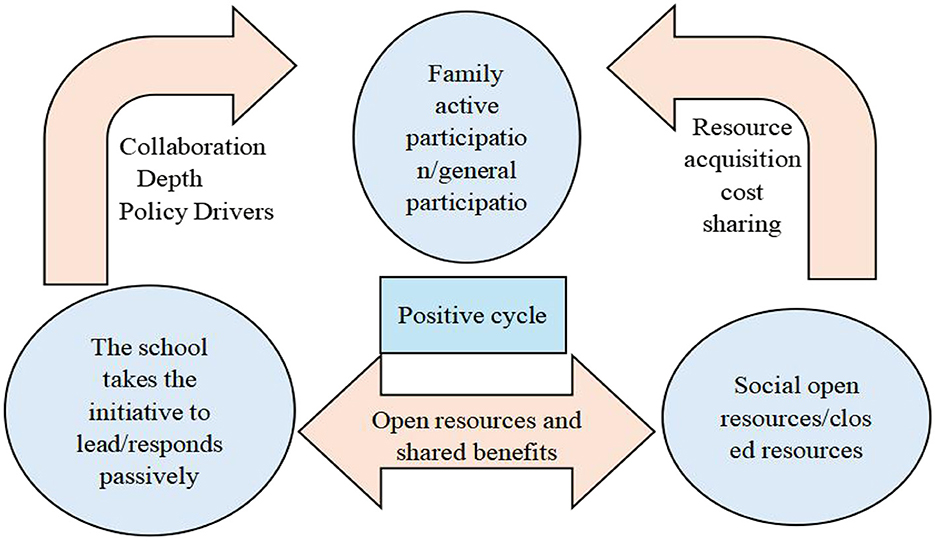
The stability analysis of social strategies focuses on boundary equilibrium points and collaborative dependence effects. When the proportion of society choosing “opening mental resources” z^* = 0 (i.e., complete “not opening resources”), the stability condition requires satisfying, and at this time, the state of social resource closure is sustainable; when z^* = 1 (i.e., complete “opening resources”), the stability condition also depends on, indicating that the strategy of social resource opening becomes a stable equilibrium. The uniqueness of social strategies lies in that their stability highly depends on the cooperation levels of families (x) and schools (y): when the collaborative effect coefficient kη is greater than the cost c_r of social resource opening, and both families and schools tend to cooperate actively (x,y → 1), society is more inclined to open resources, forming a positive cycle of tripartite collaboration. Policy interventions can reduce the cost c_r of social resource opening through cost subsidy mechanisms (such as government purchasing services or tax relief), and at the same time, enhance the enthusiasm of social participation by increasing the collaborative effect coefficient kη (such as strengthening the publicity of home-school cooperation and establishing resource sharing platforms), promoting the system to evolve toward a high-collaboration equilibrium (Seligman et al., 2009).

3 Analysis of the overall equilibrium strategy

Based on the asymptotic stability analysis of the strategic evolution of families, schools, and society, this chapter reveals the local equilibrium conditions and policy sensitivities of each subject's behavioral adjustments. However, the stability of a single subject does not equate to the maximization of the overall collaborative effectiveness of the system (Sandholm, 2010). As a dynamically complex system, the equilibrium state of collaborative mental health education for college students depends not only on the strategic choices of the three parties but also on the interactive feedback among the subjects and the synergistic effects of external policy interventions (Fehr and Fischbacher, 2003). To further explore the global evolutionary path and optimization mechanism of tripartite collaboration, this section will, from the perspective of the overall system, combine the eigenvalue analysis of the Jacobian matrix and the simulation of government regulation parameters to deeply discuss the stability conditions of different equilibrium points and the dynamic impacts of policy levers on the effectiveness of collaborative education.

In the context of collaborative mental health education for college students, the strategic choices of families, schools, and society interact with each other, potentially leading to various equilibrium states. This section will explore the stability conditions and practical implications of different equilibrium points by analyzing the evolutionary stable strategies (ESS) of the system and the eigenvalues of the Jacobian matrix.

3.1 Analysis of evolutionarily stable strategies

3.1.1 Equilibrium point solution

Based on the tripartite replicator dynamic equations, the equilibrium points of the system can be obtained by solving the following system of equations:

$\begin{array}{l}\{\begin{array}{c}F(x)=x(1-x)\left[\alpha \mu -c_f-{\alpha }^{\prime }+yz(\lambda \gamma \delta \eta -r_f)\right]=0\\ F(y)=y(1-y)\left[\beta \nu -c_s-{\beta }^{\prime }+xz((1-\lambda )\gamma \delta \eta -r_s)\right]=0\\ F(z)=z(1-z)\left[xy(k\eta -c_r)\right]=0\\ \end{array}\end{array}$

By solving these equations, the following equilibrium points can be derived (Table 3).

Table 3

Table 3. Calculation and analysis of eigenvalues of the Jacobian matrix at each equilibrium point.

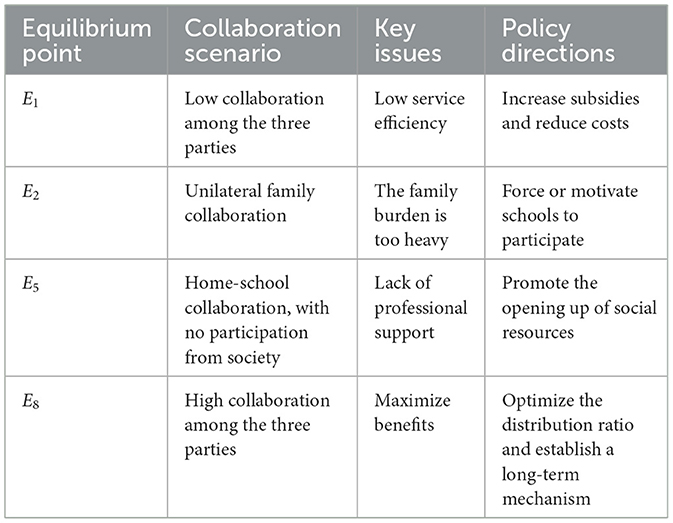
Scenario 1: Households choose general participation (x = 0), schools choose passive response (y = 0), and society chooses not to open resources (z = 0). The stability condition is that the cost of household participation exceeds the benefits ($R^f+\alpha s_f<C_{DC}^h$) and the cost of school leadership exceeds the benefits ($R_{BC}^h+\beta S_p<C_{BC}^h$). In reality, this manifests as low collaboration among the government, households, and schools, resulting in inefficient mental health services, insufficient resource integration, and limited intervention effectiveness. The root causes include inadequate government financial subsidies or lack of policy guidance to motivate collaboration, as well as high collaboration costs due to cumbersome cross-departmental communication, information-sharing barriers, and ambiguous responsibilities. To address this, a dual-policy intervention system is needed: enhancing participation incentives through increased financial subsidies, voucher systems, and reward funds, while reducing collaboration costs via digital platforms, standardized protocols, clear responsibility lists, and third-party evaluations to drive a shift toward efficient collaboration.

Scenario 2: Households choose active participation (x = 1), schools choose passive response (y = 0), and society chooses not to open resources (z = 0). The stability condition is that household participation benefits exceed costs ($R_{DC}^h+\alpha s_f>C_{DC}^h$), but school leadership costs exceed benefits ($R_{BC}^h+\beta S_p<C_{BC}^h$) and society's cost of opening resources exceeds benefits ($R_c^h>R_c^h-c_c$). In reality, households bear excessive responsibility for psychological education, while schools lack motivation due to absent evaluation mechanisms or insufficient resources, and societal institutions remain closed due to no incentives. Policies should integrate mental health education into school evaluations, mandate home-school collaboration mechanisms, and use government-purchased services to guide societal institutions to open resources, lowering barriers for households to access professional support.

Scenario 3: Households choose general participation (x = 0), schools choose active leadership (y = 1), and society chooses not to open resources (z = 0). The stability condition is that school leadership benefits exceed costs ($R_{DC}^h+\beta S_p>C_{dc}^h$), but household participation costs exceed benefits $R_{BC}^h+\alpha s_f<C_{BC}^h$) and society's cost of opening resources exceeds benefits ($R_c^h>R_c^e-c_c$). In reality, the implementation of positive education means transforming schools into educational places with a positive atmosphere (Kristjánsson, 2012). Schools provide mental health services alone, but low household engagement and closed societal resources limit services to campuses, failing to address deeper family influences. Policies should reduce household participation costs through community outreach, parent training, and subsidies, while establishing school-society cooperation funds and encouraging professional institutions to enter schools to bridge service gaps.

Scenario 4: Households choose general participation (x = 0), schools choose passive response (y = 0), and society chooses to open resources (z = 1). The stability condition is that societal benefits of opening resources exceed costs ($R_c^e-c_c>R_c^h$), but household participation costs exceed benefits (${R_{BC}}^h+\alpha s_f<{C_{BC}}^h$) and school leadership costs exceed benefits (${R_{BC}}^h+\beta S_p<{C_{BC}}^h$). In reality, societal institutions open resources, but low participation from households and schools leads to underutilization due to lack of awareness or access. Policies should promote home-school awareness of resources, establish mechanisms for “societal resources in schools,” and develop digital platforms to improve resource matching.

Scenario 5: Households choose active participation (x = 1), schools choose active leadership (y = 1), and society chooses not to open resources (z = 0). The stability condition is that home-school collaboration benefits exceed costs ($R_{DC}^h+R_{BC}^h+\alpha s_f+\beta S_p>C_{DC}^h+C_{BC}^h$), but societal costs of opening resources exceed benefits (${R_c}^h>{R_c}^e-c_c$). In reality, home-school collaboration forms but lacks professional societal support, limiting services to prevention. Societal institutions avoid participation due to high costs and low returns. Universities should establish a supportive ecosystem for college students from the institutional level to promote their psychological development (Brendtro, 2006). Policies should offer tax breaks or subsidies to societal institutions participating in collaboration, establish standards, and use government endorsement to build trust.

Scenario 6: Family chooses active participation (x = 1), school chooses passive response (y = 0), society chooses open resources (z = 1). Stability conditions: family-society collaboration revenue exceeds costs ($R_{DC}^h+R_c^e+\alpha s_f>C_D^{h}C+2c_c$). School-led costs exceed revenue ($R_{BC}^h+\beta S_p<C_{BC}^h$). Real-world performance: preliminary cooperation between families and social institutions, but schools rejects resource intervention due to management restrictions or lack of motivation, leading to fragmentation between in-school data and social services. Policy recommendations: legislate to clarify schools' obligations to open resources and incorporate them into evaluations; develop a home-school-community psychological data sharing platform to achieve cross-scenario data synchronization (Em et al., 2025).

Scenario 7: Family chooses general participation (x = 0), school chooses active leadership (y = 1), society chooses open resources (z = 1). Stability conditions: school-society collaboration revenue exceeds costs ($R_{BC}^h+Rce+\beta S_p>C_{BC}^h+2c_c$). Family participation costs exceed revenue ($R_{DC}^h+\alpha s_f<C_{DC}^h$). Real-world performance: schools collaborate with social institutions to provide services and during the growth process of college students, schools form a cooperative relationship with them, guiding college students to become people with love, responsibility, and initiative (Waters et al., 2017) but low family participation hinders the continuation of intervention effects into home scenarios. Policy recommendations: develop “family-friendly” service products to lower participation thresholds; offer point rewards and social resource redemption for active families to enhance initiative.

Scenario 8: Family chooses active participation (x = 1), school chooses active leadership (y = 1), society chooses open resources (z = 1). Stability conditions: tripartite collaboration revenue exceeds costs for all parties $({R_{DC}}^h+{R_{BC}}^h+R{c}_e+\alpha s_f+\beta S_p>{C_{DC}}^h+{C_{BC}}^h+c_c$). Reasonable revenue distribution ratio: fairness in λh:λs:λc. Real-world performance: deep tripartite collaboration, where families cooperate with schools and society provides professional support; services cover the entire chain and achieve systemic effects. Policy recommendations: establish special funds and clarify revenue distribution to ensure long-term cooperation; develop monitoring platforms and dynamically adjust policies based on psychological improvement data to enhance synergistic efficiency (Table 4).

Table 4

Table 4. Analysis of home-school-society collaboration equilibria and policy recommendations.

Analysis of each equilibrium point provides targeted recommendations for policymakers to guide the system toward the high-collaboration equilibrium (E8).

(1) Interior equilibrium analysis

In the evolutionary game model of home-school-society collaboration for college students' mental health, the analysis of interior equilibrium points focuses on the dynamic balance where the strategic proportions of all three parties are in intermediate states. If an interior equilibrium (x*, y*, z*)upepsilon(0,1)3 exists, it must satisfy with the core being the dynamic matching of benefits and costs across all three parties' strategic choices. Given x*, y*upepsilon(0,1), the existence of an interior equilibrium particularly depends on the balance between the costs and benefits of social resource opening—when the expected benefits of social resource opening (e.g., long-term social benefits from collaborative effects) equal its costs (e.g., service inputs from professional institutions), social strategic choices reach a critical point, thereby influencing the strategic equilibrium of families and schools.

This analysis indicates that the tripartite collaboration system may exhibit intermediate states of incomplete collaboration, whose stability depends on the effective allocation of social resources and dynamic adjustments to cost-benefit ratios. This provides a theoretical basis for “fine-tuning” policy interventions. For example, moderation subsidies or optimized benefit distribution can nudge the cost-benefit balance of social resource opening toward the equilibrium point, preventing the system from settling into extreme states of low or high collaboration.

(2) Practical implications of equilibrium points

In the tripartite evolutionary game model of collaborative psychological education for college students' mental health among families, schools, and society, different equilibrium points characterize differentiated collaboration states and their real-world implications:

Low-collaboration equilibrium [e.g., E1 = (0,0,0)] manifests as non-cooperation among all three parties, resulting in inefficient mental health services. This reflects the typical dilemma of insufficient incentives and resource integration in current practice. Partial-collaboration equilibria demonstrate unilateral or bilateral cooperation limitations: E₂ = (1, 0, 0): households alone participate actively. E3 = (0, 1, 0): schools alone take leadership. E4 = (0, 0, 1): society alone opens resources. E5 = (1, 1, 0): household-school collaboration without societal resources. These states exhibit inefficiencies such as resource wastage or intervention discontinuities due to missing stakeholder engagement. High-collaboration equilibrium [E8 = (1, 1, 1)] achieves tripartite synergy, maximizing mental health service effectiveness as the system's ideal state (Table 5).

Table 5

Table 5. Eigenvalue sign conditions and stability conclusions for each equilibrium point.

3.1.2 Analysis of stability

Equilibrium points such as E₁, E₂, E₃, E₄, and E₅ remain stable under specific conditions. For example, E₁ maintains low collaboration because the benefits for all three parties are lower than the costs, while E5 fails to attract social participation due to the high costs of opening resources. E₆ = (1, 0, 1) and E₇ = (0, 1, 1) are conditionally stable, depending on optimized benefit distribution and reduced family costs, respectively. The stability of E₈ requires that the collaborative benefits for families, schools, and society all exceed their respective costs, i.e., the benefits of family participation, school leadership, and social resource opening must each be greater than their costs.

3.1.3 Policy interventions

Policy interventions should focus on three work together aspects: enhancing collaborative benefits, reducing collaboration costs, and promoting social participation. In particular, the following policy measures can be considered:

Optimizing benefits: Ensure positive net benefits through government subsidies (α for families, β for schools) and benefit distribution mechanisms (λ). Reducing costs: Establish special funds to lower family psychological education costs (e.g., free courses) and school service costs (e.g., facility sharing). Incentivizing society: Use tax incentives to reduce the cost of social resource opening (cc) and attract professional institutions. Example: When family subsidies (α > 0.35), school subsidies (β > 0.4), and social incentives (θ > 0.25) exceed critical values, and the benefit distribution ratio is reasonable (e.g., λ = 0.4, λ = 0.4, λ = 0.2), the system can stably converge to E8. Conversely, if any party's cost-benefit balance is disrupted (e.g., excessively high family participation costs), corresponding parameters (e.g., increasing α) should be dynamically adjusted to restore equilibrium.

3.1.4 Conclusion

Achieving high-collaboration equilibrium requires systematic policy support. Governments should use levers such as subsidies, resource allocation, and incentives to break the low-collaboration deadlock and establish dynamic adjustment mechanisms to respond to real-world feedback. This will promote long-term, stable, and efficient collaboration among families, schools, and society, providing sustainable institutional guarantee for college students' mental health services.

3.2 Tripartite collaborative evolution analysis considering government regulation

In the previous section, we analyzed the equilibrium points and stability conditions of the tripartite evolutionary game, revealing the strategic interactions among families, schools, and society in the collaborative mental health education of college students. However, achieving a stable evolution toward high-collaboration equilibrium often requires overcoming critical cost-benefit thresholds that spontaneous interactions among the three parties may not suffice to address. Therefore, the role of the government as an external regulator becomes particularly crucial. This section further explores how the government can intervene in the strategic choices of the three parties through policy tools (e.g., subsidies, incentives, and resource allocation) to optimize the system's evolutionary path and promote a more efficient and stable equilibrium in the collaborative education system.

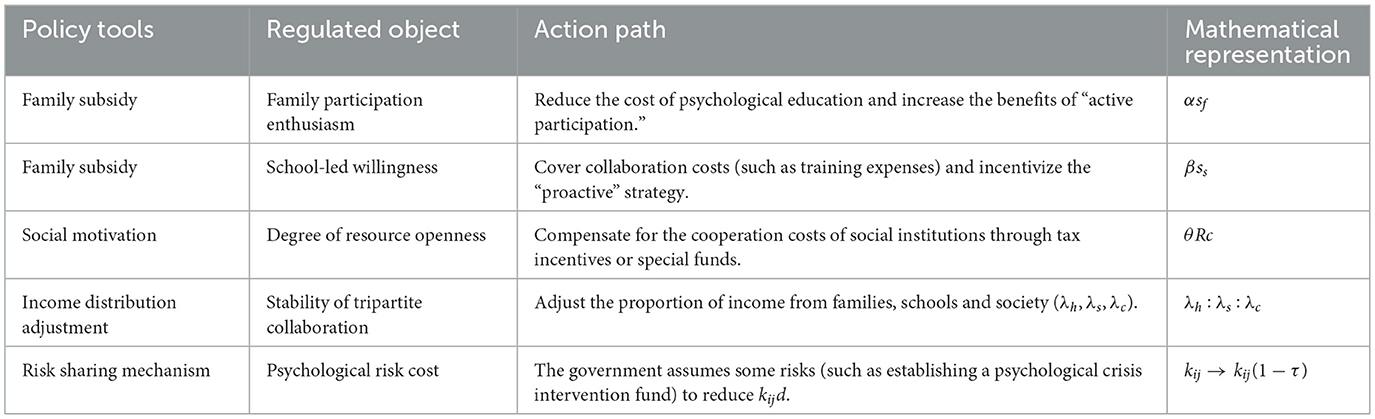
As a key external regulator in the collaborative mental health education system for college students, the government directly influences the strategic choices of families, schools, and society through policy tools such as subsidies, legislation, and resource allocation. This section incorporates government regulation parameters (α, β, θ, S_m, S_p, etc.) into the evolutionary game model to analyze their intervention paths and effects on the system equilibrium.

Stability changes of equilibrium points under government regulation taking the high-collaboration equilibrium E8 = (1, 1, 1) as an example, its stability conditions require that the collaborative benefits of families, schools, and society all exceed their respective costs. The specific core logic is as follows:

When the government's subsidy ratio for families (such as α) is sufficient to make the net benefit of families' “active participation” exceed that of “general participation” (i.e., the benefit of families' participation in psychological education $R_{DC}^h$ minus the cost C_f is still higher than the benefit of passive participation R_f), the family strategy will stabilize at “active participation.” Here, α is the subsidy ratio, and Sf is the maximum subsidy amount for families, indicating that the subsidy must reach a critical value to cover the participation costs of families and provide additional incentives.

The stability of the school's “active leadership” strategy requires that its benefits (such as the sum of the government subsidy βSs and the mental health service benefit) are higher than the difference between the benefit of “passive response” (${R_{BC}}^h$) and the collaboration cost (C_s). Here, β is the school subsidy ratio, and Ss is the maximum subsidy amount for schools, indicating that the government needs to reduce the net cost of schools' active participation through financial support.

The stability condition for society's “open resources” strategy is that its benefits (such as the cooperation benefit $R_c^e$ and the government incentive θR_c) are higher than the difference between the benefit of “not opening resources” (${R_c}^h$) and the opening cost (C_c). Here, θ is the social incentive ratio, and Rc is the total social cooperation benefit, indicating that the resource opening costs of social institutions need to be compensated through incentive mechanisms.

$\begin{array}{l}\{\begin{array}{cc}\text{Family}:& \alpha \mu +\lambda h\gamma \delta \eta >cf(1-\tau )+{\alpha }^{\prime }+rf\\ \text{University}:& \beta v+{\lambda }_s\gamma \delta \eta >c_s(1-\tau )+{\beta }^{\prime }+r_s\\ \text{Society}:& k\eta (1+\theta )>cr(1-\tau )\\ \end{array}\end{array}$

The subsidy ratios (α, β) and the incentive ratio (θ) in the above conditions need to reach specific critical values (such as α > 0.35, β > 0.4, θ > 0.25) to promote the three parties' strategies to stabilize in a high-collaboration state. For example, when the family subsidy α exceeds the critical value, the family participation rate will significantly increase and remain stable, and the same applies to the regulatory parameters of schools and society. These critical values provide a quantitative basis for the government to formulate policies, ensuring that the subsidy and incentive efforts are sufficient to break through the “non-collaborative inertia” of the three parties and form a stable collaborative education mechanism. The specific mechanisms through which these key government parameters influence the strategic choices of families, schools, and society are systematically summarized in Table 6.

Table 6

Table 6. Correlation mechanisms between government regulation parameters and tripartite strategies.

3.3 Simulation of government regulation scenarios

Scenario 1: In the single-policy scenario where only the government's subsidy ratio α for households is adjusted, the proportion x of households choosing “active participation in psychological education” significantly increases, reflecting the direct incentive effect of subsidies on households' willingness to participate. However, since the school subsidy β and social incentive θ are not adjusted simultaneously, schools may maintain a “passive response” strategy due to higher dominant costs than benefits, and social institutions may remain “unwilling to open resources” due to the lack of cooperation incentives. This leads the system to converge to a partial collaboration equilibrium point E5 = (1, 1, 0), where households participate actively, schools take the initiative, but society does not open resources. The limitation of this scenario is that single policies struggle to drive tripartite coordination, and potential strategy lags in schools and society may cause resource misallocation. For example, household needs and school services lack support from professional social resources, affecting the overall effectiveness of mental health services.

Scenario 2: When the government implements a coordinated regulation policy by simultaneously increasing the household subsidy α, school subsidy β, and social incentive θ, the collaboration motivation of the three parties is fully activated: households reduce participation costs due to increased subsidies, schools enhance their willingness to take the initiative due to financial support, and social institutions are more inclined to open resources due to increased incentives. This systematic policy intervention can rapidly drive the system to converge to a high-collaboration equilibrium point E8 = (1, 1, 1), i.e., the ideal state where households participate actively, schools take the initiative, and society opens resources. Data examples show that when α = 0.6, β = 0.5, and θ = 0.4, the tripartite collaboration probability can increase to 85%, indicating that coordinated regulation effectively breaks the low-collaboration deadlock, forms a positive cycle of tripartite linkage through multiple incentives, and significantly improves the efficiency and effectiveness of collaborative mental health education.

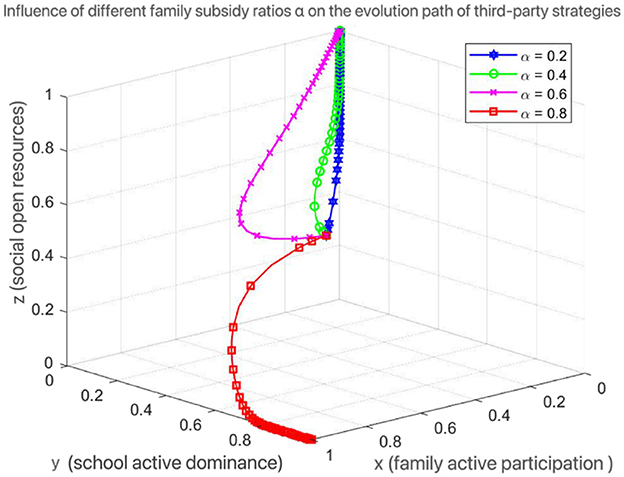
Scenario 3: Dynamically adjusting the profit distribution ratios (λ_h, λ_s, λ_n) for households, schools, and society can effectively prevent any party from withdrawing from collaboration due to insufficient profits, thereby enhancing system stability. For instance, when setting λ_h = 0.4, λ_s = 0.4, and λ_n = 0.2, the profit distribution among the three parties becomes more balanced: households and schools, as core education entities, receive higher profit shares to incentivize their continuous collaborative investment; although social institutions have a slightly lower share, their willingness to open resources is maintained through stable profit expectations. This distribution model alleviates the risk of cooperation breakdown caused by interest imbalance, particularly in the early stages of collaboration or scenarios with significant resource input disparities. Through an institutionalized profit distribution mechanism, it guides the three parties to form long-term stable collaborative relationships and promotes the system's evolution toward high-collaboration equilibrium.

3.4 Numerical simulation validation

In the evolutionary game model of home-school-society tripartite collaboration for college students' mental health, government regulation strategies significantly influence the strategic choices of the three parties and the system's equilibrium state. Numerical simulations comparing the equilibrium results under three scenarios—no regulation, single subsidy, and coordinated regulation (see Table 7)—clearly reveal the practical effects of different policy interventions.

Table 7

Table 7. Comparison of equilibria before and after government coordination.

In the unregulated (baseline) state, the household participation rate (x = 0.35), school initiative rate (y = 0.28), and social openness rate (z = 0.12) all remain low, with slow system convergence. This indicates that without external intervention, the three parties generally prefer low-collaboration strategies due to high collaboration costs and insufficient benefits, leading to a “fragmented” dilemma in mental health services.

The single-subsidy policy (adjusting only α = 0.5) significantly increases the household participation rate (x = 0.72), but the improvements in the school initiative rate (y = 0.31) and social openness rate (z = 0.15) are limited, with a moderate convergence speed. This confirms the limitation of single policies: while household enthusiasm is stimulated, schools maintain passive responses due to the lack of financial support (β unadjusted), and social institutions remain resource-closed due to the absence of incentives (θ unadjusted), resulting in the system only achieving a partial equilibrium of “active household participation, low collaboration from schools and society” (e.g., E5). The overall collaborative efficiency is insufficient.

Coordinated regulation (α = 0.5, β = 0.4, θ = 0.3) demonstrates the advantages of systematic policies: the household participation rate (x = 0.89), school initiative rate (y = 0.85), and social openness rate (z = 0.78) all significantly increase, with the fastest system convergence speed. This shows that simultaneously adjusting subsidy ratios (α, β) and incentive coefficients (θ) can form a tripartite linkage effect—households reduce participation costs due to subsidies, schools enhance initiative due to financial support, and social institutions open resources due to profit incentives—ultimately driving the system rapidly toward high-collaboration equilibrium (E8) (see Table 7 for details).

3.5 Analysis of tripartite coevolution considering government regulation

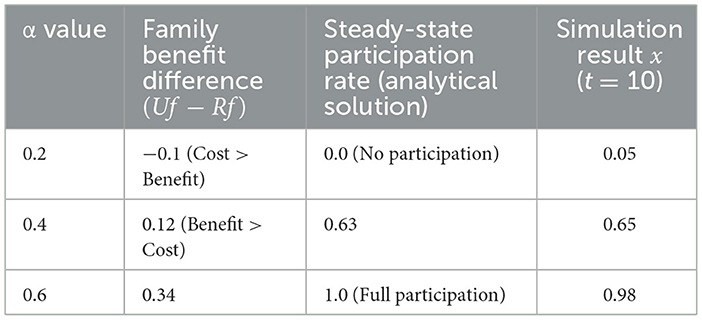
In the three party evolutionary game model of college students' mental health cooperative education, the quantitative influence of government regulation parameters such as subsidy ratio α, β, θ on the choice of three party strategies can be deeply revealed through numerical examples and sensitivity analysis. Taking the action mechanism of family subsidy ratio α on family participation rate x as an example, it has influence through cost-benefit reconstruction mechanism. The increase of α will directly increase the expected benefit of family “active participation” strategy and reduce the net cost. Widening the difference in returns from “average participation” creates positive incentives that drive up the household participation rate x. For quantitative analysis, the initial parameters are set as family participation cost c_f = 0.5, other subsidy related parameters α'= 0.2, synergy benefit coefficient μ = 1.0, comprehensive benefit term $-c_{AO}^s+\beta s_s$, family risk cost, and the school dominance rate/and social openness rate/are fixed to simulate the middle cooperation level scenario. When α ≤ 0.35, the cost of family active participation is higher than the benefit, and the family tends to participate generally. For example, when α = 0.2, the benefit difference is −0.1, the steady participation rate is 0, and the simulation result x = 0.05; When α > 0.35, the profit difference is positive, and the participation rate increases significantly. For example, when α = 0.4, the profit difference is 0.12, the steady participation rate is 0.63, the simulation result x = 0.65, when α = 0.6, the profit difference is 0.34, the steady participation rate reaches 1, and the simulation result x = 0.98 is close to the complete participation state, which reflects the threshold effect and the marginal increasing law. Moreover, the analytical solution is highly consistent with the simulation results to verify the reliability of the model. This indicates that the government needs to set α above 0.35 to break through the cost-benefit threshold, simultaneously optimize β and θ to avoid single policy leading to families fighting alone, and enhance policy effectiveness by reducing the inherent cost of families or improving the synergistic benefit coefficient, which provides quantitative basis for formulating differentiated subsidy policies and emphasizes the necessity of multi-agent collaborative intervention (see Table 8 for details).

Table 8

Table 8. Difference of family income and participation rate under different family subsidy ratio α.

(1) The influence of β on y

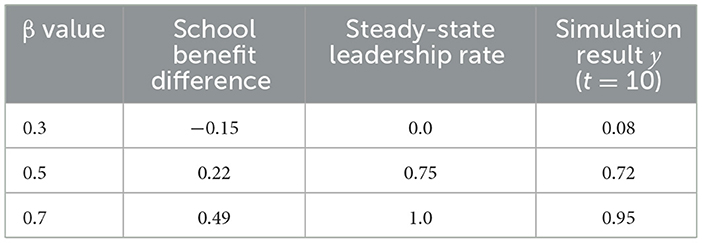
In the home-school-community three-way evolutionary game model of college students' mental health cooperative education, the influence of government regulation parameters on three-way strategy can be further clarified through numerical examples and sensitivity analysis. Taking the effect mechanism of β on y, β increases the net benefit by covering the cost of school collaboration (such as teacher training cost). The initial parameters are set as school collaboration cost c_s = 0.6, other subsidy related parameters β′ = 0.3, synergy benefit coefficient v = 1.2, comprehensive benefit term (1−λ)γδη = 0.7, school risk cost r_s = 0.4, and fixed family participation rate/and social openness rate z = 0.6. The results show that when β = 0.3, the benefit difference is −0.15, Schools maintain passive coping (steady state dominance 0, simulation y = 0.08), while the return difference is 0.22 when β = 0.5, steady state dominance 0.75 (simulation y = 0.72), return difference 0.49 when β = 0.7, schools are completely active dominant (steady state y = 1, simulation y = 0.95), and y increases about 64% when β increases from 0.3 to 0.5, but the marginal effect decreases when β > 0.7, which needs to be combined with financial budget optimization (see Table 9 for details).

Table 9

Table 9. Difference and dominance ratio of school income under different school subsidy ratio β.

(2) Influence of social incentive ratio θ on social openness ratio z

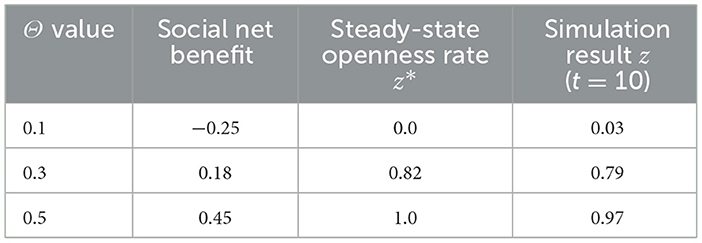
The influence of social incentive ratio θ on social openness rate z is reflected in compensating the cost of resource opening $\theta R_c^c$ by revenue sharing c_c, encouraging social institutions to choose the strategy of “open resources,” setting initial parameters as social opening cost c_c = 0.8, synergy coefficient kη = 1.0, social revenue $R_{AO}^c=0.5,R_{PO}^c=0.3$, under different school strategies, and fixing x = 0.8, y = 0.7. The data show that when θ = 0.1, social net revenue −0.25, maintaining resource closure (steady state z = 0, simulation z = 0.03), net return 0.18 when θ = 0.3, steady state open rate 0.82 (simulation z = 0.79), net return 0.45 when θ = 0.5, complete open (steady state z = 1, simulation z = 0.97), and z rises rapidly when θ > 0.25. The government can optimize resource investment through stepped incentives (such as θ = 0.4) (see Table 10 for details).

Table 10

Table 10. Numerical analysis of the influence of social incentive ratio θ on social openness rate.

(3) Simulation of comprehensive regulation effect

The simulation of comprehensive regulation effect shows that the convergence steps of the system exceed 100 and the cooperation rate is low without regulation (x = 0.35, y = 0.28, z = 0.12), when only adjusting α = 0.5 and β = 0.4, the home-school collaboration rate increased significantly (x = 0.89, y = 0.78), but the social openness rate is only 0.45, while the cooperative regulation α = 0.6, β = 0.5, θ = 0.4, the tripartite cooperation rate reaches 0.95, 0.92, 0.88, respectively, and the convergence steps are only 25. It is verified that the multi-dimensional policy linkage can significantly accelerate the system to converge to the high cooperative equilibrium E, and when α > 0.5, β > 0.4, θ > 0.3, the cooperation rate exceeds 85% (see Table 11 for details).

Table 11

Table 11. Cooperation rate and convergence steps of home-school-community under different control combinations.

(4) Policy recommendations supplement

Based on the above analysis, policy recommendations include differentiated subsidy design, such as setting α ≥ 0.5 for low-income families, increasing β to 0.6 for rural schools, and dynamically adjusting θ for social institutions according to service effects (For example, θ = 0.3 + 0.1 × service satisfaction). At the same time, the government needs to monitor the critical values of family α > 0.35, school β > 0.4 and society θ > 0.25 in real time, and update the parameters according to the cooperation effect every semester to form a dynamic adjustment mechanism to continuously optimize the efficiency of home-school-community collaborative education.

4 Simulation analysis of three-way evolutionary game

In order to verify the applicability of home-school-community three-way evolutionary game model in college students' mental health collaborative education, and further analyze the influence of government regulation parameters (such as family subsidy ratio α, school subsidy ratio β, social incentive ratio θ), cooperation cost, resource opening income and other key variables on the system evolution path and results, this section carries out numerical simulation analysis based on the ideal evolutionary stable state (1, 1, 1).

Matlab R2022b was used for simulation. Referring to the replication dynamic equation and parameter setting in Section 1, the evolution path and equilibrium evolution trend of the strategy under the change of key variables were analyzed one by one on the basis that the initial probability of the strategy was 0.4.

4.1 Three-way evolutionary path simulation

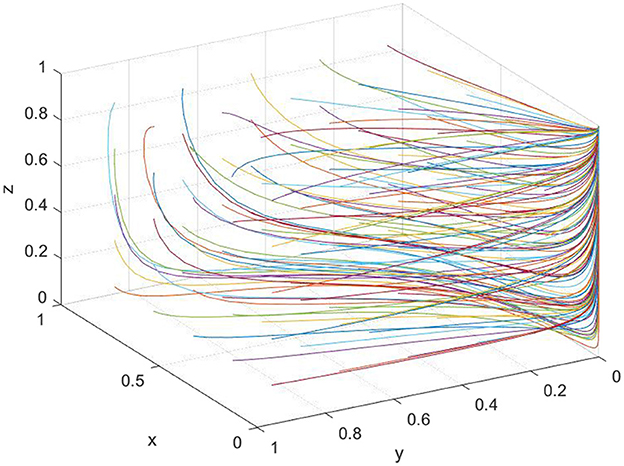
Substituted the basic parameters into the model, and set the initial strategy selection probability as: family active participation x = 0.4, school active dominance y = 0.4, social open resources z = 0.4. The simulation evolution path is shown in Figure 2.

Figure 2

Figure 2. System evolution path.

As can be seen from Figure 2, the final evolution of the system tends to a stable state (1, 1, 1), indicating that families, schools, and society finally choose to cooperate in mental health services, verifying the feasibility and stability of the evolutionary game model under the background of collaborative education. Next, this paper will examine the impact of key policy parameters on evolutionary paths.

4.2 Influence of family subsidy ratio α on evolution results

In order to explore the impact of government subsidies on the evolution of the system, let α be 0.2, 0.4, 0.6, 0.8, and the other parameters remain unchanged. The simulation results are shown in Figure 3.

Figure 3

Figure 3. Effect of α change on system evolution results.

Figure 3 shows that as α increases, the proportion of families choosing “active participation” increases significantly. When α < 0.3, the system tends to (0, y, z), and the family participation intention is insufficient; when α > 0.5, the family strategy converges rapidly to 1, and the system evolves to a highly cooperative state. It shows that increasing family subsidies properly can effectively stimulate their cooperative power, which is the key to building a stable cooperative system.

4.3 The influence of β ratio of school subsidy on evolution results

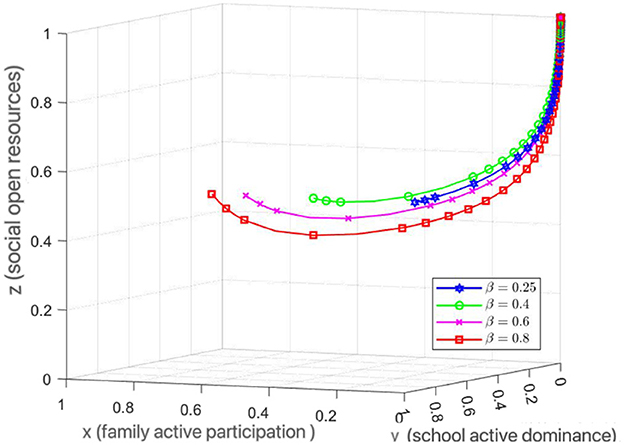
In order to study the promotion effect of school subsidy on system collaboration, β is set to be 0.25, 0.4, 0.6 and 0.8. The simulation results are shown in Figure 4.

Figure 4

Figure 4. Effect of β change on system evolution results.

Figure 4 shows that the proportion of school “active” strategies increases significantly with β. The critical threshold of β is between 0.35 and 0.45. Below this value, schools tend to be passive; above this value, active strategies quickly dominate and the system evolves more easily into a cooperative state (x, 1, z). Therefore, enhancing school policy support will enhance their dominant willingness and reduce the risk of collaboration lag.

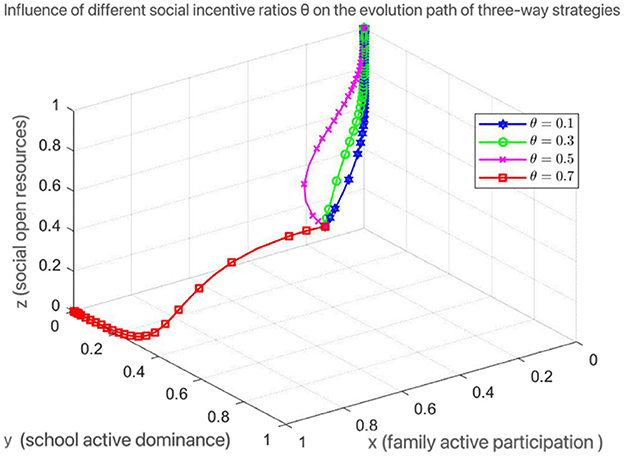
4.4 Influence of social incentive ratio θ on evolution results

Set θ = 0.1, 0.3, 0.5, 0.7, and examine their impact on social resource opening strategies. The simulation results are shown in Figure 5.

Figure 5

Figure 5. Effect of θ variation on system evolution results.

Figure 5 shows that below θ 0.25, society remains essentially “closed” (z = 0); above θ 0.4, the proportion of openness rises sharply, eventually tending to 1. It shows that the cooperation tendency of social institutions is highly sensitive to incentive mechanism, and the design of revenue sharing system is the core of promoting resource flow.

5 Conclusion

Based on the realistic demand of college students' mental health collaborative education, this paper systematically analyzes the key factors of participation strategies by constructing an evolutionary game model involving family, school and society, and draws the following main conclusions and practical enlightenment.

For families, their participation strategies are mainly influenced by government subsidies, participation costs and expected benefits. Model simulations show that higher government subsidies can significantly increase the probability of families choosing “active participation,” especially when combined with low participation costs and high expected returns. However, when the cost of family participation is too high or the expected benefits are insufficient, their willingness to participate will be significantly inhibited.

It is suggested that government departments should establish differentiated subsidy policies: raise subsidy standards for families with economic difficulties (Heng et al., 2025), and carry out universal education on mental health knowledge to reduce their psychological threshold for participation (Chin et al., 2024). Schools should optimize the home-school communication mechanism, reduce parents' time cost through digital platform (Stephan et al., 2019), and improve the convenience of participation.

For schools, the choice of dominant strategy mainly depends on financial support, professional resources supply and risk management ability. Simulation results suggest that when government support covers at least 40% of the mental health service costs, the school's “active leadership” strategy is more likely to reach a stable equilibrium under the model conditions. In addition, the openness of social resources directly affects school service effectiveness, and there is a significant positive correlation between the two.

The administrative department of education shall improve the special fund guarantee mechanism for mental health and establish a scientific performance appraisal system (Thon et al., 2022). At the same time, schools need to strengthen the construction of professional teams, improve risk response capabilities, and actively build cooperation platforms with social institutions to realize resource sharing and complementary advantages.

For social institutions, resource opening decisions are mainly influenced by revenue allocation ratio, operating cost, and synergy effect. When the proportion of income distribution exceeds 30%, the willingness of social institutions to choose “open resources” is significantly enhanced. It is worth noting that the participation of families and schools will amplify the marginal benefits of social resources through synergy, forming a positive feedback mechanism.

It is suggested to establish government-led income distribution guidelines and improve the psychological service procurement mechanism involving social institutions. At the same time, supporting policies such as tax preference and brand publicity can be adopted to reduce the operating costs of social institutions and enhance their enthusiasm for continuous participation.

International evidence demonstrates that the family-school-community collaborative education mechanism yields significant improvements in adolescent mental health outcomes. For instance, In Ghana, research shows that support from parents, classmates, and teachers significantly boosts student engagement (Ansong et al., 2017). In South Korea, Gyeonggi Province's “Shared School Program” has promoted cooperation among universities and community organizations to support youth education and wellbeing. In Cambodia, recent national endeavors have focused on enhancing research capacity and scholarly pursuits within higher education institutions, recognizing the foundational role of robust academic ecosystems in fostering student development, including psychosocial wellbeing (Em and Khampirat, 2025). While detailed quantitative evaluations are limited, reports indicate improvements in mental health support accessibility and service coordination. In the United States, federal initiatives such as the School-Based Mental Health Services program have allocated substantial funding—over $500 million in recent years—to expand mental health workforce capacity in schools. These efforts have led to improvements in crisis intervention outcomes and access to care, although success rates vary across districts. These cases collectively demonstrate that tripartite collaboration not only enhances mental health service efficiency but also substantially improves student psychological wellbeing. This study establishes a theoretical foundation and practical framework for university mental health education through such collaborative mechanisms, with potential to achieve similarly positive outcomes in practice.

This study reveals the inherent mechanism of home-school-community collaboration through evolutionary game theory, quantitatively analyzes the impact of policy intervention on system equilibrium, and provides theoretical basis for improving college students' mental health service system. Future research can further explore the following directions: one is to introduce time delay effect to analyze the dynamic response process of policy implementation; the other is to investigate the impact of regional differences on synergy effects; and the third is to study the transformation effect of digital technology on traditional synergy models. These expansions will help to build a more accurate and efficient new model of collaborative education.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

JG: Data curation, Writing – review & editing, Writing – original draft, Investigation. FT: Data curation, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This article was a phased research result of the 2025 Excellent Project of Ideological and Political Work in Colleges and Universities of Shanxi Provincial Department of Education entitled “The Charm of Shanxi Merchants: Digital Intelligence Education” — Innovating the In-depth Integration of College Cultural Relics Activation and Practical Education Resources (Project No.: 2025002). This work was supported by “Shanxi Provincial High-Quality Development Research Project — 2025 Project Approval List of Family Construction Think Tank Special Topic”, undertaking Unit: Shanxi University of Finance and Economics (Project Number: SXGZL2025ZXD1032).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2025.1660557/full#supplementary-material

References

Albert, B. (1977). Social Learning Theory. Englewood Cliffs, NJ: Prentice Hall.

Google Scholar

Ansong, D., Okumu, M., Bowen, G. L., Walker, A. M., and Eisensmith, S. R. (2017). The role of parent, classmate, and teacher support in student engagement: evidence from Ghana. Int. J. Educ. Dev. 54, 51–58. doi: 10.1016/j.ijedudev.2017.03.010

Crossref Full Text | Google Scholar

Ayiro, L., Misigo, B. L., and Dingili, R. (2023). Stress levels, coping strategies, and mental health literacy among secondary school students in Kenya. Front Educ. 8:1099020. doi: 10.3389/feduc.2023.1099020

Crossref Full Text | Google Scholar

Brendtro, L. K. (2006). The Vision of Urie Bronfenbrenner: Adults Who are Crazy About Kids. Reclaiming Child Youth. 15, 162–166. doi: 10.4135/9781446212127.n22

Crossref Full Text | Google Scholar

Bronfenbrenner, U. (1979). The Ecology of Human Development: Experiments by Nature and Design. Cambridge: Harvard University Press.

Google Scholar

Cavioni, V., Grazzani, I., and Ornaghi, V. (2020). Mental health promotion in schools: a comprehensive theoretical framework. Int. J. Emot. Educ. 12, 65–82. Available online at: https://www.um.edu.mt/library/oar/handle/123456789/55039

Google Scholar

Chacon, G. P., Daniels, K. M., and Lobel, R. (2017). The role of surge pricing on a service platform with self-scheduling capacity. Manuf. Serv. Oper. Manag. 19, 368–384. doi: 10.1287/msom.2017.0618

PubMed Abstract | Crossref Full Text | Google Scholar

Chen, X., Zhang, X., and Jin, Y. (2023). Implications and practical paths of mental health education in collaboration with families, schools, and communities in China. Front. Educ. Res. 6, 12–18. doi: 10.25236/FER.2023.060703

Crossref Full Text | Google Scholar

Chin, P., Sam, R., Serey, M., and Em, S. (2024). Exploring the benefits and drawbacks of directing undergraduates' self-study pursuits: an in-depth analysis through literature review. J. Gen. Educ. Humanit. 3, 117–132. doi: 10.58421/gehu.v3i2.210

Crossref Full Text | Google Scholar

Chu, W., and Wei, L. (2024). Home, school, and community: building a “trinity” education mechanism based on collaboration. Adv. Educ. Human. Soc. Sci. Res. 10:1. doi: 10.56028/aehssr.10.1.198.2024

Crossref Full Text | Google Scholar

Em, S., and Khampirat, B. (2025). “Facilitating scholarly pursuits in higher education: cambodia's endeavors toward research advancement,” in Enhancing Research Output in Higher Education: Research Proposals, Profiles, and Publishing, ed. A. A. Mdikana (Hershey: IGI Global), 39–66.

Google Scholar

Em, S., Mok, S., Sam, R., Pen, D., and Serey, M. (2025). “Implications and considerations of AI-generative tools for higher education practices: opportunities, challenges, and future directions,” in Examining AI Disruption in Educational Settings: Challenges and Opportunities, ed. M. W. Kessinger (Hershey: IGI Global), 297–332. doi: 10.4018/979-8-3693-7873-1.ch011

Crossref Full Text | Google Scholar

Fehr, E., and Fischbacher, U. (2003). The nature of human altruism. Nature 425, 785–791. doi: 10.1038/nature02043

PubMed Abstract | Crossref Full Text | Google Scholar

Fengxian, Z. (2024). An analysis of collaboration between school, family and community in education. Lect. Notes Educ. Psychol. Public Media 54, 262–266. doi: 10.54254/2753-7048/54/20241679

Crossref Full Text | Google Scholar

Gintis, H. (2017). Individuality and Entanglement: The Moral and Material Bases of Social Life. Princeton University Press. doi: 10.2307/j.ctvc779cx

Crossref Full Text | Google Scholar

Heng, S., Chhourn, B., Loch, R., Mok, S., and Em, S. (2025). Correlation of home environment among personality and academic performance of undergraduates in Cambodia. J. Gen. Educ. Humanit. 4, 211–226. doi: 10.58421/gehu.v4i1.385

Crossref Full Text | Google Scholar

Koenig, J., Farhat, L. C., and Bloch, M. H. (2025). From adolescence into young adulthood-the importance of a longitudinal perspective across development in child and adolescent mental health. J. Child Psychol. Psychiatry 66, 1–3. doi: 10.1111/jcpp.14094

PubMed Abstract | Crossref Full Text | Google Scholar

Kristjánsson, K. (2012). Positive psychology and positive education: old wine in new bottles? Educ. Psychol. 47, 86–105. doi: 10.1080/00461520.2011.610678

Crossref Full Text | Google Scholar

Liu, S., and Xiao, X. (2023). Research on the problems and countermeasures in home-school cooperation of mental health education in elementary and middle schools: from Bronfenbrenner's ecosystem theory perspective. Front. Educ. Res. 6:63110. doi: 10.25236/FER.2023.063110

Crossref Full Text | Google Scholar

Liu, Y. (2025). Efficacy of home-school collaboration in enhancing college students' mental health. J. Eval. Clin. Pract. 31:e14273. doi: 10.1111/jep.14273

PubMed Abstract | Crossref Full Text | Google Scholar

Lu, M., Gao, Y., and Wan, Q. (2021). Research on evolutionary game of collaborative innovation in supply chain under digitization background. Math. Probl. Eng. 2021:1–18. doi: 10.1155/2021/3511472

Crossref Full Text | Google Scholar

Luyu, L. A. (2025). Review and prospect of home-school collaborative education in the past 20 years. Adv. Educ. Technol. Psychol. 9:1. doi: 10.23977/aetp.2025.090101

Crossref Full Text | Google Scholar

Nou, H., Mok, S., Lim, S., and Em, S. (2025). The relationship between students' attitudes towards cooperative learning strategies and their academic achievement. J. Soc. Knowl. Educ. 6, 200–210. doi: 10.37251/jske.v6i2.1606

Crossref Full Text | Google Scholar

Organization for Economic Co-operation and Development (2021). Public Finance Mechanisms for Mental Health. Paris: OECD Publishing.

Google Scholar

Ostrom, E. (1990). Governing the Commons: The Evolution of Institutions for Collective Action. Cambridge: Cambridge University Press.

Google Scholar

Perc, M., Jordan, J. J., Rand, D. G., Wang, Z., Boccaletti, S., and Szolnoki, A. (2021). Statistical physics of human cooperation in institutional networks. Nat. Hum. Behav. 5, 712–725.

Google Scholar

Sandholm, W. H. (2010). Population Games and Evolutionary Dynamics. Cambridge: MIT Press.

Google Scholar

Sandholm, W. H. (2020). Population Games and Evolutionary Dynamics, 2nd Edn. Cambridge: MIT Press.

Google Scholar

Seligman, M. E. P., Ernst, R. M., Gillham, J., et al. (2009). Positive education: positive psychology and classroom interventions. Oxf. Rev. Educ. 35, 293–311. doi: 10.1080/03054980902934563

Crossref Full Text | Google Scholar

Smith, J. M. (1982). Evolution and the Theory of Games. Cambridge: Cambridge University Press.

Google Scholar

Stephan, M., Markus, S., and Gläser-Zikuda, M. (2019). Students' achievement emotions and online learning in teacher education. Front. Educ. 4:109. doi: 10.3389/feduc.2019.00109

Crossref Full Text | Google Scholar

Tang, L. (2023). Research on the construction of a long-term mechanism for college students' mental health education from the perspective of home-school-community collaboration. Lect. Notes Educ. Arts Manag. Soc. Sci. 3, 54–60. doi: 10.18063/lne.v3i1.579

Crossref Full Text | Google Scholar

Thon, H., Em, S., Pang, S., and Nhor, R. (2022). Students' motivational factors behind acquiring shadow education and reasons for creating new generation schools in Cambodia. J. Gen. Educ. Humanit. 1, 201–212. doi: 10.58421/gehu.v1i4.51

Crossref Full Text | Google Scholar

Urie, B. (1979). The Ecology of Human Development: Experiments by Nature and Design. London: Harvard University Press.

Google Scholar

Waters, L., Sun, J., Rusk, R., Cotton, A., and Arch, A. (2017). “Positive education: visible wellbeing and positive functioning in students,” in Wellbeing, Recovery and Mental Health, eds. M. Slade, L. Oades, and A. Jarden (Cambridge: Cambridge University Press), 245–264.

Google Scholar

Weibull, J. W. (1997). Evolutionary Game Theory. MIT press.

Google Scholar

Williams, L., Mullins, J. L., Israel, B., et al. (2025). Culture, campus, and confidence: unpacking discrimination's impact on mental health among diverse college students. Front. Educ. 10:1614475. doi: 10.3389/feduc.2025.1614475

Crossref Full Text | Google Scholar

World Bank (2023). Digital Solutions for Public Service Delivery: Lessons from Global Experiences. Washington: World BankGroup.

Google Scholar

World Health Organization (2021). World Mental Health Report: Transforming Mental Health for All. Geneva: WHO.

Google Scholar

World Health Organization (2022). Mental Health Policy Package: Community Engagement. Geneva: WHO.

Google Scholar

Xiaoli, C. (2024). Research on the dilemma and path of mental health education for college students from the perspective of home-school cooperation. J. Contemp. Educ. Res. 8, 63–68. doi: 10.26689/jcer.v8i7.7751

Crossref Full Text | Google Scholar

Zhang, Q., Lin, S., Liu, J., and Jin, Y. (2022). A game perspective on collaborative learning among students in higher education. Cogent Educ. 9:2115617. doi: 10.1080/2331186X.2022.2115617

Crossref Full Text | Google Scholar

Zhang, Y., Liu, H., and Zhang, L. (2020). Policy simulation with evolutionary algorithms for collaborative governance in public services. J. Comput. Sci. 45:101178.

Google Scholar