Analysis of high school students' mental models of angles

Angles are a foundational concept in mathematics with wide applications in science and engineering, yet students often struggle with understanding the mathematical concepts behind them. Existing research has focused largely on misconceptions, leaving the cognitive structures behind these difficulties underexplored. To this end, we leveraged the “Fidelities Model of Conceptual Development” (short: FG-FF framework) to explore students cognitions of angles. The FG-FF framework, originally developed in physics education, distinguishes two cognitive dimensions in learner's mental models. Firstly, a Gestalt, which refers to its visual structure and appearance, and secondly a Functionality, which encompasses how well a model captures conceptual dynamics. The degrees in which both cognitive dimensions are related to reality—Fidelity of Gestalt (FG) and Functional Fidelity (FF)—enable a distinct typification of learners with respect to their mental models. While promising in science education, this framework has seen limited use in mathematics to date. To explore the explanatory power of this framework with regards to mental models in mathematics education, we conducted a cross-sectional survey with N = 403 high school students, using a newly developed instrument tailored to assess FG and FF in the context of mental models of angles. Confirmatory factor analysis confirmed a strong two-factor model (CFI = 0.96, RMSEA = 0.03, SRMR = 0.05) with solid reliability (ω_FF = 0.78, ω_FG = 0.66), validating the framework's relevance for mathematics education. The findings further suggest that effective teaching of geometry should intentionally guide students from visually grounded, Gestalt-oriented representations toward more abstract, functionally coherent understandings of mathematical concepts. By focusing on this progression, educators can design learning sequences that better connect perceptual intuition with formal reasoning, fostering deeper conceptual understanding of angles and related geometric ideas.

1 Introduction

The concept of angles is fundamental in mathematics and science and has critical applications in engineering, architecture, and computer graphics (Roseno et al., 2015). In physics, angles are essential to describe projectile motion, calculate forces, and analyze wave behavior (cf. Abdel-Malek and Siam, 2024). Engineers rely on angular measurements when designing structures, machines, and electrical circuits (cf. Wang et al., 2024). In computer graphics, angles are utilized to render three-dimensional objects, manipulate images, and create realistic animations (cf. Lu et al., 2020). Architects use angles to design buildings, optimize spatial arrangements, and ensure structural integrity (cf. Ma et al., 2022). Without a clear and accurate mental model of the angle concept, students may struggle to grasp these fundamental principles and their applications, which can limit their opportunities to pursue careers in the fields of science, technology, engineering, and mathematics.

Despite its importance, research consistently shows that students across age groups and educational contexts face persistent difficulties in understanding angles (Sari et al., 2021). Existing research has focused mainly on documenting and reporting the diverse range of misconceptions students exhibit when learning about angles, with comparatively less emphasis on elucidating the underlying mental processes that contribute to these misconceptions (Amoah and Assem, 2018). This disparity has led to the development of less effective pedagogical interventions, as educators often lack a comprehensive understanding of the specific cognitive challenges students face (Bütüner and Filiz, 2017). Addressing this gap in the literature is crucial for designing effective instructional strategies that promote a deeper and more accurate understanding of angles.

This study aims to investigate the cognitive structures that influence high school students' understanding of angles, a fundamental concept in geometry. While prior research has primarily focused on identifying students' misconceptions, this study takes a different approach by examining the mental models students use through the theoretical framework of Functional Fidelity (FF) and Fidelity of Gestalt (FG)—ideas that have predominantly been applied in physics and science education but are rarely utilized in mathematics. By using FF and FG, this study moves beyond cataloging misconceptions to analyze the cognitive structures that shape how students reason about angles. Unlike prior work that focuses on observable errors, this approach examines the underlying patterns and inconsistencies in students' mental models (cf. Sadijah and Malang, 2022). Addressing this gap is essential, as a deeper understanding of these reasoning processes can directly inform the design of interventions that target the roots of conceptual difficulty rather than its symptoms.

2 Research background

2.1 The angle concept: a brief overview

In education, angles often remain undefined from a mathematical standpoint. Instead, educators use various approaches that try to capture intuitive ideas, e.g. by describing angles as an amount of turning between two lines, the union of two rays, or the interior region between the intersection of two lines (Keiser, 2004; Richardson and Koyunkaya, 2017). However, (Veith and Bitzenbauer, 2021) have described how these intuitive approaches can lead to misconceptions, especially with regards to the differentiation between angles and their measure. From a mathematical standpoint, the definition of angles becomes rather trivial: Given three points A, B and C, then the ordered pair ([AB, [AC) is called angle between the two rays [AB and [AC. The rays [AB and [AC are called sides (or legs) and A the vertex of the angle. A very important implication of this definition is that angles can not be visualized directly as they are not figures. Instead, they are an abstract tuple of two mathematical objects, and visually representing them via both rays is similar to visualizing the mapping rule of a function ℝ → ℝ using its graph: While the objects themselves are not part of the plane in the sense that they consist of points, one can think of them as being represented by geometric figures for illustrative purposes.

Although this definition of angles may appear simple, it presents complex learning challenges in mathematics and physics education, often becoming a stumbling block for students at various levels (Bütüner and Filiz, 2017). This complexity arises from its dual nature, reflected in both static and dynamic interpretations, which can lead to misconceptions that hinder a comprehensive understanding (Johnson et al., 2021). To effectively help students develop a strong grasp of angles, educators must explore these different perspectives and examine common misconceptions.

At its core, the concept of an angle encompasses both geometric and kinematic properties, resulting in distinct definitions and interpretations that students must reconcile to develop a clear and accurate mental model of the concept. The static definition, rooted in Euclidean geometry, describes an angle as the intersection of two rays sharing a common endpoint, much like the opening of a pair of scissors (Susanto, 2020). While this static view is intuitive for visualizing angles in geometric figures, it does not account for the dynamic element of rotation and directional change. The dynamic definition of an angle characterizes it as a measure of rotation, indicating the amount of turn needed to align one ray with another within the same plane (Bütüner and Filiz, 2017). This perspective emphasizes angles as transformations, focusing on changes in orientation and direction. The distinct differences between these static and dynamic viewpoints can pose a significant challenge for students, as they must reconcile two seemingly different interpretations of the same concept. Additionally, the concept of an angle extends beyond the static and dynamic perspectives to include alternative characterizations, such as sector angles and the inclination between half-lines (Mitchelmore and White, 2000). The variety of definitions highlights the complexity of the concept of angles and emphasizes the need for educators to address these different perspectives in their teaching explicitly. Because of this complexity and the dual nature of angles, students often encounter misconceptions that hinder their understanding and application of this fundamental concept.

Research has identified a range of student misconceptions about angles, primarily arising from the difficulties in reconciling static and dynamic definitions of angles. For educators, recognizing the complex nature of angles and the common misconceptions that students hold is essential for promoting a deeper, more nuanced understanding. Henderson and Taimina (2005) further emphasize this complexity by arguing that no single formal definition can adequately capture the richness of our experiences with angles. Their perspective highlights the subjective and intuitive elements of angle perception, indicating that a thorough understanding requires more than simply memorizing formal definitions. In the next section, we will review existing studies on how students think when learning about angles.

2.2 Students' mental models in conceptualizing angles

Students' conceptions about angles have been widely studied, revealing persistent misconceptions across age groups and contexts. Biber et al. (2013) investigated the errors and misunderstandings of eighth-grade students in a Turkish middle school using a mixed-methods approach. Through four open-ended questions, the researchers found that students frequently relied on the physical appearance of geometric figures rather than their mathematical properties. A notable misconception involved applying properties valid in specific geometric situations to inappropriate contexts. Many students also struggled to understand parallelism in relation to angles.

These findings align with broader research suggesting that students often struggle to grasp the abstract nature of angle concepts. For example, Clements and Sarama (2020) highlighted that children commonly confuse the size of angles with their visual representation, leading to incorrect classifications of acute and obtuse angles. Similarly, Battista (1999) observed that students had difficulty recognizing angle congruence, especially when the angles appeared differently oriented or positioned.

In another qualitative study, Özen Ünal and Urun (2021) examined sixth-grade students' misconceptions about angles in a public school in western Turkey. Using 17 open-ended questions and content analysis, the researchers found that students struggled with defining angles, comparing angle measures, and understanding adjacent, complementary, and supplementary angles.

Interestingly, misconceptions were also prevalent among high-achieving students. Bütüner and Filiz (2017), in a mixed-methods study of 233 sixth graders in Trabzon, Turkey, found that even top-performing students misidentified straight and right angles when presented in unfamiliar orientations. They attributed this to potentially misleading representations in textbooks. This highlights the importance of not assuming conceptual understanding based solely on performance and underscores the need for diagnostic assessments and metacognitive reflection in instruction.

These patterns of inaccurate reasoning about angles are not new. Earlier research (Gal, 2011; Gal and Linchevski, 2010; Keiser, 2004; Lehrer et al., 1988; Woodward, 1978) has consistently shown that angle concepts pose cognitive challenges. Common misconceptions include beliefs that angle size depends on the length of its arms (Bustang et al., 2013; Munier and Merle, 2009), the arc's size (Devichi and Munier, 2013), or the area enclosed between the arms (Clausen-May, 2008; Kim and Lee, 2014; Wilson and Adams, 1992). These findings underscore the need for instructional approaches that address and rectify these deeply ingrained misconceptions.

Recent educational research has shifted its focus from investigating students' misconceptions to examining the mental models or internal representations that influence how learners understand and process mathematical concepts (Al-Mutawah et al., 2019). These models are particularly important in geometry, where visual-spatial understanding plays a crucial role (Pinilla, 2024). However, little research has been conducted on the structure of students' mental models on specific aspects of geometry. This is an area that still requires further investigation, and the present study aims to fill this research gap. The following section outlines the theoretical framework that underpins this study.

2.3 Fidelity of gestalt and functional fidelity

The term mental model, which has been widely used in the science education literature (e.g. Ke et al., 2005; Pedrera et al., 2025; Gogus, 2013; Coll, 2006), can be traced back to Craik's original notion of an internal representation of something external (Nersessian, 1993). In educational contexts, the term is often used to describe student misconceptions, conceptions, preconceptions, or internal representations of phenomena.

However, in mathematics education, mental model is not always the preferred term, though it does appear (Gogus, 2013; Greca and Moreira, 2002). In German-speaking contexts, for example, the concept is commonly referred to as Grundvorstellung (translated as “foundational idea”), although it is frequently rendered as mental model in English-language publications (Vom Hofe and Blum, 2016). We have chosen to use the term mental model in this work to align both with the established translation of Grundvorstellung and with its widespread use across science education disciplines to describe and analyze learners' conceptual knowledge.

Furthermore, the term mental model aligns with the terminology used in the Fidelities Model of Conceptual Development (short: FG-FF framework), which underpins the present research questions. The FG-FF framework was initially proposed by Ubben (2020) and further elaborated by Bitzenbauer and Ubben (2025). It introduces several key ideas:

1. A mental model consists of two components: a Gestalt, which refers to its (often visual) structure, appearance, or more generally its surface-level representation; and a Functionality, which encompasses the set of behaviors, processes, or dynamics the model is intended to represent. For example, the Gestalt of an angle might be the visual pattern of two rays extending from a common point, while its Functionality is the relational measure between those rays.

2. A mental model's Gestalt and Functionality relate independently to the phenomenon they represent, each with its own degree of fidelity. This means that a learner might perceive the Gestalt of a model—its structure or appearance—as visually similar to the actual entity, even if the model fails to reflect the way the entity behaves or functions. Conversely, a model might accurately represent functional relationships (Functionality) while appearing quite dissimilar to the real-world phenomenon. Fidelity of Gestalt (FG) thus refers to how closely the model resembles the represented object in appearance, while Functional Fidelity (FF) refers to how well it captures the object's dynamic or conceptual characteristics. The FG and FF hypothesis emphasizes that these two dimensions can vary independently and should both be considered when analyzing how students construct and use mental models in educational settings.

Applying the FG and FF hypothesis allows us not only to examine the content of learners' mental models (as is common in existing research), but also to investigate how learners relate these models to real-world phenomena and to instructional representations such as graphs, diagrams, and videos. It also helps identify which dimension—Gestalt or Functionality—needs to be addressed more directly in order to promote deeper conceptual understanding.

This approach is supported by findings from research originally conducted in quantum physics education (Ubben and Heusler, 2021; Ubben and Bitzenbauer, 2022; Bitzenbauer and Ubben, 2025), which show that FG and FF are mostly independent dimensions: learners can hold models that appear visually accurate but fail to function correctly, and vice versa. Furthermore, experts tend to exhibit high Functional Fidelity even when their Gestalts are abstract and less visually concrete.

In mathematics education, these dimensions correspond to familiar challenges related to representation and abstraction. Visual tools (such as diagrams, figures, or manipulatives) can enhance concrete understanding (Glenberg et al., 2004) but may obscure underlying relationships if used uncritically (Brown et al., 2009). Conversely, symbolic reasoning and formal notation promote functional understanding (Kaminski et al., 2009; Uttal et al., 2009), yet may fail to connect with learners' intuitive or real-world experiences, leading to meaningless processing of symbols (Nathan, 2012). Studies often suggest that learners typically move from concrete, visually faithful representations toward more abstract, functionally rich models (for a more in-depth review of this we refer the reader to Fyfe et al., 2014). They also show, however, that concrete examples often may limit the mathematical abstraction process (Uttal et al., 1997; Goldstone and Sakamoto, 2003; Sloutsky et al., 2005), which was one of the problems which initially led to the FG-FF framework, only that it was in the contexts of physics education (Bitzenbauer and Ubben, 2025).

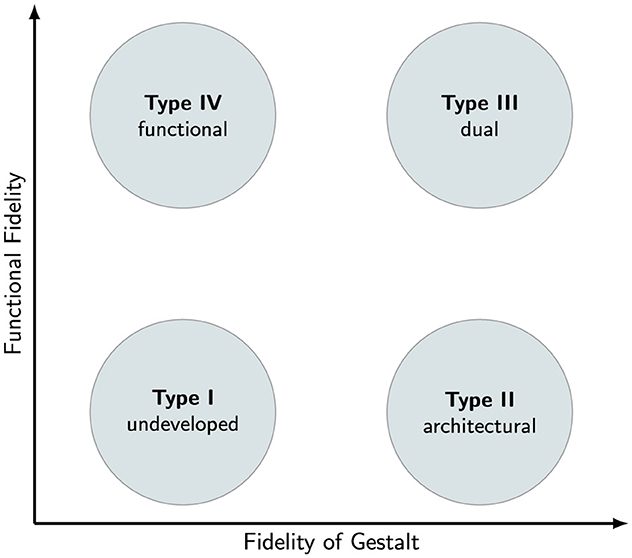
The FG-FF framework contributes to the ongoing discussion by offering a structured way to model the shift in understanding through distinct types of mental model understanding. These types emerge from different combinations of Functional Fidelity (FF) and Fidelity of Gestalt (FG), which, as previous studies have shown, represent largely independent dimensions of learners' mental representations (Ubben and Heusler, 2021; Bitzenbauer and Ubben, 2025). Related to this, Ubben (2020) and Ubben and Bitzenbauer (2022) proposed four archetypal ways to interpret a mental model, each characterizing a unique way in which learners relate their internal models to the phenomena they aim to represent:

1. Type I—Undeveloped understanding (low FG, Low FF): at this stage, the mental model neither visually resembles the phenomenon nor captures its underlying functionality. Such models are superficial and primarily declarative, reproducing isolated facts or processes without deeper conceptual insight. In mathematics education, this might mean that learners can rearrange symbols and formulae, but can not apply them to real world problems (cf. Nathan, 2012).

2. Type II—Architectural understanding (high FG, low FF): here, the learner constructs a model that appears visually accurate and well-organized, but lacks a grasp of the functional relationships involved. The emphasis is on surface appearance rather than deeper meaning or mechanism. In mathematics education, it has been reported that familiar concrete objects (high FG) can facilitate learning (cf. Petersen and McNeil, 2013).

3. Type III—Dual (replica) understanding (high FG, high FF): in this case, the mental model both resembles the phenomenon and correctly represents its functional aspects. It offers a coherent and concrete representation that bridges visual and dynamic elements. However, such models often remain tied to specific contexts, limiting the learner's ability to transfer or generalize the conceptual understanding. This phenomenon has been readily reported in the mathematics education literature as well (cf. Brown et al., 2009; Uttal et al., 1997; Goldstone and Sakamoto, 2003; Sloutsky et al., 2005).

4. Type IV—Functional understanding (low FG, high FF): at this level, learners are no longer dependent on visual similarity. Instead, they focus on the core functions and dynamics of the concept. These models are typically abstract, yet reflect deep, transferable understanding that can be applied flexibly to new situations. This is arguably the abstract understanding of mental models as well that is often desired as the more expert understanding (cf. Kaminski et al., 2009; Uttal et al., 2009).

A visual overview of this categorization is presented in Figure 1. Ubben (2020) and Bitzenbauer and Ubben (2025) argue that learning processes typically follow a developmental trajectory from Type I to Type IV. Initially, the learner may not see the model as meaningfully connected to reality (Type I). As visual familiarity increases (raising FG), the learner may achieve Type II. Through interaction with the model—either mentally or through real-world engagement—Functional Fidelity can increase, leading to Type III, where the model resembles and behaves like the phenomenon. Research with learners aged 14 and older suggests that Type III understanding is commonly reached and corresponds to frameworks like diSessa's “knowledge in pieces,” (DiSessa, 2018) where isolated “knowledge isles” allow for prediction and explanation within familiar contexts, but hinder transfer and abstraction.

Figure 1

Figure 1. Type grid of the FG-FF framework with all four distinct types.

Importantly, reducing Gestalt fidelity at later stages allows for abstraction and the transfer of functional ideas beyond the original learning context. This enables learners to apply mathematical concepts in new scenarios or use them to model previously unencountered problems. Studies in quantum physics education have shown that Types III and IV are the most frequently achieved forms of understanding at the secondary and post-secondary level. Notably, in one study, all participating experts (professors) demonstrated a Type IV understanding. These findings are reinforced by evidence that conceptual (i.e., abstract) knowledge correlates positively with FF and negatively with FG.

3 Research rationale

This data from science education raise the question of whether the FG-FF framework can be similarly applied within mathematics education. Initial exploratory studies suggest that students' mental models in mathematics may also vary along the dimensions of Gestalt and Functional Fidelity (Veith et al., 2022a,b), but a systematic empirical investigation—comparable to those conducted in physics education—has yet to be undertaken.

The mathematical concept of the angle offers a particularly suitable case for such an exploration. Angles are inherently abstract constructs (see Section 2.1), yet they are typically introduced through strongly visual instructional methods that emphasize concrete representations, leading to several problems (see Section 2.2). This tension between abstraction and visual representation aligns closely with the distinctions captured by the FG-FF hypothesis. As such, the angle concept serves as an ideal testbed for examining how students' mental models relate to both the appearance and the functionality of mathematical ideas.

To address this gap, the present study is guided by the following research questions:

1. How well does the FG-FF hypothesis align with students' understanding of their mental models of angles?

2. Which types of model understanding, as defined by the FG-FF framework, are prevalent among high school learners?

4 Methods

4.1 Study design and sample

We conducted a cross-sectional survey study to explore students' mental model of angles. The instrument was administered digitally via LimeSurvey to N = 403 secondary school students (N₁ = 172 male, N₂ = 225 female, N₃ = 6 did not provide any information) from South Africa. The students did not receive specific instruction in angles prior to test administration. Data collection was conducted in May 2025. All participants were on the verge between lower and upper secondary school, i.e. ranging from Grades 9 and 10 to 11 and 12. All students possessed foundational knowledge of angles, including the ability to identify, classify and measure various types of angles, and apply angle relationships in plane geometric figures such as triangles and parallel lines. Only fully completed responses were further analyzed.

4.2 Instrument development

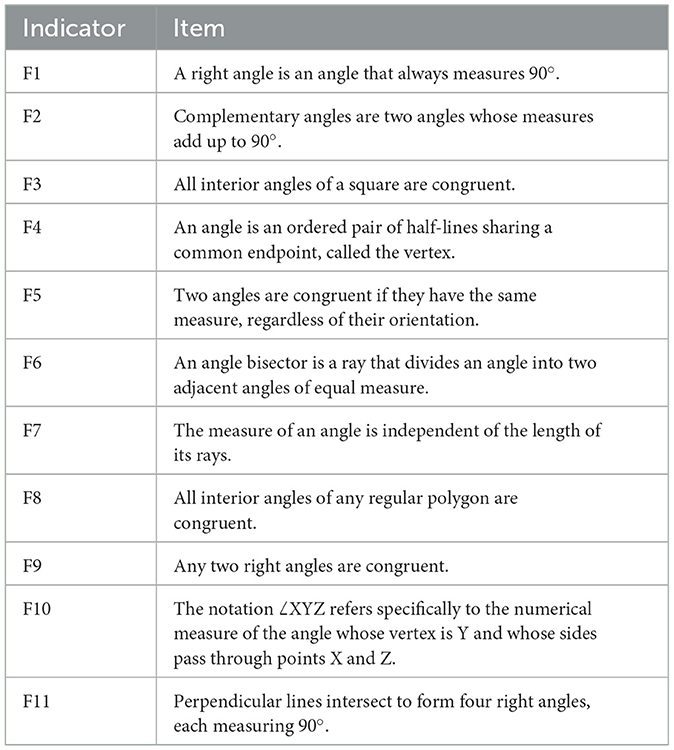
Since our theoretical framework has not yet been investigated in the context of mathematics education, we had to develop the items from scratch. To this end, we adopted items from prior test instruments regarding angles (Unal and Urun, 2021) and reworked them in terms of model understanding so that they more accurately capture purely functional and gestalt aspects (cf. Section 2.3). Gestalt aspects, i.e. visual or perceptual features, were captured by phrasings referring to size, position or shape (e.g. G5: “The area enclosed by the angle's rays shows how big the angle is”). Functional aspects, on the other hand, were expressed through abstract, relational and measurement-oriented formulations (e.g. F9: “The measure of an angle is independent of the length of its rays”). In other words, while Gestalt-oriented items often referenced the apparent size or spatial configuration of an angle as a visual entity, Functional items emphasized properties such as congruency (angles being congruent rather than “identical”) and measurement (angles having a measure rather than being a number). This linguistic and conceptual differentiation was essential in guiding the development process since prior research found that the distinction between angles and their measures plays a crucial role in mathematics education (Veith and Bitzenbauer, 2021). The instrument was subsequently reviewed by (a) two experts in physics education to ensure that the underlying mental models are captured in the sense of the FF-FG framework and (b) two experts in mathematics education for linguistic clarity and content validity before being distributed to the participants. An overview of all items is provided in Appendix Tables 5, 6.

4.3 Data analysis regarding RQ1

To evaluate whether the data align with the theoretical structure proposed by the FG-FF framework, we performed a confirmatory factor analysis (CFA), adhering to the approach described by Bitzenbauer and Ubben (2025). CFA was chosen because our primary goal was to verify this theoretical structure by examining the relationships between observed variables and their corresponding latent constructs, thereby

“allowing us to assess how well a hypothesized factor structure ‘fits' the observed data” (Russell, 2002, p.1638).

Initially, we assessed the assumption of multivariate normality using Mardia's test, available in the MVN package in R (cf. Jackson et al., 2009). Since the test indicated a violation of normality, we employed robust maximum likelihood estimation, utilizing the Yuan-Bentler mean-adjusted estimator as implemented in the lavaan package (Yuan and Bentler, 1998).

The data analysis was conducted using R 4.4.2 and its packages lavaan, MVN, semTools and semPlot.

4.3.1 Global model fit

We gauged the overall fit of the model using a combination of established fit indices: the χ²-test, the Comparative Fit Index (CFI), the Root Mean Square Error of Approximation (RMSEA), and the Standardized Root Mean Residual (SRMR). In line with the guidelines by Schermelleh et al. (2003), we interpreted CFI values ≥0.95, RMSEA values ≤ 0.05, and SRMR values ≤ 0.05 as indicative of good model fit. To further evaluate model adequacy and complexity, we compared alternative model specifications using the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC). These indices reward model simplicity while penalizing excessive parameterization, with lower scores denoting preferable models (Vrieze, 2012). Whereas AIC emphasizes predictive performance, BIC applies a more conservative penalty for complexity, especially in large samples. Complementing these comparisons, we also conducted Likelihood Ratio Tests (LRTs), which offer a formal statistical method for assessing whether a more complex, nested model significantly outperforms a simpler one. Using both information criteria and LRTs enabled a more thorough evaluation of competing models by integrating goodness-of-fit with statistical rigor (Buzick, 2010; Chakrabarti and Ghosh, 2011).

4.3.2 Local model fit

To inspect local fit at the indicator level, we examined standardized factor loadings (λ), corresponding measurement error variances (1−λ²), and indicator reliabilities (λ²). The model did not permit cross-loadings. Following the guidelines of Kline (1998), we removed any item with a loading below 0.30 from the final model. At the latent construct level, we assessed reliability using McDonald's ω, which is suitable when loadings vary across indicators, and reliability was deemed sufficient for ω values above 0.70 (cf. McDonald, 1999). We also calculated the Average Extracted Variance (AEV) for each latent factor. According to the Fornell-Larcker criterion, discriminant validity is supported when the AEV of a factor exceeds the squared correlations it shares with other factors (cf. Fornell and Larcker, 1981).

4.4 Data analysis regarding RQ2

Research Question 2 was investigated by analyzing basic descriptive statistics for all indicators in a first step. These include the distribution of responses, arithmetic means, standard deviations (SD), and median values. Additionally, we leveraged the results of the CFA to analyze students' model thinking by situating them within the type grid explained in Section 2.3. To this end, we derived two composite metrics to represent the respective latent constructs from the factor loadings (λ): the FF-score for factor FF and the FG-score for factor FG. These scores were calculated as weighted averages of the observed indicators, with weights corresponding to the standardized factor loadings, as follows:

$\begin{array}{l}\text{FF-score}=\frac{{\displaystyle {\sum }_{i=1}^{11}}{\lambda }_i\text{F}i}{{\displaystyle {\sum }_{i=1}^{11}}{\lambda }_i}\text{and}\text{FG-score}=\frac{{\displaystyle {\sum }_{j=1}^9}{\lambda }_i\text{G}j}{{\displaystyle {\sum }_{j=1}^9}{\lambda }_j}\end{array}$

This approach ensures that indicators with higher loadings—i.e., those more strongly associated with the latent factor—contribute more heavily to the corresponding composite score.

Lastly, we grouped the students into either lower secondary (10th grade and lower) and upper secondary (11th grade and above) to check whether the cohorts differ in terms of these scores. Since the prerequisite of normality for these scores was violated, we refrained from conducting t-tests. Instead, we compared their scores using the non-parametric Mann-Whitney-U Test. We present the results of the Mann–Whitney U-test in the format [U(N₁, N₂) = U, p; r] where U denotes the test statistic, N₁ and N₂ indicate the sample sizes of the two groups being compared, p represents the associated p-value and r is the effect size (cf. Nachar, 2003). Statistical significance is interpreted such that p-values below 0.01 indicate a significant effect, while values below 0.001 are considered highly significant. To assess the strength of significant effects, we additionally report the effect size using the rank-biserial correlation coefficient r. Following the guidelines proposed by Kerby (2014), we interpret 0.2 < r < 0.4 as medium-sized effects and r≥0.4 as large effects.

5 Results

5.1 Results regarding RQ1

5.1.1 Results regarding global model fit

Table 1 presents a comprehensive overview of the two tested models and their associated fit indices. As model constraints are relaxed from the two-factor to the one-factor model, there is a corresponding decline in the CFI, illustrating that model fit deteriorates with reduced structure. This is paralleled by increasing values for the SRMR and the RMSEA, further supporting the trend. Furthermore, the two-factor model yields the lower χ² value and is able to meet all the conventional fit criteria listed in the second column, in contrast to the one-factor model. Moreover, a likelihood ratio test (conducted via lavtestLRT from the lavaan package) shows that the two-factor model is statistically highly significant superior to the one-factor model, with p < 0.001. With a CFI of 0.95, SRMR of 0.05, and RMSEA of 0.03, it satisfies the standard benchmarks for good fit discussed in Section 4.3. Lastly, the Akaike (AIC) and Bayesian (BIC) information criteria values also suggest a better balance between fit and parsimony. In summary, the two-factor model outperforms the one-factor model in each criterion, substantiating the hypothesized two-factor structure from the theoretical framework guiding this study. Based on these considerations, we focus on reporting the local fit statistics of the two-factor model in the next section.

Table 1

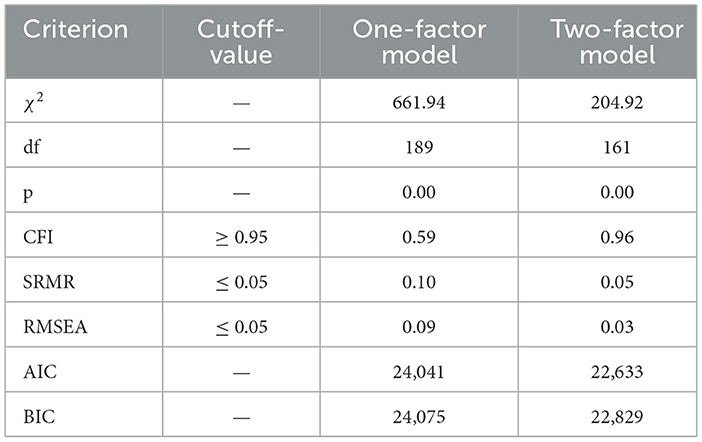
Table 1. Results of the confirmatory factor analysis on the model level for both models under investigation.

5.1.2 Results regarding local model fit

The local fit indices, including item-level estimates and reliability scores, are summarized in Table 2. To identify the model and ensure comparability, latent variables were standardized by fixing their variances to 1, allowing all item loadings to be estimated freely (Bitzenbauer and Ubben, 2025). All items display satisfactory loadings above the commonly used threshold of 0.30 and range from 0.341 (F4) to 0.640 (F9). At the factor level, the reliability estimate is strong in the case of the FF factor (ω_FF = 0.78) and satisfactory in the case of the FG factor (ω_FG = 0.66) considering the shorter scale length. The associated path diagram for this model is depicted in Figure 2. Additionally, the inter-factor correlation is only 0.16 and thus its square is succeeded by the AEV value of either factor. Thus, discriminant validity according to the Fornell-Larcker criterion can be assumed for our model (Fornell and Larcker, 1981). Taken together, the CFA findings are robust and support a nuanced two-dimensional structure underlying mathematics students' mental model of angles.

Table 2

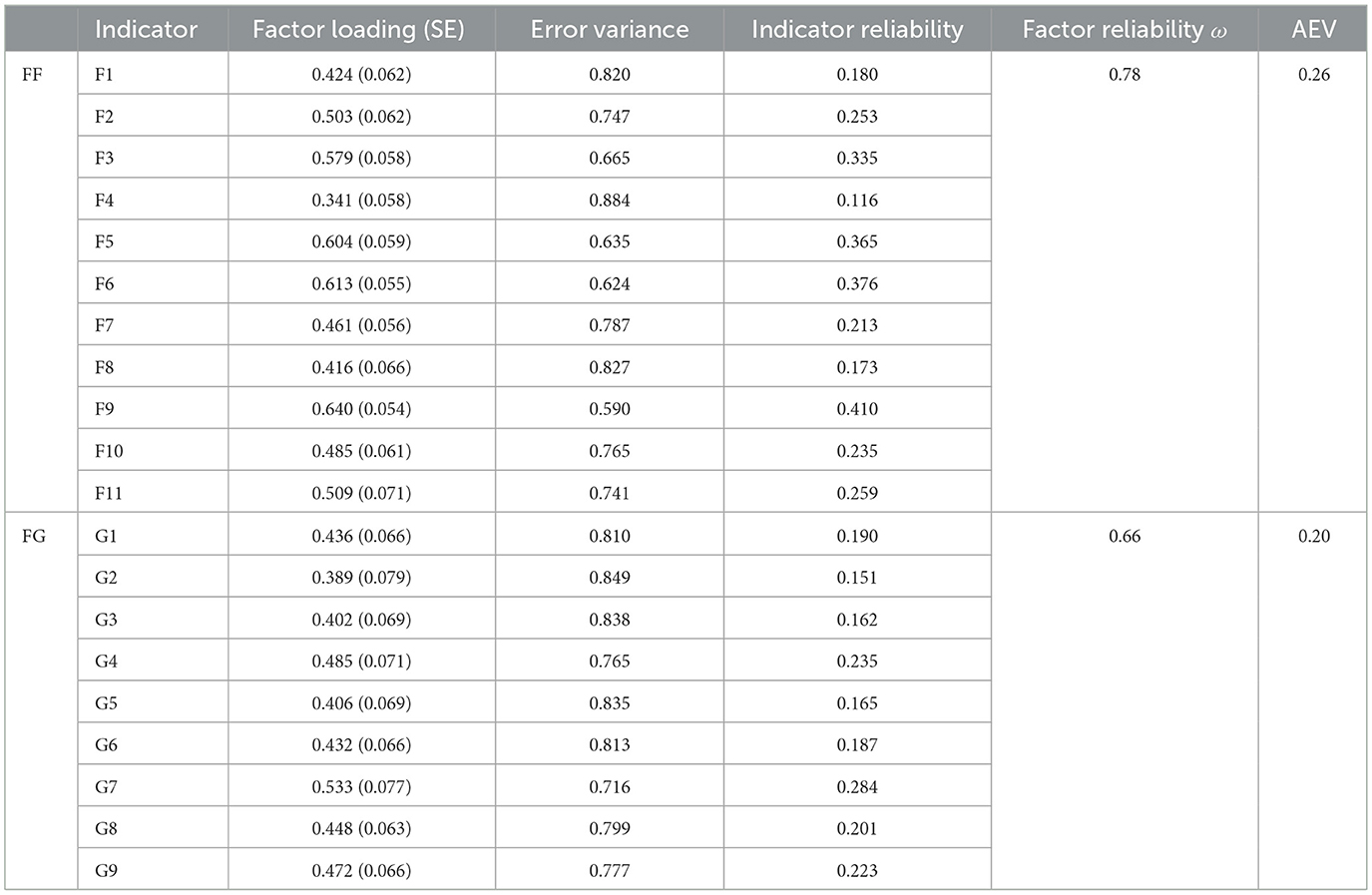
Table 2. Results of the confirmatory factor analysis for the two-factor model including item estimates (i.e. factor loadings, standard error and error variance) as well as reliability calculations (i.e., indicator reliability, factor reliability, and average extracted variance).

Figure 2

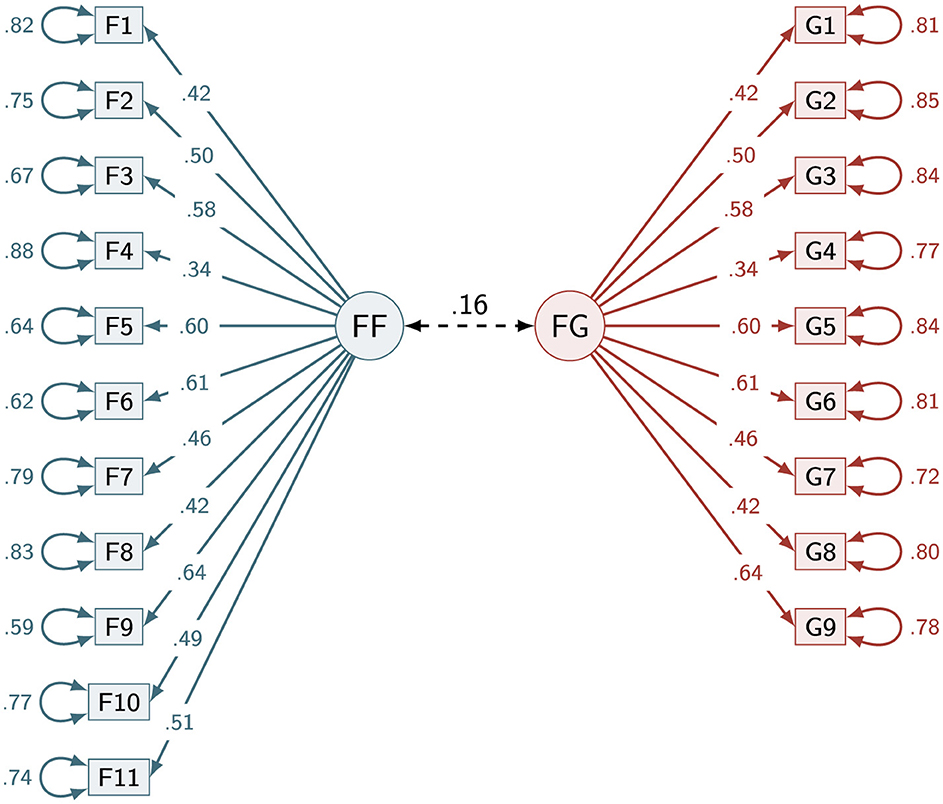
Figure 2. Path diagram of the two-factor model. Decimal numbers on the single-sided arrows indicate factor loadings, while numbers on the double-sided arrows indicate error variances of the respective item. The correlation between both factors is 0.16.

5.2 Results regarding RQ2

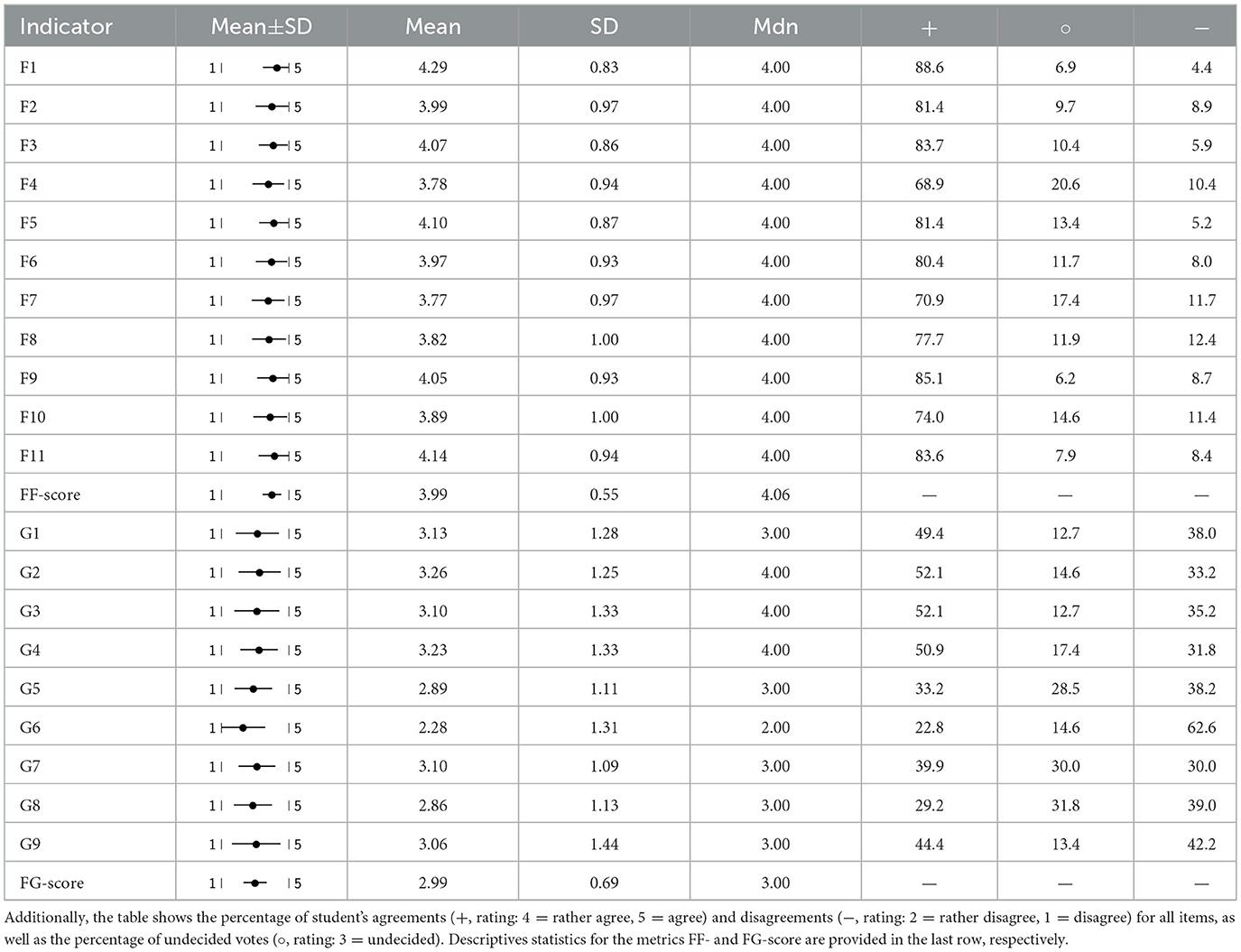
The second research question was investigated by looking at the students' responses to the items. An overview for each item in terms of descriptive statistics is provided in Table 3. For the indicators of FF, mean values range from 3.77 (F7) to 4.29 (F1), with standard deviations between 0.83 (F1 )and 1.00 (F10). Medians are consistently 4 across all items. Agreement percentages (+) for these items vary between 68.9% (F4) and 88.6% (F1), while disagreement rates (−) range from 4.4% (F1) to 12.4% (F8). The proportion of undecided responses (°) falls between 6.2% (F9) and 20.6% (F4). Regarding the indicators of FG, mean values span from 2.28 (G6) to 3.26 (G2), with standard deviations ranging from 1.09 (G7) to 1.44 (G9). In contrast to FF, median values vary between 2 and 4. Agreement levels (+) lie between 22.8% (G6) and 52.1% (G2, G3), while disagreement rates (−) vary from 30.0% (G7) to 62.6% (G6). Undecided responses (°) show a broader range, from 12.7% (G1, G3) to 31.8% (G8). Overall a clear trend is observable, with indicators for FF receiving more agreement in general and responses for FG indicators spreading across a larger range. To shed more light on the significance of these findings, the data will subsequently be divided into two cohorts with regard to the participants' age.

Table 3

Table 3. Descriptive statistics including mean, standard deviation and median.

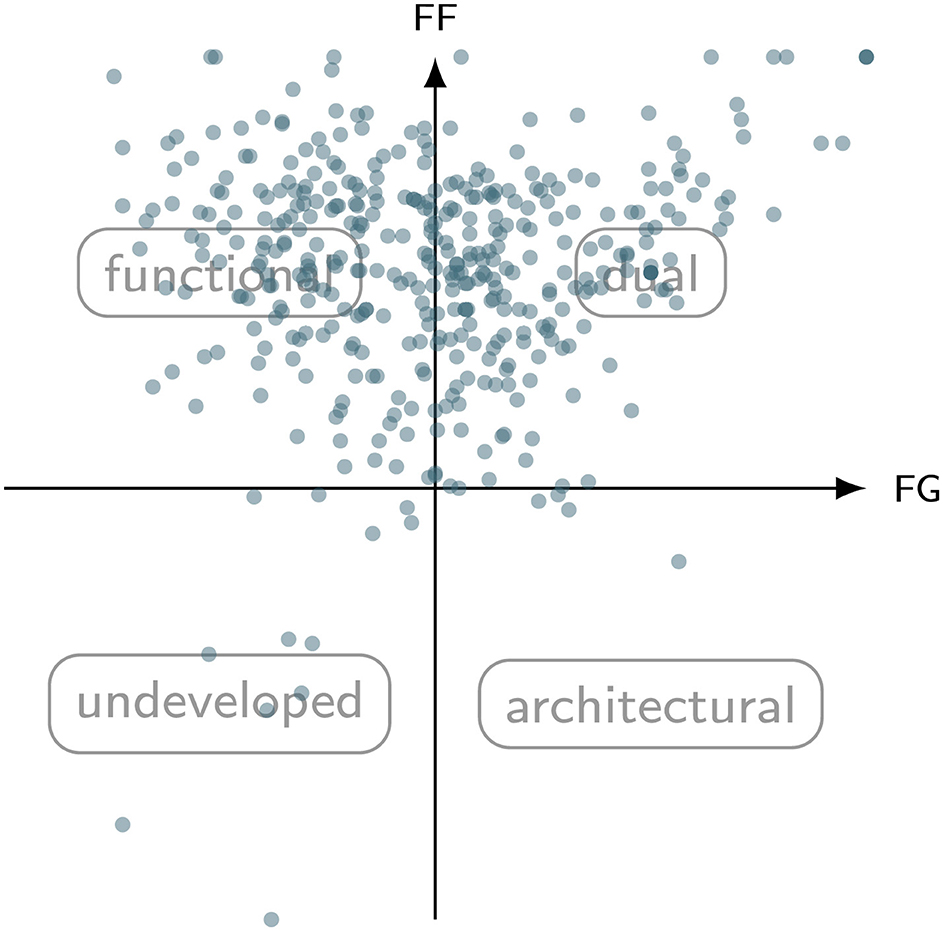
The type grid is presented in Figure 3, illustrating the classification of learners' mental models of angles according to the metrics FF- and FG-score (cf. Table 3). The dual and functional types make up the majority of the sample, with 49.38% belonging to the functional type and 46.40% belonging to the dual type. Only a small share of students are situated within the low functionality types: 2.98% of students have an undeveloped mental model and 1.24% can be associated with the architectural type. The differentiation between lower and upper secondary school with regards to these types is presented in Figure 4. The visualization suggests that the older students (red nodes) dominate in terms of functional thinking and also exhibit a lower FG-score. This visual discrepancy is further reflected by the results of the Mann–Whitney-U-tests: While for the FG-score, the younger cohort exhibits higher values on a highly significant statistical level [U_{(253, 140)} = 12, 123, p < 0.001; r = 0.32], the exact opposite is true for the FF-score [U_{(253, 140)} = 10, 532, p < 0.001; r = 0.41]. Descriptive statistics for the respective groups are reported alongside the test statistics in Table 4 and visualized in terms of boxplots in Figures 5, 6.

Figure 3

Figure 3. Type grid of the FG-FF framework for the entire sample.

Figure 4

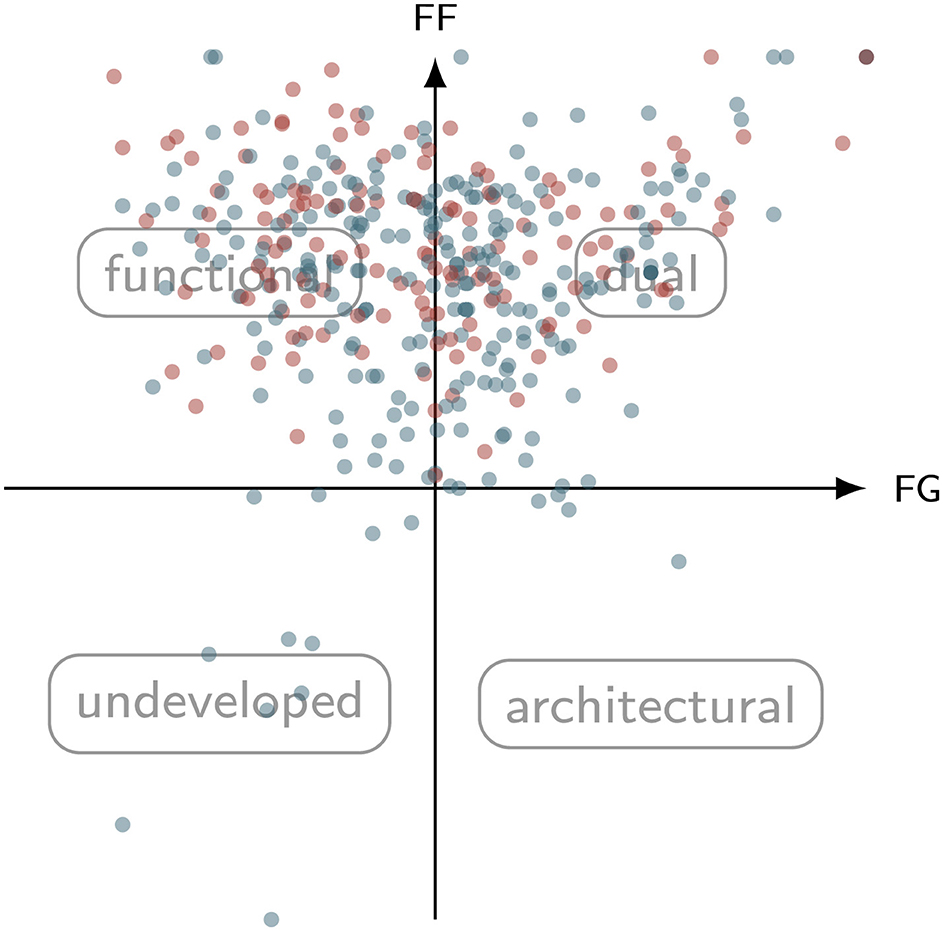
Figure 4. Type grid of the FG-FF framework where blue nodes denote students of grade 10 or below (N₁ = 253) and red nodes denote students of grade 11 or higher (N₂ = 140).

Table 4

Table 4. Results of the Mann–Whitney-U test, including descriptive statistics (i.e., sample size of the cohort, mean values, standard deviation (SD), and standard error (SE)) as well as the test statistics U, p-values and respective effect-sizes.

Figure 5

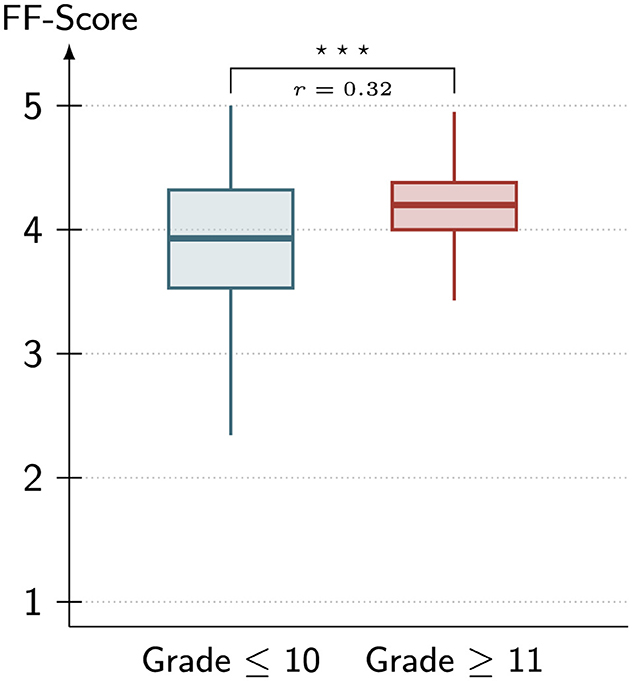
Figure 5. Boxplots of the variable FF-Score for both cohorts. Whiskers indicate 1.5 times the interquartile range. r is the biserial rank correlation and the stars indicate the level of statistical significance (***p < 0.001).

Figure 6

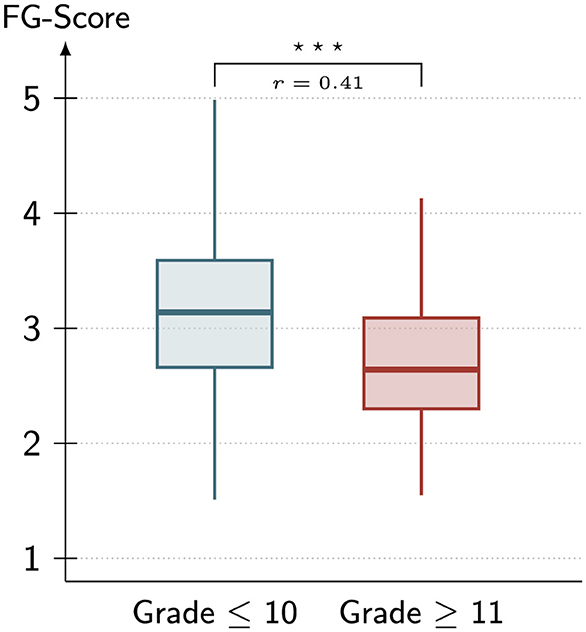
Figure 6. Boxplots of the variable FG-Score for both cohorts. Whiskers indicate 1.5 times the interquartile range. r is the biserial rank correlation and the stars indicate the level of statistical significance (***p < 0.001).

6 Discussion

6.1 Discussion regarding RQ1

The results of the confirmatory factor analysis strongly support the hypothesized two-factor structure distinguishing between Functional Fidelity (FF) and Fidelity of Gestalt (FG). As shown in Table 1, the two-factor model meets all conventional cut-off criteria for good model fit, including a Comparative Fit Index (CFI) of 0.96, a Standardized Root Mean Square Residual (SRMR) of 0.05, and a Root Mean Square Error of Approximation (RMSEA) of 0.03. These values indicate an excellent fit of the model to the data. In contrast, the one-factor model falls substantially short of these standards, with a low CFI (0.59), elevated SRMR (0.10), and an RMSEA of 0.09—values that are commonly interpreted as signs of poor fit. Furthermore, information-theoretic measures such as the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC) also favor the two-factor model, indicating a more optimal balance between model complexity and explanatory power.

These findings confirm that FF and FG are best understood as empirically distinct constructs, validating the theoretical assumption underlying the FG-FF hypothesis. The poorer performance of the one-factor model suggests that collapsing both constructs into a single latent dimension obscures meaningful distinctions in how learners conceptualize the visual vs. functional aspects of the target concept (in our case: angles). This distinction is consistent with research in mathematics education indicating that perceptual and conceptual reasoning often emerge along separate developmental trajectories (e.g., Battista, 1999; Biber et al., 2013; Clements and Sarama, 2020). Similar two-dimensional frameworks have been proposed in studies on geometrical reasoning and functional interpretation (Portnoy et al., 2006), which further supports the validity of distinguishing between form-based and function-based mental representations.

The local model fit indices presented in Table 2 further reinforce this conclusion. All items show satisfactory factor loadings above the 0.30 threshold, ranging from 0.341 (F4) to 0.640 (F9), indicating that each item contributes meaningfully to its respective latent construct. The reliability estimates for the two factors—ω_FF = 0.78 and ω_FG = 0.66—are considered strong and acceptable respectively, especially in light of the fewer items loading on the FG factor. Moreover, the low inter-factor correlation (r = 0.16) suggests that FF and FG capture largely independent dimensions of students' mental models. Since the squared correlation between the factors is lower than the Average Extracted Variance (AEV) for either factor, discriminant validity is also supported according to the Fornell-Larcker criterion (Fornell and Larcker, 1981).

In summary, answering RQ1, the model testing confirms the theoretical distinction between Functional Fidelity and Fidelity of Gestalt. The empirical fit of the two-factor model, both globally and locally, provides robust support for applying the FG-FF framework in the analysis of students' mental models. These results justify the continued use of this dual-construct structure in subsequent analyses and interpretations throughout this study. They also extend prior work by operationalizing this distinction quantitatively, rather than inferring it solely from task-based performance as in earlier studies (Devichi and Munier, 2013). A clearer synthesis of FG and FF within existing models of conceptual change in geometry (e.g. Gennen (2023)) may further strengthen the theoretical grounding.

6.2 Discussion regarding RQ2

Since the FG and FF scales exhibit only negligible correlation, a type grid analogous to that proposed by Ubben and Heusler (2021) could be generated, enabling the classification of students' mental model archetypes. The results indicate that the majority of participants in this study fell into either Type III (Dual Understanding) or Type IV (Functional Understanding), which aligns with previous findings (Ubben and Heusler, 2021). These results resonate with previous studies identifying common misconceptions in angle understanding. Research by Biber et al. (2013), Clements and Sarama (2020) and Battista (1999) among others, has shown that many students rely heavily on visual cues when reasoning about angles. However, unlike studies where visual-dependence dominated across age groups (Bütüner and Filiz, 2017), the present findings suggest a stronger shift toward functional reasoning in older cohorts.

Only a small fraction of learners exhibited a Type II understanding (high FG, low FF), suggesting a focus on surface-level visual features without a grasp of underlying functional relationships for these few participants. Similarly, very few students demonstrated Type I (Undeveloped Understanding), implying that in the studied grade levels, students had either not formed any meaningful conception of angles or had only developed abilities to work with angles without meaningful understanding.

A comparison between students below grade 11 and those in grade 11 or higher revealed statistically significant differences: Functional Fidelity increased with age, while Gestalt Fidelity decreased. This trend points toward a developmental shift from visually grounded to more abstract, functional understandings of angles—consistent with the findings of Ubben et al. (2023) regarding expert cognition. However, as the present study employed a cross-sectional design, these differences should be interpreted as cohort-level trends rather than individual developmental trajectories. This pattern echoes research on conceptual reorganization in geometry in adolescence (Weigand et al., 2025), where the decline in context-dependent perception is accompanied by increased reliance on invariant properties of shapes.

These findings hold important implications for instructional design. The observed progression supports pedagogical strategies that begin by fostering concrete intuition and then transition toward encouraging abstract reasoning and structural understanding, which indeed have been suggested previously (cf. Volodin et al., 2025; Xie et al., 2024; Pulvermüller, 2023; Azmidar et al., 2017). Specifically, classroom interventions might include contrasting examples that dissociate angle size from visual length or orientation, the use of dynamic geometry environments to emphasize rotational invariance, and guided reflection prompts that help students articulate dual type reasoning more fluently.

The rarity of Type II models suggests that visualizations are not limiting development but rather that students of the examined grades are generally able to proceed from visual input to more functionally coherent mental models.

While few students in this study exhibited low-functionality models, it remains an open question whether such types—particularly Types I and II—are more prevalent among younger students. For example, it has been found before that surface level aspects/gestalt are extremely important for younger learners (Petersen and McNeil, 2013). Future research should extend this investigation to younger age groups to explore whether these types are more commonly observed earlier in the learning trajectory. Longitudinal designs would allow researchers to track transitions between FG- and FF-dominant types, building on similar developmental pathways proposed in angle conception research (Simpson et al., 2024).

7 Conclusion

This study advances current understanding of students' conceptualizations of angles by applying the FG–FF framework to uncover the cognitive structures underlying their reasoning. Unlike prior research that has predominantly focused on cataloging misconceptions (e.g., Battista, 1999; Biber et al., 2013; Clements and Sarama, 2020), this work highlights that Gestalt-based and functionally abstract reasoning represent empirically distinguishable mental model types with clear implications for learning (Ubben and Heusler, 2021). By demonstrating that these dimensions are not merely descriptive but structurally separable, the study contributes a novel lens for conceptual analysis in mathematics education (Devichi and Munier, 2013).

The findings suggest that students do not move uniformly from visual to abstract reasoning; instead, they exhibit patterned variations that can inform pedagogical intervention (Bütüner and Filiz, 2017). One of the key contributions of this research lies in illustrating the potential for hybrid reasoning, where elements of Gestalt and functional thinking coexist (Ubben et al., 2023). This opens promising avenues for future work on how such models develop and transition over time.

Nevertheless, the study offers an initial, rather than definitive, validation of the FG–FF framework. Three directions for further refinement emerge. First, additional psychometric work is needed to strengthen the reliability of FG measurements and further substantiate the structural distinctiveness of both constructs (Ubben and Heusler, 2021). Second, extending research to younger learners may clarify developmental trajectories and reveal when functional abstraction begins to emerge (Petersen and McNeil, 2013). Third, integrating quantitative findings with qualitative data (e.g., interviews, task-based reasoning, or classroom observations) would deepen insight into how students mobilize these cognitive dimensions in practice (Devichi and Munier, 2013).

A critical next step is moving beyond observational designs to explore instructional impact. There is a pressing need for experimental or design-based research that tests how targeted teaching strategies can facilitate shifts from Gestalt-dominant reasoning (Type II) toward more functionally grounded understanding (Type IV) (Iberi, 2023). Such studies could help identify specific classroom practices, representations, and learning sequences that actively support cognitive transition rather than assuming it will occur naturally (Weigand et al., 2025). For teachers, actionable guidance derived from students' mental models—such as prompts that redirect attention from perceptual features to invariant functional relations—would be particularly beneficial (Clements and Sarama, 2020).

Finally, while angles provide a productive case due to their dual visual–abstract nature, the FG–FF framework holds potential beyond this context. Applying it to other mathematical domains—such as symmetry, fractions, or functions—may reveal similar structural dynamics and further test its explanatory scope across the curriculum (Battista, 1999). Through continued refinement, cross-topic application, and intervention-oriented research, the FG–FF framework can evolve into a powerful tool for understanding and improving conceptual development in both primary and secondary mathematics education (Weigand et al., 2025).

8 Limitations and outlook

While the findings of this study offer valuable insights into students' mental models of angles through the lens of the FG-FF hypothesis, several limitations should be noted and recommendations for further research derived.

First, the study employs a cross-sectional design, which allows for the observation of age-related trends but does not permit conclusions about individual developmental trajectories. Longitudinal research would be necessary to confirm whether the observed patterns reflect actual learning progressions over time. Our study does not establish cause-and-effect relationships. Consequently, the validity of our findings pertains primarily to the structural level, i.e. providing evidence that Fidelity of Gestalt and Functional Fidelity represent empirically distinct dimensions of student cognition. Future research should leverage this empirical substantiation by applying this framework, tracing how students' mental models evolve over time, and by identifying critical transition points between Gestalt-dominant and functionally abstract reasoning.

Second, the study relies solely on self-report data collected through Likert-scale items. While confirmatory factor analysis supports the underlying structure, Likert-scale responses may not fully capture the complexity of learners' cognitive models or their application in problem-solving contexts. Future studies may benefit from combining quantitative approaches with qualitative data sources, such as student interviews or think-aloud protocols, to gain deeper insights into students' reasoning processes.

Third, although the FG-FF framework assumes a conceptual distinction between Gestalt and Functional Fidelity, the actual boundary between visual and functional reasoning in students' thinking may be more fluid than the model suggests. Hybrid forms of reasoning that combine both aspects could exist but remain undetected through the current measurement design.

Additionally, the FG factor showed lower internal consistency compared to the FF factor. This may be due to the smaller number of items, the broader variability in student interpretation of visual prompts, or an inherent conceptual looseness of the Gestalt dimension. Further refinement of FG items and piloting with broader samples could improve measurement reliability.

The content focus of the study is also limited to the mathematical concept of angles. While angles present a compelling case due to their simultaneously visual and abstract nature, the generalizability of the FG-FF framework to other mathematical or scientific concepts remains an open question. Future research could explore how this dual-dimensional framework applies to other mathematical concepts whose abstract nature get circumvented by visualization, such as functions or fractions. First attempts to explore the explanatory power of this framework have been made in the context of group theory (Veith et al., 2022a), where the study of symmetry groups of geometric figures hinted at similar cognitive dynamics: Students were asked to determine the symmetry group of a given geometric figure, yet those who focused predominantly on the Gestalt of the figure—interpreting it in terms of familiar shapes such as triangles or rectangles—frequently failed to identify the correct set of symmetries. This suggests that an overemphasis on visual resemblance can inhibit recognition of the underlying functional relationships.

In addition, the relationship between both cognitive dimensions and secondary variables needs to be investigated more thoroughly. As elaborated in Section 2.3, a statistically significant relationship between both constructs and conceptual understanding has been found in physics (the degree of FG being negatively correlated to conceptual understanding, while the degree of FF was positively correlated), raising the question whether this result can be extended into mathematics, and whether evidence can be gathered for correlations with other cognitive constructs, such as procedural or declarative knowledge.

Moreover, the current sample includes only high school students. The developmental dynamics of younger learners, particularly those in prepubescent stages where abstraction abilities are still emerging, remain unexplored. It is plausible that younger students exhibit a higher prevalence of undeveloped or architectural mental models. Expanding the age range to include primary or lower secondary students would allow for a more comprehensive picture of how these mental model types evolve.

Finally, the study is observational and does not involve any instructional intervention. As such, it does not provide evidence on how specific teaching strategies might influence transitions between mental model types. Future experimental or design-based studies could explore how targeted instruction fosters the shift from Gestalt-focused to functionally abstract understanding.

In the end, while this study supports the validity of the FG-FF hypothesis in the context of angle learning, further research is needed to refine the framework, extend its application, and explore its instructional implications more directly.

Data availability statement

All data can be obtained by the corresponding author upon reasonable request.

Ethics statement

The studies involving humans were approved by the Limpopo Department of Basic Education (South Africa) Ethics Committee. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants' legal guardians/next of kin.

Author contributions

JV: Conceptualization, Formal analysis, Investigation, Methodology, Visualization, Writing – original draft. EM: Conceptualization, Investigation, Writing – original draft. MU: Methodology, Writing – original draft, Writing – review & editing. FH: Data curation, Methodology, Writing – review & editing. PB: Conceptualization, Methodology, Supervision, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This study was supported by the Open Access Publishing Fund of Leipzig University.

Acknowledgments

The authors express sincere gratitude to Joe Munosiwani and Reneilwe Bridget Moloto for their valuable assistance in the data collection process. Their support and commitment significantly contributed to the successful completion of this research.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Generative AI statement

The author(s) declare that Gen AI was used in the creation of this manuscript. The authors stated that Generative AI tools (e.g., ChatGPT by OpenAI) were used to check the English language clarity of the manuscript only. No content generation was performed by AI.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdel-Malek, A. R., and Siam, O. A. (2024). Critical launch angle for projectile motion. ERU Res. J. 3, 1471–1479. doi: 10.21608/erurj.2024.251675.1095

Crossref Full Text | Google Scholar

Al-Mutawah, M. A., Thomas, R., Eid, A., Mahmoud, E. Y., and Fateel, M. J. (2019). Conceptual understanding, procedural knowledge and problem-solving skills in mathematics: high school graduates work analysis and standpoints. Int. J. Educ. Pract. 7, 258–273. doi: 10.18488/journal.61.2019.73.258.273

Crossref Full Text | Google Scholar

Amoah, C. A., and Assem, H. D. (2018). Assessing pre-service science teachers' conception of geometric optics (transmission of light) in the selected special science colleges of education in Ghana. Int. J. Sci. Res. Manag. 6, 389–394. doi: 10.18535/ijsrm/v6i6.el04

Crossref Full Text | Google Scholar

Azmidar, A., Darhim, D., and Dahlan, J. A. (2017). Enhancing students' interest through mathematics learning. J. Phys. Conf. Ser. 895:012072. doi: 10.1088/1742-6596/895/1/012072

Crossref Full Text | Google Scholar

Battista, M. (1999). The importance of spatial structuring in geometric reasoning. Teach. Child Math. 6, 170–177. doi: 10.5951/TCM.6.3.0170

Crossref Full Text | Google Scholar

Biber, C., Tuna, A., and Korkmaz, S. (2013). The mistakes and the misconceptions of the eighth-grade students on the subject of angles. Eur. J. Sci. Math. Educ. 1, 50–59. doi: 10.30935/scimath/9387

Crossref Full Text | Google Scholar

Bitzenbauer, P., and Ubben, M. S. (2025). The structure of learners' perceptions of models (not only) in quantum physics: spotlight on fidelity of gestalt and functional fidelity. EPJ Quantum Technol. 12:16. doi: 10.1140/epjqt/s40507-025-00316-7

Crossref Full Text | Google Scholar

Brown, M. C., McNeil, N. M., and Glenberg, A. M. (2009). Using concreteness in education: real problems, potential solutions. Child Dev. Perspect. 3, 160–164. doi: 10.1111/j.1750-8606.2009.00098.x

Crossref Full Text | Google Scholar

Bustang, B., Zulkardi, Z., Darmawijoyo, H., Dolk, M., and van Eerde, D. (2013). Developing a local instruction theory for learning the concept of angle through visual field activities and spatial representations. Int. Educ. Stud. 6, 58–70. doi: 10.5539/ies.v6n8p58

Crossref Full Text | Google Scholar

Bütüner, S. O., and Filiz, M. (2017). Exploring high-achieving sixth-grade students' erroneous answers and misconceptions on the angle concept. Int. J. Math. Educ. Sci. Technol. 48, 533–554. doi: 10.1080/0020739X.2016.1256444

Crossref Full Text | Google Scholar

Buzick, H. M. (2010). Testing for heterogeneous factor loadings using mixtures of confirmatory factor analysis models. Front. Psychol. 1:165. doi: 10.3389/fpsyg.2010.00165

PubMed Abstract | Crossref Full Text | Google Scholar

Chakrabarti, A., and Ghosh, J. K. (2011). “AIC, BIC and recent advances in model selection," in Philosophy of Statistics, Volume 7 of Handbook of the Philosophy of Science, eds. P. S. Bandyopadhyay, and M. R. Forster (North-Holland: Elsevier), 583–605. doi: 10.1016/B978-0-444-51862-0.50018-6

Crossref Full Text | Google Scholar

Clausen-May (2008). Another angle on angles. Aust. Prim. Math. Classroom 13, 4–8.

Google Scholar

Clements, D. H., and Sarama, J. (2020). Learning and Teaching Early Math: The Learning Trajectories Approach. New York, NY: Routledge. doi: 10.4324/9781003083528

Crossref Full Text | Google Scholar

Coll, R. K. (2006). “The role of models, mental models and analogies in chemistry teaching," in Metaphor and Analogy in Science Education (Cham: Springer), 65–77. doi: 10.1007/1-4020-3830-5_6

Crossref Full Text | Google Scholar

Devichi, C., and Munier, V. (2013). About the concept of angle in elementary school: Misconceptions and teaching sequences. J. Math. Behav. 32, 1–9. doi: 10.1016/j.jmathb.2012.10.001

Crossref Full Text | Google Scholar

DiSessa, A. A. (2018). “A friendly introduction to “knowledge in pieces": modeling types of knowledge and their roles in learning," in Invited Lectures from the 13th International Congress on Mathematical Education (Cham: Springer), 65–84. doi: 10.1007/978-3-319-72170-5_5

Crossref Full Text | Google Scholar

Fornell, C., and Larcker, D. F. (1981). Evaluating structural equation models with unobservable variables and measurement error. J. Mark. Res. 20, 39–50. doi: 10.1177/002224378101800104

Crossref Full Text | Google Scholar

Fyfe, E. R., McNeil, N. M., Son, J. Y., and Goldstone, R. L. (2014). Concreteness fading in mathematics and science instruction: a systematic review. Educ. Psychol. Rev. 26, 9–25. doi: 10.1007/s10648-014-9249-3

Crossref Full Text | Google Scholar

Gal, H. (2011). From another perspective—training teachers to cope with problematic learning situations in geometry. Educ. Stud. Math. 78, 183–203. doi: 10.1007/s10649-011-9321-6

Crossref Full Text | Google Scholar

Gal, H., and Linchevski, L. (2010). To see or not to see: analyzing difficulties in geometry from the perspective of visual perception. Educ. Stud. Math. 74, 163–183. doi: 10.1007/s10649-010-9232-y

Crossref Full Text | Google Scholar

Gennen, T. (2023). Conceptual change and education: the neglected potential of developmental teaching approaches. Hum. Dev. 67, 88–107. doi: 10.1159/000530247

Crossref Full Text | Google Scholar

Glenberg, A. M., Gutierrez, T., Levin, J. R., Japuntich, S., and Kaschak, M. P. (2004). Activity and imagined activity can enhance young children's reading comprehension. J. Educ. Psychol. 96:424. doi: 10.1037/0022-0663.96.3.424

Crossref Full Text | Google Scholar

Gogus, A. (2013). Evaluating mental models in mathematics: a comparison of methods. Educ. Technol. Res. Dev. 61, 171–195. doi: 10.1007/s11423-012-9281-2

Crossref Full Text | Google Scholar

Goldstone, R. L., and Sakamoto, Y. (2003). The transfer of abstract principles governing complex adaptive systems. Cogn. Psychol. 46, 414–466. doi: 10.1016/S0010-0285(02)00519-4

PubMed Abstract | Crossref Full Text | Google Scholar

Greca, I. M., and Moreira, M. A. (2002). Mental, physical, and mathematical models in the teaching and learning of physics. Sci. Educ. 86, 106–121. doi: 10.1002/sce.10013

Crossref Full Text | Google Scholar

Henderson, D., and Taimina, D. (2005). Experiencing Geometry: Euclidean and Non-Euclidean with History. New York, NY: Pearson/Prentice Hall.

Google Scholar

Iberi, H. (2023). “The challenge of teaching and learning angles: a pedagogic intervention,” in Proceedings of the British Society for Research into Learning Mathematics, Vol. 43. (London).

Google Scholar

Jackson, D., Gillaspy, J. A., and Purc-Stephenson, R. (2009). Reporting practices in confirmatory factor analysis: an overview and some recommendations. Psychol. Methods 14, 6–23. doi: 10.1037/a0014694

PubMed Abstract | Crossref Full Text | Google Scholar

Johnson, H. L., Tzur, R., Gardner, A., Hodkowski, N. M., Lewis, A., McClintock, E., et al. (2021). A new angle: a teacher's transformation of mathematics teaching practice and engagement in quantitative reasoning. Res. Math. Educ. 28, 88–108. doi: 10.1080/14794802.2021.1988688

Crossref Full Text | Google Scholar

Kaminski, J. A., Sloutsky, V. M., and Heckler, A. (2009). Transfer of mathematical knowledge: the portability of generic instantiations. Child Dev. Perspect. 3, 151–155. doi: 10.1111/j.1750-8606.2009.00096.x

Crossref Full Text | Google Scholar

Ke, J.-L., Monk, M., and Duschl, R. (2005). Learning introductory quantum physics: sensori-motor experiences and mental models. Int. J. Sci. Educ. 27, 1571–1594. doi: 10.1080/09500690500186485

Crossref Full Text | Google Scholar

Keiser, J. M. (2004). Struggles with developing the concept of angle: comparing sixth-grade students' discourse to the history of the angle concept. Math. Think. Learn. 6, 285–306. doi: 10.1207/s15327833mtl0603_2

Crossref Full Text | Google Scholar

Kerby, D. S. (2014). The simple difference formula: an approach to teaching nonparametric correlation. Compr. Psychol. 3. doi: 10.2466/11.IT.3.1

Crossref Full Text | Google Scholar

Kim, O. K., and Lee, J. H. (2014). Representations of angle and lesson organization in Korean and american elementary mathematics curriculum programs. KAERA Res. Forum 1, 28–37.

Google Scholar

Kline, R. B. (1998). Measurement Models and Confirmatory Factor Analysis. New York, NY: Guilford Press, 189–243.

Google Scholar

Lehrer, R., Guckenberg, T., and Lee, O. (1988). Comparative study of the cognitive consequences of inquiry-based logo instruction. J. Educ. Psychol. 80, 543–553. doi: 10.1037/0022-0663.80.4.543

Crossref Full Text | Google Scholar

Lu, X., Schaefer, S., Luo, J., Ma, L., and He, Y. (2020). Low rank matrix approximation for 3D geometry filtering. IEEE Trans. Vis. Comput. Graph. 28, 1835–1847. doi: 10.1109/TVCG.2020.3026785

PubMed Abstract | Crossref Full Text | Google Scholar

Ma, J., Zhang, J., Xu, J., Ai, R., Gu, W., and Chen, X. (2022). Overlaptransformer: an efficient and yaw-angle-invariant transformer network for lidar-based place recognition. IEEE Robot Autom. Lett. 7, 6958–6965. doi: 10.1109/LRA.2022.3178797

Crossref Full Text | Google Scholar

McDonald, R. P. (1999). Test Theory: A Unified Treatment. New York, NY: Psychology Press.

Google Scholar

Mitchelmore, M., and White, P. (2000). Development of angle concepts by progressive abstraction and generalisation. Educ. Stud. Math. 41, 209–238. doi: 10.1023/A:1003927811079

Crossref Full Text | Google Scholar

Munier, V., and Merle, H. (2009). Interdisciplinary mathematics-physics approaches to teaching the concept of angle in elementary school. Int. J. Sci. Educ. 31, 1857–1895. doi: 10.1080/09500690802272082

Crossref Full Text | Google Scholar

Nachar, N. (2003). The Mann-Whitney U: a test for assessing whether two independent samples come from the same distribution. Tutor. Quant. Methods Psychol. 4, 13–20. doi: 10.20982/tqmp.04.1.p013

Crossref Full Text | Google Scholar

Nathan, M. J. (2012). Rethinking formalisms in formal education. Educ. Psychol. 47, 125–148. doi: 10.1080/00461520.2012.667063

Crossref Full Text | Google Scholar

Nersessian, N. J. (1993). “In the theoretician's laboratory: thought experimenting as mental modeling," in PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association, Vol. 1992 (Cambridge: Cambridge University Press), 291–301. doi: 10.1086/psaprocbienmeetp.1992.2.192843

Crossref Full Text | Google Scholar

Özen Ünal, D., and Urun, O. (2021). Sixth-grade students' some difficulties and misconceptions on angle concept. J. Qual. Res. Educ. 1, 125–154. doi: 10.14689/enad.27.7

Crossref Full Text | Google Scholar

Pedrera, O., Barrutia, O., and Díez, J. R. (2025). Unveiling students' mental models and learning demands: an empirical validation of secondary students' model progression on plant nutrition. Res. Sci. Educ. 1–28. doi: 10.1007/s11165-024-10225-x

Crossref Full Text | Google Scholar

Petersen, L. A., and McNeil, N. M. (2013). Effects of perceptually rich manipulatives on preschoolers' counting performance: established knowledge counts. Child Dev. 84, 1020–1033. doi: 10.1111/cdev.12028

PubMed Abstract | Crossref Full Text | Google Scholar

Pinilla, R. K. (2024). Spatial reasoning in mathematics standards: Identifying how early elementary educators are systematically supported to teach spatial skills. Front. Educ. 9:1407388. doi: 10.3389/feduc.2024.1407388

Crossref Full Text | Google Scholar

Portnoy, N., Grundmeier, T. A., and Graham, K. J. (2006). Students' understanding of mathematical objects in the context of transformational geometry: implications for constructing and understanding proofs. J. Math. Behav. 25, 196–207. doi: 10.1016/j.jmathb.2006.09.002

Crossref Full Text | Google Scholar

Pulvermüller, F. (2023). Neurobiological mechanisms for language, symbols and concepts: clues from brain-constrained deep neural networks. Prog. Neurobiol. 230:102511. doi: 10.1016/j.pneurobio.2023.102511

PubMed Abstract | Crossref Full Text | Google Scholar

Richardson, S. E., and Koyunkaya, M. Y. (2017). Fostering students' development of the concept of angles using technology. Austr. Prim. Math. Classroom 22, 13–20. doi: 10.3316/informit.735348654464798

Crossref Full Text | Google Scholar

Roseno, A., Stage, V. C., Hoerdeman, C., Díaz, S., Geist, E., Duffrin, M. W., et al. (2015). Applying mathematical concepts with hands-on, food-based science curriculum. Sch. Sci. Math. 115, 14–21. doi: 10.1111/ssm.12097

PubMed Abstract | Crossref Full Text | Google Scholar

Russell, D. W. (2002). In search of underlying dimensions: the use (and abuse) of factor analysis in personality and social psychology bulletin. Pers. Soc. Psychol. Bull. 28, 1629–1646. doi: 10.1177/014616702237645

Crossref Full Text | Google Scholar

Sadijah, C., and Malang, S. U. (2022). Students' mental model in understanding quadrilateral concept: a five-level analysis. Turk. J. Comput. Math. Educ. 13, 547–558. doi: 10.17762/turcomat.v13i2.12676

Crossref Full Text | Google Scholar

Sari, M., Tertemiz, N., and Demirci, N. (2021). A study on 5th grade students' achievement levels and misconceptions in the concept of angle. Int. J. Prog. Educ. 17, 338–356. doi: 10.29329/ijpe.2021.329.22

Crossref Full Text | Google Scholar

Schermelleh, K., Moosbrugger, H., and Müller, H. (2003). Evaluating the fit of structural equation models: tests of significance and descriptive goodness-of-fit measures. Methods Psychol. Res. 8, 23–74. doi: 10.23668/psycharchives.12784

Crossref Full Text | Google Scholar

Simpson, A., Shokeen, E., Katirci, N., and Williams-Pierce, C. (2024). Elementary students' shared understanding of angle during an educational robotics task. Front. Educ. 9:1425307. doi: 10.3389/feduc.2024.1425307

Crossref Full Text | Google Scholar

Sloutsky, V. M., Kaminski, J. A., and Heckler, A. F. (2005). The advantage of simple symbols for learning and transfer. Psychon. Bull. Rev. 12, 508–513. doi: 10.3758/BF03193796

PubMed Abstract | Crossref Full Text | Google Scholar

Susanto, D. A. (2020). Problematic of definition and terminology affecting primary teachers' mathematical knowledge for teaching geometry. J. Phys. Conf. Ser. 1567:22096. doi: 10.1088/1742-6596/1567/2/022096

Crossref Full Text | Google Scholar

Ubben, M. (2020). Typisierung des Verständnisses mentaler Modelle mittels empirischer Datenerhebung am Beispiel der Quantenphysik (Volume 304). Berlin: Logos Verlag Berlin. doi: 10.30819/5181

Crossref Full Text | Google Scholar

Ubben, M. S., and Bitzenbauer, P. (2022). Two cognitive dimensions of students' mental models in science: fidelity of gestalt and functional fidelity. Educ. Sci. 12:163. doi: 10.3390/educsci12030163

Crossref Full Text | Google Scholar

Ubben, M. S., and Heusler, S. (2021). Gestalt and functionality as independent dimensions of mental models in science. Res. Sci. Educ. 51, 1349–1363. doi: 10.1007/s11165-019-09892-y

Crossref Full Text | Google Scholar

Ubben, M. S., Veith, J. M., Merzel, A., and Bitzenbauer, P. (2023). Quantum science in a nutshell: fostering students' functional understanding of models. Front. Educ. 8:1192708. doi: 10.3389/feduc.2023.1192708

Crossref Full Text | Google Scholar

Unal, O. D., and Urun, O. (2021). Sixth-grade students' some difficulties and misconceptions on angle concept. J. Qual. Res. Educ. 27, 125–154.

Google Scholar

Uttal, D. H., O'Doherty, K., Newland, R., Hand, L. L., and DeLoache, J. (2009). Dual representation and the linking of concrete and symbolic representations. Child Dev. Perspect. 3, 156–159. doi: 10.1111/j.1750-8606.2009.00097.x

Crossref Full Text | Google Scholar

Uttal, D. H., Scudder, K. V., and DeLoache, J. S. (1997). Manipulatives as symbols: a new perspective on the use of concrete objects to teach mathematics. J. Appl. Dev. Psychol. 18, 37–54. doi: 10.1016/S0193-3973(97)90013-7

Crossref Full Text | Google Scholar

Veith, J., Bitzenbauer, P., and Girnat, B. (2022a). Exploring learning difficulties in abstract algebra: the case of group theory. Educ. Sci. 12:516. doi: 10.3390/educsci12080516

Crossref Full Text | Google Scholar

Veith, J., Bitzenbauer, P., and Girnat, B. (2022b). Teaching and learning group theory: empirical insights facilitated by the ci2gt. Educ. Sci. Available online at: https://www.mdpi.com/2227-7102/12/6/376

Google Scholar

Veith, J. M., and Bitzenbauer, P. (2021). Two challenging concepts in mathematics education: Subjectspecific thoughts on the complex unit and angles. Eur. J. Sci. Mathem. Educ. 9, 244–251. doi: 10.30935/scimath/11251

Crossref Full Text | Google Scholar

Volodin, S., Khodr, H., Dillenbourg, P., and Johal, W. (2025). Going down the abstraction stream with augmented reality and tangible robots: the case of vector instruction. arXiv [preprint]. arXiv/2504.14562. doi: 10.48550/arXiv.2504.14562

Crossref Full Text | Google Scholar

Vom Hofe, R., and Blum, W. (2016). “Grundvorstellungen” as a category of subject-matter didactics. J. Mathematik-Didaktik 37, 225–254. doi: 10.1007/s13138-016-0107-3

Crossref Full Text | Google Scholar

Vrieze, S. I. (2012). Model selection and psychological theory: a discussion of the differences between the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). Psychol. Methods 17, 228–243. doi: 10.1037/a0027127

PubMed Abstract | Crossref Full Text | Google Scholar

Wang, S., Ma, R., Cao, F., Luo, L., and Li, X. (2024). A review: high-precision angle measurement technologies. Sensors 24, 1755–1755. doi: 10.3390/s24061755

PubMed Abstract | Crossref Full Text | Google Scholar

Weigand, H.-G., Hollebrands, K., and Maschietto, M. (2025). Geometry education at secondary level-a systematic literature review. ZDM-Math. Educ. 1–15. doi: 10.1007/s11858-025-01703-1

Crossref Full Text | Google Scholar

Wilson, P. S., and Adams, V. M. (1992). A dynamic way to teach angle and angle measure. Arithmetic Teach. 39, 6–13. doi: 10.5951/AT.39.5.0006

Crossref Full Text | Google Scholar

Woodward, E. (1978). Different angles on measuring angles. Sch. Sci. Math. 78, 385–387. doi: 10.1111/j.1949-8594.1978.tb09382.x

Crossref Full Text | Google Scholar

Xie, H., Maharjan, R. S., Tavella, F., and Cangelosi, A. (2024). From concrete to abstract: a multimodal generative approach to abstract concept learning. arXiv [preprint]. arXiv:2410.02365. doi: 10.48550/arXiv:2410.02365

Crossref Full Text | Google Scholar

Yuan, K.-H., and Bentler, P. (1998). Structural equation modeling with robust covariances. Sociol. Methodol. 28, 363–396. doi: 10.1111/0081-1750.00052

Crossref Full Text | Google Scholar

Appendix

Table A1

Table A1. Overview of all indicators for the factor FG and the corresponding item phrasings.

Table A2

Table A2. Overview of all indicators for the factor FF and the corresponding item phrasings.