Impact of Large-Scale Mobile Electric Vehicle Charging in Smart Grids: A Reliability Perspective

The charging load of electric vehicles (EVs) is characterized by uncertainty and flexibility, which burdens the distribution network, especially when there is a high penetration of distributed generation (DG) in smart grids. Large-scale EV mobility integration not only affects smart grid operation reliability but also the reliability of EV charging services. This paper aims at estimating the comprehensive impacts caused by spatial-temporal EV charging from the perspective of both electricity system reliability and EV charging service reliability. First, a comprehensive reliability index system, including two novel indexes quantifying EV charging service reliability, is proposed. Then, considering traffic constraints and users’ charging willingness, a spatial-temporal charging load model is introduced. In the coupled transportation and grid framework, the reliability impacts from plenty of operation factors are analyzed. Moreover, the electricity system reliability and EV charging service reliability correlated with DG integration are discussed. A coupled transportation grid system is adopted to demonstrate the effectiveness and practicability of the proposed method. The numerical results analyze reliability impacts from EV penetration level, trip chain, EV battery capacity, DG installation location, and capacity. The proposed studies reveal that when the EV capacity ratio to DG capacity is 3:1, the system reliability reaches the maximum level.

Highlights

1) Impacts on reliability are studied from the perspective of both electricity system and EV charging service.

2) A spatial-temporal simulation strategy for mobile EV charging load is proposed.

3) A coupled transportation and grid framework is used for reliability assessment.

4) Reliability impacts from EV penetration level, trip chain, EV battery capacity, DG installation location and capacity are quantified.

Introduction

The problems of carbon emissions and energy shortage have been increasingly serious nowadays, which has captured people’s attention on sustainable and clean energy. Thus, the application of electric vehicles (EVs) has attracted much attention recently (Shafiee et al., 2013; Veldman and Verzijlbergh, 2015; Patil and NagoKalkhambkar, 2021). According to an industry report forecast, sales for EVs in 2021 will be between 1.8 and 2 million, of which more than 80% will be private cars. Moreover, several countries, such as China, Japan, America, Germany, etc., provide lavish subsidies to EV users to promote the development of electric vehicles. For instance, Germany provided up to 1.2 billion euros of subsidies to individual EV users. In addition, the construction of charging infrastructure has also caused broad concern. It is predicted that, in China, by the end of 2021, the number of public charging piles will exceed 1.15 million, while the number for the private will be close to 1.5 million. And for battery swapping stations, the number will approach 1,000. Hence, EV penetration in smart grids is increased significantly. However, while environmental stress is relieved due to EV high penetration in smart grids, the potential risk of electricity system operation is also increased as EVs are charged stochastically based on traffic constraints and users’ subjective willingness. This problem will be even more serious with the increasing penetration of distributed generation (DG) whose output power is also uncertain. On the other hand, with the large scale of EV integration, the reliability of EV charging services cannot be ignored as well. For EV users, the purpose of their charging behavior is to guarantee their own demand, while they are also an important part of electricity load. Hence, electricity system reliability and EV charging service reliability may conflict sometimes. However, there is still relatively little research on this field. As a result, impacts of EV integration on the coupled system considering EV spatial-temporal mobile charging should be investigated to make a trade-off between electricity system reliability and charging service reliability and to obtain a strategy for EV and DG coordination operation.

The transportation network and distribution network are closely coupled and interacted due to EV charging and movement. An integrated traffic-power framework proposed in Xiang et al. (2018) described the interactions between the evolution coherence of EV charging load and traffic flow. Reference Acha et al. (2010) discussed the impacts of different EV charging strategies on distribution system energy losses, which showed that distribution system operation can be optimized by EV coordination. Reference Sun et al. (2020) proposed a day-ahead robust, cost-minimizing scheduling strategy for EV overnight charging in low voltage distribution networks. In Hoog et al. (2015), EV charging was formulated as a linear optimization problem considering distribution network constraints, such as transformer capacity, voltage, and current magnitude limits. A mixed-integer linear programming model for EV coordinate charging in unbalanced distribution networks was presented in Franco et al. (2015), considering loads imbalance and three-phase circuits. However, traffic characteristics were not considered in the process of EV charging load modeling in these works, which was not in accordance with the load characteristics of EVs.

As participants in both urban transportation networks and distribution networks, characteristics of EV mobile charging load are closely associated with users’ travel habits and traffic constraints. Furthermore, the larger the scale of EV integration, the tighter the correlation among different participants. On this basis, some scholars have studied how to model transportation characteristics accurately. In Xiang et al. (2016), the siting and sizing of EV charging stations were discussed considering traffic constraints. In Luo et al. (2020a), an EV charging strategy was proposed considering traffic speed and EV numbers in charging stations. A mathematical model of EV charging demand was introduced in Xia et al. (2019), where some important factors were considered, such as seasons, travel patterns, and traffic congestion. In Su et al. (2020), a novel control method was proposed to control imbalanced feeder power on EV flexible charging. In Xiang et al. (2019), existing EV charging modeling methods were summarized from the temporal and spatial dimension perspectives. On this basis, a scale EV evolution model of charging load was introduced in Xiang et al. (2019). In Ding et al. (2020), a multiperiod restoration model for distribution networks considering the coordination of mobile EVs, routing repair crews, and microgrids was proposed, which showed that EV could help with restoration during a system outage. Reference Su et al. (2019) investigated distribution network planning problems with aggregated EV charging, which took into account EV charging behavior and driving patterns. In Manbachi et al. (2016), impacts of EV integration with different penetration on quasi Volt-VAR Optimization in distribution networks were evaluated, where EV types, mixes, and ZIP modeling were illustrated to model EV and loads. But it was ignored in these studies that EV charging was stochastic, being based on users’ own charging willingness to a great extent.

The existing research evaluates the impacts of electric vehicle integration on system reliability which is generally analyzed in terms of electricity system reliability. In contrast, the reliability of EV charging services is rarely discussed. In Cheng et al. (2020), considering spatial-temporal EV charging load predicting, the reliability of the distribution network was evaluated with large-scale electric vehicle integration. In Xu and Chung (2016), evaluation of the distribution network reliability was extended considering EVs’ operation in different modes, including vehicle-to-home and vehicle-to-grid. Reference Sadeghian et al. (2019) analyzed the reliability impact of radial distribution systems considering demand response and EVs’ flexible charging and discharging. A probabilistic reliability assessment method was introduced in Anand et al. (2020) to evaluate the effect of stochastic EV charging power on distribution network reliability. In Guner and Ozdemir (2020), reliability enhancement of distribution network was analyzed considering storage capacity of electric vehicles parking lots. The potential of battery-exchange stations in improving distribution system reliability was investigated in Farzin et al. (2016), where the conclusion that system reliability could be notably improved based on the location of the battery-exchange station was obtained. In Huang et al. (2020), a data-driven reliability evaluation method was proposed to quantify EV penetrated system reliability employing slice sampling and diffusion estimator. However, in these studies the reliability of the electricity system was studied while EV charging service reliability was ignored, which is impractical since the basic purpose of EV charging is to ensure users’ own charging demand. In Meng et al. (2021), optimal planning for EV charging infrastructure was introduced to maximize both distribution network and EV charging service reliability. Although EV charging service reliability was considered in Meng et al. (2021), it was based on EV users’ traveling reliability rather than considering the reliability of EV charging power.

The impacts of distributed generation (DG) integration on urban distribution networks cannot be ignored for its intermittent and uncertain power characteristics Xiang et al. (2020). When DG penetration in the grid reaches a certain level, conventional generator capacity will be less than the total load capacity (Ge and Wang, 2013). In this case, the uncertainty of DG output may lead to a system outage, particularly when large-scale electric vehicle charging has occurred in the system. A DG planning model taking into account network reconfiguration and demand-side management was proposed in Zhang et al. (2018). In Cui et al. (2019), collaborative planning of distribution network and distributed generation was introduced, considering the flexible operation of heat pump load. Reference Das et al. (2020) analyzed the impacts of DG integration on optimal reactive power dispatch. In Luo et al. (2020b), an optimization model to determine the coordinated allocation of EV charging stations and DG was proposed. In Colmenar-Santos et al. (2019), a charging strategy was designed to increase DG penetration in the electricity system by electric vehicle dispatching. Impacts of EV integration on wind-thermal electricity systems were explored in Göransson et al. (2010) to reduce carbon emissions. An optimal bidding strategy considering plug-in EVs and DG was proposed to maximize microgrids and distribution system profits in Bostan et al. (2020), where coordination of energy resources was also optimized for system contingency. In Luo et al. (2019), an optimization model for joint locating and sizing of EV charging infrastructure and DG was presented taking into account real-time charging navigation. But it cannot be ignored that the coordination operation of EV and DG may lead to system instability since the power was stochastic for both. Reliability impacts of DG and EV operation in coordination on smart grids should be analyzed.

Considering insufficiency in these studies, the reliability impacts of large-scale mobile EV integration on electricity system-based sequential Monte Carlo method are discussed in this paper. The main contributions of this paper are as follows:

1) A comprehensive reliability assessment method that quantifies both electricity system reliability and EV charging service reliability is proposed. Two novel indexes aiming to quantify EV charging power reliability are put forward to evaluate the curtailing extent of charging energy in each bus and analyze the charging energy not supplied from a holistic perspective.

2) A spatial-temporal mobile EV charging load model based on the vehicle-transportation-grid trajectory is proposed considering EV traffic characteristics and users’ charging willingness. In the coupled transportation and grid framework, reliability impacts considering plenty of operation factors are comprehensively analyzed.

3) Reliability impacts of DG integration on the grid with large-scale mobile EV deployment are quantified. The coordinated operation strategy of EVs and DG is discussed as well. DG installation locations can be selected to coordinate the reliability level of the distribution system and EV charging service. Moreover, the optimal DG capacity configuration, which brings the highest system reliability level, is provided.

The rest of this paper is organized as follows: in Mobile Electric vehicle Charging Load Modeling, spatial-temporal mobile EV charging load modeling is introduced; the reliability evaluation method for both system and EV charging service-based sequential Monte Carlo is proposed in Reliability Assessment; Framework provides a detailed description of the research framework employed in this paper; Numerical simulations about coupled system reliability with EV mobility and DG integration are performed in Case Study; and Conclusion draws some conclusions.

Mobile Electric vehicle Charging Load Modeling

As an uncertain load coupling transportation system and distribution system, EVs should be modeled spatially and temporally. In this section, EV mobile trajectory is formulated first based on a trip chain and Dijkstra algorithm. Then flexible charging of EV is modeled, including EV trip time, SOC consumption, charging mode selection, and users’ charging willingness.

Electric Vehicle Mobile Trajectory Modeling

EV charging load is different from conventional load due to its traffic characteristics. EV traveling starting point, destination, traveling distance, and users’ habits will influence the charging behavior. Considering transportation constraints, EV state of charge (SOC) is determined through its travel trajectory. As a result, transportation topology should be modeled first. In this paper, graph theory is employed for bidirectional transportation network modeling (Tang and Wang, 2016). In graph theory, a set of vertices are linked by the corresponding disjoint edges, while the roads are modeled by the edges, and transportation system nodes are modeled via the set of vertices.

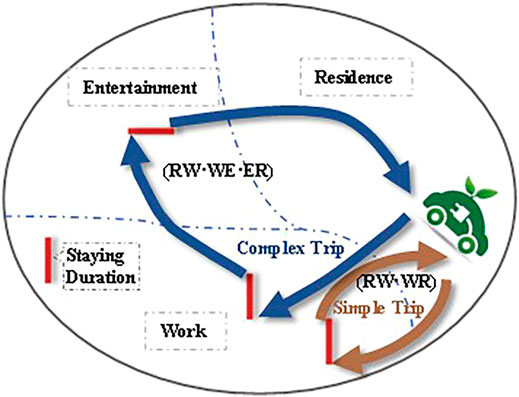
After transportation topology is obtained, EV mobile behavior should be modeled. The mobile behavior of EV users can be understood as a spatial and temporal interacting process, normally starting from one certain point and finally arriving at the destination, which can be simply categorized into three basic aspects: work, entertainment, and residence. A trip chain is usually utilized to reflect EV dynamic travel characteristics (Liang et al., 2020) and is therefore employed in this paper to provide a better description of user’s travel patterns.

Assuming every trip starts at home, and after staying in several places, i.e., workplaces, EV users eventually return to home. Then trip chains are obtained to simulate EV users traveling behaviors depicted in Figure 1. The set of trip chains are described in Table 1 as follows:

$C=\left\{C_1,C_2\right\}(1)$

where C represents the whole set of trip chains; C₁ represents the simple chain which means there is only one activity during the trip; accordingly, C₂ represents the complex chain, which means that more than one activity has occurred during the trip; R represents the residence area; W is the work area, and E is for an entertainment area.

FIGURE 1

FIGURE 1. EV traveling trajectory with two types of trip chains.

TABLE 1

TABLE 1. Trip chain of EVs.

The Dijkstra algorithm proposed by Dijkstra in 1959 is a common algorithm to find the shortest path from a point to any other point in graph theory (Dijkstra, 1959). Assuming EV users will travel in the shortest path to save time and energy. Then specific traveling path is obtained based Dijkstra algorithm when the trip starting point and destination are determined.

Electric Vehicle Charging Load Predicting

In this section, EV traveling state, including traveling time and SOC consumption is modeled. As a flexible charging load, users’ charging willingness and charging pattern are also discussed.

Electric Vehicle Traveling State Modeling

According to the statistics of the UK Ministry of Transport in 2016 (Li et al., 2019), the traveling time can be fitted to a normal distribution, which can be seen as follows:

$f\left(t;\mu ,\sigma \right)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left(-\frac{{\left(t-\mu \right)}^2}{2{\sigma }^2}\right)(2)$

where $\mu$ is the expected value of EV traveling time; $\sigma$ is the standard deviation; and $\mu$ and $\sigma$ are trip chain type and traveling points respectively.

Then EV parking time and restarting time can be calculated based on EV traveling speed:

$T_{Road}^i={\displaystyle \sum _{road=1}^W\frac{S_{road}}{V_{E_{road}}}}(3)$

$T_{park}^i=T_{start}^i+T_{Road}^i(4)$

$T_{start}^{i+1}=T_{park}^i+T_{stay}^i(5)$

where $T_{Road}$ is the traveling duration in the ith trip; W is the nodes number that the ith trip includes; Sroad is the road length; $V_{E_{road}}$ represents the traveling speed; T_park is the point of parking time; T_start is the point of starting time of next trip; T_stay is the staying duration in the destination of the ith trip.

If EV is charged during the trip, then Eq 4 can be corrected:

$T_{park}^i=T_{start}^i+T_{Road}^i+T_{mid}^i(6)$

where $T_{mid}$ is the midway charging duration in the ith trip.

SOC of EV is dependent on users driving length. If SOC is lower than its threshold value after a driving distance, then EV should be charged to ensure the next trip ends successfully. Thus, making sure SOC be able to support the next trip for each period is essential. Assuming that SOC is decreased linearly with the increase of traveling distance, SOC at one certain point during the trip can be calculated as follows:

$SO{C}_{T_{park}}^i=SO{C}_{T_{start}}^i-\frac{{\displaystyle \sum _{Road=1}^W{S}_{Road}}\times b}{Cap}(7)$

where $SO{C}_{T_{park}}^i$ is the SOC after arriving at a destination; $SO{C}_{T_{start}}^i$ is the initial SOC during the trip; b is the power consumption per mileage; Cap is the EV battery capacity.

User Charging Pattern Modeling

Before EV charging mode selection, users should decide whether EV should be charged first. Based on the current SOC, the EV traveling distance that can be supported before reaching the threshold is formulated as follows:

$S^{SO{C}_m}=\frac{\left(SO{C}_{T_{start}}^i-SO{C}_m\right)\times Cap}{b}(8)$

where $SO{C}_m$ is the SOC threshold value.

If the following formula is met, then the n_f th node is the midway charging node:

$0<S^{SO{C}_m}-{\displaystyle \sum _{road=1}^W{S}_{road}}<\xi (9)$

where $\xi$ is a prespecified value.

Naturally, the duration for midway charging can be calculated as follows:

$T_{mid}=\frac{1-SO{C}_{T_{start}}^i+b\times \left({\displaystyle \sum _{road=1}^{n_f}{S}_{road}}\right)/Cap}{Power}Cap(10)$

where Power is the charging power based on the charging pattern.

However, considering users charging willingness, sometimes EV will still be charged even though the current SOC can support the next trip. In this case, users will choose to charge or not based on business urgency, or their behavioral habits, etc. Consequently, a user charging demand model is adopted in this paper to describe the charging probability based on fuzzy theory (Liu et al., 2018a). Define DEG_SOC as the index to measure the sufficiency extent of SOC for the next trip:

$DE{G}_{SOC}=\frac{SO{C}_{T_{park}}^i\times Cap}{b\times S^{i+1}}(11)$

where Sⁱ⁺¹ is the traveling distance for the next trip.

Then, the membership function M(DEG_SOC) representing the fuzzy set of charging willingness is formulated as follows:

$M\left(DE{G}_{SOC}\right)=\{\begin{array}{cc}0,& DE{G}_{SOC}\ge X\\ 1,& DE{G}_{SOC}\le Y\\ \frac{1}{2}\left\{1+\sin \left[\frac{\pi }{X-Y}\left(\frac{X+Y}{2}-DE{G}_{SOC}\right)\right]\right\},& Y<DE{G}_{SOC}<X\end{array}(12)$

where X is the fuzzy coefficient. When the value of DEG_SOC is bigger than X, it means that SOC is adequate, and there is no need for charging; Y is the elastic coefficient. If DEG_SOC is smaller than Y, the next trip cannot be supported based on the current SOC. As a result, when DEG_SOC is between X and Y, users have the willingness to charge. The closer to X the value is, the weaker the charging demand is, and vice versa. The value of M ranges from 0 to 1.

After users decide to charge for EV, then the charging pattern should be discussed. EV users usually charge for EV at night when a full-day trip ended, as they should be prepared for the next day’s trip, and electricity price in the evening is generally lower than during the day. For the charging mode, a slow-charging mode is preferred at night when there is enough time for the charging since frequent fast charging may accelerate battery aging. For other situations, the charging pattern should be analyzed. If SOC cannot be charged to the full state through slow-charging mode during the parking time, the fast-charge mode should be adopted, which can be expressed as follows:

$\frac{Powe{r}_{slow}\times T_{stay}^i}{Cap}<1-SO{C}_{T_{park}}^i(13)$

where $Powe{r}_{slow}$ is the slow-charging power.

Reliability Assessment

As the mobile EV charging load model proposed is time-dependent and the system state is continuously changed, the sequential Monte Carlo simulation is adopted in this paper to evaluate electricity system reliability (Sankarakrishnan and Billinton, 1995). In the process of composite reliability evaluation, the optimization with the objective of minimum load curtailment is performed:

$Loa{d}_{shed}=\min {\displaystyle \sum _{j=1}^{N_L}{E}_j}(14)$

subject to

$P_{inj}+E-P_{LD}=0$

$Q_{inj}+E_Q-Q_{LD}=0$

$\underset{¯}{P_G}\le P_G\le \overline{P_G}$

$\underset{¯}{Q_G}\le Q_G\le \overline{Q_G}$

$\underset{¯}{V}\le V\le \overline{V}(15)$

where E_j is the load shedding in bus j; N_L is the number of distribution system load buses; P_inj and Q_inj are the vectors of active and reactive power injections respectively; E and E_Q are the vectors of corresponding active and reactive load curtailment; P_LD and Q_LD are the vectors of active and reactive power loads; P_G and Q_G are the vectors of active and reactive generating power and $\underset{¯}{P_G}$, $\overline{P_G}$, $\underset{¯}{Q_G}$, and $\overline{Q_G}$ are the vectors of their power limits respectively; V is the vector of bus voltage magnitude; and $\underset{¯}{V}$ and $\overline{V}$ are the vectors of corresponding limits.

In this part, three common reliability indexes to capture interruption duration, frequency, and load curtailment are introduced. In addition, two novel indexes aiming at EV charging service reliability are proposed to complement the existing indexes. All indexes are calculated based on sequential Monte Carlo simulation.

Reliability Indexes Calculation

For the distribution system, reliability indexes of SAIFI (system average interruption frequency index), SAIDI (system average interruption duration index), and EENS (expected energy not supplied) are adopted to perform reliability assessment, which can be calculated as Eqs 16–18. Additionally, two reliability indexes aiming at describing EV stochastic characteristics, i.e., POCCE (percentage of curtailed charging energy) and CENS (charging energy not supplied), are proposed to quantify EV charging service reliability. The two indexes are proposed from the perspective of EV charging power reliability. For POCCE, it is put forward to evaluate the curtailing extent of charging energy in each bus, which shows weaknesses of the charging service system. It should be noticed that in some charging points the value of POCCE is quite large while the total charging power is low. However, it still should be valued as EV charging service reliability is aimed at every EV user charging satisfaction not the charging reliability in society. For CENS, similar to distribution system index EENS, it is proposed to analyze the charging energy not supplied as a whole. It is assumed that when a system outage has occurred, EV charging load is considered to be curtailed first. Consequently, CENS can be regarded as a part of EENS. The calculation formulas are presented as follows:

$SAIFI=\frac{{\displaystyle \sum _{i_c=1}^{N_c}{\displaystyle \sum _{j=1}^{N_L}{f}_{i_c}^j{u}_j}}}{N_Y{\displaystyle \sum _{j=1}^L{u}_j}}(16)$

$SAIDI=\frac{{\displaystyle \sum _{i_c=1}^{N_c}{\displaystyle \sum _{j=1}^{N_L}{T}_{down\_i_c}^j{u}_j}}}{N_Y{\displaystyle \sum _{j=1}^{N_L}{u}_j}}(17)$

$EENS=\frac{{\displaystyle \sum _{i_c=1}^{N_c}{\displaystyle \sum _{j=1}^{N_L}{E}_{i_c}^j\times T_{down\_i_c}^j}}}{N_Y}(18)$

$POCCE=\frac{{\displaystyle \sum _{i_c=1}^{N_c}E{V}_{i_c}^j}}{{\displaystyle \sum _{i_f=1}^{N_f}EVloa{d}_{i_c}^j}}\times 100\%(19)$

$CENS=\frac{{\displaystyle \sum _{i_c=1}^{N_c}{\displaystyle \sum _{j=1}^{N_L}E{V}_{i_c}^j\times T_{down\_i_c}^j}}}{N_Y}(20)$

where N_c is the number of simulated cycles, where each cycle including an outage period $T_{down\_i_c}^j$ and a working period $T_{up\_i_c}^j$; N_f is the number of the outage periods; N_Y is the simulation year; u_j is the number of users in load bus j; $f_{i_c}^j$ is the interruption frequency in bus j; $E_{i_c}^j$ is the load curtailment; $EVloa{d}_{i_c}^j$ is the EV charging load; $E{V}_{i_c}^j$ is the curtailment of EV charging load. It should be noticed that $E{V}_{i_c}^j$, which refers to EV charging load shedding, is included in $E_{i_c}^j$.

Reliability Evaluation Based Sequential Monte Carlo Simulation

Components faults in the distribution network are relevant to environmental and operational factors. Different factors, such as service time, production defects, temperature, etc., can lead to component fault with a specified probability (Spinato et al., 2009). The faults can be considered an independent component to be modeled as a Markovian component with two states, up and down (Sulaeman et al., 2017).

Assuming that the duration of components in each state obeys an exponential distribution, the random state of the system is obtained by combining the operation states of components. Additionally, the electricity system reliability index is calculated based on the optimal power flow (OPF) solved by MATPOWER. Specific steps of the reliability assessment based on sequential Monte Carlo are as follows:

1) Set up the initial system state and input the original data, including grid topology, power load, charging load, power generation, etc.

2) According to the failure rate and repair rate of components, the time series state of components is extracted, and the component state matrix is generated. The duration of down and upstate is obtained as follows:

$T_{down\_i_c}^j=-\frac{1}{{\mu }_j}\ln N_{rand}(21)$

$T_{up\_i_c}^j=-\frac{1}{{\lambda }_j}\ln N_{rand}(22)$

where ${\mu }_j$ and ${\lambda }_j$ are the repair state and failure state respectively; N_rand is a random number evenly distributed between 0 and 1.

3) According to the component state matrix, the optimal power flow is calculated when a component failure occurred. If part of the load is curtailed, the system is considered in a failure state. Based on the simulation results, the reliability indexes are calculated based on Eqs 16–20.

4) In the process of sequential Monte Carlo evaluation, a stopping criterion is adopted when calculated parameters during the simulation are tended to be stable, which can be seen as Eq 23. If the inequation is met, the simulation stops.

$\beta =\frac{\sqrt{V\left({\beta }_{n_{MC}}\right)}}{E\left[{\beta }_{n_{MC}}\right]}\le \epsilon (23)$

where $\beta$ is the variation coefficient; E[·] is the expectation function; ${\beta }_{n_{MC}}$ is the reliability index (such as EENS) after n_MC simulation cycles; V(·) is the variance function; $\epsilon$ is a predetermined tolerance.

Framework

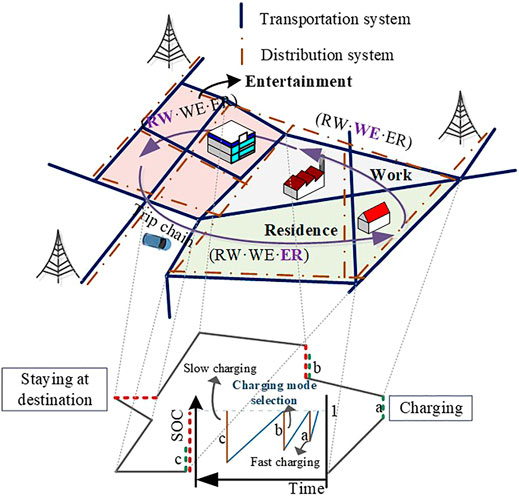
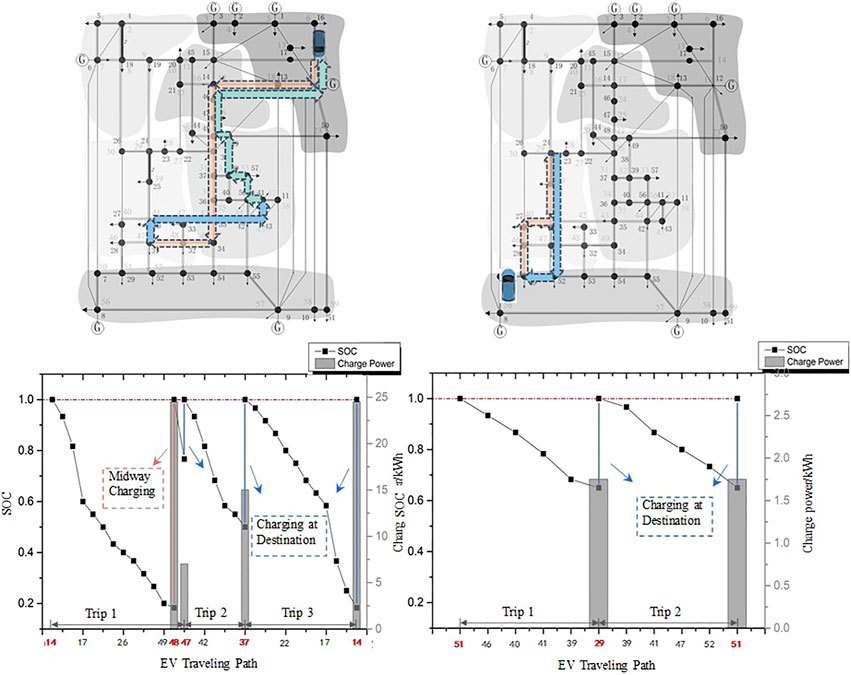
In this section, the overall framework of the proposed method is introduced. The coupled system framework-based spatial-temporal EV charging mobility is shown in Figure 2. The upper half part of the figure is the coupled transportation and distribution system, while the lower half is EV mobile trajectory-based “RW•WE•ER” trip chain and its corresponding SOC variation. Letter “a” represents the fast-charging mode adopted for midway charging during the trip in Figure 2. After the EV user gets home (the destination of the third trip), the EV is charged through low-charging mode as the letter “c” shows. Letter “b” means charging mode should be determined based on Eqs 12, 13. As can be seen, the users prefer to charge for EV at the destination of the first trip rather than the second trip.

FIGURE 2

FIGURE 2. Coupled system framework based spatial-temporal mobile EV charging.

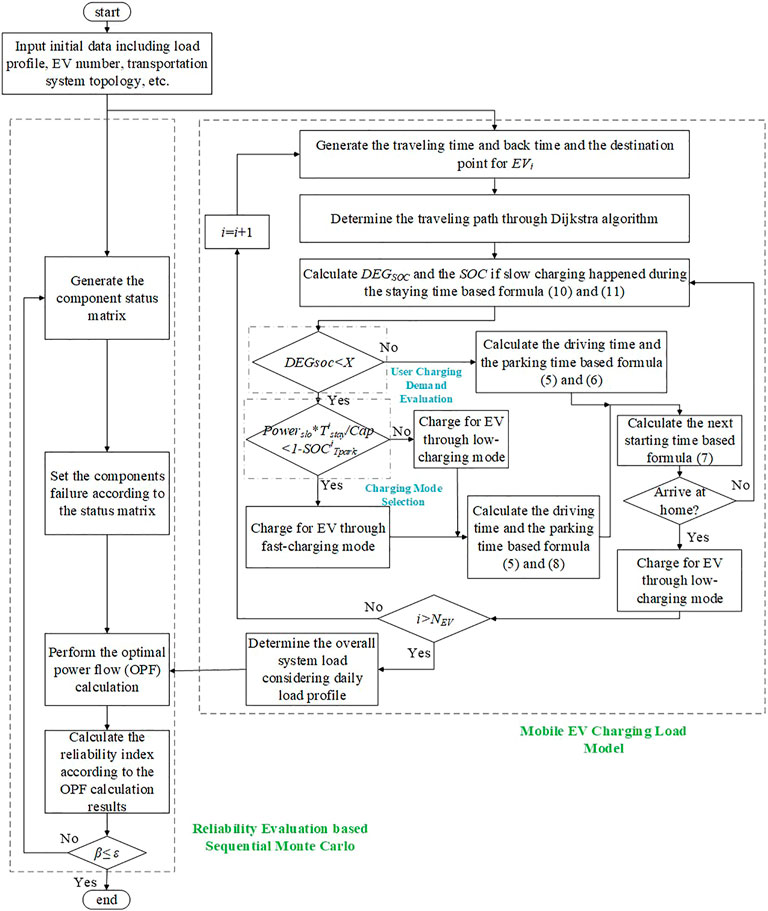
Solution steps of the proposed method are shown in Figure 3, which are divided into two parts: the mobile EV charging load modeling and the reliability evaluation based on sequential Monte Carlo.

FIGURE 3

FIGURE 3. Flowchart of reliability evaluation considering spatial-temporal EV charging load.

For the first part, the spatial-temporal EV charging load is modeled. Firstly, EV traveling starting time and back time are obtained according to a normal distribution. Then, the EV traveling path is obtained through the trip chain and Dijkstra path search algorithm. Considering EV users’ charging willingness, Eqs 12, 13 are calculated to decide whether to charge for EV or not during the trip. If EV users choose to charge, the slow-charging mode is preferred first. However, the fast-charging mode is chosen if SOC cannot be charged to the full state through slow charging mode during the staying time. When EV users get home, EVs will be charged through low-charging mode due to factors such as preparation for the next trip, lower electricity price, etc. The spatial-temporal EV charging load can be obtained when the whole EV time-space trajectory simulation is accomplished.

After EV charging load modeling, the total system load can be determined by combining the initial system load and EV charging load. The components are modeled as the Markovian components with two states, up and down. The optimal power flow (OPF) calculation is performed to obtain the system state with the minimum load shedding. If load curtailment occurs, the system state is identified as a failure. According to the OPF results, the reliability indexes are calculated. Repeat these steps until solutions are converged.

Case Study

In this section, simulations based on the IEEE 57-node test system and a coupled transportation system are performed. EV spatial and temporal characteristics are analyzed first. Then system reliability is deeply evaluated based on different EV penetration levels, trip chain, EV battery capacity, DG integrating location, and capacity.

Simulation Settings

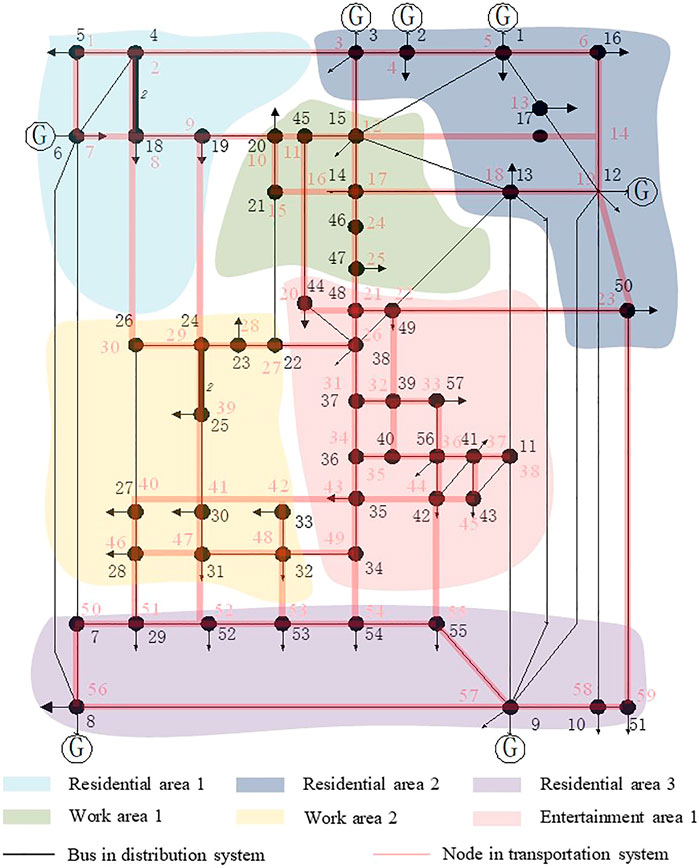
The topology of coupled IEEE 57-bus system and 59-node transportation system is depicted in Figure 4. In the distribution system, there are 80 branches, seven generators, and 57 buses containing 42 load buses. The number of total users is 932. As for the transportation system, it is divided into six areas: three residential areas, two work areas, and one entertainment area. The matching nodes of the transportation system and the distribution system buses are shown in Supplementary Appendix Tables A–C. Moreover, the length of each road is illustrated in Supplementary Appendix Table D.

FIGURE 4

FIGURE 4. Coupled system of distribution and transportation network.

For the parameters of EVs, the battery capacity of each EV is set to be 30 kWh, and the fast-charging power and low-charging power are 20 and 6 kW, respectively. The whole generator capacity is 1976 MW in the 57-bus system. It is defined that the penetration level of EV is the ratio of the fast charging power of the whole fleet to the total generator capacity. For example, a 10% penetration level means there are 9800 EVs in the coupled system (Cheng et al., 2013). Private EV is adopted as the analysis object in this paper as the traveling mode of private cars is more flexible. The parameters of X and Y are set to 2 and 1.2 respectively.

The sequential Monte Carlo method is adopted in this paper, and the step size of the sequential simulation is set to 15 min. The failure rate of the feeder is set to 0.002, and the repair rate is 0.25. The failure of the generator is not considered. Virtual generators that have high generating and operation costs are connected to load buses to calculate load curtailment. The daily load profile data is obtained from Ge et al. (2014).

Electric Vehicle Spatial-Temporal Simulations

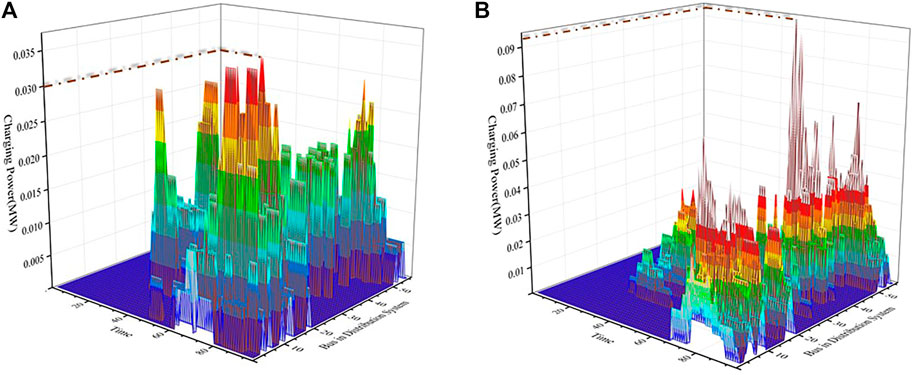
Charging load simulation for a working day and a resting day is performed in this section to evaluate the difference of charging load in different typical days. Assuming in a working day, simple trip chain accounts for 40%, and complex trip chain accounts for 60%. For resting day, 40% of people will choose to rest at home, and the complex and straightforward trip chain accounts for 50 and 10%, respectively. The charging load of 200 electric vehicles in working day and resting day are simulated, respectively, as shown in Figure 5.

FIGURE 5

FIGURE 5. Daily EV charging load in resting and working day.

It can be seen in Figure 5 that the EV charging load on the working day is much bigger than the one on the resting day, where the peak value of working-day charging power is triple that of the resting day. In addition, for both resting and working days, the time from 7:30 to 10:30 and 16:00 to 23:00 are high-demand charging periods. Moreover, different from the resting days, the charging demand is heavy in the evening, as people will often choose to charge for EV after work. As for the charging location, it can be seen that charging demand at the entertainment area on a resting day is more distinct than that on a working day. In contrast, the charging power on a working day is much higher than that on a resting day in a residential area.

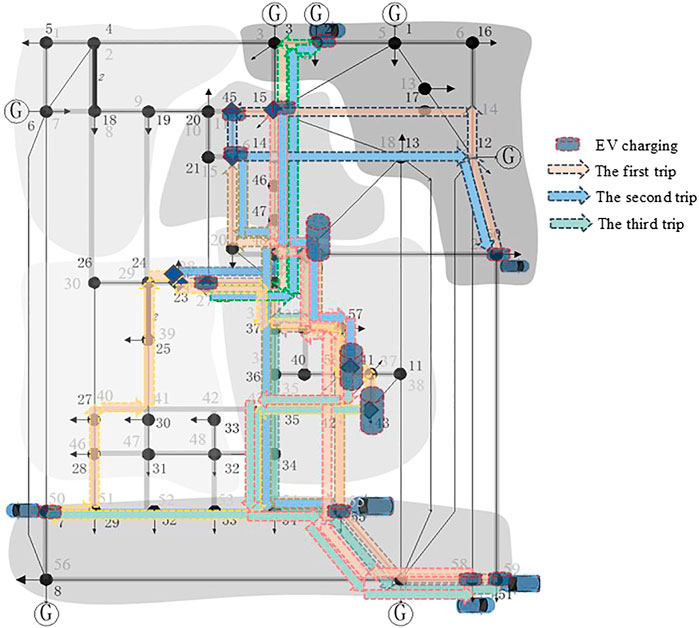
EV is charged movably and indeterminately due to its traffic characteristics. Six electric vehicles’ traveling trajectories and charging power are presented in Figure 6. Overall, the distribution of EV trajectory is mainly distributed at the central road of the transportation network. Compared to the upper part of the network depicted in Figure 6, EV charging in the lower part is more centralized. It can be noticed that the Entertainment area is located in the lower part of the transportation network, and so is Work area 2, which both lead to a high traffic density there. Consequently, the charging demand in these places is larger than the one in upper part of the system. As a result, EV charging in the lower part is more concentrated.

FIGURE 6

FIGURE 6. Description of EVs’ traveling trajectory and charging demand.

To draw EV spatial-temporal characteristics more clearly, a complex trip chain and a simple trip chain are extracted to be compared, as shown in Figure 7.

FIGURE 7

FIGURE 7. The spatial-temporal EV mobile trajectory and corresponding SOC variation.

From Figure 7, we can see the first trajectory is presented as a complex trip train that passes through residential area 2 (the start point), work area 1, entertainment area 1, work area 2 (the destination 1), entertainment area 1 (the destination 2), work area 1 and residential area 2 (destination 3, i.e., home). As the first trip (from residential area 2 to work area 2) is a long trip, EV is charged midway at node 48 to support the next trip. For the second simple trip chain, it can be noticed that SOC is dropped to the same value at both two destinations (node 29 and node 51). This is because the two trips have the same distance according to the Dijkstra path search algorithm.

Reliability Evaluation Based Sequential Monte Carlo

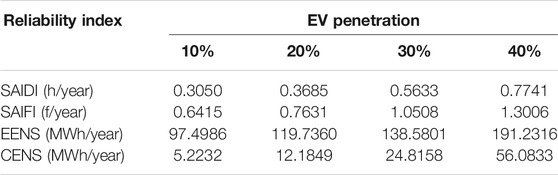
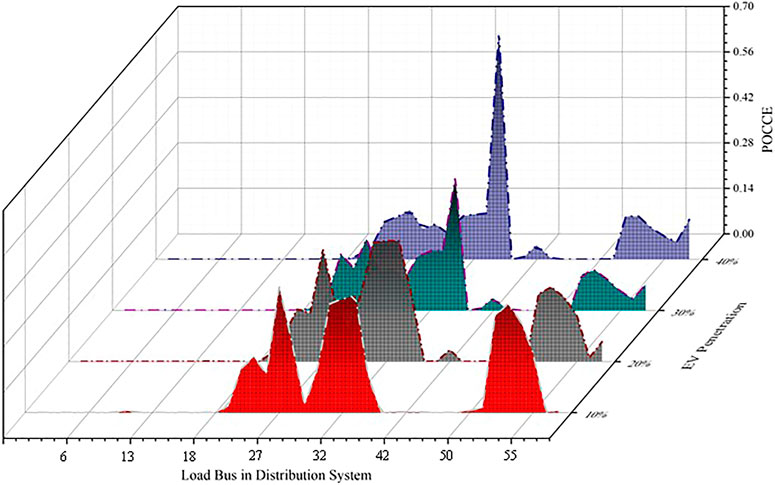
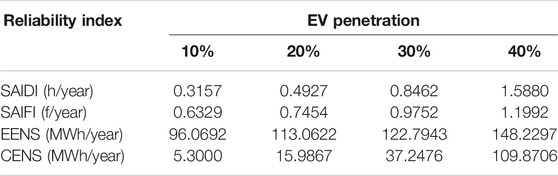
In this section, reliability indexes based on different EV penetration and trip chains are simulated. Besides, effects on the coupled system reliability due to EV charging based on different EV battery capacities are also discussed. Reliability indexes are shown in Table 2 and Figure 8 are based on EV penetration from 10 to 40%. The ratio of simple trip chain to complex trip chain is 1:9.

TABLE 2

TABLE 2. Reliability indexes based on different EV penetration.

FIGURE 8

FIGURE 8. Reliability index POCCE based different EV penetration.

From the data above, it is not difficult to find that all reliability indexes, including CENS and POCCE, worsen with EV penetration increasing. Moreover, it is noteworthy that there is a trend towards worsening POCCE value, which means that although the total EV charging power has been increased, the growth rate of curtailed charging power is more significant than before. As a result, a conclusion can be drawn that EV charging service reliability will be more seriously influenced by the growth of charging demand. Besides, there is a large capacity of charging power curtailment in buses 27, 32, 33, 35, 52, 53, and 54, which shows that the EV charging demand in the lower part of the network is more robust than the results obtained from Electric Vehicle Spatial-Temporal Simulations. To analyze the reliability level of different load buses, the loss of energy and charging energy in each load bus are compared in Figure 9.

FIGURE 9

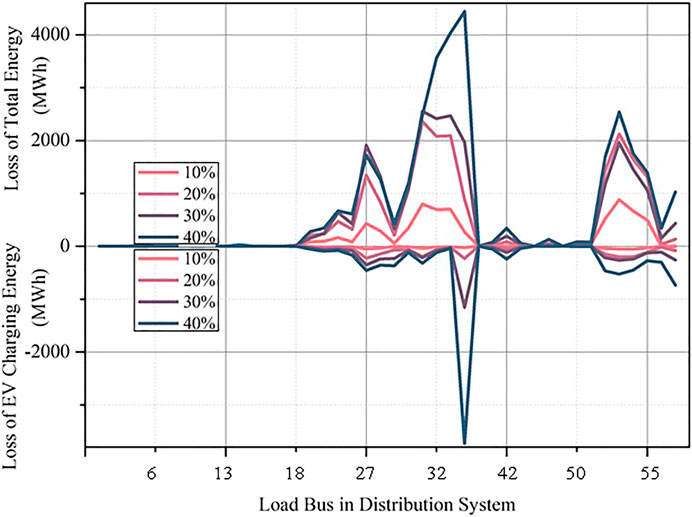
FIGURE 9. Loss of total energy and EV charging energy at each load bus in a year based on different EV penetration.

By comparing the two kinds of curves of “Loss of Total Energy” and “Loss of EV Charging Energy” in Figure 9, it is easy to realize that the buses with poor reliability level are consistent with the results in Figure 8 as well, which verifies the validity of the comprehensive reliability assessment method proposed in this paper. There may be three explanations for the phenomenon. First, the generators are mostly located at the upper part of the system, where the reliability level of buses is much higher. Besides, the lower part structure of the network is sparse; if there is a branch breaking down, nearby buses will severely be affected. Furthermore, high traffic density leads to a heavier load in the lower part.

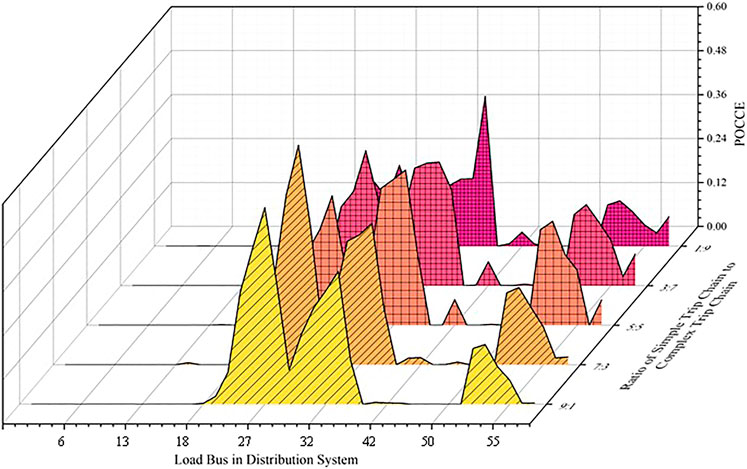
EV traffic characteristics are much correlated to users’ behaviors. The reliability indexes based on different ratios of the trip chains are shown in Table 3 and Figure 10. The penetration level of EV is set to be 30% uniformly.

TABLE 3

TABLE 3. Reliability indexes based on a different ratio of trip chain.

FIGURE 10

FIGURE 10. The reliability index POCCE based on a different ratio of trip chain.

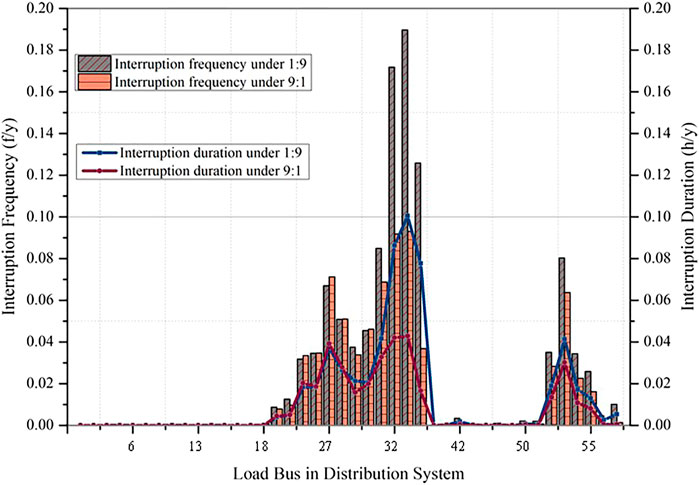
It can be noticed that with the decreasing of the complex trip chain proportion, the value of all reliability indexes is basically on a downward trend, which means system reliability has been improved. This is because, for the complex trip chain, the EV traveling trajectory is more complex. Therefore, the charging demand becomes more robust. As the proportion of the complex trip chain decreased, the system is less burdensome, and the reliability level is significantly improved. To see the difference further intuitively, the interruption frequency and duration in each load bus-based trip chain of 1:9 and 9:1 are shown in Figure 11.

FIGURE 11

FIGURE 11. Interruption frequency and duration based trip chain of 1:9 and 9:1.

From Figure 11, we can observe that the buses with high-reliability levels are basically in line with the previous results. And the interruption frequency and duration with the trip chain ratio of 1:9 is larger than the one with a ratio of 5:5, which is also consistent with the data in Table 3.

However, the above simulations are based on the constant capacity of each electric vehicle. In reality, different EV models may have various battery capacities. Thus, analyzing the effect of EV operation with different capacities is mandatory and practical. Keep the total EV capacity constant, i.e., the penetration level is the same as the data in Table 3. Increase the battery capacities of each EV to 30 kWh and the fast-charging power and low-charging power to 20 and 6 kW, respectively. The results are shown in Table 4.

TABLE 4

TABLE 4. Reliability indexes with increased battery EV capacity based on different EV penetration.

To compare the data in Tables 2, 4 more intuitively, the corresponding change rate of the reliability index is calculated. The results are shown in Figure 12.

FIGURE 12

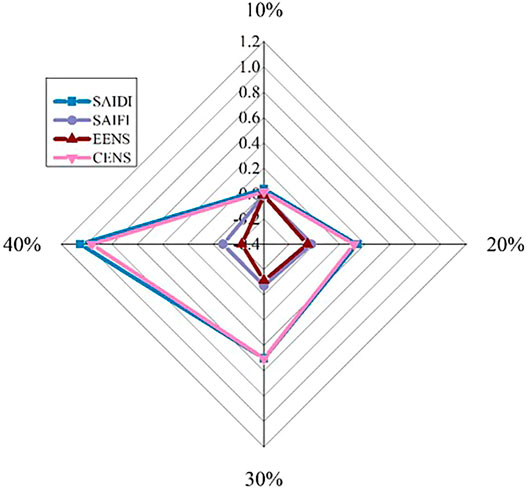
FIGURE 12. Change rate of reliability index with increased EV battery capacity based on different EV penetration.

It can be seen that the change rates of index “SAIDI” and “CENS” are greater than zero with penetration 10–40%, while the change rates of index “SAIFI” and “EENS” are less than zero. It means that after increasing EV battery capacity, “SAIDI” and “CENS” are increased and “SAIFI” and “EENS” are decreased, and as EV penetration increases, the change becomes more obvious. It may because EV users will have more unsatisfactory charging requirements in the event of a power outage when the capacity of the EV battery increases. Additionally, it may lead to a large amount of charging load at a certain moment, making the system burden much heavier. Consequently, the system becomes more complex to maintain steady-state operation. Hence, the Index “SAIDI” is increased. Since the total EV capacity is constant, the increase of EV charging power at certain moments leads to the charging power decrease at other moments. As a result, the frequency failure of the system and the amount of load curtailment are diminished.

Reliability evaluation With Electric Vehicle and Distributed Generation Integration

Due to the development of green energy and the requirements of national policies, the amount of DG in smart grids has been considerably increased. EV and DG are both characterized by their power uncertainty. Hence, system operation will be significantly influenced when they are jointly integrated into grids. This part describes the effect of DG integration on both EV charging service and distribution system reliability considering EV charging. Among all types of uncertain resources, the photovoltaic (PV) power characteristics differ greatly from charging load characteristics, as its power supply is cut off at night while EV is mainly charged at that time. In this case, PV is chosen to represent the uncertainty of DG.

In this section, two PVs with different capacities are integrated into the coupled system to evaluate its operation on system reliability. Considering the topology of the distribution system and traffic density, different PV installation locations may result in different reliability impacts. The PV installation location is determined based on the coupled system reliability. Aiming at improving EV charging service reliability, locations can be obtained by selecting buses with the two most considerable values based on Eq 24. And for distribution network reliability, it is determined based on Eq 25.

${\alpha }_j={\displaystyle \sum _{\ell }\left(\frac{POCC{E}_j}{{\displaystyle \sum _j^{N_L}POCC{E}_j}}+\frac{{\displaystyle \sum _{i_c=1}^{N_c}E{V}_{i_c}^j\times T_{down\_i_c}^j}}{{\displaystyle \sum _j^{N_L}{\displaystyle \sum _{i_c=1}^{N_c}E{V}_{i_c}^j\times T_{down\_i_c}^j}}}\right)}(24)$

${\beta }_j={\displaystyle \sum _{\ell }\frac{{\displaystyle \sum _{i_c=1}^{N_c}{E}_{i_c}^j\times T_{down\_i_c}^j}}{{\displaystyle \sum _j^{N_L}{\displaystyle \sum _{i_c=1}^{N_c}{E}_{i_c}^j\times T_{down\_i_c}^j}}}}(25)$

where $\ell$ represents the set of EV penetration from 10 to 40%.

Based on the two formulas above, bus 27 and bus 35 are selected for PV installation locations based on EV charging service reliability, and bus 31 and bus 33 for distribution system reliability. The daily time-varying output of PV can be seen from Liu et al. (2018b); however, the failure of PV is not considered. Keep the total system generation capacity constant and increase the total PV capacity from 100 to 400 MW, respectively, i.e., the capacity of a single PV cluster is from 50 to 200 MW. The penetration of EV is set to be 30%. The calculated reliability indexes are shown in Table 5.

TABLE 5

TABLE 5. Reliability indexes with PV integration.

Table 5 shows that by selecting PV to installation location based on electricity system reliability, the overall reliability level of the system is much better. However, it can be noticed that the value of “CENS/EENS” with PV location in bus 31 and 33 is higher than the one with PV location in bus 27 and 35. It means that although the overall reliability level is improved by selecting PV location bus-based electricity system reliability, EV charging service reliability will be more obviously enhanced if PV is integrated into bus 27 and 35, which gives further verification on the validity of the novel reliability indexes.

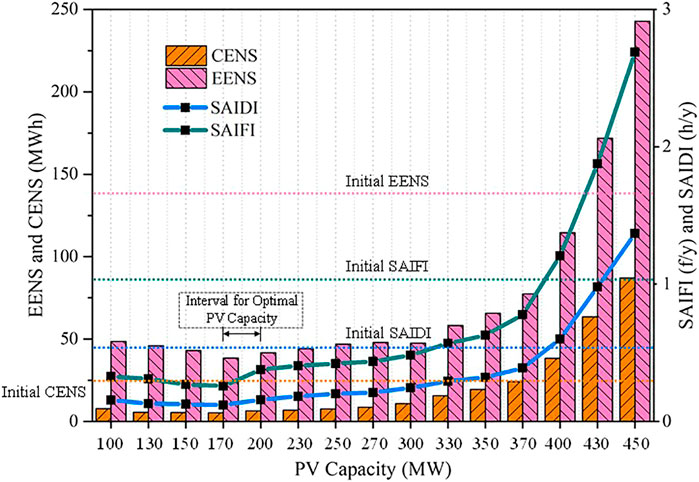
Besides, it can be noticed that with the increase of PV integration capacity, both distribution system reliability and EV charging reliability are improved first and then decreased. To see trends more visually, select bus 31 and 33 as the integration locations, and the reliability indexes with PV capacity from 100 to 450 MW are shown in Figure 13.

FIGURE 13

FIGURE 13. Reliability indexes with PV integration-based capacity from 100 to 450 MW.

When PV capacity is from 100 to 170 MW, the indexes are all on a downward trend, which means as PV penetration increases, the electricity system reliability level is improved. Consequently, the optimal PV capacity leading to the highest reliability is about 170 MW. As PV is integrated into the system, the operation of the distribution network is changed from a single power supply mode by the main power grid to a more flexible multi-terminal power supply mode by both the power main grid and PV. EV can be supplied by DG, which alleviates the system burden to a great extent. Besides, the basic power supply can be ensured by PV output in some areas when there is a system failure occurred. It means that when the ratio of EV capacity to DG capacity is 3:1, the coordinated optimal operation strategy is obtained. However, when PV capacity exceeds 200MW, the electricity system reliability level starts to decline. It is noteworthy that when PV capacity is increased by more than 370 MW, the reliability index starts to keep proliferating. Furthermore, when PV capacity reaches 400 MW, the system reliability level is even lower than the initial reliability level without PV integration. PV cannot undertake the main load for its intermittency and uncertainty, especially when there are numerous flexible EV charging loads.

Conclusion

Reliability impacts of large-scale mobile EV integration on both electricity system and EV charging service system in a coupled transportation and grid framework are explored in this paper. The case study results indicate the following:

• With the increase in EV penetration level and proportion of the complex trip chain, the reliability level for both the electricity system and EV charging service shows a downward trend. EV charging service reliability will be more severely affected by the growth of charging demand.

• Through increasing EV battery capacity, indexes “SAIDI” and “CENS” are increased while “SAIFI” and “EENS” are decreased. As EV penetration increases, the change becomes more obvious. The results implicate that both distribution network reliability and EV charging service reliability can be improved significantly by increasing EV battery capacity if there is enough backup power during the peak period.

• DG installation locations can be determined to coordinate the reliability level of the distribution system and EV charging service. Appropriate DG capacity can improve system reliability, but once a certain threshold is exceeded, the system will rapidly collapse. When DG capacity is about 170 MW, i.e., the ratio of EV capacity to DG capacity is 3:1, the highest system reliability level is reached. However, when DG capacity exceeds 370 MW, system reliability starts to deteriorate rapidly.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Appendix Material, further inquiries can be directed to the corresponding author.

Author Contributions

PX, YX: Conceptualization, methodology; PX: Writing—original draft preparation; YX, JL: Supervision; JG, WX, WS, ZJ, SJ, HZ: Writing—reviewing and editing.

Funding

This work was supported by the National Natural Science Foundation of China (51807127, 52111530067), the Sichuan Science and Technology Program (2020YFSY0037).

Conflict of Interest

Authors JG and WX were employed by company State Grid Sichuan Economic Research Institute. Author ZJ was employed by company State Grid Chongqing Shiqu Power Supply Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.688034/full#supplementary-material

References

Acha, S., Green, T. C., and Shah, N. (2010). Effects of Optimised Plug-In Hybrid Vehicle Charging Strategies on Electric Distribution Network Losses. New Orleans, LA, USA: IEEE PES T&D, 1–6.

Anand, M. P., Bagen, B., and Rajapakse, A. (2020). Probabilistic Reliability Evaluation of Distribution Systems Considering the Spatial and Temporal Distribution of Electric Vehicles. Int. J. Electr. Power Energ. Syst. 117, 105609. doi:10.1016/j.ijepes.2019.105609

CrossRef Full Text | Google Scholar

Bostan, A., Nazar, M. S., Shafie-khah, M., and Catalão, J. P. S. (2020). An Integrated Optimization Framework for Combined Heat and Power Units, Distributed Generation and Plug-In Electric Vehicles. Energy 202, 117789. doi:10.1016/j.energy.2020.117789

CrossRef Full Text | Google Scholar

Cheng, L., Chang, Y., Lin, J., and Singh, C. (2013). Power System Reliability Assessment with Electric Vehicle Integration Using Battery Exchange Mode. IEEE Trans. Sustain. Energ. 4 (4), 1034–1042. doi:10.1109/tste.2013.2265703

CrossRef Full Text | Google Scholar

Cheng, S., Wei, Z., Shang, D., Zhao, Z., and Chen, H. (2020). Charging Load Prediction and Distribution Network Reliability Evaluation Considering Electric Vehicles’ Spatial-Temporal Transfer Randomness. IEEE Access 8, 124084–124096.

Google Scholar

Colmenar-Santos, A., Muñoz-Gómez, A.-M., Rosales-Asensio, E., and López-Rey, Á. (2019). Electric Vehicle Charging Strategy to Support Renewable Energy Sources in Europe 2050 Low-Carbon Scenario. Energy 183, 61–74. doi:10.1016/j.energy.2019.06.118

CrossRef Full Text | Google Scholar

Cui, Q., Bai, X., and Dong, W. (2019). Collaborative Planning of Distributed Wind Power Generation and Distribution Network with Large-Scale Heat Pumps. CSEE J. Power Energ. Syst. 5 (3), 335–347.

Google Scholar

Das, T., Roy, R., and Mandal, K. K. (2020). Impact of the Penetration of Distributed Generation on Optimal Reactive Power Dispatch. Prot. Control. Mod. Power Syst. 5 (1), 31. doi:10.1186/s41601-020-00177-5

CrossRef Full Text | Google Scholar

Dijkstra, E. W. (1959). A Note on Two Problems in Connexion with Graphs. Numer. Math. 1, 269–271. doi:10.1007/bf01386390

CrossRef Full Text | Google Scholar

Ding, T., Wang, Z., Jia, W., Chen, B., Chen, C., and Shahidehpour, M. (2020). Multiperiod Distribution System Restoration with Routing Repair Crews, mobile Electric Vehicles, and Soft-Open-point Networked Microgrids. IEEE Trans. Smart Grid 11 (6), 4795–4808. doi:10.1109/tsg.2020.3001952

CrossRef Full Text | Google Scholar

Farzin, H., Moeini-Aghtaie, M., and Fotuhi-Firuzabad, M. (2016). Reliability Studies of Distribution Systems Integrated with Electric Vehicles under Battery-Exchange Mode. IEEE Trans. Power Deliv. 31 (6), 2473–2482. doi:10.1109/tpwrd.2015.2497219

CrossRef Full Text | Google Scholar

Franco, J. F., Rider, M. J., and Romero, R. (2015). A Mixed-Integer Linear Programming Model for the Electric Vehicle Charging Coordination Problem in Unbalanced Electrical Distribution Systems. IEEE Trans. Smart Grid 6 (5), 2200–2210. doi:10.1109/tsg.2015.2394489

CrossRef Full Text | Google Scholar

Ge, S., Guo, J., Liu, H., and Zeng, P. (2014). Impacts of Electric Vehicle’s Ordered Charging on Power Grid Load Curve Considering Demand Side Response and Output of Regional Wind Farm and Photovoltaic Generation. Power Syst. Tech. 38 (07), 1806–1811.

Google Scholar

Ge, S., and Wang, H. (2013). Reliability Evaluation of Distribution Networks Including Distributed Generations Based on System State Transition Sampling. Automation Electric Power Syst. 37 (02), 28–35.

Google Scholar

Göransson, L., Karlsson, S., and Johnsson, F. (2010). Integration of Plug-In Hybrid Electric Vehicles in a Regional Wind-thermal Power System. Energy Policy 38 (10), 5482–5492. doi:10.1016/j.enpol.2010.04.001

CrossRef Full Text | Google Scholar

Guner, S., and Ozdemir, A. (2020). Reliability Improvement of Distribution System Considering EV Parking Lots. Electric Power Syst. Res. 185, 106353. doi:10.1016/j.epsr.2020.106353

CrossRef Full Text | Google Scholar

Hoog, J. d., Alpcan, T., Brazil, M., Thomas, D. A., and Mareels, I. (2015). Optimal Charging of Electric Vehicles Taking Distribution Network Constraints into Account. IEEE Trans. Power Syst. 30 (1), 365–375.

Google Scholar

Huang, S., Ye, C., Liu, S., Zhang, W., Ding, Y., Hu, R., et al. (2020). Data-driven Reliability Assessment of an Electric Vehicle Penetrated Grid Utilizing the Diffusion Estimator and Slice Sampling. CSEE J. Power Energ. Syst., 1–9.

Google Scholar

Li, H., Du, Z., Chen, L., Guan, L., and Zhou, B. (2019). Trip Simulation Based Load Forecasting Model and Vehicle-To-Grid Evaluation of Electric Vehicles. Automation Electric Power Syst. 43 (21), 88–96.

Google Scholar

Liang, H., Lee, Z., and Li, G. (2020). A Calculation Model of Charge and Discharge Capacity of Electric Vehicle Cluster Based on Trip Chain. IEEE Access 8, 142026–142042. doi:10.1109/access.2020.3014160

CrossRef Full Text | Google Scholar

Liu, D., Lv, L., Liu, J., Gao, H., and Zhou, C. (2018). Coordinated Planning of Capacity of DG and TOU price Considering Time-Varying Characteristics of DG and Types of Load in Micro-grid. Electr. Meas. Instrumentation 55 (12), 45–53.

Google Scholar

Liu, H., Zhang, X., Liu, C., Zhang, J., and Ge, S. (2018). Timing Interactive Analysis of Electric Private Vehicle Traveling and Charging Demand Considering the Sufficiency of Charging Facilities. Proc. CSEE 38 (18), 5469–5478.

Google Scholar

Luo, L., Gu, W., Wu, Z., and Zhou, S. (2019). Joint Planning of Distributed Generation and Electric Vehicle Charging Stations Considering Real-Time Charging Navigation. Appl. Energ. 242, 1274–1284. doi:10.1016/j.apenergy.2019.03.162

CrossRef Full Text | Google Scholar

Luo, L., Wu, Z., Gu, W., Huang, H., Gao, S., and Han, J. (2020). Coordinated Allocation of Distributed Generation Resources and Electric Vehicle Charging Stations in Distribution Systems with Vehicle-To-Grid Interaction. Energy 192, 116631. doi:10.1016/j.energy.2019.116631

CrossRef Full Text | Google Scholar

Luo, Y., Feng, G., Wan, S., Zhang, S., Li, V., and Kong, W. (2020). Charging Scheduling Strategy for Different Electric Vehicles with Optimization for Convenience of Drivers, Performance of Transport System and Distribution Network. Energy 194, 116807. doi:10.1016/j.energy.2019.116807

CrossRef Full Text | Google Scholar

Manbachi, M., Sadu, A., Farhangi, H., Monti, A., Palizban, A., Ponci, F., et al. (2016). Impact of EV Penetration on Volt-VAR Optimization of Distribution Networks Using Real-Time Co-simulation Monitoring Platform. Appl. Energ. 169, 28–39. doi:10.1016/j.apenergy.2016.01.084

CrossRef Full Text | Google Scholar

Meng, J., Xiang, Y., Gu, C., Chen, S., and Liu, J. (2021). Collaborative Optimization Planning of Electric Vehicle Charging Infrastructure for Reliability Improvement. Electric Power Automation Equipment, 1–9.

Google Scholar

Patil, H., and Nago Kalkhambkar, V. (2021). Grid Integration of Electric Vehicles for Economic Benefits: a Review. J. Mod. Power Syst. Clean Energ. 9 (1), 13–26. doi:10.35833/mpce.2019.000326

CrossRef Full Text | Google Scholar

Sadeghian, O., Nazari-Heris, M., Abapour, M., Taheri, S. S., and Zare, K. (2019). Improving Reliability of Distribution Networks Using Plug-In Electric Vehicles and Demand Response. J. Mod. Power Syst. Clean. Energ. 7 (5), 1189–1199. doi:10.1007/s40565-019-0523-8

CrossRef Full Text | Google Scholar

Sankarakrishnan, A., and Billinton, R. (1995). Sequential Monte Carlo Simulation for Composite Power System Reliability Analysis with Time Varying Loads. IEEE Trans. Power Syst. 10 (3), 1540–1545. doi:10.1109/59.466491

CrossRef Full Text | Google Scholar

Shafiee, S., Fotuhi-Firuzabad, M., and Rastegar, M. (2013). Investigating the Impacts of Plug-In Hybrid Electric Vehicles on Power Distribution Systems. IEEE Trans. Smart Grid 4 (3), 1351–1360. doi:10.1109/tsg.2013.2251483

CrossRef Full Text | Google Scholar

Spinato, F., Tavner, P. J., van Bussel, G. J. W., and Koutoulakos, E. (2009). Reliability of Wind Turbine Subassemblies. IET Renew. Power Gener. 3, 387–401. doi:10.1049/iet-rpg.2008.0060

CrossRef Full Text | Google Scholar

Su, J., Lie, T. T., and Zamora, R. (2020). Integration of Electric Vehicles in Distribution Network Considering Dynamic Power Imbalance Issue. IEEE Trans. Ind. Applicat. 56 (5), 5913–5923. doi:10.1109/tia.2020.2990106

CrossRef Full Text | Google Scholar

Su, J., Lie, T. T., and Zamora, R. (2019). Modelling of Large-Scale Electric Vehicles Charging Demand: A New Zealand Case Study. Electric Power Syst. Res. 167, 171–182. doi:10.1016/j.epsr.2018.10.030

CrossRef Full Text | Google Scholar

Sulaeman, S., Tian, Y., Benidris, M., and Mitra, J. (2017). Quantification of Storage Necessary to Firm up Wind Generation. IEEE Trans. Ind. Applicat. 53 (4), 3228–3236. doi:10.1109/tia.2017.2685362

CrossRef Full Text | Google Scholar

Sun, W., Neumann, F., and Harrison, G. P. (2020). Robust Scheduling of Electric Vehicle Charging in LV Distribution Networks under Uncertainty. IEEE Trans. Ind. Applicat. 56 (5), 5785–5795. doi:10.1109/tia.2020.2983906

CrossRef Full Text | Google Scholar

Tang, D., and Wang, P. (2016). Probabilistic Modeling of Nodal Charging Demand Based on Spatial-Temporal Dynamics of Moving Electric Vehicles. IEEE Trans. Smart Grid 7 (2), 627–636.

Google Scholar

Veldman, E., and Verzijlbergh, R. A. (2015). Distribution Grid Impacts of Smart Electric Vehicle Charging from Different Perspectives. IEEE Trans. Smart Grid 6 (1), 333–342. doi:10.1109/tsg.2014.2355494

CrossRef Full Text | Google Scholar

Xia, Y., Hu, B., Xie, K., Tang, J., and Tai, H.-M. (2019). An EV Charging Demand Model for the Distribution System Using Traffic Property. IEEE Access 7, 28089–28099. doi:10.1109/access.2019.2901857

CrossRef Full Text | Google Scholar

Xiang, Y., Hu, S., Liu, Y., Zhang, X., and Liu, J. (2019). Electric Vehicles in Smart Grid: a Survey on Charging Load Modelling. IET Smart Grid 2, 25–33. doi:10.1049/iet-stg.2018.0053

CrossRef Full Text | Google Scholar

Xiang, Y., Liu, J., Li, R., Li, F., Gu, C., and Tang, S. (2016). Economic Planning of Electric Vehicle Charging Stations Considering Traffic Constraints and Load Profile Templates. Appl. Energ. 178, 647–659. doi:10.1016/j.apenergy.2016.06.021

CrossRef Full Text | Google Scholar

Xiang, Y., Liu, Z., Liu, J., Liu, Y., and Gu, C. (2018). Integrated Traffic-Power Simulation Framework for Electric Vehicle Charging Stations Based on Cellular Automaton. J. Mod. Power Syst. Clean. Energ. 6 (4), 816–820. doi:10.1007/s40565-018-0379-3

CrossRef Full Text | Google Scholar

Xiang, Y., Wang, Y., Su, Y., Sun, W., Huang, Y., and Liu, J. (2020). Reliability Correlated Optimal Planning of Distribution Network with Distributed Generation. Electric Power Syst. Res. 186, 106391. doi:10.1016/j.epsr.2020.106391

CrossRef Full Text | Google Scholar

Xu, N. Z., and Chung, C. Y. (2016). Reliability Evaluation of Distribution Systems Including Vehicle-To-home and Vehicle-To-Grid. IEEE Trans. Power Syst. 31 (1), 759–768. doi:10.1109/tpwrs.2015.2396524

CrossRef Full Text | Google Scholar

Zhang, S., Cheng, H., Wang, D., Zhang, L., Li, F., and Yao, L. (2018). Distributed Generation Planning in Active Distribution Network Considering Demand Side Management and Network Reconfiguration. Appl. Energ. 228, 1921–1936. doi:10.1016/j.apenergy.2018.07.054

CrossRef Full Text | Google Scholar

Glossary

T_Road traveling duration in a trip

W nodes number that a trip includes

Sroad road length

$V_{E_{road}}$ traveling speed

T_park point of parking time

T_start point of traveling starting time

T_stay staying duration in the destination

T_mid midway charging duration

$SO{C}_{T_{park}}$ SOC after arriving at a destination

$SO{C}_{T_{start}}$ initial SOC

$S$ traveling distance

b power consumption per mileage

Cap EV battery capacity

$Powe{r}_{slow}$ slow-charging power

X fuzzy coefficient

Y elastic coefficient

$S^{SO{C}_m}$ traveling distance before reaching SOC threshold

$SO{C}_m$ SOC threshold value

N_L number of distribution system load buses

Power charging power based charging mode selection

E_j load shedding in bus j

P_inj, Q_inj vectors of active and reactive power injections

E, E_Q vectors of corresponding active and reactive load curtailment

P_LD and Q_LD vectors of active and reactive power loads

P_G, Q_G vectors of active and reactive generating power

$\underset{¯}{P_G}$, $\overline{P_G}$ vectors of active power limits

$\underset{¯}{Q_G}$, $\overline{Q_G}$ vectors of reactive power limits

V vector of bus voltage magnitude

$\underset{¯}{V}$, $\overline{V}$ vectors of bus voltage limits

N_c number of simulated cycles

$T_{down\_i_c}^j$ outage period

N_f number of the outage periods

N_Y simulation year

u_j number of users in load bus j

$f_{i_c}^j$ interruption frequency of bus j

$E_{i_c}^j$ load curtailment of node j

$EVloa{d}_{i_c}^j$ EV charging load in bus j

$E{V}_{i_c}^j$ curtailment of EV charging load in node j

${\mu }_j$ repair state

${\lambda }_j$ failure state

N_rand a random number evenly distributed between 0 and 1

$\beta$ variation coefficient