System Design and Application of Supercritical and Transcritical CO2 Power Cycles: A Review

Wang, Enhua; Peng, Ningjian; Zhang, Mengru

doi:10.3389/fenrg.2021.723875

REVIEW article

Front. Energy Res., 10 November 2021

Sec. Process and Energy Systems Engineering

Volume 9 - 2021 | https://doi.org/10.3389/fenrg.2021.723875

System Design and Application of Supercritical and Transcritical CO₂ Power Cycles: A Review

Enhua Wang*

Ningjian Peng

Mengru Zhang

School of Mechanical Engineering, Beijing Institute of Technology, Beijing, China

Improving energy efficiency and reducing carbon emissions are crucial for the technological advancement of power systems. Various carbon dioxide (CO₂) power cycles have been proposed for various applications. For high-temperature heat sources, the CO₂ power system is more efficient than the ultra-supercritical steam Rankine cycle. As a working fluid, CO₂ exhibits environmentally friendly properties. CO₂ can be used as an alternative to organic working fluids in small- and medium-sized power systems for low-grade heat sources. In this paper, the main configurations and performance characteristics of CO₂ power systems are reviewed. Furthermore, recent system improvements of CO₂ power cycles, including supercritical Brayton cycles and transcritical Rankine cycles, are presented. Applications of combined systems and their economic performance are discussed. Finally, the challenges and potential future developments of CO₂ power cycles are discussed. CO₂ power cycles have their advantages in various applications. As working fluids must exhibit environmentally-friendly properties, CO₂ power cycles provide an alternative for power generation, especially for low-grade heat sources.

Introduction

Carbon dioxide (CO₂) was first patented in 1850 as a refrigerant (Bodinus, 1999). In the 1930s and 1940s, with the advent of chlorofluorocarbons (CFCs), CO₂ was gradually replaced. At present, environmental protection is a critical requirement in power system design. Therefore, CO₂, as a natural working fluid, attracts attention again (Kim et al., 2004). In 1969, Angelino studied the feasibility of applying a CO₂ power cycle for nuclear power generation (Angelino, 1968). Recently, many studies have focused on the CO₂ power cycle for high-temperature coal-fired power plants, solar power systems, and low-grade waste heat recovery (Wang et al., 2018b; Lee and Sanchez, 2020).

The average thermal efficiency of standalone CO₂ cycles is approximately 40%. However, if a combined cycle is used, the thermal efficiency may rise to 50–60% (Crespi et al., 2017). The supercritical CO₂ (sCO₂) Brayton cycle has the advantages of high efficiency, compact size, and a moderate operation temperature of 400–750°C. However, the sCO₂ Brayton cycle is still at an early stage of deployment. Liu et al. (Liu et al., 2019) reviewed various sCO₂ cycles in terms of working fluid properties, structural configurations, applications, thermodynamic and thermoeconomic performances, experimental systems, and main component designs, including turbines, compressors, and printed circuit heat exchangers (PCHEs). Stein and Buck (Stein and Buck, 2017) presented several advanced CO₂ power cycles for concentrated solar power (CSP) applications. Wang et al. (Wang et al., 2017) compared six different system layouts with reheating coupled with a molten salt energy storage system. Wu et al. (Wu et al., 2020) analyzed various sCO₂ Brayton cycles for small modular reactors, generation IV reactors, and fusion reactors. White et al. (White et al., 2021) summarized the technical and operational challenges of sCO₂ power cycles, including turbomachinery and heat exchanger design, material selection, and optimal operation and control methods. Kumar and Srinivasan (Kumar and Srinivasan, 2016) reported the advancements in several transcritical CO₂ (tCO₂) cycles for solar power generation.

The aforementioned studies primarily focused on sCO₂ power cycles or a specific application area. However, recent advancements in system design, the technical challenges, and tCO₂ cycles for various applications require further investigation. CO₂ power cycles have many different system configurations for different applications. It is necessary to select the most suitable configuration to maximize the performance of a specific application. This paper summarizes the system configurations and operation characteristics of various CO₂ power cycles. State-of-the-art technical progress of sCO₂ Brayton cycles and tCO₂ Rankine cycles are discussed. Applications in combined power systems and economic performance are also discussed. This study can act as a reference for the system design of novel CO₂ power cycles.

Thermophysical Properties of CO₂

Compared with conventional refrigerants, CO₂ as working fluid has the following advantages:

1) non-toxic, non-corrosive, non-flammable, and will not cause an explosion;

2) rich reserves and cost-effectiveness;

3) moderate critical pressure, and good stability in the application temperature range;

4) good compatibility with other materials and lubricants;

5) high density at the supercritical state, small expander volume, and compact heat exchanger;

6) critical temperature and pressure can adapt to a variety of external heat sources;

7) environmentally friendly properties, zero ozone depletion potential (ODP), global warming potential (GWP) is 1;

8) thermodynamic and transport properties of CO₂ are known, which are conducive to power cycle design;

9) high thermal stability, high-temperature heat exchanger (directly exchange heat with a heat source to reduce heat loss), low system complexity.

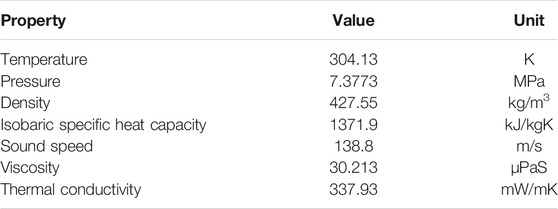
High precision is crucial for the estimation of thermophysical properties. Generally, the Span and Wagner equation of state (EoS) is used, which has an uncertainty of 0.03–0.05% in density, 0.03–1% in the speed of sound, and 0.15–1.5% in heat capacity (Span and Wagner, 1996; Span and Wagner, 2003). Additionally, the EoSs of Kunz and Wagner (Kunz et al., 2007), MBWR, and FEQ (Schmidt-Wagner) (Ely et al., 1987) can be used to calculate the properties of mixtures containing CO₂. Table 1 lists the important thermophysical properties of CO₂ at the critical point. A review of the thermodynamic and transport properties of supercritical CO₂ can be found in Nikolai et al. (Nikolai et al., 2019). Because the thermophysical properties of CO₂ in subcritical and supercritical states differ significantly, the thermodynamic state of a CO₂ power cycle at the pump inlet should be designed accordingly so that it is not too close to the critical point. Figure 1A shows the curves of density, isobaric specific heat capacity, thermal conductivity, and viscosity of CO₂ at a pressure of 9 MPa. These properties fluctuated significantly near the critical point. Figure 1B shows the curves of the isobaric specific heat capacity under different pressures. Near the critical point, the specific heat capacity increased rapidly. In power cycles using pure CO₂ as the working fluid, impurities in CO₂ may affect the performance of the compressor and cooler (Vesely et al., 2019). Therefore, the impurity concentrations should be less than 1%.

TABLE 1

TABLE 1. Thermophysical properties of CO₂ at the critical point.

FIGURE 1

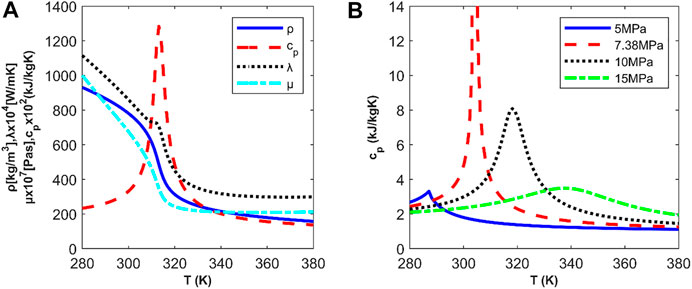
FIGURE 1. Thermophysical properties of CO₂: (A) Pressure is 9 MPa; (B) Isobaric specific heat capacity under different pressures.

The variations in the thermophysical properties significantly affect the heat transfer calculation. It is important to select an appropriate heat transfer correlation based on the working conditions of CO₂. For shell-and-tube heat exchangers, the Krasnoshchekov-Protopopov correlation (Petukhov, 1970) can be used. The heat transfer of single-phase CO₂ in the subcritical state can be estimated using the Petukhov correlation (Petukhov et al., 1961). The convective heat transfer coefficient of the gas-liquid flow can be obtained using the Cavallini-Zecchin correlation (Cavallini and Zecchin, 1974). The pressure drop of CO₂ in the condenser can be determined using the Kedzierski-Goncalves correlation (Kedzierski and Goncalves, 1999). Reznicek et al. (Reznicek et al., 2020) evaluated the predicted error of heat transfer, which was within 5%, and the error in the pressure drop was less than 10%. Recently, PCHEs have been used to exchange heat between supercritical CO₂ and high-temperature heat sources. The convective heat transfer coefficient in a PCHE can be calculated using the Gnielinski correlation (Dostal et al., 2004; Carstens et al., 2006).

CO₂ is not flammable and can be used as a retardant to suppress the flammability of hydrocarbons. Therefore, CO₂ is useful for applications with strict safety requirements. Generally, when the mole fraction of CO₂ in a mixture reaches 30%, the mixture is non-combustible (Drysdale, 1999). Therefore, some power cycles use zeotropic mixtures containing CO₂ and organic fluids to control the flammability while maintaining high efficiency. Mixtures such as CO₂/R161(C₂H₅F), CO₂/R1234ze(CF₃CH=CHF), and CO₂/R134a(CH₂FCF₃) are not sensitive to variations in the CO₂ fraction, while the net power outputs of some mixtures may gradually decrease with an increase in the CO₂ fraction (Sánchez and da Silva, 2018). The CO₂ fraction also affects the heat transfer area. The glide temperature should be constrained within a reasonable range. A high glide temperature may cause separation of the mixture and reduce its thermodynamic performance (Chys et al., 2012).

Configurations of CO₂ Power Cycles

CO₂ power systems are classified as closed supercritical Brayton cycles and transcritical Rankine cycles. Supercritical CO₂ is cooled in the sCO₂ Brayton cycle, while it is condensed to a subcritical state in the tCO₂ Rankine cycle. The performance of the CO₂ power cycle can be improved by pre-cooling, intercooling, reheating, pre-compression, and recompression. Generally, sCO₂ Brayton cycles are divided into single-flow and split-flow configurations. Figure 2 shows the fundamental single-flow layouts, where recuperation, intercooling, reheating, inter-recuperation, pre-compression, and split expansion are employed. The recuperation configuration can effectively utilize the waste heat at the turbine outlet to improve thermal efficiency. Intercooling can reduce the input power of the compressor. Reheating can increase the expansion work of turbines.

FIGURE 2

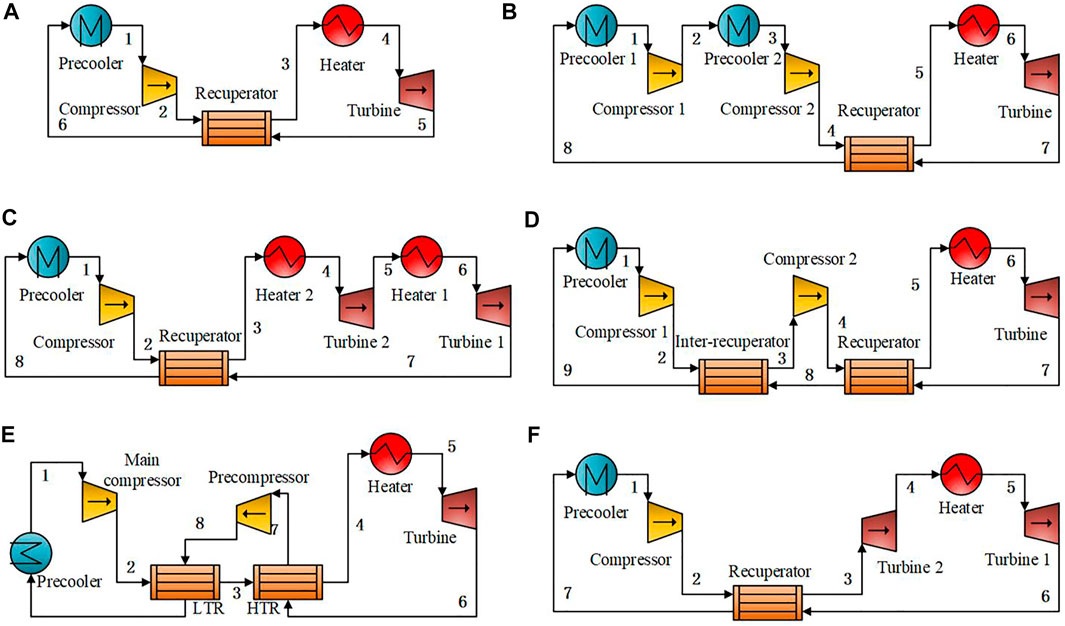
FIGURE 2. Configurations of single-flow sCO₂ Brayton cycles: (A) Recuperation; (B) Intercooling; (C) Reheating; (D) Inter-recuperation; (E) Pre-compression; (F) Split expansion (adapted from (Ahn et al., 2015)).

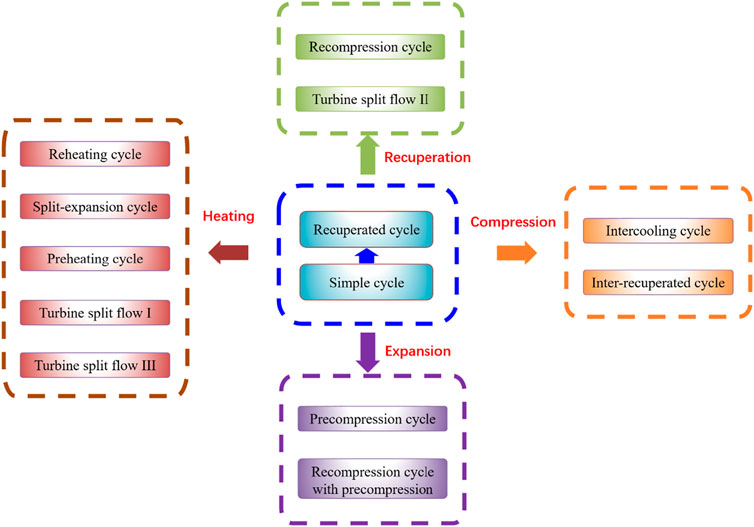
The configurations of split-flow sCO₂ cycles are shown in Figure 3. Recompression, modified recompression with pre-compression, pre-heating, and five different turbine split-flow configurations are displayed. The cooling pressure of the sCO₂ Brayton cycle is greater than 7.38 MPa, leading to a small expansion ratio. However, the temperature at the turbine outlet is still very high. To further improve the utilization efficiency of this part of waste heat, two-stage recuperation and pre-compression can be adopted based on a single-channel configuration or a split-flow configuration with split expansion. For the recompression configuration, a fluid with a low flow rate and high specific heat at the cold side, after the split flow, can exchange heat fully with the fluid with a high flow rate and low specific heat at the hot side inside the low-temperature regenerator. Thus, the pinch-point problem is alleviated, and the system thermal efficiency is improved. For the modified recompression cycle with pre-compression, the working fluid continues to expand to a subcritical state from the turbine outlet to increase the expansion work and then compresses the working fluid to a supercritical state. The working fluid flow is split between the low-temperature recuperator and high-temperature recuperator for the configurations of turbine split flow. Hence, the energy at the outlet of turbine 1 can be comprehensively utilized. For the pre-heating cycle, turbine split flows IV and V, two heaters are installed, which are suitable for applications with two different heat sources.

FIGURE 3

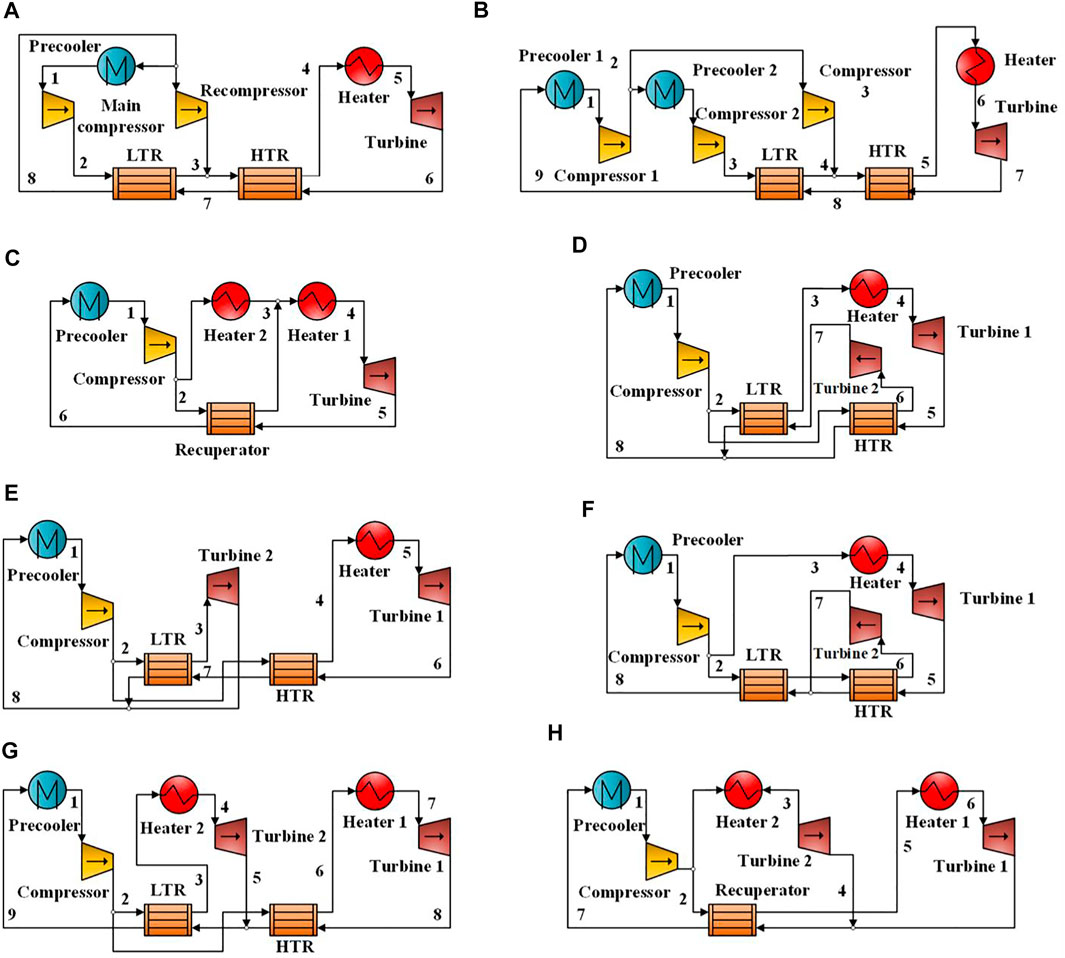
FIGURE 3. Configurations of split-flow sCO₂ Brayton cycles: (A) Recompression; (B) Modified recompression; (C) Pre-heating; (D) Turbine split flow I; (E) Turbine split flow II; (F) Turbine split flow III; (G) Turbine split flow IV; (H) Turbine split flow V (adapted from (Ahn et al., 2015)).

Typical configurations of single-flow and split-flow sCO₂ cycles were analyzed in Ahn et al. (Ahn et al., 2015). For a high-temperature heat source with a large specific heat capacity, the recompression cycle exhibited high thermal efficiency. Based on a heat source of 545°C from a sodium-cooled fast reactor, the performances of these configurations were compared, and the thermal efficiency of the recompression cycle was the highest at 43.83%. For CSP applications, the recompression sCO₂ cycle also exhibited high performance. However, for a heat source with a small heat capacity, the recompression cycle is not the best option. For exhaust heat recovery from a gas turbine, an investigation indicated that the performance of the pre-heating cycle was better than that of the single-stage recuperated cycle and the recompression cycle (Ayub et al., 2018). Even when the recompression cycle was used, the pinch-point problem persisted because of the large temperature variation of the exhaust gas and the small temperature variation of CO₂ in the heater. Therefore, it is important to match the heat sources. When a split expansion is introduced, a part of the working fluid flows into the high-pressure expander (Huang et al., 2016). Manente et al. (Manente and Costa, 2020) investigated three configurations of the sCO₂ Brayton cycle, including the turbine flow I, turbine flow II, and the pre-heating cycle. The overall heat recovery efficiency of the turbine flow II cycle reached 22.3% for a heat source of 600°C. The split expansion configuration with reheating and intercooling is also helpful for improving the performance (Cho et al., 2015; Kim et al., 2016).

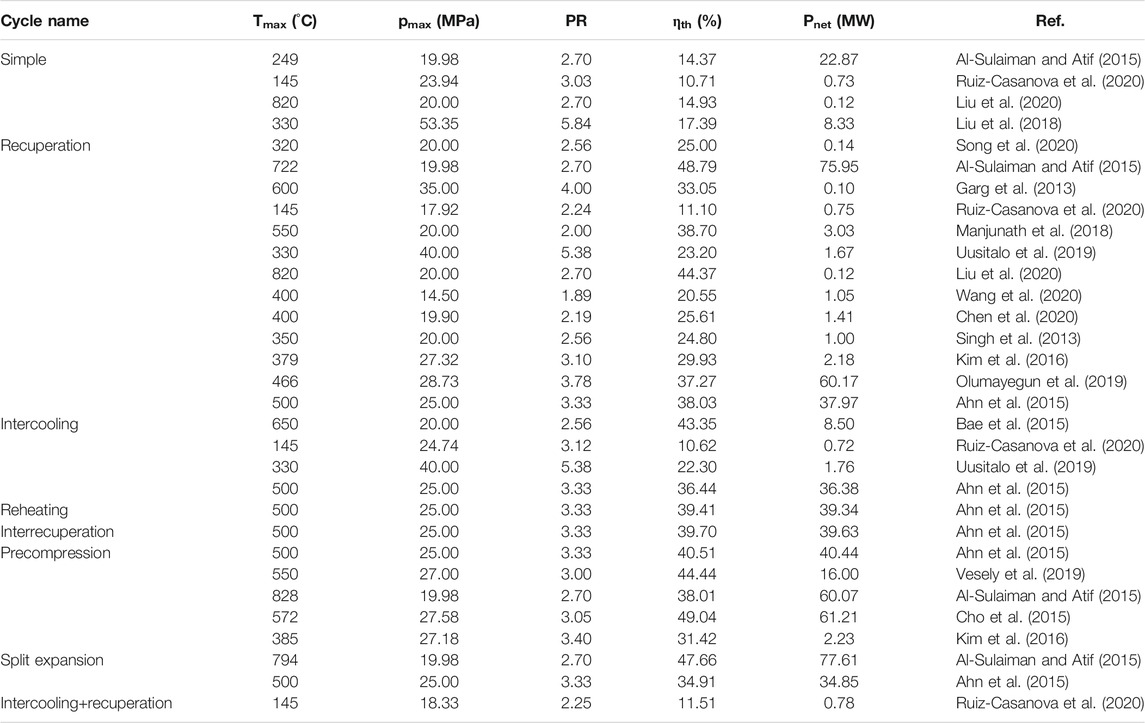
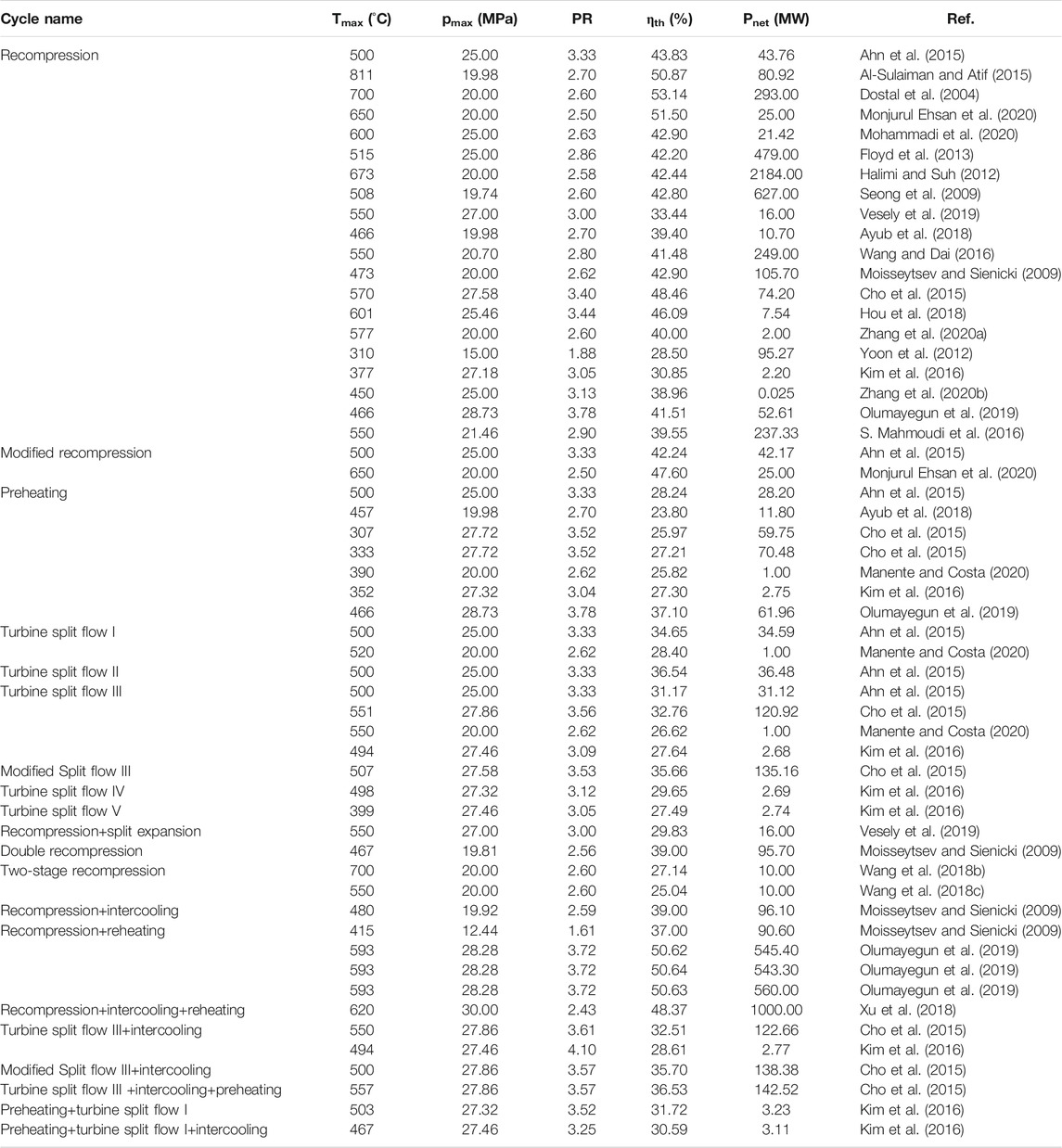
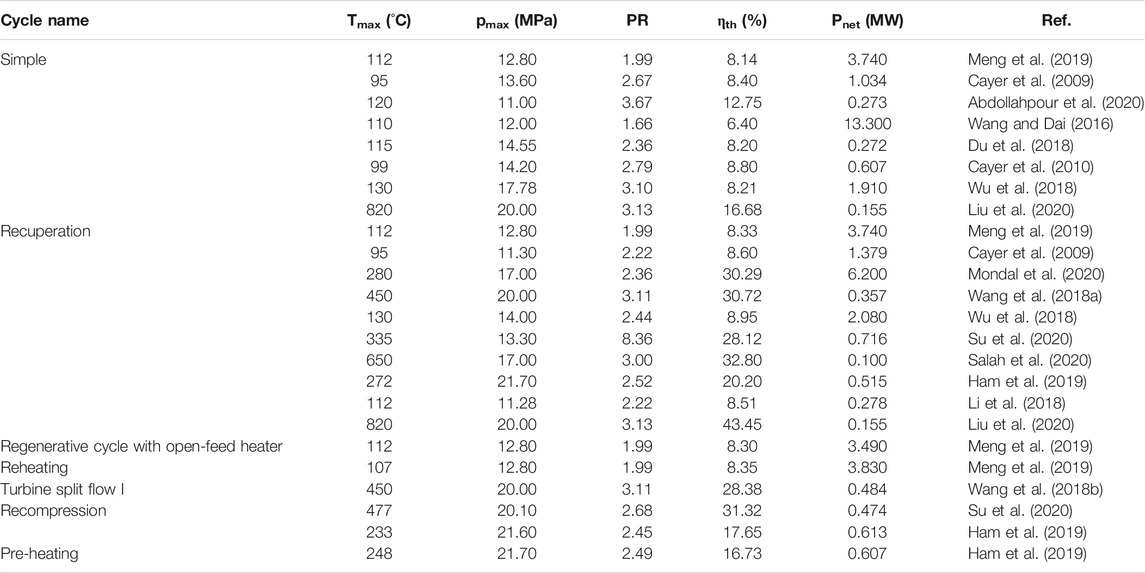
The boundary conditions reported in existing literature for single-flow layouts, including the maximum temperature and pressure, expansion pressure ratio, thermal efficiency, and net power, are listed in Table 2. Figure 4 provides a more intuitive comparison. The diameter of each circle is proportional to the thermal efficiency or net power. The maximum pressure at the turbine inlet was less than 30 MPa, while a maximum pressure of 53.35 MPa was used for theoretical analysis. The maximum temperature was 828°C. Generally, the thermal efficiency improves as the maximum temperature of sCO₂ increases. The simple sCO₂ cycle has a relatively lower thermal efficiency than the other layouts and is comparable only when the maximum temperature is small. The boundary conditions for the split-flow layouts are presented in Table 3 and Figure 5. The maximum temperature was primarily in the range of 450–650°C, and the maximum pressure was between 20 and 25 MPa. The architectures of these split-flow cycles are complicated and more suitable for large power devices with MW- or even GW-class power output. The results for the thermal efficiency of the recompression cycle cover the range of the other layouts, indicating that the split-flow layouts are well suited for high-temperature applications with a single heat source.

TABLE 2

TABLE 2. Boundary conditions of sCO₂ cycles with single-flow layouts.

FIGURE 4

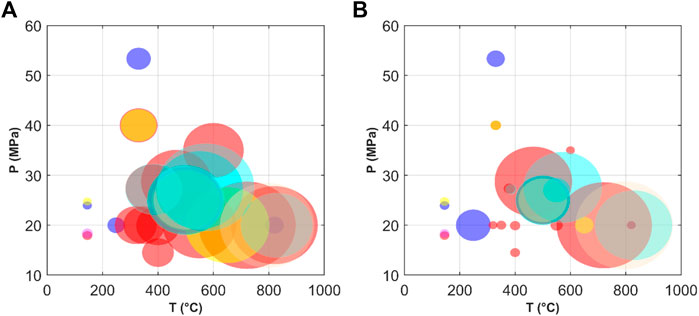
FIGURE 4. Boundary conditions of single-flow sCO₂ cycles as a function of the maximum operation temperature and pressure: (A) Thermal efficiency; (B) Net power output (legend: www.frontiersin.org simple recuperation intercooling reheating inter-recuperation pre-compression split expansion intercooling+recuperation).

TABLE 3

TABLE 3. Boundary conditions of sCO₂ cycles with split-flow layouts.

FIGURE 5

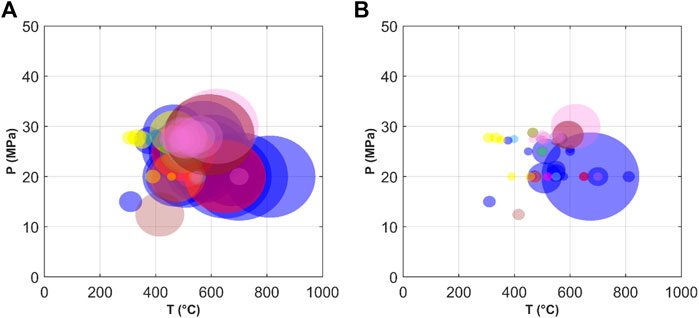
FIGURE 5. Boundary conditions of split-flow sCO₂ cycles as a function of the maximum operation temperature and pressure: (A) Thermal efficiency; (B) Net power output (legend: www.frontiersin.org recompression modified recompression pre-heating turbine split flow I turbine split flow II turbine split flow III turbine split flow IV turbine split flow V combined cycle).

Typical sCO₂ cycles are compared in Tables 4, 5. There are four ways to improve the system performance, as shown in Figure 6. The recuperated cycle is a basic improvement of the simple configuration. The recompression cycle and the turbine split flow II are designed to improve the regeneration effect. If the compression process is considered, the intercooling cycle and the inter-recuperated cycle are optimum improvements. The expansion process can be enhanced via the pre-compression cycle or the recompression cycle with pre-compression. If the heating process is considered, the other five configurations can be employed to improve heat transfer. There is no single configuration that is well suited for all applications. During the system design process, specific operation situations, temperatures of the heat source and sink, system size, and cost should be considered. A comparison of different configurations must be performed, and the most appropriate configuration should be chosen.

TABLE 4

TABLE 4. Comparison of single-flow sCO₂ cycles.

TABLE 5

TABLE 5. Comparison of split-flow sCO₂ cycles.

FIGURE 6

FIGURE 6. Improvement paths for sCO₂ Brayton cycles.

In the tCO₂ Rankine cycle, CO₂ is condensed through a heat sink. Generally, the tCO₂ Rankine cycle is used when the ambient temperature is lower than the critical temperature of CO₂. The thermal efficiency of a tCO₂ Rankine cycle can approach or even exceed that of a traditional Rankine cycle as the turbine inlet temperature increases. Furthermore, the structure of the CO₂ Rankine cycle is simpler and more compact. For low-temperature heat sources, the system configurations of the tCO₂ cycle are relatively simple. The boundary conditions reported in the existing literature for tCO₂ cycles are listed in Table 6, and are also plotted in Figure 7. The maximum temperature for the simple tCO₂ cycle was less than 130°C. However, the temperature range for the recuperation cycle covered a large interval of up to 820°C. Accordingly, the thermal efficiency of the recuperation layout was much higher in the high operation temperature regions. The efficiency of the other cycles showed no evident advantages over the recuperation cycle. At present, most studies on tCO₂ cycles are mainly focused on small power devices with a power output of 200–600 kW. The characteristics of the four configurations (Meng et al., 2019) are compared in Table 7. For the simple configuration and the regenerative cycle with an open-feed heater, the thermal efficiencies increased significantly with an increase in the inlet temperature of the expander and for a large inlet pressure of the expander. For the reheating cycle, the inlet temperature of the expander had a negligible effect on the thermal efficiency. For the regenerative cycle, the allowable range of the expander inlet pressure was relatively narrow when the inlet temperature of the expander was low.

TABLE 6

TABLE 6. Boundary conditions of tCO₂ cycles.

FIGURE 7

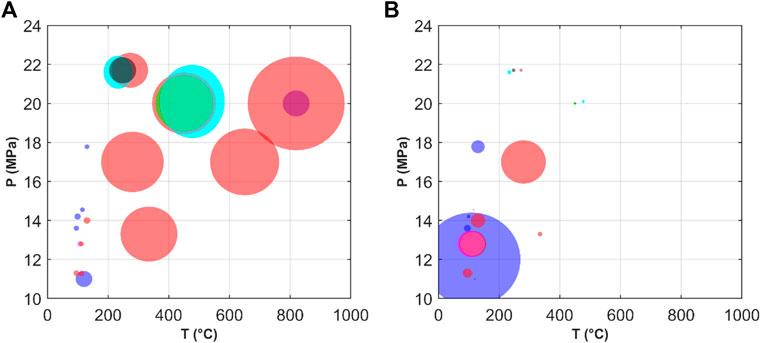
FIGURE 7. Boundary conditions of tCO₂ cycles as a function of the maximum operation temperature and pressure: (A) Thermal efficiency; (B) Net power output (legend: www.frontiersin.org simple, recuperation, regenerative cycle with open-feed heater reheating turbine split flow I recompression pre-heating).

TABLE 7

TABLE 7. Comparison of tCO₂ Rankine cycles for low-temperature sources.

Performance Characteristics of CO₂ Power Cycles

The temperature and pressure of supercritical CO₂ at the inlet of the high-pressure turbine are the two key parameters affecting the system performance. With an increase in the turbine inlet temperature, the system efficiency gradually increases, especially when the turbine inlet temperature is low (Chen et al., 2005). However, the maximum temperature at the turbine inlet is limited by the heat source temperature. Furthermore, the condensation temperatures and efficiencies of the turbine and pump have significant influences. For a simple CO₂ power cycle, the system efficiency increases proportionally with improvements in the turbine efficiency. The variations in the pump efficiency also have a significant effect owing to the large mass flow rate of CO₂. As the expansion ratio increases, the system efficiency first increases and then decreases. This is because the pump consumes more power if the expansion ratio is too large. Therefore, the optimal expansion ratio should be determined. Additionally, not only the thermodynamic performance but also other indexes such as system volume, cost, economy, safety, toxicity, and durability must be evaluated. Multi-objective optimization methods should be used to optimize the working parameters of the CO₂ power cycle. There is no single set of working parameters that can optimize all indexes simultaneously (Cayer et al., 2010). As the inlet temperature of the compressor increases, the power consumption of the compressor increases and the thermal efficiency of the sCO₂ cycle decreases gradually. Thus, the inlet temperature of the compressor should be close to the critical temperature. However, small variations in the working pressure and temperature can cause apparent changes in the thermal and physical properties of CO₂. The power consumption fluctuates abruptly around the critical point. Therefore, the temperature at the compressor inlet should not be too close to the critical point (Liu et al., 2020).

CO₂ turbines have some advantages, such as smaller size, less leakage, and shock loss. The turbine size of a sCO₂ cycle is significantly smaller than that of a subcritical organic Rankine cycle (ORC). On the other hand, operating conditions for higher speed and greater pressure require a higher mechanical strength of the turbo-generator, especially for the bearing and seal design. The choice of working fluid also affects the geometric parameters of the turbine (Uusitalo et al., 2019). For the turbine, the Stodola elliptic formula (Cooke, 1984) is normally adopted. A one-dimensional mean-line model is used to provide a more accurate estimation of turbine efficiency (Modi et al., 2015; Peng et al., 2020). Three different mean-line models were compared for a CO₂ turbine (Lee and Gurgenci, 2020). The total turbine loss based on the Aunger model (Aungier, 2006) was almost the same as the Moustapha model (Moustapha et al., 2003). However, a higher loss was observed in the Whitfield-Baines model (Whitfield and Baines, 1990) because of the large flow rate inside the rotor.

Air cooling is not suitable for steam Rankine cycles. However, air cooling has some advantages in sCO₂ power cycles, such as a smoother temperature match profile, lower exergy loss, smaller corrosion and scale deposition, and sediment accumulation. For CSP systems, the sCO₂ cycle using air cooling can save a large amount of water, which is critical in inland regions. When the ambient temperature is high, hybrid cooling combing air and water is another option that can reduce performance degradation (Ehsan et al., 2020).

Applications of sCO₂ Cycles

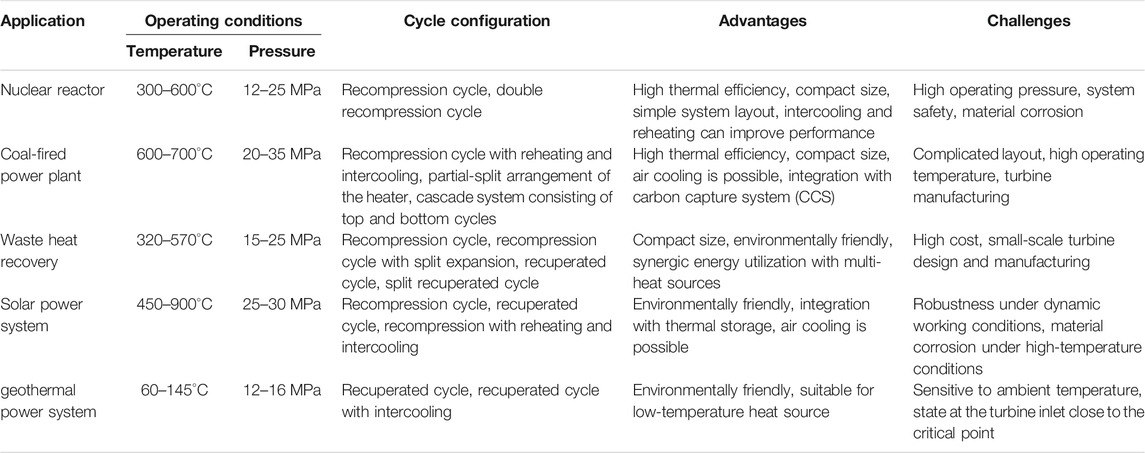
In this section, recent progress in sCO₂ cycles in nuclear and coal-fired power plants, waste heat recovery, concentrated solar systems, and geothermal power devices are presented.

Nuclear Reactor

The recuperated sCO₂ cycle is often used in high-temperature gas-cooled reactors, which have high thermal efficiency, relatively low turbine inlet temperature, compact size, and simple layout (Yoon et al., 2012; Bae et al., 2015). However, the heat transfer rate in the recuperator is limited by the pinch point (Utamura, 2010). In the last two decades, MIT carried out many investigations on sCO₂ power cycles for nuclear reactors and obtained some significant results. To improve the performance, a recompression cycle has been proposed, and the split-flow arrangement can effectively alleviate this issue. Based on a 600 MW reactor, Dostal et al. (Dostal et al., 2004) analyzed the performance of a recompression sCO₂ cycle. The turbine efficiency is not sensitive to variations in the working pressure and temperature because of the large and almost invariant mass flow rate in this cycle (Zhang et al., 2020a). However, the real gas effect of supercritical CO₂ should be considered when designing CO₂ turbines (Lee et al., 2012).

The recompression sCO₂ cycle can be applied to a fourth-generation sodium-cooled fast reactor. Thus, the risk of a chemical reaction between Na and water in the conventional steam Rankine cycle is avoided. KAERI designed a recompression sCO₂ cycle based on the KALIMER 600 system. The rated power was 600 MW. Two centrifugal compressors and a four-stage axial turbine were designed. The estimated thermal efficiency was 42.8% (Seong et al., 2009). The recompression sCO₂ cycle is also promising for fusion reactors. The estimated thermal efficiency was 42.44%, as reported by Halimi and Suh (Halimi and Suh, 2012). In the recompression cycle, the flow-split ratio is an important parameter. As the flow-split ratio declines, the cycle efficiency increases. However, the heat transfer area of the low-temperature recuperator also increases. Therefore, the flow-split ratio should be selected based on a trade-off between these two factors (Cha et al., 2009). Although the recompression cycle has a higher efficiency than other configurations, investigations indicate that further improvement of the recompression cycle is difficult (Moisseytsev and Sienicki, 2009).

Supercritical CO₂ in a nuclear reactor exhibits very high pressure, which is not conducive to the safety of commercial plants. The working pressure of current nuclear reactors is below 15 MPa although it can be as high as 25 MPa. The maximum working pressure can be decreased by combining the split expansion cycle with the recompression cycle while maintaining a high efficiency level. An investigation showed that the thermal efficiency of the system decreased slightly from 43.88 to 43.11% with a small increase in the heat transfer area, when the inlet temperature of the high-pressure turbine was reduced to 390°C, and the inlet pressure decreased from 20 to 15 MPa (Guo et al., 2018).

For the recompression cycle, the temperature at the inlet of the main compressor is higher than that of the recompressor. If the compressors maintain a constant speed, the split ratio declines as the ambient temperature increases, leading to an apparent decrease in performance. Thus, a proper control strategy is required to maintain high performance under off-design conditions (Floyd et al., 2013). However, the thermophysical properties of supercritical CO₂ vary greatly around the critical point, making it difficult to maintain control precision. Generally, control strategies such as constant flow rate and constant reactor outlet temperature are adopted. However, the reactor outlet temperature is low under small-load conditions if a constant flow rate strategy is employed. Furthermore, the system parameters fluctuate greatly, and the transient response time is long when a constant reactor outlet temperature is maintained. An optimal control strategy based on the operating parameters of the compressor was designed by Du et al. (Du et al., 2020a), and the response time of the system was shortened.

Coal-fired Power Plant

The steam Rankine cycle is a popular technology used in coal-fired power plants. To improve energy efficiency, an ultra-supercritical steam Rankine cycle with two-stage reheating is under development. However, owing to the limitations of the material and other technical constraints, the efficiency improvement of the ultra-supercritical steam Rankine cycle has stagnated. Investigations suggest that the sCO₂ Brayton cycle is a feasible alternative technology. Recently, the application of sCO₂ cycles to coal-fired power plants has attracted significant attention. Li et al. reviewed various applications of sCO₂ cycles for pulverized coal power plants, circulating fluidized bed devices, and oxy-coal power systems (Li et al., 2020).

The working temperature of the sCO₂ cycle for a coal-fired power plant can be as high as 900°C; the recompression cycle is ideal for this. Reheating is also a useful approach in this regard. Zhou et al. (Zhou et al., 2018) analyzed the performance of a recompression cycle with reheating and two-stage intercooling. Compared with the original 1000 MW single-stage reheating ultra-supercritical steam Rankine cycle (605°C/603°C/274 bar), the optimized thermal and exergy efficiencies of the sCO₂ cycle reached 47.64 and 81.25%, respectively. However, the flow rate of CO₂ increased significantly, resulting in an excessive pressure drop in the heat exchange process in the boiler, which made it difficult to fully utilize the flue gas energy. Xu et al. designed a partial-split strategy to halve the flow rate and length of the heat exchangers in the boiler (Xu et al., 2018). As a result, the overall pressure drop was reduced to 1/8. Furthermore, the exhaust temperature of the flue gas was reduced to below 120°C by diverting part of the working fluid after intercooling to recover the waste heat of the flue gas. Based on this strategy, a 1000 MW sCO₂ power generation system was proposed (Sun et al., 2018). A cascade system was designed to comprehensively utilize the waste heat of flue gas in a large temperature range of 120–1500°C. The top cycle was a recompression sCO₂ cycle with two-stage reheating, whereas the bottom cycle was a conventional recompression cycle. The heat addition of the bottom cycle can be regulated by adjusting the flow distribution between the top and bottom cycles. When the maximum working temperature was set to 620°C with a maximum pressure of 30 MPa, the cycle thermal efficiency and power generation efficiency reached 51.22% and 48.37%, respectively. In addition, Zhao found that the most energetic, promising Brayton cycle, among 1000 alternatives, was a double reheating-double recompression-reheating layout, which had a cycle efficiency of up to 51.4% (Zhao, 2018).

Coal-fired power plants are the main source of CO₂ emissions. Integration with carbon capture and storage devices is useful for alleviating the greenhouse gas effect. A two-stage cascade sCO₂ cycle with a carbon capture unit was evaluated by Olumayegun et al. (Olumayegun et al., 2019). The top cycle was a recompression configuration with one-stage reheating, and the bottom one was a recompression cycle. The carbon capture unit was a CO₂ capture system based on monoethanolamine solvent. CO₂ was absorbed by the adsorption tower and then dissociated in the separation column. The system thermal efficiency was 3.34–3.86%, higher than that of the traditional steam power cycle. After using the carbon capture unit, the thermal efficiency decreased by 11.2% but was still 0.68–1.31% higher than that of the traditional steam power cycle with carbon capture.

Waste Heat Recovery

A CO₂ cycle can be used as the bottom cycle to recover the exhaust heat of a heat engine, such as a gas turbine or internal combustion engine, and the overall energy efficiency can be improved. Hou et al. (Hou et al., 2018) designed a combined cycle consisting of a gas turbine, a recompression sCO₂ cycle, a steam Rankine cycle, and an ORC with a zeotropic working fluid. Compared with the traditional gas-steam combined system, the efficiency of the new combined system was increased by 2.33%. In marine applications, the combined power cycle can be coupled with the refrigeration cycle, and the energy efficiency of the entire system can be enhanced further. A CO₂ power system was integrated with a compression refrigeration cycle using CO₂ as the working fluid (Manjunath et al., 2018). The exhaust heat of the gas turbine was used to drive the regenerative sCO₂ cycle. The precooler of the sCO₂ cycle was integrated with the cooler of the compression refrigeration cycle. The output power of the combined system increased by 18%.

Two typical heat sources exist in an internal combustion engine, that is, exhaust gas and coolant. Novel sCO₂ cycles were designed to recover the different types of waste heat. Figure 8 shows the modified recompression sCO₂ cycle. Two heat exchangers were installed to recover the waste heat of the exhaust gas in series. The cycle efficiency increased as the inlet temperature of the high-pressure turbine increased, although the net power output decreased. Under the design conditions, the waste heat recovery efficiency was 17.86% greater than that of the recompression cycle, and the optimized heat recovery efficiency reached 74.83% (Zhang et al., 2020b). To recover the exhaust and cooling simultaneously, Song et al. designed a sCO₂ cycle with two-stage regeneration, and the maximum output power of the engine was increased by 6.9% (Song et al., 2018). The cooling water from the jacket was used to preheat the CO₂, and the exhaust gas was used to preheat and evaporate CO₂. To enhance energy efficiency, a split channel was used to reduce the CO₂ temperature at the outlet of the low-temperature preheater.

FIGURE 8

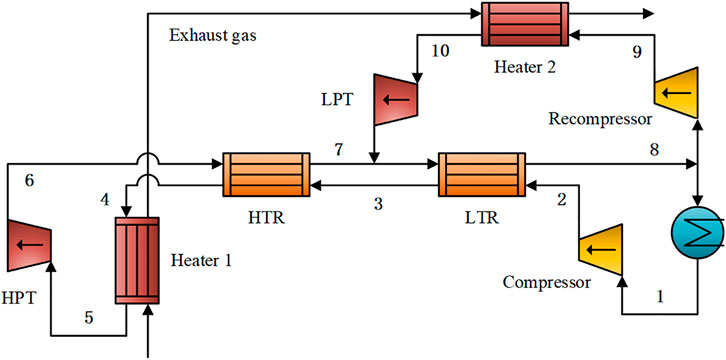
FIGURE 8. A modified recompression sCO₂ cycle for engine waste heat recovery (adapted from (Zhang et al., 2020b)).

Concentrated Solor Power System

The performance of sCO₂ cycles has been investigated for high-temperature solar thermal power systems. The thermal efficiency was approximately 32% with a source temperature of 600°C and a compressor inlet pressure of 85 bar (Garg et al., 2013). Al-Sulaiman and Atif (Al-Sulaiman and Atif, 2015) evaluated five different configurations of sCO₂ cycles for a solar power plant with a heliostat field. The highest thermal efficiency was obtained by the recompression cycle with an integrated system efficiency of 40%. The regenerative cycle also showed a comparable performance. Singh et al. (Singh et al., 2013) analyzed the dynamic performance of a direct-heated regenerative sCO₂ cycle for large-scale solar power generation. In summer, the compressor inlet pressure increases owing to the abundant solar radiation, leading to a decrease in the net power output. In winter, CO₂ might change to a subcritical state at the outlet of the cooler owing to low ambient temperature. Active control is required to ensure optimal operation of the system during all seasons.

Solar radiation varies significantly at different times of the day. A heat storage device was installed to alleviate the influence of temperature fluctuations. Wang et al. (Wang et al., 2018c) studied a CSP system with heat storage. The recompression sCO₂ cycle was integrated with reheating and intercooling. The solar circuit was coupled with the sCO₂ cycle via a heat storage device. A salt mixture (8.1 wt% NaCl + 31.3 wt% KCl + 60.6 wt% ZnCl₂) was used in the heat storage device to balance the energy fluctuations of the heat addition process. Based on the radiation data of a typical sunny day in western China, the total photoelectric efficiency could reach 19.17–22.03%, which was higher than that of traditional tower solar systems.

When the power output fluctuates frequently, the performances of the turbine and compressor degrade significantly and may even cause the failure of the control strategy. For every 1% reduction in the turbine efficiency, the system efficiency and relative power output could be decreased by 0.431 and 1.713%, respectively (Son et al., 2020). Therefore, to improve the robustness of the sCO₂ cycle, the variations in the efficiencies of the turbine and compressor should be fully evaluated during the system design stage, rather than assuming a constant efficiency (Wang et al., 2020). The turbine power output of a commercial sCO₂ system may be greater than 10 MW (Sienicki et al., 2011). For a large-scale system, a multi-stage axial-flow turbine can be used with high efficiency. Because of the variability of solar radiation, the operation characteristics of the CSP system under transient processes need to be verified to ensure that the entire system can operate continuously. An indirect sCO₂ system with a heat storage device is more suitable and can maintain a stable system power output.

A radial turbine can be used in a sCO₂ cycle owing to its low expansion ratio. El Samad et al. (El Samad et al., 2020) designed a single-stage radial turbine for a 100 MW sCO₂ cycle. A total pressure of 29.7 MPa and a temperature of 1173 K were specified at the turbine inlet. The expansion ratio was 4.95, with a mass flow rate of 354.2 kg/s. The total-to-static efficiency exceeded 83%. For CO₂ turbines, the bearing is an important part. Du et al. (Du et al., 2020b) designed an effective dry gas sealing structure. Compared with the conventional shroud or labyrinth design, the leakage loss was reduced, and the aerodynamic performance was improved. A special hybrid hydrostatically assisted hydrodynamic gas foil bearing is also a good option. However, the upper limit of the allowable temperature with a coating is 650°C, which limits its applicability. Another option is the rare-earth element magnetic bearing.

Large-scale high-temperature solar thermal power systems are generally built in desert areas where solar radiation is abundant and air cooling is required (Monjurul Ehsan et al., 2020). Air cooling is feasible for sCO₂ cycles in CSP applications. A good temperature match inside the cooler is realized, and the exergy loss is reduced. A comparison between the steam Rankine cycle and the sCO₂ cycle for power generation from solar energy indicated that the net thermal efficiency of the sCO₂ cycle was 32.9%, while it was 28.2% for the steam Rankine cycle (Shrivastava and Prabu, 2016).

Geothermal Power Generation

Geothermal sources have a much lower temperature than nuclear reactors and coal-fired power plants. Generally, the tCO₂ Rankine cycle is more suitable for low-grade energies. A relatively low condensation temperature is required to ensure the operation of a tCO₂ power system. However, it may be difficult to condense CO₂ if the ambient temperature is high. Few investigations have evaluated the feasibility of the sCO₂ cycle for the utilization of geothermal energy. Ruiz-Casanova et al. (Ruiz-Casanova et al., 2020) compared four different configurations and reported that intercooling could reduce the mass flow of CO₂ and thus decline the compression work. Regeneration slightly increased the mass flow rate of CO₂, resulting in an increase in the power output. Among the four configurations, the performance of the regenerative sCO₂ cycle with intercooling was the best, with optimal thermal and exergy efficiencies of 11.51% and 52.49%, respectively.

For high-temperature applications, special attention should be paid to the corrosivity of CO₂ and impurities in the system materials. Some materials can form a protective oxide film on the surface, such as chromium oxide and alumina, and have good compatibility with CO₂. Haynes 230 (Haynes International, 2007) or 617 alloy (Li et al., 2008) can be used for high thermal fatigue resistance.

Several MW-level CO₂ experimental systems, which concentrated on simple and recuperated configurations, have been built. More experimental systems need to be developed to validate the theoretical results. Furthermore, during the development of experimental system, technical issues can be discovered, and expertise can be gained aiding future engineering development.

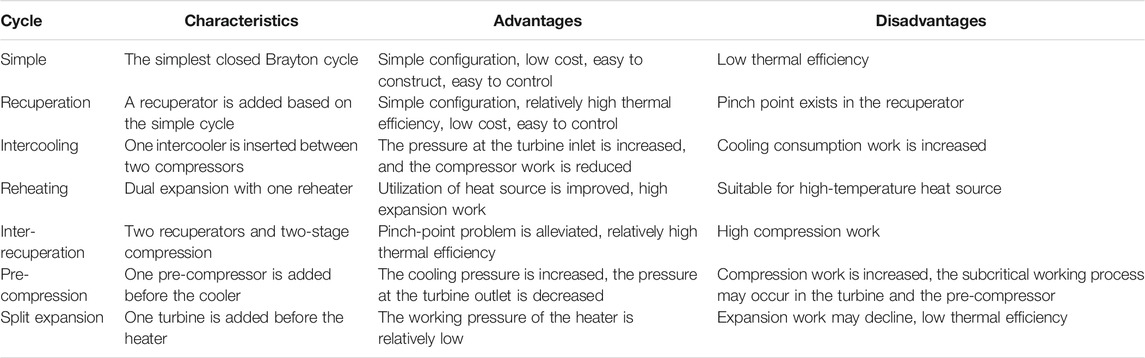
Compared with the conventional steam Rankine cycle, the sCO₂ cycle has low critical pressure, high density, high heat transfer rate, high specific power, and small size (Feng and Wang, 2019), thereby making it suitable for various heat sources. In this section, recent advancements in the sCO₂ cycle in the applications of nuclear reactors, coal-fired power plants, waste heat recovery, CSP systems, and geothermal power plants are presented. Table 8 shows the operating conditions of the sCO₂ cycles for these applications, and the corresponding advantages and disadvantages are listed.

TABLE 8

TABLE 8. Characteristics of sCO₂ cycles for different applications.

Applications of tCO₂ Rankine Cycles

A tCO₂ cycle is suitable for low-grade energy utilization if the ambient temperature is lower than 30°C, such as in low-temperature geothermal and solar power generation. Compared with an ORC, a tCO₂ cycle takes advantage of its environmentally friendly properties and compact size. The configurations of the tCO₂ cycle for low-temperature heat sources are limited, with most focusing on the simple or recuperated cycle. Compared with the working fluids of ethane, toluene, siloxane D₄, and water, the exergy efficiency of a simple or regenerative tCO₂ cycle is greater, and the system size is smaller; however, the thermal efficiency is lower (Cardemil and da Silva, 2016). The recuperated tCO₂ cycle can improve the thermal efficiency and net power output and reduce the maximum pressure of the system in comparison to the simple tCO₂ cycle (Wu et al., 2018). Additionally, the performance degradation of the recuperated cycle under off-design conditions is lower.

Water cooling is favorable for most applications. The temperature of the geothermal water at the evaporator outlet is generally constrained to over 70°C to prevent the precipitation of silica from geothermal water. Owing to this constraint, the CO₂ flow rate decreases gradually with the reduction in cooling water temperature, and the net power output increases at first and then decreases. There is an optimal cooling water temperature that maximizes the net power output. Air cooling is also feasible in cold climate regions. If the cooling water temperature is too high, it is impossible to condense the subcritical CO₂. Pan et al. (Pan et al., 2020) proposed a self-condensing tCO₂ cycle. In the proposed cycle, CO₂ is cooled to a saturated vapor state by cooling water and then expanded to a subcritical two-phase state through an expansion valve. Subsequently, they are separated. The system can operate steadily at a cooling water temperature as high as 30°C. Furthermore, a tCO₂ cycle can be integrated with liquefied natural gas (LNG) gasification equipment, where LNG is used as the heat sink of the tCO₂ cycle, and the overall system efficiency can be improved significantly (Abdollahpour et al., 2020). Another feasible method is to use a mixture containing CO₂ and a small amount of another fluid with a high boiling point, such as C₆F₆ (Lasala et al., 2015), C₆F₁₄ (Lasala et al., 2014), or TiCl₄ (Bonalumi et al., 2020). The condensation temperature is greater than the critical temperature of pure CO₂. Such a system has a high potential for CSP applications in hot regions.

At present, Echogen provides commercial products of tCO₂ power cycle: EPS100, EPS35, and EPS30 (Ecogen Inc (2021). Ecogen, 2021), with a net power output of 8, 1.8, and 1.5 MW, respectively. A recuperated configuration with air cooling is employed. These systems are designed for waste heat recovery with a supply temperature of 500–532°C. Compared with the conventional steam Rankine cycle, the tCO₂ system has a smaller size and lower cost of electricity. The small-scale tCO₂ cycle is still in the development stage. Ge et al. (Ge et al., 2018) developed a 5 kW experimental recuperated tCO₂ cycle. A single-stage axial-flow turbine with a reactivity of 0.5, and an expansion ratio of 1.5 was used. A radial turbine is more suitable for a small-scale tCO₂ cycle than an axial turbine. When the system operates under dynamic conditions, a suitable control strategy is required to adjust the operation parameters. Generally, the optimal pressure control method with an adjustable nozzle blade is slightly better than the conventional pressure sliding method with a fixed nozzle (Du et al., 2018).

There are some disadvantages to tCO₂ cycles, including high operating pressure, difficult condensation, and low thermal efficiency. To overcome these disadvantages, a binary mixture consisting of CO₂ and an organic working fluid can be used (Shu et al., 2018). The organic working fluid has a higher critical temperature than the CO₂. Thus, zeotropic mixtures containing CO₂ can alleviate the condensation problem of the tCO₂ cycle (Xia et al., 2020). However, the total heat transfer area of the system increases owing to the increase in the size of the condenser.

Combined Power Cycle

The CO₂ power cycle is generally used alone, but it can also be combined with other cycles. Figure 9 shows the possible ways of forming a combined power system based on a sCO₂ cycle. According to the principle of synthetically cascaded utilization of energy, a combined power cycle can improve the overall energy efficiency.

FIGURE 9

FIGURE 9. Possible approaches for the combined system based on sCO₂ cycles.

A combined power system can be used for a single heat source. For example, a CO₂ power cycle is cascaded with a bottoming ORC. Mondal et al. (Mondal et al., 2020) designed a combined system consisting of a tCO₂ cycle and an ORC for the waste heat recovery of a marine engine. The operating pressure of the tCO₂ cycle decreased, which was conducive for leakage reduction and system reliability. The results showed that it could save 8–9.5% of fuel per year. Such a combined cycle was used for waste heat recovery of a gas turbine, and the overall thermal efficiency and levelized cost of electricity reached 52.1% and 52.8 $/MWh, respectively (Mohammadi et al., 2020). Compared with the standalone CO₂ power cycle, the combined system had a higher heat recovery potential and better thermoeconomic performance. For high-temperature heat sources, a sCO₂ cycle can be integrated with a tCO₂ cycle. Su et al. (Su et al., 2020) designed such a sCO₂-tCO₂ combined system for the waste heat recovery of a gas turbine. The heat sink was an LNG. The thermal and exergy efficiencies of the combined system were 52.94% and 30.27% at the design point. When a simple tCO₂ cycle is employed as the bottom cycle, the expansion ratio of the turbine is lower than that of an ORC cycle, leading to better off-design performance (Wang and Dai, 2016). Additionally, a combined system integrating a sCO₂ cycle with the Kalina cycle is also feasible. The sCO₂ cycle is used as the top cycle. The heat rejection of the precooler in the sCO₂ cycle can be transmitted to the Kalina cycle. The results showed that the exergy efficiency of the combined system could be improved by 10% (S. Mahmoudi et al., 2016).

Various types of heat sources may exist in industrial processes. A CO₂ power cycle can be cascaded with an ORC or a conventional steam Rankine cycle to fully utilize these different energies. For example, a combined system of the sCO₂ cycle and ORC can be designed to reclaim waste heat from engine exhaust and coolant. The topping sCO₂ cycle is used to recover the waste heat of the exhaust gas, and the bottoming ORC is used to absorb the heat rejection of the sCO₂ cycle, waste heat of the engine coolant, and residual heat of the exhaust gas. The maximum net power output and minimum specific investment cost of the combined system were 58% and 4% higher than those of the single sCO₂ power cycle (Song et al., 2020). Combined systems have broad potential for engine waste heat recovery and other similar industrial applications.

A CO₂ power cycle can be integrated with other power systems in parallel to form a complex synthetic energy system. For example, a sCO₂ cycle was designed for a waste incineration power plant by Hao et al. (Chen et al., 2020). The sCO₂ cycle was operated together with a coal-fired steam Rankine cycle in parallel. Compared with the separated sCO₂ power system, the waste-to-electricity efficiency was enhanced by 8.34%. Economic analysis showed that the payback period was reduced by 4.2 years. Meanwhile, the net present value of the waste power generation project was increased by 18.17 M$. Compressed air energy storage systems are used to solve the problem of solar energy discontinuity and improve the flexibility of solar energy utilization. Meng et al. (Meng et al., 2020) designed a solar tCO₂ cycle to recover the waste energy of high-temperature compressed air, and the energy efficiency was evidently improved.

Toshiba proposed a tCO₂ cycle combined with an oxy-fuel gas turbine, called the Allam cycle (Iwai et al., 2015; Allam et al., 2017; Suzuki et al., 2019). CO₂ was used as the working fluid and heated in the combustor during combustion. Oxy-fuel and oxygen were delivered to the combustor, and the products were steam and CO₂. A turbine inlet pressure of 31 MPa and inlet temperature of 727°C were obtained. Subsequently, the burned gases were expanded, and a separator was installed to separate the water. Gaseous CO₂ was condensed to a liquid state, and the redundant CO₂ was extracted after pressurization. In 2016, a 50 MWe demo system was built, and a 300 MWe system fueled with natural gas was planned. Compared with conventional power plants with carbon capture, a net efficiency of 59% for natural gas and 51% for coal can be achieved by the Allam cycle. In addition, nearly 100% of CO₂ can be captured with low projected capital and O&M costs.

Economic Analysis of CO₂ Cycle

Economic performance is an important factor affecting decision-making. The conventional model based on chemical engineering plant cost index (CEPCI) is generally employed to estimate the capital cost (Turton et al., 2009; Kwon et al., 2016). Liu et al. (Liu et al., 2018) analyzed the economic performance of a sCO₂ cycle recovering the flue gas heat of a 600 MW coal-fired power plant. The sCO₂ cycle could reduce energy consumption compared with the traditional economizer method. The payback period of the system was 3.067 years, and the net present value could reach 16.132 million US dollars with a service life of 20 years, manifesting good economic performance. Cayer (Cayer et al., 2009) estimated the performance of a tCO₂ cycle for industrial waste gas at a temperature of 100°C and a flow rate of 314.5 kg/s. The results showed that the regenerator was conducive to reducing the maximum working pressure of the system. However, the UA value of the regenerative cycle was larger than that of the simple cycle. Wang et al. (Wang et al., 2018c) compared the performances of three tCO₂ cycles. The single-stage tCO₂ cycle had a good economic performance over the entire temperature range of the heat source. The two-stage cycle had a better economic performance only when the heat source temperature was higher than 530°C, and a multi-objective optimization algorithm was required if both the thermodynamic and economic performances were to be considered simultaneously. Li et al. (Li et al., 2018) established an economic model for a tCO₂ cycle based on the NSGA-II algorithm. The optimized system thermal and exergy efficiencies were 8.51% and 29.59%, respectively.

Generally, CO₂ power cycles have a higher cost than ORCs, which is the main factor restricting commercial production. Using zeotropic mixtures containing CO₂ is a feasible option that can reduce costs while maintaining high efficiency (Xia et al., 2018). At present, few investigations have focused on the economic performance of CO₂ power cycles. More efforts are required for various industrial applications to provide a comprehensive comparison among the conventional steam Rankine cycle, ORC, Kalina, and other power systems.

Technical Challenges and Possibilities of Future Development

Although CO₂ power cycles have great potential for industrial applications, some technical challenges still need to be overcome. Figure 10 shows the main challenges and possible directions for future development. First, CO₂ is a natural working fluid with environmentally friendly characteristics, such as zero ODP and low GWP. However, CO₂ is a limiting substance in the occupational exposure limit standard for hazardous factors in the workplace. CO₂ with a concentration greater than 2% will cause fatal harm to human beings in a closed space. Generally, the concentration of CO₂ prescribed in the hygiene requirements is less than 5000 ppm. Therefore, CO₂ gas leakage detection and the formulation of relevant safety specifications are needed to provide safety support for the industrial application of CO₂ power cycles.

FIGURE 10

FIGURE 10. Technical challenges and possible future developments of CO₂ power cycles.

The characteristics of fluid flow and heat transfer of supercritical CO₂ need to be investigated experimentally such that accurate correlations can be developed for a wide range of CO₂ power cycles. PCHEs that can operate under high-pressure and temperature conditions are suitable for applications with a compact size requirement. Flow passage optimization and reduction of pressure drops of PCHEs should be investigated further. Furthermore, CO₂ can be used as a flame retardant and blended with an organic working fluid. The thermophysical properties of zeotropic mixtures containing CO₂ should be measured to provide accurate data for industrial applications. Thus, a high-fidelity economic model and a comprehensive analysis can be performed.

The energy efficiency of the high-temperature sCO₂ power cycle increases with an increase in the maximum working pressure. However, the high operating temperature poses a severe challenge to metal materials. The material strength should be improved, and the wall thickness must be increased. In addition, it is possible to control the maximum working pressure to a reasonable level and improve the system efficiency by reducing the exergy loss of the components. For coal-fired power plants, the design of a high-temperature sCO₂ power cycle needs to be considered together with the design of carbon capture and carbon storage devices to meet the carbon neutrality target.

CO₂ power cycles take advantages of environmentally friendly properties, low cost, high output power, and are best suited for solar and geothermal sources. For solar power applications, a solar collector with high concentrating performance can enhance the operating temperature and system efficiency. Combining it with a heat storage device can effectively suppress fluctuations in solar energy. Furthermore, it can be integrated with domestic heat supply such that comprehensive energy utilization is realized, and the energy efficiency is improved greatly. This has good prospects in micro-distributed energy supply systems. For low-temperature geothermal power generation, few investigations have focused on the CO₂ power system, and more research and engineering developments are needed. A supercritical state is observed for the sCO₂ cycle during the cooling process, and air cooling is feasible, especially for areas with water shortages. A tCO₂ cycle is more suitable for areas at high latitudes or altitudes with low ambient temperatures or areas with abundant water resources.

The high-pressure and high-temperature operating conditions of CO₂ power systems are a severe challenge to the reliability and durability of the system components, which require careful verification in engineering practice. Supercritical CO₂ with high density has a significant impact on the high-speed rotating vanes of the turbine and compressor, and the mechanical stress of the blades must be specified in the design. To ensure reliable sealing and improve the compactness of the system, the compressor, alternator, and turbine are designed as an integrated turbine-alternator-compressor (TAC). Generally, high heat loss occurs owing to the heat transfer between the different parts of the TAC. It is necessary to reduce the heat loss of the turbine to a very low level while simultaneously ensuring good cooling of the alternator. The optimal regulation of the compressor and turbine under off-design conditions needs to be further studied.

Conclusion

In this paper, recent advancements in the system design and applications of supercritical/transcritical CO₂ power cycles are discussed. Single-flow and split-flow CO₂ power cycles have their own advantages. New CO₂ power cycles can be designed by enhancing the processes of heating, recuperation, compression, and expansion. For a high-temperature heat source with a large specific heat capacity, the recompression configuration is suitable owing to its high efficiency and relatively simple structure. The split expansion configuration with reheating and intercooling is more suitable for heat sources with a small specific heat capacity. In addition, the CO₂ power system combining the single-flow and split-flow cycles may provide a method to improve energy efficiency further, and fully utilize the advantages of both configurations. Furthermore, novel systems may be designed by combining the sCO₂ cycle with the tCO₂ cycle if the ambient temperature is low. The CO₂ power cycle can also be integrated with refrigeration and heating devices to realize the comprehensive utilization of energy, which is of great significance for applications such as distributed energy systems.

Different sCO₂ Brayton cycles have been investigated extensively for nuclear reactors, coal-fired plants, CSP, and high-temperature waste heat recovery. However, few investigations have focused on tCO₂ cycles. More efforts are required to evaluate the feasibility and potential of different tCO₂ Rankine cycles for low-grade heat sources, especially for small-scale applications. In practice, a comprehensive analysis of the CO₂ power cycle, including an evaluation of its economic performance, is required. To accelerate the industrial application of CO₂ power cycles, more efforts should be devoted to engineering activities, including component manufacturing, system seal, reliability and durability, system control, and optimization, in the future.

Author Contributions

EW contributes to conceptualization, literature survey, paper drafting, and funding acquisition. NP is mainly responsible for the data curation and writing paper. MZ contributes to the paper modification, resources, visualization.

Funding

This research work was supported by the National Natural Science Foundation of China (Grant No. 51876009).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

CEPCI, chemical engineering plant cost index; CFC, chlorofluorocarbon; CHP, combine heat and power; CSP, concentrated solar power; GWP, global warming potential; HPT, high-pressure turbine; HTR, high-temperature recuperator; ICE, internal combustion engine; LNG, liquefied natural gas; LPT, low-pressure turbine; LTR, low-temperature recuperator; ODP, ozone depletion potential; ORC, organic Rankine cycle; PCHE, printed circuit heat exchanger; RC, Rankine cycle; sCO₂, supercritical CO₂ power cycle; TAC, turbine-alternator-compressor; tCO₂, transcritical CO₂ power cycle; VCC, vapor compression cycle.

References

Abdollahpour, A., Ghasempour, R., Kasaeian, A., and Ahmadi, M. H. (2020). Exergoeconomic Analysis and Optimization of a Transcritical CO₂ Power Cycle Driven by Solar Energy Based on Nanofluid with Liquefied Natural Gas as its Heat Sink. J. Therm. Anal. Calorim. 139, 451–473. doi:10.1007/s10973-019-08375-6