A Comprehensive Study on Maximum Power Point Tracking Techniques Based on Fuzzy Logic Control for Solar Photovoltaic Systems

Maximum power point tracking (MPPT) methods based on fuzzy logic control (FLC) is a popular application in recent years. However, different kinds of fuzzy control methods lack comparative study, which led to confusion in practice. Hence, a comprehensive study on these methods is essential. Unfortunately, very few attempts have been made in this regard. In this paper, four FLC methods are selected for comparative analysis. Furthermore, the design details and experimental result will also be given to help choose and measure these methods, which presents a clear image of the technology of FLC based MPPT to readers.

1 Introduction

Due to the increasingly serious environmental problems, low carbon economy has received people’s attention. Photovoltaic (PV) energy becomes a promising alternative as it is omnipresent, environment friendly, and has less operational and maintenance costs. An efficient maximum power point tracking (MPPT) technique is necessary that is expected to track the maximum power point (MPP) at all environmental conditions and then force the PV system to operate at that MPP (Sivakumar et al., 2015; Saravanan and Ramesh Babu, 2016; Kandemir et al., 2017; Al-Dhaifallah et al., 2018; Yang et al., 2018a; Yang et al., 2018b; Li X. et al., 2019a; Yang et al., 2019a; Li X. et al., 2019b; Yang et al., 2019b; Yang et al., 2019c; Li S. et al., 2020; Yang et al., 2020b; Eltamaly, 2021; Li F. et al., 2021).

In recent years, many advanced control techniques have been associated with the MPPT control such as fuzzy logic control (FLC) in order to increase the efficiency of solar panels. Several FLC methods are compared and reviewed in the literature (Dounis et al., 2013; Boukenoui et al., 2016; Kwan and Wu, 2016; Ouchen et al., 2016; Mohamed et al., 2017; Nabipour et al., 2017; Yilmaz et al., 2018; Youssef et al., 2018; Li X. et al., 2019c; Loukil et al., 2020; Verma et al., 2020; Jin et al., 2021; Rajesh et al., 2021; Tang et al., 2021). In this paper, four FLC methods are selected for comparative analysis. Then, comprehensive study has been made to compare the FLC methods regarding their features of input variables. Furthermore, the control effect has also been studied. Finally, the correctness of the conclusion is verified by simulation and experiment.

The paper is organized as follows. In Section 2, FLC MPPT techniques are extracted from a vast literature survey. Then, the comparative analysis of the four methods will be verified by experiments in Section 3. The concluding remarks are presented in Section 4.

2 Review of MPPT Algorithms Based on Fuzzy Logic Control

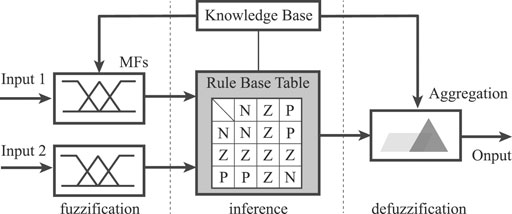
Generally, three stages can be identified in FLC MPPT’s control Figure 1. In the first stage, the numerical input variables are converted into equivalent linguistic variables as input fuzzy sets. In the second stage, the input fuzzy sets are calculated into output fuzzy sets through the inference with the fuzzy rule base table. In the last stage, the output fuzzy sets are converted back to numerical variables as the output.

FIGURE 1

FIGURE 1. The work progress of a FLC method.

On the other hand, the design of FLC method is also divided into three stages. Firstly, the input variables should be selected to identify the position of work power point (WPP) related to MPP, and the output variable should be chosen to execute the command of the controller. After that, the rules of FLC methods should be set based on the study of PV characteristics. Finally, the parameters of FLC methods should be configured on the basis of the variable characteristic.

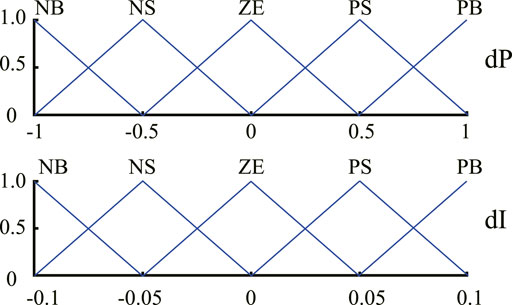
In FLC, the values of variable are expressed of linguistic variables such as PB (positive big), PS (positive small), ZE (zero), NS (negative small), and NB (negative big) using basic fuzzy subset. Each of these acronyms is defined by mathematical membership functions (MFs). Moreover, the setting of parameters involves two aspects: ranges and adjustments.

According to the consultation of other literature data and personal summary, four extant methods of fuzzy controls are compared. In addition, for ease of comparison, the output variable of the four methods should be consistent. The difference of duty cycle (dD) is the universal choice, and the range and parameters of $dD$ are same in different methods (Rezk and Eltamaly, 2015). And boost circuit is chosen as the DC-DC converter. $dD$ are expressed of linguistic variables such as LB (left big), LS (left small), ZE (zero), RS (right small), and RB (right big) using basic fuzzy subset, as shown in Figure 2.

FIGURE 2

FIGURE 2. The output of all FLC methods.

2.1 dP&dV Method and dP&dI Method

The $\text{dP\&dV}$ method is one of the most widely used in the industry (Boukenoui et al., 2017; Farajdadian and Hassan Hosseini, 2019). For the $\text{dP\&dV}$ method, the first and second inputs refer to Eqs. 1, 2, respectively.

$dP\left(k\right)=P\left(k\right)-P\left(k-1\right)(1)$

$dV\left(k\right)=V\left(k\right)-V\left(k-1\right)(2)$

where $P\left(k\right)$ and $V\left(k\right)$ are PV output power and voltage, respectively at time k. According to the principle of dP&dV method, the basic operation principle can be expressed by:

$\{\begin{array}{cc}dP>0,dV>0\text{or}dP<0,dV<0& \text{Left}\text{of}\text{MPP}\\ dP>0,dV<0\text{or}dP<0,dV>0& \text{Right}\text{of}\text{MPP}\end{array}(3)$

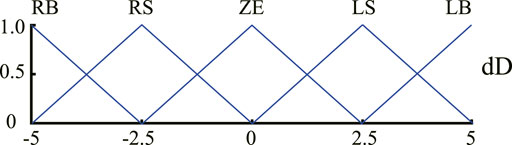
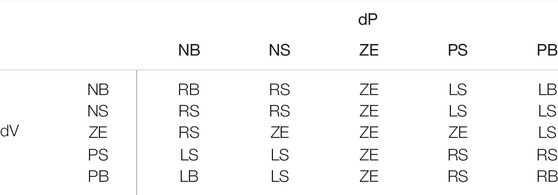
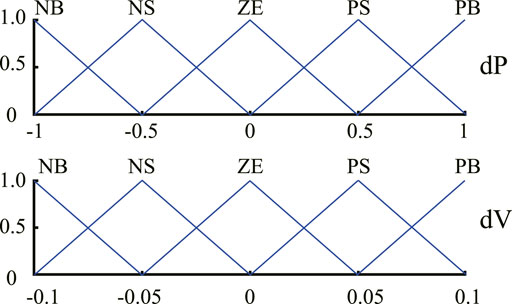
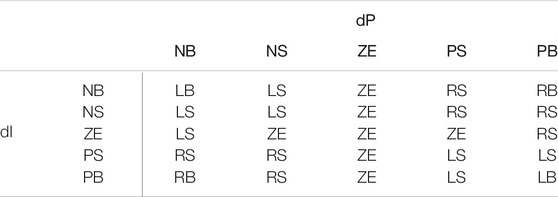
Based on Eqs. 1–3, fuzzy rules are summarized in Table 1, and the MFs of $dP$ and $dV$ is shown as Figure 3.

TABLE 1

TABLE 1. The rules of dP&dV method.

FIGURE 3

FIGURE 3. The MFs of dP&dV method.

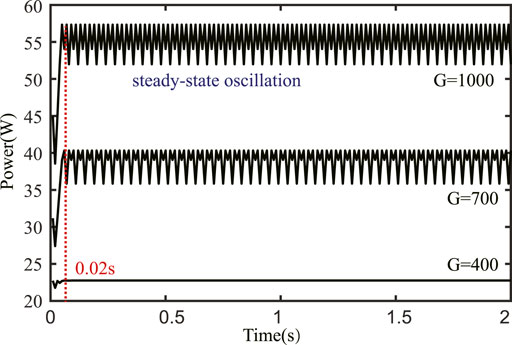
As shown in Figure 4, the steady-state oscillation is significant when the irradiation is large. On the contrary, the steady-state oscillation disappears when the solar irradiance level is low. The tracking speed of this method is relatively fast, which helps to keep up with PV changes quickly.

FIGURE 4

FIGURE 4. The tracking effect of dP&dV method.

The $\text{dP\&dI}$ method is another popular method, which is similar to the $\text{dP\&dV}$ method. For the $\text{dP\&dV}$ method, the first and second inputs refer to Eqs. 4, 5, respectively.

$dP\left(k\right)=P\left(k\right)-P\left(k-1\right)(4)$

$dI\left(k\right)=I\left(k\right)-I\left(k-1\right)(5)$

where $P\left(k\right)$ and $I\left(k\right)$ are PV output power and voltage, respectively at time k. According to the principle of dP&dI method, the operation principle can be expressed by:

$\{\begin{array}{cc}dP>0,dI<0\text{or}dP<0,dV>0& \text{Left}\text{of}\text{MPP}\\ dP>0,dI>0\text{or}dP<0,dI<0& \text{Right}\text{of}\text{MPP}\end{array}(6)$

Based on Eqs 4–6, fuzzy rules are summarized in Table 2, and the MFs of $dP$ and $dI$ is shown as Figure 5.

TABLE 2

TABLE 2. The rules of dP&dI method.

FIGURE 5

FIGURE 5. The MFs of dP&dI method.

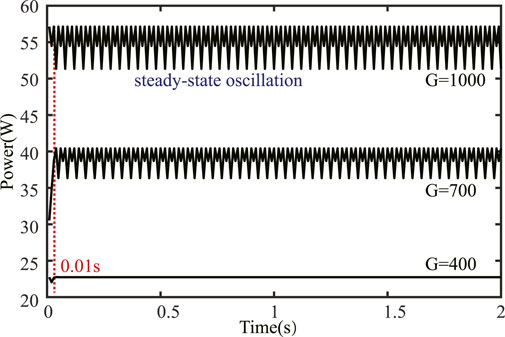
As shown in Figure 6, the steady-state oscillation is hard when the irradiation is large. On the contrary, the steady-state oscillation disappears when the irradiance decreases. The tracking speed of this method is relatively faster, which help to keep up with PV changes quickly.

FIGURE 6

FIGURE 6. The tracking effect of dP&dI method.

The characteristics of the two methods can be summarized as follow:

• The control logic is simple and rules are easy to design.

• It is easy to produce steady-state oscillation.

• The tracking speed of the two methods is faster.

2.2 E&dE Method

For the $\text{E\&dE}$ method, the first and second inputs refer to Eqs. 7, 8, respectively (Danandeh and Mousavi G, 2018; Bhukya and Nandiraju, 2020).

$E\left(k\right)=\frac{dP}{dV}=\frac{P\left(k\right)-P\left(k-1\right)}{V\left(k\right)-V\left(k-1\right)}(7)$

$dE\left(k\right)=E\left(k\right)-E\left(k-1\right)(8)$

where $P\left(k\right)$ and $V\left(k\right)$ are PV output power and voltage respectively at time k. According to the principle of E&dE method, the operation principle can be expressed by:

$\{\begin{array}{c}E>0\text{Left}\text{of}\text{MPP}\\ E<0\text{Right}\text{of}\text{MPP}\end{array}(9)$

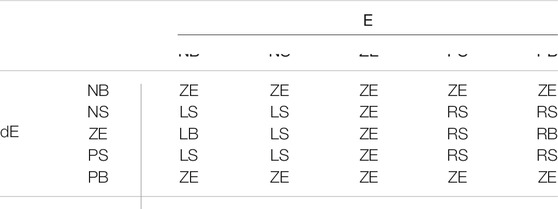
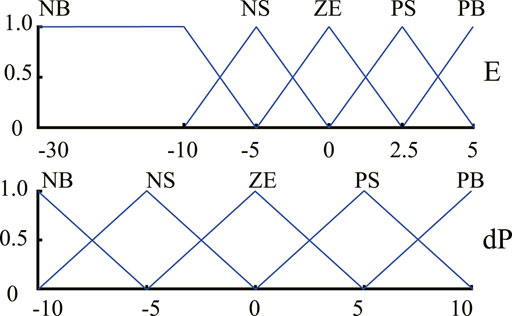
Based on Eqs. 7–9, fuzzy rules are summarized in Table 3, and the MFs of E and $dE$ is shown as Figure 7.

TABLE 3

TABLE 3. The rules of E&dE method.

FIGURE 7

FIGURE 7. The MFs of E&dE method.

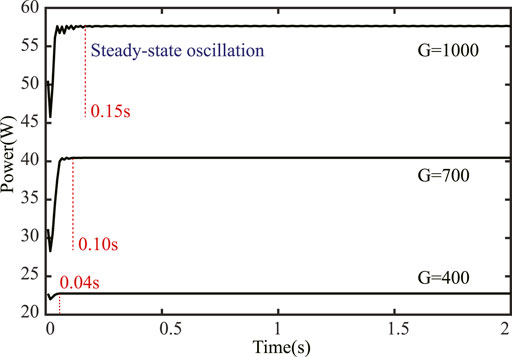
As shown in Figure 8, the steady-state oscillation still exists and is mainly decided by the solar exposure level. The tracking speed of this method is relatively slower, which is not suitable to cope with the rapid change of irradiation.

FIGURE 8

FIGURE 8. The tracking effect of E&dE method.

The characteristics of $\text{E\&dE}$ method can be summarized as follow:

• The tracking speed of the two methods is faster. The control logic is simple and rules are easy to design.

• The steady-state oscillation is slight.

• The tracking speed of $\text{E\&dE}$ method is slow.

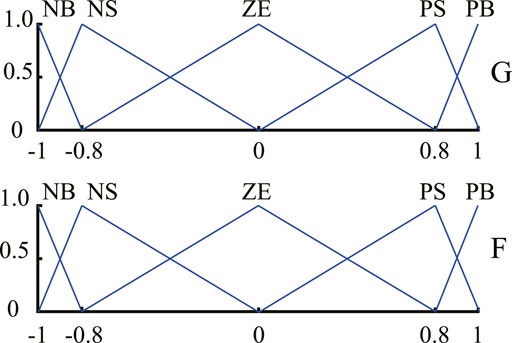
2.3 G&F Method

For the $\text{G\&F}$ method, the first and second inputs refer to Eq. 10 (Chen Y.-T. et al., 2016).

$\{\begin{array}{c}G=1-\left|\frac{dI}{dV}\right|/\left|\frac{I}{V}\right|\\ F=1-\left|\frac{I}{V}\right|/\left|\frac{dI}{dV}\right|\end{array}(10)$

According to the principle of G&F method, the operation principle can be expressed by:

$\{\begin{array}{cc}G>0\text{and}F<0& \text{Left}\text{of}\text{MPP }\\ F>0\text{and}G<0& \text{Right}\text{of}\text{MPP }\end{array}$

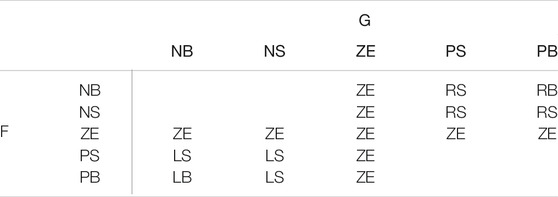
According to the above formulas, fuzzy rules can be designed, as shown in Table 4, and the MFs of G and F is shown as Figure 9.

TABLE 4

TABLE 4. The rules of G&F method.

FIGURE 9

FIGURE 9. The MFs of G&F method.

As shown in Figure 10, the steady-state oscillation is well canceled in this scheme. The tracking speed of this method is appropriate, which is enough to cope with the rapid change of irradiation.

FIGURE 10

FIGURE 10. The tracking effect of G&F method.

The characteristics of $\text{E\&dE}$ method can be summarized as follow:

• The control logic is ingenious and rules are less.

• The steady-state oscillation is not found.

• The tracking speed of $\text{E\&dE}$ method is moderate.

2.4 The Composite Methods

After the combination of other control techniques, many FLC methods have been developed based on the above methods.

The beta-parameter based MPPT algorithm are derived from E&dE method (Li X. et al., 2019c). This method adds an input variable, β, to E&dE method, and changes the fuzzy rule based on the value of β, as shown in Table 5. The dilemma between the rules number and the universality for various operating conditions can be effectively solved with this new algorithm. In addition, it can simplify the Fuzzy rule membership functions since the number of fuzzy rules can be reduced.

TABLE 5

TABLE 5. The rules of β method.

The FLC-MPPT based on genetic algorithm and small-signal analysis are derived from dP&dV method (Mohamed et al., 2017). Then, proper FLC-MPPT control design was performed by means of combining genetic algorithm and the analytical design formulas. This method use the small-signal model with combination of a stochastic searching technique based on genetic algorithm to get the accurate design parameters of dP&dV method.

The FLC MPPT based on firefly algorithm are derived from dP&dV method (Farajdadian and Hassan Hosseini, 2019) This method utilize the firefly algorithm to design fuzzy controller membership functions for a better effectiveness. After optimizing the parameters by firefly algorithm, the MPPT method will have better dynamic performance and perform well at all irradiation levels.

Another MPPT method which is well adapted with microcontrollers is Neural networks (NN) method. Artificial neural network (ANN) emerged at the same time that fuzzy logic emerged and both are considered a part of soft computation. In complex neural networks, higher number of hidden layers are used. Number of layers and neurons of each layer and the functions employed in layers depend on user’s knowledge. Input variables might be array parameters like V and I, weather information like temperature and solar irradiation or a combination of them. Output variable is usually duty cycle of the inverter.

3 Simulation Result and Experimental Evaluation

As shown in Figure 11, this experiment utilized Host PC, Real-Time Model Simulator (MT6016), Interface board, and Oscilloscope.

FIGURE 11

FIGURE 11. Experimental platform.

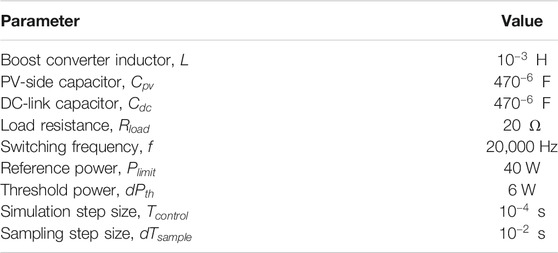
The PV model of EN50530 and boost converter are utilized in this experience (Chen P.-C. et al., 2015; Park and Choi, 2017; Ayop and Tan, 2018; Yang et al., 2020a; Li X. et al., 2021). Table 6 lists main electrical parameters of the selected PV module in EN50530, and Table 7 lists main electrical parameters of the PV system.

TABLE 6

TABLE 6. Main parameters for EN50530 PV modules.

TABLE 7

TABLE 7. Main parameters for the PV system.

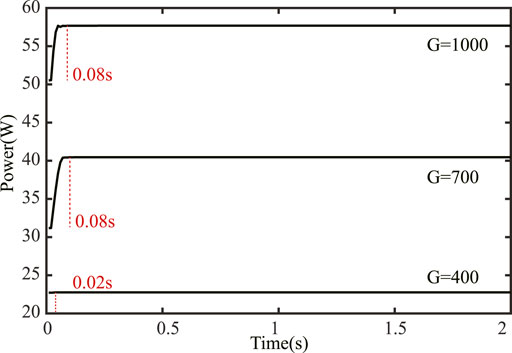
The results of the real-time simulation platform are consistent with the theoretical analysis. As shown in Figure 12, the tracking process of $\text{dP\&dV}$ method was successful in the whole process. However, with the irradiation intensifies, the oscillation becomes more obvious. This not only leads to the power loss, but also brings a large variation of voltage, which will seriously affect the power quality. Furthermore, the oscillation in $\text{E\&dE}$ and $\text{G\&F}$ methods is far smaller than the $\text{dP\&dV}$ method. The tracking speed of $\text{E\&dE}$ method is slower than that of the $\text{G\&F}$ method.

FIGURE 12

FIGURE 12. The real-time experiences of all methods.

4 Conclusion

In this paper, four MPPT programs based FLC are compared. It can be concluded that, the selection of input variables determines the difficulty of the final control effects, based on the analysis of the design process and tracking effects. The correctness of the theoretical analysis is proved by simulation results and experiment evaluations.

However, this paper does not describes the MPPT progresses which combine FLC with other technologies in detail. Because, this paper focuses on the comparative analysis of the difference of basic FLC methods. The introduction of additional methods does not benefit comparative analysis.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

TZ, JD, and XL contributed to conception and design of the study and wrote sections of the manuscript. TZ performed the statistical analysis and wrote the first draft of the manuscript. XL provides guidance. SD proof reading. All authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Dhaifallah, M., Nassef, A. M., Rezk, H., Nisar, K. S., and Nisar, K. S. (2018). Optimal Parameter Design of Fractional Order Control Based INC-MPPT for PV System. Solar Energy 159, 650–664. doi:10.1016/j.solener.2017.11.040

CrossRef Full Text | Google Scholar

Ayop, R., and Tan, C. W. (2018). Design of Boost Converter Based on Maximum Power Point Resistance for Photovoltaic Applications. Solar Energy 160, 322–335. doi:10.1016/j.solener.2017.12.016

CrossRef Full Text | Google Scholar

Bhukya, L., and Nandiraju, S. (2020). A Novel Photovoltaic Maximum Power Point Tracking Technique Based on Grasshopper Optimized Fuzzy Logic Approach. Int. J. Hydrogen Energy 45 (16), 9416–9427. doi:10.1016/j.ijhydene.2020.01.219

CrossRef Full Text | Google Scholar

Boukenoui, R., Ghanes, M., Barbot, J.-P., Bradai, R., Mellit, A., and Salhi, H. (2017). Experimental Assessment of Maximum Power Point Tracking Methods for Photovoltaic Systems. Energy 132, 324–340. doi:10.1016/j.energy.2017.05.087

CrossRef Full Text | Google Scholar

Boukenoui, R., Salhi, H., Bradai, R., and Mellit, A. (2016). A New Intelligent MPPT Method for Stand-Alone Photovoltaic Systems Operating Under Fast Transient Variations of Shading Patterns. Solar Energy 124, 124–142. doi:10.1016/j.solener.2015.11.023

CrossRef Full Text | Google Scholar

Chen, P.-C., Chen, P.-Y., Liu, Y.-H., Chen, J.-H., and Luo, Y.-F. (2015). A Comparative Study on Maximum Power Point Tracking Techniques for Photovoltaic Generation Systems Operating Under Fast Changing Environments. Solar Energy 119, 261–276. doi:10.1016/j.solener.2015.07.006

CrossRef Full Text | Google Scholar

Chen, Y.-T., Jhang, Y.-C., and Liang, R.-H. (2016). A Fuzzy-Logic Based Auto-Scaling Variable Step-Size MPPT Method for PV Systems. Solar Energy 126, 53–63. doi:10.1016/j.solener.2016.01.007

CrossRef Full Text | Google Scholar

Danandeh, M. A., and Mousavi G, S. M. (2018). A New Architecture of INC-Fuzzy Hybrid Method for Tracking Maximum Power Point in PV Cells. Solar Energy 171, 692–703. doi:10.1016/j.solener.2018.06.098

CrossRef Full Text | Google Scholar

Dounis, A. I., Kofinas, P., Alafodimos, C., and Tseles, D. (2013). Adaptive Fuzzy Gain Scheduling PID Controller for Maximum Power Point Tracking of Photovoltaic System. Renew. Energy 60, 202–214. doi:10.1016/j.renene.2013.04.014

CrossRef Full Text | Google Scholar

Eltamaly, A. M. (2021). A Novel Musical Chairs Algorithm Applied for MPPT of PV Systems. Renew. Sustain. Energy Rev. 146, 111135. doi:10.1016/j.rser.2021.111135

CrossRef Full Text | Google Scholar

Farajdadian, S., and Hassan Hosseini, S. M. (2019). Design of an Optimal Fuzzy Controller to Obtain Maximum Power in Solar Power Generation System. Solar Energy 182, 161–178. doi:10.1016/j.solener.2019.02.051

CrossRef Full Text | Google Scholar

Jin, J. X., Wang, J., Yang, R. H., Zhang, T. L., Mu, S., Fan, Y. J., et al. (2021). A Superconducting Magnetic Energy Storage With Dual Functions of Active Filtering and Power Fluctuation Suppression for Photovoltaic Microgrid. J. Energy Storage 38, 102508. doi:10.1016/j.est.2021.102508

CrossRef Full Text | Google Scholar

Kandemir, E., Cetin, N. S., and Borekci, S. (2017). A Comprehensive Overview of Maximum Power Extraction Methods for PV Systems. Renew. Sustain. Energy Rev. 78, 93–112. doi:10.1016/j.rser.2017.04.090

CrossRef Full Text | Google Scholar

Kwan, T. H., and Wu, X. (2016). Maximum Power Point Tracking Using a Variable Antecedent Fuzzy Logic Controller. Solar Energy 137, 189–200. doi:10.1016/j.solener.2016.08.008

CrossRef Full Text | Google Scholar

Li, F., Lin, D., Tao, Y., Li, J., Wang, K., Zhang, X., et al. (2021). Adaptive Rapid Neural Optimization: A Data-Driven Approach to MPPT for Centralized TEG Systems. Electr. Power Syst. Res. 199, 107426. doi:10.1016/j.epsr.2021.107426

CrossRef Full Text | Google Scholar

Li, S., Ping, A., Liu, Y., Ma, X., and Li, C. (2020). A Variable-Weather-Parameter MPPT Method Based on a Defined Characteristic Resistance of Photovoltaic Cell. Solar Energy 199, 673–684. doi:10.1016/j.solener.2020.02.065

CrossRef Full Text | Google Scholar

Li, X., Wang, Q., Wen, H., and Xiao, W. (2019a). Comprehensive Studies on Operational Principles for Maximum Power Point Tracking in Photovoltaic Systems. IEEE Access 7, 121407–121420. doi:10.1109/access.2019.2937100

CrossRef Full Text | Google Scholar

Li, X., Wen, H., Hu, Y., Du, Y., and Yang, Y. (2021). A Comparative Study on Photovoltaic MPPT Algorithms Under en50530 Dynamic Test Procedure. IEEE Trans. Power Electron. 36 (4), 4153–4168. doi:10.1109/tpel.2020.3024211

CrossRef Full Text | Google Scholar

Li, X., Wen, H., Hu, Y., and Jiang, L. (2019b). A Novel Beta Parameter Based Fuzzy-Logic Controller for Photovoltaic MPPT Application. Renew. Energy 130, 416–427. doi:10.1016/j.renene.2018.06.071

CrossRef Full Text | Google Scholar

Li, X., Wen, H., Hu, Y., and Jiang, L. (2019c). Drift-Free Current Sensorless MPPT Algorithm in Photovoltaic Systems. Solar Energy 177, 118–126. doi:10.1016/j.solener.2018.10.066

CrossRef Full Text | Google Scholar

Loukil, K., Abbes, H., Abid, H., Abid, M., and Toumi, A. (2020). Design and Implementation of Reconfigurable MPPT Fuzzy Controller for Photovoltaic Systems. Ain Shams Eng. J. 11 (2), 319–328. doi:10.1016/j.asej.2019.10.002

CrossRef Full Text | Google Scholar

Mohamed, A. A. S., Berzoy, A., and Mohammed, O. A. (2017). Design and Hardware Implementation of FL-MPPT Control of PV Systems Based on GA and Small-Signal Analysis. IEEE Trans. Sustain. Energy 8 (1), 279–290. doi:10.1109/tste.2016.2598240

CrossRef Full Text | Google Scholar

Nabipour, M., Razaz, M., Seifossadat, S. G., and Mortazavi, S. S. (2017). A New MPPT Scheme Based on a Novel Fuzzy Approach. Renew. Sustain. Energy Rev. 74, 1147–1169. doi:10.1016/j.rser.2017.02.054

CrossRef Full Text | Google Scholar

Ouchen, S., Betka, A., Abdeddaim, S., and Menadi, A. (2016). Fuzzy-Predictive Direct Power Control Implementation of a Grid Connected Photovoltaic System, Associated With an Active Power Filter. Energy Convers. Manag. 122, 515–525. doi:10.1016/j.enconman.2016.06.018

CrossRef Full Text | Google Scholar

Park, J.-Y., and Choi, S.-J. (2017). A Novel Simulation Model for PV Panels Based on Datasheet Parameter Tuning. Solar Energy 145, 90–98. doi:10.1016/j.solener.2016.12.003

CrossRef Full Text | Google Scholar

Rajesh, T., Gunapriya, B., Sabarimuthu, M., Karthikkumar, S., Raja, R., and Karthik, M. (2021). Frequency Control of PV-Connected Micro Grid System Using Fuzzy Logic Controller. Mater. Today Proc. 45, 2260–2264. International Conference on Advances in Materials Research - 2019. doi:10.1016/j.matpr.2020.10.255

CrossRef Full Text | Google Scholar

Rezk, H., and Eltamaly, A. M. (2015). A Comprehensive Comparison of Different MPPT Techniques for Photovoltaic Systems. Solar Energy 112, 1–11. doi:10.1016/j.solener.2014.11.010

CrossRef Full Text | Google Scholar

Saravanan, S., and Ramesh Babu, N. (2016). Maximum Power Point Tracking Algorithms for Photovoltaic System - A Review. Renew. Sustain. Energy Rev. 57, 192–204. doi:10.1016/j.rser.2015.12.105

CrossRef Full Text | Google Scholar

Sivakumar, P., Abdul Kader, A., Kaliavaradhan, Y., and Arutchelvi, M. (2015). Analysis and Enhancement of PV Efficiency with Incremental Conductance MPPT Technique Under Non-Linear Loading Conditions. Renew. Energy 81, 543–550. doi:10.1016/j.renene.2015.03.062

CrossRef Full Text | Google Scholar

Tang, L., Wang, X., Xu, W., Mu, C., and Zhao, B. (2021). Maximum Power Point Tracking Strategy for Photovoltaic System Based on Fuzzy Information Diffusion Under Partial Shading Conditions. Solar Energy 220, 523–534. doi:10.1016/j.solener.2021.03.047

CrossRef Full Text | Google Scholar

Verma, P., Garg, R., and Mahajan, P. (2020). Asymmetrical Interval Type-2 Fuzzy Logic Control Based MPPT Tuning for PV System Under Partial Shading Condition. ISA Trans. 100, 251–263. doi:10.1016/j.isatra.2020.01.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, B., Wang, J., Zhang, X., Yu, T., Yao, W., Shu, H., et al. (2020a). Comprehensive Overview of Meta-Heuristic Algorithm Applications on PV Cell Parameter Identification. Energy Convers. Manag. 208, 112595. doi:10.1016/j.enconman.2020.112595

CrossRef Full Text | Google Scholar

Yang, B., Wang, J., Zhang, X., Zhang, M., Shu, H., Li, S., et al. (2019a). MPPT Design of Centralized Thermoelectric Generation System Using Adaptive Compass Search Under Non-Uniform Temperature Distribution Condition. Energy Convers. Manag. 199, 111991. doi:10.1016/j.enconman.2019.111991

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Shu, H., Zhu, D., An, N., Sang, Y., et al. (2018a). Energy Reshaping Based Passive Fractional-Order PID Control Design and Implementation of a Grid-Connected PV Inverter for MPPT Using Grouped Grey Wolf Optimizer. Solar Energy 170, 31–46. doi:10.1016/j.solener.2018.05.034

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Shu, H., Zhu, D., An, N., Sang, Y., et al. (2018b). Perturbation Observer Based Fractional-Order Sliding-Mode Controller for MPPT of Grid-Connected PV Inverters: Design and Real-Time Implementation. Control Eng. Pract. 79, 105–125. doi:10.1016/j.conengprac.2018.07.007

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Zhang, X., Li, H., Shu, H., Sang, Y., et al. (2019b). Dynamic Leader Based Collective Intelligence for Maximum Power Point Tracking of PV Systems Affected by Partial Shading Condition. Energy Convers. Manag. 179, 286–303. doi:10.1016/j.enconman.2018.10.074

CrossRef Full Text | Google Scholar

Yang, B., Zhang, M., Zhang, X., Wang, J., Shu, H., Li, S., et al. (2020b). Fast Atom Search Optimization Based MPPT Design of Centralized Thermoelectric Generation System Under Heterogeneous Temperature Difference. J. Clean. Prod. 248, 119301. doi:10.1016/j.jclepro.2019.119301

CrossRef Full Text | Google Scholar

Yang, B., Zhong, L., Zhang, X., Shu, H., Yu, T., Li, H., et al. (2019c). Novel Bio-Inspired Memetic Salp Swarm Algorithm and Application to MPPT for PV Systems Considering Partial Shading Condition. J. Clean. Prod. 215, 1203–1222. doi:10.1016/j.jclepro.2019.01.150

CrossRef Full Text | Google Scholar

Yilmaz, U., Kircay, A., and Borekci, S. (2018). PV System Fuzzy Logic MPPT Method and PI Control as a Charge Controller. Renew. Sustain. Energy Rev. 81, 994–1001. doi:10.1016/j.rser.2017.08.048

CrossRef Full Text | Google Scholar

Youssef, A., Telbany, M. E., and Zekry, A. (2018). Reconfigurable Generic FPGA Implementation of Fuzzy Logic Controller for MPPT of PV Systems. Renew. Sustain. Energy Rev. 82, 1313–1319. doi:10.1016/j.rser.2017.09.093

CrossRef Full Text | Google Scholar