- 1School of Renewable Energy, Shenyang Institute of Engineering, Shenyang, China
- 2Key Laboratory of Regional Multi-energy System Integration and Control of Liaoning Province, Shenyang, China
- 3School of Electrical Engineering, Shenyang University of Technology, Shenyang, China
- 4Liaoning Province Information Centre, Shenyang, China
In the power system, the loads and nonlinearity parameters cause the system frequency deviation, which complicates the load frequency control (LFC). To deal with the above problem, an adaptive sliding mode control (SMC) based on disturbance observer is proposed to eliminate frequency deviation for interconnected power system in this paper. Firstly, the mathematical model of the power system is established, where the power exchange between the tie line is considered as the variable of the designed sliding surface. Secondly, the nonlinear disturbance observer is constructed to estimate the parameter uncertainty and load of power system. Thirdly, combined with the estimated value of the disturbance observer and integral sliding mode surface, the SMC is designed. Moreover, considering the inherent shortcoming of SMC—the chattering problem, an adaptive strategy is applied to the SMC to ensure the stability of controller. Next, the stability of the designed SMC is proved by Lyapunov stability theory. Finally, to verify the effectiveness of the proposed controller, several simulations are presented.
Introduction
LFC is a crucial technology for stable operation of modern large-scale interconnected power systems. Due to random uncertainty such as the power demand, the power generation, the communication time lag, the device parameter, etc. The frequency and power exchange in a large range power system will fluctuate or escape from the planned tolerance. When unexpected uncertainty occurs in power system, the purpose of frequency control is to quickly stabilize the system frequency and exchange power between interconnected systems within an acceptable plan (Dou et al., 2017). Driven by the rapid development of technology, power generation units, electrical equipment, and communication systems, power systems have become more complex (Wang et al., 2021b). Therefore, an effective frequency control strategy urgently needs to be proposed to manage the challenge of complex systems.
Furthermore, micro-grid can fully exploit renewable energy to reduce carbon emission. Based on the advantages of the micro-grid, the system has been widely established. However, when micro-grid encounters the intermittency of renewable resource, the rapid fluctuations of load and the uncertainties of internal parameters, frequency regulation is more complex (Kahrobaeian and Mohamed, 2012; Khooban et al., 2017; Lu et al., 2017). To stabilize the frequency, many mature control algorithms have been implemented to solve LFC problems, such as intelligent control, adaptive control (Rashidi et al., 2004), robust control (Huang et al., 2016; Jiang et al., 2012), fuzzy control (Yousef et al., 2014), proportional-integral differentiation (PID) control (Khodabakhshian and Edrisi, 2008; Tan, 2010), etc.
PID control is the common control tool to damp frequency oscillation for micro-grid which is treated as a linear model (Bevrani and Hiyama, 2008; Kamwa et al., 2001). The PID controllers are the simple and easy control tool which can powerfully tuned for several specific operation points (Wangdee and Billinton, 2006). As the integration of renewable energy power generation, the characteristics of power system are non-linear, thus the PID control has no ability to eliminate frequency deviation, especially when the actual work point of micro-grid deviates far from the expected work point (Tang et al., 2015). In (Farahani et al., 2012), the PID controller were optimized to eliminate frequency deviation. The main idea is to tune the gains of PID controller by the lozi map-based chaotic algorithm. Thus, a scheduling PID control strategy based on optimized parameters was applied to microgrid. Similarly, T. Chaiyatham proposed the fuzzy logic-PID controller which utilizes bee colony optimization to tune the fuzzy logic-PID controllers of micro-grid (Chaiyatham et al., 2019). For non-reheat thermal system, Gonggui Chen et al. utilized the fuzzy PID controller based on the Improved Ant Colony Optimization algorithm against system frequency deviation (Chen et al., 2020). Lim et al. (Lim et al., 1998) solved the LFC problem for the unmeasurable state in micro-grid using the robust control theory. Meanwhile, the adaptive control schemes were validated with system parameter uncertainties (Pan and Liaw, 1989).
Generally, as a well-known control method, SMC is a non-linear variable structure controller, whose control is discontinuity. As the advantages of strong robustness properties and quick response, it has been studied extensively (Li et al., 2017; Li et al., 2018; Ai-Hamouz and AbdeI-Magid, 1993; Wang et al., 2021a; Mi et al., 2013). Therefore, SMC is an alternative control strategy to address load frequency problems in micro-grid. Due to external disturbances of renewable energy and parameter variations in internal system, SMC has gained significant research attentions in the field of LFC. AI Hamouz designed a variable structure controller using linear sliding surface, where a step disturbance was considered in the simulation (Ai-Hamouz and AbdeI-Magid, 1993). Therefore, there is a problem with this control strategy. In Sivaramakrishnan et al. (1984), a SMC was presented through the pole assignment technique, where the parametric uncertainties were studied with the matched condition. However, when the power grid is working normally, the system parameters cannot always meet the matched condition. Yang Mi proposed SMC based on proportion-lintegral sliding mode surface, and this method was proved that micro-grid can be immune to the external disturbances with matched and unmatched conditions. However, the aforementioned control strategy was studied based on the proportional-integral controller which has overshoot (Mi et al., 2013). In recent years, considering the parameter uncertainty and the complexity of external disturbances, the advanced SMC method based on disturbance observer was proposed (Li et al., 2016; Mu et al., 2017; Wang et al., 2019; Ma et al., 2017; Liu et al., 2016; Ginoya et al., 2014). In Mu et al. (2017), SMC with neural network observer was constructed, where the measured values were used to control law and it was proven to be superior in the simulation. However, the uncertainties of system parameters are not demonstrated. Ark Dev proposed a SMC based on Luenberger observer (Dev and Sarkar, 2019). However, the Luenberger observer is applied in the absence of rigorous theoretical proof.
In this paper, a disturbance observer, which estimates the matched and unmatched disturbances in the power system, is applied in the LFC. Furthermore, an adaptive SMC strategy based on disturbance observer is investigated to eliminate frequency deviation.
The main contributions of this paper are described as.
1) The disturbance observers are proposed and applied to estimate the disturbances of the multi-area interconnected power system, which effectively track matching and unmatching disturbances.
2) SMC is improved to eliminate frequency deviation. Firstly, comparing the traditional proportional-integral sliding mode surface, the area control error (ACE) and estimated value are taken as state variables into the novel sliding mode surface, which ensures that the frequency deviation and the ACE converge to the equilibrium point. Secondly, to address the chattering of controller, the adaptive law is designed.
Model of Power System
In the power system, the frequency deviation is caused by the fluctuation of the load. The function of LFC is to eliminate frequency deviation. The system proposed in many documents has been applied to LFC. In this chapter, the mathematical model of the power system is established where the types of disturbances are elaborated.
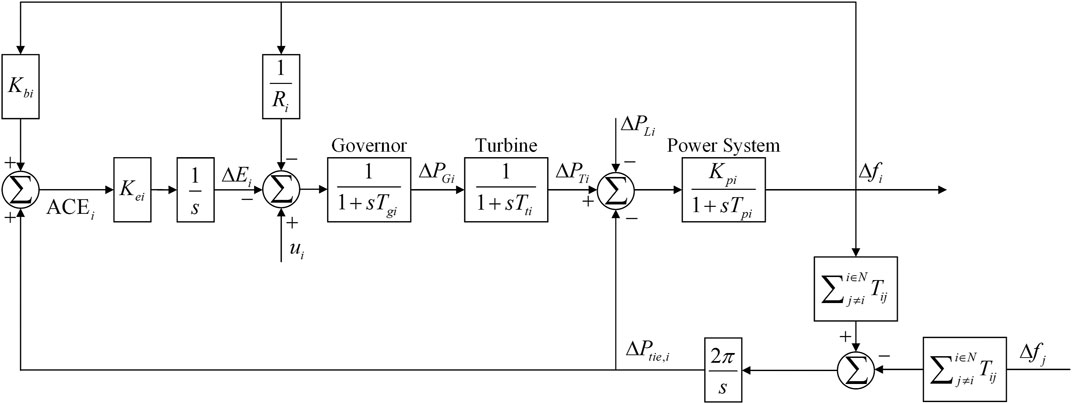
LFC block diagram of i th area power system is illustrated in Figure 1. Due to the complexity of the power system structure, it is regarded as a nonlinear system in practice. However, since the load fluctuation is very small, linearized power system model is approved for theoretical analysis. In this section,
The mathematical dynamics of
where
In this paper, the
Based on Eq. 1, the matrix form of power system can be expressed as
where
where
When the system is working, there is uncertainty in the system matrix, which is an important factor leading to frequency deviation. In this section, the uncertainty of system parameters and load disturbances are regarded as concentrated disturbances which are characterized by linearity and nonlinearity. Then, according to Eq. 3, we get
where
where
Design of SMC With Disturbance Observer
Design of Disturbance Observer
In the power system, there are matching and mismatching disturbances, which are unknown. The uncertainty and load satisfy the following assumption:
Assumption 1
Based on Assumption 1, the concentrated disturbance can be expressed as follows
With the concentrated disturbance composed of system parameter uncertainty and load, a nonlinear disturbance observer is designed to estimate the unknown disturbance as follows
where
Design of SMC
SMC has been proven to be a powerful controller in many documents, and it is adopted to many fields, such as aircraft, robots, and inverted pendulums. Traditionally, there are two crucial steps in SMC, which are the sliding surface and the control law. The sliding surface ensures that the system state reaches the equilibrium point, and the control law drives the state of the space to the sliding surface. For matching and matching disturbances, the proportional-integral sliding surface is generally adopted in SMC.
where
The improved sliding surface is
where
In SMC, the chattering problem is difficult to address. In this paper, the adaptive control is used to slow down the output chattering of the controller. Based on Eq. 9, the adaptive controller can be obtained
where
where
Stability Analysis
In this section, the stability of disturbance observer and SMC is proved.
Stability Analysis of Disturbance Observer
To prove that the disturbance observer can track matched/unmatched disturbances, the following assumptions are necessary.
Assumption 2 The derivative of the disturbance in the system satisfies
Assumption 3 The error
where
Proof:
Based on Assumption 3, the derivative of the error is given
By means of Eq. 14, it can be concluded that the observer can estimate the disturbance in a finite time.
Stability Analysis of Improved SMC
For an adaptive controller Eq. 10, it is necessary to prove the stability of system Eq. 4. Next, the Lyapunov approach is adopted to analysis the stability of the system under the controller.
Proof:
The Lyapunov function is constructed as follows:
where
Differentiating improved sliding surface Eq. 9, we get
Substituting Eq. 4, we get
Using Eqs 6, 10, 11, the
where
Simulation Analysis
Several simulations are presented for improved SMC in this section. In the simulation, frequency deviation of single and interconnected systems is analyzed. First, in presence of load fluctuation, the control performances are presented, such as, the frequency deviation, the sliding mode surface, and the controller output. Secondly, when there are parameter uncertainties and load disturbances in the interconnected system, the designed SMC performance is analyzed. The parameters of the system are shown in Table 1 (Mi et al., 2013).
Single-Area Power System
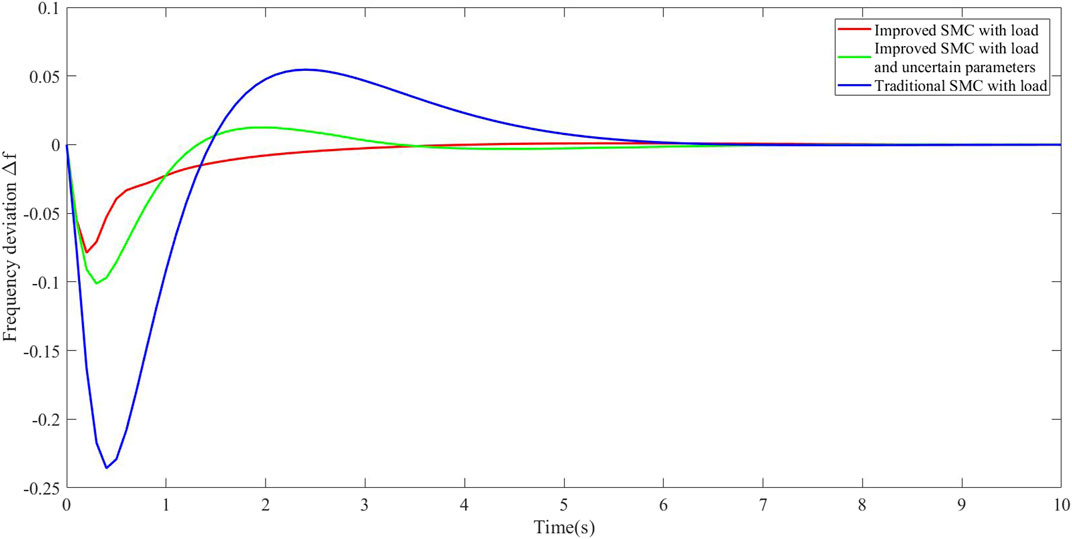
The step load disturbances are applied to the system. The load disturbance is applied to the system, which is a −0.1 p.u. disturbance applied on the system at 0–10 s. Moreover, the parameter uncertainty in the single system is analyzed. The parameters of disturbance observer, SMC and parameter uncertainty are as follows:
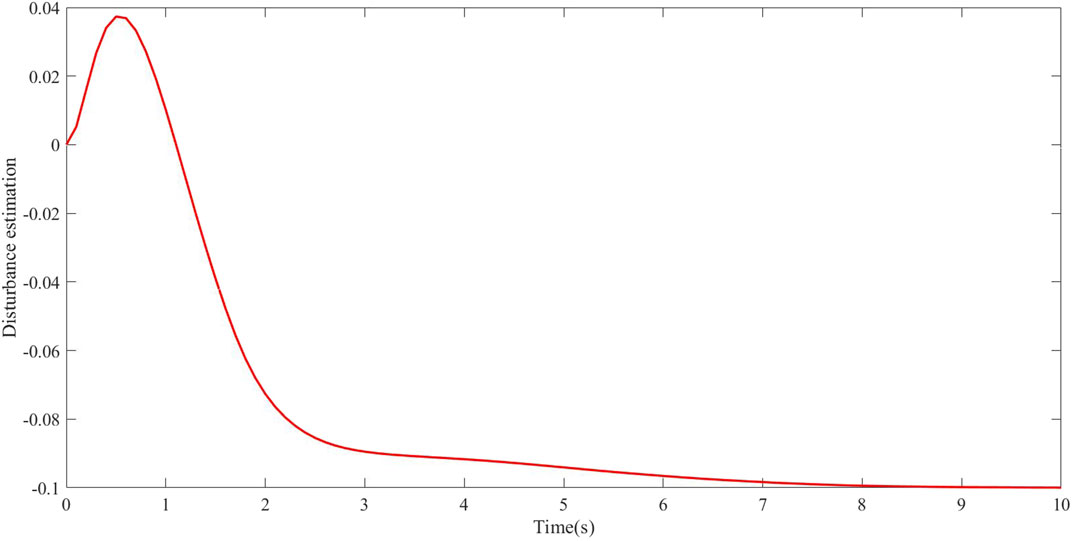
The frequency deviation with traditional SMC and improved SMC is shown in Figure 2. Compared with the traditional SMC, the designed SMC effectively suppresses the frequency deviation. In addition, the control strategy has been verified to effectively eliminate the frequency deviation caused by the uncertainty of the system parameters. From Figure 3, it concludes that the designed disturbance observer can track the load disturbance.
Multi-Area Power System
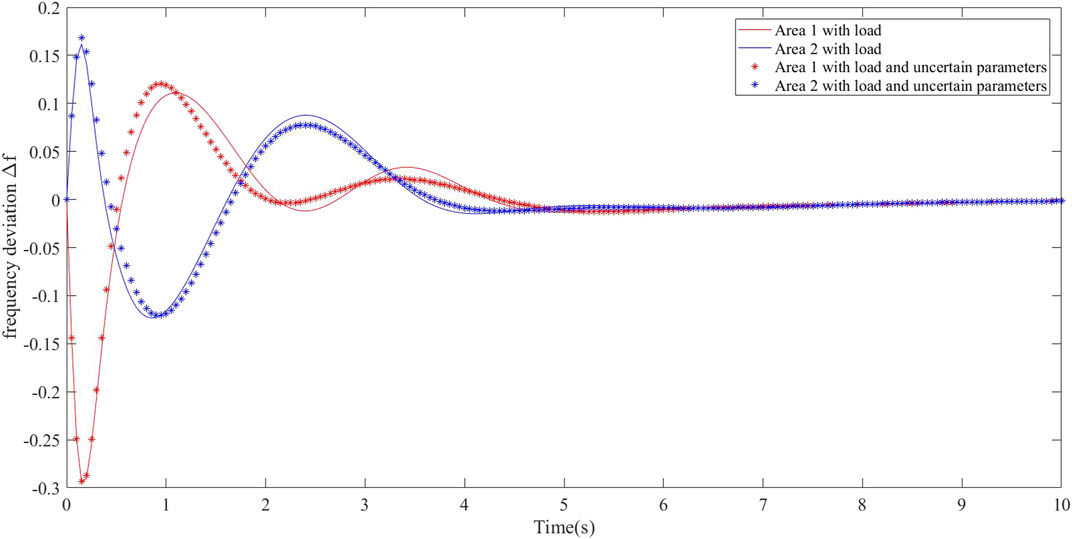
There are linear disturbances and parameter uncertainties in multi-area systems
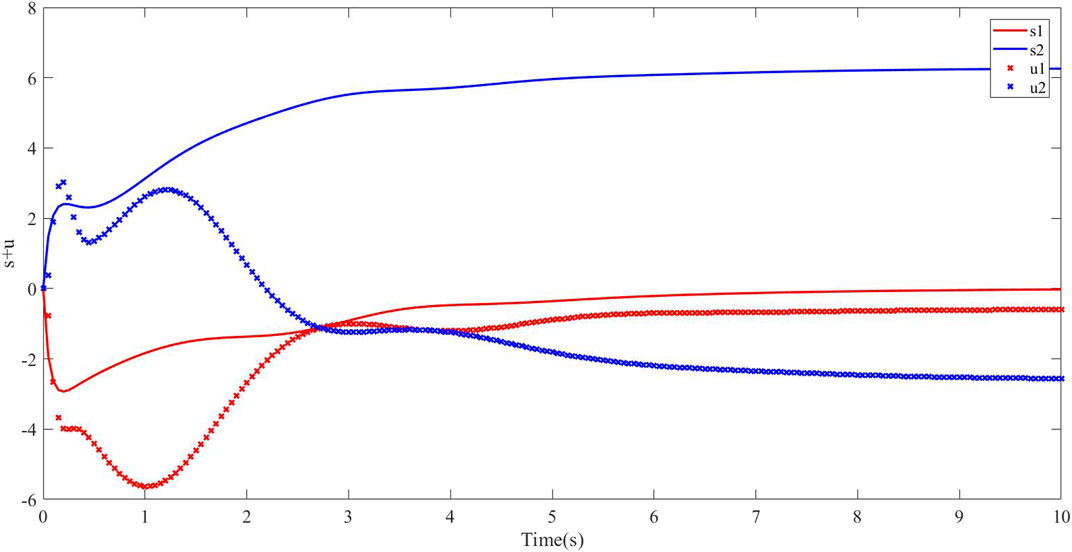
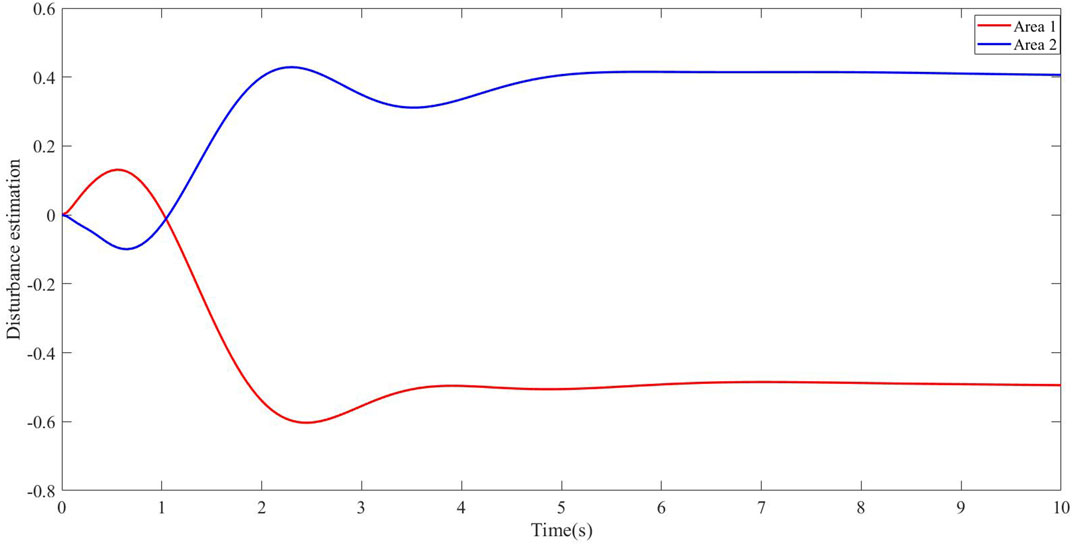
In multi-area systems, it can be concluded that when the system has disturbances and nonlinear parameter uncertainties, the system frequency can be eliminated with the designed SMC from Figure 4. In addition, we can know that the power exchange of tie line converges to zero at 10 s from Figure 5. The sliding mode surface and control law in the system are presented in Figure 6. In Figure 7, the estimated values of the disturbance observer in area 1 and area 2 can effectively estimate the load disturbance.
Conclusion
In this paper, the frequency in the power system, regarded as the most basic feature of the power system, is solved by the designed control strategy. An improved SMC is proposed, which guarantees the stability of the system with disturbances. Firstly, the disturbance observer is used in LFC, which calculates the disturbance. Furthermore, it is proved by Lyapunov stability theory. Secondly, the adaptive SMC based on the disturbance observer is designed, which destroys the conservativeness of the traditional SMC. Then, it is proved to ensure the system stability. Finally, several simulation results are presented. In addition, for power systems with nonlinear characteristics, the advanced control strategy will be further studied.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
SL provided the main idea of this paper. MW and YZ were responsible for the writing work of this paper. HW and QL carried out the simulation.
Funding
This work was supported by Liaoning Revitalization Talents Program (XLYC1907138), Natural Science Foundation of Liaoning Province (2019-MS-239), Key R&D Program of Liaoning Province (2020JH2/10300101) and Technology Innovation Talent Fund of Shenyang (Grant Nos. RC190360, RC200252).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ai-Hamouz, Z. M., and AbdeI-Magid, Y. L. (1993). Variable Structure Load Frequency Controllers for Multiarea Power Systems. Int. J. Electr. Power Energ. Syst. 15 (5), 293–300.
Bevrani, H., and Hiyama, T. (2008). Robust Decentralised PI Based LFC Design for Time Delay Power Systems. Energ. Convers. Management 49 (2), 193–204. doi:10.1016/j.enconman.2007.06.021
Chaiyatham, T., Ngamroo, I., Pothiya, S., and Vachirasricirikul, S. (2019). Design of Optimal Fuzzy Logic-PID Controller Using Bee colony Optimization for Frequency Control in an Isolated Wind-Diesel System. 2009 Proceedings of the Transmission & Distribution Conference & Exposition: Asia and Pacific, Seoul Korea (South) 1–4. doi:10.1109/TD-ASIA.2009.5356804
Chen, G., Li, Z., Zhang, Z., and Li, S. (2020). An Improved ACO Algorithm Optimized Fuzzy PID Controller for Load Frequency Control in Multi Area Interconnected Power Systems. IEEE Access 8, 6429–6447. doi:10.1109/access.2019.2960380
Dev, A., and Sarkar, M. K. (2019). Robust Higher Order Observer Based Non-linear Super Twisting Load Frequency Control for Multi Area Power Systems via Sliding Mode. Int. J. Control. Autom. Syst. 17 (7), 1814–1825. doi:10.1007/s12555-018-0529-4
Dou, C., Yue, D., Guerrero, J. M., Xie, X., and Hu, S. (2017). Multiagent System-Based Distributed Coordinated Control for Radial DC Microgrid Considering Transmission Time Delays. IEEE Trans. Smart Grid 8 (5), 2370–2381. doi:10.1109/tsg.2016.2524688
Farahani, M., Ganjefar, S., and Alizadeh, M. (2012). PID Controller Adjustment Using Chaotic Optimisation Algorithm for Multi-Area Load Frequency Control. IET Control. Theor. Appl. 6 (13), 1984–1992. doi:10.1049/iet-cta.2011.0405
Ginoya, D., Shendge, P. D., and Phadke, S. B. (2014). Sliding Mode Control for Mismatched Uncertain Systems Using an Extended Disturbance Observer. IEEE Trans. Ind. Electron. 61 (4), 1983–1992. doi:10.1109/tie.2013.2271597
Huang, C., Yue, D., Xie, X., and Xie, J. (2016). Anti-windup Load Frequency Controller Design for Multi-Area Power System with Generation Rate Constraint. Energies 9 (5), 1–18. doi:10.3390/en9050330
Jiang, L., Yao, W., Wu, Q. H., Wen, J. Y., and Cheng, S. J. (2012). Delay-dependent Stability for Load Frequency Control with Constant and Time-Varying Delays. IEEE Trans. Power Syst. 27 (2), 932–941. doi:10.1109/tpwrs.2011.2172821
Kahrobaeian, A., and Mohamed, Y. A.-R. I. (2012). Interactive Distributed Generation Interface for Flexible Micro-grid Operation in Smart Distribution Systems. IEEE Trans. Sustain. Energ. 3 (2), 295–305. doi:10.1109/tste.2011.2178045
Kamwa, I., Grondin, R., and Hebert, Y. (2001). Wide-area Measurement Based Stabilizing Control of Large Power Systems-A Decentralized/hierarchical Approach. IEEE Trans. Power Syst. 16 (1), 136–153. doi:10.1109/59.910791
Khodabakhshian, A., and Edrisi, M. (2008). A New Robust PID Load Frequency Controller. Control. Eng. Pract. 16 (9), 1069–1080. doi:10.1016/j.conengprac.2007.12.003
Khooban, M. H., Niknam, T., Blaabjerg, F., and Dragičević, T. (2017). A New Load Frequency Control Strategy for Micro-grids with Considering Electrical Vehicles. Electric Power Syst. Res. 143, 585–598. doi:10.1016/j.epsr.2016.10.057
Li, H., Shi, P., and Yao, D. (2017). Adaptive Sliding-Mode Control of Markov Jump Nonlinear Systems with Actuator Faults. IEEE Trans. Automat. Contr. 62 (4), 1933–1939. doi:10.1109/tac.2016.2588885
Li, H., Shi, P., Yao, D., and Wu, L. (2016). Observer-based Adaptive Sliding Mode Control for Nonlinear Markovian Jump Systems. Automatica 64, 133–142. doi:10.1016/j.automatica.2015.11.007
Li, H., Wang, J., Wu, L., Lam, H.-K., and Gao, Y. (2018). Optimal Guaranteed Cost Sliding-Mode Control of Interval Type-2 Fuzzy Time-Delay Systems. IEEE Trans. Fuzzy Syst. 26 (1), 246–257. doi:10.1109/tfuzz.2017.2648855
Lim, K. Y., Wang, Y., Guo, G., and Zhou, R. (1998). A New Decentralized Robust Controller Design for Multi-Area Load Frequency Control via Incomplete State Feedback. Optimal Control. Appl. Methods 19 (5), 1998. doi:10.1002/(sici)1099-1514(199809/10)19:5<345:aid-oca634>3.0.co;2-5
Liu, X., Kong, X., and Lee, K. Y. (2016). Distributed Model Predictive Control for Load Frequency Control with Dynamic Fuzzy Valve Position Modelling for Hydrothermal Power System. IET Control. Theor. Appl. 10 (4), 1653–1664. doi:10.1049/iet-cta.2015.1021
Lu, X., Yu, X., Lai, J., Guerrero, J. M., and Zhou, H. (2017). Distributed Secondary Voltage and Frequency Control for Islanded Microgrids with Uncertain Communication Links. IEEE Trans. Ind. Inf. 13 (2), 448–460. doi:10.1109/tii.2016.2603844
Ma, M., Zhang, C., Liu, X., and Chen, H. (2017). Distributed Model Predictive Load Frequency Control of the Multi-Area Power System after Deregulation. IEEE Trans. Ind. Electron. 64 (6), 5129–5139. doi:10.1109/tie.2016.2613923
Mi, Y., Fu, Y., Wang, C., and Wang, P. (2013). Decentralized Sliding Mode Load Frequency Control for Multi-Area Power Systems. IEEE Trans. Power Syst. 28 (4), 4301–4309. doi:10.1109/tpwrs.2013.2277131
Mu, C., Liu, W., Xu, W., and Rabiul Islam, M. (2017). Observer-based Load Frequency Control for Island Microgrid with Photovoltaic Power. Int. J. Photoenergy 2017, 1–11. doi:10.1155/2017/2851436
Pan, C. T., and Liaw, C. M. (1989). An Adaptive Controller for Power System Load-Frequency Control. IEEE Trans. Power Syst. 4 (1), 122–128. doi:10.1109/59.32469
Rashidi, M., Rashidi, F., Arjomand, A. S., and Sahragard, J. (2004). Design of a Robust and Adaptive Load Frequency Controller for Multi-Area Power Networks with System Parametric Un-certainties Using TDMLP Neural Network. IEEE International Conference on Systems, Man and Cybernetics. 3698–3703. The Hague, Netherlands. 10-13 Oct. 2004.
Sivaramakrishnan, A. Y., Hariharan, M. V., and Srisailam, M. C. (1984). Design of Variable-Structure Load-Frequency Controller Using Pole Assignment Technique. Int. J. Control 40 (3), 487–498. doi:10.1080/00207178408933289
Tang, Y., Yang, J., Yan, J., and He, H. (2015). Intelligent Load Frequency Controller Using GrADP for Island Smart Grid with Electric Vehicles and Renewable Resources. Neurocomputing 170, 406–416.
Wang, R., Sun, Q., Hu, W., Li, Y., Ma, D., and Wang, P. (2021a). SoC-based Droop Coefficients Stability Region Analysis of the Battery for Stand-Alone Supply Systems with Constant Power Loads. IEEE Trans. Power Electron. 36 (7), 7866–7879. doi:10.1109/tpel.2021.3049241
Wang, R., Sun, Q., Ma, D., and Liu, Z. (2019). The Small-Signal Stability Analysis of the Droop-Controlled Converter in Electromagnetic Timescale. IEEE Trans. Sustain. Energ. 10 (3), 1459–1469. doi:10.1109/tste.2019.2894633
Wang, R., Sun, Q., Tu, P., Xiao, J., Gui, Y., and Wang, P. (2021b). Reduced-order Aggregate Model for Large-Scale Converters with Inhomogeneous Initial Conditions in Dc Microgrids. IEEE Trans. Energ. Convers. 36 (3), 2473–2484. doi:10.1109/tec.2021.3050434
Wangdee, W., and Billinton, R. (2006). Considering Load-Carrying Capability and Wind Speed Correlation of WECS in Generation Adequacy Assessment. IEEE Trans. Energ. Convers. 21 (3), 734–741. doi:10.1109/tec.2006.875475
Wen Tan, W. (2010). Unified Tuning of PID Load Frequency Controller for Power Systems via IMC. IEEE Trans. Power Syst. 25 (1), 341–350. doi:10.1109/tpwrs.2009.2036463
Keywords: load frequency control, interconnected power system, the disturbance observer, the adaptive control, sliding mode control
Citation: Wei M, Lin S, Zhao Y, Wang H and Liu Q (2021) An Adaptive Sliding Mode Control Based on Disturbance Observer for LFC. Front. Energy Res. 9:733910. doi: 10.3389/fenrg.2021.733910
Received: 30 June 2021; Accepted: 07 September 2021;
Published: 21 September 2021.
Edited by:
Dazhong Ma, Northeastern University, ChinaCopyright © 2021 Wei, Lin, Zhao, Wang and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sheng Lin, bGluc2hlbmdfc2llQDE2My5jb20=
 Mofan Wei1,2
Mofan Wei1,2 Sheng Lin
Sheng Lin