PMSM Wind Farm Aggregation Algorithm Based on Power Equivalence Principle

With the continuing increase of offshore wind farm power scale, it is urgent to propose a simplified wind farm model, which aggregates the entire wind farm into single or several aggregated wind turbine generators (WTGs), aiming to save computing resources and improve simulation speed. A novel aggregation algorithm that considers the power loss of offshore submarine cable is proposed, which is different from the traditional wind farm modeling method that adopts amplifying transformer as aggregation medium. Moreover, multi machine aggregation (MMA) algorithm is furtherly proposed to improve the aggregation accuracy. Simulation results verify that the proposed aggregation method can present the dynamic characteristics of wind farm with high accuracy, and can be popularized for other types of wind farm.

Introduction

In recent years, the penetration of wind energy and the scale of wind farm are increasing rapidly (Zou et al., 2014), at the same time, since the energy efficiency for offshore wind energy is relatively higher than onshore wind energy, so there is an obvious trend that the application focus is shifting from offshore to onshore wind farm. On the other hand, wind power is inherently random and intermittent (Sanchez et al., 2012), with the continuing increase of wind power scale, this will impose adverse impact on the stability operation of large scale wind farm, so before the construction of wind farm, it is necessary to conduct a comprehensive feasibility analysis, aiming to analyze the interactive behavior between wind farm and power grid (Xue et al., 2013; Muljadi et al., 2006). Nowadays the modeling of wind farm is usually focused on onshore wind farm with doubly-fed induction generator (DFIG) as the main generator type, but as for offshore wind farm, it usually adopts permanent magnet synchronous motor (PMSM) as the main generator type, so there is also an urgent need to conduct research and analysis on PMSM offshore wind farm and its aggregation application.

For engineering practice, the impact of wind power integrated into power grid is usually analyzed from the perspective of “wind farm” (Ding et al., 2013), if detailed model is adopted for each WTG in one single wind farm, this will lead to an incredible increase in the scale of simulation, one effective solution is to build a simplified wind farm aggregation model to increase the simulation speed while maintaining accuracy. Previous researches have already focused on single machine aggregation (SMA) (Mercado-Vargas et al., 2015) and multi machine aggregation (MMA) (Badr et al., 2015). For SMA aggregation, the entire wind farm will be integrated into one single large WTG, the interface characteristics of single aggregated WTG is the same compared with that of wind farm (L. M. Fernandez et al., 2005). For MMA aggregation, the entire wind farm will be aggregated into several large WTGs according to certain indexes, normally the wind speed will be the selected as the main grouping index. (H. Dong, 2018). Amplifying transformer is usually adopted to conduct the aggregation work, (Conroy et al., 2009)- (Slootweg et al., 2003), the primary winding is connected to a single WTG, while the output power from the secondary winding is amplified with an artificial constant, this method is easy to conduct and understand, but the most obvious drawback is that the mechanism of adopting amplifying transformer as aggregation medium still needs further verification, and the dynamic characteristics of transmission line or cable is neglected (Yang et al., 2012; Ali et al., 2013), all these shortcomings will severely influence the aggregation accuracy, making aggregation model less convincing. Different from the aggregation method which adopts amplifying transformer, aggregation algorithm is used to calculate the aggregated generator parameter according to the single WTG parameter as well as the number of WTGs in wind farm (Chowdhury et al., 2010; Li et al., 2011).

At present, some results have been achieved in the research of dynamic aggregation modeling of onshore wind farms. However, unlike onshore wind farms, offshore wind turbines have a larger unit capacity and use cable lines as the main collection lines, this is one of the most significant difference from that used on onshore wind farm, besides, the impact brought by the submarine cable cannot be ignored. The modalities of the aggregation model of wind turbines are more abundant (Wang et al., 2018; Badr et al., 2015), and the dynamic characteristics of the collection lines of wind farms have also become a main object of aggregation research, which cannot be ignored.

At the same time, unlike the overhead line collection lines of onshore wind farms, the charging capacity of the cable collection lines of offshore wind farms is very large, generally 20–25 times than that of the overhead line circuits, which is equivalent to the reactive power compensation equipment being connected in parallel, so ignoring the transmission line capacitance in the conventional aggregation method will bring great errors, and the aggregation result will also have a significant difference between the detailed model and the aggregated model. (Teng et al., 2019; Du et al., 2019).

In this paper, a comprehensive aggregation algorithm is proposed considering the power loss of offshore wind farm submarine cable, including the aggregation of WTG electrical parameters, pneumatic parameters as well as the integration of transmission line, the power equivalent principle is also used to calculate all the aggregation parameters of wind farm, simulation results verify that the proposed aggregation algorithm can match well with detailed model, while MMA model is more accurate than SMA to reflect the operation of wind farm in various wind speed environment.

Modeling of Offshore PMSM Wind Farm

Structure of Offshore PMSM Wind Farm

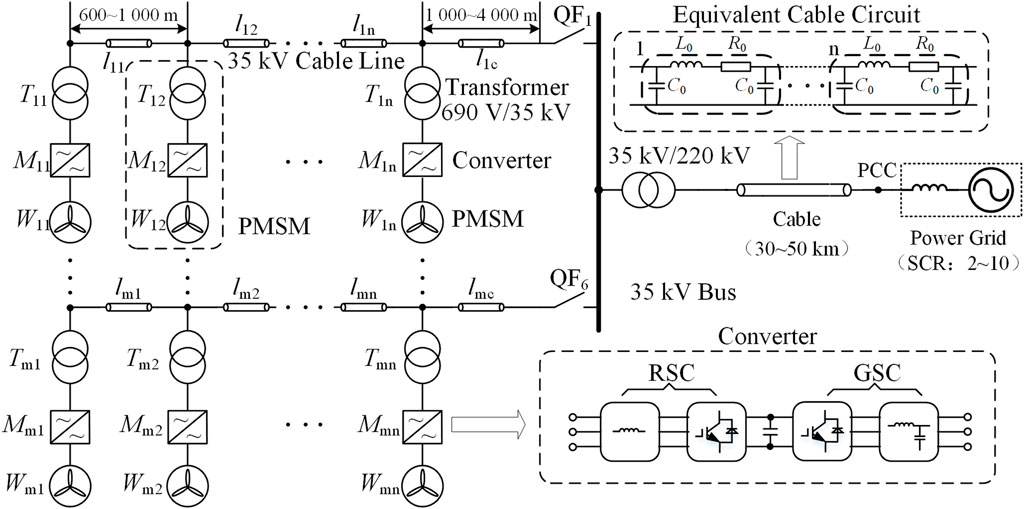
Offshore wind farm usually adopts permanent magnet synchronous motor (PMSM) as the main generation type due to its relative higher power rating compared with that of tradition doubly-fed induction generator (DFIG). As is shown in Figure 1, one single wind farm usually consists of up to 16 feeders which are connected to collection bus, for each feeder in wind farm, up to 12 WTGs are connected in series in each feeder. A typical simplified PMSM wind farm is selected to conduct aggregation simulation research in this paper, six feeders are linked to 35 kV collection bus with three or four WTG connected in series in one single feeder, altogether 34 WTGs are included in this wind farm.

FIGURE 1

FIGURE 1. Topological structure of PMSM wind farm.

Operation and Control of PMSM Wind Farm

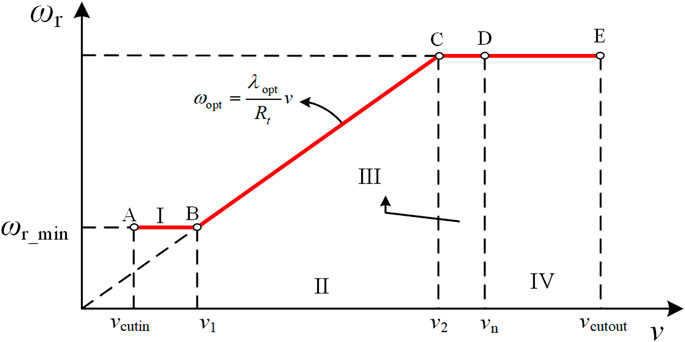
As is shown in Figure 2, the working interval within the full wind speed range for PMSM can be divided into four operation modes, which are I-low constant speed mode, II-MPPT mode, III-high constant speed mode and IV-constant power mode respectively, x-axis represents the wind speed v, and y-axis refers to rotor speed ω_r.

FIGURE 2

FIGURE 2. Operation mode division under full wind condition.

When wind speed locates within [v_cutin, v₁], the purpose is to control the rotor speed to stabilize at a low constant speed ω_{r_min}. With the increase of wind speed, PMSM then enters the MPPT stage, PMSM will operate at a particular rotor speed so as to catch the maximum power from wind, both tip speed ratio λ and rotor speed will be controlled at their optimal value λ_opt and ω_{r_opt.} When wind speed exceeds v₂, rotor speed reaches the rated value ω_{r_max}, PMSM will then operate at high constant speed ω_{r_max} until exceeding the rated power, afterwards the pitch angle regulator will be activated and PMSM will operate at constant power mode.

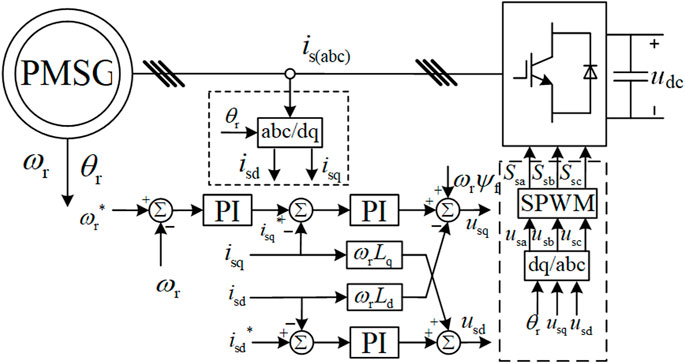
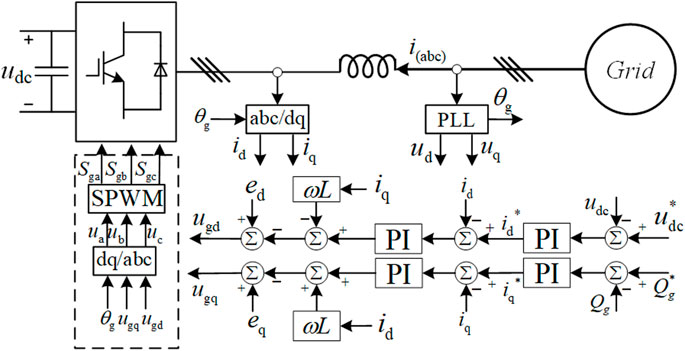
Each PMSM WTG in the target research wind farm adopts traditional Vector Control (VC) strategy to decouple the control of WTG active power and reactive power, the control diagram for PMSM rotor side converter (RSC) and grid side converter (GSC)is shown in Figures 3, 4 respectively.

FIGURE 3

FIGURE 3. Control diagram of PMSM RSC.

FIGURE 4

FIGURE 4. Control diagram of PMSM GSC.

PMSM RSC adopts rotor flux linkage oriented vector control strategy, the control purpose of this control strategy is to control RSC active power and reactive power independently. As is shown in Figure 3, two cascaded control loops are included in RSC control strategy, the control object of active power control loop is PMSM rotor speed ω_r, so as to track the MPPT point given a specific wind speed. For reactive power control loop, the d-axis reference current i_sd^* is set to zero, so that the PMSM electromagnetic torque can only be influenced by q-axis stator current i_sq, which is exactly the output of rotor speed closed loop.

The control diagram of PMSM GSC is shown in Figure 4, GSC is aimed at controlling dc-link voltage and balancing active power through dc-link capacitor, the GSC d axis reference current is obtained from the output of dc-link voltage regulator and the q axis reference current is get via reactive power regulator.

Aggregation Principle and Algorithm

Submarine cable is considered as one important aggregation object in this paper, which is less emphasized in traditional amplifying transformer aggregation strategy, the conditions that the aggregation of wind farm must meet are:

1) The amplitude and phase of voltage at PCC of aggregation model is equal to that of wind farm detailed model.

2) The total capacity of aggregation model is the sum of the capacities of all WTGs in the detailed model.

3) The consumed active power inside the aggregation model is equal to that of wind farm detailed model.

4) The inductive and capacitive reactive power of aggregation model is equal to that of wind farm detailed model.

PMSM WTG Parameter Aggregation

Based on the principles listed above, the equivalent parameters of aggregated PMSM WTG can be calculated with Eq. 1, 2, where a total of m WTGs with the same generation type are aggregated into one single WTG.

$\{\begin{array}{l}{S}_{eq}=\sum _{i=1}^m{S}_i=m{S}_n\\ X_{s-eq}=\frac{x_s}{m}{r}_{s-eq}=\frac{r_s}{m}{B}_{c\_eq}=m{B}_c\end{array}(1)$

$\{\begin{array}{cc}{H}_{t\_eq}=H_t& H_{g\_eq}=H_g\\ K_{s\_eq}=K_s& D_{s\_eq}=D_s\\ S_{T\_eq}=m{S}_T& Z_{T\_eq}=\frac{Z_T}{m}\end{array}(2)$

S_n is the rated capacity of one single WTG, x_s, r_s and B_c are the reactance, resistance and admittance of the WTG; m is the total number of WTGs in the same cluster; S_T is the rated capacity of the transformer; Z_T is the impedance of the transformer; H_t and H_g is the inertia time constant of the wind turbine and generator.

As for the aggregation of wind speed, there are a variety of aggregation methods to calculate the aggregated wind speed for wind farm. When the element of wake effect is not taken in account, then the aggregated wind speed is the same as the speed for single WTG:

$v_{eq}=v(3)$

However, when taking wake effect into consideration, then the calculation of aggregated wind speed is based on the power curve of WTG, firstly the power of each WTG in wind farm needs to be calculated and then get the average power, so that the aggregated wind speed can be drawn from the average wind speed as well as the given WTG power curve, assuming that the number of WTGs that will be aggregated is m, then the output power can be calculated as:

$P_m=f\left(v_m\right)(4)$

Based on the power equation in Eq. 4, the aggregated wind speed can be calculated from:

$v_{eq}=\frac{1}{m}{\displaystyle \sum _{i=1}^m{f}^{-1}\left(v_k\right)}(5)$

PMSM Wind Farm Aggregation Considering Submarine Cable Power Loss

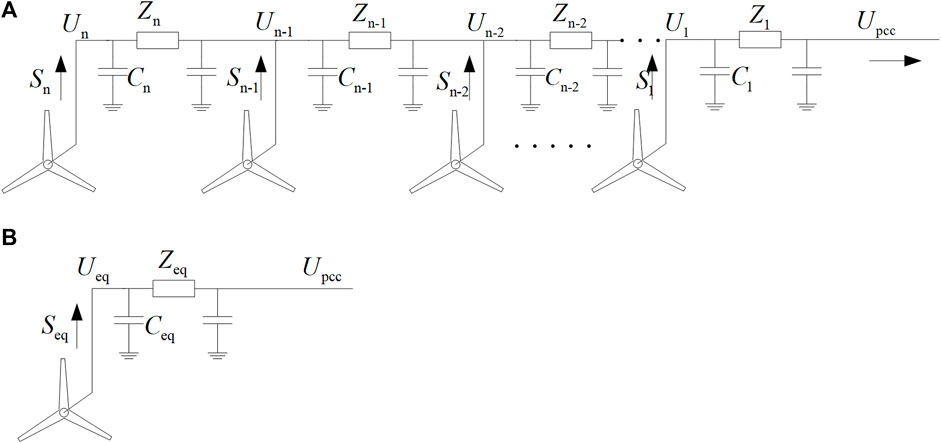
For offshore PMSM wind farm, the ground capacitance is usually 20–25 times than that of overhead lines. So it cannot be ignored in the SMA analysis. Active power equivalent principle is applied in the aggregation of offshore submarine cable, as is shown in Figure 5, S_i and U_i represent the output power and terminal voltage of the ith WTG on the feeder respectively, C_i and Z_i represent the capacitance and impedance of the ith cable line on the feeder respectively, U_pcc represents the voltage at the PCC point. And S_eq and U_eq represent the equivalent output power and terminal voltage of the aggregated WTG separately, C_eq and Z_eq represent the equivalent capacitance and impedance of the aggregated cable line.

FIGURE 5

FIGURE 5. Transmission Line Aggregation process. (A) Before Equivalence. (B) After Equivalence.

Based on the power equivalent principle, in order to calculate SMA submarine cable parameter, the power loss of the impedance on the nth cable at the end of the feeder, and the power loss of the impedance of the mth cable on the feeder can be expressed as:

$\{\begin{array}{l}\Delta S_n={\left(S_n-j\frac{1}{2}{C}_n{U}_n^2\right)}^2{Z}_n/U_n^2\\ \Delta S_m=\frac{{\left({\displaystyle \sum _{i=m}^{n-1}\left(S_i-j\frac{1}{2}\left(C_{i+1}+C_i\right)U_i^2+\Delta S_{i+1}\right)}-j\frac{1}{2}{C}_n{U}_n^2\right)}^2{Z}_m}{U_m^2}\end{array}(6)$

Based on Eq. 6, the power loss of all submarine cables on one feeder, and the power loss on the equivalent circuit can be expressed as:

$\{\begin{array}{l}\Delta S_{z\text{total}}=\Delta S_1+\Delta S_2+\dots +\Delta S_n\\ \Delta S_{zeq}=\frac{{\left(S_{eq}-j\frac{1}{2}{C}_{eq}{U}_{eq}^2\right)}^2{Z}_{eq}}{U_{eq}^2}\end{array}(7)$

The expression of equivalence impedance Z_eq can be calculated based on the power equivalent principle of ΔS_ztotal = ΔS_zeq:

$Z_{eq}=\frac{\Delta S_{z\text{total}}}{{\left(S_{eq}-j\frac{1}{2}{C}_{eq}{U}_{eq}^2\right)}^2}{U}_{eq}^2(8)$

Besides, according to the principle that the reactive power consumed on the capacitor before and after the cable line equivalence is the same, the equivalent capacitor can be expressed as:

$C_{\text{eq}}=\frac{\left(C_n{U}_n^2+C_n{U}_{n-1}^2+C_{n-1}{U}_{n-1}^2+\dots +C_2{U}_2^2+C_1{U}_2^2+C_1{U}_1^2\right)}{\left(U_{eq}^2+U_1^2\right)}(9)$

Equations 1–9 are the main calculation algorithm for PMSM wind farm single machine aggregation. When referring multi machine aggregation, wind speed for each WTG is selected as the main grouping index, all WTGs in a wind farm are grouped into four groups according to the WTG operation mode so as to minimize the aggregation error, since the operation mode is directly related to the wind speed and wind speed can be well estimated and calculated through various prediction algorithm, so it is easy to group one single wind farm based on wind speed for each WTG.

Simulation Results

Simulation Verification of SMA for Grid Fault Situation.

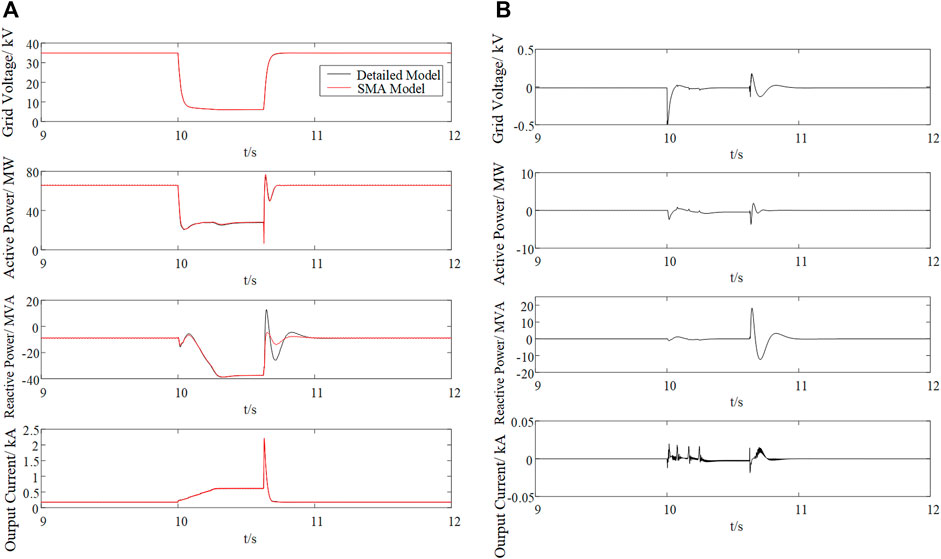
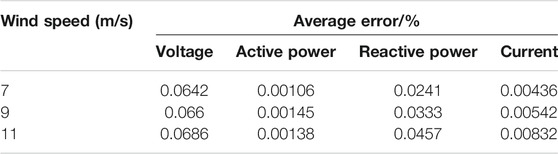
Simulation verification is firstly carried out between detailed model and SMA model under the wind speed of 7, 9, and 11 m/s respectively. A three-phase short circuit fault occurs in simulation and the fault duration is 0.625 s.

Figure 6A shows the comparison between the detailed model and SMA model under the wind speed of 7 m/s. The first panel is the voltage RMS value, indicating that grid voltage drops to 20% of the normal value and lasts for 625 ms, the rest panels are output active power, reactive power and current. Figure 6B is the average error curve of active power, reactive power and current at the PCC point. Based on Figure 6A and Figure 6B, it can be seen that the two curves overlap well with each other in steady state. Although there is a deviation in the dynamic process, it is not very large, which means that the SMA model can reflect the dynamic process of the detailed model.

FIGURE 6

FIGURE 6. 7 m/s LVRT response comparison. (A) Comparison Results (B) Error Results.

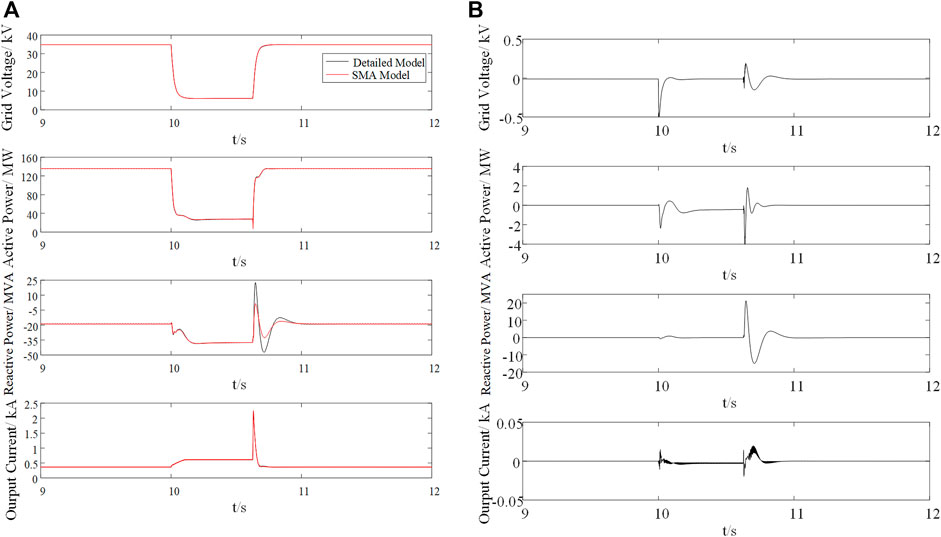
Similar conclusions can also be found in Figure 7, 8, where the wind speed are 9 and 11 m/s respectively.

FIGURE 7

FIGURE 7. 9 m/s LVRT response comparison. (A) Comparison Results (B) Error Results.

FIGURE 8

FIGURE 8. 11 m/s LVRT response comparison. (A) Comparison Results (B) Error Results.

In order to investigate the aggregation accuracy of SMA model, we define the average error E_x as an important index to quantify the aggregation accuracy, as is shown as:

$E_x=\frac{1}{n}\frac{{\displaystyle \sum _{i=1}^n\left(X_{eqi}-X_i\right)}}{X_N}\times 100\%(10)$

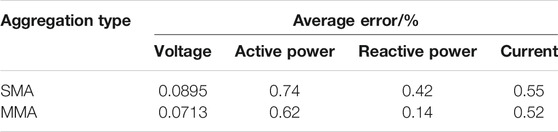
where x is the parameter to be investigated, n is the number of sampling points, the subscript eq indicates the equivalent parameter of the aggregation model while N indicates the rated value. As is shown from Tables 1–3, the average error comparison before, during and after grid fault are listed respectively for further analysis.

TABLE 1

TABLE 1. Average error before grid fault between SMA and detailed model.

It can be seen from Table 1 that for different wind speeds, when the collection line is a cable line, the results of the wind farm aggregation model match well with the detailed wind model, the average error of voltage, current and active power is within 0.12%, while the error of reactive power is within 0.05%, which can fully prove the correctness of the aggregation method proposed in this paper. As the wind speed increases, it can be seen that the magnitude of the error is also increasing. The reason is that the output parameter is increased with the increase of wind speed, but the base value used in the evaluation method is unchanged, which results in the increase of average error, but the increase is still within the normal range.

Comparing Table 1, Table 2, and Table 3, it can be seen that the average error during grid fault process is larger than that before and after grid fault. The main reason is that the line parameters are calculated at the rated power for the convenience of simulation, during grid fault process, the output active power is less than that in steady state, which causes the loss on the line of the aggregated model to be different from detailed model.

TABLE 2

TABLE 2. Average error during grid fault between SMA and detailed model.

TABLE 3

TABLE 3. Average error after grid fault between SMA and detailed model.

Simulation Verification Between SMA and MMA Algorithm.

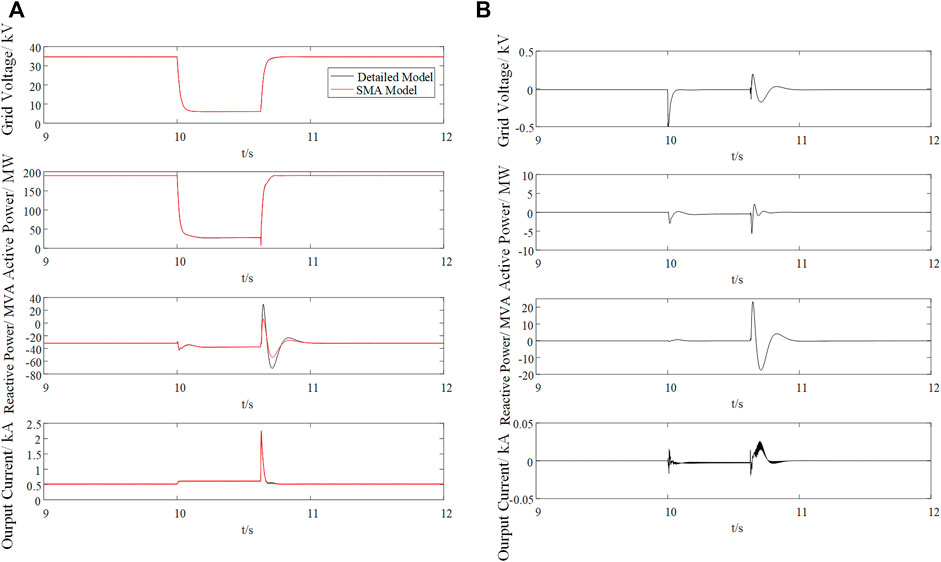
Wind speed of each wind turbine generator is randomly set to compare the aggregation accuracy between SMA and MMA algorithm. Wind speed for each WTG is selected as the main grouping index, as is shown in Figure 2, the wind speed of wind turbine generator determines the operation mode, so all wind turbine generators running in the same operation mode are grouped together to be aggregated into one WTG.

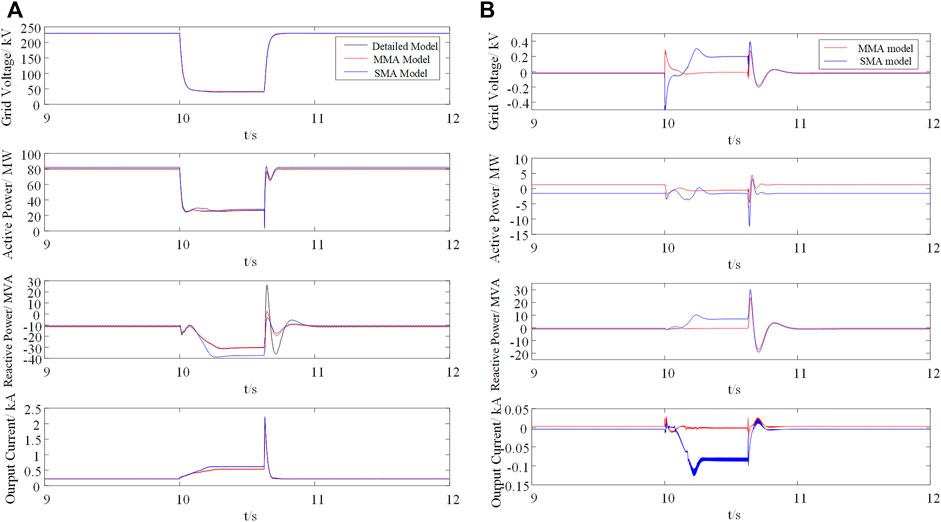
Simulation results are shown in Figure 9 to compare the aggregation accuracy between detailed model, MMA model and SMA model. A three-phase symmetrical short-circuit fault occurs in the simulation at t = 10 s, the amplitude of grid voltage drop is 20% of the rated voltage. The first panel of Figure 9A is the grid voltage while the rest panels are output active power, reactive power and current. Figure 9B shows the error curve of PCC point voltage RMS, output active power, output reactive power and output current. Combining the two figures, it can be seen that the MMA model has higher accuracy than SMA model, MMA can better reflect the dynamic process of the detailed model in the dynamic process.

FIGURE 9

FIGURE 9. Comparisons between SMA and MMA algorithm. (A) Comparison Results (B) Error Results.

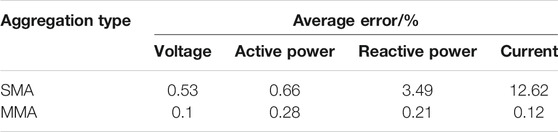
From the above simulation results, although the response trend of SMA model, MMA model and detailed model are basically the same, there are still dynamic errors during the whole process, so that a quantitative analysis is still needed to calculate the error before and during grid fault. The results are shown in the following table.

Comparing Table 4 and Table 5, it can be seen that the MMA model has higher accuracy than SMA model. When wind turbines are in different operation modes, the SMA model is not sufficient enough to characterize the entire wind farm, the average error between MMA model and the detailed model are smaller than that between SMA model and the detailed model, showing that grouping wind farm according to wind speed can effectively improve the aggregation accuracy.

TABLE 4

TABLE 4. Average error before grid fault between SMA, MMA and detailed model.

TABLE 5

TABLE 5. Average error during grid fault between SMA, MMA and detailed model.

Conclusion

This paper proposes a comprehensive aggregation algorithm with the consideration of the power loss of offshore wind farm submarine cable. The aggregation algorithm includes the aggregation of WTG electrical parameters, pneumatic parameters as well as the integration of transmission line, the power equivalent principle is used to calculate all the aggregation parameters of wind farm. Detailed conclusions are:

1) The aggregated model can comprehensively reflect the dynamic characteristics of wind farm under different working conditions.

2) Simulation results verify that the proposed aggregation algorithm can match well with detailed model, while MMA model is more accurate than SMA to reflect the operation of wind farm in various wind speed environment (Sanchez et al., 2012; Mercado-Vargas et al., 2015).

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

HS is responsible for the research on novel aggregation algorithm and analysis. XC is responsible for the research on novel aggregation algorithm and analysis together with HS. HY is responsible for the collection of wind farm parameter and the set-up of simulation platform. JZ is responsible for the collection of wind turbine generator parameter. YQ is responsible for the simulation of wind turbine generator and the novel aggregation algorithm. ZZ is responsible for the simulation of aggregated wind farm and the accuracy analysis of the aggregation algorithm.

Funding

Project Supported by the State Key Laboratory of Advanced Power Transmission Technology (SGTYHT/18-JS-206).

Conflict of Interest

Authors HY and JZ were employed by the State Key Laboratory of Advanced Power Transmission Technology of Global Internet Research Institute Energy Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a shared affiliation, though no other collaboration, with several of the authors HS, XC, YQ, and ZZ at the time of the review.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ali, M., Ilie, I.-S., Milanovic, J. V., and Chicco, G. S. (2013). Wind Farm Model Aggregation Using Probabilistic Clustering. IEEE Trans. Power Syst. 28, 309–316. doi:10.1109/TPWRS.2012.2204282

CrossRef Full Text | Google Scholar

Badr, M. A., Atallah, A. M., and Bayoumi, M. A. S. (2015). Comparison between Aggregation Techniques for PMSG Wind Farm. Energ. Proced. 74, 1162–1173. doi:10.1016/j.egypro.2015.07.759

CrossRef Full Text | Google Scholar

Badr, M. A., Atallah, A. M., and Bayoumi, M. A. (2015). Modifying the Aggregated Wind Farm Model with a Controller. Adv. Energ. Res. 3 (3), 133–142. doi:10.12989/eri.2015.3.3.133

CrossRef Full Text | Google Scholar

Chowdhury, M. A., Hosseinzadeh, N., Billah, M. M., and Haque, S. A. (2010). Dynamic DFIG Wind Farm Model with an Aggregation Technique. Int. Conf. Electr. Computer Eng. (ICECE 2010) 2010, 330–333. doi:10.1109/ICELCE.2010.5700695

CrossRef Full Text | Google Scholar

Conroy, J., and Watson, R. S. (2009). Aggregate Modelling of Wind Farms Containing Full-Converter Wind Turbine Generators with Permanent Magnet Synchronous Machines: Transient Stability Studies. IET Renew. Power Gener. 3, 39–52. doi:10.1049/iet-rpg:20070091

CrossRef Full Text | Google Scholar

Ding, N., Lu, Z., Qiao, Y., and Min, Y. (2013). Simplified Equivalent Models of Large-Scale Wind Power and Their Application on Small-Signal Stability. J. Mod. Power Syst. Clean. Energ. 1, 58–64. doi:10.1007/s40565-013-0005-3

CrossRef Full Text | Google Scholar

Dong, H., Bai, Y., Li, X., Li, H., and Ma, M. Aggregation Modeling of Wind Farms Based on Multi Machine Representation. Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), 1–6. October 2018. Beijing, China, doi:10.1109/EI2.2018.8582531

CrossRef Full Text | Google Scholar

Du, W., Dong, W., Wang, H., and Cao, J. (2019). Dynamic Aggregation of Same Wind Turbine Generators in Parallel Connection for Studying Oscillation Stability of a Wind Farm. IEEE Trans. Power Syst. 34 (6), 4694–4705. doi:10.1109/TPWRS.2019.2920413

CrossRef Full Text | Google Scholar

Feng Xue, F., Xiao-Fang Song, X.-F., Kang Chang, K., Tian-Ci Xu, T.-C., Feng Wu, F., and Yu-Qing Jin, Y.-Q. S. (July 2013). Equivalent Modeling of DFIG Based Wind Farm Using Equivalent Maximum Power Curve. Proceedings of the 2013 IEEE Power & Energy Society General Meeting, 1–5. Vancouver, BC, Canada, doi:10.1109/PESMG.2013.6672848

CrossRef Full Text | Google Scholar

Fernandez, L. M., Garcia, C. A., Jurado, F., and Saenz, J. R. (June 2005). Aggregation of Doubly Fed Induction Generators Wind Turbines under Different Incoming Wind Speeds. Proceedings of the 2005 IEEE Russia Power Tech., 1–6. St. Petersburg, Russia, doi:10.1109/PTC.2005.4524685

CrossRef Full Text | Google Scholar

Li, S., Liu, Z., and Jia, Y. Dynamic Aggregation of Doubly-Fed Induction Generators (DFIGs) for Stability Analysis of Wind Power Systems. Proceedings of the IEEE Power and Energy Society General Meeting, 1–6. July 2011. Detroit, MI, USA, doi:10.1109/PES.2011.6038990

CrossRef Full Text | Google Scholar

Mercado-Vargas, M. J., Gómez-Lorente, D., Rabaza, O., and Alameda-Hernandez, E. (2015). Aggregated Models of Permanent Magnet Synchronous Generators Wind Farms. Renew. Energ. 83, 1287–1298. doi:10.1016/j.renene.2015.04.040

CrossRef Full Text | Google Scholar

Muljadi, E., Butterfield, C. P., Ellis, A., Mechenbier, J., Hochheimer, J., Young, R., et al. (June 2006). Equivalencing the Collector System of a Large Wind Power Plant. Proceedings of the2006 IEEE Power Engineering Society General Meeting 1, 9. Montreal, QC, Canada, doi:10.1109/PES.2006.1708945

CrossRef Full Text | Google Scholar

Sanchez, A. G., Molina, M. G., and Lede, A. M. R. (2012). Dynamic Model of Wind Energy Conversion Systems with PMSG-Based Variable-Speed Wind Turbines for Power System Studies. Int. J. Hydrogen Energ. 37, 10064–10069. doi:10.1016/j.ijhydene.2011.12.077

CrossRef Full Text | Google Scholar

Slootweg, J. G., de Haan, S. W. H., Polinder, H., and Kling, W. L. S. (2003). General Model for Representing Variable Speed Wind Turbines in Power System Dynamics Simulations. IEEE Trans. Power Syst. 18, 144–151. doi:10.1109/TPWRS.2002.807113

CrossRef Full Text | Google Scholar

Teng, W., Wang, X., Wang, X., Meng, Y., and Shi, W. (2019). An Improved Support Vector Clustering Approach to Dynamic Aggregation of Large Wind Farms. Csee Jpes 5, 2. doi:10.17775/CSEEJPES.2016.01600

CrossRef Full Text | Google Scholar

Wang, P., Zhang, Z., Huang, Q., Wang, N., Zhang, X., and Lee, W.-J. (2018). Improved Wind Farm Aggregated Modeling Method for Large-Scale Power System Stability Studies. IEEE Trans. Power Syst. 33, 6332–6342. doi:10.1109/TPWRS.2018.2828411

CrossRef Full Text | Google Scholar

Yang, D., Ban, L., Xiang, Z., Du, N., Zheng, B., and Wu, Z. S. (July 2012). An Aggregation Method of Wind Farm Model for Electromagnetic Transient Simulation Analysis. Proceedings of the 2012 IEEE Power Electronics and Machines in Wind Applications, 1–5. Denver, CO, USA, doi:10.1109/PEMWA.2012.6316356

CrossRef Full Text | Google Scholar

Zou, J., Peng, C., Yan, Y., Zheng, H., and Li, Y. S. (2014). A Survey of Dynamic Equivalent Modeling for Wind Farm. Renew. Sustainable Energ. Rev. 40, 956–963. doi:10.1016/j.rser.2014.07.157

CrossRef Full Text | Google Scholar