- 1Electrical Power and Machines Engineering Department, Faculty of Engineering, Helwan University, Cairo, Egypt
- 2Faculty of Science and Engineering, Swansea University, Wales, United Kingdom
- 3Academy of Scientific Research and Technology (ASRT), Cairo, Egypt
Interconnecting two or more microgrids can help improve power system performance under changing operational circumstances by providing mutual and bidirectional power assistance. This study proposes two interconnected AC microgrids based on three renewable energy sources (wind, solar, and biogas). The wind turbine powers a permanent magnet synchronous generator. A solar photovoltaic system with an appropriate inverter has been installed. In the biogas generator, a biogas engine is connected to a synchronous generator. M1 and M2, two interconnected AC microgrids, are investigated in this study. M2 is connected to a hydro turbine, which provides constant power. The distribution power loss, frequency, and voltage of interconnected AC microgrids are modeled as a multi-objective function (OF). Minimizing this OF will result in optimal power flow and frequency enhancement in interconnected AC microgrids. This research is different from the rest of the research works that talk about the virtual inertia control (VIC) method, as it not only improves frequency using an optimal controller but also achieves optimal power flow in microgrids. In this paper, the following five controllers have been studied: proportional integral controller (PI), fractional-order PI controller (FOPI), fuzzy PI controller (FPI), fuzzy fractional-order PI controller (FFOPI), and VIC based on FFOPI controller. The five controllers are tuned using particle swarm optimization (PSO) to minimize the (OF). The main contribution of this paper is the comprehensive study of the performance of interconnected AC microgrids under step load disturbances, the eventual grid following/forming contingencies, and the virtual inertia control of renewable energy resources used in the structure of the microgrids, and simulation results are recorded using the MATLAB™ platform. The voltages and frequencies of both microgrids settle with zero steady-state error following a disturbance within 0.5 s with less overshoots/undershoots (3.7e-5/-0.12e-3) using VIC. Moreover, the total power losses of two interconnected microgrids must be considered for the different controllers to identify which one provides the best optimal power flow.
1 Introduction
Due to growing concerns about environmental factors, greenhouse gases (particularly CO2), and global warming, renewable energy sources (RESs) are now quickly developing all over the world. As a result, several issues with the integration of renewable energy into networks have been discussed in the literature, along with potential solutions. The primary traits of RESs that make it difficult to integrate them with the grid and the load are intermittent availability of the input source, which results in highly intermittent and unreliable power output, low flux density, meaning they require more space per unit of power generation than conventional generators, and low inertia. RESs, such as the solar photovoltaic system (SPVS) and wind energy converting system (WECS), have lower inertia than conventional sources, which reduces the grid’s ability to enhance stability.
In the literature, different integrations of RESs and their data have been discussed. The stability of microgrids is a significant part of interest. Some of the aspects of microgrids have been discussed and introduced in the literature by many authors (Farrokhabadi et al., 2020). Sustained low-frequency deviations are one of the problems in microgrids, as studied by Kundur et al. (2006), El-Fergany and El-Hameed (2017), and Firdaus et al. (2020). Another problem is voltage control in microgrid systems (Tu et al., 2018; Delavari and Naderian, 2019). There is literature in which these problems are solved separately and jointly. A microgrid comprising solar and wind needs a backup because of its intermittent nature. Inverter-connected battery backup is one of the proposals suggested in the study by Jayawardana et al. (2019) and Sharma et al. (2020). The other proposal is a connected diesel/biogas-based generating plant (Barik and Das, 2018). Many control strategies are performed in a wind–solar–diesel system using various optimizing techniques (Sheng and Zhang, 2017; Rezkallah et al., 2019; Puchalapalli et al., 2020). Some proposals have been given on AC and DC microgrids (Liang et al., 2019; Guo et al., 2021). Also, the rate of generation deviation in the SPVS is very high because of cloud changes (Zhao et al., 2020). The PV plant of the SPVS is connected to the power system via an inverter. So, control of the PV unit is presented by the control of the inverter (Chao et al., 2020).
The output power of the wind turbine is proportional to the square of the rotor diameter and the cube of the wind speed because of the aerodynamic characteristics (Yaramasu et al., 2015). The permanent magnet synchronous generator (PMSG) is commonly utilized in the WECS. However, the PMSG is robust and does not need separate field control (Gencer, 2016). The SPVS and WECS are coupled to the point of common coupling (PCC) by power inverters. Also, the connected inverter delivers virtual inertia to the network (Xi et al., 2018). There is literature that shows that the virtual inertia of the WECS and SPVS based on inverters can almost act as conventional generators that can be used for the dynamic stability of the power grid. However, an energy buffer must be saved (Johnson et al., 2020).
For a low-power network not like the SPVS and WECS, a biogas generator (BG) and diesel generator can be utilized as the controlled generation unit, as the fuel input BG-based generator can be controlled. Urban electrification has improved extremely in the previous decade. In improving countries, electrification has been carried out, but continuous power provision remains troublesome. These areas yet face power cuts for some time. The main cause for disturbed power provided are deprived grid supplies, reliance on conventional generation, weak power infrastructure, faraway distance transmission, and the value of urban and industrial parts (Ubilla et al., 2014; Suryakiran et al., 2018). In the literature, many methods of microgrids have been presented by the authors. However, to donate to a self-sufficient city interconnected with power availability relying on load segregation and setting priority loads has not been reasonable. So, a stability study of interconnected microgrids has been proposed to observe the network dynamics while sharing the power between two microgrids to guarantee an uninterrupted power supply.
The other effort to restrain the
The converter loss may share over 50% of the total distribution loss (Dabbaghjamanesh et al., 2020) in the AC microgrid. So, considering it in the control arrangements would be significant in decreasing the distribution power loss. In the study by Yuan et al. (2020), the overall distribution power loss of two interconnected AC microgrids is further almost fitted by a function of active and reactive power. Then, the optimization function is used to share the active and reactive power of each generation unit. The total distribution power loss of two interconnected AC microgrids, namely, power loss of each area and line loss, are modeled as the objective function of power loss of each generation unit and the AC link between two areas. In addition, sharing power between two areas is considered to cover the load’s demand according to the objective function. Therefore, the distribution loss minimization can be realized by adaptively adjusting the optimal parameters of the controller offline.
With sharing power among generation units (Boyd and Vandenberghe, 2004; Wang et al., 2021), a distributed optimization algorithm is presented for global distribution loss minimization. The simulation results validate the proposed control strategy for reducing the distribution power loss of two interconnected AC microgrids. The last challenge is enhancing the microgrid’s frequency under high penetration levels of renewable generation units. One solution is to install fast-reacting energy storage systems (ESS) with virtual inertia controllers via low-inertia power generation units; such controllers have been extensively studied in recent years (Boicea, 2014; Vorobev et al., 2017; Jiang et al., 2020; Abubakr et al., 2021; Fawzy et al., 2021; Kerdphol et al., 2021). Each control technique has its own advantages and restriction. The microgrid system’s position enables ideal energy management. To maximize power flow inside the setup, a local energy management system may regulate generators (and presumably loads, as well). Depending on the kind of operation, several objectives are set for energy management: grid-connected or an island (Akinyele et al., 2018). In the grid-connected mode, the typical goals are to reduce the price of energy import at the PCC, advance the power factor at the PCC, and optimize the voltage profile through the microgrid (Hashemi and Vahidinasab, 2021). In the islanded mode, which is used in the study by Hashemi and Vahidinasab (2021), the main aim of power management is to improve the system and motivate high reliability and flexibility in terms of frequency and voltage. Opposite to these inclusive reviews, which focused on virtual inertia topologies execution (Tamrakar et al., 2017), virtual inertia and frequency control for distributed energy generation units (Singh and Seethalekshmi, 2020), and inertia valuation improvement in power systems (Fernández-Guillamón et al., 2019), we focused on the virtual inertia control method designed to enhance the frequency deviation trouble in islanded AC interconnected microgrids. In particular, we strived to extinguish why definite control methods are more effective in different conditions and which control methods will prefer publicity in the next years. Finally, we propose some analysis for the virtual inertia control method utilized in AC interconnected microgrid applications.
Despite the rich literature review, and much research dealing with power quality enhancement in interconnected microgrids, the contributions of this paper are manifold. 1) In contrast to Suryakiran et al. (2018) and Singh et al. (2021), the novelty of this modeling is demonstrated to achieve not only the sharing of the active and reactive power of all generation units in both microgrids but also the sharing between both microgrids through a tie line to guarantee the conception of an uninterrupted power supply. 2) Contrary to Deng et al. (2020), Yang et al. (2020), and Singh et al. (2021), the novelty of this work is demonstrated in the use a multi-objective function for minimizing voltage deviation, frequency deviation, and the total distribution power loss at the same time to achieve simultaneous optimal power management and frequency enhancement of the AC interconnected microgrid. 3) Complementary to Tamrakar et al. (2017), Fawzy et al. (2021), Kerdphol et al. (2021), and Mohamed et al. (2022), the proposed ESS based on virtual inertia control is a grid-forming element that can operate with a RES without requiring conventional energy sources. As a result, it not only improves the supply reliability during grid-forming unit outages but also solves the frequency regulation problem and enhances optimal power management in islanded AC interconnected microgrids. 4) In addition to Elshenawy et al. (2022), Ghany Mohamed Abdel Ghany et al. (2018), Jiang et al. (2020), Nathan Kutz and Brunton (2022), Mohamed et al. (2022), and Singh et al. (2021), under step load disturbances, and severe disturbances such as eventual grid following/forming contingencies, the improvement of the system performance using a PI, FOPI, FPI, FFOPID, and VIC based on FFOPI controllers for mitigating frequency and voltage oscillation and achieving optimal power management in two AC interconnected microgrids with a multi-objective function is investigated. 5) The PSO technique is utilized to automatically optimize the controller parameters while considering the system nonlinearity, converters and line dynamics, and the interaction components. This technique helps to reduce design work and costs. Additionally, any other optimization technique may be implemented in future work to be compared with the PSO technique.
The fundamental idea and challenge of this research is to design an appropriate optimal controller for controlling the frequency, voltage, and optimal power management of two interconnected microgrids. The parameters of each controller are optimized using particle swarm optimization (PSO). This paper deals with a unique frequency control method called VIC to stabilize the microgrid frequency and achieve optimal power management using an adaptive controller. PI, FOPI, FPI, FFOPID, and VIC based on FFOPI controllers are demonstrated. This model is developed based on realistic city generation availability. It is tested under step load disturbances and severe contingencies disturbance to achieve not only the sharing of the active and reactive power of all generation units in both microgrids but also the sharing between both microgrids through a tie line to guarantee the conception of an uninterrupted power supply.
This paper is organized as follows: In Section 2, the system under study and the mathematical modeling of the individual components system are explained. FPI and FFOPI block diagrams, membership functions, rules, and PSO techniques used in the optimization of five controller parameters are presented in Section 3. The stability study and power quality enhancement problems and the utilized multi-objective function are stated in Section 4. The virtual inertia control is proposed in Section 5. The results and discussions are given in Section 6. Finally, the conclusions of the presented work are summarized in Section 7. The system parameters, list of symbols, and list of abbreviations are in the Supplementary Appendix.
2 System under study and mathematical modeling of the two interconnected microgrids’ components
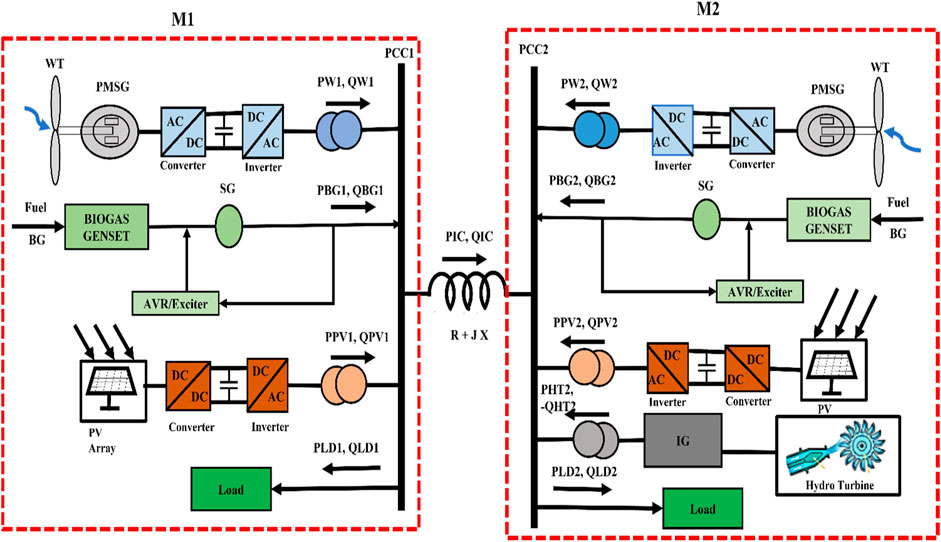
The novelty of this modeling, in contrast to the studies by Suryakiran et al. (2018) and Singh et al. (2021), is demonstrated to achieve not only the sharing of the active and reactive power of all generation units in both microgrids but also the sharing between both microgrids through a tie line to guarantee the conception of an uninterrupted power supply through a continuous generation–demand balance. The interconnected system is modeled with the assumption that microgrid M1 has 50 kW of surplus power that is transmitted to microgrid M2. The power transferred through the interconnection changes at a steady state under all conditions. The microgrid systems handle any changes in demand or generation on a local level. Figure 1 depicts the interconnected microgrid system as a single-line diagram (SLD).
Real and reactive power balance may be described by Eqs 1, 2 in a steady state:
For a small disturbance in power flows, Eqs 1, 2 can be written as follows:
A change in real power demand/generation would result in a change in the frequency of the system, which, in the Laplace domain, can be given as
Similarly, a change in reactive power mismatch results in a change in system bus voltage given by
2.1 Modeling of the WECS with the PMSG
The WECS considers a wind turbine with a permanent magnet synchronous generator that is coupled to the common bus via an AC/DC/AC power electronic interface and transformer. Like a synchronous generator with internal reactance
A small perturbation in power flows can be expressed in the Laplace domain as follows:
where
The delay due to inertia of the system has been accounted as follows:
2.2 Modeling of solar PV systems with an inverter (SPVS)
The power that a PV panel produces is in the form of a direct current. Therefore, before connecting to the common bus, the power is passed through a DC/DC/AC power electronic interface and then connected to the bus through a transformer. Like the WECS, the power flow equations considering XTPV as internal reactance are given by
For a small perturbation, Eqs 13, 14 can be written in the Laplace domain as
where
The delay due to inertia of the system has been accounted as follows:
2.3 Modeling of the BG
The BG model has been adopted from the study by Suryakiran et al. (2018). Reactive power control in biogas is carried out by the voltage regulation action of the automatic voltage regulator (AVR) and exciter. Considering the dynamic state after neglecting the saturation function, the equations for real and reactive powers are derived and given as follows:
where
2.4 Modeling of the HT
A constant input hydro turbine has been considered. The total active and reactive power flow from the induction generator considering the generator side equation is given by
The negative sign of reactive power shows the power is being taken by the IG. The term
where K7 =
2.5 Modeling of AC interconnection
An AC short transmission line has been considered while modeling the interconnection. The line has a high R/X ratio, meaning it cannot be considered lossless. The power flow through such a line is given by
where
where
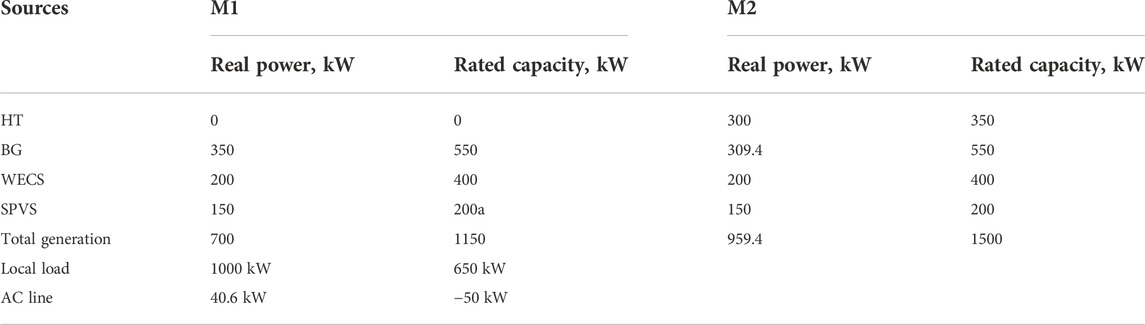
The microgrids are modeled using the abovementioned individual models of sources. The data for microgrid M2 have been taken from the studies by Suryakiran et al. (2018) and Singh et al. (2021), and the data for M1 have resulted from slight changes in the data for M2. M2 has been designed to meet the energy needs of a group of four medium-sized villages, each of which is projected to need about 1600 kW. The maximum diversification demand for M2 is 1000 kW (approx.). The power supply has a frequency of 50 Hz and a rated voltage of 1 pu. The M1 model was created for a group of four villages: two small and two mediums. The rated generation capacity of M1 is 1,150 kW, the maximum demand that can be accommodated is 700 kW, 50 Hz, and the rated voltage is 1 pu. A constant power of 50 kW is transmitted from the M1 microgrid to the M2 microgrid through an AC interconnection, and after losses, 40.6 KW is delivered to the M2 microgrid. The steady-state generation parameters of two microgrids, overall demand power, power transfer from AC interconnection, and generation from all the generation units in M1 and M2 are summarized in Table 1.
3 Fuzzy PI and fuzzy fractional-order PI for interconnected microgrids
The FPI controller has three coefficients, and the three are normalized gains K1, K2, and K3, as shown in Figure 2A, whereas the FFOPI controller has four coefficients, three of them are normalized gains K1, K2, and K3, and one is fractional-order control system λ, as shown in Figure 2B. FPI and FFOPI have two inputs, named error
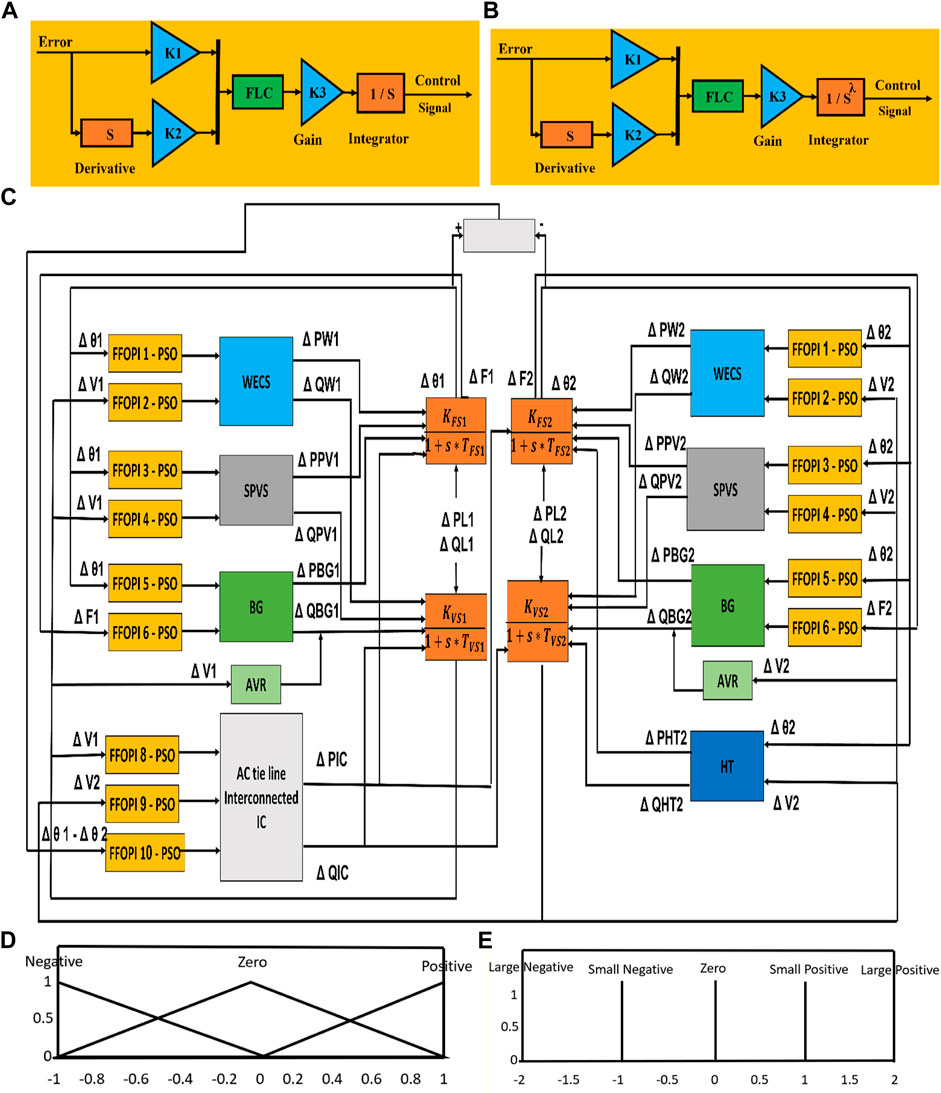
FIGURE 2. Block diagram of controller, complete transfer function block diagram of the interconnected microgrid system and membership for E and CE, (A) FPI controller, (B) FFOPI controller, (C) complete transfer function block diagram of the interconnected microgrid system, (D) input membership, (E) output membership.
PSO simulates the collective behavior of a swarm in searching for food. The algorithm is an iterative process that aims to find a solution that satisfies a fitness function within a search space (Abdelwahab et al., 2020). Yet, PSO includes several updates in order to the inherited composite nature (Elnozahy et al., 2020). The PSO technique is based on the assumption that particles update their velocity and location at each iteration. Thus, the current location
For the suggested PI, FOPI, FPI, FFOPI, and VIC based on FFOPI controllers, the PSO is used in this study to improve the controller’s parameters. The parameters for the optimization method are as follows: population = 50; iterations = 70; velocity clamping factor v = 2; cognitive
PSO is devoted to searching the optimized parameters of FPI and FFOPI controllers to minimize the following multi-objective function:
The fuzzy logic (FLC) rules are listed as follows in Table 2. Figures 2D,E show the membership of output and input, where: N = negative, p = positive, SP = small positive, Z = zero, SN = small negative, LP = large positive, and LN = large negative (Ghany Mohamed Abdel Ghany et al., 2018). Any crisp value is defined in two fuzzy sets due to the uniform distribution of the input sets, which are triangle and cross neighbor sets with a membership value of 0.5. For ease of defuzzification, the output membership functions are assumed to be uniformly distributed singletons.
The first phase in the design method is to transfer the PI and FOPI gains to the linear fuzzy controller by replacing the known PI and FOPI with a linear FPI and linear FFOPI. According to the feedback error signal e(n), the traditional PI controller and FOPI controller signal u(n) at any given time instant n can be stated either in absolute form, as in Eqs 32, 33, or incremental form, as in Eqs 34, 36.
where Ts is the sampling period, Kp and KI are the proportional and integral gains, respectively, and λ is the integral fractional-order control system. The most often used defuzzification technique uses the concept of the center of gravity and is expressed as follows:
where u (ui) represents the element’s membership grade or weight, which is the result of the rule i.
4 Multi-objective function for interconnected microgrids
Simulation has been used to demonstrate the stability study (SS) in two interconnected systems for a disturbance such as an increase in real and reactive power demand in both microgrids by each one, increased load variation, and emergency/recovery from generation. The five controllers can reduce the step disturbance-induced steady-state error in frequency and voltage in the interconnected microgrids. The distribution power loss (DPL) in two interconnected microgrids is composed of eight parts: three parts for the first microgrid, which includes the power loss from the wind, PV, and biogas sources; four parts for the second microgrid, which includes the power loss from the wind, PV, biogas, and hydro turbine; and one part for the AC interconnected line power loss. The average conduction losses of the PMSG, rectifier, inverter, and transformer are included in the wind power loss, whereas the average conduction losses of the DC-DC converter, inverter, and transformer are included in the PV power loss. The average conduction losses of the synchronous generator are included in the BG power loss, the average conduction losses of the hydro turbine and induction generator are included in the HT power loss, and the average conduction losses of the tie line impedance are included in the line power loss. The distribution power loss of two interconnected microgrids is given by
where
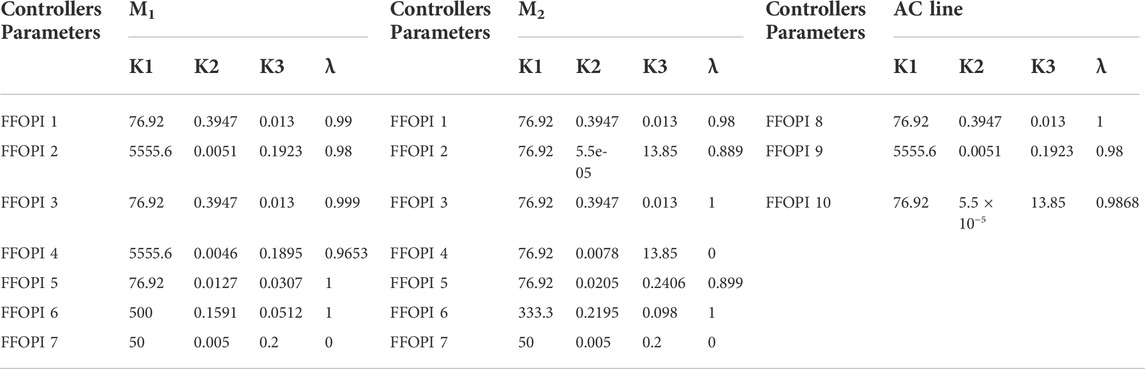
To guarantee power quality enhancement, the OF must include two terms. The first term will achieve the stability study by minimizing the OF based on ITSE criteria of voltage and frequency of two interconnected microgrids, whereas the second term will achieve the optimal power flow by minimizing the OF based on ITSE criteria of DPL of two interconnected microgrids. The five controllers’ parameters are tuned using the PSO algorithm for minimizing the OF based on ITSE criteria of voltage, frequency, and distribution power loss of two interconnected microgrids, as shown in Equation 41, and the tuned values are listed in Table 3.
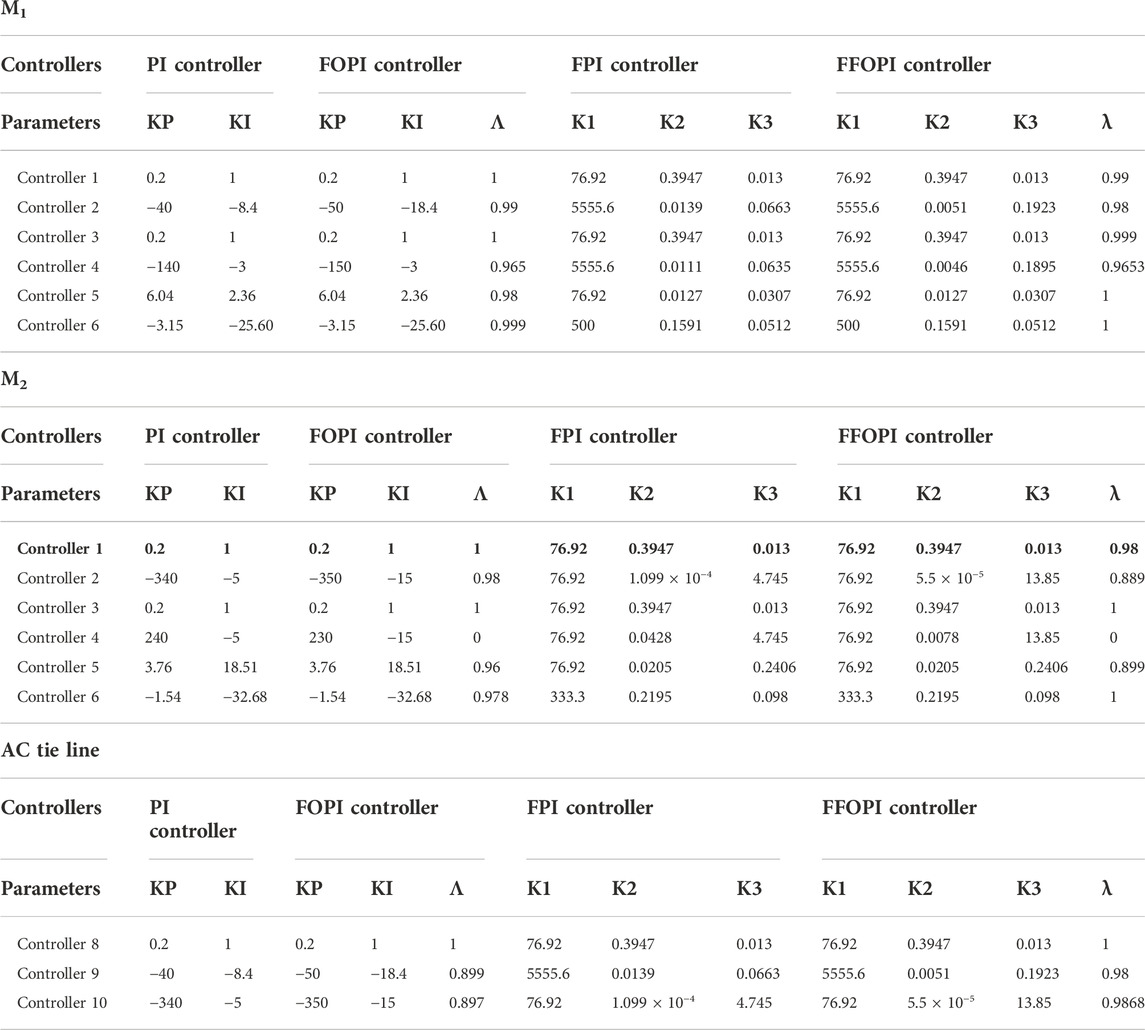
TABLE 3. Controller gains of microgrid system M1 and M2 and the tie line for PI, FOPI, FPI, and FFOPI controllers.
5 Virtual inertia control for interconnected microgrids
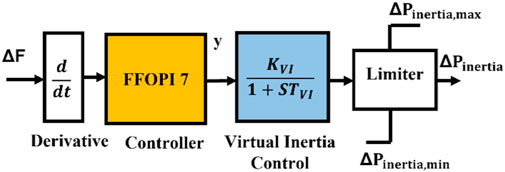
The virtual synchronous generator (VSG) supplies the substitutional power to the actual synchronous machine (Abubakr et al., 2021; Fawzy et al., 2021). This generator can be used to improve the frequency stability in networks with a high level of renewable power. Virtual inertia (VI) is a certain part of the VSG applied to serve the lack of inertia utilizing a power injection technique. The restrictions of the virtual inertia system cannot provide active frequency support. So, an additional robust controller must be utilized to face nonlinearities in low-inertia systems. The virtual inertia control structure Figure 3 contains a derivative unit, a designed controller FFOPI, virtual inertia control (energy storage system and virtual inertia variable gain), and a power limiter
During the last decade, the energy storage system (ESS) became an important unit in renewable energy networks since it can provide frequency smoothness and balance for further dispatch. The simplified ESS model can be distinguished as follows:
For minimizing the OF, The FFOPI controller is tuned using the ITSE criterion. The parameters of the FFOPI controller are tuned using the PSO algorithm based on ITSE criteria, as shown in Eq. 41. The tuned gain parameters of FFOPI are given in Table 4. The parameters Kv1 and Tv1 are determined by PSO also, which equals 0.8 and 10, respectively.
6 Result and discussion
In this section, the stability study, optimal power management, and virtual inertia control of the proposed two interconnected microgrids using five controllers based on PSO through multi-objective function are investigated by each controller including multiple disturbances. Each controller includes load disturbances and contingency/recovery of generation. The simulations result of the studied microgrid is carried out using MATLAB/Simulink software. The PI, FOPI, FPI, FFOPI, and VIC based on FFOPI controllers using PSO through multi-objective function will be discussed in each disturbance. The data of the system considered for simulation studies are given in Supplementary Appendix.
6.1 Load variation disturbance
The variation in the electric load affects the interconnected microgrid frequency and power, so the interconnected microgrid control shall interact with such disturbances to provide satisfactory performance. These fluctuations include a step load change. The interconnected system has been simulated for an increase in real and reactive power demand in both microgrids by 0.01 pu each.
The change in frequencies and voltages of microgrids M1 and M2 are shown in Figure 4. It can be observed that the five controllers are adequate to mitigate the steady-state error in frequency and voltage caused by step load variation disturbances in the interconnected microgrids. The dynamic specification [settling time (Ts), overshoot (Os), and undershoot (Us)] of frequencies and voltage deviation at each controller is summarized in Table 5.
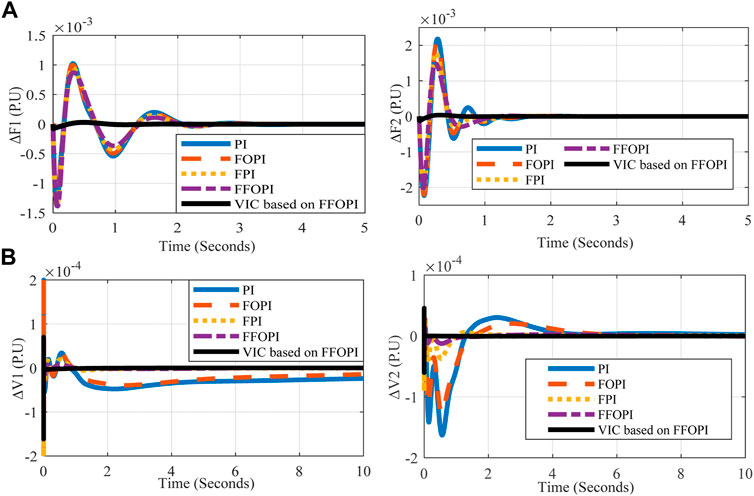
FIGURE 4. Interconnected microgrid’s frequency and voltage measurements versus time for each controller at load disturbance (A) ΔF1 (P.U), ΔF2 (P.U) and (B) ΔV1 (P.U), ΔV2 (P.U).
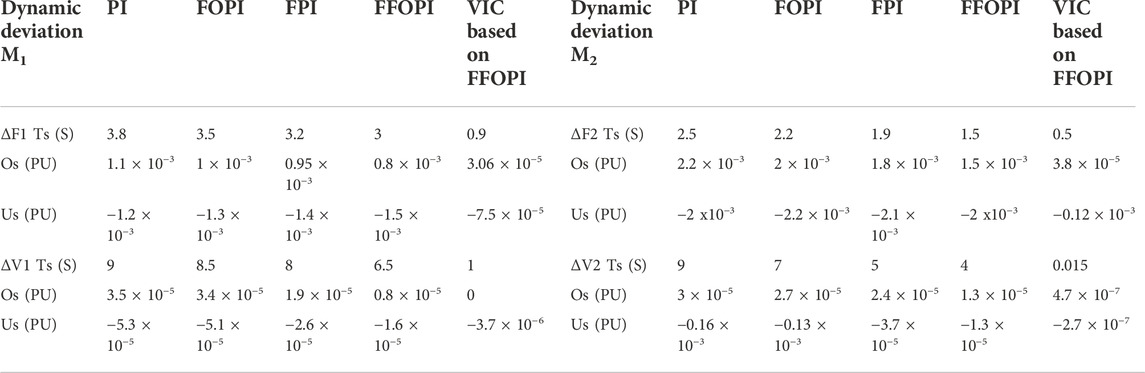
TABLE 5. Dynamic specification of frequencies and voltage deviation for each controller at load disturbance.
From Table 5, after the comparison between five controllers, the VIC based on FFOPI minimizes overshoots Os/undershoots Us, improves system stability, and reduces settling time Ts of the system for both frequency deviation of two interconnected microgrids. As a result, employing VIC based on FFOPI offered a superior response in terms of frequency enhancement compared to other controllers.
A shorter settling time and less overshoots/undershoots in frequency magnitudes indicate a quicker restoration of the kinetic energy of the rotating electrical machines in the system, which would mean a faster correction of power–demand imbalances.
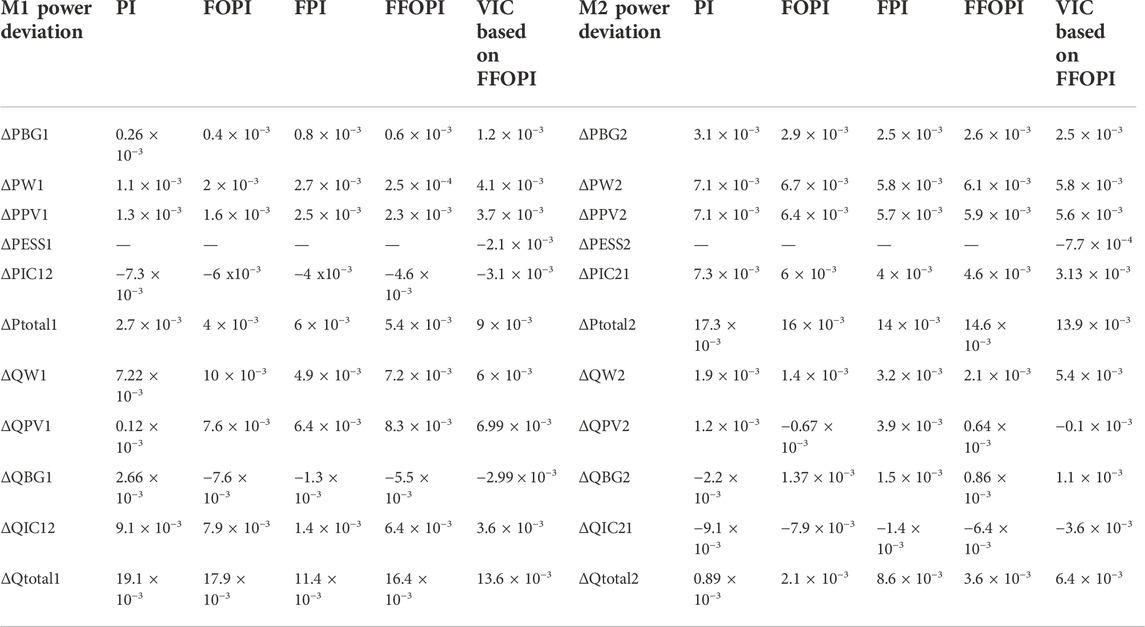
The power imbalance during this disturbance is compensated according to Table 6, explaining the power sharing of each generation unit in two microgrids at each controller through a multi-objective function to minimize the total power loss. The investigation of Figures 5, 6 can be justified by looking at Table 6.
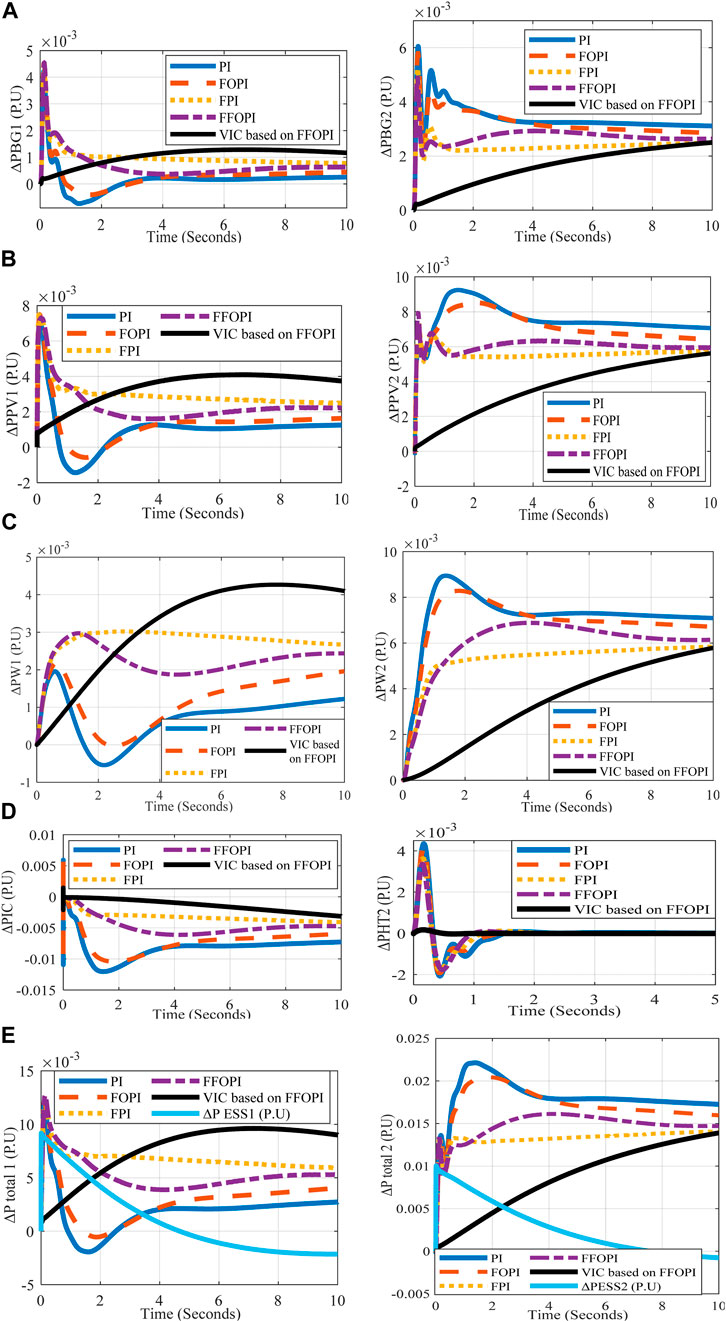
FIGURE 5. M1 and M2’s active power measurements versus time for each controller at load disturbance (A) ΔPBG1 (PU), ΔPBG2 (PU), (B) ΔPPV1 (PU), ΔPPV2 (PU), (C) ΔPw1 (PU), ΔPw2 (PU), (D) ΔPHT2 (PU), ΔPIC (PU), and (E) ΔPtotal1 (PU), ΔPtotal2 (PU).
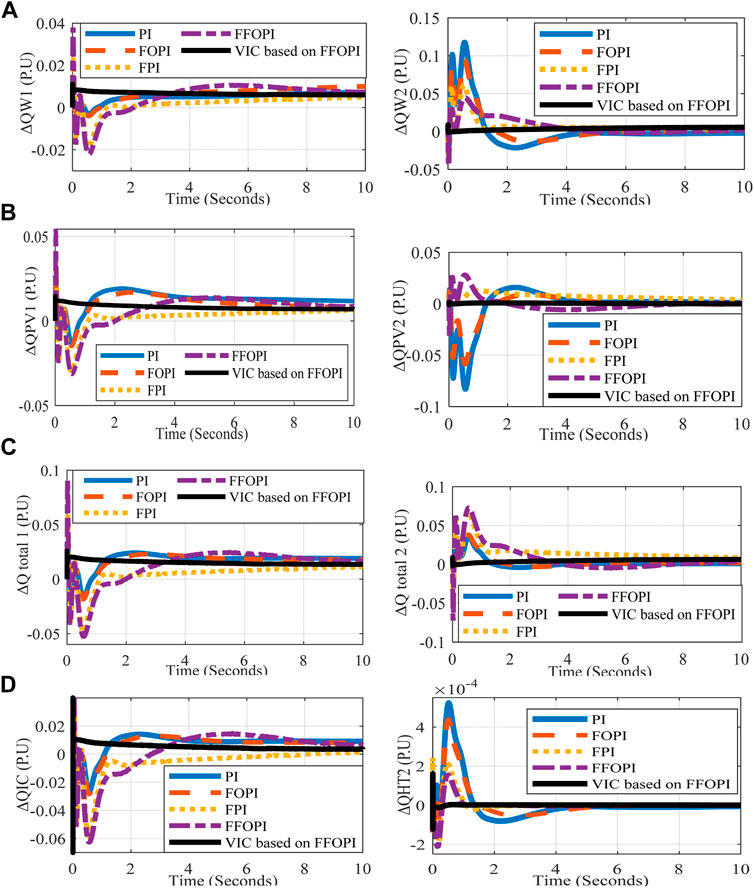
FIGURE 6. M1 and M2’s reactive power measurements versus time for each controller at load disturbance (A) ΔQw1 (PU), ΔQW2 (PU), (B) ΔQPV1 (PU), ΔQPV2 (PU), (C) ΔQtotal 1 (PU), ΔQtotal 2 (PU), and (D) ΔQIC (PU), ΔQHT2 (PU).
From Table 6, the ESS through VIC acts as a load to support the frequency. The power loss of two interconnected microgrids can be calculated by using Eq. 40, which is recorded as 7.2 e-9 for PI controllers, 2.5 e-9 for FOPI, 1.3 e-11 for FPI, 6.5 e-12 for FFOPI, and 1.4 e-13 for VIC based on FFOPI due to the minimum value of power-sharing (ΔPIC and ΔQIC) through the tie line at VIC case, so the VIC based on FFOPI controller provided a superior response with respect to frequency enhancement and optimal power management compared to other controllers.
6.2 Contingency event disturbance analysis
In this section, microgrid will be subjected to a large disturbance in this part that will result in a severe power imbalance, impact frequency and power response, as well as a brief outage of the tie line.
6.2.1 Case 1: Disconnecting the tie line with load variation disturbance
Other severe disturbances include the sudden outage of the tie line, which prevents power from transferring from one microgrid to another. Each microgrid is in charge of satisfying the demand load at its PCC. The tie line between two microgrids is activated at zero seconds in a sudden outage, while the load change demand is maintained at 0.01 pu throughout the simulation period. This variance results in a power differential between the power that is generated and that which is required, which may affect the microgrid’s power management and frequency.
The inertia of the BG and the virtual inertia of the inverter linked to the PVS and WECS instantly of each microgrid correct for the frequency variation. However, using ESS could improve stability during a disturbance period until the BG’s isochronous governor intervenes to restore the steady-state frequency; as a result, using VIC offered a superior response in terms of frequency enhancement. Figure 7 shows the change in frequencies and voltages of microgrids M1 and M2. The dynamic specification (Ts, Os, and Us) of frequencies and voltage deviation at each controller is summarized in Table 7.
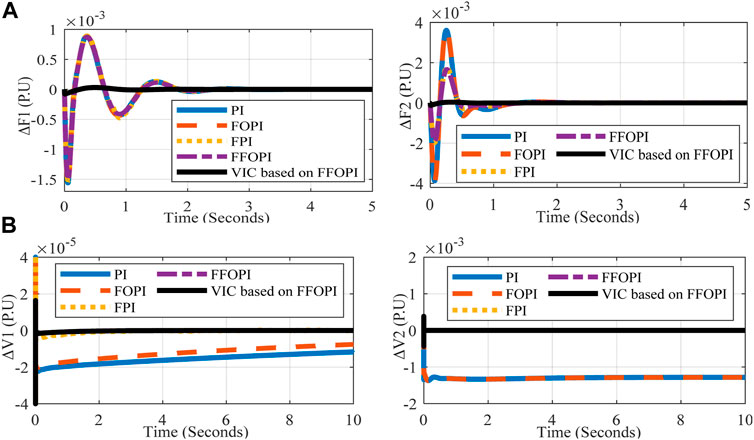
FIGURE 7. Interconnected microgrid’s frequency and voltage measurements versus time for each controller at disconnected tie line disturbance (A) ΔF1 (P.U), ΔF2 (P.U) and (B) ΔV1 (P.U), ΔV2 (P.U).
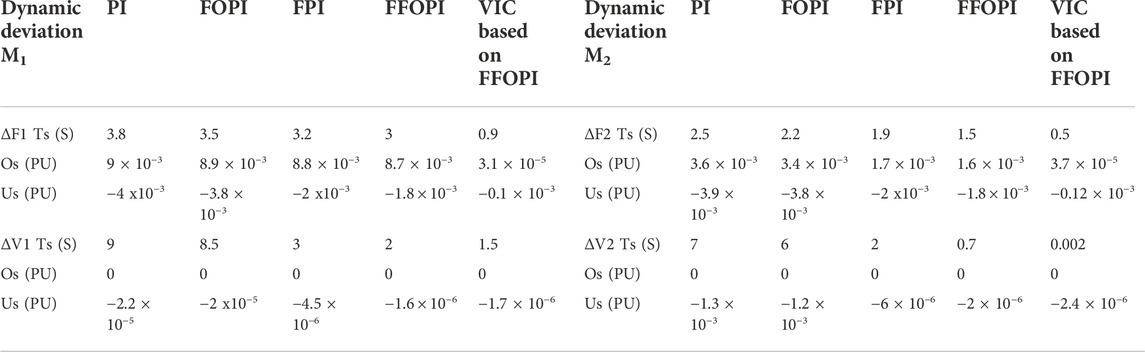
TABLE 7. Dynamic specification of frequencies and voltage deviation for each controller at disconnecting the tie line.
From Table 7, after the comparison between five controllers, the VIC based on FFOPI provided the best response properties of Ts, Os, and Us of the system for both frequency deviation of two interconnected microgrids. As a result, using VIC based on FFOPI offered a better response in terms of frequency enhancement when compared to other controllers.
Table 8 illustrates the power sharing of each generating unit in M1 and M2 balance for the power imbalance during this disturbance at each controller through multi-objective functions which supported the minimum total power loss. Table 8 facilitates the investigation of Figures 8, 9.
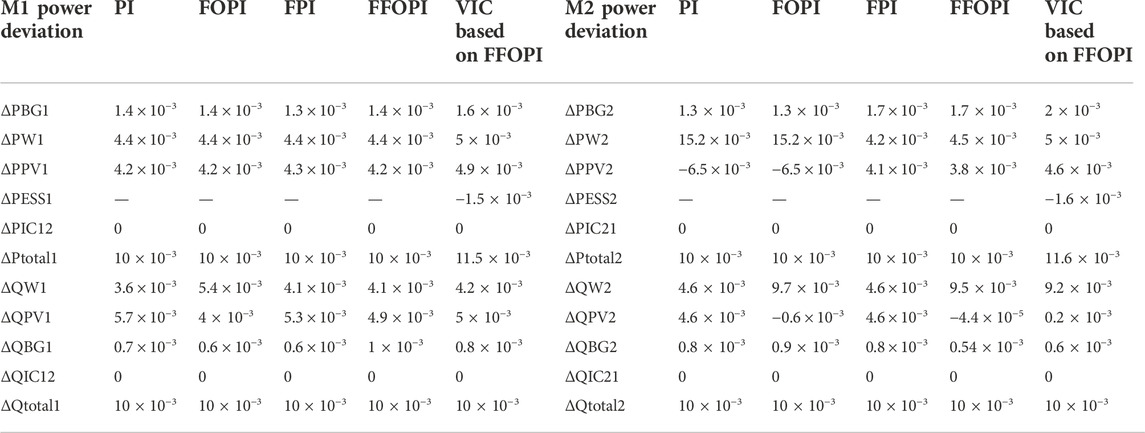
TABLE 8. Power flow in pu of microgrid system M1 and M2 for each controller at disconnecting the tie line.
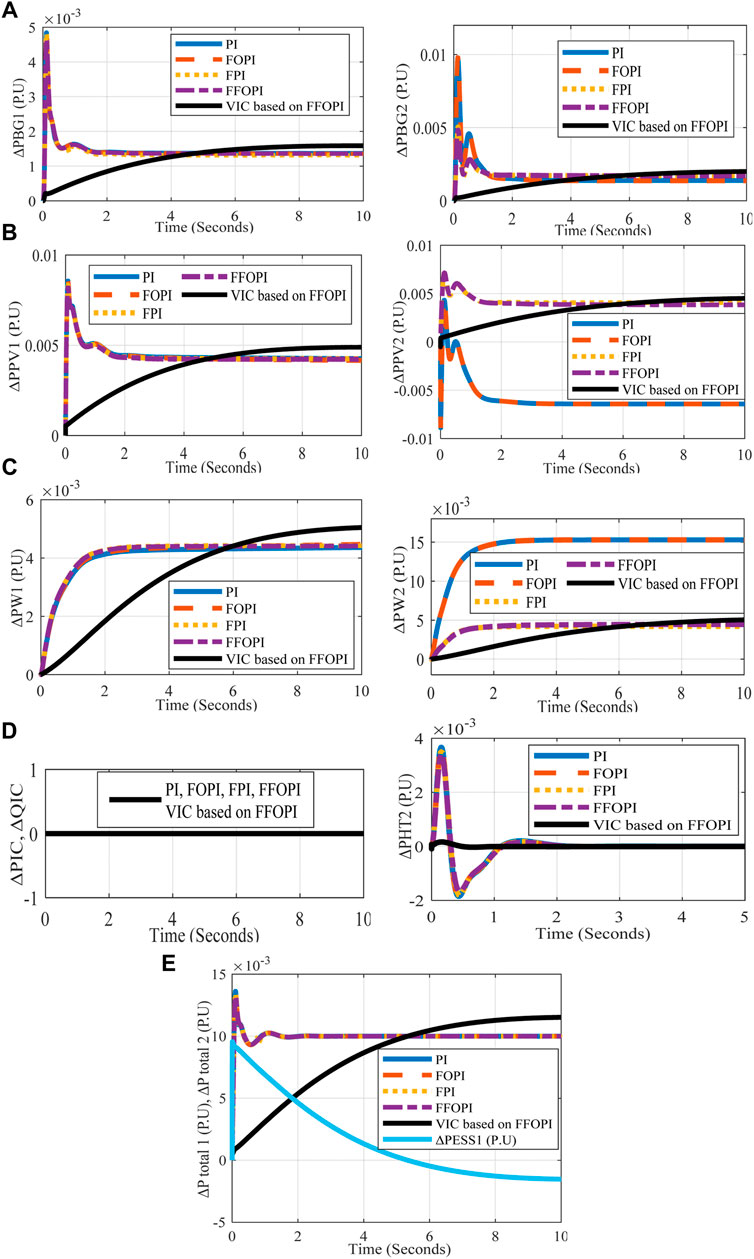
FIGURE 8. M1 and M2’s active power measurements versus time for each controller at disconnected tie line disturbance (A) ΔPBG1 (PU), ΔPBG2 (PU), (B) ΔPPV1 (PU), ΔPPV2, (C) ΔPw1 (PU), ΔPw2 (PU), (D) ΔPHT2 (PU), ΔPIC (PU), and (E) ΔPtotal 1 (PU), ΔPtotal 2 (PU).
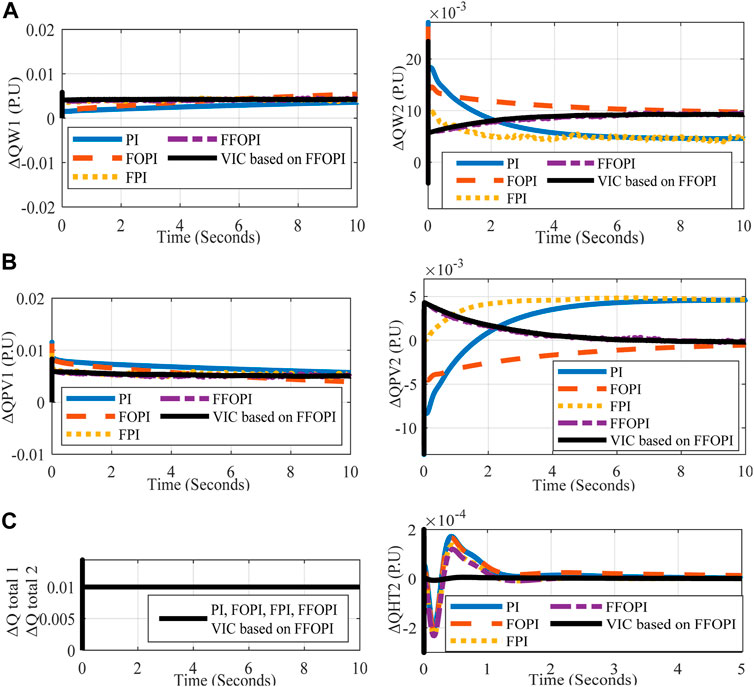
FIGURE 9. M1 and M2’s reactive power measurements versus time for each controller at disconnected tie line disturbance (A) ΔQw1 (PU), ΔQW2 (PU), (B) ΔQPV1 (PU), ΔQPV2 (PU), (C) ΔQtotal 1 (PU), ΔQtotal 2 (PU), and ΔQHT2 (PU).
From Table 8, the ESS through VIC acts as a load to support the frequency. Eq. 40 mentioned in Section 4 can be used to calculate the power loss of two interconnected microgrids, and the results are 8.9 e-11 for PI controller, 9.97 e-13 for FOPI, 1.6 e-13 for FPI, 6.4 e-15 for FFOPI, and 1.6 e-15 for VIC based on FFOPI. As a result, the best frequency performance and the optimal power flow are achieved in the case of VIC based on FFOPI during the disturbance of disconnecting the tie line.
From the analysis of the total power loss at each disturbance, the magnitude of the total power loss of two interconnected microgrids at disconnected tie line disturbance is smaller than the magnitude of total power loss at the load disturbance due to the lossless power of the tie line at disconnected tie line disturbance.
6.2.2 Case 2: Disconnecting the BG with load variation disturbance
Other severe disturbances include the sudden outage of the BG, which causes a severe reduction in the generated power. In a sudden outage, the BG in each microgrid is applied at zero second, whereas the load change demand is kept constant at 0.01 pu during the simulation period. This variation creates a power imbalance between the generated and demanded power, which can cause deviation in the microgrid frequency and power management.
The virtual inertia of the PVSS and WECS, as well as the virtual inertia control of the ESS in the case of VIC, instantly adjusts the frequency deviation. Figure 10 displays the variations in frequencies and voltages of microgrids M1 and M2. The dynamic specification of frequencies and voltage deviation at each controller can be summarized in Table 9.
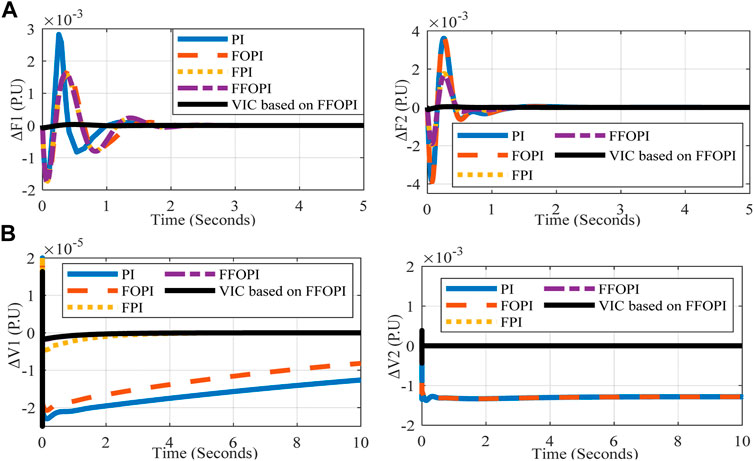
FIGURE 10. Interconnected microgrid’s frequency and voltage measurements versus time for each controller at disconnected BG disturbance (A) ΔF1 (P.U), ΔF2 (P.U) and (B) ΔV1 (P.U), ΔV2 (P.U).
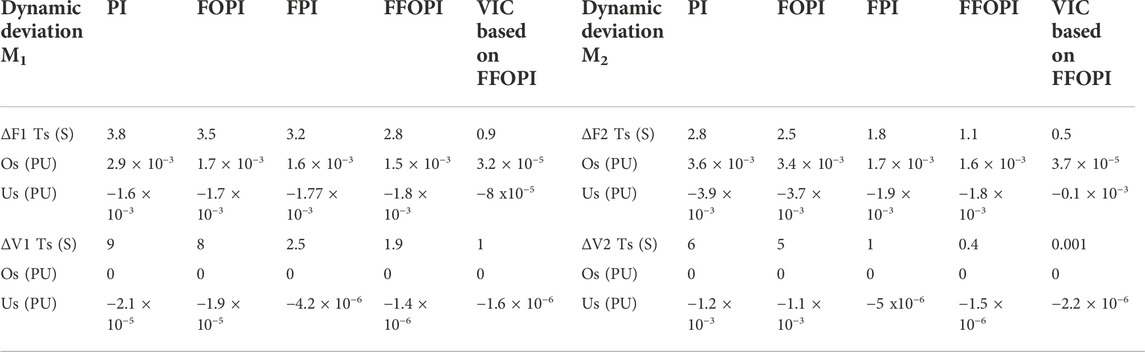
TABLE 9. Dynamic specification of frequencies and voltage deviation for each controller at disconnecting the BG.
From Table 9, after the comparison between five controllers, the VIC based on FFOPI minimizes Os and Us, improves system stability, and reduces Ts of the system for both frequency deviation of two interconnected microgrids. As a result, using VIC offered a superior response in terms of frequency enhancement compared to other controllers. Due to the system’s low inertia, in this case, it can be seen that the overshoot of the frequency response in the case of an outage BG is larger than the outage of the tie line.
Table 10 illustrates the power sharing of each generating unit in two microgrids that are used to compensate for the power imbalance that results from this disturbance at each controller through multi-objective functions to minimize the total power loss. Table 10 provides justification for the analysis of Figures 11, 12.
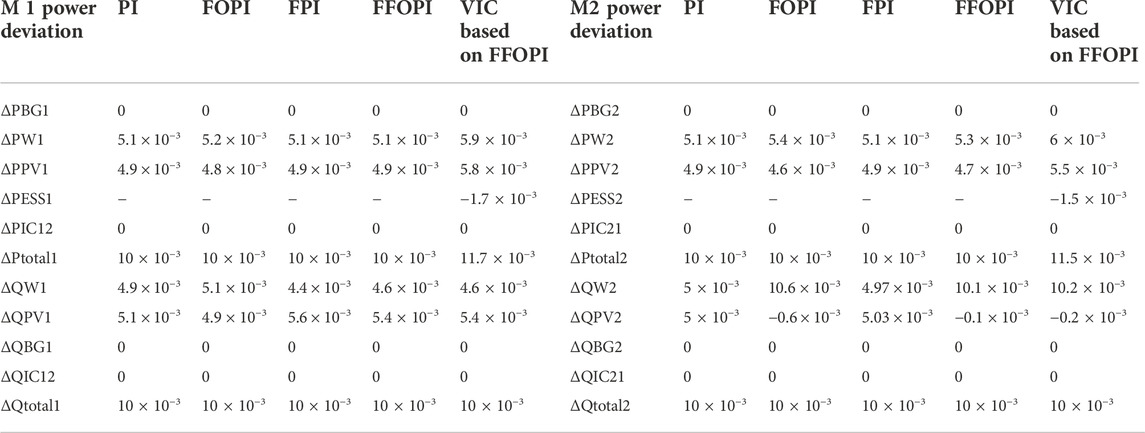
TABLE 10. Power flow in pu of microgrid system M1 and M2 for each controller at disconnecting the BG.
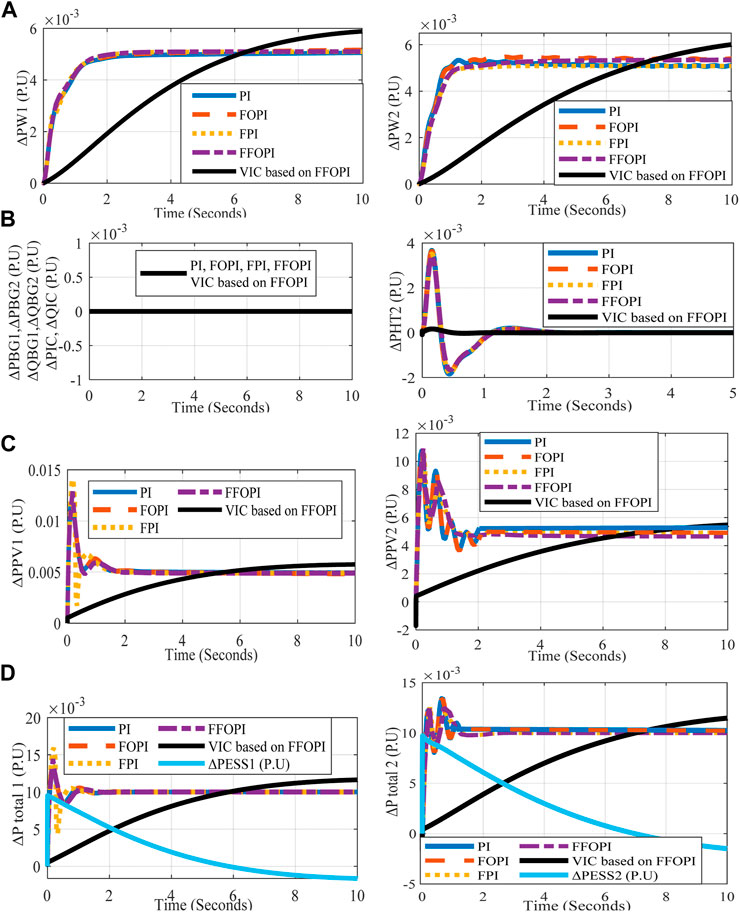
FIGURE 11. M1 and M2’s active power measurements versus time for each controller at disconnected BG disturbance (A) ΔPw1 (PU), ΔPw2 (PU), (B) ΔPBG1 (PU), ΔPBG2 (PU), ΔPHT2 (PU), ΔPIC (PU), (C) ΔPPV1 (PU), ΔPPV2 (PU), and (D) ΔPtotal 1 (PU), ΔPtotal 2 (PU).
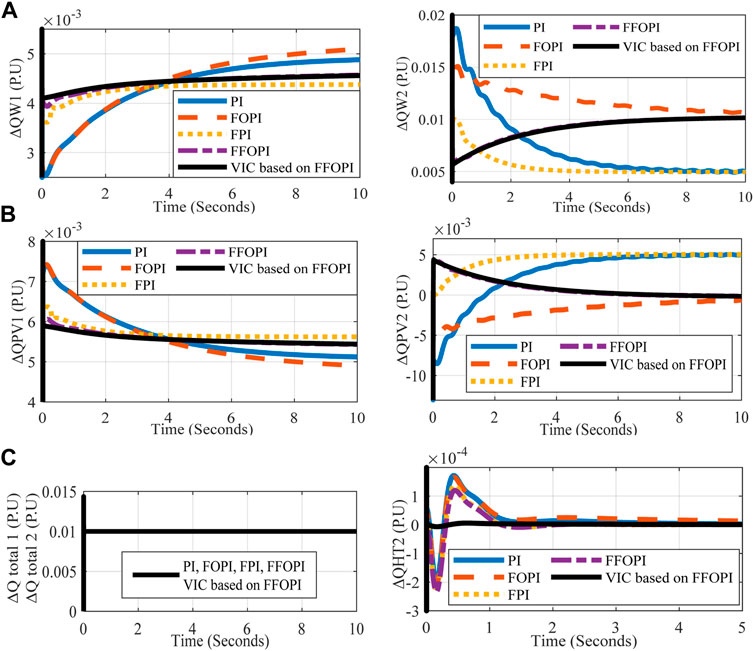
FIGURE 12. M1 and M2’s reactive power measurements versus time for each controller at disconnected BG disturbance (A) ΔQw1 (PU), ΔQw2 (PU), (B) ΔQPV1 (PU), ΔQPV2 (PU), and (C) ΔQtotal1 (PU), ΔQtotal 2 (PU), ΔQHT2 (PU).
From Table 10, the ESS through VIC acts as a load to support the frequency. Eq. 40 can be used to compute the power loss of two linked microgrids. It gives results of 8.9 e-12 for PI controller, 9.97 e-14 for FOPI, 1.6 e-14 for FPI, 6.4 e-16 for FFOPI, and 1.6 e-16 for VIC based on FFOPI. In comparison to other controllers, the VIC based on FFOPI controller offered a better response in terms of frequency enhancement and optimal power management.
From the analysis of the total power loss at each disturbance, the magnitude of the total power loss of two interconnected microgrids at disconnected BG disturbance is smaller than the magnitude of the total power loss at load disturbance and disconnected tie line disturbance due to the lossless power of the tie line and BG at disconnected BG disturbance.
7 Conclusion
In developing nations, the demand for clean but intermittent energy sources, as well as power, is expanding. Power delivery that is dependable and consistent is incredibly tough. The deployment of microgrids has been proposed as a solution to the problem of grid outages. There were two types of microgrids considered: those without diesel engine support and those with diesel engine support. The microgrid M1 lacked diesel engine support, but the microgrid M2 featured hydro turbine support. These two microgrids are linked by an AC short transmission cable. It has been proposed that additional power generated in M2 be transmitted to M1 in order to maintain a steady supply of electricity for the group of villages represented by M2. Renewable energy sources found in the microgrids M1 and M2 include photovoltaic (PV) modules, WECS, and biogas gensets. To achieve optimal power management in two AC-linked microgrids and increase frequency stability, a power injection mechanism employing a multi-objective function was used to compensate for the lack of inertia when subjected to varied shocks of load fluctuation and generation contingencies. To reduce frequency and voltage oscillations, the research examined how to tune PI, FOPI, FPI, FPI, FFOPI, and VIC based on FFOPI controllers using PSO.
Variations in load and other power sources can induce a power imbalance between generated and demand power, causing deviations in microgrid frequency and power management. The inertia of the BG, as well as the virtual inertia of the inverter coupled to the PVS and WECS in the absence of VIC, balances the energy imbalance. However, the compensation utilized in the absence of VIC is applied in the event of VIC, with the ESS acting as a load to sustain the frequency. The best power sharing between each generating unit is used in each controller to compensate for the power differential during disturbances via a multi-objective function, with the total power loss recorded as the smallest value in the case of VIC based on FFOPI compared to other controllers due to the smallest value of power-sharing (PIC and QIC) through the tie line at VIC based on FFOPI controller. The findings show that, when compared to other controllers, the VIC-based FFOPI controller delivers the best frequency performance and power flow.
The seriousness of contingencies can have a significant influence on system dynamics. Without VIC, a tie line or BG outage affects microgrid stability but does not cause microgrid instability due to the inertia of the BG and virtual inertia of the inverter connected to the PVSS and WECS of each microgrid in the case of a tie line outage, and the virtual inertia of the inverter connected to the WECS and PVSS in the case of a BG outage. Using the ESS, on the other hand, may improve stability throughout the disturbance period until the BG’s isochronous governor reacts to restore the steady-state frequency. The power imbalance during a contingency disturbance is balanced by the optimal power sharing of each generation unit in each controller via a multi-objective function that supported the minimum total power loss in the case of the VIC based on FFOPI controller; thus, using the VIC based on FFOPI controller provided a superior response in terms of frequency enhancement and optimal power management when compared to the other controllers. Without VIC, the overshoot of frequency response in case of outage BG is bigger than in other circumstances (disturbances) due to the system’s low inertia in case of outage BG.
The voltages and frequencies of both microgrids vary within acceptable limits and subsequently settle with zero steady-state error following a disturbance within 0.5s with smaller overshoots/undershoots (3.7e-5/-0.1e-3) using VIC based on FFOPI, demonstrating the technical viability of the model and VIC approach. The power loss of two linked microgrids was 7.2 e-9 for PI controllers, 2.5 e-9 for FOPI, 1.3 e-11 for FPI, 6.5 e-12 for FFOPI, and 1.4 e-13 for VIC based on FFOPI due to the minimal value of power sharing (ΔPIC and ΔQIC) across the tie line in the case of VIC during load disturbance. The magnitude of total power loss of two linked microgrids was 1.6 e-16 pu in the case of VIC based on FFOPI controller due to the lossless power of tie line and BG at unconnected BG disturbance. As a consequence, when compared to other situations, the VIC based on FFOPI controller produced a higher response in terms of frequency augmentation and effective power management.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
ME: conceptualization, methodology, software, formal analysis, resources, data curation, writing—original draft, and visualization. AF, HE, and AE: validation, investigation, writing—review and editing, visualization, and supervision. SK: software, formal analysis, validation, investigation, writing—review and editing, and visualization.
Acknowledgments
The authors would like to acknowledge the support from Swansea University, the Faculty of Science and Engineering, and the Astute Wales project to conduct this work. The ASTUTE 2020 (Advanced Sustainable Manufacturing Technologies) operation, supporting manufacturing companies across Wales, was part-funded by the European Regional Development Fund through the Welsh Government and the participating Higher Education Institutions under grant number APCFSE11.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.1035097/full#supplementary-material
SUPPLEMENTARY TABLE A1 | Microgrid 1 parameters values.
SUPPLEMENTARY TABLE A2 | Microgrid 2 parameters values.
SUPPLEMENTARY TABLE A3 | Hydro turbine and AC tie line parameters values.
References
Abdelwahab, S. A. M., Hamada, A. M., and Abdellatif, W. S. E. (2020). Comparative analysis of the modified perturb & observe with different MPPT techniques for PV grid connected systems. Int. J. Renew. Energy Res. 10, 1. doi:10.20508/ijrer.v10i1.10375.g7850
Abubakr, H., Mohamed, T. H., Hussein, M. M., Guerrero, J. M., and Agundis-Tinajero, G. (2021). Adaptive frequency regulation strategy in multi-area microgrids including renewable energy and electric vehicles supported by virtual inertia. Int. J. Electr. Power & Energy Syst. 129, 106814. doi:10.1016/j.ijepes.2021.106814
Akinyele, D., Belikov, J., and Levron, Y. (2018). Challenges of microgrids in remote communities: A steep model application. Energies 11 (2), 432. doi:10.3390/en11020432
Barik, A. K., and Das, D. C. (2018). Expeditious frequency control of solar photovoltaic/biogas/biodiesel generator based isolated renewable microgrid using grasshopper optimisation algorithm. IET Renew. Power Gener. 12, 1659–1667. doi:10.1049/iet-rpg.2018.5196
Boicea, V. A. (2014). Energy storage technologies. The past and the present. Proc. IEEE 102, 1777–1794. doi:10.1109/jproc.2014.2359545
Boyd, S., and Vandenberghe, L. (2004). Convex optimization. Cambridge, MA, U.K: Cambridge Univ. press. doi:10.1017/cbo9780511804441.001
Chao, P., Li, W., Liang, X., Shuai, Y., Sun, F., and Ge, Y. (2020). A comprehensive review on dynamic equivalent modeling of large photovoltaic power plants. Sol. Energy 210, 87–100. doi:10.1016/j.solener.2020.06.051
Dabbaghjamanesh, M., Kavousi-Fard, A., Mehraeen, S., Zhang, J., and Dong, Z. Y. (2020). Sensitivity analysis of renewable energy integration on stochastic energy management of automated reconfigurable hybrid AC–DC microgrid considering DLR security constraint. IEEE Trans. Ind. Inf. 16, 120–131. doi:10.1109/tii.2019.2915089
Delavari, H., and Naderian, S. (2019). Backstepping fractional sliding mode voltage control of an islanded microgrid. IET Gener. Transm. &. Distrib. 13, 2464–2473. doi:10.1049/iet-gtd.2018.5909
Deng, J., Mao, Y., and Yang, Y. (2020). Distribution power loss reduction of standalone DC microgrids using adaptive differential evolution-based control for distributed battery systems. Energies 13, 2129. doi:10.3390/en13092129
El-Fergany, A. A., and El-Hameed, M. A. (2017). Efficient frequency controllers for autonomous two-area hybrid microgrid system using social-spider optimiser. IET Gener. Transm. &. Distrib. 11, 637–648. doi:10.1049/iet-gtd.2016.0455
Elnozahy, A., Yousef, A. M., Ghoneim, S. S., Abdelwahab, S. A., Mohamed, M., and Abo-Elyousr, F. K. (2020). Optimal economic and environmental indices for hybrid PV/Wind-Based battery storage system. J. Electr. Eng. Technol. 16, 2847–2862. doi:10.1007/s42835-021-00810-9
Elshenawy, M., Fahmy, A., Elsamahy, A., Kandil, S. A., and El Zoghby, H. M. (2022). Optimal power management of interconnected microgrids using virtual inertia control technique. Energies 15 (19), 7026. doi:10.3390/en15197026
Farrokhabadi, P. M., Mostafa, C., Claudio, A. S., John, W. N., Ehsan, F., Mendoza-Araya, P. A., et al. (2020). Microgrid stability definitions, analysis, and examples. IEEE Trans. Power Syst. 35, 13–29. doi:10.1109/tpwrs.2019.2925703
Fawzy, A., Bakeer, A., Magdy, G., Atawi, I. E., and Roshdy, M. (2021). Adaptive virtual inertia-damping system based on model predictive control for low-inertia microgrids. IEEE Access 9, 109718–109731. doi:10.1109/access.2021.3101887
Fernández-Guillamón, E., Gómez-Lázaro, E., MuljadiMolina-García, Á., and Molina-Garcia, A. (2019). Power systems with high renewable energy sources: A review of inertia and frequency control strategies over time. Renew. Sustain. Energy Rev. 115, 109369. doi:10.1016/j.rser.2019.109369
Firdaus, A., Sharma, D., and Mishra, S. (2020). Dynamic power flow based simplified transfer function model to study instability of low-frequency modes in inverter-based microgrids. IET Gener. Transm. &. Distrib. 14, 5634–5645. doi:10.1049/iet-gtd.2020.0818
Gencer, A. “Modelling and analysis of operation PMSG based WECS under different load conditions,” in Proceedings of the 2016 IEEE 8th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Ploiesti, Romania, June 2016. doi:10.1109/ECAI.2016.7861198
Ghany Mohamed Abdel Ghany, M. A., Bensenouci, A., Bensenouci, M. A., and Nazih Syed-Ahmad, M. “Fuzzy fractional-order PID tuned via relative rate observer for the Egyptian load frequency regulation,” in Proceedings of the IEEE 2018 Twentieth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, December 2018, 18–20. doi:10.1109/mepcon.2018.8635142
Guo, L., Fu, X., and Zeng, J. (2021). Editorial: Power management for AC/DC hybrid microgrid. Front. Energy Res. 9. doi:10.3389/fenrg.2021.801894
Hasanzadeh, S., Dehghan, S. M., and Khoramikia, H. (2021). Droop control method based on fuzzy adaptive virtual resistance for DC microgrids. Int. J. Power Electron. 14, 197. doi:10.1504/ijpelec.2021.10039547
Hashemi, S. M., and Vahidinasab, V. (2021). Energy management systems for microgrids. Berlin, Germany: Springer International Publishing, 61–95. doi:10.1007/978-3-030-59750-4_3
Jayawardana, A., Agalgaonkar, A. P., Robinson, D. A., and Fiorentina, M. (2019). Optimisation framework for the operation of battery storage within solar rich microgrids. IET Smart Grid 2, 504–513. doi:10.1049/iet-stg.2019.0084
Jiang, Y., Pates, R., and Mallada, E. (2020). Dynamic droop control in low-inertia power systems. IEEE Trans. Autom. Contr. 1, 3518–3533. doi:10.1109/tac.2020.3034198
Jiang, Y., Yang, Y., Tan, S. C., and Hui, S. Y. R. (2020). Distributed sliding mode observer-based secondary control for DC microgrids under cyber-attacks. IEEE J. Emerg. Sel. Top. Circuits Syst. 1, 144–154. doi:10.1109/jetcas.2020.3046781
Johnson, S. C., Rhodes, J. D., and Webber, M. E. (2020). Understanding the impact of non-synchronous wind and solar generation on grid stability and identifying mitigation pathways. Appl. Energy 262, 114492. doi:10.1016/j.apenergy.2020.114492
Kerdphol, T., Rahman, F. S., Watanabe, M., and Mitani, Y. (2021). Virtual inertia synthesis and control. Cham, Switzerland: Springer International Publishing. doi:10.1007/978-3-030-57961-6
Kundur, P., Paserba, J., Vittal, V., and Andersson, G. (2006). Closure of definition and classification of power system stability. IEEE Trans. Power Syst. 21, 446. doi:10.1109/tpwrs.2005.861952
Liang, B., Kang, L., He, J., Zheng, F., Xia, Y., Zhang, Z., et al. (2019). Coordination control of hybrid AC/DC microgrid. J. Eng. (Stevenage). 16, 3264–3269. doi:10.1049/joe.2018.8505
Mohamed, M. M., El Zoghby, H. M., Sharaf, S. M., and Mosa, M. A. (2022). Optimal virtual synchronous generator control of battery/supercapacitor hybrid energy storage system for frequency response enhancement of photovoltaic/diesel microgrid. J. Energy Storage 51, 104317. doi:10.1016/j.est.2022.104317
Nathan Kutz, J., and Brunton, S. L. (2022). “Reduced-order models (ROMs),” in Data-driven science and engineering (Cambridge, MA, USA: Cambridge University Press), 449–484. doi:10.1017/9781009089517.017
Puchalapalli, S., Tiwari, S. K., Singh, B., and Goel, P. K. (2020). A microgrid based on wind-driven DFIG, DG, and solar PV array for optimal fuel consumption. IEEE Trans. Ind. Appl. 56, 4689–4699. doi:10.1109/tia.2020.2999563
Qian, X., Yang, Y., Li, C., and Tan, S. C. (2020). Operating cost reduction of DC microgrids under real-time pricing using adaptive differential evolution algorithm. IEEE Access 8, 169247–169258. doi:10.1109/access.2020.3024112
Rezkallah, M., Singh, S., Chandra, A., Singh, B., Tremblay, M., Saad, M., et al. (2019). Comprehensive controller implementation for wind-PV-diesel based standalone microgrid. IEEE Trans. Ind. Appl. 55, 5416–5428. doi:10.1109/tia.2019.2928254
Sharma, R., Kewat, S., and Singh, B. (2020). Robust MMSOGI-FLL control algorithm for power quality improvement of solar PV-SyRG pico hydro-BES based islanded microgrid with dynamic load. IET power electron 13, 2874–2884. doi:10.1049/iet-pel.2019.1002
Sheng, S., and Zhang, J. (2017). Capacity configuration optimisation for stand-alone micro-grid based on an improved binary bat algorithm. J. Eng. (Stevenage). 13, 2083–2087. doi:10.1049/joe-.2017.0696
Singh, D., and Seethalekshmi, K. A. “A review on various virtual inertia techniques for distributed generation,” in Proceedings of the IEEE International Conference on Electrical and Electronics Engineering, Gorakhpur, India, February 2020, 14–15. doi:10.1109/ice348803.2020.9122959
Singh, Vinit Kumar, Venkata Suryakiran, Bhamidipati, Verma, Ashu, and Bhatti, T. S. (2021). Modelling of a renewable energy-based AC interconnected rural microgrid system for the provision of uninterrupted power supply. IET Energy Syst. Integr. 3, 172–183. doi:10.1049/esi2.12015
Suryakiran, B. V., Singh, V. K., Verma, A., and Bhatti, T. S. (2018). Stability study of integrated microgrid system. In: ICSCS 2018, 837. Singapore: Springer, 817–825. doi:10.1007/978-981-13-1936-5_83
Tamrakar, U., Shrestha, D., Maharjan, M., Bhattarai, B., Hansen, T., and Tonkoski, R. (2017). Virtual inertia: Current trends and future directions. Appl. Sci. 7, 654. doi:10.3390/app7070654
Tu, C., Xiao, F., Guo, Q., and Lan, Z. “High voltage quality control strategy of microgrid main inverter for islanded microgrid,” in Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, November 2018, 4–7. doi:10.1109/PEAC.2018.8590352
Ubilla, K., Jimenez-Estevez, G. A., Hernadez, R., Reyes-Chamorro, L., Hernandez Irigoyen, C., Severino, B., et al. (2014). Smart microgrids as a solution for rural electrification ensuring long-term sustainability through cadastre and business models. IEEE Trans. Sustain. Energy 5, 1310–1318. doi:10.1109/tste.2014.2315651
Vorobev, P., Huang, P. H., Hosani, M. A., Kirtley, J. L., and Turitsyn, K. “A framework for development of universal rules for microgrids stability and control,” in Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, Australia, December 2017, 12–15. doi:10.1109/cdc.2017.8264418
Wang, Y., Zhao, Q., and Wang, X. (2021). An asynchronous gradient descent based method for distributed resource allocation with bounded variables. IEEE Trans. Autom. Contr. 1, 6106–6111. doi:10.1109/tac.2021.3131557
Xi, J., Geng, H., Ma, S., Chi, Y., and Yang, G. (2018). Inertial response characteristics analysis and optimisation of PMSG-based VSG-controlled WECS. IET Renew. Power Gener. 12, 1741–1747. doi:10.1049/iet-rpg.2018.5250
Yang, Y., Qin, Y., Tan, S. C., and Hui, S. Y. R. (2019). Efficient improvement of photovoltaic-battery systems in standalone DC microgrids using a local hierarchical control for the battery system. IEEE Trans. Power Electron. 34, 10796–10807. doi:10.1109/tpel.2019.2900147
Yang, Y., Qin, Y., Tan, S. C., and Hui, S. Y. R. (2020). Reducing distribution power loss of islanded AC microgrids using distributed electric springs with predictive control. IEEE Trans. Ind. Electron. 67, 9001–9011. doi:10.1109/tie.2020.2972450
Yaramasu, V., Wu, B., Sen, P. C., Kouro, S., and Narimani, M. (2015). High-power wind energy conversion systems: Stateof- the-art and emerging technologies. Proc. IEEE 103, 740–788. doi:10.1109/jproc.2014.2378692
Yuan, Y., Wang, D., Liu, F., and DengChen, Z. (2020). Efficiency-prioritized droop control strategy of AC microgrid. IEEE J. Emerg. Sel. Top. Power Electron. 1, 2936–2950. doi:10.1109/jestpe.2020.2967756
Zhao, D., Qian, M., Ma, J., and Yamashita, K. (2020). Photovoltaic generator model for power system dynamic studies. Sol. Energy 210, 101–114. doi:10.1016/j.solener.2020.06.077
Nomenclature
List of symbols
List of abbreviations
RES Renewable energy system
PCC Point of common coupling
VSG Virtual synchronous generator
ESS Energy storage system
WECS Wind energy converting system
SPVS Solar photovoltaic system
BG Biogas genset
HT Hydro turbine
PMSG Permanent magnet synchronous generator
SLD Single-line diagram
SS Stability study
DPLM Distribution power loss minimization
VIC Virtual inertia control
FFOPI Fuzzy fractional-order PI
PSO Particle swarm optimization
ITSE Integral time square error
OF Objective function based on equ.41
Keywords: contingency of the power system, fuzzy fractional-order PI (FFOPI), fuzzy PI (FPI), multi-objective optimization, power quality enhancement, virtual inertia control
Citation: Elshenawy M, Fahmy A, Elsamahy A, El Zoghby HM and Kandil SA (2022) Improving frequency response for AC interconnected microgrids containing renewable energy resources. Front. Energy Res. 10:1035097. doi: 10.3389/fenrg.2022.1035097
Received: 02 September 2022; Accepted: 15 November 2022;
Published: 05 December 2022.
Edited by:
Dan Lu, Alfred University, United StatesReviewed by:
Zhenxiong Wang, Xi’an Jiaotong University, ChinaLiang Zhang, Northeast Electric Power University, China
Copyright © 2022 Elshenawy, Fahmy, Elsamahy, El Zoghby and Kandil. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ashraf Fahmy, YS5hLmZhaG15QHN3YW5zZWEuYWMudWs=
 Mahmoud Elshenawy
Mahmoud Elshenawy Ashraf Fahmy
Ashraf Fahmy Adel Elsamahy
Adel Elsamahy Helmy M. El Zoghby1
Helmy M. El Zoghby1