A Multi-Agent Game-Based Incremental Distribution Network Source–Load–Storage Collaborative Planning Method Considering Uncertainties

How to obtain the optimal decision-making scheme based on the investment behavior of various stakeholders is an important issue that needs to be solved urgently in incremental distribution network planning. To this end, this article introduces the virtual player “Nature” to realize the combination of the game theory and robust optimization and proposes an incremental distribution network source–load–storage collaborate planning method with a multi-agent game. First, the planning and decision-making models of a DG investment operator, a distribution network (DN) company, power consumers, and a distributed energy storage (DES) investment operator are constructed, respectively. Then the static game behaviors between the DG investment operator and distribution network company, as well as the DG investment operator and the DES investment operator, are analyzed based on the transfer relations between these four participants. At the same time, robust optimization is used to deal with the uncertainty of the DG output, and the virtual player “Nature” is introduced to study the dynamic game behavior between the DG investment operator and the distribution company. Finally, a dynamic–static joint game planning model is proposed. The simulation results verify the correctness and effectiveness of the proposed method.

1 Introduction

With the steady progress of pilot reform, incremental distribution business in China began to become open to social capital (Liu and Yang, 2021). At the same time, distributed generation (DG) investors, power consumers participating in demand side response (DSR), and distributed energy storage (DES) investors, in the role of independent entities, started to participate in the investment and operation of the distribution network. The diversification of investors has become one of the most significant characteristics of China’s incremental distribution network (Ma and Wang, 2017; Liu et al., 2020; Shen and Raksincharoensak, 2021a; Ma et al., 2021). Additionally, more uncertainties have been injected into it. Therefore, it is of great theoretical and practical significance to study the incremental distribution network planning method considering multiple independent participants and uncertainties (Li et al., 2020; Li et al., 2021a; Shen and Raksincharoensak, 2021b).

At present, distribution network planning considering multiple investment entities have attracted increasing research attention among investment operators and academic communities (Su et al., 2016; Li et al., 2017; Zhu et al., 2020; Li et al., 2021b). Su et al. (2016) analyzed the cost–benefit relationship between DG investment operators and distribution network companies after the access of DGs, establishing the model of optimizing DG capacity. Li et al. (2017) proposed a three-layer planning model of an active distribution network considering the interests of distribution network companies, DG operators, and consumers. Although the benefits or costs of different entities are modeled independently in the aforementioned article, the whole planning model is based on the overall rationality, aiming for optimizing the weighted sum, rather than the independent optimization of each investment entity. This cannot inflect the market mechanism of the actual incremental distribution network, deteriorating its economic performance (Liao et al., 2018). Therefore, it is a promising way to construct an incremental distribution network planning model based on individual rationality and game theory, improving the planning decision efficiency (Li and Xu, 2020a; Shen et al., 2022a).

Currently, the game issue in distribution network planning has been widely studied (Mei et al., 2011; Lu et al., 2014; Wen et al., 2016). Based on the complete information from the dynamic game theory, Mei et al. (2011) took photovoltaic, energy storage, and power grid as game participants, analyzed the game relationship between them in the market environment, and established a coordinated planning model of the optical storage network. According to the possible alliance relationship between wind power generation, photovoltaic power generation, and energy storages, Wen et al. (2016) proposed five non-cooperative and cooperative game planning modes and obtained the optimal capacity allocation scheme under them. The aforementioned references analyzed the game relation between each participant, establishing various game models from the perspective of dynamic and static and cooperative and non-cooperative. However, the uncertainties of distribution network are not considered, and the accuracy of planning cannot be guaranteed in the large-scale access of distributed power (Lu et al., 2014).

In this article, the main contributions are summarized as follows:

(1) By introducing the virtual player “Nature,” the deep integration of the game theory and robust optimization was realized.

(2) Considering multi-agent dynamic and static game, a source–load–storage collaborative planning method for incremental distribution networks was proposed.

(3) The uncertainty of DG output is fully considered. The network topology is actively changed to enhance robustness in large fluctuations of the DG output, and the planning result is more reasonable.

The correctness and effectiveness of the proposed method are verified in a modified IEEE 33-bus distribution network system.

2 Planning Model of Each Investment Entity

2.1 DG Investment Operator

2.1.1 Objective

The objective is to maximize the total operation cost of DG investment operators while satisfying prevailing physical constraints (Shi et al., 2016; Li and Xu, 2020b). The details can be generally described as follows:

$\max C^{DG}(x_i,N_i)=C_S^{DG}+C_C^{DG}-(C_I^{DG}+C_{OM}^{DG}),(1)$

$\{\begin{array}{l}{C}_S^{DG}={\displaystyle \sum _{t=1}^{{\mathrm{\Omega }}_t}{\theta }_{es1}\cdot P_t^{DG}}+{\displaystyle \sum _{t=1}^{{\mathrm{\Omega }}_t}{\theta }_{es2}\cdot P_{qt}^{DG}}\\ C_C^{DG}={\displaystyle \sum _{t=1}^{{\mathrm{\Omega }}_t}{\theta }_{gc}\cdot P_t^{DG}}\\ C_I^{DG}=({\theta }_{sg}\cdot {\displaystyle \sum _{i=1}^{{\mathrm{\Omega }}_i}{x}_i}\cdot P_{sg}^{DG}\cdot N_i)\cdot \frac{r{(1+r)}^{LT}}{{(1+r)}^{LT}-1}\\ C_{OM}^{DG}={\displaystyle \sum _{t=1}^{{\mathrm{\Omega }}_t}{\theta }_{om}\cdot P_t^{DG}}\end{array}.(2)$

2.1.2 Constrains

The constraint conditions of the DG investment operator planning model mainly include the restriction of the number of nodes to be selected in DG and the constraint of the DG output (Jin et al., 2017; Shen et al., 2020a; Shen et al., 2020b).

$N_{i.\min }\le N_i\le N_{i.\max },(3)$

$P_{\min }^{DG}\le P_t^{DG}\le P_{\max }^{DG}.(4)$

2.2 Distribution Network Company

2.2.1 Objective

The objective is to maximize their income of DN company, and the mathematical expression of the model can be expressed as follows:

$\max C^{DN}\left(y_i\right)=C_S^{DN}-(C_I^{DN}+C_L^{DN}+C_{B1}^{DN}+C_{B2}^{DN}+C_{B3}^{DES}).(5)$

$\{\begin{array}{l}{C}_S^{DN}={\displaystyle \sum _{t=1}^{{\mathrm{\Omega }}_t}{\psi }_{es}\cdot (P_t^{load}-(P_t^{it}+P_t^{out}-P_t^{in}))}\\ C_I^{DN}=({\psi }_{sg}\cdot {\displaystyle \sum _{j=1}^{{\mathrm{\Omega }}_j}{y}_j}\cdot l_j)\cdot \frac{r{(1+r)}^{LT}}{{(1+r)}^{LT}-1}\\ C_L^{DN}={\displaystyle \sum _{t=1}^{{\mathrm{\Omega }}_t}{\psi }_{es}\cdot P_t^{loss}}\\ C_{B1}^{DN}={\displaystyle \sum _{t=1}^{{\mathrm{\Omega }}_t}{\psi }_{eb1}\cdot (P_t^{load}-P_t^{DG}-P_t^{DES}-(P_t^{it}+P_t^{out}-P_t^{in}))}\\ C_{B2}^{DN}={\displaystyle \sum _{t=1}^{{\mathrm{\Omega }}_t}{\psi }_{eb2}\cdot P_t^{DG}\cdot T_t}\\ C_{B3}^{DES}={\displaystyle \sum _{t=1}^{{\mathrm{\Omega }}_t}{\psi }_{eb3}\cdot P_t^{DES}\cdot T_t}\end{array}.(6)$

2.2.2 Constrains

The constraint conditions of the distribution network company planning model mainly include new line investment constraint, branch flow constraint, and safety constraint.

${\displaystyle \sum _{k=1}^{{\mathrm{\Omega }}_k}{y}_{j,k}}=1,(7)$

$\{\begin{array}{c}{P}_{i.t}=U_{i.t}\cdot {\displaystyle \sum _{j\in i}{U}_{j.t}\cdot (G_{ij}\cdot \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{ij}+{\mathrm{B}}_{ij}\cdot \mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{ij})}\\ Q_{i.t}=U_{i.t}\cdot {\displaystyle \sum _{j\in i}{U}_{j.t}\cdot (G_{ij}\cdot \mathrm{s}\mathrm{i}\mathrm{n}{\theta }_{ij}-{\mathrm{B}}_{ij}\cdot \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{ij})}\end{array},(8)$

$\{\begin{array}{c}{U}_{i.\min }\le U_{i.t}\le U_{i.\max }\\ P_{ij.t}\le P_{ij.\max }\end{array}.(9)$

2.3 Power Consumers

2.3.1 Objective

The objective function of the power consumer planning model is $C^{US}$. The details are as follows:

$C^{US}(P^{it},P^{out},P^{in})=C_B^{US}+C_C^{US},(10)$

$\{\begin{array}{l}{C}_B^{US}={\displaystyle \sum _{t=1}^{{\mathrm{\Omega }}_t}{\omega }_{eb}\cdot (P_t^{it}+P_t^{out}-P_t^{in})}\\ C_C^{US}={\displaystyle \sum _{t=1}^{{\mathrm{\Omega }}_t}{\omega }_{gc}\cdot P_t^{it}}\end{array}.(11)$

2.3.2 Constrains

The constraints of the power consumer planning model mainly include transfer load power constraints and interruptible load power constraints according to the demand-side response mode (Guo and Liu, 2017; Shen et al., 2021b).

$\{\begin{array}{c}{\lambda }_{\min }{P}_t^{load}\le P_t^{out}\le {\lambda }_{\max }{P}_t^{load}\\ {\mu }_{\min }{P}_t^{load}\le P_t^{in}\le {\mu }_{\max }{P}_t^{load}\end{array},(12)$

${\displaystyle \sum _{t=1}^{{\mathrm{\Omega }}_t}{P}_t^{out}}={\displaystyle \sum _{t=1}^{{\mathrm{\Omega }}_t}{P}_t^{in}},(13)$

$P_{\min }^{it}\le P_t^{it}\le P_{\max }^{it}.(14)$

2.4 DES Investment Operator

2.4.1 Objective

The objective function $C^{DES}$ of distributed energy storage investment operators mainly includes the profit of energy price difference $C_S^{DES}$, government daily subsidy $C_C^{DES}$, DES investment cost $C_I^{DES}$, and energy storage equipment operation and maintenance cost $C_{OM}^{DES}$. The details are as follows:

$\max C^{DES}=C_S^{DES}+C_C^{DES}-(C_I^{DES}+C_{OM}^{DES}),(15)$

$\{\begin{array}{l}{C}_S^{DES}={\displaystyle \sum _{t=1}^{{\mathrm{\Omega }}_t}{\psi }_{eb3}}{P}_t^{DES}{T}_t-{\displaystyle \sum _{t=1}^{{\mathrm{\Omega }}_t}{\theta }_{es2}}{P}_t^{DG}{T}_t-{\displaystyle \sum _{t=1}^{{\mathrm{\Omega }}_t}{\lambda }_{es}}{P}_t^{DN}{T}_t\\ C_C^{DES}=C_I^{DES}\times 15\%/(365\cdot N)\\ C_I^{DES}=(K_{in}{C}_{AC}+K_P{P}_{\max })\cdot \frac{r{(1+r)}^{LT}}{{(1+r)}^{LT}-1}\\ C_{OM}^{DES}=K_O{P}_{\max }+K_M{E}_{dis.year}\\ C_{day}=C_I^{DES}/(N\cdot 365)+K_O\cdot P_{\max }/365+K_M\cdot E_{dis.day}\end{array}.(16)$

2.4.2 Constrains

The constraint conditions of the DES investment operator planning model mainly include the active power output constraint and residual capacity constraint of energy storage equipment.

$\{\begin{array}{l}{P}_{cha.\min }\le P_{cha}\le P_{cha.\max }\\ P_{dis.\min }\le P_{dis}\le P_{dis.\max }\end{array},(17)$

$SO{C}_{\min }\le SOC\le SO{C}_{\max }.(18)$

3 Multi-Agent Game Behavior in Incremental Distribution Network Planning

3.1 Transfer Relation Among Entities

The planning investment entities of this study are the DG investment operator, DN company, power consumer, and the DES investment operator. After the access of DG, the uncertainty of its output would affect the security operation of the DN. Therefore, the output of DG is considered as a special decision variable to characterize its uncertainty, and “Nature” is introduced as a virtual entity (Shen et al., 2017; Wang et al., 2021; Zhang et al., 2021; Yang et al., 2022a).

The DG investment operator selects the location and capacity under the current grid structure, transmitting the information to the DN companies, “Nature,” and the DES investment operator. Thereby, the DES investment operator would determine its decision result according to DG’s location and capacity.

The active response measures are formulated by power consumers after receiving time-of-use price information and interruptible load incentive information, that is, it determines the power of transfer load and interruptible load, feeding back to DN companies in the form of an equivalent load.

After the DN company knowing the location of DG and the current power grid structure, its planning would be interfered by “Nature.” Therefore, when the output of DG is transmitted to the DN company, it would accept the transmission information from other entities and decide to establish a new line to form a new power grid structure.

3.2 Dynamic and Static Combined Game Analysis

In this study, considering four entities and “Nature,” a dynamic–static joint game pattern was put forward. The static game behaviors were formed between the DG investment operator and distribution network company, as well as the DG investment operator and the DES investment operator. At the same time, a dynamic game was formed between the distribution network company and “Nature.”(Mei et al., 2016).

The final game equilibrium state is described as follows:

$\{\begin{array}{c}{\mathit{f}}^{\ast }=\arg \max C^{DG}(\mathit{f},{\mathit{y}}^{\ast },{\mathit{p}}^{\ast })\\ \begin{array}{l}{\mathit{y}}^{\ast }=\mathrm{argmax}{C}^{DN}({\mathit{f}}^{\ast },\mathit{y},{\mathit{p}}^{\ast })\\ {\mathit{p}}^{\ast }=\arg \max C^{DES}({\mathit{f}}^{\ast },{\mathit{y}}^{\ast },\mathit{p})\end{array}\end{array},(19)$

where ${\mathit{f}}^{\ast }$, ${\mathit{y}}^{\ast }$, and ${\mathit{p}}^{\ast }$ are the planning strategies of the DG investment operator, DN company, and the DES investment operator under an equilibrium state, respectively, and $\arg \max (·)$ represents the set of variables when the objective is maximized.

4 Case Study

4.1 Instance and Setup

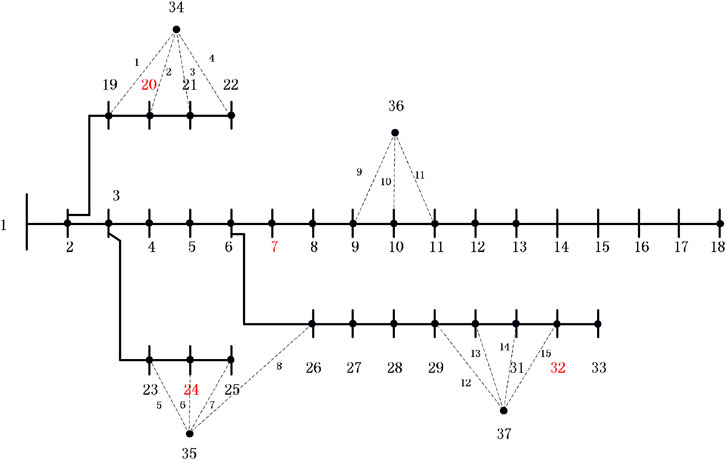
In this study, we test the performance of the proposed approach using a case study based on the modified IEEE 33-bus distribution system (Li et al., 2021c; Li et al., 2021d; Yang, 2021; Yang et al., 2021; Yang et al., 2022b). Its structure is shown in Figure 1. The system consists of 37 branches. A total load of 3715 kW + 2700 kvar and a reference voltage of 12.66 kV are considered in this system.

FIGURE 1

FIGURE 1. IEEE33 node distribution system.

DG is considered as photovoltaic power generation. At the same time, the optional access position of photovoltaic power generation is {7, 20, 24, and 32}. Other relevant parameters of DG are shown in Table 1. Meanwhile, the relevant parameters of DES are shown in Table 2. No. 33 ∼ 37 is the new load node, and the total capacity is 460 kW. In this study, the planned cycle is 5 years, and the new capacity of original load nodes is 5% at the planned level. The solid lines indicate the existing lines, and the dotted line indicates the line to be selected for new load access. Other relevant parameters of DN are shown in Table 3. The specific parameters are as follows.

TABLE 1

TABLE 1. DG relevant parameters.

TABLE 2

TABLE 2. DES relevant parameters.

TABLE 3

TABLE 3. Distribution network relevant parameters.

4.2 Simulation Results and Analysis

4.2.1 Planning Results

The following two cases are studied to validate the effectiveness of the proposed approach.

Case 1: Incremental distribution network planning without game theory.

Case 2: Incremental distribution network planning using game theory without considering the uncertainty of DG output.

Case 3: Incremental distribution network planning using game theory with considering the uncertainty of DG output, that is, the game model established in this study.

The planning results under the two cases are shown in Table 4.

TABLE 4

TABLE 4. Planning results of different market participants in the two cases.

The results of the three cases are compared in Table 4. It can be seen that optimal planning schemes of the DG investment operator and the DES investment operator are the same in Cases 2 and 3 but different from those in Case 1, and the planning results of the distribution network company in the three scenarios are disparate.

4.2.2 Necessity Analysis of Multi-Agent Game

Under Cases 1 and 2, the necessity of considering a multi-agent game by comparing the costs and benefits of the DG investment operator, DN company, and DES investment operator is illustrated. The specific results are shown in Table 5.

TABLE 5

TABLE 5. Costs, benefits, and net income of each entity.

As can be seen from Table 5 (A), the DG electricity sale revenue, DG investment cost, DG operation, maintenance cost, and government subsidies in Case 2 are, respectively, 140 yuan, 200 yuan, 81,500 yuan, 70,000 yuan, and 70,000 yuan higher than those of Case 1. The reason is that the installed capacity of DG expands after considering the multi-agent game, making the investment cost increase. Meanwhile, with the rapid development of DG output, other costs and benefits would increase.

As shown in Table 5 (B), in Case 2, the electricity sales revenue, investment cost, and government subsidy of the DES investment operator are all increased, compared with Case 1. This is because after considering the multi-agent game, the DES investment operator can adjust its investment decision according to the increase in DG installed capacity to maximize the overall benefit.

From Table 5 (C), compared with Case 1, the increase in electricity sales revenue is lesser than that enhanced in other costs. Therefore, Case 2 has no advantage in the net income of the DN company. The main reason is that after the multi-agent game is considered in Case 2, the length of new lines is longer, which makes the investment cost and network loss increase. At the same time, the installed capacity of DG is increased. Based on the principle of preferential absorption of DG and DES, the DN company purchases more power from the investment operators of DG and DES. When the total purchased power is certain, the purchase power from main network is cut down. Moreover, the available power supply increases on fault and the expected power shortage decreases. Therefore, the failure cost is reduced.

From tab 5, the sum of net income of the DG investment operator, DN company, and DES investment operator in Case 2 is less than that of Case 1 by 94,400 yuan, but the net income of the DG investment operator and DES investment operator is more than that of Case 1 by 46,600 yuan and 54,600 yuan, respectively. The reason is that in Case 1, the optimization goal of planning is to maximize the overall benefits of the DG investment operator, DN company, and DES investment operator. However, the overall benefit maximization is at the expense of the DG investment operator and DES investment operator. In Case 2, the planning scheme is obtained after the continuous game of multiple entities. The decision combination of each entity forms a Nash equilibrium point, that is, no participant can obtain better results by independent strategy change. This approach is more in line with market mechanisms, as well as the benefits of all market participants would be taken into account.

4.2.3 The Necessity Analysis of Considering Uncertainty in Multi-Agent Game Model

The decision of the DN company would only be affected by considering the uncertainty of the output of the DG. However, the planning results of the DG investment operator and DES investment operator in Cases 2 and 3 are the same, as well as the costs and benefits remained unchanged. Therefore, by comparing the costs and benefits of the DN company in Cases 2 and 3, it could illustrate the necessity of adopting robust optimization to deal with the uncertainty of the DG output.

From Table 6, compared with Case 2, the electricity sale revenue, investment cost, network loss cost, failure cost, and power purchase cost from the main network increase by 105,700 yuan, 94,800 yuan, 46,400 yuan, 500 yuan, and 146,900 yuan, respectively. This is because the uncertainty of the DG output is taken into account in Case 3. As well as the DN company would make a decision after observing the worst interference in the DG output. Therefore, the investment decision-making is more conservative. This leads to a longer length of the new line and increased investment costs. At the same time, the system load is bigger in the worst scenario. However, the DG output is smaller, and more load need to be supplied from the main network. The load cannot be absorbed locally to the maximum extent, thus resulting in increased costs.

TABLE 6

TABLE 6. Costs, benefits, and net income of DN company.

In order to further verify the robustness of the grid scheme in Case 3, Monte Carlo simulation is used in this study to randomly select 10,000 sample data within the uncertain interval of the DG output. The specific results are shown in Table 7.

TABLE 7

TABLE 7. Robustness check.

It can be seen from Table 7 that the mean and maximum value of the network loss cost in the sample data of Case 2 are higher than 757,500 yuan, and the maximum value of the failure cost is higher than 24,900 yuan. The situation of flow off-limit ratio accounts for 11.78%. However, the mean and maximum value of the network loss cost in the sample data of Case 3 are lower than 8,123,000 yuan, and the mean and maximum value of the failure cost are lower than 25,600, There is no power flow exceeding the limit.

Since the method in this study is based on robust optimization, the worst possible scenario of photovoltaic power output is fully considered. Therefore, the grid scheme in Case 3 could ensure that the operating cost would not increase and security constraints would not be violated, when the output of DG fluctuates within the uncertainty interval.

5 Conclusion

In this study, the game theory and the thought of robust optimization are integrated into the planning of incremental distribution network, and a multi-agent game based incremental distribution network source–load–storage collaborative planning method considering uncertainties is proposed. The simulation results are as follows:

1) Compared with the traditional method, by accurately simulating the game behavior of market entities, it can be ensured to continuously optimize their own decisions in the process of game, maximizing their own benefits and improving the market vitality and the effectiveness of planning decisions.

2) By introducing virtual game player “Nature,” the planning model based on the game theory can fully consider the influence of uncertain factors on planning decisions, optimizing the planning decisions actively to improve the benefits of the system.

The future study mainly focuses on the following two points. First, the uncertainty of the new energy output is only studied in this study. However, the safety risk of the power grid and other important uncertain factors does not consider. How to introduce the aforementioned uncertain factors into the game planning model has the value of further research. Second, for energy storage systems, the lithium battery is only selected as the energy storage device. Therefore, to improve the overall economic benefit of new energy stations, the influence of more types of energy storage device needs to be considered.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

NY: conceptualization, methodology, validation, formal analysis, investigation, writing—review and editing, supervision, and project administration. YH: methodology, software, validation, formal analysis, investigation, data curation, writing—original draft, and visualization. BD: methodology, software, and validation. TQ: writing—review and editing, supervision, and project administration. LD: writing—review and editing, supervision, and project administration. XY: data curation and project administration. JY: data curation and project administration. YH: validation, investigation, and funding acquisition. SW: validation, investigation, and funding acquisition. LZ: investigation and funding acquisition. BZ: investigation and funding acquisition. WX: supervision and project administration. YR: supervision and project administration

Funding

This work was supported by the National Natural Science Foundation of China under Grant 51607104. (Corresponding author: NY.).

Conflict of Interest

Author BT is employed by Substation Transportation Inspection Branch State Grid Huangshi Power Supply Company. Authors XY, JY, and WX are employed by State Grid Yichang Electric Power Company. Author YR was employed by Economic and Technological Research Institute, State Grid Hubei Electric Power Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Guo, T., and Liu, Y. (2017). Game Theory Based Reconfiguration Optimization for Distribution Network with Distributed Generations. Power Syst. Prot. Control. 45 (7), 28. doi:10.7667/PSPC160488

CrossRef Full Text | Google Scholar

Jin, Q., and Cheng, W., (2017). Coordinated Planning Model for Photovoltaic Station, Storage Battery and Grid Based on Complete Information Dynamic GameAutomation of Electric Power Systems. 41.

Google Scholar

Li, H., Deng, J., Feng, P., Pu, C., Arachchige, D. D., and Cheng, Q. (2021d). Short-Term Nacelle Orientation Forecasting Using Bilinear Transformation and ICEEMDAN Framework. Front. Energ. Res. 68 (9), 8930–8941. doi:10.3389/fenrg.2021.780928

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Yuan, S., Feng, P., and Arachchige, D. (2021c). Monitoring and Identifying Wind Turbine Generator Bearing Faults Using Deep Belief Network and EWMA Control Charts. Front. Energ. Res., 770. doi:10.3389/fenrg.2021.799039

CrossRef Full Text | Google Scholar

Li, Y., Gao, D. W., Gao, W., Zhang, H., and Zhou, J. (2020). Double-Mode Energy Management for Multi-Energy System via Distributed Dynamic Event-Triggered Newton-Raphson Algorithm. IEEE Trans. Smart Grid 11, 5339–5356. doi:10.1109/TSG.2020.3005179

CrossRef Full Text | Google Scholar

Li, Y., Gao, W., Yan, W., Huang, S., Wang, R., Gevorgian, V., et al. (2021a). Data-driven Optimal Control Strategy for Virtual Synchronous Generator via Deep Reinforcement Learning Approach. J. Mod. Power Syst. Clean Energ. 9 (no. 4), 919–929. doi:10.35833/MPCE.2020.000267

CrossRef Full Text | Google Scholar

Li, Z., Jiang, W., Abu-Siada, A., Li, Z., Xu, Y., and Liu, S. (2021b). Research on a Composite Voltage and Current Measurement Device for HVDC Networks. IEEE Trans. Ind. Electron. 68, 8930–8941. doi:10.1109/TIE.2020.3013772

CrossRef Full Text | Google Scholar

Li, Z., Lei, X., and Qiu, S. (2017). Coordinated Planning of Active Distribution Network Considering “Source-Grid-Load” Benefits. Powver System Technology. 2017 41 (2), 378–386. doi:10.1109/TPWRS.2020.3039538

CrossRef Full Text | Google Scholar

Li, Z., and Xu, Y. (2020a). A Risk-Averse Adaptively Stochastic Method for MultiEnergy Ship Operation under Diverse Uncertainties. IEEE Trans. Power Svstems. doi:10.1109/TPWRS.2020.3039538

CrossRef Full Text | Google Scholar

Li, Z., and Xu, Y. (2020b). Optimal Deployment of Heterogeneous Energy Storage System in a Residential Multi-Energy Microgrid with Demand Side Management. IEEE Trans. Ind. Inform. Early access 17 (2), 991–1004. doi:10.1109/TII.2020.2971227

CrossRef Full Text | Google Scholar

Liao, S., Xu, J., Sun, Y., Bao, Y., and Tang, B. (2018). Control of Energy-Intensive Load for Power Smoothing in Wind Power Plants. IEEE Trans. Power Syst. 33, 6142–6154. doi:10.1109/TPWRS.2018.2834940

CrossRef Full Text | Google Scholar

Liu, L.-N., and Yang, G.-H. (2021). Distributed Optimal Economic Environmental Dispatch for Microgrids over Time-Varying Directed Communication Graph. IEEE Trans. Netw. Sci. Eng. 8, 1913–1924. doi:10.1109/TNSE.2021.3076526

CrossRef Full Text | Google Scholar

Liu, Y., Yang, N., Dong, B., Wu, L., Yan, J., Shen, X., et al. (2020). “Multi-Lateral Participants Decision-Making: A Distribution System Planning Approach with Incomplete Information Game,” in IEEE Access, 8, 88933–88950. doi:10.1109/ACCESS.2020.2991181

CrossRef Full Text | Google Scholar

Lu, Q., Chen, L., and Mei, S. (2014). Typical Applications and Prospects of Game Theory in Power System. Proc. CSEB 34, 8013. doi:10.13334/j0258-8013

CrossRef Full Text | Google Scholar

Ma, H., Zheng, K., Jiang, H., and Yin, H. (2021). A Family of Dual-Boost Bridgeless Five-Level Rectifiers with Common-Cor Inductors. IEEE Trans. Power Electron, 12565–12578. doi:10.1109/TPEL2021.3078533

CrossRef Full Text | Google Scholar

Ma, Q., and Wang, Y. (2017). Investment Risk Analysis of Power Grid Enterprises under Incremental Distribution Businesses Opening. Electric Power Construction 38 (09), 139. doi:10.3969/j.issn.1000-7229.2017.09.020

CrossRef Full Text | Google Scholar

Mei, S., Liu, F., and Wei, W. (2016). Engineering Game Theory Foundation and Power System Application [M], 2016. Beijing: Science Press, 216.

Google Scholar

Mei, S., Wang, Y., and Liu, F. (2011). A Game Theory Based Planning Model and Analysis for Hybrid Power System With Wind Generators-Photovoltaic Panels-Storage Batteries. Automation Electric Power Syst. 35 (20), 13–19. doi:10.1097/MCC.0b013e328344b397

CrossRef Full Text | Google Scholar

Shen, X., Ouyang, T., Khajorntraidet, C., Li, Y., Li, S., and Zhuang, J. (2022a). Mixture Density Networks-Based Knock Simulator. Ieee/asme Trans. Mechatron. 27, 159–168. doi:10.1109/tmech.2021.3059775

CrossRef Full Text | Google Scholar

Shen, X., Ouyang, T., Yang, N., and Zhuang, J. (2021b). Sample-Based Neural Approximation Approach for Probabilistic Constrained Programs. IEEE Trans. Neural Netw. Learn. Syst., 1–8. doi:10.1109/tnnls.2021.3102323

CrossRef Full Text | Google Scholar

Shen, X., and Raksincharoensak, P. (2021). Pedestrian-Aware Statistical Risk Assessment. IEEE Trans. Intell. Transport. Syst., 1–9. doi:10.1109/TITS.2021.3074522

CrossRef Full Text | Google Scholar

Shen, X., and Raksincharoensak, P. (2021). Statistical Models of Near-Accident Event and Pedestrian Behavior at Non-signalized Intersections. J. Appl. Stat., 1–21. doi:10.1080/02664763.2021.1962263

CrossRef Full Text | Google Scholar

Shen, X., Zhang, X., Ouyang, T., Li, Y., and Raksincharoensak, P. (2020a). Cooperative Comfortable-Driving at Signalized Intersections for Connected and Automated Vehicles. IEEE Robot. Autom. Lett. 5 (4), 6247–6254. doi:10.1109/lra.2020.3014010

CrossRef Full Text | Google Scholar

Shen, X., Zhang, Y., Sata, K., and Shen, T. (2020b). Gaussian Mixture Model Clustering-Based Knock Threshold Learning in Automotive Engines. Ieee/asme Trans. Mechatron. 25 (6), 2981–2991. doi:10.1109/tmech.2020.3000732

CrossRef Full Text | Google Scholar

Shen, X., Zhang, Y., Shen, T., and Khajorntraidet, C. (2017). Spark advance Self-Optimization with Knock Probability Threshold for Lean-Burn Operation Mode of SI Engine. Energy 122, 1–10. doi:10.1016/j.energy.2017.01.065

CrossRef Full Text | Google Scholar

Shi, Q., Guo, L., and Zhang, X. (2016). Research on Optimal Configuration of Distributed Generation Considering Economic Benefits of the Multi-Agent. Power Syst. Prot. Control. 44 (1), 85. doi:10.7667/j.issn.1674-3415.2016.01.012

CrossRef Full Text | Google Scholar

Su, J., Zhang, P., and Liu, H. (2016). Cost-benefit Analysis of Distributed Generation and Optimization of Capacity Considering Different Stakeholders. Power Syst. Techn. 40 (4), 1128–1133. doi:10.13335/j.1000-3673.pst.2016.04.022

CrossRef Full Text | Google Scholar

Wang, C., Mei, S., Yu, H., Cheng, S., Du, L., and Yang, P. (2021). Unintentional Islanding Transition Control Strategy for Three-/Single-phase Multimicrogrids Based on Artificial Emotional Reinforcement Learning. IEEE Syst. J. 15, 5464–5475. doi:10.1109/isvst.2021.307429610.1109/jsyst.2021.3074296

CrossRef Full Text | Google Scholar

Wen, J., Zeng, B., and Zhang, J. (2016). Adjustable Robust Optimization for Distributed Wind Power Planning in Distribution. Network Power System Technology. 40, 227–233. doi:10.13335/j.1000-3673.pst.2016.01.031

CrossRef Full Text | Google Scholar

Yang, N. (2021). A Comprehensive Review of Security-Constrained Unit Commitment. J. Mod. Power Syst. Clean Energ. doi:10.35833/MPCE.2021.000255

CrossRef Full Text | Google Scholar

Yang, N., Qin, T., Wu, L., Huang, Y., Huang, Y., Xing, C., et al. (2022). A Multi-Agent Game Based Joint Planning Approach for Electricity-Gas Integrated Energy Systems Considering Wind Power Uncertainty. Electric Power Syst. Res. 204, 107673. doi:10.1016/j.epsr.2021.107673

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Wu, L., Shen, X., Jia, J., Li, Z., et al. (2022). Intelligent Data-Driven Decision-Making Method for Dynamic Multisequence: An E-Seq2Seq-Based SCUC Expert System. IEEE Trans. Ind. Inf. 18, 3126–3137. doi:10.1109/tii.2021.3107406

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Xing, C., Ye, D., and Jia, J. (2021). Deep Learning-Based SCUC Decision-Making: An Intelligent Data-Driven Approach with Self-Learning Capabilities. IET Gener. Transm. Distrib 16, 629–640. doi:10.1049/gtd2.12315

CrossRef Full Text | Google Scholar

Zhang, L., Xie, Y., Ye, J., Xue, T., Cheng, J., Li, Z., et al. (2021). Intelligent Frequency Control Strategy Based on Reinforcement Learning of Multi-Objective Collaborative Reward Function. Front. Energ. Res. 9, 525. doi:10.3389/fenrg.2021.760525

CrossRef Full Text | Google Scholar

Zhu, B., Ding, F., and Vilathgamuwa, D. M. (2020). Coat Circuits for DC-DC Converters to Improve Voltage Conversion Ratio. IEEE Trans. Power Electron. 35, 3679–3687. doi:10.1109/TPEL.2019.2934726

CrossRef Full Text | Google Scholar

Glossary

${\mathit{C}}^{\mathit{D}\mathit{G}}$ objective function of the DG investment operator

${\mathit{C}}_{\mathit{S}}^{\mathit{D}\mathit{G}}$ DG electricity sale income

${\mathit{C}}_{\mathit{I}}^{\mathit{D}\mathit{G}}$ DG investment cost

${\mathit{C}}_{\mathit{O}\mathit{M}}^{\mathit{D}\mathit{G}}$ DG operation and maintenance cost

${\mathit{C}}_{\mathit{C}}^{\mathit{D}\mathit{G}}$ government subsidies for renewable energy generation

${\mathit{\theta }}_{\mathit{e}\mathit{s}1}$ unit electricity price of DG

${\mathit{\theta }}_{\mathit{e}\mathit{s}2}$ unit photovoltaic curtailment electricity price of DG

${\mathit{\theta }}_{\mathit{g}\mathit{c}}$ subsidy cost per unit power generation of renewable energy

${\mathit{\theta }}_{\mathit{s}\mathit{g}}$ investment cost per unit capacity DG

${\mathit{x}}_{\mathit{i}}$ variables of 0 or 1, when ${\mathit{x}}_{\mathit{i}}$ = 0, meaning that the $\mathit{i}$ candidate node does not access DG. Otherwise, the candidate node $\mathit{i}$ accesses DG

${\mathit{P}}_{\mathit{t}}^{\mathit{D}\mathit{G}}$ total active power for DG at moment $\mathit{t}$

${\mathit{P}}_{\mathit{q}\mathit{t}}^{\mathit{D}\mathit{G}}$ photovoltaic curtailment of active power for DG at moment $\mathit{t}$

${\mathit{P}}_{\mathit{s}\mathit{g}}^{\mathit{D}\mathit{G}}$ rated power for a single DG

${\mathit{N}}_{\mathit{i}}$ number of DGs connected to the selected node $\mathit{i}$

$\mathit{r}$ discount rates

$\mathit{L}\mathit{T}$ life cycle of equipment

${\mathit{\theta }}_{\mathit{o}\mathit{m}}$ Unit power generation operation and maintenance costs of DG

${\mathit{C}}^{\mathit{D}\mathit{N}}$ objective function of distribution network company

${\mathit{C}}_{\mathit{S}}^{\mathit{D}\mathit{N}}$ income from electricity sales of the distribution network company

${\mathit{C}}_{\mathit{I}}^{\mathit{D}\mathit{N}}$ investment cost of new lines

${\mathit{C}}_{\mathit{L}}^{\mathit{D}\mathit{N}}$ cost of network loss

${\mathit{C}}_{\mathit{B}1}^{\mathit{D}\mathit{N}}$ cost of electricity purchase from the main network

${\mathit{C}}_{\mathit{B}2}^{\mathit{D}\mathit{N}}$ operator invested by DG

${\mathit{C}}_{\mathit{B}3}^{\mathit{D}\mathit{E}\mathit{S}}$ operator invested by DES

${\mathit{\psi }}_{\mathit{e}\mathit{s}}$ electricity price of distribution company;

${\mathit{P}}_{\mathit{t}}^{\mathit{l}\mathit{o}\mathit{a}\mathit{d}}$ primary load at moment $\mathit{t}$;

${\mathit{P}}_{\mathit{t}}^{\mathit{i}\mathit{t}}$ interruption power of interruptible load at moment $\mathit{t}$

${\mathit{P}}_{\mathit{t}}^{\mathit{o}\mathit{u}\mathit{t}}$ power transferred out of the load at moment $\mathit{t}$

${\mathit{P}}_{\mathit{t}}^{\mathit{i}\mathit{n}}$ transfer into of the load at moment $\mathit{t}$

${\mathit{P}}_{\mathit{t}}^{\mathit{D}\mathit{E}\mathit{S}}$ total active power for DES at moment $\mathit{t}$;

${\mathit{\psi }}_{\mathit{s}\mathit{g}}$ cost per unit length of the new line;

${\mathit{y}}_{\mathit{j}}$ variables of 0 or 1, when ${\mathit{y}}_{\mathit{j}}$ = 0, meaning that the line $\mathit{j}$ to be built is not selected. Otherwise, the line $\mathit{j}$ to be built is selected.

${\mathit{l}}_{\mathit{j}}$ length of the new line.

${\mathit{P}}_{\mathit{t}}^{\mathit{l}\mathit{o}\mathit{s}\mathit{s}}$ active power loss at moment $\mathit{t}$.

${\mathit{\psi }}_{\mathit{e}\mathit{b}1}$ electricity price to the higher power grid.

${\mathit{\psi }}_{\mathit{e}\mathit{b}2}$ purchase electricity prices from the DG investment operator

${\mathit{\psi }}_{\mathit{e}\mathit{b}3}$ purchase electricity prices from the DES investment operator

${\mathit{\omega }}_{\mathit{e}\mathit{b}}$ electricity price of consumers

${\mathit{\omega }}_{\mathit{g}\mathit{c}}$ compensation cost of interruptible load

${\mathit{C}}_{\mathit{B}}^{\mathit{U}\mathit{S}}$ reduced electricity cost of interruptible load after participating in the demand side response.

${\mathit{C}}_{\mathit{C}}^{\mathit{U}\mathit{S}}$ compensation cost of interruptible load after participating in the demand side response ${\mathit{C}}^{\mathit{D}\mathit{E}\mathit{S}}$ the objective function of distributed energy storage investment operators

${\mathit{C}}_{\mathit{S}}^{\mathit{D}\mathit{E}\mathit{S}}$ profit of energy price difference

${\mathit{C}}_{\mathit{C}}^{\mathit{D}\mathit{E}\mathit{S}}$ government daily subsidy

${\mathit{C}}_{\mathit{I}}^{\mathit{D}\mathit{E}\mathit{S}}$ investment cost of DES

${\mathit{C}}_{\mathit{O}\mathit{M}}^{\mathit{D}\mathit{E}\mathit{S}}$ operation and maintenance cost of energy storage equipment

${\mathit{K}}_{\mathit{i}\mathit{n}}$ coefficient of DES investment cost per unit capacity

${\mathit{K}}_{\mathit{p}}$ coefficient of DES power related cost

${\mathit{K}}_{\mathit{m}}$ coefficient of DES maintenance cost

${\mathit{K}}_{\mathit{o}}$ coefficient of DES annual operating cost

$\mathit{S}\mathit{O}{\mathit{C}}_{\mathit{min}}$ minimum remaining capacity of lithium battery, 20–30% of the total battery capacity generally

$\mathit{S}\mathit{O}{\mathit{C}}_{\mathit{max}}$ maximum remaining capacity of lithium battery, 80–100% of the total battery capacity generally

${\mathit{f}}^{\ast }$ planning strategies of DG investment operator under equilibrium state

${\mathit{y}}^{\ast }$ planning strategies of DN company under equilibrium state

${\mathit{p}}^{\ast }$ planning strategies of the DES investment operator under equilibrium state

$\mathit{arg}\mathit{max}(·)$ set of variables when the objective is maximized