A Novel Pre-Synchronization Control Method Based on Open-Loop Phase Detection for the Maritime VSC-HVDC System

Maritime island grids based on renewable energy are being rapidly developed, which poses a new challenge to the traditional pre-synchronization process of grid connection. Aiming at the problems of impulse current out of limit and long steady-state regulation time, a novel pre-synchronization control method is provided based on open-loop phase detection, which is realized by replacing the frequency detection method of the difference judgment part. The open-loop detection model of voltage phase and amplitude based on the synchronous rotating coordinate system is established first. Then the voltage phase is linearized to control the output frequency and finally reduces the voltage deviation through the compensation of virtual power to achieve the effect of a smooth grid connection. The novel pre-synchronization method has a fast response speed and no regulator effect, which can synchronize the actual values of output voltage amplitude, phase, and frequency. Simulation results verify the excellent performance of the proposed method in island stable operation and grid connection under disturbance.

1 Introduction

Voltage source converter-based high voltage direct current (VSC–HVDC) systems have experienced an increasing application in the grid connection of offshore wind farms, as a power transmission carrier and control center (Barnes et al., 2017; Alghamdi and Canizares, 2021; Xiong et al., 2021a). VSC-HVDC can supply power to an island utilizing active control and reactive power independently at the grid side. The sag control can isolate the adverse effects of wind power, and the pre-synchronous control can optimize the effect of grid connection and reduce the impact of grid connection. However, when the voltage and frequency of the wind farm side fluctuates greatly, the rapidity and stability of the control algorithm will be very crucial. Therefore, it is of great significance to quickly control the converter’s active and reactive power for improving the dynamic performance of the system under disturbances.

Because the voltage, frequency, and phase are directly related to the converter’s active and reactive power, the essence of the control is to improve the speed and sensitivity of the pre-synchronization of voltage, frequency, and phase. Phase-locked loop (Blaabjerg et al., 2006) is a common method for phase and amplitude detection dynamically. The single synchronous reference frame phase-locked loop (SSRF-SPLL) (Ademi and Milutin, 2014) adopts a d-q frame transform and PI controller, which is the most widespread three-phase PLL technology in the VSC-HVDC system. It is a closed-loop control containing two integrals, which has a suppression effect on disturbance. But it is difficult to respond in real-time and achieve phase lock in the case of grid voltage imbalance.

At present, in order to improve the speed of phase detection, the methods of improving the control performance of PLL are mainly divided into structure development and algorithm improvement. For structure development, the phase output direction is proposed by increasing the control of the direct axis voltage and eliminating the integral link (Yuan et al., 2010). The input voltage is controlled before the phase lock for improving the rapidity of the phase lock (Ama et al., 2014). For algorithm improvement, the phase Angle error is analyzed based on the small signal model at the steady-state operating point of the system, obtaining the closed-loop transfer function, and improving the adaptability of the phase-locked loop in the abnormal power grid environment (Zhang et al., 2020; Mondal et al., 2021).

The phase tracking time of these improved methods are obviously shortened. But the above methods are still based on closed-loop feedback, which requires parameter testing time, and the phase difference between the output voltage of the PLL and the actual voltage cannot suddenly become zero. For these shortcomings, open-loop detection methods are studied to speed up dynamic response time, such as zero-crossing detection (Vainio and Ovaska, 1995), the wavelet transform method (Freijedo et al., 2007), weighted least squares estimation (Wu et al., 2017), and predictive digital filters (Zhen et al., 2017). But these open-loop detection methods are mostly designed for certain grid conditions and cannot cope with multiple grid distortions simultaneously. For the active power filter, a moving average filter and a heterodyne algorithm were used to obtain the phase of the distorted voltage (Xiong et al., 2022). An open-loop method in a strong power grid is proposed to quickly obtain the positive, negative, and zero sequence components based on the symmetrical component method, which was characterized by fast and accurate acquisition (Liancheng et al., 2021).

Meanwhile, the voltage-oriented control (VOC) on the rectifier and pre-synchronous control on the inverter based on open-loop detection has been studied. For the VOC, since the detection speed of the grid voltage phase directly affects the generation of the trigger pulse, it is very beneficial to improve the performance of the rectifier by increasing the capture speed of the voltage phase. For the pre-synchronous control, virtual orthogonal signals and outputted phase and frequency of output voltage are constructed based on an open-loop (Xiong et al., 2021b; Xiu et al., 2021). However, this method was applicable to single-phase phase capture and had not been verified in the maritime VSC-HVDC system (Hintz et al., 2016). directly processed the direct axis component of the voltage and obtained its rotation angular frequency by open-loop. This method abandoned the complex parameters, but cannot accurately obtain positive and negative sequence voltages in microgrids with large frequency fluctuations.

This paper presents a detection method based on an open-loop for the instantaneous detection voltage phase. The method makes the synchronous rotation coordinate system and the actual voltage vector move at a fixed angular frequency (usually the grid standard frequency). It can detect the voltage phase in real-time only by obtaining the initial phase difference without the real-time frequency of the voltage. On this basis, a novel pre-synchronization control method is provided, which is realized by modeling the phase difference between the voltage vector and after synchronous rotation and generating the actual frequency by linearizing the obtained phase. The algorithm has a fast response speed because it is not affected by the dynamic process of the regulator. Thus, it can effectively improve the frequency and phase tracking performance and reduce the risk of a grid connection failure in a harsh environment.

The rest of this paper is organized as follows. Section 2 analyzes the structure and control algorithm of the maritime VSC-HVDC system, Section 3 studies the performance of pre-synchronization control. Section 4 verifies the effectiveness of the novel pre-synchronization method. Finally, conclusion are drawn in Section 5.

2 Structure and Control Algorithm of the Maritime VSC-HVDC System

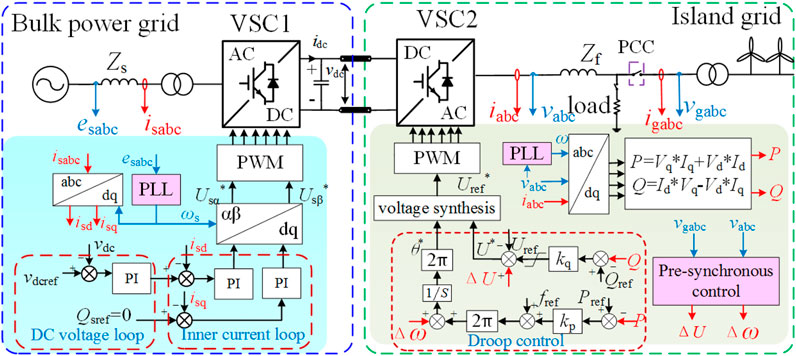
The structural model of the maritime VSC-HVDC system is shown in Figure 1, including a bulk power grid, island grid, rectifier (VSC1), inverter (VSC2), control strategy, and power lines. The power grid voltage is stably transmitted to the inverter through the rectifier, and the inverter has strong networking ability, the ability to absorb corresponding active power and reactive power according to the internal load and stability requirements, to provide power support for the island grid.

FIGURE 1

FIGURE 1. Structural model of the maritime VSC-HVDC system.

2.1 VOC Control Algorithm

In Figure 1, e_sabc and i_sabc are, respectively, the ac grid voltage and the ac grid current. v_dc is the voltage of the dc side of the rectifier, and i_dc is the dc side current. v_abc and i_abc are, respectively, the output voltage and current of the inverter. v_gabc and i_gabc are, respectively, the voltage and current of the island grid. Z_s and Z_f are the equivalent impedance of the line.

The rectifier adopts a VOC control strategy to maintain the stability of v_dc and transmission power by absorbing active and reactive power. v_dcref, Q_sref are, respectively, the reference value of v_dc and the reference value of the rectifier reactive power. ω_s is the angular frequency of grid voltage, and $U_{s\alpha }^{*}$, $U_{s\beta }^{*}$ is the modulation signal that controls the switching off of VSC1.

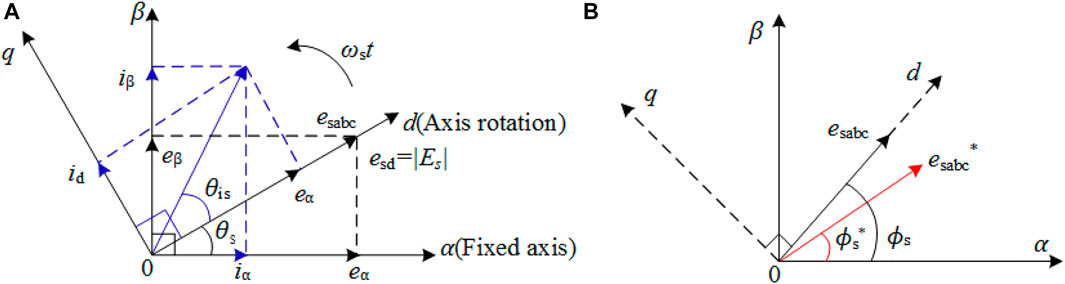
The VOC realizes the active and reactive power control via orienting the rotating coordinate systemand the voltage vector, and the vector graph based on grid voltage orientation is shown in Figure 2A. Let e_sd = |E_s|, e_sq = 0, the output power of the grid after the rectifier can be obtained

$\left\{\begin{array}{c}{P}_{\mathrm{s}}=\frac{\mathrm{3}}{\mathrm{2}}\left(e_{\mathrm{s}\mathrm{d}}{i}_{\mathrm{s}\mathrm{d}}+e_{\mathrm{s}\mathrm{q}}{i}_{\mathrm{s}\mathrm{q}}\right)=\frac{\mathrm{3}}{\mathrm{2}}|E_{\mathrm{s}}|i_{\mathrm{s}\mathrm{d}}\hfill \\ Q_{\mathrm{s}}=\frac{\mathrm{3}}{\mathrm{2}}\left(e_{\mathrm{s}\mathrm{d}}{i}_{\mathrm{s}\mathrm{q}}-e_{\mathrm{s}\mathrm{q}}{i}_{\mathrm{s}\mathrm{d}}\right)=\frac{\mathrm{3}}{\mathrm{2}}|E_{\mathrm{s}}|i_{\mathrm{s}\mathrm{q}}\hfill \end{array}\right.(1)$

here P_s is the active power, and Q_s is the reactive power. If the grid voltage is fixed, the loss of VSC1 is ignored, and the values of E_s and i_dc .remain unchanged, and Eq. 1 can be simplified to:

$P_{\mathrm{s}}=\frac{\mathrm{3}}{\mathrm{2}}|E_{\mathrm{s}}|i_{\mathrm{s}\mathrm{d}}=i_{\mathrm{d}\mathrm{c}}{v}_{\mathrm{d}\mathrm{c}}(2)$

FIGURE 2

FIGURE 2. The vector graph: (A) voltage orientation control; (B) phase-locked loop.

Because i_sd and v_dc are coupled, v_dc can be controlled through controlling i_sd, and the control of P_s can be realized. Therefore, the detection speed of the grid voltage phase directly affects the generation of the trigger pulse, thereby affecting the switching time of the rectifier.

The droop control of the inverter in the grid-connected process will produce a large current shock and power overshoot. In order to eliminate this effect, the pre-synchronization control is carried out before the grid-connected, so that the voltage amplitude difference, phase difference and frequency difference on both sides of the grid-connected switch are in a small range to close the grid-connected switch. The response speed of the pre-synchronization module is mainly determined by the detection method of voltage amplitude and phase frequency, and the commonly used detection method is a phase-locked loop. The phase-locked loop (PLL) can track and lock the phase of the AC signal in real-time, and provide phase, amplitude, and frequency information, which is widely used in converter control. The realization process of PLL is shown in Figure 2B. ${e_{\mathit{sabc}}}^{*}$ is the output voltage vector of PLL, and ${{\varphi }_s}^{*}$ is the phase angle of the voltage output by the phase-locked loop. In normal operation, the rotation speed of the actual coordinate system and the tracking control coordinate system is inconsistent, and there is a phase angle tracking error. When ${{\varphi }_s}^{*}$ = ϕ_s, the correct phase lock of e_sabc is completed. Therefore, the control process of the PLL is a closed-loop control, which uses the output value as a feedback signal to repeatedly adjust the ${{\varphi }_s}^{*}$ to complete the phase lock.

2.2 Droop Control Algorithm

The inverter adopts droop control to complete the orderly distribution of power and realize the coordinated action between the island grid and the inverter side in the dynamic process. Q and P are the active power and reactive power of the inverter respectively. U_ref, P_ref and Q_ref are voltage, active power and reactive power reference values in droop control respectively. Δω and ΔU are the pre-synchronous compensating angular frequency and compensating voltage respectively. θ^* and U^* are the phase and voltage generated by droop control respectively. ${U_{\mathit{ref}}}^{*}$ is the modulation signals that control the switching off of the inverter.

The droop control simulates the frequency and voltage regulation characteristics of the generator from the external characteristics, giving the inverter end a certain networking ability and an orderly response to the load fluctuations of the inverter end and the power demand of the island grid, avoiding complicated communication. Its characteristic equation for:

$\left\{\begin{array}{c}{f}^{*}=f_{ref}-k_{\mathrm{p}}\left(P-P_{ref}\right)\hfill \\ U^{*}=U_{ref}-k_{\mathrm{q}}\left(Q-Q_{ref}\right)\hfill \end{array}\right.(3)$

here, k_p is the active power droop coefficient, and k_q is the reactive power droop coefficient. It can be seen that k_p and k_q determine the primary frequency regulation and primary voltage regulation capabilities of the inverter side. If the inverter side voltage is not synchronized with the island voltage before grid connection, the grid connection process will have the characteristics of a large impact on the grid and long transition time, which will seriously damage the rapidity and reliability of the VSC-HVDC system. Therefore, it is necessary to perform pre-synchronization control on the voltage before grid connection, which can weaken the inrush current in advance, reduce the risk of system components being damaged, and effectively increase the grid connection speed.

Pre-synchronization control is the secondary frequency modulation and voltage regulation of the power system. When the grid connection starts, the pre-synchronization control will gradually reduce the deviation of voltage amplitude, phase, and frequency between the inverter terminal and the island grid until it reaches the grid-connected allowable value. Then close the PCC switch to achieve a smooth grid connection, and stop the pre-synchronization.

Assuming that there exists virtual impedance between the inverter and the island grid, the power transmission path at the PCC is shown in Figure 3A. The virtual complex power can be expressed as:

${\tilde{S}}_{\mathrm{P}\mathrm{C}\mathrm{C}}=v_{\text{g}}\angle 0^{\text{o}}\times \frac{v\angle \theta -v_{\text{g}}\angle 0^{\text{o}}}{Z_{\text{v}}\angle {\theta }_{\text{v}}}(4)$

where Z_v is the virtual impedance (mainly the equivalent impedance of the island grid), and θ_v is the virtual impedance Angle. If the virtual impedance is pure inductive impedance, that is Z_V = X_V∠90°, then the virtual active power and virtual reactive power are respectively:

$\left\{\begin{array}{c}\mathrm{\Delta }P=\frac{v{v}_{\text{g}}\cos \left(\theta -{\theta }_{\mathrm{v}}\right)-v_{\text{g}}^2\cos \theta }{Z_{\mathrm{v}}}=\frac{v{v}_{\text{g}}\sin \theta }{X_{\mathrm{v}}}\hfill \\ \mathrm{\Delta }Q=-\frac{v{v}_{\text{g}}\sin \left(\theta -{\theta }_{\mathrm{v}}\right)+v_{\text{g}}^2\sin {\theta }_{\mathrm{v}}}{Z_{\mathrm{v}}}=\frac{v{v}_{\text{g}}\cos \theta -v_{\text{g}}^2}{X_{\mathrm{v}}}\hfill \end{array}\right.(5)$

FIGURE 3

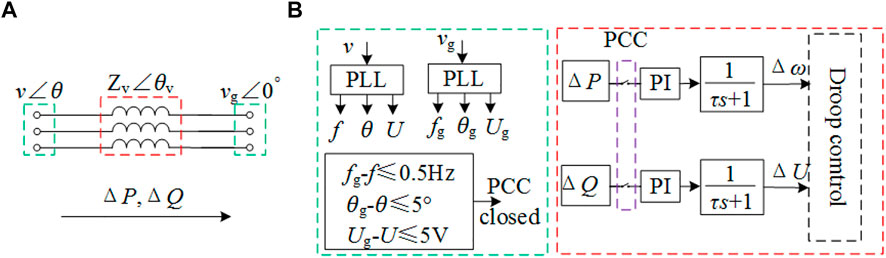
FIGURE 3. (A) Virtual Power transmission path; (B) The concrete realization process of pre-synchronization.

In order to dynamically compensate for the voltage amplitude and frequency deviation at both ends of the PCC, the PLL-based pre-synchronization method has been designed. It performs a PI adjustment on virtual active and virtual reactive power to obtain angular frequency and voltage deviation signals, which are respectively superimposed on the active and reactive power links in the droop control. And the PLL is used to detect whether the deviation meets the grid-connected conditions. The concrete realization process of the PLL-based pre-synchronization is shown in Figure 3B.

The PLL-based pre-synchronization control makes the synchronous rotating coordinate systems to lock the voltage vector, and takes the frequency as the feedback quantity. Then through PI closed-loop control, the angle between the coordinate system and the voltage vector is continuously reduced until the quadrature axis component of the voltage vector is zero. Finally, the phase, voltage amplitude, and frequency are obtained.

3 A Novel Pre-Synchronization Control Based on Open-Loop Phase Detection

3.1 Open-Loop Phase Detection

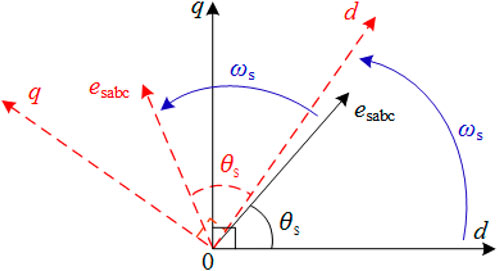
Based on the structural analysis of the phase-locked loop, it can be seen that the dynamic performance of the closed-loop phase-locked mainly depends on PI control. In the abnormal power grid environment, PI can only gradually adjust the phase output value, and the speed of phase detection is limited. Therefore, this paper proposes an open-loop detection phase technology: the traditional phase comparison method is converted into a method of superimposing the rotation angular velocity and the initial phase so that the rotation angular frequency of the synchronous rotating coordinate system is consistent with the angular frequency of the three-phase voltage. Obtain the initial phase difference between the two to accurately measure the phase. The schematic diagram of open-loop phase detection is shown in Figure 4.

FIGURE 4

FIGURE 4. Schematic diagram of open-loop phase detection.

Suppose the three-phase grid voltage e_sabc is:

$e_{sabc}=E_s\sin \left({\omega }_{s}t+{\theta }_s\right)=E_s\sin \left({\omega }_{0}t+\left({\omega }_s-{\omega }_0\right)t+{\theta }_s\right)(6)$

where θ_s is the initial phase of the grid voltage, and ω₀ is the voltage synchronous angular frequency, with ω₀ = 100π. After Park transformation of voltage, obtain ${e_{\mathrm{s}\mathrm{d}}}^{*}$ and ${e_{\mathrm{s}\mathrm{q}}}^{*}$.

$\left\{\begin{array}{c}{e_{\mathrm{s}\mathrm{d}}}^{*}=E_{\text{s}}\cos \left[\left({\omega }_s-{\omega }_0\right)t+{\theta }_s\left.\right)\right]\hfill \\ {e_{\mathrm{s}\mathrm{q}}}^{*}=E_{\text{s}}\sin \left[\left({\omega }_s-{\omega }_0\right)t+{\theta }_s\left.\right)\right]\hfill \end{array}\right.(7)$

After dividing:

$\begin{array}{ll}\hfill \frac{{e_{\mathrm{s}\mathrm{d}}}^{*}}{{e_{\mathrm{s}\mathrm{q}}}^{*}}& =\frac{1}{tan\left[\left({\omega }_s-{\omega }_0\right)t+{\theta }_s\right]}\hfill \\ \hfill & \Rightarrow \left({\omega }_s-{\omega }_0\right)t+{\theta }_s=\arctan \left({e_{\mathrm{s}\mathrm{q}}}^{*}/{e_{\mathrm{s}\mathrm{d}}}^{*}\right)\hfill \end{array}(8)$

Then the amplitude and phase of grid voltage:

$\left\{\begin{array}{c}{E}_s=\sqrt{{\left({e_{\mathrm{s}\mathrm{d}}}^{*}\right)}^2+{\left({e_{\mathrm{s}\mathrm{q}}}^{*}\right)}^2}\hfill \\ {\varphi }_s={\omega }_{0}t+\arctan \left({e_{\mathrm{s}\mathrm{q}}}^{*}/{e_{\mathrm{s}\mathrm{d}}}^{*}\right)+{\theta }_{ex}\hfill \end{array}\right.(9)$

where the value of θ_ex is related to the quadrant of the rotating coordinate system:

${\theta }_{\mathrm{e}\mathrm{x}}=\left\{\begin{array}{c}0,e_d>0,e_q>0\hfill \\ \pi ,e_d<0\hfill \\ 2\pi ,e_d>0,e_q<0\hfill \end{array}\right.(10)$

It can be seen that the voltage phase and amplitude can be detected instantaneously according to Eqs 8, 9, and the output phase component and amplitude component are not coupled, which can quickly detect and adapt to abnormal grid environment changes.

3.2 A Novel Pre-Synchronization Control Method

The PLL-based pre-synchronization control adopts closed-loop control, which affects the speed of difference judgment in the pre-synchronization process and increases the instability time of the island grid. Thus, a novel pre-synchronization method is proposed, which is to change the detection method of the difference judgment part and replace the closed-loop detection with open-loop detection. Based on the mathematical model of the three-phase grid voltage e_sabc, the voltage and phase of the inverter output voltage v_abc can be obtained.

$v_{\mathrm{a}\mathrm{b}\mathrm{c}}=U\sin \left[\left(\omega -{\omega }_n\right)t+{\omega }_{\mathrm{n}}t+{\theta }_0\right]\Rightarrow \left\{\begin{array}{c}U=\sqrt{{\left(v_{\mathrm{d}}\right)}^2+{\left(v_{\mathrm{q}}\right)}^2}\hfill \\ \theta ={\omega }_{\mathrm{n}}t+\arctan \left(v_{\mathrm{q}}/v_{\mathrm{d}}\right)+{\theta }_{\mathrm{e}\mathrm{x}}\hfill \end{array}\right.(11)$

where ω is the angular frequency of the grid voltage, and θ₀ is the initial phase of the grid voltage, and ω_n is the voltage synchronous angular frequency, with ω_n = 100π. Calculate the difference between the actual phase of the voltage and the rated phase, and obtain the frequency difference through PI control. The relationship between the phase difference and the frequency difference is:

$\mathrm{\Delta }\theta =\theta -{\theta }_N=\int \mathrm{\Delta }\omega dt=2\pi \int \mathrm{\Delta }fdt=2\pi \mathrm{\Delta }ft+\lambda (12)$

where λ = 2πn, it is the continuous change adjustment to achieve PI control. The discrete sampling process has errors and cannot be accurate to 100%. If the phase difference between the current moment and the previous time exceeds 0.99% of a cycle, the current phase difference increases by 2π, and the changes are shown in Figure 5A . As time changes, a continuously increasing phase difference curve can be obtained.

FIGURE 5

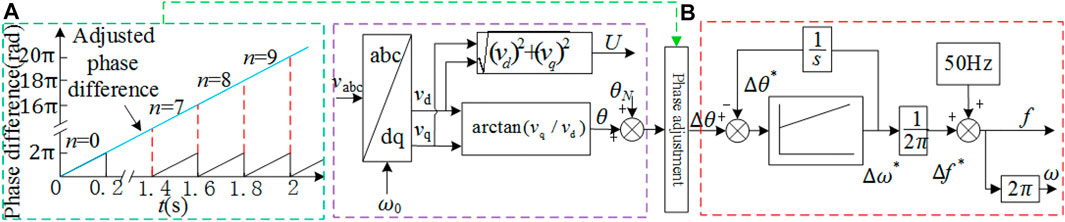
FIGURE 5. (A) Continuous change adjustment of phase difference; (B) Implementation of open-looped phase detection.

The angular frequency can be obtained by PI adjustment of the phase difference, and the novel pre-synchronization control based on open-looped frequency detection is shown in Figure 5B. In Figure 5B, Δθ^*, Δω^*, Δf^* are the feedback values of phase difference, angular frequency difference and frequency difference, respectively. When Δθ = Δθ^*, the output angular frequency difference and the feedback value of the frequency difference are the actual difference.

4 Simulation Verification

In order to verify the effectiveness of the novel pre-synchronization method, this paper builds a VSC-HVDC system in Matlab/Simulink, verifying the control effect of open-loop phase detection in the case of sudden changes in the voltage amplitude and phase changes of the grid, and analyzing the actual effects of the novel pre-synchronization control method. Related parameter settings of the VSC-HVDC system are shown in Table 1.

TABLE 1

TABLE 1. Rectifier parameter and inverter parameter.

4.1 Validation of Open-Loop Phase Detection

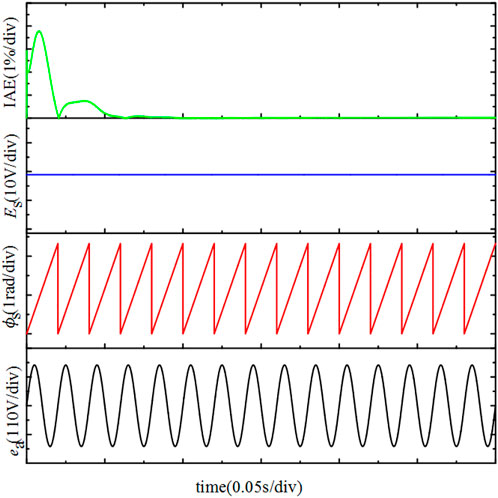
The output voltage of the power grid is maintained at 380 V, the initial phase is 0°, and the total simulation duration is 0.3 s. Figure 6 shows the actual effect of using the open-loop phase detection technology when the power grid voltage is stable. In the figure, the open-loop phase detection technology can achieve accurate measurement of voltage phase and amplitude at the initial moment of system operation. And the integral of the absolute error (IAE) of the DC voltage is always maintained within a stable value. Generally IAE$<$10% indicates that the simulation effect is very good, and the simulation results show that the open-loop phase detection technology has high-precision performance.

FIGURE 6

FIGURE 6. The detection results in steady state environment.

By comparing with the PLL algorithm, the superiority of the open-loop phase detection method is verified under the sudden change of voltage amplitude and the sudden change of phase. Figure 7A shows the results of relevant parameters after the sudden change of the grid voltage amplitude. The total simulation time is 0.8 s. The voltage drops 0.2 p.u. at 0.2 s and increases by 0.4 p.u. at 0.6 s. When the voltage amplitude changes suddenly, the open-loop phase detection method can immediately sense the amplitude change and output 0.8 p.u. However, the PLL has a time delay, and the phase output changes according to the downward trend of the linear function. Since the sudden change in voltage amplitude does not affect the phase detection result, the IAE curve of the open-loop phase detection and PLL is the same, and the maximum value of the IAE value at the sudden amplitude change is 2.5%, which is less than 10%. It shows that the error between the DC voltage and the reference value is very small, and the detection results of the two methods are basically the same when the voltage amplitude changes suddenly.

Figure 7B shows the results of related parameters after the power grid phase mutation. The total simulation time is 0.7 s, the grid voltage initial phase is 0°, the phase mutation changes to 50° at 0.3 s, and the phase mutation changes to 0° at 0.5 s. It can be seen from the figure that the measured phase of the open-loop phase detection changes synchronously with the actual phase, and its voltage amplitude is almost unchanged. However, the measured phase of the PLL gradually tracks the actual output phase within 0.16 s, and the amplitude also needs time delay to stabilize. In addition, at 0.3 and 0.5 s, the maximum IAE value of the DC voltage under the open-loop phase detection method is 2%, the IAE curve has no fluctuations, while the phase-locked loop is 20.6%, and the IAE curve fluctuation duration is 0.16 s. Obviously, the control effect of the open-loop phase detection method is better than that of the phase-locked loop.

FIGURE 7

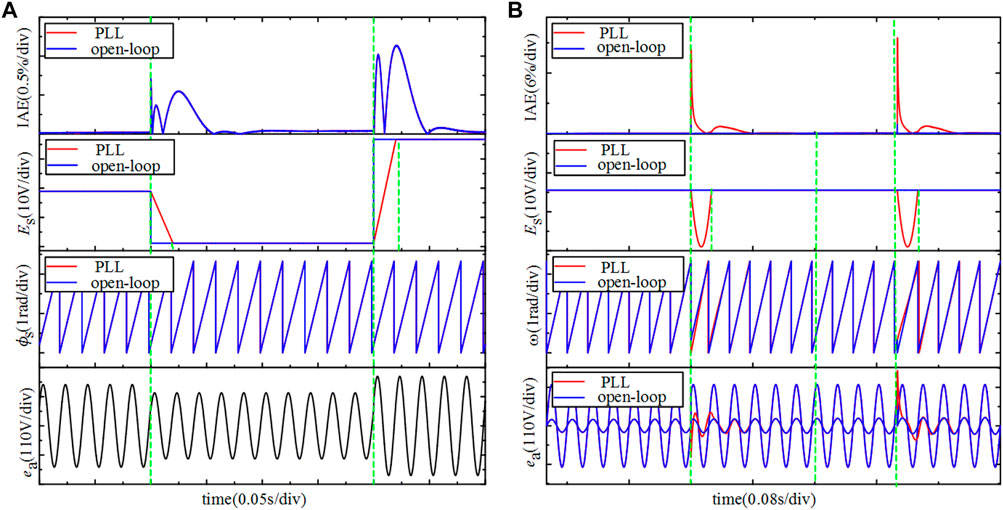
FIGURE 7. The simulation result: (A) the voltage amplitude changes suddenly; (B) the voltage phase changes suddenly.

4.2 Verification of Novel Pre-Synchronization Method

In order to verify the role of pre-synchronization in the grid connection process, Figure 8 shows the comparison result with or without pre-synchronization. The total simulation time is 1.8 s. Pre-synchronization is turned on at t = 0.3 s. The dashed line is the current change without pre-synchronization. In Figure 8, the impulse current and power oscillation spikes without pre-synchronization are too large. For example, the active power spike has reached 40% of its reference value, which seriously affects the life of power devices and power quality. When pre-synchronization existed, the current of the inverter terminal and the island grid gradually increases, there is no inrush current and power spikes and the power is output smoothly. In addition, the total time from pre-synchronized grid connection to stable operation is 200 ms, which shorter than that of a direct grid connection. The above results prove that the use of a novel pre-synchronization method can improve the grid connection quality of isolated power grids and improve the safety of the flexible and straightforward system of isolated power grids.

FIGURE 8

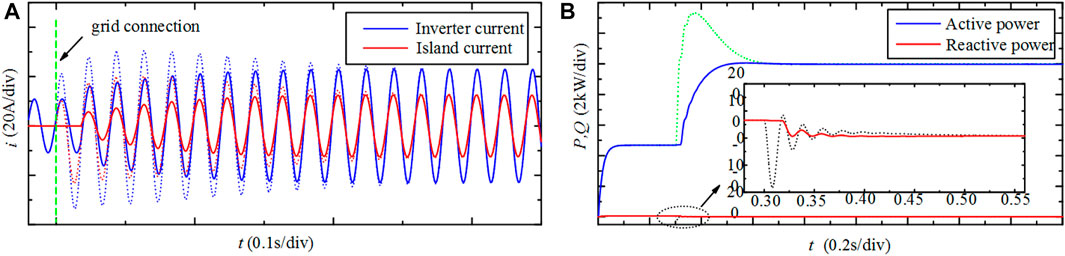
FIGURE 8. Grid connection effect under the novel pre-synchronization method: (A) the current changed; (B) the power changed.

To further verify the novel pre-synchronization method, it is compared with the PLL-based pre-synchronization method. The result is shown in Figure 9, where the initial frequency of the island grid is 49.8 Hz. As can been obtained from Figure 9, the novel pre-synchronization method has higher speed and accuracy in phase angle detection and power output than the PLL-based pre-synchronization method. When the island grid is in an unstable state, the inverter side can support the power of the island grid more timely, avoiding the further deterioration of the frequency of the island grid system.

FIGURE 9

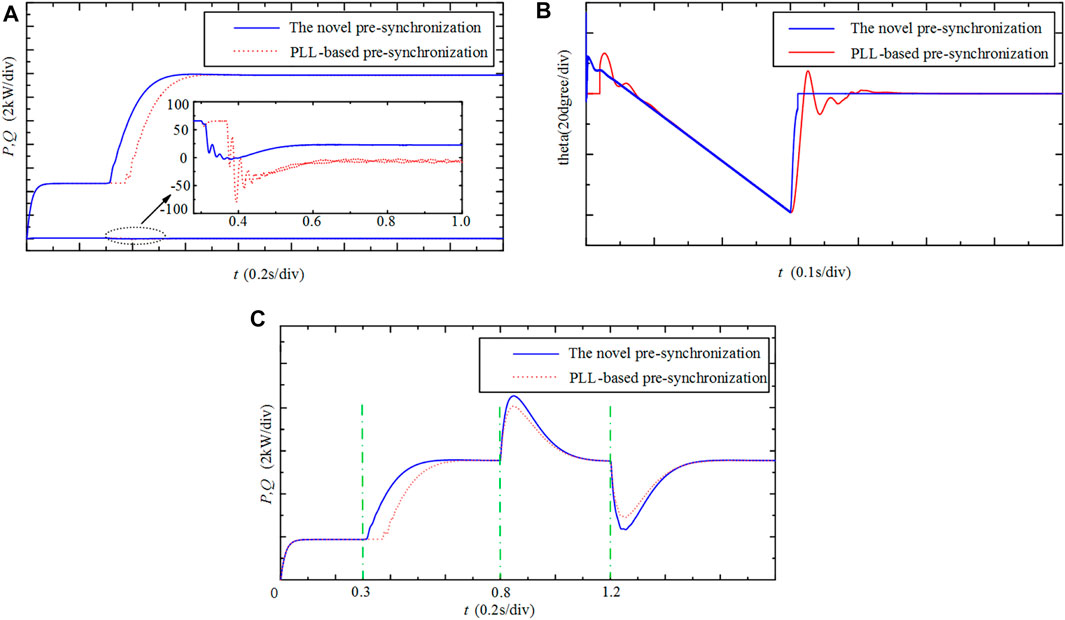
FIGURE 9. Comparison result of two pre-synchronization methods: (A) the power changed; (B) the theta changed; (C) power variation under multiple grid connection.

5 Conclusion

In order to solve the problem of grid connection in maritime island grids, a novel pre-synchronization control method based on the phase and frequency detection in the part of its difference judgment is proposed in this paper. In this method, the closed-loop structure is abandoned, and the open-loop structure is adopted to measure the voltage phase, amplitude, and frequency. It has the advantages of no PI adjustment, instantaneous output parameters, and simple structure. The proposed pre-synchronization method ensures the friendly and cooperative relationship between the island grid and the land grid, greatly reduces the impulse current and plays an important role in smoothing the power peak. Simulation results show that the quality of the grid connection of the proposed method is better than the traditional pre-synchronization method, especially when disturbed.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

JS and DW contributed to conception and design of the study. JS wrote the first draft of the manuscript. JS, DW, QG, and YQ wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work is supported by the Research Foundation of the Nanjing Institute of Technology (YKJ202017) and School-enterprise Alliance project of Jiangsu Province (NSG032039701).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

REFERENCES

Ademi, S., and Milutin, J. (2014). High-Efficiency Control of Brushless Doubly-Fed Machines for Wind Turbines and Pump Drives. Energy Convers. Manag. 81, 120–132. doi:10.1016/j.enconman.2014.01.015

CrossRef Full Text | Google Scholar

Alghamdi, B., and Canizares, C. A. (2021). Frequency Regulation in Isolated Microgrids Through Optimal Droop Gain and Voltage Control. IEEE Trans. Smart Grid 12 (2), 988–998. doi:10.1109/tsg.2020.3028472

CrossRef Full Text | Google Scholar

Ama, N., Komatsu, W., and Junior, L. M. (2014). Single and Three Phase Moving Average Filter Plls: Digital Controller Design Recipe. Electr. Power Syst. Res. 116, 276–283. doi:10.1016/j.epsr.2014.06.019

CrossRef Full Text | Google Scholar

Barnes, M., Van Hertem, D., Teeuwsen, S. P., and Callavik, M. (2017). HVDC Systems in Smart Grids. Proc. IEEE 105 (11), 2082–2098. doi:10.1109/jproc.2017.2672879

CrossRef Full Text | Google Scholar

Blaabjerg, F., Liserre, M., Teodorescu, R., and Timbus, A. V. (2006). Overview of Control and Grid Synchronization for Distributed Power Generation Systems. IEEE Trans. Ind. Electron. 53 (5), 1398–1409. doi:10.1109/tie.2006.881997

CrossRef Full Text | Google Scholar

Freijedo, F. D., Doval-Gandoy, J., Lopez, O., and Martinez-Penalver, C. (2007). “New Algorithm for Grid Synchronization Based on Fourier Series,” in European Conference on Power Electronics and Applications (Aalborg, 1–6.

CrossRef Full Text | Google Scholar

Hintz, A., Prasanna, U. R., and Rajashekara, K. (2016). Comparative Study of the Three-Phase Grid-Connected Inverter Sharing Unbalanced Three-Phase and/or Single-Phase Systems. IEEE Trans. Ind. Appl. 52 (6), 5156–5164. doi:10.1109/tia.2016.2593680

CrossRef Full Text | Google Scholar

Liancheng, X., Du, Z., Li, M., Du, L., Hao, J., and Kang, Z. (2021). A Practical and Fast Sequence Components Detection Scheme for Three-Phase Unbalanced Grid Voltage. Int. J. Electr. Power & Energy Syst. 125, 106385. doi:10.1016/j.ijepes.2020.106385

CrossRef Full Text | Google Scholar

Mondal, P., Tripathy, P., Saha, U. K., and Adda, R. (2021). A Simple Yet Robust Mechanism for the Improvement of Phase-Locked-Loop System and its Verification With Grid Side Converter Control[J]. J. Electr. Eng. Technol. doi:10.1007/s42835-021-00788-4

CrossRef Full Text | Google Scholar

Vainio, O., and Ovaska, S. J. (1995). Noise Reduction In Zero Crossing Detection by Predictive Digital Filtering. IEEE Trans. Ind. Electron. 42 (1), 58–62. doi:10.1109/41.345846

CrossRef Full Text | Google Scholar

Wu, F., Li, X., and Duan, J. (2017). Improved Elimination Scheme of Current Zero-Crossing Distortion in Unipolar Hysteresis Current Controlled Grid-Connected Inverter. IEEE Trans. Ind. Inf. 11 (5), 1111–1118. doi:10.1109/tii.2015.2470540

CrossRef Full Text | Google Scholar

Xiong, L., Liu, L., Liu, X., and Liu, Y. (2021). Frequency Trajectory Planning Based Strategy for Improving Frequency Stability of Droop-Controlled Inverter Based Standalone Power Systems. IEEE J. Emerg. Sel. Top. Circuits Syst. 11 (1), 176–187. doi:10.1109/jetcas.2021.3052006

CrossRef Full Text | Google Scholar

Xiong, L., Liu, X., Liu, L., and Liu, Y. (2022). Amplitude-Phase Detection for Power Converters Tied to Unbalanced Grids With Large X/R Ratios. IEEE Trans. Power Electron. 37 (2), 1–2112. doi:10.1109/tpel.2021.3104591

CrossRef Full Text | Google Scholar

Xiong, L., Liu, X., Zhang, D., and Liu, Y. (2021). Rapid Power Compensation Based Frequency Response Strategy for Low Inertia Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 9 (4), 4500–4513. doi:10.1109/jestpe.2020.3032063

CrossRef Full Text | Google Scholar

Xiu, L., Du, Z., Wu, B. B., Li, G., Wang, D., and Song, H. (2021). A Novel Adaptive Frequency Extraction Method for Fast and Accurate Connection Between Inverters and Microgrids. Energy 221, 119795. doi:10.1016/j.energy.2021.119795

CrossRef Full Text | Google Scholar

Yuan, Z. C., Song, Q., and Liu, W. H. (2010). A Modified Soft Phase Lock Loop Algorithm Improving the Performance in Dynamic Phase Tracking and Detection of Unbalanced Voltage[J]. Power Syst. Technol. 34 (01), 31–35.

Google Scholar

Zhang, C., Molinas, M., Foyen, S., Suul, J. A., and Isobe, T. (2020). Harmonic Domain SISO Equivalent Impedance Modeling and Stability Analysis of a Single-Phase Grid Connected VSC[J]. IEEE Trans. Power Electron. (99), 1–11. doi:10.1109/tpel.2020.2970390

CrossRef Full Text | Google Scholar

Zhen, X., Zhao, R., Blaabjerg, F., Zhang, L., and Chiang Loh, P. (2017). An Improved Flux Observer for Field-Oriented Control of Induction Motors Based on Dual Second-Order Generalized Integrator Frequency-Locked Loop[J]. IEEE J. Emerg. Sel. Top. Power Electron. (1), 513–525. doi:10.1109/jestpe.2016.2623668

CrossRef Full Text | Google Scholar