A Non-Scheduled Multi-Stage Decision-Making Approach to Control Cascading Failures

The control research on cascading failures is critical to ensure the reliability of power supply. A path-driven multi-stage corrective control model for the whole process of cascading failures is established to eliminate the risk of cascading failure. For the cascading failure process caused by overloading, the selection criterion for subsequent outage is defined according to the mechanism of propagation of cascading failures. The path-driven constraints and power relaxation constraints are extracted based on the selection criterion for a subsequent outage. A model coupled with non-scheduled multi-stage decision-making is designed by considering the flexibility of control action implementation to optimize the sum of control cost and load-shedding risk for elimination of cascading failures. The verification results show that the proposed method can reduce the probability of outages of tripped branches and successfully eliminate cascading failure.

1 Introduction

Due to human factors and external environmental factors such as natural disasters, large-scale blackouts remain difficult to avoid for modern power systems, as evinced by the many large-scale blackouts that have occurred around the world in recent years (Hines et al., 2009; Xue and Xiao, 2013). Most blackouts are found to be caused by cascading failures (Wong et al., 2007; Zeng et al., 2015; Nagpal et al., 2018). Specifically, local disturbances such as generator and transmission line outages can result in a series of successive outages through network connections, resulting in great economic losses and negative social influence. Therefore, it has important significance to quickly and accurately predict the cascading failure process and establish a targeted framework of defense for the predicted cascading failure.

According to the different modeling ideas, there are mainly two types of control approaches for cascading failure. The first type of control method is from the perspective of macroscopic system theory (Lin et al., 2018; Kornbluth et al., 2021). The control methods based on macroscopic system theory focusing on load optimization (Tu et al., 2013) and network structure reinforcement (Liu et al., 2019) are taken as preventative actions to release system operating stress and avoid blackouts. Those methods are applied to provide a reference for power system planning and design; however, it is difficult to realize cascading failure control in practical operation of the power system. Therefore, the research on cascading failure control in power systems is mainly based on reductionism, which consists of initial disturbances and control considering cascading effects.

Security constrained optimal power flow (Capitanescu et al., 2011) is a deterministic model for initial disturbances, including prevention (Azzolin et al., 2018) and correction (Bi et al., 2018), according to the timing of the implementation of control actions. The deterministic method lacks risk awareness, and overly conservative control schemes can increase control costs. Risk is a comprehensive measure of probability and results in uncertain events, including risk identification, risk assessment, and risk control. Among them, the risk identification and assessment of cascading failures have been widely discussed, and considerable results have been achieved. In addition, mathematical programming, reinforcement learning methods, and deep learning approaches (Li et al., 2022) are used to solve the above model. However, the risk control of cascading failures is still confined to the preventive control of cascading failures or the corrective control of a given cascading failure stage, especially for the initial outage. Zhai et al. (2019) compared two corrective control models of cascading failures: non-recurring corrective control and that of two consecutive cascading failure stages. The simulation results show that the two consecutive stages perform better than non-recurring corrective control. However, corrective actions are taken only at two consecutive stages, which reduces the flexibility around control timing. Subsequently, Gan et al. (2020) proposed a multi-stage corrective control model to study the predicted cascading failure. The mechanism of propagation of the cascading failure process caused by overload is not considered in the control model, that is, the influence of a control action on the branch outage probability and the constraints between outage probability of the tripped branches and in-service branches. Although the resulting control schemes can reduce the outage probability of a tripped branch, the outage probability of an in-service branch may increase significantly, even exceeding the outage probability of the tripped branch. Therefore, it is important to explore how to correct a given cascading failure process under the constraints of the cascading failure propagation mechanism. In this report, an optimal control considering the constraints of the cascading failure mechanism of propagation, the so-called path-driven multi-stage corrective control (path-driven MSCC), is presented to protect power systems against cascading failure.

This report is organized as follows. Section 2 presents an analysis of the interaction between the MSCC and the cascading effect. Extraction of path-driven constraints and power relaxation constraints is based on the mechanism of propagation of cascading failures in Section 3. And Section 4 discusses the effects of the above two constraints on the control scheme obtained by the path-driven MSCC. Section 5 concludes the report.

2 Interaction Between Cascading Failure Process and MSCC

For cascading failures caused by overload, when a branch is randomly selected as the initial disturbance, the outage probability of in-service branches can be calculated by (1), given by Zima and Andersson (2005). The selection criterion for a subsequent outage (Wei et al., 2018) is adopted, i.e., choosing the branch with largest p_i,k among all branches as the tripped branch at the (k+1)^th stage:

$p_{i,k}=\{\begin{array}{l}0,F_{i,k}\le F_i^{\text{rated}}\\ \frac{1}{F_i^{\text{max}}-F_i^{\text{rated}}}(F_{i,k}-F_i^{\text{rated}}),F_i^{\text{rated}}<F_{i,k}\le F_i^{\text{max}}\\ 1,F_{i,k}>F_i^{\text{max}}\text{. }\end{array}(1)$

In actual operation, the change of active power injections, demand response, and topology optimization can be used to correct power flow on the branches. The outage probability of in-service branches and their maximum values are also changed, as given by (1). Thus, the control action can affect the outage probability of tripped branches and even change the branches that tripped during the cascading failure process. Similarly, the network topology determined by tripped branches also affects the distribution of nodal power injections on the branches. The interaction between the cascading failure process and the MSCC continues until there are no overloaded lines in the power system.

3 Path-Driven MSCC Model

In this section, the path-driven MSCC for the whole cascading failure process is proposed, in which path-driven constraints and power relaxation constraints are taken into consideration at each cascading stage.

3.1 Objective Function

The goal of MSCC is to minimize the load-shedding risk caused by cascading failures with the lowest control cost, and the objective function f is calculated as follows:

$\min f={\displaystyle \sum _{k=1}^{v_{\text{con}}}\left({\displaystyle \prod _{m=1}^k{\pi }_m}\right)\left({\displaystyle \sum _g{\alpha }_{g}PG{D}_{g,k}}+{\displaystyle \sum _n{\beta }_{n}L{D}_{n,k}}\right)},(2)$

where v_con denotes the total number of cascading stages with corrective control actions; because the proposed multi-stage control is designed to eliminate cascading failures, v_con is an unknown variable and less than the total number of cascading stages l without corrective control. ${\pi }_k$ is the maximum of an overloaded branch probability at the (k-1)^th cascading stage, i.e., ${\pi }_k=\max \left(p_{i,k-1}\right)$. Therefore, the multiplication of ${\pi }_k$ over stages is the probability of cascading failure. PGD_g,k and LD_n,k are the power generation adjustment at unit g and load shedding at node n at the kth cascading stage. α_g and β_n are the cost coefficients of PGD_g,k and LD_n,k, respectively.

3.2 Path-Driven Constraints

In this report, the research object is the predicted cascading failure process, so the same subsequent outage selection criteria should be used in both the cascading failure prediction and the cascading failure control processes; therefore, the outage probability of the tripped branch must satisfy path-driven constraints in the MSCC model of cascading failure, given by

$p_{i,k}\ge p_{e,k}\forall e\in E_k,(3)$

where E_k is the set of in-service branches. The physical meaning of Eq. 3 is that the outage probability of predicted outage branch i at the kth stage is greater than that of other in-service branches in power systems. Eq. 3 ensures that corrective control actions can only affect the probability of an outage on a tripped branch without changing the tripped branch subject to the subsequent outage selection criteria described above.

3.3 Power Relaxation Constraints

To balance cost and load-shedding risk in corrective control, the corresponding power relaxation coefficients γ₁ and γ₂ are set for predicted tripped branches and other in-service branches. As the control relaxation coefficient decreases, the upper capacity of the power flow allowed on branches is gradually reduced in the corrective control model. At each cascading stage, the power relaxation constraints are expressed as

$\{\begin{array}{c}\left|F_{i,k}\right|\le {\gamma }_1{F}_i^{\text{rated}}k=1\text{,}2\text{,}\cdots \text{,}{v}_{\text{con}}-1\\ \left|F_{i,k}\right|\le F_i^{\text{rated}}k=v_{\text{con}}\text{, }\end{array}(4)$

$\{\begin{array}{c}\left|F_{e,k}\right|\le {\gamma }_2{F}_e^{\text{rated}}k=1\text{,}2\text{,}\cdots \text{,}{v}_{\text{con}}-1\\ \left|F_{e,k}\right|\le F_e^{\text{rated}}k=v_{\text{con}}\text{, }\end{array}(5)$

where F_i,k and F_e,_k are the active power flows on predicted tripped branches and other in-service branches, respectively. Eqs 4–5 represent power flow on branches being allowed to exceed its threshold in the former (v_con-1) stages; meanwhile, there may be differences in the degree of power relaxation for predicted tripped branches and other in-service lines.

3.4 Power Flow Constraints

At each cascading stage, the proposed model is subject to the following power flow constraints:

$P_{n,k}={\displaystyle \sum _{\mathrm{Fr}\left(i\right)}{F}_{i,k}}-{\displaystyle \sum _{\mathrm{T}\left(i\right)}{F}_{i,k}},(6)$

$P{G}_g^{min}\le P{G}_{g,k}\le P{G}_g^{min},(7)$

$0\le PG{D}_{g,k}\le PG{D}_g^{\max },(8)$

$0\le L{D}_{n,k}\text{ , }0\le {\displaystyle \sum _{m=1}^{k}L{D}_{n,m}}\le P{D}_n^{\max },(9)$

where PG_g,_k, $\mathrm{P}{\mathrm{G}}_g^{\min }$, and $\mathrm{P}{\mathrm{G}}_g^{\max }$ are power generated by unit g and its minimum and maximum capacities, respectively. $\mathrm{PG}{\mathrm{D}}_g^{\max }$ and $\mathrm{P}{\mathrm{D}}_n^{\max }$ are the maximum allowable power generation adjustment of unit g and maximum allowable load shedding of node n, respectively. Eq. 6 is the power balance equation. Eqs 7–8 limit power outputs of the generators and their power output adjustment, respectively. Eq. 9 is the load-shedding limit.

Eqs 2–9 imply that, due to the uncertainty of v_con, the path-driven MSCC model is a non-scheduled multi-stage decision-making optimization for the whole process of cascading failure. It is worth noting that control action implementation is not confined to one or more given cascading failure stages. So, there is a choice to take control actions at each cascade stage.

3.5 Solving the Path-Driven MSCC Model

The proposed model is a non-linear programming problem which is difficult to be solved directly. Therefore, we draw on the idea of the two-layer decomposition optimization scheme proposed by Liu et al. (2015), and the genetic algorithm (Shi et al., 2021) is used to solve it. The upper-level model optimizes the outage probability of predicted tripped branch for each cascading stage, and the obtained values are imported into the lower-level model. Output adjustment of unit and load shedding are optimized in the lower-level model.

4 Example Analysis

4.1 Validation of Path-Driven MSCC Model

The IEEE 39 Bus System is employed to validate the proposed method and analyze the corresponding results. The IEEE 39 Bus System consists of 10 units, 39 buses, and 46 branches. In addition, the system load in normal operation is 6,254.2 MW, and the total installed capacity is 7367 MW. The transmission capacity of branch is set to 95% of its original value, and the transmission capacity of branch 17–18 is modified to 300 MW. The active adjustment of the unit is 15% of the unit capacity; α_g and β_n are set to 1 $/MW and 100 $/MW, respectively (Carreras et al., 2001). Power relaxation coefficients γ₁ and γ₂ are both set to 1.4. The tripping of branch 1–2 is selected as the initial disturbance, and subsequently, the power flow on branch 2–3 with its rated capacity of 475 MW increases from 450.81 to 757.62 MW. The cascading effect continues to propagate until the grid is decoupled, and the cascading failure process is denoted as I_a = {1–2, 2–3, 17–18, 15–16, 1, 1, 1, 1}. Figure 1A presents the connection states of IEEE 39 Bus Systems after suffering the cascading failure process I_a. In Figure 1, the blue balls are the unit nodes, while black ones are the load nodes and red branches characterize overloaded branches. It is worth noting that the IEEE 39 node system not only is decoupled into two islands but also contains an overloaded branch in each island.

FIGURE 1

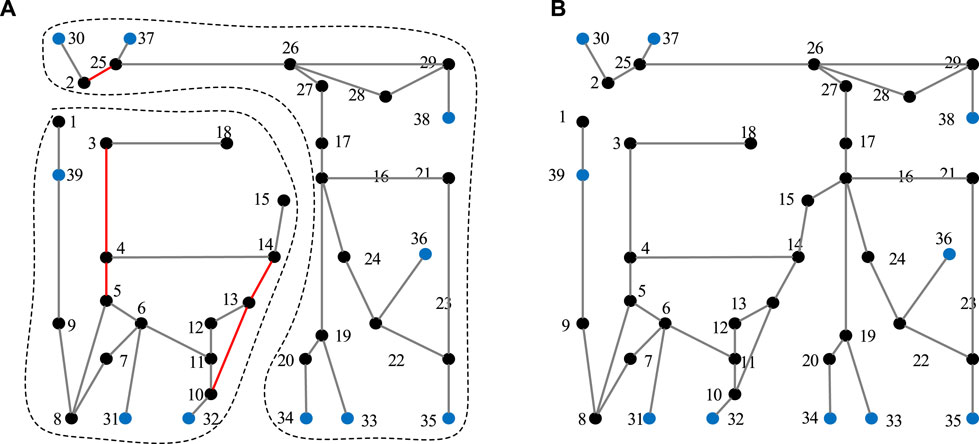
FIGURE 1. IEEE 39 Bus Systems. (A) Connection states of IEEE 39 Bus Systems without control. (B) Connection states of IEEE 39 Bus Systems with path-driven MSCC.

The proposed model is applied to devise the control schemes for the cascading failure process I_a. With corrective control, the cascading failure process is truncated from I_a to I_b = {1–2, 2–3, 17–18, 1, 0.48, 0.31}, and the connection states of IEEE 39 Bus Systems after suffering the cascading failure process I_b are shown in Figure 1B. As can be seen from Figure 1B, with corrective control, there are no multiple islands and overloaded branches in IEEE 39 Bus Systems, indicating that path-driven MSCC can successfully eliminate cascading failures in three cascading stages.

4.2 Effect of V_con

Due to the uncertainty of v_con, the proposed path-driven MSCC model is a non-scheduled multi-stage decision-making optimization facing the whole cascading failure process. In other words, the optimal control approach is designed to correct the cascading effect within the first l cascading stages. This non-scheduled model is compared with the scheduled model (i.e., v_con is restricted to a certain value), and the results are summarized in Table 1.

TABLE 1

TABLE 1. Effect of v_con on the performance of the scheduled MSCC model.

If v_con is restricted to 1, after implementing the corrective action, the power flow on branch is less than its threshold and the cascading process caused by overloaded branches ends. The MSCC will be transformed to non-recurring corrective control, and path-driven MSCC is superior to non-recurring corrective control in terms of load-shedding risk and objective function. For the scheduled MSCC model, when v_con = 3, the values of the above two indicators are the lowest at 11,412.95 and 106.05, respectively. With the scheduled constraints, the MSCC model needs to be solved repeatedly according to the value of v_con, and the solution time gradually increases as v_con increases. Then, the optimization results with different v_con values are compared, and the optimal solution is obtained. The non-scheduled MSCC model proposed in this report can be solved once to obtain the optimal solution.

4.3 Effect of Path-Driven Constraint

If the path-driven constraint is not considered in path-driven MSCC, i.e., the constraint (Eq. 3) is removed, the model is denoted as Model 2. Table 2 shows the branch outage probability ranking with the control scheme obtained by Model 2. The data listed in bold are the predicted tripped branches and their outage probability. Notably, the initial disturbance is the selected outage, so there is no ranking of branch outage probability at the first cascading stage.

TABLE 2

TABLE 2. Branch outage probability ranking with the control actions obtained by Model 2.

After control action is implemented at the third cascading stage, the outage probability of predicted tripped branch 15–16 is 0.01. In contrast, the branch with maximum outage probability is branch 4–14, and its outage probability is significantly greater than that of predicted tripped branch 15–16. From the defined criterion for candidate outage, branch 4–14 is chosen to serve as the tripped branch at the next cascading stage, so the cascading failure process will deviate from the original predicted cascading process.

Furthermore, under the corrective control obtained by using Model 2, the cascading failure process considering the selection criterion for subsequent outage is I_c = {1–2, 2–3, 17–18, 4–14, 6–11, 1, 0.49, 0.46, 0.21, 1}. It can be seen from I_c that although the control scheme obtained by Model 2 can reduce the outage probability of a tripped branch, there are still overloaded branches in the network even after four cascading stages, that is, Model 2 cannot eliminate cascading failure processes.

4.4 Effects of Power Relaxation Constraints

In this part, the power relaxation coefficient is modified to 1, denoted as Model 3. Model 3 is solved and compared with the results of Model 1, as summarized in Table 3.

TABLE 3

TABLE 3. Comparison of different control models.

As can be seen from Table 3, compared with Model 3, Model 1 provides better performance in terms of load shedding, risk of load shedding, and objective function. This is because the control scheme obtained by Model 3 needs to shed more load to satisfy the constraint whereby the power flow on a branch cannot exceed the pre-set threshold for in-service branches other than on the branch predicted to trip. As the transmission capacity of branch is further reduced, it may appear that Model 1 can provide an effective control scheme, while Model 3 fails to obtain a corrective control scheme. This is because in extreme operating conditions, when the control action is implemented to eliminate the power flow overload of one branch, it may inevitably cause the power flow overload of other branches. Therefore, the power relaxation constraints can not only help to obtain an available control scheme in extreme conditions but also reduce the control cost.

5 Conclusion

A path-driven multi-stage corrective control method considering the uncertainty of v_con is proposed to eliminate the cascading failure process. According to the mechanism of propagation of cascading failures, path-driven constraints and power relaxation constraints are extracted. Adjustments of nodal power injections including unit output adjustment and load shedding are considered corrective controls, and the proposed model is optimized by minimizing the sum of the expected control cost and load-shedding risk. The results verified that the path-driven MSCC method can correct the cascading failure process in an effective and cooperative manner. The effects of the uncertainty of v_con, path-driven constraints, and power relaxation constraints on the applicability and effectiveness of control scheme are discussed. When path-driven constraints are not considered, the obtained control scheme may fail due to change of cascading failure paths. When power relaxation constraints or the uncertainty of v_con is not considered, the resulting solutions are too conservative.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

YL and TW performed the methodology. YL was involved in data analysis and writing the original draft. TW supervised the work. JG reviewed and edited the paper.

Funding

This research was funded by the National Natural Science Foundation of China under Grant No. 52107092.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Azzolin, A., Dueñas-Osorio, L., Cadini, F., and Zio, E. (2018). Electrical and Topological Drivers of the Cascading Failure Dynamics in Power Transmission Networks. Reliab. Eng. Syst. Saf. 175, 196–206. doi:10.1016/j.ress.2018.03.011

CrossRef Full Text | Google Scholar

Bi, R., Lin, T., Chen, R., Ye, J., Zhou, X., and Xu, X. (2018). Alleviation of Post‐contingency Overloads by SOCP Based Corrective Control Considering TCSC and MTDC. IET Gener. Transm. Distrib. 12 (9), 2155–2164. doi:10.1049/iet-gtd.2017.1393

CrossRef Full Text | Google Scholar

Capitanescu, F., Martinez Ramos, J. L., Panciatici, P., Kirschen, D., Marano Marcolini, A., and Platbrood, L. (2011). State-of-the-art, Challenges, and Future Trends in Security Constrained Optimal Power Flow. Electr. Power Syst. Res. 81 (8), 1731–1741. doi:10.1016/j.epsr.2011.04.003

CrossRef Full Text | Google Scholar

Carreras, B., Lynch, V., Sachtjen, M., Dobson, I., and Newman, D. (2001). “Modeling Blackout Dynamics in Power Transmission Networks with Simple Structure,” in Proceedings of 34th IEEE Hawaii International Conference on System Sciences, Maui, Hawaii, July, 2011, 719–727. doi:10.1109/HICSS.2001.926275

CrossRef Full Text | Google Scholar

Gan, G., Geng, G., Gao, B., Zhong, W., Jiang, Q., and Huang, D. (2020). Blocking Control of Power System Cascading Failures Considering Line Outages Probability. Power Syst. techn. 44 (1), 266–272. doi:10.13335/j.1000-3673.pst.2018.2244

CrossRef Full Text | Google Scholar

Hines, P., Apt, J., and Talukdar, S. (2009). Large Blackouts in North America: Historical Trends and Policy Implications. Energy Policy 37 (12), 5249–5259. doi:10.1016/j.enpol.2009.07.049

CrossRef Full Text | Google Scholar

Kornbluth, Y., Cwilich, G., Buldyrev, S., Soltan, S., and Zussman, G. (2021). Distribution of Blackouts in the Power Grid and the Motter and Lai Model. Phys. Rev. E. 103 (3), 032309. doi:10.1103/PhysRevE.103.032309

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., Li, J., and Wang, Y. (2022). Privacy-Preserving Spatiotemporal Scenario Generation of Renewable Energies: A Federated Deep Generative Learning Approach. IEEE Trans. Industrial Inf. 18 (4), 2310–2320. doi:10.1109/TII.2021.3098259

CrossRef Full Text | Google Scholar

Lin, Y., Burghardt, K., Rohden, M., Noel, P., and D'Souza, R. (2018). Self-Organization of Dragon King Failures. Phys. Rev. E. 98 (2), 022127. doi:10.1103/PhysRevE.98.022127

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, W., Lin, Z., Wen, F., Chung, C., Xue, Y., and Ledwich, G. (2015). Sectionalizing Strategies for Minimizing Outage Durations of Critical Loads in Parallel Power System Restoration with Bi-level Programming. Int. J. Electr. Power Energy Syst. 71, 327–334. doi:10.1016/j.ijepes.2015.03.004

CrossRef Full Text | Google Scholar

Liu, D., Tse, C., and Zhang, X. (2019). Robustness Assessment and Enhancement of Power Grids from a Complex Network’s Perspective Using Decision Trees. IEEE Trans. Circuits Syst. II Exp. Briefs. 66 (5), 833–837. doi:10.1109/TCSII.2019.2909523

CrossRef Full Text | Google Scholar

Nagpal, M., Martinich, T., Jiao, Z., Manuel, S., and Zhang, H. (2018). Lessons Learned from a Regional System Blackout and Restoration in BC Hydro. IEEE Trans. Power Deliv. 33 (4), 1954–1961. doi:10.1109/TPWRD.2017.2768046

CrossRef Full Text | Google Scholar

Shi, K., Liu, H., Wang, L., Bie, Y., and Yang, Y. (2021). Theoretical Design of a Multilayer Based Spectrally Selective Solar Absorber Applied under Ambient Conditions. Front. Energy Rescl. 9, 795261. doi:10.3389/fenrg.2021.795261

CrossRef Full Text | Google Scholar

Tu, J., Xin, H., Wang, Z., Gan, D., and Huang, Z. (2013). On Self-Organized Criticality of the East China AC-DC Power System-The Role of DC Transmission. IEEE Trans. Power Syst. 28 (3), 3204–3214. doi:10.1109/TPWRS.2013.2251913

CrossRef Full Text | Google Scholar

Wei, X., Zhao, J., Huang, T., and Bompard, E. (2018). A Novel Cascading Faults Graph Based Transmission Network Vulnerability Assessment Method. IEEE Trans. Power Syst. 33 (3), 2995–3000. doi:10.1109/TPWRS.2017.2759782

CrossRef Full Text | Google Scholar

Wong, J., Su, C., and Liu, C. (2007). Study on the 729 Blackout in the Taiwan Power System. Int. J. Electr. Power Energy Syst. 29 (8), 589–599. doi:10.1016/j.ijepes.2007.02.001

CrossRef Full Text | Google Scholar

Xue, Y., and Xiao, S. (2013). Generalized Congestion of Power Systems: Insights from the Massive Blackouts in India. J. Mod. Power Syst. Clean. Energy 1 (2), 91–100. doi:10.1007/s40565-013-0014-2

CrossRef Full Text | Google Scholar

Zeng, B., Ouyang, S., Zhang, J., Shi, H., Wu, G., and Zeng, M. (2015). An Analysis of Previous Blackouts in the World: Lessons for China׳ S Power Industry. Renew. Sustain. Energy Rev. 42, 1151–1163. doi:10.1016/j.rser.2014.10.069

CrossRef Full Text | Google Scholar

Zhai, C., Zhang, H., Xiao, G., and Pan, T. (2019). A Model Predictive Approach to Protect Power Systems against Cascading Blackouts. Int. J. Electr. Power Energy Syst. 113, 310–321. doi:10.1016/j.ijepes.2019.05.029

CrossRef Full Text | Google Scholar

Zima, M., and Andersson, G. (2005). “On Security Criteria in Power Systems Operation,” in Proceeding of IEEE Power Engineering Society General Meeting, San Francisco, USA, June, 2005, 3089–3093. doi:10.1109/PES.2005.1489533

CrossRef Full Text | Google Scholar