Inertia Optimization Control and Transient Stability Analysis of Wind Power Grid-Connected System

The virtual inertia control effectively makes up for the insufficient inertia caused by the high penetration wind power grid connection. However, it has an impact on the mechanical part of the wind turbine and greatly increases the difficulty of the dynamic stability analysis of the system, resulting in limited engineering practicability. Therefore, the state equation of the wind power grid-connected system is established in this paper, and the influence of virtual inertia control on wind turbine shafting oscillation is analyzed based on the small-signal theory. Secondly, the nonlinear extended disturbance observer is designed as the compensation signal of inertia control to improve its dynamic stability supportability. Based on the integral manifold method, the shafting model of the wind turbine is reduced, and the transient energy function of shafting is established, which provided the basis for the design of the shafting stability controller. Finally, a grid-connected wind power system with high permeability is installed, and the results demonstrate that under the proposed control strategy, the swing stability of power angle is significantly improved, and the wind turbine shafting oscillation is suppressed.

1 Introduction

The power support deficiency caused by the electrical decoupling of wind turbines and the system is effectively solved with the introduction of virtual inertia control (Wang et al., 2015; Xiong et al., 2019; Li et al., 2022a). However, access to a large number of controllable inertia changes the distribution of inertia of the original system and causes an interaction with the power angle and damping characteristics of the system, even resulting in pushing the shafting oscillation of the wind turbine (Li et al., 2017; Dinkelbach et al., 2021; Mehbodniya et al., 2022). Therefore, the stability characteristics of wind power grid-connected systems should be comprehensively analyzed to optimize the virtual inertia control effect.

Wind turbines usually operate under maximum power point tracking (MPPT) control and cannot respond to frequency changes. With the increase in grid penetration, the equivalent inertia of the system decreases, threatening the system’s stable operation (Ma et al., 2017; Zeng et al., 2019; Li et al., 2022b). After the virtual inertia control is applied, the rotor’s kinetic energy of the wind turbine is used to provide power support to the system, which effectively improves the frequency modulation characteristics of the system (Ghosh et al., 2016; Wilches-Bernal et al., 2016; Wang and Tomsovic, 2018; Wang et al., 2018). However, the rapid power response generated by the virtual inertia control changes the external characteristics of the wind turbine obviously, making the dynamic stability analysis of the grid-connected wind turbine system with virtual inertia more complicated (Luo et al., 2017; Nguyen et al., 2018; Sun et al., 2019; Li et al., 2022c).

At present, a proportional-derivative controller is added to the MPPT control of variable-speed wind turbines to simulate the inertial frequency response of synchronous generators by controlling the active commands (Duckwitz and Fischer, 2017; Hu et al., 2017; Sun et al., 2022). However, the reference (Han et al., 2019) based on the small-signal analysis of the grid-connected system pointed out that the excessive virtual inertia can reduce the damping ratio of the system, prolong the transient response time, and then lead to the deterioration of the transient stability. To optimize the virtual inertia control effect, researchers have carried out extensive research. In the reference (Lao et al., 2019), the overspeed control and inertia control are combined, and the inertia is adaptively adjusted by constructing the relationship between the frequency and the inertia, thereby the frequency robustness of the system is improved. The principle of the coordinated configuration of virtual inertia and damping coefficient is given in references (Du et al., 2019; Zhang et al., 2020), but the optimal response time and overshoot cannot be accurately obtained.

According to the extended state observer theory, the system state variables and disturbances are estimated without an accurate model of the system, thereby the weakening of the control effect caused by changing parameters and inaccurate models is reduced (Imad et al., 2017). Using it in the wind turbine control link can effectively improve its auto disturbance rejection characteristics and optimize the corresponding control effect (Penne et al., 2021). In addition, reference (Jia et al., 2020) demonstrates that the virtual inertia control has the risk of reducing the small-signal stability of the system. Under this control, with the system disturbed, the output power of the wind turbine varies widely, which has an impact on its flexible shaft and even causes speed oscillation instability. Reference (Nguyen et al., 2019; Liu et al., 2021) proved the impact of virtual inertia control on the mechanical transmission chain of the wind turbine, and the rotor speed feedforward compensation is added in MPPT control to suppress the shafting oscillates, but unreasonable control coefficient is negatively affecting the dynamic stability of the system. The virtual inertia control strategy still needs to be improved to ensure the safety of the flexible shaft of the wind turbine and improve the dynamic stability of the grid-connected system. The comprehensive evaluation of the stable operation ability of the grid-connected system is the key to improving the additional controller’s friendly grid-connected function.

In this paper, by establishing the small-signal model of the wind power grid-connected system, the influence of virtual inertia on the damping characteristics of the system is analyzed, and the influence of the inertia coefficient on the electromagnetic torque damping characteristics of the wind turbine is studied combined with the two-mass model of the wind turbine. To improve the active disturbance rejection characteristic of inertia control, a nonlinear extended state observer is introduced, and a parameter design scheme based on the critical stability of shaft vibration is proposed by establishing the transient energy function of the wind turbine shaft to improve the dynamic stability of the system. Thereby the safe operation capability of the wind power grid-connected system is comprehensively improved. In section 2, a small disturbance analysis of the wind turbine grid-connected system is conducted. In Section 3, an extended disturbance observer and inertia parameter configuration principles are designed. Experimental studies to demonstrate the effectiveness of the proposed control scheme based on a typical power system with high-penetration wind power are presented in Section 4. Conclusions are presented in Section 5.

2 Small Signal Analysis of Wind Turbine Grid-Connected System

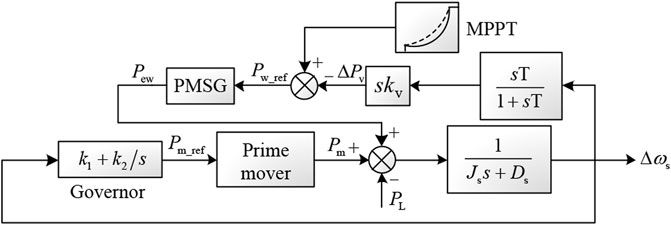
The variable speed wind turbine with virtual inertia control absorbs or releases the rotational kinetic energy by changing the wind turbine speed, adjusting the output power, and responding to the change of system frequency. Take a permanent magnet synchronous generator (PMSG) as an example. Figure 1 shows the active power control structure of the variable speed wind turbine, including MPPT control and virtual inertia controller module. Under the per-unit system, the active power control instruction of the wind turbine is the sum of the MPPT control reference instruction and the active power increment generated by the inertia controller, which can be expressed as (Wang et al., 2018)

$P_{\text{ew}}=k_{\mathrm{m}}{\omega }_{\text{w}}^2-k_{\mathrm{v}}p({\omega }_{\mathrm{s}}-{\omega }_{\text{n}})(1)$

where k_m is the MPPT coefficient of the wind turbine; k_v is the inertia control coefficient. ω_w is the angular velocity of the wind turbine; ω_s and ω_n are the angular velocity of the system synchronous generator and the rated angular velocity of the system, respectively. p is the differential operator.

FIGURE 1

FIGURE 1. Diagram of active power control of the system with virtual inertia.

The following two mass shafting models are established to analyze the dynamic stability of wind turbine shafting (Gaidi et al., 2017).

$\{\begin{array}{l}{\mathit{H}}_{\mathbf{r}}\mathit{p}{\mathit{\omega }}_{\mathrm{r}}={\mathit{P}}_{\mathbf{r}}/{\mathit{\omega }}_{\mathrm{r}}-{\mathit{K}}_{\mathrm{s}}\mathit{\theta }\\ {\mathit{H}}_{\mathbf{w}}\mathit{p}{\mathit{\omega }}_{\mathbf{w}}={\mathit{K}}_{\mathrm{s}}\mathit{\theta }-({\mathit{k}}_{\mathrm{m}}{\mathit{\omega }}_{\mathbf{w}}^{\mathbf{2}}-{\mathit{k}}_{\mathbf{v}}\mathit{p}{\mathit{\omega }}_{\mathrm{s}})\\ \mathit{p\theta }={\mathit{\omega }}_{\mathrm{r}}-{\mathit{\omega }}_{\mathbf{w}}\end{array}(2)$

where ω_r is the angular velocity of the wind turbine; θ is the torque angle of shafting; H_r and H_w are the inertia of the wind turbine and generator, respectively; K_s is the stiffness coefficient shafting; P_r is the mechanical power captured by the wind turbine.

Ignoring the damping coefficient D_s of synchronous generator, the equivalent second-order rotor motion equation of generator can be expressed as

${\mathit{H}}_{\mathbf{s}}\mathit{p}{\mathit{\omega }}_{\mathrm{s}}={\mathit{k}}_{\mathrm{1}}({\mathit{\omega }}_{\mathbf{n}}-{\mathit{\omega }}_{\mathrm{s}})+{\mathit{k}}_{\mathrm{2}}\mathit{x}-{\mathit{P}}_{\mathrm{e}}(3)$

where H_s is the equivalent inertial time constant of the system; P_e is the electromagnetic power output by the synchronous generator; x represents the output state variable of the governor, dx/dt = ω_n−ω_s; k₁ is the proportional coefficient; k₂ is the integral coefficient of the governor.

Considering the system power balance, substituting Eq. 1 into Eq. 3, the equation can be expressed as follows

$({\mathit{H}}_{\mathbf{s}}+\frac{{\mathit{k}}_{\mathrm{v}}}{{\mathit{S}}_{\mathrm{B}}})\mathit{p}{\mathit{\omega }}_{\mathrm{s}}={\mathit{k}}_{\mathrm{1}}({\mathit{\omega }}_{\mathbf{n}}-{\mathit{\omega }}_{\mathrm{s}})+{\mathit{k}}_{\mathrm{2}}\mathit{x}-\frac{{\mathit{U}}_{\mathrm{n}}^{\mathrm{2}}}{\mathit{r}{\mathit{S}}_{\mathrm{B}}}+\frac{{\mathit{k}}_{\mathrm{m}}{\mathit{\omega }}_{\mathrm{g}}^2}{{\mathit{S}}_{\mathrm{B}}}(4)$

where U_n represents the terminal voltage of the load connection point; r is the load equivalent resistance; S_B is the system capacity reference value.

Combining Eq. 2 and Eq. 4, the small-signal equation of the wind turbine grid-connected system with virtual inertia control can be expressed as

$\left[\begin{array}{l}p\mathrm{\Delta }{\omega }_s\\ p\mathrm{\Delta }x\\ p\mathrm{\Delta }{\omega }_r\\ p\mathrm{\Delta }{\omega }_w\\ p\mathrm{\Delta }\theta \end{array}\right]=\left[\begin{array}{ccccc}{a}_{11}& a_{12}& 0& a_{14}& 0\\ -1& 0& 0& 0& 0\\ 0& 0& a_{33}& 0& a_{35}\\ a_{41}& a_{42}& 0& a_{44}& a_{45}\\ 0& 0& 1& -1& 0\end{array}\right]\left[\begin{array}{l}\mathrm{\Delta }{\omega }_s\\ \mathrm{\Delta }x\\ \mathrm{\Delta }{\omega }_r\\ \mathrm{\Delta }{\omega }_w\\ \mathrm{\Delta }\theta \end{array}\right](5)$

where H_G = H_S + k_vS_B; a₁₁ = −k₁S_B/(H_GS_B); a₁₂ = −k₂/(H_GS_B); a₁₄ = 2k_mω_w0/(H_GS_B); a₃₃ = −P_r0/(H_rω²_w0); a₃₅ = −K_s/H_r; a₄₁ = −k₁k_vS_B/(H_wH_G); a₄₂ = −k₂k_v/(H_wH_G); a₄₄ = 2k_mω_w0k/H_w; k = k_v/(H_GS_B)−1; a₄₅ = K_s/H_w.

As the virtual inertia is introduced into the power system, the variable inertia distribution significantly affects system damping. Assuming the constant wind speed, the motion equation of the synchronous generator should be expressed as

$H_G{p}^2\mathrm{\Delta }{\delta }_s+k_{1}p\mathrm{\Delta }{\delta }_s-k_2\mathrm{\Delta }{\delta }_s=0(6)$

By solving the differential equation shown in Eq. 6, the real part expression of the characteristic root of the system is obtained as:

${\sigma }_{\mathrm{1,2}}=-\frac{k_1}{2H_{\text{G}}}=-\frac{k_1}{2\left(H_{\text{S}}+k_{\text{v}}{S}_{\text{B}}\right)}(7)$

According to Eq. 7, the introduction of k_v makes the equivalent inertial time constant of the system H_G increase, but the damping ratio of the synchronous generator is reduced and the characteristic roots gradually move towards the imaginary axis. Therefore, an unreasonable inertia control coefficient can even have a negative damping effect on the power angle oscillation of the synchronous generator. In addition, the virtual inertia control of the wind turbine affects the system’s dynamic characteristics and causes the stability of wind turbine shafting. Therefore, the analysis of the influence of the inertia response power of the wind turbine on shafting torsional vibration is extremely important for the safe popularization of control technology.

After the Laplace transformation of Eq. 5, ω_w can be expressed as follows

$s\mathrm{\Delta }{\omega }_{\text{w}}=[\frac{a_{14}(a_{41}-a_{42}/s)}{s-a_{11}+a_{12}/s}+a_{44}]\mathrm{\Delta }{\omega }_{\text{w}}+a_{45}\mathrm{\Delta }\theta (8)$

The coefficient of Δω_w in Eq. 8 is defined as a'₄₄, and the shafting state equation of the wind turbine with inertial control can be sorted out as

$\left[\begin{array}{l}s\mathrm{\Delta }{\omega }_{\mathrm{r}}\\ s\mathrm{\Delta }{\omega }_{\text{w}}\\ s\mathrm{\Delta }\theta \end{array}\right]=\left[\begin{array}{ccc}{a}_{33}& 0& a_{35}\\ 0& {a^{\prime }}_{44}& a_{45}\\ 1& -1& 0\end{array}\right]\left[\begin{array}{l}\mathrm{\Delta }{\omega }_{\mathrm{r}}\\ \mathrm{\Delta }{\omega }_{\text{w}}\\ \mathrm{\Delta }\theta \end{array}\right](9)$

The natural oscillation frequency of wind turbine shafting is about 1–2 Hz; therefore, the equation a'₄₄≈a₄₄ is valid. Since the inertia of the wind turbine is much greater than the inertia of the generator, i.e., H_w << H_r, as a state variable with the characteristics of rapid change, ω_w can be approximated by an integral manifold to replace, thus reducing the order of Eq. 9, to obtain the approximate expression of the analytical solution of the shafting state equation. Assume that the integral manifold of the state variable ω_w is given by

$\mathrm{\Delta }{\omega }_{\text{w}}=h(\mathrm{\Delta }{\omega }_{\mathrm{r}},\mathrm{\Delta }\theta ,\epsilon )(10)$

where ε is an infinitesimal quantity.

Let ε = H_w/(mH_r), where m>>2, and the power series expansion of Eq. 10 is given by

$\mathrm{\Delta }{\omega }_{\text{w}}=h=h_0+\epsilon h_1+{\epsilon }^2{h}_2+\cdots o\left({\epsilon }^n\right)(11)$

Substituting Eq. 11 into Eq. 9 and the expression is obtained as

$\epsilon \frac{\partial h}{\partial \mathrm{\Delta }{\omega }_{\text{w}}}p\mathrm{\Delta }{\omega }_{\text{w}}+\epsilon \frac{\partial h}{\partial \mathrm{\Delta }\theta }p\mathrm{\Delta }\theta =\frac{1}{m{H}_{\mathrm{r}}}(S_{\mathrm{1}}h+S_2\mathrm{\Delta }\theta )(12)$

where,

$\{\begin{array}{l}\frac{\mathrm{d}\mathrm{\Delta }\theta }{\mathrm{d}t}=\mathrm{\Delta }{\omega }_{\mathrm{r}}-h_0-\epsilon h_1-{\epsilon }^2{h}_2\begin{array}{c}\cdots \end{array}\\ \frac{\partial h}{\partial \mathrm{\Delta }{\omega }_{\text{w}}}=\frac{\partial h_0}{\partial \mathrm{\Delta }{\omega }_{\text{w}}}+\epsilon \frac{\partial h_1}{\partial \mathrm{\Delta }{\omega }_{\text{w}}}+{\epsilon }^2\frac{\partial h_2}{\partial \mathrm{\Delta }{\omega }_{\text{w}}}+\begin{array}{c}\cdots \end{array}\\ \frac{\partial h}{\partial \mathrm{\Delta }\theta }=\frac{\partial h_0}{\partial \mathrm{\Delta }\theta }+\epsilon \frac{\partial h_1}{\partial \mathrm{\Delta }\theta }+{\epsilon }^2\frac{\partial h_2}{\partial \mathrm{\Delta }\theta }+\begin{array}{c}\cdots \end{array}\end{array}$

The coefficients of ε⁰, ε¹, and ε² on both sides of Eq. 12 should be equal, and then the function h can be obtained as

$\{\begin{array}{l}{h}_0=-\frac{S_2}{S_{\mathrm{1}}}\mathrm{\Delta }\theta =\frac{K_{\mathrm{s}}}{2k_{\mathrm{m}}{\omega }_{\mathrm{w0}}k}\mathrm{\Delta }\theta \\ h_1=-\frac{m{H}_{\mathrm{r}}{K}_{\mathrm{s}}}{2k_{\mathrm{m}}^2{\omega }_{\mathrm{w0}}^2{k}^2}\mathrm{\Delta }{\omega }_{\mathrm{r}}+\frac{m{H}_{\mathrm{r}}{K}_{\mathrm{s}}^2}{4k_{\mathrm{m}}^3{\omega }_{\mathrm{w0}}^3{k}^3}\mathrm{\Delta }\theta \end{array}(13)$

Substituting Eq. 13 into Eq. 11, the state variable Δω_w can be approximated as

$\mathrm{\Delta }{\omega }_{\text{w}}\approx K_{\mathrm{A}}\mathrm{\Delta }\theta +K_{\mathrm{B}}\mathrm{\Delta }{\omega }_{\mathrm{r}}(14)$

where $K_{\mathrm{A}}=\frac{K_{\mathrm{s}}}{2k_{\mathrm{m}}{\omega }_{\mathrm{w0}}}+\frac{H_{\text{w}}{K}_{\mathrm{s}}^2}{4k_{\mathrm{m}}^3{\omega }_{\mathrm{w0}}^3{k}^3}$; $K_{\mathrm{B}}=-\frac{H_{\text{w}}{K}_{\mathrm{s}}}{2k_{\mathrm{m}}^2{\omega }_{\mathrm{w0}}^2{k}^2}$.

After reducing the order of the system’s state equation combined with Eq. 14, the characteristic equation can be expressed as

${\lambda }^2+(K_{\mathrm{A}}-a_{33})\lambda -K_{\mathrm{A}}{a}_{33}-(1-K_{\mathrm{B}})a_{35}=0(15)$

Therefore, the real part of the characteristic root corresponding to the shafting oscillation mode is given by

${\sigma }_{\mathrm{1,2}}=-\frac{1}{4}(\frac{K_{\mathrm{s}}}{k_{\mathrm{m}}{\omega }_{\mathrm{w0}}}+\frac{H_{\text{w}}{K}_{\mathrm{s}}^2}{2k_{\mathrm{m}}^3{\omega }_{\mathrm{w0}}^3{k}^3})-\frac{P_{\mathrm{0}}}{4H_{\mathrm{r}}{\omega }_{\mathrm{r0}}^2}(16)$

According to Eq. 16, the inertia control coefficient k_v affects the shafting oscillation mode of the wind turbine. As the control coefficient k_v increases, k also increases, σ_1,2 approaches the virtual axis of the state plane, and the dynamic stability of wind turbine shafting decreases. Therefore, a new virtual inertia control method is needed to increase the equivalent inertia of the system without causing the shaft oscillation instability of the wind turbine.

3 Virtual Inertia Optimization Based on Extended Observer

Considering the slowly changing characteristics of wind speed, the complexity of inertia control parameters is mainly affected by the penetration rate of wind power in the system. If the estimated inertia is set to H_s0, the first equation in Eq. 8 is given by

$p\mathrm{\Delta }{\omega }_{\mathrm{s}}=\frac{1}{H_{\mathrm{s}}}\mathrm{\Delta }{P}_{\mathrm{e}}+(\frac{1}{H_{\mathrm{s}}}-\frac{1}{H_{\mathrm{s}0}})\mathrm{\Delta }{P}_{\mathrm{v}}+\frac{1}{H_{\mathrm{s}0}}\mathrm{\Delta }{P}_{\mathrm{v}}(17)$

where,

$\mathrm{\Delta }{P}_{\mathrm{e}}=k_2\mathrm{\Delta }{\delta }_{\mathrm{s}}-k_1\mathrm{\Delta }{\omega }_{\mathrm{s}}+\frac{2k_{\mathrm{m}}{\omega }_{\mathrm{w}0}}{S_{\mathrm{B}}}\mathrm{\Delta }{\mathrm{\omega }}_{\mathrm{w}}$

The frequency variation is significantly affected by the system disturbance power and the controller inertia response. The expanded disturbance observer can expand the unknown disturbance affecting the controlled output of the system into new state variables. By adjusting the control coefficient, the output observation signal is gradually close to the original system state variables to realize the observation of system state variables and unknown disturbances.

For the first-order nonlinear uncertain system shown in the above equation, the expansion state variable is constructed as

$a\left(t\right)=\frac{1}{H_{\mathrm{s}}}\mathrm{\Delta }{P}_{\mathrm{e}}+(\frac{1}{H_{\text{s}}}-\frac{1}{H_{\mathrm{s0}}})\mathrm{\Delta }{P}_{\mathrm{v}}(18)$

Let the control input u = ΔP_v and the input coefficient b = 1/H_s0, the extended disturbance observer can be constructed as follows

$\{\begin{array}{l}{e}_{\omega }=\mathrm{\Delta }{\widehat{\mathrm{\omega }}}_{\mathrm{s}}-\mathrm{\Delta }{\omega }_{\mathrm{s}}\\ p\mathrm{\Delta }{\widehat{\omega }}_{\mathrm{s}}=\widehat{a}\left(t\right)+bu-{\beta }_1{e}_{\omega }\\ p\widehat{a}\left(t\right)=-{\beta }_{2}fal(e_{\omega },\alpha ,\gamma )\end{array}(19)$

where β₁ and β₂ are the adjusting gains of the nonlinear disturbance observer; α is a nonlinear factor, which generally is 0.5. γ is the filter factor related to the sampling step size of the system. fal(e_ω,α,γ) is a nonlinear function, which is expressed as

$fal(e_{\omega },\alpha ,\gamma )=\{\begin{array}{l}{\left|e_{\omega }\right|}^{\alpha }\mathrm{sign}\left(e_{\omega }\right),\left|e_{\omega }\right|>\gamma \\ \frac{e_{\omega }}{{\gamma }^{1-\alpha }},\left|e_{\omega }\right|\le \gamma \end{array}(20)$

By adjusting the parameters of the expanded disturbance observer, β₁, β₂, α, γ reasonably, the observed value can approach the actual value quickly and ensure the observation precision of the observer. According to Eq. 17 and Eq. 18, with the disturbance observer, the unbalanced power of the system caused by virtual inertia control can be expressed as

$\mathrm{\Delta }{\mathit{P}}_{\mathrm{eso}}=-{\mathit{H}}_{\mathrm{s0}}\mathit{a}\left(\mathit{t}\right)\approx -{\mathit{H}}_{\mathrm{s0}}\widehat{\mathit{a}}\left(\mathit{t}\right)(21)$

In the process of dynamic regulation, it is necessary to set the control parameters of the shafting stabilizer to avoid the threat of shafting torsional vibration caused by additional power control of the wind turbine. Let ω_θ = ω_r-ω_w, simplify Eq. 2, then the equivalent two-mass block shafting model of the wind turbine can be expressed as

$p{\omega }_{\theta }+\frac{K_{\mathrm{s}}}{H_{\text{t}}}\theta =\frac{P_{\mathrm{r0}}}{{\omega }_{\mathrm{r}}{H}_{\mathrm{r}}}+\frac{k_{\mathrm{m}}{\omega }_{\text{w}}^2}{H_{\text{w}}}-\frac{k_{\text{v}}}{H_{\text{w}}}p{\omega }_{\mathrm{s}}(22)$

where H_t = H_r×H_w/(H_r + H_w).

Taking the virtual inertia control into account, the power balance equation of the single infinite power grid can be expressed as follows

$p{\omega }_{\mathrm{s}}=\frac{S_{\mathrm{B}}}{H_{\mathrm{s}}{S}_{\mathrm{B}}+k_{\mathrm{v}}}(k_{\mathrm{m}}{\omega }_{\mathrm{w}}^2-\frac{U_{\mathrm{n}}^2}{r})(23)$

The wind turbine is controlled by an additional shafting stabilizer, and substituting the above equation is into Eq. 22, after linearization, the expression is given by

$p\mathrm{\Delta }{\omega }_{\theta }+(c_1+k_{\mathrm{s}\mathrm{s}})\mathrm{\Delta }{\omega }_{\mathrm{g}}+c_2\mathrm{\Delta }{\omega }_{\mathrm{r}}+c_3\mathrm{\Delta }\theta =0(24)$

where, c₁ = 2k_mω_w0[(k_v/(H_s + k_v/S_B)−1]/H_w; c₂ = P₀/(H_rω_w0²); c₃ = K_s/H_t; k_ss is the control coefficient of shafting stabilizer.

Since Δω_r is in the opposite phase to Δω_w, and Δω_w = nΔω_r, the expression of Δω_θ can be expressed as

$\mathrm{\Delta }{\omega }_{\theta }=\{\begin{array}{l}-(n+1)\mathrm{\Delta }{\omega }_{\text{w}}/n\\ (n+1)\mathrm{\Delta }{\omega }_{\mathrm{r}}\end{array}(25)$

where n is defined as the speed ratio between a low-speed and a high-speed shaft.

Substituting Eq. 25 into Eq. 24, the small-signal equation of state about θ is given by

${\mathit{p}}^2-\left[\frac{{\mathit{c}}_2}{1+\mathit{n}}\frac{\mathit{n}({\mathit{c}}_1-{\mathit{k}}_{\mathrm{s}})}{1+\mathit{n}}\right]\mathit{p}+{\mathit{c}}_{\mathrm{3}}\mathrm{\Delta }\mathit{\theta }=\mathrm{0}(26)$

The Lyapunov energy function of the wind turbine shafting system is constructed as

$V\left(\mathrm{\Delta }{\omega }_{\theta }\right)=\frac{1}{2}\times {\left(\mathrm{\Delta }{\omega }_{\theta }\right)}^2\ge 0(27)$

The shaft stiffness of the vital connecting parts inside the wind turbine is limited. Considering the most conservative case, when the shaft system stiffness is close to 0, and the nonlinear system is stable in the dynamic process, the first derivative of V(Δω_θ) satisfies the Eq. 28 according to the Lyapunov stability criterion. Therefore, the control coefficient configuration criterion of the stabilizer is shown in Eq. 29

$\frac{\mathrm{d}V\left(\mathrm{\Delta }{\omega }_{\theta }\right)}{\mathrm{d}t}=[\frac{n(c_1-k_{\mathrm{s}\mathrm{s}})}{1+n}-\frac{c_2}{1+n}]\mathrm{\Delta }{\omega }_{\theta }^2\le 0(28)$

$k_{\mathrm{s}\mathrm{s}}\ge 2k_{\mathrm{m}}{\omega }_{\mathrm{w}0}(\frac{k_{\mathrm{v}}}{H_{\mathrm{G}}{S}_{\mathrm{B}}}-1)-\frac{P_{\mathrm{r}0}}{n{H}_{\mathrm{r}}{\omega }_{\mathrm{r}0}^2}(29)$

According to Eq. 29, the control coefficient k_ss is set corresponding to the critical stability of the torsional vibration mode of wind turbine shafting to limit the adverse effects brought by inertia adjustment power and ensure reliable damping of shafting oscillation of wind turbine.

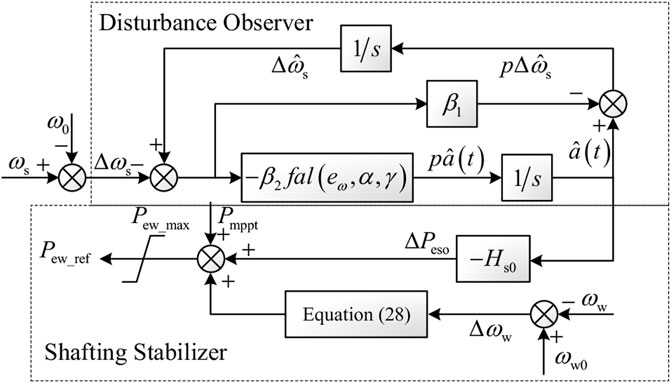
By analyzing the influence of virtual inertia on system shafting stability, a virtual inertia compensation control strategy based on an extended disturbance observer is proposed, as shown in Figure 2. As the system is disturbed and the frequency fluctuates, the angular velocity ω_s and the expansion variable a(t) are collected and input to the expanded disturbance observer. By setting its adjusting parameters k_ss reasonably, the estimated value of the system frequency and unbalanced power is rapidly approaching the actual value, and the compensation value of the output power of the inertia controller is calculated. Through Eq. 29, the control parameters of the shafting stabilization stabilizer are set, which are added with the power instruction of MPPT control and sent to the wind turbine to dynamically adjust the active power output of the wind turbine, change the power distribution of the system, and improve the system frequency supportability and shafting stability.

FIGURE 2

FIGURE 2. Diagram of virtual inertia control based on extended disturbance observer.

4 Verification and Analysis

4.1 System Structure

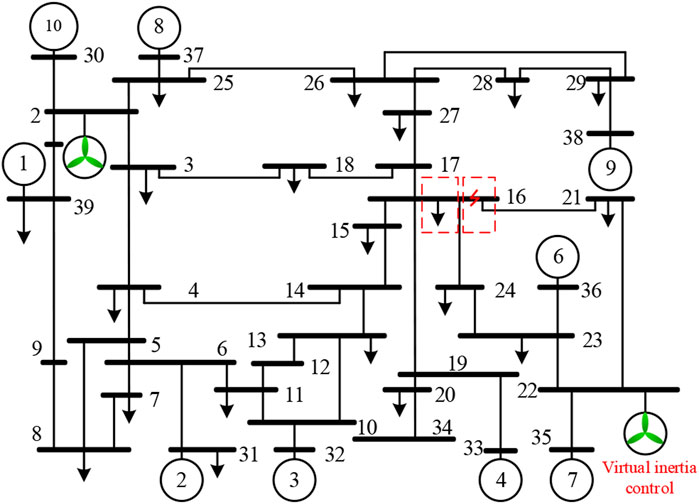
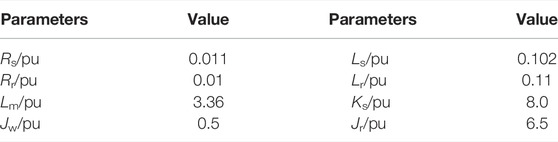
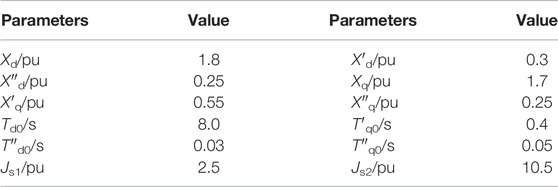
As shown in Figure 3, a 39-node New England system with the wind turbine interconnected system is established to validate the effectiveness of the proposed control strategy. The test system contains ten synchronous generators with a rated capacity of 200 MW, and two PMSG-based wind farms with 400 turbines with a rated capacity of 2MW, which are connected to the system through the bus B₃ and B₂₂, respectively. Specific simulation parameters are shown in Tables 1, 2.

FIGURE 3

FIGURE 3. Diagram of the simulation system with the wind turbine.

TABLE 1

TABLE 1. The parameters of the 2 MW PMSG.

TABLE 2

TABLE 2. The parameters of synchronous generators.

The nonlinear factor α is set as 0.5, and the filtering factor γ = 1000 h. Since the convergence effect of the expanded observer is affected by the gain coefficients β₁ and β₂, online debugging is carried out according to the estimation accuracy requirements of the observer, so that the estimated value of the output of the observer can approach the actual value at a faster speed. As β₁ = 30 and β₂ = 120, the observer can get a better convergence effect without causing a high-frequency flutter phenomenon.

4.2 The Modal Analysis

The simulation model of the system shown in Figure 3 is built in the DIgSILENT/PowerFactory, and the modal analysis of the system is conducted under the initial steady-state conditions of the system. Without virtual inertia control, the characteristic roots of the shafting oscillation mode of DFIG and the low-frequency oscillation mode of the synchronous generator in the region are −0.691 + j13.680 and −0.313 + j5.881, respectively. The corresponding phasor diagram and bar diagram of the participating factors is shown in Figure 4, respectively.

FIGURE 4

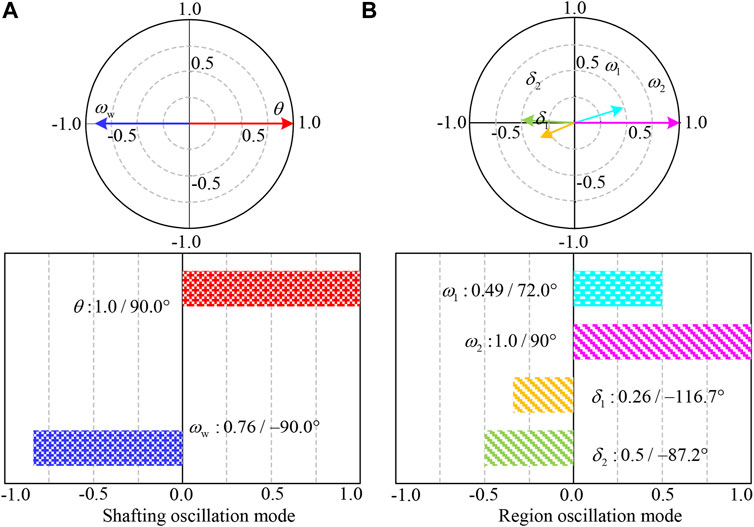
FIGURE 4. Figure shows the oscillation mode diagram of the wind turbine under the control of constant inertia, in which the (A) is the shafting oscillation mode of the wind turbine, and the (B) is the oscillation mode between the internal regions of the system.

According to the oscillation mode diagram, the shafting oscillation of the wind turbine is mainly affected by the torque angle of shafting and the angular velocity of the generator. The participation factors of the internal oscillation modes in the grid-connected system are rotor angles and angular velocities of the two synchronizers, which are consistent with the theoretical analysis results.

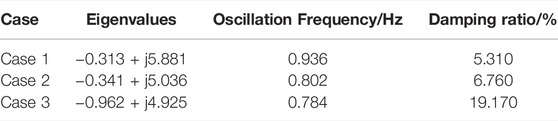
To verify the effect of the optimized inertia control scheme designed in this paper, the control coefficient k_v of constant virtual inertia is set to 30, and the shafting oscillation information of wind turbines and the information on the system static stability are calculated. As shown in Table 3, under constant inertia control, the oscillation frequency of wind turbine shafting increases greatly, which threatens the safe operation of the vital connecting parts. Compared with it, the optimized inertia control scheme designed in this paper can improve the damping ratio of the shafting oscillation mode of the wind turbine and the low-frequency oscillation mode of the system, and the oscillation frequency is also reduced Table 4. Therefore, the optimized inertia control can effectively improve the static stability of the grid-connected system based on ensuring the operating life of the wind turbine.

TABLE 3

TABLE 3. Variations of the shafting oscillation mode.

TABLE 4

TABLE 4. Variations of the region oscillation mode.

Regulating the control coefficient of inertia k_v increases from 0 to 30, the characteristic root track corresponding to each oscillation mode of the system is shown in Figure 5. Where λ₁ represents the region low-frequency oscillation mode, λ₂ represents the local low-frequency oscillation mode, and λ₃ represents the shafting oscillation mode of the wind turbine. As k_v increases from 0 to 15, λ₁ and λ₂ move away from the imaginary axis. If k_v continues to increase, the low-frequency oscillation in the region of the grid-connected system intensifies, and the overall stability decreases. The larger k_v is, the greater the active power output fluctuation of the wind turbine is, and the lower the oscillation stability of its shafting is, which is consistent with the theoretical analysis in Section 2.

FIGURE 5

FIGURE 5. Root locus of oscillation mode with k_v changing.

4.3 Dynamic Response Under Short Circuit Fault

In the following experimental tests, three control schemes are compared to verify the influence of virtual inertia control on the dynamic stability of the system. A three-phase short-circuit fault lasting 0.1 s is set at bus B₁₆, and the wind speed is kept constant at 9 m/s during the fault process.

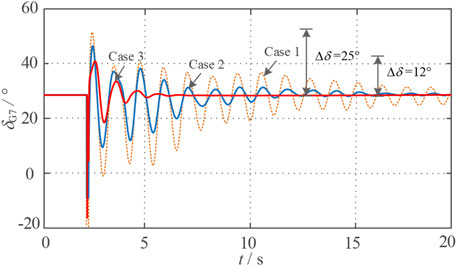
The dynamic response comparison curve of system power angle δ_G4, frequency f, and active power output of synchronous generator P_G4 are shown in Figure 6. It can be seen from Figure 6A that the traditional constant inertia control effectively increases the inertial time constant of the system, so the amplitude of the first swing of the power angle decreases after the fault. Although the fluctuation amplitude of the system frequency and power has decreased, the lower damping ratio makes the oscillation time longer, and the transient stability of the system still has a large room for improvement.

FIGURE 6

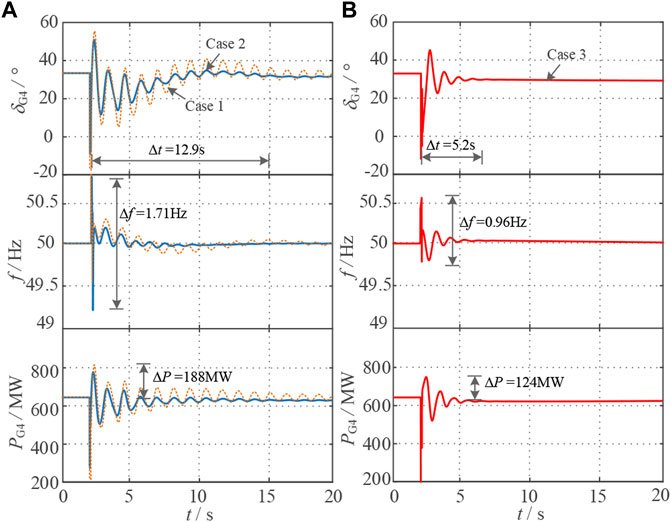
FIGURE 6. Figure shows the dynamic response curve of the system under short-circuit fault, in which no control is applied to the wind turbine in case 1, the traditional constant inertia control is applied to the wind turbine in case 2, and the optimal control proposed in this paper is applied to the wind turbine in case 3. In order to highlight the contrast effect, the response curves under case 1 and 2 are drawn as (A), and the response curves under case 3 are drawn as (B).

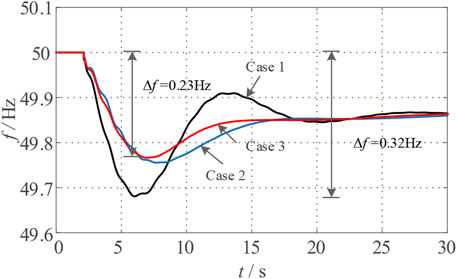
As can be seen from Figure 6B, after the optimized control strategy designed in this paper, is adopted, the time of the first pendulum oscillation of the system power angle is reduced by 59%, the maximum peak-to-peak value of the frequency fluctuation is reduced by 0.75 Hz, and the active power output of the synchronous generator G₄ is reduced by 64 MW. It can be seen from Figure 7 that the amplitude of the first swing of the power angle is decreased by 52%, and the recovery time is shortened with the damping characteristics significantly improved.

FIGURE 7

FIGURE 7. Dynamic responses of G₇ after short circuit fault.

Under the short-circuit fault, the response curves of the electromagnetic power of PMSG P_w and generator rotor speed ω_w are shown in Figure 8. The active power of the wind turbine is significantly adjusted by the constant inertia control during the system short-circuit fault, so the electromagnetic power and speed of the wind turbine fluctuate greatly, which is not conducive to the dynamic stability of the wind turbine shafting. Under the optimized inertia control strategy, the wind turbines optimize the active output and dynamic compensation system of the power deficiency by estimating system unbalanced power. Therefore, the recovery time of the wind turbine speed is shortened by 3.5 s, and the fluctuation amplitude of the speed is reduced by 6%. Meanwhile, the system dynamic stability is improved, and the shaft stability of wind turbines is assured.

FIGURE 8

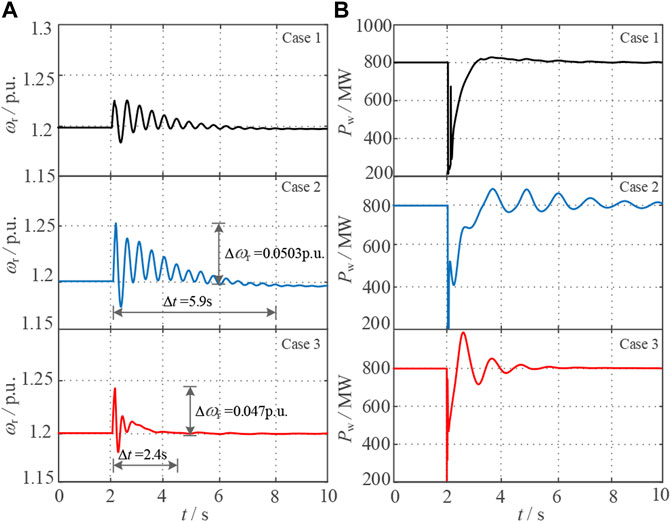
FIGURE 8. Figure shows the transient response curve of the wind turbine, in which (A) is the rotational speed curve of the wind turbine under the three simulation test cases, and (B) is the output power curve of the wind turbine.

4.4 Dynamic Response After the Load Event

To verify the frequency regulation performance of the designed inertia optimization control strategy, the initial conditions of the simulation system are changed, the load at B16 is set to suddenly increase by 1200 MW at 2 s, and the dynamic response of the system is obtained as shown in Figures 9–11.

FIGURE 9

FIGURE 9. Frequency responses of the system after the load increase.

FIGURE 10

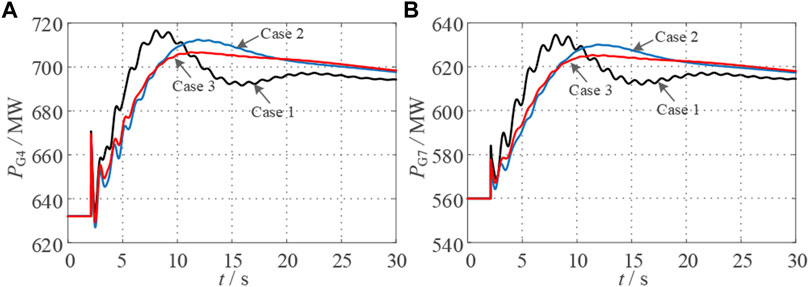
FIGURE 10. (A) shows the output power curve of the synchronous machine G₄ after a sudden load increase, and (B) shows the output power curve of the synchronous machine G₇.

FIGURE 11

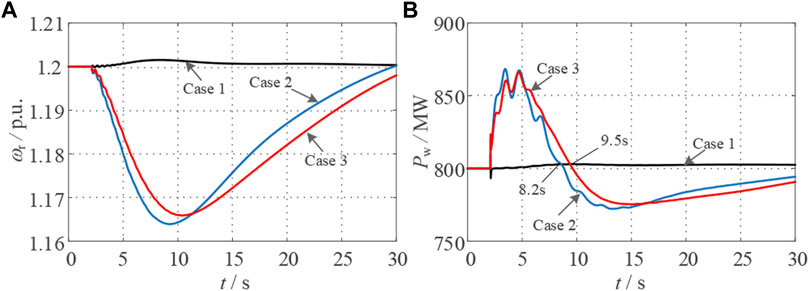
FIGURE 11. (A) shows the change curve of the rotational speed of the wind turbine after a sudden load increase, and (B) shows the output power curve of the wind turbine.

It can be seen from Figure 9 that, compared with no additional control, the frequency drop amplitude under constant inertia control is reduced by 28%, but the frequency recovery time is longer. The optimized inertia control can speed up the transient process of the system and improve the dynamic stability of the system while assisting the frequency adjustment of the system. As shown in Figures 10, 11, after the optimized inertia control proposed in this paper is applied, the rotor speed fluctuation amplitude of the wind turbine is reduced by 4%, and its output power changes more smoothly, which significantly improves the stability of the wind turbine and effectively shares the frequency modulation of the synchronous generator pressure.

5 Conclusion

In this paper, the influence of inertia control on the system and wind turbine shafting dynamic stability is analyzed by establishing the state equation of the grid-connected system of the wind turbine, and the optimal control strategy of inertia is designed. The conclusions are as follows:

1) The virtual inertia control of variable-speed wind turbines can effectively improve the system inertia weakening caused by wind turbine grid connection, but the increase of the system equivalent inertia time constant will lead to a decrease in the system damping ratio and slow power oscillation attenuation. The integral manifold method is used to reduce the order of the small-signal model of the wind turbine shafting. With the increase of the differential control coefficient k_v, the vibration modal characteristic root of the wind turbine shafting is close to the imaginary axis. Under virtual inertia control, wind turbines have an extensive range of power regulations and frequent rotational speed changes impact the mechanical life of wind turbine shafting.

2) Virtual inertial control based on a nonlinear disturbance observer is designed to optimize the virtual inertia control strategy, compensate for the support power output by the wind turbine, and reduce the virtual inertia based on ensuring the frequency modulation effect by estimating the unbalanced power generated by the system in the disturbance process. Thereby the system damping characteristics are improved, and the grid-friendly function of additional inertia control is improved. By establishing the critical stability transient energy function of the wind turbine shafting, the setting range of the k_ss control coefficient of the shafting stabilizer is given, to ensure the stability of the wind turbine oscillation.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

XZ provides the original idea; Partial theoretical analysis is implemented by WZ and LW; Simulation is realized by WS, ZW wrote the paper and proofread it. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported by the Science and technology project of State Grid Hebei Electric Power Co. Ltd. No. kj 2021-045.

Conflict of Interest

Authors WS, LW, and WZ were employed by the company State Grid Cangzhou Power Supply Company State Grid Hebei Electric Power Supply Co Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Dinkelbach, J., Nakti, G., Mirz, M., and Monti, A. (2021). Simulation of Low Inertia Power Systems Based on Shifted Frequency Analysis. Energies 14, 1860. doi:10.3390/en14071860

CrossRef Full Text | Google Scholar

Du, W., Dong, W., Wang, H., and Cao, J. (2019). Dynamic Aggregation of Same Wind Turbine Generators in Parallel Connection for Studying Oscillation Stability of a Wind Farm. IEEE Trans. Power Syst. 34 (6), 4694–4705. doi:10.1109/tpwrs.2019.2920413

CrossRef Full Text | Google Scholar

Duckwitz, D., and Fischer, B. (2017). Modeling and Design of $df/dt$ -Based Inertia Control for Power Converters. IEEE J. Emerg. Sel. Top. Power Electron. 5 (4), 1553–1564. doi:10.1109/jestpe.2017.2703814

CrossRef Full Text | Google Scholar

Gaidi, A., Lehouche, H., Belkacemi, S., Tahraoui, S., Loucif, M., and Guenounou, O. (2017). “Adaptive Backstepping Control of Wind Turbine Two Mass Model,” in 2017 6th International Conference on Systems and Control (ICSC), 168–172.

CrossRef Full Text | Google Scholar

Ghosh, S., Kamalasadan, S., Senroy, N., and Enslin, J. (2016). Doubly Fed Induction Generator (DFIG)-Based Wind Farm Control Framework for Primary Frequency and Inertial Response Application. IEEE Trans. Power Syst. 31 (3), 1861–1871. doi:10.1109/tpwrs.2015.2438861

CrossRef Full Text | Google Scholar

Han, D., Fang, J., Yu, J., Tang, Y., and Debusschere, V. (2019). “Small-Signal Modeling, Stability Analysis, and Controller Design of Grid-Friendly Power Converters with Virtual Inertia and Grid-Forming Capability,” in 2019 IEEE Energy Conversion Congress and Exposition (ECCE), 27–33.

CrossRef Full Text | Google Scholar

Hu, J., Sun, L., Yuan, X., Wang, S., and Chi, Y. (2017). Modeling of Type 3 Wind Turbines with Df/dt Inertia Control for System Frequency Response Study. IEEE Trans. Power Syst. 32 (4), 2799–2809. doi:10.1109/tpwrs.2016.2615631

CrossRef Full Text | Google Scholar

Imad, A., El Hani, S., and Echchaachouai, A. (2017). “Robust Active Disturbance Rejection Control of a Direct Driven PMSG Wind Turbine,” in 2017 International Renewable and Sustainable Energy Conference (IRSEC), 1–6.

CrossRef Full Text | Google Scholar

Jia, Y., Huang, T., Li, Y., and Ma, R. (2020). Parameter Setting Strategy for the Controller of the DFIG Wind Turbine Considering the Small-Signal Stability of Power Grids. IEEE Access 8, 31287–31294. doi:10.1109/access.2020.2973281

CrossRef Full Text | Google Scholar

Lao, H., Zhang, L., Zhao, T., and Zou, L. (2019). “Frequency Regulation Strategy for DFIG Combining Over-speed Control and Adaptive Virtual Inertia,” in 2019 IEEE Innovative Smart Grid Technologies - Asia (ISGT Asia), 1663–1666.

CrossRef Full Text | Google Scholar

Li, D., Zhu, Q., Lin, S., and Bian, X. Y. (2017). A Self-Adaptive Inertia and Damping Combination Control of VSG to Support Frequency Stability. IEEE Trans. Energy Convers. 32 (1), 397–398. doi:10.1109/tec.2016.2623982

CrossRef Full Text | Google Scholar

Li, Y., Li, J., and Wang, Y. (2022a). Privacy-preserving Spatiotemporal Scenario Generation of Renewable Energies: A Federated Deep Generative Learning Approach. IEEE Trans. Ind. Inf. 18 (4), 2310–2320. doi:10.1109/tii.2021.3098259

CrossRef Full Text | Google Scholar

Li, Y., Li, K., Yang, Z., Yu, Y., Xu, R., and Yang, M. (2022c). Stochastic Optimal Scheduling of Demand Response-Enabled Microgrids with Renewable Generations: An Analytical-Heuristic Approach. J. Clean. Prod. 330, 129840. doi:10.1016/j.jclepro.2021.129840

CrossRef Full Text | Google Scholar

Li, Y., Wang, R., and Yang, Z. (2022b). Optimal Scheduling of Isolated Microgrids Using Automated Reinforcement Learning-Based Multi-Period Forecasting. IEEE Trans. Sustain. Energy 13 (1), 159–169. doi:10.1109/tste.2021.3105529

CrossRef Full Text | Google Scholar

Liu, B., Zhao, J., Huang, Q., Milano, F., Zhang, Y., and Hu, W. (2021). Nonlinear Virtual Inertia Control of WTGs for Enhancing Primary Frequency Response and Suppressing Drivetrain Torsional Oscillations. IEEE Trans. Power Syst. 36 (5), 4102–4113. doi:10.1109/tpwrs.2021.3055262

CrossRef Full Text | Google Scholar

Luo, K., Shi, W., Shi, W., Chi, Y., Wu, Q., and Wang, W. (2017). Stability and Accuracy Considerations in the Design and Implementation of Wind Turbine Power Hardware in the Loop Platform. Csee Jpes 3 (2), 167–175. doi:10.17775/cseejpes.2017.0021

CrossRef Full Text | Google Scholar

Ma, J., Qiu, Y., Li, Y., Zhang, W., Song, Z., and Thorp, J. S. (2017). Research on the Impact of DFIG Virtual Inertia Control on Power System Small-Signal Stability Considering the Phase-Locked Loop. IEEE Trans. Power Syst. 32 (3), 2094–2105. doi:10.1109/tpwrs.2016.2594781

CrossRef Full Text | Google Scholar

Mehbodniya, A., Paeizi, A., Rezaie, M., Azimian, M., Masrur, H., and Senjyu, T. (2022). Active and Reactive Power Management in the Smart Distribution Network Enriched with Wind Turbines and Photovoltaic Systems. Sustainability 14, 4273. doi:10.3390/su14074273

CrossRef Full Text | Google Scholar

Nguyen, N., Almasabi, S., and Mitra, J. (2018). Impact of Correlation between Wind Speed and Turbine Availability on Wind Farm Reliability. IEEE Trans. Industry Appl. 55 (3), 2392–2400. doi:10.1109/ias.2018.8544643

CrossRef Full Text | Google Scholar

Nguyen, N., Almasabi, S., and Mitra, J. (2019). Impact of Correlation between Wind Speed and Turbine Availability on Wind Farm Reliability. IEEE Trans. Ind. Appl. 55 (3), 2392–2400. doi:10.1109/tia.2019.2896152

CrossRef Full Text | Google Scholar

Penne, M., Qiao, W., Qu, L., Qu, L., Huang, R., and Huang, Q. (2021). “Active Disturbance Rejection Control of Doubly-Fed Induction Generators Driven by Wind Turbines,” in 2021 IEEE Energy Conversion Congress and Exposition (ECCE), 965–972.

CrossRef Full Text | Google Scholar

Sun, L., Liu, K., Hu, J., and Hou, Y. (2019). Analysis and Mitigation of Electromechanical Oscillations for DFIG Wind Turbines Involved in Fast Frequency Response. IEEE Trans. Power Syst. 34 (6), 4547–4556. doi:10.1109/tpwrs.2019.2923012

CrossRef Full Text | Google Scholar

Sun, M., Sun, Y., Chen, L., Zou, Z., Min, Y., Liu, R., et al. (2022). Novel Temporary Frequency Support Control Strategy of Wind Turbine Generator Considering Coordination with Synchronous Generator. IEEE Trans. Sustain. Energy 13 (2), 1011–1020. doi:10.1109/tste.2022.3142914

CrossRef Full Text | Google Scholar

Wang, S., and Tomsovic, K. (2018). A Novel Active Power Control Framework for Wind Turbine Generators to Improve Frequency Response. IEEE Trans. Power Syst. 33 (6), 6579–6589. doi:10.1109/tpwrs.2018.2829748

CrossRef Full Text | Google Scholar

Wang, X., Song, P., Sun, D., and Liu, H. (2018). “Frequency Regulation Characteristics Optimization and Analysis of DFIG- VSG Based on Rotor Inertia Control,” in 2018 China International Conference on Electricity Distribution (CICED), 2051–2055.

Google Scholar

Wang, Y., Meng, J., Zhang, X., and Xu, L. (2015). Control of PMSG-Based Wind Turbines for System Inertial Response and Power Oscillation Damping. IEEE Trans. Sustain. Energy 6 (2), 565–574. doi:10.1109/tste.2015.2394363

CrossRef Full Text | Google Scholar

Wilches-Bernal, F., Chow, J. H., and Sanchez-Gasca, J. J. (2016). A Fundamental Study of Applying Wind Turbines for Power System Frequency Control. IEEE Trans. Power Syst. 31 (2), 1496–1505. doi:10.1109/tpwrs.2015.2433932

CrossRef Full Text | Google Scholar

Xiong, L., Li, P., Wu, F. W., and Wang, J. (2019). Stability Enhancement of Power Systems with High DFIG-Wind Turbine Penetration via Virtual Inertia Planning. IEEE Trans. Power Syst. 34 (2), 1352–1361. doi:10.1109/tpwrs.2018.2869925

CrossRef Full Text | Google Scholar

Zeng, X., Liu, T., Wang, S., Dong, Y., and Chen, Z. (2019). Comprehensive Coordinated Control Strategy of PMSG-Based Wind Turbine for Providing Frequency Regulation Services. IEEE Access 7, 63944–63953. doi:10.1109/access.2019.2915308

CrossRef Full Text | Google Scholar

Zhang, X., Zhu, Z., Fu, Y., and Li, L. (2020). Optimized Virtual Inertia of Wind Turbine for Rotor Angle Stability in Interconnected Power Systems. Electr. Power Syst. Res. 180, 106157. doi:10.1016/j.epsr.2019.106157

CrossRef Full Text | Google Scholar