- 1Key Laboratory of Power Grid Intelligent Dispatch and Control of Ministry of Education, Shandong University, Jinan, China
- 2Electrical Engineering Department, NFC-Institute of Engineering & Fertilizer Research, Faisalabad, Pakistan
Load restoration coordinating transmission grid, distribution grid, and microgrids is an effective measure that is taken into consideration while improving the power system resilience in extreme weather conditions. An online decision-making method is proposed to deal with the unexpected nature of power supply issues regarding the re-energization of microgrids and transmission grids. In this research work, an online multi-agent interaction technique is used for coordinated load restoration. The main algorithm comprises of two subsections, namely, a resilience index and a multi-agent-based decision-making system which are used to administer the coordination among the transmission grid, distribution grid, and microgrids. A distributionally robust optimization model is used to evaluate the power supply capability of microgrids on the basis of load restoration parameters. Finally, a step-by-step decision-making method, based on a deep Q-network, is proposed for distribution network reconfiguration considering the uncertainty of power supply capabilities of transmission grid and microgrids. Simulation results demonstrated that the proposed method can perform the online decision-making of substation load restoration, which significantly improves the load restoration efficiency.
1 Introduction
Severe climatic hazards have been observed in the last few years, leading to frequent outages and huge economic losses (Sun et al., 2019a; Perera et al., 2020; Sun and Liu, 2022). Extreme weather-induced power outages, in the United States of America, cause economic losses of $18 billion to $33 billion per annum (Shield et al., 2021). Hence, the construction of a resilient power grid to cope with extreme weather hazards has gained substantial interest from both academia and the industry point of view. A resilient power grid is capable of preventing and adapting to environmental changes, withstanding perturbations, and quick recovery from outages (Bie et al., 2017). Rapid and effective load restoration plays a key role in resilience enhancement (Wang and Gharavi, 2017). Microgrids have gained rapid development in recent years because of their flexibility to work in grid-connected and island modes (Jithendranath and Das, 2021). Grid-connected microgrids can be used as a resilient resource to restore critical loads on utility feeders (Wang et al., 2016). Coordination in different voltage level grids such as transmission grids and microgrids can significantly improve the efficiency of load restoration, especially in the case of insufficient power supply due to component failure in the transmission grid (Che and Shahidehpour, 2019; Shi et al., 2021). Therefore, it is of great interest to study the coordinated load restoration of transmission grids and microgrids for power system resilience enhancement.
Load restoration schemes are applied on either transmission or distribution grids considering security constraints (Liu et al., 2016). Load restoration is usually modeled as a combinational optimization problem, which can be solved either by mathematical programming (Gholami and Aminifar, 2017; Zhao et al., 2019) or evolutionary computation (Sun et al., 2019b; Yang et al., 2021). In order to improve the restoration efficiency, a rolling optimization strategy is proposed for transmission network recovery and load restoration with the help of a wind-storage system (Sun et al., 2022a). Taking into account different intervals of cold load pickup time, a single-time-step load restoration model, based on bi-level optimization, is proposed for the transmission grid (Sun et al., 2022b). For load restoration in distribution grids, a mixed-integer, second-order cone programming model is suggested considering the network reconfiguration and gas-fired distributed generations (Li et al., 2022). To deal with the time-dependent cold load pickup effect, the information gap decision theory has been used in the distribution grid load optimization model (Song et al., 2021). The above mentioned studies focus on the top–down approach for load restoration, whereas the bottom–up method of microgrids is not considered.
Improvement in the efficiency of load restoration under extreme weather conditions considering microgrids has become a research hot spot for resilience enhancement of power systems. The literature review divides the research work into two classes, namely, islanded microgrid formation and load restoration supported by microgrids. Generally, the former class splits an outage area into multiple islanded zones. These zones are based on the type, capacity, and location of the local generators and the demand and location of the load in the distribution grid. Each zone contains one or more microgrids to sustain during extreme weather (Chen et al., 2018; Sharma et al., 2018; Zhao et al., 2022). The latter takes microgrids as power resources and utilizes the surplus power of microgrids to restore adjacent critical load by operating subsection switches (Gao et al., 2016; Xu et al., 2018; Poudel and Dubey, 2019). The above mentioned research studies mainly focus on load restoration of one feeder in a substation, which does not dynamically coordinate power supply in other feeders. Moreover, power supply from the transmission grid is not considered, resulting in ineffective restoration.
For the entire energization of microgrids and transmission grid during load restoration, an online decision-making method based on multi-agent interaction is proposed. This method effectively coordinates among transmission grid, distribution grid, and microgrids. First, the resilience index and a multi-agent system-based decision-making framework decompose the coordinated load restoration task into several subsections. Second, the power supply from microgrids is evaluated by a distributionally robust optimization (DRO) model, and the effect of uncertainty on power supply from the transmission grid is analyzed. Finally, the deep Q-network (DQN) algorithm determines the optimal control strategies of distribution network reconfiguration for substation load restoration considering the uncertainty of power supply from microgrids and transmission grid.
The major contributions of this work are summarized as follows:
(1) A multi-agent system-based restoration decision-making framework is proposed to decompose load restoration into several subsections considering the complexity of load restoration with top–down and bottom–up power supply. Based on the characteristics of different subproblems, optimization-based and learning-based methods are proposed and applied to different agents.
(2) A Wasserstein metric-based distributionally robust optimization model is developed to deal with the uncertainty of photovoltaic (PV) generation and load in microgrids. Compared with the method considering microgrids to be conventional power sources, the proposed method is more consistent with the actual restoration situation.
(3) A reinforcement learning method, deep Q-network, is used to solve the distribution network configuration problem online. Compared with the commonly used optimization method, the proposed method has obvious advantages in computing efficiency.
The remainder of this research work is organized as follows. The substation load restoration decision-making is introduced in Section 2. The power supply capability evaluation of microgrids and transmission grids is shown in Section 3. The DQN-based online decision-making method of distribution network reconfiguration is proposed in Section 4. Case studies are analyzed in Section 5. The conclusions are drawn in Section 6.
2 Substation load restoration decision-making in extreme weather conditions
A resilience index considering weighted load restoration benefit is proposed with the objective to guide coordinated substation load restoration of the transmission grid, distribution grid, and microgrids after extreme weather. In order to obtain full energization of microgrids and transmission grids, a multi-agent, system-based decision-making framework is established for coordinated substation load restoration.
2.1 Resilience index for load restoration
To cope with the high-impact and low-probability extreme weather hazards, a resilience power system with the ability to prevent, resist, and quickly restore load is established. Effective resilience evaluation is the basis of power grid resilience enhancement. Several resilience indexes have been proposed to guide resilience enhancement of power girds before, during, and after extreme weather events, including the cost of resilience measure (Watson et al., 2014), component connectivity based on the complex-system method (Chanda and Srivastava 2016), time-to-restoration (Maliszewski and Perrings, 2012) and rapidity of restoration (Reed et al., 2009).
Time-to-restoration and rapidity of restoration are resilience indexes in the restoration phase. However, because the load needs to be restored and cut off repeatedly for substation load restoration, it is difficult to evaluate the time-to-restoration and rapidity of restoration. The resilience enhancement requires the comprehensive consideration of emergency repair and the power supply from microgrids and transmission grids. Due to unavailability of components caused by extreme weather, the substation is unable to obtain enough power supply from the transmission grid for a while. By emergency repair, the damaged components can be brought back to normal operation after a relatively long period. During this period, power system resilience can be enhanced by effectively using the various resilient resources to support as much load as possible, particularly the surplus power of microgrids.
By coordinating the power supply from microgrids and transmission grid, the critical load in the substation can be restored quickly. Because the load restoration benefit can reflect the load pickup amount and speed, this research work proposes a resilience index considering weighted load restoration benefit, as follows.
where Etotal is the resilience index; K is the restoration horizon; NM is the set of load nodes; μi,t is the load pickup state variable at time t (μi,t = 1 denotes the load is picked up; μi,t = 0 denotes the load is not picked up); ωi is the weight of load i; and Pdi is the amount of load i.
2.2 Framework of multi-agent system-based substation load restoration decision-making
During extreme weather hazards, power system components may be damaged, resulting in power outages. Due to unavailability of damaged components, the substation is unable to obtain enough power supply from the transmission grid for a period of time. On the one hand, microgrids can work in island mode and maintain stable operation during the outage. The surplus power of microgrids can provide a bottom–up power supply to restore adjacent critical loads effectively. On the other hand, the damaged components need to be recovered by emergency repair. Cooperated with emergency repair, the transmission grid can provide top–down power supply. Considering the power supply from microgrids and transmission grid for the current step, the distribution network can be reconfigured by substation switch control strategies for substation load restoration. By coordination of the transmission grid, distribution grid, and microgrids, the substation load restoration can be effectively developed to enhance power system resilience. Hence, the substation load restoration involves multiple-level power grids, each of which needs to deal with different problems simultaneously. Considering the relative independence of different levels of the power grid, the traditional centralized control method is no longer applicable. The multi-agent system based on flexible interaction is one of the effective methods to solve this problem.
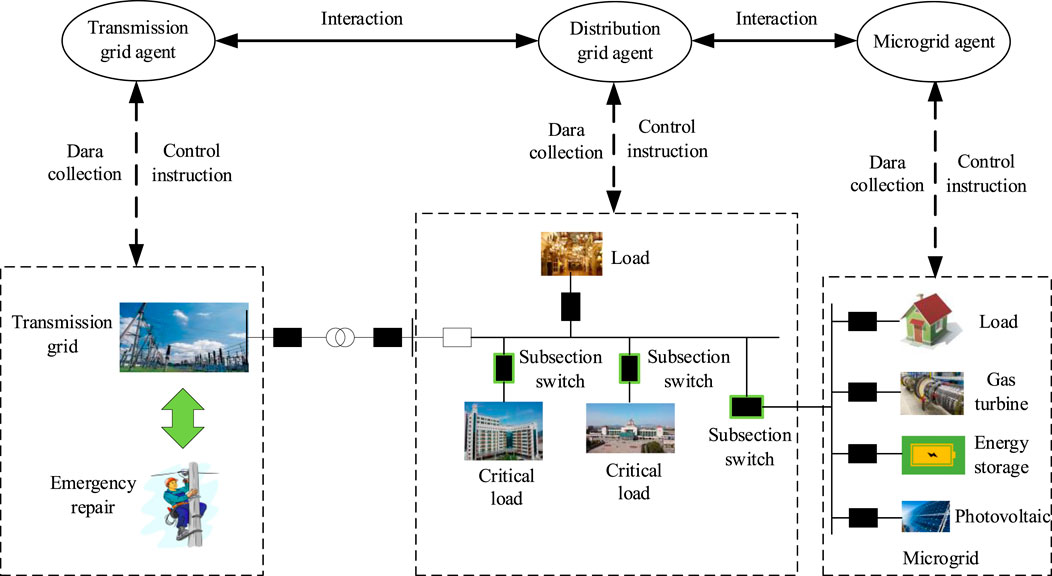
For coordination of the transmission grid, distribution grid, and microgrids, a framework of multi-agent system-based substation load restoration decision-making is established, as shown in Figure 1. The multi-agent system can provide an effective distributed autonomous control framework and mechanism. Each agent in the system not only deals with problems independently but also cooperates with other agents. According to the different external environments, the multi-agent system can adjust its own status and results at the output. It can adapt to various system structures. In addition, a multi-agent system actively achieves the main objective through information exchange and coordination, which improves system performance.
Regarding the different voltage level power grids, the proposed framework of multi-agent system-based substation load restoration decision-making comprises of three types of agents: transmission grid agent, distribution grid agent, and microgrid agent.
(1) Microgrid agent. The microgrid agent can generally collect the microgrid data, including PV generation forecast, load demand forecast, energy storage, and gas turbine status data. Based on the data, it can efficiently match the supply of resources and demand of load and evaluate the power supply capability for current and future steps. It can maintain its stable operation during the outage. For resilience index improvement, it needs to provide a power supply for critical load pickup while maintaining its stable operation.
(2) Transmission grid agent. The transmission grid agent can collect the transmission grid status and emergency repair data. Based on the data, it evaluates the power supply capability for current and future steps. For resilience index improvement, it needs to provide power supply to the substation and meet the constraints of the transmission grid.
(3) Distribution grid agent. The distribution grid agent can collect the distribution grid status and power supply evaluated data. Based on the data, it can determine the network reconfiguration strategies for substation load restoration in the current step. For resilience index improvement, it needs to make an optimal decision online considering the power supply capability of microgrids and transmission grid in the current step.
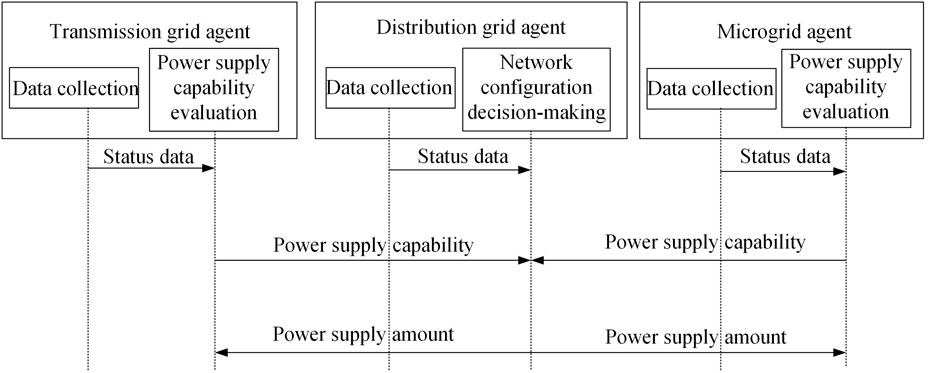
The interaction process among agents for substation load restoration in one step is shown in Figure 2. The process is described as follows: 1) agents collect the corresponding power grid status data in the current step. 2) Microgrid agent and transmission grid agent evaluate the power supply capability based on the data obtained. 3) Microgrid agent and transmission grid agent send power supply capability data to the distribution grid agent. 4) Distribution grid agent makes network configuration decisions based on the data obtained. 5) Distribution grid agent sends the required power supply amount to the transmission grid agent and microgrid agent. 6) Microgrid agent and transmission grid agent provide the corresponding power supply for the substation load restoration.
In order to achieve substation load restoration, two main techniques are considered, namely, power supply capability evaluation of microgrids and transmission grid and distribution network reconfiguration online decision-making. These techniques are further explained in the following sections.
3 Power supply capability evaluation of microgrids and transmission grid
The substation load restoration decision-making includes the power supply capability evaluation of microgrids and transmission grids. A DRO model is established to evaluate the power supply capability of microgrids (PSCMs), which is deployed in the microgrid agent. The uncertain power supply from the transmission grid influenced by emergency repair is analyzed.
3.1 Evaluation of power supply capability of microgrids
3.1.1 Wasserstein metric-based ambiguity set
Microgrids are susceptible to uncertain factors, which further influence substation load restoration. The uncertainty factors include PV generation and load remand. An efficient method is needed to deal with the uncertainty on both sides of the generation and load. In this research work, the DRO method is used, which can establish an ambiguity set containing all possible probability distributions based on historical data for fast restoration. The decision is made under the worst probability distribution condition of the ambiguity set, which solves the problem that it is difficult to accurately obtain the probability distribution. The Wasserstein metric is applied to construct an ambiguity set, which avoids the uncertainty in the process of statistical inference and further reduces the conservatism (Zhu et al., 2019).
Based on a set of samples [a1, a2, ···, aN], the empirical distribution D2 of PV and load forecast error is established as the estimation of the true distribution D1. Then, an ambiguity set containing the true distribution D1 is constructed according to the empirical distribution D2. D2 converges to D1 as N → ∞, i.e., the “distance” between D2 and D1 becomes smaller when more data are available. Wasserstein metric is a measure of the “distance” between two probability distributions, defined as follows:
where W (⋅) is the Wasserstein metric; ξ2 is the random variable subject to empirical distribution; D2; ξ1 is the random variable subject to real distribution D1; Π(⋅) is the joint distribution of D1 and D2; d (ξ2, ξ1) = ||ξ2-ξ1||; ||⋅|| can be any norm, and 1-norm is used in this research work for its superior numerical tractability in DRO (Duan et al., 2018).
According to (Zhu et al., 2019), the ambiguity set A is defined as follows:
where A is an ambiguity set of the underlying true distribution; ℜ(Ξ) is the set of all probability distributions subject to supporting space Ξ; and A is a Wasserstein ball of radius ε (N) centered at the empirical distribution D2.
Based on the Wasserstein metric, the ambiguity set is constructed, including the true distribution of PV and load prediction error. The ambiguity set contains all possible probability distributions at a given confidence level β. The radius of the Wasserstein ball is related to the given sample number N and confidence level β. The confidence level β can be changed by adjusting the radius.
Given a confidence level of the ambiguity set as β, it can be calculated as follows (Duan et al., 2018):
where N is the sample number and S is a constant, which can be acquired by solving the optimization Eq. 5.
where ρ is the auxiliary variable and μ is the sample mean.
3.1.2 Evaluation model for power supply capability of microgrids
Considering the uncertainties of generation and load, the objective function of the evaluation model for PSCM is to provide the power supply as much as possible. Meanwhile, in order to reduce the load switching number, the power supply needs to be stabilized during the load restoration process. The objective function is shown as follows:
where PM,t is the power supply of the microgrid at step t and ψ is the penalty term coefficient. The absolute value of the penalty term represents the power supply deviation between adjacent steps. By introducing auxiliary variables PM1,t, PM2,t and adding the corresponding constraints Eqs 8,9, the objective function Eq. 6 can be transformed into the linear form Eq. 7.
The constraints of the evaluation model for PSCM are presented as follows:
(1) Controllable distributed generator constraint.
where PG,t is the active power of the controllable distributed generator at step t and PG,max and PG,min are the maximum and minimum values of the active power of the controllable distributed generator, respectively.
(2) Energy storage operation constraint.
where Pdis,t and Pch,t are the charging and discharging power of energy storage at step t, respectively; US,t is the charging/discharging state of energy storage (1 indicates the charging state and 0 indicates the discharging state); PS,max is the maximum charging/discharging power of energy storage, which is limited by grid-connected inverter capacity; ES,min and ES,max are the minimum and maximum energy storage capacity, respectively; η is charging/discharging efficiency of energy storage; ES,0 is the energy storage capacity at initial restoration step; and Δt is the length of step.
(3) Power balance constraint.
where PPV,t is the PV generation power of the microgrid at step t and PL,t is the load amount of the microgrid at step t.
(4) Interactive power constraints between the microgrid and the substation.
where PM,max is the maximum power exchange at the point of common coupling, which is determined by the transformer capacity and specific policies.
3.1.3 Distributionally robust chance-constrained power supply capability of microgrids
For ease of exposition, the above mentioned PSCM problem under uncertain PV generation and load demand can be expressed as a compact representation.
where A, E, and F are constant-coefficient matrixes of constraints; C is the coefficient column vector corresponding to the objective function Eq. 7; b and g are constant column vectors; x and ζ are the decision variable and random variable, respectively, and the specific expression is shown as follows:
The uncertain constraint of the optimization problem Eq. 16 can be modeled as the chance-constrained form, shown as follows:
where D is the distribution of the random variable ζ and φ is the desired risk tolerance parameter. The chance-constrained Eq. 18 requires that all probability distributions in the ambiguity set hold simultaneously at least with confidence level 1-φ.
The highly nonconvex distributionally robust chance-constrained is the nonlinear constraint, which needs to be reconstructed into a linear constraint for the convenience of the solution.
At first, the ambiguity set is standardized according to Eq. 19
where ∑ is the sample covariance and μ is the sample mean. Assuming V is the uncertain set of random variables ϑ, it can be expressed as follows:
where Nw is the number of uncertainty sources in the ambiguity set; ϑi is the ith elements of ϑ; and l is the boundary of ϑ.
After normalization, the uncertainty set should satisfy the probability distribution containing the prediction error at a certain confidence level for practical application. Also, the boundary needs to be minimized in order to reduce conservatism (Zhu et al., 2019). Therefore, the model can be expressed as minimizing the boundary l with a probability constraint under the worst-case distribution, shown as follows:
where lmax is the maximum value of boundary l; M s is the probability distribution of the uncertain variable ϑ; and Mstd is the ambiguity set. The constraint of the problem Eq. 20 is a function variable optimization problem that is difficult to solve. According to duality theory, the following formulation can be obtained (Poola et al., 2021).
where (⋅)+ = max (⋅, 0); κ is dual variable.
Thus, Eq. 21 can be transformed into Eq. 23 which is easy to be solved.
Equation (23) can be solved by the nested bisection search method (Zhu et al., 2019).
After determining the boundary l, the boundary value of each random variable is determined. For a 1-dimensional random variable, the boundary vectors are v(1) = {l,l} and v(2) = {-l,-l}. Hence, according to u(i) = Σ1/2v(i)+μ, the chance constraints Eq. 18 can be safely approximated by the linear constraints Eq. 24.
To sum up, by replacing the chance constraints Eq. 18 with their corresponding deterministic constraint Eq. 24, the distributionally robust chance-constrained PSCM problem is transformed into a mixed-integer linear programming problem. This problem can be solved by a mature interior point method (CPLEX) solver.
3.2 Uncertain power supply capability from the transmission grid
After extreme weather hazards, the transmission grid components may be damaged. The transmission grid agent can collect real-time transmission grid status data from the energy management system. The damaged component data can be obtained from relays and fault indicators and the reports from the on-site repair crews (Chen et al., 2018). The transmission grid agent can also obtain distribution grid data such as load demand and restoration progress of the distribution grid and send the data such as power supply capability by interacting with the distribution grid agent. For load restoration efficiency improvement, the emergency repair should cooperate with the transmission grid dispatching to schedule the repair sequence of damaged components. Then, the available repair resources and crews are arranged according to the repair sequence. The repair time and the traveling time can be estimated by emergency repair (Zhang et al., 2020). Based on the data obtained, the transmission grid agent can evaluate the power supply capability.
In the practical load restoration process, uncertainty of actual repair and traveling time leads to uncertainty of the power supply capability of the transmission grid. In (Li et al., 2021), a decision support framework for adaptive restoration control of transmission systems is proposed, which can be used to allocate the restoration power to different substations based on real-time restoration dispatching and emergency repair information. The uncertainty of power supply capability from the transmission grid is not discussed in detail. It is assumed that the transmission grid agent can evaluate power supply capability in real-time.
4 Deep Q-network-based online decision-making of distribution network configuration for load restoration
Considering the uncertainty of the power supply capability of microgrids and transmission grid, a step-by-step decision-making method based on deep reinforcement learning is proposed and deployed in the distribution grid agent. A reinforcement learning model of distribution network configuration is established as the basis of reinforcement learning. The DQN algorithm is applied to obtain a policy network used online to search subsection switch control strategies.
4.1 Reinforcement learning model of distribution network configuration
Based on the power supply capability of microgrids and transmission grid and operation condition of feeders, the distribution grid agent should determine the on–off state of subsection switches at the feeders to restore load. Due to the randomness and intermittency of distributed renewable energy in microgrids, its power supply capability is uncertain during load restoration. Influenced by the uncertainty of repair and traveling time, the power supply capability of the transmission grid is also uncertain. However, the source of uncertain power supply capability of the transmission grid is complex, which is hard to be expressed by an accurate mathematical model. Online decision-making is more practical than the optimization method for restoration in uncertain problems (Sun et al., 2019b; Sun et al., 2022b), which can modify subsection switch control strategies based on real-time data to decrease the influence of uncertainty. The learning-based method can make decisions within several seconds to guarantee the online implementation of distribution network configuration within one dispatch step. The forecast error of renewable energy decreases as the time scale decreases. Usually, the forecast information of renewable energy generation is accurate within one dispatch step. Hence, the online decision-making method is used to handle uncertainty.
The state of the distribution network in the next step is only influenced by the current state, but not related to the past states. Hence, the distribution network configuration decision-making can be described as a Markov decision process, which can be handled by the reinforcement learning method. The reinforcement learning method can obtain knowledge by interacting with the environment, which does not need a large number of training samples for knowledge gain. The outages are infrequent in practical operation, leading to fewer historical data as training samples. Hence, the reinforcement learning method is suitable for distribution network configuration problems.
Environment, state, action, and reward are the main elements of reinforcement learning. Considering the characteristics of distribution network configuration, the elements are defined as follows to establish a reinforcement learning model of distribution network configuration.
(1) Environment. The environment can respond to the subsection switch control strategies of the distribution grid agent. By restoration control, the topology and operation conditions of the substation and its feeders are changed. Hence, the environment is constructed by the topology of feeders, the power supply capability evaluation model of the microgrids and transmission grid, and the operation condition calculation model.
(2) State. State is a kind of understanding and coding of the environment by the distribution grid agent. The state information that influences restoration decision-making includes power supply capability, on–off states of subsection switches, and state switch numbers of substation switches. The power supply capability influences load pickup amount. The on–off states of subsection switches influence the safe operation of feeders. Hence, the state of the distribution network configuration is expressed as follows:
where st is the state at step t; Pdown,t and Pup,t are the power supply capabilities of the transmission grid and microgrids at step t, respectively; Bi,t is the on–off state of the ith switches at step t; and NW is the number of substation switches.
(3) Action. Action refers to the means by which the distribution grid agent influences the environment. In a network configuration problem, the action can be described as the state of subsection switches in the next step, expressed as follows:
where at is the action at step t.
(4) Reward. The reward directly influences the policy established by offline learning, which further determines the online decision-making of the distribution grid agent. Hence, it is necessary to design a reasonable reward function considering the objective and constraints of network configuration. The objective of distribution network configuration is consistent with the proposed resilience index. The constraints of distribution network configuration include safe operation, power supply of microgrids, power supply of the transmission grid, and switch number of subsection switches.
If the safe operation constraint and power supply constraint of microgrids and transmission grid are not satisfied, the substation may face the risk of second power failure. If the switch number constraints of subsection switches are not satisfied, customer satisfaction is influenced. Hence, the first three kinds of constraints must be satisfied, while the subsequent constraints can be varied to some extent. The reward function is described as follows.
where rt is the reward of at step t and I0,t is a state variable that represents whether the action violates constraint at step t. If I0,t = 1, the safe operation constraint and power supply constraint of microgrids and transmission grid are not satisfied, and if I0,t = 0, the safe operation constraint and power supply constraint of microgrids and transmission grid are not satisfied; αo,t is the limit of switch number; co is the punish coefficient.
4.2 Deep Q-network algorithm for distribution network configuration
The aim of reinforcement learning is to establish a model to select the control strategies for the distribution grid agent, which is called policy function π(s, a). The policy function can obtain the probability of action, a, in a certain state, s. Q-learning is a commonly used reinforcement learning to establish a discrete array as a policy function. However, because there are a large number of states in the distribution network configuration problem, it is difficult to establish a discrete array to store the function. In addition, Monte Carlo Tree Search (MCTS) is also a kind of reinforcement learning method, which can establish a tree as a policy function. However, MCTS makes decisions based on a set of simulation results, which needs more computation time to perform simulation. For the substation load restoration problem, the decision needs to be made momentarily. The MCTS algorithm cannot meet the requirements. Hence, the DQN algorithm is selected to establish a policy function, which combines Q-learning with deep learning to obtain a Q-network by offline training.
Deep Q-network is a deep neural network with parameter θ, used to fit policy function, which can be expressed as Q (s, a, θ)≈π(s, a). The input of the deep Q-network is the load restoration state, whose output is the Q-value of every action. By offline learning, the Q-network can be used online to evaluate the Q-value of every load restoration strategy as the basis of decision-making.
The experience replay method, target network, and ε-greedy strategy are used in DQN training (Lin, 1992; Watkins and Dayan, 1992; Mnih et al., 2013), which are not presented in detail. In the training process of DQN, the decreasing gradient algorithm is used to update the Q-network based on the loss function shown as follows:
where γ is a discount factor for target Q; s’ is the state in the next step; a’ is all possible actions in state s’; θ is the parameter of the Q-network; and θ′ is the parameter of the target network, which will be updated to θ after several iterations.
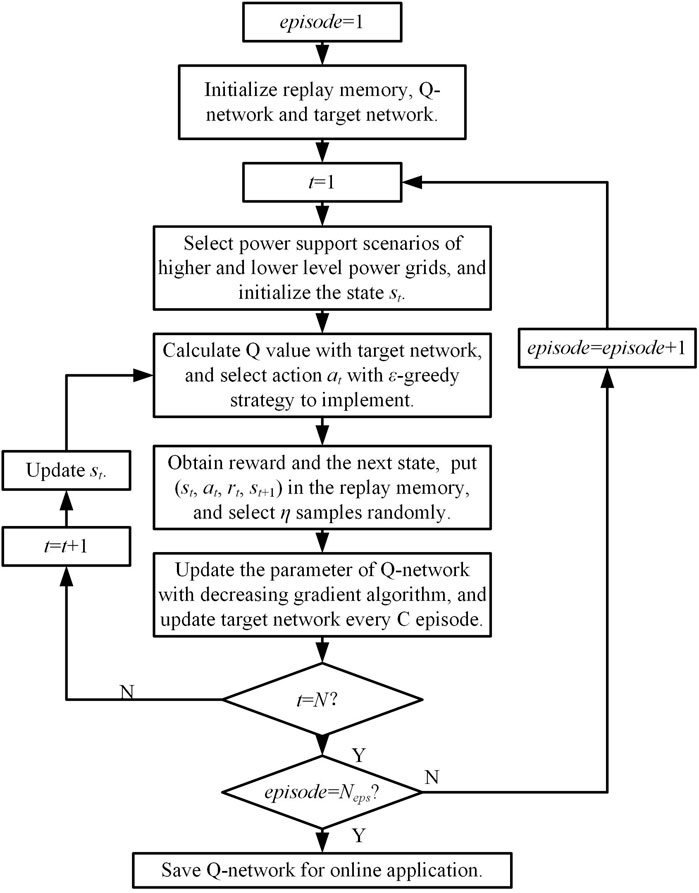
The flowchart of DQN training for distribution network configuration is shown in Figure 3. It is noticed that the scenarios of power supply capability are generated before the execution of DQN considering all possible operation states, which is important to guarantee a high generalization of DQN for distribution network configuration. Based on the scenarios, the environment of distribution network configuration is generated randomly during DQN training.
In the flowchart, Neps is the episode limitation and η is the size of the minibatch. The Adam algorithm is selected as the decreasing gradient algorithm for Q-network training (Kingma, 2015). ε in the ε-greedy strategy is updated based on the following equation.
where εini and εfin are the initial and final values of ε, respectively.
5 Case study
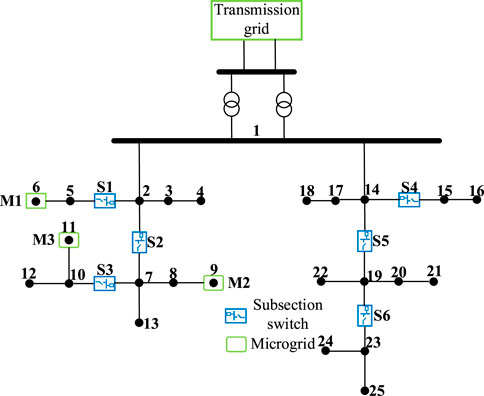
A test system is constructed to demonstrate the effectiveness of the proposed method. Two modified IEEE 13-bus systems (Yang et al., 2021) are attached to a single low-voltage bus in the station. The location of microgrids and subsection switches is shown in Figure 4. It is assumed that an extremely hot weather condition caused damage to the transmission grid, resulting in outages. Microgrids consist of controllable gas turbine, PV, load, and energy storage. Microgrid parameters, PV generation, and load demand data are referred to in the study by Zeng et al., (2019). The voltage limit is set to 0.9 to 1.1 p. u. The effectiveness of the DRO-based PSCM evaluation and DQN-based distribution network configuration decision-making is shown as follows.
5.1 Effectiveness of distributionally robust optimization-based power supply capability of microgrids evaluation
5.1.1 Power supply capability of microgrids evaluation results
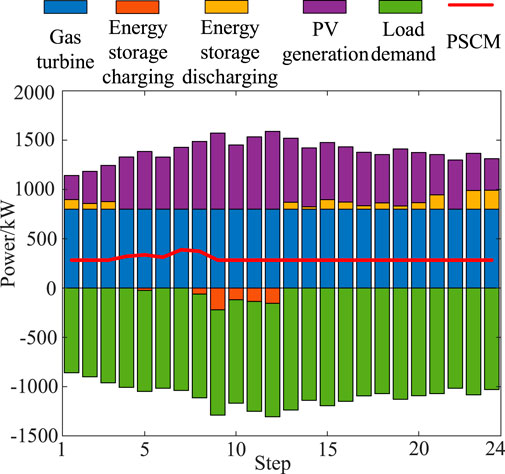
Microgrid M2 of node 9 in Figure 4 is taken as an example to illustrate. Wasserstein's ball confidence level is set to 0.95. The risk tolerance parameter φ is set to 0.05. The penalty function coefficient ψ is set to 10. For simulation purposes, the step length is set to 15 min, and the future 6 h are considered to evaluate the PSCM. In the practical load restoration process, the step length is dynamic. The proposed DRO-based PSCM evaluation model is adopted to obtain the results, as shown in Figure 5. PV generation shows a trend of gradually increasing initially and then decreasing. The energy storage charges at the step when the PV generation is high and discharges at the step when it decreases so as to ensure that the PSCM can remain stable.
5.1.2 Influence of risk tolerance parameters
The risk tolerance parameter φ represents the risk acceptance level of decision makers. In order to compare the influence of the risk acceptance level, different φ values are set to evaluate the PSCM, as shown in Table 1. A high-risk tolerance parameter indicates that decision-makers have a high-risk acceptance level. As a result, the PSCM is relatively higher, which leads to a high load restoration efficiency but a decrease in security. With the decrease in risk tolerance, the PSCM decreases, leading to reduced load restoration efficiency. In the practical load restoration process, reasonable risk tolerance parameters can be determined according to the risk preference.
5.1.3 Comparison with robust optimization
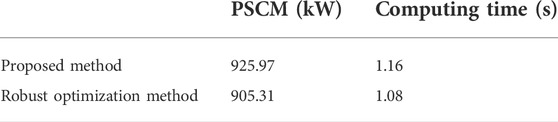
To further illustrate the performance of the Wasserstein distance-based DRO method, comparison results with the robust optimization method (Zeng et al., 2019) are shown in Table 2. The table shows that the method in this research work can obtain a higher PSCM. Compared to robust optimization, the DRO-based method can reduce the conservativeness of the calculation result using a similar calculation time. The conservatism of the calculation result is related to the confidence level and the sample size because the radius of the Wasserstein ball determines the range of possible probability distributions included in the ambiguity set. The robust optimization method is equivalent to the Wasserstein ball with a confidence level of 1, which contains all possible probability distributions. Some extreme distributions with a low probability of occurrence can be excluded from the Wasserstein ball to obtain a Wasserstein ball with a smaller radius. Compared with the robust optimization method, the proposed method can consider the distribution probability, and it has the ability to adjust the robustness flexibly to balance the safety and risk of load restoration under an uncertain environment.
5.2 Effectiveness of deep Q-network-based distribution network configuration decision-making
5.2.1 Training process of deep Q-network
The structures of the Q-network and target network are set to [144,100, 70, 40, and 36]. The values of hyperparameters of DQN training are shown in Table 3, which are set by comparing the training results of several sets of parameters. The environment of the distribution network configuration reinforcement learning model is determined by the power supply capability scenarios of microgrids and transmission grids. Based on the historical data of PV and load, the DRO-based method is adopted to calculate the power supply capability of microgrids in different scenarios. Based on the capacity of the substation, the power supply capability of the transmission grid is generated randomly. In every iteration, the power supply capability scenarios are obtained randomly as the environment of distribution network configuration simulation to generate the training data of the Q-network.
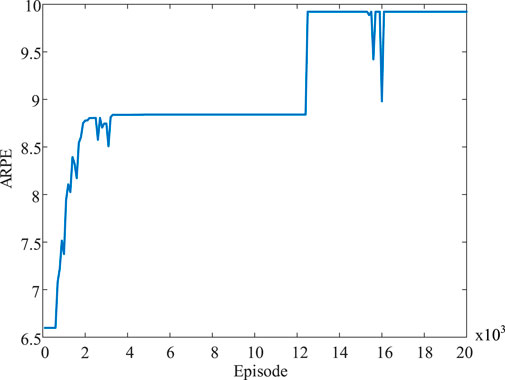
The average reward of distribution network configuration by Q-network in 30 test scenarios is calculated per 100 episodes to show the training process of DQN, which is defined as the average rewards per episode (ARPE). The training process of DQN is shown in Figure 6. It is noticed that DQN training with 20,000 episodes takes about 20 h. It can be seen that the ARPE increases rapidly in the first 2,000 episodes, and the curve is flat along with training. After 12,000 episodes, the curve is roughly stable along with training. The Q-network after 20,000 episodes is used online for distribution network configuration.
5.2.2 Substation load restoration process
Considering the power supply capability from microgrids and transmission grid, the subsection switch control strategies are determined by the DQN-based distribution network configuration decision-making method. The restoration duration is 6 h, and PV is in the enrichment period. The step length is set to 15 min. Figure 7 shows the operation process of substation load restoration from step 6 to step 7. In every step, the PSCMs of M1, M2, and M3 are evaluated by the proposed DRO-based method at first. Then, the subsection switch control strategies are determined by the proposed DQN-based method based on the PSCM information received from the transmission grid and microgrid agents. In step 6, the PSCMs of M1, M2, and M3 are 569, 1475, and 1053kW, respectively. The power supply capability of the transmission grid is 7274 kW; S2, S3, S4, S5, and S6 are closed; and S1 is open. In step 7, the PSCMs of M1, M2, and M3 are 869, 827, and 1427kW, respectively. The power supply capability of the transmission grid is 8515 kW. Due to the larger power supply capability from transmission grids and microgrids, all subsection switches are closed.
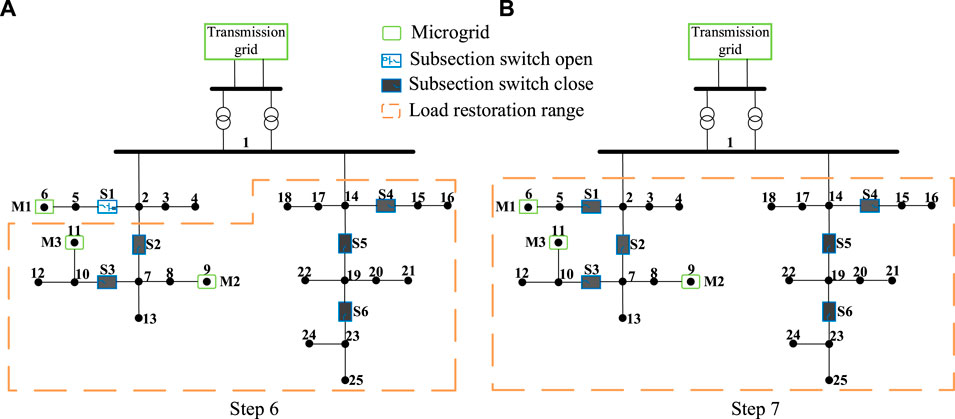
FIGURE 7. Operation process of substation load restoration. (A) The step 6 of substation load restoration process. (B) The step 7 of substation load restoration process.
5.2.3 Comparison results in different restoration scenarios
The proposed method is compared with the two methods to show its effectiveness. The main differences between different methods are shown in Table 4. The method proposed by Li et al. (2021) is referred to as Method 1, which does not consider the power supply of microgrids. The method proposed by Ding et al. (2017) is referred to as Method 2, which considers the microgrids as the controllable power supply. Four restoration scenarios are set to obtain restoration results with different methods. In scenario 1, restoration duration is 3 h and PV is in the enrichment period; In scenario 2, restoration duration is 6 h and PV is in the enrichment period; In scenario 3, restoration duration is 6 h and PV is in the barren period; and in scenario 4, restoration duration is 9 h and PV is in the barren period.
The load restoration results represented by load restoration benefits in different scenarios are shown in Figure 8. In all scenarios, the proposed method can obtain better restoration results than the other methods. It can be seen that the gaps between the lines of the proposed method and Method 1 widen as restoration duration increases, which proves the importance of a bottom–up power supply. The load restoration process is delayed by Method 2 due to restoration failure at some steps, especially when PV is in the barren period. Microgrids are regarded as the controllable power supply with a certain ramp rate, which is not consistent with the actual restoration situation. Restoration failure occurs in case of large fluctuations in power supply of microgrids, resulting in obstruction of the restoration process by Method 2. Especially during a barren period, the fluctuation in the PV output is intense, which leads to frequent restoration failure and makes load restoration benefit with Method 2 even lower than that of Method 1. Hence, the proposed method can gain better results in different scenarios by considering the uncertainty of renewable energy.
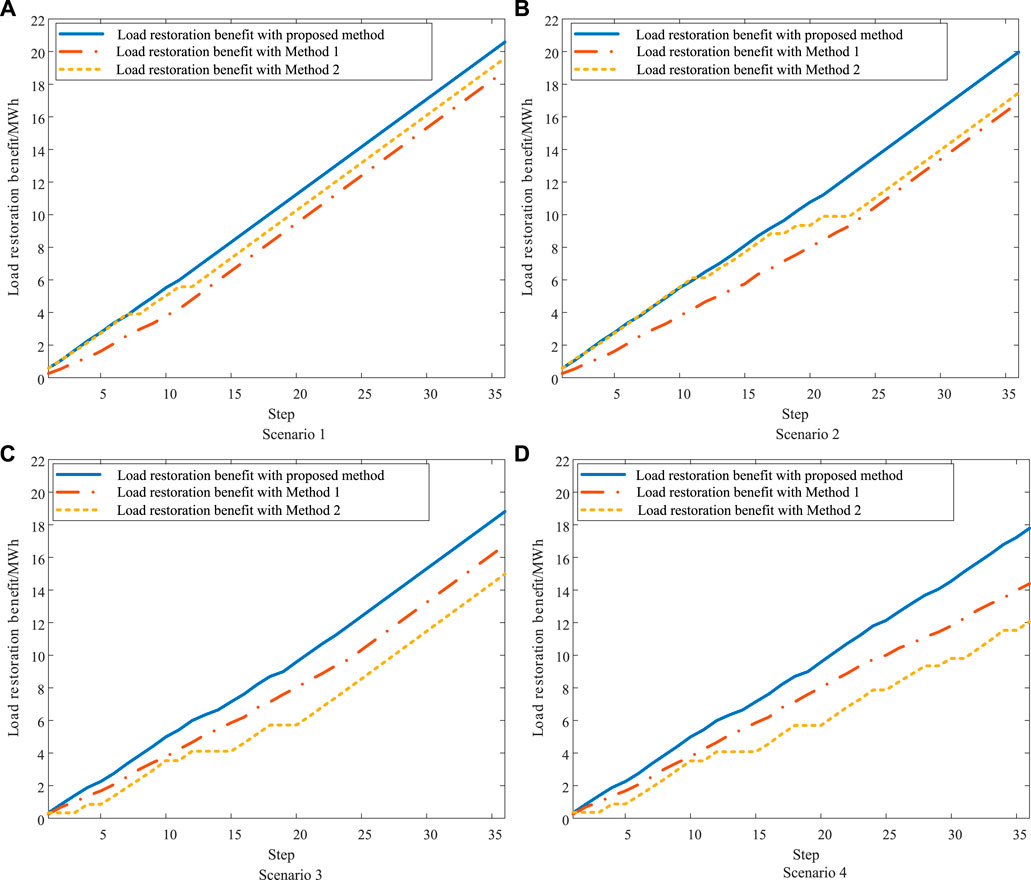
FIGURE 8. Load restoration results in different scenarios. (A) Load restoration benefit with three methods in scenario 1. (B) Load restoration benefit with three methods in scenario 2. (C) Load restoration benefit with three methods in scenario 3. (D) Load restoration benefit with three methods in scenario 4.
5.2.4 Comparison with the optimization-based method
The proposed DQN-based method for distribution network configuration is compared with the commonly used optimization-based method (Wang et al., 2016; Arif and Wang, 2017; Chen et al., 2018) under 100 scenarios to illustrate its performance further. Due to the characteristics of the algorithm, the computation time of the learning-based method must be shorter than that of the optimization-based method. Hence, the key to comparison is to compare the efficiency of restoration results. The PSO algorithm is adopted to represent the optimization-based method for comparison, which is executed several times in different scenarios to obtain the optimal results. For the PSO algorithm, the number of populations and iterations is set to 30 and 20, respectively. The computation time of PSO is about 13756s, while DQN takes 0.05s. The comparison results are shown in Table 5. Although the average load restoration benefit of the DQN method in this work is lesser, the computation time is much shorter than that of the PSO algorithm. The DQN method can be applied to online load restoration decision-making under an uncertain environment.
6 Conclusion
The aim of this investigation is to improve load restoration through effective coordination between the transmission grid, distribution grid, and microgrids, with the help of a multi-agent system-based online decision-making method. The work focuses on improving the substation load restoration efficiency through step-by-step control strategies. DRO and deep reinforcement learning are deployed in different types of agents to improve the efficiency of decision-making. The conclusions drawn are as follows. 1) The multi-agent system-based online decision-making framework decomposes the substation load restoration task into several subsections and allocates them to different agents, which are consistent with the practical transmission grid, distribution grid, and microgrids. This approach online provides the control strategies to improve the load restoration efficiency with top–down and bottom–up methods. 2) The DRO-based method can evaluate the power supply capability from microgrids as the basis for decision-making, by considering the uncertainty of PV generation and load demand, to guarantee reliable restoration. 3) The DQN-based distribution network configuration decision-making method generates a policy network by offline learning to make subsection switch control strategies for online substation load restoration, which can maintain rapid computation speed by scarifying some degree of optimality.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
RF and RS contributed to the conception and design of the study. RF and RS performed the case study. RF organized the article structure and wrote the manuscript. YL and R u H contributed to manuscript revision and reading.
Funding
This work was supported by project ZR2021QE221 supported by Shandong Provincial Natural Science Foundation.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Arif, A., and Wang, Z. (2017). Networked microgrids for service restoration in resilient distribution systems. IET Gener. Transm. &. Distrib. 11, 3612–3619. doi:10.1049/iet-gtd.2017.0380
Bie, Z., Lin, Y., Li, G., and Li, F. (2017). Battling the extreme: A study on the power system resilience. Proc. IEEE 105, 1253–1266. doi:10.1109/JPROC.2017.2679040
Chanda, S., and Srivastava, A. K. (2016). Defining and enabling resiliency of electric distribution systems with multiple microgrids. IEEE Trans. Smart Grid 7, 2859–2868. doi:10.1109/TSG.2016.2561303
Che, L., and Shahidehpour, M. (2019). Adaptive formation of microgrids with mobile emergency resources for critical service restoration in extreme conditions. IEEE Trans. Power Syst. 34, 742–753. doi:10.1109/TPWRS.2018.2866099
Chen, B., Chen, C., Wang, J., and Butler-Purry, K. L. (2018). Sequential service restoration for unbalanced distribution systems and microgrids. IEEE Trans. Power Syst. 33, 1507–1520. doi:10.1109/TPWRS.2017.2720122
Ding, T., Lin, Y., Li, G., and Bie, Z. (2017). A new model for resilient distribution systems by microgrids formation. IEEE Trans. Power Syst. 32, 4145–4147. doi:10.1109/TPWRS.2017.2650779
Duan, C., Fang, W., Jiang, L., Yao, L., and Jun, L. (2018). Distributionally robust chance-constrained approximate AC-OPF with Wasserstein metric. IEEE Trans. Power Syst. 33, 4924–4936. doi:10.1109/tpwrs.2018.2807623
Gao, H., Chen, Y., Xu, Y., and Liu, C. C. (2016). Resilience-oriented critical load restoration using microgrids in distribution systems. IEEE Trans. Smart Grid 7, 2837–2848. doi:10.1109/TSG.2016.2550625
Gholami, A., and Aminifar, F. (2017). A hierarchical response-based approach to the load restoration problem. IEEE Trans. Smart Grid 8, 1700–1709. doi:10.1109/TSG.2015.2503320
Jithendranath, J., and Das, D. (2021). Stochastic planning of islanded microgrids with uncertain multi-energy demands and renewable generations. IET Renew. Power Gener. 14, 4179–4192. doi:10.1049/iet-rpg.2020.0889
Kingma, D. P., and Ba, J. (2014). Adam: A method for stochastic optimization. arXiv 1049 preprint. arXiv preprint arXiv:1412.6980. doi:10.48550/arXiv.1412.6980
Li, G., Yan, K., Zhang, R., Jiang, T., Li, X., and Chen, H. (2022). Resilience-oriented distributed load restoration method for integrated power distribution and natural gas systems. IEEE Trans. Sustain. Energy 13, 341–352. doi:10.1109/TSTE.2021.3110975
Li, Z., Xue, Y., Wang, H., and Hao, L. (2021). Decision support system for adaptive restoration control of transmission system. J. Mod. Power Syst. Clean Energy 9, 870–885. doi:10.35833/MPCE.2021.000030
Lin, L. (1992). Self-improving reactive agents based on reinforcement learning, planning and teaching. Mach. Learn. 8, 293–321. doi:10.1007/BF00992699
Liu, Y., Fan, R., and Terzija, V. (2016). Power system restoration: A literature review from 2006 to 2016. J. Mod. Power Syst. Clean. Energy 4, 332–341. doi:10.1007/s40565-016-0219-2
Maliszewski, P. J., and Perrings, C. (2012). Factors in the resilience of electrical power distribution infrastructures. Appl. Geogr. 32, 668–679. doi:10.1016/j.apgeog.2011.08.001
Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Antonoglou, I., Wierstra, D., et al. (2013). Playing atari with deep reinforcement learning. arXiv:1312.5602.
Perera, A. T. D., Nik, V. M., Chen, D., Scartezzini, J.-L., and Hong, T. (2020). Quantifying the impacts of climate change and extreme climate events on energy systems. Nat. Energy 5, 150–159. doi:10.1038/s41560-020-0558-0
Poola, B. K., Hota, A. R., Bolognani, S., Callaway, D. S., and Cherukuri, A. (2021). Wasserstein distributionally robust look-ahead economic dispatch. IEEE Trans. Power Syst. 36, 2010–2022. doi:10.1109/TPWRS.2020.3034488
Poudel, S., and Dubey, A. (2019). Critical load restoration using distributed energy resources for resilient power distribution system. IEEE Trans. Power Syst. 34, 52–63. doi:10.1109/TPWRS.2018.2860256
Reed, D. A., Kapur, K. C., and Christie, R. D. (2009). Methodology for assessing the resilience of networked infrastructure. IEEE Syst. J. 3, 174–180. doi:10.1109/JSYST.2009.2017396
Sharma, A., Srinivasan, D., and Trivedi, A. (2018). A decentralized multi-agent approach for service restoration in uncertain environment. IEEE Trans. Smart Grid 9, 3394–3405. doi:10.1109/TSG.2016.2631639
Shi, Q., Li, F., Olama, M., Dong, J., Xue, Y., Starke, M., et al. (2021). Post-extreme-event restoration using linear topological constraints and DER scheduling to enhance distribution system resilience. Int. J. Electr. Power & Energy Syst. 131, 107029. doi:10.1016/j.ijepes.2021.107029
Shield, S. A., Quiring, S. M., and Pino, J. V. (2021). Major impacts of weather events on the electrical power delivery system in the United States. Energy 218. 119434. doi:10.1016/j.energy.2020.119434
Song, M., Nejad, R. R., and Sun, W. (2021). Robust distribution system load restoration with time-dependent cold load pickup. IEEE Trans. Power Syst. 36, 3204–3215. doi:10.1109/TPWRS.2020.3048036
Sun, L., Liu, W., Chung, C. Y., Ding, M., and Ding, J. (2022a). Rolling optimization of transmission network recovery and load restoration considering hybrid wind-storage system and cold load pickup. Int. J. Electr. Power & Energy Syst. 141, 108168. doi:10.1016/j.ijepes.2022.108168
Sun, L., Yang, Z., Li, M., Ding, M., and Liang, B. (2022b). A Bi-level approach to load restoration strategy considering variant length of time steps. IET Generation Trans. Dist. 16, 319–332. doi:10.1049/gtd2.12307
Sun, R., and Liu, Y. (2022). Hybrid reinforcement learning for power transmission network self-healing considering wind power. IEEE Trans. Neural Netw. Learn. Syst., 1–11. doi:10.1109/TNNLS.2021.3136554
Sun, R., Liu, Y., and Wang, L. (2019a). An online generator start-up algorithm for transmission system self-healing based on MCTS and sparse autoencoder. IEEE Trans. Power Syst. 34, 2061–2070. doi:10.1109/TPWRS.2018.2890006
Sun, R., Liu, Y., Zhu, H., Azizipanah-Abarghooee, R., and Terzija, V. (2019b). A network reconfiguration approach for power system restoration based on preference-based multiobjective optimization. Appl. Soft Comput. 83, 105656. doi:10.1016/j.asoc.2019.105656
Wang, J., and Gharavi, H. (2017). Power grid resilience [scanning the issue]. Proc. IEEE 105, 1199–1201. doi:10.1109/JPROC.2017.2702998
Wang, Z., Chen, B., Wang, J., and Chen, C. (2016). Networked microgrids for self-healing power systems. IEEE Trans. Smart Grid 7, 310–319. doi:10.1109/TSG.2015.2427513
Watkins, C. J. C. H., and Dayan, P. (1992). Q-learning. Q-learning. Mach. Learn. 8, 279–292. doi:10.1007/BF00992698
Watson, J.-P., Guttromson, R., Silva-Monroy, C., Jeffers, R., Jones, K., Ellison, J., et al. (2014). Conceptual framework for developing resilience metrics for the electricity, ol, and gas sectors in the United States. Albuquerque, NM, USA: Sandia National Lab. SAND2014-18019Tech. Rep. doi:10.2172/1177743
Xu, Y., Liu, C. C., Schneider, K., Tuffner, F., and Ton, D. (2018). Microgrids for service restoration to critical load in a resilient distribution system. IEEE Trans. Smart Grid 9, 426–437. doi:10.1109/TSG.2016.2591531
Yang, L., Xu, Y., Sun, H., Chow, M., and Zhou, J. (2021). A multiagent system based optimal load restoration strategy in distribution systems. Int. J. Electr. Power & Energy Syst. 124, 106314. doi:10.1016/j.ijepes.2020.106314
Zeng, J., Wang, Q., Liu, J., Chen, J., and Chen, H. (2019). A potential game approach to distributed operational optimization for microgrid energy management with renewable energy and demand response. IEEE Trans. Ind. Electron. 66, 4479–4489. doi:10.1109/TIE.2018.2864714
Zhang, G., Zhang, F., Zhang, X., Meng, K., and Dong, Z. Y. (2020). Sequential disaster recovery model for distribution systems with Co-optimization of maintenance and restoration crew dispatch. IEEE Trans. Smart Grid 11, 4700–4713. doi:10.1109/TSG.2020.2994111
Zhao, J., Li, F., Mukherjee, S., and Sticht, C. (2022). Deep reinforcement learning-based model-free on-line dynamic multi-microgrid formation to enhance resilience. IEEE Trans. Smart Grid 13, 2557–2567. doi:10.1109/tsg.2022.3160387
Zhao, J., Wang, H., Liu, Y., Azizipanah-Abarghooee, R., and Terzija, V. (2019). Utility-oriented online load restoration considering wind power penetration. IEEE Trans. Sustain. Energy 10, 706–717. doi:10.1109/TSTE.2018.2846231
Keywords: deep reinforcement learning, distributionally robust optimization, load restoration, microgrid, multi-agent, resilience, Smart Grid
Citation: Fan R, Sun R, Liu Y and Hassan Ru (2022) An online decision-making method based on multi-agent interaction for coordinated load restoration. Front. Energy Res. 10:992966. doi: 10.3389/fenrg.2022.992966
Received: 13 July 2022; Accepted: 01 August 2022;
Published: 15 September 2022.
Edited by:
Bo Yang, Kunming University of Science and Technology, ChinaReviewed by:
Xiaoshun Zhang, Northeastern University, ChinaXiaohan Jiang, Kunming University of Science and Technology, China
Copyright © 2022 Fan, Sun, Liu and Hassan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yutian Liu, bGl1eXRAc2R1LmVkdS5jbg==
 Rui Fan
Rui Fan Runjia Sun
Runjia Sun Yutian Liu1*
Yutian Liu1* Rizwan ul Hassan
Rizwan ul Hassan