Solving optimal power flow problems via a constrained many-objective co-evolutionary algorithm

The optimal power flow problem in power systems is characterized by a number of complex objectives and constraints, which aim to optimize the total fuel cost, emissions, active power loss, voltage magnitude deviation, and other metrics simultaneously. These conflicting objectives and strict constraints challenge existing optimizers in balancing between active power and reactive power, along with good trade-offs among many metrics. To address these difficulties, this paper develops a co-evolutionary algorithm to solve the constrained many-objective optimization problem of optimal power flow, which evolves three populations with different selection strategies. These populations are evolved towards different parts of the huge objective space divided by large infeasible regions, and the cooperation between them renders assistance to the search for feasible and Pareto-optimal solutions. According to the experimental results on benchmark problems and the IEEE 30-bus, IEEE 57-bus, and IEEE 118-bus systems, the proposed algorithm is superior over peer algorithms in solving constrained many-objective optimization problems, especially the optimal power flow problems.

1 Introduction

Optimal power flow (OPF) is a prominent area of power system optimization, where the primary goal is to identify the optimal operations and management strategies for power systems, so as to maximize the profit and ensure safety and reliability. It optimizes a set of control variables including active power generation of generators, bus voltages of generators, transformer tap ratios, and reactive power of shunt compensators, achieving the optimization of specific objectives and the satisfaction of multiple constraints (Warid et al., 2018). Conventional OPF problems consider a single objective with various forms, and there has been a growing interest in the study of multi-objective optimal power flow (MOOPF) (Chen et al., 2018). MOOPF allows for a more comprehensive evaluation of economic efficiency, environmental friendliness, and power system reliability, providing a broader perspective on power system optimization. Recently, many-objective optimal power flow (MaOOPF) has also gained attention for its thorough consideration of the operational status of power systems (Zhang et al., 2019), including fuel costs, emissions, voltage magnitude deviations, and active power losses. In short, studying OPF, MOOPF, and MaOPF is essential for advancing the optimization of power systems, while these problems pose challenges to optimizers due to the various objectives and constraints characterized by non-linearity, non-convexity, and high dimensionality (Li et al., 2021).

In the past, mathematical programming methods have been utilized to address OPF problems with a single objective, such as interior point method (Momoh and Zhu, 1999), linear programming (Mota-Palomino and Quintana, 1986), and nonlinear programming (Habibollahzadeh et al., 1989). However, the non-convex landscapes and strict constraints entrap mathematical programming methods in local optimums, preventing them from finding the global optimal solutions. To overcome this issue, metaheuristics have emerged to solve OPF problems in the last decade. These include the adaptive constraint differential evolution (Li et al., 2021), the enhanced differential evolution with self-adaptive penalty constraint handling technique (Li et al., 2020), the improved chaotic flower pollination algorithm (Daqaq et al., 2022), the modified Gaussian bare-bones Levy-flight firefly algorithm (Alghamdi, 2022), and the probabilistic optimal power flow calculation method based on adaptive diffusion kernel density estimation (Li et al., 2019a). These metaheuristics have demonstrated promising performance in solving single-objective OPF problems, but the consideration of a single metric limits their applications in complex power systems.

On the other hand, MOOPF refers to highly nonlinear constrained multi-objective optimization problems, which is more practical but requires the balance between multiple conflicting metrics (Biswas et al., 2020). To solve MOOPF problems effectively, multi-objective evolutionary algorithms and swarm intelligence algorithms have been customized. For instance, a modified multi-objective evolutionary algorithm based on decomposition was suggested in (Zhang et al., 2016), a hybrid bat algorithm with constrained Pareto fuzzy dominance was suggested in (Chen et al., 2019), and the selection and mutation strategies of differential evolution were embedded in an enhanced variant of NSGA-III in (Huang et al., 2018). Recently, an improved heap optimization algorithm was suggested for MOOPF (Shaheen et al., 2022), and the multi-objective particle swarm optimization algorithm (Shaheen et al., 2022) and its improved version (Qian and Chen, 2022) were also employed for MOOPF.

With the continuous development of power systems, the need for extending MOOPF to MaOOPF turns out to be urgent. MaOOPF is crucial for promoting the sustainable development of power systems, as it involves a greater number of objectives suitable for the planning of modern power systems. The introduction of more objectives makes the optimization problems more challenging, and high-performance optimizers have been put on the agenda. So far, only a few optimizers have been used to address MaOOPF problems, including the two-step knee point-driven evolutionary algorithm (Li and Li, 2018), an improved NSGA-III with adaptive elimination strategy (Zhang et al., 2019), an MOEA/D with many-stage dynamical resource allocation strategy (Zhang et al., 2020), a many-objective gradient-based optimizer (Premkumar et al., 2021), and the many-objective marine predators algorithm (Khunkitti et al., 2022).

Evolutionary algorithms have shown effectiveness in solving various complex problems Tian et al. (2019b); Xiang et al. (2022); Yang et al. (2022), including those with many objectives and constraints. Evolutionary many-objective optimization has been developed for 2 decades, where a number of evolutionary algorithms have shown effectiveness in solving various many-objective optimization problems (Li et al., 2015). State-of-the-art many-objective evolutionary algorithms strike a balance between many objectives by using four categories of ideas, including diversity enhancement (Li et al., 2014; Zhang et al., 2015b), new dominance relations (Zhu et al., 2016; Tian et al., 2019a), objective decomposition (Zhang and Li, 2007; Deb and Jain, 2013), and performance indicators (Tian et al., 2016; Tian et al., 2018). Also, evolutionary constrained multi-objective optimization has gained attention in recent years, and some evolutionary algorithms have shown effectiveness in handling constrained multi-objective optimization problems (Liang et al., 2023). Existing constrained multi-objective evolutionary algorithms handle complex constraints with several ideas, such as constrained dominance principle (Deb et al., 2002), penalty functions (Xia et al., 2020), multi-stage frameworks (Tian et al., 2022), and co-evolutionary frameworks (Tian et al., 2021). However, the development of evolutionary constrained many-objective optimization is in its infancy, where the large infeasible regions located in high-dimensional objective spaces significantly hamper the approximation of constrained Pareto fronts. Currently, the majority of multi-objective evolutionary algorithms can only cross through infeasible regions in low-dimensional objective spaces, whereas few are scalable to many-objective optimization (Ming et al., 2022a; Ming et al., 2022b).

Focusing on the MaOOPF problems in power systems, this work proposes a co-evolutionary algorithm for solving constrained many-objective optimization problems. More specifically, the proposed algorithm suggests a co-evolutionary framework with three populations, which are separately evolved considering different priorities of objectives and constraints. These populations are responsible for searching different parts of the high-dimensional objective space, so as to break through large infeasible regions more easily. According to the experimental comparisons with state-of-the-art counterparts, the proposed algorithm exhibits superiority on not only MaOOPF problems but also challenging benchmark problems with up to ten objectives and five constraints.

The rest of this paper is organized as follows. From the perspective of constrained many-objective optimization, Section 2 introduces the mathematical definition of the MaOOPF problem considered in this work. In Section 3, the detailed procedure of the proposed co-evolutionary algorithm is presented. To verify the effectiveness of the proposed algorithm, Section 4 conducts comparative experiments on benchmark problems and MaOOPF problems. Finally, conclusions and future work are given in Section 5.

2 Problem formulation

Figure 1 illustrates the input and output of optimal power flow with respect to the IEEE 30-bus system. The input represents the topological structure and requirements of the power system, including conductance, susceptance, rated voltage, and many other parameters. The output represents the control variables (i.e., decision variables) to be optimized, including voltages of generators, transformer tap ratios, reactive power of shunt compensator, and active power of generators. By considering economic viability, carbon emission limitations, energy efficiency, safety, and stability, MaOOPF provides a comprehensive evaluation of power systems. Its objectives are to maximize operational efficiency while enhancing energy utilization and environmental benefits, and its constraints are to strike a balance between power outputs and demands. In the following, the mathematical definition of the MaOOPF problem is detailed from the perspective of constrained many-objective optimization.

FIGURE 1

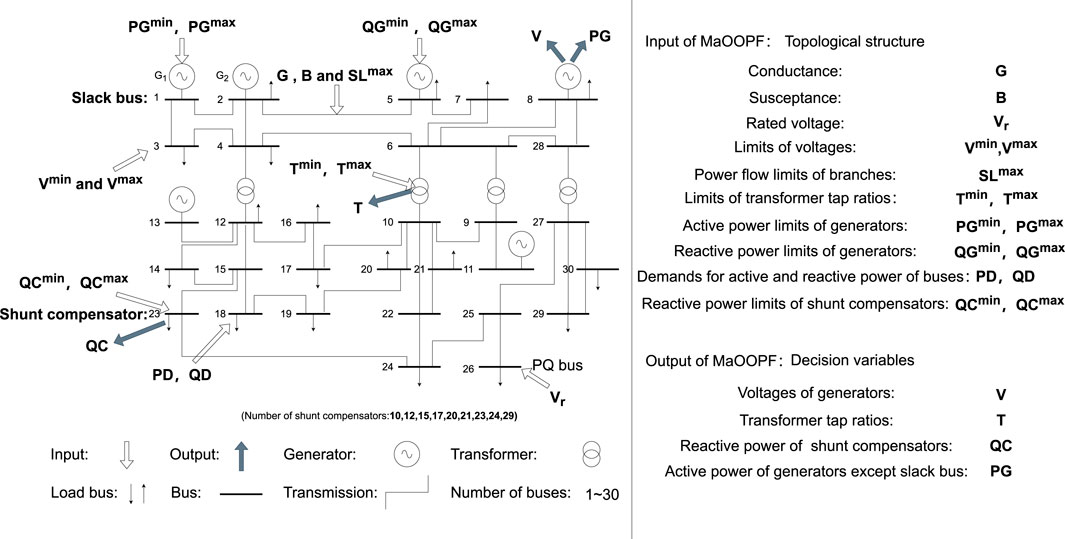
FIGURE 1. Illustration of the input and output of optimal power flow with respect to the IEEE 30-bus system.

2.1 Constrained many-objective optimization problems

In general, a problem involving four or more objectives and subject to a set of constraints is referred to as a constrained many-objective optimization problem, which can be mathematically represented using the following definition:

$\begin{array}{cc}\hfill \text{minimize\hspace{0.17em}}& \mathit{f}\left(\mathit{x}\right)=\left(f_1\left(\mathit{x}\right),f_2\left(\mathit{x}\right),\dots ,f_m\left(\mathit{x}\right)\right)\hfill \\ \hfill \text{\hspace{0.17em}subject\hspace{0.17em}to\hspace{0.17em}}& \mathit{h}\left(\mathit{x}\right)=\left(h_1\left(\mathit{x}\right),\dots ,h_p\left(\mathit{x}\right)\right)=\mathbf{0}\hfill \\ \hfill & \mathit{g}\left(\mathit{x}\right)=\left(g_1\left(\mathit{x}\right),\dots ,g_q\left(\mathit{x}\right)\right)\le \mathbf{0}\hfill \\ \hfill \text{\hspace{0.17em}where\hspace{0.17em}}& \mathit{x}=\left(x_1,x_2,\dots ,x_d\right)\in \mathbf{X}\hfill \\ \hfill & \mathbf{X}=\left\{\mathit{x}\mid \mathit{l}\le \mathit{x}\le \mathit{u}\right\}\hfill \\ \hfill & \mathit{l}=\left(l_1,l_2,\dots ,l_d\right),\mathit{u}=\left(u_1,u_2,\dots ,u_d\right)\hfill \end{array},(1)$

where f(x) are m ≥ 4 objectives to be optimized simultaneously, h(x) are p equality constraints, and g(x) are q inequality constraints. Besides, $\mathit{x}=\left(x_1,x_2,\dots ,x_d\right)$ denotes a solution consisting of d decision variables in the decision space X.

A solution in X that satisfies all the p + q constraints is referred to as a feasible solution, otherwise, it is considered an infeasible solution. A solution that is not Pareto dominated by any other solutions in X is referred to as a global optimal solution, where y dominates x indicates that f_i(y) ≤ f_i(x) for all i = 1, …, m and f_j(y) < f_j(x) for at least one j = 1, …, m. Note that only minimization problems are considered for consistency. The goal of solving a constrained many-objective optimization problem is to find a set of feasible and global optimal solutions, which spread evenly in the high-dimensional objective space. That is, the obtained solution set should be of good convergence, diversity, and feasibility.

2.2 Mathematical definition of MaOOPF

The core of optimal power flow is to ensure the balance between power outputs and demands, which are represented by the following power balance equations (Li et al., 2021):

$\begin{array}{cc}\hfill P{G}_i=& P{D}_i+V_i\sum _{j=1}^{nb}{V}_j\left(G_k\cos {\theta }_{i\to j}+B_k\sin {\theta }_{ij}\right)=0,\hfill \\ \hfill & i=1,\dots ,nb,k=1,\dots ,nl\hfill \\ \hfill Q{G}_i=& Q{D}_i+V_i\sum _{j=1}^{nb}{V}_j\left(G_k\cos {\theta }_{ij}+B_k\sin {\theta }_{ij}\right)=0,\hfill \\ \hfill & i=1,\dots ,nb,k=1,\dots ,nl\hfill \\ \hfill T_t=& V_i{V}_j,t=1,\dots ,nt,i,j\text{\hspace{0.17em}are\hspace{0.17em}the\hspace{0.17em}buses\hspace{0.17em}}\hfill \\ \hfill & \text{connected\hspace{0.17em}to\hspace{0.17em}transformer\hspace{0.17em}}t\hfill \\ \hfill Q{C}_c=& V_c^2{B}_c,c=1,\dots ,nc\hfill \end{array},(2)$

where PG_i and QG_i denote the active power and reactive power outputs of the generator at bus i, respectively, PD_i and QD_i denote the active power and reactive power demands of bus i, G_k and B_k denote the conductance and susceptance of the kth branch between bus i and bus j, respectively, θ_ij denotes the voltage phase angle difference between the starting bus i and the ending bus j of a branch, T_t denotes the transformer tap ratio of transformer t, and QC_c denotes the reactive power of shunt compensator c. Besides, nb is the number of buses, nl is the number of branches, nt is the number of transformers, and nc is the number of shunt compensators.

While some constrained multi-objective optimization models directly involve the above equality constraints to be handled by optimizers (Kumar et al., 2021), they are difficult to be satisfied by metaheuristics using stochastic search paradigms. Therefore, the Newton-Ralph method based power flow calculation provided by Matpower (Zimmerman et al., 2010) is employed to satisfy these equality constraints, and thus only inequality constraints should be handled by metaheuristics. The input of power flow calculation consists of some topological structure parameters (i.e., conductance G, susceptance B, voltage limits V^min, V^max, power limits PG^min, PG^max, and power demands PD, QD) and decision variables (i.e., voltages of generators V_G, transformer tap ratios T, reactive power of shunt compensators QC, and active power of generators PG_1,…,ng−1). The output of power flow calculation consists of state variables used in objective and constraint calculation, including voltages of buses V, active power of slack bus PG_ng, reactive power of generators QG, phase angles θ, and power flow of branches SL.

Afterwards, five objectives and a series of constraints can be calculated accordingly (Zhang et al., 2019). The first objective f₁ minimizes the total fuel cost, which is defined as

$f_1=TFC=\sum _{i=1}^{ng}\left(a_i+b_{i}P{G}_i+c_{i}P{G}_i^2\right),(3)$

where ng is the number of generators, PG_i is the active power output of the ith generator, and a_i, b_i, c_i are fixed fuel cost coefficients of the ith generator. The second objective f₂ minimizes the total emission, which is defined as

$f_2=TE=\sum _{i=1}^{ng}{\alpha }_i+{\beta }_{i}P{G}_i+{\gamma }_{i}P{G}_i^2+{\varrho }_i{e}^{\left({\lambda }_{i}P{G}_i\right)},(4)$

where α_i, β_i, γ_i, ϱ_i, λ_i represent fixed emission coefficients of the ith generator. The third objective f₃ minimizes the active power loss, which is defined as

$f_3=APL=\sum _{k=1}^{nl}\left(G_k\left(V_i^2+V_j^2-2V_i{V}_j\cos {\theta }_{ij}\right)\right),(5)$

where nl is the number of branches, G_k is the conductance of the kth branch, V_i, V_j are the voltages of two buses connected to the ith branch, and θ_ij is the voltage phase angle difference between the two buses. The fourth objective f₄ minimizes the voltage magnitude deviation, which is defined as

$f_4=VMD=\sum _{i=1}^{npq}\left|\left(V_i-V_r\right)\right|,(6)$

where npq is the number of PQ buses, and V_r is the rated voltage of 1.0 per unit. The last objective f₅ minimizes the voltage stability index, which is defined as

$f_5=VSI=\underset{j=1,\dots ,npq}{\max }\left(L_j\right),(7)$

where the L-index of the jth PQ bus is calculated by

$L_j=\left|1-\sum _{i=1}^{ng}{F}_{ji}\frac{V_i}{V_j}\right|,(8)$

and Jacobian matrix F is obtained using the Y bus matrix (Khunkitti et al., 2022).

In addition to the five objectives, a series of inequality constraints need to be satisfied, which are defined based on the upper and lower bounds of the corresponding variables. The generator constraints include

$\begin{array}{cc}\hfill P{G}_{ng}^{\mathit{min}}& \le P{G}_{ng}\hfill \\ \hfill P{G}_{ng}& \le P{G}_{ng}^{\mathit{max}}\hfill \\ \hfill Q{G}_i^{\mathit{min}}& \le Q{G}_i\hfill \\ \hfill Q{G}_i& \le Q{G}_i^{\mathit{max}},i=1,\dots ,ng\hfill \end{array},(9)$

where PG_ng is the active power of slack bus and QG_i is the reactive power of the generator at bus i. Besides, the security constraints include

$\begin{array}{cc}\hfill V_i^{\min }& \le V_i\hfill \\ \hfill V_i& \le V_i^{\max },i=1,\dots ,npq\hfill \\ \hfill S{L}_k& \le S{L}_{\mathit{k}}^{\max },k=1,\dots ,nl\hfill \end{array},(10)$

where V_i is the voltage at the PQ bus i and SL_k is the power flow of the kth branch.

With the above decision variables, objectives, and constraints, the MaOOPF problem considered in this work can be mathematically written as

$\begin{array}{cc}\hfill \text{minimize\hspace{0.17em}}& \mathit{f}\left(\mathit{x}\right)=\left(f_1\left(\mathit{x}\right),f_2\left(\mathit{x}\right),\dots ,f_5\left(\mathit{x}\right)\right)\hfill \\ \hfill \text{\hspace{0.17em}subject\hspace{0.17em}to\hspace{0.17em}}& \mathit{g}\left(\mathit{x}\right)=\left(g_1\left(\mathit{x}\right),\dots ,g_q\left(\mathit{x}\right)\right)\le \mathbf{0}\hfill \\ \hfill \text{\hspace{0.17em}where\hspace{0.17em}}& \mathit{x}=\left(P{G}_1,\dots ,P{G}_{ng-1},V_1,\dots ,V_{ng},T_1,\dots ,T_{nt},\right.\hfill \\ \hfill & \left.Q{C}_1,\dots ,Q{C}_{nc}\right)\in \mathbf{X}\hfill \\ \hfill & \mathbf{X}=\left\{\mathit{x}\mid \mathit{l}\le \mathit{x}\le \mathit{u}\right\}\hfill \\ \hfill & \mathit{l}=\left(P{G}_1^{\mathit{min}},\dots ,P{G}_{ng-1}^{\mathit{min}},0.94,\dots ,0.94_{ng},\right.\hfill \\ \hfill & \left.0.9,\dots ,0.9_{nt},0,\dots ,0_{nc}\right)\hfill \\ \hfill & \mathit{u}=\left(P{G}_1^{\mathit{max}},\dots ,P{G}_{ng-1}^{\mathit{max}},1.06,\dots ,1.06_{ng},\right.\hfill \\ \hfill & \left.1.1,\dots ,1.1_{nt},5,\dots ,5_{nc}\right)\hfill \end{array}.(11)$

This optimization model includes d = 2ng − 1 + nt + nc continuous decision variables with different ranges, five objectives, and q = 2 + 2ng + 2npq + nl inequality constraints, which pose challenges to existing optimizers. Therefore, a constrained many-objective co-evolutionary algorithm is customized in the next section.

3 The proposed algorithm

The proposed algorithm, termed three-population based constrained many-objective co-evolutionary algorithm (TPCMaO), evolves three populations with different search behaviors. In this section, we first give the general framework of the proposed algorithm. Then, we elaborate on the key components of the proposed algorithm, i.e., the selection strategies for the three populations.

3.1 General framework of TPCMaO

To date, co-evolutionary algorithms have shown their effectiveness in solving complex constrained optimization problems in many works (Li et al., 2019b; Tian et al., 2021; Qiao et al., 2022a; Sun et al., 2023). These algorithms often co-evolve multiple populations, where one population is used to solve the original problem and the other populations are used to solve helper problems. However, as discussed in (Zhang et al., 2023), the effectiveness of existing co-evolutionary algorithms is prone to be affected, since they cannot always maintain the relatedness between the helper problem and the original problem. Thus, to solve the challenging MaOOPF problems, in this paper, we propose a three-population based co-evolutionary many-objective evolutionary algorithm TPCMaO. While TPCMaO co-evolves two populations to solve the original problem and an unconstrained helper problem that are not highly related, it also evolves one population to solve a constraint-relaxed helper problem, which aims to enable the original and helper problems to maintain a good relatedness.

Figure 2 depicts the general framework of the proposed TPCMaO. For the three co-evolved populations, P1, P2, and P3 are used to solve the original constrained problem f_original, unconstrained helper problem f_helper1, and constraint-relaxed helper problem f_helper2, respectively. They adopt the same mating selection strategy to obtain parent solutions and the same offspring reproduction operator to generate offspring solutions, but they differ with each other in obtaining the combined populations and performing environmental selection.

FIGURE 2

FIGURE 2. The general framework of TPCMaO.

Algorithm 1.Procedure of the proposed TPCMaO.

Input: N (population size), FE_max (maximum number of function evaluations)

Output: P (final population)

1:  [P1, P2, P3] ← Randomly generate N solutions to initialize each population;

2:  Evaluate P1, P2, and P3 by f_original, f_helper1, and f_helper2, respectively;

3:  FE = 3N;

4:  while FE ≤ FE_max do

5:   [S1, S2, S3] ← Select N solutions from P1, P2, and P3 by the binary tournament selection method, respectively;

6:   O1 ← Generate N/2 offspring solutions based on S1 by genetic operators;

7:   O2 ← Generate N/2 offspring solutions based on S2 by genetic operators;

8:   O3 ← Generate N offspring solutions based on S3 by genetic operators;

9:   FR ← Calculate the ratio of feasible solutions in P2 ∪ O2;

10:   if FR > 0.5 then

11:    H1 ← P1 ∪ O1 ∪ P2 ∪ O2;

12:   else

13:    H1 ← P1 ∪ O1 ∪ O2;

14:   end if

15:   H2 ← P2 ∪ O2 ∪ O1;

16:   H3 ← P3 ∪ O3;

17:   Evaluate H1, H2, and H3 by f_original, f_helper1, and f_helper2, respectively;

18:   FE = FE + 2N;

19:   P1 ← Select N solutions from H1 based on constraint dominance principle;

20:   P2 ← Select N solutions from H2 based on unconstraint dominance principle;

21:   P3 ← Select N solutions from H3 based on ϵ-constraint dominance principle;

22:  end while

23:  return N optimal solutions in P1 ∪ P3;

Algorithm 1 presents the detailed procedure of TPCMaO. To begin with, TPCMaO generates three initial populations with N solutions in a random manner. After the three populations are evaluated by f_original, f_helper1, and f_helper2, respectively, TPCMaO enters the main loop until termination. At each generation, TPCMaO first uses the binary tournament selection method to obtain three parent populations, namely, S1, S2, and S3. Based on the three parent populations, three offspring populations O1, O2, and O3 are then generated using simulated binary crossover operator [Deb and Agrawal (1995)] and polynomial mutation operator [Deb and Goyal (1996)]. Next, TPCMaO combines parent and offspring solutions to obtain three hybrid populations, namely, H1, H2, and H3. Specifically, the combination of H1 is determined by the ratio of feasible solutions in P2 ∪ O2, H2 consists of the solutions in P2, O2, and O1, and H3 is obtained by combining P3 and O3. Afterwards, TPCMaO evaluates the solutions in H1, H2, and H3 by f_original, f_helper1, and f_helper2, respectively. Finally, TPCMaO selects the populations for the next-generation from the combined populations by three different environmental selection strategies. That is, the problems f_original, f_helper1, and f_helper2 are totally the same except for the consideration of constraints. More specifically, the original problem f_original is defined in Eq. 1 without equality constraints, the unconstrained helper problem f_helper1 is defined as

$\begin{array}{cc}\hfill \text{minimize\hspace{0.17em}}& \mathit{f}\left(\mathit{x}\right)=\left(f_1\left(\mathit{x}\right),f_2\left(\mathit{x}\right),\dots ,f_m\left(\mathit{x}\right)\right)\hfill \\ \hfill \text{\hspace{0.17em}where\hspace{0.17em}}& \mathit{x}=\left(x_1,x_2,\dots ,x_d\right)\in \mathbf{X}\hfill \\ \hfill & \mathbf{X}=\left\{\mathit{x}\mid \mathit{l}\le \mathit{x}\le \mathit{u}\right\}\hfill \\ \hfill & \mathit{l}=\left(l_1,l_2,\dots ,l_d\right),\mathit{u}=\left(u_1,u_2,\dots ,u_d\right)\hfill \end{array},(12)$

and the constraint-relaxed helper problem f_helper2 is defined as

$\begin{array}{cc}\hfill \text{minimize\hspace{0.17em}}& \mathit{f}\left(\mathit{x}\right)=\left(f_1\left(\mathit{x}\right),f_2\left(\mathit{x}\right),\dots ,f_m\left(\mathit{x}\right)\right)\hfill \\ \hfill \text{\hspace{0.17em}subject\hspace{0.17em}to\hspace{0.17em}}& \mathit{g}\left(\mathit{x}\right)=\left(g_1\left(\mathit{x}\right),\dots ,g_q\left(\mathit{x}\right)\right)\le ϵ\hfill \\ \hfill \text{\hspace{0.17em}where\hspace{0.17em}}& \mathit{x}=\left(x_1,x_2,\dots ,x_d\right)\in \mathbf{X}\hfill \\ \hfill & \mathbf{X}=\left\{\mathit{x}\mid \mathit{l}\le \mathit{x}\le \mathit{u}\right\}\hfill \\ \hfill & \mathit{l}=\left(l_1,l_2,\dots ,l_d\right),\mathit{u}=\left(u_1,u_2,\dots ,u_d\right)\hfill \end{array},(13)$

where ϵ is set according to (Fan et al., 2019).

When the number of function evaluations FE reaches the maximum number of function evaluations FE_max, TPCMaO terminates and selects N optimal solutions from P1 ∪ P3 as the final results. In the following, we introduce the three environmental selection strategies, which are the key components of the proposed algorithm.

3.2 Environmental selection strategies of TPCMaO

In the proposed algorithm, solutions in population P1 are evaluated by f_original considering all constraints, which enables the algorithm to pay efforts to constraint satisfaction. By contrast, solutions in population P2 are evaluated by f_helper1 without considering any constraint, which enables solutions to cross through infeasible regions and converge to the Pareto front quickly. Besides, with the purpose of finding more feasible regions, solutions in population P3 are evaluated by f_helper2, which regards solutions in constraint-relaxed boundaries as feasible solutions. The above diversified purposes drive the proposed TPCMaO to update populations P1, P2, and P3 via different environmental selection strategies. More specifically, the evolution of the three populations is based on the selection strategy of SPEA2 with shift based density estimation (Li et al., 2014), which shows high effectiveness in many-objective optimization and is flexible to be embedded in other algorithms (Tian et al., 2020). On the other hand, the difference in the selection strategies for the three populations lies in the dominance relations, where the constraint dominance principle, unconstraint dominance principle, and ϵ-constraint dominance principle are used for populations P1, P2, and P3, respectively.

In the case that population P1 is evolved for constraint satisfaction, solutions that survive for the next-generation should be those with smaller constraint violation values and better objective values. For this aim, TPCMaO first calculates the ratio of feasible solutions in P2 ∪ O2. If the ratio of feasible solutions FR is larger than 0.5, which means that the union of P2 and O2 potentially contains high-quality feasible solutions beneficial to the evolution of population P1, TPCMaO combines all solutions in P1, O1, P2, and O2 to obtain H1. Otherwise, TPCMaO combines all solutions in P1, O1, and O2 to obtain H1. Then, TPCMaO calculates the fitness value of each solution in H1 by the method in (Li et al., 2014) and selects N solutions with the smallest fitness values to form the new population P1. It is worth noting that, in the process of calculating fitness values, the dominance relations of solutions are determined by the constraint dominance principle (Deb et al., 2002).

Considering that population P2 is evolved for driving solutions to cross through infeasible regions and converge to the Pareto front quickly, solutions that survive for the next-generation should be those with better objective values. Thus, TPCMaO only combines O1 with P2 and O2, since offspring solutions in O1 are possibly of better convergence than parent solutions in P1. Then, TPCMaO calculates the fitness value of each solution in H2 by the method in (Li et al., 2014) and selects N solutions with the smallest fitness values to form the new population P2. It is worth noting that, in the process of calculating fitness values, the dominance relations of solutions are determined by non-dominated sorting that does not consider any constraint (Zhang et al., 2015a).

From Figure 2; Algorithm 1, it can be observed that population P3 is evolved independently, which is different from populations P1 and P2 that interact with each other frequently. That is, when offspring population O3 is generated, it is directly combined with parent population P3 to obtain hybrid population H3. Then, TPCMaO calculates the fitness value of each solution in H3 by the method in (Li et al., 2014) and selects N solutions with the smallest fitness values to form the new population P3. It is worth noting that, in the process of calculating fitness values, the dominance relations of solutions are determined by the ϵ-constraint dominance principle (Takahama and Sakai, 2006; Ji et al., 2022), which is different from the methods used for populations P1 and P2. Specifically, given two solutions x and y, if the constraint violation values of them are both smaller than ϵ, the solution with better objective values dominates the other one. Otherwise, the solution with a smaller constraint violation value dominates the other one. In the proposed algorithm, the value of ϵ is updated by the method suggested in (Fan et al., 2019).

4 Experimental studies

In this section, the proposed algorithm is first compared with state-of-the-art algorithms on challenging constrained many-objective benchmark problems. Then, the proposed algorithm is verified on MaOOPF problems. The experiments are conducted on PlatEMO (Tian et al., 2017).

4.1 Experimental settings

Firstly, the proposed TPCMaO is compared with CCMO (Tian et al., 2021), MTCMO (Qiao et al., 2022b), DCNSGA-III (Jiao et al., 2021), TriP (Ming et al., 2022b), and CMME (Ming et al., 2022a) on the 16 ZXH-CF (Zhou et al., 2020) benchmark problems. In these test problems, the number of objectives m is set to 5, 8, and 10, and the number of decision variables d is set to 10 + m. Then, the proposed TPCMaO is compared with the five competitors on three power systems, namely, the IEEE 30-bus, IEEE 57-bus, and IEEE 118-bus systems. Table 1 presents the statistics of the three power systems, and the detailed information and related data can be found from (Zimmerman et al., 2010; Zhang et al., 2019; Premkumar et al., 2021). In the experiments, the performance on the ZXH-CF benchmark problems is assessed by IGD (Zitzler et al., 2003), and the performance on the power systems is measured by HV (While et al., 2006). Besides, we take the Wilcoxon rank sum test with a significance level of 0.05 to verify the difference between compared algorithms and the proposed TPCMaO, where the symbols +, −, and ≈ indicate that the result obtained by a compared algorithm is significantly better, significantly worse, and statistically similar to that of the proposed TPCMaO, respectively. In the following, the detailed parameter settings are given.

(1) The maximum number of function evaluations FE_max is adopted as the termination criterion, which is set to 50,000 and 80,000 for the experiments on benchmark problems and power systems, respectively.

(2) The population size N is set to 100 for each algorithm on all test instances.

(3) All the compared algorithms adopt simulated binary crossover (Deb and Agrawal, 1995) and polynomial mutation (Deb and Goyal, 1996) for offspring generation. The crossover probability is set to 1, the mutation probability is set to 1/d with d denoting the number of decision variables, and the distribution index of both crossover and mutation is set to 20.

(4) The algorithm-specific parameters in the compared algorithms are set to the same as those in their original papers, while the proposed TPCMaO does not have any algorithm-specific parameter.

TABLE 1

TABLE 1. Statistics of three power systems.

4.2 Experimental results on ZXH-CF problems

The 16 ZXH-CF benchmark problems are scalable to have any number of objectives and decision variables, posing challenges to existing algorithms in evolving towards the constrained Pareto fronts. Besides, they present difficulties by introducing convergence-hardness related constraints and diversity-hardness related constraints. More specifically, the convergence-hardness related constraints introduce infeasible barriers in approaching the optimums, and the diversity-hardness related constraints restrict the feasible optimal regions to make the benchmark problems have different shapes of Pareto fronts.

Table 2 presents the IGD results obtained by CCMO, MTCMO, DCNSGA-III, TriP, CMME, and the proposed TPCMaO on the 16 ZXH-CF problems with 5, 8, and 10 objectives. As shown in the table, TPCMaO achieves the best overall performance, obtaining 45 best results out of the 48 test instances. By contrast, CCMO, MTCMO, and DCNSGA-III only obtain one best result, respectively, while TriP and CMME do not obtain any best result. According to the Wilcoxon rank sum test results, the proposed TPCMaO outperforms CCMO, MTCMO, DCNSGA-III, TriP, and CMME on 46, 46, 45, 48, and 47 problems, respectively, which indicates that the proposed TPCMaO is significantly better than state-of-the-art algorithms in solving constrained many-objective optimization problems.

TABLE 2

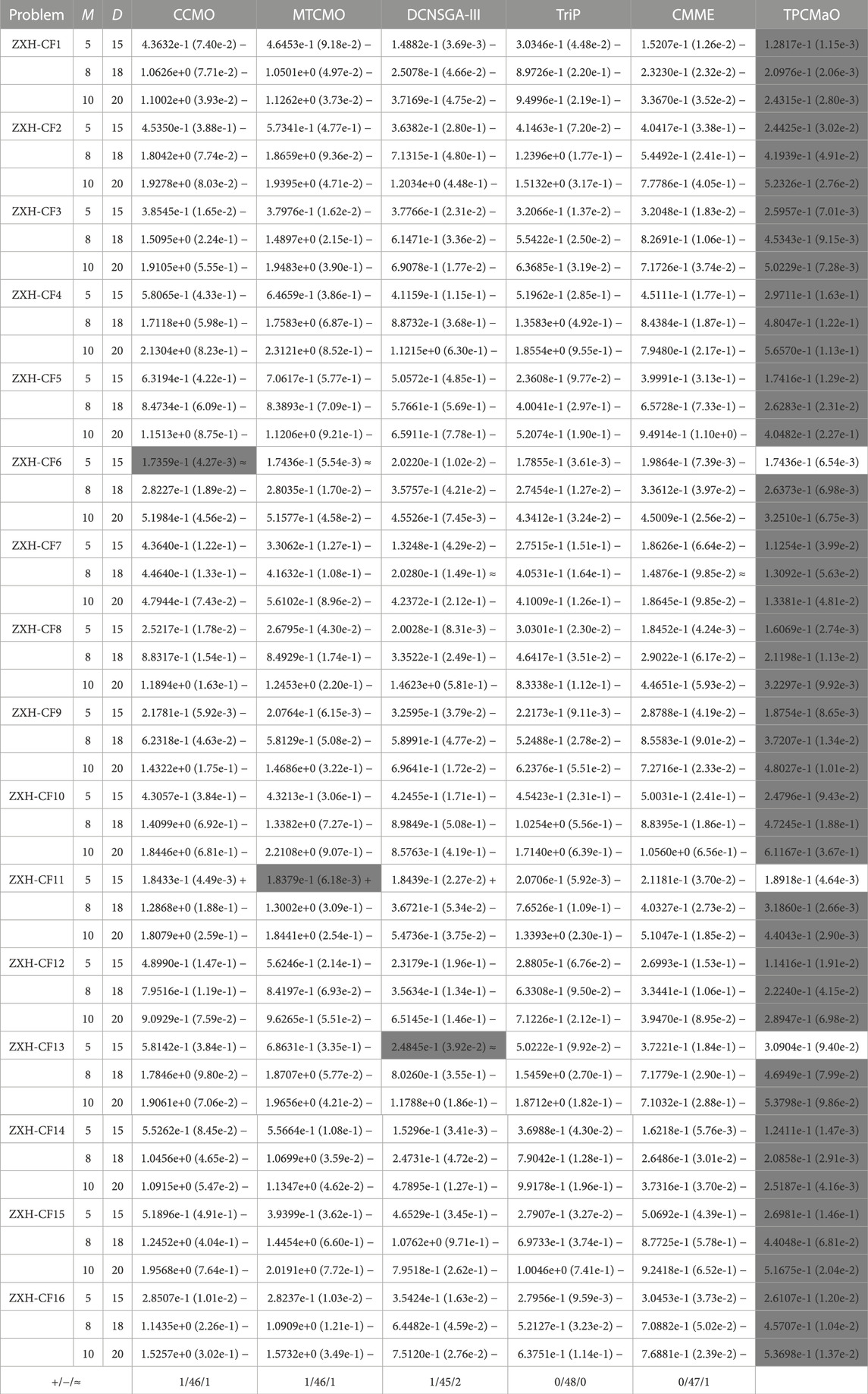
TABLE 2. IGD results obtained by CCMO, MTCMO, DCNSGA-III, TriP, CMME, and TPCMaO on the ZXH-CF benchmark problems. The best result in each row is highlighted.

For visual comparisons, Figure 3 depicts the parallel coordinates of Pareto fronts obtained by CCMO, MTCMO, DCNSGA-III, TriP, CMME, and the proposed TPCMaO on 5-objective ZXH-CF2, in the run associated with the median IGD value. It can be seen that the Pareto fronts obtained by DCNSGA-III, CMME, and the proposed TPCMaO are obviously better than those obtained by CCMO, MTCMO, and TriP in terms of both convergence and diversity. Besides, the Pareto front approximated by TPCMaO has better diversity than those obtained by DCNSGA-III and CMME. In short, the proposed TPCMaO exhibits the best performance among the six compared algorithms.

FIGURE 3

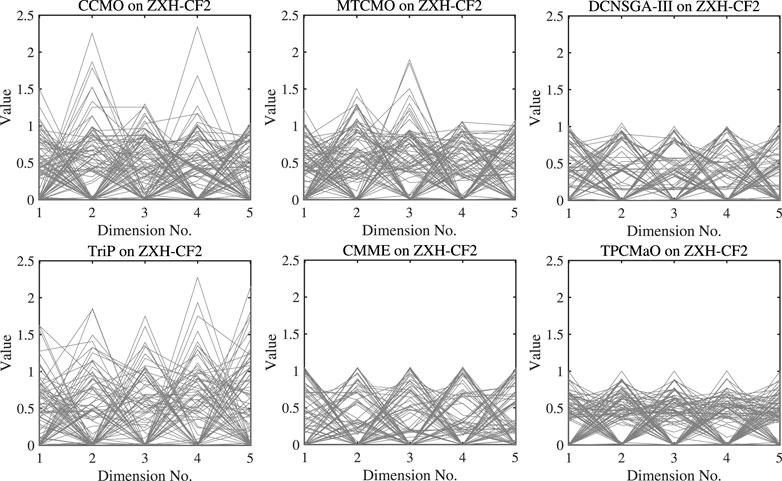
FIGURE 3. The parallel coordinates of Pareto front obtained by each algorithm on 5-objective ZXH-CF2 in the run associated with the median IGD value.

4.3 Experimental results on power systems

Table 3 presents the HV results obtained by CCMO, MTCMO, DCNSGA-III, TriP, CMME, and the proposed TPCMaO on the MaOOPF problems of the IEEE 30-bus, IEEE 57-bus, and IEEE 118-bus systems. It can be seen that TPCMaO exhibits the best overall performance, obtaining the best results on the IEEE 57-bus and IEEE 118-bus systems, followed by TriP gaining the best result on the IEEE 30-bus system. According to the Wilcoxon rank sum test results, TPCMaO is not worse than the five competitors on any test instance. By contrast, TPCMaO is significantly better than CCMO, MTCMO, DCNSGA-III, TriP, and CMME on 3, 3, 3, 2, and 3 test instances, respectively.

TABLE 3

TABLE 3. HV results obtained by CCMO, MTCMO, DCNSGA-III, TriP, CMME, and the proposed TPCMaO on the IEEE 30-bus, IEEE 57-bus, and IEEE 118-bus systems. The best result in each row is highlighted.

Figures 4–6 depict the parallel coordinates of Pareto fronts obtained by each algorithm on the IEEE 30-bus, IEEE 57-bus, and IEEE 118-bus systems. In comparison with CCMO, MTCMO, DCNSGA-III, and TriP, the Pareto fronts approximated by TPCMaO on the three instances are obviously better in terms of both convergence and diversity. Compared with CMME, TPCMaO obtains competitive results on the IEEE 30-bus and IEEE 57-bus systems and slightly worse result on the IEEE 118-bus system.

FIGURE 4

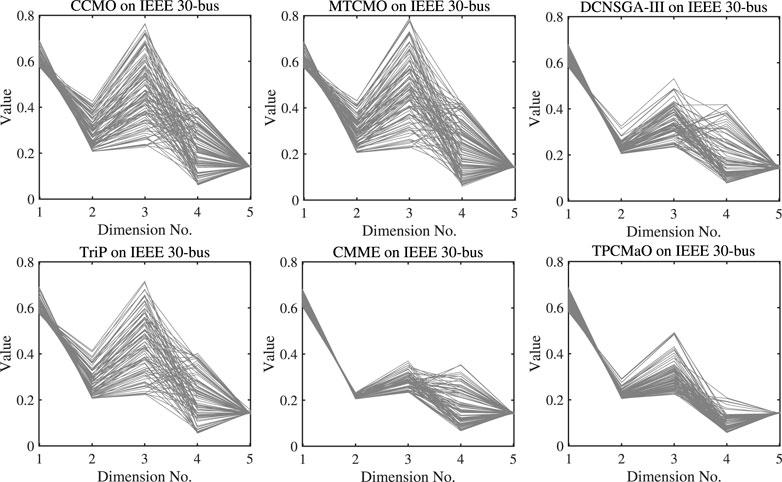
FIGURE 4. The parallel coordinates of Pareto front obtained by each algorithm on the IEEE 30-bus system in the run associated with the median HV value.

FIGURE 5

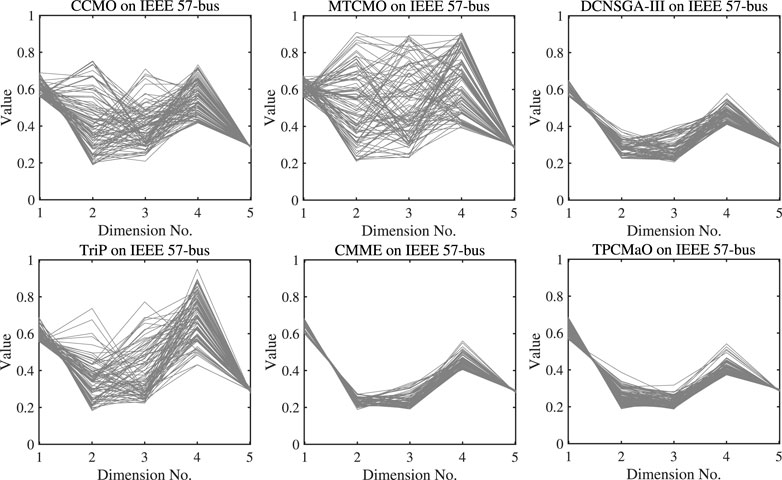
FIGURE 5. The parallel coordinates of Pareto front obtained by each algorithm on the IEEE 57-bus system in the run associated with the median HV value.

FIGURE 6

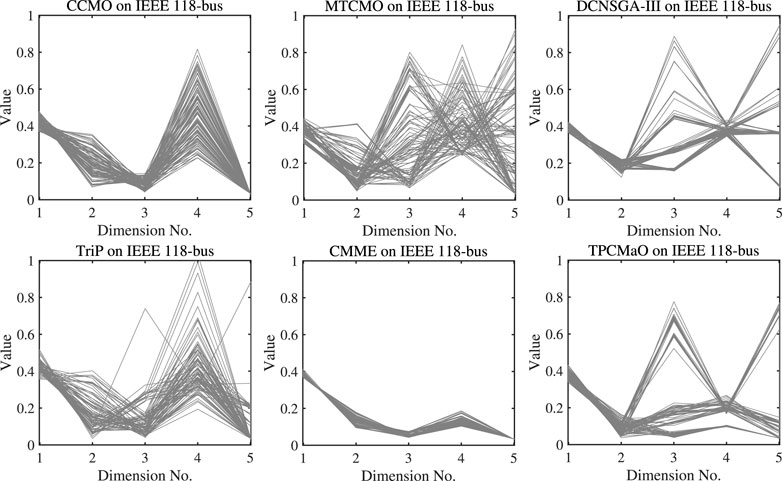
FIGURE 6. The parallel coordinates of Pareto front obtained by each algorithm on the IEEE 118-bus system in the run associated with the median HV value.

Figure 7 plots the convergence curves with median HV values obtained by TPCMaO and five compared algorithms on the three instances. On the IEEE 30-bus system, TPCMaO and TriP exhibit obviously better convergence performance than the other four algorithms. Although the convergence efficiency of TPCMaO is a bit inferior to TriP on the IEEE 30-bus system, TPCMaO achieves competitive result at the end of evolution. On the IEEE 57-bus and IEEE 118-bus systems, it can be seen that TPCMaO achieves obviously better convergence performance than the five compared algorithms. It is worth noting that, on the IEEE 118-bus system, DCNSGA-III and TriP do not obtain any feasible solutions until termination; thus, their convergence curves are unavailable.

FIGURE 7

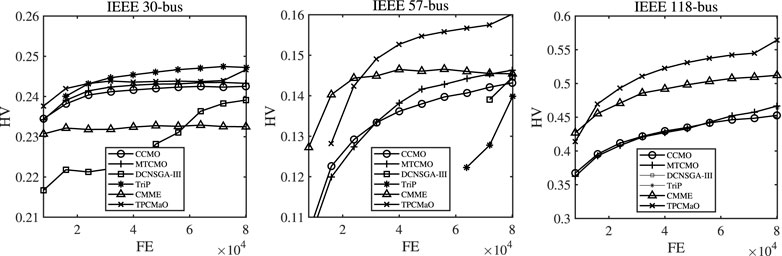
FIGURE 7. Convergence curves with the median HV values obtained by CCMO, MTCMO, DCNSGA-III, TriP, CMME, and the proposed TPCMaO on the IEEE 30-bus, IEEE 57-bus, and IEEE 118-bus systems. FE denotes the number of function evaluations.

To provide a more detailed analysis of experimental results obtained by TPCMaO and compared algorithms, Table 4 lists the result obtained by each algorithm on each objective of the IEEE 57-bus system. As shown in the table, TPCMaO obtains the best results on the objectives of TFC and APL in terms of both minimum and mean values. By contrast, MTCMO and DCNSGA-III obtain the best results on VMD and VSI, respectively, and the remaining two algorithms obtain competitive results on the objective of TE. In short, none of the six algorithms can obtain the best results on all objectives, since the five objectives have distinct difference in terms of numerical magnitude, which is prone to cause search bias. However, it can still be seen that the proposed TPCMaO obtains the best overall performance among the six algorithms. To summarize, the proposed algorithm is superior over state-of-the-art constrained many-objective evolutionary algorithms on both benchmark problems and MaOOPF problems.

TABLE 4

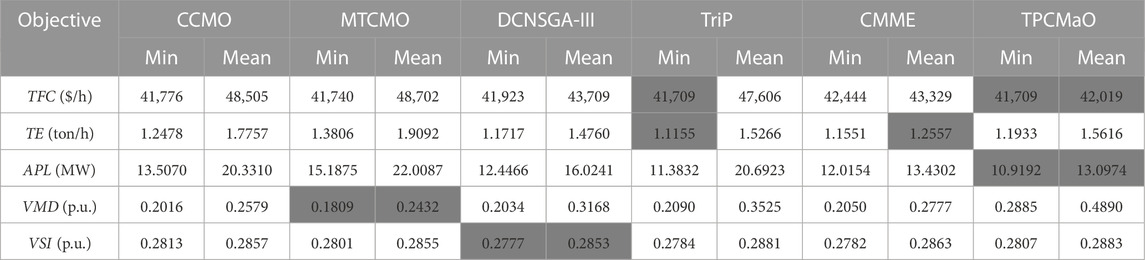
TABLE 4. Objective values obtained by CCMO, MTCMO, DCNSGA-III, TriP, CMME, and TPCMaO on the IEEE 57-bus system. The best result in each row is highlighted.

5 Conclusion

Optimal power flow with many objectives and constraints plays an important role in power systems. To address this challenging optimization task, in this paper, we have proposed a new co-evolutionary constrained many-objective evolutionary algorithm, where three populations are co-evolved with different purposes. Specifically, the first population is evolved for obtaining the Pareto front, the second population is evolved for improving the speed of convergence, and the third population is evolved for finding more feasible regions. The three populations explore different parts of the high-dimensional objective space divided by large infeasible regions, striking a good balance between convergence, diversity, and feasibility for solving constrained many-objective optimization problems.

Experimental results on both benchmark problems and MaOOPF problems reveal that the proposed algorithm achieves better overall performance than five state-of-the-art competitors. However, while the proposed algorithm obtains better results on some objectives, it also shows slightly worse performance on some other objectives, such as VMD and VSI. Thus, in the future, we prepare to design novel strategies to alleviate the search bias, which is beneficial for decision-makers to consider all objectives comprehensively. Furthermore, it is also desirable to use the proposed algorithm to conduct cascading failures in power systems (Fang et al., 2021).

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

YT: Writing–original draft. ZS: Validation, Writing–review and editing. YZ: Methodology, Writing–original draft. LZ: Investigation, Writing–review and editing. HZ: Formal Analysis, Writing–review and editing. XZ: Funding acquisition, Writing–review and editing.

Funding

The authors declare financial support was received for the research, authorship, and/or publication of this article. This work was supported in part by the National Natural Science Foundation of China (Nos 62276001, 62136008, U20A20306, U21A20512), in part by the Anhui Provincial Natural Science Foundation (No. 2308085J03), and in part by the Excellent Youth Foundation of Anhui Provincial Colleges (No. 2022AH030013).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alghamdi, A. S. (2022). Optimal power flow of renewable-integrated power systems using a Gaussian bare-bones Levy-flight firefly algorithm. Front. Energy Res. 697. doi:10.3389/fenrg.2022.921936

CrossRef Full Text | Google Scholar

Biswas, P. P., Suganthan, P. N., Mallipeddi, R., and Amaratunga, G. A. J. (2020). Multi-objective optimal power flow solutions using a constraint handling technique of evolutionary algorithms. Soft Comput. 24, 2999–3023. doi:10.1007/s00500-019-04077-1

CrossRef Full Text | Google Scholar

Chen, G., Qian, J., Zhang, Z., and Sun, Z. (2019). Applications of novel hybrid bat algorithm with constrained pareto fuzzy dominant rule on multi-objective optimal power flow problems. IEEE Access 7, 52060–52084. doi:10.1109/access.2019.2912643

CrossRef Full Text | Google Scholar

Chen, G., Yi, X., Zhang, Z., and Lei, H. (2018). Solving the multi-objective optimal power flow problem using the multi-objective firefly algorithm with a constraints-prior Pareto-domination approach. Energies 11, 3438. doi:10.3390/en11123438

CrossRef Full Text | Google Scholar

Daqaq, F., Ouassaid, M., Kamel, S., Ellaia, R., and El-Naggar, M. F. (2022). A novel chaotic flower pollination algorithm for function optimization and constrained optimal power flow considering renewable energy sources. Front. Energy Res. 10. doi:10.3389/fenrg.2022.941705

CrossRef Full Text | Google Scholar

Deb, K., and Agrawal, R. B. (1995). Simulated binary crossover for continuous search space. Complex Syst. 9, 115–148.

Google Scholar

Deb, K., and Goyal, M. (1996). A combined genetic adaptive search (GeneAS) for engineering design. Comput. Sci. Inf. 26, 30–45.

Google Scholar

Deb, K., and Jain, H. (2013). An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: solving problems with box constraints. IEEE Trans. Evol. Comput. 18, 577–601. doi:10.1109/tevc.2013.2281535

CrossRef Full Text | Google Scholar

Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 6, 182–197. doi:10.1109/4235.996017

CrossRef Full Text | Google Scholar

Fan, Z., Li, W., Cai, X., Li, H., Wei, C., Zhang, Q., et al. (2019). Push and pull search for solving constrained multi-objective optimization problems. Swarm Evol. Comput. 44, 665–679. doi:10.1016/j.swevo.2018.08.017

CrossRef Full Text | Google Scholar

Fang, J., Wu, J., Zheng, Z., and Tse, C. K. (2021). Revealing structural and functional vulnerability of power grids to cascading failures. IEEE J. Emerg. Sel. Top. Circuits Syst. 11, 133–143. doi:10.1109/jetcas.2020.3033066

CrossRef Full Text | Google Scholar

Habibollahzadeh, H., Luo, G. X., and Semlyen, A. (1989). Hydrothermal optimal power flow based on a combined linear and nonlinear programming methodology. IEEE Trans. Power Syst. 4, 530–537. doi:10.1109/59.193826

CrossRef Full Text | Google Scholar

Huang, J., Wu, Q. H., Li, Z. G., and Zheng, J. H. (2018). “Multi-objective optimal power flow problem using DE-NSGA-III algorithm,” in Proceedings of the 2018 IEEE Innovative Smart Grid Technologies-Asia, Singapore, May 2018 (IEEE), 693–698.

CrossRef Full Text | Google Scholar

Ji, J.-Y., Zeng, S., and Wong, M. L. (2022). ϵ-constrained multiobjective differential evolution using linear population size expansion. Inf. Sci. 609, 445–464. doi:10.1016/j.ins.2022.07.108

CrossRef Full Text | Google Scholar

Jiao, R., Zeng, S., Li, C., Yang, S., and Ong, Y.-S. (2021). Handling constrained many-objective optimization problems via problem transformation. IEEE Trans. Cybern. 51, 4834–4847. doi:10.1109/tcyb.2020.3031642

PubMed Abstract | CrossRef Full Text | Google Scholar

Khunkitti, S., Siritaratiwat, A., and Premrudeepreechacharn, S. (2022). A many-objective marine predators algorithm for solving many-objective optimal power flow problem. Appl. Sci. 12, 11829. doi:10.3390/app122211829

CrossRef Full Text | Google Scholar

Kumar, A., Wu, G., Ali, M., Luo, Q., Mallipeddi, R., Suganthan, P., et al. (2021). A benchmark-suite of real-world constrained multi-objective optimization problems and some baseline results. Swarm Evol. Comput. 67, 100961. doi:10.1016/j.swevo.2021.100961

CrossRef Full Text | Google Scholar

Li, B., Li, J., Tang, K., and Yao, X. (2015). Many-objective evolutionary algorithms: A survey. ACM Comput. Surv. 48, 1–35. doi:10.1145/2792984

CrossRef Full Text | Google Scholar

Li, G., Lu, W., Bian, J., Qin, F., Wu, J., Song, J., et al. (2019a). Development and validation of a CIMP-associated prognostic model for hepatocellular carcinoma. Front. Energy Res. 7, 128–141. doi:10.1016/j.ebiom.2019.08.064

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, K., Chen, R., Fu, G., and Yao, X. (2019b). Two-archive evolutionary algorithm for constrained multiobjective optimization. IEEE Trans. Evol. Comput. 23, 303–315. doi:10.1109/tevc.2018.2855411

CrossRef Full Text | Google Scholar

Li, M., Yang, S., and Liu, X. (2014). Shift-based density estimation for Pareto-based algorithms in many-objective optimization. IEEE Trans. Evol. Comput. 18, 348–365. doi:10.1109/tevc.2013.2262178

CrossRef Full Text | Google Scholar

Li, S., Gong, W., Hu, C., Yan, X., Wang, L., and Gu, Q. (2021). Adaptive constraint differential evolution for optimal power flow. Energy 235, 121362. doi:10.1016/j.energy.2021.121362

CrossRef Full Text | Google Scholar

Li, S., Gong, W., Wang, L., Yan, X., and Hu, C. (2020). Optimal power flow by means of improved adaptive differential evolution. Energy 198, 117314. doi:10.1016/j.energy.2020.117314

CrossRef Full Text | Google Scholar

Li, Y., and Li, Y. (2018). Two-step many-objective optimal power flow based on knee point-driven evolutionary algorithm. Processes 6, 250. doi:10.3390/pr6120250

CrossRef Full Text | Google Scholar

Liang, J., Ban, X., Yu, K., Qu, B., Qiao, K., Yue, C., et al. (2023). A survey on evolutionary constrained multi-objective optimization. IEEE Trans. Evol. Comput. 27, 201–221. doi:10.1109/tevc.2022.3155533

CrossRef Full Text | Google Scholar

Ming, F., Gong, W., Wang, L., and Lu, C. (2022b). A tri-population based co-evolutionary framework for constrained multi-objective optimization problems. Swarm Evol. Comput. 70, 101055. doi:10.1016/j.swevo.2022.101055

CrossRef Full Text | Google Scholar

Ming, F., Gong, W., Wang, L., and Gao, L. (2022a). A constrained many-objective optimization evolutionary algorithm with enhanced mating and environmental selections. IEEE Trans. Cybern. 53, 4934–4946. doi:10.1109/tcyb.2022.3151793

CrossRef Full Text | Google Scholar

Momoh, J. A., and Zhu, J. Z. (1999). Improved interior point method for OPF problems. IEEE Trans. Power Syst. 14, 1114–1120. doi:10.1109/59.780938

CrossRef Full Text | Google Scholar

Mota-Palomino, R., and Quintana, V. H. (1986). Sparse reactive power scheduling by a penalty function-linear programming technique. IEEE Trans. Power Syst. 1, 31–39. doi:10.1109/tpwrs.1986.4334951

CrossRef Full Text | Google Scholar

Premkumar, M., Jangir, P., Sowmya, R., and Elavarasan, R. M. (2021). Many-objective gradient-based optimizer to solve optimal power flow problems: analysis and validations. Eng. Appl. Artif. Intell. 106, 104479. doi:10.1016/j.engappai.2021.104479

CrossRef Full Text | Google Scholar

Qian, J., and Chen, G. (2022). Improved multi-goal particle swarm optimization algorithm and multi-output BP network for optimal operation of power system. IAENG Int. J. Appl. Math. 52.

Google Scholar

Qiao, K., Yu, K., Qu, B., Liang, J., Song, H., and Yue, C. (2022a). An evolutionary multitasking optimization framework for constrained multiobjective optimization problems. IEEE Trans. Evol. Comput. 26, 263–277. doi:10.1109/tevc.2022.3145582

CrossRef Full Text | Google Scholar

Qiao, K., Yu, K., Qu, B., Liang, J., Song, H., Yue, C., et al. (2022b). Dynamic auxiliary task-based evolutionary multitasking for constrained multi-objective optimization. IEEE Trans. Evol. Comput. 27, 642–656. doi:10.1109/tevc.2022.3175065

CrossRef Full Text | Google Scholar

Shaheen, A. M., El-Sehiemy, R. A., Hasanien, H. M., and Ginidi, A. R. (2022). An improved heap optimization algorithm for efficient energy management based optimal power flow model. Energy 250, 123795. doi:10.1016/j.energy.2022.123795

CrossRef Full Text | Google Scholar

Sun, Z., Ren, H., Yen, G. G., Chen, T., Wu, J., An, H., et al. (2023). An evolutionary algorithm with constraint relaxation strategy for highly constrained multiobjective optimization. IEEE Trans. Cybern. 53, 3190–3204. doi:10.1109/tcyb.2022.3151974

PubMed Abstract | CrossRef Full Text | Google Scholar

Takahama, T., and Sakai, S. (2006). “Constrained optimization by the ϵ constrained differential evolution with gradient-based mutation and feasible elites,” in Proceedings of the 2006 IEEE Congress on Evolutionary Computation, Vancouver, BC, Canada, July 2006.

Google Scholar

Tian, Y., Cheng, R., Zhang, X., Cheng, F., and Jin, Y. (2018). An indicator based multi-objective evolutionary algorithm with reference point adaptation for better versatility. IEEE Trans. Evol. Comput. 22, 609–622. doi:10.1109/tevc.2017.2749619

CrossRef Full Text | Google Scholar

Tian, Y., Cheng, R., Zhang, X., and Jin, Y. (2017). PlatEMO: A matlab platform for evolutionary multi-objective optimization [educational forum]. IEEE Comput. Intell. Mag. 12, 73–87. doi:10.1109/mci.2017.2742868

CrossRef Full Text | Google Scholar

Tian, Y., Cheng, R., Zhang, X., Su, Y., and Jin, Y. (2019a). A strengthened dominance relation considering convergence and diversity for evolutionary many-objective optimization. IEEE Trans. Evol. Comput. 23, 331–345. doi:10.1109/tevc.2018.2866854

CrossRef Full Text | Google Scholar

Tian, Y., Yang, S., Zhang, L., Duan, F., and Zhang, X. (2019b). A surrogate-assisted multiobjective evolutionary algorithm for large-scale task-oriented pattern mining. IEEE Trans. Emerg. Top. Comput. Intell. 3, 106–116. doi:10.1109/tetci.2018.2872055

CrossRef Full Text | Google Scholar

Tian, Y., Zhang, T., Xiao, J., Zhang, X., and Jin, Y. (2021). A coevolutionary framework for constrained multiobjective optimization problems. IEEE Trans. Evol. Comput. 25, 102–116. doi:10.1109/tevc.2020.3004012

CrossRef Full Text | Google Scholar

Tian, Y., Zhang, X., Cheng, R., and Jin, Y. (2016). “A multi-objective evolutionary algorithm based on an enhanced inverted generational distance metric,” in Proceedings of the 2016 IEEE Congress on Evolutionary Computation, Vancouver, BC, Canada, July 2016, 5222–5229.

CrossRef Full Text | Google Scholar

Tian, Y., Zhang, Y., Su, Y., Zhang, X., Tan, K. C., and Jin, Y. (2022). Balancing objective optimization and constraint satisfaction in constrained evolutionary multiobjective optimization. IEEE Trans. Cybern. 52, 9559–9572. doi:10.1109/tcyb.2020.3021138

PubMed Abstract | CrossRef Full Text | Google Scholar

Tian, Y., Zheng, X., Zhang, X., and Jin, Y. (2020). Efficient large-scale multiobjective optimization based on a competitive swarm optimizer. IEEE Trans. Cybern. 50, 3696–3708. doi:10.1109/tcyb.2019.2906383

PubMed Abstract | CrossRef Full Text | Google Scholar

Warid, W., Hizam, H., Mariun, N., and Wahab, N. I. A. (2018). A novel quasi-oppositional modified Jaya algorithm for multi-objective optimal power flow solution. Appl. Soft Comput. 65, 360–373. doi:10.1016/j.asoc.2018.01.039

CrossRef Full Text | Google Scholar

While, L., Hingston, P., Barone, L., and Huband, S. (2006). A faster algorithm for calculating hypervolume. IEEE Trans. Evol. Comput. 10, 29–38. doi:10.1109/tevc.2005.851275

CrossRef Full Text | Google Scholar

Xia, Z., Liu, Y., Lu, J., Cao, J., and Rutkowski, L. (2020). Penalty method for constrained distributed quaternion-variable optimization. IEEE Trans. Cybern. 51, 5631–5636. doi:10.1109/tcyb.2020.3031687

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiang, X., Tian, Y., Zhang, X., Xiao, J., and Jin, Y. (2022). A pairwise proximity learning-based ant colony algorithm for dynamic vehicle routing problems. IEEE Trans. Intelligent Transp. Syst. 23, 5275–5286. doi:10.1109/tits.2021.3052834

CrossRef Full Text | Google Scholar

Yang, S., Tian, Y., He, C., Zhang, X., Tan, K. C., and Jin, Y. (2022). A gradient guided evolutionary approach to training deep neural networks. IEEE Trans. Neural Netw. Learn. Syst. 33, 4861–4875. doi:10.1109/tnnls.2021.3061630

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, J., Tang, Q., Li, P., Deng, D., and Chen, Y. (2016). A modified MOEA/D approach to the solution of multi-objective optimal power flow problem. Appl. Soft Comput. 47, 494–514. doi:10.1016/j.asoc.2016.06.022

CrossRef Full Text | Google Scholar

Zhang, J., Wang, S., Tang, Q., Zhou, Y., and Zeng, T. (2019). An improved NSGA-III integrating adaptive elimination strategy to solution of many-objective optimal power flow problems. Energy 172, 945–957. doi:10.1016/j.energy.2019.02.009

CrossRef Full Text | Google Scholar

Zhang, J., Zhu, X., and Li, P. (2020). MOEA/D with many-stage dynamical resource allocation strategy to solution of many-objective OPF problems. Int. J. Electr. Power & Energy Syst. 120, 106050. doi:10.1016/j.ijepes.2020.106050

CrossRef Full Text | Google Scholar

Zhang, Q., and Li, H. (2007). MOEA/D: A multi-objective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 11, 712–731. doi:10.1109/tevc.2007.892759

CrossRef Full Text | Google Scholar

Zhang, X., Tian, Y., Cheng, R., and Jin, Y. (2015a). An efficient approach to non-dominated sorting for evolutionary multi-objective optimization. IEEE Trans. Evol. Comput. 19, 201–213. doi:10.1109/tevc.2014.2308305

CrossRef Full Text | Google Scholar

Zhang, X., Tian, Y., and Jin, Y. (2015b). A knee point driven evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 19, 761–776. doi:10.1109/tevc.2014.2378512

CrossRef Full Text | Google Scholar

Zhang, Y., Tian, Y., Jiang, H., Zhang, X., and Jin, Y. (2023). Design and analysis of helper-problem-assisted evolutionary algorithm for constrained multiobjective optimization. Inf. Sci. 648, 119547. doi:10.1016/j.ins.2023.119547

CrossRef Full Text | Google Scholar

Zhou, Y., Xiang, Y., and He, X. (2020). Constrained multiobjective optimization: test problem construction and performance evaluations. IEEE Trans. Evol. Comput. 25, 172–186. doi:10.1109/tevc.2020.3011829

CrossRef Full Text | Google Scholar

Zhu, C., Xu, L., and Goodman, E. D. (2016). Generalization of Pareto-optimality for many-objective evolutionary optimization. IEEE Trans. Evol. Comput. 20, 299–315. doi:10.1109/tevc.2015.2457245

CrossRef Full Text | Google Scholar

Zitzler, E., Thiele, L., Laumanns, M., Fonseca, C., and da Fonseca, V. (2003). Performance assessment of multiobjective optimizers: an analysis and review. IEEE Trans. Evol. Comput. 7, 117–132. doi:10.1109/tevc.2003.810758

CrossRef Full Text | Google Scholar

Zimmerman, R. D., Murillo-Sánchez, C. E., and Thomas, R. J. (2010). Matpower: steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans. power Syst. 26, 12–19. doi:10.1109/tpwrs.2010.2051168

CrossRef Full Text | Google Scholar