Dynamic pricing optimization for commercial subcontracting power suppliers engaging demand response considering building virtual energy storage

Commercial buildings have abundant flexible energy resources for demand response (DR). The electricity price for tenants in the commercial building is generally issued by a subcontracting power supplier (SPS), and the tenants cannot directly interact with the energy retailer. Therefore, the incentive for tenants to participate in DR is insufficient, and their potential is not fully explored. To address these issues, this paper proposes a dynamic pricing method based on the Stackelberg game, helping tenants actively participate in DR. Then, with the optimized energy consumption of the tenants, a virtual energy storage model of the commercial building is constructed by aggregating the adjustable capabilities of flexible energy resources such as air-conditioning (AC) and electric vehicles (EVs) in the public area. Finally, simulation tests are conducted based on a real commercial building to demonstrate the effectiveness of the game-theoretic pricing approach and validate the role of virtual energy storage of the building in DR.

1 Introduction

Commercial buildings are equipped with flexible and adjustable devices such as PV and energy storage devices, which are important resources for participating in DR. However, PV is characterized by volatility and randomness, and energy storage devices are expensive and have a short cycle life (Sparacino et al., 2012), limiting their ability to participate in DR. Due to the energy-buffering and time-shifting effects of air-conditioning (AC) loads and electric vehicles (EVs) in commercial buildings, they exhibit virtual energy storage characteristics similar to energy storage systems, which can be optimized and scheduled in conjunction with PV and energy storage devices for DR (Barala et al., 2021). It should be noted that flexible resource regulation needs to prioritize load demand and comfort, and its direct adjustment potential is limited. It is also necessary to adjust tenants’ electricity consumption behavior by changing electricity prices in order to increase the amount of electricity that commercial buildings participate in DR. Nevertheless, in the current environment, commercial buildings generally have SPS, and energy retailers cannot directly supply electricity to tenants. Tenants cannot directly participate in DR and receive rewards, leading to a lack of motivation. Therefore, in the context of the existence of SPS, this paper focuses on studying how to effectively schedule flexible resources and how to formulate dynamic electricity prices to incentivize tenants’ participation in DR.

In the commercial building, the controllable loads, such as AC loads and EVs, possess characteristics of flexible and controllable operation. These loads can be regarded as virtual energy storage (VES) units for regulation purposes, thereby achieving the objective of demand-side management in commercial buildings. The essence of VES is to effectively achieve DR goals while minimizing any negative impact on users, and it is considered a new flexible source. To optimize the scheduling of building internal AC loads and EVs participating in DR, it is necessary to establish a VES model. Jin et al. (2017) developed a VES model based on building thermal storage capacity. By analyzing the charging and discharging characteristics of VES and user comfort, a dynamic economic scheduling model based on AC virtual energy storage was established. Vijayalakshmi et al. (2022) developed a VES system using DR management to mitigate the power fluctuations of PV through the combination of AC virtual energy storage and battery energy storage. Comparative analysis of optimized scheduling demonstrates that the participation of VES can reduce the capacity requirements of energy storage devices. Chai et al. (2023) proposed a two-stage optimization technique to determine the charging and discharging schedule of EVs participating in building DR plans. Simulation results indicate that the convenience of EV owners’ travel has received more attention in the proposed model. However, the aforementioned papers lack sufficient research on the methods of load adjustment for tenants in commercial buildings and thus unable to effectively coordinate the VES and tenant load in commercial buildings.

During the DR period, the SPS needs to establish a reasonable electricity price to incentivize tenants to adjust their own electricity consumption behavior (Shi et al., 2020; Shi et al., 2022). After signing DR contracts with the energy retailer, the SPS generates compensation and electricity price curves with the aim of maximizing its own profits (Cui et al., 2023). Consequently, commercial building tenants are only able to maximize their own profits based on the pricing set by the SPS and provide feedback on their load and response curves. This process constitutes a typical Stackelberg game model (Xu et al., 2021; Xu et al., 2023) that analyzes the strategic behavior of a DR aggregator, responsible for the optimization of its DR providers’ bids in a wholesale market. The DR resource consists of an aggregation of residential electric heating systems, governed by a physical load model and user-specified comfort constraints. To consider the uncertainty associated with wind generation and electric demands, a scenario-based stochastic programming model has been adopted in this work. The results show the effectiveness of the Stackelberg game model used for the interaction between the aggregator and consumers (Song et al., 2020; Sun et al., 2021) The aforementioned study did not take into account the specific scenarios that exist within the SPS of commercial buildings. Further research is needed to investigate the dynamic game and collaborative control processes between the SPS and tenants.

Overall, the current research has not considered the special scenarios of commercial buildings with SPS, resulting in underutilization of flexible resources such as VES in the buildings. Additionally, the lack of a reasonable dynamic pricing for the SPS motivates tenants’ participation effectively in DR. To address these issues, this paper proposes a dynamic price optimization method that considers VES within commercial buildings. By employing Stackelberg game theory, the method determines the dynamic optimal price, thereby encouraging commercial buildings to participate in DR. The specific contributions of this study are as follows:

(1) A virtual energy storage model in commercial buildings was developed, considering the AC load and EVs as generalized storage participating in DR scheduling. The virtual energy storage scheduling and tenants’ participation in demand response were coordinated to construct the DR benefit model for the SPS.

(2) In order to effectively motivate tenants to participate in DR, this article establishes a dynamic price game optimization model based on the profit model of SPS and tenants in commercial buildings. This model is used to solve the optimal pricing between SPS and tenants and analyzes the existence of equilibrium solutions for this model.

2 A utility model for commercial building tenant DR based on price incentives

In the current policy context, there are limitations to increasing the revenue of commercial building SPS through excessive electricity price hikes. However, SPS can participate in DR by effectively utilizing the abundant flexible load resources within commercial buildings, thereby reducing electricity costs in a reasonable and compliant manner.

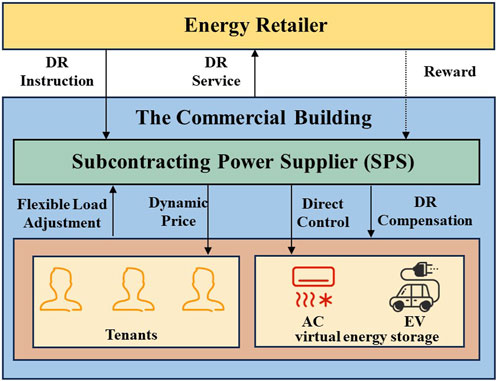
The electricity supply process in commercial buildings consists of three entities: the energy retailer, SPS, and tenants. The SPS cannot directly intervene in tenant’s electricity consumption behavior but can directly control the load in the public area. In order to ensure their own electricity consumption, tenants need to sign a separate contract with the SPS. In this case, the SPS can regulate price to incentivize tenants to change their electricity consumption behavior. The energy retailer, on the other hand, enters into a price contract with the SPS and supplies electricity to the entire commercial building, with no direct price interaction with the tenants.

Figure 1 shows that in the commercial building involved in demand response, the energy retailer sends a demand response instruction to the SPS, and the SPS after receiving the instruction designs a dynamic price while satisfying the tenant’s electricity demand to incentivize the tenant to reduce the electricity load during the demand response time period (Darwazeh et al., 2022). Each tenant optimizes its own electricity consumption behavior with the change in dynamic price and achieves the optimal balance between electricity consumption cost and satisfaction. In this paper, we mainly consider virtual energy storage for AC and EVs in commercial buildings. SPS can directly control the virtual energy storage for AC in commercial buildings to participate in demand response scheduling and realize the smoothing of the load curve (Tiwari and Pindoriya, 2022). At the same time, the SPS can incentivize the EVs at the charging piles to participate in the demand response scheduling by means of price compensation, and the SPS can effectively reduce the load during the demand response period by responding to the demand response commands of the power retailer in the above two ways and obtain the profit from the energy retailer according to the actual demand response capacity.

Figure 1

Figure 1. DR relationship in a commercial building.

2.1 Dynamic pricing design for commercial buildings based on price incentives

This paper explores the use of dynamic electricity pricing as a mean for commercial buildings to encourage tenants’ participation in DR. Under this approach, tenants are charged according to the time-of-use (TOU) electricity pricing when they do not participate in DR. However, when they participate, the electricity prices for different time periods are adjusted according to a predetermined price adjustment ratio. The actual electricity price curve, denoted as $e^{\prime }=\left[e_1^{\prime },e_2^{\prime },\cdots ,e_t^{\prime }\right]$, allows tenants to decide whether or not to respond to the price adjustments based on their electricity consumption needs.

The actual electricity price during time period t can be represented as a function of the price adjustment ratio:

$e_t^{\prime }=\phi \left(t\right)e_t\delta \left(t\right)+\varphi \left(t\right)e_t\left(1-\delta \left(t\right)\right),(1)$

where $\phi \left(t\right)$ are rates of electricity price adjustment and $\delta \left(t\right)$ is the binary variable, where the value of 1 denotes an increase in the tenant load and the value of 0 signifies a reduction in the tenant load.

Due to the disadvantaged position of tenants in the electricity purchasing process, they can only respond to the electricity price offered by the SPS (Li et al., 2022). Therefore, in order to protect the basic interests of tenants, it is necessary to impose constraints on the actual electricity price $e_t^{\prime }$:

${e_{\mathit{min}}\le e}_t^{\prime }\le e_{\mathit{max}},(2)$

where $e_{\mathit{min}}$ and $e_{\mathit{max}}$ represent the minimum and maximum actual electricity prices during time period t, respectively.

2.2 A utility model for commercial building tenants based on dynamic time-of-use electricity pricing

Due to the large variety and decentralized distribution of flexible loads in tenants, it is difficult to count the specific loads. In this paper, the tenant loads of commercial buildings are broadly categorized into two types: adjustable loads and rigid loads. Assuming that the tenant set N of a commercial building consists of n tenants, the total load of the tenant k in time period t is $P_{k,t}$, where the adjustable load is $P_{k,t}^{\text{DR}}$, and the other rigid load is $P_{k,t}^{\text{EL}}$. The total load of tenant k during time period t can be calculated as follow in Eq. 3 (Li et al., 2021; Yasir et al., 2023):

$P_{k,t}=P_{k,t}^{\text{DR}}+P_{k,t}^{\text{EL}}.(3)$

The electricity consumption of tenant k in time period t is as follow in Eq. 4:

$E_{k,t}^{tenant}={\int }_t^{t+∆t}{P}_{k,t}dt.(4)$

For a tenant k, the utility function $u_{k,t}\left(E_{k,t}^{tenant,DR},{\omega }_k\right)$ that represents the tenant k’s participation in DR during time period t can be defined as follows (Sun et al., 2021):

$u_{k,t}\left(E_{k,t}^{tenant,DR},{\omega }_k\right)=\left(e_t-e_t^{\prime }\right)\left(E_{k,t}^{plan}-E_{k,t}^{tenant,DR}\right)-{\omega }_k\left(E_{k,t}^{DR}-E_k^{ideal}\right),(5)$

where $e_t$ is the electricity price during the period t; $e_t^{\prime }$ is the actual purchase price of electricity for tenants during the time period t; $E_{k,t}^{plan}$ is tenant k’s planned electricity consumption during time period t; $E_{k,t}^{tenant,DR}$ is the response electricity of tenant k during time period t; $E_k^{ideal}$ is the ideal response electricity of tenant k; and ${\omega }_k$ is the coefficient of electricity preference for tenant k.

Various electricity prices for tenant k and the utility function for participating in DR can be derived from Eqs 2, 5. Consequently, the profit of tenant k can be expressed as Eq. 6.

$I_k^{tenant}={\sum }_{t=1}^T{u}_{k,t}\left(E_{k,t}^{tenant,DR},{\omega }_k\right)-e_t\left(E_{k,t}^{plan}-E_{k,t}^{tenant,DR}\right).(6)$

The amount of electricity that tenants can adjust is subjected to constraints imposed by electricity prices and the limit of adjustable electricity. The adjustable electricity limit for tenant k during time period t is defined in Eq. 7.

$\left\{\begin{array}{ll}0\le E_{k,t}^{tenant,DR}\le E_{k,t,\mathit{max}}^{cutDR}& \delta \left(t\right)=0,\\ E_{k,t,\mathit{max}}^{addDR}\le E_{k,t}^{tenant,DR}\le 0& \delta \left(t\right)=1,\end{array}\right.(7)$

where $Q_{k,t,\mathit{max}}^{cutDR}$ and $Q_{k,t,\mathit{max}}^{addDR}$ represent the maximum extent to which the user can reduce and increase the load, respectively, whose values can be obtained through Eqs 8, 9; and $\delta \left(t\right)$ is the binary variable, where the value of 1 denotes an increase in the tenant load, while the value of 0 signifies a reduction in the tenant load.

$E_{k,t,\mathit{max}}^{cutDR}=p_{cut,t}{E}_{k,t}^{plan},(8)$

$E_{k,t,\mathit{max}}^{addDR}=p_{add,t}{E}_{k,t}^{plan},(9)$

where $p_{cut,t}$ and $p_{add,t}$ represent the maximum reduction and increase ratios of adjustable loads for tenants during time period t, respectively. Additionally, $E_{k,t}^{tenant,DR}$ must also satisfy upper and lower limit constraints. The constraint is shown in Eq. 10.

$E_{k,t,\mathit{min}}^{tenant,DR}\le E_{k,t}^{tenant,DR}\le E_{k,t,\mathit{max}}^{tenant,DR}.(10)$

3 A profit model of DR for the subcontracting power supply in commercial buildings

According to the analysis in the previous section, the load of commercial buildings can be divided into public area load and tenant load based on regional energy use scenarios. The main energy loads in public areas include building lighting, central AC, and charging stations in underground garages. In addition, existing commercial buildings usually have a certain amount of new energy generation equipment to reduce electricity costs and ensure power supply for important loads in extreme situations (Miglioli et al., 2023).

Since the main way to reduce energy consumption in lighting loads is to replace energy-saving lamps and improve energy efficiency, it is difficult to reduce energy loads by turning off the light sources in DR scenarios (Han, et al., 2022). At the same time, other loads within the public area generally encounter the problem of being more difficult to regulate and having a small adjustable range. Therefore, when considering the energy consumption optimization of the public area loads, this paper mainly focuses on central AC and EV loads. Since both types of loads have certain cross-temporal energy transfer capabilities, they can be regarded as virtual energy storage devices participating in DR regulation. Therefore, after introducing the basic models of central AC and EVs, the two types of loads are collectively established as a VES model of SPS in commercial buildings.

3.1 A VES model for the SPS in commercial buildings

3.1.1 Electric vehicle model

Electric vehicles are considered significant flexible resources in commercial buildings. This article regards EVs as VES and involves them in DR regulation. The battery charge status ($SO{C}_i$) of an individual EV user i can be expressed as follows (Jin et al., 2023):

${SOC}_{i,t+1}^{EV}={SOC}_{i,t}^{EV}+\frac{\left({\omega }_{i,t}^c{P}_{i,t}^{EV,c}{\mu }_c\Delta t-\frac{{\omega }_{i,t}^d{P}_{i,t}^{EV,d}\Delta t}{{\mu }_d}\right)}{B},(11)$

$T_{c,i}=\frac{\left(SO{C}_{e,i}-SO{C}_i\right)B}{P_{i,t}^{EV,c}{\mu }_c\Delta t},(12)$

$T_{d,i}=\frac{\left(SO{C}_i-SO{C}_{\min }\right){\mu }_{d}B}{P_{i,t}^{EV,d}\Delta t},(13)$

where $B$ represents the capacity of the EV battery; $P_{i,t}^{EV,c}$ denotes the charging power of user i during time period t; $P_{i,t}^{EV,d}$ represents the discharging power of user i during time period t; ${\omega }_{i,t}^c$ is the charging coefficient, where ${\omega }_{i,t}^c=1$ indicates that the EV is in a charging state and ${\omega }_{i,t}^c=0$ indicates that the EV is in a non-charging state; ${\omega }_{i,t}^d$ is the discharging coefficient, where ${\omega }_{i,t}^d=1$ indicates that the EV is in a discharging state and ${\omega }_{i,t}^d=0$ indicates that the EV is in a non-discharging state; ${\mu }_c$ and ${\mu }_d$ are the charging and discharging efficiencies of the EV battery, respectively; $T_{c,i}$ is the minimum number of time periods required to meet the user’s charging expectations; $SO{C}_{e,i}$ represents the user’s desired state of charge upon departure; and $SO{C}_{\min }$ is the predetermined critical state of charge for the battery.

The constraints of EV models encompass various factors, such as battery state constraint, battery charge continuity constraint, charge state constraint, user’s expected charge constraint, and charge/discharge rate constraint. Battery state constraint can be represented using the state variable ${\omega }_{i,t}^c$. When an EV is connected to a charging station and is in a controllable state of charging and discharging, ${\omega }_{i,t}^c=1$. When the EV is in a traveling state, ${\omega }_{i,t}^c=0$. However, the battery of the EV can only exhibit charging, discharging, or idle states. Therefore, the constraint of the battery state of the EV is as follows:

${\omega }_{i,t}^c+{\omega }_{i,t}^d\le {\omega }_{i,t^i}^{in}.(14)$

The battery state of charge at time t, denoted as ${SOC}_{i,t}^{EV}$, is subjected as follows:

${SOC}_{\mathit{min}}\le {SOC}_{i,t}^{EV}\le 1.(15)$

Finally, the charging and discharging of EVs must also meet the constraints of charging and discharging rates.

$\left\{\begin{array}{l}0\le P_{i,t}^{EV,c}\le P_{\mathit{max}}^{EV,c},\\ 0\le P_{i,t}^{EV,d}\le P_{\mathit{max}}^{EV,d},\end{array}\right.(16)$

where $P_{\mathit{max}}^{EV,c}$ and $P_{\mathit{max}}^{EV,d}$ represent the maximum values of EV charging and discharging, respectively.

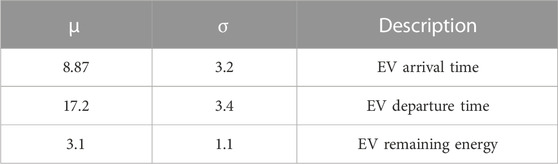
For EVs, there is a large uncertainty in the arrival and departure times and initial state of charge (SOC) of individual EVs. By analyzing the results of a survey conducted by the Federal Highway Administration of the US Department of Transportation in 2009 on household driving trips across the US, it is possible to roughly obtain the probability density distributions of EV arrival times at charging piles in commercial buildings during the weekday period, probability density distributions of departure times, and probability density distributions of mileage traveled in the charging intervals. The corresponding fitted curve functions are shown in Eqs 17–19 (U.S. Department of Transportation and Highway Administration, 2009).

$f_1\left(x\right)=\left\{\begin{array}{c}\frac{1}{\sqrt{2\pi }{\sigma }_l}\exp \left(-\frac{{\left(x-{\mu }_l\right)}^2}{2{\sigma }_l^2}\right),0<x\le {\mu }_l+12,\\ \frac{1}{\sqrt{2\pi }{\sigma }_l}\exp \left(-\frac{{\left(x-24-{\mu }_l\right)}^2}{2{\sigma }_l^2}\right),{\mu }_l+12<x\le 24,\end{array}\right.(17)$

$f_a\left(x\right)=\left\{\begin{array}{c}\frac{1}{\sqrt{2\pi }{\sigma }_a}\exp \left(-\frac{{\left(x+24-{\mu }_a\right)}^2}{2{\sigma }_a^2}\right),0<x\le {\mu }_a-12,\\ \frac{1}{\sqrt{2\pi }{\sigma }_a}\exp \left(-\frac{{\left(x-{\mu }_a\right)}^2}{2{\sigma }_a^2}\right),{\mu }_a-12<x\le 24,\end{array}\right.(18)$

$f_t\left(x\right)=\frac{1}{\sqrt{2\pi }{\sigma }_{t}x}\exp \left(-\frac{{\left(\ln x-{\mu }_t\right)}^2}{2{\sigma }_t^2}\right).(19)$

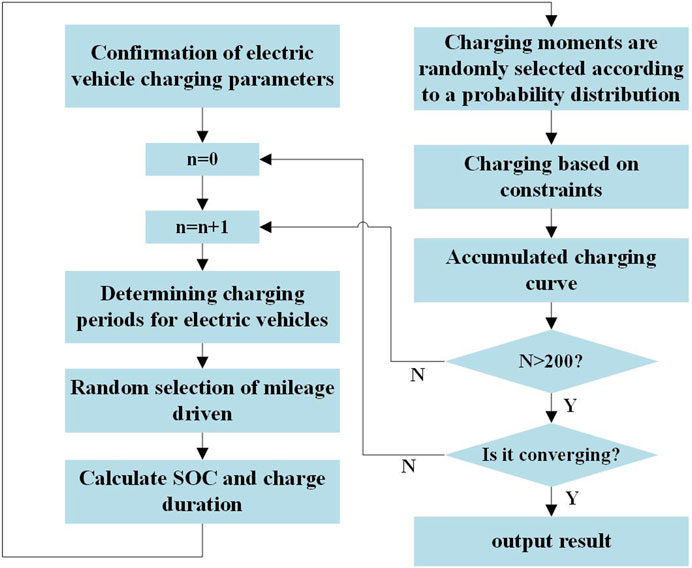
According to the expression of probability density random distribution such as charging start moment and daily journey, the Monte Carlo method is applied for random sampling to determine the charging behavior of EVs in the charging station, and then the corresponding data are used to calculate the real SOC of EVs. The specific process is shown in Figure 2.

Figure 2

Figure 2. Flowchart for predicting electric vehicle charging behavior.

Based on the time of EV access to the charging post and the remaining power obtained from Monte Carlo simulation, all EVs in the charging station at a certain time period can be classified into adjustable loads that participate in the response and rigid loads that do not participate in the response. The state of charge of the battery when the EV user leaves the charging station should satisfy the user’s expectation, and the EV user’s expected electricity constraint is

${SOC}_i^E\le {SOC}_i^{in}+{{\displaystyle \sum }}_{\mathrm{t}=1}^{\mathrm{T}}\left({\omega }_{\mathrm{i},\mathrm{t}}^{\mathrm{c}}{{\displaystyle \int }}_t^{t+∆t}{P}_{i,t}^{EV,c}dt{\mu }_{\mathrm{c}}-\frac{{\omega }_{\mathrm{i},\mathrm{t}}^{\mathrm{d}}{{\displaystyle \int }}_t^{t+∆t}{P}_{i,t}^{EV,d}dt}{{\mu }_{\mathrm{d}}}\right)/B\le 1,(20)$

where ${SOC}_i^E$ is the desired charge state when EV user i leaves the charging station and ${SOC}_i^{in}$ is the charge state when EV user i enters the charging station. If the time of accessing the charging pile cannot meet the user’s expected electricity requirement or the electricity is lower than the critical electricity when EV accesses, it is considered that this part of energy storage cannot participate in the regulation (Zhu et al., 2023). Otherwise, it is considered that the energy storage can participate in the demand response to adjust the charging and discharging strategy. In this paper, we consider the EV adjustable load in the charging station under each time period, aggregated to an energy storage device to consider the overall dispatchable electricity capacity. At this point, the EV discharge available to the commercial building in time period t is

$E_t^{EV,DR}={\sum }_{\mathrm{i}=1}^{{\mathrm{N}}_2}\left[{\omega }_{i,t}^c{P}_{i,t}^{EV,c}{\mu }_{\mathrm{c}}\Delta t+{\omega }_{i,t}^d{P}_{i,t}^{EV,d}\Delta t/{\mu }_{\mathrm{d}}\right].(21)$

3.1.2 Air-conditioning model

The enclosure structure of a building endows the internal air-conditioning system with the ability to store and release energy, thereby exhibiting characteristics similar to a VES system. This enables it to be considered VES and participate in DR (Chen et al., 2021). In commercial buildings, the internal tenants are dispersed and occupy smaller spaces, making it inconvenient to regulate the temperature control load. On the other hand, the public areas have larger spaces, and the AC can be directly controlled by the SPS. Therefore, this study disregards the AC load of the tenants and only considers the AC load of the public areas as VES participating in DR.

In order to effectively improve the capacity of DR of commercial buildings, this study considers the AC load as VES participating in regulation during DR periods. By fully utilizing the stored cooling energy in public areas, the transfer of cooling power supply time is achieved (Zhang, et al., 2022). To facilitate the analysis of the VES regulation capacity of the SPS in commercial buildings, the charging and discharging power of VES is defined as the difference between the cooling/heating power produced by AC and the dissipative cooling/heating load, which is expressed as follows:

$Q_t^{AC,VES}=Q_t^{AC}-Q_t^{diss},(22)$

where $Q_t^{AC,VES}$ represents the VES power of the AC system. When $Q_t^{AC,VESS}>0$, the VES is in the “energy storage” state, and when $Q_t^{AC,VESS}<0$, it is in the “energy dissipation” state. $Q_t^{AC}$ is the cooling/heating power of the air-conditioning unit in time period t, obtained from Eq. 23, and $Q_t^{diss}$ is the outward heat transfer power from the building at time t, obtained from Eq. 24:

$Q_t^{AC}=P_t^{AC}\times COP,(23)$

where $P_t^{AC}$ is the electric power of inverter AC and $COP$ is the energy efficiency ratio of the inverter AC.

${\int }_t^{t+∆t}{Q}_t^{diss}\text{dt}={\sum }_{k=1}^n{h}_k{A}_k\left(T_{k,t}-T_t\right),(24)$

where $Q_t^{diss}$ varies with the temperature difference between indoor and outdoor. $h_k$ is the combined heat transfer coefficient between the kth enclosure in the building and the outside world (including neighboring spaces); $A_k$ is the area of the kth enclosure in the space; $T_{k,t}$ is the temperature of the kth enclosure; and $T_t$ is the temperature of the indoor space during the time period t.

In commercial buildings, the factors that influence the limit of VES capacity in AC systems are primarily related to human thermal comfort indicators. Therefore, the range of temperature constraints within the building can be expressed as follows:

$T_{\mathit{min}}\le T_t\le T_{\mathit{max}},(25)$

where $T_{\mathit{min}}$ and $T_{\mathit{max}}$ represent the acceptable upper and lower limits of indoor temperature for users, respectively. According to Eqs 24, 25, the virtual energy storage heat capacity V of the AC can be obtained as follows:

$V={\sum }_{k=1}^n{h}_k{A}_k\left(T_{\mathit{max}}-T_{\mathit{min}}\right).(26)$

${SOC}_t^{AC}$ is the charge state of the AC virtual energy storage at period t, as shown in Eq. 27, which ranges from 0 to 1. When $T_t=T_{\mathit{min}}$, ${SOC}_t^{AC}=0$, and when $T_t$ = $T_{\mathit{max}}$, ${SOC}_t^{AC}=1$.

$\left\{\begin{array}{c}{SOC}_{t+1}^{AC}={SOC}_t^{AC}+\frac{{\int }_t^{t+∆t}{Q}_t^{diss}dt}{E_t^{AC}},\\ 0\le {SOC}_t^{AC}\le 1.\end{array}\right.(27)$

Therefore, the electricity from the virtual storage of air conditioners that participates in the demand response at time period t is as follows:

$E_t^{AC}={\int }_t^{t+∆t}\left(P_t^{AC,plan}-P_t^{AC}\right)dt,(28)$

where $P_t^{AC,plan}$ is the AC load without taking into account the virtual energy storage regulation and $P_t^{AC}$ is the actual AC load.

3.1.3 Virtual energy storage model

In order to better illustrate the dynamic processes of AC and EVs, they are considered generalized energy storage devices participating in DR scheduling. The model of the generalized energy storage model is as follow in Eq. 29 (Bu, et al., 2023):

$\left[\begin{array}{c}SO{C}_{t+1}^{AC}\\ SO{C}_{t+1}^{EV}\end{array}\right]=\left[\begin{array}{c}SO{C}_t^{AC}\\ SO{C}_t^{EV}\end{array}\right]+{\left[\begin{array}{c}\frac{\mathrm{\Sigma }{\mathcal{h}}_k{A}_k\left(T_{k,t}-T_t\right)}{COP}\\ {\omega }_t^c{P}_t^{EV,c}{\mu }_c\Delta t-{\omega }_t^d\frac{P_t^{EV,d}}{{\mu }_d}\Delta t\end{array}\right]}^{\mathrm{T}}\left[\begin{array}{c}1/E^{AC}\\ 1/B\end{array}\right],(29)$

where $SO{C}_t^{AC}$ represents the virtual SOC of the AC during the energy storage period $t$ and $SO{C}_t^{EV}$ represents the virtual SOC of the EVs during the energy storage period $t$. The definition for the $E^{AC}$ remaining variables can be found in Eqs 11–28.

3.2 The profit model of SPS

The SPS signs a contract with the energy retailer to participate in DR and generate profit. This is achieved by adjusting the electricity purchase price $e^{\prime }$ for tenants, incentivizing their participation in DR activities and maximizing their own interests. The expression for the profit of SPS is as follow in Eq. 30.

$I_{\text{SPS}}={\displaystyle {\sum }_{t=1}^T}{\left((E\right.}_t^{DR}{p}_t^{DR}-E_t^{retailer}{p}_t^{retailer}-{E_t^{EV}{,}_t{e}_{EV}-C}_{re}^{\text{DR}}),(30)$

where $E_t^{DR}$ represents the actual electricity involved in DR; $p_t^{DR}$ is the contractual price associated with participating in DR; $E_t^{retailer}$ denotes the purchased electricity by the SPS during time period t; $p_t^{retailer}$ is the electricity price during time period t; $E_{EV,t}$ represents the electricity generation by EVs during time period t; $e_{ev}$ represents the subsidy price for EVs participating in DR during time period t; and $C_{re}^{\text{DR}}$ represents the compensation cost for providing DR to tenants.

The electricity $E_t^{DR}$ for commercial buildings participating in DR shall be satisfied, as shown in the following Eq. 31.

$E_t^{DR}=E_t^{EV}+E_t^{AC}+{\displaystyle {\sum }_{k=1}^n}{E}_{k,t}^{tenant,DR}.(31)$

The actual purchased electricity $E_{\text{grid},t}$ of the SPS electricity during the time period t is as follow in Eq. 32.

$E_t^{grid}=E_t^{public}+E_t^{tenant}-E_t^{PV}+E_t^{EV},(32)$

where $E_t^{public}$ represents the electricity consumption in the public area during time period t; $E_t^{tenant}$ represents the electricity consumption by tenants during time period t; $E_t^{PV}$ represents the PV during time period t,; and $E_t^{EV}$ represents the electricity amount of EV charging/discharging during time period t.

is as follow in Eq. 33.

$C_{re}^{\text{DR}}=\left(e_t-e_t^{\prime }\right)E_t^{tenant},(33)$

where $e_t$ is the customer tariff before response; $e_t^{\prime }$ is the dynamic tariff of the customer after response, which is obtained from Eq. 1; and $E_t^{tenant}$ is the actual electricity consumption of the tenant after participating in DR.

4 A Stackelberg game model for the dynamic optimal pricing of commercial building SPS

This section considers the game process between the SPS and the participating DR tenants in the operation of commercial buildings and constructs a Stackelberg game model for the optimal pricing of the SPS. After signing a DR contract with the energy retailer, the SPS will generate compensation prices and electricity price curves with the goal of maximizing its own profits. Therefore, commercial building tenants can only maximize their own profits based on the pricing set by the SPS and provide feedback on their load and response curves. This process constitutes a typical Stackelberg game model, with the SPS as the decision-maker and the individual tenants as followers. Therefore, using a backward induction approach (Li et al., 2022), the profits of the SPS $I_{SPS}$ is maximized based on dynamic price $e^{\prime }$, then the adjusted dynamic price $e^{\prime }$ is substituted into the tenant’s profits, and the DR electricity $E_{k,t}^{DR}$ for each time period is optimized.

4.1 Stackelberg game model based on the dynamic time-of-use electricity price

In the Stackelberg game problem, both the SPS of commercial buildings and each individual tenant aim to maximize their own profits. The optimal strategy for tenant k satisfies the following Eq. 34.

$\left\{\begin{array}{c}{\mathit{Q}}^{*}=\underset{Q_{k,t}^{DR}}{\mathrm{argmax}}{I}_k^{tenant},\\ \mathrm{s}.\mathrm{t}.\text{\hspace{0.17em}eq\hspace{0.17em}}\left(7\right),\left(8\right),\left(9\right).\end{array}\right.(34)$

The optimal strategy of SPS satisfies the following Eq. 35.

$e^{\prime *}=\underset{e_t^{\prime }}{\mathrm{argmax}}{I}_{SPS}.(35)$

To obtain the ideal electricity number of tenants responding to dynamic pricing, it is crucial to solve the utility model of tenants. Initially, we need to examine the electricity prices $e_t^{\prime }$ during various time periods and calculate the first-order partial derivative of the profit function for tenant k in relation to DR electricity $E_{k,t}^{DR}$ in the time period t (Zhou et al., 2021; Bhatti and Broadwater, 2020). Examine method is as follow in Eq. 36.

$\frac{\partial I_k^{tenant}}{\partial E_{k,t}^{DR}}=e_t^{\prime }-2{\omega }_k\frac{E_{k,t}^{DR}-E_k^{ideal}}{E_{k,t}^{DR}},(36)$

where $\frac{\partial I_k^{tenant}}{\partial E_{k,t}^{DR}}=0$, and the optimal DR electricity of tenant k at time period t ${E_{k,t}^{DR}}^{*}$ can be obtained as follow in Eq. 37.

${E_{k,t}^{DR}}^{*}=\frac{E_k^{ideal}}{1-\frac{e_t^{\prime }}{2{\omega }_k}}.(37)$

Based on the deduction presented in Section 4.1, assuming the strategy combination of tenants and SPS denoted as $\mathit{S}=\left\{{\left\{{\mathit{Q}}_{\mathit{k}},{\mathit{\omega }}_{\mathit{k}}\right\}}_{kϵN},{\mathit{e}}^{\prime }\right\}$, where ${\left\{{\mathit{Q}}_{\mathit{k}},{\mathit{\omega }}_{\mathit{k}}\right\}}_{kϵN}$ represents the strategy set of tenant k and ${\mathit{e}}^{\prime }$ represents the strategy set of the SPS. The sufficient and necessary condition for ${\mathit{S}}^{*}$ to be an equilibrium solution in game theory is given in the following equation. After adjusting to strategy $\beta$, all participants satisfy the Eq. 38.

$W_{\beta }\left({\mathit{S}}^{*}\Vert s_{\beta }\right)\le W_{\beta }\left({\mathit{S}}^{*}\right),(38)$

where $W_{\beta }$ represents the adjusted profit after implementing strategy $s_{\beta }$ and ${\mathit{S}}^{*}\Vert s_{\beta }$ represents that participant $\beta$ individually changes its own strategy, while the strategies of other participants remain unchanged. This implies that in the equilibrium solution ${\mathit{S}}^{*}$, no participants can achieve higher benefits by unilaterally altering their own strategy.

For any tenant k in a commercial building, given a known dynamic price $e^{\prime }$, the tenant’s objective function is dependent on $Q_k^{DR}$, and it is continuous and differentiable everywhere. There must exist at least one optimal strategy in a closed domain to achieve game equilibrium. Similarly, when the tenant’s DR electricity $Q_k^{DR}$ is given, the optimization problem for the SPS becomes a function about $e^{\prime }$, with a closed feasible domain, and there always exists an optimal strategy to maximize profits.

4.2 Optimization process of the Stackelberg game model

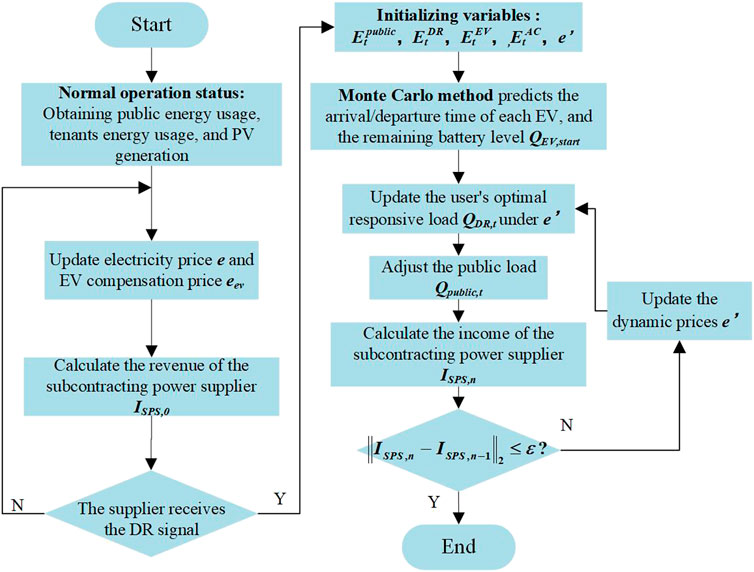
In the process of Stackelberg game between SPS and tenants, the SPS acts as the dominant player, while tenants determine their response strategies based on the pricing strategy of the SPS and their own electricity demands. Therefore, the pricing strategy of the SPS is the most crucial component of the game strategy combination. By designing a dynamic pricing optimization algorithm for the SPS, the optimal solution of the Stackelberg game model can be obtained. The optimization process of the Stackelberg game model is illustrated in Figure 3. The primary processes encompass the following:

1) During the normal operational phase, the SPS disseminates information regarding electricity price for commercial tenants. These tenants then purchase electricity at price e. The SPS calculates its own profit $I_{SPS,0}$ based on the total load curve during normal operating hours and the photovoltaic generation curve.

2) When the SPS receives an invitation to demand response, they adjust the price curve to optimize tenants’ response, thus entering into a game of strategy between the SPS and the tenants.

3) Using the Monte Carlo method, the prediction of daily electric vehicle charging load is conducted, along with the initialization of tenant load and tenant electricity price.

4) During the load response phase, SPS solves for optimal dynamic price using a fixed-step iterative loop approach. Tenants adjust their response electricity based on the revised price information and calculate their profits. The SPS adjusts the price and calculates its profit $I_{SPS,n}$ based on tenants’ feedback.

5) Compare the results of the nth and n-1th games; if the difference between the two games satisfies ${‖I_{SPS,n}-I_{SPS,n-1}‖}_2\ge \epsilon$, update the dynamic electricity price and return to process 2.

6) Obtain the optimal pricing and exit the loop.

Figure 3

Figure 3. Flowchart of the optimization algorithm.

5 Simulation results

5.1 Basic parameter settings

This study focuses on the analysis of energy optimization and dynamic time-of-use electricity pricing for a selected commercial building SPS (US Department of Transportation). The optimization period T is set to 24 h, with intervals of 0.25 h for the optimization periods. The computational model is implemented using Python 3.8 and utilizes the Gurobi for Python solver for objective function calculations.

The basic parameter settings include the following:

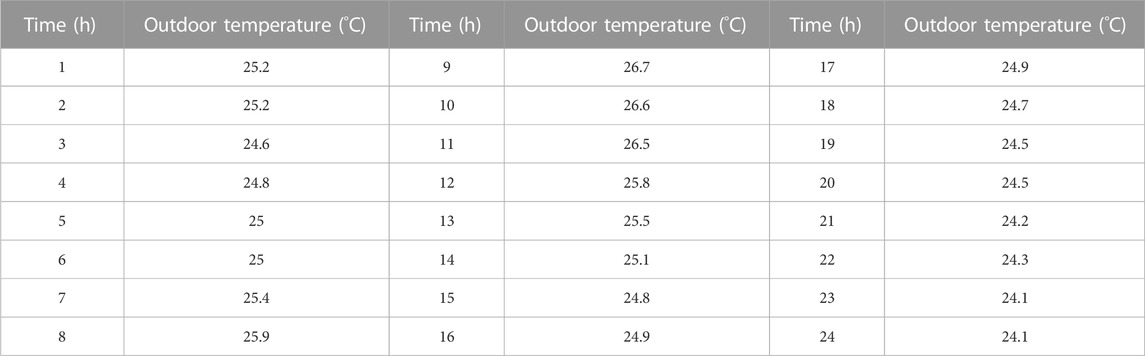
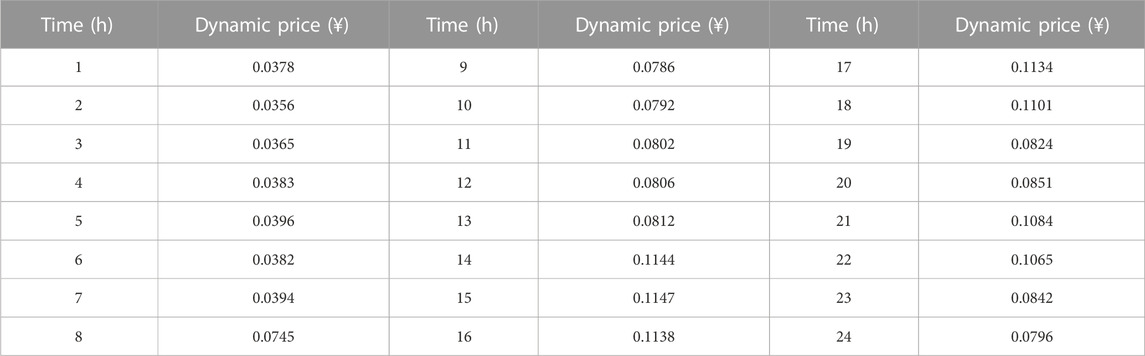
1) The outdoor hourly climate temperature is shown in Table 1, while the indoor comfort temperature is set at 25°C–27°C (Afroz et al., 2018).

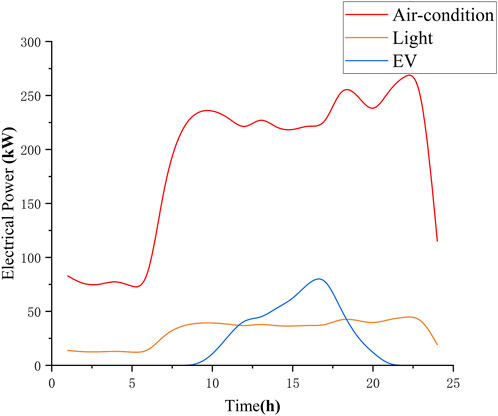
2) The energy load in the public areas of the building is mainly composed of AC load, lighting load, and electric vehicle load, as depicted in Figure 4, where EV loads are simulated using the Monte Carlo method, the probabilistic model is shown in Eqs 17–19, and the required parameters are shown in Table 2.

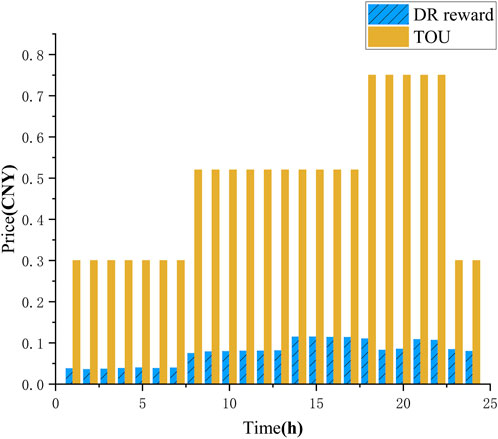
3) The electricity price for commercial buildings is 1.2 CNY/(kWh) during peak hours (12:00–14:00; 19:00–22:00), 0.8 CNY/(kWh) during off-peak hours (9:00–12:00; 22:00–24:00), and 0.3 CNY/(kWh) during valley hours (00:00–09:00). The purchase price for merchants is 0.7 CNY/kWh. The time-of-use electricity price and DR revenue prices are shown in Figure 5.

4) It is assumed that there are 100 merchants in the commercial building, and their comfort preferences are randomly sampled within the range of 0.6–1.2. Each merchant’s maximum adjustable load is set at 30% of the merchant’s own energy demand.

Table 1

Table 1. Outdoor temperature settings.

Figure 4

Figure 4. Electric demand curves in the public area.

Table 2

Table 2. Settings for the EV model.

Figure 5

Figure 5. Histograms of TOU and DR reward.

5.2 Dynamic electricity price adjustment and profit analysis

The adjustment results of the total load curve under the optimal pricing strategy are illustrated in Figure 6A. It can be observed that upon receiving the DR signal, the SPS will adjust the response price curve and communicate it to the tenants, thereby incentivizing them to optimize their response electricity. Before 10:00 and after 23:00, the building energy consumption produces a significant drop due to the end of the business hours of the commercial building, and at the same time, during the time period when the demand response is considered, the loads are forced to turn on or turn off in order to ensure the overall economy, which leads to an abnormal scheduling of the energy consumption curve. After adopting the dynamic price game scheduling strategy, the energy load of the commercial building during business hours can ensure the demand response requirements, while the overall process is smoother, which ensures the tenants’ energy comfort.

Figure 6

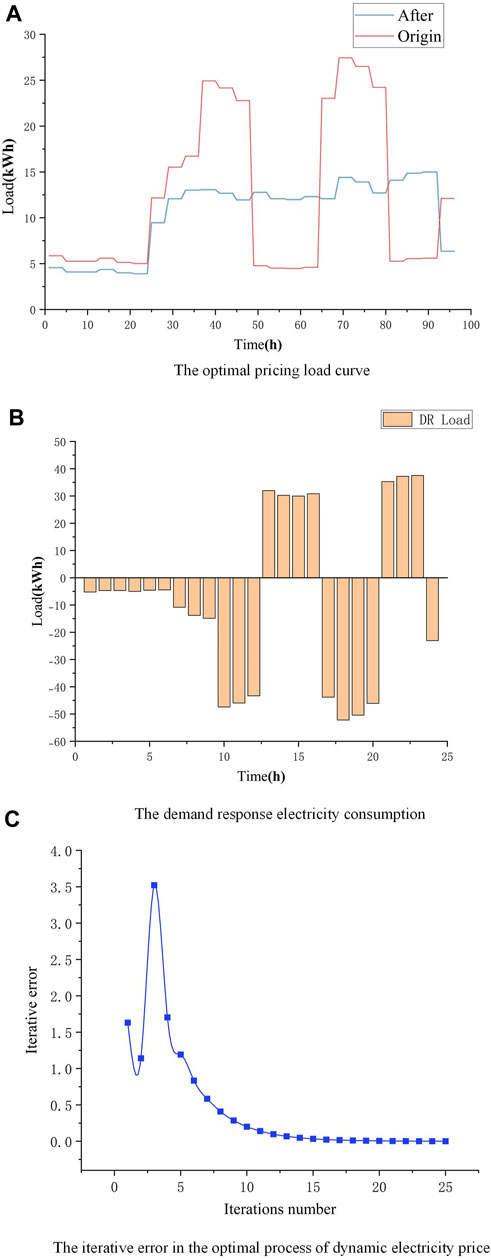
Figure 6. User load curve and response power with the optimal pricing strategy. (A) Optimal pricing load curve. (B) Demand response electricity consumption. (C) Iterative error in the optimal process of the dynamic electricity price.

The incentivizing effect of the dynamic price adjustment on tenant response power can also be seen by the change in load response power, as shown in Figure 6B. The tenants reduce their own energy demand outside the hours of high load demand in the middle of the day and at night, when the PV is mainly used for flexible equipment such as AC and EVs in the public areas, which serves as an accumulation of electricity. During the tenants’ peak hours (11:00–14:00; 17:00–20:00), the building’s flexible conditioning equipment can be used to better support the tenants’ energy use and reduce the need for external power supply.

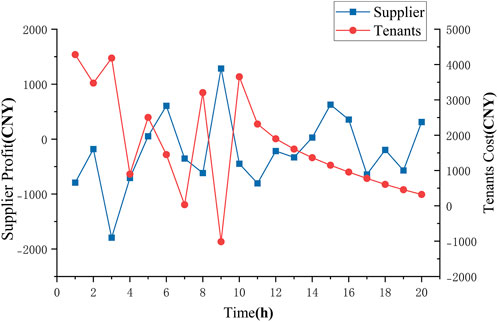
Figure 6C illustrates the iterative curve of the price game process, where after approximately 10 price adjustments, the profits of both the tenants and the SPS gradually stabilize, reaching the final game equilibrium. Figure 7 shows that the profit of the SPS decreases from an initial value of 3,538.14 CNY to 1,006.37 CNY after 10 adjustments. The initially high profit of the SPS can be attributed to the unreasonable initial dynamic response electricity price set at the beginning of the iteration, resulting in the tenants obtaining excessive profits. After several rounds of game adjustments, the SPS gradually transfers its profit to the tenants, leading to a decrease and stabilization of its own profit, which aligns with the game process between the SPS and the tenants in real scenarios. The results of the electricity price adjustments in Figure 8 and the response electricity in Figure 6B also indicate that the fluctuation in tenants’ electricity expenditure costs is significantly related to the electricity price set by the SPS. By modifying the dynamic electricity price, the tenants’ participation in DR can be effectively incentivized. The final dynamic price is shown in Table 3.

Figure 7

Figure 7. Variation in supplier profit and tenants’ cost.

Figure 8

Figure 8. Results of electricity price adjustment.

Table 3

Table 3. Dynamic price results.

5.3 Analysis of the effects of VES

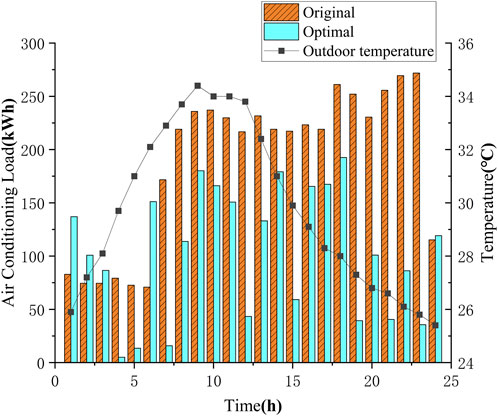
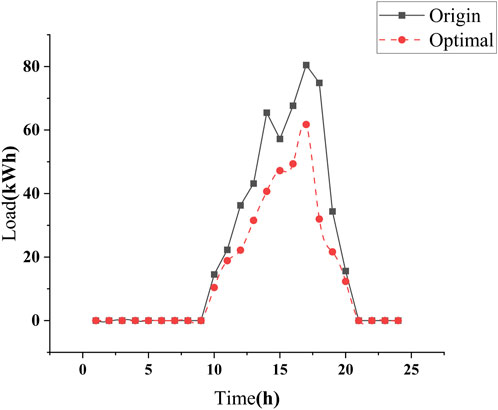
The thermal inertia of the building structure allows for the balancing of energy consumption at different times through the implementation of variable energy strategies, taking advantage of the insulation provided by the building envelope during AC operation. This increases the flexibility of energy strategies and reduces the demand for building energy during peak periods by utilizing temporal and spatial transformations. Additionally, with the guidance of electricity price, EV owners who would typically charge their vehicles during peak hours can choose to adjust their charging schedule or even supply electricity back to the building, resembling the process of energy storage and discharge. This method, which exploits the flexible energy potential of devices rather than utilizing battery energy storage equipment, is referred to as VES in buildings.

Figures 9, 10 show that based on the existing AC load curve, the consideration of building thermal inertia has resulted in a significant reduction in the AC load demand during high temperature periods (which also coincide with peak electricity prices), without noticeably compromising users’ comfort within the building. Additionally, by utilizing EV for reverse charging, a certain amount of energy load can be provided during peak periods while also offering economic benefits to EV owners.

Figure 9

Figure 9. Results of air-conditioning load adjustment.

Figure 10

Figure 10. Results of EV load adjustment.

6 Conclusion

This study focuses on the issue of electricity trading in commercial buildings that involves a process of subcontracting power supply. It investigates DR strategies for commercial buildings. First, it addresses the problem of insufficient motivation for tenants due to the lack of a reasonable incentive mechanism from the SPS to tenants. It proposes a dynamic time-of-use pricing optimization for the SPS. Second, this study constructs a VES model by exploring the flexible potential of AC loads and EVs in public areas. Lastly, based on Stackelberg game theory, it transforms the price game between the SPS and tenants into a two-stage dynamic optimization process. The existence of equilibrium solutions for this game optimization problem is analyzed, achieving the cost-optimal strategy for the SPS to participate in DR. Simulation tests are conducted in a specific commercial building environment, and the results demonstrate the following:

(1) The utilization of a game-theoretic model based on Stackelberg game theory aligns with the actual scenario of the game process between the SPS and the tenants. The dynamic electricity price obtained through the game between the SPS and the tenants can effectively incentivize the tenants to participate in DR.

(2) VES plays a positive role in DR. By regulating AC virtual energy storage, the demand for AC load can be adjusted without compromising comfort. By reverse charging buildings with EVs, a certain amount of energy load can be provided during DR periods.

The dynamic pricing optimization proposed in this article is more aligned with real commercial building environments. This approach holds significant implications for guiding DR participation among SPSs in commercial buildings.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

HH: conceptualization and writing–original draft. YN: conceptualization and writing–original draft. YJ: writing–original draft. ZT: writing–review and editing. YQ: writing–review and editing. XZ: writing–review and editing.

Funding

The author declare that financial support was received for there search, authorship, and/or publication of this article. This study was supported by the Technology Project of State Grid Jiangsu Electric Power Company (Grant No. J2022096).

Conflict of interest

Authors HH, YN, YJ, ZT, YQ, and XZ were employed by Nanjing Power Supply Company of State Grid Jiangsu Electric Power Co., Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Afroz, Z., Urmee, T., Shafiullah, G., and Higgins, G. (2018). Real-time prediction model for indoor temperature in a commercial building. Appl. Energy 231, 29–53. doi:10.1016/j.apenergy.2018.09.052

CrossRef Full Text | Google Scholar

Barala, C., Mathuria, , and Bhakar, R. (2021). “Virtual energy storage systems: challenges and opportunities,” in 2021 9th IEEE International Conference on Power Systems (ICPS), Kharagpur, India, December 16-18, 2021, 1–6.

CrossRef Full Text | Google Scholar

Bhatti, B., and Broadwater, R. (2020). Distributed nash equilibrium seeking for a dynamic micro-grid energy trading game with non-quadratic payoffs. Energy 202, 117709. doi:10.1016/j.energy.2020.117709

CrossRef Full Text | Google Scholar

Bu, L., Chen, X., Gan, L., Yu, K., Zhou, Y., Cao, J., et al. (2023). Low-carbon operation method of the building based on dynamic carbon emission factor of power system. IET Smart Grid 6 (1), 67–85. doi:10.1049/stg2.12085

CrossRef Full Text | Google Scholar

Chai, Y., Che, H., Tan, C., Tan, W., Yip, S., and Gan, M. (2023). A two-stage optimization method for Vehicle to Grid coordination considering building and Electric Vehicle user expectations. Int. J. Electr. Power & Energy Syst. 148, 108984. doi:10.1016/j.ijepes.2023.108984

CrossRef Full Text | Google Scholar

Chen, X., Bu, L., Chen, C., Gan, L., and Yu, K. (2021). An operational optimization method of regional multi-energy system considering thermal quasi-dynamic characteristics. CSEE J. Power Energy Syst. doi:10.17775/CSEEJPES.2020.03830

CrossRef Full Text | Google Scholar

Cui, F., An, D., and Zhang, G. (2023). A game strategy for demand response based on load monitoring in smart grid. Front. Energy Res. 11. doi:10.3389/fenrg.2023.1240542

CrossRef Full Text | Google Scholar

Darwazeh, D., Duquette, J., Gunay, B., Wilton, I., and Shillinglaw, S. (2022). Review of peak load management strategies in commercial buildings. Sustain. Cities Soc. 77, 103493. doi:10.1016/j.scs.2021.103493

CrossRef Full Text | Google Scholar

Han, H., Wei, T., Wu, h., Xu, X., Zang, H., Sun, G., et al. (2022). A low-carbon dispatch strategy for power systems considering flexible demand response and energy storage. Front. Energy Res. 10. doi:10.3389/fenrg.2022.883602

CrossRef Full Text | Google Scholar

Jin, X., Mu, Y., Jia, H., Wu, J., Jiang, T., and Yu, X. (2017). Dynamic economic dispatch of a hybrid energy microgrid considering building based virtual energy storage system. Appl. Energy 194, 386–398. doi:10.1016/j.apenergy.2016.07.080

CrossRef Full Text | Google Scholar

Jin, Y., Xie, J., Zhou, C., Zhang, J., Xu, M., and Yang, X. (2023). A peak-regulating method of aggregating electric vehicle groups based on improved FCM algorithm. High. Volt. Eng. 1-12. doi:10.13336/j.1003-6520.hve.20230320

CrossRef Full Text | Google Scholar

Li, S., Zhang, L., Nie, L., and Wang, J. (2022b). Trading strategy and benefit optimization of load aggregators in integrated energy systems considering integrated demand response: a hierarchical Stackelberg game. Energy 249, 123678. doi:10.1016/j.energy.2022.123678

CrossRef Full Text | Google Scholar

Li, Z., Jia, F., Mate, A., Jabbari, S., Chakraborty, M., Tambe, M., et al. (2022a). Solving structured hierarchical games using differential backward induction. Proceedings of the thirty-eighth conference on uncertainty in artificial intelligence PMLR 180, 1107–1117. https://proceedings.mlr.press/v180/li22a.html

Google Scholar

Li, Z., Su, S., Jin, X., Chen, H., Li, Y., and Zhang, R. (2021). A hierarchical scheduling method of active distribution network considering flexible loads in office buildings. Int. J. Electr. Power & Energy Syst. 131, 106768. doi:10.1016/j.ijepes.2021.106768

CrossRef Full Text | Google Scholar

Miglioli, A., Aste, N., Pero, C., and Leonforte, F. (2023). Photovoltaic-thermal solar-assisted heat pump systems for building applications: integration and design methods. Energy Built Environ. 4 (Issue 1), 39–56. doi:10.1016/j.enbenv.2021.07.002

CrossRef Full Text | Google Scholar

Shi, Q., Chen, C., Mammoli, A., and Li, F. (2020). Estimating the profile of incentive-based demand response (IBDR) by integrating technical models and social-behavioral factors. IEEE Trans. Smart Grid 11 (1), 171–183. doi:10.1109/tsg.2019.2919601

CrossRef Full Text | Google Scholar

Shi, W., Qin, W., Wang, L., Yao, H., Jing, X., Zhu, Y., et al. (2022). Regional power grid LSTM dispatching strategy considering electric vehicle demand and time of use price difference. Proc. CSEE 42 (10), 3573–3587. doi:10.13334/j.0258-8013.pcsee.202473

CrossRef Full Text | Google Scholar

Song, Z., Shi, J., Li, S., Chen, Z., Yang, W., and Zhang, Z. (2020). Day ahead bidding of a load aggregator considering residential consumers demand response uncertainty modeling. Appl. Sci. 10 (20), 7310. doi:10.3390/app10207310

CrossRef Full Text | Google Scholar

Sparacino, A., Reed, G., Kerestes, R., Grainger, B., and Smith, Z. (2012). “Survey of battery energy storage systems and modeling techniques,” in 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22 - 26 July 2012, 1–8.

CrossRef Full Text | Google Scholar

Sun, W., Liu, X., Xiang, W., and Li, H. (2021). Master-Slave game based optimal pricing strategy for load aggregator in day-ahead electricity market. Automation Electr. Power Syst. 45 (01), 159–167.

Google Scholar

Tiwari, A., and Pindoriya, N. (2022). Automated demand response in smart distribution grid: a review on metering infrastructure, communication Technology and optimization models. Electr. Power Syst. Res. 206, 107835. doi:10.1016/j.epsr.2022.107835

CrossRef Full Text | Google Scholar

U.S. Department of TransportationFederal Highway Administration (2009). National household travel survey (EB/OL]. [2011-06-01].

Google Scholar

Vijayalakshmi, K., Vijayakumar, K., and Nandhakumar, K. (2022). Prediction of virtual energy storage capacity of the air-conditioner using a stochastic gradient descent based artificial neural network. Electr. Power Syst. Res. 208, 107879. doi:10.1016/j.epsr.2022.107879

CrossRef Full Text | Google Scholar

Xu, B., Wang, J., Guo, M., Lu, J., Li, G., and Han, L. (2021). A hybrid demand response mechanism based on real-time incentive and real-time pricing. Energy 231, 120940. doi:10.1016/j.energy.2021.120940

CrossRef Full Text | Google Scholar

Xu, G., Liu, L., Lu, Y., Zhao, Y., Zhang, L., and Song, S. (2023). Perception and decision-making for demand response based on dynamic classification of consumers. Int. J. Electr. Power & Energy Syst. 148, 108954. doi:10.1016/j.ijepes.2023.108954

CrossRef Full Text | Google Scholar

Yasir, A., Ghulam, H., Khursheed, A., Khalid, R., Ahmad, K., and Musaed, A. (2023). A sustainable approach for demand side management considering demand response and renewable energy in smart grids. Front. Energy Res. 11. doi:10.3389/fenrg.2023.1212304

CrossRef Full Text | Google Scholar

Zhang, J., Zhou, X., Lei, S., and Luo, M. (2022). Energy and comfort performance of occupant-centric air conditioning strategy in office buildings with personal comfort devices. Build. Simul. 15, 899–911. doi:10.1007/s12273-021-0852-1

CrossRef Full Text | Google Scholar

Zhou, Y., Ding, H., Liang, Y., Ji, Z., Wu, Z., and Hu, Q. (2021). “Dynamic pricing of integrated energy service providers based on master-slave game,” in 2021 IEEE Sustainable Power and Energy Conference, Nanjing, China, Nov. 25 - 27, 2021, 1891–1896.

CrossRef Full Text | Google Scholar

Zhu, L., Huang, H., Gao, S., He, Y., and Bian, Y. (2023). Research on optimal load allocation of electric vehicle considering wind power consumption. Proc. CSEE 41 (S1), 194–203. doi:10.13334/j.0258-8013.pcsee.211929

CrossRef Full Text | Google Scholar