Decentralized asynchronous adaptive federated learning algorithm for securely prediction of distributed power data

Introduction: Improving the precision and real-time speed of electricity data prediction while safeguarding data privacy and security holds immense significance for all power system participants’ decision-making. To surmount the issues of exorbitant computational expenses and privacy breaches of traditional centralized prediction methods, this paper proposes a decentralized asynchronous adaptive federated learning algorithm for securely prediction of distributed power data, which makes predictions from distributed data more flexible and secure.

Methods: First, each regional node trains its own deep neural network model locally. After that, the node model parameters are uploaded to the decentralized federated learning chain for ensuring local data protection. Asynchronous aggregated update of the global prediction model is then achieved via block mining and shared maintenance. The algorithm has been enhanced based on the traditional federated learning algorithm, which introduces an asynchronous mechanism while adaptively adjusting the regional node model weights and local update step size to overcomes the inefficiency of traditional methods.

Results and Discussion: The experimental analysis of actual electricity price data is conducted to compare and analyze with the centralized prediction model, study the impact of model adoption and parameter settings on the results, and compare with the prediction performance of other federated learning algorithms. The experimental results show that the method proposed in this paper is highly accurate, efficient, and safe.

1 Introduction

Power time-series data has a significant impact on power system operation, planning and decision making. It can support decision making and optimization in load forecasting and dispatching, fault detection and handling, energy planning and market trading. However, with the development of distributed energy resources, the rise of microgrids and the Energy Internet, and the application of intelligent and digital technologies, several factors have contributed to making power systems become distributed (Liu et al., 2021). Meanwhile, power industries, which are a vital part of national energy security, have data on energy supply and demand, grid stability, etc. Therefore, it is necessary to develop an efficient method applicable to the analysis and prediction of distributed power data, which can reduce the cost of data transmission and processing, and also ensure the security of private data in the power industry (Ali et al., 2023).

Currently, researchers have conducted relevant studies on the analysis and prediction of time series data in distributed power systems. The primary methods employed encompass traditional time series analysis and intelligent data mining techniques. In the time series approach, statistical analysis is conducted on power time series data to identify its characteristics, patterns, and trends, which are then utilized to derive predictive values (Badhiye et al., 2022; Frizzo et al., 2023). Some of the more classical time series models include Autoregressive (AR), Moving Average (MA), and Autoregressive Moving Average (ARMA). Furthermore, data mining methods are employed to capture potential non-linear relationships in the formation process of power time series data, thus enhancing prediction accuracy (Wang et al., 2023; Zhang et al., 2023). Commonly utilized intelligent methods include Random Forest (RF), Support Vector Machine (SVM), Deep Neural Network (DNN), Recurrent Neural Network (RNN), Convolutional Neural Network (CNN), Long Short-Term Memory (LSTM), and Gated Recurrent Unit (GRU), among others.

The above methods for predicting electricity time series data usually adopt a centralized computing model, collecting all the data and concentrating them in a central node for model training and prediction analysis. During the training of the centralized predictive model, all data is transmitted and stored on the central server, the model is trained on the central server, and the update of the model is applied directly on the central server (Ahmed et al., 2022). However, the transmission of large amounts of data during centralised learning poses a risk to user privacy (Mcmahan et al., 2017). Meanwhile, the centralized mode has some problems, such as high data acquisition cost, low real-time performance, large resource consumption, and insufficient adaptability to the rapid change of the distributed power system (Li et al., 2020a).

To overcome the shortcomings of centralized tariff prediction models, some studies have applied techniques such as distributed computing and federated learning to power systems, which delegate data processing and analysis tasks to multiple edge nodes to improve efficiency, real-time performance and security. Federated learning methods can perform model training and parameter updating without exposing data and achieve better privacy results. For example, in FedAvg (Mcmahan et al., 2017), participating nodes perform local training and upload model parameters to the server, which performs parameter aggregation and model updating and distributes the global model to nodes, iteratively performing the above steps until convergence.

However, traditional federated learning methods do not perform well in the presence of heterogeneity in the system (Li et al., 2020b). In a fluctuating and undulating distributed power system, the conditions in each region are heterogeneous, and there may be problems such as inconsistent data distribution in each region, different data volumes, different data transmission efficiencies, and different computing power (Yu et al., 2019; Zeng et al., 2023). If an inappropriate data analysis and prediction method is used, the results obtained will have a negative impact on strategy analysis and decision making.

To address the limitations of the above methods, this paper proposes a decentralized asynchronous adaptive federated learning algorithm (DAAFed) for securely prediction of distributed power data. The main contributions of this study are summarized as follows.

1) A decentralized distributed framework has been developed for predicting regional time series data. Each regional node trains its own local data prediction model using its unique data. Next, the parameters of the deep network model are uploaded. With the use of blockchain technology, the aggregation update of the global prediction model is realized through the generation of blocks and the common maintenance of block sets.

2) The conventional federated learning algorithm is improved by the integration of a time-synchronous mechanism, which adopts the adaptive adjustment of the regional node model weight and the local update step size, thereby improving the accuracy and efficiency of distributed data prediction.

3) The proposed method will be validated using measured data from different regions in Spain. By comparing and analyzing the results with a centralized prediction model, investigating the impact of model adoption and parameter settings on the results, and comparing the prediction performance with other federated learning algorithms, the experimental results validate that the proposed method is able to balance safety, accuracy and efficiency.

The rest of this article is organized as follows. Sections 2, 3 present a review of related work and the basic model for power time series data prediction, respectively. The decentralized asynchronous adaptive federated learning method proposed in this article is explained in Section 4. Then, in Section 5, we perform simulation experiments to verify the effectiveness of the method proposed in this paper. Finally, Section 6 concludes this article.

2 Related work

In distributed machine learning, federated learning, as an emerging artificial intelligence technology, can ensure data privacy while performing efficient machine learning, providing a new way to solve the “data silo” problem. Federated learning algorithms have been gradually applied to various problems, such as healthcare (Chen et al., 2023), communication (Qu et al., 2023), language modelling (Wu et al., 2020), transportation (Qi et al., 2023), etc. Federated learning was proposed by Google in 2017, where global models are trained through the cooperation of edge devices without sharing training data. In this approach, training is performed by edge devices, and the weights of the training results are shared with a central server to perform weight updates. And the updated weights are then sent back to the edge devices for a new round of training.

The basic federated learning methods are only suitable for certain environments, so there are also some improved federated learning methods that can be useful in different environments. A federated learning approach in conjunction with deep autoencoder networks based on representation learning was proposed by Husnoo et al. (2023) to enable monitoring and data collection subsystems in distributed grid regions to collaboratively train attack detection models for accurate detection of power system and network security anomalies without sharing sensitive power-related data. The K-means was used to cluster power data locally at the utility, followed by federated learning to build accurate power prediction models for each class of power data in conjunction with other local clients (He and Zhao, 2022). A combined federated learning and deep reinforcement learning scheme for ultra-short term wind power prediction has been proposed by Li et al. (2023a), which uses a deep deterministic policy gradient algorithm as the basic prediction model to improve prediction accuracy, and then integrates the prediction model into the federated learning framework.

Recently, blockchain-based federated learning approaches have become increasingly popular. Blockchain provides tamper-proof and non-repudiation guarantees for the data stored in its ledger. Therefore, storing local and global models in the blockchain helps to improve the overall integrity of the system. Blockchain nodes can also collaborate to maintain the stored data and detect any malicious intentions of the participants. In addition, the execution of smart contracts is deterministic, which allows the federated learning process to be executed correctly and fairly. Intelligent encryption was redesigned to take advantage of the decentralized nature of blockchain technology to design collaborative intelligent federated learning frameworks for automated diagnosis without violating the trustworthiness metrics of privacy, security and data sharing encountered in smart city healthcare systems (Mohamed et al., 2023). Privacy-sensitive energy data can be stored locally at edge producer-consumer nodes without disclosure to third parties, and only the learned local model weights are shared using a blockchain network. Smart contracts are also used to handle the integration of local machine learning predictive models with the blockchain, enabling model parameter scaling and reducing blockchain overhead (Antal et al., 2022). A blockchain federated learning based object detection scheme was proposed by Li et al. (2023b), which eliminates central authority by using a distributed InterPlanetary File System (IPFS). The global model is periodically aggregated when multiple local model parameters are uploaded to the IPFS. Nodes can retrieve the global model from the IPFS. This method has been used in face detection, animal detection, unsafe content detection, vehicle detection, etc.

3 Preliminary

The characteristics and patterns of electricity time series data are intricately linked to the geographical location and regional environment of each distributed area. Factors such as electricity demand, load peaks and troughs, weather conditions, power generation structure, and network configuration in different regions all contribute to the distinct characteristics of electricity data. To address the challenge of predicting electricity time series data in diverse regions and to more effectively capture the non-linear relationships and data features of electricity prices, this study adopts a deep neural network model for accurate predictions at the edge nodes. Specifically, we focus on investigating and analyzing the commonly used CNN and LSTM, as well as their combination, to achieve accurate forecasting.

Let ${\mathrm{\Omega }}_k$ represent the model of the kth node, and the sample data used for training the prediction includes various feature data such as load information $L_k$, generation information $G_k$, weather information $W_k$, date information $D_k$, along with the corresponding labeled data for prediction target $P_k$. The representation can be expressed as Eqs 1, 2:

${\mathit{x}}_{\mathit{k}}=\left[{\mathit{L}}_{\mathit{k}},{\mathit{G}}_{\mathit{k}},{\mathit{W}}_{\mathit{k}},{\mathit{D}}_{\mathit{k}}\right](1)$

${\mathit{y}}_{\mathit{k}}=\left[{\mathit{P}}_{\mathit{k}}\right](2)$

Training of each node is based on both the model as well as the sample data. The prediction accuracy is higher when the value of the loss function is small. The commonly used loss function, Root Mean Square Error (RMSE), can be expressed as in Eq. 3:

$\mathit{l}\left(\mathit{\Omega }\left({\mathit{x}}_{\mathit{k}}\right),{\mathit{y}}_{\mathit{k}}\right)=\sqrt{\frac{\mathbf{1}}{\mathit{n}}{\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}{\left(\mathit{\Omega }\left({\mathit{x}}_{\mathit{i}}\right)-{\mathit{y}}_{\mathit{i}}\right)}^{\mathbf{2}}}(3)$

where $n$ is the total number of samples at the kth node, $x_i\in x_k$, $y_i\in y_k$, and $\mathrm{\Omega }\left(x_i\right)$ is the prediction output of the model.

Considering the efficient utilization of computing resources in each region and the paramount importance of data security, this study adopts the federated learning framework for model training and parameter updating in the region-specific prediction. Each edge node possesses data transmission and computation capabilities, making it advantageous to delegate computation tasks to the edge nodes, thereby ensuring accurate and efficient time series data prediction in a trustworthy environment.

In contrast to the traditional centralized learning model that uploads raw data to a central server for model training, the federated learning framework assigns the model training task to distributed local devices. Subsequently, the global model is updated on the server side by exchanging certain parameters. The process of prediction for each region using the federated learning framework comprises the following steps:

1) The server defines the general task of prediction, including the determination of global variables such as the choice of prediction model, training rounds, and aggregation rounds.

2) As in Eq. 4, each node determines the initial local model based on the global model $\omega$. The node then trains the local model ${\mathrm{\Omega }}_k$ using local data, encompassing generation, load, climate, and date information. The node then uploads the parameters $v_k$, such as local model weights, to the server.

${\mathit{v}}_{\mathit{k}}\leftarrow \mathit{L}\mathit{o}\mathit{c}\mathit{a}\mathit{l}\mathit{U}\mathit{p}\mathit{d}\mathit{a}\mathit{t}\mathit{e}\left(\mathit{\omega },{\mathit{x}}_{\mathit{k}},{\mathit{y}}_{\mathit{k}}\right),\mathit{k}=\mathbf{1,2},\dots ,\mathit{K}(4)$

3) As in Eq. 5, the server globally aggregates the model parameters from each node according to the specified mechanism to construct a new global model $\omega$.

$\mathit{\omega }\leftarrow \mathit{G}\mathit{l}\mathit{o}\mathit{b}\mathit{a}\mathit{l}\mathit{U}\mathit{p}\mathit{d}\mathit{a}\mathit{t}\mathit{e}\left({\mathit{v}}_{\mathbf{1}},{\mathit{v}}_{\mathbf{2}},\dots ,{\mathit{v}}_{\mathit{K}}\right)(5)$

4) Each node receives the latest global model as the initial model for the next round of training and iteratively performs steps 2) and 3) until the model prediction reaches the desired accuracy.

4 Methodology

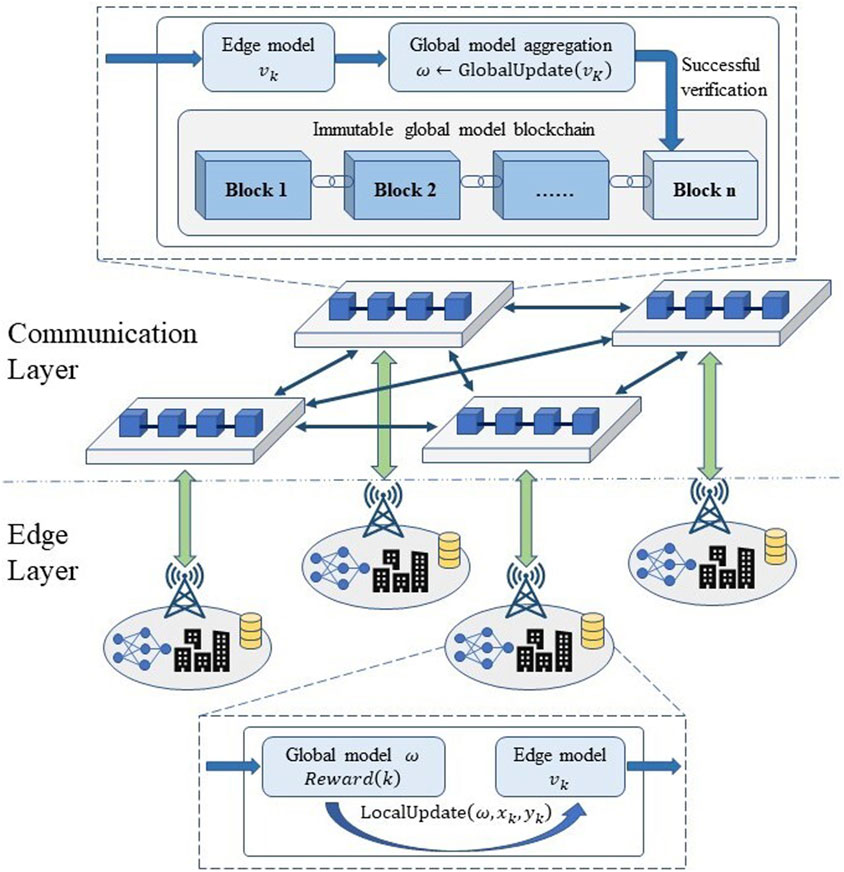
In this section, a decentralized asynchronous adaptive federated learning algorithm is proposed, which is oriented towards the secure prediction of distributed power data. As shown in Figure 1, the distributed regional time-series data prediction framework designed in this paper has a two-layer structure. The edge layer consists of each actual compute node, including the local power network and real-time data. The communication layer is the communication link between nodes, which is used to aggregate and update the model under the cooperation. First, each regional node locally trains its own deep network model ${\mathrm{\Omega }}_k$ and uploads the node prediction model parameters $v_k$ to the federated learning chain to realize local data protection. Then, the global model $\omega$ is updated asynchronously based on the distributed ledger mechanism in blockchain technology, and the aggregation of global models is realized by block mining, and each regional node obtains the latest global model $\omega$ through the shared immutable blockchain for subsequent prediction tasks.

FIGURE 1

FIGURE 1. Distributed regional electricity price forecasting framework.

4.1 Traditional federated learning algorithm

Within the federated learning framework, each participating node conducts local training and uploads model parameters to the server. The server aggregates parameters and updates the model, distributing the global model to each node. These procedures are iterative and continue until convergence is achieved. The most commonly used model aggregation algorithm for federated learning is FedAvg. The total number of nodes is $K$, the kth node contributes data samples as $S_k$, then the number of samples of this node is $\left|S_k\right|$, and the total number of data samples is $S={\sum }_{k=1}^K\left|S_k\right|$.

As in Eq. 6, the global objective function that requires optimization is $\min F\left(\omega \right)$, where $\omega \in R^d$:

$\mathit{F}\left(\mathit{\omega }\right)=\frac{\mathbf{1}}{\mathit{S}}{\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{S}}{\mathit{f}}_{\mathit{i}}\left(\mathit{\omega }\right)(6)$

where $f_i\left(\omega \right)=l\left(x_i,y_i;\omega \right)$ represents the prediction loss for the sample $\left(x_i,y_i\right)$ under the model parameter $\omega$, then Eq. 6 can be rewritten as Eqs 7, 8:

${\mathit{F}}_{\mathit{k}}\left({\mathit{v}}_{\mathit{k}}\right)=\frac{\mathbf{1}}{\left|{\mathit{S}}_{\mathit{k}}\right|}{\sum }_{\left({\mathit{x}}_{\mathit{i}},{\mathit{y}}_{\mathit{i}}\right)\in {\mathit{S}}_{\mathit{k}}}{\mathit{f}}_{\mathit{i}}\left({\mathit{v}}_{\mathit{k}}\right)(7)$

$\mathit{F}\left(\mathit{\omega }\right)={\sum }_{\mathit{k}=\mathbf{1}}^{\mathit{K}}\frac{\left|{\mathit{S}}_{\mathit{k}}\right|}{\mathit{S}}{\mathit{F}}_{\mathit{k}}\left({\mathit{v}}_{\mathit{k}}\right)(8)$

where $F_k\left(v_k\right)$ is the loss function of the kth node, while $F\left(\omega \right)$ is the overall federated loss function.

Each iteration process of FedAvg comprises a local update and a global update. During every iteration, the following process is undertaken:

Initially, the latest global model from the server is received as the local model for the current round during the local update of each node. Then, $e$ iterations of the local model are carried out, updating the model parameter ${\omega }^k$ for the kth node in each iteration as in Eq. 9:

${\mathit{v}}_{\mathit{k}}^{\mathit{t}}={\mathit{v}}_{\mathit{k}}^{\mathit{t}}-\mathit{\eta }\nabla {\mathit{F}}_{\mathit{k}}\left({\mathit{v}}_{\mathit{k}}^{\mathit{t}}\right)(9)$

where, $\eta$ is the learning rate of the local update at each node.

Secondly, once the local update is executed, the model parameters are uploaded to the server. Subsequently, a server-side global aggregation update is implemented using the following aggregation formula as in Eq. 10:

${\mathit{\omega }}_{\mathit{t}+\mathbf{1}}={\sum }_{\mathit{k}=\mathbf{1}}^{\mathit{K}}\frac{\left|{\mathit{S}}_{\mathit{k}}\right|}{\mathit{S}}{\mathit{v}}_{\mathit{k}}^{\mathit{t}}(10)$

4.2 Asynchronous adaptive mechanism

The asynchronous adaptive federated learning algorithm proposed in this paper makes improvements based on the FedAvg algorithm. In the process of global model aggregation, an asynchronous mechanism and adaptive adjustment of node model weights based on the determination of time obsolescence are introduced. In the process of updating local node models, personalized learning and adaptive step length adjustment are introduced to ensure asynchronous real-time and regional personalization, and to improve the prediction accuracy while enhancing the generalization ability of the global model. The specific implementation process of the asynchronous adaptive federal learning algorithm is shown as follow.

First, the overall objective function is determined based on Eq. 10. In the asynchronous adaptive federal learning algorithm, the overall objective function is Eq. 11:

$\mathit{min}{\sum }_{\mathit{k}=\mathbf{1}}^{\mathit{K}}\frac{\left|{\mathit{S}}_{\mathit{k}}\right|}{\mathit{S}}{\mathit{F}}_{\mathit{k}}\left({\mathit{v}}_{\mathit{k}}\right)(11)$

Let ${\lambda }_k=\frac{\left|S_k\right|}{S}$ denote the weight of each node. Then add model personalization constraints as in Eq. 12:

$\mathit{s}.\mathit{t}.{‖{\mathit{v}}_{\mathit{k}}-\mathit{\omega }‖}^{\mathbf{2}}\le {\mathit{T}}_{\mathit{k}}(12)$

where $\left\{T_k,k=\mathrm{1,2},\dots ,K\right\}$ is the model personalization tolerance threshold, which is used to reflect the difference between the global model and the local model to achieve the personalized learning of the node’s local model. The above optimization objective function with constraints can be rewritten by using the Lagrange equation as in Eq. 13:

$\mathit{L}\left({\mathit{v}}_{\mathit{k}},\mathit{\omega },{\mathit{\mu }}_{\mathit{k}}\right)={\sum }_{\mathit{k}=\mathbf{1}}^{\mathit{K}}{\mathit{\lambda }}_{\mathit{k}}{\mathit{F}}_{\mathit{k}}\left({\mathit{v}}_{\mathit{k}}\right)+\frac{{\mathit{u}}_{\mathit{k}}}{\mathbf{2}}\left({‖{\mathit{v}}_{\mathit{k}}-\mathit{\omega }‖}^{\mathbf{2}}-{\mathit{T}}_{\mathit{k}}\right)(13)$

The partial derivative of this objective function can be obtained:

${\nabla }_{{\mathit{v}}_{\mathit{k}}}\mathit{L}={\mathit{\lambda }}_{\mathit{k}}\nabla {\mathit{F}}_{\mathit{k}}\left({\mathit{v}}_{\mathit{k}}\right)+{\mathit{u}}_{\mathit{k}}\left({\mathit{v}}_{\mathit{k}}-\mathit{\omega }\right)(14)$

${\nabla }_{\mathit{\omega }}\mathit{L}={\sum }_{\mathit{k}=\mathbf{1}}^{\mathit{K}}{\mathit{u}}_{\mathit{k}}\left({\mathit{v}}_{\mathit{k}}-\mathit{\omega }\right)(15)$

${\nabla }_{{\mathit{u}}_{\mathit{k}}}\mathit{L}=\frac{\mathbf{1}}{\mathbf{2}}\left({‖{\mathit{v}}_{\mathit{k}}-\mathit{\omega }‖}^{\mathbf{2}}-{\mathit{T}}_{\mathit{k}}\right)(16)$

where $k=\mathrm{1,2},\dots ,K$.

Secondly, in the aggregation of global models, the asynchronous characteristics of multi-node collaboration should be considered. Asynchronous training allows each node to update model parameters independently with the server without worrying about the calculation pace of other nodes. In the case of asynchronous training, the model parameter update on the server side is carried out asynchronously, that is, there is no need to wait for the progress of other nodes that are being calculated. Considering the different time required for each node to complete the local task, this paper assumes that global aggregation begins whenever a single edge node completes uploading model parameters. Therefore, the variable ${\phi }_k\left(t\right)\in \left\{\mathrm{0,1}\right\}$ is introduced to indicate the completion of node updates as in Eq. 17:

${\mathit{\phi }}_{\mathit{k}}\left(\mathit{t}\right)=\left\{\begin{array}{c}\mathbf{1},\mathit{k}\mathit{t}\mathit{h}\mathit{n}\mathit{o}\mathit{d}\mathit{e}\mathit{c}\mathit{o}\mathit{m}\mathit{p}\mathit{l}\mathit{e}\mathit{t}\mathit{e}\mathit{s}\mathit{u}\mathit{p}\mathit{d}\mathit{a}\mathit{t}\mathit{e}\mathit{a}\mathit{t}\mathit{t}\\ \mathbf{0},\mathit{o}\mathit{t}\mathit{h}\mathit{e}\mathit{r}\mathit{s}\end{array}\right.(17)$

The above variables satisfy the constraints as in Eq. 18:

${\sum }_{\mathit{k}=\mathbf{1}}^{\mathit{K}}{\mathit{\phi }}_{\mathit{k}}\left(\mathit{t}\right)=\mathbf{1}(18)$

According to Eq. 15, the global model aggregation is given by:

$\mathit{\omega }\left({\mathit{t}}_{\mathbf{1}}\right)=\mathit{\omega }\left({\mathit{t}}_{\mathbf{0}}\right)+{\sum }_{\mathit{k}=\mathbf{1}}^{\mathit{K}}{\mathit{\phi }}_{\mathit{k}}\left({\mathit{t}}_{\mathbf{1}}\right){\mathit{\beta }}_{\mathit{k}}\left({\mathit{t}}_{\mathit{k}},{\mathit{t}}_{\mathbf{1}}\right)\left({\mathit{v}}_{\mathit{k}}\left({\mathit{t}}_{\mathbf{1}}\right)-\mathit{\omega }\left({\mathit{t}}_{\mathbf{0}}\right)\right)(19)$

where $t_1$ is the generation moment of the global model of the current generation, which is also the moment when the local model of the kth node completes this update, $t_0$ is the generation moment of the global model of the previous generation, $t_k$ is the generation moment of the global model adopted by the local model of the kth node when it performs the current update, ${\beta }_k$ is the weight adaptive adjustment function based on the determination of the temporal staleness, which is determined according to the before and after of the local update of the kth node. If this model is outdated, the current node model is given a smaller weight, the specific form can be defined as:

${\mathit{\beta }}_{\mathit{k}}\left({\mathit{t}}_{\mathit{k}},{\mathit{t}}_{\mathbf{1}}\right)={\mathit{\beta }}_{\mathit{m}}\mathit{cos}\left(\frac{\mathit{\pi }\left({{\mathit{t}}_{\mathbf{1}}-\mathit{t}}_{\mathit{k}}\right)}{\mathbf{2}\left({\mathit{t}}_{\mathbf{1}}+\mathit{\epsilon }\right)}\right)(20)$

where ${\beta }_m$ is the maximum learning weight, $\epsilon$ is a constant value close to zero. And when $t_k$ is similar to $t_1$, ${\beta }_k$ takes a value close to ${\beta }_m$.

$\frac{\partial {\mathit{\beta }}_{\mathit{k}}}{\partial {\mathit{t}}_{\mathit{k}}}={\mathit{\beta }}_{\mathit{m}}\mathit{sin}\left(\frac{\mathit{\pi }\left({{\mathit{t}}_{\mathbf{1}}-\mathit{t}}_{\mathit{k}}\right)}{\mathbf{2}\left({\mathit{t}}_{\mathbf{1}}+\mathit{\epsilon }\right)}\right)\left(\frac{\mathit{\pi }}{\mathbf{2}\left({\mathit{t}}_{\mathbf{1}}+\mathit{\epsilon }\right)}\right)>\mathbf{0}(21)$

$\frac{\partial {\mathit{\beta }}_{\mathit{k}}}{\partial {\mathit{t}}_{\mathbf{1}}}={-\mathit{\beta }}_{\mathit{m}}\mathit{sin}\left(\frac{\mathit{\pi }\left({{\mathit{t}}_{\mathbf{1}}-\mathit{t}}_{\mathit{k}}\right)}{\mathbf{2}\left({\mathit{t}}_{\mathbf{1}}+\mathit{\epsilon }\right)}\right)\left(\frac{\mathit{\pi }\left({\mathit{t}}_{\mathit{k}}+\mathit{\epsilon }\right)}{\mathbf{2}{\left({\mathit{t}}_{\mathbf{1}}+\mathit{\epsilon }\right)}^{\mathbf{2}}}\right)<\mathbf{0}(22)$

$\frac{{\partial }^{\mathbf{2}}{\mathit{\beta }}_{\mathit{k}}}{\partial {{\mathit{t}}_{\mathit{k}}}^{\mathbf{2}}}=-{\mathit{\beta }}_{\mathit{m}}\mathit{cos}\left(\frac{\mathit{\pi }\left({{\mathit{t}}_{\mathbf{1}}-\mathit{t}}_{\mathit{k}}\right)}{\mathbf{2}\left({\mathit{t}}_{\mathbf{1}}+\mathit{\epsilon }\right)}\right){\left(\frac{\mathit{\pi }}{\mathbf{2}\left({\mathit{t}}_{\mathbf{1}}+\mathit{\epsilon }\right)}\right)}^{\mathbf{2}}<\mathbf{0}(23)$

$\frac{{\partial }^{\mathbf{2}}{\mathit{\beta }}_{\mathit{k}}}{\partial {{\mathit{t}}_{\mathbf{1}}}^{\mathbf{2}}}=-{\mathit{\beta }}_{\mathit{m}}\mathit{cos}\left(\frac{\mathit{\pi }\left({{\mathit{t}}_{\mathbf{1}}-\mathit{t}}_{\mathit{k}}\right)}{\mathbf{2}\left({\mathit{t}}_{\mathbf{1}}+\mathit{\epsilon }\right)}\right){\left(\frac{\mathit{\pi }\left({\mathit{t}}_{\mathit{k}}+\mathit{\epsilon }\right)}{\mathbf{2}{\left({\mathit{t}}_{\mathbf{1}}+\mathit{\epsilon }\right)}^{\mathbf{2}}}\right)}^{\mathbf{2}}+\mathbf{2}{\mathit{\beta }}_{\mathit{m}}\mathit{sin}\left(\frac{\mathit{\pi }\left({{\mathit{t}}_{\mathbf{1}}-\mathit{t}}_{\mathit{k}}\right)}{\mathbf{2}\left({\mathit{t}}_{\mathbf{1}}+\mathit{\epsilon }\right)}\right)\left(\frac{\mathit{\pi }\left({\mathit{t}}_{\mathit{k}}+\mathit{\epsilon }\right)}{\mathbf{2}{\left({\mathit{t}}_{\mathbf{1}}+\mathit{\epsilon }\right)}^{\mathbf{3}}}\right)(24)$

The values of ${\beta }_k$ vary with $t_k$ and $t_1$ as shown in Figure 2. According to Eqs 21–24, ${\beta }_k$ increases with the increase of $t_k$, and the magnitude of the increase decreases gradually, indicating that when the local model is updated with the newer global model, the weight of the updated node model should be increased accordingly. Also ${\beta }_k$ decreases with the increase of $t_1$. When $t_k$ is smaller, $\frac{{\partial }^2{\beta }_k}{\partial {t_1}^2}>0$, which means ${\beta }_k$ is convex. When $t_k$ is larger, $\frac{{\partial }^2{\beta }_k}{\partial {t_1}^2}<0$, which means ${\beta }_k$ is concave. It indicates that the global model parameters obtained at the early stage of prediction have large weights only at the early stage, and their weights decrease rapidly in the later stage of prediction.

FIGURE 2

FIGURE 2. Weight adaptive adjustment function.

Convergence analysis is carried out on the aggregation of the global model. When $T\to \infty$, the algorithm is considered convergent if the statistic $R\left(T\right)={\sum }_{t=1}^T\left[F\left(\omega \left(t\right)\right)-F\left({\omega }^{*}\right)\right]$ meets the predetermined convergence criteria that $R\left(T\right)/T\to 0$, which means $\omega \to \arg \min {\sum }_{t=1}^{T}F\left(\omega \left(t\right)\right)\triangleq {\omega }^{*}$, $\omega$ converges to ${\omega }^{*}$ to minimize the objective function.

The convergence analysis is shown as in Eq. 25.

$\mathit{R}\left(\mathit{T}\right)={\sum }_{\mathit{t}=\mathbf{1}}^{\mathit{T}}\left[\mathit{F}\left(\mathit{\omega }\left(\mathit{t}\right)\right)-\mathit{F}\left({\mathit{\omega }}^{*}\right)\right]\le {\sum }_{\mathit{t}=\mathbf{1}}^{\mathit{T}}<\mathit{\omega }\left(\mathit{t}\right)-\mathit{v},\mathit{\omega }\left(\mathit{t}\right)-{\mathit{\omega }}^{*}>$

$\le {\sum }_{\mathit{t}=\mathbf{1}}^{\mathit{T}}\frac{\mathbf{1}}{\mathbf{2}{\mathit{\beta }}_{\mathit{t}}}\left[{‖\mathit{\omega }\left(\mathit{t}\right)-{\mathit{\omega }}^{*}‖}^{\mathbf{2}}-{‖\mathit{\omega }\left({\mathit{t}}^{\prime }\right)-{\mathit{\omega }}^{*}‖}^{\mathbf{2}}\right]+\frac{{\mathit{\beta }}_{\mathit{t}}}{\mathbf{2}}{‖\mathit{\omega }\left(\mathit{t}\right)-\mathit{v}‖}^{\mathbf{2}}(\mathrm{25a})$

According to (22), it can be inferred that ${\beta }_t$ decreases monotonically. Using the assumption that ${‖\omega \left(t\right)-{\omega }^{*}‖}^2\le D^2$ and local node personalization constraints ${‖\omega \left(t\right)-v‖}^2\le G^2$, the above equation can be simplified and transformed as follows:

$\mathit{R}\left(\mathit{T}\right)\le \frac{\mathbf{1}}{\mathbf{2}{\mathit{\beta }}_{\mathbf{1}}}{\mathit{D}}^{\mathbf{2}}+{\mathit{D}}^{\mathbf{2}}{\sum }_{\mathit{t}=\mathbf{2}}^{\mathit{T}}\left(\frac{\mathbf{1}}{{\mathbf{2}\mathit{\beta }}_{\mathit{t}}}-\frac{\mathbf{1}}{\mathbf{2}{\mathit{\beta }}_{\mathit{t}-\mathbf{1}}}\right)+\frac{{\mathit{G}}^{\mathbf{2}}}{\mathbf{2}}{\mathit{\beta }}_{\mathit{T}}=\frac{{\mathit{D}}^{\mathbf{2}}}{\mathbf{2}{\mathit{\beta }}_{\mathit{T}}}+\frac{{\mathit{G}}^{\mathbf{2}}}{\mathbf{2}}{\mathit{\beta }}_{\mathit{T}}\le \frac{{\mathit{D}}^{\mathbf{2}}}{\mathbf{2}{\mathit{\beta }}_{\mathit{min}}}+\frac{{\mathit{G}}^{\mathbf{2}}{\mathit{\beta }}_{\mathit{max}}}{\mathbf{2}}(\mathrm{25b})$

Consequently, $R\left(T\right)$ has an upper bound and mean value of the statistic $R\left(T\right)/T\to 0$ when $T\to \infty$, ensuring the convergence of the global model aggregation.

Furthermore, for the update process of the edge model, according to Eqs 14, 16, the update process can be expressed as follow:

${\mathit{v}}_{\mathit{k}}\left({\mathit{t}}_{\mathbf{1}}\right)={\mathit{v}}_{\mathit{k}}\left({\mathit{t}}_{\mathit{k}}\right)-{\mathit{\eta }}_{\mathbf{1}}\left(\nabla {\mathit{F}}_{\mathit{k}}\left({\mathit{v}}_{\mathit{k}}\left({\mathit{t}}_{\mathit{k}}\right)\right)\right)\times \left[{\mathit{\lambda }}_{\mathit{k}}\nabla {\mathit{F}}_{\mathit{k}}\left({\mathit{v}}_{\mathit{k}}\left({\mathit{t}}_{\mathit{k}}\right)\right)+{\mathit{u}}_{\mathit{k}}\left({\mathit{v}}_{\mathit{k}}\left({\mathit{t}}_{\mathit{k}}\right)-\mathit{\omega }\left({\mathit{t}}_{\mathit{k}}\right)\right)\right](26)$

${\mathit{u}}_{\mathit{k}}\left({\mathit{t}}_{\mathbf{1}}\right)={\mathit{u}}_{\mathit{k}}\left({\mathit{t}}_{\mathit{k}}\right)-{\mathit{\eta }}_{\mathbf{2}}\left({‖{\mathit{v}}_{\mathit{k}}\left({\mathit{t}}_{\mathit{k}}\right)-\mathit{\omega }\left({\mathit{t}}_{\mathit{k}}\right)‖}^{\mathbf{2}}\right)\times \left({‖{\mathit{v}}_{\mathit{k}}\left({\mathit{t}}_{\mathit{k}}\right)-\mathit{\omega }\left({\mathit{t}}_{\mathit{k}}\right)‖}^{\mathbf{2}}-{\mathit{T}}_{\mathit{k}}\right)(27)$

where ${\eta }_1$ and ${\eta }_2$ are the adaptive adjustment function of the step size, which can be expressed as

$\mathit{\eta }\left(\mathit{z}\right)=\mathit{max}\left\{{\mathit{\eta }}_{\mathit{min}},\mathit{min}\left\{{\mathit{\eta }}_{\mathit{max}},{\mathit{p}}^{\mathit{q}*\mathit{z}}\right\}\right\}(28)$

where ${\eta }_{\mathit{min}}$ is the minimum value of the step, ${\eta }_{\mathit{max}}$ is the maximum value of the step, $p>1$ and $q>0$, $z$ is the independent variable of the adaptive function, and $\eta \left(z\right)$ is a non-decreasing function taking values in the interval $\left[{\eta }_{\mathit{min}},{\eta }_{\mathit{max}}\right]$. As in Eq. 28, it is indicated that when the gradient of the loss function is small and the local model is close to the global model, the step size is adaptively reduced to prevent non-convergence in the learning of the local model. Compared with the fixed step size, the adaptive step size can adjust the amplitude of the parameter changing direction along the gradient according to the training stage, and improve the convergence rate while ensuring the convergence accuracy.

Convergence analysis of the update process of the edge model is performed. Since the parameters of the above process are solved according to a variant of gradient descent, a proof is required:

$\mathit{E}{‖{\mathit{v}}_{\mathit{k}}\left({\mathit{t}}_{\mathbf{1}}\right)-{\mathit{\omega }}^{*}‖}^{\mathbf{2}}\le \mathit{l}\left({\mathit{v}}_{\mathit{k}}\left({\mathit{t}}_{\mathit{k}}\right)-{\mathit{\omega }}^{*}\right)(29)$

As in Eq. 29, the distance between the parameters of the current iteration and the optimal parameters ${\omega }^{*}$ is less than the distance between the parameters of the previous iteration and the optimal parameters ${\omega }^{*}$, which means that the upper bound of the distance between the parameters of the current iteration and the optimal parameters is decreasing.

There are some assumptions on the functions $F_1,\dots ,F_K$ for the algorithm as the premise of convergence analysis:

1) As in Eq. 30, $F_1,\dots ,F_K$ are all L-smooth: for all $v$ and $\omega$,

${\mathit{F}}_{\mathit{k}}\left(\mathit{v}\right)\le {\mathit{F}}_{\mathit{k}}\left(\mathit{\omega }\right)+{\left(\mathit{v}-\mathit{\omega }\right)}^{\mathit{T}}\nabla {\mathit{F}}_{\mathit{k}}\left(\mathit{\omega }\right)+\frac{\mathit{L}}{\mathbf{2}}{‖\mathit{v}-\mathit{\omega }‖}^{\mathbf{2}}(30)$

2) As in Eq. 31, $F_1,\dots ,F_K$ are all $\mu$-convex: for all $v$ and $\omega$,

${\mathit{F}}_{\mathit{k}}\left(\mathit{v}\right)\ge {\mathit{F}}_{\mathit{k}}\left(\mathit{\omega }\right)+{\left(\mathit{v}-\mathit{\omega }\right)}^{\mathit{T}}\nabla {\mathit{F}}_{\mathit{k}}\left(\mathit{\omega }\right)+\frac{\mathit{\mu }}{\mathbf{2}}{‖\mathit{v}-\mathit{\omega }‖}^{\mathbf{2}}(31)$

3) The variance of the stochastic gradient is bounded as in Eq. 32:

$\mathit{E}‖\nabla {\mathit{F}}_{\mathit{k}}\left(\mathit{v}\right)-\nabla {\mathit{F}}_{\mathit{k}}\left(\mathit{\omega }\right)‖\le {\mathrm{\sigma }}_{\mathit{k}}^{\mathbf{2}}(32)$

4) The expectation of the 2-Norm of the stochastic gradient is consistently bounded as in Eq. 33:

${\mathit{E}‖\nabla {\mathit{F}}_{\mathit{k}}\left(\mathit{v}\right)‖}_{\mathbf{2}}^{\mathbf{2}}\le {\mathit{G}}^{\mathbf{2}}(33)$

Meanwhile, we measure the system heterogeneity by $\mathrm{\Gamma }$ as in Eq. 34, which denotes the difference between the optimal value of the global objective function and the weighted local objective function. $\mathrm{\Gamma }$ converges to 0 when the data are distributed iid independently and identically.

$\mathit{\Gamma }={\mathit{F}}^{*}-{\sum }_{\mathit{k}}{\mathit{\lambda }}_{\mathit{k}}{\mathit{F}}_{\mathit{k}}^{*}(34)$

Let $v^{\prime }{=v}_k\left(t_1\right)$ and $v{=v}_k\left(t_k\right)$, then

$\mathit{E}{‖{\mathit{v}}^{\prime }-{\mathit{\omega }}^{*}‖}^{\mathbf{2}}$

$=\mathit{E}{\left|\left|\mathit{v}-{\mathit{\omega }}^{*}-{\mathit{\eta }}_{\mathbf{1}}\nabla {\mathit{F}}_{\mathit{k}}\left(\mathit{v}\right)\times \left[{\mathit{\lambda }}_{\mathit{k}}\nabla {\mathit{F}}_{\mathit{k}}\left(\mathit{v}\right)+{\mathit{u}}_{\mathit{k}}\left(\mathit{v}-\mathit{\omega }\right)\right]\right|\right|}^{\mathbf{2}}$

$=\mathit{E}({‖\mathit{v}-{\mathit{\omega }}^{*}‖}^{\mathbf{2}}+{{\mathit{\eta }}_{\mathbf{1}}}^{\mathbf{2}}{\left[{\mathit{\lambda }}_{\mathit{k}}\nabla {\mathit{F}}_{\mathit{k}}\left(\mathit{v}\right)+{\mathit{u}}_{\mathit{k}}\left(\mathit{v}-\mathit{\omega }\right)\right]}^{\mathbf{2}}-\mathbf{2}{\mathit{\eta }}_{\mathbf{1}}\times$

$\left.<\mathit{v}-{\mathit{\omega }}^{*},\left[{\mathit{\lambda }}_{\mathit{k}}\nabla {\mathit{F}}_{\mathit{k}}\left(\mathit{v}\right)+{\mathit{u}}_{\mathit{k}}\left(\mathit{v}-\mathit{\omega }\right)\right]\nabla {\mathit{F}}_{\mathit{k}}\left(\mathit{v}\right)>\right)(35)$

in which

$-\mathbf{2}{\mathit{\eta }}_{\mathbf{1}}<\mathit{v}-{\mathit{\omega }}^{*},\left[{\mathit{\lambda }}_{\mathit{k}}\nabla {\mathit{F}}_{\mathit{k}}\left(\mathit{v}\right)+{\mathit{u}}_{\mathit{k}}\left(\mathit{v}-\mathit{\omega }\right)\right]\nabla {\mathit{F}}_{\mathit{k}}\left(\mathit{v}\right)>$

$=-\mathbf{2}{\mathit{\eta }}_{\mathbf{1}}<\mathit{v}-\mathit{\omega }+\mathit{\omega }-{\mathit{\omega }}^{*},\left[{\mathit{\lambda }}_{\mathit{k}}\nabla {\mathit{F}}_{\mathit{k}}\left(\mathit{v}\right)+{\mathit{u}}_{\mathit{k}}\left(\mathit{v}-\mathit{\omega }\right)\right]\nabla {\mathit{F}}_{\mathit{k}}\left(\mathit{v}\right)>$

$\le -\mathbf{2}{\mathit{\eta }}_{\mathbf{1}}\left[{\mathit{u}}_{\mathit{k}}{\mathit{T}}_{\mathit{k}}+\frac{\mathit{\mu }}{\mathbf{2}}{‖\mathit{v}-{\mathit{\omega }}^{*}‖}^{\mathbf{2}}\right]+\mathbf{6}\mathrm{\Gamma }\mathbf{L}{{\mathit{\eta }}_{\mathbf{1}}}^{\mathbf{2}}-{\mathit{\lambda }}_{\mathit{k}}{\mathit{T}}_{\mathit{k}}(36)$

${\left[{\mathit{\lambda }}_{\mathit{k}}\nabla {\mathit{F}}_{\mathit{k}}\left(\mathit{v}\right)+{\mathit{u}}_{\mathit{k}}\left(\mathit{v}-\mathit{\omega }\right)\right]}^{\mathbf{2}}$

$={{\mathit{\lambda }}_{\mathit{k}}}^{\mathbf{2}}{\nabla {\mathit{F}}_{\mathit{k}}\left(\mathit{v}\right)}^{\mathbf{2}}+{{\mathit{u}}_{\mathit{k}}}^{\mathbf{2}}{‖\mathit{v}-\mathit{\omega }‖}^{\mathbf{2}}+\mathbf{2}{\mathit{\lambda }}_{\mathit{k}}{\mathit{\mu }}_{\mathit{k}}\nabla {\mathit{F}}_{\mathit{k}}\left(\mathit{v}\right)\left(\mathit{v}-\mathit{\omega }\right)$

$\le {{\mathit{\lambda }}_{\mathit{k}}}^{\mathbf{2}}{\mathit{G}}^{\mathbf{2}}+{{\mathit{u}}_{\mathit{k}}}^{\mathbf{2}}{\mathit{T}}_{\mathit{k}}+\mathbf{2}{\mathit{\lambda }}_{\mathit{k}}{\mathit{u}}_{\mathit{k}}\frac{\mathit{\mu }}{\mathbf{2}}{\mathit{T}}_{\mathit{k}}(37)$

In summary, the original equation can be converted as follow:

$\mathit{E}{‖{\mathit{v}}^{\prime }-{\mathit{\omega }}^{*}‖}^{\mathbf{2}}\le \left(\mathbf{1}-{\mathit{\eta }}_{\mathbf{1}}\mathit{\mu }\right){\mathit{E}‖\mathit{v}-{\mathit{\omega }}^{*}‖}^{\mathbf{2}}{+{{\mathit{\eta }}_{\mathbf{1}}}^{\mathbf{2}}\mathit{B}-(\mathit{\lambda }}_{\mathit{k}}+\mathbf{2}{\mathit{\eta }}_{\mathbf{1}}{\mathit{u}}_{\mathit{k}}){\mathit{T}}_{\mathit{k}}(38)$

$\mathit{B}=\mathbf{6}\mathit{\Gamma }\mathit{L}+{{\mathit{\lambda }}_{\mathit{k}}}^{\mathbf{2}}{\mathit{G}}^{\mathbf{2}}+{{\mathit{u}}_{\mathit{k}}}^{\mathbf{2}}{\mathit{T}}_{\mathit{k}}+{\mathit{\lambda }}_{\mathit{k}}{\mathit{u}}_{\mathit{k}}\mathit{\mu }{\mathit{T}}_{\mathit{k}}(39)$

As in Eqs 35–39, this convergence analysis is formally similar to that of FedAvg. However the equation in this paper subtracts one more positive term, which show that the iterative process is convergent.

4.3 Decentralization mechanism

Considering the demand for distributed power time-series data prediction and the disadvantages of centralized processing, the approach of applying blockchain technology in this case is proposed in this paper in order to decentralize prediction, leveraging its global data ledger sharing and non-tamperability, which can further ensure the trust, security, transparency and traceability of data in the power industry.

In this paper, the federated learning global model parameter updating process described in the previous subsection is implemented by placing it on a blockchain. The blockchain guarantees the operation of a shared and trusted distributed ledger on a peer-to-peer network, which in the prediction scenario of this paper is the shared set of global model parameters blocks. The global model used for prediction is placed on the blockchain for updating so that it is not under the control of any single node, but each regional node has equal rights to validate and access the global model in the blockchain in such a way that it not only avoids a single point of failure, but also protects against data attacks in terms of security.

The workflow of the communication layer of the decentralized federated learning framework used in this paper broadly includes the processes of block generation, consensus verification and global maintenance. The decentralized implementation of the prediction framework includes the following:

1) Setting permissions for each regional participant, only participants with permissions for electricity data prediction can jointly train the federation model, and new nodes can join and receive the current federation model only if they meet the permission conditions when accessing.

2) After each edge node completes a round of local training, it packages and broadcasts the privacy protected local model parameters and other data to the network, which includes the local task start time $t_k$, the local task completion time $t_1$, the local model parameters $v_k\left(t_1\right)$, and the task completion situation ${\phi }_k\left(t_1\right)$ and other data to be recorded.

The local update is completed to form a data packet:

${\mathit{T}\mathit{X}}_{\mathbf{0}}=\left\{{\mathit{t}}_{\mathit{k}},{\mathit{t}}_{\mathbf{1}},{\mathit{v}}_{\mathit{k}}\left({\mathit{t}}_{\mathbf{1}}\right),\dots \right\}(40)$

3) Each edge node collects the latest packet ${TX}_0$ broadcast in the network, completes the update of the global model by block mining, calculates the global model aggregation $\omega \left(t_1\right)$, and packages the data before and after the aggregation.

The global aggregation is completed to form a data packet:

${\mathit{T}\mathit{X}}_{\mathbf{1}}=\left\{{\mathit{\phi }}_{\mathit{k}}\left({\mathit{t}}_{\mathbf{1}}\right),\mathit{\omega }\left({\mathit{t}}_{\mathbf{1}}\right),\dots \right\}(41)$

4) The node that completes block mining packages the above packets to form a block, and broadcasts it to the network of nodes waiting for verification. The block consists of a block body and a block header, where the block body contains the data before and after aggregation, and the block header contains the predecessor hash and the root hash, and the specific process of block generation includes:

Local updating and global aggregation of data packets together form the block body:

${\mathit{B}\mathit{o}\mathit{d}\mathit{y}}_{\mathit{N}}=\left\{\mathit{T}\mathit{X}\right\}=\left\{{\mathit{T}\mathit{X}}_{\mathbf{0}},{\mathit{T}\mathit{X}}_{\mathbf{1}},\dots \right\}(42)$

Hash algorithm achieves the irreversible mapping from plaintext to ciphertext, this paper uses SHA256 to calculate the hash value. The successor hash is the hash value of the previous block and the root hash is generated based on the hash value of the packet $\left\{TX\right\}$:

$\mathit{P}\mathit{r}\mathit{e}\mathit{v}\mathit{H}\mathit{a}\mathit{s}\mathit{h}=\mathit{H}\mathit{a}\mathit{s}\mathit{h}\left({\mathit{H}\mathit{e}\mathit{a}\mathit{d}\mathit{e}\mathit{r}}_{\mathit{N}-\mathbf{1}}\right)(43)$

$\mathit{R}\mathit{o}\mathit{o}\mathit{t}\mathit{H}\mathit{a}\mathit{s}\mathit{h}=\mathit{M}\mathit{e}\mathit{r}\mathit{k}\mathit{l}\mathit{e}\mathit{T}\mathit{r}\mathit{e}\mathit{e}\left(\left\{\mathit{T}\mathit{X}\right\}\right)(44)$

The successor hash and the root hash together form the block header of the block:

${\mathit{H}\mathit{e}\mathit{a}\mathit{d}\mathit{e}\mathit{r}}_{\mathit{N}}=\left\{\mathit{P}\mathit{r}\mathit{e}\mathit{v}\mathit{H}\mathit{a}\mathit{s}\mathit{h},\mathit{R}\mathit{o}\mathit{o}\mathit{t}\mathit{H}\mathit{a}\mathit{s}\mathit{h}\right\}(45)$

The block header and the block body together form the block:

${\mathit{B}\mathit{l}\mathit{o}\mathit{c}\mathit{k}}_{\mathit{N}}=\left\{{\mathit{H}\mathit{e}\mathit{a}\mathit{d}\mathit{e}\mathit{r}}_{\mathit{N}},{\mathit{B}\mathit{o}\mathit{d}\mathit{y}}_{\mathit{N}}\right\}(46)$

5) After receiving blocks, all nodes in the network collaboratively verify updates to the global model. The fastest node to complete verification within each region sends its signature to the other nodes for verification. Once all nodes have reached a consensus, the block is added to the global model block set. The most recent global model, along with signatures and timestamps, form new blocks and attach to the blockchain. Finally, each node receives a copy of the most recent global model block to synchronise the model. Additionally, all nodes collectively store and maintain the block set of the global model.

At the same time, as shown in Eqs 47, 48, the node that successfully mines a new block can obtain the block reward $BlockReward\left(k\right)$, which in turn encourages the nodes to jointly maintain the update of the global model. Meanwhile, the node under the proof-of-work mechanism can obtain the reward $f\left(S_k\right)$ proportional to the size of the sample data, which in turn encourages the participants to contribute the data and the model. After joining the prediction federation, participants can obtain additional financial benefits by earning rewards while obtaining accurate prediction models.

$\mathit{R}\mathit{e}\mathit{w}\mathit{a}\mathit{r}\mathit{d}\left(\mathit{k}\right)=\mathit{B}\mathit{l}\mathit{o}\mathit{c}\mathit{k}\mathit{R}\mathit{e}\mathit{w}\mathit{a}\mathit{r}\mathit{d}\left(\mathit{k}\right)+\mathit{f}\left({\mathit{S}}_{\mathit{k}}\right)(47)$

$\mathit{B}\mathit{l}\mathit{o}\mathit{c}\mathit{k}\mathit{R}\mathit{e}\mathit{w}\mathit{a}\mathit{r}\mathit{d}\left(\mathit{k}\right)=\left\{\begin{array}{c}\mathit{B}\mathit{a}\mathit{s}\mathit{e}\mathit{R}\mathit{e}\mathit{w}\mathit{a}\mathit{r}\mathit{d},\mathbf{\text{successful\hspace{0.17em}mining}}\\ \mathbf{0},\mathbf{\text{others}}\end{array}\right.(48)$

4.4 The overall process

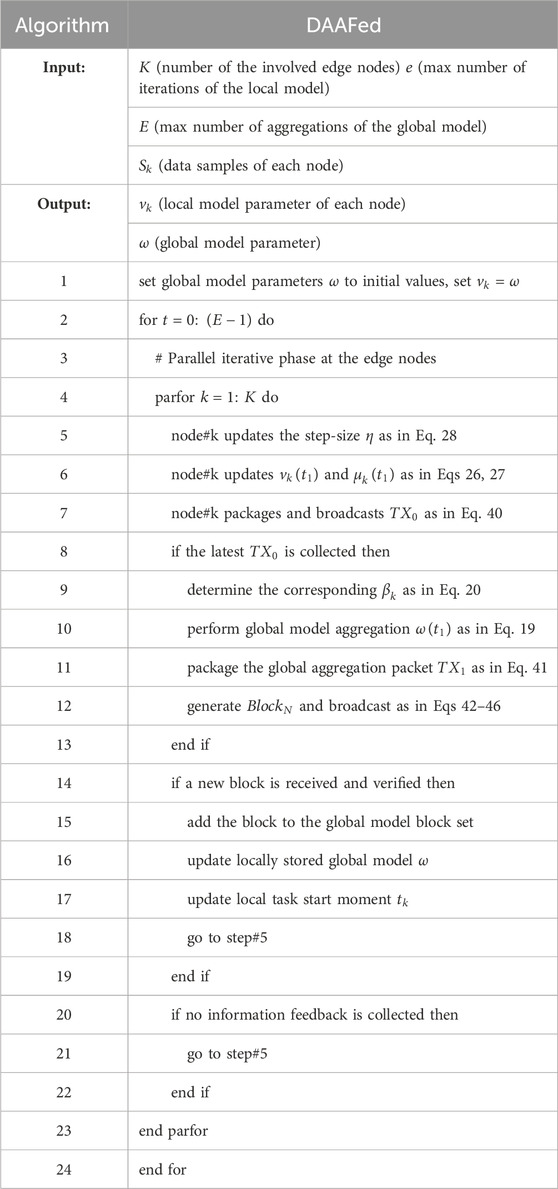
In summary, the pseudo-code of the decentralized asynchronous adaptive federated learning algorithmic process is shown in Table 1. Combining the advantages of federated learning and blockchain, the framework achieves privacy protection for local multi-source data while removing the dependence on a centralized central server. The approach improves training reliability and reduces communication costs, while ensuring the scalability of the edge node network and reducing the risk of single point of failure.

TABLE 1

TABLE 1. Pseudocode of DAAFed.

5 Experiments and results

5.1 Data and setup

The proposed method is implemented on a high performance server equipped with Intel Xeon Gold 6136 and NVIDIA TITAN XP. The Python libraries, including TensorFlow and Keras are used to build our model. The experimental data was selected as a dataset of historical data from 1st January 2015 to 31st December 2018 for five regions of the Spanish electricity market, which consists of time-series data on electricity price, generation, load, weather, and date information, sampled every 1 h, where the price of electricity is used as a label for the prediction. Missing values and outliers in the series are filled and replaced using linear interpolation, normalization is used before prediction training to prevent the effect of different magnitudes, and inverse normalization is used for prediction output to restore the relevance of the output data.

5.2 Analysis of the overall implementation effect

First of all, to show the overall implementation effect of the proposed framework in this paper, the data set is divided into training set, validation set and test set for prediction training, the RMSE of the training set and validation set in the iterative process is recorded, and finally the prediction of the test set is performed and the result is compared with the real value, and the partial tariff prediction results and RMSE iteration curves of the nodes are shown in Figure 3.

FIGURE 3

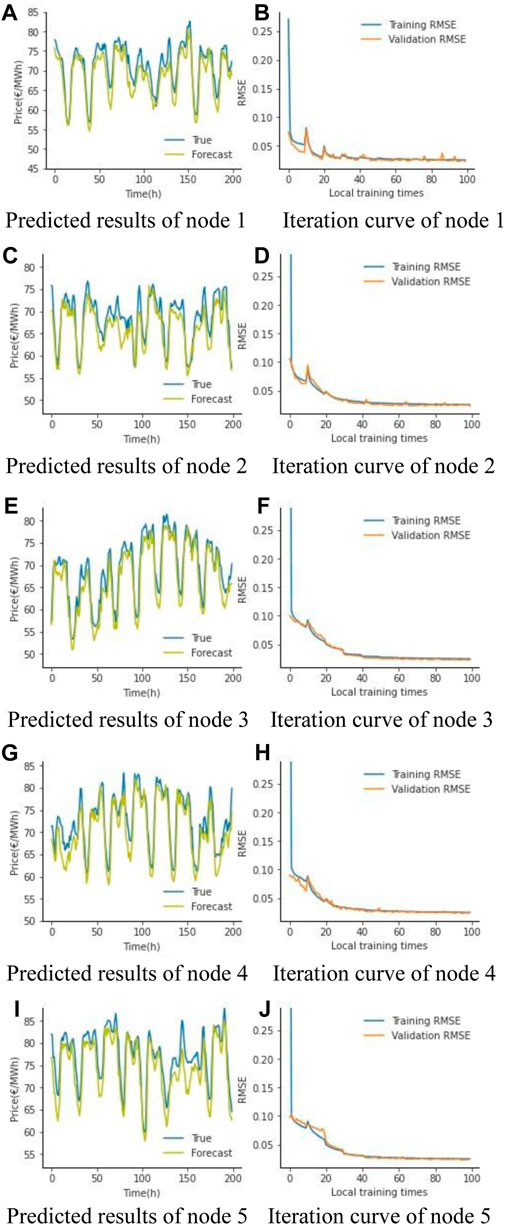
FIGURE 3. Overall predicted results and performance. (A) Predicted results of node 1. (B) Iteration curve of node 1. (C) Predicted results of node 2. (D) Iteration curve of node 2. (E) Predicted results of node 3. (F) Iteration curve of node 3. (G) Predicted results of node 4. (H) Iteration curve of node 4. (I) Predicted results of node 5. (J) Iteration curve of node 5.

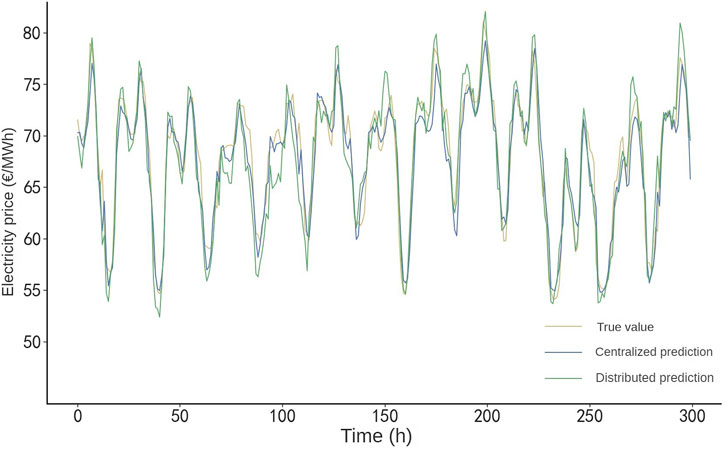
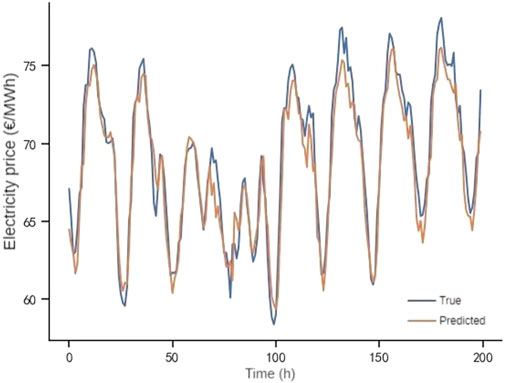
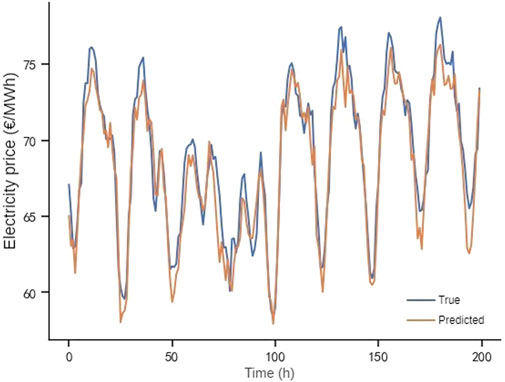
To verify the improvement of the prediction performance of the proposed framework in this paper, the distributed regional tariff prediction model and the centralized tariff prediction model are compared and analyzed, and the prediction results of the two are shown in Figure 4.

FIGURE 4

FIGURE 4. Comparison of centralized and distributed prediction.

As shown in Figure 4, the predicted and actual values of the two prediction models are relatively close to each other, and the predicted value of the distributed model is slightly different from the actual value, because the samples used for training in the centralized model are the data of all nodes, while the samples used for training in each node in the distributed model are only the local data, but the distributed model strengthens the correlation between nodes by protecting the transmission of the model parameters and overcomes the phenomenon of data islanding.

The prediction performances of the distributed and centralized modes are shown in Table 2, except for the prediction accuracy, the distributed mode mostly outperforms the centralized mode. In terms of running time, since the computational tasks are assigned to each edge node in the distributed mode, and only local data is used for single-point training, the computational volume of a single computational unit is greatly reduced, and the single-point training time in the distributed mode is less than that in the centralized mode. In terms of data transmission, only the model parameters are transmitted in the distributed mode, which protects the data of each node and does not reveal the private data such as power generation information and user habits, and “53601” represents the sum of the elements of the weight matrix and bias vector of the prediction model. The centralized mode requires the transmission of all sample data, which has the risk of data leakage, where “5 × 35064 × 33” means that there are 35,064 sample data in each of the five nodes, and each sample contains 33 dimensions of data. Therefore, the distributed model can effectively reduce the amount of data transmitted in a single transmission and provide a certain level of security to protect the privacy of electricity.

TABLE 2

TABLE 2. Comparison of centralized and distributed prediction.

5.3 Comparative analysis of edge node prediction models

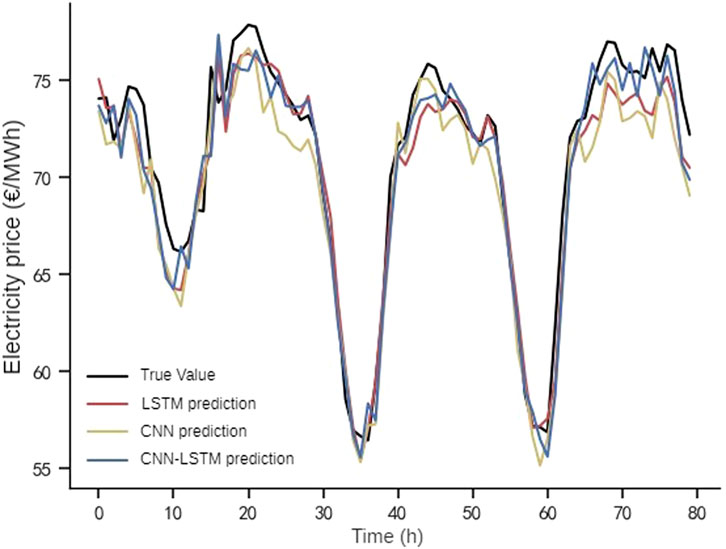
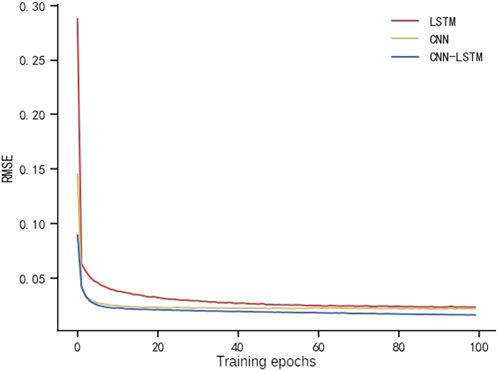
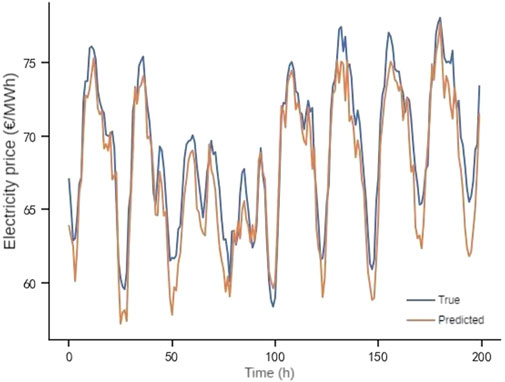
Choosing a more appropriate model for distributed prediction at the edge nodes can effectively improve the overall prediction accuracy. To improve the implementation effect of the method proposed in this paper, LSTM model, CNN model and CNN-LSTM model are used at the edge nodes to predict the electricity price for the same data set. The model parameters are adjusted based on the method proposed in the related literature, and the prediction performance under the three models is compared and analyzed, as shown in Figure 5. The RMSE is calculated again after converting the model output into real size, and the results of the RMSE of each model evaluation index are shown in Table 3.

FIGURE 5

FIGURE 5. Comparison of prediction results under different models.

TABLE 3

TABLE 3. Comparison of RMSE under different models.

From Figures 5, 6 and Table 3, it can be seen that the overall prediction value of CNN-LSTM is closest to the real value, and the efficiency of the training iteration is also higher. The main reason is that CNN-LSTM combines the advantages of CNN and LSTM, capturing both local and global temporal features at different time scales through sliding window and loop structure, while the feature of parameter sharing of convolutional layer reduces the number of parameters of LSTM network and improves the computational efficiency. Therefore, choosing CNN-LSTM model for prediction at edge nodes can have good accuracy and efficiency.

FIGURE 6

FIGURE 6. Comparison of iteration curves under different models.

5.4 Comparative analysis of federated learning algorithms

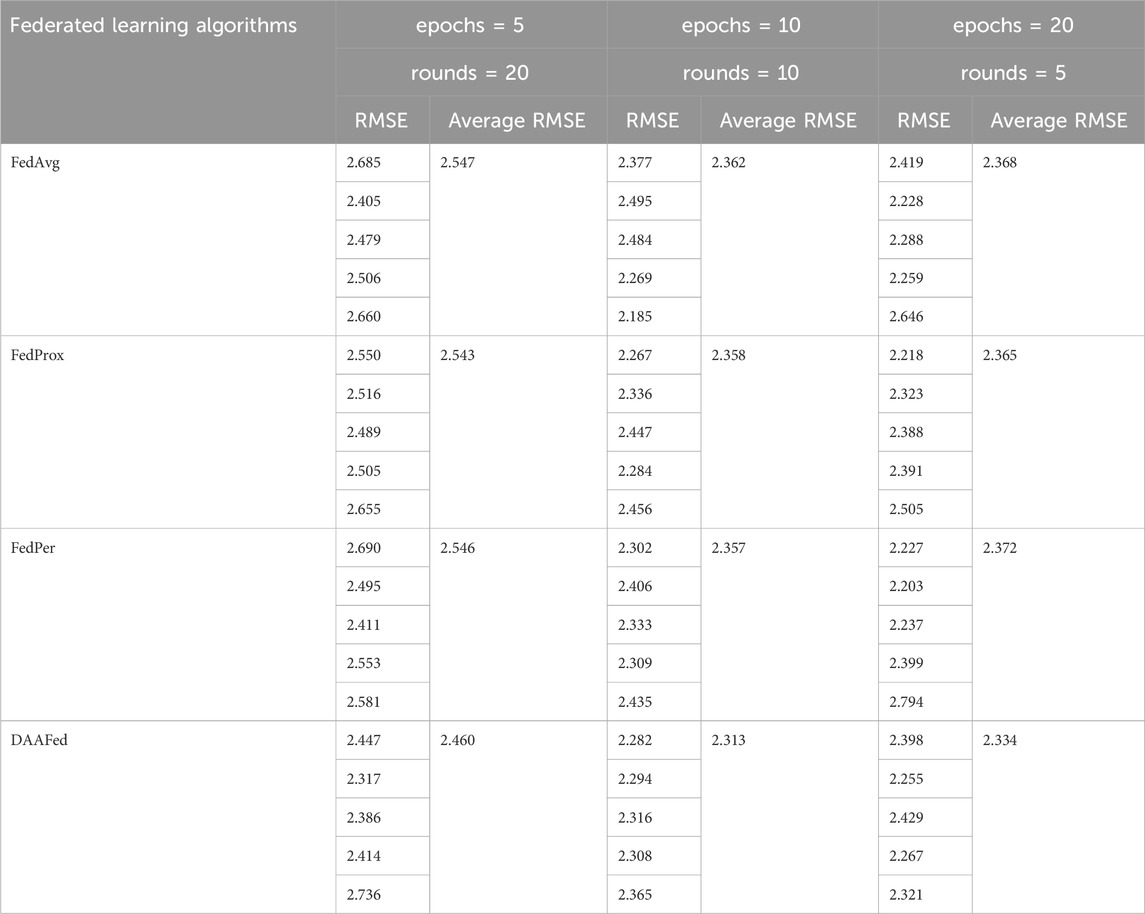
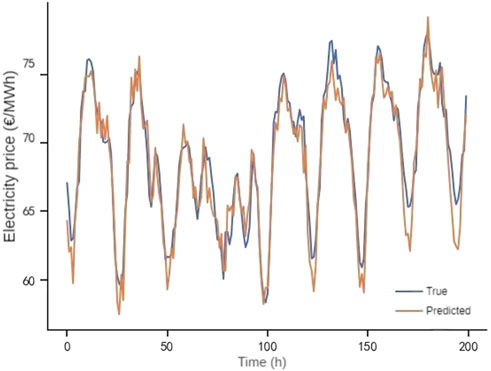
To verify that the DAAFed algorithm proposed in this paper has better prediction performance, FedAvg, FedProx (Li et al., 2020b), FedPer (Arivazhagan et al., 2019) and DAAFed are used to predict the electricity price on the same dataset, and the prediction performance of the above algorithms are compared and analysed. FedProx adds regularization terms to constrain the similarity between the global model and the local model to prevent overfitting (Li et al., 2020a). Each node model in FedPer has its own personalization layer that preserves the characteristics of the node data (Arivazhagan et al., 2019).

The RMSE and average RMSE for each node using the above federated learning algorithms with different iteration settings are shown in Table 4. FedProx adds a regularization term to limit the similarity between the global model and the local model and prevent overfitting; and each node has its own personalization layer in each node’s model in FedPer, which is used to preserve the node data’s own characteristics. Table 4 shows that the prediction performance of these two improved algorithms is similar to that of FedAvg. The DAAFed algorithm used in this paper has a smaller error compared to the other three algorithms, because the asynchronous mechanism used in the aggregation of the global model allows the nodes to update the model based on the latest global model, and at the same time, the step size is adaptively adjusted in the updating of the node’s local model, so the model learns to the better parameter faster, and thus the overall performance is better. Therefore, the overall performance is better.

TABLE 4

TABLE 4. Comparison of RMSE under different federated learning algorithms.

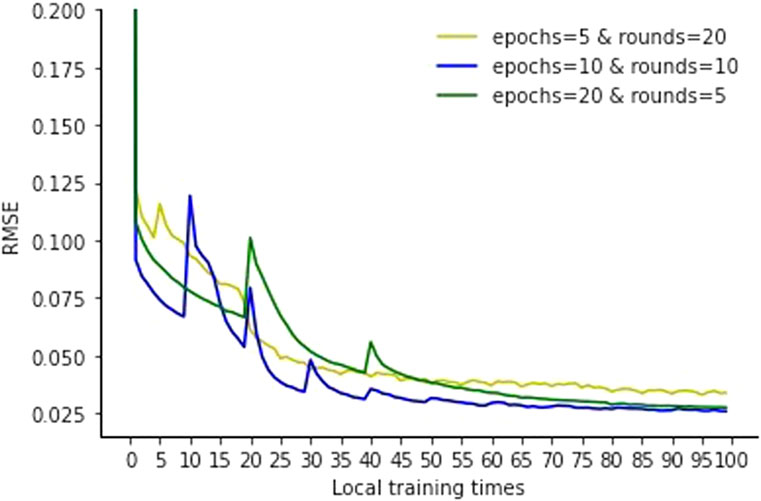
From Table 4, it can be seen that setting different local iteration epochs and global aggregation rounds has different prediction effects, and choosing the appropriate settings can fully exploit the advantages of the federated learning framework.

Figure 7 shows the iteration curves under different settings. It shows that when epochs = 10 and rounds = 10 there is better iteration efficiency than the other two settings. When epochs = 5 there is a slower decrease in the iteration curve because when the number of local iterations is small, the local model of each node does not have enough performance and cannot make full use of the local data. When epochs = 20 there is a slow decrease in the iteration curve before global aggregation, which means that a higher number of local iterations leads to a slower decrease of the iteration curve before global aggregation. This means that if the number of local iterations is high, it can lead to overfitting, which affects the ability of global model generalization, so the setting of epochs = 10 and rounds = 10 can give better federated learning results.

FIGURE 7

FIGURE 7. Comparison of iteration curves under different iteration parameter settings.

Based on this setting, the prediction results of a node under each of the above algorithms are shown in Figures 8–11, from which it can be seen that the predicted value of DAAFed is closer to the real value compared to several other federated learning algorithms.

FIGURE 8

FIGURE 8. Predicted results of FedAvg.

FIGURE 9

FIGURE 9. Predicted results of FedProx.

FIGURE 10

FIGURE 10. Predicted results of FedPer.

FIGURE 11

FIGURE 11. Predicted results of DAAFed.

6 Conclusion

In order to solve the problems of high computational cost and low data security under the traditional centralized electricity data forecasting method, this paper proposes a distributed regional electricity market electricity price forecasting method based on decentralized adaptive federated learning. The following conclusions are drawn from the analysis of the arithmetic example of the Spanish electricity market.

Compared to the conventional centralized prediction method, the distributed data prediction method reduces the amount of prediction calculation and data transmission, and approaches the centralized prediction accuracy in the implementation process, while protecting the local data in each region. Precise selection of prediction models on each node and appropriate configuration of the number of local iterations and global update rounds can be highly effective in enhancing the accuracy and efficiency of prediction. Compared to the Federated Learning algorithm, DAAFed enhances prediction accuracy by introducing an asynchronous adaptive mechanism. The validity of this proposed method is verified.

At present, privacy protection is becoming increasingly important in the power industry, which brings new challenges to distributed electricity price prediction. Therefore, how to further consider the protection effect of privacy protection mechanism and communication efficiency optimization will be the focus of the next research work.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

QL: Writing–original draft, Writing–review and editing, Conceptualization, Methodology, Validation. DL: Software, Supervision, Writing–review and editing. HC: Funding acquisition, Resources, Writing–review and editing. XiL: Formal Analysis, Project administration, Writing–review and editing. XuL: Data curation, Methodology, Visualization, Writing–review and editing. WC: Conceptualization, Investigation, Writing–review and editing.

Funding

The authors declare financial support was received for the research, authorship, and/or publication of this article. This research is supported by the State Grid Information and Telecommunication Group scientific and technological innovation projects “Research on Power Digital Space Technology System and Key Technologies” (Grant No. SGIT0000XMJS2310456).

Conflict of interest

Authors QL, DL, XiL, and WC were employed by State Grid Information & Telecommunication Group Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmed, F. K., Hussain, J. S., Attique, M. K., Sharif, M., Tariq, U., and Kadry, S. (2022). A review on federated learning towards image processing. Comput. Electr. Eng. 99, 107818. doi:10.1016/j.compeleceng.2022.107818

CrossRef Full Text | Google Scholar

Ali, H., Chandren, R., Kamrul, M., Paw, J. K. S., and Singh, M. J. (2023). Big data analytics using cloud computing based frameworks for power management systems: status, constraints, and future recommendations. Sensors 23 (6), 2952. doi:10.3390/s23062952

PubMed Abstract | CrossRef Full Text | Google Scholar

Antal, M., Mihailescu, V., Cioara, T., and Anghel, I. (2022). Blockchain-based distributed federated learning in smart grid. Mathematics 10 (23), 4499. doi:10.3390/math10234499

CrossRef Full Text | Google Scholar

Arivazhagan, M., Aggarwal, V., and Singh, A. (2019). Federated learning with personalization layers. ArXiv:1912.00818. Available at: https://doi.org/10.48550/arXiv.1912.00818.

Google Scholar

Badhiye, S., Chatur, P., and Raghuwanshi, M. (2022). Time series forecasting using range regression automata. International journal of uncertainty. Fuzziness Knowledge-Based Syst. 30 (06), 1035–1063. doi:10.1142/S0218488522500325

CrossRef Full Text | Google Scholar

Chen, Y., Lu, W., Qin, X., Wang, J., and Xie, X. (2023). MetaFed: federated learning among federations with cyclic knowledge distillation for personalized healthcare. IEEE Trans. neural Netw. Learn. Syst. 2023, 1–12. doi:10.1109/tnnls.2023.3297103

CrossRef Full Text | Google Scholar

Frizzo, S., Oriel, L., Cocco, V., and Coelho, L. d. S. (2023). Aggregating prophet and seasonal trend decomposition for time series forecasting of Italian electricity spot prices. Energies 16 (3), 1371. doi:10.3390/en16031371

CrossRef Full Text | Google Scholar

He, W., and Zhao, L. (2022). Application of federated learning algorithm based on K-means in electric power data. J. New Media 4 (4), 191–203. doi:10.32604/jnm.2022.032994

CrossRef Full Text | Google Scholar

Husnoo, M., Anwar, A., Reda, H., Hosseinzadeh, N., Islam, S., Mahmood, A., et al. (2023). FedDiSC: a computation-efficient federated learning framework for power systems disturbance and cyber attack discrimination. Energy AI 14, 100271. doi:10.1016/j.egyai.2023.100271

CrossRef Full Text | Google Scholar

Li, T., Anit, K., Ameet, T., and Smith, V. (2020a). Federated learning: challenges, methods, and future directions. IEEE Signal Process. Mag. 37 (3), 50–60. doi:10.1109/msp.2020.2975749

CrossRef Full Text | Google Scholar

Li, T., Sahu, A., and Zaheer, M. (2020b). Federated optimization in heterogeneous networks. Proc. Mach. Learn. Syst. 2020 (2), 429–450. doi:10.48550/arXiv.1812.06127

CrossRef Full Text | Google Scholar

Li, Y., Wang, R., Li, Y., Zhang, M., and Long, C. (2023a). Wind power forecasting considering data privacy protection: a federated deep reinforcement learning approach. Appl. Energy 329, 120291. doi:10.1016/j.apenergy.2022.120291

CrossRef Full Text | Google Scholar

Li, Y., Yan, Y., Liu, Z., Yin, C., Zhang, J., and Zhang, Z. (2023b). A federated learning method based on blockchain and cluster training. Electronics 12 (19), 4014. doi:10.3390/electronics12194014

CrossRef Full Text | Google Scholar

Liu, Y., Wang, G., Guo, W., Zhang, Y., Dong, W., Wei, G., et al. (2021). Power data mining in smart grid environment. J. Intelligent Fuzzy Syst. 40 (2), 3169–3175. doi:10.3233/jifs-189355

CrossRef Full Text | Google Scholar

Mcmahan, H., Moore, E., and Ramage, D. (2017). “Communication-efficient learning of deep networks from decentralized data,” in Proceedings of the 20th International Conference on Artificial Intelligence and Statistics(AISTATS), 1273–1282.

Google Scholar

Mohamed, A., Ibrahim, A., Hossam, H., and Karam, S. (2023). Towards efficient and trustworthy pandemic diagnosis in smart cities: a blockchain-based federated learning approach. Mathematics 11 (14), 3093. doi:10.3390/math11143093

CrossRef Full Text | Google Scholar

Qi, T., Chen, L., Li, G., Li, Y., and Wang, C. (2023). FedAGCN: a traffic flow prediction framework based on federated learning and Asynchronous Graph Convolutional Network. Appl. Soft Comput. J. 138, 110175. doi:10.1016/j.asoc.2023.110175

CrossRef Full Text | Google Scholar

Qu, Z., Li, Y., Liu, B., Gupta, D., and Tiwari, P. (2023). DTQFL: a digital twin-assisted quantum federated learning algorithm for intelligent diagnosis in 5G mobile network. IEEE J. Biomed. health Inf. 2023, 1–10. doi:10.1109/jbhi.2023.3303401

CrossRef Full Text | Google Scholar

Wang, Z., Zhou, M., Zhao, Y., Zhang, F., Wang, J., Qian, B., et al. (2023). Electrical power edge-end interaction modeling with time series label noise learning. Electronics 12 (18), 3987. doi:10.3390/electronics12183987

CrossRef Full Text | Google Scholar

Wu, X., Liang, Z., and Wang, J. (2020). FedMed: a federated learning framework for language modeling. Sensors 14, 4048. doi:10.3390/s20144048

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, H., Yang, S., and Zhu, S. (2019). “Parallel restarted SGD with faster convergence and less communication: demystifying why model averaging works for deep learning,” in Proceedings of the AAAI Conference on Artificial Intelligence, 5693–5700.

CrossRef Full Text | Google Scholar

Zeng, M., Wang, X., Pan, W., and Zhou, P. (2023). Heterogeneous training intensity for federated learning:a deep reinforcement learning approach. IEEE Trans. Netw. Sci. Eng. 10 (2), 990–1002. doi:10.1109/tnse.2022.3225444

CrossRef Full Text | Google Scholar

Zhang, X., Zhong, C., Zhang, J., and Wang, T. (2023). Robust recurrent neural networks for time series forecasting. Neurocomputing 526, 143–157. doi:10.1016/j.neucom.2023.01.037

CrossRef Full Text | Google Scholar