Two-stage robust planning method for distribution network energy storage based on load forecasting

A two-stage robust planning method for energy storage in distribution networks based on load prediction is proposed to address the uncertainty of active load in energy storage planning. First, considering the uncertainty of active load, a short-term load forecasting model combining the mutual information method and BiLSTM is established based on k-means++ clustering. Second, based on the results of load forecasting, a comprehensive norm-constrained uncertainty set is constructed, and a two-stage robust model for distribution network energy storage planning is established. The first stage aims to minimize the annual investment cost of the energy storage system, while the second stage aims to minimize the daily operating cost of the distribution network. At the same time, a second-order cone relaxation transformation model with non-convex constraints is introduced to ultimately achieve the optimal economy of the distribution network in energy storage planning. Finally, the effectiveness of the proposed method and model is validated on the IEEE 33-node distribution network model using the MATLAB platform.

1 Introduction

For the development of a high-proportion renewable energy source (RES), the access of a large number of RESs and the increase in load demand have brought new challenges for the flexible and efficient operation of the power system, and energy storage technology is considered to be an important means to solve the instability of RES output and demand (Yang et al., 2022a; Yang et al., 2022b; Yang et al., 2022c). Therefore, it is necessary to study how to plan energy storage in the distribution network (Nan et al., 2018; Yang et al., 2022d).

At present, there is a lot of research on energy storage planning conducted by many scholars. Huang et al. (2023) proposed a new power system energy storage planning method considering the demand response resources. Zhu and Shan (2023) established a distributed robust capacity planning model based on the uncertainty of new energy output, which fully considers the flexibility of system operation. Lan et al. (2022) proposed a hybrid energy storage model in order to smooth wind power fluctuations. The energy storage capacity of an isolated island microgrid was configured by Li et al. (2016). In the work of Li et al. (2016), Lan et al. (2022), Huang et al. (2023), and Zhu and Shan (2023), energy storage planning is only based on a local power system or a microgrid and does not extend to the distribution network. Ren et al. (2019), Zhang et al. (2023a), Yang et al. (2023), and Zheng et al. (2023) established the energy storage planning model in the distribution network. Among them, Zheng et al. (2023) considered the long-term and short-term energy storage joint planning of the source and storage transport under the high proportion of wind power penetration. Yang et al. (2023) considered the energy storage planning of auxiliary service income. Zhang et al. (2023a) guided the energy storage location by evaluating the distribution of system inertia and then planned the energy storage capacity with the minimum investment and system operating cost as the goal. Ren et al. (2019) considered both active and reactive power, and a model of optimal location and capacity allocation for battery energy storage power stations was established based on the improved system impedance matrix. Although Li et al. (2016), Ren et al. (2019), Lan et al. (2022), Zhang et al. (2023a), Huang et al. (2023), Yang et al. (2023), Zheng et al. (2023), and Zhu and Shan (2023) have carried out research on the planning of energy storage power stations, the focus is only on energy storage. With the increasing load demand in power systems, its uncertainty will become a factor that cannot be ignored in energy storage planning.

At this stage, the main methods of dealing with uncertainty problems in power systems are stochastic optimization (SO) (Lei et al., 2022; Zuo et al., 2022) and robust optimization (RO) (Ma et al., 2023; Wang et al., 2023). While maximizing the expected benefits, SO may not be feasible to achieve without involving other possible uncertainties. RO methods can guarantee robustness within a pre-specified set of uncertainties, but the decision process violates unpredictability, and complex “min–max” structures can lead to computational difficulties. In addition, RO is unable to merge distribution information, leading to overly conservative solutions. Distributed robust optimization (DRO) resolves the problem of difficult and overly conservative parameter acquisition by making decisions under the worst probability distribution of random variables. For DRO, however, a fuzzy set based on moment information (Wu and Fang, 2023) is limited in the information it can describe and does not include the true distribution well. The uncertain output of RES in the work of Wang et al. (2022) is based on the coupling of the Kullback–Leibler (KL) divergence. Although the calculation amount is reduced, the KL divergence is an asymmetric measure. If the two distributions are far apart, the KL divergence value is meaningless. Fuzzy assemblies based on Wasserstein metrics (Hou et al., 2023; Liu et al., 2023) lead to computational difficulties.

Regardless of the method of uncertainty, one source of data is based on the predicted value. In the work of Feng et al. (2019), Cai et al. (2020), and Han et al. (2021), load prediction was carried out based on the machine learning method. Cecati et al. (2015), Wang et al. (2015), and Su et al. (2017) made use of the artificial neural network method, which is one of the popular applications at present. However, Cecati et al. (2015), Wang et al. (2015), Su et al. (2017), Feng et al. (2019), Cai et al. (2020), and Han et al. (2021) ignored the timing of load in their work. Zhang et al. (2017) and Zheng et al. (2020) used the long short-term memory (LSTM) network and Jixiang et al. (2019) used the bidirectional long short-term memory (BiLSTM) network to well solve the temporal problems in the process of load prediction, but the factors affecting load change are not fully considered. Peng et al. (2020) and Jinpeng et al. (2021) considered the key factors affecting load, such as date and weather, in the process of load forecasting, but effective information on load fluctuation was not extracted, and load forecasting was not applied to energy storage planning.

To sum up, considering the shortcomings of the existing research, this paper proposes a two-stage robust planning method for energy storage in a distribution network based on load prediction. First, in order to extract effective and comprehensive forecasting information from load fluctuations and improve forecasting accuracy, a mutual information (MI) method and BiLSTM short-term load forecasting model considering feature importance fluctuations are established based on k-means++ clustering. Based on load prediction, a DRO uncertainty set with comprehensive norm constraints is constructed to establish a two-stage distribution network energy-storage planning model. The first stage aims at the minimum annual investment cost of energy storage, the second stage aims at the minimum daily operating cost of the distribution network, and the second-order cone relaxation transformation model is introduced. Finally, the economy and effectiveness of the proposed model and method are verified on the IEEE 33-node distribution network model.

2 Load model

2.1 Load clustering

One of the characteristics of a power system load is its periodicity. Developing short-term load forecasting based on the periodic characteristics of the load is the basis for improving the forecasting accuracy. The periodicity of the load is reflected in the overall change law of 24 h a day with a similar trend (Zhang et al., 2023b; Fu et al., 2023). In addition, the daily load scenario is affected by a variety of factors (date characteristics, temperature, humidity, etc.) and can be divided into different types, and the importance of the input characteristics also shows obvious differences. Aiming at the above characteristics, this paper first performs cluster analysis on the daily load curve based on the k-means++ algorithm.

As an improvement of k-means, k-means++ is used to make the distance between the initial cluster centers as far as possible in the process of cluster initialization to avoid the problem of local optimization of cluster centers to select relatively better cluster centers. The k-means++ algorithm effectively solves the initial center selection problem of the k-means algorithm, but it does not provide an effective solution for the selection of cluster number k.

This cluster takes meteorological characteristics as input to subdivide the daily load scenarios. Meteorological features include different types of data, such as temperature and humidity. Since temperature is a significant factor affecting the variation of daily load, the temperature of a day is selected as the input of clustering, and the final result of daily load scene division is obtained.

2.2 Wave matrix

The MI method is used to measure the importance of input features, and the extracted MI value is used to represent the importance value of the input features. The greater the MI value, the greater the correlation between the input features and load, that is, the greater the importance value. MI comes from the concept of entropy in information theory, which reflects the correlation between any two random variables. The MI value between the input feature and the load is used to characterize the importance value of the input feature. Therefore, based on dividing different daily load scenarios from the original database, the importance value fluctuation matrix of the input features is extracted for the specific scenarios.

The formula for calculating the MI value $M\left(\mathrm{{\rm A}},\mathrm{{\rm B}}\right)$ is as follows:

$M\left(\mathrm{{\rm A}},\mathrm{{\rm B}}\right)={\displaystyle \sum _{\alpha }}{\displaystyle \sum _{\beta }}{h}_{\mathrm{A}\mathrm{B}}\left(\alpha ,\beta \right){\log }_2\frac{h_{\mathrm{A}\mathrm{B}}\left(\alpha ,\beta \right)}{h_{\mathrm{A}}\left(\alpha \right)h_{\mathrm{B}}\left(\beta \right)},(1)$

where $h_{\mathrm{{\rm A}}\mathrm{{\rm B}}}\left(\alpha ,\beta \right)$ is the joint probability density function of variables $\alpha$ and $\beta$, A and B are variable sets, and $h_{\mathrm{{\rm A}}}\left(\alpha \right)$ and $h_{\mathrm{{\rm B}}}\left(\beta \right)$ are the edge probability density functions of their corresponding variables.

The steps for constructing the importance fluctuation matrix are as follows:

Step 1. According to the clustering result of the daily load scenario, the load data are divided into n groups according to the number of load sampling points in a day. Then, the output load dataset is as follows:

$P=\left[P_1,P_2,...,P_t,...,P_n\right],(2)$

where $P_t$ is the load output during the t period.

Step 2. The input feature matrix E corresponding to the above output load dataset is taken.

$\mathbf{E}=\left[\begin{array}{ccccc}{E}_{1,1}& \cdots & E_{t,1}& \cdots & E_{n,1}\\ E_{1,2}& \cdots & E_{t,2}& \cdots & E_{n,2}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ E_{1,m}& \cdots & E_{t,m}& \cdots & E_{n,m}\end{array}\right],(3)$

where $E_{t,m}$ is input to the mth feature of ${\mathrm{P}}_{\mathrm{t}}$.

Step 3. The MI value ${\mathbf{E}}_{\mathit{t}}$ of the input and output load in the t period is calculated, and normalization processing is carried out.

${\mathbf{E}}_t=\left[\begin{array}{c}M\left(E_{t,1},P_t\right)\\ M\left(E_{t,2},P_t\right)\\ ⋮\\ M\left(E_{t,m},P_t\right)\end{array}\right],(4)$

where $M\left(E_{t,1},P_t\right)$ is the level of importance of the class 1 input in the t period.

Step 4. t iteratively solves the input importance values at different moments from 1 to n and obtains the input importance fluctuation matrix M with time.

$\mathbf{M}=\left[\begin{array}{ccccc}M\left(E_{1,1},P_1\right)& \cdots & M\left(E_{t,1},P_t\right)& \cdots & M\left(E_{n,1},P_n\right)\\ M\left(E_{1,2},P_1\right)& \cdots & M\left(E_{t,2},P_t\right)& \cdots & M\left(E_{n,2},P_n\right)\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ M\left(E_{1,m},P_1\right)& \cdots & M\left(E_{t,m},P_t\right)& \cdots & M\left(E_{n,m},P_n\right)\end{array}\right].(5)$

2.3 BiLSTM model

Considering that there is a certain relationship between the load in the current period and the load in the previous and later periods in short-term load forecasting, BiLSTM, which considers two-way time information, is chosen as the underlying model of short-term load forecasting. The calculation formula of BiLSTM is as follows:

$\overrightarrow{r_t}=\overrightarrow{U_{LSTM}}\left(r_{t-1},m_t,a_{t-1}\right),(6)$

$\stackrel{⃖}{r_t}=\stackrel{⃖}{U_{LSTM}}\left(r_{t+1},m_t,a_{t+1}\right),(7)$

${\mathrm{\Psi }}_t=b_t\overrightarrow{r_t}+c_t\stackrel{⃖}{r_t}+a_{t-1},(8)$

where $\overrightarrow{r_t}$ and $\stackrel{⃖}{r_t}$ are the predicted load values before and after the t period; $\overrightarrow{U_{LSTM}}\left(·\right)$ and $\stackrel{⃖}{U_{LSTM}}\left(·\right)$ represent the forward and backward calculation process of LSTM, respectively; $m_t$ is the input feature at time t; $b_t$, $c_t,$ and $a_{t-1}$ are optimization parameters; and ${\mathrm{\Psi }}_t$ is the load prediction value of BiLSTM during the t period.

2.4 MI-BiLSTM prediction process

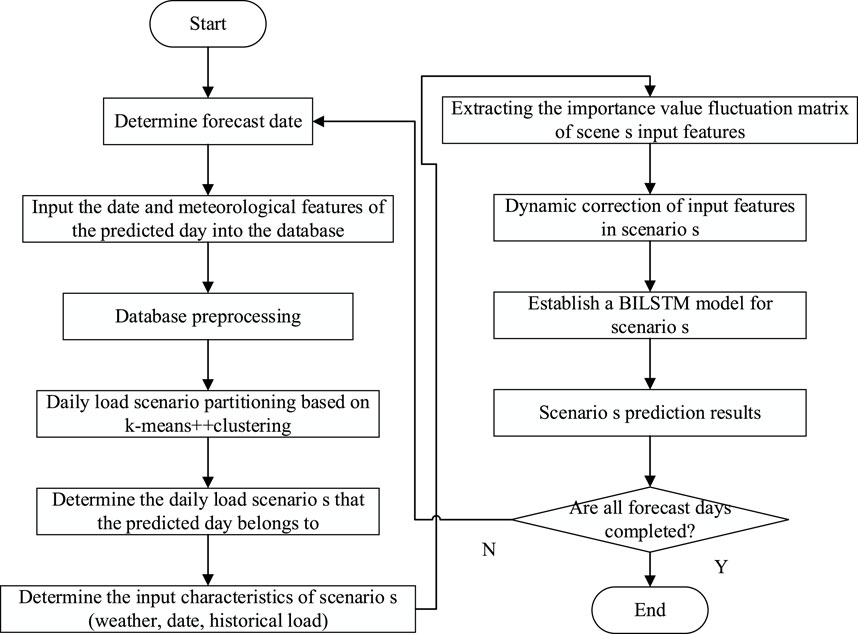
The process of the short-term load forecasting method based on MI-BiLSTM is shown in Figure 1. At the same time, in order to make up for the time-invariance of the weight-sharing structure of the BiLSTM model, the extracted importance value fluctuation matrix M is used as the input feature of BiLSTM.

FIGURE 1

FIGURE 1. Flow chart of load forecast.

2.5 An uncertain set of loads

Based on the load prediction results of each scenario and combined with the comprehensive norm constraints in DRO (including 1-norm and infinite norm), the uncertainty set of predicted load values is constructed to enhance the robustness of the power system operation (Li et al., 2021; Li et al., 2023a). The uncertainty set $\mathit{Q}$ is shown as follows:

$\mathit{Q}=\left\{\left\{p_s\right\}\left|\begin{array}{l}{\displaystyle \sum _{s=1}^S}\left|p_s-p_{s.0}\right|\le {\omega }_1\\ \underset{1\le s\le S}{\max }\left|p_s-p_{s.0}\right|\le {\omega }_{\infty }\\ {\displaystyle \sum _{s=1}^S}{p}_s=1\\ p_s\ge 0,s=1,2,...,\mathrm{S}\end{array}\right.\right\},(9)$

where $p_{s.0}$ is the initial probability value of the predicted sth discrete scenario, $p_s$ is the actual probability value of the sth discrete scenario when the system is running, ${\omega }_1$ and ${\omega }_{\infty }$ are the 1-norm threshold and the infinite norm threshold, respectively, for the constraints satisfied, and S is the number of scenes.

Meanwhile, the probability distribution of the load scenario satisfies the following confidence constraints:

$\left\{\begin{array}{l}\mathrm{Pr}\left\{{\displaystyle \sum _{s=1}^S}\left|p_s-p_{s.0}\right|\le {\omega }_1\right\}\le {\xi }_1\\ \mathrm{Pr}\left\{\underset{1\le s\le S}{\max }\left|p_s-p_{s.0}\right|\le {\omega }_{\infty }\right\}\le {\xi }_{\infty }\\ {\xi }_1=1-2{Se}^{-\frac{2W{\omega }_1}{S}}\\ {\xi }_{\infty }=1-2{Se}^{-2W{\omega }_{\infty }}\end{array}\right.,(10)$

where ${\xi }_1$ and ${\xi }_{\infty }$ are the confidence levels and W is the load initial sample number.

3 Two-stage planning model

Based on the constructed load uncertainty set, a two-stage energy storage planning model of a distribution network is established (Zhou et al., 2023). Then, the non-convex constraints of the model are transformed based on second-order cone relaxation, and finally, the operation optimization problem of the distribution network is solved.

3.1 First-stage model

The first-stage model aims to minimize the annual investment cost of energy storage, and the specific expression is as follows:

${\mathrm{C}}_1=\frac{r{\left(1+\mathrm{r}\right)}^{\mathrm{Y}}}{{\left(1+\mathrm{r}\right)}^{\mathrm{Y}}-1}\left({\zeta }_1{P}_{bat}+{\zeta }_2{Q}_{bat}\right),(11)$

where r is the annual interest rate, Y is the operating life of the system, $P_{bat}$ and $Q_{bat}$ are the maximum power and capacity configured for energy storage, and ${\zeta }_1$ and ${\zeta }_2$ are the unit installation cost of energy storage power and capacity, respectively.

3.2 Second-stage model

The objective function of the second-stage model is the lowest daily operating cost $C_2$ of the distribution network, which includes the network loss cost $C_3$, energy storage charge and discharge cost $C_4$, and distribution network generation cost $C_5$. The specific expression is as follows:

${\mathrm{C}}_2={\mathrm{C}}_3+{\mathrm{C}}_4+{\mathrm{C}}_5,(12)$

${\mathrm{C}}_3={\displaystyle \sum _{t=1}^{\mathrm{T}}}{P}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}.t}{\gamma }_1={\displaystyle \sum _{t=1}^{\mathrm{T}}}{\displaystyle \sum _{ij\in \mathrm{\Omega }}}{r}_{ij}{I}_{ij.t}^2,(13)$

${\mathrm{C}}_4={\displaystyle \sum _{t=1}^{\mathrm{T}}}\left(P_{i.t}^{\mathrm{c}\mathrm{h}\mathrm{a}}+P_{i.t}^{\mathrm{d}\mathrm{i}\mathrm{s}}\right){\gamma }_2,(14)$

${\mathrm{C}}_5={\displaystyle \sum _{t=1}^{\mathrm{T}}}{\gamma }_{3.t}{P}_{i.t}^{\mathrm{g}\mathrm{r}\mathrm{i}\mathrm{d}},(15)$

where $P_{loss.t}$ is the power loss of the grid at time t, $P_{i.t}^{cha}$ and $P_{i.t}^{dis}$ are the charge and discharge power stored at node i at time t, $P_{i.t}^{grid}$ is the power generation power of the grid at node i at time t, ${\gamma }_1$ is the cost of unit grid loss, ${\gamma }_2$ is the charge and discharge power cost per unit of energy storage, ${\gamma }_{3.t}$ is the time-of-use price of the grid, $r_{ij}$ is the resistance on the branch ij, and $I_{ij.t}$ is the current on the branch ij at time t.

3.3 Constraint condition

(1) Power flow constraint

$P_{i.t}={\displaystyle \sum _{k\in \delta \left(j\right)}}{P}_{jk.t}-{\displaystyle \sum _{i\in \pi \left(j\right)}}\left(P_{ij.t}-r_{ij}{I}_{ij.t}^2\right)+g_j{V}_{j.t}^2,(16)$

$P_{i.t}=P_{i.t}^{\mathrm{W}\mathrm{T}}+P_{i.t}^{\mathrm{P}\mathrm{V}}+P_{i.t}^{\mathrm{g}\mathrm{r}\mathrm{i}\mathrm{d}}-P_{s.i.t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}},(17)$

$Q_{i.t}={\displaystyle \sum _{k\in \delta \left(j\right)}}{Q}_{jk.t}-{\displaystyle \sum _{i\in \pi \left(j\right)}}\left(Q_{ij.t}-x_{ij}{I}_{ij.t}^2\right)+b_j{V}_{j.t}^2,(18)$

$Q_{i.t}=Q_{i.t}^{\mathrm{g}\mathrm{r}\mathrm{i}\mathrm{d}}-Q_{i.t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}},(19)$

$V_{j.t}^2=V_{i.t}^2-2\left(P_{ij.t}{r}_{ij}+Q_{ij.t}{x}_{ij}\right)+I_{ij.t}^2\left(r_{ij}^2+x_{ij}^2\right),(20)$

$I_{ij.t}^2=\frac{P_{ij.t}^2+Q_{ij.t}^2}{V_{i.t}^2},(21)$

where $\delta \left(j\right)$ and $\pi \left(j\right)$ are a collection of branch nodes, with j as the first and as the end, $x_{ij}$ is the reactance on the branch ij, $g_j$ and ${\mathrm{b}}_{\mathrm{j}}$ are the admittance of node j, $P_{i.t}$ and $Q_{i.t}$ are the active and reactive work at node i, $V_{j.t}$ is the voltage at node j at time t, $P_{ij.t}$ and $Q_{ij.t}$ are, respectively, the active and reactive power of the branch ij in time t, $P_{i.t}^{\mathrm{W}\mathrm{T}}$, $P_{i.t}^{\mathrm{P}\mathrm{V}}$, and $P_{s.i.t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}$ are, respectively, the WT and PV output at node i in the t period and the active load in the s scenario, and $Q_{i.t}^{\mathrm{g}\mathrm{r}\mathrm{i}\mathrm{d}}$ and $Q_{i.t}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}$ are, respectively, the reactive power and reactive power load emitted by the power grid at node i of the time period t.

Here, equation 21 uses second-order cone relaxation to deal with nonlinearity (Li et al., 2023b), specifically as follows:

${‖\begin{array}{l}2P_{ij.t}\\ 2Q_{ij.t}\\ I_{ij.t}^2-V_{i.t}^2\end{array}‖}_2\le I_{ij.t}^2-V_{i.t}^2.(22)$

(2) Current constraint

$0\le I_{ij.t}\le I_{ij.t}^{\max },(23)$

where $I_{ij.t}^{\max }$ is the maximum current on the branch ij at time t.

(3) Voltage constraint

$V_{i.t}^{\min }\le V_{i.t}\le V_{i.t}^{\max },(24)$

where $V_{i.t}^{\min }$ and ${\mathrm{V}}_{\mathrm{i}.\mathrm{t}}^{\max }$ are the minimum and maximum voltages at node i at time t.

(4) Energy storage constraints

$\left\{\begin{array}{c}0\le P_{i.t}^{\mathrm{c}\mathrm{h}\mathrm{a}}\le B_{i.t}^{\mathrm{c}\mathrm{h}\mathrm{a}}{P}_{\max }^{\mathrm{c}\mathrm{h}\mathrm{a}}\\ 0\le P_{i.t}^{dis}\le B_{i.t}^{\mathrm{d}\mathrm{i}\mathrm{s}}{P}_{\max }^{dis}\\ B_{i.t}^{\mathrm{c}\mathrm{h}\mathrm{a}}+B_{i.t}^{\mathrm{d}\mathrm{i}\mathrm{s}}\le 1,B_{i.t}^{\mathrm{c}\mathrm{h}\mathrm{a}},B_{i.t}^{dis}\in \left\{0,1\right\}\\ E_{t+1}=E_t+{\eta }_{cha}{P}_{i.t}^{cha}-P_{i.t}^{\mathrm{d}\mathrm{i}\mathrm{s}}/{\eta }_{dis}\\ E_0=E_T\end{array}\right.,(25)$

where $B_{i.t}^{\mathrm{c}\mathrm{h}\mathrm{a}}$ and $B_{i.t}^{\mathrm{d}\mathrm{i}\mathrm{s}}$ are the charge and discharge markers for the t period, $P_{\max }^{\mathrm{c}\mathrm{h}\mathrm{a}}$ and $P_{\max }^{\mathrm{d}\mathrm{i}\mathrm{s}}$ are the maximum charge and discharge power, $E_t$ is the energy storage capacity at time t, and ${\eta }_{\mathrm{c}\mathrm{h}\mathrm{a}}$ and ${\eta }_{\mathrm{d}\mathrm{i}\mathrm{s}}$ are the charge and discharge efficiency.

3.4 Robust model

According to equations 11–15, the energy storage capacity, power, and charging and discharging variables are designed as the variables of the first stage, while the remaining variables are variables of the second stage (Li et al., 2023c). For concise expression, the above model is expressed in the matrix form as follows:

$\underset{\mathit{x}}{\min }{\mathit{a}}^{\mathrm{T}}\mathit{x}+\underset{\left\{p_s\right\}\in \mathit{Q}}{\max }\underset{{\mathit{y}}_s,\mathit{z},\mathit{u}}{\min }{\displaystyle \sum _{s=1}^{\mathrm{S}}}{p}_s\left({\mathit{z}}^{\mathrm{T}}C\mathit{z}+{\mathit{b}}^{\mathrm{T}}\mathit{u}\right),(26)$

$s.t.\left\{\begin{array}{l}\mathit{D}\mathit{x}\le \mathit{e}\\ {‖\mathit{F}\mathit{z}+\mathit{f}‖}_2\le \mathit{G}\mathit{z}+\mathit{g}\\ \mathit{H}\mathit{z}+{\mathit{K}\mathit{y}}_s+\mathit{J}\mathit{u}\le \mathit{l}\\ \mathit{L}{p}_s\le \mathit{o}\end{array}\right.,(27)$

where $\mathit{x}$, ${\mathit{y}}_s$, $\mathit{z}$, and $\mathit{u}$ are the decision variables and the rest are the coefficient matrices.

4 Model solving

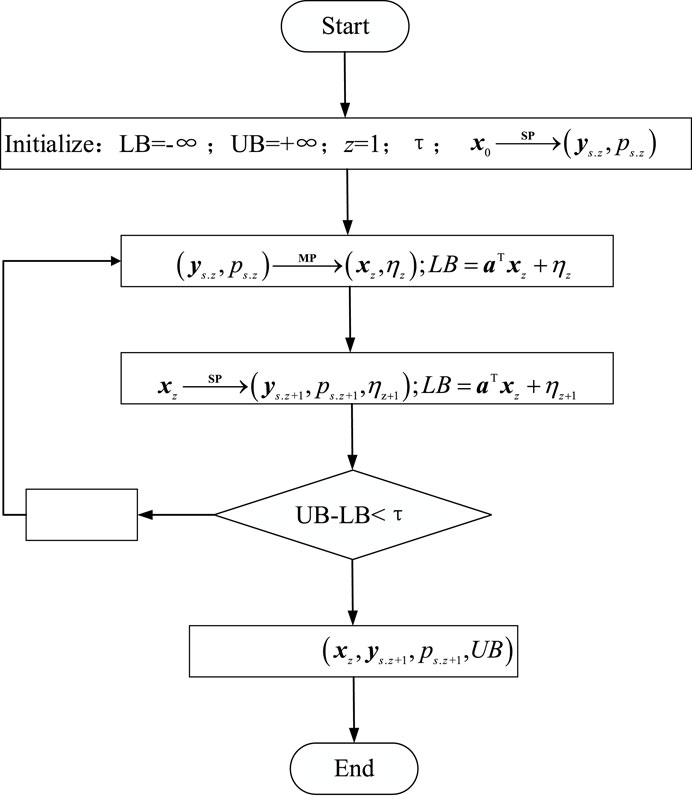
The robust model in equation 27 is decomposed into the master problem (MP) and sub-problem (SP) for solving life-science identifiers.

MP is shown as follows:

$\left(\mathrm{M}\mathrm{P}\right)\underset{\mathit{x},\eta }{\min }{\mathit{a}}^{\mathrm{T}}\mathit{x}+\eta ,(28)$

$\eta \ge {\displaystyle \sum _{s=1}^{\mathrm{S}}}{p_{s.\lambda }}^{*}\left({\mathit{z}}^{\mathrm{T}}C\mathit{z}+{\mathit{b}}^{\mathrm{T}}\mathit{u}\right),(29)$

where $\mathrm{\eta }$ is the upper bound value and $\mathrm{\lambda }$ is the number of iterations.

SP is used to solve the lowest daily operating cost of the distribution network under the worst scenario probability distribution when the variables are given in the first stage, as follows:

$\left(\mathrm{S}\mathrm{P}\right)\underset{\left\{p_s\right\}\in \mathit{Q}}{\max }\underset{{\mathit{y}}_s,\mathit{z},\mathit{u}}{\min }{\displaystyle \sum _{s=1}^{\mathrm{S}}}{p}_s\left({\mathit{z}}^{\mathrm{T}}C\mathit{z}+{\mathit{b}}^{\mathrm{T}}\mathit{u}\right).(30)$

Since the variables and constraints in equation 30 are not directly related to the variables and constraints in the second stage, the inner solution can be obtained first and then the outer solution.

${\upsilon }_s=\underset{{\mathit{y}}_s,\mathit{z},\mathit{u}}{\min }\left({\mathit{z}}^{\mathrm{T}}C\mathit{z}+{\mathit{b}}^{\mathrm{T}}\mathit{u}\right),(31)$

$\mathcal{l}=\underset{\left\{p_s\right\}\in \mathit{Q}}{\max }{\displaystyle \sum _{s=1}^{\mathrm{S}}}{p}_s{\upsilon }_s.(32)$

The process of solving the two-stage robust model can be seen in Figure 2.

FIGURE 2

FIGURE 2. Solution flow chart.

5 Case study

5.1 Basic parameter

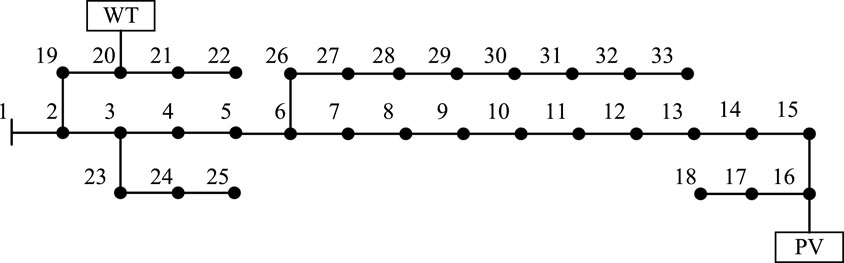
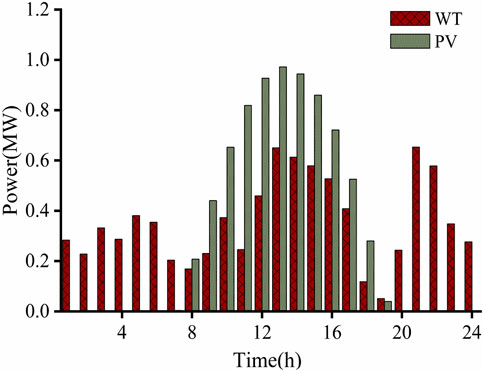
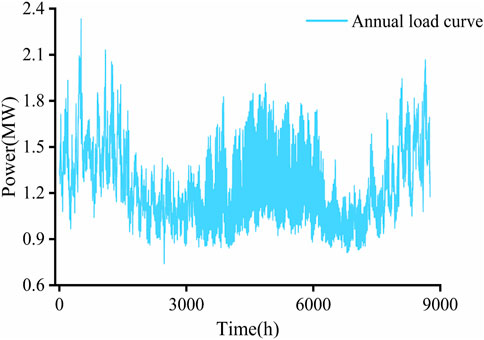
Here, the grid parameters of IEEE 33 nodes are used, among which the 16th node is connected to the photovoltaic and the 20th node is connected to the fan. The allowable voltage range of nodes is 0.95–1.05 pu. The specific network architecture is shown in Figure 3. The original data of typical daily PV, fan, and 1-year active load are shown in Figures 4 and 5. The unit installation cost of energy storage power and capacity is 1,008 yuan/kw and 1,400 yuan/kw, respectively, the annual bank interest rate is 0.05, the operating life is 10 years, and the TOU price is referenced (Yang et al., 2023). The following examples are simulated and analyzed by MATLAB.

FIGURE 3

FIGURE 3. 33-node network architecture.

FIGURE 4

FIGURE 4. Output of wind turbines and photovoltaics.

FIGURE 5

FIGURE 5. Annual load curve.

5.2 Comparative analysis of load forecasting results

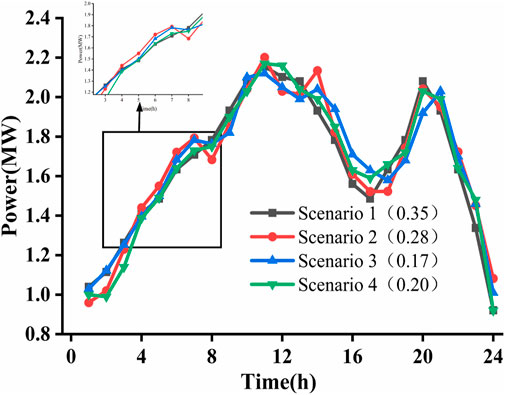
The annual load data of a region in the east of China are used as daily k-means++ clustering, and the four best types of scenarios and the probability of each scenario are divided by simulation, as shown in Figure 6. The mean absolute percentage error (MAPE) and root mean square error (RMSE) are used to analyze the load forecasting results. After scene clustering, the annual load curve is clustered into four different daily load scenarios, and the day-ahead forecasting is carried out.

FIGURE 6

FIGURE 6. Load clustering scenario and its probability.

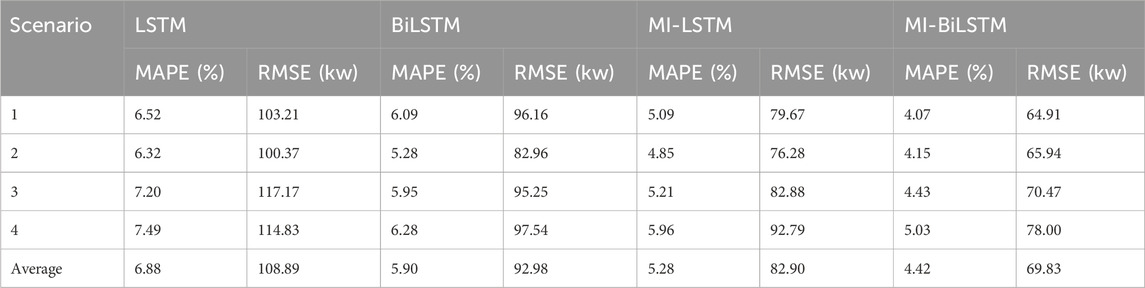
Four different models, LSTM, BiLSTM, MI-LSTM, and MI-BiLSTM, are selected for comparison. Since the main work of prediction is to extract the importance value fluctuation matrix and modify the original input features, the relevant parameters of the deep neural network model should be controlled to remain unchanged during comparison, and the original input features and modified features should be observed to change the accuracy of prediction by substituting them into the model. Therefore, the parameter settings of the LSTM and MI-LSTM models are consistent, and the parameter settings of the BiLSTM and MI-BiLSTM models are also consistent. The hyperparameters of the LSTM and BiLSTM models are optimized by the control variable method. MAPE and RMSE are recorded under different daily load scenarios. The prediction results under the four methods are shown in Table 1.

TABLE 1

TABLE 1. Comparison of the prediction results of different models under different scenarios.

As can be seen from Table 1, among the four models, the LSTM model has the lowest average prediction accuracy, while the established BiLSTM model has higher prediction accuracy compared to the LSTM model due to the consideration of bidirectional information, and the MI-LSTM model has a significantly improved prediction accuracy compared with the LSTM model due to the consideration of the fluctuation of the importance of input features. For the MI-BiLSTM model, the prediction accuracy is better than that of the other models in four different daily load scenarios, which indicates that the fluctuation matrix of importance value extracted by the MI method has a more obvious improvement effect on accuracy compared with other methods.

In scenarios one to four, the MAPE of the MI-BiLSTM model was 2.45%, 2.17%, 2.77%, and 2.46%, respectively. Compared with other models in all the scenarios, the average value of the MI-BiLSTM model is the lowest, and so is its RMSE.

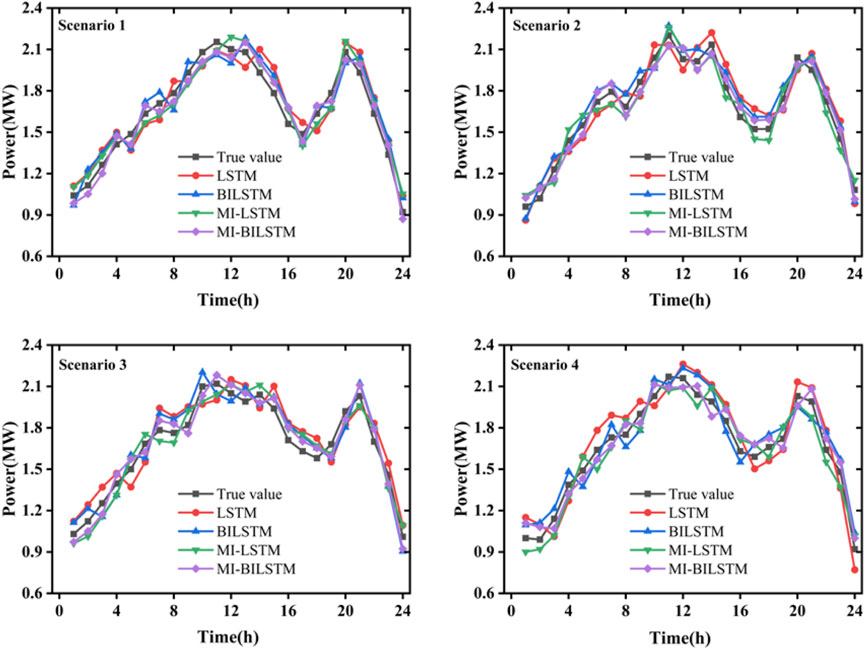
The comparison of the results of different models is shown in Figure 7. As can be seen from Figure 7, the prediction accuracy of the MI-BiLSTM model is the highest among the four models. At the peaks and troughs of the load curve, the model not only considers the bidirectional information flow but also realizes the dynamic tracking of the fluctuation of the importance value of the input features, which has a better fitting effect for the real load curve.

FIGURE 7

FIGURE 7. Comparison of load forecasting under different scenarios.

5.3 Energy storage planning analysis

In order to verify the effectiveness and economy of energy storage planning, the following three schemes were compared.

Case 1. Considering neither energy storage planning nor incorporating wind turbines or photovoltaics.

Case 2. Considering incorporating WT and PV without considering energy storage planning.

Case 3. Considering incorporating wind turbines, photovoltaics, and energy storage.

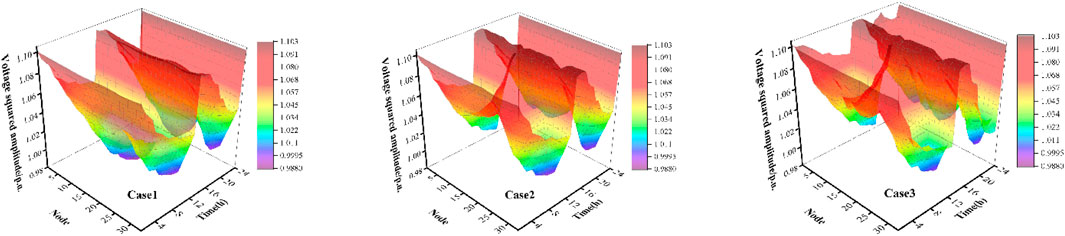
The indicators, energy storage capacity configuration results, and node position pairs under different schemes are shown in Table 2, and the node voltage is shown in Figure 8.

According to Table 2 and Figure 8, although there is no energy storage investment cost in Case 1 without considering the installation of energy storage and distributed energy, the daily operating cost and electricity distribution cost of the distribution network are higher than those in other schemes, and the voltage fluctuation of Case 1 is also significantly different from that of the other schemes. Case 2 has more distributed energy than Case 1. Although the network loss cost increases, the other indicators are improved. Case 3 has the lowest daily operating cost after planning energy storage, and the fundamental reason is that the increase in energy storage meets more load demand and reduces the power generation in the distribution network. Although the network loss increases by 320.855 yuan compared with Case 1, it is negligible when considering the reduced operating cost.

As can be seen from Figure 8, the voltage of all the cases is within a reasonable range; Case 1 has the largest voltage fluctuation, Case 2 has a slight improvement compared with Case 1, and Case 3 has a significant improvement compared with Case 1 and Case 2.

It is not difficult to see that the implementation of energy storage planning for the distribution network on the basis of load forecasting has improved the operating costs, voltage fluctuations, and network losses of the distribution network.

TABLE 2

TABLE 2. Comparison of the indicators and configuration results.

FIGURE 8

FIGURE 8. Voltage fluctuations of different cases.

5.4 Comparison of uncertain methods

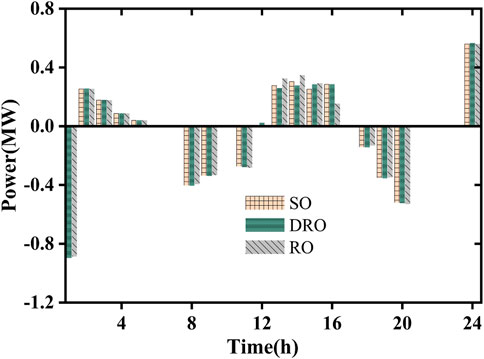
To verify the advantages of the DRO energy storage planning presented in this article, the results of DRO are compared with those of SO and RO. Among them, SO is optimized based on the expected value of the load forecast, while RO considers the worst case based on the expected value of the load forecast, and the expected value of the load forecast fluctuates ±10%. Table 3 shows the comparison of the energy storage planning results under different uncertain methods. Figure 9 and Figure 10 are the comparison of power generation and energy storage charging and discharging of the distribution network, respectively.

TABLE 3

TABLE 3. Comparison of the energy storage planning results under different uncertain methods.

FIGURE 9

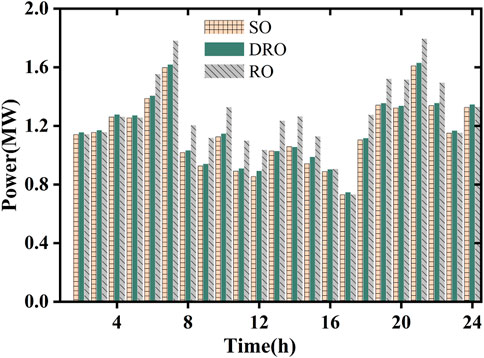
FIGURE 9. Comparison of generation power in the distribution network under different uncertainty methods.

FIGURE 10

FIGURE 10. Comparison of energy storage charging and discharging under different uncertain methods.

As can be seen from Table 3 and Figures 9 and 10, in terms of distribution network operating costs, the SO results are the most aggressive, RO is the most conservative, and DRO is somewhere in between. The reasons for this are the following.

RO ignored the distribution information of the load and only considered the worst-case system operation, which led to an increase in the cost of power purchase to meet the load demand. Second, the configured energy storage charge and discharge cannot meet the worst-case load at all times, so the energy storage capacity decreases, which also increases the power generation of the distribution network unit.

In contrast, SO considers only a single empirical distribution, while DRO considers the worst distribution of load compliance in an uncertain concentration, which results in the lowest daily operating costs in SO.

In summary, the DRO model presented here takes into account the distribution information in the known load sample data and optimizes it for the worst-case scenario, effectively balancing robustness and economy.

6 Conclusion

In order to track the fluctuation of the importance value of input features and further improve the prediction accuracy, a MI-BiLSTM short-term load forecasting method considering the fluctuation of importance value of the features is proposed on the basis of k-means++ clustering. Then, based on load forecasting, a comprehensive norm-constrained uncertainty set is constructed. A two-stage robust model for energy storage planning of a distribution network is constructed to optimize the network loss. After a case analysis, the following conclusions are reached:

1) The MI-BiLSTM short-term load forecasting method using a feature importance value fluctuation matrix can make up for the defects of LSTM and improve the forecasting accuracy.

2) Under various daily load scenarios, the prediction methods presented in this paper show higher prediction accuracy. This shows that the method is not limited to a specific scenario and has good adaptability and stability.

3) Based on load prediction, energy storage planning for a distribution network not only reduces the daily operating cost of the distribution network but also improves the power flow distribution of the system, further reduces network loss, and improves voltage fluctuation, which is of practical significance.

4) For uncertainty, the DRO method based on comprehensive norm can improve the robustness of the uncertainty set, and compared with SO and RO, this method has a better performance in planning and economic problems and the effect is stable.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

YH: writing–review and editing and data curation. YM: writing–original draft.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Science and Technology Project of State Grid Shanghai Electric Power Company (No. 52090022004J).

Conflict of interest

Authors MY, HZ, KJ, YL, and XT were employed by State Grid Shanghai Electric Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from Science and Technology Project of State Grid Shanghai Electric Power Company (No. 52090022004J). The funder had the following involvement: study design, collection, analysis, interpretation of data, the writing of this article.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cai, S., Zhang, B., and Tang, D. (2020). Fisher information method for processing weather factors in short-term load forecasting. Electr. Power Autom. Equip. 40 (3), 141–146. doi:10.16081/j.epae.202002027

CrossRef Full Text | Google Scholar

Cecati, C., Kolbusz, J., Różycki, P., Siano, P., and Wilamowski, B. M. (2015). A novel RBF training algorithm for short-term electric load forecasting and comparative studies. IEEE Trans. Industrial Electron- ics 62 (10), 6519–6529. doi:10.1109/tie.2015.2424399

CrossRef Full Text | Google Scholar

Feng, Y. T., Zhang, P. X., Yang, M., Li, Q., and Zhang, A. (2019). Short term load forecasting of offshore oil field microgrids based on DA-SVM. Energy Procedia 158, 2448–2455. doi:10.1016/j.egypro.2019.01.318

CrossRef Full Text | Google Scholar

Fu, W., Jiang, X., Li, B., Tan, C., Chen, B., and Chen, X. (2023). Rolling bearing fault diagnosis based on 2D time-frequency images and data augmentation technique. Meas. Sci. Technol. 34 (4), 045005. doi:10.1088/1361-6501/acabdb

CrossRef Full Text | Google Scholar

Han, J., Yan, L., and Li, Z. (2021). A task-based day-ahead load forecasting model for stochastic economic dispatch. IEEE Trans. Power Syst. 36 (6), 5294–5304. doi:10.1109/tpwrs.2021.3072904

CrossRef Full Text | Google Scholar

Hou, H., Gan, M., and Wu, X. (2023). Two-stage distribu-tionally robust optimal scheduling for port multi-energy microgrid considering mobile hydrogen energy storage. Proc. CSEE, 1–18. doi:10.13334/j.0258-8013.pcsee.223327

CrossRef Full Text | Google Scholar

Huang, Y., Zhang, Y., and Xia, Z. (2023). Power system power planning method considering the value of demand response resources and energy storage capacity. J. Shanghai Jiao Tong Univ. 57 (04), 432–441. doi:10.16183/j.cnki.jsjtu.2021.477

CrossRef Full Text | Google Scholar

Jinpeng, C., Zhijian, Hu, and Weinan, C. (2021). Load prediction of integrated energy system based on combination of quadratic modal decomposition and deep bidirectional long shortterm memory and multiple linear regression. Automation Electr. Power Syst. 45 (13), 85–94. doi:10.7500/AEPS20200829004

CrossRef Full Text | Google Scholar

Jixiang, Lu, Qipei, Z., and Zhihong, Y. (2019). Short-term load forecasting method based on CNN-LSTM hybrid neural network model. Automa- tion Electr. Power Syst. 43 (8), 131–137.

Google Scholar

Lan, Ma, Xie, L., and Lin, Ye (2022). Wind power fluctuation suppression strategy based on hybrid energy storage Bi-level programming model. Power Syst. Technol. 46 (03), 1016–1029. doi:10.13335/j.1000-3673.pst.2021.0569

CrossRef Full Text | Google Scholar

Lei, P., Wei, Z., and Chen, S. (2022). Multi-stage stochastic optimization dispatch model for AC-DC hybrid distribution power network. Power Syst. Prot. Control 50 (14), 23–32. doi:10.19783/j.cnki.pspc.211212

CrossRef Full Text | Google Scholar

Li, L., Hu, Bo, and Xie, K. (2016). Capacity optimization of hybrid energy storage systems in isolated microgrids based on discrete Fourier transform. Automation Electr. Power Syst. 40 (12), 108–116.

Google Scholar

Li, Z., Wu, L., Xu, Y., Wang, L., and Yang, N. (2023a). Distributed tri-layer risk-averse stochastic game approach for energy trading among multi-energy microgrids. Appl. Energ. 2023, 120282, 120282. doi:10.1016/j.apenergy.2022.120282

CrossRef Full Text | Google Scholar

Li, Z., Wu, L., Xu, Y., and Zheng, X. (2021). Stochastic-weighted robust optimization based bilayer operation of a multi-energy building microgrid considering practical thermal loads and battery degradation. IEEE Trans. Sustain. Energ. 13 (2), 668–682. doi:10.1109/TSTE.2021.3126776

CrossRef Full Text | Google Scholar

Li, Z., Xu, Y., Wang, P., and Xiao, G. (2023b). Restoration of multi energy distribution systems with joint district network recon figuration by a distributed stochastic programming approach. IEEE Trans. Smart Grid, 1–13. doi:10.1109/TSG.2023.3317780

CrossRef Full Text | Google Scholar

Li, Z., Xu, Y., Wang, P., and Xiao, G. (2023c). Coordinated preparation and recovery of a post-disaster multi-energy distribution system considering thermal inertia and diverse uncertainties. Appl. Energ. 336, 120736. doi:10.1016/j.apenergy.2023.120736

CrossRef Full Text | Google Scholar

Liu, H. 1, Li, H., and Ma, J. (2023). Distribu tionally robust optimal dispatching of integrated electricity and heating system considering source-load uncertainty. Electr. Power Autom. Equip., 1–14. doi:10.16081/j.epae.202302008

CrossRef Full Text | Google Scholar

Ma, H., Hu, J., and Tong, Y. (2023). A two-stage ro bust planning approach for data center microgrids considering flexibility. Proc. CSEE, 1–13. doi:10.13334/j.0258-8013.pcsee.221146

CrossRef Full Text | Google Scholar

Nan, Y., DiZhou, Y. Z., Jiazhan, C., Daojun, C., and Xiaoming, W. (2018). Research on modelling and solution of stochastic SCUC under AC power flow constraints. IET Generation Transm. Distribution 12 (15), 3618–3625. doi:10.1049/iet-gtd.2017.1845

CrossRef Full Text | Google Scholar

Peng, X., Pan, K., and Zhang, D. (2020). Piecewise short-term load forecasting based on adaptive seasonal load category and important point segment. Power Syst. Technol. 44 (2), 603–613. doi:10.13335/j.1000-3673.pst.2018.1705

CrossRef Full Text | Google Scholar

Ren, H., Kang, J., and Qian, L. (2019). Comparison and analysis of location methods for energy storage devices in multi-machine power systems. Distrib. Energy 4 (2), 23–29. doi:10.16513/j.cnki.10-1427/tk.2019.02.004

CrossRef Full Text | Google Scholar

Su, X., Liu, T., Cao, H., Jiao, H., Yu, Y., He, C., et al. (2017). A multiple distributed BP neural networks approach for short-term load forecasting based on Hadoop framework. Proc. CSEE 37 (17), 4966–4973. doi:10.13334/j.0258-8013.pcsee.160747

CrossRef Full Text | Google Scholar

Wang, C., Zhang, X., and Ling, K. (2023). Two-stage adaptive robust optimal scheduling based on the interval probability uncertainty set for microgrids. Proceed- ings CSEE, 1–14.

Google Scholar

Wang, D., Shi, X., and Yin, J. (2015). Prediction on hourly load of air conditioning by RBF support vector machine. Trans. China Electrotech. Soc. 30, 531–535. Supple- ment 1. doi:10.19595/j.cnki.1000-6753.tces.2015.s1.092

CrossRef Full Text | Google Scholar

Wang, Q., Zhang, X., Yi, C., Li, Z., and Xu, D. (2022). A novel shared energy storage planning method considering the correlation of renewable uncertainties on the supply side. IEEE Trans. Sustain. Energy 13 (4), 2051–2063. doi:10.1109/tste.2022.3179837

CrossRef Full Text | Google Scholar

Wu, M., and Fang, F. (2023). Distributionally robust opti mization of electricity-heat-hydrogen integrated energy system with wind and solar uncertainties. Trans. China Electrotech. Soc., 1–14. doi:10.19595/j.cnki.1000-6753.tces.220759

CrossRef Full Text | Google Scholar

Yang, N., Dong, Z., Wu, L., Zhang, L., Shen, X., Chen, D., et al. (2022b). A comprehensive review of security-constrained unit commitment. J. Mod. Power Syst. Clean Energy 10 (3), 562–576. doi:10.35833/mpce.2021.000255

CrossRef Full Text | Google Scholar

Yang, N., Qin, T., Wu, L., Huang, Yu, Huang, Y., Xing, C., et al. (2022d). A multi-agent game based joint planning approach for electricity-gas integrated energy systems considering wind power uncertainty. Electr. Power Syst. Res. 204, 107673. doi:10.1016/j.epsr.2021.107673

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Wu, L., Shen, X., Jia, J., Li, Z., et al. (2022a). Intelligent data-driven decision-making method for dynamic multisequence: an E-Seq2Seq-based SCUC expert system. IEEE Trans. Industrial Inf. 18 (5), 3126–3137. doi:10.1109/tii.2021.3107406

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Xing, C., Ye, Di, Jia, J., Chen, D., et al. (2022c). Deep learning-based SCUC decision-making: an intelligent data-driven approach with self-learning capabilities. Wiley-Blackwell) 16 (4), 629–640. doi:10.1049/gtd2.12315

CrossRef Full Text | Google Scholar

Yang, X., Liu, X., and Qi, G. U. O. (2023). Coordin-ated planning of energy storage and flexible retrofit of thermal power units considering ancillary service income. Power Syst. Technol. 47 (04), 1350–1362. doi:10.13335/j.1000-3673.pst.2022.1306

CrossRef Full Text | Google Scholar

Zhang, T. F., Liu, D., and Yue, D. (2017). “Rough neuron based RBF neural networks for short-term load forecasting,” in 2017 IEEE International Conference on Energy Internet, Beijing,China, April 17-21, 2017, 291–295. doi:10.1109/ICEI.2017.58

CrossRef Full Text | Google Scholar

Zhang, Y., Xie, X., Fu, W., Chen, X., Hu, S., Zhang, L., et al. (2023b). An optimal combining attack strategy against economic dispatch of integrated energy system. IEEE Trans. Circuits Syst. II Express Briefs 70 (1), 246–250. doi:10.1109/tcsii.2022.3196931

CrossRef Full Text | Google Scholar

Zhang, Z., Zhou, M., and Wu, Z. (2023a). Energy storage location and capacity planning method consi-dering dynamic frequency support. Proc. CSEE 43 (07), 2708–2721. doi:10.13334/j.0258-8013.pcsee.212928

CrossRef Full Text | Google Scholar

Zheng, R., Zhang, S., and Xianyong, X. (2020). Shortterm load forecasting of multi-layer long short-term memory neural network considering temperature fuzziness. Electr. Power Autom. Equip. 40 (10), 181–186. doi:10.16081/j.epae.202008016

CrossRef Full Text | Google Scholar

Zheng, Y., Jiang, Y., and Zhang, J. (2023). Joint planning optimization of source-storage-transport-ation considering long and short-term energy storage under high proportion of wind power penetration. Electr. Power Autom. Equip. 43 (03), 63–71. doi:10.16081/j.epae.202205054

CrossRef Full Text | Google Scholar

Zhou, D., Xie, P., Huang, Y., Cheng, G., Tang, W., Zou, K., et al. (2023). Optimization method of power grid material warehousing and allocation based on multi-level storage system and reinforcement learning. Comput. Electr. Eng. 109, 108771. doi:10.1016/j.compeleceng.2023.108771

CrossRef Full Text | Google Scholar

Zhu, X., and Shan, Y. (2023). Dispatching strategy of aggregator considering fuzzy random uncertainty. Electr. Power Autom. Equip. 43 (06), 152–159+167. doi:10.16081/j.epae.202206007

CrossRef Full Text | Google Scholar

Zuo, F., Zhang, Y., and Zhao, Q. (2022). Two-stage stochastic optimization for operation scheduling and capacity allocation of integrated energy production unit considering supply and demand uncertainty. Proc. CSEE 42 (22), 8205–8215. doi:10.13334/j.0258-8013.pcsee.220343

CrossRef Full Text | Google Scholar