- 1School of Energy Resources, China University of Geosciences, Beijing, China
- 2Research Institute of Petroleum Exploration and Development of CNPC, Beijing, China
The Blasingame method is a valuable tool for analysing the diminishing production challenge in the presence of variable bottomhole pressure and diverse production conditions. It is essential to highlight that the Blasingame method views the closed reservoir as the outer boundary condition for its model. This paper introduces the concept of the equivalent well control radius and formulates the Blasingame method based on the fluid flow characteristics inherent in twin-well production, taking into account the influence of inter-well interference. This study provides an in-depth analysis of production variations in reservoirs with inter-well interference by examining Blasingame type-curve definitions of the dimensionless parameters. Additionally, it investigates key factors impacting production, including neighbouring wells’ production, distance, and opening time: variations in all three parameters lead to different levels of interference between wells, which manifests itself in the regularised production integral derivative curve with different lengths and heights of convexity. Numerical simulations employing orthogonality are conducted to validate the reliability of this method. The results of these simulations offer theoretical support for the precise evaluation of reservoirs facing similar challenges.
1 Introduction
In reservoirs with strong inter-well connectivity, neighbouring well interference can significantly impact test well pressures during the declining development process (Yuan and Wang, 2013; Guo et al., 2022; Wang et al., 2023). It has been well-established that reservoir dynamic description techniques, centred on single-well test well analysis and modern declining production analysis techniques, are effectively applied in reservoirs characterised by small single-well control ranges and poor inter-well connectivity (Zhang, 2004). However, reservoirs with high permeability and good connectivity are often multi-well systems (Zhang et al., 2006; Lin and Yang, 2007; Li and Luo, 2009). Therefore, interpreting such reservoirs using a single-well dynamic description can be misleading (Pang et al., 2012; Gan et al., 2022; Wang et al., 2023). Currently, the industry typically employs the superposition principle method to study the dynamic information of test wells in a multi-well system with inter-well interference (Onur et al., 1991; Li et al., 1994; Zhou et al., 2022). Jiaen Lin, Qiguo Liu, and Yonglu Jia demonstrated the late ‘upward curvature’ of the pressure recovery derivative curve in test wells by using the well test analysis technique (Dong and Zhai, 1996; Lin et al., 1996; Liu et al., 2002; Lin and Yang, 2005b; Liu et al., 2006; Jia et al., 2008; Deng et al., 2015). Hedong Sun provided a theoretical proof of this phenomenon while establishing an analysis method for multi-well pressure recovery test wells under neighbouring well interference conditions (Sun, 2016; Alarji. H et al., 2022). With the deepening of research, many scholars have explored the multi-well production model under the influence of multiple factors. Zeng Yang established a model for interpreting well tests in injection wells that consider interference from neighbouring wells (Zeng Y et al., 2020; Zhao et al., 2022). Cao established a well test interpretation model for finite inflow fractured wells under multi-well interference (Wei et al., 2022b).
The analytical solution of the multi-well production model discussed in previous studies is primarily used for analysing test wells (Jiang et al., 2019; Chen, 2023). The model assumes an infinite reservoir as the outer boundary condition, which simplifies the analysis. This paper introduces a closed reservoir as the outer boundary condition, introduces the ‘normalisation factor’, and applies the model’s solution to the Blasingame-type curves (Chen et al., 2017; Xu et al., 2021).
Modern methods of diminishing yield analysis and well test analysis are based on the classical seepage basis, but the two methods use different accuracy of evaluation data in the analysis process (Sun, 2013; Spivey, 2016; Wei et al., 2022a). Modern methods of diminishing yield analysis require less precision in the data and are, therefore, less difficult and costly to obtain. Blasingame and others creatively introduced the proposed time of material equilibrium and regularised yields to establish a plate of decreasing curves called the Blasingame plate (Mccray, T.L, 1990; Palacio and Blasingame, 1993). It is epoch-making in the modern analysis of diminishing yield.
2 Modelling and solving
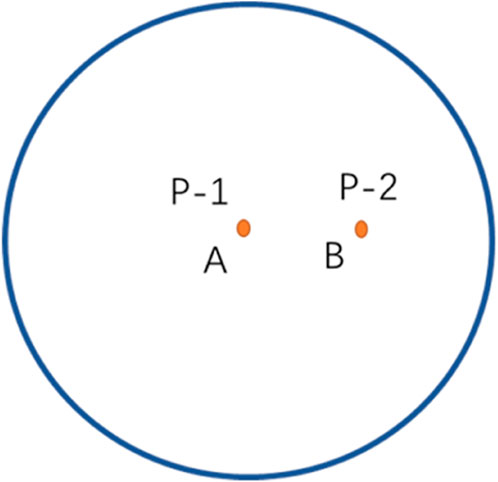
Figure 1 shows a circular stratigraphic well deployment map.
From Figure 1, the middle point of a circular formation with supply radius re and closed outer boundary, there is a well P-1 producing at a constant yield qi, while at point B, there is another well P-2 producing at a yield q2, and the distance from point A to point B is L.
Other assumptions are as follows: the reservoir is homogeneous and isotropic, with impermeable boundaries above and below; the reservoir pores are filled with a single-phase, micro-compressible fluid, and the flow is in accordance with Darcy’s law; the effect of gravity is neglected; and the effects of the skin effect and the wellbore storage effect are not considered.
2.1 Equivalent well control radius
The pull-down spatial pressure solution for point A of the double-well production, Eq. 1, can be obtained according to the Duhamel superposition principle (Wang, 2015):
where
When L tends to 0, the pressure response of the unsteady seepage stage at point A is equivalent to the pressure response of well P-1 when it produces individually at a constant production rate
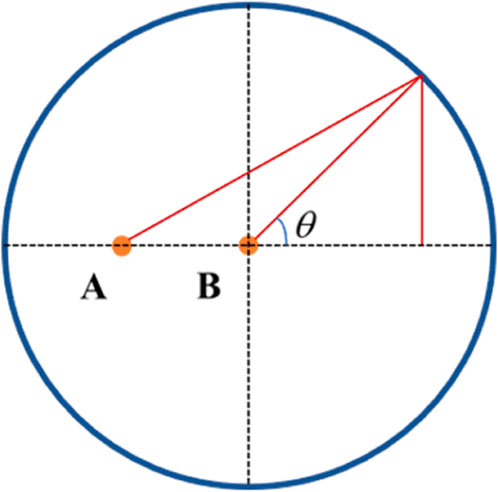
Figure 2 shows a conceptual diagram of the reD2 solution. Overall, in Figure 2, the flow stage at point A, when the two wells are producing, can be simplified as the infinite radial flow stage, the proposed steady-state stage. In turn, the pressure solution at point A when well P-2 is producing alone can be simplified as the pressure solution for one well in the centre of a circular closed reservoir with constant production, while the simplified well control radius expression for well B is given in this paper.
The average of the distances from point B to the circular closure boundary at the simplified drain radius is as follows:
where
From Eqs 2–4, we can derive
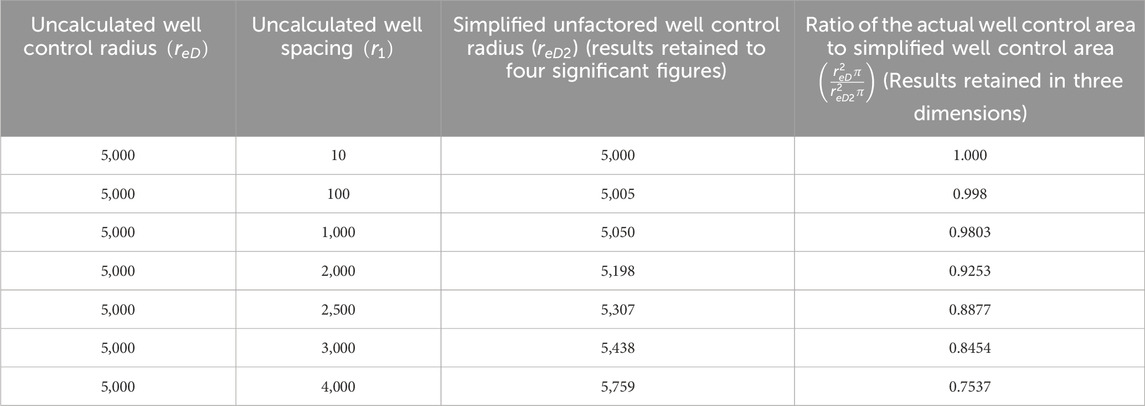
Table 1 lists the equivalent well control radius error rating table. After obtaining the simplified well control radius using this method, the corresponding equivalent well control area is further calculated and compared with the actual well control area. It is found that the simplified well control area is more accurate at
2.2 Modelling
The fixed solution problem for p-1 wells can be described as follows:
The fixed solution problem for p-2 wells can be described as follows:
The dimensionless variables are defined as follows:
where
2.3 Solution of the mathematical model
A Laplace transformation of Eqs 5–15 yields
The boundary conditions within the P-1 well are expressed as
The boundary conditions within the P-2 well are expressed as
Substituting Eq. 16 and Eq. 17 into Eq. 19, we have Eq. 20
Substituting Eq.16 and Eq.18 into Eq. 19, we have Eq. 21
Eq. 22 can be obtained from the Duhamel superposition principle:
3 Plotting Blasingame-type curves
Plots of the rate solution qD under a constant BHFP and the reciprocal of the pressure solution at a constant rate (1/pD) in the coordinate system are shown in Figure 3A. The figure indicates that the two curves almost overlap in the transient flow period and are dispersed in the boundary-dominated flow period. Palacio and Blasingame (1993) replaced dimensionless time tD with dimensionless material balance time tcD and plotted the above curves again. The result shows that the two curves overlap, as shown in Figure 3B. In other words, the solutions of variable flow rate and constant flow rate are equivalent due to the introduction of material balance time tcD. Therefore, the Blasingame method is applicable to the condition of a variable BHFP and also to the condition of a variable flow rate (Liu, 2010; Yu, 2020).
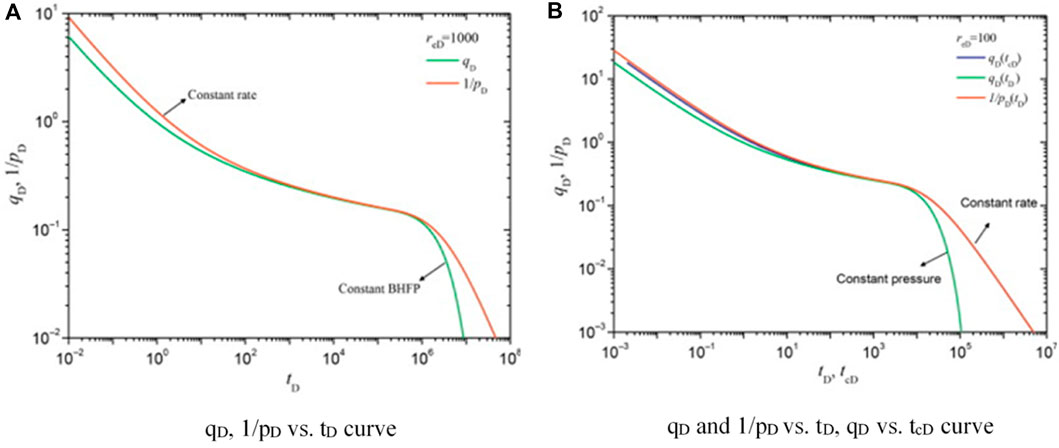
Figure 3. Comparison of fixed production pressure inverse, fixed production output, and fixed production material balance time output curves (A). qD, 1/pD vs. tD curve; (B). qD and 1/pD vs. tD, qD vs. tcD curve (Hedong Sun, 2015).
3.1 Blasingame-type curve definitions of the dimensionless parameters
Blasingame-type curve definitions of the dimensionless parameters are formed by introducing normalisation coefficients,
Here, Blasingame-type curve definitions of the dimensionless parameters are as follows:
Define the dimensionless material balance time as Eq. 23
Define the dimensionless decline flow rate Eq. 24
Define the dimensionless cumulative production as Eq. 25
Define the dimensionless decline flow rate integral function as Eq. 26
Define the dimensionless decline flow rate integral derivative as Eq. 27
3.2 Blasingame-type curves and model validation
Figure 4 shows an unstable analysis curve of production from double straight wells in homogeneous reservoirs. From Figure 4, taking reD = 5,000 and qB = 4 as an example, the crude oil flow can be roughly divided into an early radial flow stage, a stage influenced by the interference of neighbouring wells, and a later stage when the influence of the interfering wells is weakened (unsteady flow stage). The following section addresses the effect of well spacing, neighbouring well production, and neighbouring well start time factors on the Blasingame curve.
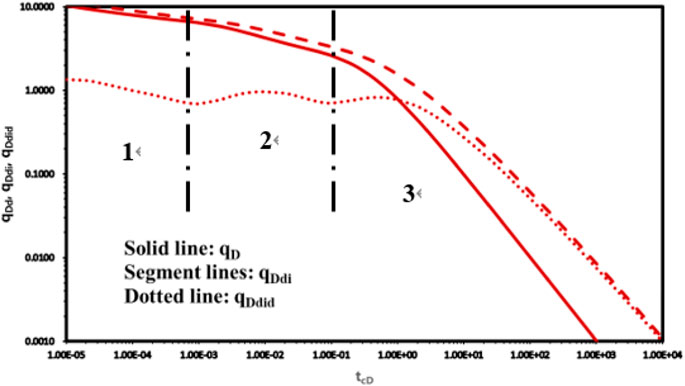
Figure 4. Unstable analysis curve of production from double straight wells in homogeneous reservoirs.
3.2.1 Effect of well spacing
Figure 5 shows the effect of different distances between two wells on the Blasingame curve when two wells in a circular homogeneous confined reservoir are producing at the same rate with simultaneous fixed production. From Figure 5, the early unstable flow stage of typical curves is a set of curves corresponding to different dimensionless well spacings,
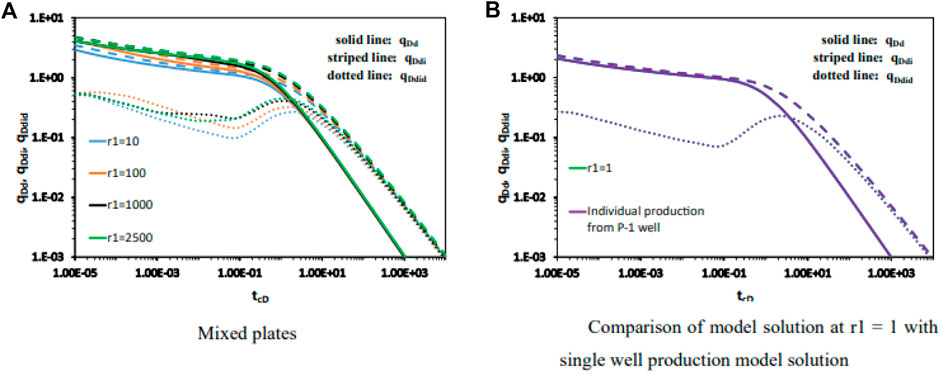
Figure 5. Effect of different distances between two wells on the Blasingame curve when two wells in a circular homogeneous confined reservoir are producing at the same rate with simultaneous fixed production (A) Mixed plates; (B) Comparison of model solution at r1=1 with single well production model solution.
Let
3.2.2 Effect of well spacing
Figure 6 shows the effect of Blasingame curves on P-2 delayed production from twin wells in circular homogeneous confined reservoirs producing at the same rate of constant production. Typical curves are a set of curves corresponding to the different dimensionless material balance time delays of P-2 wells (with fixed production rates, denoted as qi) during the opening of the well. For the same production rate and constant well spacing, the larger is
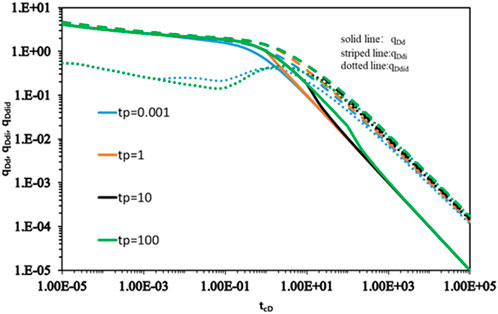
Figure 6. Effect of Blasingame curves on P-2 delayed production from twin wells in circular homogeneous confined reservoirs producing at the same rate of constant production.
3.2.3 Effect of production size of neighbouring wells
Figure 7 shows the effect of Blasingame curves in circular homogeneous closed reservoirs with two wells producing P-2 at different rates at the same time. Figure 7 shows that the type curves are a set of curves corresponding to the production of P-2 wells of different unfactored times. Under the condition of simultaneous production with the same well spacing, the larger
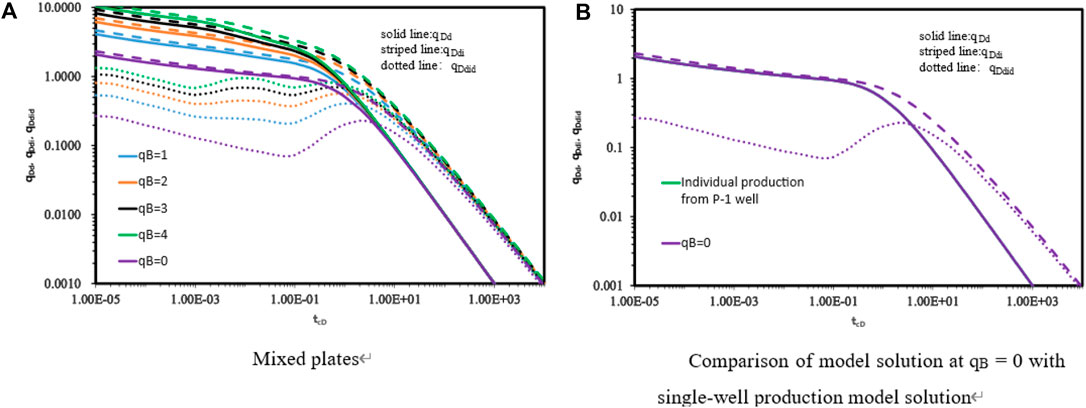
Figure 7. Effect of Blasingame curves in circular homogeneous closed reservoirs with two wells producing P-2 at different rates at the same time (A) Mixed plates; (B) Comparison of model solution at qB=0 with single well production model solution.
Let
4 Comparative analysis of numerical simulations
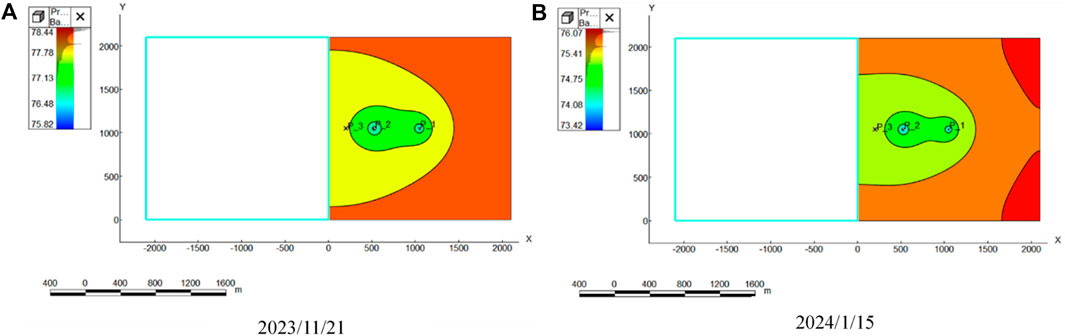
Figures 8, 9 show the reservoir pressure map and plot of the bottomhole pressure, production, and cumulative production over time for the centre point wells.
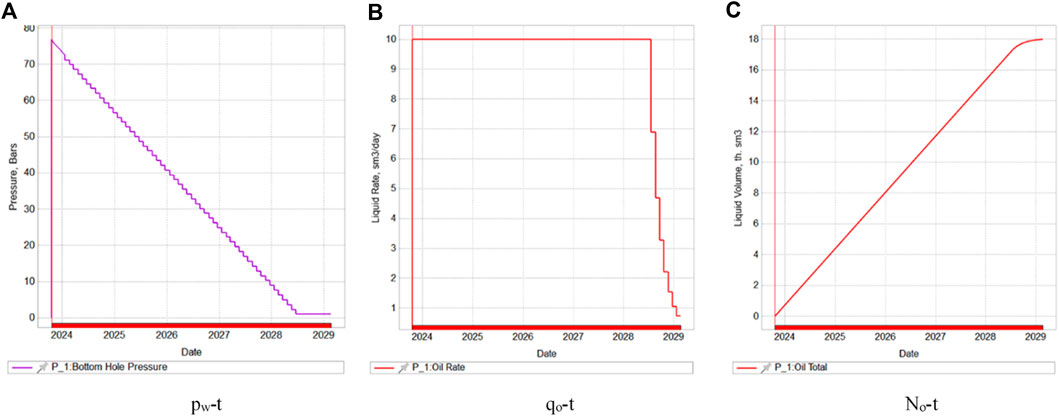
Figure 9. Plot of bottomhole pressure, production, and cumulative production over time for centre-point wells (A). pw-t; (B). qo-t; (C). No-t.
From Figures 8, 9, tNavigator software was used to establish a 2000 m × 2000 m × 20 m reservoir 3-D model, with a grid step of 5 m, net-to-gross ratio of 0.1, porosity of 0.1, X-axis permeability of 100 mD, X-axis permeability of 100 mD, Z-axis permeability of 10 mD, an initial pressure of 80 MPa, a support depth of 110 m, a single-component model, a well at the centre point producing at a fixed rate, and another well at the grid coordinates (100, 100, 1) producing at the same rate, and two wells producing at the same time, and obtaining the data on the bottomhole pressure, the production rate, and the cumulative production rate of the wells at the centre point with the change of time.
4.1 Data processing
To regularise the resultant data from numerical model runs,
Calculate the material balance time by Eq. 28
Calculate the normalised rate by Eq. 29
Calculate the normalised rate integral by Eq. 30
Calculate the normalised rate integral derivative by Eq. 31
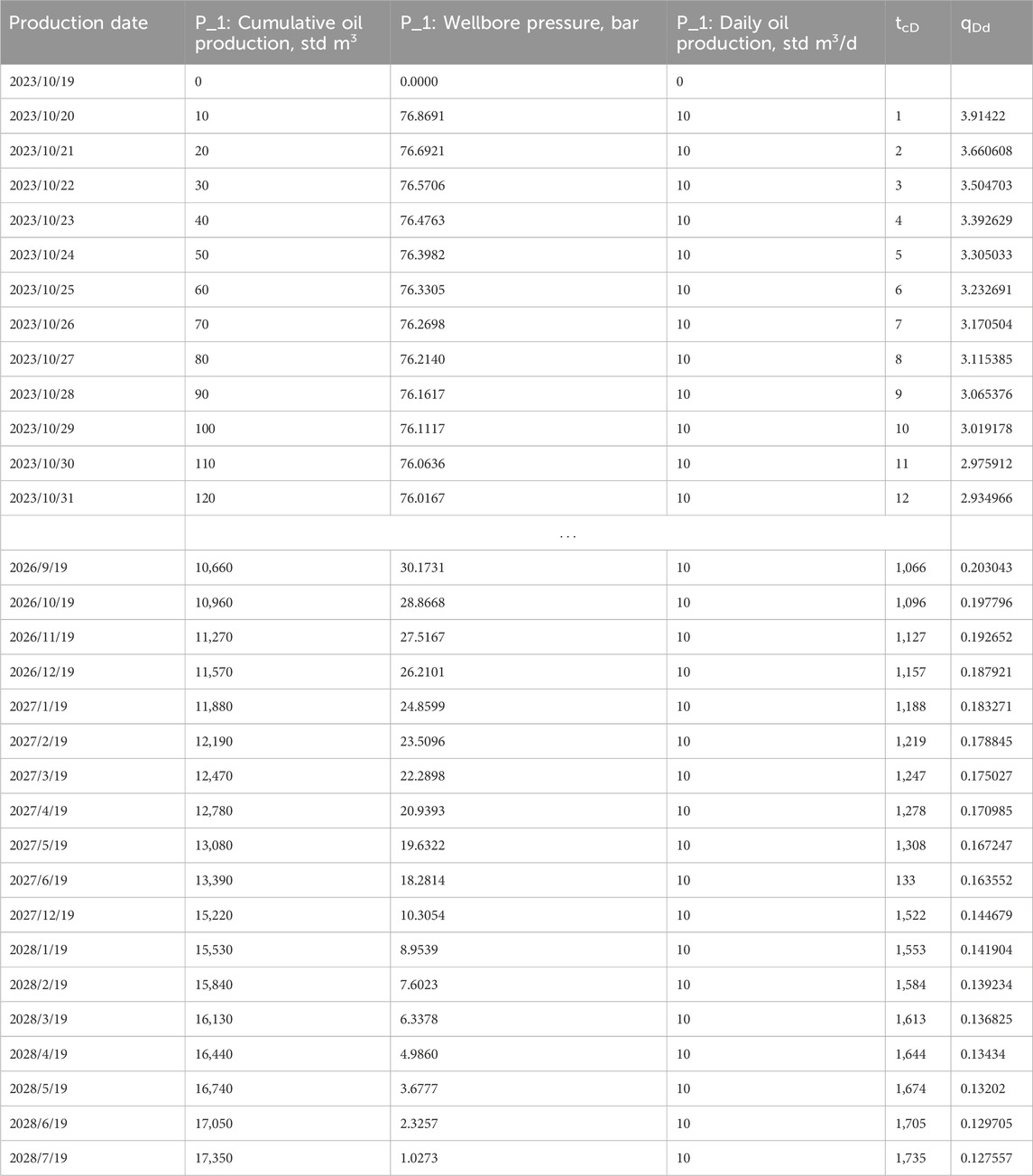
Table 2 is the numerical simulation data–production data regularisation table.
4.2 Data fitting
Figure 10 shows measured curve fitting results from plotting the three relational curves, qd-tc, qdi-tc, and qdid-tc, fitting the Blasingame yield instability analysis plate, and recording the fitted values, where the three relational curves can be used simultaneously or individually.
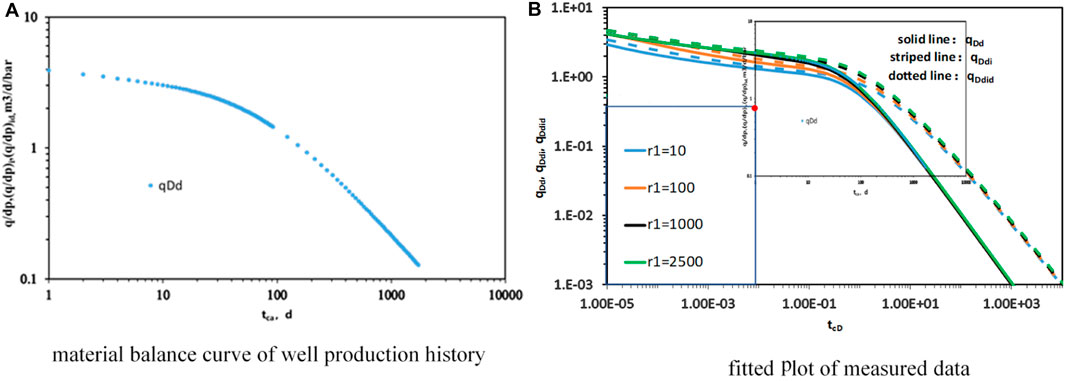
Figure 10. Measured curve fitting results (A) material balance curve of well production history; (B) fitted plot of measured data.
Using the theoretical fit points (8 × 10−3, 0.4), the actual fit points can be obtained (1, 0.7).
The dynamic reserve at the centre point can be calculated according to the following Eq 32:
as
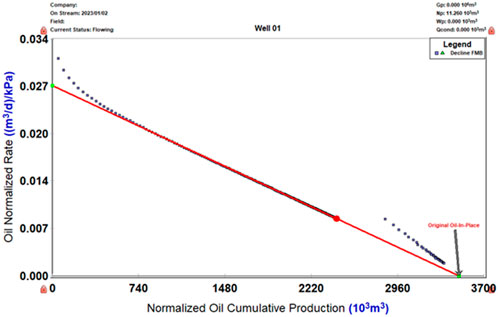
Additionally, the flowing material balance method (FMB) is listed for comparison to verify the accuracy of the method used in this article.
Figure 11 shows the equilibrium curves for the flowing material balance.
FMB is a method similar to the traditional material balance equation. However, it differs from the traditional material balance equation in that it uses dynamic pressure data instead of static pressure data for storage evaluation. Additionally, it differs from the flow material balance method, which uses flow pressure for dynamic storage evaluation. Once the reservoir is producing and has achieved a steady-state flow, the following relationship can be established (Eq. 33):
The dynamic reserves N can be determined from the intercept results if the
From Figure 11, the dynamic reserves calculated for the P-1 well’s reservoir are
5 Conclusion
In this paper, the dual-well model is solved analytically by the equivalent well control radius method, and the following conclusions are reached:
(1) Based on establishing a constant production model that takes into account the effect of the presence of inter-well interference, the method of equivalent well control radius is used to simplify the treatment of the external boundary conditions of neighbouring wells that are not at the centre point of a circular closed reservoir. The range of applicability of the method is verified by comparing the equivalent well control surface with the actual well control area, and it is found that the method is more accurate when
(2) Based on the method of equivalent well control radius, a sensitivity analysis of the Blasingame curve for the dual-well model can be conducted with respect to the parameters of adjacent well production, well spacing, and adjacent well opening time: the Blasingame normalised dimensionless decline flow rate integral curve is shifted downward when inter-well interference occurs, returning to a straight line later in the season. The Blasingame normalised dimensionless decline flow rate integral curve is shifted downward in the early stage, and the shape of the curve in the later stage is determined by the parameters. The Blasingame normalised dimensionless decline flow rate integral derivative curve has convex bulges, and the higher the degree of interference between the wells, the higher the bulges are, and the earlier they appear.
(3) Using the double-well production Blasingame curve plate for decreasing production analysis, the interpreted dynamic reserve results are more accurate for reservoirs with inter-well interferences, and the method in this paper can provide technical support for the fine evaluation of such reservoirs.
(4) Shortcomings: At present, the method is only applicable to analytical solutions and is used under the condition that r1 (distance between wells) > reD (actual well control radius). This is somewhat inapplicable to more complex models, such as composite media models, and requires further investigation.
Data availability statement
The original contributions presented in the study are included in the article/supplementary materials; further inquiries can be directed to the corresponding author.
Author contributions
PD: writing–original draft. QW: writing–review and editing. JZ: writing–review and editing. YW: writing–review and editing. DW: supervision and writing–review and editing. YH: software, supervision, and writing–review and editing. PL: validation and writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article from The National Natural Science Foundation of China (Grant No. 52074344).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alarji, H., Clark, S., and Regenauer-Lieb, K. (2022). Wormholes effect in carbonate acid enhanced oil recovery methods. Adv. Geo-Energy Res. 6 (6), 492–501. doi:10.46690/ager.2022.06.06
Chen, M., Wang, Z., Sun, H., Chang, C., Fuller, P. M., and Lu, J. (2017). Ventral medullary control of rapid eye movement sleep and atonia. Petroleum Sci. Bull. 2 (1), 53–62. doi:10.1016/j.expneurol.2017.01.002
Chen, Y. Q., Wang, X., and Liu, Y. (2023). The problems and derivation of Blasingame's steady-state pressure drop equation for variable production wells and its application. J. China Offshore Oil Gas 35 (6), 70–77. doi:10.2118/JCM-2023-35-6-070
Deng, Q., Nie, R., Jia, Y., Wang, X., Chen, Y., and Xiong, Y. (2015). “A new method of pressure buildup analysis for a well in a multi-well reservoir,” in SPE North Africa Technical Conference and Exhibition, Cairo, Egypt, September 14-16, 2015.
Dong, J., and Zhai, Y. (1996). “Study on theoretical curve of well test under multi-well interference conditions,” in Proceedings of the 5th National Symposium on Seepage Hydraulics SPE Asia Pacific Improved Oil Recovery Conference, Kuala Lumpur, Malaysia, October 25-26, 1999 (Beijing: Petroleum Industry Press), 188–193.
Gan, X., Yi, J., Ou, J., Yuan, Q., Deng, Z., Yan, P., et al. (2022). Numerical well test technology of gas well pressure recovery based on inter-well interference model. Well Test. Oil Gas Wells 31 (3), 9–15. doi:10.19680/j.cnki.1004-4388.2022.03.002
Guo, J., Ning, B., Yan, H., Jia, C., and Li, Y. (2022). Production performance analysis for deviated wells in carbonate gas reservoirs with multiple heterogeneous layers. Front. Energy Res. 10. doi:10.3389/fenrg.2022.861780
Jiang, R. Z., He, J. X., and Jiang Yu, F. H. (2019). Establishment and application of Blasingame's production decline analysis method for fractured horizontal wells in shale gas reservoirs. Acta Pet. Sin. 40 (12), 1503–1510. doi:10.7623/syxb201912009
Li, X., and Luo, J. (2009). Application research on the well test analysis model under the influence of adjacent wells. Well Test. 18 (2), 5–7. doi:10.3969/j.issn.1004-4388.2009.02.002
Lin, J., Liu, W., and Chen, Q. (1996). Application of the analysis theory of multi-well system for water injection development. Petroleum Explor. Dev. 23 (3), 58–63.
Lin, J., and Yang, H. (2005b). Pressure buildup analysis for a well in a closed, bounded multi-well reservoir. Chin. J. Chem. Eng. 13 (4), 441–450. doi:10.1002/cite.200590223
Lin, J., and Yang, H. (2007). “Analysis of well-test data in a multi-well reservoir with water injection,” in SPE Annual Technical Conference and Exhibition, Anaheim, California, November 11-14, 2007.
Liu, Q., Chen, Y., Zhang, L., and Wang, W. (2006). Study on the model and interpretation method of interference well testing without shutting in. Well Test. 15 (1), 10–12. doi:10.3969/j.issn.1004-4388.2006.01.004
Liu, X., Zou, C., Jiang, Y., and Yang, X. (2010). Basic principles and applications of modern production decline analysis. Nat. Gas. Ind. 30 (5), 50–54. doi:10.3787/j.issn.1000-0976.2010.05.012
Liu, Y., Chen, H., Zhang, D., Zhou, R., and Liu, Y. (2002). Numerical well test analysis of oil wells under the condition of adjacent well influence. Well Test. 11 (5), 4–7. doi:10.3969/j.issn.1004-4388.2002.05.002
Liu, Y., Jia, Y., Kang, Y., and Huo, J. (2008). A survey of genetic simulation software for population and epidemiological studies. Drill. Prod. Technol. 31 (1), 79–86. doi:10.1186/1479-7364-3-1-79
Li, S., Zhou, R., and Huang, B. (1994). Theoretical analysis and application of interference pressure among adjacent wells. Petroleum Explor. Dev. 1 (1), 84–88. 128.
Mccray, T. L. (1990). Reservoir analysis using production decline data and adjusted time. United States: Texas A&M University.
Onur, M., Serra, K. V., and Reynolds, A. C. (1991). Analysis of pressure buildup data from a well in a multi-well system. SPE Form. Eval. 6 (1), 101–110. doi:10.2118/18123-pa
Palacio, J. C., and Blasingame, T. A. (1993). Decline-curve analysis using type curves analysis of gas well production data. SPE 25909.
Pang, J., Lei, G., Liu, H., and Zhang, X. (2012). Evaluation of well-to-well interference in gas wells using the material balance method. Sci. Technol. Eng. 12 (26), 6787–6789. 6793. doi:10.3969/j.issn.1671-1815.2012.26.049
Spivey, J. P., and John Lee, W. (2016). Practical well test interpretation methods, translated by yongxin han, H Sun, xg Deng, and Y shi. Beijing: Petroleum Industry Press.
Sun, H. (2005). Advanced production decline analysis and application. Oxford: Gulf Professional Publishing.
Sun, H. (2013). Modern production decline analysis method and application of oil and gas wells. Beijing: Petroleum Industry Press.
Sun, H. (2016). Analysis method of multi-well pressure recovery well test under the condition of adjacent well interference. Nat. Gas. Ind. 36 (5), 62–68. doi:10.3787/j.issn.1000-0976.2016.05.009
Wang, F. (2015). Diagnosis of nonlinear reservoir behaviour for correctly applying the superposition principle and deconvolution. J. Nat. Gas Sci. Eng. 26, 630–641. doi:10.1016/j.jngse.2015.07.004
Wang, Y., Dai, Z., Chen, Li, Shen, X., Chen, F., and Soltanian, M. R. (2023). An integrated multi-scale model for CO2 transport and storage in shale reservoirs. Appl. Energy 331, 120444. doi:10.1016/j.apenergy.2022.120444
Wang, Y.-W., and Dai, Z.-X. (2023). A hybrid physics-informed data-driven neural network for CO2 storage in depleted shale reservoirs. Petroleum Sci. 16 (1), 109–120. doi:10.3969/j.issn.1000-9585.2023.01.014
Wei, C., Cheng, S., Bai, J., Li, Z., Shi, W., Wu, J., et al. (2022b). Analytical well test analysis method for finite conductivity fractured well under multi-well interference. Petroleum Geol. Oilfield Dev. Daqing 41 (4). doi:10.19597/J.ISSN.1000-3754.202103018
Wei, C., Cheng, S., Jiang, B., Li, Z., Shi, W., Wu, J., et al. (2022a). Analytical well test analysis method for finite conductivity fractured wells under multi-well interference. Daqing Petroleum Geol. Dev. 41 (4), 90–97. doi:10.19597/J.ISSN.1000-3754.202103018
Xu, Y., Liu, Q., Xiaoping, Li, Wang, X. J., Liang, H. S., Zeng, Z. C., et al. (2021). Fbf1 regulates mouse oocyte meiosis by influencing Plk1. Nat. Gas. Ind. 41 (6), 74–83. doi:10.1016/j.theriogenology.2021.01.018
Yu, Q., Hu, X., Li, Y., and Jia, Y (2020). Dynamic evaluation method of oil well parameters and reservoir parameters in drilling large caves. Oil Gas Geol. 41 (3), 647–654. doi:10.11743/ogg20200320
Zeng, T., Jia, Y., Wang, H., Tang, D., and Zhang, W. (2006). Analysis of the finite multi-well system well test model and template curve. Xinjiang Pet. Geol. 27 (1), 86–88. doi:10.3969/j.issn.1001-3873.2006.01.024
Zeng, Y., Kang, X., Tang, E., Liang, D., and Cheng, S. (2020). A new well test interpretation model for injection polymer wells considering adjacent well interference. J. Chengdu Univ. Technol. Sci. Technol. Ed. 47 (1), 85–91. doi:10.3969/j.issn.1671-9727.2020.01.08
Zhang, L., Xiang, Z., Li, Y., Li, X., and Liu, Q. (2006). Impact of well-to-well interference on oil-water two-phase flow numerical well test curves. J. Hydrodynamics Ser. A 21 (6), 805–810.
Zhang, X., Jia, Y., Yan, T., Peng, H., Wergedal, J. E., Guttierez, G. G., et al. (2004). Local ex vivo gene therapy with bone marrow stromal cells expressing human BMP4 promotes endosteal bone formation in mice. Well Test. Technol. 25 (3), 4–15. doi:10.1002/jgm.477
Zhao, J., Wang, L., Liu, S., Kang, Z., Yang, D., and Zhao, Y. (2022). Numerical simulation and thermo-hydro-mechanical coupling model of in situ mining of low-mature organic-rich shale by convection heating. Adv. Geo-Energy Res. 6 (6), 502–514. doi:10.46690/ager.2022.06.07
Keywords: twin-well production, mobile phase, equivalent well control radius, Blasingame-type curves, declining yield curve, explanatory plate
Citation: Du P, Wang Q, Zhang J, Wang Y, Wang D, Han Y and Liu P (2024) The Blasingame method considering the effect of inter-well interference in a circular homogeneous closed reservoir. Front. Energy Res. 12:1376848. doi: 10.3389/fenrg.2024.1376848
Received: 26 January 2024; Accepted: 20 March 2024;
Published: 10 May 2024.
Edited by:
Yan Peng, China University of Petroleum, Beijing, ChinaReviewed by:
Yilong Yuan, Jilin University, ChinaYuhao Zhou, China University of Petroleum (East China), China
Copyright © 2024 Du, Wang, Zhang, Wang, Wang, Han and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Pengcheng Liu, bHBjQGN1Z2IuZWR1LmNu
 Pengfei Du1
Pengfei Du1 Yanwei Wang
Yanwei Wang Pengcheng Liu
Pengcheng Liu