- 1Institute of Energy and Climate Research–Theory and Computation of Energy Materials (IEK-13), Forschungszentrum Jülich GmbH, Jülich, Germany
- 2Chair of Theory and Computation of Energy Materials, Faculty of Georesources and Materials Engineering, RWTH Aachen University, Aachen, Germany
- 3Jülich Aachen Research Alliance, JARA Energy and Center for Simulation and Data Science (CSD), Jülich, Germany
- 4Institute of Energy and Climate Research–Materials Synthesis and Processing (IEK-1), Forschungszentrum Jülich GmbH, Jülich, Germany
- 5Department of Chemistry for Materials, Graduate School of Engineering, Mie University, Tsu, Japan
This study explores multi-component garnet-based materials as solid electrolytes for all-solid-state lithium batteries. Through a combination of computational and experimental approaches, we investigate the thermodynamic and structural properties of lithium lanthanum zirconium oxide garnets doped with various elements. Applying density functional theory, the influence of dopants on the thermodynamic stability of these garnets was studied. Probable atomic configurations and their impact on materials’ properties were investigated with the focus on understanding the influence of these configurations on structural stability, phase preference, and ionic conductivity. In addition to the computational study, series of cubic-phase garnet compounds were synthesized and their electrochemical performance was evaluated experimentally. Our findings reveal that the stability of cubic phase in doped Li-garnets is primarily governed by enthalpy, with configurational entropy playing a secondary role. Moreover, we establish that the increased number of doping elements significantly enhances the cubic phase’s stability. This in-depth understanding of materials’ properties at atomic level establishes the basis for optimizing high-entropy ceramics, contributing significantly to the advancement of solid-state lithium batteries and other applications requiring innovative material solutions.
1 Introduction
In recent years, solid-state batteries (SSBs) have gained considerable interest, primarily due to the safety concerns associated with conventional lithium-ion batteries (Tarascon and Armand, 2001; Armand and Tarascon, 2008). Employing metallic lithium as an anode in SSBs offers enhanced energy density and capacity, which are critical attributes for application in electric vehicles (EVs) (Manthiram et al., 2017; Li et al., 2021). Moreover, SSBs inherently enhance safety, as their solid electrolytes are not prone to the leakage and flammability issues associated with liquid electrolytes in conventional lithium-ion batteries (Sun et al., 2023). Additionally, SSBs demonstrate increased durability under thermal and mechanical stress, which contributes to longer battery life and improved reliability (Yu et al., 2023). A key challenge in SSB development is finding suitable replacements for the liquid electrolytes used in conventional lithium-ion batteries. Among the candidates, garnet-type solid electrolytes, such as Li7La3Zr2O12 (LLZO), have emerged as promising candidates owing to their thermodynamic stability against lithium metal and relatively high conductivity (∼10−3S/cm at 25°C) compared to other solid electrolytes (Duan et al., 2018; Liu et al., 2018).
LLZO exists in two phases: a tetragonal phase with an I41/acd space group and a cubic phase with an
The enhancement of cubic-phase stability and ionic conductivity at lower temperatures remains a priority for advancing the performance of solid-state lithium batteries. One innovative approach involves the “high-entropy” concept, where introducing multiple elements into a material can increase configurational entropy, leading to single disorder phase at lower temperatures. The high-entropy concept has garnered significant attention across various fields due to its ability to enhance materials performance (Kowalski, 2020; Amiri and Shahbazian-Yassar, 2021; Ma et al., 2021). For example, high-entropy alloys (HEAs) or mixed metal-oxides have demonstrated remarkable durability, catalytic activity, radiation damage resistance and unique properties attributed to the synergistic effects of mixed elements in a single-phase solid solution (Li et al., 2015; Tomboc et al., 2020). The application of high-entropy principles extends to ceramics as well. For instance, research on high-entropy fluorides (HEFs) has highlighted their potential as high-capacity cathode materials for lithium-ion batteries (Cui et al., 2022), and He et al. (2023) demonstrates that the high-entropy approach can improve structural stability upon electrochemical cycling in Prussian White (PW) sodium-ion cathodes. In the context of lithium garnet systems like LLZO, the high-entropy approach has yielded enhanced room temperature conductivity and ease of synthesis, attributable to the induced disorder from high entropy (Stockham et al., 2022).
Configurational entropy, Sconf, is crucial in determining the phase stability of high-entropy materials. In thermodynamics, the relative phase stability is governed by the Gibbs free energy, ΔG = ΔH − TΔStot, where the total entropy, ΔStot, includes different contributions such as vibrational, magnetic, electronic, charge, and configurational entropies. Among these, the impact of contributions such as vibrational entropy is often considered negligible due to their minor magnitude relative to configurational entropy (Shang et al., 2011; Wouters et al., 2020). Therefore, this discussion primarily focuses on the significance of Sconf in the context of Gibbs free energy.
When the disordering enthalpy is large, the synthesis temperature required for achieving a disordered single phase can be lowered by the increased Sconf. The Sconf, assuming full disordering, can be calculated as (Finkeldei et al., 2017):
where xi is the concentration ratio of element i, and R is the universal gas constant. In garnets, this concept is extended to include sublattices:
Here, ms represents the multiplicity of sublattice s, and xi,s are the mole fractions of element i at sublattice s. An increase in elemental diversity elevates ΔStot, potentially lowering the synthesis temperature required for an atomic configuration to disorder. However, it remains controversial whether enthalpy or entropy predominantly influences structural stability of a disordered compound (Otto et al., 2013). There is also a question if an ideal, full disordering is realized in real materials (e.g., Navrotsky, 2010; Finkeldei et al., 2017; Kowalski, 2020).
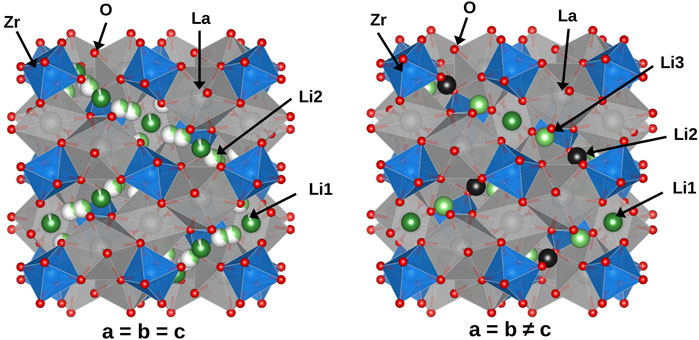
Atomistic modelling is a useful tool to decipher the role of enthalpy and entropy in disordered multi-compound materials (Finkeldei et al., 2017; Kowalski, 2020). For these calculations, correct input structures are essential to correctly calculate the thermodynmic properties. However, the description of lithium vacancy distribution in computational studies on LLZO has been notably inconsistent. For example, Tian et al. (2018) reported a distribution of 13 Li atoms at the Li1 site and 43 at the Li2 site. Conversely, Xu et al. (2012) filled the 24d site completely, distributing the remaining Li ions randomly within the center of the 48g site. This inconsistency is mirrored in experimental studies, where the exact occupancy of Li at these sites remains a subject of debate, often because of the limitations of techniques like X-ray diffraction (XRD) and nuclear magnetic resonance (NMR). For instance, Awaka et al. (2011) determined the occupancies at Li1 and Li2 sites to be 0.94 and 0.35, respectively, while Xie et al. (2011) found them to be 0.56 and 0.44 using neutron diffraction.
To address these challenges, various methods for the distribution of atoms in structural models have been developed. One common strategy involves minimizing the Coulomb energy (Bonilla et al., 2019; Binninger et al., 2020; Jung et al., 2022). Another method is the use of Special Quasirandom Structures (SQS), which mimic a fully disordered state, and is particularly suited for high-entropy materials (Zunger et al., 1990). These approaches aim to provide more accurate and representative structural models for DFT analysis, thereby enhancing the reliability of computational predictions regarding LLZO’s thermodynamic properties.
In this study, we systematically increase the number of doping elements in garnet Li7La3Zr2O12, which in turn incrementally raises the configurational entropy, with the aim of elucidating the thermodynamic properties of the multi-doped material. We employ DFT to select dopants that offer the highest thermodynamic stability, and examine the impact of various atomic configurations on structural stability of the garnet. Specifically, the structural stability of different atomic configurations distributed by the SQS method and minimized-Coulomb energy are compared. Additionally, we conducted experiments to compare the synthesizability and ionic conductivity between different compounds with varying dopant levels. Through a combination of computational and experimental work, we aim to provide valuable insights into the impact of atomic distribution on enthalpy, and the role of entropy in structural stabilization in multi-doped LLZO.
2 Methods
2.1 Computational approach
First-principle DFT calculations were conducted using the Quantum-ESPRESSO software (gpu-enabled version 7.2), based on plane-wave DFT (Giannozzi et al., 2009; 2020). Ultrasoft pseudopotentials were utilized in all DFT calculations (Vanderbilt, 1990). For thermodynamic calculations, the PBE exchange-correlation functional was applied (Perdew et al., 1996), while structural parameters were calculated using the PBEsol exchange-correlation functional (Perdew et al., 2008). The expected improvement in describing structural parameters with PBEsol functional, as expected by its design (Perdew et al., 2008), was demonstrated in many of our previous studies (e.g., Blanca Romero et al., 2014; Connor et al., 2021; Kowalski et al., 2021; Ting and Kowalski, 2023). The supercell unit was set as Li56La24Zr16O96 for pure LLZO. Calculations were performed with a plane-wave cutoff energy of 50 Ry and a 4 × 4 × 4 Monkhorst-Pack k-point mesh (Monkhorst and Pack, 1976) to ensure convergence. Structural optimizations were carried out with convergence thresholds of 10–5 for energy and 10–4/a0 (where a0 is the Bohr radius) for forces.
The investigated systems were based on cubic-LLZO (c-LLZO) with space group Ia-3d and tetragonal-LLZO (t-LLZO) with space group I41/acd. In pure LLZO, both structures feature 8-fold coordinated La sites and 6-fold coordinated Zr sites. The Li sites differ between these two crystal structures. In c-LLZO, Li occupies tetrahedral 24d (Li1 site) and octahedral 96h (Li2 site), as depicted in Figure 2A. In t-LLZO, there are three Li sites: tetrahedral 8a (Li1), and two groups of octahedral sites, 16f (Li2) and 32g (Li3), shown in Figure 2B. In the initial DFT structure of c-LLZO, Li distribution is considered at positions 24d and 48g, with post-relaxation displacement to 96h (Figure 2C).
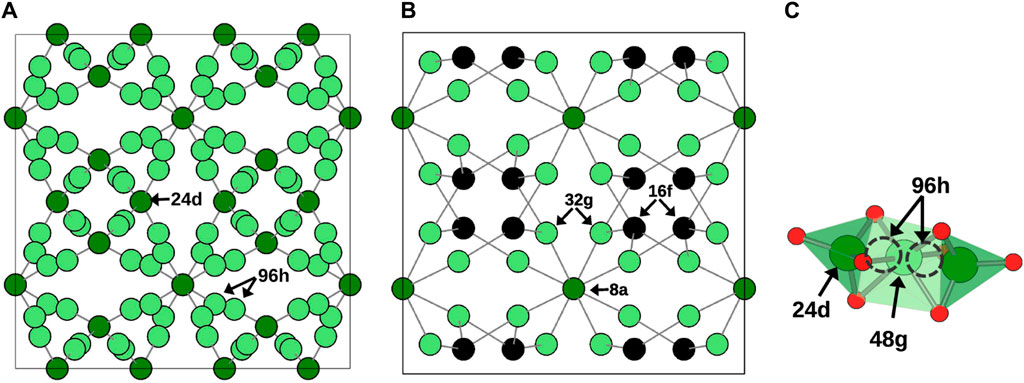
Figure 2. Li sublattice in (A) c-LLZO. (B) t-LLZO. (C) Li site at 96h is displaced from 48g in c-LLZO in DFT initial structure.
In our calculations, various dopants were selected to investigate their entropic effects, with compositions detailed in Table 1. Initially, partial Zr4+ was replaced with a A5+ element, reducing the Li number from seven to six to induce more Li-vacancies and consequently higher configurational entropy. The number of Li atoms was kept constant in subsequent compositions. This enabled us to focus on the investigation of entropic contribution from the dopant concentration. In HEG2, alongside A5+, partial Zr4+ was substituted with B5+ and C4+. HEG3 involved further replacement of partial La3+ with D3+, gradually increasing configurational entropy.

Table 1. The chemical composition of investigated compounds and the oxidation state (O.S.) of the dopants.
Element distribution in multi-doped LLZO was categorized into Li-vacancy and metal-ion groups. Two methodologies were utilized: the Special Quasirandom Structure and a Coulomb-energy-based approach. SQS, executed via the ATAT package (van de Walle et al., 2013), distributes elements in a minimal-size supercell to resemble a fully random solid solution (Zunger et al., 1990). The Coulomb-energy-based (CE-based) method arranges atoms to minimize the Ewald Summation for Coulomb interactions, optimized through Monte Carlo sampling (Binninger et al., 2020). When species share the same oxidation number, we preferentially selected structures with higher symmetry. This strategic choice is underpinned by insights suggesting that structural symmetry plays a role in enhancing stability. Specifically, symmetry in a structure can lead to a reduction in the system’s degrees of freedom and overall energy, making the structure inherently more stable (Borisov et al., 2019). We calculated the 50 structures with the lowest Coulomb energies using DFT and chose the one with the minimum computed energy for our analysis.
With two groups of distribution and two methodologies, we systematically explored element distribution in four distinct ways: I. both groups using SQS; II. both using the CE-based method; III. one group via SQS and the other through CE-based method; IV. the inverse of arrangement III. These configurations are referred to as LiSQS/MSQS, LiCE/MCE, LiSQS/MCE, and LiCE/MSQS, respectively, where ‘Li’ refers to the Li-vacancy group and ‘M’ to the metal-ion group.
In calculating configurational entropy, Li-site vacancies are treated as distinct species. Notably, in c-LLZO’s cubic phase, despite Li occupying 96h positions, the placement of two Li atoms in adjacent sites is energetically unfavorable, leading to their treatment as a single site. This reduces the site count from 96h to 48g (Figure 2C). Thus, for configurational entropy calculations in the cubic phase, the total number of Li sites is considered to be 72, with 24 at Li1 and 48 at Li2 sites. The Li concentration in tetragonal and cubic phases is calculated based on the distribution of Li atoms over available sites.
2.2 Experimental approach
The high-entropy garnets were synthesized by conventional solid-state reaction. The starting materials Li2CO3, La(OH)3, ZrO2, TiO2, Ta2O5, Sb2O5, and Nd2O3 were mixed in stoichiometric amounts with 5 wt% Li2CO3 in excess by ball-milling in hexane. After dried, the powder was placed on a gold sheet inside an alumina crucible for calcination at 850°C for 12 h in air. After cooled down, the calcined powder was ball-milled again in hexane. The fine powder was pressed to form pellets at 13.7 MPa by using uniaxial hydraulic press, and the pellets were subsequently pressed at 150 MPa in an isostatic press. The obtained pellets were sandwiched between two gold sheets and sintered in an alumina crucible, and sintered in air at 1,050°C for 12 h. The sintered pellets were collected and stored in the Argone-filled glovebox.
The samples were characterized for their phase purities by X-ray diffraction (XRD) on a Bruker D4 Endeavor device (Bruker, Germany) using Cu Kα radiation equipped with a 1D detector LynxEye. The qualitative phase analyses were done using Panalytical’s HighScore software, and LeBail profile fitting for lattice parameters of the investigated samples were carried out using the software Jana2006 based on the structure model in the cubic space group of Ia-3d (ICSD 158372).
The Li-ion conductivities of HEGs were measured by electrochemical impedance spectroscopy (EIS). Prior to the EIS measurements, the HEGs pellets were polished on 400, 800, 1,500 and 4,000 grid sandpapers, and sandwiched by two lithium metal foils with a diameter of 6 mm. Such Li|HEG|Li symmetric assembly was then sealed in a pouch bag with two Ni bars as current collectors for the EIS measurements. EIS was measured in the frequency range from 10 MHz to 1 Hz with an electrical field perturbation of 50 mV using an impedance analyzer by Novocontrol Technologies, or in the frequency range from 1 MHz to 0.1 Hz with an electrical field perturbation of 10 mV using a frequency response analyzer by Solartron Analytical. A fitting of the impedance spectrum was conducted in the software ZView (Scribner) to obtain bulk conductivity.
3 Results and discussion
3.1 Dopant selection
Table 2 lists the studied dopants, their ionic radii (Shannon, 1976) and reported doping positions from prior studies. Dopant selection was based on the similarity of their ionic radii to either Zr4+ or La3+ and their doping positions. The formation Enthalpies from oxides (ΔHf,ox) of the considered compounds were calculated using total DFT energies of reactants and products. We then selected those with the lowest ΔHf,ox for further evaluation. Atomistic structures of products in the cubic phase were generated using SQS. For HEG1, HEG2, and HEG3, ΔHf,ox was determined by the energy difference between reactants and products, as described in the following reaction:
The results in Figure 3 show that Sb has the lowest formation enthalpy among the elements considered for element A in Li6La3ZrAO12, leading to the identification of HEG1 as Li6La3ZrSbO12. For HEG2, Ta/Ti combination was by 5 kJ/mol slightly more favorable compared to the Nb/Ti combination. Therefore, HEG2 was considered as Li6La3Zr0.5Sb0.5Ta0.5Ti0.5O12. Nd was chosen as the dopant D in HEG3 based on its thermodynamic stability. Notably, Sb-doped LLZO (HEG1) demonstrated the lowest ΔHf,ox relative to HEG2 and HEG3. A subtle change in ΔHf,ox was observed when transitioning from three-element-doped HEG2 to four-element-doped HEG3. This trend suggests that careful dopant selection leads to minor changes in ΔHf,ox, but enhancing the configurational entropy (ΔSconf) with the addition of more dopant types.
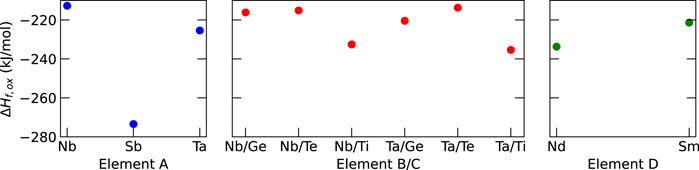
Figure 3. Computed formation enthalpies from oxides (ΔHf,ox) for selected dopants. The dopants with the lowest ΔHf,oxwere chosen, namely, Sb, Ta, Ti, and Nd for A, B, C, and D dopants, respectively. For reference, the experimental ΔHf,oxvalue for t-LLZO is −168.0 kJ mol−1 (Il’ina et al., 2019).
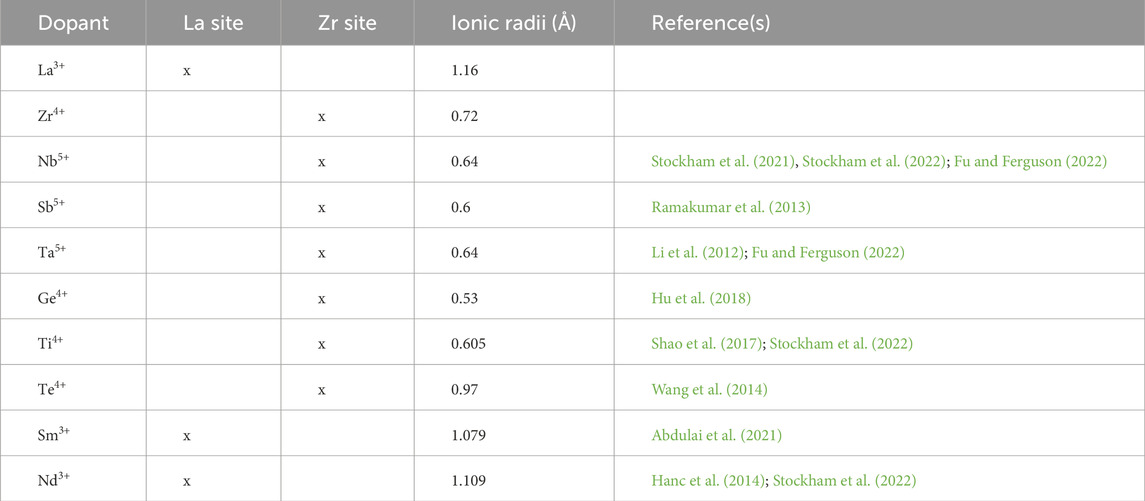
Table 2. List of considered dopants and their ionic radii, with references from a comprehensive database (Shannon, 1976).
Following the computational predictions, we proceeded with the synthesis of the compounds. HEG1, with composition Li6La3ZrSbO12, was successfully synthesized in a cubic phase. However, challenges emerged during the electrochemical performance assessment of HEG2. A potential issue identified was the high titanium content in HEG2, which might cause a reduction of Ti4+ to Ti3+, leading to a transformation of the garnet from an electrical insulator to a conductor. To address this, we modified the composition of HEG2, reducing the Ti content from Li6La3Zr0.5Sb0.5Ta0.5Ti0.5O12 to Li6La3Zr0.75Sb0.5Ta0.5Ti0.25O12 and correspondingly adjusting the Zr content. For HEG3, we maintained the mole fraction in the Zr-sublattice and introduced Nd doping to the La-sublattice. This resulted in the Li6La1.5Nd1.5Zr0.75Sb0.5Ta0.5Ti0.25O12 model compound.
3.2 Effect of Li distribution on structural relaxation
The distribution of elements in the cubic phase was modelled in four distinct ways, as described in Section 2.1: LiSQS/MSQS, LiCE/MCE, LiSQS/MCE, and LiCE/MSQS. The computed entropies illustrated in Figure 4 provide insights into the relative stability and phase preference across these different distribution methods. Contrary to our initial expectations, the LiCE/MCE atomic distribution resulted in the highest computed energies (enthalpies) for all three compounds, indicating the least stability of such arrangement. As opposite, the LiSQS/MSQS method resulted in the lowest energy, suggesting the fully disordered structure as the most stable one for each of the considered compounds. We note that this is in contrast to a common expectation of disordered compounds having higher formation enthalpies than ordered compounds with identical stoichiometry (e.g., Kowalski, 2020). After structural relaxation, we assessed lattice parameters and the position of Li to determine if the structures were in cubic or tetragonal phases. We emphasize the importance of examine the Li position, since the lattice parameters for relaxed structures can vary even in the cubic phase. We note that Li-vacancy distribution could influence phase stability, particularly when the number of dopant elements is low. For example, the relaxation of HEG1 structure that was determined from electrostatic calculations (LiCE/MCE) transitioned from cubic to tetragonal phase, while HEG2 and HEG3 maintained their cubic phase.
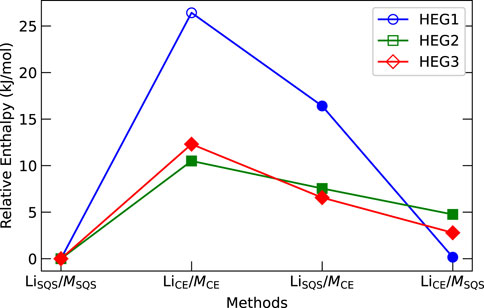
Figure 4. Computed energy (enthalpy) comparison of HEG1, HEG2, and HEG3 using different atomic distribution methods. Energies are normalized by subtracting the lowest computed value for each compound. Filled and hollow markers denote cubic and tetragonal phases, respectively. Marker shapes represent the compounds: circles for HEG1, squares for HEG2, and diamonds for HEG3.
Analysis of Li distribution before and after structural relaxation shows that the site occupancies and displacement degrees depend on the distribution methods, as shown in Table 3. The CE-based method tended to fill the Li1 site and distribute remaining Li atoms to the Li2 site, contrasting with the SQS method where occupancies of Li1 and Li2 sites were identical. After relaxation, some Li atoms migrated from tetrahedrally coordinated Li1 to octahedrally coordinated Li2 sites. The displacement, particularly at Li1 sites, appear to be influenced by the occupancy after relaxation. For each compound, the higher the occupancy at the Li1 site, the greater the displacement degree observed, as reported in Table 3. This relationship was not found at Li2 sites. These findings suggest that the occupation of the Li1 site may influence structural displacement, affecting other properties such as ionic conductivity, activation energy, and diffusion paths. This appears to contrast with previous reports, which indicate that variations in Li + ion arrangements do not significantly impact DFT results (Rettenwander et al., 2014). Our results, however, underscore the importance of Li distribution in not only influencing phase stability but also other intrinsic material properties. The choice of atom distribution method, therefore, is not trivial and demands careful consideration.

Table 3. Li site occupancy and displacement comparison for HEG compounds obtained with different distribution methods. Initial and relaxed occupancies for Li1 and Li2 sites in the cubic phase are listed, along with displacement post-relaxation. The displacement is calculated from the deviation of each Li-O bond from average Li-O bond distance. For HEG1 with LiCE/MCE, which transitioned to a tetragonal phase, the occupancy of each Li site is specified.
We further investigate the influence of Li- and M-group atomic distribution on the thermodynamic stability of the phases. We uncover a nuanced relationship between changes in the atomic distributions of Li- and M-groups and their thermodynamic stability impacts. Figure 5 illustrates the enthalpy variation from different sublattice distribution methods for HEG1, HEG2, and HEG3 compounds. Specifically, we find that variation of energy is more sensitive to the M-group’s atomic distribution than the Li-group’s arrangement. This phenomenon is evident in the energy difference, where shifts in the M-group distribution yielded larger variances (Figure 5). For instance, the energy difference is more pronounced in HEG1 when the M-group atoms change from an SQS to a CE distribution, compared to the same change in the Li-group. The result suggests that the structural stability and electronic characteristics of the compounds are markedly more sensitive to the configuration of the M-group atoms than of the Li-group. This sensitivity could be attributed to the higher oxidation state of M ions (e.g., Zr4+, Ta5+) compared to Li+, making the electrostatic effects more impactful on enthalpy. These findings underscore the importance of the atomic configuration of dopant in modulating the compound’s energy profile and emphasize the importance of targeted distribution method selection to optimize material properties.
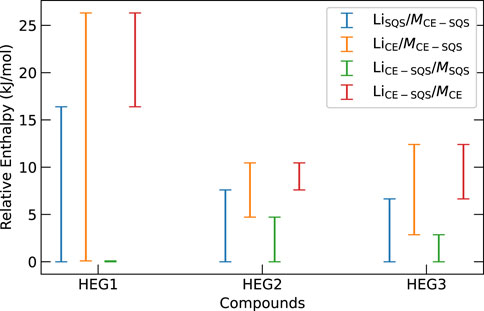
Figure 5. Enthalpy variations for HEG1, HEG2, and HEG3 highlight the effects of differing M- and Li-group atomic distributions on thermodynamics. Each notation, such as LiSQS/MCE−SQS, indicates enthalpy difference
To investigate the influence of Coulomb interactions on the structural stability of high entropy garnets, the Ewald summation was performed for both initial and relaxed states of HEG1, HEG2, and HEG3. Figure 6 shows the obtained significant variations in Coulomb energy. These variations were more pronounced in structures with increased number of doping elements, particularly for those configured with LiSQS/MSQS. The complexity introduced by increasing number of dopants contributed to this trend, highlighted by the increased displacement within the tetrahedral Li1 site (details in Table 3), with displacement degrees of 0.133, 0.199, and 0.214 for the respective structures. An example that underscores this observation is the comparison between the relaxed structures of HEG1 and HEG3. Despite identical Li occupancies, the larger displacement degree in HEG3 — a consequence of the greater number of doping elements—especially at the Li1 site, leads to extended interatomic distances. This, in turn, results in a more substantial impact on electrostatic energy. Hence, it is evident that increased displacement of Li atoms significantly influencing the electrostatic energy.
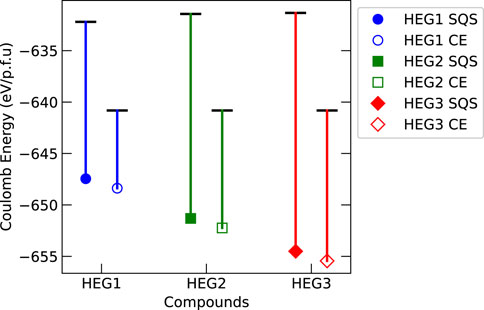
Figure 6. Comparison of Coulomb energy difference before and after structural relaxation for HEG1, HEG2, and HEG3 compounds, of which the structure configuration is distributed by LiSQS/MSQS (SQS, filled markers) and LiCE/MCE (CE, hollow markers) methods. The energy of each compound’s unrelaxed structure is denoted by a horizontal bar, while the relaxed structure energy is depicted using colored markers: blue circle for HEG1, green square for HEG2, and red diamond for HEG3. A vertical line connects each unrelaxed energy bar to its corresponding relaxed energy marker, visually representing the energy shift upon relaxation.
A direct correlation between Coulomb and total DFT energies for the unrelaxed structures of high entropy garnet compounds is found, which is in line with the findings presented in Binninger et al. (2020). However, this correlation diminishes after structural geometry relaxation. For the relaxed structures across the three high entropy garnet compounds, the SQS structure exhibited the lowest computed enthalpies, whereas the CE-based model resulted in the highest computed enthalpies. In contrast, results from Ewald summation revealed an opposing trend, showing that both before and after structural relaxation, the CE-based model consistently yielded the lowest Coulombic energies. The inconsistency between DFT and Ewald summation results is likely attributable to changes in interatomic distances and electronic structures that occur during the relaxation process. These changes facilitate charge redistribution and electron delocalization, which in turn diminish the applicability of the localized point-charge model for the Coulomb energy in the relaxed state. Thus, our findings suggest that while CE-based atomic distributions effectively identify atomic configurations with the lowest energy dominated by Coulomb interactions, their predictive accuracy for determining the lowest-energy configurations decreases in materials with higher covalency and structural complexity, such as high-entropy garnet LLZO. In these materials, the CE-based methods are less reliable for determining the most stable, low-energy configurations.
3.3 Thermodynamic characterization of high-entropy garnet compounds
In order to gain a deeper understanding of the thermodynamic properties of high-entropy garnet compounds HEG1, HEG2, and HEG3, we performed calculations of their configurational entropy and compared these findings with their enthalpy values. Figure 7 shows the enthalpy differences between the tetragonal and cubic phases of these compounds. For pure LLZO, the enthalpy of the tetragonal phase is lower by
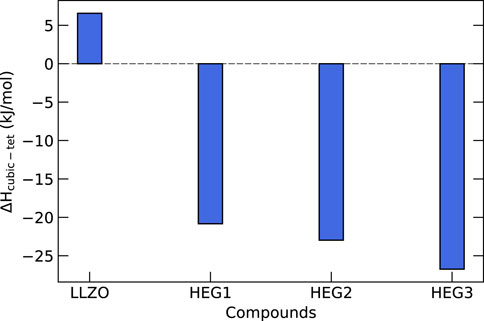
Figure 7. Enthalpy differences (in kJ/mol of formula unit) between cubic and tetragonal phases for HEG compounds. Each difference is derived by subtracting the computed enthalpy of the tetragonal phase from that of the cubic phase. The computed enthalpy are based on the SQS-distributed atomic configurations, which have been demonstrated to exhibit the lowest energies for these compounds (see Figure 4). An exception is made for t-LLZO, where a fully ordered configuration is used.
Afterwards, we compare the configurational entropies of the garnet compounds, as detailed in Table 4. For the fully ordered LLZO in its tetragonal phase, the configurational entropy

Table 4. The configurational entropy per formula unit calculated from Eq. 2 for different compounds in tetragonal
The analysis further reveals that introducing Li vacancies and increasing the number of dopants leads to an increase in the configurational entropy. For the compounds HEG1, HEG2, and HEG3, regardless of the variety and concentration of dopants, a consistent difference in configurational entropy—approximately 13 J/mol/K per formula unit—is observed between the cubic and tetragonal phases. This difference is mainly due to the greater number of possible Li sites in the cubic phase compared to the tetragonal phase, as reflected in Eq. 2. However, it is important to note that this entropy difference is relatively minor when compared to the enthalpy difference between the two phases. These observations suggest that while configurational entropy does play a role in stabilizing the cubic phase, enthalpy is the main driving force in the formation of this phase. We note, however, that entropy and enthalpy of a partially or fully disordered materials are correlated (e.g. Kowalski, 2020). This finding emphasizes the significant role of enthalpy in dictating the phase stability in high-entropy garnet compounds, particularly under varying conditions of dopant concentrations and structural configurations.
It has been suggested that the ideal Li content to form a conductive garnet with cubic structure is 5 < Li < 6.6 per formula unit (Bernstein et al., 2012). This can be seen, for example, in Li7– 3x–yMxLa3Zr2−yByO12 (M = Al, Ga, B = Ta) (Allen et al., 2012; Thompson et al., 2014; Baklanova et al., 2018). At Li contents larger than 6.6, the cubic structure undergoes a reduction of symmetry to a tetragonal polymorph and the ionic conductivity decreases. Our result is aligned with this observation. For Li content of 7, the stable structure appears to be tetragonal and as Li content reduces to 6, cubic phase is favorable. Jung et al. (2022) discusses that the cubic phase stabilization in the garnet with multiple dopants is presumably caused by an entropy effect rather than the enthalpy effect for a constant lithium content of 7.0 in Li7La3M2O12 (M = Zr, Hf, Sn, Sc, Ta). In our calculation, we observe a different scenario. The main stability driver is enthalpy, and configurational entropy provides extra stabilization of cubic phase.
3.4 Experimental result
The high-entropy garnet compounds HEG1, HEG2, and HEG3 were synthesized utilizing conventional solid-state reaction methodologies. The X-ray diffraction (XRD) patterns of HEG1, HEG2 and HEG3 are shown in Supplementary Figure S1. Additionally, Thermogravimetric Analysis/Differential Thermal Analysis (TGA/DTA) was performed to examine the thermal stability of HEG2, confirming the thermal stability of the garnet material (see Supplementary Figure S2). The experimentally measured lattice parameters were in close agreement with theoretical predictions, as reported in Table 5, underscoring the effectiveness of the PBEsol functional for accurate prediction of structural parameters. This alignment between experimental and computational results not only validates the synthesis process but also reinforces the reliability of the computational methods employed in this study.
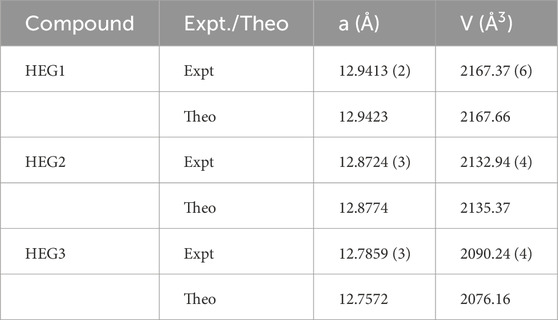
Table 5. The lattice parameters measured from X-ray diffraction pattern for HEG1, HEG2 and HEG3 (Expt.) compared with the computed lattice parameters (Theo.). The reported theoretical lattice parameters are from the SQS structures of each compounds.
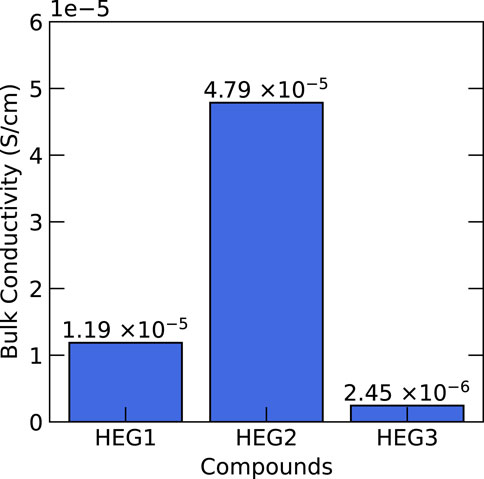
Subsequent to synthesis, we conducted a comprehensive analysis of the electrochemical properties of these compounds, focusing on bulk Li-ion conductivity. The Electrochemical Impedance Spectroscopy (EIS) spectra of HEG1, HEG2, and HEG3 are presented in Supplementary Figure S3. The results, illustrated in Figure 8, revealed that HEG2 exhibited superior ionic conductivity compared to its counterparts. In contrast, HEG3, despite exhibiting the most significant displacement indicative of higher local disorder (see Table 3), displayed the lowest conductivity. This outcome challenges the previously suggested hypothesis by Zeng et al. (2022) regarding the enhancement of ionic conductivity via local disorder and site percolation in high-entropy materials. The minimal influence of entropy and the amount of doping elements on ionic conductivity suggests that these parameters may not be the primary drivers of conductivity in high-entropy garnet compounds. Detailed experimental data encompassing the influence of cation doping on the microstructure and additional electrochemical characterizations are presented in Ye et al. (2022).
Our findings indicate a more intricate interplay between local structural disorder, site percolation, and ionic conductivity than previously anticipated. This complexity warrants a deeper investigation. The insights from this analysis not only contribute to our understanding of the electrochemical behavior of high-entropy garnets but also open avenues for future research, particularly in optimizing these materials for advanced energy storage applications.
4 Conclusion
This study provides a comprehensive computational and experimental analysis of the entropy effect on stability of high-entropy garnet-type LLZO. By employing computational approaches, we effectively selected thermodynamically stable dopants for single-, three-, and four-element-doped LLZO, leading to the study of three high-entropy garnet compounds: Li6La3ZrSbO12 (HEG1), Li6La3Zr0.75Sb0.5Ta0.5Ti0.25O12 (HEG2), and Li6La1.5Nd1.5Zr0.75Sb0.5Ta0.5Ti0.25O12 (HEG3).
Our study conclusively demonstrates that the cubic phase of high-entropy garnet compounds HEG1, HEG2, and HEG3 is more favorable than the tetragonal phase, primarily due to enthalpic advantages, with the configurational entropy contributing as a secondary factor to the stability enhancement. Through detailed DFT calculations, we have shown for the first time that increasing the diversity of selected doping elements significantly improves the cubic phase’s stability, highlighting the profound impact of dopant variety on the thermodynamic stability of these materials. Additionally, our thorough analysis indicates that metal distribution has a more profound effect on thermodynamic stability compared to lithium distribution, highlighting the importance of atomic arrangement in these compounds. We also found that disordered structures are energetically favored in HEG1, HEG2, and HEG3, over relatively ordered phases predicted by minimal Coulombic energy considerations. This preference for disordered configurations, revealed through extensive DFT calculations across various atomic configurations, suggests a complex interplay between thermodynamic stability and atomic distribution and request further investigation.
Experimentally, we successfully synthesized three high-entropy cubic-phase garnet compounds with reduced synthesis temperatures, a feat attributable to the increased configurational entropy. However, despite obtaining cubic-phase multicomponent garnets, improvements in bulk ionic conductivity with increased doping were not as significant as expected. This outcome indicates that the interplay between ionic diffusion mechanisms and the composition of HEGs is complex and requires further elucidation.
This work not only advances our understanding of the thermodynamic aspects of high-entropy garnet compounds but also highlights the intricate relationship between atomic distribution, phase stability, and ionic transport properties in these materials. The insights gained from this study pave the way for future research aimed at optimizing the performance of high-entropy ceramics in energy storage and other advanced technological applications.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
Y-YT: Writing–review and editing, Writing–original draft, Visualization, Validation, Project administration, Methodology, Investigation, Formal Analysis, Data curation, Conceptualization. RY: Writing–review and editing, Writing–original draft, Validation, Methodology, Investigation, Formal Analysis, Data curation, Conceptualization. ED: Writing–review and editing. QM: Writing–review and editing. ST: Writing–review and editing. DM: Writing–review and editing. NI: Writing–review and editing. MF: Writing–review and editing. ME: Writing–review and editing. OG: Writing–review and editing. PKa: Methodology, Writing–review and editing, Supervision. PKo: Methodology, Writing–review and editing, Supervision.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The support from the Japan Society for the Promotion of Science (JSPS) is acknowledged for funding the experimental part of this research. Jülich Aachen Research Alliance - Center for Simulation and Data Science (JARA-CSD, Project No. cjiek61) is acknowledged for funding the computational part of this research.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2024.1393914/full#supplementary-material
References
Abdulai, M., Dermenci, K. B., and Turan, S. (2021). Lanthanide doping of Li7La3−xMxZr2O12 (M=Sm, Dy, Er, Yb; x=0.1–1.0) and dopant size effect on the electrochemical properties. Ceram. Int. 47, 17034–17040. doi:10.1016/j.ceramint.2021.03.010
Allen, J. L., Wolfenstine, J., Rangasamy, E., and Sakamoto, J. (2012). Effect of substitution (Ta, Al, Ga) on the conductivity of Li7La3Zr2O12. J. Power Sources 206, 315–319. doi:10.1016/j.jpowsour.2012.01.131
Amiri, A., and Shahbazian-Yassar, R. (2021). Recent progress of high-entropy materials for energy storage and conversion. J. Mater. Chem. A 9, 782–823. doi:10.1039/D0TA09578H
Armand, M., and Tarascon, J.-M. (2008). Building better batteries. Nature 451, 652–657. doi:10.1038/451652a
Awaka, J., Kijima, N., Hayakawa, H., and Akimoto, J. (2009). Synthesis and structure analysis of tetragonal Li7La3Zr2O12 with the garnet-related type structure. J. Solid State Chem. 182, 2046–2052. doi:10.1016/j.jssc.2009.05.020
Awaka, J., Takashima, A., Kataoka, K., Kijima, N., Idemoto, Y., and Akimoto, J. (2011). Crystal structure of fast lithium-ion-conducting cubic Li7La3Zr2O12. Chem. Lett. 40, 60–62. doi:10.1246/cl.2011.60
Baklanova, Y. V., Tyutyunnik, A. P., Tarakina, N. V., Fortes, A. D., Maksimova, L. G., Korona, D. V., et al. (2018). Stabilization of cubic Li7La3Hf2O12 by Al-doping. J. Power Sources 391, 26–33. doi:10.1016/j.jpowsour.2018.04.066
Bernstein, N., Johannes, M. D., and Hoang, K. (2012). Origin of the structural phase transition in Li7La3Zr2O12. Phys. Rev. Lett. 109, 205702. doi:10.1103/PhysRevLett.109.205702
Binninger, T., Marcolongo, A., Mottet, M., Weber, V., and Laino, T. (2020). Comparison of computational methods for the electrochemical stability window of solid-state electrolyte materials. J. Mater. Chem. A 8, 1347–1359. doi:10.1039/C9TA09401F
Blanca Romero, A., Kowalski, P. M., Beridze, G., Schlenz, H., and Bosbach, D. (2014). Performance of DFT+U method for prediction of structural and thermodynamic parameters of monazite-type ceramics. J. Comput. Chem. 35, 1339–1346. doi:10.1002/jcc.23618
Bonilla, M. R., García Daza, F. A., Carrasco, J., and Akhmatskaya, E. (2019). Exploring Li-ion conductivity in cubic, tetragonal and mixed-phase Al-substituted Li7La3Zr2O12 using atomistic simulations and effective medium theory. Acta Mater. 175, 426–435. doi:10.1016/j.actamat.2019.06.033
Borisov, S. V., Magarill, S. A., and Pervukhina, N. V. (2019). Crystallographic analysis of symmetry-stability relations in atomic structures. J. Struct. Chem. 60, 1191–1218. doi:10.1134/S0022476619080018
Connor, T., Cheong, O., Bornhake, T., Shad, A. C., Tesch, R., Sun, M., et al. (2021). Pyrochlore compounds from atomistic simulations. Front. Chem. 9, 733321. doi:10.3389/fchem.2021.733321
Cui, Y., Sukkurji, P. A., Wang, K., Azmi, R., Nunn, A. M., Hahn, H., et al. (2022). High entropy fluorides as conversion cathodes with tailorable electrochemical performance. J. Energy Chem. 72, 342–351. doi:10.1016/j.jechem.2022.05.032
Duan, H., Zheng, H., Zhou, Y., Xu, B., and Liu, H. (2018). Stability of garnet-type Li ion conductors: an overview. Solid State Ionics 318, 45–53. doi:10.1016/j.ssi.2017.09.018
Finkeldei, S., Kegler, P., Kowalski, P. M., Schreinemachers, C., Brandt, F., Bukaemskiy, A. A., et al. (2017). Composition dependent order-disorder transition in NdxZr1−xO2– 0.5x pyrochlores: a combined structural, calorimetric and ab initio modeling study. Acta Mater. 125, 166–176. doi:10.1016/j.actamat.2016.11.059
Fu, Z., and Ferguson, J. (2022). Processing and characterization of an Li7La3Zr0.5Nb0.5Ta0.5Hf0.5O12 high-entropy Li–garnet electrolyte. J. Am. Ceram. Soc. 105, 6175–6183. doi:10.1111/jace.18576
Geiger, C. A., Alekseev, E., Lazic, B., Fisch, M., Armbruster, T., Langner, R., et al. (2011). Crystal chemistry and stability of “Li7La3Zr2O12” garnet: a fast lithium-ion conductor. Inorg. Chem. 50, 1089–1097. doi:10.1021/ic101914e
Giannozzi, P., Baroni, S., Bonini, N., Calandra, M., Car, R., Cavazzoni, C., et al. (2009). QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502. doi:10.1088/0953-8984/21/39/395502
Giannozzi, P., Baseggio, O., Bonfà, P., Brunato, D., Car, R., Carnimeo, I., et al. (2020). Quantum ESPRESSO toward the exascale. J. Chem. Phys. 152, 154105. doi:10.1063/5.0005082
Hanc, E., Zajac, W., and Molenda, J. (2014). Synthesis procedure and effect of Nd, Ca and Nb doping on structure and electrical conductivity of Li7La3Zr2O12 garnets. Solid State Ionics 262, 617–621. doi:10.1016/j.ssi.2013.11.033
He, Y., Dreyer, S. L., Ting, Y.-Y., Ma, Y., Hu, Y., Goonetilleke, D., et al. (2023). Entropy-mediated stable structural evolution of prussian white cathodes for long-life Na-ion batteries. Angew. Chem. 136, e202315371. doi:10.1002/anie.202315371
Hu, S., Li, Y.-F., Yang, R., Yang, Z., and Wang, L. (2018). Structure and ionic conductivity of Li7La3Zr2−xGexO12 garnet-like solid electrolyte for all solid state lithium ion batteries. Ceram. Int. 44, 6614–6618. doi:10.1016/j.ceramint.2018.01.065
Il’ina, E. A., Raskovalov, A. A., and Reznitskikh, O. G. (2019). Thermodynamic properties of solid electrolyte Li7La3Zr2O12. J. Chem. Thermodyn. 128, 68–73. doi:10.1016/j.jct.2018.08.009
Jung, S.-K., Gwon, H., Kim, H., Yoon, G., Shin, D., Hong, J., et al. (2022). Unlocking the hidden chemical space in cubic-phase garnet solid electrolyte for efficient quasi-all-solid-state lithium batteries. Nat. Commun. 13, 7638. doi:10.1038/s41467-022-35287-1
Kowalski, P. M. (2020). Formation enthalpy of Ln2B2O7-type (B=Ti,Sn,Hf,Zr) compounds. Screen. Mater 189, 7–10. doi:10.1016/j.scriptamat.2020.07.048
Kowalski, P. M., He, Z., and Cheong, O. (2021). Electrode and electrolyte materials from atomistic simulations: properties of LixFePO4 electrode and zircon-based ionic conductors. Front. Energy Res. 9. doi:10.3389/fenrg.2021.653542
Larraz, G., Orera, A., and Sanjuán, M. L. (2013). Cubic phases of garnet-type Li7La3Zr2O12: the role of hydration. J. Mater. Chem. A 1, 11419–11428. doi:10.1039/C3TA11996C
Li, C., Wang, Z.-y., He, Z.-j., Li, Y.-j., Mao, J., Dai, K.-h., et al. (2021). An advance review of solid-state battery: challenges, progress and prospects. Sustain. Mater. Technol. 29, e00297. doi:10.1016/j.susmat.2021.e00297
Li, Y., Han, J.-T., Wang, C.-A., Xie, H., and Goodenough, J. B. (2012). Optimizing Li+ conductivity in a garnet framework. J. Mater. Chem. 22, 15357–15361. doi:10.1039/C2JM31413D
Li, Y., Kowalski, P. M., Beridze, G., Birnie, A. R., Finkeldei, S., and Bosbach, D. (2015). Defect formation energies in A2B2O7 pyrochlores. Scr. Mater. 107, 18–21. doi:10.1016/j.scriptamat.2015.05.010
Liu, Q., Geng, Z., Han, C., Fu, Y., Li, S., He, Y.-b., et al. (2018). Challenges and perspectives of garnet solid electrolytes for all solid-state lithium batteries. J. Power Sources 389, 120–134. doi:10.1016/j.jpowsour.2018.04.019
Ma, Y., Ma, Y., Wang, Q., Schweidler, S., Botros, M., Fu, T., et al. (2021). High-entropy energy materials: challenges and new opportunities. Energy Environ. Sci. 14, 2883–2905. doi:10.1039/D1EE00505G
Manthiram, A., Yu, X., and Wang, S. (2017). Lithium battery chemistries enabled by solid-state electrolytes. Nat. Rev. Mater 2, 16103–16116. doi:10.1038/natrevmats.2016.103
Matsui, M., Takahashi, K., Sakamoto, K., Hirano, A., Takeda, Y., Yamamoto, O., et al. (2013). Phase stability of a garnet-type lithium ion conductor Li7La3Zr2O12. Dalton Trans. 43, 1019–1024. doi:10.1039/C3DT52024B
Meier, K., Laino, T., and Curioni, A. (2014). Solid-state electrolytes: revealing the mechanisms of Li-ion conduction in tetragonal and cubic LLZO by first-principles calculations. J. Phys. Chem. C 118, 6668–6679. doi:10.1021/jp5002463
Monkhorst, H. J., and Pack, J. D. (1976). Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192. doi:10.1103/PhysRevB.13.5188
Navrotsky, A. (2010). Thermodynamics of solid electrolytes and related oxide ceramics based on the fluorite structure. J. Mater. Chem. 20, 10577–10587. doi:10.1039/C0JM01521K
Otto, F., Yang, Y., Bei, H., and George, E. P. (2013). Relative effects of enthalpy and entropy on the phase stability of equiatomic high-entropy alloys. Acta Mater. 61, 2628–2638. doi:10.1016/j.actamat.2013.01.042
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/PhysRevLett.77.3865
Perdew, J. P., Ruzsinszky, A., Csonka, G. I., Vydrov, O. A., Scuseria, G. E., Constantin, L. A., et al. (2008). Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100, 136406. doi:10.1103/PhysRevLett.100.136406
Ramakumar, S., Satyanarayana, L., Manorama, S. V., and Murugan, R. (2013). Structure and Li+ dynamics of Sb-doped Li7La3Zr2O12 fast lithium ion conductors. Phys. Chem. Chem. Phys. 15, 11327–11338. doi:10.1039/C3CP50991E
Rettenwander, D., Blaha, P., Laskowski, R., Schwarz, K., Bottke, P., Wilkening, M., et al. (2014). DFT study of the role of Al3+ in the fast ion-conductor Li7– 3xAl3+xLa3Zr2O12 garnet. Chem. Mater. 26, 2617–2623. doi:10.1021/cm5000999
Shang, S. L., Wang, Y., Kim, D. E., Zacherl, C. L., Du, Y., and Liu, Z. K. (2011). Structural, vibrational, and thermodynamic properties of ordered and disordered Ni1−xPtx alloys from first-principles calculations. Phys. Rev. B 83, 144204. doi:10.1103/PhysRevB.83.144204
Shannon, R. D. (1976). Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. A 32, 751–767. doi:10.1107/S0567739476001551
Shao, C., Yu, Z., Liu, H., Zheng, Z., Sun, N., and Diao, C. (2017). Enhanced ionic conductivity of titanium doped Li7La3Zr2O12 solid electrolyte. Electrochimica Acta 225, 345–349. doi:10.1016/j.electacta.2016.12.140
Shin, D. O., Oh, K., Kim, K. M., Park, K.-Y., Lee, B., Lee, Y.-G., et al. (2015). Synergistic multi-doping effects on the Li7La3Zr2O12 solid electrolyte for fast lithium ion conduction. Sci. Rep. 5, 18053. doi:10.1038/srep18053
Stockham, M. P., Dong, B., James, M. S., Li, Y., Ding, Y., Kendrick, E., et al. (2021). Evaluation of Ga0.2Li6.4Nd3Zr2O12 garnets: exploiting dopant instability to create a mixed conductive interface to reduce interfacial resistance for all solid state batteries. Dalton Trans. 50, 13786–13800. doi:10.1039/D1DT02474D
Stockham, M. P., Dong, B., and Slater, P. R. (2022). High entropy lithium garnets – testing the compositional flexibility of the lithium garnet system. J. Solid State Chem. 308, 122944. doi:10.1016/j.jssc.2022.122944
Sun, H., Kang, S., and Cui, L. (2023). Prospects of LLZO type solid electrolyte: from material design to battery application. Chem. Eng. J. 454, 140375. doi:10.1016/j.cej.2022.140375
Tarascon, J.-M., and Armand, M. (2001). Issues and challenges facing rechargeable lithium batteries. Nature 414, 359–367. doi:10.1038/35104644
Thompson, T., Wolfenstine, J., Allen, J. L., Johannes, M., Huq, A., David, I. N., et al. (2014). Tetragonal vs. cubic phase stability in Al – free Ta doped Li7La3Zr2O12 (LLZO). J. Mater. Chem. A 2, 13431–13436. doi:10.1039/C4TA02099E
Tian, H.-K., Xu, B., and Qi, Y. (2018). Computational study of lithium nucleation tendency in Li7La3Zr2O12 (LLZO) and rational design of interlayer materials to prevent lithium dendrites. J. Power Sources 392, 79–86. doi:10.1016/j.jpowsour.2018.04.098
Ting, Y.-Y., and Kowalski, P. M. (2023). Refined DFT+U method for computation of layered oxide cathode materials. Electrochimica Acta 443, 141912. doi:10.1016/j.electacta.2023.141912
Tomboc, G. M., Kwon, T., Joo, J., and Lee, K. (2020). High entropy alloy electrocatalysts: a critical assessment of fabrication and performance. J. Mater. Chem. A 8, 14844–14862. doi:10.1039/D0TA05176D
Vanderbilt, D. (1990). Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 41, 7892–7895. doi:10.1103/PhysRevB.41.7892
van de Walle, A., Tiwary, P., de Jong, M., Olmsted, D. L., Asta, M., Dick, A., et al. (2013). Efficient stochastic generation of special quasirandom structures. Calphad 42, 13–18. doi:10.1016/j.calphad.2013.06.006
Wang, D., Zhong, G., Dolotko, O., Li, Y., McDonald, M. J., Mi, J., et al. (2014). The synergistic effects of Al and Te on the structure and Li+-mobility of garnet-type solid electrolytes. J. Mater. Chem. A 2, 20271–20279. doi:10.1039/C4TA03591G
Wouters, C., Sutton, C., Ghiringhelli, L. M., Markurt, T., Schewski, R., Hassa, A., et al. (2020). Investigating the ranges of (meta)stable phase formation in (InxGa1 x)2O3: impact of the cation coordination. Phys. Rev. Mater. 4, 125001. doi:10.1103/PhysRevMaterials.4.125001
Xie, H., Alonso, J. A., Li, Y., Fernández-Díaz, M. T., and Goodenough, J. B. (2011). Lithium distribution in aluminum-free cubic Li7La3Zr2O12. Chem. Mater. 23, 3587–3589. doi:10.1021/cm201671k
Xu, M., Park, M. S., Lee, J. M., Kim, T. Y., Park, Y. S., and Ma, E. (2012). Mechanisms of Li+ transport in garnet-type cubic Li3+xLa3M2O12 (M = Te, Nb, Zr). Phys. Rev. B 85, 052301. doi:10.1103/PhysRevB.85.052301
Ye, R., Ting, Y.-Y., Dashjav, E., Ma, Q., Taminato, S., Mori, D., et al. (2022). Preparation and electrochemical properties of Li6La3Zr0.7Ti0.3Ta0.5Sb0.5O12 high-entropy Li-garnet solid electrolyte. Front. Energy Res. doi:10.3389/fenrg.2024.1379576
Yu, X., Chen, R., Gan, L., Li, H., and Chen, L. (2023). Battery safety: from lithium-ion to solid-state batteries. Engineering 21, 9–14. doi:10.1016/j.eng.2022.06.022
Zeng, Y., Ouyang, B., Liu, J., Byeon, Y.-W., Cai, Z., Miara, L. J., et al. (2022). High-entropy mechanism to boost ionic conductivity. Science 378, 1320–1324. doi:10.1126/science.abq1346
Keywords: solid electrolyte, garnet, ionic conductor, DFT, high-entropy, solid-state lithium battery, thermodynamic and structural property, dopant effect
Citation: Ting Y-Y, Ye R, Dashjav E, Ma Q, Taminato S, Mori D, Imanishi N, Finsterbusch M, Eikerling MH, Guillon O, Kaghazchi P and Kowalski PM (2024) Thermodynamic and structural characterization of high-entropy garnet electrolytes for all-solid-state battery. Front. Energy Res. 12:1393914. doi: 10.3389/fenrg.2024.1393914
Received: 29 February 2024; Accepted: 06 May 2024;
Published: 30 May 2024.
Edited by:
Zhong Ma, University of Shanghai for Science and Technology, ChinaCopyright © 2024 Ting, Ye, Dashjav, Ma, Taminato, Mori, Imanishi, Finsterbusch, Eikerling, Guillon, Kaghazchi and Kowalski. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yin-Ying Ting, eS50aW5nQGZ6LWp1ZWxpY2guZGU=
 Yin-Ying Ting
Yin-Ying Ting Ruijie Ye
Ruijie Ye Enkhtsetseg Dashjav4
Enkhtsetseg Dashjav4 Nobuyuki Imanishi
Nobuyuki Imanishi Martin Finsterbusch
Martin Finsterbusch Michael H. Eikerling
Michael H. Eikerling Piotr M. Kowalski
Piotr M. Kowalski