Parameter extraction of photovoltaic cell models using electric eel foraging optimizer

Solar energy has emerged as a key solution in the global transition to renewable energy sources, driven by environmental concerns and climate change. This is largely due to its cleanliness, availability, and cost-effectiveness. The precise assessment of hidden factors within photovoltaic (PV) models is critical for effectively exploiting the potential of these systems. This study employs a novel approach to parameter estimation, utilizing the electric eel foraging optimizer (EEFO), recently documented in the literature, to address such engineering issues. The EEFO emerges as a competitive metaheuristic methodology that plays a crucial role in enabling precise parameter extraction. In order to maintain scientific integrity and fairness, the study utilizes the RTC France solar cell as a benchmark case. We incorporate the EEFO approach, together with Newton-Raphson method, into the parameter tuning process for three PV models: single-diode, double-diode, and three-diode models, using a common experimental framework. We selected the RTC France solar cell for the single-diode, double-diode, and three-diode models because of its significant role in the field. It serves as a reliable evaluation platform for the EEFO approach. We conduct a thorough evaluation using statistical, convergence, and elapsed time studies, demonstrating that EEFO consistently achieves low RMSE values. This indicates that EEFO is capable of accurately estimating the current-voltage characteristics. The system’s smooth convergence behavior further reinforces its efficacy. Comparing the EEFO with competing methodologies reinforces its competitive advantage in optimizing solar PV model parameters, showcasing its potential to greatly enhance the usage of solar energy.

1 Introduction

Concern over the environment’s decline and the severe effects of climate change has grown over the past few decades, partly due to the excessive use of conventional fossil fuels like coal, oil, and gas. As a result, renewable energy sources have garnered significant attention (Mohamed et al., 2024). Solar energy stands out as a very potential sustainable alternative due to its clean, abundant, cost-effective, and widespread characteristics (Li B. et al., 2021). Photovoltaic (PV) systems can efficiently utilize this limitless energy resource, with meticulous modeling closely ensuring the system’s performance precision (Yesilbudak, 2024).

PV system modeling commonly utilizes three prominent models of PV cells: the single-diode model, the double-diode model, and the more complex three-diode model. However, the datasheets provided by PV manufacturers do not provide certain physical parameters found in these models (Abdel-Basset et al., 2020). Finding these hidden traits accurately is important for many areas, such as evaluating performance, making sure quality, and the very important task of tracking the maximum power point in PV systems (Li M. et al., 2021; Wang et al., 2021; Memon et al., 2023).

Efficient exploitation and integration of solar cells and modules into renewable energy systems necessitate a comprehensive understanding of the characteristics that define their behavior (Yousri et al., 2020; Sun et al., 2021; Zheng et al., 2022). The utilization of parameter estimation techniques has become essential in this context. There is a lot of research that looks at how optimization methods for parameter extraction in PV models have changed recently (Luo et al., 2018; Sheng et al., 2019; Chen L. et al., 2023; Almunem et al., 2024; Ekinci et al., 2024; Hussain et al., 2024; Singla et al., 2024). A number of metaheuristic algorithms were used in the study to solve the difficult problem of accurately predicting parameters that are needed to make PV systems work as efficiently as possible.

For example, one of the studies proposes a hybrid algorithm that combines bird mating optimizer with Lambert W-function (LBMO) and Wang’s analytical method called (WLBMO) to optimize parameters of the single diode model (Saadaoui et al., 2024). Its effectiveness is evaluated on the RTC solar cell and three commercial photovoltaic models. The WLBMO algorithm achieves significant error rate reductions of 92.856%, 1.147%, 49.732%, and 89.221% for the R.T.C France solar cell, Photowatt-PWP201, STM6-40/36, and KC200GT modules, highlighting its pivotal role in optimizing solutions. In another study, the Jaya algorithm has been improved for precise parameter extraction (Choulli et al., 2024). This new version uses individual performance metrics, weighting factors, and population averages to avoid incorrect solutions and promote the best-suggested solution. It also incorporates a Gaussian mutation strategy for improved population quality. The improved algorithm is superior in stability, precision, and convergence speed for photovoltaic parameter estimation in single-diode, double-diode, triple-diode, and photovoltaic module models. The study in (Ramachandran et al., 2024) aims to develop an objective function for accurately estimating the initial root parameters of PV models. The objective function is designed using the first-order Berndt-Hall-Hall-Hausman numerical method and the non-linear damping parameter of the Levenberg-Marquardt technique. The enhanced Henry gas solubility optimization (EHGSO) algorithm is combined with the sine-cosine mutualism phase of symbiotic organisms search to efficiently estimate unknown parameters. The proposed EHGSO methodology is tested on single diode and double diode PV models, showing excellent agreement with experimental data and superiority compared to other algorithms. The study reported in (Han et al., 2024) proposes an improved multi-verse optimizer, INMVO, which integrates an iterative chaos map and the Nelder–Mead simplex method to accurately extract unknown parameters from PV models. The proposed INMVO has a balance between exploration and exploitation, and has been tested on four well-known PV models. The results show its effectiveness and reliability, and it can be implemented as an advanced tool for extracting parameters in various PV models. In Ru (2024), the chaos learning butterfly optimization algorithm (CLBOA) is proposed as a new method for extracting PV model parameters. It uses a Cauchy mutation to jump out of local optima, a chaos learning strategy to learn from optimal individuals, and randomization to increase population diversity. Compared to other algorithms, CLBOA outperforms them in convergence performance, parameters extraction accuracy, running time, and improvement index. It was applied to the YL PV power station model of Guizhou Power Grid in China, proving its strong potential for PV parameter extraction. Apart from the above studies, the weighted mean of vectors (INFO) algorithm demonstrated statistical superiority, achieving high accuracy and reliability in parameter extraction for various PV cells and modules (Demirtas and Koc, 2022). INFO’s application extended to single and double diode models, showcasing its potential in advancing the integration of solar energy systems (Izci et al., 2022). Lastly, the dandelion optimizer coupled with the Newton-Raphson numerical method proved effective in accurately determining parameters for different PV models, highlighting its superiority in terms of accuracy, reliability, and convergence (Elhammoudy et al., 2023). Recently, a novel research field successfully combining machine learning and swarm intelligence approaches has emerged, proving to be capable of obtaining outstanding results in various areas. For instance, hybrid methods between metaheuristics and machine learning have been shown to significantly enhance optimization performance (Malakar et al., 2020; Bacanin et al., 2021). These approaches harness the strengths of both paradigms to address complex optimization problems more effectively.

Cumulatively, this research provides significant contributions to the dynamic field of optimization strategies for solar parameter extraction, thereby facilitating the development of more effective and environmentally friendly photovoltaic systems. Every strategy presents distinct advantages and advancements, thereby facilitating future progress in the realm of renewable energy. Nevertheless, the aforementioned methodologies demonstrate limitations, including slow convergence and insufficient population diversity. In addition, due to the intrinsic unpredictability of metaheuristics, their rates of convergence and stability sometimes meet expectations. Furthermore, most previous research has focused on predicting parameters for single-diode and double-diode models, limiting the exploration of the three-diode model (Hassan et al., 2024; Kumari et al., 2024).

This work aims to address the crucial job of parameter estimation in PV models, with a specific emphasis on a novel and effective methodology. The electric eel foraging optimizer (EEFO) method (Alzakari et al., 2024) is proposed as a novel and effective metaheuristic technique for parameter estimation in PV models in response to the discovered gap. The present optimizer is a sophisticated optimization technique that draws inspiration from the social predation behaviors exhibited by electric eels. This study represents the inaugural report on the potential of this optimizer for extracting parameters in PV models. To reach better results the EEFO is implemented in conjunction with the Newton–Raphson method (Izci et al., 2024), ensuring their coordination throughout the process. Our investigation focuses on the RTC France solar cell, specifically examining single-diode, double-diode, and three-diode models as case studies. Our objective is to ensure consistency and fairness throughout the study. We implemented a standardized experimental framework to ensure consistency. The integration of the EEFO brought forth a methodical and effective strategy for navigating the complex parameter space of solar PV models. We carefully adjusted the parameters of the single-diode model, double-diode model, and three-diode model. We selected the RTC France solar cell as the primary case study due to its notable importance in the field of solar photovoltaics, which makes it a reliable platform for assessing the efficacy of the EEFO across different solar cell models.

In order to ensure a thorough evaluation and analysis of the results, we conducted statistical, convergence, and elapsed time examinations. The analysis yielded vital information, enabling us to draw significant conclusions about the effectiveness of the EEFO in optimizing various solar cell models. The empirical findings of several model improvements employing the EEFO demonstrate a notable level of precision in parameter estimation. Regular proposals of this approach consistently show low root mean square error (RMSE) values, indicating its superior performance in accurately assessing current and voltage properties. The EEFO demonstrates smooth convergence behavior. The performance measures of the EEFO method provide a high level of concordance between the experimental and estimated values, hence indicating the precise modeling capabilities of the proposed approach. The gravitational search algorithm (Rashedi et al., 2009), whale optimization algorithm (Mirjalili and Lewis, 2016), slime mould algorithm (Chen H. et al., 2023), arithmetic optimization algorithm (Abualigah et al., 2021) and sinh cosh optimizer (Bai et al., 2023) are some of the new and competitive methods used in comparison tests. We also delve into a comprehensive statistical analysis comparing the EEFO’s performance with alternative methods (Diab et al., 2020; Houssein et al., 2021; Nicaire et al., 2021; Rezk et al., 2021; Beşkirli and Dağ, 2022; Fan et al., 2022; Kharchouf et al., 2022; Premkumar et al., 2022; Yu et al., 2022; 2023; Ayyarao and Kishore, 2023; Bogar, 2023; Chauhan et al., 2023; Gu et al., 2023; Li et al., 2023; Maden et al., 2023; Qaraad et al., 2023; Izci et al., 2024; Kullampalayam Murugaiyan et al., 2024; Wu et al., 2024), further establishing its competitive edge in the realm of solar PV model parameter optimization. In light of the above discussion, the contributions of this study cam briefly be listed as follows:

1 - Introduction of the EEFO method for the first time in the context of PV model parameter estimation.

2 - Implementation of EEFO in conjunction with the Newton–Raphson method to ensure robust and precise parameter estimation.

3 - Comprehensive evaluation of the EEFO on the RTC France solar cell, using single-diode, double-diode, and three-diode models to validate its effectiveness.

4 - Detailed statistical, convergence, and elapsed time analyses to assess the performance of EEFO against state-of-the-art optimization algorithms.

5 - Demonstration of EEFO’s superior performance in terms of low RMSE, smooth convergence behavior, and precise modeling capabilities.

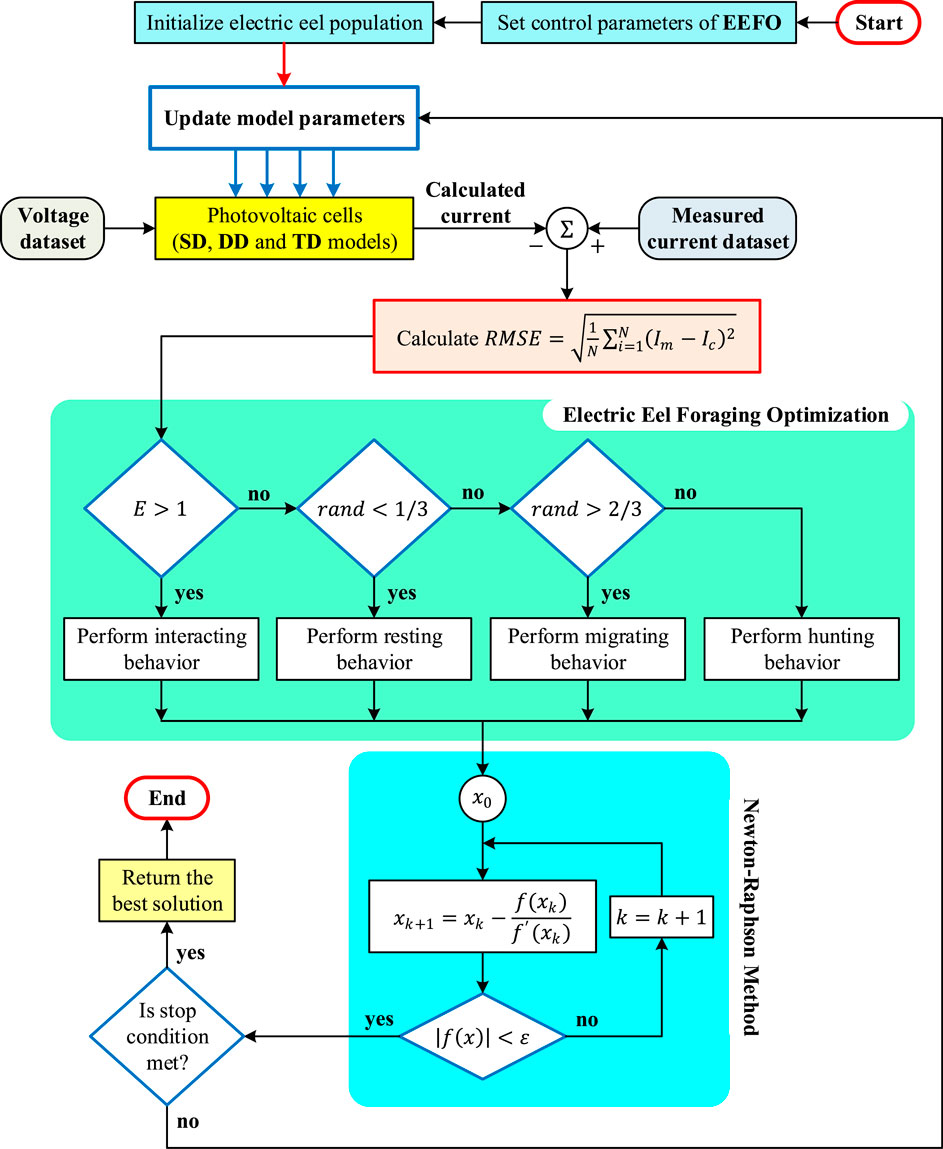
2 Electric eel foraging optimizer

The exceptional predatory capability of electric eels, indigenous to South America, was used as a source of inspiration for the development of electric eel foraging optimization (EEFO) (Zhao et al., 2024). According to Bastos et al. (2021), the EEFO encompasses the social predation activities of electric eels, which encompass interactions, resting, migrating, and hunting. The subsequent subsections provide a description of the mathematical representations pertaining to foraging behaviors.

2.1 Interacting

EEFO utilizes a cooperative methodology, drawing inspiration from the social predation behavior of eels, wherein each electric eel assumes the role of a candidate solution. At every stage, the most optimal candidate solution acts as the desired target. This interaction phase replicates the process of global exploration, in which each eel actively participates with others according to their respective places. In particular, eels interact with a partner that is randomly picked from the entire population, and they modify their positions in response to the disparity between the selected eel and the center of the population. In addition, eels engage in interactions with partners that are randomly selected from the population. They adjust their locations by assessing the difference between a randomly chosen eel and a position that is produced randomly within the search space. Interactions encompass a phenomenon known as churn, which denotes stochastic movements occurring in diverse directions. The churn is represented mathematically as

$C=n_1\times B.(1)$

where $n_1\sim N\left(0,1\right)$ and $B=\left[b_1,b_2,\dots b_k,\dots b_d\right]$. Here, the function $b\left(k\right)$ is equal to 1 when $k$ is equal to $g$, while $b\left(k\right)$ is equal to 0 for all other values of $k$. The value of $g$ is decided by generating a random permutation of the numbers from 1 to $d$. The interactive behavior is defined as

$\left\{\begin{array}{c}\left\{\begin{array}{c}{v}_i\left(t+1\right)=x_j\left(t\right)+C\times \left(\overline{x}\left(t\right)-x_i\left(t\right)\right),p_1>0.5\\ v_i\left(t+1\right)=x_j\left(t\right)+C\times \left(x_r\left(t\right)-x_i\left(t\right)\right),p_1\le 0.5\end{array}\right.fit\left(x_j\left(t\right)\right)<fit\left(x_i\left(t\right)\right)\\ \left\{\begin{array}{c}{v}_i\left(t+1\right)=x_i\left(t\right)+C\times \left(\overline{x}\left(t\right)-x_j\left(t\right)\right),p_2>0.5\\ v_i\left(t+1\right)=x_i\left(t\right)+C\times \left(x_r\left(t\right)-x_j\left(t\right)\right),p_2\le 0.5\end{array}\right.fit\left(x_j\left(t\right)\right)\ge fit\left(x_i\left(t\right)\right)\end{array}\right..(2)$

Here, $x_r$ is calculated as the product of the lower bound ($Low$) and the sum of a random number ($r$) multiplied by the difference between the upper bound ($Up$) and the lower bound. The variables $p_1$ and $p_2$ represent random numbers chosen from the range between 0 and 1. The suitability of the proposed position for the $ith$ electric eel is denoted by $fit\left(x_i\right)$, where $x_j$ is the position of an eel chosen randomly from the current population, with $j\ne i$. Furthermore, the expression for $\overline{x}\left(t\right)$ is

$\overline{x}\left(t\right)=\frac{1}{n}{\sum }_{i=1}^n{x}_i\left(t\right)(3)$

Here, $n$ represents the population size. According to Eq. 3, the interaction behavior of electric eels allows them to move to different spots in the search space, which greatly helps in exploring the complete search space in the EEFO algorithm.

2.2 Resting

It is crucial to establish a designated resting region before electric eels engage in resting behavior in the EEFO algorithm. In order to improve the efficiency of the search process, a specific resting area is assigned inside the region where one particular dimension of an electric eel’s position vector aligns with the main diagonal of the search space. Creating a resting region involves standardizing both the area being searched and the position of the eel, which can range from 0 to 1. Afterwards, a dimension is selected at random from the eel’s position and projected onto the major diagonal of the normalized search space. This determines the central point of the eel’s resting region. The expression for the manifestation of resting behavior is given by Eq. 4.

$v_i\left(t+1\right)=R_i\left(t+1\right)+n_2\times \left(R_i\left(t+1\right)-round\left(rand\right)\times x_i\left(t\right)\right)(4)$

Here, $n_2$ follows a normal distribution with mean 0 and standard deviation 1, and $R_i$ represents the resting posture.

2.3 Hunting

Electric eels have a hunting tactic that goes beyond just swarming when they find their victim. Instead, they demonstrate cooperative behavior by organizing themselves into a huge circular formation to surround the prey. Throughout this process, they maintain continuous communication and collaboration with other eels, accomplished by the use of mild electric organ discharges. As the eels interact more, the size of the electrified circle decreases. Ultimately, the eels direct the group of fish from the depths of the ocean to shallower regions, rendering them easier to catch as prey. Consistent with this pattern of behavior, the electrified circle functions as the authorized hunting zone. At this stage, the prey initiates strategic moves throughout the hunting area, rapidly and repeatedly changing locations out of fear. The hunting behavior shown by eels, which is defined by their curling action, may be elucidated as follows:

$v_i\left(t+1\right)=H_{prey}\left(t+1\right)+\eta \times \left(H_{prey}\left(t+1\right)-round\left(rand\right)\times x_i\left(t\right)\right)(5)$

where η is the curling factor as defined by Zhao et al. (2024), and Hprey represents the prey’s current location relative to its former position inside the hunting region.

2.4 Migrating

Electric eels have a natural inclination to go from their resting location to the hunting area when they detect prey. In order to quantitatively express this migratory tendency, the following equation is utilized:

$v_i\left(t+1\right)=-r_5\times R_i\left(t+1\right)+r_6\times (H_r\left(t+1\right)-L\times \left(H_r\left(t+1\right)-x_i\left(t\right)\right)(6)$

In this context, $H_r$ denotes any point inside the hunting area, while $r_5$ and $r_6$ are arbitrary values selected from the interval (0,1). The Levy flight function, represented as $L$, is included into the exploitation phase of EEFO to avoid becoming trapped in local optima.

2.5 Transition from exploration to exploitation

The exploration and exploitation transitions in EEFO are significantly influenced by an energy factor, which plays a key role in optimizing the algorithm’s performance (Wang et al., 2019; Izci et al., 2020). The energy factor value of the eel is used to determine whether to choose exploration or exploitation. It is technically described as

$E\left(t\right)=4\times \sin \left(1-\frac{t}{T}\right)\times \mathit{ln}\frac{1}{r_7}(7)$

where $r_7$ is a random number between 0 and 1.

3 Problem definition for solar photovoltaic system and application of EEFO

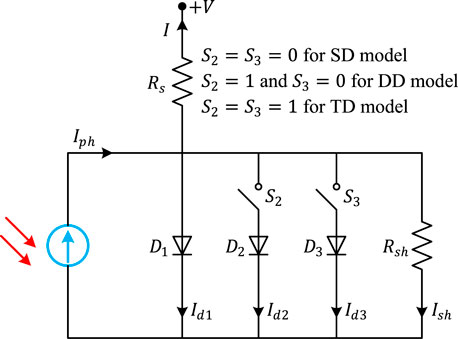
PV cells are semiconductor devices that have the ability to directly convert sunlight into electrical energy. The precise determination of photovoltaic cell parameters holds significant importance in the development, examination, and enhancement of solar systems. The characteristics that have a substantial impact on the overall performance and efficiency of PV cells are the series resistance ($R_s$), shunt resistance ($R_{sh}$), diode ideality factor, and diode saturation current ($I_{sd}$). Researchers and engineers frequently employ mathematical models that elucidate the electrical characteristics of PV cells in order to determine these parameters. The single-diode (SD), double-diode (DD), and three-diode (TD) are three often employed models to represent the electrical equivalent circuit of PV systems. Figure 1 demonstrates the equivalent circuit of those models and the related switch ($S_2$ and $S_3$) configurations to obtain those models. This section examines the aforementioned models and their significance in the context of estimating parameters for photovoltaic cells. Furthermore, the execution of the suggested approach to extract those parameters is also addressed.

Figure 1

Figure 1. Equivalent circuits of SD, DD and TD models.

3.1 Single-diode (SD) model

The SD model offers a streamlined and efficient mathematical depiction of the electrical properties demonstrated by a PV cell. According to this model, the PV cell may be accurately represented as a single diode that is coupled in parallel with a current source. Although the SD model is simple, it effectively represents the essential characteristics of the PV cell’s electrical response while also being computationally efficient. The current-voltage (I-V) relationship of a PV cell in the SD model may be defined as follows:

$I=I_{ph}-I_{sd}\left(e^{\frac{\left(V+I{R}_s\right)}{\left(n{V}_t\right)}}-1\right)-\frac{\left(V+I{R}_s\right)}{R_{sh}}(8)$

In this context, $I$ denotes the current produced by the PV cell, $V$ represents the voltage across the terminals of the PV cell, $I_{ph}$ stands for the current generated by the cell when exposed to light, $I_{sd}$ refers to the current at which the diode ($D_1$ – see Figure 1) in the cell becomes saturated, $R_s$ signifies the resistance in series with the cell, $R_{sh}$ denotes the resistance in parallel with the cell, $n$ represents the ideality factor of the diode, and $V_t$ represents the thermal voltage, which is approximately equal to $kT/q$. Here, $k$ represents Boltzmann's constant, $T$ represents the temperature in Kelvin, and $q$ represents the elementary charge.

3.2 Double-diode (DD) model

The DD model offers an advanced approach to simulate the behavior of PV cells by including extra diodes to accurately represent their complex electrical characteristics. This improved version incorporates an additional diode ($D_2$ – See Figure 1) that precisely targets recombination losses in the PV cell, resulting in a more detailed and accurate depiction of the PV cell’s real-world properties. The I-V relationship of a PV cell in the DD model is expressed by the following equation:

$I=I_{ph}-I_{sd1}\left(e^{\frac{\left(V+I{R}_s\right)}{\left(n_1{V}_t\right)}}-1\right)-I_{sd2}\left(e^{\frac{\left(V+I{R}_s\right)}{\left(n_2{V}_t\right)}}-1\right)-\frac{\left(V+I{R}_s\right)}{R_{sh}}.(9)$

Here, $I_{sd2}$ represents the diode saturation current of the extra diode, $n_1$ represents the ideality factor of the main diode ($D_1$), and $n_2$ represents the ideality factor of the additional diode ($D_2$).

3.3 Three-diode (TD) model

The TD model is a sophisticated depiction of a PV cell that offers a more precise characterization of its behavior in comparison to SD and DD models. The current-voltage relationship in this model is expressed as $I=I_{ph}-I_{d1}-I_{d2}-I_{d3}-I_{sh}$ where $I_{d1}$ represents the current flowing through diode $D_1$, $I_{d2}$ represents the current flowing through diode $D_2$, and $I_{d3}$ represents the current flowing through diode $D_3$. To compute the total current flowing through the PV cell, one must add up the individual currents passing through the three diodes in the TD model. The equation may be expressed as

$I=I_{ph}-I_{sd1}\left(e^{\frac{V+I{R}_s}{n_1{V}_t}}-1\right)-I_{sd2}\left(e^{\frac{V+I{R}_s}{n_2{V}_t}}-1\right)-I_{sd3}\left(e^{\frac{V+I{R}_s}{n_3{V}_t}}-1\right)-\frac{V+I{R}_s}{R_{sh}}.(10)$

Here, the variables $n_1$, $n_2$, and $n_3$ represent the ideality factors of the diodes $D_1$, $D_2$, and $D_3$, respectively.

3.4 Recommended novel approach

In order to effectively examine a practical solar system, it is essential to possess a precise PV model that accurately mimics its behavior under various operating situations (Ridha et al., 2022). Such a model necessitates suitable characteristics that differentiate one PV system from another. Consequently, the process of determining the values of the parameters for the solar PV model becomes an optimization issue, which requires the use of an objective function. The objective function is determined by comparing the measured data values from a physical system with the data values received from the model. When the estimated values of the model closely align with the observed values, it signifies a similarity to the physical system. The objective function ($F_{Obj}$) for parameter estimation in solar PV models is determined by calculating the root mean square error (RMSE) between the observed and estimated values, which quantifies their similarity. The RMSE is a metric that quantifies the average difference between the measured current-voltage curve ($I_m$) and the calculated current-voltage curve ($I_c$) using a set of estimated parameters as demonstrated in the following equation:

$F_{Obj}=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(I_m-I_c\right)}^2}(11)$

Here, $N$ denotes the total number of data points. RMSE quantifies the extent of the total difference between the model and the observed data. The current may be determined by solving the nonlinear equations obtained from the analogous circuits, namely, Eqs 8–10. The standard objective function estimates the current as follows:

$I_c=I_{ph}-I_{sd}\left(e^{\frac{\left(V+I_m{R}_s\right)}{\left(n{V}_t\right)}}-1\right)-\frac{\left(V+I_m{R}_s\right)}{R_{sh}}(12)$

By substituting Eq. 12 into Eq. 11, we obtain the following expression for the SD model:

$F_{Obj}=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(I_m-\left\{I_{ph}-I_{sd}\left(e^{\frac{\left(V+I_m{R}_s\right)}{\left(n{V}_t\right)}}-1\right)-\frac{\left(V+I_m{R}_s\right)}{R_{sh}}\right\}\right)}^2}(13)$

For the DD model, this will be:

$F_{Obj}=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(I_m-\left\{I_{ph}-I_{sd1}\left[e^{\frac{\left(V+I_m{R}_s\right)}{\left(n_1{V}_t\right)}}-1\right]-I_{sd2}\left[e^{\frac{\left(V+I_m{R}_s\right)}{\left(n_2{V}_t\right)}}-1\right]-\frac{\left(V+I_m{R}_s\right)}{R_{sh}}\right\}\right)}^2.}(14)$

Lastly, for TD model, the following expression will be obtained:

$F_{Obj}=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(I_m-\left\{I_{ph}-I_{sd1}\left[e^{\frac{\left(V+I_m{R}_s\right)}{\left(n_1{V}_t\right)}}-1\right]-I_{sd2}\left[e^{\frac{\left(V+I_m{R}_s\right)}{\left(n_2{V}_t\right)}}-1\right]-I_{sd3}\left[e^{\frac{\left(V+I_m{R}_s\right)}{\left(n_3{V}_t\right)}}-1\right]-\frac{\left(V+I_m{R}_s\right)}{R_{sh}}\right\}\right)}^2.}(15)$

The equations presented in Eqs 8–10 demonstrate a profoundly nonlinear characteristic. Therefore, if we substitute ($I=I_m$) in Eq. 11 to estimate the current, the results would be erroneous because of the equation’s nonlinearity. Various approaches, including the Taylor series, Newton-Raphson method, Lambert W function, and others, can be used to solve the nonlinear Eqs 8–10 (Ayyarao, 2022; Ekinci et al., 2024; Izci et al., 2024). In this work, we have opted to employ the iterative Newton-Raphson (N-R) approach for parameter extraction. This approach has significant benefits, such as excellent precision and a relatively low computing load. The optimization approach is implemented in tandem with the N-R method, guaranteeing their synchronization throughout the process.

The N-R technique is an iterative algorithm that necessitates a beginning point, $x_0$, and a termination condition. After $k$ rounds, the revised solution may be expressed as $x_{k+1}=x_k-f\left(x\right)/f^{\prime }\left(x\right)$. The ultimate solution is obtained when the magnitude of $f\left(x\right)$ is smaller than a certain tolerance, $\epsilon$. The current for the SD, DD, and TD models is calculated using Eqs 16–18 accordingly. This is done by solving the nonlinear equations $SD\left(x\right)$, $DD\left(x\right)$, and $TD\left(x\right)$, where $x$ denotes $I$.

$SD\left(x\right)=I_{ph}-I_{sd}\left[e^{\frac{\left(V+x{R}_s\right)}{\left(n{V}_t\right)}}-1\right]-\frac{\left(V+x{R}_s\right)}{R_{sh}}-x(16)$

$DD\left(x\right)=I_{ph}-I_{sd1}\left[e^{\frac{\left(V+x{R}_s\right)}{\left(n_1{V}_t\right)}}-1\right]-I_{sd2}\left[e^{\frac{\left(V+x{R}_s\right)}{\left(n_2{V}_t\right)}}-1\right]-\frac{\left(V+x{R}_s\right)}{R_{sh}}-x(17)$

$TD\left(x\right)=I_{ph}-I_{sd1}\left[e^{\frac{\left(V+x{R}_s\right)}{\left(n_1{V}_t\right)}}-1\right]-I_{sd2}\left[e^{\frac{\left(V+x{R}_s\right)}{\left(n_2{V}_t\right)}}-1\right]-I_{sd3}\left[e^{\frac{\left(V+x{R}_s\right)}{\left(n_3{V}_t\right)}}-1\right]-\frac{\left(V+x{R}_s\right)}{R_{sh}}-x(18)$

This approach is employed to calculate the value of the objective function during the parameter optimization procedure. During the optimization process, the algorithm transfers the solar PV cell variables to the N-R technique, which computes the value of the objective function. To solve the nonlinear equations in Eqs 16–18 at a certain voltage, the N-R approach is used. This method yields output current values with an error ($\epsilon$) that is less than ${10}^{-4}$. There are two major obstacles in this approach. First and foremost, the selection of the starting point significantly impacts the ultimate answer. Furthermore, it is essential to minimize the duration of the execution. These problems can be surmounted with a straightforward measure. The measured current is chosen as the initial value since it is anticipated that the estimated current will be in close proximity to the observed current. Figure 2 demonstrates the procedure of parameter extraction by integrating the N-R approach using the EEFO.

Figure 2

Figure 2. Parameter extraction of PV models using EEFO and N-R methods.

4 Comparative simulation results

This section provides a comprehensive discussion and evaluation of the R.T.C. France solar photovoltaic cell. The considered cell has 26 current-voltage data set that have been obtained at a temperature of 33°C. It is worth mentioning that the all comparative simulations are executed using MATLAB R2023a on a personal computer with an 12th Gen Intel(R) Core(TM) i7-12700H processor 2.30 GHz, 32 GB RAM, under Windows 10 64-bit operating system.

4.1 Compared metaheuristic algorithms and parameter settings

The efficacy of the EEFO (Zhao et al., 2024) was evaluated more accurately by contrasting it with five distinct metaheuristic algorithms. The selected algorithms include the gravitational search algorithm (GSA) (Rashedi et al., 2009) and the whale optimization algorithm (WOA) (Mirjalili and Lewis, 2016), which are widely used. On the other hand, the slime mould algorithm (SMA) (Chen H. et al., 2023), arithmetic optimization algorithm (AOA) (Abualigah et al., 2021), and sinh cosh optimizer (SCHO) (Bai et al., 2023) are the most recent additions. The control parameters for all algorithms are listed as follows.

- EEFO: No other parameters

- GSA: $G_0=100$ and $a=20$

- WOA: $a$ linearly decreases from two to 0

- SMA: $z=0.03$

- AOA: $\alpha =5$ and $\mu =0.499$

- SCHO: $ct=3.6$, $u=0.388$, $m=0.45$, $ϵ=0.003$, $n=0.5$, $\alpha =4.6$, $\beta =1.55$, $p=10$ and $q=9$

The population size for all algorithms was fixed at 50, and the total number of iterations was set at 400. This was done to create equitable conditions for conducting comparisons. According to provided control parameters, GSA and AOA necessitate the modification of two additional control parameters, whereas WOA and SMA only require the adjustment of one. However, SCO necessitates the modification of nine control parameters, with the exception of population size and total number of iterations. The primary advantage of the EEFO is its ability to optimize without the need for parameters, making it very desired for solving the given optimization issue.

4.2 Results of single-diode model

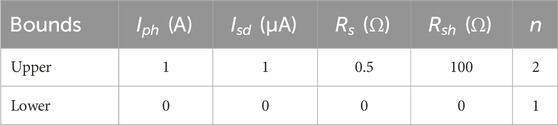
Table 1 provides the lower and maximum limits for the 5 parameters that need to be optimized in a single diode model. In order to achieve the lowest value for the RMSE objective function, it is crucial that the $I_{ph}$, $I_{sd}$, $R_s$, $R_{sh}$ and $n$ parameters be accurately predicted within the specified limitations.

Table 1

Table 1. The parameter limits of single-diode model.

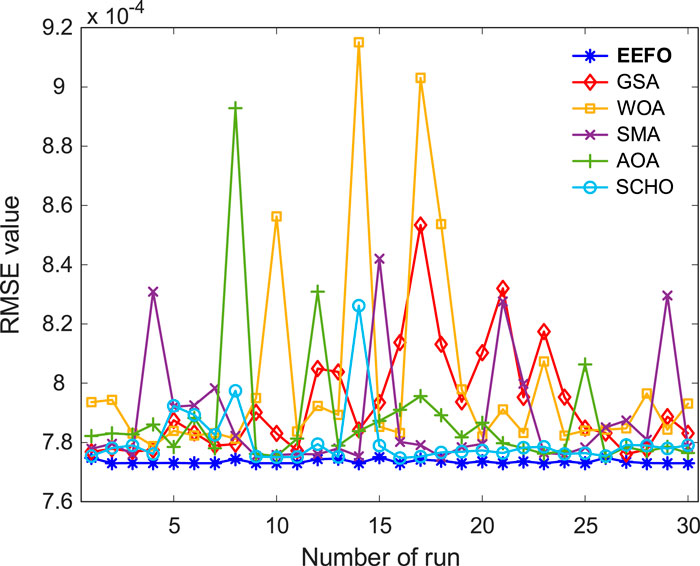
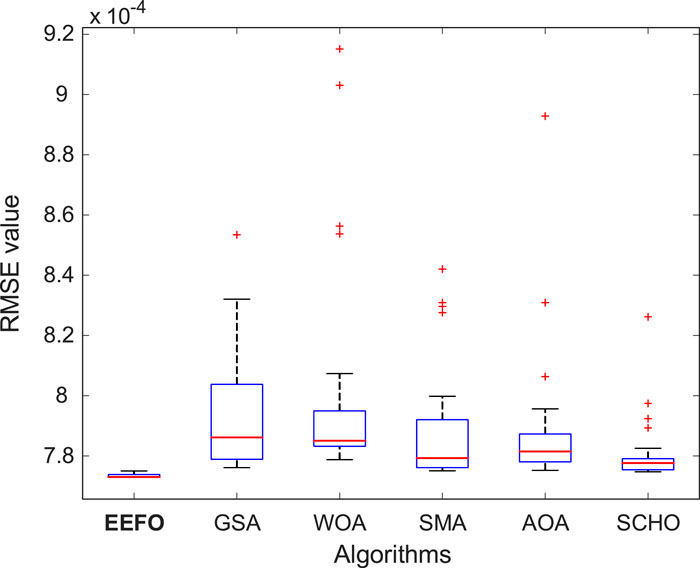
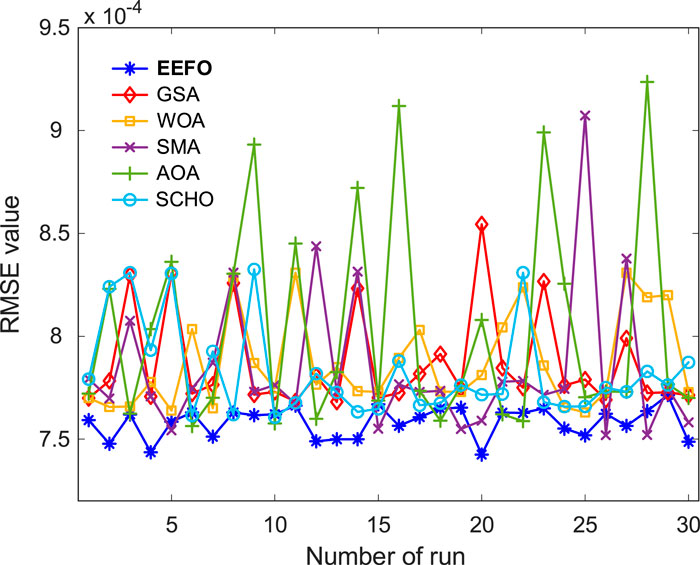
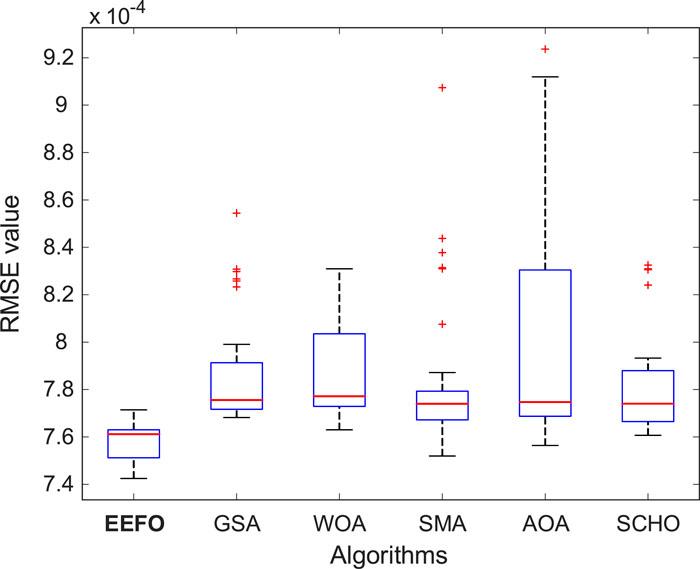
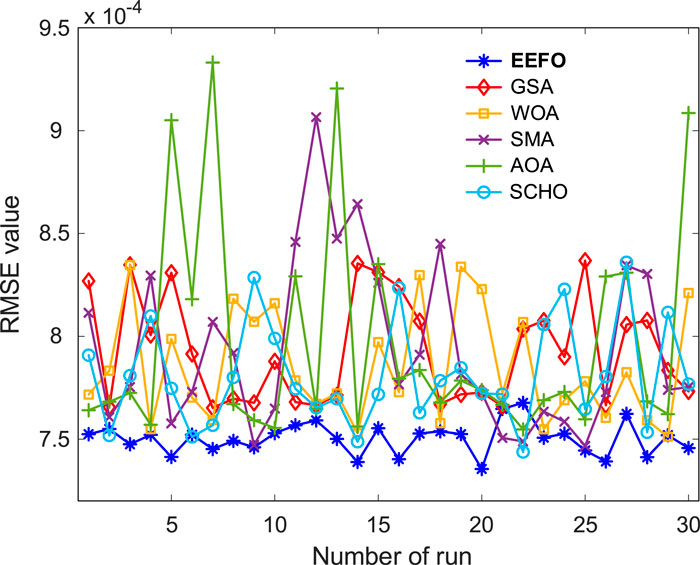
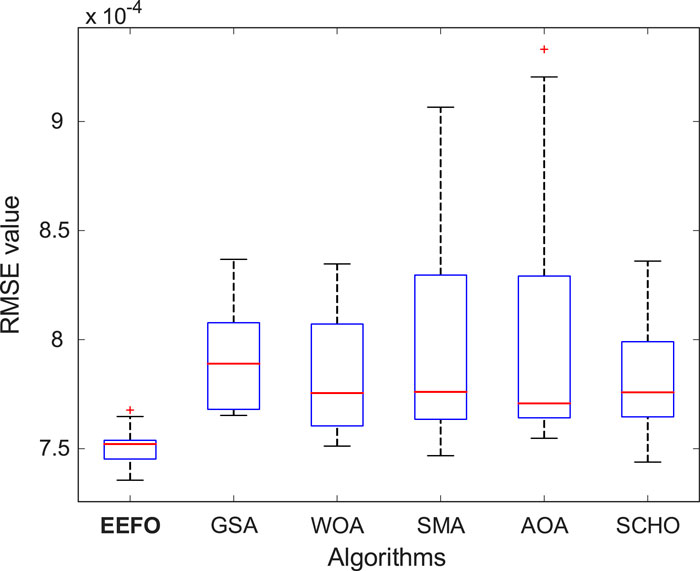
Figures 3, 4 display the graphical outcomes of 30 iterations of the EEFO, GSA, WOA, SMA, AOA, and SCHO algorithms. Figure 3 displays the RMSE values achieved with the EEFO method, which are consistently low and outperform other algorithms in each run. In addition, the inspection of the box plot in Figure 4 clearly shows that the RMSE range of the EEFO method is minimal, which indicates its statistical success and stability.

Figure 3

Figure 3. Obtained RMSE values with respect to all runs for single diode model.

Figure 4

Figure 4. Boxplot analysis of EEFO, GSA, WOA, SMA, AOA and SCHO for single-diode model.

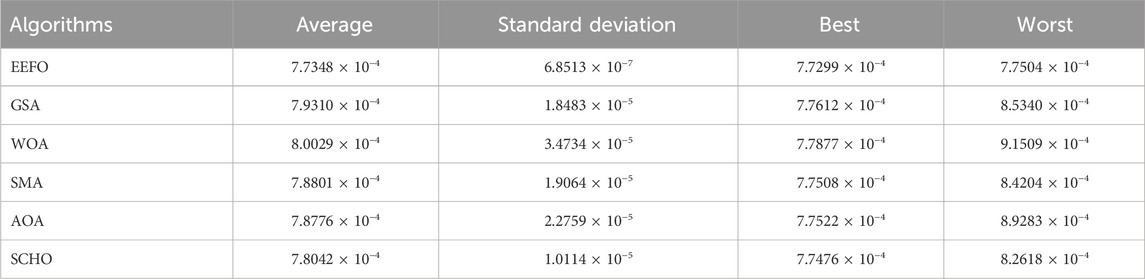
Table 2 presents the statistical outcomes of all methods in the single diode model for the RMSE objective function. The RMSE objective function minimized by the EEFO method has an average, standard deviation and best values of 7.7348 × 10⁻⁴, 6.8513 × 10⁻⁷, and 7.7299 × 10⁻⁴ in the table. These numerical values are the most minimal in comparison to other methods. In addition, the highest RMSE value obtained from the EEFO method is considerably smaller than the average and lowest RMSE values achieved by the GSA, WOA, SMA, and AOA algorithms. The numerical findings validate the excellence of the EEFO method and its resilient statistical framework. The values of the most accurate estimated $I_{ph}$, $I_{sd}$, $R_s$, $R_{sh}$ and $n$ parameters from the optimal run of all methods are provided in Table 3.

Table 2

Table 2. Statistical metric values of RMSE for single-diode model.

Table 3

Table 3. Estimated parameters of single-diode model.

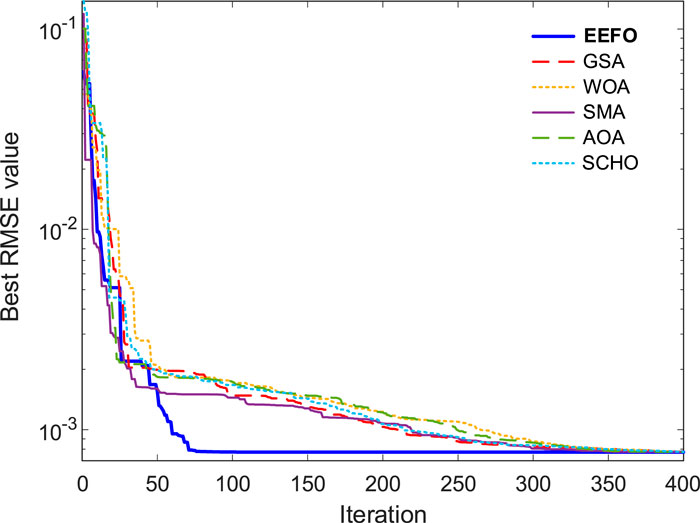
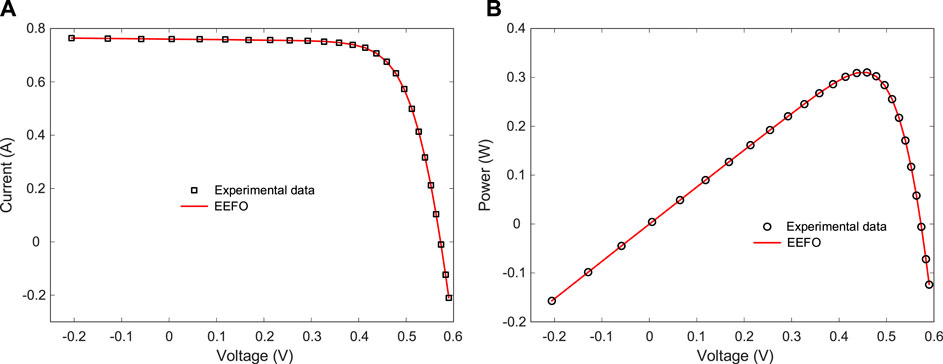
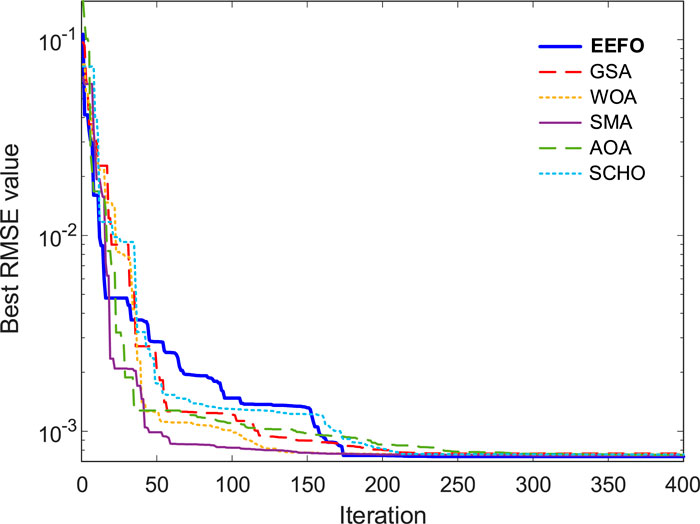
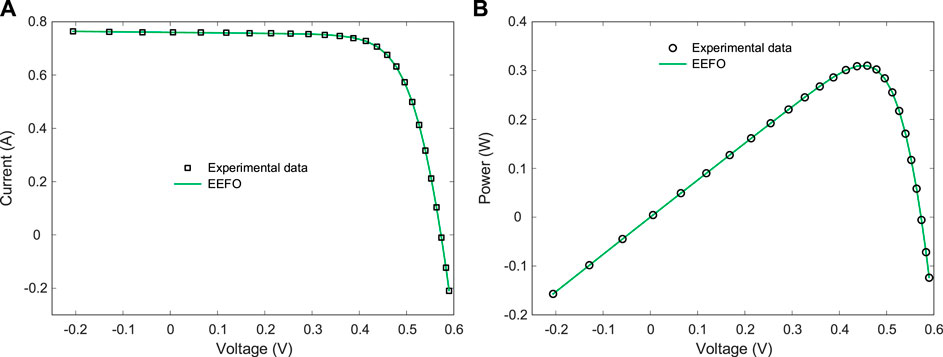
Figure 5 shows the change of the convergence curves for the RMSE objective function with respect to the algorithm’s number of iterations. As shown in the figure, compared to the GSA, WOA, SMA, AOA and SCHO algorithms, the best RMSE value was achieved with the least iteration with EEFO. Figure 6 shows the I-V and P-V curves of the EEFO-based single diode model and 26 experimental data. The EEFO algorithm has been overlapping with experimental data because it makes the parameter extraction very precise and accurate.

Figure 5

Figure 5. Detailed convergence curves of EEFO, GSA, WOA, SMA, AOA and SCHO for single-diode model.

Figure 6

Figure 6. I-V (A) and P-V (B) curve characteristics for single-diode model.

4.3 Results of double-diode model

The parameters to be optimized in the double diode model are $I_{ph}$, $I_{sd1}$, $I_{sd2}$, $R_s$, $R_{sh}$, $n_1$ and $n_2$. The lower and upper boundaries of these 7 parameters are listed in Table 4. In Figure 7, RMSE values are given for 30 running of all algorithms. Other algorithms (GSA, WOA, SMA, AOA, and SCHO) except for the EEFO are subject to high fluctuations in RMSE values in each run. As with the single-diode model, the EEFO algorithm finds RMSE values close to each run, indicating statistical stability for the double diode model, as well. Figure 8 shows the results of the boxplot analysis of all algorithms. As is clear from the figure, the EEFO algorithm affirms its superiority as a statistical structure over other comparison algorithms due to the absence of data at endpoints in the boxplot and the lowest median value.

Table 4

Table 4. The parameter limits of double-diode model.

Figure 7

Figure 7. Obtained RMSE values with respect to all runs for double diode model.

Figure 8

Figure 8. Boxplot analysis of EEFO, GSA, WOA, SMA, AOA and SCHO for double-diode model.

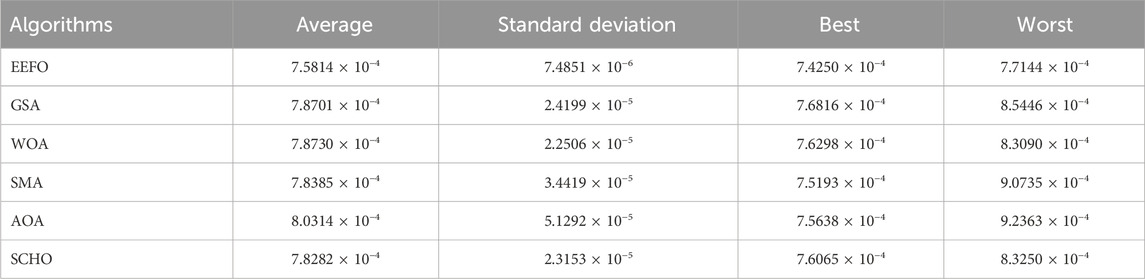
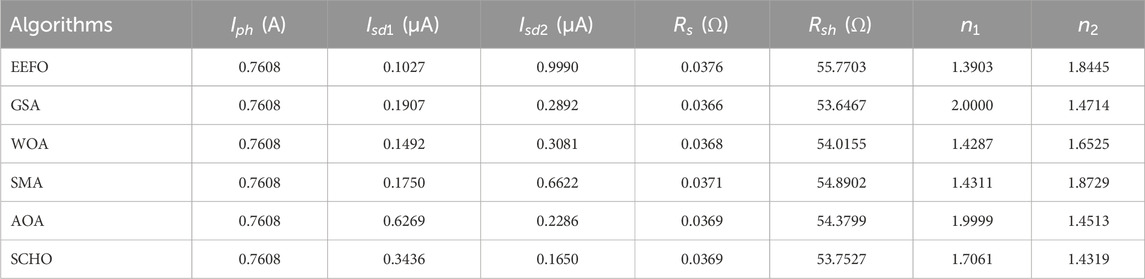
Table 5 shows the statistical metrics of the RMSE objective function for the double diode model. Considering the numerical values in the table, the lowest average (7.5814 × 10⁻⁴), the standard deviation (7.4851 × 10⁻⁶), the best (7.4250 × 10⁻⁴) and the worst (7.7144 × 10⁻⁴) values were obtained using the EEFO. As was the case for the single-diode model, the best RMSE metrics were found with EEFO. Table 6 shows the parameters of the double-diode model optimized using EEFO, GSA, WOA, SMA, AOA and SCHO methods.

Table 5

Table 5. Statistical metric values of RMSE for double-diode model.

Table 6

Table 6. Estimated parameters of double-diode model.

Comparative convergence curves of the algorithms are provided in detail in Figure 9. The EEFO has reached the lowest RMSE (7.4250 × 10⁻⁴) without sticking to the local minimum. The GSA, WOA, SMA, AOA, and SCHO algorithms started to reach lower values between 300 and 400 iterations. However, the EEFO approaches the lowest value earlier than 250th iteration. The I-V and P-V curves of the system optimized with EEFO are shown in Figure 10. As can be seen from the figure, 26 experimental data are compatible with EEFO’s estimates for all voltage ranges.

Figure 9

Figure 9. Detailed convergence curves of EEFO, GSA, WOA, SMA, AOA and SCHO for double-diode model.

Figure 10

Figure 10. I-V (A) and P-V (B) curve characteristics for double-diode model.

4.4 Results of three-diode model

Table 7 shows the boundaries of the three-diode model with 9 parameters. For all algorithms, the RMSE values obtained from 30 runs are shown in Figure 11. On the other hand, the comparative box plot analysis is shown in Figure 12. From these figures one can see the superiority of the EEFO since it has achieved fewer fluctuations and the lowest RMSE values in all runs compared to GSA, WOA, SMA, AOA, and SCHO algorithms.

Table 7

Table 7. The parameter limits of three-diode model.

Figure 11

Figure 11. Obtained RMSE values with respect to all runs for three diode model.

Figure 12

Figure 12. Boxplot analysis of EEFO, GSA, WOA, SMA, AOA and SCHO for three-diode model.

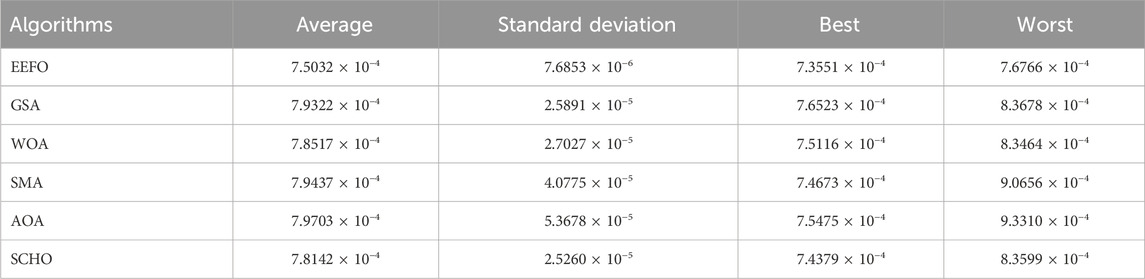
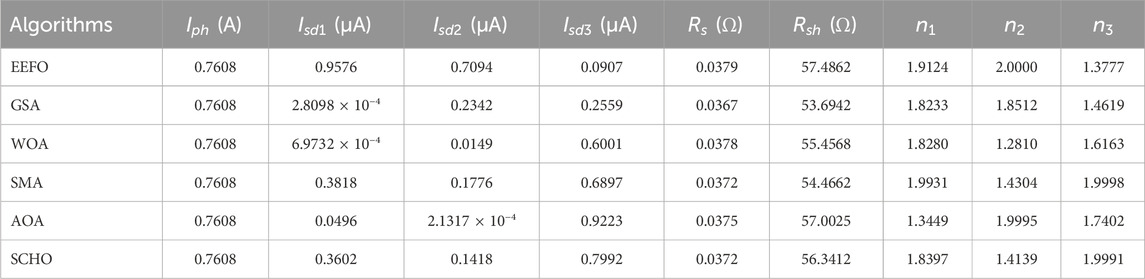
The fundamental statistical metrics of the algorithms in terms of RMSE values are listed in Table 8. As were the same case with the other two diode models, the three diode model had the lowest average (7.5032 × 10⁻⁴), the standard deviation (7.6853 × 10⁻⁶), the best (7.3551 × 10⁻⁴) and the worst (7.6766 × 10⁻⁴) values with the EEFO algorithm. The values of the parameters $I_{ph}$, $I_{sd1}$, $I_{sd2}$, $I_{sd3}$, $R_s$, $R_{sh}$, $n_1$, $n_2$ and $n_3$ optimized with EEFO, WOA, SMA, AOA and SCHO are given in Table 9.

Table 8

Table 8. Statistical metric values of RMSE for three-diode model.

Table 9

Table 9. Estimated parameters of three-diode model.

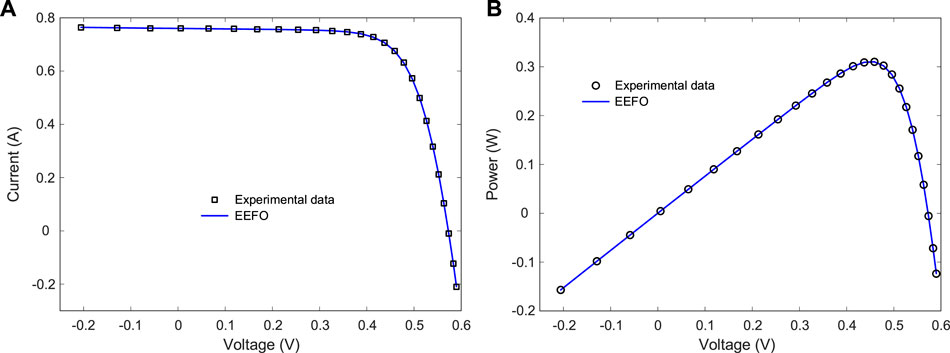
Comparative convergence profiles for the three-diode model are shown in Figure 13. As illustrated in the figure, the only algorithm that achieves the lowest RMSE value with the least iteration is EEFO. Due to its better exploration-exploitation balance and the no requirement of adjustable additional parameters, the EEFO finds global solutions in the shortest possible time without stagnating to the local minimum. The I-V and P-V curves of the three-diode model optimized with EEFO are shown in Figure 14. This figure indicates that the EEFO can estimate the parameters with good accuracy since the current and power data estimated by the EEFO is almost identical with that of the experimental results.

Figure 13

Figure 13. Detailed convergence curves of EEFO, GSA, WOA, SMA, AOA and SCHO for three-diode model.

Figure 14

Figure 14. I-V (A) and P-V (B) curve characteristics for three-diode model.

4.5 Comparison of elapsed times

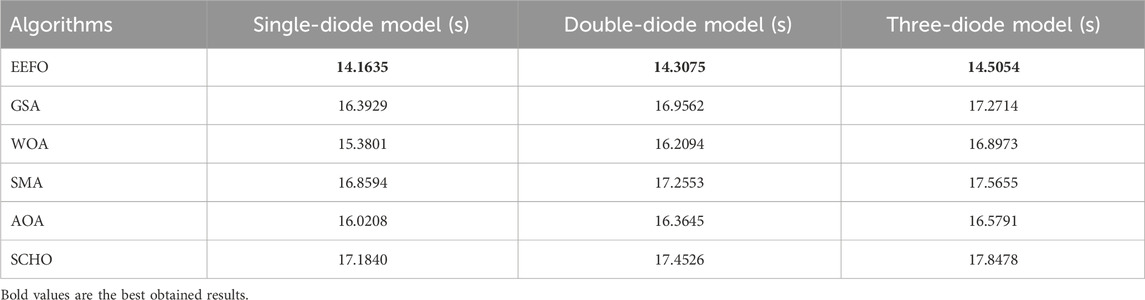
It is important for an algorithm to be able to perform the optimization task as quickly as possible while achieving the best results during the optimization process. Table 10 shows the average run times of EEFO, GSA, WOA, SMA, AOA and SCHO algorithms for different diode models. When the numerical values in the table are considered, the shortest calculation times for all diode models are obtained using the EEFO. Furthermore, since the estimated number of parameters is highest in the three-diode model, the increase in calculation time compared to the other two diode models is normal, however, this is also negligible for EEFO. As these results show, compared to other algorithms, the EEFO algorithm not only minimizes the RMSE objective function, but also completes this optimization process as quickly as possible.

Table 10

Table 10. Elapsed times for all diode models.

4.6 Comparison of best RMSE values with recently reported studies

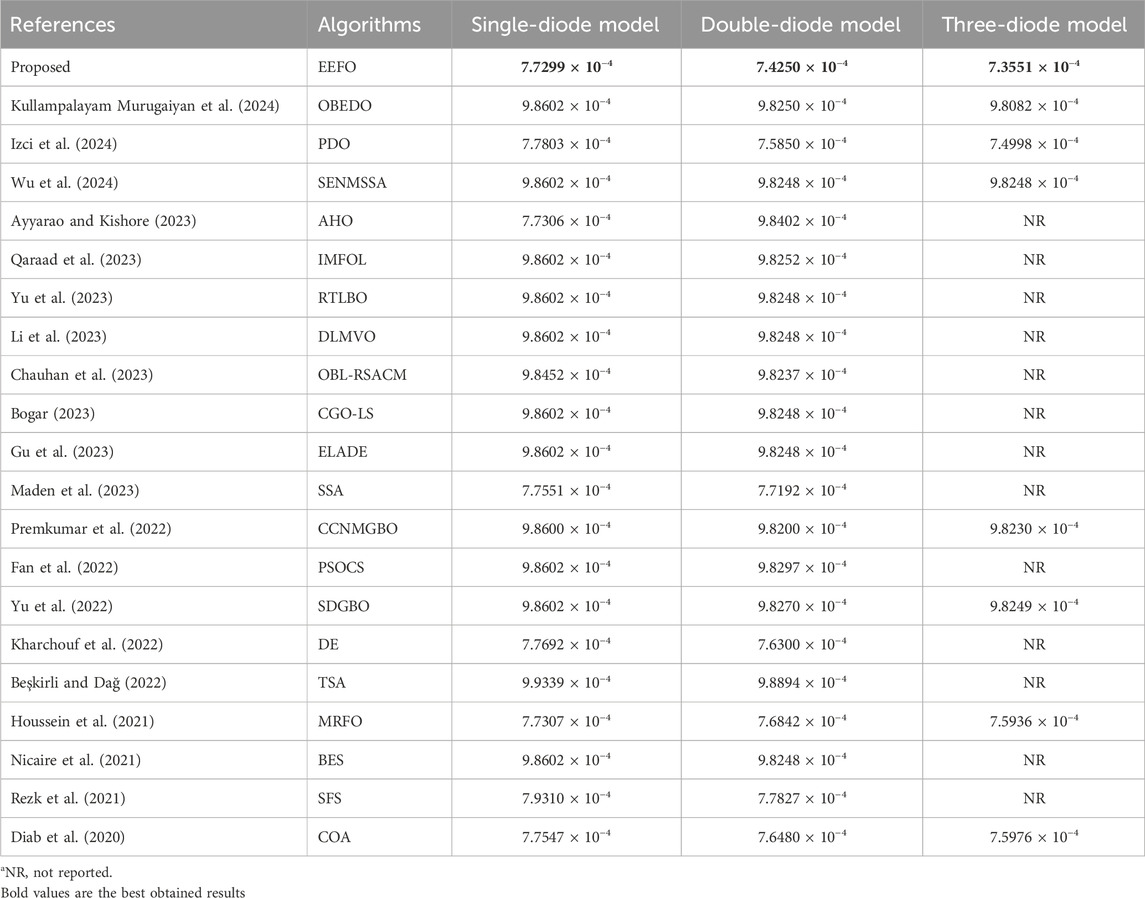
The success and superiority of the proposed EEFO for the extraction of the parameters of different photovoltaic models is compared in this section by employing the best algorithms published in reputable journals between 2020 and 2024. The 20 methods (Diab et al., 2020; Houssein et al., 2021; Nicaire et al., 2021; Rezk et al., 2021; Beşkirli and Dağ, 2022; Fan et al., 2022; Kharchouf et al., 2022; Premkumar et al., 2022; Yu et al., 2022; 2023; Ayyarao and Kishore, 2023; Bogar, 2023; Chauhan et al., 2023; Gu et al., 2023; Li et al., 2023; Maden et al., 2023; Qaraad et al., 2023; Izci et al., 2024; Kullampalayam Murugaiyan et al., 2024; Wu et al., 2024) are employed and the respective comparison and the best RMSE values are shown in Table 11. In the single diode model, the lowest RMSE value was found with the EEFO at 7.7299 × 10⁻⁴. Its closest competitor seems to be the approach reported in (Ayyarao and Kishore, 2023) which is at 7.7306 × 10⁻⁴. Similarly, the best RMSE values for EEFO’s two-diode and three-diode models are 7.4250 × 10⁻⁴ and 7.3551 × 10⁻⁴, respectively. The nearest competitor (Izci et al., 2024) found RMSE values for two diode and three diode models as 7.5850 × 10⁻⁴ and 7.4998 × 10⁻⁴, respectively. As is clear from this comparison table, the proposed EEFO-based approach can achieve better results by finding the lowest RMSE value. This makes it superior to the previously reported approaches in the literature as it allows us to estimate more precise parameter values.

Table 11

Table 11. Comparison of RMSE values.

4.7 Discussion

A comprehensive analysis was conducted initially, comparing the GSA, WOA, SMA, AOA, and SCHO algorithms with the Newton-Raphson-supported EEFO method. This is the first report in the literature regarding the presented technique with the aim of improving the parameter extraction of solar systems. The EEFO method successfully obtained precise and accurate parameter values for three different diode models. This was achieved by minimizing the RMSE, maintaining consistent statistical performance, and approaching the global solution with minimal iterations, without getting trapped in local minima. The completion of these operations took the minimum possible time frame for the EEFO compared to the competitors. Based on the RMSE, the EEFO method was shown to be the most effective approach among the twenty strategies currently documented in the literature for diode models. EEFO may be efficiently used to a diverse range of optimization problems that need the prediction of additional factors in real-world scenarios as the behavior of the diode models optimized with EEFO aligns well with the experimental data.

5 Conclusion

The increasing fears regarding environmental deterioration and the pressing necessity to address climate change have stimulated the investigation of renewable energy sources as feasible substitutes for traditional fossil fuels. Solar energy has emerged as a feasible solution owing to its vast availability, environmentally friendly characteristics, and cost-effectiveness. Photovoltaic (PV) systems, which utilize solar energy, are crucial in the shift towards sustainability. However, accurately modeling these systems is still difficult due to the intricate nature of the process. Traditional photovoltaic (PV) modeling often depends on well-established models like the single-diode, double-diode, and three-diode models. However, the absence of specific physical characteristics in manufacturer datasheets presents challenges in accurately assessing and improving performance. Nevertheless, recent progress in parameter estimate methods, namely, by employing metaheuristic algorithms, has greatly enhanced the precision and effectiveness of PV system modeling. Numerous optimization techniques, such as the bald eagle search method and the artificial hummingbird methodology, have exhibited their effectiveness in precisely forecasting parameters for diverse photovoltaic (PV) models. However, current approaches demonstrate several drawbacks, including sluggish convergence and inadequate population variety. Additionally, the investigation of the three-diode model has received limited attention in the literature. In order to tackle these issues, the present study presents the electric eel foraging optimizer (EEFO) method, an innovative metaheuristic approach that draws inspiration from the social predation behaviors observed in electric eels. The EEFO method presents a methodical and efficient strategy for navigating the intricate parameter space of solar photovoltaic (PV) models. It has demonstrated encouraging outcomes in several scenarios, including single-diode, double-diode, and three-diode models. The improved efficacy of the EEFO in accurately calculating parameters for solar PV models is supported by statistical analysis and comparative tests conducted against competing approaches. The precision and reliability of the model in simulating current and voltage parameters are shown by its smooth convergence behavior and consistent ability to yield low root mean square error values.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

DI: Conceptualization, Investigation, Methodology, Project administration, Resources, Software, Writing–original draft. SE: Conceptualization, Investigation, Methodology, Resources, Software, Visualization, Writing–review and editing. LA: Data curation, Supervision, Validation, Writing–review and editing. MS: Project administration, Resources, Supervision, Validation, Writing–review and editing. MR: Resources, Supervision, Validation, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdel-Basset, M., Mohamed, R., Mirjalili, S., Chakrabortty, R. K., and Ryan, M. J. (2020). Solar photovoltaic parameter estimation using an improved equilibrium optimizer. Sol. Energy 209, 694–708. doi:10.1016/j.solener.2020.09.032

CrossRef Full Text | Google Scholar

Abualigah, L., Diabat, A., Mirjalili, S., Abd Elaziz, M., and Gandomi, A. H. (2021). The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 376, 113609. doi:10.1016/j.cma.2020.113609

CrossRef Full Text | Google Scholar

Almunem, A., Muhsen, D. H., Haider, H. T., and Khatib, T. (2024). A novel method for modeling of photovoltaic modules based on arithmetic optimization algorithm and cuckoo search. Opt. (Stuttg) 298, 171591. doi:10.1016/j.ijleo.2023.171591

CrossRef Full Text | Google Scholar

Alzakari, S. A., Izci, D., Ekinci, S., Alhussan, A. A., and Hashim, F. A. (2024). A new control scheme for temperature adjustment of electric furnaces using a novel modified electric eel foraging optimizer. AIMS Math. 9, 13410–13438. doi:10.3934/math.2024654

CrossRef Full Text | Google Scholar

Ayyarao, T. S. L. V. (2022). Parameter estimation of solar PV models with quantum-based avian navigation optimizer and Newton–Raphson method. J. Comput. Electron 21, 1338–1356. doi:10.1007/s10825-022-01931-8

CrossRef Full Text | Google Scholar

Ayyarao, T. S. L. V., and Kishore, G. I. (2023). Parameter estimation of solar PV models with artificial humming bird optimization algorithm using various objective functions. Soft Comput. 28, 3371–3392. doi:10.1007/s00500-023-08630-x

CrossRef Full Text | Google Scholar

Bacanin, N., Stoean, R., Zivkovic, M., Petrovic, A., Rashid, T. A., and Bezdan, T. (2021). Performance of a novel chaotic firefly algorithm with enhanced exploration for tackling global optimization problems: application for dropout regularization. Mathematics 9, 2705. doi:10.3390/math9212705

CrossRef Full Text | Google Scholar

Bai, J., Li, Y., Zheng, M., Khatir, S., Benaissa, B., Abualigah, L., et al. (2023). A sinh cosh optimizer. Knowl. Based Syst. 282, 111081. doi:10.1016/j.knosys.2023.111081

CrossRef Full Text | Google Scholar

Bastos, D. A., Zuanon, J., Rapp Py-Daniel, L., and de Santana, C. D. (2021). Social predation in electric eels. Ecol. Evol. 11, 1088–1092. doi:10.1002/ece3.7121

PubMed Abstract | CrossRef Full Text | Google Scholar

Beşkirli, A., and Dağ, İ. (2022). An efficient tree seed inspired algorithm for parameter estimation of Photovoltaic models. Energy Rep. 8, 291–298. doi:10.1016/j.egyr.2021.11.103

CrossRef Full Text | Google Scholar

Bogar, E. (2023). Chaos game optimization-least squares algorithm for photovoltaic parameter estimation. Arab. J. Sci. Eng. 48, 6321–6340. doi:10.1007/s13369-022-07364-6

CrossRef Full Text | Google Scholar

Chauhan, S., Vashishtha, G., and Kumar, A. (2023). Approximating parameters of photovoltaic models using an amended reptile search algorithm. J. Ambient. Intell. Humaniz Comput. 14, 9073–9088. doi:10.1007/s12652-022-04412-9

CrossRef Full Text | Google Scholar

Chen, H., Li, C., Mafarja, M., Heidari, A. A., Chen, Y., and Cai, Z. (2023a). Slime mould algorithm: a comprehensive review of recent variants and applications. Int. J. Syst. Sci. 54, 204–235. doi:10.1080/00207721.2022.2153635

CrossRef Full Text | Google Scholar

Chen, L., Han, W., Shi, Y., Zhang, J., and Cao, S. (2023b). A photovoltaic parameter identification method based on Pontogammarus maeoticus swarm optimization. Front. Energy Res. 11. doi:10.3389/fenrg.2023.1204006

CrossRef Full Text | Google Scholar

Choulli, I., Elyaqouti, M., hanafi Arjdal, E., Ben hmamou, D., Saadaoui, D., Lidaighbi, S., et al. (2024). DIWJAYA: JAYA driven by individual weights for enhanced photovoltaic model parameter estimation. Energy Convers. Manag. 305, 118258. doi:10.1016/j.enconman.2024.118258

CrossRef Full Text | Google Scholar

Demirtas, M., and Koc, K. (2022). Parameter extraction of photovoltaic cells and modules by INFO algorithm. IEEE Access 10, 87022–87052. doi:10.1109/ACCESS.2022.3198987

CrossRef Full Text | Google Scholar

Diab, A. A. Z., Sultan, H. M., Do, T. D., Kamel, O. M., and Mossa, M. A. (2020). Coyote optimization algorithm for parameters estimation of various models of solar cells and PV modules. IEEE Access 8, 111102–111140. doi:10.1109/ACCESS.2020.3000770

CrossRef Full Text | Google Scholar

Ekinci, S., Izci, D., and Hussien, A. G. (2024). Comparative analysis of the hybrid gazelle-Nelder–Mead algorithm for parameter extraction and optimization of solar photovoltaic systems. IET Renew. Power Gener. 18, 959–978. doi:10.1049/rpg2.12974

CrossRef Full Text | Google Scholar

Elhammoudy, A., Elyaqouti, M., Arjdal, E. H., Ben Hmamou, D., Lidaighbi, S., Saadaoui, D., et al. (2023). Dandelion Optimizer algorithm-based method for accurate photovoltaic model parameter identification. Energy Convers. Manag. X 19, 100405. doi:10.1016/j.ecmx.2023.100405

CrossRef Full Text | Google Scholar

Fan, Y., Wang, P., Heidari, A. A., Chen, H., Hamza, T., and Mafarja, M. (2022). Random reselection particle swarm optimization for optimal design of solar photovoltaic modules. Energy 239, 121865. doi:10.1016/j.energy.2021.121865

CrossRef Full Text | Google Scholar

Gu, Z., Xiong, G., Fu, X., Mohamed, A. W., Al-Betar, M. A., Chen, H., et al. (2023). Extracting accurate parameters of photovoltaic cell models via elite learning adaptive differential evolution. Energy Convers. Manag. 285, 116994. doi:10.1016/j.enconman.2023.116994

CrossRef Full Text | Google Scholar

Han, Y., Chen, W., Heidari, A. A., Chen, H., and Zhang, X. (2024). Balancing exploration–exploitation of multi-verse optimizer for parameter extraction on photovoltaic models. J. Bionic Eng. 21, 1022–1054. doi:10.1007/s42235-024-00479-6

CrossRef Full Text | Google Scholar

Hassan, M. H., Kamel, S., Ramadan, A., Domínguez-García, J. L., and Zeinoddini-Meymand, H. (2024). Optimizing photovoltaic models: a leader artificial ecosystem approach for accurate parameter estimation of dynamic and static three diode systems. IET Generation, Transm. Distribution 18, 1026–1058. doi:10.1049/gtd2.13121

CrossRef Full Text | Google Scholar

Houssein, E. H., Zaki, G. N., Diab, A. A. Z., and Younis, E. M. G. (2021). An efficient Manta Ray Foraging Optimization algorithm for parameter extraction of three-diode photovoltaic model. Comput. Electr. Eng. 94, 107304. doi:10.1016/j.compeleceng.2021.107304

CrossRef Full Text | Google Scholar

Hussain, M. T., Hussan, M. R., Tariq, M., Sarwar, A., Ahmad, S., Poshtan, M., et al. (2024). Archimedes optimization algorithm based parameter extraction of photovoltaic models on a decent basis for novel accurate RMSE calculation. Front. Energy Res. 11. doi:10.3389/fenrg.2023.1326313

CrossRef Full Text | Google Scholar

Izci, D., Ekinci, S., Dal, S., and Sezgin, N. (2022). “Parameter estimation of solar cells via weighted mean of vectors algorithm,” in 2022 Global Energy Conference (GEC), Batman, Turkey, 26-29 October 2022 (IEEE), 312–316. doi:10.1109/GEC55014.2022.9986943

CrossRef Full Text | Google Scholar

Izci, D., Ekinci, S., Demiroren, A., and Hedley, J. (2020). “HHO algorithm based PID controller design for aircraft pitch angle control system,” in 2020 International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), Ankara, Turkey, 26-28 June 2020 (IEEE), 1–6. doi:10.1109/HORA49412.2020.9152897

CrossRef Full Text | Google Scholar

Izci, D., Ekinci, S., and Hussien, A. G. (2024). Efficient parameter extraction of photovoltaic models with a novel enhanced prairie dog optimization algorithm. Sci. Rep. 14, 7945. doi:10.1038/s41598-024-58503-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Kharchouf, Y., Herbazi, R., and Chahboun, A. (2022). Parameter’s extraction of solar photovoltaic models using an improved differential evolution algorithm. Energy Convers. Manag. 251, 114972. doi:10.1016/j.enconman.2021.114972

CrossRef Full Text | Google Scholar

Kullampalayam Murugaiyan, N., Chandrasekaran, K., Manoharan, P., and Derebew, B. (2024). Leveraging opposition-based learning for solar photovoltaic model parameter estimation with exponential distribution optimization algorithm. Sci. Rep. 14, 528. doi:10.1038/s41598-023-50890-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumari, P. A., Basha, C. H. H., Puppala, R., Fathima, F., Dhanamjayulu, C., Chinthaginjala, R., et al. (2024). Application of DSO algorithm for estimating the parameters of triple diode model-based solar PV system. Sci. Rep. 14, 3867. doi:10.1038/s41598-024-53582-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, B., Chen, H., and Tan, T. (2021a). PV cell parameter extraction using data prediction–based meta-heuristic algorithm via extreme learning machine. Front. Energy Res. 9. doi:10.3389/fenrg.2021.693252

CrossRef Full Text | Google Scholar

Li, J., Dang, J., Xia, C., Jia, R., Wang, G., Li, P., et al. (2023). Dynamic leader multi-verse optimizer (dlmvo): a new algorithm for parameter identification of solar PV models. Appl. Sci. 13, 5751. doi:10.3390/app13095751

CrossRef Full Text | Google Scholar

Li, M., Li, C., Huang, Z., Huang, J., Wang, G., and Liu, P. X. (2021b). Spiral-based chaotic chicken swarm optimization algorithm for parameters identification of photovoltaic models. Soft Comput. 25, 12875–12898. doi:10.1007/s00500-021-06010-x

CrossRef Full Text | Google Scholar

Luo, X., Cao, L., Wang, L., Zhao, Z., and Huang, C. (2018). Parameter identification of the photovoltaic cell model with a hybrid Jaya-NM algorithm. Opt. (Stuttg) 171, 200–203. doi:10.1016/j.ijleo.2018.06.047

CrossRef Full Text | Google Scholar

Maden, D., Çelik, E., Houssein, E. H., and Sharma, G. (2023). Squirrel search algorithm applied to effective estimation of solar PV model parameters: a real-world practice. Neural Comput. Appl. 35, 13529–13546. doi:10.1007/s00521-023-08451-x

CrossRef Full Text | Google Scholar

Malakar, S., Ghosh, M., Bhowmik, S., Sarkar, R., and Nasipuri, M. (2020). A GA based hierarchical feature selection approach for handwritten word recognition. Neural Comput. Appl. 32, 2533–2552. doi:10.1007/s00521-018-3937-8

CrossRef Full Text | Google Scholar

Memon, Z. A., Akbari, M. A., and Zare, M. (2023). An improved cheetah optimizer for accurate and reliable estimation of unknown parameters in photovoltaic cell and module models. Appl. Sci. 13, 9997. doi:10.3390/app13189997

CrossRef Full Text | Google Scholar

Mirjalili, S., and Lewis, A. (2016). The whale optimization algorithm. Adv. Eng. Softw. 95, 51–67. doi:10.1016/j.advengsoft.2016.01.008

CrossRef Full Text | Google Scholar

Mohamed, R., Abdel-Basset, M., Sallam, K. M., Hezam, I. M., Alshamrani, A. M., and Hameed, I. A. (2024). Novel hybrid kepler optimization algorithm for parameter estimation of photovoltaic modules. Sci. Rep. 14, 3453. doi:10.1038/s41598-024-52416-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Nicaire, N. F., Steve, P. N., Salome, N. E., and Grégroire, A. O. (2021). Parameter estimation of the photovoltaic system using bald eagle search (BES) algorithm. Int. J. Photoenergy 2021, 1–20. doi:10.1155/2021/4343203

CrossRef Full Text | Google Scholar

Premkumar, M., Jangir, P., Ramakrishnan, C., Kumar, C., Sowmya, R., Deb, S., et al. (2022). An enhanced Gradient-based Optimizer for parameter estimation of various solar photovoltaic models. Energy Rep. 8, 15249–15285. doi:10.1016/j.egyr.2022.11.092

CrossRef Full Text | Google Scholar

Qaraad, M., Amjad, S., Hussein, N. K., Badawy, M., Mirjalili, S., and Elhosseini, M. A. (2023). Photovoltaic parameter estimation using improved moth flame algorithms with local escape operators. Comput. Electr. Eng. 106, 108603. doi:10.1016/j.compeleceng.2023.108603

CrossRef Full Text | Google Scholar

Ramachandran, M., Sundaram, A., Ridha, H. M., and Mirjalili, S. (2024). Estimation of photovoltaic models using an enhanced Henry gas solubility optimization algorithm with first-order adaptive damping Berndt-Hall-Hall-Hausman method. Energy Convers. Manag. 299, 117831. doi:10.1016/j.enconman.2023.117831

CrossRef Full Text | Google Scholar

Rashedi, E., Nezamabadi-pour, H., and Saryazdi, S. (2009). GSA: a gravitational search algorithm. Inf. Sci. (N Y) 179, 2232–2248. doi:10.1016/j.ins.2009.03.004

CrossRef Full Text | Google Scholar

Rezk, H., Babu, T. S., Al-Dhaifallah, M., and Ziedan, H. A. (2021). A robust parameter estimation approach based on stochastic fractal search optimization algorithm applied to solar PV parameters. Energy Rep. 7, 620–640. doi:10.1016/j.egyr.2021.01.024

CrossRef Full Text | Google Scholar

Ridha, H. M., Hizam, H., Mirjalili, S., Othman, M. L., and Ya’acob, M. E. (2022). Zero root-mean-square error for single- and double-diode photovoltaic models parameter determination. Neural Comput. Appl. 34, 11603–11624. doi:10.1007/s00521-022-07047-1

CrossRef Full Text | Google Scholar

Ru, X. (2024). Parameter extraction of photovoltaic model based on butterfly optimization algorithm with chaos learning strategy. Sol. Energy 269, 112353. doi:10.1016/j.solener.2024.112353

CrossRef Full Text | Google Scholar

Saadaoui, D., Elyaqouti, M., Assalaou, K., Ben Hmamou, D., Lidaighbi, S., Arjdal, E., et al. (2024). Extraction of single diode PV cell/module model parameters using a hybrid BMO approach with Lambert’s W function. Int. J. Ambient Energy 45. doi:10.1080/01430750.2024.2304331

CrossRef Full Text | Google Scholar

Sheng, H., Li, C., Wang, H., Yan, Z., Xiong, Y., Cao, Z., et al. (2019). Parameters extraction of photovoltaic models using an improved moth-flame optimization. Energies (Basel) 12, 3527. doi:10.3390/en12183527

CrossRef Full Text | Google Scholar

Singla, M. K., Gupta, J., Alsharif, M. H., and Kim, M.-K. (2024). A modified particle swarm optimization rat search algorithm and its engineering application. PLoS One 19, e0296800. doi:10.1371/journal.pone.0296800

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, L., Wang, J., and Tang, L. (2021). A powerful bio-inspired optimization algorithm based PV cells diode models parameter estimation. Front. Energy Res. 9. doi:10.3389/fenrg.2021.675925

CrossRef Full Text | Google Scholar

Wang, G.-G., Deb, S., and Cui, Z. (2019). Monarch butterfly optimization. Neural Comput. Appl. 31, 1995–2014. doi:10.1007/s00521-015-1923-y

CrossRef Full Text | Google Scholar

Wang, L., Chen, Z., Guo, Y., Hu, W., Chang, X., Wu, P., et al. (2021). Accurate solar cell modeling via genetic neural network-based meta-heuristic algorithms. Front. Energy Res. 9. doi:10.3389/fenrg.2021.696204

CrossRef Full Text | Google Scholar

Wu, H., Chen, Y., Cai, Z., Heidari, A. A., Chen, H., and Zhang, Y. (2024). Super-evolutionary mechanism and Nelder-Mead simplex enhanced salp swarm algorithm for photovoltaic model parameter estimation. IET Renew. Power Gener. doi:10.1049/rpg2.12973

CrossRef Full Text | Google Scholar

Yesilbudak, M. (2024). A comparative study on accurate parameter estimation of solar photovoltaic models using metaheuristic optimization algorithms. Electr. Power Components Syst. 52, 1001–1021. doi:10.1080/15325008.2023.2283843

CrossRef Full Text | Google Scholar

Yousri, D., Rezk, H., and Fathy, A. (2020). Identifying the parameters of different configurations of photovoltaic models based on recent artificial ecosystem-based optimization approach. Int. J. Energy Res. 44, 11302–11322. doi:10.1002/er.5747

CrossRef Full Text | Google Scholar

Yu, S., Chen, Z., Heidari, A. A., Zhou, W., Chen, H., and Xiao, L. (2022). Parameter identification of photovoltaic models using a sine cosine differential gradient based optimizer. IET Renew. Power Gener. 16, 1535–1561. doi:10.1049/rpg2.12451

CrossRef Full Text | Google Scholar

Yu, X., Hu, Z., Wang, X., and Luo, W. (2023). Ranking teaching–learning-based optimization algorithm to estimate the parameters of solar models. Eng. Appl. Artif. Intell. 123, 106225. doi:10.1016/j.engappai.2023.106225

CrossRef Full Text | Google Scholar

Zhao, W., Wang, L., Zhang, Z., Fan, H., Zhang, J., Mirjalili, S., et al. (2024). Electric eel foraging optimization: a new bio-inspired optimizer for engineering applications. Expert Syst. Appl. 238, 122200. doi:10.1016/j.eswa.2023.122200

CrossRef Full Text | Google Scholar

Zheng, Y., Zhang, E., and An, P. (2022). Peafowl optimization algorithm based PV cell models parameter identification. Front. Energy Res. 10. doi:10.3389/fenrg.2022.985523

CrossRef Full Text | Google Scholar