A method of determining the carbon emission reduction contribution of regional distribution networks based on spherical fuzzy sets

Introduction: An innovative methodology is proposed to delve into the pivotal role of regional distribution networks (RDNs) in fostering low-carbon development.

Methods: The methodology first constructs an evaluation framework encompassing various dimensions and then integrates spherical fuzzy sets (SFSs) with the best-worst method (BWM), enabling the precise calculation of indicator weight parameters. Subsequently, we employ the measurement of alternatives and ranking according to compromise solution (MARCOS) with SFSs to process and synthesize decision making information.

Results: Take the Shanghai region as an example, results show that C4 has the highest performance and C10 has the lowest.

Discussion: In conclusion, this research presents a significant step forward in understanding the importance of RDNs in promoting low-carbon development and offers a practical approach for decision-makers to assess and enhance the performance of RDNs.

1 Introduction

With the continuous promotion of the dual-carbon target, the gradual increase in renewable energy penetration in urban power grids has brought about problems of strong intermittency and uncertainty, making urban energy security face severe challenges (Zhang and Kang, 2022). As an important part of the power system, the contribution of the regional distribution network to carbon emission reduction directly affects the low-carbon process of the overall power industry. By optimizing power transmission and distribution, regional distribution networks (RDNs) can effectively reduce the line loss of the power grid and improve energy efficiency (Yue et al., 2024; Cheng et al., 2024). Thus, RDNs bear great responsibility in the process of sustainable development of urban energy. However, the current research on the carbon emission of RDNs mostly focuses on traceability, collaboration, and reduction optimization and thus lacks quantitative determination of the contribution of carbon emission reduction, which weakens the green support capacity of RDNs and makes it difficult to guarantee the effectiveness of new energy production, transmission, and consumption in the urban green development process (Yang et al., 2024; Yang S. et al., 2023; Sang et al., 2024). Therefore, accurately identifying and effectively quantifying the green support capacity of RDNs is a key link to achieving the dual-carbon goal, and the study of the carbon emission reduction contribution of RDNs has become a key research direction in urban green development.

At present, in the field of carbon emission reduction quantification, existing research revolves around the low-carbonized economic operation of integrated energy systems in parks, the analysis of carbon emission reduction benefits on the urban user side, the effectiveness of green energy access, and multi-modal transportation networks aiming at carbon emission minimization. In order to solve the contradiction between the power consumption of carbon capture devices and the demand for carbon capture, Paulino E. Labis proposes a near-end strategy optimization algorithm based on the real-time response to uncertain source loads, which demonstrates the effectiveness and advancement of this method in decarbonized operation (Labis et al., 2011). Yi Xie takes the urban user side as the main body, adopts the marginal carbon emission factor to calculate the expected carbon reduction of user-side energy storage, and analyzes in-depth the influence of user-side energy storage behavior on the total carbon emission of the system, which demonstrates that the carbon-reducing cloud energy storage model can bring better carbon reduction advantages (Xie et al., 2023). Lijuan Yao centers on green energy access work, combines a variety of hierarchical control algorithms to explore the effectiveness of green energy access in the load system, and provides clean energy output tracking services to verify the effectiveness of the method (Yao et al., 2023). For low-carbon multi-modal transport planning problem research, Qin Huang proposed the Harris Hawk optimization algorithm so that the low-carbon objectives and low-cost objectives are optimized, verifying the correctness of the model (Huang et al., 2023). Puliang Du proposed a quantum spherical fuzzy environment decision-making framework for determining the carbon reduction contribution of power companies (Du et al., 2024). Although scholars have carried out some research in the field of carbon emission reduction quantifications, the research for determining the carbon emission reduction contribution of RDNs is still to be explored.

The research on the determination of carbon emission reduction contributions of RDNs involves many aspects of economics, technology, environment, and management, covering many fields such as electric energy substitution, emerging technology, smart logistics, and line loss management, making it a typical multi-attribute decision-making problem under fuzzy environment (Sun et al., 2021; Li et al., 2023; Du et al., 2023; Xue and Tsai, 2022). In recent years, research on multi-attribute decision-making problems in fuzzy environments mostly involves three aspects: indicator weight determination, decision-making method, and fuzzy information characterization. Among them, Qiushuang Wei constructs a best-worst method, interval type-2 fuzzy, preference ranking organization method for enrichment evaluations (BWM-IT2F-PROMETHEE-II) model to calculate indicator weights and recognize the solution of barriers based on the fact that barriers to the implementation of carbon sink projects have the problems of complexity, multiplicity, and uncertainty. The PROMETHEE-II method is cumbersome and requires a complicated calculation process when dealing with large-scale datasets and real-time decision-making, and the interrelationships among the programs are not taken into account (Wei et al., 2023). Therefore, Yongji Wu proposes the measurement of alternatives and ranking according to the compromise solution (MARCOS) method, which effectively avoids the above problems and considers the impact of decision makers’ preferences on the evaluation process (Wu et al., 2023). Xiaomin Gong develops a hybrid decision-making framework to address the problem of renewable energy hosting potential assessment using an interval 2-type fuzzy best-worst method for determining indicator weights and introduces an extended MARCOS method for ranking alternatives (Gong et al., 2021). Based on a spherical fuzzy environment, Rajput Laxmi portrays the importance of indicators and effectively preserves the uncertainty of multi-dimensional information (Laxmi et al., 2024). In addition, the spherical fuzzy set (SFS), as a kind of fuzzy number with three-dimensional degrees of affiliation, non-affiliation, and hesitation, is more in line with the actual situation than the existing linear relationship, which opens up a new way to deal with complex decision-making problems and is widely used in the field of fuzzy decision-making to recognize the effective transformation of fuzzy information (Geng and Li, 2023).

Based on the above analysis, this article proposes a decision-making framework determining the carbon emission reduction contribution of RDNs based on the BWM-MARCOS in an SFS environment to fill the gaps in existing research. First, an indicator system is constructed from economic, technological, environmental, and management dimensions to perceive the carbon emission reduction contribution of RDNs for the first time. Second, the collected expert semantic evaluation information is converted into spherical fuzzy numbers with the BWM to recognize the subjective assignment of the relevant indicators, effectively solving the limitations of traditional methods in dealing with complex and multi-dimensional uncertain information. Then, the weights are incorporated into the developed SFS-MARCOS model for accurate determination relative to traditional methods, which considers the influence of decision makers’ preferences on the evaluation process and improves the scientificity and practicability of decision-making. Finally, the effectiveness of the proposed modeling approach is verified by taking 11 RDNs in Shanghai as examples.

2 Evaluation indicators for carbon emission reduction contribution of RDNs

2.1 Construction of the indicator system

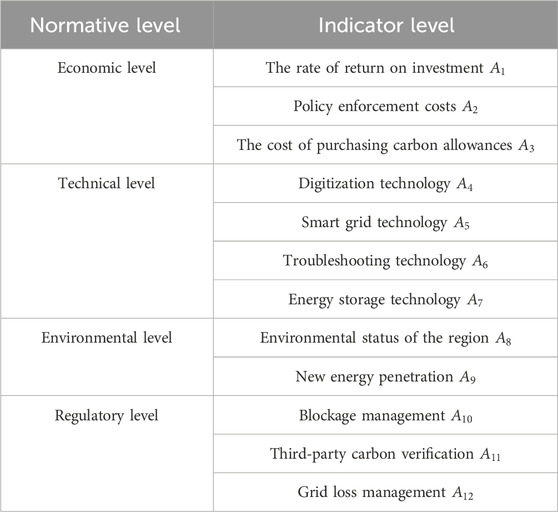
Existing studies mainly diagnose the degree of influence of important operation-related parameters of electricity enterprises on carbon emissions from a global perspective; however, there is a lack of a set of indicator systems to perceive the contribution of carbon emission reduction of RDNs, making it difficult to explain the support of urban green transformation (Yang Y. et al., 2023). In order to solve the above problems, the carbon emission reduction contribution evaluation indicator system of RDNs is constructed from four dimensions of economy, technology, environment, and management, as shown in Table 1.

Table 1

Table 1. Carbon emission reduction contribution indicator system for RDNs.

2.2 Analysis of the indicator system

2.2.1 Economic dimension

The rate of return on investment ($A_1$) (Avdasheva and Orlova, 2020): A measure of the ratio of investment in carbon reduction projects in the distribution grid to long-term benefits. A high ROI indicates that the project is economically viable, as shown in Equation 1.

${\mathrm{U}}_I=\frac{C_I}{C_R}\times 100\%,(1)$

where ${\mathrm{U}}_I$, $C_I,$ and $C_R$, respectively, represent the rate of return on investment, the cost of investment on distribution networks, and the return.

Policy enforcement costs ($A_2$): Policy implementation costs refer to the various expenses that the government must pay in the process of promoting the implementation of carbon emission reduction policies, including the costs of policy publicity, supervision, subsidies, and tax exemptions. These are the economic costs paid by the government to guide and support the electric industry and all sectors of society in participating in carbon emission reduction.

The cost of purchasing carbon allowances ($A_3$) (Zhong et al., 2024): These costs are the fees that enterprises or individuals must pay in order to obtain a certain number of carbon emission allowances in the carbon emission trading market. As an economic incentive, the purchase fee of carbon allowances can encourage industries to reduce carbon emissions, improve energy efficiency, and promote green and low-carbon development.

2.2.2 Technical level

Digital technology ($A_4$) (Sun et al., 2021): The use of the Internet, big data, artificial intelligence, blockchain, artificial intelligence, and other new-generation information technology at all levels of the distribution networks to carry out systematic and comprehensive changes.

Smart grid technology ($A_5$) (Sun et al., 2021): An integrated, high-speed two-way communication network that supports the application of advanced sensing and measurement technologies, advanced equipment technologies, advanced control methods, and advanced decision support system technologies.

Fault handling technology ($A_6$) (Liu et al., 2023): Detect and locate fault points in the distribution network in a timely manner so that remedial measures can be taken quickly to reduce the time of unplanned power outages caused by faults. Rationally arrange maintenance plans and resource allocation to avoid unnecessary waste of resources and duplication of work, thereby improving overall operational efficiency and indirectly reducing carbon emissions.

Energy storage technology ($A_7$) (Li et al., 2024): The process of storing energy through a medium or device and releasing it when needed. Stored surplus renewable energy can be released during peak energy demand to ensure a stable supply of renewable energy.

2.2.3 Environmental level

Environmental status of the region ($A_8$): The conditions of air quality, water quality conditions, soil quality, plant ecology, animal ecology, human health, and natural resource conditions. When the environmental state of an area is better, it can not only utilize resources more efficiently and reduce energy consumption in the production process but also reduce the negative impact on the environment.

New energy penetration rate ($A_9$) (Sun et al., 2021): The proportion of power generation from new energy projects in the areas to total power generation, as shown in Equation 2.

$P_{NE}=\frac{C_{NEG}}{{\mathrm{C}}_{TG}}\times 100\%,(2)$

where $P_{NE}$, $C_{NEG},$ and ${\mathrm{C}}_{TG}$, respectively, represent the new energy penetration rate, the amount of new energy power generation, and the total power generation of RDNs.

2.2.4 Management level

Blockage management ($A_{10}$) (Qiu et al., 2024): The integration and utilization of renewable energy can be prioritized by adjusting power generation plans and load allocation. Because the carbon intensity of renewables is much lower than that of fossil fuels, increasing the proportion of renewable energy can help reduce the overall carbon emissions of regional distribution grids.

Third-party carbon verification ($A_{11}$): Verification of the greenhouse gas emission reports submitted by carbon emission entities participating in carbon emission trading by independent third-party service providers to ensure the validity and accuracy of the emission data submitted by carbon emission entities.

Grid line loss management ($A_{12}$) (Xue and Tsai, 2022): The power losses and damages incurred in transmission, substation, distribution, and marketing during the transmission of electrical energy from power plants to customers. With the rapid development of renewable energy, the distribution system must strengthen its ability to absorb and dispatch renewable energy.

3 Spherical fuzzy set theory

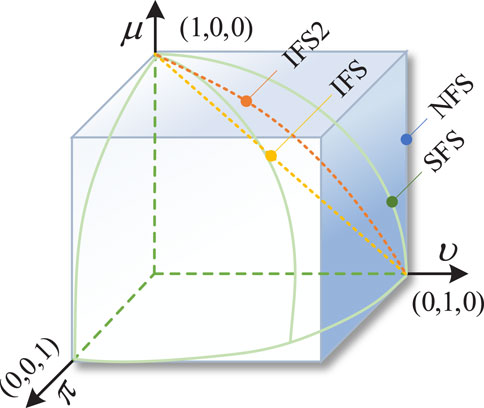
Fuzzy sets are powerful tools for dealing with uncertain information and are widely used in areas such as evaluation decision making (Yu et al., 2021). Spherical Fuzzy Sets (SFSs) is a concept that extends the traditional fuzzy sets, which contains extended forms of traditional fuzzy sets such as Intuitionistic Fuzzy Sets (IFS), Intuitionistic Fuzzy Sets of the second type (IFS2) and Neutrosophic Fuzzy Sets (NFS), providing more powerful tools for decision analysis, data processing, and other fields. Figure 1 illustrates the differences between IFS, IFS2, NFS, and SFS. For example, the affiliation dimension for the rating “absolutely much important” can be set to be close to 0.9, and the neutrality and non-affiliation dimensions can be set to be close to 0.1.

Figure 1

Figure 1. Geometric representation of IFS, IFS2, NFS, and SFS.

First, an SFS can transform semantic evaluation into fuzzy numbers, providing a wider value domain for each parameter, better dealing with uncertainty and expert’s hesitation, and accurately reflecting decision maker’s preferences and judgments, which is a significant feature of an SFS that distinguishes them from other fuzzy sets. In addition, decision makers often rely on subjective judgment and experience when assessing the contribution of regional distribution grids to carbon emission reduction. An SFS can allow decision makers to express their subjective judgments in a more flexible and precise way, thus better reflecting the actual situation. Finally, an SFS can enhance decision support by helping decision makers better understand and analyze the relationships between various factors and thus make more rational decisions.

Therefore, this article adopts the SFS to accurately characterize the evaluation information of high-dimensional uncertainty indicators in the carbon emission reduction contribution of RDNs.

3.1 Definition of spherical fuzzy sets

$AD=\left\{A{D}_t|t=1,2,...,K\right\}$ is the set of semantic evaluations provided by the decision expert $D_t$. $A{D}_t$ is converted to a spherical fuzzy number ${\stackrel{\sim }{A}}_S$ on the argument domain $U$, as shown in Equation 3.

${\stackrel{\sim }{A}}_S=\left\{u,\left({\mu }_{{\stackrel{\sim }{A}}_S}\left(u\right),{\upsilon }_{{\stackrel{\sim }{A}}_S}\left(u\right),{\pi }_{{\stackrel{\sim }{A}}_S}\left(u\right)\right)|u\in U\right\}.(3)$

${\mu }_{{\stackrel{\sim }{A}}_S}:U\in \left[0,1\right]{\upsilon }_{{\stackrel{\sim }{A}}_S}:U\in \left[0,1\right]{\pi }_{{\stackrel{\sim }{A}}_S}:U\in \left[0,1\right].(4)$

The values ${\mu }_{{\stackrel{\sim }{A}}_S}$, ${\upsilon }_{{\stackrel{\sim }{A}}_S}$, and ${\pi }_{{\stackrel{\sim }{A}}_S}$, which are the degree of subordination, non-subordination, and hesitation of $u$ to ${\stackrel{\sim }{A}}_S$, respectively, are satisfied:

$0\le {\mu }_{{\stackrel{\sim }{A}}_S}^2\left(u\right)+{\upsilon }_{{\stackrel{\sim }{A}}_S}^2\left(u\right)+{\pi }_{{\stackrel{\sim }{A}}_S}^2\left(u\right)\le 1,\forall u\in U.(5)$

3.2 Operations on spherical fuzzy numbers

The basic operations of ${\stackrel{\sim }{A}}_S=\left({\mu }_{{\stackrel{\sim }{A}}_S}\left(u\right),{\upsilon }_{{\stackrel{\sim }{A}}_S}\left(u\right),{\pi }_{{\stackrel{\sim }{A}}_S}\left(u\right)\right)$ and ${\stackrel{\sim }{B}}_S=\left({\mu }_{{\stackrel{\sim }{A}}_S}\left(u\right),{\upsilon }_{{\stackrel{\sim }{A}}_S}\left(u\right),{\pi }_{{\stackrel{\sim }{A}}_S}\left(u\right)\right)$ for any two spherical fuzzy numbers ${\stackrel{\sim }{A}}_S$ and ${\stackrel{\sim }{B}}_S$, where $\lambda$ is real and $\lambda \ge 0$, are as follows:

${\stackrel{\sim }{A}}_S\oplus {\stackrel{\sim }{B}}_S=\left\{{\left({{\mu }^2}_{{\stackrel{\sim }{A}}_S}+{{\mu }^2}_{{\stackrel{\sim }{B}}_S}-{{\mu }^2}_{{\stackrel{\sim }{A}}_S}{{\mu }^2}_{{\stackrel{\sim }{B}}_S}\right)}^{1/2}\right.,v_{{\stackrel{\sim }{A}}_S}{v}_{{\stackrel{\sim }{B}}_S},\left.{\left[\left(1-{{\mu }^2}_{{\stackrel{\sim }{B}}_S}\right){{\pi }^2}_{{\stackrel{\sim }{A}}_S}+\left(1-{{\mu }^2}_{{\stackrel{\sim }{A}}_S}\right){{\pi }^2}_{{\stackrel{\sim }{B}}_S}-{{\pi }^2}_{{\stackrel{\sim }{A}}_S}{{\pi }^2}_{{\stackrel{\sim }{B}}_S}\right]}^{1/2}\right\},(6)$

$\lambda \cdot {\stackrel{\sim }{A}}_S=\left\{\sqrt{1-{\left(1-{{\mu }^2}_{{\stackrel{\sim }{A}}_S}\right)}^{\lambda }},v_{{\stackrel{\sim }{A}}_S}^{\lambda },\right.\left.\sqrt{{\left(1-{{\mu }^2}_{{\stackrel{\sim }{A}}_S}\right)}^{\lambda }-{\left(1-{{\mu }^2}_{{\stackrel{\sim }{A}}_S}-{{\pi }^2}_{{\stackrel{\sim }{A}}_S}\right)}^{\lambda }}\right\},(7)$

where $\lambda >0$. The spherical distance between ${\stackrel{\sim }{A}}_S$ and ${\stackrel{\sim }{B}}_S$ is expressed as

$D\left({\stackrel{\sim }{A}}_S,{\stackrel{\sim }{B}}_S\right)=\arccos \left\{1-\frac{1}{2}\left[{\left({{\mu }_{{\stackrel{\sim }{A}}_S}}^2-{{\mu }_{{\stackrel{\sim }{B}}_S}}^2\right)}^2\right.\right.\left.\left.+{\left({v_{{\stackrel{\sim }{A}}_S}}^2-{v_{{\stackrel{\sim }{B}}_S}}^2\right)}^2+{\left({{\pi }_{{\stackrel{\sim }{A}}_S}}^2-{{\pi }_{{\stackrel{\sim }{B}}_S}}^2\right)}^2\right]\right\},(8)$

where the defining factor $\frac{2}{\pi }$ makes the spherical distance between the spherical fuzzy numbers to be $\left[0,1\right]$, instead of $\left[0,\frac{2}{\pi }\right]$ because ${\mu }_{{\stackrel{\sim }{A}}_S}^2\left(u\right)+v_{{\stackrel{\sim }{A}}_S}^2\left(u\right)+{\pi }_{{\stackrel{\sim }{A}}_S}^2\left(u\right)=1$, which is obtained by simplification:

$D\left({\stackrel{\sim }{A}}_S,{\stackrel{\sim }{B}}_S\right)=\frac{2}{\pi }{\displaystyle \sum _{i=1}^n}\arccos \left[{\mu }_{{\stackrel{\sim }{A}}_S}\left(u_i\right){\mu }_{{\stackrel{\sim }{B}}_S}\left(u_i\right)\right.+v_{{\stackrel{\sim }{A}}_S}\left(u_i\right)v_{{\stackrel{\sim }{B}}_S}\left(u_i\right)+{\pi }_{{\stackrel{\sim }{A}}_S}\left(u_i\right){\pi }_{{\stackrel{\sim }{B}}_S}\left(u_i\right)].(9)$

The spherical weighted arithmetic mean operation of ${\stackrel{\sim }{A}}_{Si}\left(i=1,2,...,n\right)$ is as follows

$\begin{array}{l}{M}_w\left(A_{S1},A_{S2},...,A_{Sn}\right)=w_1{A}_{S1}+w_2{A}_{S2}+...+w_n{A}_{Sn}\\ =\left\{\sqrt{1-{{\displaystyle \prod _{i=1}^n}\left(1-{\mu }_{A_{Si}}^2\right)}^{w_i}},{\displaystyle \prod _{i=1}^n}{v}_{A_{Si}}^{w_i}\right.,\left.\sqrt{{{\displaystyle \prod _{i=1}^n}\left(1-{\mu }_{A_{Si}}^2\right)}^{w_i}-{{\displaystyle \prod _{i=1}^n}\left(1-{\mu }_{A_{Si}}^2-{\pi }_{A_{Si}}^2\right)}^{w_i}}\right\},\end{array}(10)$

where $w_i\in \left[0,1\right]$, ${\displaystyle {\sum }_{i=1}^n}{w}_i=1$. The clear value of the spherical fuzzy number ${\stackrel{\sim }{A}}_S$ is calculated as follows:

$\mathit{Def}\left({\stackrel{\sim }{A}}_S\right)={\left({\mu }_{{\stackrel{\sim }{A}}_S}-{\pi }_{{\stackrel{\sim }{A}}_S}\right)}^2-{\left(v_{{\stackrel{\sim }{A}}_S}-{\pi }_{{\stackrel{\sim }{A}}_S}\right)}^2.(11)$

4 Evaluation method for carbon emission reduction contribution of RDNs

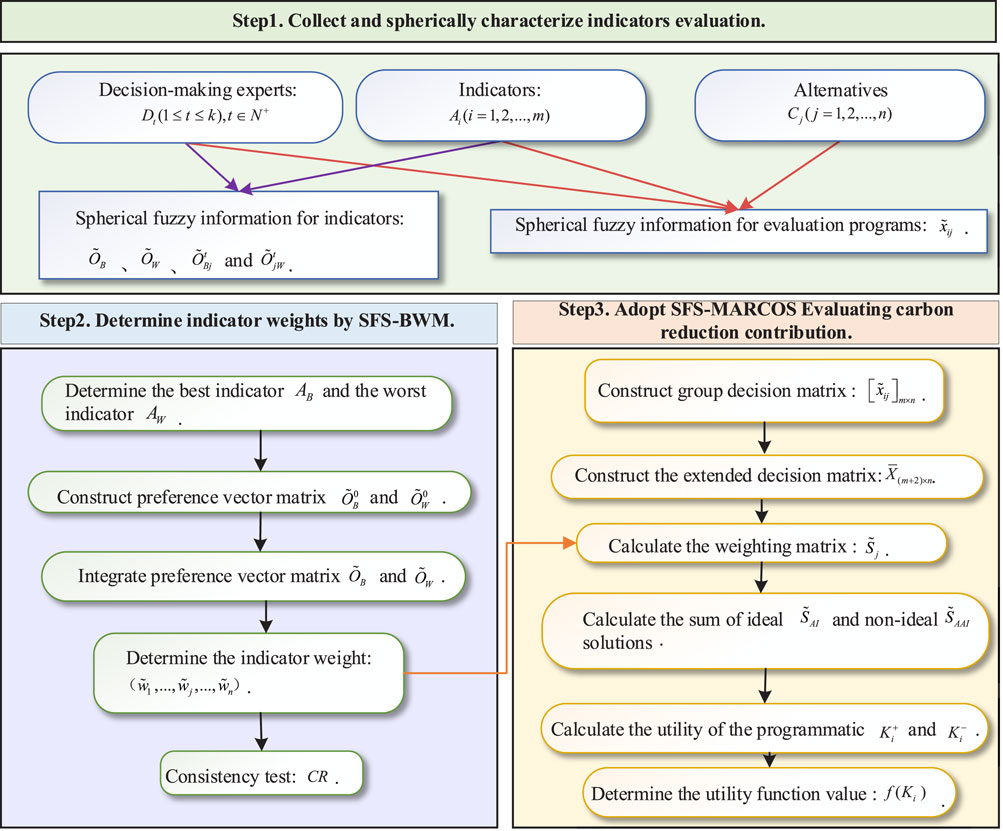
Considering the uncertainty of indicator evaluation, a hybrid model is proposed for analyzing the carbon emission reduction contribution of RDNs. The evaluation process consists of three stages, as shown in Figure 2. When evaluating the carbon emission reduction contribution of urban RDNs, the alternative to be evaluated is $C_j\left(j=1,2,...,n\right)$, the evaluation indicator is $A_i\left(i=1,2,...,m\right)$, and the decision-making expert is $D_t\left(1\le t\le k\right),t\in N^{+}$. According to Table 2, the semantic evaluation information of qualitative indicators is converted into spherical fuzzy numbers, where ${\stackrel{\sim }{x}}_{t,ij}=\left({\mu }_{t,ij},v_{t,ij},{\pi }_{t,ij}\right)$ denotes the spherical fuzzy evaluation information of the expert $D_t$ for regional distribution network $C_j$ in indicator $A_i$. The decision assembly information ${\stackrel{\sim }{x}}_{ij}$ is denoted as:

${\stackrel{\sim }{x}}_{ij}={\displaystyle \sum _{t=1}^k}{w}_t{\stackrel{\sim }{x}}_{t,ij},(12)$

where $w_t$ represents the expert’s ability in the relevant domain and satisfies $w_t\ge 0$, ${\displaystyle {\sum }_{t=1}^k}{w}_t=1$. The degree of expert semantic evaluation can be compared by using Equations 9 and 10.

Figure 2

Figure 2. Evaluation process of carbon emission reduction contribution of RDNs.

Table 2

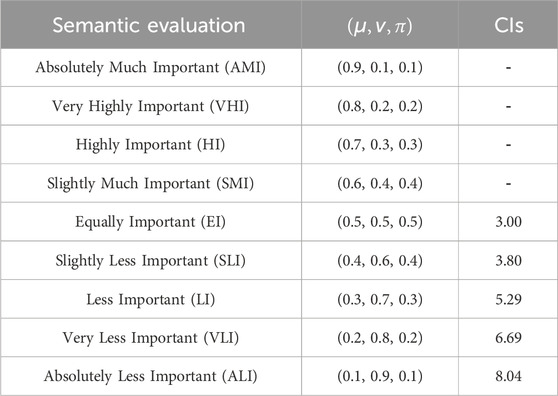
Table 2. Semantic evaluation and corresponding spherical fuzzy numbers applied to SFS-BWM and SFS-MARCOS.

4.1 Measurement of indicator weights

The weights play a crucial role in the model-solving process; however, the constructed indicator system contains a variety of uncertain information. Accordingly, accurate quantification of indicator weights will become a key problem in determining carbon emission reduction contributions.

The evaluation indicator system constructed in this study has many indicators. The commonly used indicator weight determination methods (for example, hierarchical analysis) are cumbersome and complex to calculate, so this article adopts the BWM to prioritize the priority ranking of the indicator assignment weights to obtain consistent results through less pairwise comparison information (Xiao et al., 2023). In addition, the “best-worst” comparison can more directly reflect the relative importance of each criterion, which can help researchers identify the key influencing factors more quickly and formulate targeted emission reduction measures (Jia et al., 2019). The BWM method ensures the scientificity and rationality of the decision-making results through steps such as consistency checking, which helps reduce the influence of subjective judgments on the decision-making results and improves the objectivity and accuracy of the study.

Therefore, the BWM is expanded into the SFS to develop a new method of determining indicator weights. The specific steps are as follows:

a. For the constructed evaluation indicator system $A_i$, determine the best and the worst indicators, denoted as $A_B$ and $A_W$, respectively.

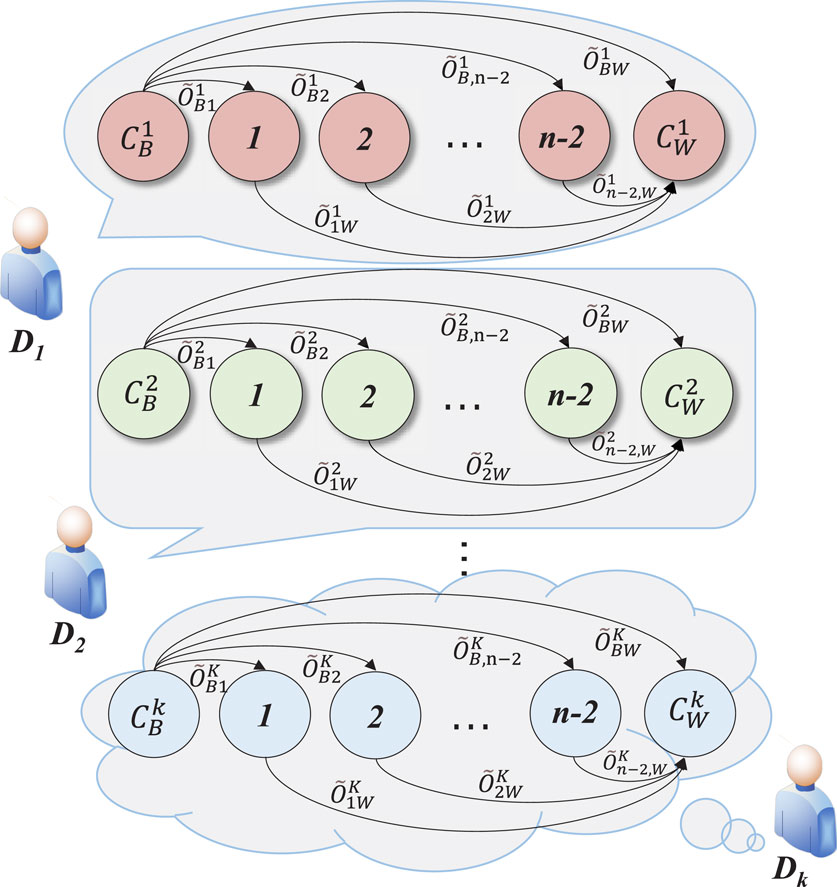
b. Construct the preference vector matrices ${\stackrel{\sim }{O}}_B^0$ and ${\stackrel{\sim }{O}}_W^0$.

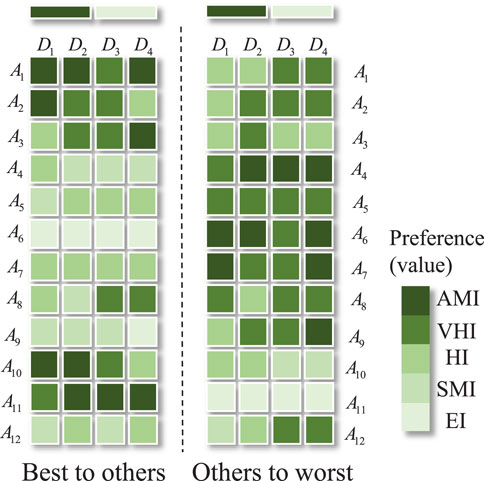
The preference comparison shown in Figure 3 is carried out and converted into the corresponding spherical fuzzy numbers, as shown in Table 2.

Figure 3

Figure 3. Preferential comparison.

${\stackrel{\sim }{O}}_B^t$ and ${\stackrel{\sim }{O}}_W^t$ separately represent the vector of fuzzy preferences of the best indicator $A_B$ over the other indicators provided, and the other indicators over the worst indicator $A_W$ provided by the expert $D_t$. The form of ${\stackrel{\sim }{O}}_B^t$ is as follows:

${\stackrel{\sim }{O}}_B^t=\left({\stackrel{\sim }{O}}_{B1}^t,{\stackrel{\sim }{O}}_{B2}^t,...,{\stackrel{\sim }{O}}_{Bn}^t\right),(13)$

where ${\stackrel{\sim }{O}}_{Bj}^t=\left({\mu }_{Bj}^t,v_{Bj}^t,{\pi }_{Bj}^t\right)$. Integrate the $K$ fuzzy preference vectors ${\stackrel{\sim }{O}}_B^t\left(t=1,2,...,k\right)$ provided by experts in the matrix ${\stackrel{\sim }{O}}_B^0$. It is as follows:

${\stackrel{\sim }{O}}_B^0=\left[\begin{array}{cccc}{\stackrel{\sim }{O}}_{B1}^1& {\stackrel{\sim }{O}}_{B2}^1& \cdots & {\stackrel{\sim }{O}}_{Bn}^1\\ {\stackrel{\sim }{O}}_{B1}^2& {\stackrel{\sim }{O}}_{B2}^2& \cdots & {\stackrel{\sim }{O}}_{Bn}^2\\ ⋮& ⋮& \ddots & ⋮\\ {\stackrel{\sim }{O}}_{B1}^K& {\stackrel{\sim }{O}}_{B2}^K& \cdots & {\stackrel{\sim }{O}}_{Bn}^K\end{array}\right].(14)$

Similarly, the fuzzy preference vectors of other indicators are compared to the worst indicator ${\stackrel{\sim }{O}}_W^t\left(t=1,2,...,k\right)$ in matrix ${\stackrel{\sim }{O}}_W^0$. It is as follows:

${\stackrel{\sim }{O}}_W^0=\left[\begin{array}{cccc}{\stackrel{\sim }{O}}_{1W}^1& {\stackrel{\sim }{O}}_{2W}^1& \cdots & {\stackrel{\sim }{O}}_{nW}^1\\ {\stackrel{\sim }{O}}_{1W}^2& {\stackrel{\sim }{O}}_{2W}^2& \cdots & {\stackrel{\sim }{O}}_{nW}^2\\ ⋮& ⋮& \ddots & ⋮\\ {\stackrel{\sim }{O}}_{1W}^K& {\stackrel{\sim }{O}}_{2W}^K& \cdots & {\stackrel{\sim }{O}}_{nW}^K\end{array}\right].(15)$

c. Integrate the preference vector matrices ${\stackrel{\sim }{O}}_B$ and ${\stackrel{\sim }{O}}_W$.

According to Equations 3–7, integrate matrix ${\stackrel{\sim }{O}}_B^0$ and matrix ${\stackrel{\sim }{O}}_W^0$ into matrix ${\stackrel{\sim }{O}}_B$ and matrix ${\stackrel{\sim }{O}}_W$ as follows:

${\stackrel{\sim }{O}}_B=\left({\stackrel{\sim }{O}}_{B1},{\stackrel{\sim }{O}}_{B2},...,{\stackrel{\sim }{O}}_{Bn}\right),(16)$

${\stackrel{\sim }{O}}_W=\left({\stackrel{\sim }{O}}_{1W},{\stackrel{\sim }{O}}_{2W},...,{\stackrel{\sim }{O}}_{nW}\right),(17)$

where ${\stackrel{\sim }{O}}_{BB}=\left(0.5,0.5,0.5\right)$, ${\stackrel{\sim }{O}}_{WW}=\left(0.5,0.5,0.5\right)$, ${\stackrel{\sim }{O}}_{Bj}$, and ${\stackrel{\sim }{O}}_{jW}$ are calculated as follows:

${\stackrel{\sim }{O}}_{Bj}=\frac{1}{k}{\displaystyle \sum _{t=1}^k}{\stackrel{\sim }{O}}_{Bj}^t=\left\{\sqrt{1-{\left(1-{\mu }_{Bj}^2\right)}^{\frac{1}{k}}},v_{Bj}^{\frac{1}{k}}\right.\left.,\sqrt{{\left(1-{\mu }_{Bj}^2\right)}^{\frac{1}{k}}-{\left(1-{\mu }_{Bj}^2-{\pi }_{Bj}^2\right)}^{\frac{1}{k}}}\right\}.(18)$

${\stackrel{\sim }{O}}_{jW}=\frac{1}{k}{\displaystyle \sum _{t=1}^k}{\stackrel{\sim }{O}}_{jW}^t=\left\{\sqrt{1-{\left(1-{\mu }_{jW}^2\right)}^{\frac{1}{k}}},v_{jW}^{\frac{1}{k}}\right.\left.,\sqrt{{\left(1-{\mu }_{jW}^2\right)}^{\frac{1}{k}}-{\left(1-{\mu }_{jW}^2-{\pi }_{jW}^2\right)}^{\frac{1}{k}}}\right\}.(19)$

d. Determination of indicator weights.

Calculate the clear values of matrix ${\stackrel{\sim }{O}}_B$ and matrix ${\stackrel{\sim }{O}}_W$ as follows:

$R\left({\stackrel{\sim }{O}}_B\right)=\left(R\left({\stackrel{\sim }{O}}_{B1}\right),R\left({\stackrel{\sim }{O}}_{B2}\right),...,R\left({\stackrel{\sim }{O}}_{Bn}\right)\right),(20)$

$R\left({\stackrel{\sim }{O}}_W\right)=\left(R\left({\stackrel{\sim }{O}}_{1W}\right),R\left({\stackrel{\sim }{O}}_{2W}\right),...,R\left({\stackrel{\sim }{O}}_{nW}\right)\right),(21)$

where ${\stackrel{\sim }{w}}_B$ is the weight of the best indicator $A_B$, ${\stackrel{\sim }{w}}_W$ is the weight of the worst indicator $A_W$, and ${\stackrel{\sim }{w}}_j$ is the weight of the indicator $A_i$. R(⋅) is obtained from Equation 11 ${\stackrel{\sim }{w}}_j$ is satisfied:

$\min \left|\frac{{\stackrel{\sim }{w}}_B}{{\stackrel{\sim }{w}}_j}-R\left({\stackrel{\sim }{O}}_{Bj}\right)\right|.(22)$

$\min \left|\frac{{\stackrel{\sim }{w}}_j}{{\stackrel{\sim }{w}}_W}-R\left({\stackrel{\sim }{O}}_{jW}\right)\right|.(23)$

It implies that the optimal weights of the indicators are consistent between the optimal indicators compared to the other indicators and between the other indicators compared to the worst indicators as follows:

$\frac{{\stackrel{\sim }{w}}_B}{{\stackrel{\sim }{w}}_j}=R\left({\stackrel{\sim }{O}}_{Bj}\right).(24)$

$\frac{{\stackrel{\sim }{w}}_j}{{\stackrel{\sim }{w}}_W}=R\left({\stackrel{\sim }{O}}_{jW}\right).(25)$

Let the objective value be $\stackrel{\sim }{\xi }$ and construct an optimization model to determine the best weights of the indicators. It is as follows:

$\begin{array}{l}\min \stackrel{\sim }{\xi }\\ s.t.\left\{\begin{array}{l}\left|w_B/w_j-R\left({\stackrel{\sim }{O}}_{Bj}\right)\right|\le \stackrel{\sim }{\xi }\\ \left|w_j/w_W-R\left({\stackrel{\sim }{O}}_{jW}\right)\right|\le \stackrel{\sim }{\xi .}\\ {\displaystyle \sum _{t=1}^k}{\stackrel{\sim }{w}}_j=1\\ \begin{array}{l}0\le {\stackrel{\sim }{w}}_j\le 1\\ j=1,2,...,n\end{array}\end{array}\right.\end{array}(26)$

Solve the model by Lingo software to determine the indicator weight set $\left({\stackrel{\sim }{w}}_1,...,{\stackrel{\sim }{w}}_j,...,{\stackrel{\sim }{w}}_n\right)$.

e. Consistency test.

The consistency ratio ($CR$) is a key indicator to test the consistency of pairwise comparisons, and the consistency indices ($C{I}_s$) under different semantic evaluations have been given, as shown in Table 2. The consistency ratio $CR$ is determined from the $C{I}_s$ and the target value ${\xi }^{*}$. The formula is given below:

$CR=\frac{{\xi }^{*}}{CI,}(27)$

where $CR$ is closer to 0, indicating higher consistency, and $CR$ is closer to 1, indicating lower consistency, where $CR\in \left[0,1\right]$.

4.2 Evaluation of carbon emission reduction contribution based on SFS-MARCOS

Based on multi-dimensional indicator weights, the multi-attribute decision-making method is extended into the spherical fuzzy environment to calculate the carbon emission reduction contribution of RDNs. Considering that the decision-making process needs to deal with a large and highly uncertain amount of information, this research applies the MARCOS method. It is compared with common multi-attribute decision-making methods such as the multi-attributive border approximation area comparison (MABAC), the fuzzy comprehensive evaluation (FCE), the complex proportional assessment (COPRAS), and the preference ranking organization method for enrichment evaluations (PROMETHEE)-Ι and PROMETHEE-Ⅱ (Jia et al., 2019; Zhang et al., 2024; Rani et al., 2020; Seikh and Mandal, 2023; Yu et al., 2023).

MARCOS considers the inverse ideal solution and the ideal solution in the formation of the initial matrix, and at the same time, covers many indicators and decision scenarios and maintains stability (Thangaraj et al., 2023). Therefore, this article extends MARCOS into an SFS environment to determine the contribution of RDNs to carbon emission reduction. The specific steps are as follows:

a. Constructing a group decision matrix ${\left[{\stackrel{\sim }{x}}_{ij}\right]}_{m\times n}$.

${\left[{\stackrel{\sim }{x}}_{ij}\right]}_{m\times n}=\begin{array}{c}{A}_1\\ A_2\\ ⋮\\ A_m\end{array}\begin{array}{c}\begin{array}{cccc}{C}_1& C_2& \cdots & C_n\end{array}\\ \left[\begin{array}{cccc}{\stackrel{\sim }{x}}_{11}& {\stackrel{\sim }{x}}_{12}& \cdots & {\stackrel{\sim }{x}}_{1n}\\ {\stackrel{\sim }{x}}_{21}& {\stackrel{\sim }{x}}_{22}& \cdots & {\stackrel{\sim }{x}}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\stackrel{\sim }{x}}_{m1}& {\stackrel{\sim }{x}}_{m2}& \cdots & {\stackrel{\sim }{x}}_{mn}\end{array}\right],\end{array}(28)$

where $A_m$ denotes the $m.th$ type of indicator and $C_n$ denotes the $n.th$ alternative. In addition, ${\stackrel{\sim }{x}}_{ij}=\left({\mathrm{\mu }}_{ij},v_{ij},{\mathrm{\pi }}_{ij}\right)$, ${\stackrel{\sim }{x}}_{ij}$ is calculated as follows:

${\stackrel{\sim }{x}}_{ij}=\frac{1}{k}{\displaystyle \sum _{t=1}^k}{\stackrel{\sim }{x}}_{ij.}^t(29)$

b. Construct the extended population decision matrix ${\overline{X}}_{\left(m+2\right)\times n}$.

The ideal solution $AI$ and anti-ideal solution $AAI$ are introduced into the group decision matrix ${\left[{\stackrel{\sim }{x}}_{ij}\right]}_{m\times n}$ to obtain the extended group decision matrix:

${\overline{X}}_{\left(m+2\right)\times n}=\begin{array}{c}AAI\\ A_1\\ A_2\\ ⋮\\ \begin{array}{l}{A}_m\\ AI\end{array}\end{array}\begin{array}{c}\begin{array}{cccc}{C}_1& C_2& \cdots & C_n\end{array}\\ \left[\begin{array}{cccc}\begin{array}{l}{\stackrel{\sim }{x}}_{aa1}\\ {\stackrel{\sim }{x}}_{11}\end{array}& \begin{array}{l}{\stackrel{\sim }{x}}_{aa2}\\ {\stackrel{\sim }{x}}_{12}\end{array}& \cdots & \begin{array}{l}{\stackrel{\sim }{x}}_{aan}\\ {\stackrel{\sim }{x}}_{1n}\end{array}\\ {\stackrel{\sim }{x}}_{21}& {\stackrel{\sim }{x}}_{22}& \cdots & {\stackrel{\sim }{x}}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ \begin{array}{l}{\stackrel{\sim }{x}}_{m1}\\ {\stackrel{\sim }{x}}_{a1}\end{array}& \begin{array}{l}{\stackrel{\sim }{x}}_{m2}\\ {\stackrel{\sim }{x}}_{a2}\end{array}& \cdots & \begin{array}{l}{\stackrel{\sim }{x}}_{mn}\\ {\stackrel{\sim }{x}}_{an}\end{array}\end{array}\right],\end{array}(30)$

where $AI$ represents the ideal solution of indicator $A_j$, and $AAI$ represents the anti-ideal solution of indicator $A_j$. ${\stackrel{\sim }{x}}_{aj}$ and ${\stackrel{\sim }{x}}_{aaj}$ are calculated as follows:

$\begin{array}{l}{\stackrel{\sim }{x}}_{aj}=\left({\mu }_{aj},v_{aj},{\pi }_{aj}\right)\\ =\left\{\begin{array}{c}\left(\min {\mu }_{ij},\max v_{ij},\min {\pi }_{ij}\right),\begin{array}{cc}if& j\in C\end{array},\\ \left(\max {\mu }_{ij},\min v_{ij},\min {\pi }_{ij}\right),\begin{array}{cc}if& j\in D\end{array}\end{array}\right.\end{array}(31)$

$\begin{array}{l}{\stackrel{\sim }{x}}_{aaj}=\left({\mu }_{aaj},v_{aaj},{\pi }_{aaj}\right)\\ =\left\{\begin{array}{c}\left(\max {\mu }_{ij},\min v_{ij},\min {\pi }_{ij}\right),\begin{array}{cc}if& j\in C\end{array}\\ \left(\min {\mu }_{ij},\max v_{ij},\min {\pi }_{ij}\right),\begin{array}{cc}if& j\in D\end{array}\end{array}\right.\end{array},(32)$

where $D$ and $C$ denote the benefit and cost indicators, respectively.

c. Calculate the weighting matrix ${\stackrel{\sim }{S}}_j$.

${\stackrel{\sim }{S}}_j=w_1{x}_{1j}+...+w_i{x}_{ij}+...+w_m{x}_{mj}\left(j=1,2,...,n\right).(33)$

In the formula, ${\stackrel{\sim }{S}}_j$ is in the form of $\left({\mu }_i,v_i,{\pi }_i\right)$. $w_i{x}_{ij}$ is calculated by Equation 10 as follows:

$w_i{x}_{ij}=\left.\left\{\sqrt{1-{\left(1-{{\mu }^2}_{{\stackrel{\sim }{x}}_{ij}}\right)}^{w_i}},\right.v_{{\stackrel{\sim }{x}}_{ij}}^{w_i},\sqrt{{\left(1-{\mu }_{{\stackrel{\sim }{x}}_{ij}}^2\right)}^{w_i}-{\left(1-{\mu }_{{\stackrel{\sim }{x}}_{ij}}^2-{\pi }_{{\stackrel{\sim }{x}}_{ij}}^2\right)}^{w_i}}\right\}.(34)$

d. The sum ${\stackrel{\sim }{S}}_{AAI}$, ${\stackrel{\sim }{S}}_{AI}$ of ideal and non-ideal solutions is calculated:

${\stackrel{\sim }{S}}_{AAI}=w_1{x}_{AAI1}+...+w_i{x}_{AAIi}+...+w_m{x}_{AA\text{Im}}={\displaystyle \sum _{i=1}^m}{w}_i{\stackrel{\sim }{x}}_{AAIi}.(35)$

${\stackrel{\sim }{S}}_{AI}=w_1{x}_{AI1}+...+w_i{x}_{AIi}+...+w_m{x}_{A\text{Im}}={\displaystyle \sum _{i=1}^m}{w}_i{\stackrel{\sim }{x}}_{AIi}.(36)$

e. The utility degree of the solution is calculated:

$K_i^{+}=\frac{R\left({\stackrel{\sim }{S}}_i\right)}{R\left({\stackrel{\sim }{S}}_{aai}\right)}.(37)$

$K_i^{-}=\frac{R\left({\stackrel{\sim }{S}}_i\right)}{R\left({\stackrel{\sim }{S}}_{ai}\right).}(38)$

In the formula, $K_i^{+}$ and $K_i^{-}$ represent the utility degree of indicator $A_i$ associated with ideal solution $AI$ and anti-ideal solution $AAI$, respectively, $R\left({\stackrel{\sim }{S}}_i\right)$ represents the clear value of ${\stackrel{\sim }{S}}_i$.

f. Determine the utility function value $f\left(K_i\right)$.

$f\left(K_i\right)=\frac{K_i^{+}+K_i^{-}}{1+\frac{1-f\left(K_i^{+}\right)}{f\left(K_i^{+}\right)}+\frac{1-f\left(K_i^{-}\right).}{f\left(K_i^{-}\right)}}(39)$

where $f\left(K_i^{+}\right)$ and $f\left(K_i^{-}\right)$ denote the utility functions of the ideal solution $AI$ and the anti-ideal solution $AAI$, respectively. It is shown below:

$f\left(K_i^{+}\right)=\frac{K_i^{+}}{K_i^{+}+K_i^{-}}.(40)$

$f\left(K_i^{-}\right)=\frac{K_i^{-}}{K_i^{+}+K_i^{-.}}(41)$

Finally, based on Equations 12–41, the utility function values of the calculated solutions, $f\left(K_i\right)$ are used to rank the perceived carbon emission reduction contributions of the RDNs.

5 Case study

5.1 Case overview and model implementation

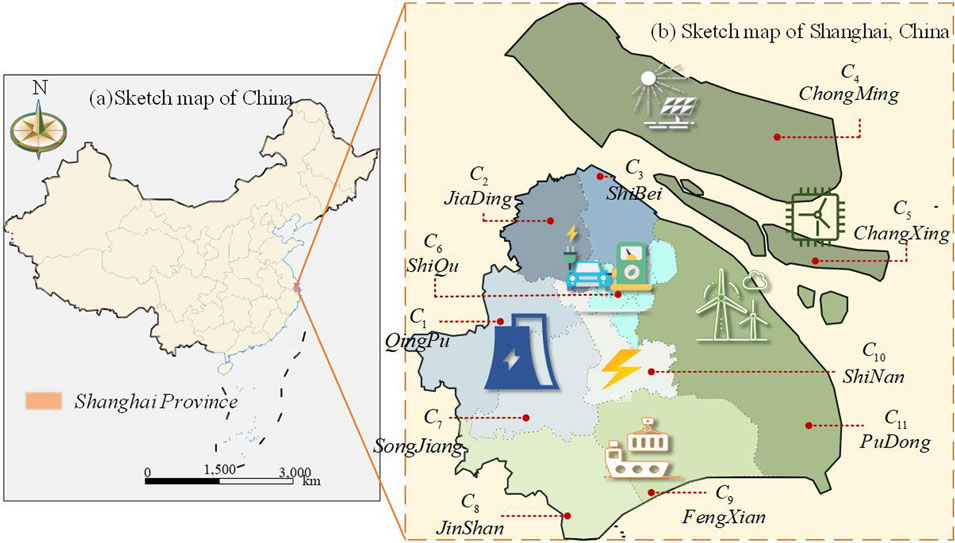
Shanghai has promoted renewable energy and a circular economy in Chongming Island, where distributed power supply, new energy generation, and intelligent operation and maintenance have achieved certain successes, driving the city’s economy toward low-carbon development. However, the significant contribution of regional carbon emission reduction is not currently perceived in depth, and the role of corresponding mitigation initiatives to support the green transformation of cities is not clearly defined. Therefore, this article selects 11 RDNs in Shanghai for analysis.

The evaluation system contains 12 indicators. $A_1$, $A_4$–$A_{11}$ are revenue-based indicators, and $A_2$, $A_3$, and $A_{12}$ are cost-based indicators. The decision-making expert group consists of the director of the finance department of the Chongming area, the deputy dean of the School of Economics and Management of Shanghai University of Electric Power, the head of the low-carbon evaluation team of the Economic Research Institute, and the personnel of the operation and maintenance center of Shibei Area, who provide pairwise comparative information on the indicators and information on the evaluation of the alternatives, as shown in Figures 5, 6., respectively. After their discussion, it was determined that the best indicator was $A_6$ and the worst indicator was $A_{11}$. The case study adopts the SFS-BWM and SFS-MARCOS modeling proposed in this article to quantify the carbon emission reduction contribution of RDNs and analyze the results, and Figure 4 shows the area of each RDN.

a. Conversion of pairwise comparison preference information and alternative evaluation information into spherical fuzzy numbers.

Figure 4

Figure 4. Area of RDNs in Shanghai.

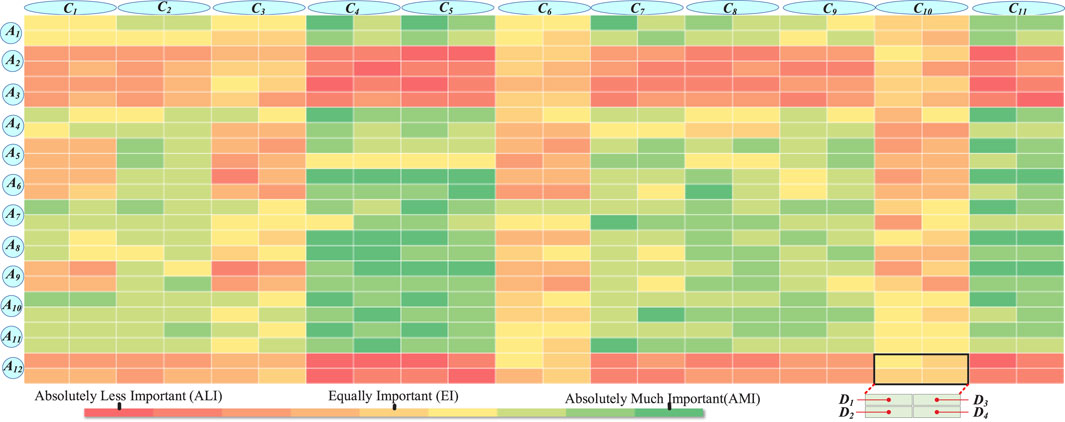
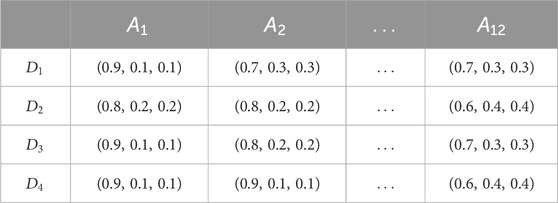
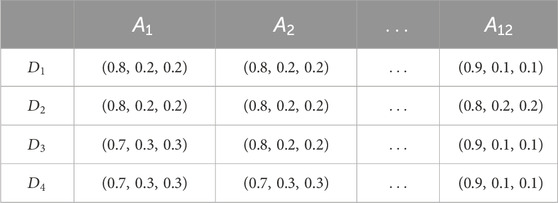
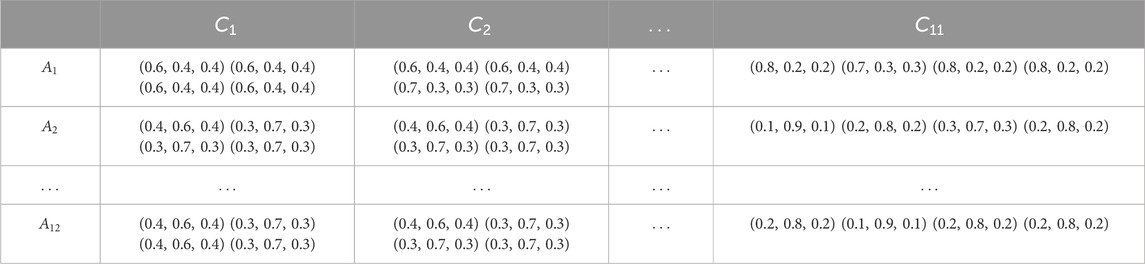
The pairwise comparison preference information and alternative evaluation information provided by the experts, as shown in Figures 5, 6, respectively, are converted into spherical fuzzy numbers, as shown in Tables 3–5. ${\stackrel{\sim }{O}}_{7W}^1$ is denoted as (0.9.0.1, 0.1), and ${\stackrel{\sim }{x}}_{11}^1$ is denoted as (0.6, 0.4, 0.4).

b. Integration of pairwise comparative preference information and alternative indicator performance evaluation information provided by experts.

Figure 5

Figure 5. Semantic evaluation information from experts for Shanghai RDN indicators.

Figure 6

Figure 6. Expert determination of pairwise comparative preference information.

Table 3

Table 3. Preferences of the best indicator over other indicators.

Table 4

Table 4. Preferences of other indicators over the worst indicator.

Table 5

Table 5. Information on expert evaluation of the performance of alternative indicators.

The pairwise comparative preferences and indicator performance evaluations provided by the four experts are integrated to generate the group preference information of the best indicators relative to other indicators ${\stackrel{\sim }{O}}_{Bi}$, the group spherical fuzzy preference information of other indicators for the worst indicators ${\stackrel{\sim }{O}}_{iW}$, and the group evaluation information of the RDN ${\stackrel{\sim }{x}}_{ij}$.

c. Indicator weight calculation.

The clear values of $R\left({\stackrel{\sim }{O}}_{Bi}\right)$ and $R\left({\stackrel{\sim }{O}}_{iW}\right)$ for the vectors ${\stackrel{\sim }{O}}_{Bi}$ and ${\stackrel{\sim }{O}}_{iW}$, are generated, and the weights of the indicators ${\stackrel{\sim }{w}}_j$ are determined by Lingo calculation, as shown in Figure 7.

d. Consistency test.

Figure 7

Figure 7. Indicator weight parameters.

The target value $\stackrel{\sim }{\xi }$ is obtained as 0.18 by using Equation 26, and the consistency ratio $CR$ is calculated as 0.038 by using Equation 27, which is much smaller than 1 and close to 0. This low value indicates that BWM shows strong consistency in determining the weights of indicators.

e. Determination of ideal solution $AI$ and anti-ideal solution $AAI$.

Considering the influence of the indicators on the contribution of areas to carbon emission reduction, the ideal solution $AI$ and the anti-ideal solution $AAI$ of the indicator system are determined.

f. Calculate the ideal solution $S\left(AI\right)$ and anti-ideal solution $S\left(AAI\right)$.

The indicator weights obtained in step c are brought into the operation of a spherical fuzzy number to obtain the ideal solution $S\left(AI\right)$ and the anti-ideal solution $S\left(AAI\right)$ of each indicator. The clear values of the ideal solution $S\left(AI\right)$ and the anti-ideal solution $S\left(AAI\right)$ are obtained through Equation 6.

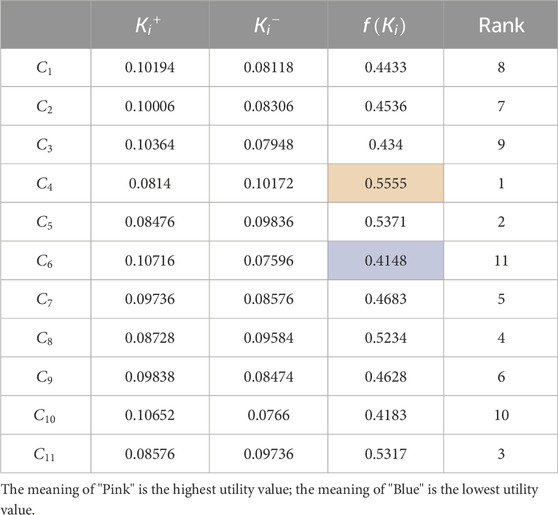
g. Calculate and rank the utility function value $f\left(K_i\right)$.

Equations 37, 38 are used to obtain the utility degree $K_i^{+}$ of alternative $A_i$ with the ideal solution $AI$ and the utility degree $K_i^{-}$ of alternative $A_i$ with the anti-ideal solution $AAI$. In addition, Equations 40 and 41 are used to obtain the utility function $f\left(K_i^{+}\right)$ is 1.03 and $f\left(K_i^{-}\right)$ is −0.03. Based on this, Equation 39 is used to obtain the utility function value $f\left(K_i\right)$ of the carbon emission reduction contribution of the RDNs, as shown in Table 6.

Table 6

Table 6. Program utility degree, utility function value, and rankings.

5.2 Result analysis

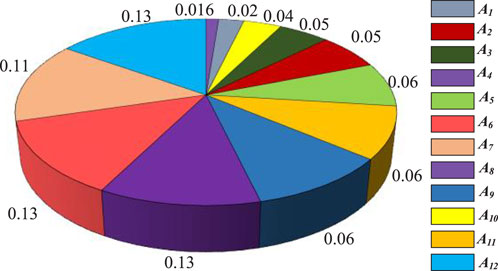
The indicator weight parameters of RDNs in terms of their perceived carbon emission reduction contributions are shown in Figure 7. The weight parameters of the indicators obtained by the SFS-BWM indicate that $A_4$, $A_6$, $A_{12}$, and $A_7$ are four relatively important indicators. After the investigation, big data and artificial intelligence can predict energy demand more accurately, fault handling technology effectively processes and transforms energy, and energy storage technology can store and utilize energy to solve the contradiction between supply and demand in the power system so the evaluation of indicator weights is consistent with the actual situation, and the assignment of indicators is reasonable. However, the performance of indicators $A_6$, $A_8$, and $A_{12}$ is unevenly distributed among RDNs that must make targeted improvements according to their own situation. Meanwhile, the weight of $A_4$ is generally low, and the application of digitization technology in areas must still be strengthened. In the future, in order to improve their carbon emission reduction contribution, the RDNs will still face many challenges in low-carbon development. Therefore, they must continue to improve their equipment investment, technological innovation, environmental protection, and comprehensive management.

Under the influence of multi-dimensional indicators, the SFS-MARCOS method is used to calculate the carbon emission reduction contribution of RDNs, as shown in Figure 8. The results show that $C_4$ has the highest performance and $C_{10}$ has the lowest. Chongming has sufficient photovoltaic power and wind power generation sources and is now connected to the new energy installed capacity of 35 kV above, totaling 529 MW. The second-ranked Pudong region has created several green factories, green supply chains, green products, and green parks. Shanghai’s first green finance regulations have been implemented in the Pudong New Area. Changxing County has established a regulatory forcing mechanism to guide enterprises to increase investment in green manufacturing. In addition, the low-carbon agricultural development practice area of Langxia Town, Jinshan District, has realized the reduction, low-carbonization, and resource utilization of agricultural waste through projects such as the resource utilization of livestock and poultry manure.

Figure 8

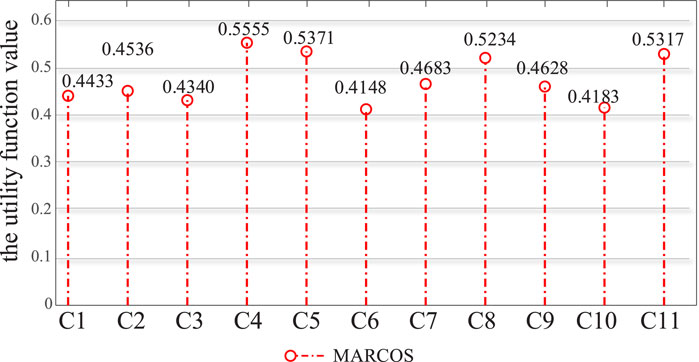
Figure 8. The evaluation results of carbon emission reduction contribution of RDNs under the MARCOS.

The economic development in the southern region of the city heavily relies on high-energy-consuming and high-emission industries, with the electricity sector being the primary contributor to this challenge, so the total amount and intensity of carbon emissions from the south grid are high. For areas with low contribution to carbon emission reduction, a variety of measures should be taken according to local conditions to improve the effect of carbon emission reduction. Therefore, the case results are in line with the actual situation, which verifies the reliability of the modeling method and shows that the evaluation is effective.

5.3 Sensitivity analysis

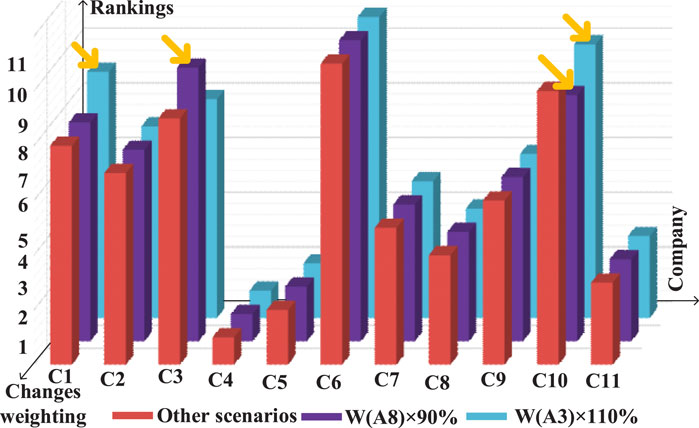
In order to analyze the influence of indicator weights on the rankings of carbon emission reduction contribution of areas, sensitivity analysis based on weight fluctuation was implemented. For this analysis, all indicator weights were reduced or increased by 10% from the original, as shown in Figure 9.

Figure 9

Figure 9. Ranking results of sensitivity analysis for indicator weight fluctuations.

Assuming that the original weight of $A_i$ becomes ${w_i}^{\prime }=\alpha w_i$, the weights of other indicators will change accordingly $w_o^{\prime }=\beta w_o\left(i\ne o\right)$. The modified weights satisfy $\alpha w_i+{\displaystyle {\sum }_{o=1,o\ne i}^{12}}\beta w_o=1$, where $\alpha$ takes the values of 90% and 110%.

When indicator $A_8$ is reduced by 10%, the ranking of carbon emission reduction contribution of the original RDNs changes. $C_3$ changes from ninth to tenth place, and $C_{10}$ changes from tenth to ninth. In addition, when indicator $A_3$ was increased by 10%, the carbon reduction contribution of $C_3$ moved forward by one place from ninth to eighth, while $C_1$ changed from eighth to ninth, exchanging rankings with each other. Changes in the weights of the remaining indicators did not bring about a change in the ranking of the carbon emission reduction contributions of RDNs.

This indicates that the environmental conditions of the region where areas $C_3$ and $C_{10}$ are located have a significant impact on the carbon emission reduction contribution of areas. When the regional environmental condition deteriorates ($A_8$ indicator decreases), the carbon emission reduction contribution of some areas may fall in the ranking, while other areas may benefit from it and rise. This reflects the more prominent influence of environmental policies, regional resource utilization efficiency, and other factors on the carbon emission reduction contribution ability of RDNs in $C_3$ and $C_{10}$. Indicator $A_3$, changes in the cost of purchasing carbon allowances, can also affect the ranking of RDNs in terms of their contribution to carbon emission reductions. Increased costs may prompt areas to optimize equipment operations and improve energy efficiency, thereby increasing carbon emission reduction contributions. Conversely, changes in costs may also affect areas’ emission reduction efforts or willingness to invest. It is worth noting that this change is bidirectional, that is, cost increases are positive for some areas (e.g., $C_3$) and negative for others (e.g., $C_1$). This further emphasizes the importance of cost control and operational efficiency in the reduction of carbon emissions by RDNs.

5.4 Comparative analysis

In order to verify the feasibility and superiority of the SFS-MARCOS method in evaluating the carbon emission reduction contribution of RDNs, MABAC, FCE, COPRAS, PROMETHEE-Ι, and PROMETHEE-II are used to replace the MARCOS method. The application of MABAC in sorting problems is based on the distances of the alternatives from the border approximation areas. The FCE calculates the comprehensive evaluation value based on the set of weights and the single-factor judgement matrix, thus obtaining the overall evaluation of the evaluation object. The COPRAS considers the relative importance of the options and takes into account the actual validity of the options when dealing with the alternatives to ensure the comprehensiveness and practicability of the assessment results. The PROMETHEE combines the concepts of ideal and anti-ideal solutions and evaluates the solutions by constructing preference and aversion functions. The different results obtained by the different methods are analyzed, and the following rankings of utility function value of RDNs’ carbon emission reduction contribution are obtained, as shown in Figure 10.

Figure 10

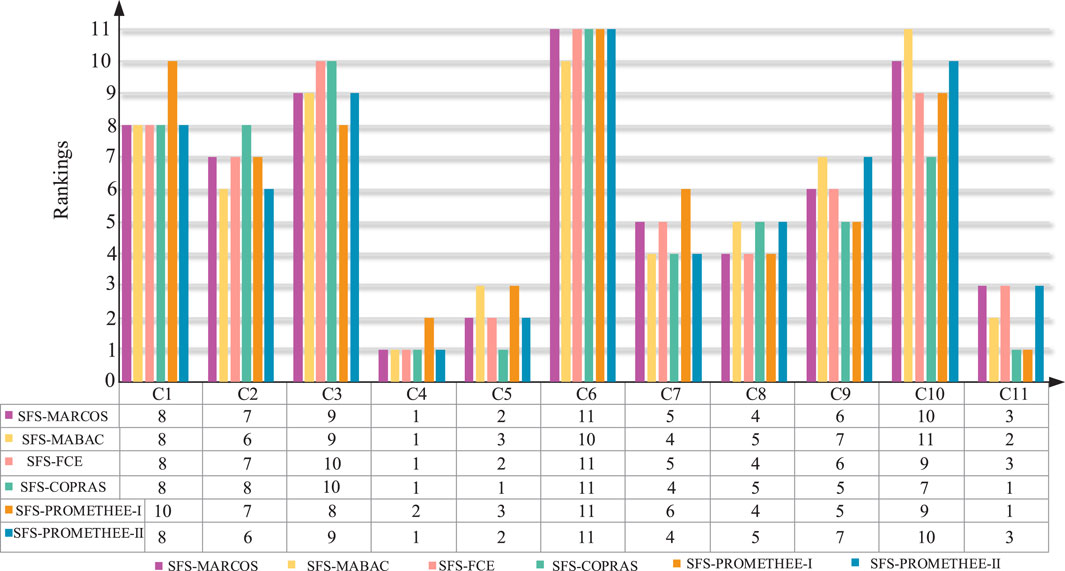
Figure 10. The rankings of the evaluation results of different decision-making methods in SFS environments.

As can be seen in Figure 10, the carbon reduction contribution of $C_4$ is the highest, and this result is largely consistent across the various decision-making methods, except for SFS-COPRAS and SFS-PROMETHEE-Ι. $C_4$ finishes in the second-best place in the SFS-PROMETHEE-Ι. All the methods unanimously identify that the carbon reduction contribution of $C_6$ is lower than that of other RDNs. Except for the SFS-MABAC calculations, which yielded the second-lowest C6 ranking. In addition, it can be clearly seen that the carbon emission reduction contribution of $C_5$ and $C_{11}$ is in the top three of all methods, $C_6$, $C_{10}$, and $C_3$ are in the bottom three of all methods, and the remaining $C_1$, $C_2$, $C_7$, and $C_8$ are evenly ranked in the middle four. The difference in the rankings of the largest and smallest carbon reduction contribution of each RDN under all decision-making methods does not differ by more than two places. The only exception is the COPRAS method in $C_{10}$, which ranks seventh and is due to the fact that COPRAS focuses more on a combined assessment of guideline scores and weights, with each area having a score under each guideline, which contributes to the differences in ranking results. The slight difference in the comparison results is within the acceptable range due to the variability of the method characteristics. All in all, the robustness and effectiveness of the ranking results by the suggested framework are verified.

Under the premise of ensuring the completeness of the decision-making evaluation information, it is compared with the SFS-MABAC, SFS-FCE, SFS-COPRAS, SFS-PROMETHEE-Ι, and SFS-PROMETHEE-Ⅱ methods to make the evaluation result objective and authentic and to verify that the SFS-MARCOS method is feasible, effective, and meets the needs of decision-making in practice.

6 Conclusion

In this article, a novel multi-attribute decision-making BWM-MARCOS method based on SFS is proposed for the realm of carbon emission reduction contribution determination, whose characteristics are as follows:

a. This article constructs the indicator system from four dimensions of economy, technology, environment, and management to provide an all-round determination of the carbon emission reduction contribution of RDNs.

b. The SFS-BWM method is adopted to calculate the importance degree of the indicators, circumvent the cumbersome and complicated arithmetic procedures, and avoid the loss of information in the evaluation.

c. The SFS-MARCOS method is used to deal with a large amount of uncertain data, is robust to data changes, solves the problem of data changes in the presence of a certain amount of noise, and ensures the stability of the evaluation results.

Eleven areas in Shanghai are analyzed as examples to verify the effectiveness and feasibility of the proposed method. The next step of the study will incorporate quantitative information on the basis of qualitative research and redesign the indicator system to support the low-carbon development of other industries. In the future, research can leverage big data and machine learning techniques to automate data collection and analysis, reducing subjectivity and enhancing accuracy. Multi-regional case studies can be conducted to test the generalizability and applicability of the proposed model.

To this end, we offer the following recommendations for carbon reduction in RDNs:

a. Strengthen the application of digital and intelligent technologies.

b. Optimize the energy structure and increase the penetration of new energy sources.

c. Implement scientific investment management and cost control.

d. Enhance environmental regulation and third-party carbon verification.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

PD: conceptualization, funding acquisition, methodology, project administration, software, supervision, visualization, writing–original draft, and writing–review and editing. MY: data curation, formal analysis, investigation, methodology, software, validation, visualization, writing–original draft, and writing–review and editing. WH: methodology, project administration, resources, supervision, writing–original draft, and writing–review and editing. PW: conceptualization, methodology, project administration, resources, visualization, writing–original draft, and writing–review and editing. QX: conceptualization, formal analysis, methodology, software, validation, visualization, writing–original draft, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research received support from the Shanghai Yangfan Program (23YF1414300).

Conflict of interest

Author PW was employed by the Economic and Technological Research Institute of State Grid Fujian Electric Power Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Avdasheva, S., and Orlova, Y. (2020). Effects of long-term tariff regulation on investments under low credibility of rules: rate-of-return and price cap in Russian electricity grids. Energy Policy 138, 111276. doi:10.1016/j.enpol.2020.111276

CrossRef Full Text | Google Scholar

Cheng, S., Cheng, Y., He, C., Fu, T., and Wang, C. (2024). Distributed synergistic planning of distribution networks-multiple integrated energy systems considering uncertainty. Electr. Power Autom. Equip., 1–19. doi:10.16081/j.epae.202404004

CrossRef Full Text | Google Scholar

Du, P., Gong, X., Han, B., and Zhao, X. (2023). Carbon-neutral potential analysis of urban power grid: a multi-stage decision model based on RF-DEMATEL and RF-MARCOS. Expert Syst. Appl. 234, 121026. doi:10.1016/j.eswa.2023.121026

CrossRef Full Text | Google Scholar

Du, P., Zhou, B., and Yang, M. (2024). Carbon emission reduction contribution analysis of electricity enterprises in urban green development: a quantum spherical fuzzy sets-based decision framework. Technol. Forecast. Soc. Change 200, 123181. doi:10.1016/j.techfore.2023.123181

CrossRef Full Text | Google Scholar

Geng, X., and Li, Y. (2023). Methodology research for spherical fuzzy quality function deployment considering psychological preferences. Univ. Shanghai Sci. Technol. 45 (5), 523–533. doi:10.13255/j.cnki.jusst.20220628001

CrossRef Full Text | Google Scholar

Gong, X., Yang, M., and Du, P. (2021). Renewable energy accommodation potential evaluation of distribution network: a hybrid decision-making framework under interval type-2 fuzzy environment. J. Clean. Prod. 286, 124918. doi:10.1016/j.jclepro.2020.124918

CrossRef Full Text | Google Scholar

Huang, Q., Zhang, H., Ma, L., and Yang, J. (2023). Hybrid Harris hawks optimization algorithm for solving low-carbon multimodal transportation problem with fuzzy demand. Appl. Res. Comput. 40 (10), 2978–2983. doi:10.19734/j.issn.1001-3695.2023.03.0061

CrossRef Full Text | Google Scholar

Jia, F., Liu, Y., and Wang, X. (2019). An extended MABAC method for multi-criteria group decision making based on intuitionistic fuzzy rough numbers. Expert Syst. Appl. 127, 241–255. doi:10.1016/j.eswa.2019.03.016

CrossRef Full Text | Google Scholar

Labis, P. E., Visande, R. G., Pallugna, R. C., and Caliao, N. D. (2011). The contribution of renewable distributed generation in mitigating carbon dioxide emissions. Renew. Sustain. Energy Rev. 15 (9), 4891–4896. doi:10.1016/j.rser.2011.07.064

CrossRef Full Text | Google Scholar

Laxmi, R., Ismat, B., and Sanjay, K. (2024). Spherical fuzzy analytic hierarchy process and linear assignment model based MCGDM method with its application in ranking of states for their business climate. Expert Syst. Appl. 238, 122247. doi:10.1016/j.eswa.2023.122247

CrossRef Full Text | Google Scholar

Li, B., Liao, K., Yang, J., and He, Z. (2024). A data-driven fault detection scheme for DC distribution networks based on the adaptive boosting technique. Appl. Energy 374, 123949. doi:10.1016/j.apenergy.2024.123949

CrossRef Full Text | Google Scholar

Li, B., Xia, X., and Li, Q. (2023). Research on the influence of carbon allowance trading on the improvement of carbon emission reduction technology and the coordination mechanism. Chin. J. Manag. Sci. 575, 1003–207x. doi:10.16381/j.cnki.issn1003-207x.2023.0576

CrossRef Full Text | Google Scholar

Liu, X., Mei, S., Ding, R., Zhong, S., Zhang, X., Xie, N., et al. (2023). Compressed air energy storage engineering status, development trend and application prospects. Automation Electr. Syst. 43 (10), 38–47. doi:10.16081/j.epae.202309005

CrossRef Full Text | Google Scholar

Qiu, H., Shi, K., Wang, R., Zhang, L., Liu, X., and Cheng, X. (2024). A novel temporal–spatial graph neural network for wind power forecasting considering blockage effects. Renew. Energy 227, 120499. doi:10.1016/j.renene.2024.120499

CrossRef Full Text | Google Scholar

Rani, P., Mishra, A. R., and Mardani, A. (2020). An extended Pythagorean fuzzy complex proportional assessment approach with new entropy and score function: application in pharmacological therapy selection for type 2 diabetes. Appl. Soft Comput. 94, 106441. doi:10.1016/j.asoc.2020.106441

CrossRef Full Text | Google Scholar

Sang, L., Xu, Y., Sun, H., and Wu, W. (2024). Carbon-aware distribution network operation approach via fusing learning and optimization. Proc. CSEE, 1–11.

Google Scholar

Seikh, M. R., and Mandal, U. (2023). Interval-valued Fermatean fuzzy Dombi aggregation operators and SWARA based PROMETHEE II method to bio-medical waste management. Expert Syst. Appl. 226, 120082. doi:10.1016/j.eswa.2023.120082

CrossRef Full Text | Google Scholar

Sun, Y., Li, Z., and Bao, H. (2021). Multi-energy heterogeneous load regulation framework and key technology analysis under clean heating mode. Proc. CSEE 41 (20), 6827–6842. doi:10.13334/j.0258-8013.pcsee.210798

CrossRef Full Text | Google Scholar

Thangaraj, M., Samayan, N., and Selvaraj, G. (2023). Sustainable renewable energy system selection for self-sufficient households using integrated fermatean neutrosophic fuzzy stratified AHP-MARCOS approach. Renew. Energy 218, 119324. doi:10.1016/j.renene.2023.119292

CrossRef Full Text | Google Scholar

Wei, Q., Zhou, C., Liu, Q., Zhou, W., and Huang, J. (2023). A barrier evaluation framework for forest carbon sink project implementation in China using an integrated BWM-IT2F-PROMETHEE II method. Expert Syst. Appl. 230, 120612. doi:10.1016/j.eswa.2023.120612

CrossRef Full Text | Google Scholar

Wu, Y., Yan, W., Du, P., Gong, X., and Zhou, M. (2023). Mengxia zhou. Regional evaluation study of VFTO interference to secondary side cables based on cloud model and MARCOS. IEEE Trans. neural Netw. Learn. Syst. 10, 1–14. doi:10.1109/TNNLS.2023.3325537

CrossRef Full Text | Google Scholar

Xiao, J., Cai, M., Gao, Y., and Zhou, K. (2023). Consensus model for interval-value non-additive BWM considering risk attitude. Control Decis. 39 (6), 2097–2105. doi:10.13195/j.kzyjc.2022.2099

CrossRef Full Text | Google Scholar

Xie, Y., Li, Y., Liu, Y., Du, E., Xu, Q., and Zhang, N. (2023). Preliminary exploration of carbon reduction demand side cloud energy storage model: operation model and benefit analysis. Proc. CSEE 61, 1–13. doi:10.13334/j.0258-8013.pcsee.23150

CrossRef Full Text | Google Scholar

Xue, X., and Tsai, P. W. (2022). Integrating Energy Smart Grid’s ontologies through multi-objective particle swarm optimization algorithm with competitive mechanism. Sustain. Energy Technol. Assessments 53, 102442. doi:10.1016/j.seta.2022.102442

CrossRef Full Text | Google Scholar

Yang, S., Lao, K. W., Hui, H., and Chen, Y. (2024). Secure distributed control for demand response in power systems against deception cyber-attacks with arbitrary patterns. IEEE Trans. Power Syst., 1–12. doi:10.1109/tpwrs.2024.3381231

CrossRef Full Text | Google Scholar

Yang, S., Lao, K. W., Hui, H., Chen, Y., and Dai, N. (2023a). Real-time harmonic contribution evaluation considering multiple dynamic customers. CSEE J. Power Energy Syst., 1–13. doi:10.17775/CSEEJPES.2022.06570

CrossRef Full Text | Google Scholar

Yang, Y., Hao, J., Wang, X., Feng, X., Du, X., and Zheng, L. (2023b). Global diagnosis and analysis of carbon emission reduction by combining data stacked-layer optimization model. Proc. CSEE 43 (S1), 153–164. doi:10.13334/j.0258-8013.pcsee.231399

CrossRef Full Text | Google Scholar

Yao, L., Cai, R., Qian, J., and Wu, X. (2023). Aggregation and control model construction of hybrid load system for supply and demand balance in low-carbon zone. Power Syst. Technol. 47 (8), 3153–3166. doi:10.13335/j.1000-3673.pst.2023.0432

CrossRef Full Text | Google Scholar

Yu, D., Liu, Y., and Xu, Z. (2023). Analysis of knowledge evolution in PROMETHEE: a longitudinal and dynamic perspective. Inf. Sci. 642, 119151. doi:10.1016/j.ins.2023.119151

CrossRef Full Text | Google Scholar

Yu, Q., Liao, Y., Cao, J., and Hou, F. (2021). QUALIFLEX and LINMAP-based approach for multi-attribute decision making problems with simplified neutrosophic hesitant fuzzy sets. Operations Res. Manag. Sci. 30 (6), 77–82. doi:10.12005/orms.2021.0183

CrossRef Full Text | Google Scholar

Yue, F., Liu, H., Su, X., and Chen, S. (2024). Carbon tracing method for RDNs considering load side electricity substitution. Guangdong Electr. power 37 (02), 47–55. doi:10.3969/j.issn.1007-290X.2024.02.006

CrossRef Full Text | Google Scholar

Zhang, Y., Wang, S., Liu, J., Liu, D., Li, T., and Wu, W. (2024). A corrosion assessment methodology based on triangular intuitionistic fuzzy comprehensive evaluation (TIFCE) with analytic network process (TIFANP): an application to external corrosion of the storage tank floor. Expert Syst. Appl. 238©, 121896. doi:10.1016/j.eswa.2023.121896

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Z., and Kang, C. (2022). Challenges and prospects for constructing the new-type power system towards a carbon neutrality future. Proc. CSEE 42 (8), 2806–2819. doi:10.13334/j.0258-8013.pcsee.220467

CrossRef Full Text | Google Scholar

Zhong, X., Zhong, W., Lin, Z., Zhou, G., Lai, L. L., Xie, S., et al. (2024). Localized electricity and carbon allowance management for interconnected discrete manufacturing systems considering algorithmic and physical feasibility. Appl. Energy 372, 123791. doi:10.1016/j.apenergy.2024.123791

CrossRef Full Text | Google Scholar