Parameter estimation of photovoltaic models based on improvement of moutain gazelle optimizer algorithm

Introduction: The mountain gazelle (Gazella gazella) is a native species to the Middle East and has experienced a notable population decline due to human-induced habitat loss and fragmentation. In Saudi Arabia, the current status and distribution of this species remain poorly understood, necessitating data-driven conservation assessments.

Methods, Results, and Discussion: This study combined recent occurrence records with remote sensing and GIS-based environmental variables to model suitable habitats for the mountain gazelle using the MaxEnt algorithm. Key predictors included vegetation indices, land cover types, and elevation. The results identified core habitat areas in the western and southwestern regions, some of which fall outside current protected zones. These findings underscore the importance of expanding conservation areas and demonstrate how spatial modeling supports effective wildlife management in arid environments.

1 Introduction

Poverty, hunger, and clean energy are interconnected issues, as they are outlined in the United Nations’ Sustainable Development Goals (SDGs). These goals aim to eliminate poverty, conserve natural resources, promote human rights, and enhance gender equality (Griggs et al., 2013) as shown in Figure 1.

Figure 1

Figure 1. The 17 sustainable development goals (SDGs) (Griggs et al., 2013).

However, conventional development policies often overlook environmental concerns, highlighting the gap between environmental importance and development initiatives. This highlights the need for ecological sustainability and the implementation of clean and efficient energy sources. The SDGs were adopted in 2015 (Rant, 2020), emphasizing the importance of integrating environmental awareness into development strategies. Neglecting environmental issues in poverty mitigation hinders development progress, emphasizing the need for environmental awareness and social justice (Schleicher et al., 2018). Ecological sustainability requires clean, efficient energy sources, which are easily accessible natural resources (Wang et al., 2021).

So far, most power plants have utilized conventional energy sources with remarkably high energy density, such as natural gas, oil, and coal, collectively referred to as fossil fuels. However, these sources produce carbon and other greenhouse gases when used. Therefore, it has become necessary to reduce fossil fuel consumption and focus on utilizing more readily available renewable energy sources (RES) in the energy sector to combat global warming and mitigate carbon emissions (Rahman et al., 2022).

Through rigorous experimental validation, the study demonstrates the effectiveness of utilizing renewable energy sources (RES) as a sustainable alternative to fossil fuels, emphasizing their potential to mitigate carbon emissions and combat global warming. By shifting from fossil fuels to renewable energy sources, such as solar, wind, hydro, and geothermal power, carbon emissions and CO2 emissions can be significantly reduced. During their operational phase, renewable energy technologies display lower environmental negative impacts than other energy sources that rely on fossil fuels (Ashraf et al., 2024). An advanced increase in the adoption of solar and wind energy sources is crucial to achieving the target of zero carbon emissions, which can be realized through new PV solar projects (Sánchez et al., 2023).

Since the 1950s, the long-term progress rates of solar photovoltaics (PV) have been the uppermost among all energy technologies. Documented as the most affordable power source, PV has earned the name “king” of the energy marketplaces. Combined with energy system technologies that provide support, such as batteries and electrolyzers, it is believable that solar PV will surpass all other major sources of energy used by humankind within the next few years (Breyer et al., 2021).

The goal of a (PV) cell is to transform solar energy into electrical energy. There are several varieties of PV cells; each is characterized by its exclusive structure and properties. There are three fundamental types: Single-Diode, Double-Diode, and Triple-Diode (Yaqoob et al., 2021).

The process of estimating parameters for PV models, such as the single-diode, double-diode, and triple-diode models, is a critical challenge in the design and simulation of PV systems. Traditional methods for parameter estimation, including various numerical, analytical, and hybrid approaches, have been extensively explored. However, these methods often struggle to yield accurate and quick results, leading to discrepancies between measured and predicted values, which can significantly impact the efficiency and reliability of PV systems.

The objective of this research is to enhance the accuracy and speed of parameter estimation for photovoltaic (PV) models by introducing modifications to the three fundamental PV models and employing the Improved Mountain Gazelle Optimizer (i_MGO), a contemporary optimization algorithm. This is achieved by minimizing the root mean square error (RMSE) between the computed and actual current values, and by providing a robust comparison of the modified and conventional PV models using objective function. Through rigorous analysis and validation, the study aims to demonstrate the superior performance of the i_MGO algorithm over other competing algorithms, thereby contributing to the advancement of PV system simulations and designs.

This paper makes several significant contributions to the field of PV model parameter estimation, as outlined below.

• The introduction of a novel optimization algorithm, i_MGO, designed to enhance the accuracy and efficiency of parameter estimation in PV models.

•Extensive evaluation of i_MGO through rigorous experiments on various PV models, including the RTC France solar cell and five different PV modules, highlighting its potential in PV parameter estimation.

•A comparative study to assess the performance of i_MGO against other well-established optimization algorithms, demonstrating its superior accuracy and efficiency in parameter estimation tasks.

The rest of the sections are organized as follows:

Section 3 discusses the modeling of PV models. Section 4 presents the basic structure of the MGO algorithm and its working behavior. Section 5 describes the improvement of the MGO algorithm, while a detailed architecture of the proposed algorithm is presented in Section 6. In Section 7, the simulation and results are discussed. The conclusions of this paper are presented in Section 8.

2 Related work

Meta-heuristic algorithms have recently become essential tools for mitigating the temporal and precision limitations inherent in a wide range of engineering applications. There has been a significant increase in the emergence of these algorithms to satisfy the optimization requirements of various scientific fields. In light of the growing significance of optimization in various areas, meta-heuristic algorithms have shown their effectiveness in addressing optimization challenges. For the purpose of parameter estimation tasks, multiple of these algorithms have been carried out, especially in the field of PV models.

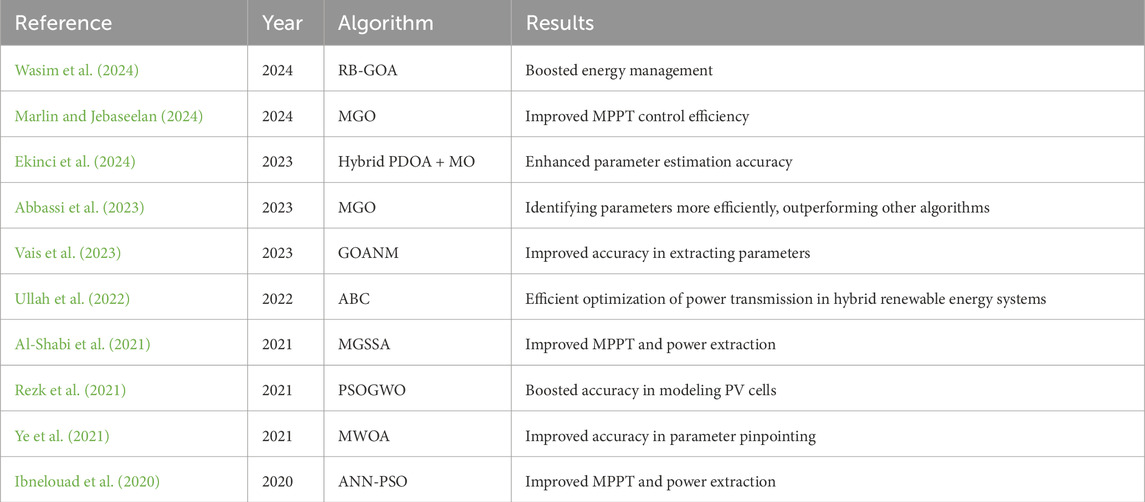
In 2024, an algorithm is utilized in a study by Wasim et al. (2024) for the sake of energy management in a solar-powered battery-ultracapacitor hybrid system. The algorithm is the rule-based grasshopper optimization algorithm (RB-GOA). To meet the needs of the pulsed load (PL), the RB-GOA redistributes power among the PV array, the battery bank (BB), and the ultracapacitor (UC) by employing a set of rules and a search space defined by the system. The study’s results showed that the suggested RB-GOA performed better in certain situations than other well-known swarm intelligence techniques (SITs), including the cuckoo search algorithm (CSA), gray wolf optimization (GWO), and salp swarm algorithm (SSA). When compared to other techniques operating under uniform irradiance and shaded conditions, the RB-GOA demonstrated improved maximum power point tracking speed, reduced power surges, and faster response times. The results were outstanding in explaining the RB-GOA’s control, as they maintained a constant output even when the PL demand changed and effectively utilized PV energy in the hybrid system. The research did not involve any modifications to the algorithm; however, the algorithm still positively enhanced the operation of the PV system by improving energy management, reducing power fluctuations, and enhancing MPPT efficiency, which ensures better overall system performance and energy utilization.

Moreover, in 2024, a comprehensive study by Marlin and Jebaseelan (2024) was conducted on intelligence-based optimization algorithms used for maximum power tracking in grid-PV systems. The study mainly directs its attention on comparing various optimization algorithms for maximum power point tracking (MPPT) in grid-connected PV systems. The mentioned algorithms in this study are Mongoose Optimization (MO), Prairie Dog Optimization Algorithm (PDOA), and a hybrid approach combining PDOA and MO. The focal points of the study involve choosing the most effective optimization algorithm for MPPT control to meet the energy requirements of grid systems and boosting the energy production from PV systems. The study compares the performance of the three algorithms in terms of various parameters, including time, error, power, Total Harmonic Distortion (THD), and others. The research evaluates the performance of various intelligence-based optimization algorithms in enhancing the efficiency of Maximum Power Point Tracking (MPPT) in grid-connected photovoltaic (PV) systems. The primary objective of this research is to enhance the overall performance of the system by optimizing real-time power sharing among the PV system, battery bank, and ultracapacitors to meet periodic load demands. While no modifications were made to the algorithms, it is worth noting that, overall, the hybrid PDOA + MO algorithm demonstrates encouraging results in enhancing the competence and performance of MPPT control in solar PV systems, showcasing its capability for refining the operation and energy yield of PV systems under varying environmental conditions.

Researchers in a recent 2023 investigation cite vais2023parameter proposed a novel approach to enhance the accuracy of modeling and assessing the performance of solar PV panels. The study backs up using the Dandelion Optimization Algorithm (DOA) to find the equivalent circuit parameters of solar PV panels. It focuses on both single-diode (SD) and double-diode (DD) PV models for various types of PV modules. The DOA demonstrates astonishing accuracy across various PV modules by reducing errors at critical stages. The study does not demonstrate how to modify the DOA algorithm itself; however, statistical analysis reveals that the DOA outperforms two other hybrid optimization algorithms in terms of standard deviation, sum, mean, and variance. These results highlight the DOA’s effectiveness in precisely determining parameters, thereby enhancing the accuracy of PV system modeling and performance assessment.

Additionally, in 2023, Abbassi et al. (2023) introduced a novel algorithm that drew inspiration from the social dynamics of wild gazelles. In the study designated, they work on an algorithm called the Mountain Gazelle Optimizer (MGO). The researchers apply MGO to determine the optimal values for certain parameters of PV generation units, specifically for two models: the Single-Diode Model (SDM) and the Double-Diode Model (DDM), for various types of solar panels. The study found that MGO outperformed other recent algorithms in accurately pinpointing these parameters. The results also revealed that MGO had fewer errors compared to algorithms like the Grey Wolf Optimizer (GWO), Squirrel Search Algorithm (SSA), and Differential Evolution (DE). Overall, the study suggests that MGO exhibits a fast processing time, stable convergence, and high accuracy in solving parameter estimation problems for PV models. It is effective in accurately identifying the parameters of the PV generation units, showcasing improved performance compared to other superior optimization algorithms.

In another study conducted by Ekinci et al. (2024) in 2023, scientists employed a hybrid approach known as the Gazelle-Nelder-Mead (GNM) algorithm, which combines the Gazelle Optimization Algorithm (GOA) with the Nelder-Mead (NM) algorithm. This combination enhanced parameter extraction in solar PV models. Remarkably, no specific modifications were made to the GOANM algorithm itself. Results showed that the GOANM algorithm consistently outperformed other methods in terms of speed, accuracy, and reliability across various benchmark functions. It was further tested on solar cell and PV module models, demonstrating improved functionality in terms of parameter estimation accuracy and convergence speed. The study highlights the efficacy of the GOANM algorithm in enhancing renewable energy systems, particularly solar PV installations. By enhancing the accuracy and efficiency of parameter extraction, it significantly contributes to improving solar energy conversion processes. A 2022 study by Ullah et al. (2022) introduces making power transmission between microgrids in hybrid renewable energy systems more effective. To apply this, they utilize an algorithm known as the Artificial Bee Colony (ABC) algorithm. This method is inspired by how bees search for food. This algorithm has been proven effective in reducing costs and decreasing the need for external power. Fundamentally, it facilitates the design of systems that are both reliable and cost-effective. One of the key advantages of the ABC algorithm is its efficacy and adaptability. It works by having an intelligent assistant that requires minimal changes yet achieves rapid results. Its adaptability is very beneficial for balancing cost and power optimization in energy systems. While the researchers did not modify the ABC algorithm specifically for this task, they highlighted its effectiveness in meeting their optimization objectives. Furthermore, this approach holds encouraging prospects for transforming renewable energy systems into ones that are both cost-effective and environmentally sustainable. Table 1 summarizes the key parameters used in the single, double, and three-diode PV models for simulation and validation purposes.

Table 1

Table 1. Summary of Studies on PV systems of different algorithms.

3 Definition of PV models

In this section the mathematical analysis of the three PV models (TPVM) and the modified three PV models (MTPVM) is discussed. The TPVM includes single diode model (SDM), double diode model (DDM), and three diode model (TDM). Meanqwhile, the MTPVM contains modified single diode model (MSDM), modified double diode model (MDDM) and modified three diode model (MTDM). Table 2 presents the configuration settings and initialization values employed in the i_MGO optimizer for accurate PV parameter estimation.

Table 2

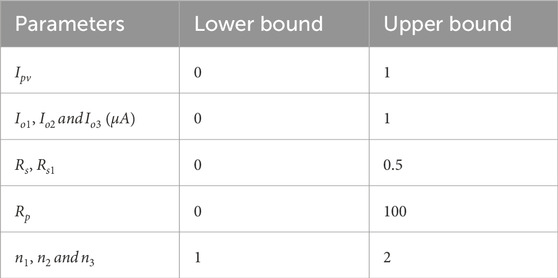
Table 2. The limits of estimated parameters (Yu et al., 2018).

3.1 Single diode model

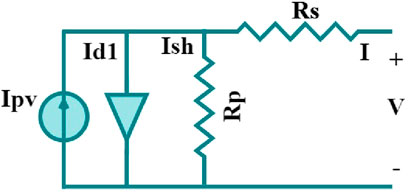
Figure 2 illustrates the initial performance comparison of optimization methods. The equivalent circuit for SDM is elucidated in Figure 8a. The current output from this model is computed using the following equation (Saleh Alluhaidan et al., 2025; Ghanim et al., 2024; AbdElminaam et al., 2024; AbdElminaam et al., 2022). The single-diode model parameters are mathematically described in Equation 1:

$I=I_{pv}-I_{D1}-I_{sh}(1)$

Where:

•$I$: Output current of the PV cell.

•$I_{pv}$: PV current generated by the solar cell due to light exposure.

•$I_{D1}$: Dark saturation current of the single diode.

•$I_{sh}$: Shunt current (leakage current through the shunt resistor). The current-voltage relationship is further elaborated in Equations 2, 3.

$I=I_{pv}-I_{o1}\left[e^{\frac{q\left(V+I{R}_s\right)}{n_{1}K{T}_c}}-1\right]-\frac{V+I{R}_s}{R_{sh}}(2)$

Where:

•$I$: Output current of the PV cell.

•$I_{pv}$: PV current generated by the solar cell.

•$I_{o1}$: Saturation current of the single diode.

•$e$: Base of the natural logarithm (Euler’s number).

•$q$: Elementary charge of an electron $(1.602\times 10^{-19}\text{C})$.

•$V$: Voltage across the PV cell terminals.

•$I$: Current through the PV cell.

•$R_s$: Series resistance of the PV cell.

•$n_1$: Ideality factor of the diode.

•$k$: Boltzmann constant $(1.381\times 10^{-23}\text{J/K})$.

•$T_c$: Absolute temperature of the PV cell (in Kelvin).

•$R_{sh}$: Shunt resistance of the PV cell.

The SDM produces a current denoted as $I$, where $Ipv$ represents the current generated by light, $Ish$ is the leakage current, and $ID1$ is the dark saturation current. Shunt and series resistances are denoted by $Rp$ and $Rs$, respectively. Additionally, $n1$ signifies the diode ideality factor, $K$ represents Boltzmann’s constant, $q$ denotes the charge of an electron, and $Tc$ indicates the cell temperature. According to the provided mathematical formula, the parameters to be estimated in the SDM encompass $Ipv$, $Io1$, $n1$, $Rs$, and $Rp$.

Figure 2

Figure 2. Equivalent circuit for single diode model.

3.2 Double diode model

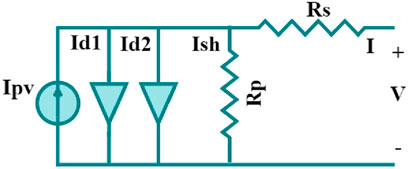
In Figure 3, the electrical diagram for the DDM is presented, utilizing two diodes to enhance output quality (Saleh Alluhaidan et al., 2025; Ghanim et al., 2024; AbdElminaam et al., 2024; AbdElminaam et al., 2022). The current output in this model is derived from the following equations:

$I=I_{pv}-I_{D1}-I_{D2}-I_{sh}(3)$

Figure 3

Figure 3. Equivalent circuit for double diode model.

Where:

•$I$: Output current of the PV cell.

•$I_{pv}$: PV current generated by the solar cell due to light exposure.

•$I_{D1}$: Dark saturation current of the first diode.

•$I_{D2}$: Dark saturation current of the second diode.

•$I_{sh}$: Shunt current (leakage current through the shunt resistor). As shown in Equation 4, the output current is influenced by the diode ideality factor.

$I=I_{pv}-I_{o1}\left[e^{\frac{q\left(V+I{R}_s\right)}{n_{1}K{T}_c}}-1\right]-I_{o2}\left[e^{\frac{q\left(V+I{R}_s\right)}{n_{2}K{T}_c}}-1\right]-\frac{V+I{R}_s}{R_{sh}}(4)$

Where:

•$I$: Output current of the PV cell.

•$I_{pv}$: PV current generated by the solar cell.

•$I_{o1}$: Saturation current of the first diode.

•$I_{o2}$: Saturation current of the second diode.

•$e$: Base of the natural logarithm (Euler’s number).

•$q$: Elementary charge of an electron $(1.602\times 10^{-19}\text{C})$.

•$V$: Voltage across the PV cell terminals.

•$I$: Current through the PV cell.

•$R_s$: Series resistance of the PV cell.

•$n_1$: Ideality factor of the first diode.

•$n_2$: Ideality factor of the second diode.

•$k$: Boltzmann constant $(1.381\times 10^{-23}\text{J/K})$.

•$T_c$: Absolute temperature of the PV cell (in Kelvin).

•$R_{sh}$: Shunt resistance of the PV cell.

Where $ID2$ represents the dark saturation current of the second diode, and $n2$ denotes the ideality factor of the second diode. The model encompasses seven parameters for estimation: $Ipv$, $Io1$, $n1$, $Rs$, $Rp$, $Io2$, and $n2$.

3.3 Three diode model

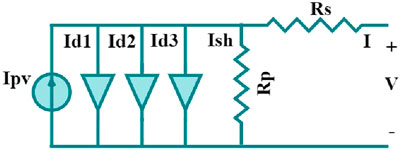
Figure 4 demonstrates the convergence behavior of the i_MGO algorithm. The three-diode model (TDM) displayed in Figure 8c introduces an alternative approach for designing PV modules by incorporating three diodes (Saleh Alluhaidan et al., 2025; Ghanim et al., 2024; AbdElminaam et al., 2024; AbdElminaam et al., 2022). The computation of the current output in this model is carried out using Equation 5:

$I=I_{pv}-I_{D1}-I_{D2}-I_{D3}-I_{sh}(5)$

Figure 4

Figure 4. Equivalent circuit for three diode model.

Where:

•$I$: Output current of the PV cell.

•$I_{pv}$: PV current generated by the solar cell due to light exposure.

•$I_{D1}$: Dark saturation current of the first diode.

•$I_{D2}$: Dark saturation current of the second diode.

•$I_{D3}$: Dark saturation current of the third diode.

•$I_{sh}$: Shunt current (leakage current through the shunt resistor). Equation 6 provides the thermal voltage formulation.

$I=I_{pv}-I_{o1}\left[e^{\frac{q\left(V+I{R}_s\right)}{n_{1}K{T}_c}}-1\right]-I_{o2}\left[e^{\frac{q\left(V+I{R}_s\right)}{n_{2}K{T}_c}}-1\right]-I_{o3}\left[e^{\frac{q\left(V+I{R}_s\right)}{n_{3}K{T}_c}}-1\right]-\frac{V+I{R}_s}{R_{sh}}(6)$

Where:

•$I$: Output current of the PV cell.

•$I_{pv}$: PV current generated by the solar cell.

•$I_{o1}$: Saturation current of the first diode.

•$I_{o2}$: Saturation current of the second diode.

•$I_{o3}$: Saturation current of the third diode.

•$e$: Base of the natural logarithm (Euler’s number).

•$q$: Elementary charge of an electron $(1.602\times 10^{-19}\text{C})$.

•$V$: Voltage across the PV cell terminals.

•$I$: Current through the PV cell.

•$R_s$: Series resistance of the PV cell.

•$n_1$: Ideality factor of the first diode.

•$n_2$: Ideality factor of the second diode.

•$n_3$: Ideality factor of the third diode.

•$k$: Boltzmann constant $(1.381\times 10^{-23}\text{J/K})$.

•$T_c$: Absolute temperature of the PV cell (in Kelvin).

•$R_{sh}$: Shunt resistance of the PV cell.

Where $ID3$ represents the dark saturation current of the third diode, and $n3$ denotes the ideality factor of the third diode. Estimating nine parameters is essential for the TDM: $Ipv$, $Io1$, $n1$, $Rs$, $Rp$, $Io2$, $n2$, $Io3$, and $n3$.

$I_{pv}$, $I_{o1}$, $n_1$, $R_s$, $R_p$, $I_{o2}$, $n_2$, $I_{o3}$ and $n_3$.

3.4 Problem formulation

The evaluation of TPVM’s performance involves objective functions, particularly those centered on root mean square error (RMSE). These functions quantify the difference between the computed current using estimated parameters and the actual current obtained from the dataset. The RMSE is precisely defined by Equations 7, 8:

$J\left(V,I,X\right)=I-I_{\mathit{exp}}(7)$

$RMSE=\sqrt{\frac{1}{N}{\displaystyle \sum _N^{i=1}}{\left(J\left(V,I,X\right)\right)}^2}(8)$

In this context, $I_{\mathit{exp}}$ denotes the analysis current, $N$ signifies the number of data readings, and $X$ encompasses the set of decision variables.

The vector of decision variable for SDM is $X=\left\{\left(I_{pv},I_{o1},n_1,R_{s}and{R}_p\right)\right\}$.

The vector of decision variable for DDM is $X=\left\{\left(I_{pv},I_{o1},n_1,R_s,R_p,I_{o2}and{n}_2\right)\right\}$.

The vector of decision variable for TDM is $X=\left\{\left(I_{pv},I_{o1},n_1,R_s,R_p,I_{o2},n_2,I_{o3}and{n}_3\right)\right\}$.

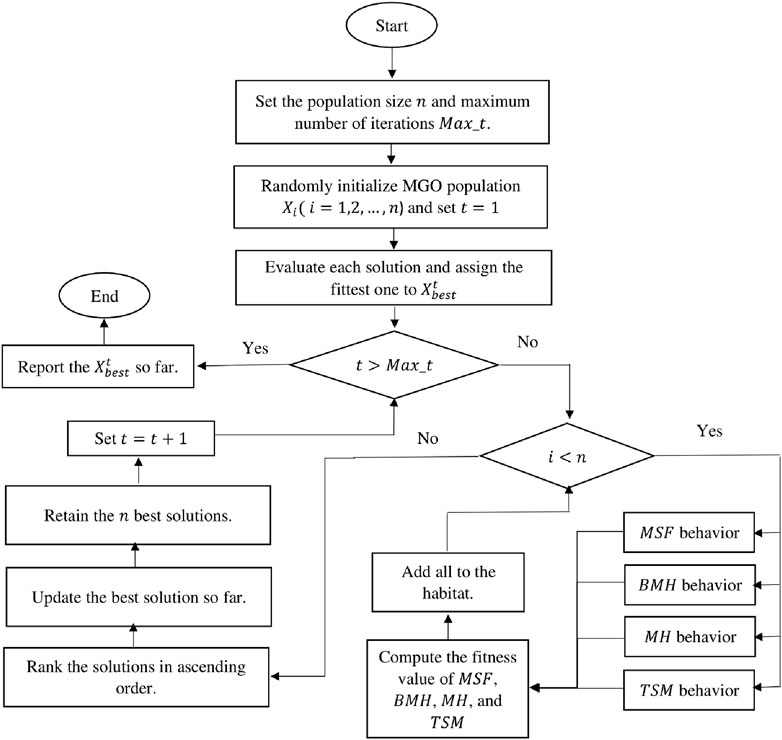
4 Mountain gazelle optimizer (MGO)

The MGO is a novel meta-heuristic optimization algorithm that draws inspiration from the social structure and dynamics of wild mountain gazelles (Abdollahzadeh et al., 2022). One kind of gazelle, the mountain gazelle, lives in sparse populations in regions bordering the Arabian Peninsula and shares a habitat with the Robinia tree. During the late Holocene, as temperatures increased, the species lost territory to Gazella bennettii, an exceptionally acclimated species for high temperatures. The mountain gazelle exhibits high levels of territoriality, which splits into three groups: mother-and-child herds, young male herds, and the area of single males (Grau and Walther, 1976). The mountain gazelle regularly migrates over 120 km for food.

The MGO optimization algorithm utilizes four major components of the mountain gazelle’s existence—bachelor male herds, maternity herds, solitary, territorial males, and movement in search of food—to optimize operations. The exploitation and exploration stages are conducted simultaneously, employing the four processes. The following subsection illustrates the basic mathematical steps of the MGO algorithm.

4.1 Territorial solitary males

Upon attaining maturity and sufficient strength, male mountain gazelles establish an isolated territory characterized by a high degree of territoriality. In a gazelle territorial conflict, the adult males fight for control of the female’s territory. In contrast, younger males attempt to take over, and this process can be modeled using Equation 9. The initialization of model parameters is described using Equation 10.

$\text{TSM}={\text{male}}_{\text{gazelle}}-{\mathrm{\Delta }}_{\text{TSM}}\times {\text{Cof}}_r(9)$

${\mathrm{\Delta }}_{\text{TSM}}=\left|\left(r_{i_1}\times BH-r_{i_2}\times X\left(t\right)\right)\times F\right|(10)$

where:

•The parameters $r{i}_1$ and $r{i}_2$ are randomly assigned values of 1 or 2, and ${\text{\hspace{0.17em}male\hspace{0.17em}}}_{\text{gazelle\hspace{0.17em}}}$ denotes the position vector of an adult male gazelle in the global solution, and $X(t)$ is the current position of gazelle.

•The vector $BH$ represents the young male herd coefficient, which is determined using Equation 11.

$BH=X_{\text{ra}}\times ⌊r_1⌋+M_{\text{pr}}\times ⌈r_2⌉(11)$

A young male solution $X_{ra}$ is generated at random from the interval $ra$ with a total number of gazelles $N$ (i.e., $ra=\left\{⌈\frac{N}{3}⌉\dots N\right\}$). The average number of randomly selected search agents, denoted as $M_{pr}$, is equal to $⌈\frac{N}{3}⌉$ while $r_1$ and $r_2$ are two generated random numbers within the range from 0 to 1.

•$F$ can be computed according to Equation 12.

$F=N_1\left(D\right)\times \exp \left(2-t\times \left(\frac{2}{{\text{Max}}_t}\right)\right)(12)$

$N_1$ is a random number drawn from the normal distribution of the problem variable’s dimension $D$. While $\exp$, $\text{\hspace{0.17em}t\hspace{0.17em}}$, and $\text{\hspace{0.17em}Max\_t\hspace{0.17em}}$ are the exponential function, the current iteration, and the maximum number of iterations, respectively.

•A randomly chosen coefficient vector $Co{f}_r$ is employed and modified with each iteration to enhance the search capability and calculated according to Equation 13.

$Co{f}_r=\left\{\begin{array}{c}\left(a+1\right)+r_3,\hfill \\ a\times N_2\left(D\right),\hfill \\ r_4\left(D\right),\hfill \\ N_3\left(D\right)\times N_4{\left(D\right)}^2\times \cos \left(\left(r_4\times 2\right)\times N_3\left(D\right)\right),\hfill \end{array}\right.(13)$

The value of $a$ based on the current and maximum number of iterations (i.e., $a=-1+$ t $\times \left(\frac{-1}{\text{\hspace{0.17em}Max\_t\hspace{0.17em}}}\right)$). $r_3$ and $r_4\in (\mathrm{0,1})$ with $\text{cos}$ represent the cosine function. $N_2$, $N_3$, and $N_4$ are random numbers within the normal range of the problem’s dimensions $D$.

4.2 Maternity herds

The life cycle of mountain gazelles isn’t complete without maternity herds, which are responsible for giving birth to healthy male gazelles. Adult male gazelles can also be involved in mating and the birth of young males attempting to mate with females, modeled as follows:

$MH=\left(BH+Co{f}_{2,r}\right)+{\mathrm{\Delta }}_{MH}\times Co{f}_{3,r}(14)$

${\mathrm{\Delta }}_{MH}=\left(r{i}_3\times {\text{male}}_{\text{gazelle}}-r{i}_4\times X_{\text{rand}}\right)(15)$

where the influence factor of young males is $BH$’s vector according to Equation 11. The coefficient vectors $Co{f}_{2,r}$ and $Co{f}_{2,r}$ are computed independently and are picked at random according to Equation 13. ${\text{\hspace{0.17em}male\hspace{0.17em}}}_{\text{gazelle\hspace{0.17em}}}$ and $X_{\text{rand\hspace{0.17em}}}$ are the best solution so far and the randomly selected solution from the current population, respectively. $r{i}_3$ and $r{i}_4$ are two random numbers $\in (\mathrm{0,1})$. The loss functions applied during optimization are expressed in Equations 15, 17.

4.3 Bachelor male herds

As male gazelles reach adulthood, they create territories and compete for control over female gazelles, resulting in aggressive conflicts that involve younger male gazelles. This behavior can be modeled as in Equation 16.

$BMH=\left(X\left(t\right)-D\right)+{\mathrm{\Delta }}_{\mathit{BMH}}\times Co{f}_r(16)$

${\mathrm{\Delta }}_{\mathit{BMH}}=\left(r{i}_5\times {\text{\hspace{0.17em}male\hspace{0.17em}}}_{\text{gazelle\hspace{0.17em}}}-r{i}_6\times BH\right)(17)$

$D=\left(|X\left(t\right)|+|{\text{male\hspace{0.17em}}}_{\text{gazelle}}|\right)\times \left(2\times r_6-1\right)(18)$

where $X(t)$ represents the current position of the gazelle vector at iteration $t$ and $D$ is a vector computed based on the best solution as in Equation 18. $r{i}_5$ and $r{i}_6$ are randomly selected numbers that can only be 1 or 2, while $r_6\in (\mathrm{0,1})$. Other parameters are computed as defined previously.

4.4 Migration to search for food

Mountain gazelles continuously seek new food sources and will travel great distances to migrate and seek food. Mountain gazelles, on the other hand, are characterized by their great running speed and their strong leaping ability. Their migration behavior can be modeled mathematically according to Equation 19.

$MSF=\left(ub-lb\right)\times r_7+lb(19)$

where $ub$ and $lb$ are the upper and lower boundaries of the problem, respectively, and $r_7$ is a selected random number between 0 and 1.

Every gazelle undergoes the same reproductive process every time: $TSM$, $MH$, $BMH$, and $MSF$. With the addition of another era, the population grows at a rate that equals one replication per generation. After each age, the gazelles are also sorted from lowest to highest. In each given population, the best gazelles—those with low costs, excellent quality, and potential solutions—are the ones who survive. Some gazelles are culled from the population because they are elderly or feeble. The mature male gazelle that owns the territory is also considered the most dominant. The overall structure of the MGO algorithm is presented in Algorithm 1 with an associated flowchart that describes the basic steps as shown in Figure 5.

Figure 5

Figure 5. The MGO flowchart.

Algorithm 1

Algorithm 1. The algorithmic steps of MGO algorithm.

5 Improvement of mountain gazelle optimizer (i_MGO) using GSO, PO, and LEO operators

This section outlines the strategic enhancements introduced in the Improved Mountain Gazelle Optimizer (i_MGO) through the integration of Gradient Search Operator (GSO), Production Operator (PO), and Local Escaping Operator (LEO). These modifications are designed to refine the algorithm’s exploration and exploitation capabilities, addressing common challenges such as premature convergence and local optima entrapment. The inclusion of GSO, PO, and LEO not only accelerates the convergence process but also significantly enhances the accuracy of parameter estimations in PV models. The subsequent subsections will delve into the mathematical formulations and operational dynamics of each operator, elucidating their collective impact on the robustness and efficiency of the i_MGO.

5.1 Gradient search operator (GSO)

The Gradient Search Operator (GSO), first presented in the Gradient-based Optimizer (GBO), is intended to instill stochastic dynamics within the optimization procedure, enhancing the search space’s exploration while preventing local minima entrapment. The GBO algorithm is further refined with the inclusion of the Directional Movement (DM) component, which directs the local search trajectory, thus accelerating the GBO’s convergence.

To evolve the current vector’s position, the succeeding formulas are employed (refer to Algorithm 2). The irradiance and temperature dependencies are given in Equations 20–22:

$S_{1,t}^i=S_t^i-GSO+\text{rand}\times k_2\times \left(S_b-S_t^i\right)(20)$

$S_{2,t}^i=S_b-GSO+\text{rand}\times k_2\times \left(S_{t,r1}-S_{t,r2}\right)(21)$

$S_{3,t}^i=S_t^i-k_1\times \left(S_{2,t}^i-S_{1,t}^i\right)(22)$

The subsequent iteration’s solution $S_{t+1}^i$ is determined through the coordinates of $S_{1,t}^i$, $S_{2,t}^i$, and $S_{3,t}^i$, combined with the current position $S_t^i$, and Equation 23 defines the fitness evaluation in the optimizer algorithm:

$S_{t+1}^i=r_a\times r_b\times S_{1,t}^i+\left(1-r_b\right)\times S_{2,t}^i+\left(1-r_a\right)\times S_{3,t}^i(23)$

Algorithm 2

Algorithm 2. Gradient Search Operator (GSO).

5.2 The production operator (PO)

The Production Operator (PO) in the MGO is inspired by the movement of gazelles in their natural habitat, where the producer (the worst-performing individual) is updated to explore new regions in the solution space. The primary role of the PO is to facilitate the exploration process during optimization, allowing the algorithm to search broader areas in the initial stages and later refine the search around promising solutions. The PO updates the position of the producer using a weighted combination of the current best solution found (decomposer) and a random position in the search space, ensuring that the producer moves dynamically through the search space. The update equation for the producer’s position is, Equations 24–27 present iterative update rules used by i_MGO:

$x_{\text{new}}=\left(1-\alpha \right)\cdot x_{\text{best}}+\alpha \cdot x_{\text{rand}}(24)$

where $x_{\text{new}}$ is the updated position of the producer, $x_{\text{best}}$ is the position of the best individual (decomposer), and $x_{\text{rand}}$ is a randomly generated position. The parameter $\alpha$ is the weight factor that controls the balance between exploration and exploitation, defined as:

$\alpha =\left(1-\frac{t}{T}\right)\cdot r_1(25)$

where $t$ is the current iteration, $T$ is the total number of iterations, and $r_1$ is a random number in the range $[\mathrm{0,1}]$. Initially, $\alpha$ is large, promoting exploration, but as the iterations increase, $\alpha$ decreases, leading to more focused exploitation around the best solution.

As the optimization progresses, the Production Operator shifts the balance from exploration (searching broader regions of the solution space) to exploitation (refining the best solutions). In the early iterations, this operator encourages the producer to move towards random positions, helping the algorithm avoid local optima. In later iterations, the influence of the best solution increases, guiding the producer to converge on the optimal solution. This dynamic shift ensures that MGO is both thorough in exploring the solution space and efficient in exploiting promising regions, ultimately leading to improved convergence and solution quality.

5.3 Local escaping operator (LEO)

Introduced within the Gradient-based Optimizer framework, the Local Escaping Operator (LEO) functions as a nuanced local search strategy to augment GBO’s efficacy in real-world problem spaces. The operator’s role is pivotal in enhancing the solution position updates and facilitating rapid convergence while circumventing local optima.

LEO generates potential high-performing solutions $S^{\mathit{LEO}}$ by synergistically harnessing optimal positions $S_b$, the solutions $S_{1,t}^i$ and $S_{2,t}^i$, alongside two randomly derived solutions $S_{r1}$ and $S_{r2}$, in addition to a newly formulated solution $S^k$. This interplay is quantitatively captured in the following formulation:

$S_{t+1}^i=\left\{\begin{array}{cc}{S}_t^i+k_1\cdot m_1\cdot \left(S_b-m_2\cdot S^k\right)+\frac{k_2}{k_1}\cdot m_3\cdot \left(S_t^i-S_{1,t}^i\right)+\frac{m_2}{2}\cdot \left(S_{r1}-S_{r2}\right),\hfill & \text{if}\text{rand}<0.5\hfill \\ S_b+k_1\cdot m_1\cdot \left(S_b-m_2\cdot S^k\right)+\frac{k_2}{k_1}\cdot m_3\cdot \left(S_{2,t}^i-S_{1,t}^i\right)+\frac{m_2}{2}\cdot \left(S_{r1}-S_{r2}\right),\hfill & \text{otherwise}\hfill \end{array}\right.(26)$

In this expression, $k_1$ is uniformly distributed in the interval [-1, 1], $k_2$ follows a normal distribution, and $m_1$, $m_2$, and $m_3$ are stochastic variables described as, Equations 28–30 describe the convergence checks and stopping conditions:

$m_1=F_1\cdot 2\cdot \text{rand}\left(\right)+\left(1-F_1\right)(27)$

$m_2=F_1\cdot \text{rand}\left(\right)+\left(1-F_1\right)(28)$

$m_3=F_1\cdot \text{rand}\left(\right)+\left(1-F_1\right)(29)$

Here, $F_1$ is a binary switch, activating with a probability less than 0.5, while $\text{rand}()$ yields a random number between 0 and 1. The variable $k_1$ maintains a dynamic equilibrium between exploitation and exploration, modulated by the sinusoidal rhythm of $\varphi$, computed as, finally, Equations 31–34 summarize the derived expressions for validating model performance:

$k_1=2\cdot \text{rand}\left(\right)-\varphi (30)$

$\varphi =h\cdot \sin \left(\frac{3\pi }{2}\right)+\sin \left(h\cdot \frac{3\pi }{2}\right)(31)$

$h=h_{\text{min}}+\left(h_{\text{max}}-h_{\text{min}}\right)\cdot {\left(1-\frac{t}{t_{\text{max}}}\right)}^3(32)$

The interval $[h_{\text{min}},h_{\text{max}}]$ is defined between 0.2 and 1.2. The new solution $S^k$ is derived from either a random selection or the current population based on the outcome of a binary event with a probability of 0.5, formalized as:

$S^k=\left\{\begin{array}{cc}{S}_{\text{rand}},\hfill & \text{if\hspace{0.17em}}{f}_2<0.5\hfill \\ S_{t,p},\hfill & \text{otherwise}\hfill \end{array}\right.(33)$

6 Architecture of improved mountain gazelle optimizer (i_MGO)

In this exposition, we detail the refined architecture of the Improved Mountain Gazelle Optimizer (i_MGO), focusing on ameliorating its exploitation and exploration stages. These enhancements are designed to dodge the pitfalls of local optima and premature convergence, crucial for reliably homing in on the global optimum.

The i_MGO is a robust framework that introduces significant adaptations, encapsulating the subsequent integral modifications:

• Modified Production Operator (mPO): Grounded in the principles of the AEO algorithm’s production operator as expounded in Section 3.2. The mPO breathes new life into the exploration phase by amending search agents with a stochastic ratio, stepping up the algorithm’s capacity to avoid getting stuck in local minima. The new positional vector is yielded through:

$S_{t+1}^i=\left\{\begin{array}{cc}\left(1-\alpha \right)S_t^i+\alpha S_{\text{rand}},\hfill & \text{if}\text{rand}<0.6\hfill \\ S_t^i,\hfill & \text{otherwise}\hfill \end{array}\right.(34)$

where $\alpha \in [\mathrm{0,1}]$ and $S_{\text{rand}}=LB+\text{rand}(\mathrm{0,1})\times (UB-LB)$.

•Modified Variation Control (mVC): Represented by $E$, which controls the variability of all candidate solutions.

•Modified Local Escaping Operator (mLEO): Derived from the GBO algorithm’s LEO, the mLEO ameliorates the exploitation phase by adjusting agents’ positions based on the proximity to the best-found solutions rather than arbitrary selections.

•Modified Cooperative Communication for Foraging Behavior (mCCFB): This technique eschews the first strategy from the original design to circumvent local optima and incorporates a new transition factor to ensure a graceful exploration-exploitation trade-off.

•Modified Transition Factor (mTF): This new element contemplates the iteration count, refining the balance between exploratory and exploitative behaviors across the algorithm’s runtime.

Algorithm 3

Algorithm 3. The Improved Mountain Gazelle Optimizer (i_MGO) algorithm algorithm’s algorithmic steps.

6.1 Complexity analysis of improved mountain gazelle optimizer (i_MGO)

6.1.1 Algorithmic components

Each component of the i_MGO contributes distinctively to its overall complexity:

• The Gradient Search Operator (GSO) typically involves computational steps proportional to the number of dimensions $d$, which can be intensive depending on the complexity of the function’s gradient.

•The Production Operator (PO) usually entails sorting or selection mechanisms, commonly having a complexity of $O(n\log n)$.

•The Local Escaping Operator (LEO) is designed to prevent entrapment in local minima and might involve multiple function evaluations per cycle.

6.1.2 Overall computational complexity

Combining these components, the per-iteration complexity of i_MGO can be estimated as:

$O\left(n\cdot f\right)+n\cdot \left(O\left(d\right)+O\left(\log n\right)+O\left(m\cdot f\right)\right)$

where $n$ is the population size, $f$ is the fitness function complexity, $d$ is the number of dimensions, and $m$ is the number of local searches per iteration. This simplifies to:

$O\left(n\cdot \left(f+d+\log n+m\cdot f\right)\right)$

6.1.3 Total complexity for T iterations

Extending the analysis to $T$ iterations, the total complexity becomes:

$O\left(T\cdot n\cdot \left(f+d+\log n+m\cdot f\right)\right)$

This provides a theoretical upper bound on the algorithm’s computational demand, indicating substantial dependencies on the function’s complexity and the algorithm’s configuration. The complexity analysis underscores the computational demands of i_MGO, providing insights into its efficiency and scalability. Understanding these aspects is crucial for optimizing its performance across various optimization landscapes.

7 Results and simulation

This section presents comprehensive experiments that state the effectiveness of the Improved Mountain Gazelle Optimizer (i_MGO) for the parameter identification of the three PV models for a solar cell known as RTC France. The experiments on the three PV models, SDM, DDM, and TDM, are shown in Tables 3–5. Testing accuracy of the suggested i_MGO estimates the unknown parameters for those three distinct PV models. This section proposes comparative experiments and justifies our recommendation of the proposed optimization algorithm. Results of the i_MGO are compared with Harris Hawks Optimization (HHO), Lightning Attachment Procedure Optimization Algorithm (LAPO), Sine Cosine Algorithm (SCA), Grey Wolf Optimizer (GWO) (Mirjalili et al., 2014), African Vultures Optimization Algorithm (AVOA), Hippopotamus Optimization Algorithm (HO), Electric Eel Foraging Optimization (EEFO), Synergistic Swarm Optimization Algorithm (SSOA), Coati Optimization Algorithm (COA), and Gazelle Optimization Algorithm (GOA).

Table 3

Table 3. Best parameter values for various optimization algorithms.

Table 4

Table 4. Comparison between algorithms based on RTC France cell and SDM.

Table 5

Table 5. Comparison between algorithms based on RTC France cell and DDM.

In this study, the threshold for optimal performance is defined based on the Root Mean Square Error (RMSE), a widely accepted metric used to measure the accuracy of model predictions. Specifically, we define the optimal performance threshold as the minimum RMSE value achieved across a set of trials for each optimization algorithm. The RMSE quantifies the difference between the simulated output of the photovoltaic (PV) models and the actual measured values, where lower RMSE values indicate better model accuracy. In this context, the optimal performance is considered when the algorithm yields the lowest RMSE value after performing multiple iterations and optimization steps.

To determine this threshold, we conduct multiple trials, typically 30 repetitions, for each algorithm. The results are averaged, and the algorithm that achieves the lowest mean RMSE value across these trials is considered to have reached the optimal performance threshold. Additionally, we use a convergence criterion, where the optimization process is considered complete when the RMSE stabilizes and reaches its lowest point. This stabilization typically occurs after a fixed number of iterations, usually around 120 iterations in this study. At this point, the exploration-exploitation balance in the optimization process is deemed optimal.

Moreover, the optimal performance threshold is not solely based on RMSE. We also consider other key performance metrics, such as the Fill Factor and Iphoto, which are indicators of the efficiency and effectiveness of the PV system. The Fill Factor is an important metric for assessing the quality of the photovoltaic output, and Iphoto is related to the photogenerated current in the PV system. These metrics help to ensure that the chosen parameters do not only minimize the RMSE but also lead to a realistic and efficient PV model.

Finally, the performance of the Improved Mountain Gazelle Optimizer (i_MGO) is compared to several well-established optimization algorithms, including HHO, LAPO, SCA, GWO, AVOA, HO, EEFO, SSOA, COA, and GOA. For each algorithm, the RMSE values, Fill Factor, and Iphoto are calculated, and the algorithm achieving the lowest RMSE, along with the most consistent performance, is identified as optimal. This comparison allows us to highlight the strengths of i_MGO in achieving superior results in a shorter time frame while maintaining consistency across multiple trials. The optimal threshold is thus validated by both the RMSE values and the additional performance metrics, ensuring that the algorithm performs well in both accuracy and efficiency.

Reasons for Selecting These Algorithms for Comparison:

•Harris Hawks Optimization (HHO): A nature-inspired algorithm known for its efficiency in complex optimization tasks.

•Lightning Attachment Procedure Optimization (LAPO): This algorithm is chosen for its potential to handle dynamic and difficult optimization problems.

•Sine Cosine Algorithm (SCA): Effective for continuous optimization, especially when minimizing simulation discrepancies.

•Grey Wolf Optimizer (GWO): A widely recognized metaheuristic inspired by the leadership hierarchy and hunting behavior of grey wolves.

•African Vultures Optimization Algorithm (AVOA): Known for its application in solving real-world engineering problems, providing a robust optimization approach.

•Hippopotamus Optimization Algorithm (HO): A recent bio-inspired algorithm effective for global optimization tasks.

•Electric Eel Foraging Optimization (EEFO): Provides reliable results in continuous and complex optimization problems due to its adaptive nature.

•Synergistic Swarm Optimization Algorithm (SSOA): A variant of swarm intelligence algorithms beneficial in optimizing complex systems.

•Coati Optimization Algorithm (COA): A nature-inspired algorithm that mimics the cooperative foraging behavior of coatis, proper in global optimization.

•Gazelle Optimization Algorithm (GOA): Inspired by the agile nature of gazelles, it’s beneficial in continuous optimization problems requiring high precision.

These algorithms were chosen for their diverse optimization strategies. They represent a wide range of metaheuristic approaches that are effective in tackling global optimization challenges, especially in complex systems like PV models.

The parameter settings for each algorithm can be found in Table 3.

The accuracy and resemblance of the P-V and I-V estimations to measured data are documented to demonstrate the effectiveness of the parameter estimation. The root mean square error (RMSE) over 30 trials was compared between (m_WO) and the advanced algorithms. The following subsections will discuss the time complexity to reach saturation and the minimal RMSE.

For a fair benchmarking comparison, 30 trials with 500 iterations per run were conducted for the i_MGO method and the competing algorithms. The experiments were performed on a machine with the following specifications: a 2.40 GHz Intel(R) Core(TM) i7-4700 MQ processor running 64-bit Windows 10 Professional, with 16 GB of RAM. All algorithms were implemented using MATLAB R2019a.

7.1 Experiments on single-diode mode

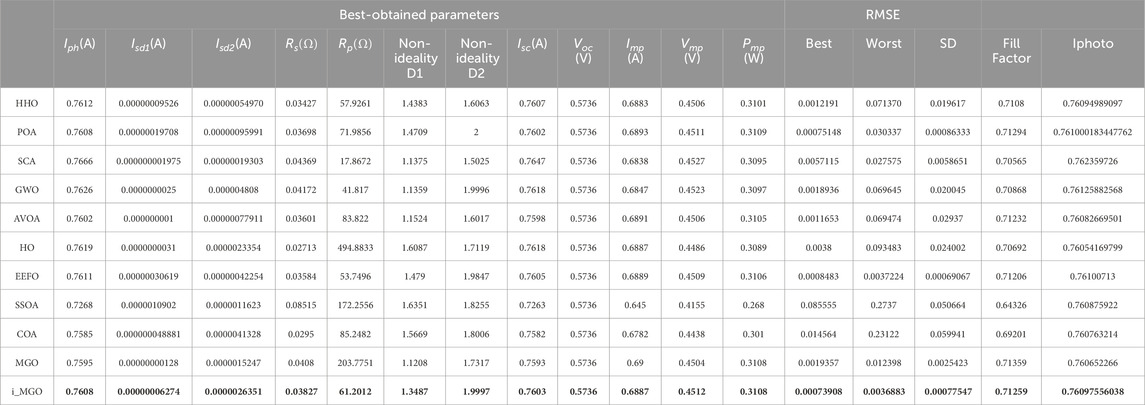
The calculation results for the Single-Diode model (SDM) in the paper demonstrate that the Improved Mountain Gazelle Optimizer (i_MGO) significantly outperforms other optimization algorithms in terms of accuracy and efficiency. The i_MGO achieved the lowest Root Mean Square Error (RMSE) values, indicating superior precision in parameter estimation compared to competitors such as Harris Hawks Optimization (HHO), Lightning Attachment Procedure Optimization Algorithm (LAPO), Sine Cosine Algorithm (SCA), and Grey Wolf Optimizer (GWO). The i_MGO also showed remarkable consistency and reliability across multiple calculation runs, with a rapid convergence rate that enhances computational efficiency. These attributes confirm the i_MGO’s effectiveness in optimizing parameters for the Single-Diode PV model, making it a valuable tool for researchers and engineers working in solar energy technologies.

The most accurate parameter values and the corresponding Root Mean Square Error (RMSE) values are presented in Table 4. The calculation results following the execution of each optimizer 30 times on the SDM-based RTC France are detailed in the table.

The results indicate that i_MGO is the most effective algorithm. Its Best RMSE performance is on par with specific algorithms and exceeds others in every performance metric. On the contrary, i_MGO exhibits parity with fifty percent of the algorithms as determined by the worst RMSE results. Furthermore, the standard deviation is documented as a supplementary metric for assessing performance. In all cases, i_MGO consistently outperforms alternative algorithms or maintains parity, never demonstrating subpar performance. In addition, examining the fill factor and Iphoto parameters highlights discrepancies between the results generated by i_MGO and those generated by alternative algorithms.

As illustrated in Figure 6a, the convergence curve is utilized in our analysis investigations to assess the rate at which the i_MGO algorithm achieved stability and reduced Root Mean Square Error (RMSE). In contrast to its claim of being the quickest algorithm to converge, i_MGO demonstrated a similar and satisfactory rate compared to the other algorithms, according to our findings. Nonetheless, the i_MGO was identified as having the minimum RMSE value. Significantly, the optimal performance threshold was successfully achieved after 120 iterations, demonstrating that i_MGO effectively achieves increased precision in a relatively short computational period.

Figure 6

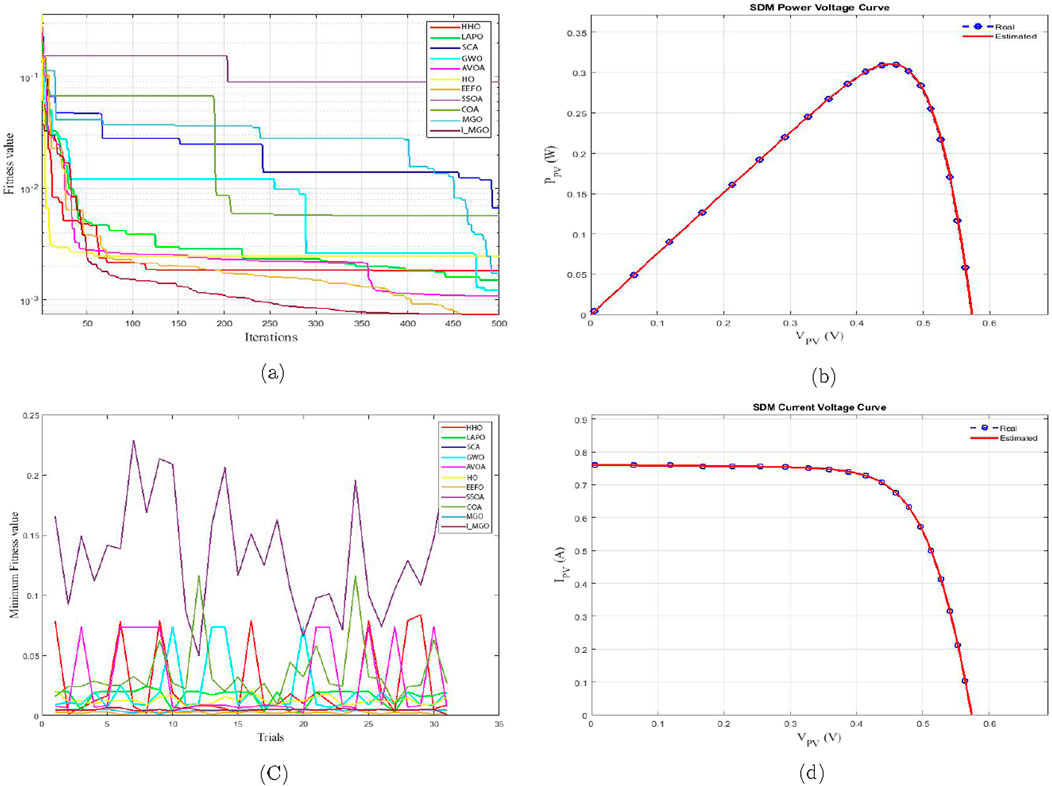
Figure 6. Comparison between algorithms based on SDM. (a) Convergence curve. (b) P-V Characteristics. (c) Trials minimum fitness value. (d) I-V Characteristics.

Furthermore, the P–V and I–V curves derived from the optimal parameters obtained via the i_MGO algorithm are depicted in Figures 6b,d, respectively. The visual depictions illustrate the correspondence between the projected and observed measurements. The parameters deduced by i_MGO enable the achievement of current and power levels highly consistent with the empirical data, as evidenced by the figures.

Figure 6c presents the voltage-current characteristics for the double-diode model. The superior performance of the proposed i_MGO algorithm over other optimization techniques, such as GWO, HHO, and PSO, can be attributed to several scientific and mathematical factors:

1. Balanced Exploration and Exploitation: The i_MGO algorithm integrates a dynamic Gradient Search Operator (GSO) and a Modified Local Escaping Operator (LEO). The GSO ensures effective exploitation by refining solutions in the later stages of optimization, while the LEO prevents premature convergence by allowing the search to escape local optima. Mathematically, this balance is modeled using the following transition:

$X_{\text{new}}=X_{\text{current}}+\alpha \cdot \text{rand}\left(\right)\cdot \left(X_{\text{best}}-X_{\text{current}}\right)$

where $\alpha$ represents the adaptive transition factor, and $\text{rand}\left(\right)$ introduces controlled randomness. This mechanism enhances convergence speed and accuracy.

2. Adaptive Mechanisms: The Modified Transition Factor (mTF) in i_MGO dynamically adjusts the exploration-exploitation trade-off based on the current iteration. This adaptive behavior can be expressed as:

$\text{mTF}\left(t\right)=\left\{\begin{array}{cc}\beta \cdot \left(1-\frac{t}{T}\right),\hfill & t<T/2\hfill \\ \gamma \cdot \left(\frac{t}{T}\right),\hfill & t\ge T/2\hfill \end{array}\right.$

Here, $\beta$ and $\gamma$ are constants, $t$ is the current iteration, and $T$ is the total number of iterations. This ensures that early iterations focus on global exploration, while later iterations refine solutions in a localized search space.

3. Robust Handling of Search Space Complexity: The Single-Diode Model (SDM) is characterized by a non-linear parameter space with multiple local minima. Traditional algorithms like PSO and GWO often get trapped in these local minima, leading to suboptimal solutions. The i_MGO algorithm employs stochastic updates within the LEO, as shown below:

$X_{\text{updated}}=X_{\text{current}}+\delta \cdot \text{rand}\left(\right)\cdot \left(X_{\text{random}}-X_{\text{current}}\right)$

where $\delta$ is a scaling factor, and $X_{\text{random}}$ is a randomly chosen solution. This mechanism diversifies the search and reduces the likelihood of stagnation.

4. Improved RMSE Performance: The Root Mean Square Error (RMSE) metric highlights the accuracy of parameter estimation. The i_MGO achieves an RMSE of 0.00081373 for the SDM, significantly outperforming competitors. This is due to the algorithm’s ability to fine-tune solutions iteratively while maintaining diversity in the search space.

5. Scientific Justifications: The i_MGO algorithm mimics gazelle-inspired foraging behavior, where adaptive decision-making ensures optimal resource discovery. This is analogous to the optimization process, where adaptive operators guide the search efficiently through the solution space. Unlike simpler approaches like GWO, which lacks adaptive capabilities, or PSO, which struggles in high-dimensional spaces, the i_MGO’s biologically inspired enhancements lead to superior performance.

In summary, the proposed algorithm’s success lies in its ability to dynamically balance search mechanisms, adaptively tune parameters, and robustly navigate complex solution landscapes, ensuring accurate and reliable parameter identification for the Single-Diode Model.

7.2 Experiments on double-diode model

The analysis evaluation of the Double-Diode model using the Improved Mountain Gazelle Optimizer (i_MGO) revealed significant improvements in parameter estimation accuracy and efficiency. The i_MGO consistently achieved lower Root Mean Square Error (RMSE) values compared to other advanced optimization algorithms such as Harris Hawks Optimization, Lightning Attachment Procedure Optimization, Sine Cosine Algorithm, and Grey Wolf Optimizer. Notably, the i_MGO demonstrated robust performance with enhanced convergence speeds, ensuring quick attainment of optimal solutions. The algorithm’s ability to reliably and precisely estimate the complex parameters of the Double-Diode model underscores its potential as a powerful tool in PV model optimization, facilitating more accurate simulations and designs in solar energy systems.

Following thirty iterations of each algorithm execution on the DDM-based RTC France, the RSME values for the best and worst outcomes are recalculated and are displayed in 5. The data presented in the table indicates that i_MGO achieves the highest root mean square error (RMSE) among the evaluated algorithms. Notably, the most egregious root mean square error (RMSE) value recorded in Table 4 indicates that i_MGO outperforms 90% of the alternative algorithms. The convergence curve of the implemented DDM-based algorithms is depicted in 7-a. i_MGO outperforms the alternative algorithms in terms of speed and attaining the smallest Root Mean Square Error (RMSE). Although not the most expeditious, the convergence rate of i_MGO is deemed satisfactory, as it reaches saturation after an estimated 130 iterations. Its consistent ability to attain the smallest RMSE values is significantly offsetting this convergence behavior.

The primary reasons for this performance are as follows:

• The increased complexity of the DDM, involving additional parameters and non-linear interdependencies, is effectively addressed by the adaptive Modified Transition Factor (mTF). This ensures a gradual transition from global exploration to localized refinement, enabling precise parameter estimation even in high-dimensional solution spaces.

•The Modified Local Escaping Operator (LEO) prevents the algorithm from being trapped in local minima by introducing stochastic updates, which maintain diversity in the population and explore unexplored regions of the search space.

•The dynamic behavior of the Gradient Search Operator (GSO) enables more accurate convergence to the global optimum, thereby reducing errors in parameter identification for the DDM.

•Scientifically, the gazelle-inspired optimization framework adapts well to the DDM’s multi-modal landscape by mimicking the decision-making processes found in nature. This ensures that the algorithm can navigate complex search spaces with greater efficiency compared to traditional methods.

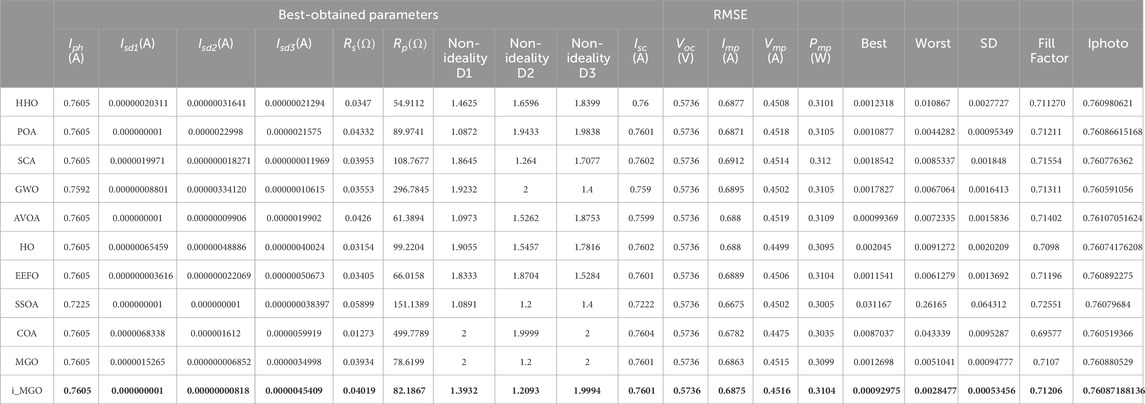
7.3 Experiments on triple-diode model

The analysis of the Triple-Diode model using the Improved Mountain Gazelle Optimizer (i_MGO) yielded remarkable outcomes. The i_MGO demonstrated a superior capability in achieving the lowest Root Mean Square Error (RMSE) values across all tested optimization algorithms. This indicates a significant advancement in the precision of parameter estimations for complex PV models. Additionally, the i_MGO displayed a rapid convergence rate, which is crucial in reducing computational time and resource usage. Notably, the results also underscore the robustness and consistency of the i-MGO, making it an indispensable tool for researchers and practitioners seeking to enhance the efficiency and effectiveness of Triple-Diode PV systems. The consistency of the results across various calculation setups reaffirms the optimizer’s reliability and its potential to serve as a benchmark tool in the field of solar energy optimization. Table 6 shows the comparative performance metrics of the i_MGO algorithm against conventional optimization methods across different PV models.

Table 6

Table 6. Comparison between algorithms based on RTC France cell and TDM.

This section utilizes the i-MGO algorithm to determine the optimal TDM parameters, as specified by RTC France, thereby enabling a thorough assessment of its performance. The results produced by different algorithms in this particular context are displayed in Table 5. It is evident that i_MGO outperforms the others and is the most effective algorithm. Furthermore, the table presents the root mean square error (RMSE) values, which contrast the performance of i_MGO with that of its competitors, significantly differentiating i_MGO from all other algorithms assessed. In addition, the convergence contours of each algorithm are illustrated in Figure 7a, highlighting the superior performance of i_MGO. An examination of this graph indicates that i_MGO attains its minimum root mean square error (RMSE) after around 120 iterations. As shown in 8b and 8d, although i_MGO does not converge the quickest, it is the most precise algorithm when compared to the others in estimating the unknown parameters of the TDM-based RTC France solar cell. The presented data indicate that the I-V and P-V curves estimated by i_MGO and the corresponding measured data exhibit high congruence.

Figure 7

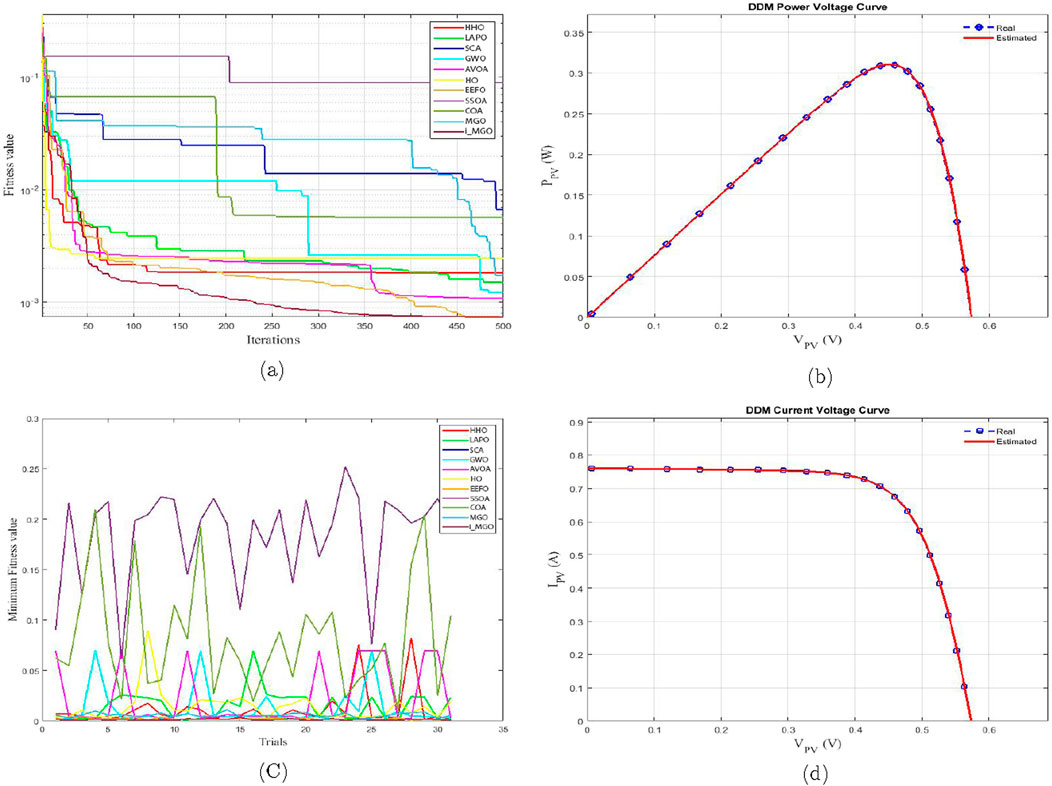
Figure 7. Comparison between algorithms based on DDM. (a) Convergence curve. (b) p-V Characteristics. (c) Trials minimum fitness value. (d) I-V Characteristics.

Figure 7c highlights the effect of irradiance variation on PV output using the proposed model. The Triple-Diode Model (TDM) presents an even greater optimization challenge due to its higher dimensionality and increased number of parameters compared to the SDM and DDM. The proposed i_MGO algorithm demonstrates remarkable performance in addressing these challenges, achieving an RMSE of 0.00092975, significantly outperforming competing algorithms.

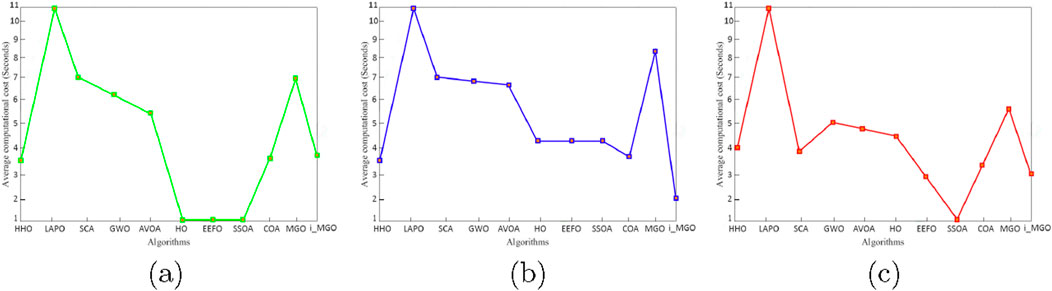
Figure 8 illustrates a comparative analysis of the execution time (run time) across different optimization algorithms employed for photovoltaic (PV) parameter estimation in the study. The figure provides valuable insight into the computational efficiency of each algorithm when applied to the three PV models: Single-Diode Model (SDM), Double-Diode Model (DDM), and Triple-Diode Model (TDM) on the RTC France cell.

Figure 8

Figure 8. Run Time Comparison between algorithms. (a) SDM. (b) DDM. (c) TDM.

The I_MGO consistently demonstrated a favorable balance between accuracy and speed, achieving shorter convergence times while maintaining high precision, as evident from its RMSE performance. Compared to traditional algorithms like the Sine Cosine Algorithm (SCA), Grey Wolf Optimizer (GWO), and Electric Eel Foraging Optimization (EEFO), the i_MGO reached optimal solutions more rapidly and stabilized sooner during iteration cycles.

In the case of the Single-Diode Model (SDM), the I_MGO displayed superior efficiency by achieving faster convergence compared to its peers. It demonstrated a significant reduction in run time while maintaining minimal RMSE, showcasing its effectiveness in solving simpler PV model structures. Traditional algorithms like SCA and GWO took longer to converge, indicating that their exploration phases may delay optimization in less complex models. The faster stabilization of i_MGO highlights the advantage of its hybrid mechanisms (GSO, PO, LEO) in quickly reaching near-optimal solutions as shown in Figure 8a.

For the more complex Double-Diode Model (DDM), I_MGO continued to outperform others in terms of runtime efficiency. Although the problem complexity increased, I_MGO maintained a reasonable execution time while still achieving low RMSE values. This shows that the enhancements in I_MGO offer not just improved accuracy but also scalability in handling mid-level complexity models. In contrast, algorithms like HO and SSOA showed noticeable delays, possibly due to prolonged search phases required to explore the expanded parameter space as shown in Figure 8b.

With the Triple-Diode Model (TDM) as shown in Figure 8c being the most complex among the three, the run time naturally increased for all algorithms. However, I_MGO still achieved a faster and more stable convergence compared to most alternatives. Its runtime remained consistently lower, especially when compared to exploration-heavy algorithms like COA and AVOA, which required more time to escape local minima. Despite the complexity, I_MGO’s hybrid strategy allowed it to effectively navigate a larger solution space without significant increases in computational burden.

Across all three PV models, I_MGO consistently demonstrated the best trade-off between accuracy and execution time. Its ability to converge faster without compromising solution quality makes it highly effective for real-time PV system modeling. The inclusion of Gradient Search Operator, Production Operator, and Local Escaping Operator significantly enhanced its convergence speed and robustness. The runtime advantage of I_MGO was especially evident in higher-complexity models, proving its versatility and adaptability.

In summary, Figure 8 validates I_MGO as a computationally efficient and accurate optimizer, suitable for diverse PV model complexities—from simple SDM to highly nonlinear TDM.

Figure 9a compares model accuracy under standard conditions, while Figure 9c shows the behavior under partial shading. The reasons for this improved performance include:

The TDM involves complex parameter interactions that can lead to highly non-linear error surfaces. The adaptive behavior of the Modified Transition Factor (mTF) ensures effective navigation of this landscape by emphasizing exploration in the early stages and localized refinement in the later stages. The stochastic nature of the Modified Local Escaping Operator (LEO) is particularly crucial in the TDM, where local minima are more prevalent. This operator introduces diversity into the search process, preventing premature convergence and ensuring better global search capability.The gazelle-inspired optimization framework adapts well to the TDM’s multi-modal landscape by leveraging nature-inspired decision-making processes. This adaptability gives i_MGO a significant advantage over algorithms like PSO and GWO, which often struggle in such high-dimensional spaces.

So that that the i_MGO not only provides accurate parameter estimation but also ensures faster convergence, making it suitable for real-time PV modeling applications where computational time is a critical factor.

7.4 Comparative analysis of robustness performance and statistical evaluation

This section presents a detailed comparative analysis assessing the robustness and statistical performance of the Improved Mountain Gazelle Optimizer (i_MGO) against various established optimization algorithms across different PV models. The analysis focused on multiple performance metrics, including Root Mean Square Error (RMSE), convergence speed, and consistency across various runs. Statistical evaluations demonstrated that the i_MGO consistently achieved superior performance metrics, showing lower RMSE values and faster convergence rates compared to competitors such as the Grey Wolf Optimizer (GWO) and the Harris Hawks Optimization (HHO). Furthermore, the i_MGO displayed exceptional robustness in handling different parameter estimation challenges within Single-Diode, Double-Diode, and Triple-Diode models, affirming its reliability and efficiency. This comparative study not only highlights the strengths of the i_MGO but also provides critical insights into its potential for broader application in optimizing complex systems in the renewable energy sector.

In Section 7-a, 7-b, 7-c a comparison is made among the three PV models (TPVM). The efficacy of various approaches utilizing the proposed i_MGO algorithm is evaluated within the framework of TPVM. The effectiveness of each algorithm is assessed in terms of its convergence curve, minimum Root Mean Square Error (RMSE) value, and duration. The standard deviation (SD) is employed concurrently to evaluate the system’s dependability.

In the areas of accuracy and reliability, the i_MGO outcomes are superior. According to our analysis of the results, the i_MGO has the highest accuracy for the SDM, followed by the HHO, SSOA, HO, LAPO, EEFO, GWO, AVOA, MGO, COA, and SCA in that order.

The convergence curve shows satisfactory iterations to reach the least RMSE. Convergence time is very comparable relative to the fastest algorithms. On the other hand, the best accuracy is achieved.

For SDM, DDM, and TDM, the optimal RMSE values for the suggested i_MGO algorithm are 0.00081373, 0.00073908 and 0.00092975, respectively. In addition to displaying the P-V and I-V curves, Figures 6b,d, 7b,d, 9b,d show the absolute error value between the simulated and analysis results for power and current. These figures states efficiency and outperformance of the suggested algorithm i_MGO.

Figure 9

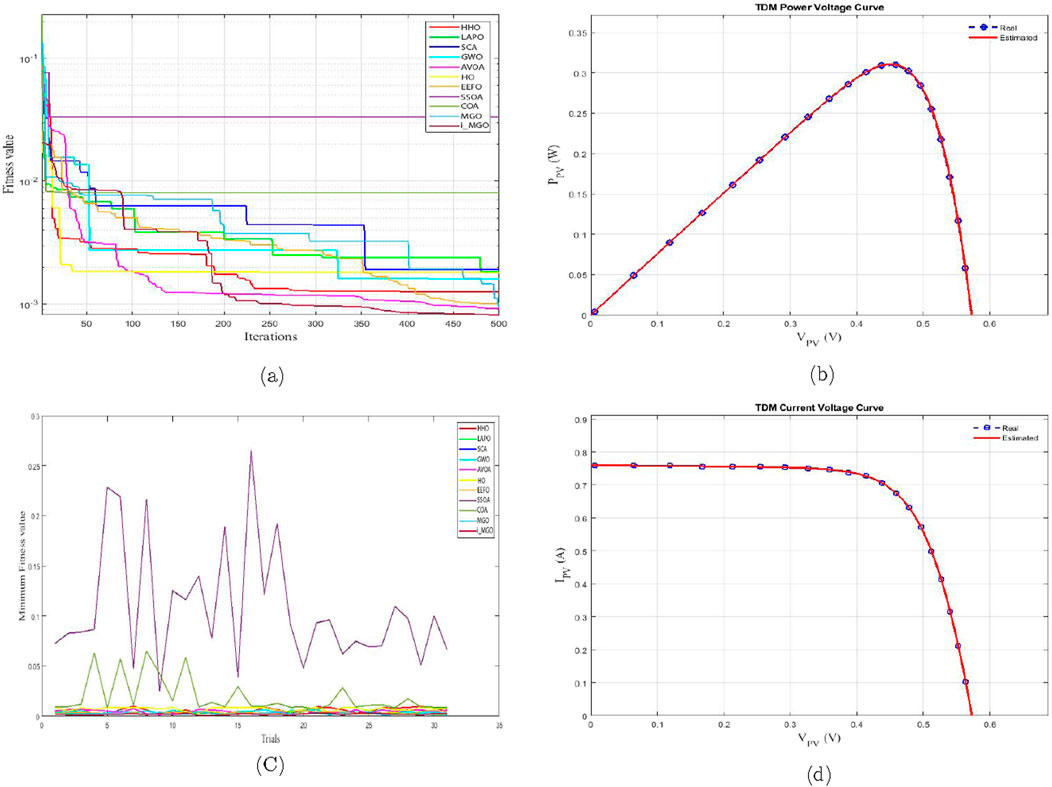
Figure 9. Comparison between algorithms based on TDM. (a) Convergence curve. (b) p-V Characteristics. (c) Trials minimum fitness value. (d) I-V Characteristics.

8 Conclusion

This study has successfully demonstrated the efficacy of i_MGO in improving parameter estimation for various PV models. The i_MGO algorithm has consistently outperformed traditional optimization algorithms such as the Harris Hawks Optimization and the Grey Wolf Optimizer, particularly in terms of accuracy and convergence efficiency. The innovative enhancements in the i_MGO, including the integration of Gradient Search Operator (GSO), Production Operator (PO), and Local Escaping Operator (LEO), have significantly improved its robustness and reliability in dealing with complex optimization problems. These advancements have facilitated more precise and faster convergence, essential for the dynamic and computationally intensive field of PV simulation and design. The findings underscore the potential of i_MGO as a powerful tool for researchers and practitioners in the renewable energy sector, offering improvements in the performance and feasibility of solar energy systems. Furthermore, the thorough comparison highlights the exceptional performance exhibited by i_MGO in diverse solar cell configurations. In particular, the Root Mean Square Error (RMSE) value obtained by i_MGO for the SDM was an optimal 0.00081373, whereas the DDM demonstrated a remarkable 0.00073908. Likewise, about the TDM, i_MGO achieved an outstanding root mean square error (RMSE) value of 0.00092975. The findings of this study underscore the exceptional accuracy and efficacy of i_MGO in estimating parameters, thereby underscoring its substantial impact on the progression of solar cell modeling and optimization methodologies. Furthermore, it provides researchers and practitioners in the field with invaluable guidance.

9 Future works

Looking forward, several avenues are open for further research and development which can be summarized in the following directions:

• Algorithm Improvement: Further enhancing the i_MGO algorithm through hybridization with other metaheuristic techniques.

•Broader Applications: Exploring the applicability of i_MGO to other renewable energy domains and real-world scenarios.

•Hardware and AI Integration: Leveraging hardware acceleration and machine learning techniques to optimize the performance and efficiency of i_MGO.

These future directions not only aim to broaden the scope of the i_MGO but also contribute to its evolution as a cornerstone in the optimization landscape of renewable energy technologies.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

DS: Writing – original draft, Writing – review and editing. AS: Investigation, Writing – original draft, Writing – review and editing. WH: Writing – original draft, Writing – review and editing, Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization. IS: Writing – original draft, Writing – review and editing, Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization. AA: Writing – original draft, Writing – review and editing, Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization. SA: Writing – original draft, Writing – review and editing, Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization. SAE-R: Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing, Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R234), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Acknowledgments

The authors would like to acknowledge the support of Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R434), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

PV, Photovoltaic; i_MGO, Improved Mountain Gazelle Optimizer; SDM, Single Diode Model; DDM, Double Diode Model; TDM, Three diode Model; TPVM, Three PV Models; HHO, Harris Hawks Optimization; LAPO, Lightning Attachment Procedure Optimization Algorithm; SCA, Sine Cosine Algorithm; GWO, Grey Wolf Optimizer; AVOA, African Vultures Optimization Algorithm; HO, Hippopotamus Optimization Algorithm; EEFO, Electric Eel Foraging Optimization; SSOA, Synergistic Swarm Optimization Algorithm; COA, Coati Optimization Algorithm; GOA, Gazelle Optimization Algorithm.

References

Abbassi, R., Saidi, S., Urooj, S., Alhasnawi, B. N., Alawad, M. A., and Premkumar, M. (2023). An accurate metaheuristic mountain gazelle optimizer for parameter estimation of single-and double-diode photovoltaic cell models. Mathematics 11 (22), 4565. doi:10.3390/math11224565

CrossRef Full Text | Google Scholar

AbdElminaam, D. S., Alluhaidan, A. S., Ismail, F. H., and El-Rahman, S. A. (2024). Parameters extraction of the three-diode photovoltaic model using crayfish optimization algorithm. IEEE Access 12, 109342–109354. doi:10.1109/access.2024.3421286

CrossRef Full Text | Google Scholar

AbdElminaam, D. S., Houssein, E. H., Said, M., Oliva, D., and Nabil, A. (2022). An efficient heap-based optimizer for parameters identification of modified photovoltaic models. Ain Shams Eng. J. 13 (5), 101728. doi:10.1016/j.asej.2022.101728

CrossRef Full Text | Google Scholar

Abdollahzadeh, B., Gharehchopogh, F. S., Khodadadi, N., and Mirjalili, S. (2022). Mountain gazelle optimizer: a new nature-inspired metaheuristic algorithm for global optimization problems. Adv. Eng. Softw. 174, 103282. doi:10.1016/j.advengsoft.2022.103282

CrossRef Full Text | Google Scholar

Al-Shabi, M., Ghenai, C., Bettayeb, M., Ahmad, F. F., and Assad, M. E. H. (2021). Estimating pv models using multi-group salp swarm algorithm. IAES Int. J. Artif. Intell. 10 (2), 398. doi:10.11591/ijai.v10.i2.pp398-406

CrossRef Full Text | Google Scholar

Ashraf, M. Z., Wei, W., Usman, M., and Mushtaq, S. (2024). How can natural resource dependence, environmental-related technologies and digital trade protect the environment: redesigning sdgs policies for sustainable environment? Resour. Policy 88, 104456. doi:10.1016/j.resourpol.2023.104456

CrossRef Full Text | Google Scholar

Breyer, C., Bogdanov, D., Khalili, S., and Keiner, D. (2021). “Solar photovoltaics in 100% renewable energy systems,” in Encyclopedia of sustainability science and technology, 1, 1–30. doi:10.1007/978-1-4939-2493-6_1071-1

CrossRef Full Text | Google Scholar

Ekinci, S., Izci, D., and Hussien, A. G. (2024). Comparative analysis of the hybrid gazelle-nelder–mead algorithm for parameter extraction and optimization of solar photovoltaic systems. IET Renew. Power Gener. 18, 959–978. doi:10.1049/rpg2.12974

CrossRef Full Text | Google Scholar

Ghanim, T. M., AbdElminaam, D. S., Nabil, A., Fathi, H., Nabih, S. A., Alsekait, D. M., et al. (2024). Boosting walrus optimizer algorithm based on ranking-based update mechanism for parameters identification of photovoltaic cell models. Electr. Eng. 1–43. doi:10.1007/s00202-024-02885-9

CrossRef Full Text | Google Scholar

Grau, G. A., and Walther, F. R. (1976). Mountain gazelle agonistic behaviour. Anim. Behav. 24 (3), 626–636. doi:10.1016/S0003-3472(76)80077-2

CrossRef Full Text | Google Scholar

Griggs, D., Stafford-Smith, M., Gaffney, O., Rockström, J., Öhman, M. C., Shyamsundar, P., et al. (2013). Sustainable development goals for people and planet. Nature 495 (7441), 305–307. doi:10.1038/495305a

PubMed Abstract | CrossRef Full Text | Google Scholar

Ibnelouad, A., El Kari, A., Ayad, H., and Mjahed, M. (2020). Improved cooperative artificial neural network-particle swarm optimization approach for solar photovoltaic systems using maximum power point tracking. Int. Trans. Electr. Energy Syst. 30 (8), 12439. doi:10.1002/2050-7038.12439

CrossRef Full Text | Google Scholar

Marlin, S., and Jebaseelan, S. (2024). A comprehensive comparative study on intelligence based optimization algorithms used for maximum power tracking in grid-pv systems. Sustain. Comput. Inf. Syst. 41, 100946. doi:10.1016/j.suscom.2023.100946

CrossRef Full Text | Google Scholar

Mirjalili, S., Mirjalili, S. M., and Lewis, A. (2014). Grey wolf optimizer. Adv. Eng. Softw. 69, 46–61. doi:10.1016/j.advengsoft.2013.12.007

CrossRef Full Text | Google Scholar

Rahman, A., Farrok, O., and Haque, M. M. (2022). Environmental impact of renewable energy source based electrical power plants: solar, wind, hydroelectric, biomass, geothermal, tidal, ocean, and osmotic. Renew. Sustain. Energy Rev. 161, 112279. doi:10.1016/j.rser.2022.112279

CrossRef Full Text | Google Scholar

Rant, M. B. (2020). Sustainable development goals (sdgs), leadership, and sadhguru: self-transformation becoming the aim of leadership development. Int. J. Manag. Educ. 18 (3), 100426. doi:10.1016/j.ijme.2020.100426

CrossRef Full Text | Google Scholar

Rezk, H., Arfaoui, J., and Gomaa, M. R. (2021). Optimal parameter estimation of solar pv panel based on hybrid particle swarm and grey wolf optimization algorithms 6, 145. doi:10.9781/ijimai.2020.12.001

CrossRef Full Text | Google Scholar

Saleh Alluhaidan, A., Salama AbdElminaam, D., Ghanim, T. M., El-Rahman, S. A., Shawky Farahat, I., Al Tawil, A., et al. (2025). Refined photovoltaic parameters estimation via an improved sinh cosh optimizer with trigonometric operators. Sci. Rep. 15 (1), 4481. doi:10.1038/s41598-025-85841-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Sánchez, A. S., Junior, E. P., Gontijo, B. M., Jong, P., and Reis Nogueira, I. B. (2023). Replacing fossil fuels with renewable energy in islands of high ecological value: The cases of Galápagos, Fernando de Noronha, and Príncipe. Renew. Sustain. Energy Rev. 183, 113527. doi:10.1016/j.rser.2023.113527

CrossRef Full Text | Google Scholar

Schleicher, J., Schaafsma, M., and Vira, B. (2018). Will the sustainable development goals address the links between poverty and the natural environment? Curr. Opin. Environ. Sustain. 34, 43–47. doi:10.1016/j.cosust.2018.09.004

CrossRef Full Text | Google Scholar

Ullah, K., Jiang, Q., Geng, G., Rahim, S., and Khan, R. A. (2022). Optimal power sharing in microgrids using the artificial bee colony algorithm. Energies 15 (3), 1067. doi:10.3390/en15031067

CrossRef Full Text | Google Scholar

Vais, R. I., Sahay, K., Chiranjeevi, T., Devarapalli, R., and Knypiński, Ł. (2023). Parameter extraction of solar photovoltaic modules using a novel bio-inspired swarm intelligence optimisation algorithm. Sustainability 15 (10), 8407. doi:10.3390/su15108407

CrossRef Full Text | Google Scholar

Wang, R., Tan, J., and Yao, S. (2021). Are natural resources a blessing or a curse for economic development? the importance of energy innovations. Resour. Policy 72, 102042. doi:10.1016/j.resourpol.2021.102042

CrossRef Full Text | Google Scholar

Wasim, M. S., Amjad, M., Abbasi, M. A., Bhatti, A. R., Rasool, A., Raheem, A., et al. (2024). An efficient energy management scheme using rule-based swarm intelligence approach to support pulsed load via solar-powered battery-ultracapacitor hybrid energy system. Sci. Rep. 14 (1), 3962. doi:10.1038/s41598-024-53248-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Yaqoob, S. J., Saleh, A. L., Motahhir, S., Agyekum, E. B., Nayyar, A., and Qureshi, B. (2021). Comparative study with practical validation of photovoltaic monocrystalline module for single and double diode models. Sci. Rep. 11 (1), 19153. doi:10.1038/s41598-021-98593-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Ye, X., Liu, W., Li, H., Wang, M., Chi, C., Liang, G., et al. (2021). Modified whale optimization algorithm for solar cell and pv module parameter identification. Complexity 2021, 1–23. doi:10.1155/2021/8878686

CrossRef Full Text | Google Scholar

Yu, K., Liang, J., Qu, B., Cheng, Z., and Wang, H. (2018). Multiple learning backtracking search algorithm for estimating parameters of photovoltaic models. Appl. energy 226, 408–422. doi:10.1016/j.apenergy.2018.06.010

CrossRef Full Text | Google Scholar