Chance-constrained optimal schedule of battery energy storage considering the uncertainties of renewable generation

Since renewable energy generation has strong uncertainties and pure conventional unit dispatch schemes are limited by the unit-operating capacities, such scheduling is inapplicable for power systems with high proportions of renewable energy sources (RESs). We propose an optimal scheduling model for battery energy storage systems (BESSs) by considering the uncertainties of RESs. The probability distribution of renewable energy generation is characterized using a Gaussian mixture model that effectively captures its stochastic nature. Chance constraints are incorporated into the dispatch model to enhance system security while ensuring sufficient reserve capacity to mitigate fluctuations in the RES outputs. Furthermore, these constraints are transformed into their deterministic equivalents using quantile-based methods. Case studies were then conducted on two systems to demonstrate the ability of the proposed model to improve system security and economic efficiency. The results indicate that incorporating BESSs can significantly reduce the system risk probability and operational costs, particularly under scenarios with high RES penetration. The model also highlights the tradeoffs between BESS capacity and system risk levels as well as constraint settings and economic benefits to provide valuable insights for practical applications. It is expected that future efforts in this field will be focused on extending the model to include the impacts of BESSs on branch power transmission risks.

1 Introduction

The global shift toward renewable energy sources (RESs) has become the cornerstone of efforts to reduce greenhouse gas emissions and combat climate change. However, the growing reliance on wind, solar, and other RESs has introduced challenges owing to their intermittent and unpredictable nature. To address these challenges, battery energy storage systems (BESSs) have emerged as critical components for enhancing the stability and reliability of modern power systems. BESSs can store excess energy generated during periods of high renewable output and discharge it when the generation is low, thereby smoothing the fluctuations and ensuring more stable power supply. Additionally, BESSs can provide ancillary services such as frequency regulation, voltage support, and peak shaving, which are essential for maintaining grid stability. These capabilities make a BESS a key technology for integrating a greater proportion of renewable energy into a power grid.

The optimal dispatch of a BESS has been studied extensively, where researchers have focused on various aspects, such as economic dispatch and integration with renewable energy. For instance, Chen et al. (2020) proposed a two-stage chance-constrained unit commitment model considering a BESS to cooptimize the day-ahead energy and reserve schedules, demonstrating the potential to enhance system flexibility and promote wind consumption. Similarly, Li et al. (2016) formulated a stochastic unit commitment approach with wind power forecast uncertainty and energy storage; they presented a two-step framework for evaluating the potential value of energy storage in power systems with renewable generation, thereby demonstrating the ability of a BESS to decrease curtailment of wind generation while reducing load and reserve shortfalls. Nguyen et al. (2015) defined a lifetime cost function to indicate the cost incurred by a BESS for dispatching 1 kWh of wind energy while determining the optimal battery capacity. Jiang et al. (2018) aimed to maximize the benefits of wind-storage union systems and established an optimal capacity model by considering BESS investment costs, wind curtailment savings, and auxiliary service compensation; further, they explored the roles of BESSs in alleviating the variability and uncertainty of wind output as well as the system costs of auxiliary services. However, the unpredictable nature of renewable generation has necessitated the development of dispatch models that can account for uncertainties; this has motivated the development of stochastic and robust optimization methods.

Stochastic optimization models have been widely used to manage the uncertainties associated with RESs. For example, in rolling scheduling, Gu and Xie (2017) used the deterministic scheduling model for the time period close to the current time and leveraged the stochastic scheduling model for the longer time periods to generate the random scene; then, they used the parallel algorithm to accelerate the solution. They also proposed the criteria for comparing the effects of stochastic and deterministic scheduling. Gangammanavar et al. (2016) proposed a stochastic programming framework for subhourly economic dispatch to address renewable energy integration. This framework modeled slow-response resources at hourly intervals and fast-response resources at subhourly intervals. By using stochastic decomposition, this method improved cost prediction and efficiency over traditional models, as demonstrated on the IEEE RTS96 and Illinois systems.

Robust optimization has also gained attention for ensuring reliable BESS dispatches under a wide range of scenarios. For instance, Wu et al. (2014) established a one-stage robust optimization model by considering the uncertainty of wind power output to solve the rolling scheduling problem and ensure the safe operation of the system by establishing the allowable output range of wind power. Zeng and Zhao (2013) utilized the spatial correlation of wind power output to build a prediction model for wind power and established a robust rolling economic dispatch model. Xie et al. (2014) proposed a general column-constraint generation algorithm for solving two-stage robust optimization. By assuming that the generator output will be adjusted linearly according to the renewable energy output, Jabr (2013) established a two-stage DC power flow scheduling model. Another notable contribution is the work by Zhao et al. (2013), who proposed a multistage robust economic dispatch model wherein the uncertainty set in each stage is dynamically updated based on the uncertainty set of the previous stage to capture the variation of renewable energy output more accurately. Here, the first-stage decision variables represent the immediate dispatch decisions, while the dispatch decisions for the subsequent stages are treated as the second-stage decision variables.

As a special form of stochastic optimization, chance-constrained optimization relaxes the constraints of traditional optimization. Since these constraints involve random variables, they may not be met for all possible values of the random variables. Chance constraints ensure that the probability of the constraints being satisfied exceeds a certain threshold, thereby converting deterministic constraints into probabilistic ones. Bolognani et al. (2017) proposed a chance-constrained optimization method suitable for fast online solutions and applied it to power grid dispatching; here, it is assumed that the sample set of uncertain variables can be obtained from historical data. In the offline stage, the feasible region of chance-constrained optimization is constructed from the sample information. In the online decision-making stage, it is only necessary to solve the deterministic optimization problem based on the measurement information and feasible region determined in the offline stage, which offers high computational efficiency. Zhao et al. (2023) proposed a data-driven chance-constrained dispatch strategy for integrated power and natural gas systems to handle uncertainties from wind power prediction errors; through numerical experiments on a modified IEEE 33-bus system, they demonstrated enhanced economic operation, reduced total costs, and improved robustness against uncertainties compared to traditional methods.

Scheduling methods based on stochastic optimization often model renewable energy generation as random variables. Consequently, the probability model of the random variables is closely related to the accuracy of the optimization results and efficiency of the solution method. In recent years, Gaussian mixture models (GMMs) have been employed to model uncertainties in power systems. GMMs demonstrate strong performance by accurately representing arbitrary probability density functions and possess desirable mathematical properties, such as invariance under linear transformations, making them well-suited for applications in probabilistic power flow analyses and chance-constrained optimization problems. In their application to uncertainty modeling and probabilistic power flow analysis, Singh et al. (2010) employed a GMM to describe the uncertainty of the distribution network load and noted that it effectively fits different probability distributions. Valverde et al. (2013) employed GMMs to describe the probabilistic model of individual loads in the distribution network by selecting appropriate component combinations through the weighted least-squares approach; this approach was also used to obtain the probability distributions of voltage and power flow in probabilistic power flow analysis and state estimation. Additionally, they proposed a component clustering and reduction method for GMMs. Wang et al. (2017a) utilized a high-dimensional GMM to describe the joint probability distribution of random power injection; based on the linear transformation invariance of the GMM and linear power flow model, the expression for probability distribution of the branch power flow was obtained analytically.

In the application of GMMs to stochastic optimization scheduling, Wang et al. (2017b) investigated chance-constrained economic dispatch by considering wind power uncertainty; they used a GMM to describe the joint probability distribution of power generation across multiple wind farms and approximated the cumulative distribution function of the GMM through a piecewise linear combination of quartic polynomials. The quantiles of the random variables in the chance constraints were determined by solving these quartic equations. Viafora et al. (2020) considered the uncertainties of dynamic power limits on transmission lines and wind power by constructing a joint probability distribution model using a Gaussian copula. They employed a GMM for the fitting and investigated the optimal power flow problem under chance constraints, where the quantiles of the random variables were calculated using a lookup table during the transformation of the chance constraints.

Despite the advancements in BESS dispatch strategies, there remain challenges in optimizing BESS operations under the uncertainties associated with renewable generation. We aim to address this by developing an integrated optimization framework that leverages chance-constrained stochastic optimization methods to mitigate the uncertainties of renewable generation. The proposed approach seeks to enhance the operational efficiencies of BESSs by ensuring that they can effectively mitigate the variability of renewable resources while maintaining grid stability and economic viability.

2 Methodology

In this study, we consider the day-ahead operation of a power system. The schedule of the BESS is cooptimized with the generation schedules of conventional generators, such as thermal units and hydraulic stations, in the day-ahead dispatch stage. The power demand of the loads is obtained from the day-ahead forecast as deterministic inputs. The actual generation from the RESs are regarded as random variables, and their probability distribution is modeled with the GMM, which is introduced in detail in the following sections.

2.1 Objective function of the dispatch model

The objective of day-ahead dispatch is to minimize the total operational cost of the power system, including the fuel cost of conventional units and cycle aging cost for a single optimization dispatch cycle. The objective function of the dispatch model is expressed as in Equation 1

$Obj=\min {\displaystyle \sum _{t=1}^T}\left({\displaystyle \sum _{i=1}^{N_G}}\left(a_i{P}_{i,t}^2+b_i{P}_{i,t}+c_i\right)+{\displaystyle \sum _{j=1}^{N_E}}{\displaystyle \sum _{k=1}^{N_K}}{\omega }_k{P}_{j,k,t}^{e,dis}\right),(1)$

where $T$ is the total period of optimization; $N_G$ is the number of conventional units; $a_i$, $b_i$, and $c_i$ are the coefficients of the quadratic fuel cost function of the conventional units; $P_{i,t}$ is the generation schedule of the ith conventional unit at the tth period; $N_K$ is the segment of the piecewise linear aging cost model for battery index $k$; ${\omega }_k$ is the middle value in segment $k$; $N_E$ is the number of BESSs; $P_{j,t}^{e,ch}$ and $P_{j,t}^{e,dis}$ are the charging and discharging powers of the jth BESS at the tth period. The relationship between the depth of discharge (DoD) of the battery and its capacity degradation is non-linear; to address this, we apply an approach that approximates the impact of a single-cycle DoD on battery degradation through piecewise linearization (Zhang et al., 2022). The piecewise linear model can be expressed by Equations 2–5

$\omega \left(h_t\right)={\omega }_i\text{\hspace{0.17em}if\hspace{0.17em}}{h}_t\in \left(\frac{i-1}{N_K},\frac{i}{N_K}\right),i=1,2,\dots ,N_K(2)$

$Q_{\text{cycle}}\left(h_t\right)=A\exp \left(\frac{-E_a}{RT}\right){\left(h_t{E}_{rate}\right)}^z(3)$

${\omega }_i=\frac{C}{{\eta }^{dis}{E}_{rate}}{k}_i(4)$

$k_i=\frac{1}{2}\left[Q_{cycle}\left(\frac{i}{N}\right)-Q_{cycle}\left(\frac{i-1}{N}\right)\right],(5)$

where $Q_{\text{cycle}}$ is the capacity fading of the battery over a single cycle; $A$ is the Arrhenius constant; $z$ is the reaction rate constant; $R$ is the molar gas constant; $E_a$ is the activation energy; $T$ is the absolute temperature; $E_{rate}$ is the battery capacity; $C$ is the replacement cost; $h_t$ is the depth of the cycle at time t; ${\eta }^{dis}$ is the discharge efficiency factor.

2.2 Constraints of the dispatch model

The dispatch schedules of the conventional units and BESSs must maintain the balance and security of the power system, so the dispatch model considers the physical constraints expressed in Equations 6–12.

${\displaystyle \sum _{i=1}^{N_G}}{P}_{i,t}+{\displaystyle \sum _{j=1}^{N_E}}{P}_{j,t}^e+{\displaystyle \sum _{k=1}^{N_R}}{P}_{k,t}^R={\displaystyle \sum _{d=1}^{N_D}}{L}_{d,t}(6)$

${P_i^{\mathit{min}}\le P}_{i,t}\le P_i^{\mathit{max}}(7)$

$P_{i,t}^e=P_{i,t}^{e,dis}-P_{i,t}^{e,ch}(8)$

$P_i^{e,\mathit{min}}\le P_{i,t}^e\le P_i^{e,\mathit{max}}(9)$

$E_{i,t+1}^e=E_{i,t}^e-\frac{P_{i,t}^{e,dis}}{{\eta }_i^{dis}}\Delta t+{\eta }_i^{ch}{P}_{i,t}^{e,ch}\Delta t(10)$

$E_{i,t}^{e,\mathit{min}}\le E_{i,t}^e\le E_{i,t}^{e,\mathit{max}}(11)$

$-S_l^{\mathit{max}}\le {\displaystyle \sum _{i=1}^{N_G}}{s}_{l-i}{P}_{i,t}+{\displaystyle \sum _{j=1}^{N_B}}{s}_{l-j}{P}_{j,t}^e+{\displaystyle \sum _{k=1}^{N_B}}{s}_{l-k}{P}_{k,t}^R+{\displaystyle \sum _{d=1}^{N_D}}{s}_{l-d}{L}_{d,t}\le S_l^{\mathit{max}}(12)$

In the power balance constraint of Equation 6, $P_{j,t}^e$ is the net power of the BESS, which is equal to the difference between the discharging and charging powers shown in Equation 8. $N_R$ is the number of RESs, $P_{k,t}^R$ is the day-ahead schedule of forecast generation of the kth RES in the tth period less than its forecast; $N_D$ is the number of power loads; $L_{d,t}$ is the power demand of the dth load in the tth period. Constraint Equation 7 restricts the generation schedule of the conventional units to the upper bound $P_i^{\mathit{max}}$ and lower bound $P_i^{\mathit{min}}$. Constraint Equation 9 ensures that the discharging and charging powers of the BESS do not exceed the upper bound $P_i^{e,\mathit{max}}$ or lower bound $P_i^{e,\mathit{min}}$. The energy stored in the BESS is denoted by $E_{i,t}^e$ and has temporal dependence between periods, as shown in Equation 10, where ${\eta }_i^{dis}$ and ${\eta }_i^{ch}$ are the efficiency factors of discharging and charging, respectively. $\Delta t$ is the length of the period. The energy of the BESS is restricted by its storage capacity, as shown in Equation 11. The power flow in each branch l is restricted according to Equation 12, where $s_{l-i}$ denotes the power transfer distribution factor calculated from the DC power flow model and $S_l^{\mathit{max}}$ is the maximal transmission capacity of branch l.

It is worth noting that the actual generation of the RES is stochastic and will not always follow the day-ahead forecast $P_{k,t}^R$, so we use ${\stackrel{\sim }{P}}_{k,t}^R$ to represent the actual power generation of the RES to emphasize this uncertainty. The deviation of the actual renewable energy generation and its deterministic forecast ${\stackrel{\sim }{P}}_{k,t}^R-P_{k,t}^R$ introduce a power imbalance in the system and must be compensated by other power sources with regulation flexibilities. Therefore, sufficient reserve capacity should be allocated among the conventional units and BESSs to ensure that they can respond to fluctuations of renewable generation at the intraday stage after day-ahead dispatch. Here, we use chance constraints to formulate the constraints of the reserve capacity.

$Prob\left\{{\displaystyle \sum _{i=1}^{N_G}}{r}_{i,t}^{+}+{\displaystyle \sum _{j=1}^{N_E}}{r}_{j,t}^{e+}\ge \left({\displaystyle \sum _{k=1}^{N_R}}{P}_{k,t}^R-{\displaystyle \sum _{k=1}^{N_R}}{\stackrel{\sim }{P}}_{k,t}^R\right)\right\}\ge 1-{\alpha }^{+}(13)$

$Prob\left\{{\displaystyle \sum _{i=1}^{N_G}}{r}_{i,t}^{-}+{\displaystyle \sum _{j=1}^{N_E}}{r}_{j,t}^{e-}\ge \left({\displaystyle \sum _{k=1}^{N_R}}{\stackrel{\sim }{P}}_{k,t}^R-{\displaystyle \sum _{k=1}^{N_R}}{P}_{k,t}^R\right)\right\}\ge 1-{\alpha }^{-}(14)$

Here, $r_{i,t}^{+}$ and $r_{i,t}^{-}$ are the upward and downward reserve capacities of the ith conventional unit in the tth period, respectively; $r_{j,t}^{e+}$ and $r_{j,t}^{e-}$ are the upward and downward reserve capacities of the jth BESS in the tth period, respectively; $Prob$ refers to the probability of an event; ${\alpha }^{+}$ and ${\alpha }^{-}$ represent the tolerable risk levels where the upward and downward reserves are insufficient, respectively. The constraints in Equations 13, 14 indicate that the sufficiency of upward and downward reserves is guaranteed with a high probability, except in extreme scenarios where the actual renewable generation deviates severely from its forecast.

We also have the constraints shown in Equations 15–18, where the available reserve capacity of the conventional units is restricted by the ramping capability $R_i$ as well as the space between the current generation and upper/lower bounds. Similarly, the available reserve capacity of the BESS is constrained by its stored energy, as shown in Equations 19–22.

$R_i\ge r_{i,t}^{+}\ge 0(15)$

$r_{i,t}^{+}\le P_i^{\mathit{max}}-P_{i,t}(16)$

$R_i\ge r_{i,t}^{-}\ge 0(17)$

$r_{i,t}^{-}\le P_{i,t}-P_i^{\mathit{min}}(18)$

$\frac{E_{i,t}^e}{\Delta t}\ge r_{i,t}^{e+}\ge 0(19)$

$r_{i,t}^{e+}\le P_i^{e,\mathit{max}}-P_{i,t}^e(20)$

$\frac{E_{i,t}^e}{\Delta t}\ge r_{i,t}^{e-}\ge 0(21)$

$r_{i,t}^{e-}\le P_{i,t}^e-P_i^{e,\mathit{min}}(22)$

2.3 Probabilistic model of renewable generation

Owing to the limitations of using normal distribution to describe random variables in engineering practice, such as the fact that the symmetry of a normal distribution relative to the mean may not always hold in practice, we use a GMM to describe the probability distribution of renewable generation. Each component of the GMM is normally distributed, and the probability density function is a convex combination of the probability density functions of all normally distributed components. A GMM with K components and N dimensions is used to describe the joint probability distribution of $\xi$, and its probability density function is expressed by Equations 23–25

$\begin{array}{c}{PDF}_{\xi }={\displaystyle \sum _{k=1}^K}{\omega }_{k}N\left(\left.\mathrm{x}\right|{\mathrm{\mu }}^k,{\mathrm{\Sigma }}^k\right)\\ ={\displaystyle \sum _{k=1}^K}{\omega }_k\frac{\exp \left(-\frac{1}{2}{\left(x-{\mathrm{\mu }}^k\right)}^T{\left({\mathrm{\Sigma }}^k\right)}^{-1}\left(x-{\mathrm{\mu }}^k\right)\right)}{\sqrt{{\left(2\pi \right)}^N\left|{\mathrm{\Sigma }}^k\right|}}\end{array}(23)$

${\omega }_k>0(24)$

${\displaystyle \sum _{k=1}^K}{\omega }_k=1,(25)$

where ${\mathrm{\mu }}^k$ and ${\mathrm{\Sigma }}^k$ represent the mean vector and covariance matrix of each normally distributed component, respectively; ${\omega }_k$ is the weight coefficient of each normally distributed component, which is non-negative with a total sum of 1.

The GMM has stronger fitting ability than a single normal distribution. By setting the model parameters reasonably, such as the number of components, weight coefficients of the components, mean, and covariance, we can accurately characterize any probability distribution. In this work, we fit the GMM using historical generation forecast data and actual output data from wind and photovoltaic power plants under the jurisdiction of the Electric Reliability Council of Texas. The fitted variable was the error between the actual and predicted values, with its dimensionality equal to the number of renewable energy sites. The fitted parameters were ${\mathrm{\mu }}^k$ and ${\mathrm{\Sigma }}^k$, for which ${\omega }_k$ was selected beforehand based on average log-likelihood to ensure high likelihood while retaining a moderate number of component parameters to avoid a negative impact on the subsequent computational speed.

2.4 Chance-constraint transformation in the probabilistic model

In the probabilistic optimization model, we represent the safety constraints as risk-controllable chance constraints. These constraints contain random variables that cannot be solved directly using existing solvers, so they must be transformed into deterministic constraints. For example, constraint Equation 13 can be rewritten as Equation 26.

$Prob\left\{-{\displaystyle \sum _{k=1}^{N_R}}{\stackrel{\sim }{P}}_{k,t}^R\le {\displaystyle \sum _{i=1}^{N_G}}{r}_{i,t}^{+}+{\displaystyle \sum _{j=1}^{N_E}}{r}_{j,t}^{e+}-{\displaystyle \sum _{k=1}^{N_R}}{P}_{k,t}^R\right\}\ge 1-{\alpha }^{+}(26)$

The left-hand side expression $-{\sum }_{k=1}^{N_R}{\stackrel{\sim }{P}}_{k,t}^R$ is a linear combination of the actual generation power of the RES, which can be written in the form $s^{\mathrm{T}}\mathrm{\xi }$ , where $s^{\mathrm{T}}={-1}^{\mathrm{T}}$, $\mathrm{\xi }={\stackrel{\sim }{P}}_{k,t}^R$ , and $1^{\mathrm{T}}$ is a column vector where each dimension is 1. According to the affine transformation invariance of the GMM (Flåm et al., 2013), the probability distribution of the linear combination $s^{\mathrm{T}}\mathrm{\xi }$ of various components of the high-dimensional random variable $\mathrm{\xi }$ can be described using a one-dimensional GMM. Therefore, $s^{\mathrm{T}}\mathrm{\xi }$ can be regarded as a one-dimensional random variable, and Equation 26 implies that the cumulative distribution function (CDF) of the random variable ${-1}^{\mathrm{T}}{\stackrel{\sim }{P}}_{k,t}^R$ at ${\sum }_{i=1}^{N_G}{r}_{i,t}^{+}+{\sum }_{j=1}^{N_E}{r}_{j,t}^{e+}-{\sum }_{k=1}^{N_R}{P}_{k,t}^R$ is greater than or equal to $1-{\alpha }^{+}$, as shown in Equation 27.

${CDF}_{{-1}^{\mathrm{T}}{\stackrel{\sim }{P}}_{k,t}^R}\left({\displaystyle \sum _{i=1}^{N_G}}{r}_{i,t}^{+}+{\displaystyle \sum _{j=1}^{N_E}}{r}_{j,t}^{e+}-{\displaystyle \sum _{k=1}^{N_R}}{P}_{k,t}^R\right)\ge 1-{\alpha }^{+}(27)$

Because a CDF is a monotonically increasing function, it is necessary that ${\sum }_{i=1}^{N_G}{r}_{i,t}^{+}+{\sum }_{j=1}^{N_E}{r}_{j,t}^{e+}-{\sum }_{k=1}^{N_R}{P}_{k,t}^R$ be greater than the variable value corresponding to the CDF of ${-1}^T{\stackrel{\sim }{P}}_{k,t}^R$ when the function value is equal to $1-{\alpha }^{+}$, which is the $1-{\alpha }^{+}$ quantile of $s^{\mathrm{T}}\mathrm{\xi }$ referred to as $Q\left({-1}^{\mathrm{T}}{\stackrel{\sim }{P}}_{k,t}^R\left|1-\right.{\alpha }^{+}\right)$.

Thus, the chance constraints in Equations 13, 14 can be transformed into deterministic constraints, as shown in Equations 28, 29.

${\displaystyle \sum _{i=1}^{N_G}}{r}_{i,t}^{+}+{\displaystyle \sum _{j=1}^{N_E}}{r}_{j,t}^{e+}-{\displaystyle \sum _{k=1}^{N_R}}{P}_{k,t}^R\ge Q\left({-1}^{\mathrm{T}}{\stackrel{\sim }{P}}_{k,t}^R\left|1-\right.{\alpha }^{+}\right)(28)$

${\displaystyle \sum _{i=1}^{N_G}}{r}_{i,t}^{-}+{\displaystyle \sum _{j=1}^{N_E}}{r}_{j,t}^{e-}+{\displaystyle \sum _{k=1}^{N_R}}{P}_{k,t}^R\ge Q\left(1^{\mathrm{T}}{\stackrel{\sim }{P}}_{k,t}^R\left|1-\right.{\alpha }^{-}\right)(29)$

3 Numerical tests

To evaluate the effectiveness of the proposed models and approaches, numerical tests were conducted. Accordingly, we conducted day-ahead dispatch tests on two systems to compare the proposed chance-constrained method with the GMM (CC-GMM) to two other algorithms, namely, limited-scenario optimization (LSO) and distributionally robust optimization (DRO). Then, the impacts of different reserve capacity constraints and BESS parameter settings on the system risk probability and operational costs were assessed. The proposed model is solved using the Gurobi optimizer.

3.1 Case settings

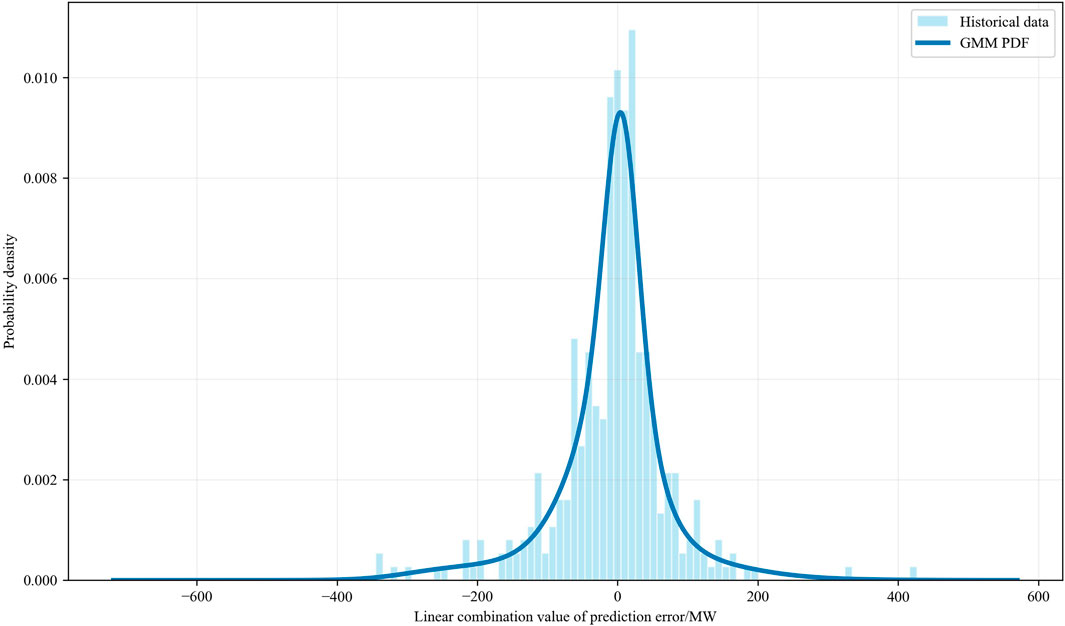
For the parameter settings, the GMM parameters of the renewable energy sites were obtained by fitting historical data. Taking the first system as an example, we configured 10 renewable energy sites and initially performed GMM fitting using historical forecast error data from these 10 sites. For different numbers of components, we calculated the average log-likelihood values of the fitted GMMs, where higher values indicated better fitting accuracy. Then, we selected a component count that achieved sufficient fitting precision without excessive complexity to obtain the final GMM parameters, including the mean vectors, covariance matrices, and component weights. Figure 1 illustrates the variation in the average log-likelihood value with respect to the number of components, based on which we set the number of Gaussian components to 15. To illustrate the accuracy of the fitted GMM, the distribution of the total renewable power output prediction errors is shown in Figure 2.

Figure 1

Figure 1. Mean log likelihood under different numbers of Gaussian mixture model (GMM) components.

Figure 2

Figure 2. Distribution of the prediction errors of the total renewable power output.

The maximum energy storage capacity of each BESS station was set, and the basic attribute parameters of the batteries are shown in Table 1; the remaining parameters have the quantitative relationships shown in Equations 30–34

$E_{i,t}^{e,\mathit{min}}=0.1·E_{i,t}^{e,\mathit{max}}(30)$

$P_i^{e,\mathit{max}}=\frac{E_{i,t}^{e,\mathit{max}}}{2}\left(MW\right)(31)$

$P_i^{e,\mathit{min}}=-P_i^{e,\mathit{max}}(32)$

${\eta }_i^{dis}={\eta }_i^{ch}=0.93(33)$

$\Delta t=1.(34)$

Table 1

Table 1. Battery attributes.

Based on these parameters, we conducted simulations on two systems: system #l is a modified 57-bus system (case 57) comprising five conventional, 10 BESS, and 10 RES units, including five wind farms and five photovoltaic power stations; system #2 is a modified 118-bus system (case 118) comprising 29 conventional, 15 BESS, and 20 RES units, including 10 wind farms and 10 photovoltaic power stations. With regard to the permissible system risk level setting, a typical system that can tolerate a certain level of risk would be assigned a risk probability of 0.05. For systems requiring high reliability where cost is not the primary constraint, a risk probability of 0.01 would be more prudent. In this case study, we consider a probability of 0.05 as the standard value. For the optimization results, if the risk probability during any period exceeds this set probability, then the method is deemed a failure. The 24-h power curves for the renewable energy sites are selected as the forecast values from a specific day in historical data while their actual power outputs remain uncertain. These actual values are obtained by adding the predicted power curves to the forecast errors modeled as random variables.

3.2 Test on system #1

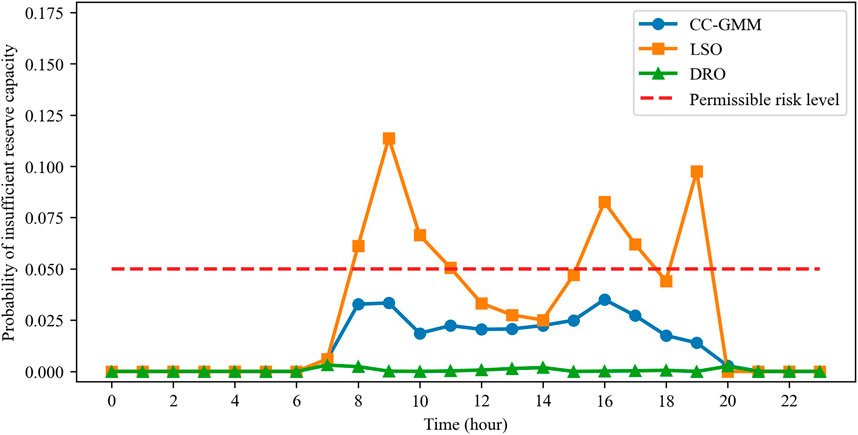
We first compared the performances of different optimization algorithms on system #1, namely, CC-GMM, LSO, and DRO. The maximum capacity of each BESS unit is 30 MWh, which is at a medium value. The permissible system risk level of 0.05 is the most critical metric here for validating the effectiveness of the method. This threshold represents the maximum acceptable probability of reserve inadequacy, and all optimization algorithms should demonstrate compliance with this requirement while maintaining economy. For CC-GMM, the reserve capacity chance constraints are set at ${\alpha }^{+}={\alpha }^{-}=0.025$ to limit the system risk probability to under 0.05. For the LSO method, we considered three discrete scenarios for the actual renewable generation outputs, namely 1.1, 1.0, and 0.9 times the forecast values; the corresponding reserve capacity constraints and branch power flow constraints under these three scenarios are simultaneously incorporated as deterministic constraints in the optimization model. The DRO method utilizes the mean vector and covariance matrix of the forecast errors calculated from historical data; it incorporates the reserve capacity constraints by considering the worst-case distributions within an ambiguity set. Given the inherent conservatism of the DRO method, we set the probability of its reserve capacity constraints at 0.05 to mitigate excessive conservativeness in the operational decisions. The comparative results of the three optimization methods are presented in Figure 3 and Table 2.

Figure 3

Figure 3. Probabilities of insufficient reserve capacities of different algorithms in system #1.

Table 2

Table 2. Objective function values of different optimization methods for system #1.

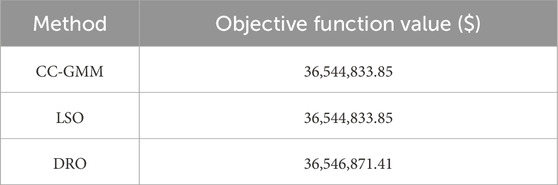
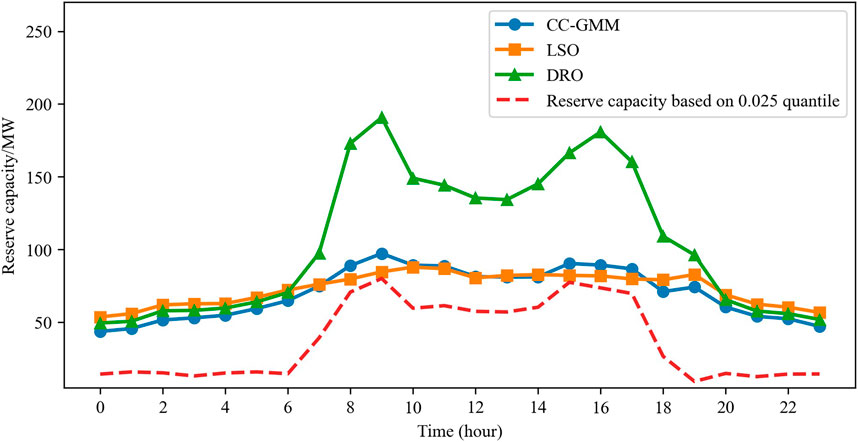
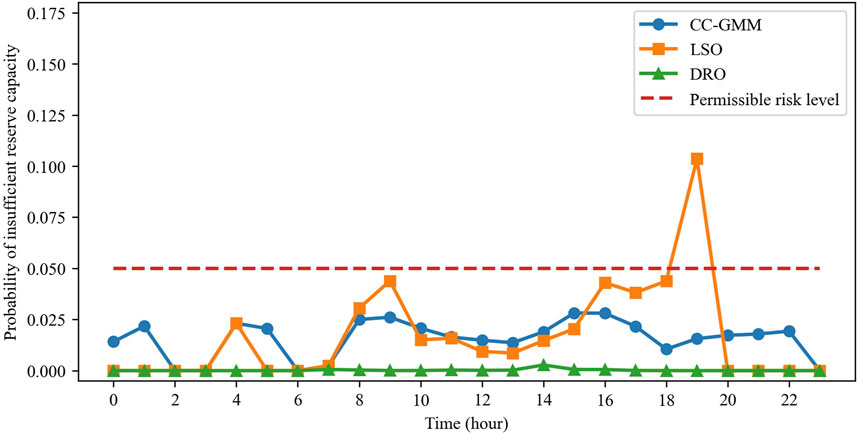
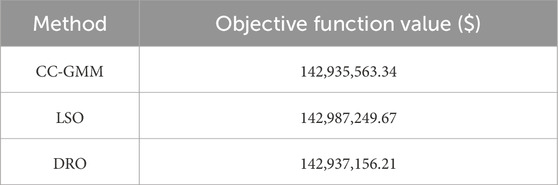
From the results, it is seen that the LSO method fails to meet the risk requirements of the system as it exceeds the allowable risk level during 8:00–11:00, 16:00–17:00, and at 19:00 hours. This is because the LSO adopts deterministic constraints under multiple scenarios, and it can at most consider scenarios with ±10% deviations in the renewable energy output in this case study. If the deviation exceeds this range, the model becomes infeasible as it cannot satisfy all the constraints simultaneously. The objectives of the LSO and CC-GMM are close while that of DRO is the highest. Both CC-GMM and DRO meet the system risk requirements at all times. However, the DRO method yields overly conservative optimization results, leading to lower economic efficiency than the CC-GMM method. Therefore, the CC-GMM method allows more effective handling of renewable energy uncertainty.

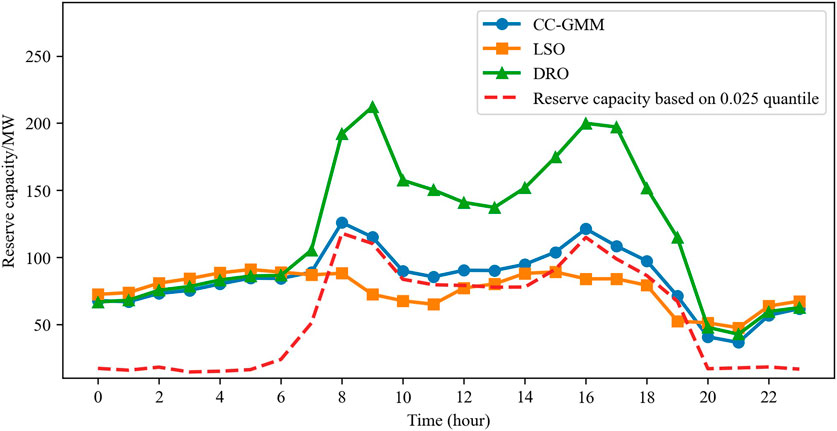
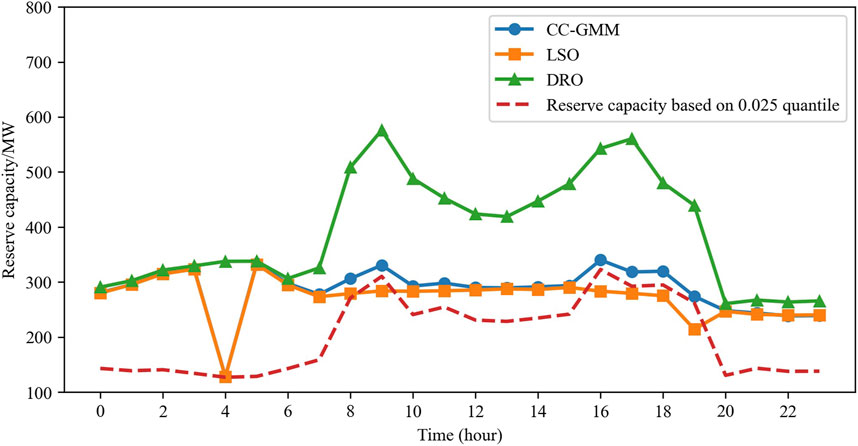
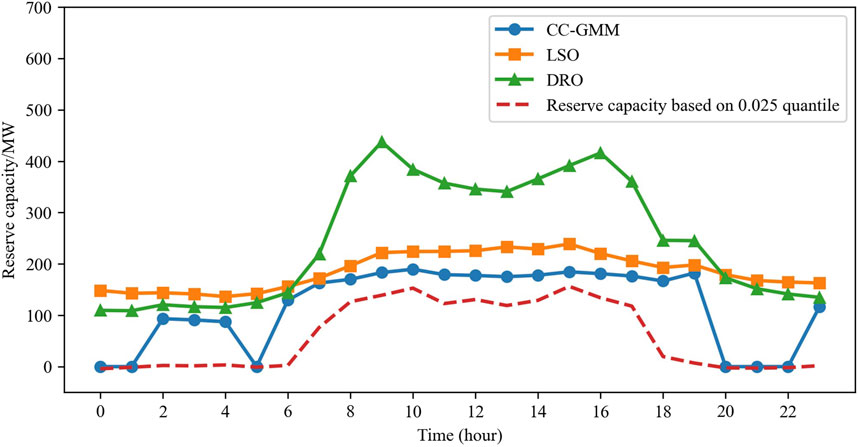
The efficacies of different algorithms are specifically reflected in the total system reserve capacity provided by their optimization results. The upward and downward reserve capacities achieved by each algorithm are shown in Figures 4, 5. The red dashed lines in the figures represent the quantile corresponding to an insufficient reserve risk probability of 0.025 calculated on the basis of the GMM. When the available reserve capacity is above this line, the probability of violation of the individual upward or downward reserve constraints is less than 0.025; when the available capacity is below the line, the probability of violation exceeds 0.025, with greater deviations indicating higher risk. Figure 4 illustrates the upward reserve of the system. For the LSO method, during 8:00–11:00, 16:00–17:00, and at 19:00 hours, the available reserve capacity is significantly below the quantile curve, resulting in the system risk probability exceeding the acceptable level during these periods. This is because LSO cannot account for situations beyond the predefined scenarios and fails to capture the true distribution of the renewable generation forecast errors, leading to unsatisfactory results. Between 7:00 and 19:00 hours, the reserve capacity provided by the CC-GMM method is generally aligned just above the quantile curve, while the reserve capacity provided by the DRO method is significantly higher for sacrificing a part of the economic performance. As shown in Figure 5 for the downward reserves, all three methods satisfy the reserve requirement corresponding to a risk probability below 0.025, with the DRO method remaining the most conservative.

Figure 4

Figure 4. Total upward reserve capacities of different algorithms in system #1.

Figure 5

Figure 5. Total downward reserve capacities of different algorithms in system #1.

Next, we verify the influences of different power parameters of the BESS units on the system risk probability. The $E_{i,t}^{e,\mathit{max}}$ of the BESS units tested in three groups are 10 MWh, 30 MWh, and 50 MWh. In these trials, we set the reserve capacity chance constraints and ${\alpha }^{+}={\alpha }^{-}=0.025$. The computed results are shown in Figure 6, which indicates the general trend; the larger the capacity of the BESS, the lower is the risk level of the system. This is attributable to the characteristics of the BESS parameter settings in this work, where a larger maximum capacity also means a greater maximum charge and greater discharge power. According to Equation 20, this enables the BESS to provide a higher reserve capacity.

Figure 6

Figure 6. Probabilities of insufficient reserve capacities for different battery energy storage system (BESS) parameters in system #1.

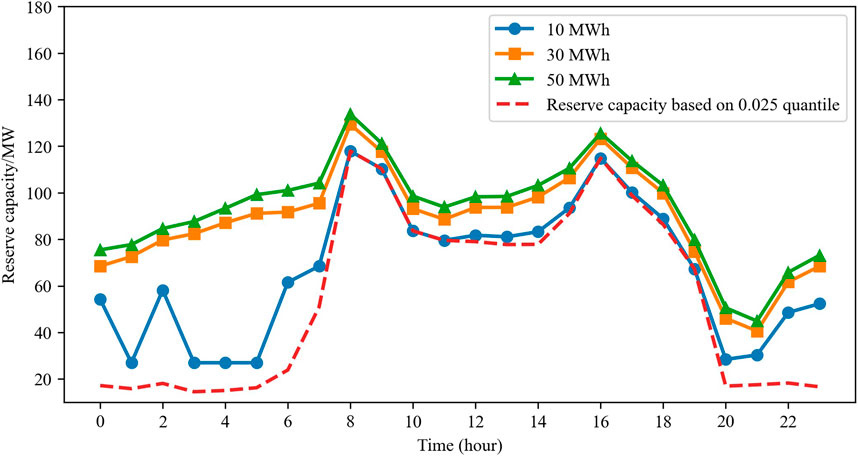
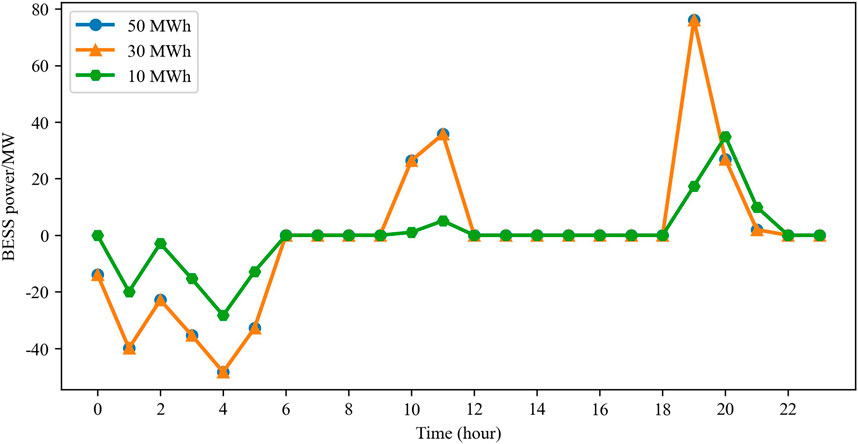
To further analyze how the BESS affects the system risk probability, we plotted the total upward reserve capacity curves and BESS power curves for BESS capacities of 10 MWh, 30 MWh, and 50 MWh, which are shown in Figures 7, 8. Figure 6 specifies that the BESS charges when the power is less than 0 and discharges when the power is greater than 0. During 0:00–5:00 hours, owing to the low load power and the fact that the RESs maintain a certain output power, the BESSs promote consumption of renewable energy through charging. During the peak load periods of 10:00–11:00 and 19:00–21:00 hours, the BESSs reduce the outputs of conventional units by discharging, thereby reducing generation costs. When the BESS capacity is 10 MWh, its charging and discharging schedule is relatively limited owing to capacity constraints, resulting in a lower reserve capacity, as shown in Figure 7; from 7:00 to 20:00 hours, the upward reserve capacity curve of this BESS nearly coincides with the 0.025 quantile reserve curve, leading to the higher corresponding risk probability noted in Figure 6. When the BESS capacity is increased to 30 MWh and 50 MWh, the charging and discharging schedules are almost identical; this is because if the generation cost savings from discharging the BESS are lower than the degradation cost incurred by discharging, the system will not plan additional discharging. Consequently, although the schedules are similar, the BESS of 50 MWh capacity can provide more reserve capacity, resulting in a slightly lower risk curve for the 50 MWh case than the 30 MWh case, as shown in Figure 6.

Figure 7

Figure 7. Total upward reserve capacities for different BESS parameters in system #1.

Figure 8

Figure 8. Power curves of BESSs with different capacities in system #1.

We further investigated the impacts of the chance-constraint probability limitations on the system risk level and objective function value under such situations. The $E_{i,t}^{e,\mathit{max}}$ of each BESS is set to 20 MWh, while ${\alpha }^{+}$ and ${\alpha }^{-}$ are both set to 0.05, 0.04, 0.03, 0.02, and 0.01 each. The computed results are shown in Figure 9 and Table 3. Figure 9 shows that as the set probability of the chance constraints decreases, the system risk level also decreases. It is worth noting that since the upward and downward reserve risks may overlap, setting the individual chance-constraint probabilities to 0.05 for both upward and downward reserves may result in the total system risk exceeding 0.05 during certain periods. As shown in Figure 9, when the individual chance-constraint probabilities are set below 0.03, the total system risk meets the requirement at all times. From Table 3, it is seen that as the probability of the chance constraints decreases, the objective function shows an increasing trend, which is in line with the notion that system security improvements are often achieved at the cost of reduced economy.

Figure 9

Figure 9. Probabilities of insufficient reserve capacities for different chance-constraint probability settings in system #1.

Table 3

Table 3. Objective function values under different chance-constraint probabilities for system #1.

3.3 Test on system #2

To further verify the effectiveness of the proposed method, we performed tests on system #2. Here, we again conducted tests on the probability of insufficient reserve capacity under different optimization methods, different BESS parameters, and different chance-constraint probability settings. The first type of experiment was on the performances of the three optimization algorithms, whose results are shown in Figures 10–12 and Table 4. Compared to Figure 4, the risk probability curves for the three methods have changed in system #2 owing to the higher number of conventional generators, renewable energy stations, and energy storage devices. As shown in Figure 10, the LSO method fails to meet the risk requirement only at 19:00 hours, while the risk probability for CC-GMM is higher than that of LSO during several other periods throughout the day. This can be explained with the upward and downward reserve capacities shown in Figures 11, 12.

Figure 10

Figure 10. Probabilities of insufficient reserve capacities of different algorithms in system #2.

Figure 11

Figure 11. Total upward reserve capacities of different algorithms in system #2.

Figure 12

Figure 12. Total downward reserve capacities of different algorithms in system #2.

Table 4

Table 4. Objective function values of different optimization methods for system #2.

In Figure 11, the downward reserve capacity provided by LSO at 19:00 hours is significantly lower than that corresponding to the 0.025 quantile, leading to the highest risk probability at this point that exceeds 0.05. Figure 12 demonstrates that all three methods provide reserves greater than the 0.025 quantile capacity for downward reserve capacity. Additionally, during nighttime when there is no photovoltaic generation, such as 0:00–6:00 and 20:00–23:00 hours, LSO exhibits the strongest downward reserve conservatism. This is because the positive forecast error of wind power is smaller than that of photovoltaic generation, and LSO allocates more downward reserve capacity as it considers up to 10% positive deviation. Thus, the total risk probability of LSO in certain periods is lower than that of CC-GMM while its objective function is the highest.

Owing to the conservatism of DRO, its risk probabilities are low throughout the day, while its objective function is higher than that of CC-GMM. These results further confirm that so long as the probability setting is reasonable, the CC-GMM method always meets the system risk requirements while maintaining good economic performance. In contrast, the LSO and DRO methods have certain shortcomings because they cannot account for the actual uncertainties of renewable energy generation, leading to suboptimal results. In the test of probability of insufficient reserve capacity in the system under different BESS parameters, the $E_{i,t}^{e,\mathit{max}}$ of the BESS units tested in the three groups are set to 10 MWh, 30 MWh, and 50 MWh. The computed risk probabilities and upward reserve capacities are shown in Figures 13, 14.

Figure 13

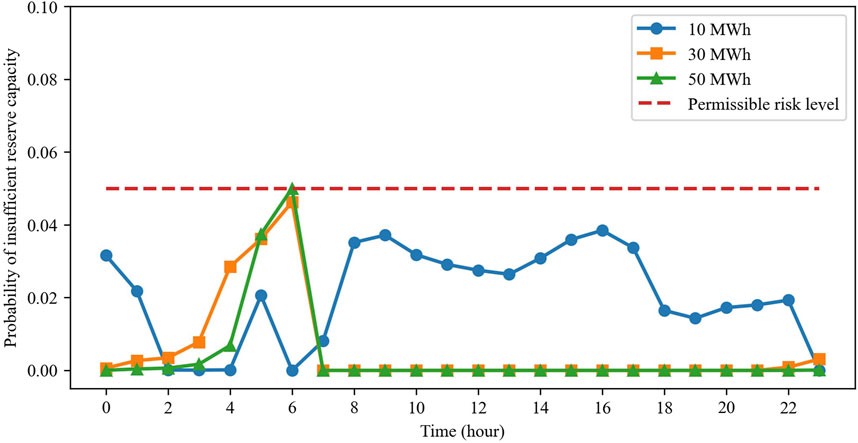
Figure 13. Probabilities of insufficient reserve capacities for different BESS parameters in system #2.

Figure 14

Figure 14. Total upward reserve capacities for different BESS parameters in system #2.

In Figure 13, the system risk probability during 0:00–6:00 hours does not show regular alteration with increase in BESS capacity. During certain periods, such as 0:00–1:00 hours, the risk is lowest for the 50 MWh system, while the risk is medium for the 30 MWh and highest for the 10 MWh systems. However, in other periods, such as at 4:00 hours, the risk is highest for the 30 MWh BESS. The reason for this can be explained using Figure 14. As seen in Figure 14, the upward reserve capacity provided by the 30 MWh system drops at 4:00 hours, just touching the reserve capacity corresponding to the 0.025 quantile. On the one hand, the reserve capacity provided by the energy storage system must satisfy the state of charge constraint, but the system cannot provide too much reserve capacity as it has to meet the charging and discharging schedules for the next period. On the other hand, this phenomenon occurs because the reserve capacity of conventional generators does not directly affect the objective function. These generators are subject to their ramping constraints and maximum/minimum power output limits, while still needing to provide sufficient reserves to meet the instantaneous demand. A simple example of this is when a generator is operating at its maximum power; it retains full downward regulation capability within its ramping constraints, and such adjustments do not incur any penalties in the objective function. Since the sole objective of the optimization solver is to minimize the objective function while satisfying the constraints, unexpected situations may arise: during certain periods, only some of the generators provide the full reserve capacity while the remaining generators provide no reserve capacity within their adjustable ranges.

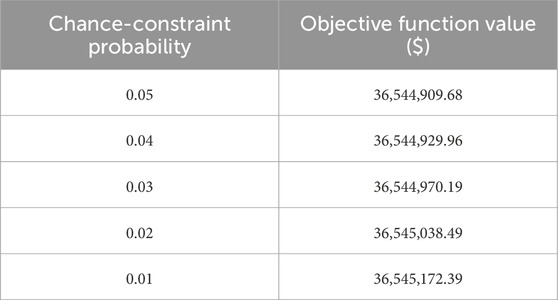
In system #2, we set lower chance-constraint probabilities of 0.05, 0.025, 0.01, 0.005, and 0.0025 to explore their impacts on system risk and the objective function; the corresponding results are shown in Figure 15 and Table 5. As seen from Figure 15, as the chance-constraint probability reduces, the system risk probability also decreases generally, which is consistent with the results shown in Figure 10. However, the changes in the objective function are different. As shown in Table 5, when the probability is reduced from 0.05 to 0.005, the objective function remains unchanged. Only when the probability is set to 0.0025 does the objective function increase significantly. This is because system #2 contains larger-scale generators and energy storage systems, allowing it higher capability to provide reserve capacity. Even with a 0.005 chance-constraint probability, the reserve capacity constraint remains relaxed. It is only when the probability is set to 0.0025 that the constraint tightens, causing the objective function to increase. Thus, the chance-constraint probability setting must comprehensively consider both the economic and security aspects of system operation.

Figure 15

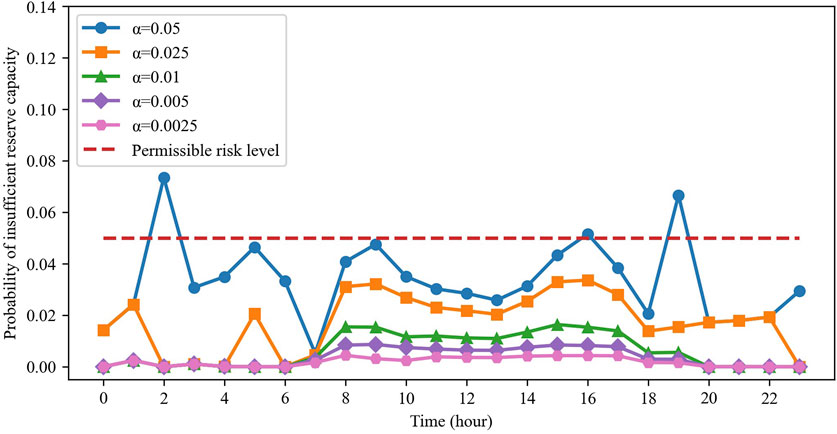
Figure 15. Probabilities of insufficient reserve capacities under different chance-constraint probability settings in system #2.

Table 5

Table 5. Objective function values under different chance-constraint probabilities for system #2.

4 Conclusion

This study proposes an optimal dispatch model of BESS called CC-GMM by considering the uncertainties of renewable generation. Here, we leverage the GMM to describe the probability distribution of the prediction errors of RESs, thereby considering the uncertainties of renewable generation. Chance constraints are incorporated into the model to ensure system security and are transformed into deterministic constraints using quantiles for the solution. The results show that involving BESSs in scheduling effectively promotes the consumption of renewable energy while improving the safety of systems containing a high proportion of RESs. Compared to the LSO and DRO methods, CC-GMM maintains good economic performance while ensuring system security. However, the proposed method can be improved in certain areas, such as considering the impact of BESS on the risk of branch transmission power in the model, to better match the actual operation of the power system; this is intended as the future direction of this research.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors without undue reservation.

Author contributions

ZL: writing – original draft, data curation, and formal analysis. DX: methodology, resources, and writing – original draft. HY: data curation, project administration, and writing – review and editing. YL: supervision, writing – review and editing, and project administration. JL: investigation, writing – review and editing, and validation. YC: validation, visualization, and writing – original draft. YY: conceptualization, investigation, and writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the State Grid Corporation of China (Risk dispatch and prevention considering energy storage and renewable generation, no. 521200230002).

Conflict of interest

Authors ZL, DX, HY, YL, and JL were employed by the State Grid Anhui Electric Power Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The authors declare that this study received funding from State Grid Corporation of China. The funder had the following involvement in the study: the study design and analysis.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bolognani, S., Arcari, E., and Dörfler, F. (2017). A fast method for real-time chance-constrained decision with application to power systems. IEEE Control Syst. Lett. 1, 152–157. doi:10.1109/LCSYS.2017.2711140

CrossRef Full Text | Google Scholar

Chen, Z., Li, Z., Guo, C., Ding, Y., and He, Y. (2020). Two-stage chance-constrained unit commitment based on optimal wind power consumption point considering battery energy storage. IET Generation, Transm. & Distribution 14, 3738–3749. doi:10.1049/iet-gtd.2019.1492

CrossRef Full Text | Google Scholar

Flåm, J. T., Zachariah, D., Vehkaperä, M., and Chatterjee, S. (2013). The linear model under mixed Gaussian inputs: designing the transfer matrix. IEEE Trans. Signal Process. 61, 5247–5259. doi:10.1109/TSP.2013.2278812

CrossRef Full Text | Google Scholar

Gangammanavar, H., Sen, S., and Zavala, V. M. (2016). Stochastic optimization of sub-hourly economic dispatch with wind energy. IEEE Trans. Power Syst. 31, 949–959. doi:10.1109/TPWRS.2015.2410301

CrossRef Full Text | Google Scholar

Gu, Y., and Xie, L. (2017). Stochastic look-ahead economic dispatch with variable generation resources. IEEE Trans. Power Syst. 32, 17–29. doi:10.1109/TPWRS.2016.2520498

CrossRef Full Text | Google Scholar

Jabr, R. A. (2013). Adjustable robust OPF with renewable energy sources. IEEE Trans. Power Syst. 28, 4742–4751. doi:10.1109/TPWRS.2013.2275013

CrossRef Full Text | Google Scholar

Jiang, X., Nan, G., Liu, H., Guo, Z., Zeng, Q., and Jin, Y. (2018). Optimization of battery energy storage system capacity for wind farm with considering auxiliary services compensation. Appl. Sci. 8, 1957. doi:10.3390/app8101957

CrossRef Full Text | Google Scholar

Li, N., Uçkun, C., Constantinescu, E. M., Birge, J. R., Hedman, K. W., and Botterud, A. (2016). Flexible operation of batteries in power system scheduling with renewable energy. IEEE Trans. Sustain. Energy 7, 685–696. doi:10.1109/TSTE.2015.2497470

CrossRef Full Text | Google Scholar

Nguyen, C.-L., Lee, H.-H., and Chun, T.-W. (2015). Cost-optimized battery capacity and short-term power dispatch control for wind farm. IEEE Trans. Industry Appl. 51, 595–606. doi:10.1109/TIA.2014.2330073

CrossRef Full Text | Google Scholar

Singh, R., Pal, B. C., and Jabr, R. A. (2010). Statistical representation of distribution system loads using Gaussian mixture model. IEEE Trans. Power Syst. 25, 29–37. doi:10.1109/TPWRS.2009.2030271

CrossRef Full Text | Google Scholar

Valverde, G., Saric, A. T., and Terzija, V. (2013). Stochastic monitoring of distribution networks including correlated input variables. IEEE Trans. Power Syst. 28, 246–255. doi:10.1109/TPWRS.2012.2201178

CrossRef Full Text | Google Scholar

Viafora, N., Delikaraoglou, S., Pinson, P., and Holbøll, J. (2020). Chance-constrained optimal power flow with non-parametric probability distributions of dynamic line ratings. Int. J. Electr. Power & Energy Syst. 114, 105389. doi:10.1016/j.ijepes.2019.105389

CrossRef Full Text | Google Scholar

Wang, Z., Shen, C., Liu, F., and Gao, F. (2017a). Analytical expressions for joint distributions in probabilistic load flow. IEEE Trans. Power Syst. 32, 2473–2474. doi:10.1109/TPWRS.2016.2612881

CrossRef Full Text | Google Scholar

Wang, Z., Shen, C., Liu, F., Wu, X., Liu, C.-C., and Gao, F. (2017b). Chance-constrained economic dispatch with non-Gaussian correlated wind power uncertainty. IEEE Trans. Power Syst. 32, 4880–4893. doi:10.1109/TPWRS.2017.2672750

CrossRef Full Text | Google Scholar

Wu, W., Chen, J., Zhang, B., and Sun, H. (2014). A robust wind power optimization method for look-ahead power dispatch. IEEE Trans. Sustain. Energy 5, 507–515. doi:10.1109/TSTE.2013.2294467

CrossRef Full Text | Google Scholar

Xie, L., Gu, Y., Zhu, X., and Genton, M. G. (2014). Short-term spatio-temporal wind power forecast in robust look-ahead power system dispatch. IEEE Trans. Smart Grid 5, 511–520. doi:10.1109/TSG.2013.2282300

CrossRef Full Text | Google Scholar

Zeng, B., and Zhao, L. (2013). Solving two-stage robust optimization problems using a column-and-constraint generation method. Operations Res. Lett. 41, 457–461. doi:10.1016/j.orl.2013.05.003

CrossRef Full Text | Google Scholar

Zhang, L., Yu, Y., Li, B., Qian, X., Zhang, S., Wang, X., et al. (2022). Improved cycle aging cost model for battery energy storage systems considering more accurate battery life degradation. IEEE Access 10, 297–307. doi:10.1109/ACCESS.2021.3139075

CrossRef Full Text | Google Scholar

Zhao, C., Wang, J., Watson, J.-P., and Guan, Y. (2013). Multi-stage robust unit commitment considering wind and demand response uncertainties. IEEE Trans. Power Syst. 28, 2708–2717. doi:10.1109/TPWRS.2013.2244231

CrossRef Full Text | Google Scholar

Zhao, Y., Li, Z., Ju, P., and Zhou, Y. (2023). Data-driven chance-constrained dispatch for integrated power and natural gas systems considering wind power prediction errors. IET Gener. Transm. Distrib. 17, 2846–2860. doi:10.1049/gtd2.12861

CrossRef Full Text | Google Scholar