Thermal performance enhancement in a hexagonal cavity filled with hybrid nanofluid and a steering-shaped insertion

Background: Steering-shaped obstacles are extensively used in various thermal engineering applications, including heat exchangers, transformers, semiconductors, microelectronics, chemical sensors, air-cooled engines, gas turbines, automotive radiators, and hydrogen fuel cells.

Aims: The main goal of this study was to examine how key dimensionless parameters—such as the Reynolds number ($Re$), Richardson number ($Ri$), Hartmann number ($Ha$), Nusselt number ($Nu$), Bejan number ($Be$), and magnetic field angle ($\gamma$)—affect the heat transfer, fluid flow, and entropy generation in a hybrid nanofluid ($Ti{O}_2-Cu-H_{2}O$) system. A mixed convection flow is analyzed inside a hexagonal cavity containing a heated steering-shaped obstacle. The cavity has two moving walls that drive the flow, whereas a magnetic field is applied at an angle. The focus is to reduce entropy generation and enhance thermal performance, which is important for improving the efficiency of advanced cooling systems.

Method and validations: The governing equations and boundary conditions are solved using the Galerkin weighted residual finite element method, with extensive validation against existing results to ensure the accuracy of the findings.

Parameters: In the study, we investigate a range of parameters: nanoparticle concentration ($\phi$) varying from 1% to 5%, $Re$ from 1 to 300, $Ha$ from 0 to 60, $Ri$ from 0.1 to 10, and $\gamma$ ranging from $0°$ to $90°$.

Results: In the study, we show that lid-driven motion of the top and bottom walls, along with a steering-shaped heated obstacle, enhances heat transfer (HT) and reduces entropy generation$(E_{gen}$). Thermal performance improves with increasing $Ri$ and $Re$ but decreases with increasing $Ha$. For fixed $Re$ = 300, at the highest magnetic field strength ($Ha$ = 60), the HT rate reaches its minimum, exhibiting a 22.41% decrease relative to the no magnetic-field condition ($Ha$ = 0). An increase in the $Ri$ number leads to a 68.76% enhancement in thermal performance. At a fixed $Ri=10$, increasing the $Re$ number from 1 to 300 leads to a 263.83% enhancement in thermal performance. The addition of $Ti{O}_2-Cu-H_{2}O$ hybrid nanofluid (HNF) further enhances thermal performance.

Conclusion: In the study, we reveal that mixed-convection (MC) HNF and heated steering-shaped obstacles play a significant role in enhancing HT and reducing $E_{avg}$ within the cavity.

Highlights

• The average Nusselt number (${Nu}_{avg}$) increases by 263.83% as the Richardson number ($Ri$) increases from 0.1 to 10.

• Hybrid nanoparticles enhance heat transfer by approximately 6.31%.

• Due to the Hartman number ($\left.Ha\right)$, entropy generation decreases by approximately 22.13%.

• This study applies to advanced cooling systems like air-cooled engines.

1 Introduction

The efficiency of thermal systems is often limited by the low thermal conductivity of heat transfer (HT) fluids such as water, ethylene glycol, and similar substances. Research workers suggest adding metallic or non-metallic particles (e.g., metal oxides and carbon nanotubes) to base fluids to enhance thermal conductivity as these particles exhibit higher thermal conductivity than the base fluid. Initially, the suspension contains micro- or millimeter-sized particles; however, issues like poor stability, erosion, and clogging arise. As a result, research workers have shifted their focus to nanoparticles (Leong et al., 2017; Rashid et al., 2023a). Studies on natural convection (NC) in cavities filled with nanofluids have been conducted worldwide, as this phenomenon can enhance HT efficiency by reducing heat loss and increasing cooling rates. It has numerous potential applications in areas such as solar collectors, petroleum reservoirs, nuclear cooling, heat exchangers, transportation, electrical machinery cooling, fire engineering, mechanical applications, HT systems, renewable energy systems, underground water movement, and geothermal resources (Saha G. et al., 2023; Kumar et al., 2015; Pavía et al., 2021; Islam et al., 2022; Alobaid et al., 2017; Devendiran and Amirtham, 2016; Mahian et al., 2021; Saha et al., 2024a; Rashid et al., 2023b). Many efforts have been made to gather fundamental data on NC flows and heat transfer in cavities (Saha et al., 2024b; Al-Amir et al., 2023; Mahmud et al., 2024; Jihan et al., 2024; Saha B. K. et al., 2024).

A numerical investigation of magnetohydrodynamics (MHD) NC with the effect of a source and sink was conducted by Ahmad et al. (2024a). They introduced fins that acted as a source and sink, with their aspect ratio affecting HT, mass transfer (MT), and entropy generation$(E_{gen}$). The results indicated that a higher Rayleigh number ($Ra$) enhanced HT and MT, whereas the Ha reduced both. Alam et al. (2024) performed a statistical and numerical study within a hexagonal cavity on MHD unsteady laminar NC with a ${Fe}_3{O}_4-H_{2}O$ nanofluid. In this study, we used response surface methodology (RSM) to assess the sensitivity of parameters such as Hartmann number ($Ha),Ra,$ and nanoparticle concentration ($\phi$). The results showed a significant increase in the average Nusselt number (${Nu}_{avg}$) with higher $\phi ,\text{magnetic\hspace{0.17em}field\hspace{0.17em}angle\hspace{0.17em}}\left(\gamma \right),$ nanoparticle type, and Ra, whereas Ha and nanoparticle diameter had opposite effects. Saha et al. (2025) investigated HT in a modified tooth-shaped cavity with an ${Al}_2{O}_3–H_{2}O$ nanofluid considering MHD natural convection. Their results indicated that higher Ra and φ improved HT by enhancing the temperature gradient and thermal properties of the nanofluid. Saha T. et al. (2023b) studied MHD NC inside a wavy cavity with a heated fin. Their results showed that streamlines and isotherms varied with fin length, and nanoparticle shape significantly impacted HT, with the Nusselt number ($Nu$) increasing by 7.65% for blade-shaped nanoparticles and 2.86% for spherical-shaped nanoparticles. A recent study by Jamy et al. (2023) examined conjugate MHD NC in an L-shaped cavity with a thick fin, finding that HT improved for $Ra\ge 10⁴$ due to $Ha$, whereas conduction dominated for $Ra\le 10⁴$.

In many practical applications, NC and external forces contribute to mixed convection (MC). This process is crucial in phase changes and the cooling of electronic devices. The magnetic field plays a key role in electrically conductive fluids and is essential for understanding the dynamics of liquid metals, plasma, electrolytes, and fusion blankets (Colak et al., 2020). Alomari et al. (2024) studied MHD MC in curvilinear lid-driven cavities with carbon nanotubes (CNTs) and an adiabatic cylinder. The results showed enhanced HT and flow with higher Reynolds number ($Re$) and Richardson number ($Ri$). Thermal performance increased by 57% as $Ri$ increased from 0.1 to 10 at $Re=41$ and by 62.5% at $Re=200$. Higher $\phi$ improved HT but reduced circulation, whereas thermal performance decreased by 34.7% as $Ha$ increased from 0 to 62 at $Re=200$. Al-Khaleel et al. (2024) investigated MHD MC in a lid-driven wavy cavity with Ostwald-de Waele nanofluids. At the highest $Re$, increasing Grashof ($Gr$) and Darcy ($Da$) numbers enhanced $Nu$ by 3% and 19%, respectively, whereas decreasing $Ha$ values increased $Nu$ by 23%. Karim et al. (2024) examined MC heat and MT in a right triangular domain. The outcomes showed that lid direction and $Re$ values significantly influence HT and MT, with lid movement serving as an effective control for flow and temperature distribution. A sensitivity study of MHD MC in a hexagonal cavity using $Ti{O}_2-H_{2}O$ nanofluid was conducted by Islam et al. (2023). The results revealed that with increasing $Re$ and$\phi ,$ the thermal performance of the nanofluid improved, whereas higher $Ha$ reduced it. Furthermore, $\phi$ and $Re$ positively influenced $Nu$, whereas $Ha$ had a negative effect. At $Ha=0$, the maximum $Nu$ was achieved at $Re=200$ and $\phi =0.1$. $Ti{O}_2-H_{2}O$ nanofluid improved HT by 17.69%, offering insights for designing efficient MC heat exchangers. The influence of various inflow conditions on MC in a T-shaped cavity with $Ti{O}_2-H_{2}O$ nanofluid was analyzed by Ruvo et al. (2023). The results revealed that uniform inflow significantly affected HT rates in the cavity, varying with $Gr$ and $Re$, and nanofluids enhanced HT, especially at $Gr>{10}^3$ for $Ri=1$. The study by Habibishandiz and Saghir (2022) investigated MC in a vertical annular porous cylinder with nanofluid and oxytactic microorganisms. Their findings showed that higher $Ha$ reduced HT, and microbes could mitigate this effect.

To enhance the properties of nanofluids, research workers introduced hybrid nanofluids (HNFs) as next-generation HT fluids (Ranga Babu et al., 2017). The synthesis of hybrid nanoparticles improves physicochemical properties that individual components or materials cannot achieve. Many studies have found that the thermal conductivity of HNF is higher than that of single nanofluids (Sajid and Ali, 2018; Saha et al., 2024a). A computational study by Hussain et al. (2021) analyzed the flow of ${Al}_2{O}_3-Cu-H_{2}O$ HNF in a horizontal channel with an open cavity. Their results showed that higher $Ri$ values enhanced HT and $E_{gen}$. Additionally, increasing $Re$ and $\phi$ boosted HT and $E_{gen}$, whereas the average Bejan number (${Be}_{avg}$) decreased. Khan et al. (2020) studied mixed-convection HT of ${Al}_2{O}_3-Cu-H_{2}O$ HNF in a split-lid-driven cavity with a Y-shaped obstacle. Their findings indicated that the split-lid motion creates symmetrical streamlines and isotherms. The local $Nu$ peaks when the lids meet, whereas ${Nu}_{avg}$ decreases with increasing $Ri$ values. Malik et al. (Al Kalbani et al., 2020) examined a wavy lid-driven cavity with HNF, and their outcomes showed that increasing $Gr,\gamma ,\phi$, and $Re$ values enhanced flow and HT, whereas higher undulations, cylinder radius, and $Ha$ reduced flow strength.

A numerical experiment on the inner adiabatic rotating cylinder inside a vented cavity with MC of HNF was conducted by Jasim et al. (2021). Their findings indicated that counterclockwise rotation enhanced convective HT, whereas clockwise rotation had the opposite effect. Additionally, for counterclockwise rotation, HT improved as the cylinder moved closer to the hot wall. The maximum HT enhancement, reaching 21% compared to the stationary cylinder, was observed when R = 0.3 and $\delta =0.5$ under the conditions Gr = 10⁴, $\phi =2\%$, $Re=100$, and $\mathrm{\Omega }=5$. Akhter et al. (2023) investigated MC HNF in a square cavity with multiple rotating obstacles. Their results showed that HT enhancement reached a maximum of 261.29% with cylinder rotation ($\omega =0–50$; $\phi =1\%;Ha=10$), decreasing with higher magnetic field strength. The lowest HT rate, 144.62% lower than that at $Ha=0$, was observed at $Ha=50$. The optimal HT, 101.2% higher than that of water, was achieved with 5% hybrid nanoparticles. Mahboobtosi et al. (2023) examined a curved stretching surface with ternary HNF suspended in polymer. Their analysis indicated that increasing $\phi$ enhanced $E_{gen}$ and reduced Bejan number ($Be$) values. They also found that as the curvature range parameter increased, $Nu$ decreased by 37%. A study on the effect of inclination angle, including heat sources and convective boundary conditions, on a porous shrinking surface was carried out by Zainodin et al. (2024). They observed that as $\phi$ increased, skin friction increased by approximately 14.79%. Altering the inclination angle led to a 3.28% increase in skin friction and a 0.0068% increase in the HT rate. Furthermore, with an increasing Biot number, HT was enhanced by approximately 174.48%. Ali et al. (2024) investigated MHD MC in an octagonal heat exchanger with HNF. Their findings revealed that thermal performance improved with increasing $Re$ and $\phi$, whereas the opposite behavior was observed for $Ha$. Additionally, introducing HNF of $Ti{O}_2-Cu-H_{2}O$ enhanced the HT capacity of water by 25.75%. A numerical experiment on NC within a hexagonal cavity using $MgO-H_{2}O$ was conducted by Sumeira et al. (Yasmin et al., 2023). Their findings indicated that convection, velocity, and HT were enhanced with an increase in $Ra$. Furthermore, related literature can be found in the study by Ikram et al. (2024), Ikram et al. (2023), and Ikram et al. (2021). Deebani et al. (2025) conducted a numerical analysis of trihybrid nanofluid flow over an extended stagnation region on a flat plate embedded in a porous medium. The study revealed that the ternary nanofluid significantly enhanced thermal performance, as reflected in the Nusselt number. Specifically, mono-nanofluids containing Go, $Ag$, and $Cu$ exhibited enhancements of 17.13%, 8.44%, and 19.20%, respectively, whereas hybrid nanofluids demonstrated improvements of 12.67%, 18.13%, and 13.65%, respectively. Raza et al. (2024a) experimentally investigated HT in heat coaxial pipes, demonstrating that incorporating nanofluids significantly improves thermal conductivity, making them effective for electronics cooling, spacecraft systems, and heat recovery applications. An investigation on tetra-hybrid nanofluid flow in a porous channel with stretching/shrinking walls was conducted by Shutaywi et al. (2024). The outcome of the experiment reveals that elevated radiation enhances radiative HT, whereas stretching and shrinking alter boundary thickness, collectively leading to an increased Nusselt number. An experiment was conducted on a trihybrid nanofluid confined between two horizontal coaxial cylinders by Raza et al. (2024b). The experimental results indicate that increasing $Ha$ leads to a reduction in the velocity profile, whereas the temperature profile exhibits an opposite trend. Conversely, higher $Re$ enhances both temperature and velocity profiles. Alhadri et al. (2022) investigated the radiative behavior of a $Cu–Al₂O₃–$water hybrid nanofluid under the influence of Joule heating and suction over a stretched surface. The incorporation of the Darcy–Forchheimer model accounted for inertial and porous medium effects, enhancing the physical relevance of the study. The result shows that the influences of suction, magnetic field, and permeability parameters are significant. On a shrinking surface, increasing the volume fraction of copper nanoparticles enhanced local skin friction while reducing the local Nusselt number. Furthermore, the study demonstrated that the artificial neural network (ANN) method effectively predicts both skin friction and local heat transfer rates. Deebani et al. (2024) investigated MHD Casson nanofluid flow with convective boundary conditions over a stretching surface. The outcome shows that an increase in the stretching and Casson parameters reduces the temperature profile, whereas higher magnetic, radiation, Eckert, thermophoresis, and Brownian motion parameters elevate it. Skin friction increases with stretching but decreases with the Casson parameter, and the reduced Nusselt number decreases with increasing Eckert, thermophoresis, and Brownian motion parameters but improves with lower radiation effects. Waqas et al. (2025) performed a numerical study to analyze the thermal and mass transport behavior of a Casson fluid within a staggered cavity, subjected to magnetohydrodynamic effects at various inclination angles. The results reveal that increasing $Re$ from 10 to 1000 enhances the Nusselt and Sherwood numbers by approximately 37.4% and 41.8%, respectively, indicating significant improvements in heat and mass transfer. Moreover, entropy generation reaches its peak at an inclination angle of 90°, whereas increasing $Ha$ leads to a notable reduction—approximately 20%—in both thermal and concentration transport rates. A comparable investigation was conducted by Majeed et al. (2025), in which the thermal and flow characteristics of a Casson fluid were examined within a hexagonal enclosure featuring a heated bottom wall and a centrally placed circular obstacle. The results indicate that increases in both $Ha$ and aspect ratio lead to elevated temperature and mass concentration within the fluid domain. Furthermore, the Nusselt number exhibits an increasing trend with higher values of the Casson number, buoyancy ratio, and inclination angle, whereas it decreases as the Lewis number (Le) increases. In contrast, the average mass transfer rate enhances with increasing Casson number, Lewis number, and buoyancy ratio but diminishes with the increases in the inclination angle and $Ha$. Ahmad et al. (2024b) conducted a comprehensive investigation into the coupled heat and mass transfer driven by NC, along with entropy generation, within a square cavity featuring four diagonally oriented corner fins and a centrally positioned circular obstacle. The study considered the influence of a non-Newtonian (Casson) fluid under the effect of an inclined magnetic field. Their findings revealed that the highest entropy generation occurs near the fin tips and along solid boundaries. An increase in the Casson parameter intensified the flow velocity, temperature distribution, and entropy production. However, the presence of fins introduced greater resistance to fluid motion, thereby reducing the Nusselt number and Sherwood numbers. Additionally, a higher $Ra$ was shown to enhance flow velocity while decreasing $Be$, indicating a shift toward entropy generation dominated by HT rather than fluid friction. Ahmad et al. (2024a) conducted an investigation on the effects of heat sources and sinks in the presence of a Casson fluid. The obtained results confirm that the inclusion of fins significantly enhances the efficiency of HT systems and influences the development of flow structures. An increase in $Ra$ intensifies both heat and mass transfers, highlighting the dominant role of buoyancy-driven convection. In contrast, an increase in $Ha$ suppresses convective motion, thereby diminishing thermal transport. Moreover, as Le increases, entropy generation associated with fluid deformation becomes more pronounced, which is also reflected in the corresponding variation of $Be$.

It is worth reiterating that various cavity geometries have been studied, including square cavities with multiple rotating rough cylinders (Akhter et al., 2023) and MC in octagonal cavities with circular obstacles (Ali et al., 2024). The present study introduces a nonrotating steering-shaped obstacle within a double lid-driven hexagonal cavity under the influence of an inclined magnetic field. To the best of the authors’ knowledge, no prior study has explored the combined effects of this specific obstacle shape with magnetic orientation on MC flow and entropy generation in an HNF environment. This unique configuration leads to distinct flow interactions and thermal characteristics that differentiate our model from previous works. The primary objective of this study is to investigate temperature distributions, flow fields, and HT behaviors; minimize $E_{gen}$; and optimize the thermodynamic performance of HT by evaluating Be for MHD MC flow inside the cavity. The numerical results are expected to provide a valuable reference for future research on MC HT using HNF within a cavity under the influence of an inclined magnetic field.

Focusing on entropy offers a deeper insight into the irreversibilities and energy losses within the system, which is essential for developing more efficient thermal management systems. In this study, we introduce a significant innovation by incorporating double lid-driven walls and a heated, steering-shaped obstacle within the hexagonal cavity. The study is conducted for an advanced cooling component, such as an air-cooled engine, which generates heat that must be efficiently dissipated to prevent overheating. The findings of our study and this design closely align with real-world applications, enhancing the practical significance of the research. Additionally, the study emphasizes the development of thermal management systems.

2 Model description

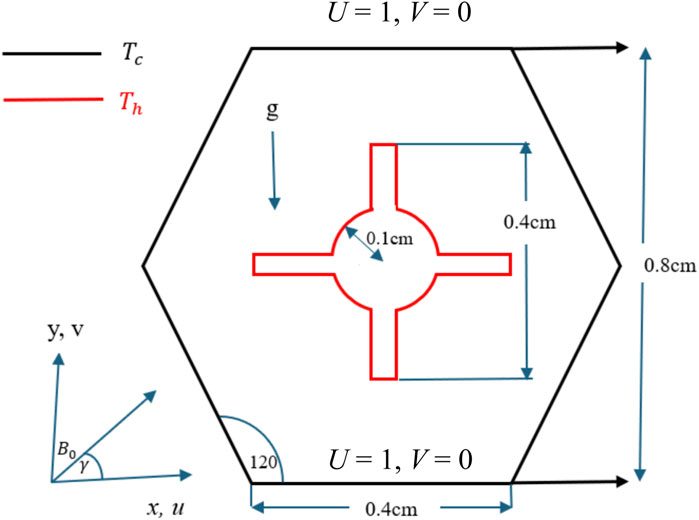
This study investigates the flow characteristics of HNF within a double lid-driven hexagonal cavity containing a steering-shaped obstacle, as shown in Figure 1. The HNF flow is considered laminar, steady, and incompressible throughout the domain. The upper and bottom walls of the cavity move with a uniform velocity in the positive x-direction, whereas the other walls remain stationary. Additionally, a heated steering-shaped obstacle (T_h) is installed inside the hexagonal cavity. All the remaining walls are maintained at a constant low temperature (T_c). The length and width of the steering-shaped obstacle are 0.4 cm and 0.04 cm, respectively. Consequently, the length and width of the entire domain are identical, each measuring 0.8 cm. The magnetic field is inclined at an angle $\gamma$, with a constant magnitude of $B_0$.

Figure 1

Figure 1. Geometry of the governing problem.

The physical relevance of the parameters used in our simulations is discussed below:

• Nanoparticle concentration ($\phi :1\%$–$5\%$): this range reflects realistic concentrations commonly used in experimental and numerical studies of nanofluids and HNF, where the enhancement in thermal conductivity without causing significant agglomeration or sedimentation is well documented. Concentrations beyond 5% can lead to stability and viscosity issues; hence, we limited the upper bound to ensure physical realism and numerical stability.

• Reynolds number ($Re$: 1–300): this range allows us to study flow regimes from creeping flow to the onset of transition in laminar flow. It covers both diffusion-dominated and convection-dominated regimes, which is essential for mixed-convection analysis and for capturing the influence of forced convection in different intensities.

• Hartmann number ($Ha:0$–$60$): the selected range covers both weak and strong magnetic field effects. This is consistent with prior studies in MHD convection, where $Ha$ ≤ 60 is sufficient to observe the suppressive influence of the Lorentz force on flow and heat transfer in enclosures.

• Richardson number ($Ri:0.1$–$10$): this dimensionless number measures the ratio of buoyancy to inertial forces. The selected range effectively captures the transition from forced convection ($Ri<1$), through mixed-convection ($Ri\approx 1$), to natural convection-dominated flow ($Ri>1$). It ensures a comprehensive investigation of different convection regimes relevant in practical applications.

• Inclination angle ($\gamma :0$–$90$): varying the inclination angle allows us to assess the impact of gravity orientation on heat and fluid flow behaviors. This range covers all relevant orientations from horizontal to vertical, commonly encountered in thermal system configurations such as solar collectors, electronic cooling devices, and building enclosures.

3 Governing equations and boundary conditions

For the purpose of enhancing our analysis, we use the continuity, momentum, and energy equations. The governing equations in two-dimensional Cartesian coordinates, based on the previously outlined assumptions, are presented as follows (Malik et al., 2024):

$\frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}=0,(1)$

$\left(U\frac{\partial U}{\partial X}+V\frac{\partial U}{\partial Y}\right)=-\frac{{\rho }_{bf}}{{\rho }_{hnf}}\frac{\partial P}{\partial X}+\frac{{\rho }_{bf}}{{\rho }_{hnf}}\frac{{\mu }_{hnf}}{{\mu }_{bf}}\frac{1}{Re}\times \left(\frac{{\partial }^{2}U}{\partial X^2}+\frac{{\partial }^{2}U}{\partial Y^2}\right)+\frac{{\rho }_{bf}}{{\rho }_{hnf}}\frac{{\sigma }_{hnf}}{{\sigma }_{bf}}\frac{{Ha}^2}{Re}\times \left(Vcos\gamma \mathit{sin}\gamma -U{\mathit{sin}}^2\gamma \right),(2)$

$\left(U\frac{\partial V}{\partial X}+V\frac{\partial V}{\partial Y}\right)=-\frac{{\rho }_{bf}}{{\rho }_{hnf}}\frac{\partial P}{\partial Y}+\frac{{\rho }_{bf}}{{\rho }_{hnf}}\frac{{\mu }_{hnf}}{{\mu }_{bf}}\frac{1}{Re}\times \left(\frac{{\partial }^{2}V}{\partial X^2}+\frac{{\partial }^{2}V}{\partial Y^2}\right)+\frac{{\rho }_{bf}}{{\rho }_{hnf}}\frac{{\sigma }_{hnf}}{{\sigma }_{bf}}\frac{{Ha}^2}{Re}\times \left(Ucos\gamma \mathit{sin}\gamma -V{\mathit{sin}}^2\gamma \right)+\frac{{\left(\rho \beta \right)}_{hnf}}{{\rho }_{hnf}{\beta }_{bf}}Ri\theta ,(3)$

$U\frac{\partial \theta }{\partial X}+V\frac{\partial \theta }{\partial Y}=\frac{1}{PrRe}\frac{K_{hnf}}{K_{bf}}\frac{{\left({\rho C}_p\right)}_{bf}}{{\left({\rho C}_p\right)}_{hnf}}\left(\frac{{\partial }^2\theta }{\partial X^2}+\frac{{\partial }^2\theta }{\partial Y^2}\right).(4)$

The dimensionless parameters presented in Equation 5 serve as the basis for Equations 1–4:

$X=\frac{x}{L},Y=\frac{y}{H},U=\frac{u}{U_0},V=\frac{v}{U_0},P=\frac{P}{\rho {U_0}^2},Ri=\frac{Gr}{{Re}^2},Re=\frac{U_{0}L}{\vartheta },Gr=\frac{g\beta \left(T_h-T_c\right)}{{\vartheta }^2}{L}^3,\vartheta =\frac{\mu }{\rho },\mathit{Pr}=\frac{\vartheta }{\alpha },Ha=B_{0}L\sqrt{\frac{\sigma }{\mu }},\theta =\frac{T-T_c}{T_h-T_c},{\alpha }_{bf}=\frac{k_{bf}}{{\left(\rho Cp\right)}_{bf}}.(5)$

Correlations of HNF between nanoparticles and base fluid are depicted in Equation 6 (Ali et al., 2024):

$\phi ={\phi }_{Cu}+{\phi }_{Ti{O}_2},$

${\rho }_{hnf}=\left(1-\phi \right){\rho }_{bf}+{\phi }_{Cu}{\rho }_{Cu}+{\phi }_{Ti{O}_2}{\rho }_{Ti{O}_2,}$

${\left(\rho C_p\right)}_{hnf}=\left(1-\phi \right){\left(\rho C_p\right)}_{bf}+{\phi }_{Cu}{\left(\rho C_p\right)}_{Cu}+{\phi }_{Ti{O}_2}{\left(\rho C_p\right)}_{Ti{O}_2,}$

$k_{hnf}=\left(\frac{k_{sp}+2k_{bf}-2\phi \left(k_{bf}-k_{sp}\right)}{k_{sp}+2k_{bf}+\phi \left(k_{bf}-k_{sp}\right)}\right)k_{bf,}$

$\phi k_{sp}={\phi }_{Cu}{k}_{Cu}+{\phi }_{Ti{O}_2}{k}_{Ti{O}_{2,}}$

${\mu }_{hnf}={\mu }_{bf}\left(1+2.5\phi +6.5{\phi }^2\right),$

${\alpha }_{hnf}=\frac{k_{hnf}}{{\left(\rho C_p\right)}_{hnf}},$

${\left(\rho \beta \right)}_{hnf}=\left(1-\phi \right){\left(\rho \beta \right)}_{bf}+{\phi }_{Cu}{\beta }_{Cu}+{\phi }_{Ti{O}_2}{\beta }_{Ti{O}_2},$

${\sigma }_{hnf}={\sigma }_{bf}\left[1+\frac{3\phi \left(\frac{{\sigma }_{sp}}{{\sigma }_{bf}}-1\right)}{\left(\frac{{\sigma }_{sp}}{{\sigma }_{bf}}+2\right)-\phi \left(\frac{{\sigma }_{sp}}{{\sigma }_{bf}}-1\right)}\right]\phi {\sigma }_{sp}={\phi }_{Cu}{\sigma }_{Cu}+{\phi }_{Ti{O}_2}{\sigma }_{Ti{O}_2.}(6)$

The specified boundary conditions for fluid velocity and temperature are detailed in Equation 7:

$\begin{array}{ccc}\text{Top\hspace{0.17em}and\hspace{0.17em}bottom\hspace{0.17em}walls}:U=1,& V=0,& \theta =0\\ \text{Steering\hspace{0.17em}shaped\hspace{0.17em}obstacles}:U=0,& V=0,& \theta =1\\ \text{Remaining\hspace{0.17em}walls}:U=0,& V=0,& \theta =0.\end{array}(7)$

Nondimensional parameters:

Nusselt number: local Nusselt number (${Nu}_l$) along the heated surface can be represented in Equation 8 (Abood et al., 2024):

${Nu}_l=\frac{k_{hnf}}{k_f}\left(\frac{\partial \theta }{\partial n}\right).(8)$

${Nu}_{avg}$ along the heated surface can be represented in Equation 9 (Abood et al., 2024):

${Nu}_{avg}=\frac{1}{S}{\displaystyle \underset{0}{\overset{s}{\int }}}{Nu}_{l}dn,(9)$

where S represents the length of the heated surface and n indicates the direction along this surface.

Entropy generation:

Dimensionless forms of $E_{gen}$, $E_{ht},$ $E_{ff},\text{and\hspace{0.17em}}{E}_{mf}$ are represented in Equations 10a, 10b, 10c, 10d, respectively (Hussain et al., 2024; H et al., 2017):

$E_{gen}=E_{ht}+E_{ff}+E_{mf,}(\mathrm{10a})$

$E_{ht}=\frac{k_{hnf}}{k_f}\left[{\left(\frac{\partial \theta }{\partial X}\right)}^2+{\left(\frac{\partial \theta }{\partial Y}\right)}^2\right],(\mathrm{10b})$

$E_{ff}=\varnothing \frac{{\mu }_{hnf}}{{\mu }_f}\left[2\left({\left(\frac{\partial U}{\partial X}\right)}^2+{\left(\frac{\partial V}{\partial Y}\right)}^2\right)+\left(\frac{\partial U}{\partial Y}+\frac{\partial V}{\partial X}\right)\right],(\mathrm{10c})$

$E_{mf}=\varnothing \frac{{\sigma }_{hnf}}{{\sigma }_f}{Ha}^2{\left(Vcos\gamma \mathit{sin}\gamma -U{\mathit{sin}}^2\gamma \right)}^2.(\mathrm{10d})$

Here, the irreversibility factor, represented by $\varnothing$ in this case, is ${10}^{-4}.$

Dimensionless $E_{avg}$ (H et al., 2017) can be computed as shown in Equation 11:

$E_{avg}=\frac{1}{v}\int E_{gen}dv=E_{ht,avg}+E_{ff,avg}+E_{mf,avg.}(11)$

Bejan number:

The local and average Bejan numbers are represented in Equations 12a, 12b, respectively (Taghizadeh and Asaditaheri, 2018):

${Be}_l=\frac{E_{ht}}{E_T},(\mathrm{12a})$

${Be}_{avg}=\int {Be}_{l}dv.(\mathrm{12b})$

4 Methodology

To solve the nondimensional governing Equations 1–4, alongside the specified boundary conditions, the domain of interest is discretized into a collection of finite elements. The numerical simulations were conducted using the finite element method (FEM)-based computational fluid dynamics (CFD) software, COMSOL Multiphysics 6.2. A numerical simulation process is presented using a flowchart in Figure 2a.

Figure 2

Figure 2. (a) Flowchart of numerical simulation. (b) Schematic presentation of the grid hexagonal cavity.

The second-order Galerkin method, a fundamental approach within FEM, works by minimizing the error between the exact and approximate solutions over the entire domain. It does so by multiplying the residuals of the governing differential equations by a set of predefined weighting functions and then integrating them over the domain. This transforms the governing partial differential equations into a system of algebraic equations that can be solved numerically. This method is adopted due to its high accuracy, rapid convergence, and ability to handle complex geometries and boundary conditions efficiently, which ensures that the approximate solution satisfies the governing equations in an average sense, leading to a stable and accurate numerical solution.

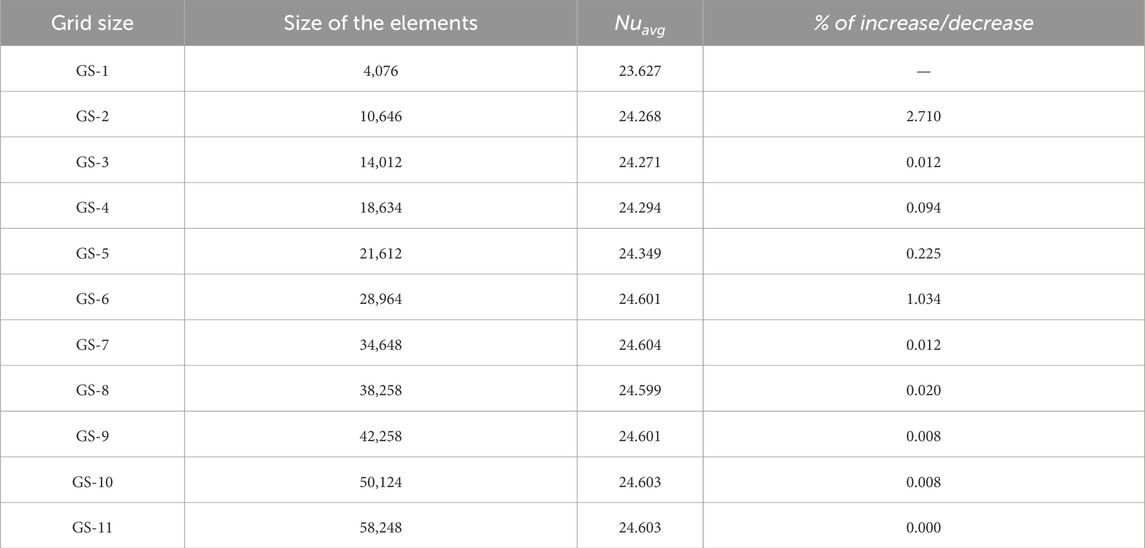
In the fluid domain, as shown in Figure 2b, the computational domain has been divided into triangular mesh elements to discretize the various flow variables within the domain. To confirm the mesh independence of the numerical solution, different grid sizes were utilized to compute Nu_avg. However, to enhance numerical stability and mitigate abrupt variations in flow behavior, the cavity’s corners were chamfered. Moreover, a refined mesh was used near these corners and along the solid boundaries to ensure computational accuracy, as depicted in Figure 2b.

5 Model validation

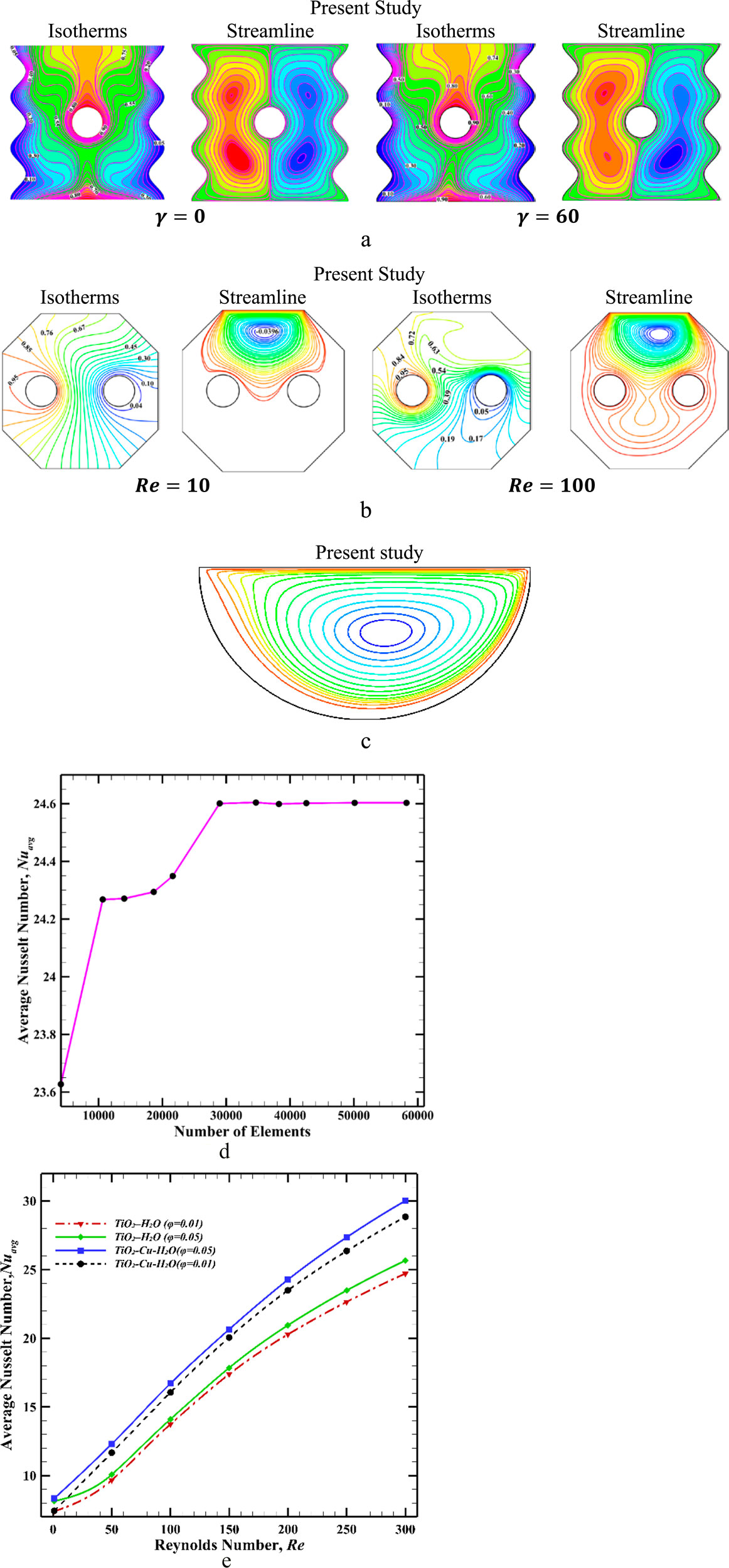
To ensure accuracy, various scenarios have been analyzed to evaluate the accuracy of the present analysis. The numerical results are compared with the results of Malik et al. (2024), who studied mixed convective HT within a wavy cavity, as shown in Figure 3a. Additionally, we investigate HT behavior within a wavy upper HNF filled lid-driven cavity. For further comparison, we utilized the findings of Ali et al. (2024), who examined MC in an octagonal cavity driven by a moving lid. Their study considered two circular cylinders, where the left cylinder was heated, and the right cylinder was cooled. The corresponding results are presented in Figure 3b. In addition, our numerical results are compared with the experimental and numerical investigation was conducted by Chen and Cheng (2004) to examine the combined influence of lid motion and buoyancy on flow dynamics and heat transfer characteristics in a lid-driven arc-shaped cavity under MC conditions, and results presented in Figure 3c.

Figure 3

Figure 3. (a) Our Streamlines and isothermals contours for varying inclined magnetic field and compared with Malik et al. (2004). (b) Our results of Ψ and θ in the cavity, for Ha = 10, φ = 0.02, γ = 0, Pr = 6.9, Ri = 1 compared with Ali et al. (2024). (c) Our Streamline profile for Gr = 10⁵, $\mathcal{R}$ = 500, Pr = 0.71 compared with Chen and Cheng (2004). (d) Calculation of the average Nusselt number for the grid independence test. (e) Comparative study of the average Nusselt number of hybrid-nanofluid $\left(Ti{O}_2-Cu-H_{2}O\right.$) and nanofluid $\left(Ti{O}_2-H_{2}O\right)$ for $\phi =\left(0.01vs0.05\right)$.

6 Grid independence test and mesh generation

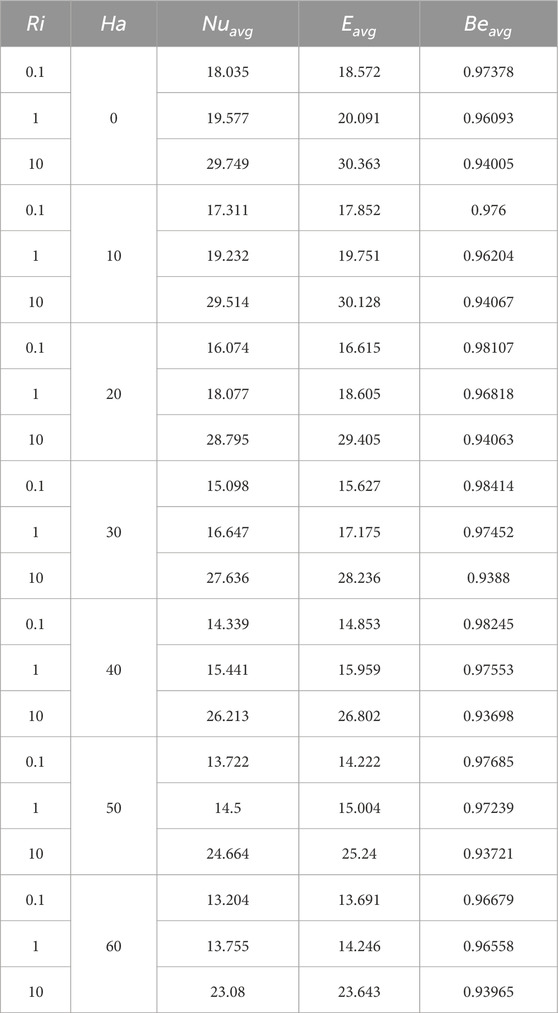
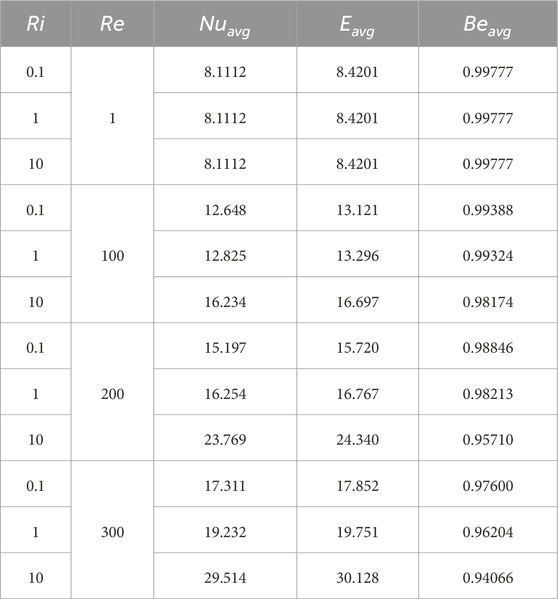
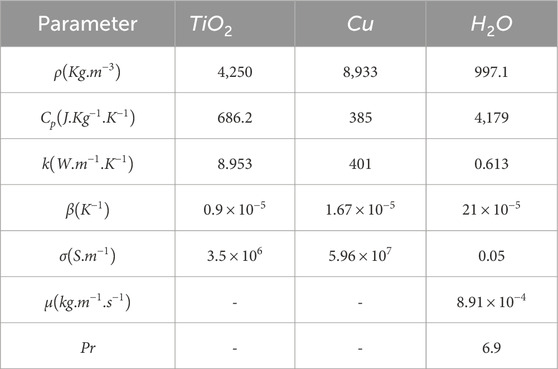
To assess grid independence, ${Nu}_{avg}$ was computed for $Re=300,Ri=10,\gamma =90$ and $0.05$, and $Ha=$ 60, using five different grid sizes, as presented in Table 1. Based on the data in Table 1 with Figure 3d, the triangular mesh element GS-7 was selected to discretize the computational domain for the present study. The physical properties of the base fluid and $Ti{O}_2-Cu-H_{2}O$ solid particles are provided in Table 2. A comparative study is conducted between HNF and nanofluid, as illustrated in Figure 3e. Taking nanofluid ($\left.Ti{O}_2-H_{2}O\right)$, thermal performance increases by 3.82%, if $\phi$ varies from 0.01 to 0.05, whereas considering HNF ($\left.Ti{O}_2-Cu-H_{2}O\right)$, thermal performance increases by 6.31% for varying $\phi$. For $Ha=60$, $\phi =0.05,Re=300,Ri=10$, and $\gamma =0$, the average Nusselt numbers for the nanofluid and HNF are 25.661 and 30.017, respectively. Therefore, it is evident that HT can be enhanced, considering HNF inside the hexagonal cavity.

Table 1

Table 1. Calculation of the Nusselt number for the grid independence test.

Table 2

Table 2. Physical properties of solid particles $Ti{O}_2,Cu$ and the base fluid (H et al., 2017).

7 Results and discussion

In this study, we examine how $Re$, $Ri$, and magnetic fields affect the temperature distribution, entropy generation, and $Be$ in a HNF enclosed within a hexagonal cavity. The governing equations are solved using the finite element method. The analysis considers several dimensionless parameters, including $Ha$ varying from 0 to 60, $\gamma$ varying from 0 to 90, $Re$ varying from 100 to 300, $Ri$ varying from 0.1 to 10, and $\phi$ varying from 0 to 0.05, while maintaining a constant $\mathit{Pr}$ of 6.9.

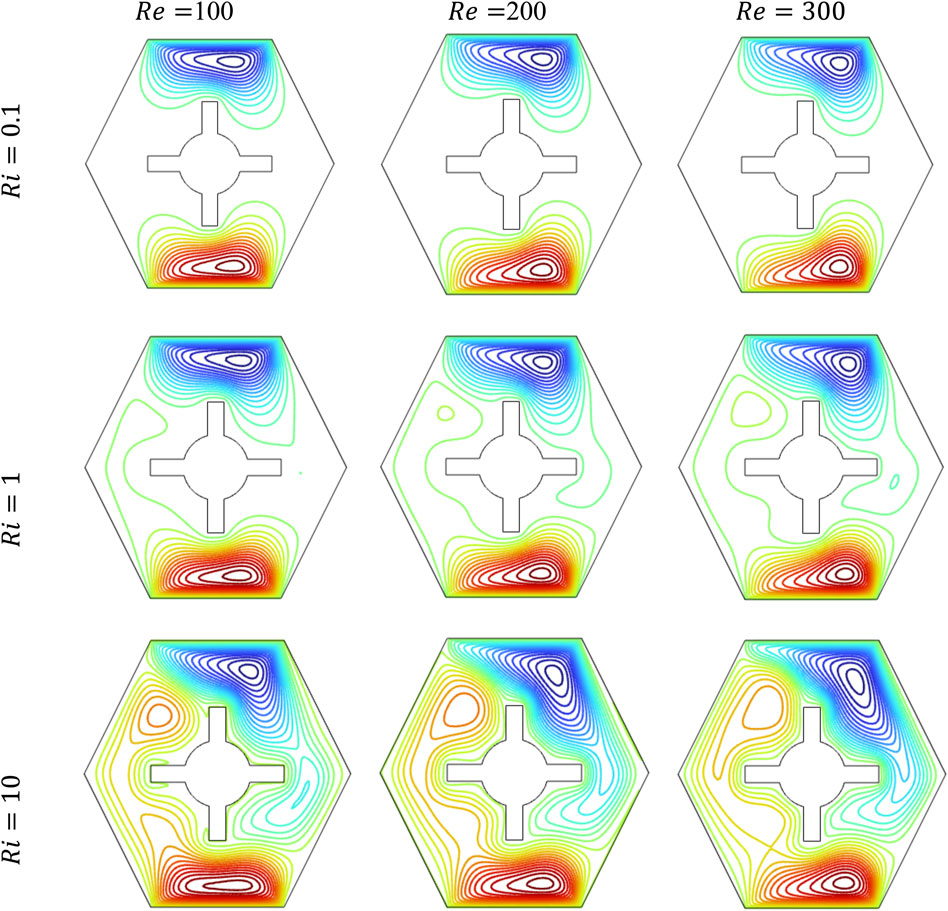
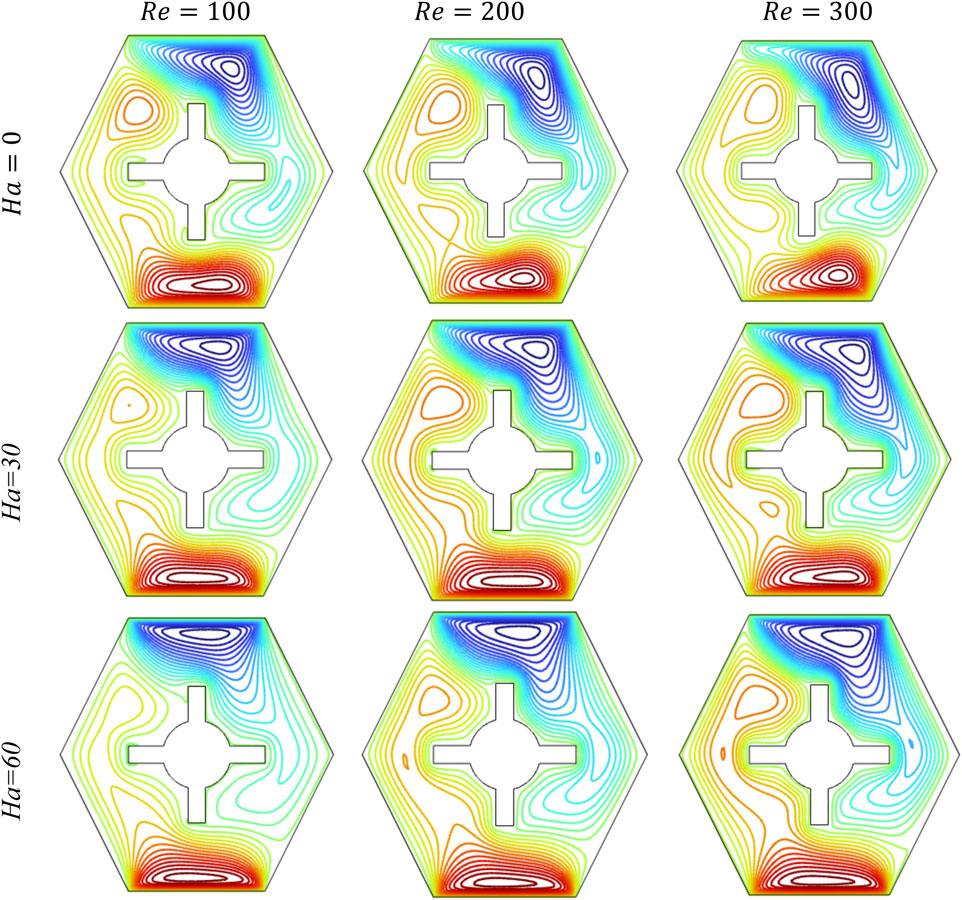
Figures 4, 5 illustrate the effects of varying $Re$ and $Ri$ on the flow streamlines and temperature distributions within the cavity. The analysis is performed at $\phi$ = 0.04, $\mathit{Pr}$ = 6.9, $Ha$ = 10, and $\gamma =30$, using $Re$ values of 100, 200, and 300 and Ri values of 0.1, 1, and 10, respectively. At $Re$ = 100, the flow forms symmetrical, well-organized recirculation zones at the upper and lower ends of the cavity, indicating moderate FC influence. As $Re$ increases to 200, the streamlines become more compact and shift toward the corners, showing enhanced flow velocity and stronger circulatory behavior due to the increased inertia force. At $Re$ = 300, the loops become even tighter and stretch along the walls, whereas the center of the cavity shows less movement. This change happens because $Ri$ = 0.1 is low, indicating that the effect of buoyancy is weak and the flow is mainly driven by the moving walls. As $Re$ increases, the force of the moving fluid becomes stronger, reducing mixing in the cavity and guiding the flow more in the direction of the lid motion.

Figure 4

Figure 4. Streamline contours for different values of $Re$ and $Ri$, when $\phi =0.04,\mathit{Pr}=6.9,Ha=10,\text{and\hspace{0.17em}}\gamma =0$.

Figure 5

Figure 5. Isotherm contour for different values of $Re$ and $Ri$, when $\phi =0.04,\mathit{Pr}=6.9,Ha=10,\text{and\hspace{0.17em}}\gamma =0$.

At a fixed $Ri$ = 1, which indicates a balanced interaction between buoyancy and inertial forces, the streamline patterns evolve noticeably with increasing $Re$. At $Re$ = 100, the flow exhibits moderate circulation with strong vortices near the moving upper and lower walls and slight disturbances appearing in the core region, suggesting the onset of buoyancy-induced convection. As $Re$ increases to 200, inertial effects grow stronger, stretching the vortices and inducing additional secondary circulations near the side boundaries, indicating the increasing dominance of FC. At $Re$ = 300, the flow becomes more active and complex, with longer vortices and distinct secondary eddies emerging appearing in the center of the cavity. This shows that stronger FC is pushing the fluid more, whereas buoyancy still affects the flow’s vertical shape. The combined effect of $Ri$ = 1 and increasing $Re$ facilitates stronger fluid mixing, higher circulation energy, and greater asymmetry in streamlines, which are characteristics crucial for improving the thermal transport system.

At a high $Ri$ = 10, buoyancy forces dominate over shear-driven motion, shaping the flow strongly by NC. At $Re$ = 100, large asymmetric vortices are observed on both sides of the inner hot steering-shaped obstacle, with widespread circulation zones indicating the dominance of thermal plumes increasing due to strong buoyant effects. When $Re$ increases to 200, the flow becomes a bit more orderly, but buoyancy is still important. The vortices begin to stretch and move as the faster fluid motion starts to resist the upward movement. At $Re$ = 300, the stronger forced flow pushes the vortices toward the cold walls and reduces the circulation in the middle.

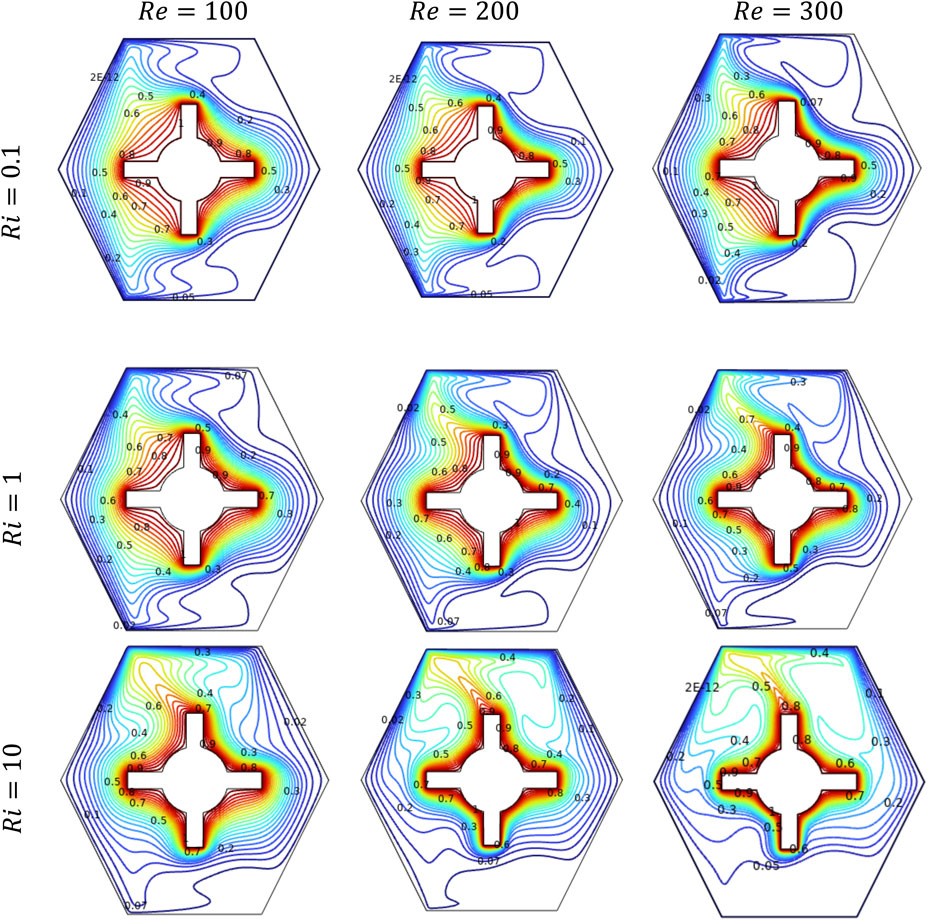
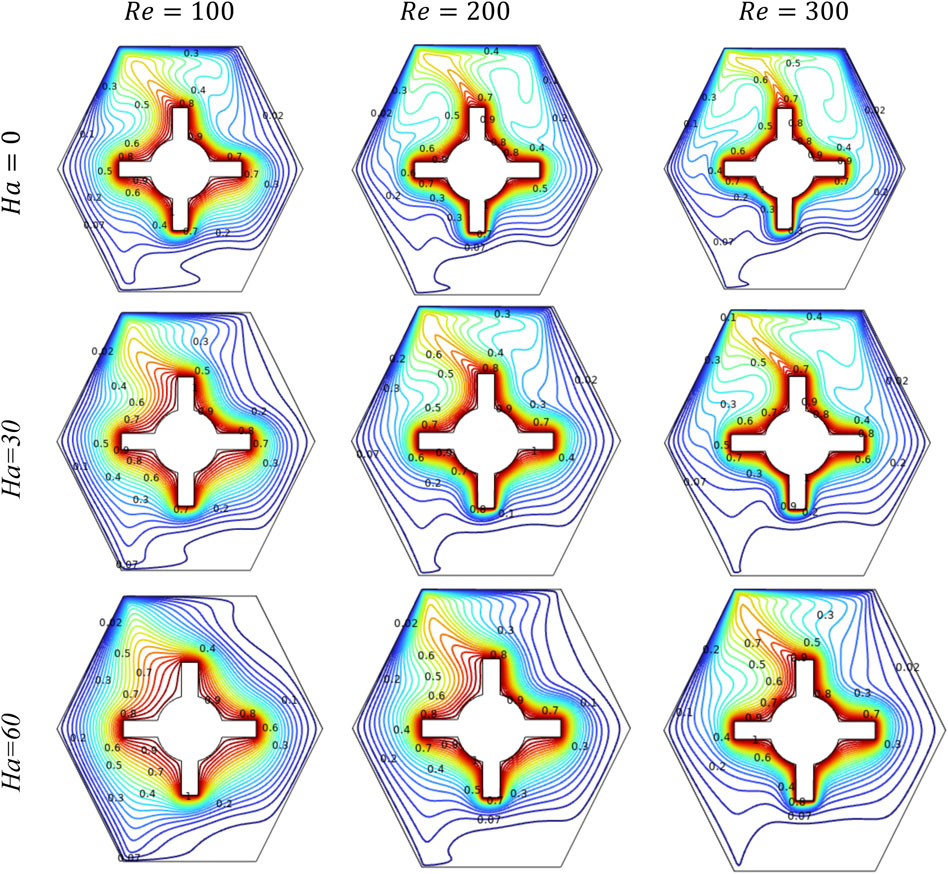
Figure 5 illustrates the influence of isotherm contours on fluid temperature regulation, emphasizing the enhanced HT within the fluid domain as $Re$ and $Ri$ vary.

When $Re$ = 100 is kept fixed, at low $Ri$ = 0.1, the isotherm contours are close to the steering-shaped hot obstacle and mostly go sideways, showing that FC from the moving walls controls the heat flow. The heat is mostly pushed by the fluid’s motion. When $Ri$ increases to 1, the isotherm contour lines start to curve more, and heat starts moving upward due to buoyancy, indicating that both FC and NC are affecting the flow. At high $Ri$ = 10, the isotherm lines distort strongly and increase vertically from the hot obstacle surface, showing that NC is now in control. In this case, heat moves mainly upward because of the temperature difference, and the effect of the moving walls becomes weaker.

At $Re$ = 200, the isotherm contours vary noticeably with increasing $Ri$. For $Ri$ = 0.1, the isotherms are closely packed and extend mainly in the horizontal direction near the hot obstacle, showing that HT is mainly driven by FC due to lid motion. As $Ri$ increases to 1, the temperature lines start to curve upward, showing that both FC and NC are occurring, and buoyancy is starting to affect the heat movement. When $Ri$ reaches 10, the isotherms curve strongly upward and become more vertical, especially near the top of the hot surface. This pattern shows that natural convection takes over. The hot fluid increases because of buoyant forces, so the moving walls matter less. Clear heat paths form, showing the change from forced flow to mixed flow, and then to flow driven mainly by heat.

At $Re=300$, the isotherm contours change significantly with varying $Ri$. At $Ri=0.1$, the isotherms are significantly aligned with the flow direction, indicating a dominant FC effect where the influence of the moving walls is pronounced, and the thermal layer is minimal. As $Ri$ increases to 1, buoyancy effects become comparable to inertial forces, leading to a more noticeable upward curvature of isotherms and the development of thermal plumes above the hot obstacle characteristic of an MC regime. At $Ri=10$, buoyancy forces dominate the flow field, causing strong vertical plume formation from the hot surfaces and suppressing the influence of the moving walls. The isotherms become nearly vertical in the core region, reflecting a shift to a buoyancy-driven HT mechanism. This progression highlights the increasing role of thermal buoyancy relative to shear-driven transport with increasing $Ri$ at constant $Re$.

Figures 6, 7 illustrate the impact of $Ha$ and $Re$ on fluid flow and temperature distributions for a fixed set of parameters: $Ri=10,\phi =0.04,\mathit{Pr}=6.9$, and $\gamma$ = 30. Now, for $Re=100$ from Figure 6 at $Ha$ = 0, the flow is predominantly governed by FC from the moving walls, forming strong asymmetric counter-rotating vortices near the hot central obstacle, with vigorous circulation zones at the upper and lower regions. As $Ha$ increases to 30, the magnetic field starts damping the flow, suppressing secondary vortices and causing streamlines to become smoother and more symmetric, particularly near the central core. At $Ha$ = 60, Lorentz forces strongly resist fluid motion, significantly weakening circulation and stretching the streamlines along the flow direction. This shows that the flow is becoming less mixed and is changing from being driven by motion to being controlled by the magnetic field, which is important to determine how heat and fluid move in magnetic convection.

Figure 6

Figure 6. Streamline contours for the different values of $Ha$ and $Re$, when $Ri=10,\phi =0.04,\mathit{Pr}=6.9,\text{and\hspace{0.17em}}\gamma =0$.

Figure 7

Figure 7. Isotherm contours for the different values of $Ha$ and $Re$, when $Ri=10,\phi =0.04,\mathit{Pr}=6.9$, and $\gamma =0$.

At $Re=$ 200, the effect of increasing $Ha$ on the streamline patterns is clearly evident. For $Ha$ = 0, the flow structure is characterized by two dominant recirculating vortices in the upper-right and lower-left regions of the cavity due to the stronger thermal plume interactions caused by elevated buoyancy forces. Streamlines near the obstacle are tightly packed and curve sharply around its surface, revealing enhanced convective activity and increased velocity gradients around the heated geometry. Additionally, secondary eddies form near the cavity corners, particularly on the upper-left and lower-right sides, suggesting complex recirculation zones driven by the combined effects of wall movement and buoyant increase of hot fluid. The inclusion of a strong magnetic field ($Ha$ = 30) leads to the suppression of fluid motion and vortex intensity, particularly near the heated obstacle. Compared to the non-magnetic case, the streamline contours become smoother and less tightly packed, indicating reduced flow velocity and weakened recirculatory motion. The top-right and bottom-left vortices persist but are more subdued, and secondary eddies near the cavity corners become less pronounced, demonstrating the stabilizing influence of the obliquely inclined magnetic field. Compared to lower $Ha$ (0,30) cases, the flow structure becomes noticeably more suppressed and ordered as the Lorentz force significantly restrains fluid motion and attenuates both primary and secondary vortices for $Ha=60$. The dominant circulation cells in the upper-right and lower-left regions persist but exhibit reduced rotational strength and tighter streamline spacing near the cavity boundaries. The flow slows down near the obstacle, shown by the stretched and flat flow lines. This means that the increasing hot flow is weaker and there is less mixing.

At $Re=300$, the flow dynamics are dominated by strong inertial effects and are significantly affected by varying $Ha$. In the absence of a magnetic field, the streamlines reveal highly convective flow behavior characterized by two prominent counter-rotating vortices above and below the heated obstacle, induced by the motion of the top and bottom walls. The presence of tightly packed streamlines near the hot central obstacle suggests strong momentum interaction and buoyancy-induced recirculation, particularly in the lower-right and upper-left quadrants, where thermal plumes are distinctly curved due to dominant inertial transport. As $Ha$ increases to 30, the Lorentz force begins to suppress secondary vortical structures and damps the velocity gradients, resulting in smoother and less distorted streamline curvature on the left region, whereas right-side flow becomes more aligned, indicating suppression of chaotic mixing. As $Ha$ increases to 60, the magnetic effect gets stronger. The top and bottom vortices become longer and more stretched in the direction of the flow, with less side movement. This shows that the magnetic field is reducing the flow. The flow lines near the obstacle become less crowded, indicating that heat-driven movement is weaker, and forced flow takes over. The magnetic field, which is sideways, slows the flow down, flattens the swirling areas, lines up the flow better, and reduces spinning, especially in the middle and left parts. In the end, the flow changes from a messy, heat-driven pattern to a smooth, steady pattern controlled by the magnetic field. This shows how movement, heat, and magnetism all affect the flow inside the hexagon area.

Regarding isotherm contours from Figure 7, at fixed $Ha$ = 0 and $Re$ = 100, the isotherms are distributed around the hot obstacle with dense clustering, signifying strong thermal diffusion and dominant conduction. As $Re$ increases to 200, the isotherms become increasingly asymmetric and begin to stretch along the flow direction, especially downstream of the obstacle, indicating enhanced convective HT. At $Re=300$, this stretching is further pronounced, and the isotherms are tightly packed near the obstacle edges, reflecting thinner thermal boundary layers and more efficient heat.

When $Ha=30$ is kept fixed, at $Re$ = 100, the isotherms remain closely spaced near the hot obstacle, indicating moderate heat diffusion and relatively weak inertial forces. As $Re$ increases to 200, the influence of advection becomes more apparent, causing the isotherms to distort further downstream due to enhanced fluid motion induced by the moving walls, yet the magnetic damping retains a relatively laminar profile. At $Re$ = 300, the inertial forces overpower diffusive effects, stretching the isotherms significantly in the flow direction and thinning the thermal boundary layers near the obstacle.

In case of fixed $Ha=60$, at $Re$ = 100, the thermal boundary layer around the hot steering-shaped obstacle is thick, and the isotherms spread due to dominance of conduction and MHD-induced damping. At $Re$ = 200, isotherms begin to compress near the top wall, indicating enhanced advection, whereas some distortion appears at the lower-left region due to inertial forces overcoming magnetic damping. At $Re$ = 300, advection becomes significant, leading to further thinning of the thermal boundary layer at the front face and expansion of isotherms downstream.

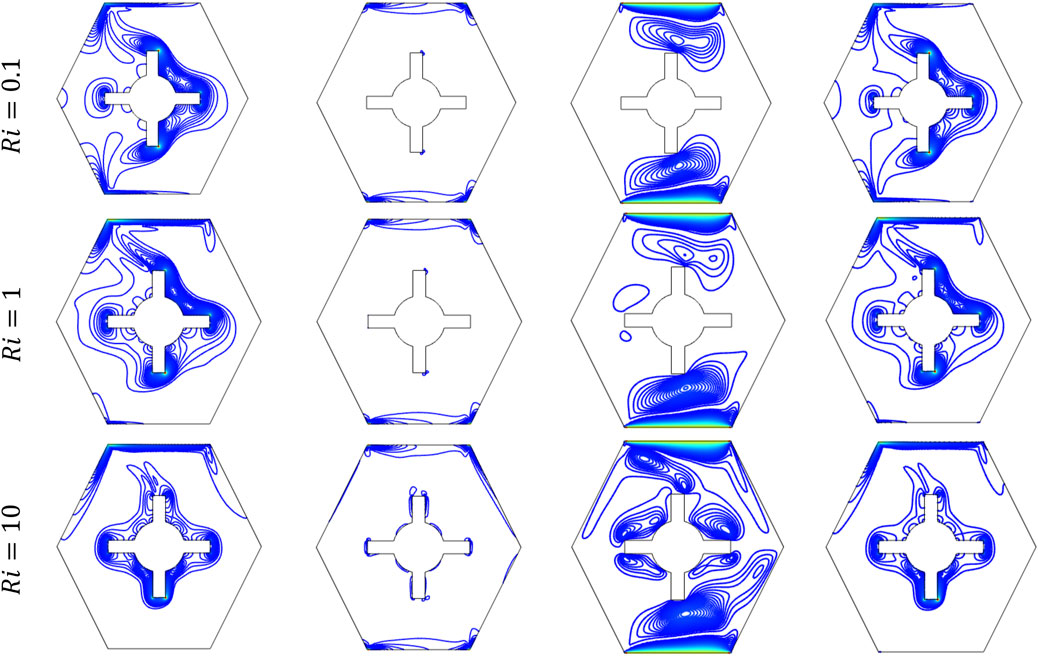
Figures 8, 9 illustrate $E_{gen}$ due to heat transfer ($E_{ht}$), fluid friction ($E_{ff}$), magnetic field ($E_{mf}$), and average entropy generation ($E_{avg}$) for different values of $Ri$ and $Ha$. When $Ri=0.1$, FC is stronger because the lid motion is much greater than the buoyancy force. This makes $E_{ht}$ gather along the flow path, especially near the moving lid walls and the edges of the hot steering-shaped obstacle, showing strong shear-driven HT. $E_{ff}$ is primarily confined to thin shear layers near the moving upper and lower walls and around the sharp corners of the hot obstacle, where velocity gradients are high. $E_{mf}$ due to the magnetic field mainly influences near-wall regions where strong velocity gradients occur, resulting in localized entropy generation confined to the upper and lower corners.

Figure 8

Figure 8. Effect of $Ri$ on $E_{ht},E_{ff},E_{mf}$, and $E_T$, when $\mathit{Pr}=6.9,\phi =0.04,Ha=10,\gamma =30$, and $Re=300$.

Figure 9

Figure 9. Effect of $Ha$ on $E_{ht},E_{ff},E_{mf}$, and $E_{avg}$, when $Ri=10,Re=300,\gamma =30,\mathit{Pr}=6.9,\text{and\hspace{0.17em}}\phi =0.04$.

At $Ri=1$, FC and buoyancy are equally strong. This creates a more mixed flow and spreads the heat over a larger area near the obstacle and the boundary walls. The entropy due to $E_{ff}$ expands slightly in the boundary regions, reflecting moderate viscous dissipation, whereas $E_{mf}$ results in asymmetrical entropy contours and becomes more irregular than that at $Ri=0.1$, especially in the upper half, indicating increased magnetic damping and energy dissipation. $E_{avg}$ becomes more irregular, distributed more asymmetrically due to complex vortex interactions.

When $Ri=10$, buoyancy becomes stronger than lid motion. This leads to more symmetric and vertically stretched $E_{ht}$ patterns around the hot obstacle. It shows that NC is now controlling the HT, resulting in a smoother but more upward-directed thermal field. In case of $E_{ff}$ NC enhances internal recirculation zones, leading to more prominent entropy generation not only near the moving boundaries but also around the surface of the obstacle, as stronger flow separation and vortical structures evolve. Moreover, the magnetic field interaction becomes more pronounced throughout the domain, spreading $E_{mf}$ across a wider area, particularly around the obstacle and along vertical flow paths. This trend reveals that as NC intensifies, the Lorentz force enhances viscous braking and thermal damping, thereby amplifying magnetic $E_{mf}$ and disrupting flow symmetry. As NC dominates, buoyancy-driven circulation structures become more prominent, giving rise to vertically oriented entropy patterns around the heated obstacle and the upper boundary layers.

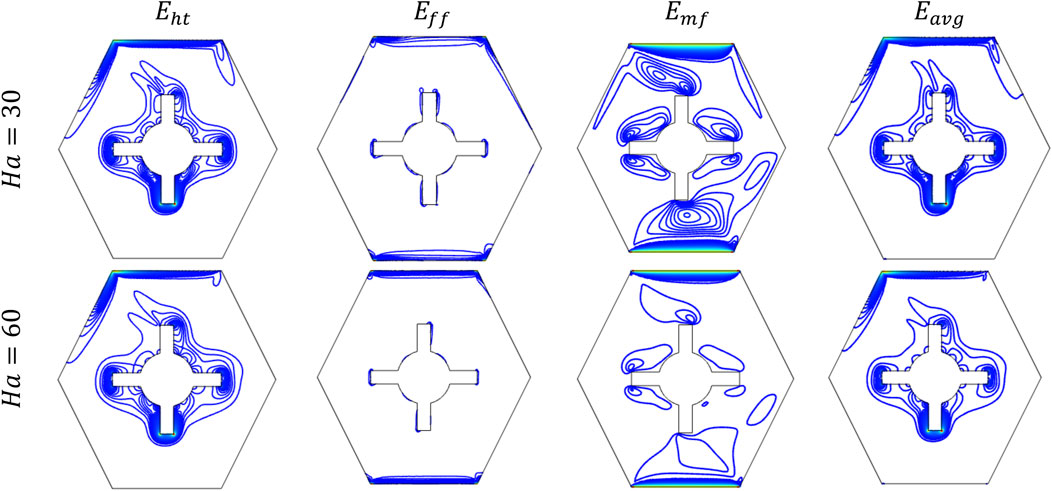
Figure 9 illustrates the effect of varying $Ha$ of entropy generation. At $Ha$ = 30, $E_{ht}$ becomes relatively complex and results in dense contours near the obstacle, indicating stronger convective thermal gradients, which enhances $E_{ht}$ due to faster fluid motion. However, at $Ha$ = 60, the lines become smoother and more spread out, showing that the stronger magnetic field reduces the flow of the fluid. This reduces heat mixing and leads to a flow that is more controlled by diffusion rather than movement. As a result, $E_{ht}$ becomes weaker and more evenly spread, showing how the magnetic field helps control and reduce entropy in MHD thermal systems.

At $Ha=30$, the flow is more active due to weaker magnetic damping, resulting in stronger velocity gradients near the moving walls and around steering shaped obstacle. This leads to higher viscous dissipation and increased $E_{ff}$. However, at $Ha=60$, the stronger magnetic field imposes greater resistance on the fluid motion, especially across the field lines, causing the flow to slow down and velocity gradients to decrease. As a result, $E_{ff}$ becomes weaker and more confined to thin layers near the moving walls, indicating a shift toward a more stable and magnetically controlled flow regime.

At $Ha=30$, the magnetic field is relatively weaker, resulting in more dispersed and structured $E_{mf}$ zones, particularly near the top and bottom walls where the motion-induced currents interact with the field. As $Ha$ increases to 60, the influence of the magnetic field becomes significantly stronger, leading to damping of fluid motion and suppression of current circulation, which reduces the magnitude and concentration of magnetic-induced entropy. This is evident from the simplified and less intense contour distributions and minimizes average entropy generation. This indicates that less energy is irreversibly lost, improving the overall thermodynamic efficiency of the system.

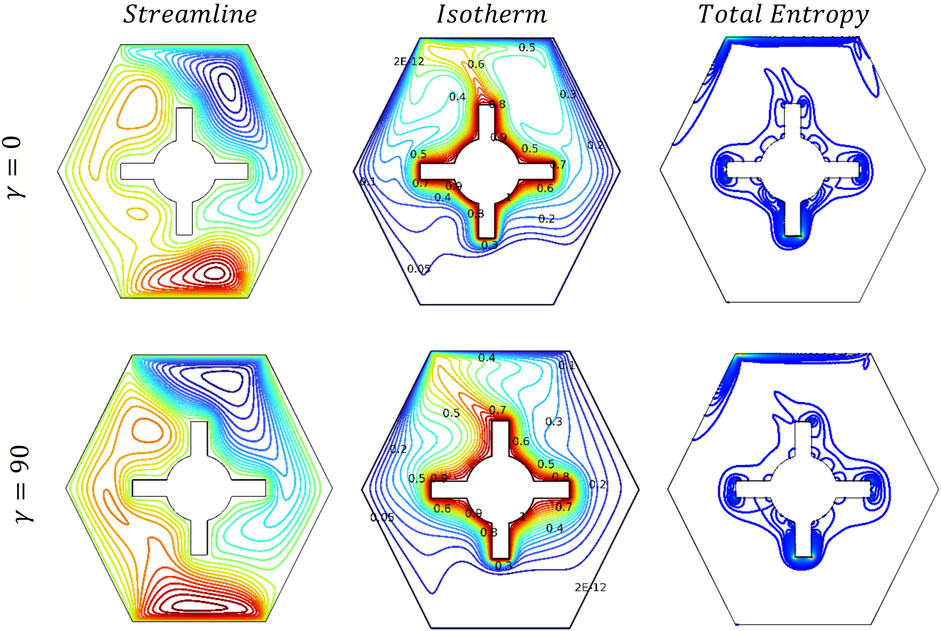
In this section, we examine the influence of magnetic field inclination on fluid flow behavior and thermal performance. A detailed analysis is conducted to assess the impact of varying magnetic field angles on heat transfer rates and flow characteristics. Figure 10 illustrates the influence of the inclined magnetic field angle ($\gamma$) on the streamline patterns, isotherm contours, and total entropy generation within the domain. When γ = 0, the magnetic field is parallel to the flow direction. The Lorentz force is weaker along this direction, so the flow forms stronger re-circulations and complex vortex patterns. Several small eddies clearly appear, especially in the top-left and bottom-right corners. At $\gamma$ = 90, the magnetic field is perpendicular to the lid motion, and the Lorentz force acts against the flow, greatly reducing the formation of secondary eddies. The flow looks more organized and has horizontal layers.

Figure 10

Figure 10. Streamline, isotherm, and total entropy generation for the different values of $\gamma$, when $Re=300,Ri=10,\phi =0.05,\mathit{Pr}=6.9$, and $Ha=10$.

At $\gamma$ = 0, the heat spreads unevenly, especially around the surface of the hot obstacle inside the domain. The closely packed isotherm lines near the hot surface of the steering-shaped obstacle show strong HT, and the hot isotherm lines mostly rise upward due to buoyancy force. When $\gamma$ = 90, the heat pattern changes. The isotherm lines become more twisted around the vertical surface of the steering-shaped obstacle, showing that the magnetic field affects how heat moves. The heat shifts downward in some areas and becomes more uneven. This suggests that the magnetic field changes the flow of heat and reduces the symmetry of the temperature distribution inside the cavity.

From Figure 10, at $\gamma$ = 0, higher entropy generation appears more clearly near the edges of the heated steering-shaped obstacle. This indicates strong temperature gradients and viscous effects in those zones, which contribute to higher irreversibility in the system. The upper part of the cavity shows more complex structures, where sharp curves in the lines suggest increased fluid motion and mixing due to both NC from the hot obstacle and FC from the moving walls. The center and the lower regions of the cavity have more confined entropy contours, showing that HT is more localized and less chaotic there. The movement of the top and bottom walls enhances the flow near those areas, but the most significant entropy is still generated close to the hot obstacle where the temperature difference is the greatest. At $\gamma$ = 90, the total entropy generation decreases due to magnetic field suppression.

7.1 Average Nusselt number

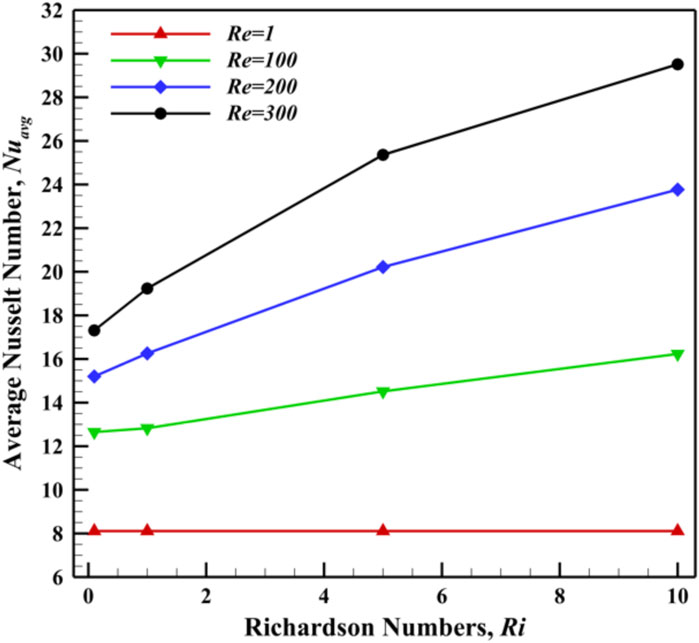
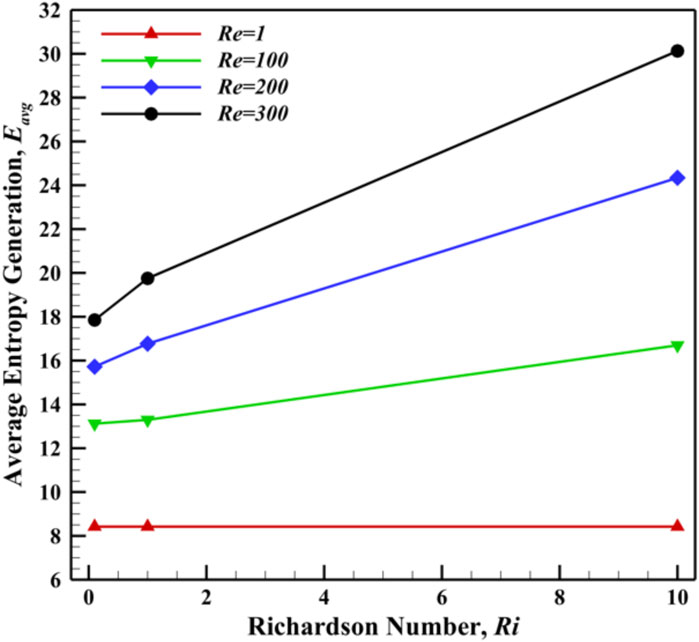
The interaction between convective HT and thermal conductivity influences the behavior of ${Nu}_{avg}$ in relation to $Ri$ and $Re$, as depicted in Figure 11. From this figure, it can be observed that for lower $Re$ (at $Re=$ 1), ${Nu}_{avg}$ remains constant at 8.112 despite an increase in $Ri$ from 0.1 to 10. This is expected because viscous forces dominate the flow dynamics, suppressing convective effects. Even as Ri increases significantly, indicating stronger buoyancy forces, the flow remains diffusion-dominated due to low $Re$, limiting convective HT and keeping ${Nu}_{avg}$.

Figure 11

Figure 11. ${Nu}_{avg}$ for different values of $Ri$ and $Re$ for $\phi =0.04,\mathit{Pr}=6.9$, and $\gamma =30$.

However, for higher $Re$ ($Re=$ 100, 200, and 300), an improvement in ${Nu}_{avg}$ is evident, as shown in Figure 11 and Table 6. As flow velocity increases, convective HT is enhanced, whereas higher $Ri$ strengthens buoyancy-driven HT. The combined effect of FC and NC leads to an increase in ${Nu}_{avg}$, reflecting improved thermal efficiency. The highest ${Nu}_{avg}$ value of 29.514 is observed at $Re=$ 300 and $Ri=$ 10.

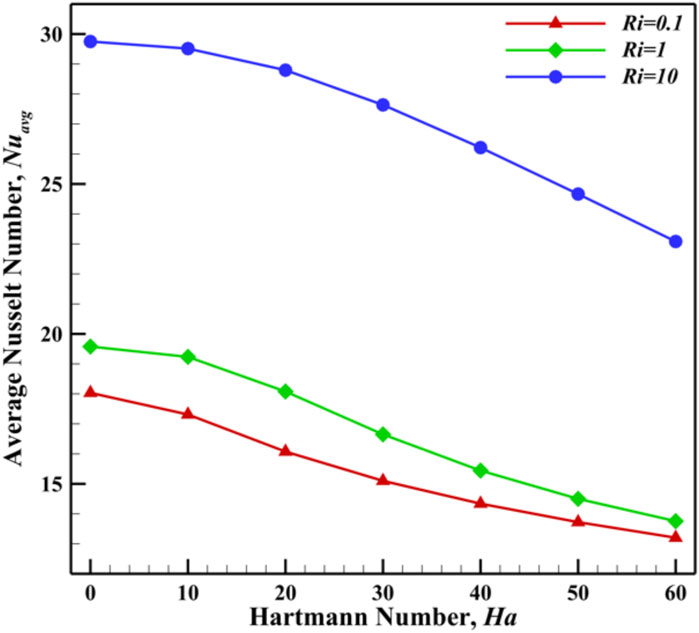
In contrast, the relationship between Ha and Ri is inverse, as shown in Figure 12 and Table 3. When $Ha=$ 0, ${Nu}_{avg}$ reaches its highest value of 29.747, whereas at $Ha=60$, it decreases to 23.08 for $Ri=10$. A similar pattern is observed across all $Ri$ cases in Figure 11. This occurs because the magnetic field suppresses fluid motion, reducing convective HT. As $Ha$ increases, the Lorentz force dampens velocity fluctuations and minimizes fluid mixing, weakening the convective HT mechanism. Consequently, HT becomes more conduction-dominated, leading to a reduction in ${Nu}_{avg}$ across all cases.

Figure 12

Figure 12. ${Nu}_{avg}$ for varying $Ha$ and $Ri$, where $\phi =0.04,\mathit{Pr}=6.9,\gamma =30,\text{and\hspace{0.17em}}Re=400$.

Table 3

Table 3. Variation of ${Nu}_{avg}$, $E_{avg}$, and ${Be}_{avg}$ for various $Ri$ and $Ha$, when $\phi$ for $Ti{O}_2-Cu-H_{2}O$ is 0.04, $Re=300$, and $\gamma =30$.

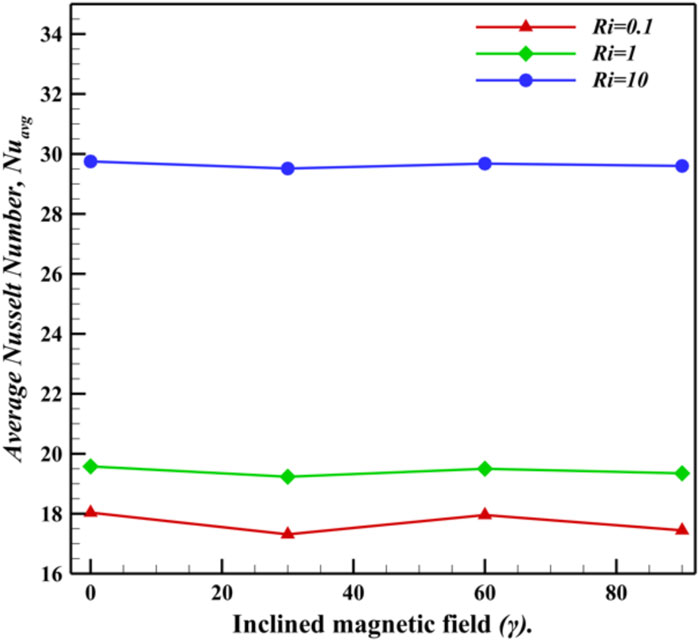
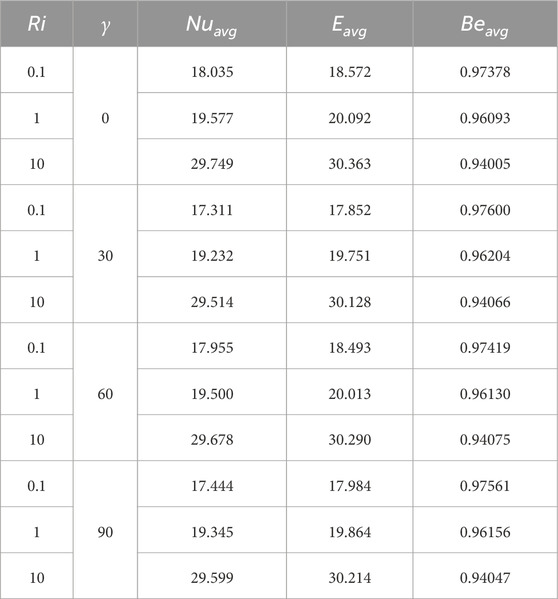
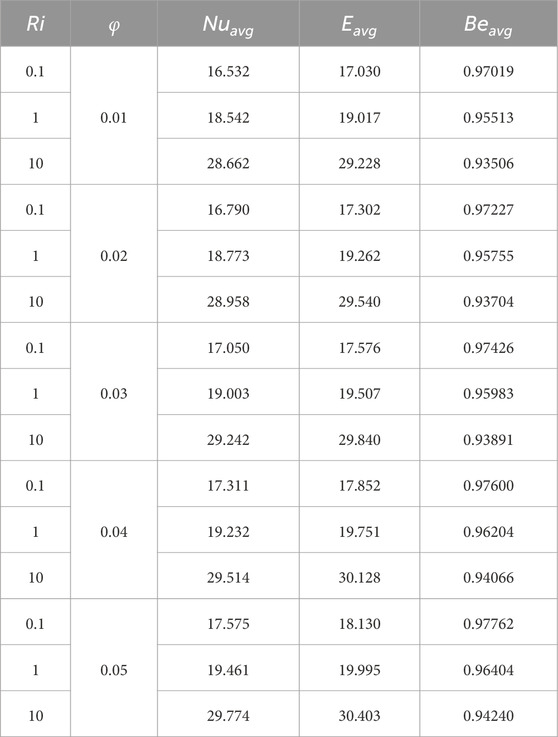
The effect of an inclined magnetic field is illustrated in Figure 13 and Table 4. The highest ${Nu}_{avg}$ occurs when $\gamma =0$, whereas the lowest values appear at $\gamma =30$ for all cases; however, the difference is not significant. Additionally, $\phi$ plays a crucial role in determining ${Nu}_{avg}$. As $\phi$ increases, the thermal conductivity of the fluid improves significantly, enhancing HT efficiency within the cavity. From Table 5, ${Nu}_{avg}$ is 28.662 for Ri = 10 and $\phi$ = 0.01, but when $\phi$ increases from 1% to 5%, ${Nu}_{avg}$ increases to 29.774—an approximate increase of 3.87%. Similarly, for Ri = 0.1, ${Nu}_{avg}$ improves by approximately 5.61%.

Figure 13

Figure 13. ${Nu}_{avg}$ for varying $\gamma$ and $Ri$ for $\phi =0.04,\mathit{Pr}=6.9,\text{and\hspace{0.17em}}Re=300$.

Table 4

Table 4. Variation of ${Nu}_{avg}$, $E_{avg},$ and ${Be}_{avg}$ for various $Ri$ and $\gamma$, when $\phi =0.04$, $Re=300,\text{and\hspace{0.17em}}Ha=10$.

Table 5

Table 5. Variation of ${Nu}_{avg}$, $E_{avg},$and ${Be}_{avg}$for various $Ri$and $\phi$, when $Re=300,Ha=10$, and $\gamma =30$.

7.2 Entropy generation

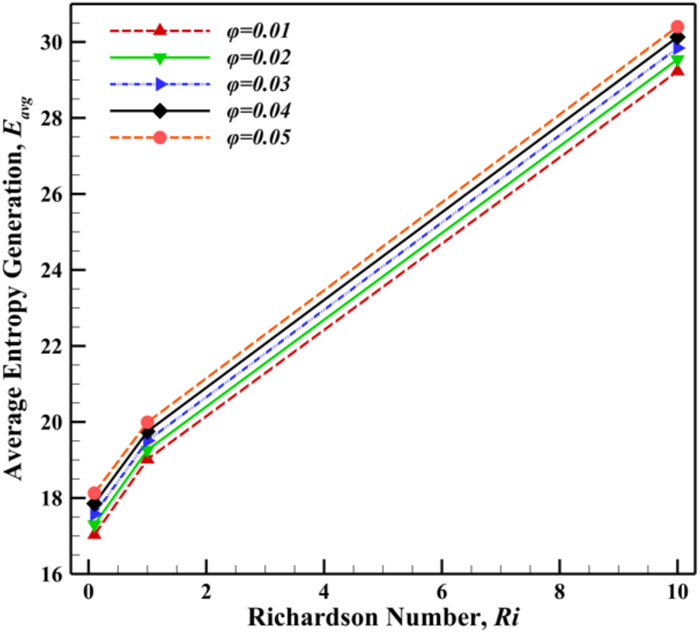
$E_{avg}$ is evaluated through irreversible processes such as $E_{ht}$, $E_{ff}$, and the magnetic field inside the cavity. Analyzing $E_{avg}$ allows for assessing system performance, identifying areas of thermal inefficiency, and guiding improvements in design efficiency. Figure 14 examines the influence of $Ri$ and $\phi$ on $E_{avg}$ at constant $Re$ = 300, $\mathit{Pr}$ = 6.9, and $\gamma =$ 30. As the nanoparticle volume fraction increases ($\phi$ = 0.01–0.05), $E_{avg}$ escalates, indicating potential areas for improving system efficiency. From Table 5, the average $E_{avg}$ is 17.03 for $Ri=0.1$, when $\phi$ = 0.01, but it increases to 18.130 when $\phi$ reaches 0.05—an approximate 6.45% increase in $E_{avg}$.

Figure 14

Figure 14. $E_{avg}$ for different values of $Ri$ and $\phi$, when$\mathit{Pr}=6.9,Re=300,\text{and\hspace{0.17em}}\gamma =30$

The effects of $Ri$ and $Re$ on $E_{avg}$ are illustrated in Figure 15. When $Ri=1$, $E_{avg}$ remains unchanged for different $Ri$ values ($Ri=$ 0.1, 1, and 10), indicating the dominance of viscous effects. However, as $Re$ increases to 100, 200, and 300, $E_{avg}$ increases due to the growing influence of inertial forces, which enhance convective HT and velocity gradients. This results in higher contributions from both thermal and viscous irreversibilities, significantly increasing overall $E_{avg}$. From Table 6, for a fixed $Ri=0.1$, $E_{avg}$ increases by approximately 112.01%, increasing from 8.4201 to 17.852. Similarly, for $Ri=10$, it increases by approximately 257.81%, reaching 30.128. However, Table 3 shows the opposite trend: $E_{avg}$ decreases with increasing $Ha$ for all $Ri$ cases.

Figure 15

Figure 15. $E_{avg}$ for varying $Re$ and $Ri$ for $\phi =0.04,\mathit{Pr}=6.9,Re=300,\text{and\hspace{0.17em}}\gamma =30$.

Table 6

Table 6. Variation of ${Nu}_{avg}$, $E_{avg}$, and ${Be}_{avg}$for various $Ri$and $Re$, when $\phi =0.04$, $Re=300,Ha=10,\text{and\hspace{0.17em}}\gamma =30$.

When $Ha=0$, the absence of a magnetic force allows more vigorous fluid motion, leading to an increase in $E_{avg}$ from 18.572 to 30.363 as $Ri$ increases from 0.1 to 10. However, at $Ha=60$, the Lorentz force significantly suppresses fluid motion and convective HT, minimizing fluid friction irreversibility and limiting entropy generation. Consequently, HT efficiency is reduced, and $E_{avg}$ decreases under a strong magnetic field.

Inclined magnetic fields also influence $E_{avg}$ inside the cavity. From Table 4, when $\gamma =0$, $E_{avg}$ is relatively high; however, no significant variation in $E_{avg}$ is observed for different $\gamma$ values.

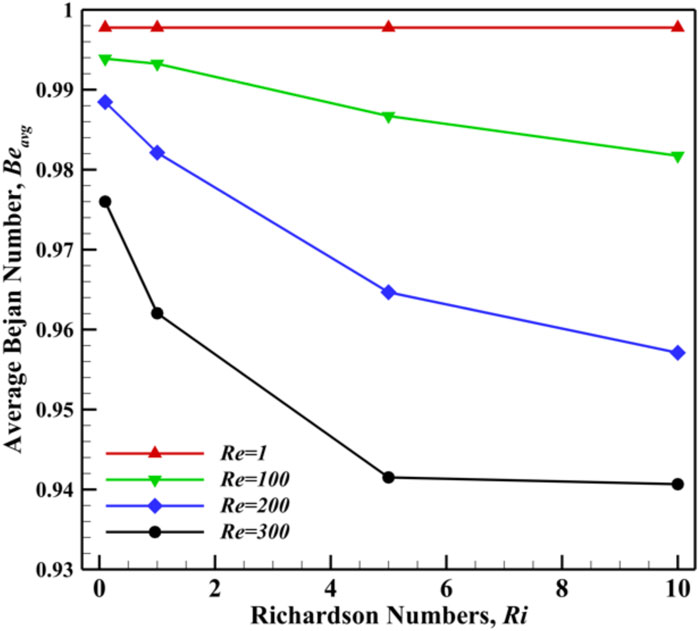
7.3 Bejan Number

The average Bejan number ($\left.{Be}_{avg}\right)$ indicates whether $E_{gen}$ is primarily due to HT irreversibility (${Be}_{avg}$ >0.5) or fluid friction irreversibility (${Be}_{avg}$ <0.5). Figure 16 presents the ${Be}_{avg}$ profiles for various Re and $Ri$ values. When $Re=1$, ${Be}_{avg}$ remains high and constant across all $Ri$ values because the flow is dominated by viscous forces, and HT is primarily conduction-driven, with negligible inertia effects. However, at higher Reynolds numbers ($Re=$ 100, 200, and 300), ${Be}_{avg}$ decreases as convective HT becomes dominant, and inertial forces strengthen. This reduces the relative contribution of $E_{avg}$ due to fluid friction, which plays a key role in determining ${Be}_{avg}$. Consequently, ${Be}_{avg}$ decreases at higher $Re$.

Figure 16

Figure 16. ${Be}_{avg}$ for varying $Re$ and $Ri$ for $\phi =0.04,\mathit{Pr}=6.9,\text{and\hspace{0.17em}}\gamma =30$.

On the other hand, as $Ha$ increases, the magnetic field strengthens, suppressing fluid motion and reducing velocity gradients, thereby minimizing HT. As a result, the dominant source of $E_{avg}$ shifts toward fluid friction irreversibility, leading to a reduction in ${Be}_{avg}$. From Table 3, for $Ri=0.1$, ${Be}_{avg}$ is 0.97378, but as $Ha$ increases from 0 to 60, ${Be}_{avg}$ decreases by 0.71%. Similarly, for $Ri=10$, ${Be}_{avg}$ decreases by 0.39%, indicating that HT remains dominant over fluid friction.

$\phi$ also affects ${Be}_{avg}$ by enhancing thermal conductivity. This reduces the dominance of convective HT relative to conductive HT, thereby increasing the contribution of $E_{avg}$ from conduction. Additionally, a higher $\phi$ increases the fluid’s viscosity, leading to greater fluid friction and further contributing to ${Be}_{avg}$. From Table 5, for a fixed $Ri=0.1$, ${Be}_{avg}$ increases by approximately 0.76%, increasing from 0.97019 to 0.97762 as $\phi$ increases from 0.01 to 0.05. Similarly, for $Ri=$ 10, it increases by approximately 0.78%, from 0.93506 to 0.94240, for the same increment in $\phi$.

8 Conclusion

A comprehensive numerical analysis on a hexagonal cavity with inner steering-shaped obstacle insertion under MHD MC using $Ti{O}_2-Cu-H₂O$ HNF is carried out in the present study. We recognize that the 2D simplification inherently neglects out-of-plane motions and secondary flow structures that can arise due to the cavity’s depth and boundary layer interactions. As such, although the present findings offer valuable qualitative insights and comparative trends, they may not fully capture the complexity of the three-dimensional (3D) behavior. However, in 2D simulation, results indicate that increasing $\phi$, $Re$, and $Ri$ enhances ${Nu}_{avg}$ and reduces ${Be}_{avg}$. The entropy generation analysis provides insights into system inefficiencies, offering a pathway to optimized design. The effects of Re and Ri on entropy generation and the average Bejan number are evaluated for various irreversibility distribution ratios. Additionally, isotherm and streamline plots are presented to illustrate flow pattern transformations and to elucidate the impact of irreversibility on entropy generation.

• $E_{gen}$ increases with $Ri$ and $\phi$, whereas $Be$ decreases with $Ri$ and $\phi$ generally. For low values of $Re$, increasing $Ri$ leads to only negligible changes in both ${Nu}_{avg}$ and ${Be}_{avg}$. In contrast, at higher $Re$, an increase in $Ri$ results in a significant increase in ${Nu}_{avg}$ and a marked decrease in ${Be}_{avg}.$

• In the absence of a magnetic field, increasing $\phi$ leads to an enhancement in $E_{gen}$; however, when a magnetic field is applied, $E_{gen}$ decreases.

• ${Nu}_{avg}$ generally decreases as $Ha$ enhances due to the damping of the fluid motion within the cavity with the magnetic field. However, increasing $Ha$ can play an effective role in controlling the fluid flow

• For higher values, $Ha$ becomes dominating in the flow regime due to the influence of the Lorentz force. ${Nu}_{avg}$ decreases by approximately 26%, 29.73%, and 22.42% as $Ha$ increases for varying $Ri$ to 0.1, 1, and 10, respectively. Similarly, when $Ha$ becomes higher, $E_{avg}$ also decreases by approximately 26.71%, 29.09%, and 22.13%. ${Be}_{avg}$ shows a slight increase with increasing $Ha$. It increases by 0.842% and 0.04% for $Ri$ 0.1 and 10, respectively, and remains stable for $Ri=$ 1.

• At fixed values of $Ha$ = 10, $Re$ = 300, and $\gamma$ = 30, with increasing $\phi$ from 0.01 to 0.05, ${Nu}_{avg}$ increases by 6.31%, 4.95%, and 3.87% for $Ri$ of 0.1,1, and 10, respectively. Moreover, $E_{avg}$ shows an increasing trend with increasing $\phi$, which are 6.45%, 5.14%, and 4.02%.

• At a fixed $Ha$ = 10, $Re$ = 300, and $\phi$ = 0.04, ${Nu}_{avg}$ and $E_{avg}$ attain their maximum and minimum values when the magnetic field inclination angle γ is 0 and 30, respectively. In contrast, ${Be}_{avg}$ exhibits the opposite trend, and it is relatively higher at $\gamma$ = 30 and lower at $\gamma$ = 0. This indicates that a horizontally applied magnetic field ($\gamma$ = 0) enhances thermal transport and overall irreversibility, whereas a more inclined field ($\gamma$ = 30) favors viscous dissipation dominance in the entropy generation mechanism.

• At a fixed $Ha$ = 10, $\phi$ = 0.04, and $\gamma$ = 30, as $Re$ increased from 1 to 300, ${Nu}_{avg}$ exhibits significant enhancement by 113.39%, 137.08%, and 263.83% for $Ri$ = 0.1,1, and 10, respectively. Similarly, $E_{avg}$ increased by 112.01%, 134.56%, and 257.81% for varying $Ri$, respectively. On the other hand, ${Be}_{avg}$ decreased by approximately 2.18%, 3.58%, and 5.72%. This decrease indicates a growing contribution of fluid friction irreversibility relative to thermal irreversibility at higher $Re$ values.

8.1 Limitation of the work

The present study investigates specific aspects of HT and $E_{gen}$ under distinct boundary conditions. Although nondimensional analysis is suitable for the scope of this research, dimensional analysis remains essential for addressing real-world applications. Additionally, the methodology used in this study is based on numerical analysis. To deepen our understanding of HT and $E_{gen}$ in the cavity, future research should focus on integrating HNFs, exploring variations in geometries, incorporating discrete heating, and investigating additional phenomena such as 3D geometry with try-HNFs. In the 2D geometry, gravity acts in the y-direction, which is a limitation of the current study. This issue could be resolved by extending the analysis to a three-dimensional geometry. Therefore, the present investigations would not only enhance our knowledge but also offer valuable insights into optimizing thermal management systems and improving efficiency across various practical applications.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

BS: Data curation, Formal Analysis, Investigation, Methodology, Resources, Software, Visualization, Writing – original draft. GB: Data curation, Investigation, Writing – review and editing. NM: Formal Analysis, Writing – original draft. MH: Methodology, Writing – review and editing. GS: Conceptualization, Supervision, Writing – review and editing. SS: Funding acquisition, Project administration, Supervision, Writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Generative AI statement

The author(s) declare that Generative AI was used in the creation of this manuscript. The authors used AI-assisted technology (ChatGPT 3.5) for language editing and grammar checking.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abood, F. A., Radhi, Z. K., Hadi, A. K., Homod, R. Z., and Mohammed, H. I. (2024). MHD mixed convection of nanofluid flow Ag- MgO/water in a channel contain a rotational cylinder. Int. J. Thermofluids 22, 100713. doi:10.1016/j.ijft.2024.100713

CrossRef Full Text | Google Scholar

Ahmad, S., Cham, B. M., Liu, D., Islam, S. U., Hussien, M. A., and Waqas, H. (2024a). Numerical analysis of heat and mass transfer of MHD natural convection flow in a cavity with effects of source and sink. Case Stud. Therm. Eng. 53, 103926. doi:10.1016/j.csite.2023.103926

CrossRef Full Text | Google Scholar

Ahmad, S., Liu, D., Waqas, H., and Munir, S. (2024b). Numerical simulation of magnetohydrodynamics double-diffusive natural convection in a cavity with non-uniform heated walls. Appl. Therm. Eng. 253, 123778. doi:10.1016/j.applthermaleng.2024.123778

CrossRef Full Text | Google Scholar

Akhter, R., Ali, M. M., Billah, M. M., and Uddin, M. N. (2023). Hybrid-nanofluid mixed convection in square cavity subjected to oriented magnetic field and multiple rotating rough cylinders. Results Eng. 18, 101100. doi:10.1016/j.rineng.2023.101100

CrossRef Full Text | Google Scholar

Alam, M. S., Huda, M. N., Rahman, M. M., and Billah, M. M. (2024). Statistical and numerical analysis of magnetic field effects on laminar natural convection heat transfer of nanofluid in a hexagonal cavity. Int. J. Thermofluids 24, 100856. doi:10.1016/j.ijft.2024.100856

CrossRef Full Text | Google Scholar

Al-Amir, Q. R., Hamzah, H. K., Ali, F. H., Hatami, M., Al-Kouz, W., Al-Manea, A., et al. (2023). Investigation of natural convection and entropy generation in a porous titled Z-staggered cavity saturated by TiO2-water nanofluid. Int. J. Thermofluids 19, 100395. doi:10.1016/j.ijft.2023.100395

CrossRef Full Text | Google Scholar

Alhadri, M., Raza, J., Yashkun, U., Lund, L. A., Maatki, C., Khan, S. U., et al. (2022). Response surface methodology (RSM) and artificial neural network (ANN) simulations for thermal flow hybrid nanofluid flow with Darcy-Forchheimer effects. J. Indian Chem. Soc. 99 (8), 100607. doi:10.1016/j.jics.2022.100607

CrossRef Full Text | Google Scholar

Ali, Md. Y., Islam, S., Alim, M. A., Biplob, R. A., and Islam, Md. Z. (2024). Numerical investigation of MHD mixed convection in an octagonal heat exchanger containing hybrid nanofluid. Heliyon 10 (17), e37162. doi:10.1016/j.heliyon.2024.e37162

PubMed Abstract | CrossRef Full Text | Google Scholar

Al Kalbani, K. S., Rahman, M. M., and Ziad Saghir, M. (2020). Entropy generation in hydromagnetic nanofluids flow inside a tilted square enclosure under local thermal nonequilibrium condition. Int. J. Thermofluids 5–6, 100031. doi:10.1016/j.ijft.2020.100031

CrossRef Full Text | Google Scholar

Al-Khaleel, M., Abderrahmane, A., Younis, O., Jamshed, W., Guedri, K., Safdar, R., et al. (2024). A Galerkin finite element-based study of MHD mixed convective of Ostwald-de Waele nanofluids in a lid-driven wavy chamber. Results Phys. 56, 107232. doi:10.1016/j.rinp.2023.107232

CrossRef Full Text | Google Scholar

Alobaid, M., Hughes, B., Calautit, J. K., O’Connor, D., and Heyes, A. (2017). A review of solar driven absorption cooling with photovoltaic thermal systems. Renew. and Sustain. Energy Rev. 76, 728–742. doi:10.1016/j.rser.2017.03.081

CrossRef Full Text | Google Scholar

Alomari, M. A., Al-Salami, Q. H., Alyousuf, F. Q. A., Alqurashi, F., and Flayyih, M. A. (2024). Numerical analysis of magnetohydrodynamic mixed convection and entropy generation in a curvelinear lid-driven cavity with carbon nanotubes and an adiabatic cylinder. Int. J. Thermofluids 24, 100852. doi:10.1016/j.ijft.2024.100852

CrossRef Full Text | Google Scholar

Chen, C. L., and Cheng, C. H. (2004). Experimental and numerical study of mixed convection and flow pattern in a lid-driven arc-shape cavity. Heat mass Transf. 41, 58–66. doi:10.1007/s00231-004-0541-5

CrossRef Full Text | Google Scholar

Colak, E., Oztop, H. F., and Ekici, O. (2020). MHD mixed convection in a chamfered lid-driven cavity with partial heating. Int. J. Heat Mass Transf. 156, 119901. doi:10.1016/j.ijheatmasstransfer.2020.119901

CrossRef Full Text | Google Scholar

Deebani, W., Raza, J., Lund, L. A., Shah, Z., and Shutaywi, M. (2024). Statistical and sensitivity analysis of MHD Casson Nanofluid with convective boundary conditions on a stretching surface. Phys. Scr. doi:10.1088/1402-4896/ada327

CrossRef Full Text | Google Scholar

Deebani, W., Raza, J., Lund, L. A., Shah, Z., and Shutaywi, M. (2025). Optimization and sensitivity analysis of heat transfer rate of tri-hybrid nanofluid of stagnation point flow. J. Algorithms and Comput. Technol. 19, 17483026251331492. doi:10.1177/17483026251331492

CrossRef Full Text | Google Scholar

Devendiran, D. K., and Amirtham, V. A. (2016). A review on preparation, characterization, properties and applications of nanofluids. Renew. and Sustain. Energy Rev. 60, 21–40. doi:10.1016/j.rser.2016.01.055

CrossRef Full Text | Google Scholar

Habibishandiz, M., and Saghir, Z. (2022). MHD mixed convection heat transfer of nanofluid containing oxytactic microorganisms inside a vertical annular porous cylinder. Int. J. Thermofluids 14, 100151. doi:10.1016/j.ijft.2022.100151

CrossRef Full Text | Google Scholar

Hussain, S., Ahmed, S. E., and Akbar, T. (2017). Entropy generation analysis in MHD mixed convection of hybrid nanofluid in an open cavity with a horizontal channel containing an adiabatic obstacle. Int. J. Heat Mass Transf. 114, 1054–1066. doi:10.1016/j.ijheatmasstransfer.2017.06.135

CrossRef Full Text | Google Scholar

Hussain, S., Jamal, M., Maatki, C., Ghachem, K., and Kolsi, L. (2021). MHD mixed convection of Al₂ O₃ –Cu–water hybrid nanofluid in a wavy channel with incorporated fixed cylinder. J. Therm. Analysis Calorim. 144 (6), 2219–2233. doi:10.1007/s10973-020-10260-6

CrossRef Full Text | Google Scholar

Hussain, S. M., Parveen, R., Katbar, N. M., Rehman, S., Abd-Elmonem, A., Abdalla, N. S. E., et al. (2024). Entropy generation analysis of MHD convection flow of hybrid nanofluid in a wavy enclosure with heat generation and thermal radiation. Rev. Adv. Mater. Sci. 63 (1), 2002–2018. doi:10.1515/rams-2024-0037

CrossRef Full Text | Google Scholar

Ikram, M. M., Saha, G., and Saha, S. C. (2023). Unsteady conjugate heat transfer characteristics in hexagonal cavity equipped with a multi-blade dynamic modulator. Int. J. Heat Mass Transf. 200, 123527. doi:10.1016/j.ijheatmasstransfer.2022.123527

CrossRef Full Text | Google Scholar

Ikram, M. M., Saha, G., and Saha, S. C. (2021). Conjugate forced convection transient flow and heat transfer analysis in a hexagonal, partitioned, air filled cavity with dynamic modulator. Int. J. Heat Mass Transf. 167, 120786. doi:10.1016/j.ijheatmasstransfer.2020.120786

CrossRef Full Text | Google Scholar

Ikram, M. M., Saha, G., and Saha, S. C. (2024). Second law analysis of a transient hexagonal cavity with a rotating modulator. Int. J. Heat Mass Transf. 221, 125039. doi:10.1016/j.ijheatmasstransfer.2023.125039

CrossRef Full Text | Google Scholar

Islam, S., Bairagi, T., Islam, T., Rana, B. M. J., Reza-E-Rabbi, S., and Rahman, M. M. (2022). Heatline visualization in hydromagnetic natural convection flow inside a prismatic heat exchanger using nanofluid. Int. J. Thermofluids 16, 100248. doi:10.1016/j.ijft.2022.100248

CrossRef Full Text | Google Scholar

Islam, S., Islam, M. M., Rana, B. M. J., Islam, M. S., Reza-E-Rabbi, S., Hossain, M. S., et al. (2023). Numerical investigation with sensitivity study of MHD mixed convective hexagonal heat exchanger using TiO₂–H₂O nanofluid. Results Eng. 18, 101136. doi:10.1016/j.rineng.2023.101136

CrossRef Full Text | Google Scholar

Jamy, R. H., Chowdhury, S., Chowdhury, F. K., and Saha, S. (2023). Analyzing overall thermal behaviour of conjugate MHD free convection in L-shaped chamber with a thick fin. Case Stud. Therm. Eng. 48, 103137. doi:10.1016/j.csite.2023.103137

CrossRef Full Text | Google Scholar

Jasim, L. M., Hamzah, H., Canpolat, C., and Sahin, B. (2021). Mixed convection flow of hybrid nanofluid through a vented enclosure with an inner rotating cylinder. Int. Commun. Heat Mass Transf. 121, 105086. doi:10.1016/j.icheatmasstransfer.2020.105086

CrossRef Full Text | Google Scholar

Jihan, J. I., Saha, B. K., Nag, P., Moon, N. J., Saha, G., and Saha, S. C. (2024). Advancing thermal efficiency and entropy management inside decagonal enclosure with and without hot cylindrical insertions. Int. J. Thermofluids 23, 100785. doi:10.1016/j.ijft.2024.100785

CrossRef Full Text | Google Scholar

Karim, M. F., Islam, S., Rahman, M. M., Paul, A., and Mandal, G. (2024). A numerical investigation on forced convection heat and mass transfer performance in a right triangular cavity. Int. J. Thermofluids 21, 100578. doi:10.1016/j.ijft.2024.100578

CrossRef Full Text | Google Scholar

Khan, Z. H., Khan, W. A., Hamid, M., and Liu, H. (2020). Finite element analysis of hybrid nanofluid flow and heat transfer in a split lid-driven square cavity with Y-shaped obstacle. Phys. Fluids 32 (9). doi:10.1063/5.0021638

CrossRef Full Text | Google Scholar

Kumar, V., Tiwari, A. K., and Ghosh, S. K. (2015). Application of nanofluids in plate heat exchanger: a review. Energy Convers. Manag. 105, 1017–1036. doi:10.1016/j.enconman.2015.08.053

CrossRef Full Text | Google Scholar

Leong, K. Y., Ku Ahmad, K. Z., Ong, H. C., Ghazali, M. J., and Baharum, A. (2017). Synthesis and thermal conductivity characteristic of hybrid nanofluids – a review. Renew. and Sustain. Energy Rev. 75, 868–878. doi:10.1016/j.rser.2016.11.068

CrossRef Full Text | Google Scholar

Mahboobtosi, M., Hosseinzadeh, K., and Ganji, D. D. (2023). Entropy generation analysis and hydrothermal optimization of ternary hybrid nanofluid flow suspended in polymer over curved stretching surface. Int. J. Thermofluids 20, 100507. doi:10.1016/j.ijft.2023.100507

CrossRef Full Text | Google Scholar

Mahian, O., Bellos, E., Markides, C. N., Taylor, R. A., Alagumalai, A., Yang, L., et al. (2021). Recent advances in using nanofluids in renewable energy systems and the environmental implications of their uptake. Nano Energy 86, 106069. doi:10.1016/j.nanoen.2021.106069

CrossRef Full Text | Google Scholar

Mahmud, T., Saboj, J. H., Nag, P., Saha, G., and Saha, B. K. (2024). Artificial neural network (ANN) approach in predicting the thermo-solutal transport rate from multiple heated chips within an enclosure filled with hybrid nanocoolant. Int. J. Thermofluids 24, 100923. doi:10.1016/j.ijft.2024.100923

CrossRef Full Text | Google Scholar

Majeed, A. H., Hasan, M. J., Waqas, H., Liu, D., Alroobaea, R., and Muhammad, T. (2025). Impact of Hartmann number and aspect ratio on the heat and mass transfer characteristics in a hexagonal enclosure with a heated circular obstacle inside. Ain Shams Eng. J. 16 (4), 103330. doi:10.1016/j.asej.2025.103330

CrossRef Full Text | Google Scholar

Malik, M. F., Turabi, Y. U. U. B., Raza, M., Imran, M., and Muhammad, T. (2024). Computational analysis of heat transfer for hybrid nanofluid flow within a wavy lid-driven cavity with entropy generation and non-uniform heating. Results Phys. 67, 108054. doi:10.1016/j.rinp.2024.108054

CrossRef Full Text | Google Scholar

Pavía, M., Alajami, K., Estellé, P., Desforges, A., and Vigolo, B. (2021). A critical review on thermal conductivity enhancement of graphene-based nanofluids. Adv. Colloid Interface Sci. 294, 102452. doi:10.1016/j.cis.2021.102452

PubMed Abstract | CrossRef Full Text | Google Scholar

Ranga Babu, J. A., Kumar, K. K., and Srinivasa Rao, S. (2017). State-of-art review on hybrid nanofluids. Renew. and Sustain. Energy Rev. 77, 551–565. doi:10.1016/j.rser.2017.04.040

CrossRef Full Text | Google Scholar

Rashid, U., Lu, D., and Iqbal, Q. (2023a). Nanoparticles impacts on natural convection nanofluid flow and heat transfer inside a square cavity with fixed a circular obstacle. Case Stud. Therm. Eng. 44, 102829. doi:10.1016/j.csite.2023.102829

CrossRef Full Text | Google Scholar

Raza, J., Lund, L. A., Ashraf, H., Shah, Z., Alshehri, M. H., and Vrinceanu, N. (2024a). Fuzzy TOPSIS optimization of MHD trihybrid nanofluid in heat pipes. Case Stud. Therm. Eng. 64, 105493. doi:10.1016/j.csite.2024.105493

CrossRef Full Text | Google Scholar

Raza, J., Mustafa, F., Lund, L. A., Shah, Z., Alshehri, M. H., and Vrinceanu, N. (2024b). Optimization of heat transfer rate of trihybrid nanofluid embedded between two horizontal coaxial cylinders by RSM. Case Stud. Therm. Eng. 60, 104637. doi:10.1016/j.csite.2024.104637

CrossRef Full Text | Google Scholar

Ruvo, T. H., Saha, S., Mojumder, S., and Saha, S. (2023). Mixed convection in an open T-shaped cavity utilizing the effect of different inflow conditions with Al₂O₃-water nanofluid flow. Results Eng. 17, 100862. doi:10.1016/j.rineng.2022.100862

CrossRef Full Text | Google Scholar

Rashid, F. L., Mohammed, H. I., Dulaimi, A., Al-Obaidi, M. A., Talebizadehsardari, P., Ahmad, S., et al. (2023b). Analysis of heat transfer in various cavity geometries with and without nano-enhanced phase change material: A review. Energy Reports, 10, 3757–3779. doi:10.1016/j.egyr.2023.10.036

CrossRef Full Text | Google Scholar

Saha, B. K., Jihan, J. I., Ahammad, Md. Z., Saha, G., and Saha, S. C. (2024c). Enhanced thermal performance and entropy generation analysis in a novel cavity design with circular cylinder. Heat. Transf. Hob. N.J. Print. 53 (3), 1446–1473. doi:10.1002/htj.22999

CrossRef Full Text | Google Scholar

Saha, B. K., Jihan, J. I., Barai, G., Moon, N. J., Saha, G., and Saha, S. C. (2025). Exploring natural convection and heat transfer dynamics of Al₂O₃-H₂O nanofluid in a modified tooth-shaped cavity configuration. Int. J. Thermofluids 25, 101005. doi:10.1016/j.ijft.2024.101005

CrossRef Full Text | Google Scholar

Saha, G., Al-Waaly, A. A., Ikram, M. M., Bihani, R., and Saha, S. C. (2024b). Unveiling the dynamics of entropy generation in enclosures: a systematic review. Int. J. Thermofluids 21, 100568. doi:10.1016/j.ijft.2024.100568

CrossRef Full Text | Google Scholar

Saha, G., Al-Waaly, A. A., Paul, M. C., and Saha, S. C. (2023a). Heat transfer in cavities: configurative systematic review. Energies 16 (5), 2338. doi:10.3390/en1605233852338

CrossRef Full Text | Google Scholar

Saha, G., Saboj, J. H., Nag, P., and Saha, S. C. (2024a). Synergistic heat transfer in enclosures: a hybrid nanofluids review. J. Nanofluids 13 (2), 524–535. doi:10.1166/jon.2024.2143

CrossRef Full Text | Google Scholar

Saha, T., Islam, T., Yeasmin, S., and Parveen, N. (2023b). Thermal influence of heated fin on MHD natural convection flow of nanofluids inside a wavy square cavity. Int. J. Thermofluids 18, 100338. doi:10.1016/j.ijft.2023.100338

CrossRef Full Text | Google Scholar

Sajid, M. U., and Ali, H. M. (2018). Thermal conductivity of hybrid nanofluids: a critical review. Int. J. Heat Mass Transf. 126, 211–234. doi:10.1016/j.ijheatmasstransfer.2018.05.021

CrossRef Full Text | Google Scholar

Shutaywi, M., Raza, J., Lund, L. A., Shah, Z., Vrinceanu, N., and Deebani, W. (2024). Optimization of heat transfer in a channel with stretching walls using a magnetized tetra-hybrid nanofluid. Adv. Mech. Eng. 16 (11), 16878132241293959. doi:10.1177/16878132241293959

CrossRef Full Text | Google Scholar

Taghizadeh, S., and Asaditaheri, A. (2018). Heat transfer and entropy generation of laminar mixed convection in an inclined lid driven enclosure with a circular porous cylinder. Int. J. Therm. Sci. 134, 242–257. doi:10.1016/j.ijthermalsci.2018.08.018

CrossRef Full Text | Google Scholar

Waqas, H., Khalid, S., Hasan, M. J., Ahmad, S., Al-Mdallal, Q. M., and Muhammad, T. (2025). Entropy generation effects with heat and mass transfer characteristics through staggered enclosure. Phys. Fluids 37 (2). doi:10.1063/5.0250212

CrossRef Full Text | Google Scholar

Yasmin, S., Khan, S. A., Fatima, N., Imran, M., Tahir, M., Waqas, H., et al. (2023). Computational analysis of MHD MgO−water nanofluid flow inside hexagonal enclosure fitted with fins. Case Stud. Therm. Eng. 43, 102788. doi:10.1016/j.csite.2023.102788

CrossRef Full Text | Google Scholar

Zainodin, S., Jamaludin, A., Nazar, R., and Pop, I. (2024). Impact of heat source on mixed convection hybrid ferrofluid flow across a shrinking inclined plate subject to convective boundary conditions. Alexandria Eng. J. 87, 662–681. doi:10.1016/j.aej.2023.12.057

CrossRef Full Text | Google Scholar

Nomenclature

${\mathit{C}}_{\mathit{p}}$ specific heat capacity (j/kgK)

${\mathit{N}\mathit{u}}_{\mathit{a}\mathit{v}\mathit{g}}$ average Nusselt number

${\mathit{E}}_{\mathit{a}\mathit{v}\mathit{g}}$ average entropy generation

${\mathit{E}}_{\mathit{g}\mathit{e}\mathit{n}}$ entropy generation

Pr Prandtl number

$\mathit{R}\mathit{e}$ Reynolds number

$\mathit{N}\mathit{u}$ $Nusseltnumber$

$\mathit{E}$ $dimensionlessentropygeneration$

$\mathit{T}$ $temperature\left(K\right)$

$\mathit{u},\mathit{v}$ $velocitycomponentsinx-andy-directions\left(m/s\right)$

$\mathit{U},\mathit{V}$ $dimensionlessvelocitycomponents$

$\mathit{x},\mathit{y}$ $dimensionalCartesiancoordinates\left(m\right)$

$\mathit{X},\mathit{Y}$ $dimensionlessCartesiancoordinates$

${\mathit{B}}_{\mathbf{0}}$ magnetic field

$\mathit{\phi }$ volume fraction

Greek symbols

$\mathit{\alpha }$ $\left.thermaldiffusivity\right($m²/s)

$\mathit{\beta }$ $thermalexpansioncoefficient$ $\left(k^{-1}\right.$)

$\varnothing$ irreversibility factor

$\mathit{\nu }$ $\left.kinematicviscosity\right($m²/s)

$\mathit{\theta }$ $dimensionlesstemperature$

$\mathit{\mu }$ $viscosity$ ($Ns/m^{-2}$)

ρ density (kg/ $m^3$)

$\mathit{g}$ gravitational acceleration (${ms}^{-2}$)

$\mathit{\sigma }$ electrical conductivity (S. $m^{-1}$)

k thermal conductivity ($\left.W.m^{-1}.K^{-1}\right)$

Subscripts

avg average

nf nanofluid

hnf hybrid-nanofluid

bf base fluid

h hot

c cold

l local

ff fluid friction

mf magnetic field

T total