- 1School of Chemical and Biomolecular Engineering, Georgia Institute of Technology, Atlanta, GA, United States
- 2KLA Corporation, Milipitas, CA, United States
All-solid-state ceramic batteries with Li metal anodes promise substantial gains in energy density, owing to the metal’s high theoretical capacity and low reduction potential, as well as enhanced safety. However, realizing these benefits requires optimization of buried grain boundaries and interfaces within and between a cell’s bulk components, through intentionally designed interfaces, targeted grain boundary engineering, rational synthesis strategies, and beyond. In this Review, we examine recent atomistic simulations that provide insights into such solutions by elucidating ion transport, electron transfer, and chemical reactivity in solid state electrolyte grain boundaries, cathode | electrolyte interfaces, cathode | cathode grain boundaries, and electrolyte interfaces in anode-free solid-state batteries. We also discuss the advantages and limitations of the various computational methods applied. Lastly, we highlight universal machine learning potentials, challenging datasets, and opportunities for tighter integration with experiments, all of which broaden the scope of modeling. These developments enable unprecedented large-scale simulations of buried solid | solid interfaces, potentially accelerating progress to understand and improve ASSB performance in silico.
Introduction to battery interfaces
All-solid-state batteries (ASSBs) enable pure Li metal anodes and offer high energy density due to their high theoretical capacity, low reduction potential, and lack of a host anode structure. Safety gains are also possible by replacing the organic, flammable electrolyte with a more thermally stable, solid-state electrolyte (SSE). Since the discovery of a SSE with ionic conductivity higher than liquid electrolytes over 10 years ago (Janek and Zeier, 2023), ASSBs have rapidly progressed toward large-scale production: In November 2024, Honda announced a roll-to-roll testing line that continuously presses the anode, SSE, and cathode layers together—similar to the production of conventional liquid Li-ion cells. The line is being used to optimize manufacturing conditions prior to large-scale production, which is projected to launch in the second half of this decade (Voelcker, 2025).
Despite these practical advances, large-scale adoption of ASSBs is hindered by the mechanical instability, high impedance, and interfacial degradation arising from myriads of solid | solid interfaces. Targeted efforts to improve performance are difficult due to the lack of unified understanding of the complex ionic, electronic, mechanical, and thermal effects that underpin degradation (Janek and Zeier, 2023), (Banerjee et al., 2020). These coupled phenomena begin at the nanoscale, starting with heterogeneities in Li diffusivity, strain fields, and electrochemical potential. While recent characterization and modeling have focused on characterizing these “patterned” particles, additional detailed efforts are needed to achieve bottom-up engineering strategies (Zhao et al., 2023). We note that this view is strongly shared by recent Perspectives (Carrasco, 2024), (Dawson, 2024).
Figure 1a shows a cost-competitive, idealized ASSB cell, at the top of charge, with the appropriate dimensions for a thick positive electrode, thin Li metal negative electrode, and a thin 20 µm layer of SSE, which also functions as the separator. Figure 1a shows that if this thin SSE is not hindered by its intrinsic Li+ conductivity (Luntz et al., 2015), then the remaining bottlenecks for ionic transport are grain boundaries within a SSE and thick positive electrode and electrode | SSE interfaces.
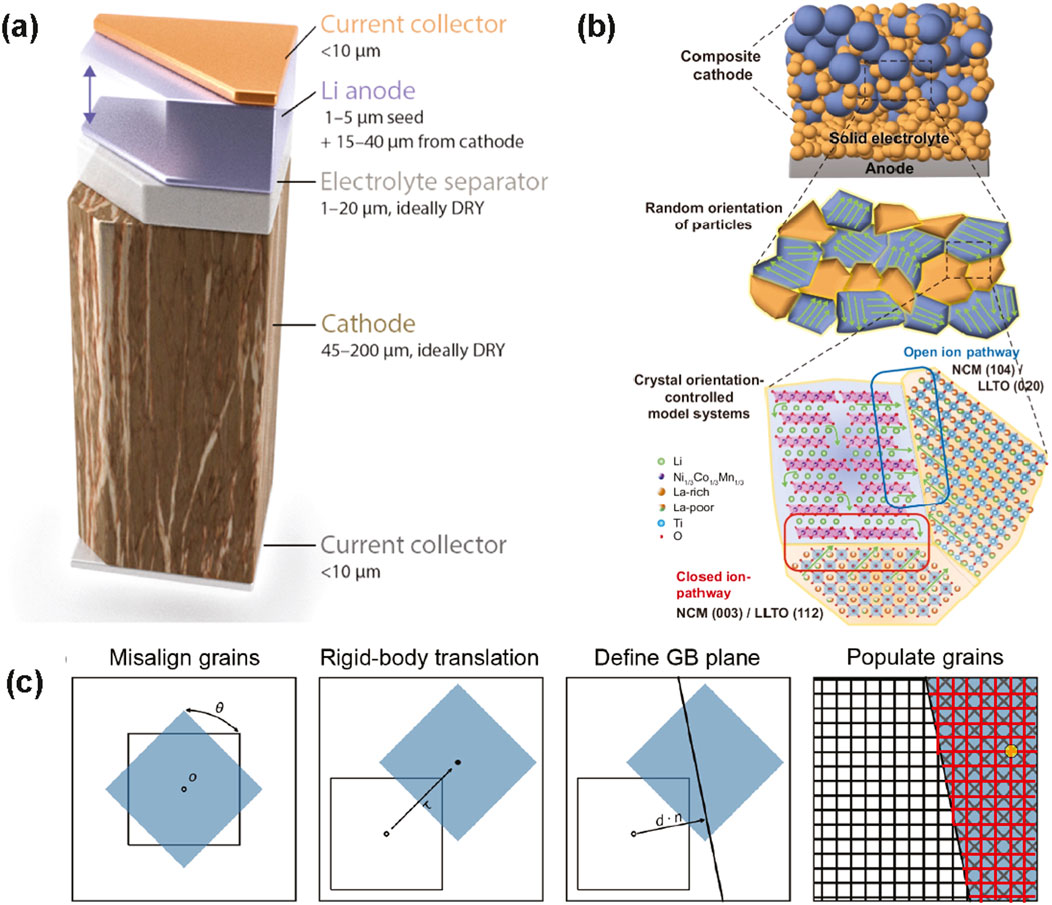
Figure 1. Explicit atomistic modeling of interfaces in an ASSB. (a) An ideal ASSB contains a thick cathode (hundreds of µm), thin solid-state electrolyte (SSE) which may also act as a separator (20 µm), and an anode-free configuration which undergoes large volume change upon charge, where Li is plated onto the current collector. Reprinted with permission from (Albertus et al., 2021). Copyright 2021 American Chemical Society. (b) Example composite particle containing a Li(Ni1/3Mn1/3 Co1/3)O2 (NMC) cathode | Li3xLa(2/3)-x⎕(1/3)−2xTiO3 (LLTO) interface for two pathways: one open pathway (blue box), where Li (green) can travel directly into LLTO, and another closed pathway (red box), where a metal-terminated surface blocks Li diffusion (Lee et al., 2024) (c) Construction of a grain boundary, where two grains are misaligned by an angle θ about a rotation axis o. The reciprocal of the fraction of coincident or overlapping points (one example: yellow circle) from the two grains, blue and white, is a parameter known as Σ. The lattice extended into the blue crystal from the white crystal are shown in red for clarity. Modified from (Dawson, 2024).
For the remainder of this report, we discuss the operation of the cell in discharge, referring to the positive electrode as the cathode and Li metal as the anode. We describe the efforts of the community in explicit modeling of solid | solid interfaces, surveying recent works from classical molecular dynamics, ab initio molecular dynamics (AIMD), and machine learning interatomic potentials (MLIPs) applied to ASSB interfaces, e.g., SSE | SSE, cathode | SSE, cathode | SSE, and SSE | anode-free interfaces. For each interface, we conclude with remaining challenges.
Interface simulations
Within a composite cathode, the particles are randomly oriented and form pathways that may be either open or blocked to Li transport (Figure 1b). These particles also contain defects, such as interstitials, stacking faults, dislocations, or grain boundaries (GBs) that allow or hinder Li diffusion. GBs, defined as solid surfaces of contact among surface slabs of different orientation (Figure 1c), are specified by a tilt angle θ and rotation axis o. In the simplest case, when only two differently oriented grains meet, the extension of the lattice from one crystal into the other (red lines in Figure 1c) results in overlapping sites (yellow circle). The reciprocal of the fraction of all overlapping sites is quantified as Σ: this value is 1 for a perfect crystal, low for a highly symmetric GB, and high for low-symmetry GB. Altogether, with the terminating slab denoted by Miller indices (hkl), the categorization of a GB is given by the notation, Σ(hkl). The notation is convenient when describing GBs within a heterogenous, bulk material, such as those within SSEs.
SSE | SSE interface
If properly engineered, GBs in the SSE can play a crucial role in preventing cell failure, as they significantly influence power density, cycle life, and safety (Yu and Siegel, 2017). Due to their different local environments compared to in the bulk, GBs exhibit deviations in ionic conductivity, electronic structure, mechanical properties (Dawson, 2024). However, the diversity of GBs can be hard to resolve, let alone interpret.
To this end, polycrystalline modeling using atomistic simulations can be a precise tool for resolving buried SSE | SSE interfaces. A recent Perspective by Dawson extensively reviews the pool of GB in SSE studied so far using atomistic modeling: Li3xLa(2/3)–xTiO3 (0 < x < 0.16, LLTO), Li3OCl, Li2OHCl, Li7La3Zr2O12 (LLZO), Li0.375Sr0.4375Ta0.75Zr0.25O3 (LSTZ0.75), LiZr2 (PO4)3 (LZP), Li10GeP2S12, Li3PS4, and Li3InCl6 (Dawson, 2024). Therefore, we only briefly mention previous works concerning modeling of GB, focusing more on the growth in methodologies (classical approaches, ab initio force fields, and machine learning force fields) used in SSE | SSE GB modeling.
The earliest studies of SSE GB have used classical molecular dynamics (CMD) to recommend processing conditions for LLZO to increase low-energy, compact GB (Yu and Siegel, 2017), resolve origins of sluggish Na conductivity in oxide-based polycrystalline Na3PO4 SSE compared to sulfide-based polycrystalline Na3PS4 (Dawson et al., 2019), and suggest nanosizing of Li10GePS12 (LGPS) to increase the dimensionality of Li-ion conductivity (Dawson and Islam, 2022). The sizes of these systems range from 103–105 atoms and are deployed for around 10 nanoseconds. They are based on classical force fields (e.g., Morse potentials) that are fitted to reproduce certain static and dynamic experimental properties (e.g., lattice constants, thermal expansion, phase transitions, shear, bulk, and elastic moduli) or freshly fitted via empirical procedures (e.g., General Utility Lattice Program (Gale and Rohl, 2003)). From these works, it is evident that findings from fitted CMD can capture the local chemical and structural environments of polycrystals occupying space on the order of 103 nm3, build experimentally consistent understandings of ion diffusion, and improve processing conditions.
CMD simulations can then inform continuum-level modeling and construct equivalent circuit models to assess how GB size controls ionic diffusion. For example, in the case of anti-perovskite Li3OCl, four candidate GBs have remarkably low GB energies and are presumed to form with high probability during synthesis. The ease of forming these GBs could explain the discrepancy between calculated single-crystal activation barriers compared to experimental measurements, especially when grain sizes are less than a few hundred nanometers (Figure 2a). (Dawson et al., 2018) Their work emphasizes that, in addition to bulk migration barriers, grain boundary migration energies are another important parameter to consider in the search for realistic high-performance SSE. This challenge is also noted by a recent computational Review for the design of fast Li conductors (Jun et al., 2024).
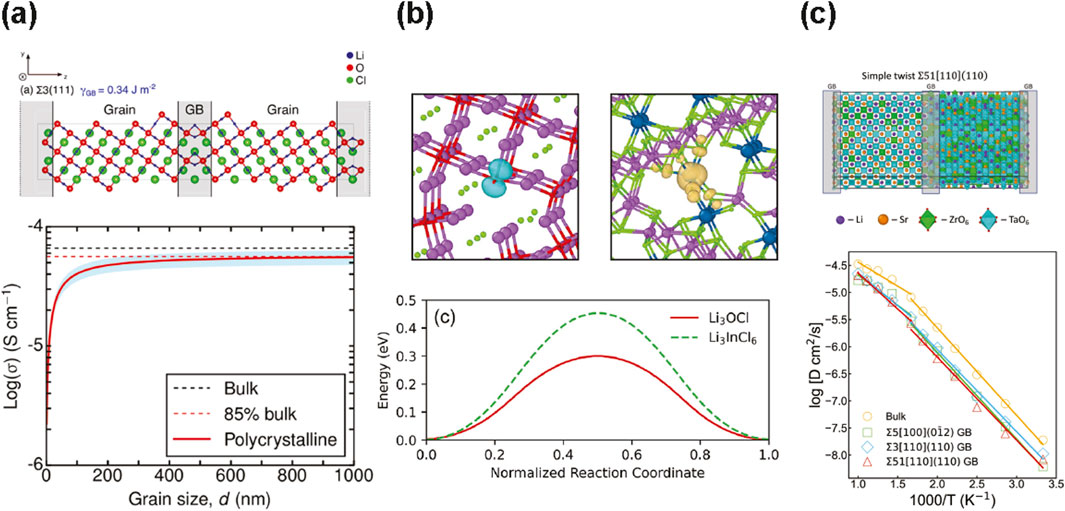
Figure 2. Examples of classical, ab initio, and machine learning molecular dynamics simulations of transport in SSE grain boundaries. (a) Grain boundary (GB) structure and energy for Σ3 (111) for Li3OCl, with equivalent GBs in grey (center and edges of supercell). High GB resistance dominates for small-enough grain sizes, according to an equivalent circuit model. Reprinted with permission from (Dawson et al., 2018). Copyright 2018 American Chemical Society. (b) Isosurface plots of electron polarons in Li3OCl (turquoise) and hole polarons Li3InCl6 (yellow), with activation barriers of 0.3 eV and 0.45 eV, respectively. The polaron hopping rate in Li3InCl6 is similar to that in TiO2, which is a good polaronic conductor (Quirk and Dawson, 2023). (c) High-index (simple twist) GB modeled using a Moment Tensor Potential, showing comparably high ionic transport as those found along low-index GB (Lee et al., 2023).
While CMD is useful for obtaining microscopic descriptions of Li diffusion via a non-reactive picture of ionic transport, it captures no electronic information. However, it is known that electron conduction in SSE can lead to unwanted Li deposition and detrimental cell shorts. For example, Demir et al. use hybrid DFT and thermodynamic arguments in a 192-atom cell to show that in cubic LLZO, Li metal nucleation can only occur around regions which relax lattice strain (e.g., GBs, voids) due to the enormous positive formation energy of neutral Li formation in the bulk (Demir et al., 2024). Their investigations reveal that GBs are effective Li metal deposition sites and candidates for dendrite formation.
Understanding mixed ionic and electronic transport along SSE GB can be achieved through AIMD which uses forces from ab initio calculations and classical Newtonian mechanics to propagate equations of motion (Car and Parrinello, 1985). Quirk and Dawson use AIMD in four SSE, Li3OCl, Li2OHCl,
While AIMD offers improved accuracy over CMD by better capturing the complex bonding expected in some high angle GBs, it remains limited to small system sizes and short timescales (e.g., typically fewer than 400 atoms and ∼100 picoseconds (ps) for Li3OCl and Li3InCl6 (Quirk and Dawson, 2023), preventing the exhaustive study of large length scales needed for high angle or amorphous GBs. Additionally, as DFT approaches have systematic errors, results of AIMD simulations must sometimes undergo a secondary analysis step, using a higher-level of theory which is even more computationally expensive (Gao et al., 2022).
Studying high angle GBs at nanometer-length scales using expensive levels of theory requires going beyond CMD or AIMD approaches. ML interatomic potentials (MLIPs), which can quite accurately reproduce electronic structure calculations, have been bridging the methods gap between the accuracy of ab initio methods and relatively lower cost of classical methods since Behler and Parinello first introduced the use of high-dimensional neural network potentials in 2008 (Behler and Parrinello, 2007). The advantage of MLIPs is that they enable quantum mechanically accurate molecular simulations of systems for now typically 103 atoms (Jacobs et al., 2025), (Deringer et al., 2019), (Unke et al., 2021) unlocking a variety of GBs and heterogenous interfaces which were once beyond the capability with solely AIMD, which reviewed earlier, is about 400 atoms evolving over ps of time. There are several classes of MLIPs (Behler, 2021). Second generation MLIPs, which historically have been the most widely used, express the total energy as a sum of mostly local atomic energy contributions. Third generation MLIPs include long-range interactions via environment-dependent partial charges, while fourth-generation MLIPs further account for long-range charge transfer.
For example, Lee et al. use a MLIP (system size: 600–900 atoms, deployed for 5–10 ns) and aberration-corrected scanning transmission electron microscopy and spectroscopy to study the origin of anomalously high GB conductivity in perovskite SSE, Li0.5ySr1-0.75y□0.25yTayZr1-yO3 (LSTZ0.75, with A-site vacancies). Its excellent transport is unlike its canonical counterpart, perovskite-type, LLTO, which has high bulk ionic conductivity, but poor GB ionic conductivity (Lee et al., 2023). It is unclear how LSTZ0.75 and LLTO, which have the same crystal structure, can exhibit drastically different GB conductivity. A Moment Tensor Potential (MTP), fitted on DFT reference energies, is used to find that Sr at the GBs tend to migrate into the bulk for both low-
While the training error of the MLIP on GB structures is about 3 meV/atom, indicating some deviation from DFT, the accuracy is comparable to other studies using MTP on ASSB GBs (Ou et al., 2024), (Jalem et al., 2023) This could be due to the lack of long-range interactions in MTP, which could be mitigated by using a third-generation MLIP. Other opportunities include extension into systems which can only be probed using MLIPs: glassy-crystalline matrices such as Li3PS4 (Urata et al., 2024) and amorphous-amorphous interfaces such as Li3B11O18 coatings on Li3PS4 SSE (Wang et al., 2023). The study of MLIP in SSE interfaces will be particularly critical in composite polymer-ceramic SSE, which is one of the most promising ASSB technologies. The reason is that composite SSE combine the advantages of high mechanical strength and interfacial contact of polymer electrolytes, with the electrochemical stability, thermal stability, ionic conductivity, and resistance to dendrite formation, of ceramic SSE (Yu and Manthiram, 2021). However, new strategies are needed to promote low-resistance, highly efficient ion-conduction networks at the composite SSE | anode and composite SSE | cathode interfaces. With this target in mind, combined atomistic and coarse-grained MLIPs may help with the design of polymer-ceramic composites.
Cathode | SSE interface
The greatest impedance occurs not at the anode | SSE interface, but at the cathode | SSE interface, suggesting that the cathode | SSE interface could be a principal hurdle in developing ASSBs (Luntz et al., 2015). However, a main challenge is that composite cathodes, made of the cathode active material carbon binder, consist of randomly-oriented crystallographic interfaces (Figure 1b). The plethora of such interfaces implies that degradation can initiate from just as many locations.
It is unclear how to connect this complex morphology and associated surface facets to observable metrics, such as capacity fade, unless measures are taken during synthesis to intentionally generate well-defined interfaces (Zahiri et al., 2021). Recent experimental progress in this area has made this possible. Zahiri et al. performed controlled electrodeposition of LiCoO2 with three halide SSE and one sulfide SSE. They find a strong dependence of Li3YCl6 instability on LiCoO2 orientation and examine this using DFT. Their calculations reveal that the (003) LiCoO2 surface has a weak and slightly repulsive interaction with the (100) Li3YCl6 surface (0.15 eV/nm2) compared to the (110) LiCoO2 surface with (100) Li3YCl6 surface (4.40 eV/nm2). Since it takes less energy to break bonds at the weak interface, overpotentials will further accelerate the decomposition. In contrast, many more bonds, such as Co-Cl, Li-O, and Y-O, form at the (110) LiCoO2 | Li3YCl6 interface, resisting decomposition. These insights guide rational fabrication of dense, additive-free cathodes with controlled electrochemical and chemical reactions and minimal capacity fade. This collaboration involving controlled experiments and electronic structure calculations is another example of validation efforts that enable rational, expedited optimization of ASSB.
In addition to thermodynamic comparisons, reaction dynamics at cathode | SSE interfaces have also been recently pursued. Golov et al. use AIMD to study reactivity at the (001) cathode | (001) Li3YCl5Br (LYCB) and (110) Li metal anode | (110) LYCB interfaces (Golov et al., 2024). Two cathode materials, LiNi0.6Mn0.2Co0.2O2 (NMC622) and LiNi0.8Mn0.1Co0.1O2 (NMC811), each containing up to ∼200 atoms, were found to promote Y-O, Li-Cl, and Li-Br bonds at the expense of Y-Cl and Y-Br bond breakage. For NMC622, 20 ps of AIMD does not reveal further structural rearrangement nor charge equilibration. On the other hand, for NMC811, more structural rearrangements are observed, specifically the formation of a bromide monochloride molecule at 15 ps, which is expected to form Br2 gas, lead to Ni reduction, and Li intercalation from LYCB into NMC811. The findings, despite occurring over a short simulation time (15–20 ps), are consistent with experimental observations that Cl2 gas evolves in NMC | Li3MCl6 (M = In, Y, Zr), and that Li loss from the SSE occurs via Li insertion into NMC. The authors suggest that dynamic evolution of NMC | LYCB can be probed, to an extent, using AIMD.
In one of the most exhaustive multiscale modeling efforts to date, Feng et al. consider 600 distinct, dense, polycrystalline LiCoO2 | LLZO interfaces using atomistically-informed mesoscale modeling, MLIP, and ML analysis (Figure 3a). (Feng et al., 2024) Using MLIP MD simulations (sampled for 4–10 ns), they calculate effective diffusivity for 600 microstructures (consisting of a two-phase polycrystal) and find a bimodal distribution when the bulk diffusivities in LCO vs. LLZO are significantly different. This behavior arises from the respective percolating channels of slow and fast phases; when more slow-diffusing phases are added to remove connectivity of fast phases, diffusivity follows a unimodal distribution. It is revealed that microstructural optimization of heterointerfaces (defined as where at least three types of interfaces meet), can form conductive-enough networks even if diffusivity at other interfaces is low. Thus, future efforts could include collaborations with experiment, such as joint efforts to intentionally promote more of these conductive heterointerfaces. Other next steps could still be in computation, given that the authors mention three limitations in the findings: lack of atomistic detail on how spatiotemporal environments control Li mobility at interfaces, lack of charge transfer in the MLIP model, and artificial smoothing of interfacial structure for mesoscale simulations. In summary, the workflow is the first to develop atomistically-informed, multiscale modeling for cathode-active materials with SSE interfaces.
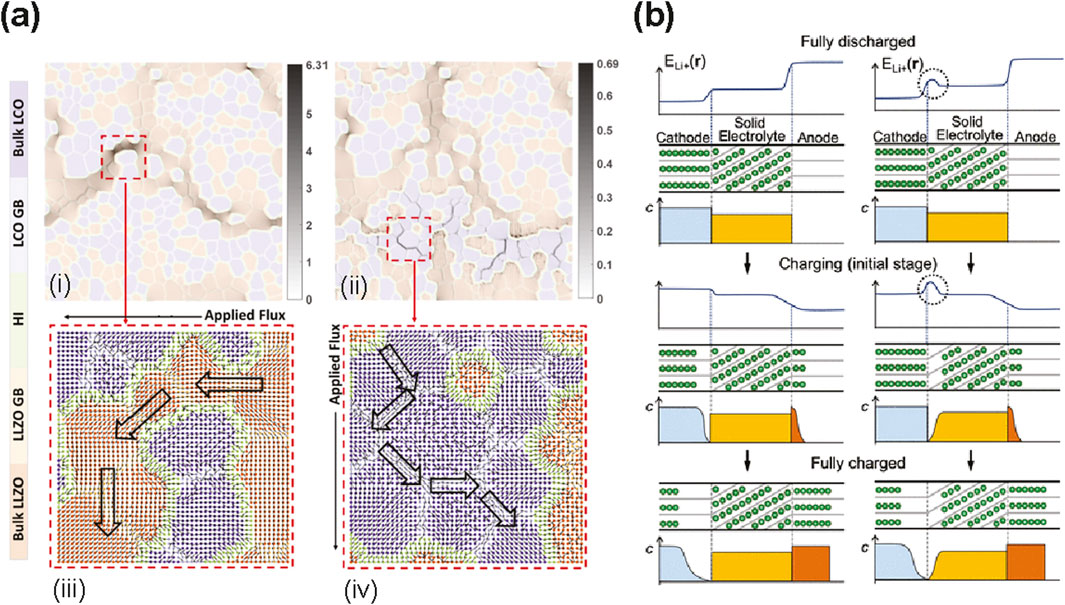
Figure 3. Considerations for modeling electrode | SSE interfaces. (a) State-of-the-art modeling of cathode | SSE interfaces for ionic conductivity showing Li flux density analysis for microstructures when flux is applied along horizontal (i,iii) and vertical (ii,iv) directions. The flux magnitude in grayscale (i,ii) and direction as vector fields (iii,iv) with streamlines (large hollow black arrows) for the most conductive phase, illustrate how Li mostly moves through bulk LLZO (i,iii), avoiding heterointerfaces, or through the LiCoO2 (LCO) grain boundaries (ii,iv). Reproduced with permission from (Feng et al., 2024). (b) Space charge layers form on the cathode side and/or the SSE side, depending on the chemical potential of Li. During charge, the concentration of Li will change as Li (green circles) is de-intercalated from the cathode (blue), transported through the SSE (yellow), and intercalated into the anode (orange). For normal interfaces (left), Li will be depleted on the cathode side at the end of charge, whereas for interfaces with high Li chemical potential (right), Li will be depleted on both the cathode and SSE sides. Reprinted with permission from (Gao et al., 2020). Copyright 2020 American Chemical Society.
Computational efforts investigating reactivity at cathode | SSE interfaces tend to use semi-local DFT approximations, typically in the form of the Perdew–Burke–Ernzerhof (PBE) (Perdew et al., 1996), due to their ability to calculate accurate formation energies within practical cost. However, semi-local DFT contains remnant self-interaction errors (Perdew and Levy, 1983), (Mori-Sánchez et al., 2008) resulting in underestimation of band gaps and relatively poorer enthalpies of formation for strongly-correlated systems containing d electrons (Zhang et al., 2018).
One way to reduce the self-interaction error in the form of charge delocalization is to solve for on-site, Coulombic Hubbard corrections via the self-consistent linear response method (Zhou et al., 2004), (Cococcioni and de Gironcoli, 2005). However, the approach is not straightforward in cathode | SSE interfaces, as transition metal oxides near the surface have locally different environments than those in the bulk, requiring spatially and chemically dependent Hubbard U and V (DFT + U + V) corrections. These systems can benefit from automated determination, and one promising approach has been to develop ML models based on equivariant neural networks, using atomic occupation matrices to predict Hubbard parameters with iterative linear response calculations per atomic site (Uhrin et al., 2025). By removing the need for manual tuning, the method may significantly expedite ab initio modeling of cathode | SSE interfaces with significantly more heterogeneous environments.
At the interface, there is a natural accumulation of vacancies due to the difference in Li chemical potential, and this forms a space charge layer (SCL) (Figure 3b). At the anode side, there is, by contrast, an accumulation of Li and depletion of vacancies. However, depending on the SSE, the formation of a SCL does not always result in depletion of Li at the interface, since stable Li adsorption sites can form, leading to a “Li pileup”, inducing an even greater SCL. Such is the case for LiCoO2 (110) | β-Li3PS4 (010). These blocked Li migration pathways can be mitigated by adding a thin LiNbO3 buffer layer which provides more Li transport pathways, reducing the SCL (Haruyama et al., 2014).
In a follow-up study using particle swam optimization via the CALYPSO method (Gao et al., 2019), the more stable (104) surface of LiCoO2 is systematically studied with β-Li3PS4 (010). It is revealed that extensive cation and anion mixing form cobalt sulfides and phosphorous oxides (Gao et al., 2020). Instead of Li adsorption forming a Li-rich region which is the case with (110) LiCoO2 | β-Li3PS4 (010), there is now Li depletion due an increase in the migration barrier at the mixed sulfide/oxide interface. The resultant Li chemical potential is now higher at the interface than in the bulk (Figure 3c), resulting in interfacial resistance, electron transfer from the SSE, and oxidative decomposition of the SSE (e.g., S oxidation).
Full-scale consideration of the SCL will require simulations of large length scales with electron transfer, which are exclusively handled with at least third-generation MLIPs with environment-dependent partial charge information (Uhrin et al., 2025). While many state-of-the-art MLIPs are second generation meaning that they do not explicitly differentiate among charges or oxidation states (e.g., MTP, as discussed in the previous section), this assumption was recently shown to be problematic for the case of thermodynamic stability in bulk LiFePO4: A pretrained CHGNet MLIP, which includes electronic degrees of freedom using magnetic moments, is successfully used with semi-grand canonical cluster expansion sampling to predict two-phase co-existence during lithiation of LiFexPO4, due to its incorporation of electronic entropy (Deng et al., 2023). Without including electronic degrees of freedom, LixFePO4 exists as a solid solution, inconsistent with experiments. From this work, it is evident that explicit differentiation between charge states may be critical for capturing thermodynamic behavior of cathode materials.
Even so, third-generation MLIPs with charge states for cathode | SSE interfaces may not be sufficient, considering that in an earlier section we reviewed that electron conduction in SSE can be facile along grain boundaries meaning that non-local charge transfer must also be a consideration. Fortunately, these new models, constituting fourth-generation MLIPs, are an area of active development (Ko et al., 2023) (Gubler et al., 2024).
In summary, electrochemical modeling of cathode | SSE interfaces remains an open challenge, owing to the un-established DFT corrections needed to study heterogeneous cathode environments and the unvetted non-local charge transfer MLIP models applied to cathode | SSE interfaces. Active work in these directions may lead to atomistically-informed understanding of how electrochemical degradation occurs, allowing for targeted design of passivating, ionically conducting cathode | SSE interfaces.
Cathode | Cathode interfaces
The cathode | cathode interface facilitates Li-ion transport within composite electrodes of ASSBs (He et al., 2021). While a well-designed particle with crystallographic alignment improves rate capability and cycling performance (Xu et al., 2020), large-scale mitigation of failure is still limited. For example, Yan et al. use STEM-HAADF to reveal that cracks nucleate from the NMC333 grain interior during cycling at high voltage (Yan et al., 2017). They find that the edge dislocation core within primary particles acts as the nucleation site for crack initiation (Figure 4a). The process is diffusion-limited, and dislocations are surmised to propagate along (003) planes, forming intragranular cracks. Indeed, crack formation along (003) is consistent with other in situ studies (Zhang et al., 2017). These findings indicate coatings are not sufficient to prevent cathode degradation at high voltage, motivating studies that focus on alleviating internal cathode strain and homogenizing Li distribution.
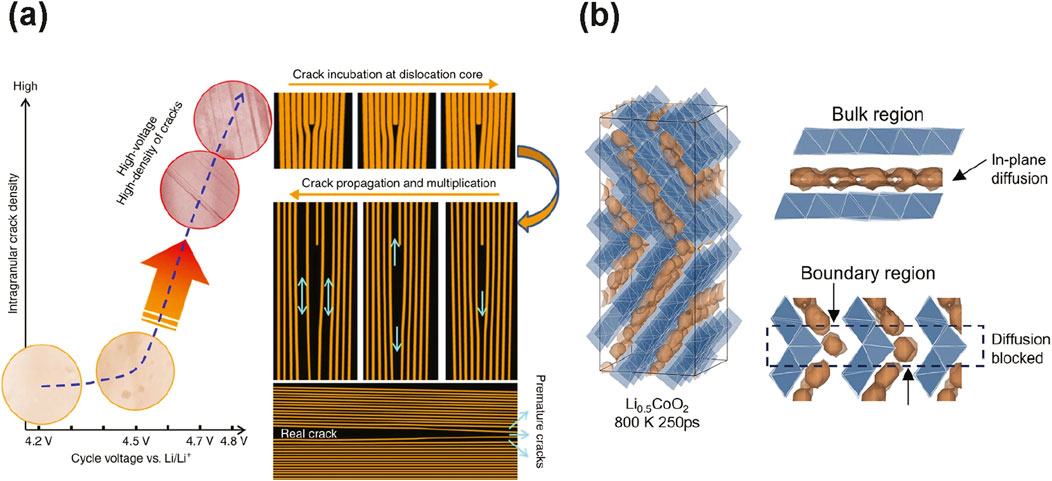
Figure 4. Examples of cathode defects that reduce electrochemical performance. (a) Significant intragranular crack density, as observed in STEM-HAADF images, is correlated with increasing cycle voltage. Schematic diagrams illustrate diffusion-limited, dislocation-assisted crack incubation and propagation (Yan et al., 2017). (b) Isosurfaces of Li (brown) in both bulk and twin boundary regions of Li0.5CoO2. Li transport in the boundary region is relatively limited compared to the bulk, resulting in reduced rate capability. Reprinted with permission from (Jiao et al., 2025). Copyright 2025 American Chemical Society.
Achieving uniform Li concentration at increasing rates is challenging for polycrystalline cathodes as their heterogeneous structure lends to heterogeneous transport. This effect can be directly quantified with computational modeling. He et al. use AIMD to investigate Li-ion migration among different GB models and statistically analyze Li migration energy profiles in the bulk, across GBs, and along GB planes in LiNi0.5Mn0.3Co0.2O2 (He et al., 2021). They find that the coherent Σ2 GB shows the lowest boundary energy (0.097 J/m2) and promotes Li diffusivity 1-2 orders of magnitude higher than that in the bulk. However, grain boundary energy alone is not sufficient for predicting Li transport, as the Σ3 GB exhibits a modestly higher GB energy (0.286 J/m2) but reduced diffusivity by 7 orders of magnitude across the GB. Disordered Σ5 and Σ9 GBs, though energetically less favorable, promotes Li diffusivity by up to 10 times compared to the bulk.
Targeted modeling efforts can also appraise strategies to prevent intergranular cracking. Hu et al. use DFT calculations and construct a straightforward dataset for the coherent Σ3 [100] (012) GB of LiNiO2 (Hu et al., 2024). They iterate through 64 metallic and semi-metallic dopants at four different well-defined locations: Li sites on the GB, Ni sites on the GB, neighboring Li sites near the GB, and neighboring Ni sites near the GB. Based on GB segregation energies and strength calculations, only group IV elements, such as Fe and Co, have beneficial roles as substitutes on Li sites. On the other hand, there are more effective dopant candidates for Ni GBs, suggesting that numerous GB engineering efforts (i.e., doping with Mg, Al, Si, Ti, Cr, Mn, Fe, Cu, Zn, Hf, or Ce) would be effective for Ni-rich cathodes as they would preferentially segregate and strengthen Ni GBs. The results align well with experimental observations, motivating systematic investigation across more complex systems.
The dynamic roles of dopants are already being investigated with a second-generation MLIP. Jiao et al. systematically assess the benefit of Al doping in LCO using experiments, characterization, and modeling (Jiao et al., 2025). Undoped LCO exhibits near perfect crystallization whereas doping increases chemical and structural heterogeneity. The extent that the structural heterogeneity is a problem is evaluated using a second generation MLIP. Simulations on thermodynamically favorable twin boundaries reveal that Li-ion diffusion is impeded at a LCO twin boundary compared to in the bulk (Figure 4b), resulting in loss of rate performance. Additionally, density of states DFT calculations on representative local configurations from MLIP simulations indicate that oxygen atoms with Li-rich environments are likely to be oxidized, as their electronic states lie close to the Fermi level. The iteration of using MLIP to inform configurations for electronic structure calculations is typical for closing the loop on MLIP simulation predictions.
It is worth mentioning again that Feng et al. also investigate Li transport in LCO bulk and LCO GBs within composite cathodes using MLIP (Feng et al., 2024). Their study reveals that the LCO bulk acts as a transport bottleneck, while LCO GBs can serve as secondary conduction pathways when LLZO connectivity is poor. In well-connected LLZO networks, Li-ion flux remains concentrated in LLZO. However, when LLZO pathways are disrupted, Li must traverse through the LCO bulk and GBs, resulting in reduced ionic conductivity. Their findings suggest that optimizing LCO GB properties through doping, grain size engineering, and interface modifications may enhance diffusion and improve rate and operational stability.
Some progress has been made in atomistic modeling of cathodes, mainly via DFT studies, AIMD, and MLIP. However, cathode-cathode interfaces remain understudied compared to other battery components. Thus, future directions simply include continued use of all methods to increase the scope of our understanding of cathode defects and grain boundaries during electrochemical cycling.
Anode-free | SSE interface
We refer the reader elsewhere for exhaustive Reviews on Li metal anode | SSE theory and computation (Krauskopf et al., 2020), (Sanchez and Dasgupta, 2024), (Seymour et al., 2023). In this section, we instead focus on recent works applying computational modeling to study anode-free | SSE interfaces as previous studies suggest that only an anode-free Li-metal SSB can be competitive with the energy density and cycle stability of Li-ion batteries (Heubner et al., 2021).
The anatomy of an anode-free ASSB is shown in Figure 1a. Upon charge, Li from the reservoir of the cathode active material diffuses through the thin SSE and is plated directly onto the current collector (CC). The uniformity of this plating is dependent on binding energy of Li atoms to the CC, nucleation overpotential, wettability, electric field, and morphology of the existing surface (Petersen et al., 2024).
In 2019, Pande and Viswanathan use computational screening to search for CCs which can stably nucleate uniform Li films upon charge (Pande and Viswanathan, 2019). Their thermodynamic calculations and first order approximations show that the use of Li alloys (e.g., Li-Zn, Li-Al, Li-B, Li-Cd, Li-Ag) may yield cells with better rate capability due to low nucleation overpotentials and higher specific energies.
Other thermodynamic evaluations include a combined DFT-experimental comparison of Li deposition onto Ag vs. Cu (Shin and Manthiram, 2022). Here, Shin and Manthiram find preferential interactions of Li with Ag (110) and Ag (111) surfaces, compared to Cu (111). This interaction suggests preferential alloying of Li with Ag forms Ag Li20, enhancing Li reversibility and Coulombic efficiency. In another joint experimental-DFT/AIMD study with an anode-free electrode made of branched polyethyleneimine, Ag nanoparticles, and LiNO3, deposited onto a Cu CC, Cho et al. use AIMD (size: 20 × 20 × 20 Å3) to find that the Li2O/Ag interfaces, which do not alloy as strongly compared to Li/Ag interfaces, can facilitate reversible alloying, uniform Li deposition, and increase capacity retention. However, the stable and facile formation of Li/Ag alloys are still necessary to act as buffers to prevent Li dendrite formation (Cho et al., 2022). The study demonstrates that AIMD can identify complex chemical interplay at mixed metallic/oxide interfaces in anode-free technology.
These studies of anode-free ASSB introduce an additional structure between the SSE and CC: a thin coating or intermediate layer, whether by construction (Li-alloys (Pande and Viswanathan, 2019)), or through chemical reaction (LiNO3 decomposition (Cho et al., 2022)). The addition of this third layer has been modeled with multiscale approaches. Recently, Xie et al. combine DFT and continuum modeling to investigate the role of a thin Ag/C composite buffer layer (BL) in SSE | BL | CC (Xie et al., 2024). The computed first-principles phase diagram, including electronic energy, configurational entropy, and phonon free energy, shows remarkable solubility of Li in Ag, creating stable alloys up to AgLi25. At the end of lithiation, Ag nanoparticles precipitate out of the BL onto the CC due to lower interfacial resistance, homogenizing the current. The integration of DFT with continuum modeling connects the thermodynamic underpinnings with interlayer structure to explain the observed Ag extrusion onto the CC. More efforts along this direction of “integrated atomistic to continuum mechanics” could help resolve the multiscale evolution of anode-free, buffer-layer-integrated current collectors in ASSB.
Additionally, as is the case for the cathode | SSE interface, including non-local charge transfer via MLIPs will also be critical at anode-free interfaces, as metallic Li deposition onto metallic buffer layers or current collectors means the electron is delocalized with respect to the deposited Li. For this reason, the modeling of metallic anode | SSE interfaces will also benefit from advances in fourth-generation MLIPs.
Summary of methods in interfacial modeling
We have discussed state-of-the-art methods for modeling grain boundaries and interfaces in ASSBs and pointed out their advantages and disadvantages. The takeaways are summarized in Table 1. Depending on the application of interest, Table 1 shows that certain methods will be more advantageous than others. For example, studying primarily ion transport in SSE grain boundaries with fitted force fields may already be sufficient with CMD. However, if there is experimental or theoretical evidence that local charge transfer reactions need to be considered, MLIP MD simulations could be useful. On another hand, if non-local charge transfer is needing to be examined, (e.g., at electrode | SSE interfaces), fourth generation MLIPs or AIMD may be the two methods of choice. In terms of cost and scalability, we refer a recent Review which discusses these tradeoffs in detail (Jacobs et al., 2025).
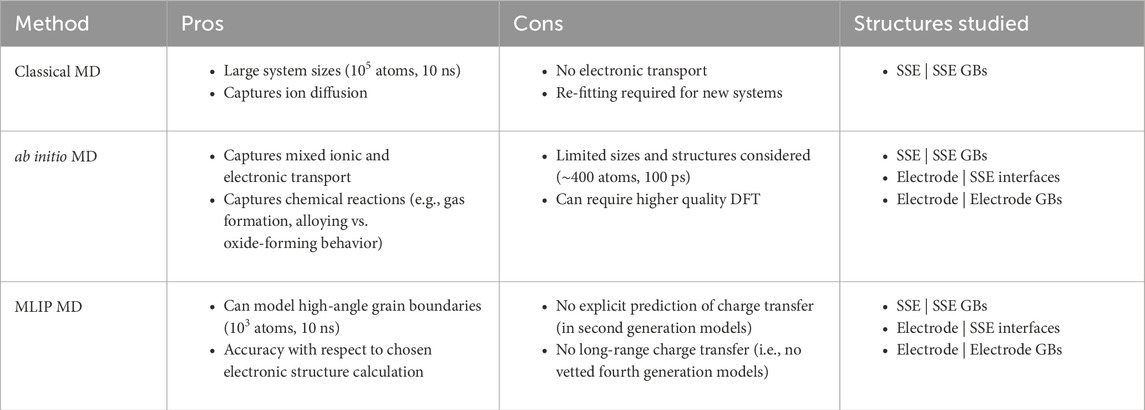
Table 1. Pros and cons for each computational approach used to study bulk heterogeneities in solid-state interfaces.
Looking ahead: challenges and opportunities in explicit atomistic modeling in ASSBs
Benchmarking open-source universal interatomic potentials
With the advent of open-source databases (dataset size), such as Materials Project (∼150k) (Jain et al., 2013), OQMD (1.2M) (Kirklin et al., 2015), AFLOW (3.5M) (Curtarolo et al., 2012), Alexandria (5M) (Schmidt et al., 2024), and OMat24 (118M) (Barroso-Luque et al., 2024), the development of open-source “Universal” MLIPs (U-MLIPs) fitted to most of the periodic table, has become possible. Starting in 2022, the first U-MLIP was developed by Chen and Ong (Chen and Ong, 2022). Trained across 187,000 energies, 16 million forces, and 1.6 million stresses from structural relaxation, the model is used to relax ∼30 million hypothetical structures for materials discovery. These efforts have been followed by the release of several other open-source models featuring modified architectures and training data: CHGNet trained on Materials Project data and ionic relaxation (MPtrj) (Deng et al., 2023), MACE-MP also trained on MPtrj, EquiformerV2 models from OMat24 (Barroso-Luque et al., 2024), and MatPES (Kaplan et al., 2025). All of these U-MLIPs bring promise to reduce the overhead time in fitting interfacial ML models in ASSBs as well as be a pre-screening tool prior to costly DFT calculations. We refer the reader to a recent Review which discusses more U-MLIPs, including proprietary models (Jacobs et al., 2025).
Efforts to benchmark and/or improve U-MLIPs are already underway. Focassio et al. find that out-of-the-box performance of M3GNet, MACE-MP-0, and CHGNet are only modestly accurate predictors of surface energies for unary systems (Focassio et al., 2025). Fine-tuning MACE and M3GNet with publicly-available data from a previous benchmarking effort (Zuo et al., 2020) improves the accuracy of all models to the point of being comparable with models trained from scratch. However, the key takeaway is sufficient dataset coverage for the target space in the first place.
In a feasibility analysis, Kwon and Kim compare CHGNet and M3GNET with PBE on new cathode materials, Mn-substituted LiMnyFe1-yPO4 as a function of Mn content and find good alignment of both U-MLIP with PBE in that all predict solid solutions. Cation-disordered relative energies in rocksalt Li2TiO3 and Li2TiS3 are also reasonably produced. However, both CHGNet and M3GNET fail for the LiFePO4 voltage profile, predicting a solid solution instead of a two-phase reaction, and underestimate the voltage (Kwon and Kim, 2024). Note that the results are consistent with the report by Deng et al., which finds that the electronic entropy (Fe2+/Fe3+ disorder, not Li+/vacancy disorder) is critical to converge on the two-phase reaction. The results suggest that U-MLIP is practical for expediting domain understanding, but not for replacing it.
Guo et al. examine diffusivity with M3GNET after comparing results with DFT-MD to set baselines for screening criteria (Guo et al., 2024). They discover 130 new candidates, after filtering for phase stability, mechanical compatibility, electrical conductivity, Li+ conductivity over 50 ps trajectories, electrochemical stability, and chemical reactivity. While M3GNET provides reasonable estimations to allow for efficient high-throughput screening, there is a systematic 150 meV underprediction of activation energy, resulting in overestimation of Li+ conductivity.
These findings indicate a persistent overstabilization of phases, which could be related to the “softening” effect of U-MLIP since training data are skewed toward equilibrium datasets (Deng et al., 2024). Nevertheless, prospects in the integration of U-MLIP for accelerated discovery and understanding of ASSBs remain bright, provided there are continuous advancements in release of open-source data and models and benchmarks on practical materials systems, such as surfaces and solid | solid interfaces.
New databases
The need for more challenging datasets to include non-equilibrium solid materials has been answered by a few teams: Zheng et al. present the ab initio amorphous materials database, consisting of a ‘5000 K amorphous database’ with 5,120 compounds and with a similar coverage, chemically, with the Materials Project. Note that 69% of the compounds contain Li, making the dataset particularly suitable for ASSBs (Zheng et al., 2024).
The Open Materials 2024 (OMat24) database from Meta, consisting of 118 million single-point energy DFT PBE/PBE + U calculations on non-equilibrium inorganic bulk materials, is the largest database to date. Barroso-Luque et al. show that pre-training an Equiformer V2 Model on OMat24, with additional fine-tuning on MPtrj and subsets of the Alexandria database, yields state-of-the-art results over the top-performing U-MLIPs (ORB MPtrj, SevenNet, MACE) (Barroso-Luque et al., 2024). Overall, the availability and amount of training data appear to develop more transferable models, increasing the urgency and importance of developing more robust, open datasets.
Integration with experiments
As introduced earlier, it is possible to grow controlled morphology of thick cathode crystals using electrodeposition from a molten salt bath (at 200–300
Collaborations can also provide synthesis and processing recommendations. Howard et al. carried out a joint computational-experimental study on LiMn2O4-LLTO cathode | SSE interface and find that cation exchange is enthalpically favorable in (111) LiMn2O4 | (111) LLTO such that the interface becomes a trap for anti-site defects (Howard et al., 2022). Experiments using pulsed laser deposition corroborate this finding, and observe that above a critical temperature, the interface becomes blurred. Efforts to design ASSB with sharp interfaces should consider a maximal synthesis temperature such that interdiffusion is kinetically limited. Thus, these experimental-computational studies can expedite rational understanding of ASSBs that behave “as designed”.
Experiments are typically done at constant potential, meaning constant electrochemical potential of electrons. However, typical ASSB calculations enforce constant Li chemical potential. The authors believe this is partly because grand canonical ensemble DFT, useful for enforcing constant potential, is still an area of active development. For example, recently Melander et al. describe that by enforcing a local electrode inner potential, instead of a global electrochemical potential (proportional to the Fermi level of a given phase) which is the standard method for grand canonical DFT, they can model outer-sphere reactions that occur in weakly interacting solute-electrode systems (Melander et al., 2024). Outer-sphere reactions are completely missed by the global Fermi level model. While these studies are for aqueous solid | liquid systems, they remain to be tested on ASSB interfaces. In summary, applying grand canonical DFT during AIMD studies of ASSB interfaces, and eventually to new generations of MLIPs, could also increase future collaborations with experiments since the effect of overpotentials can then directly be evaluated.
Entirely computationally-driven multiscale simulations are also being explored, and their success promises tighter integration with experiments. For example, as reviewed earlier, the Quantum Simulations Group at Livermore National Laboratory has studied chemo-mechanical effects of the garnet SSE Li7La3Zr2O12 | LiCoO2 interface, guiding future processing conditions (Feng et al., 2024), (Wan et al., 2024). Validation with in operando measurements may enable construction of physically accurate, digital twin models capable of predicting and understanding battery performance in silico.
Atomistic insights into degradation pathways inform recyclability
Scaling ASSBs will require not only electrochemical optimization but also materials circularity. However, as discussed earlier, degradation at interfaces can form a variety of decomposition products. In this section, we discuss how certain byproducts are beginning to pose different challenges for recycling.
For instance, we described how breakdown during cycling between LiCoO2 (104) β-Li3PS4 interface results in easy formation of interfacial reaction, involving both cation (Co, P) and anion (O, S) mixing (Gao et al., 2020). Polysulfide phases (e.g., P2S64-, Li2Sx), found to varying degrees at different cathode | β-Li3PS4 interfaces (Wissel et al., 2024), exhibit intrinsically low solubility in both inorganic acids and organic solvents typically used in hydrometallurgical recycling processes (Adeoye et al., 2023). Their accumulation near the cathode–electrolyte interface forms chemically inert, amorphous passivation layers that impede Li+ transport, hinders redox activity, and blocks mass transport of protons and metal ions (e.g., Li+) to and from the underlying LiCoO2 matrix (Marana et al., 2023). Such sulfide-rich interphases can critically suppress metal dissolution. In chalcopyrite systems, similar elemental sulfide, disulfide, and polysulfide layers have been shown to reduce Cu recovery to below 10% (Wei et al., 2023), suggesting comparable risks for ASSB recycling.
The presence of Al in spent ASSBs, such as through doping or via the current collector, poses a major problem for hydrometallurgical recovery. This is because after dissolution, Al precipitates as amorphous γ-AlOOH at pH 4.5–4.8 (Kordloo et al., 2025). The poorly crystalline phase has high surface area and adsorptive capacity, physical entrapping and chemisorbing Ni2+, Co2+, and Mn2+ at undercoordinated oxygen environments (Zou et al., 2024). This leads to transition metal losses during co-precipitation, consistent with the non-selective recovery of Co observed at both pH 8.5–8.8 and 9.2–9.5, ultimately reducing product purity and recovery efficiency (Ihrig et al., 2022). To address this, several studies recommend modifying solvent systems—such as using organic acids (e.g., oxalic acid) or complexing agents—to suppress Al dissolution, and implementing two-step strategies where Al is removed prior to transition metal leaching (Schneider et al., 2023). Others emphasize that pH control and tuning complexation equilibria are essential to minimize co-precipitation during downstream separation (Makwarimba et al., 2022). More recent solvometallurgical approaches using deep eutectic solvents have shown promise in selectively leaching Ni, Co, and Mn while avoiding Al(OH)3 gel formation altogether (Ebrahimi et al., 2023). Taken together, these findings support the view that Al mitigation is critical, that solvent choice matters, and that future recycling strategies should focus on removing or passivating Al early in the process.
In summary, atomistic modeling that identify degradation products can begin to foreshadow downstream limitations using current recycling methods. Given that some degradation products are unavoidable, advancements in new recycling methods are critical (Ma et al., 2025).
Conclusion
We have reviewed the latest computational developments for explicit modeling of interfacial atomistics in ASSBs, focusing on works which use DFT, classical MD, ab initio MD, and machine learning potentials to uncover thermodynamic and kinetics in SSE | SSE, cathode | SSE, cathode | cathode, and anode-free | SSE interfaces. Given their multiscale nature, modeling of interfaces can reveal phenomena starting at the atomistic level: Classical MD with equivalent circuit models can illustrate the effect of grain size on macroscopic diffusion; AIMD simulations can uncover the onset of electronic and/or chemical degradation, (e.g., Li dendrite formation, gas evolution); ML potentials can model both transport and degradation mechanisms at nanometer-length and nanosecond-time scale. However, further work in methods and case studies are needed; urgent directions include development/deployment of fourth-generation machine learning potentials and benchmarking of machine learning potentials at solid | solid interfaces. Additionally, we have discussed universal machine learning potentials, the release of challenging datasets, and directions for joint experimental-computation efforts as promising developments that will in parallel enable expedited and robust understanding of chemical, electronic, thermal, and mechanical evolution of ASSB interfaces. Continued dedicated efforts in these directions may achieve in silico insight into buried heterointerfaces at unprecedented length and time scales, accelerating practical adoption of ASSBs.
Author contributions
JY: Conceptualization, Investigation, Writing – original draft, Writing – review and editing. XR: Investigation, Writing – review and editing. AO: Writing – review and editing, Investigation.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. JY acknowledges support from startup funds at the Georgia Institute of Technology School of Chemical and Biomolecular Engineering.
Conflict of interest
Author AO was employed by KLA Corporation.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Adeoye, H. A., Dent, M., Watts, J. F., Tennison, S., and Lekakou, C. (2023). Solubility and dissolution kinetics of sulfur and sulfides in electrolyte solvents for lithium–sulfur and sodium–sulfur batteries. J. Chem. Phys. 158 (6), 064702. doi:10.1063/5.0132068
Albertus, P., Anandan, V., Ban, C., Balsara, N., Belharouak, I., Buettner-Garrett, J., et al. (2021). Challenges for and pathways toward Li-Metal-Based all-solid-state batteries. ACS Energy Lett. 6 (4), 1399–1404. doi:10.1021/acsenergylett.1c00445
Banerjee, A., Wang, X., Fang, C., Wu, E. A., and Meng, Y. S. (2020). Interfaces and interphases in all-solid-state batteries with inorganic solid electrolytes. Chem. Rev. 120 (14), 6878–6933. doi:10.1021/acs.chemrev.0c00101
Barroso-Luque, L., Shuaibi, M., Fu, X., Wood, B. M., and Dzamba, M. (2024). “Open materials 2024 (OMat24) inorganic materials dataset and models”
Behler, J. (2021). Four generations of high-dimensional neural network potentials. Chem. Rev. 121 (16), 10037–10072. doi:10.1021/acs.chemrev.0c00868
Behler, J., and Parrinello, M. (2007). Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 98 (14), 146401. doi:10.1103/PhysRevLett.98.146401
Car, R., and Parrinello, M. (1985). Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 55 (22), 2471–2474. doi:10.1103/PhysRevLett.55.2471
Carrasco, J. (2024). A theoretical perspective on solid-state ionic interfaces. Philosophical Trans. R. Soc. A Math. Phys. Eng. Sci. 382 (2281), 20230313. doi:10.1098/rsta.2023.0313
Chen, C., and Ong, S. P. (2022). A universal graph deep learning interatomic potential for the periodic table. Nat. Comput. Sci. 2 (11), 718–728. doi:10.1038/s43588-022-00349-3
Cho, S., Kim, D. Y., Lee, J., Kang, J., Lee, H., Kim, G., et al. (2022). Highly reversible lithium host materials for high-energy-density anode-free lithium metal batteries. Adv. Funct. Mater 32 (47), 2208629. doi:10.1002/adfm.202208629
Cococcioni, M., and de Gironcoli, S. (2005). Linear response approach to the calculation of the effective interaction parameters in the method. Phys. Rev. B 71 (3), 035105. doi:10.1103/PhysRevB.71.035105
Curtarolo, S., Setyawan, W., Hart, G. L., Jahnatek, M., Chepulskii, R. V., Taylor, R. H., et al. (2012). AFLOW: an automatic framework for high-throughput materials discovery. Comput. Mater Sci. 58, 218–226. doi:10.1016/j.commatsci.2012.02.005
Dawson, J. A., Canepa, P., Clarke, M. J., Famprikis, T., Ghosh, D., and Islam, M. S. (2019). Toward understanding the different influences of grain boundaries on ion transport in sulfide and oxide solid electrolytes. Chem. Mater. 31 (14), 5296–5304. doi:10.1021/acs.chemmater.9b01794
Dawson, J. A., Canepa, P., Famprikis, T., Masquelier, C., and Islam, M. S. (2018). Atomic-scale influence of grain boundaries on Li-ion conduction in solid electrolytes for all-solid-state batteries. J. Am. Chem. Soc. 140 (1), 362–368. doi:10.1021/jacs.7b10593
Dawson, J. A., and Islam, M. S. (2022). A nanoscale design approach for enhancing the Li-ion conductivity of the Li10GeP2S12 solid electrolyte. ACS Mater Lett. 4 (2), 424–431. doi:10.1021/acsmaterialslett.1c00766
Dawson, J. A. (2024). Going against the grain: atomistic modeling of grain boundaries in solid electrolytes for solid-state batteries. ACS Mater. Au 4 (1), 1–13. doi:10.1021/acsmaterialsau.3c00064
Demir, S., Tekin, A., Chan, Y. T., Scheurer, C., Reuter, K., Luntz, A. C., et al. (2024). Factors affecting the electron conductivity in single crystal Li7La3Zr2O12 and Li7P3S11. ACS Appl. Energy Mater 7 (6), 2392–2404. doi:10.1021/acsaem.3c03092
Deng, B., Choi, Y., Zhong, P., Riebesell, J., Anand, S., Li, Z., et al. (2024). Overcoming systematic softening in universal machine learning interatomic potentials by fine-tuning.
Deng, B., Zhong, P., Jun, K., Riebesell, J., Han, K., Bartel, C. J., et al. (2023). CHGNet as a pretrained universal neural network potential for charge-informed atomistic modelling. Nat. Mach. Intell. 5 (9), 1031–1041. doi:10.1038/s42256-023-00716-3
Deringer, V. L., Caro, M. A., and Csányi, G. (2019). Machine learning interatomic potentials as emerging tools for materials science. Adv. Mater. 31 (46), 1902765. doi:10.1002/adma.201902765
Ebrahimi, E., Kordloo, M., Khodadadmahmoudi, G., Rezaei, A., Ganjali, M., and Azimi, G. (2023). Solvometallurgical recycling of spent LiNixCoyMnzO2 (NCM) cathode material using ternary choline chloride-ethylene glycol-p-toluenesulfonic acid deep eutectic solvent. Hydrometallurgy 222, 106184. doi:10.1016/j.hydromet.2023.106184
Feng, L., Wang, B., Kim, K., Wan, L. F., Wood, B. C., and Heo, T. W. (2024). Machine-learning-assisted deciphering of microstructural effects on ionic transport in composite materials: a case study of Li7La3Zr2O12-LiCoO2. Energy Storage Mater 73, 103776. doi:10.1016/j.ensm.2024.103776
Focassio, B., Freitas, L. P. M., and Schleder, G. R. (2025). Performance assessment of universal machine learning interatomic potentials: challenges and directions for materials’ surfaces. ACS Appl. Mater Interfaces 17 (9), 13111–13121. doi:10.1021/acsami.4c03815
Gale, J. D., and Rohl, A. L. (2003). The general utility lattice Program (GULP). Mol. Simul. 29 (5), 291–341. doi:10.1080/0892702031000104887
Gao, B., Gao, P., Lu, S., Lv, J., Wang, Y., and Ma, Y. (2019). Interface structure prediction via CALYPSO method. Sci. Bull. (Beijing) 64 (5), 301–309. doi:10.1016/j.scib.2019.02.009
Gao, B., Jalem, R., Ma, Y., and Tateyama, Y. (2020). Li+ transport mechanism at the heterogeneous cathode/solid electrolyte interface in an all-solid-state battery via the first-principles structure prediction scheme. Chem. Mater. 32 (1), 85–96. doi:10.1021/acs.chemmater.9b02311
Gao, B., Jalem, R., Tian, H.-K., and Tateyama, Y. (2022). Revealing atomic-scale ionic stability and transport around grain boundaries of garnet Li7La3Zr2O12 solid electrolyte. Adv. Energy Mater 12 (3), 2102151. doi:10.1002/aenm.202102151
Golov, A., Lian, J. X., and Carrasco, J. (2024). Interface stability and reaction mechanisms of Li3YCl5Br with high-voltage cathodes and Li metal anode: insights from ab initio simulations. ACS Appl. Mater Interfaces 16, 57870–57877. doi:10.1021/acsami.4c12938
Gubler, M., Finkler, J. A., Schäfer, M. R., Behler, J., and Goedecker, S. (2024). Accelerating fourth-generation machine learning potentials using quasi-linear scaling particle mesh charge equilibration. J. Chem. Theory Comput. 20, 7264–7271. doi:10.1021/acs.jctc.4c00334
Guo, X., Wang, Z., Yang, J.-H., and Gong, X.-G. (2024). Machine-learning assisted high-throughput discovery of solid-state electrolytes for Li-ion batteries. J. Mater. Chem. A 12 (17), 10124–10136. doi:10.1039/D4TA00721B
Haruyama, J., Sodeyama, K., Han, L., Takada, K., and Tateyama, Y. (2014). Space–charge layer effect at interface between oxide cathode and sulfide electrolyte in all-solid-state lithium-ion battery. Chem. Mater. 26 (14), 4248–4255. doi:10.1021/cm5016959
He, X., Sun, H., Ding, X., and Zhao, K. (2021). Grain boundaries and their impact on Li kinetics in layered-oxide cathodes for Li-ion batteries. J. Phys. Chem. C 125 (19), 10284–10294. doi:10.1021/acs.jpcc.1c02400
Heubner, C., Maletti, S., Auer, H., Hüttl, J., Voigt, K., Lohrberg, O., et al. (2021). From lithium-metal toward anode-free solid-state batteries: current developments, issues, and challenges. Adv. Funct. Mater 31 (51), 2106608. doi:10.1002/adfm.202106608
Howard, J. D., Evmenenko, G., Kim, J. J., Warburton, R. E., Patel, S., Fister, T. T., et al. (2022). Understanding the solid-state electrode–electrolyte interface of a model system using first-principles statistical mechanics and thin-film x-ray characterization. ACS Appl. Mater. 14 (5). doi:10.1021/acsami.1c20988
Hu, Y., Zhang, Y., Wen, B., and Dai, F.-Z. (2024). Grain boundary engineering in Nickel-rich cathode: a combination of high-throughput first-principles and interpretable machine learning study. Acta Mater 276, 120144. doi:10.1016/j.actamat.2024.120144
Ihrig, M., Finsterbusch, M., Laptev, A. M., Tu, C. h., Tran, N. T. T., Lin, C. a., et al. (2022). Study of LiCoO 2/Li 7 La 3 Zr 2 O 12:Ta interface degradation in all-solid-state lithium batteries. ACS Appl. Mater Interfaces 14 (9), 11288–11299. doi:10.1021/acsami.1c22246
Jacobs, R., Morgan, D., Attarian, S., Meng, J., Shen, C., Wu, Z., et al. (2025). A practical guide to machine learning interatomic potentials – status and future. Curr. Opin. Solid State Mater Sci. 35, 101214. doi:10.1016/j.cossms.2025.101214
Jain, A., Ong, S. P., Hautier, G., Chen, W., Richards, W. D., Dacek, S., et al. (2013). Commentary: the Materials Project: a materials genome approach to accelerating materials innovation. Apl. Mater 1 (1), 011002. doi:10.1063/1.4812323
Jalem, R., Chandrappa, M. L. H., Qi, J., Tateyama, Y., and Ong, S. P. (2023). Lithium dynamics at grain boundaries of β-Li 3 PS 4 solid electrolyte. Energy Adv. 2 (12), 2029–2041. doi:10.1039/D3YA00234A
Janek, J., and Zeier, W. G. (2023). Challenges in speeding up solid-state battery development. Nat. Energy 8 (3), 230–240. doi:10.1038/s41560-023-01208-9
Jiao, S., Li, Y., Lin, T., Feng, S., Zhang, C., Pan, H., et al. (2025). Achieving high-performance defect-free LiCoO 2 cathode via a dopant-free approach. J. Am. Chem. Soc. Jun 147, 22839–22850. doi:10.1021/jacs.5c05162
Jun, K., Chen, Y., Wei, G., Yang, X., and Ceder, G. (2024). Diffusion mechanisms of fast lithium-ion conductors. Nat. Rev. Mater 9, 887–905. doi:10.1038/s41578-024-00715-9
Kaplan, A. D., Liu, R., Qi, J., Ko, T. W., Deng, B., Riebesell, J., et al. (2025). A foundational potential energy surface dataset for materials.
Kirklin, S., Saal, J. E., Meredig, B., Thompson, A., Doak, J. W., Aykol, M., et al. (2015). The Open Quantum Materials Database (OQMD): assessing the accuracy of DFT formation energies. NPJ Comput. Mater 1 (1), 15010. doi:10.1038/npjcompumats.2015.10
Ko, T. W., Finkler, J. A., Goedecker, S., and Behler, J. (2023). Accurate fourth-generation machine learning potentials by electrostatic embedding. J. Chem. Theory Comput. 19 (12), 3567–3579. doi:10.1021/acs.jctc.2c01146
Kordloo, M., Khodadadmahmoudi, G., Barati, M. R., and Rezaei, A. (2025). Effect of leaching media on selective precipitation of Al, Ni, Co, and Mn in the NMC battery recycling process. Sep. Purif. Technol. 363, 132093. doi:10.1016/j.seppur.2025.132093
Krauskopf, T., Richter, F. H., Zeier, W. G., and Janek, J. (2020). Physicochemical concepts of the lithium metal anode in solid-state batteries. Chem. Rev. 120 (15), 7745–7794. doi:10.1021/acs.chemrev.0c00431
Kwon, D., and Kim, D. (2024). Machine learning interatomic potentials in engineering perspective for developing cathode materials. J. Mater. Chem. A 12 (35), 23837–23847. doi:10.1039/D4TA03452J
Lee, S., Park, H., Kim, J. Y., Kim, J., Choi, M. J., Han, S., et al. (2024). Unveiling crystal orientation-dependent interface property in composite cathodes for solid-state batteries by in situ microscopic probe. Nat. Commun. 15 (1), 7947. doi:10.1038/s41467-024-52226-4
Lee, T., Qi, J., Gadre, C. A., Huyan, H., Ko, S. T., Zuo, Y., et al. (2023). Atomic-scale origin of the low grain-boundary resistance in perovskite solid electrolyte Li0.375Sr0.4375Ta0.75Zr0.25O3. Nat. Commun. 14 (1), 1940. doi:10.1038/s41467-023-37115-6
Luntz, A. C., Voss, J., and Reuter, K. (2015). Interfacial challenges in solid-state Li ion batteries. J. Phys. Chem. Lett. 6 (22), 4599–4604. doi:10.1021/acs.jpclett.5b02352
Ma, X., Meng, Z., Bellonia, M. V., Spangenberger, J., Harper, G., Gratz, E., et al. (2025). The evolution of lithium-ion battery recycling. Nat. Rev. Clean. Technol. 1 (1), 75–94. doi:10.1038/s44359-024-00010-4
Makwarimba, C. P., Tang, M., Peng, Y., Lu, S., Zheng, L., Zhao, Z., et al. (2022). Assessment of recycling methods and processes for lithium-ion batteries. iScience 25 (5), 104321. doi:10.1016/j.isci.2022.104321
Marana, N. L., Casassa, S., Sgroi, M. F., Maschio, L., Silveri, F., D’Amore, M., et al. (2023). Stability and formation of the Li 3 PS 4/Li, Li 3 PS 4/Li 2 S, and Li 2 S/Li interfaces: a theoretical study. Langmuir 39 (51), 18797–18806. doi:10.1021/acs.langmuir.3c02354
Melander, M. M., Wu, T., Weckman, T., and Honkala, K. (2024). Constant inner potential DFT for modelling electrochemical systems under constant potential and bias. NPJ Comput. Mater 10 (1), 5. doi:10.1038/s41524-023-01184-4
Mori-Sánchez, P., Cohen, A. J., and Yang, W. (2008). Localization and delocalization errors in density functional theory and implications for band-gap prediction. Phys. Rev. Lett. 100 (14), 146401. doi:10.1103/PhysRevLett.100.146401
Ou, Y., Ikeda, Y., Scholz, L., Divinski, S., Fritzen, F., and Grabowski, B. (2024). Atomistic modeling of bulk and grain boundary diffusion in solid electrolyte using machine-learning interatomic potentials. Phys. Rev. Mater 8 (11), 115407. doi:10.1103/PhysRevMaterials.8.115407
Pande, V., and Viswanathan, V. (2019). Computational screening of current collectors for enabling anode-free lithium metal batteries. ACS Energy Lett. 4 (12), 2952–2959. doi:10.1021/acsenergylett.9b02306
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77 (18), 3865–3868. doi:10.1103/PhysRevLett.77.3865
Perdew, J. P., and Levy, M. (1983). Physical content of the exact Kohn-Sham orbital energies: band gaps and derivative discontinuities. Phys. Rev. Lett. 51 (20), 1884–1887. doi:10.1103/PhysRevLett.51.1884
Petersen, D., Gronenberg, M., Lener, G., Leiva, E. P. M., Luque, G. L., Rostami, S., et al. (2024). Anode-free post-Li metal batteries. Mater Horiz. 11, 5914–5945. doi:10.1039/D4MH00529E
Quirk, J. A., and Dawson, J. A. (2023). Design principles for grain boundaries in solid-state lithium-ion conductors. Adv. Energy Mater 13 (32), 2301114. doi:10.1002/aenm.202301114
Sanchez, A. J., and Dasgupta, N. P. (2024). Lithium metal anodes: advancing our mechanistic understanding of cycling phenomena in liquid and solid electrolytes. J. Am. Chem. Soc. 146 (7), 4282–4300. doi:10.1021/jacs.3c05715
Schmidt, J., Cerqueira, T. F., Romero, A. H., Loew, A., Jäger, F., Wang, H. C., et al. (2024). Improving machine-learning models in materials science through large datasets. Mater. Today Phys. 48, 101560. doi:10.1016/j.mtphys.2024.101560
Schneider, K., Kiyek, V., Finsterbusch, M., Yagmurlu, B., and Goldmann, D. (2023). Acid leaching of Al- and Ta-substituted Li7La3Zr2O12 (LLZO) solid electrolyte. Met. (Basel) 13 (5), 834. doi:10.3390/met13050834
Seymour, I. D., Quérel, E., Brugge, R. H., Pesci, F. M., and Aguadero, A. (2023). Understanding and engineering interfacial adhesion in solid-state batteries with metallic anodes. ChemSusChem 16 (12), e202202215. doi:10.1002/cssc.202202215
Shin, W., and Manthiram, A. (2022). Fast and simple Ag/Cu ion exchange on Cu foil for anode-free lithium-metal batteries. ACS Appl. Mater Interfaces 14 (15), 17454–17460. doi:10.1021/acsami.2c01980
Uhrin, M., Zadoks, A., Binci, L., Marzari, N., and Timrov, I. (2025). Machine learning Hubbard parameters with equivariant neural networks. NPJ Comput. Mater 11 (1), 19. doi:10.1038/s41524-024-01501-5
Unke, O. T., Chmiela, S., Sauceda, H. E., Gastegger, M., Poltavsky, I., Schütt, K. T., et al. (2021). Machine learning force fields. Chem. Rev. 121 (16), 10142–10186. doi:10.1021/acs.chemrev.0c01111
Urata, S., Bertani, M., and Pedone, A. (2024). Applications of machine-learning interatomic potentials for modeling ceramics, glass, and electrolytes: a review. J. Am. Ceram. Soc. 107 (12), 7665–7691. doi:10.1111/jace.19934
Wan, L., Yuan, S., Wang, B., Kim, K., Heo, T. W., and Wood, B. C. (2024). Understanding interfacial degradation in all solid-state lithium batteries from multiscale simulations. PRiME, 313. doi:10.1149/ma2024-022313mtgabs
Wang, C., Aykol, M., and Mueller, T. (2023). Nature of the amorphous–amorphous interfaces in solid-state batteries revealed using machine-learned interatomic potentials. Chem. Mater. 35 (16), 6346–6356. doi:10.1021/acs.chemmater.3c00993
Wei, Z., Yang, X., Li, W., Ma, Q., Wu, X., and Li, Y. (2023). An improved understanding of chalcopyrite leaching mechanisms: the influence of anisotropic crystal planes. Minerals 13 (11), 1461. doi:10.3390/min13111461
Wissel, K., Haben, A., Küster, K., Starke, U., Kautenburger, R., Ensinger, W., et al. (2024). Direct recycling of β-Li 3 PS 4 -based all-solid-state Li-ion batteries: interactions of electrode materials and electrolyte in a dissolution-based separation process. Adv. Energy Sustain. Res. 5 (7). doi:10.1002/aesr.202300280
Xie, F., Diallo, M. S., Kim, H., Tu, Q. H., and Ceder, G. (2024). The microscopic mechanism of lithiation and delithiation in the Ag/C buffer layer for anode-free solid-state batteries. Adv. Energy Mater 14 (10), 2302960. doi:10.1002/aenm.202302960
Xu, Z., Jiang, Z., Kuai, C., Xu, R., Qin, C., Zhang, Y., et al. (2020). Charge distribution guided by grain crystallographic orientations in polycrystalline battery materials. Nat. Commun. 11 (1), 83. doi:10.1038/s41467-019-13884-x
Yan, P., Zheng, J., Gu, M., Xiao, J., Zhang, J.-G., and Wang, C.-M. (2017). Intragranular cracking as a critical barrier for high-voltage usage of layer-structured cathode for lithium-ion batteries. Nat. Commun. 8 (1), 14101. doi:10.1038/ncomms14101
Yu, S., and Siegel, D. J. (2017). Grain boundary contributions to Li-ion transport in the solid electrolyte Li7La3Zr2O12 (LLZO). Chem. Mater. 29 (22), 9639–9647. doi:10.1021/acs.chemmater.7b02805
Yu, X., and Manthiram, A. (2021). A review of composite polymer-ceramic electrolytes for lithium batteries. Energy Storage Mater 34, 282–300. doi:10.1016/j.ensm.2020.10.006
Zahiri, B., Patra, A., Kiggins, C., Yong, A. X. B., Ertekin, E., Cook, J. B., et al. (2021). Revealing the role of the cathode–electrolyte interface on solid-state batteries. Nat. Mater 20 (10), 1392–1400. doi:10.1038/s41563-021-01016-0
Zhang, H., Omenya, F., Yan, P., Luo, L., Whittingham, M. S., Wang, C., et al. (2017). Rock-salt growth-induced (003) cracking in a layered positive electrode for Li-ion batteries. ACS Energy Lett. 2 (11), 2607–2615. doi:10.1021/acsenergylett.7b00907
Zhang, Y., Kitchaev, D. A., Yang, J., Chen, T., Dacek, S. T., Sarmiento-Pérez, R. A., et al. (2018). Efficient first-principles prediction of solid stability: towards chemical accuracy. NPJ Comput. Mater 4 (1), 9. doi:10.1038/s41524-018-0065-z
Zhao, H., Deng, H. D., Cohen, A. E., Lim, J., Li, Y., Fraggedakis, D., et al. (2023). Learning heterogeneous reaction kinetics from X-ray videos pixel by pixel. Nature 621 (7978), 289–294. doi:10.1038/s41586-023-06393-x
Zheng, H., Sivonxay, E., Gallant, M., Luo, Z., McDermott, M., Huck, P., et al. (2024). The ab initio amorphous materials database: empowering machine learning to decode diffusivity.
Zhou, F., Cococcioni, M., Marianetti, C. A., Morgan, D., and Ceder, G. (2004).“First-principles prediction of redox potentials in transition-metal compounds with $\mathrm{LDA}+U$,” Phys. Rev. B 70 (23), 235121. doi:10.1103/PhysRevB.70.235121
Zou, Y., Chernyaev, A., Seisko, S., Sainio, J., and Lundström, M. (2024). Removal of iron and aluminum from hydrometallurgical NMC-LFP recycling process through precipitation. Min. Eng. 218, 109037. doi:10.1016/j.mineng.2024.109037
Keywords: interfacial modeling, density functional theory, classical potentials, machine learning interatomic potentials, solid state batteries
Citation: Yang JH, Rao X and Ooi AWS (2025) Buried No longer: recent computational advances in explicit interfacial modeling of lithium-based all-solid-state battery materials. Front. Energy Res. 13:1621807. doi: 10.3389/fenrg.2025.1621807
Received: 01 May 2025; Accepted: 15 July 2025;
Published: 13 August 2025.
Edited by:
Howard Qingsong TU, Rochester Institute of Technology (RIT), United StatesReviewed by:
Selva Chandrasekaran Selvaraj, University of Illinois Chicago, United StatesXiang Chen, Tsinghua University, China
Copyright © 2025 Yang, Rao and Ooi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Julia H. Yang, amh5YW5nQGdhdGVjaC5lZHU=
 Julia H. Yang
Julia H. Yang Xinqiang Rao
Xinqiang Rao Amanda Whai Shin Ooi
Amanda Whai Shin Ooi