Lightweight state-of-charge estimation method for lithium-ion batteries based on lumped semi-empirical model

Efficient and accurate state-of-charge (SOC) estimation of lithium-ion batteries under complex conditions is challenging. To address this, we develop a battery performance prediction framework using a lumped semi-empirical model, incorporating three critical factors: state-of-health (SOH), depth of discharge (DOD), and operational load. Systematic evaluations, including hybrid pulse power characterization (HPPC) tests and new European driving cycle (NEDC) simulations, were conducted to validate the model’s predictive capability across varying SOH and DOD levels. Building on this foundation, we pro-pose an SOC estimation methodology that leverages the model’s framework, analyzing three distinct aging states (unaged, mildly aged, and seriously aged) and comparing offline versus online parameter identification approaches. To enhance accuracy in low SOC regimes, a segmented training strategy is introduced. Additionally, a comparison was made between four different SOC estimation methods. Experimental results show that the lumped semi-empirical model is suitable for complex working conditions of lithium-ion batteries, and the proposed method exhibits high accuracy and robustness in SOC estimation across typical discharge ranges, and it effectively balances estimation accuracy and computational burden, making it beneficial for engineering applications.

1 Introduction

The worldwide natural environment has deteriorated in recent years, and resources have been severely depleted. Energy conservation and emissions reduction are important resolutions for each country’s development. The transportation industry is also speeding up its research on the zero carbon economy. New energy electric vehicles and electric air-craft become the new direction and hotspot domains of future development. As the optimum selection for the current new energy electric vehicles and aircraft power reserves, the performance and service reliability of lithium-ion batteries (LIBs) are essential variables and bottlenecks affecting the development of the new energy industry. To accurately manage the endurance and health conditions of lithium-ion batteries for efficient management and intelligent maintenance, the battery management system (BMS) evaluates the SOC, SOH, state-of-power (SOP), and state-of-function (SOF) of the battery by collecting and analyzing external parameters such as current and voltage (Wang et al., 2012; Verbrugge, 2008; Ge et al., 2021).

The SOC of lithium-ion batteries reflects the remaining available power inside the battery (Hannan et al., 2017). Accurate estimation of the SOC batteries helps maximize the capabilities of the battery, improves the service safety and extends battery life. Popular estimation methods currently include the open-circuit voltage method, discharge experiment method, ampere hour integration method, Kalman filtering method, data-driven method, and fusion model estimation method. The open-circuit voltage (Gong et al., 2021) method and discharge experiment method (Li-ping et al., 2014) are mostly used for laboratory offline tests to estimate SOC; the ampere-hour integration method (Luo et al., 2020) is a relatively simple and practical online SOC estimation method, but this method cannot accurately obtain the initial SOC, which is prone to cumulative errors, resulting in low estimation accuracy. The Kalman filter method (Wei et al., 2018) uses the closed-loop estimation to estimate SOC and corrects the initial SOC value to enhance the robustness of the estimation results. However, the algorithm used in this method is complex, with a large number of calculations and a long calculation period, which makes the filtering effect not ideal (Bizeray et al., 2015). Compared with the Kalman filter algorithm, the data-driven algorithm (Ren et al., 2018) does not require the establishment of an accurate lithium-ion battery model, and it can better deal with complex nonlinear systems when estimating SOC. The data-driven algorithm requires large-scale and high-quality data for training which is computer storage and central processors demanding. Due to the high computational resources and computational time, it is difficult to popularize and apply in engineering (He et al., 2021). In general, the above methods are mainly divided into three categories: experimental method, model estimation method, and data-driven method. Although the experimental method can easily obtain the values of SOC state variables of the lithium-ion battery, the prediction results are heavily affected by the initial value of SOC, temperature, and aging state of the lithium-ion battery, making it unpractical in engineering (Nejad et al., 2016). The data-driven method has a high computational cost and is difficult to be applied to SOC online estimation. The training results directly affect the accuracy of SOC estimation and have weak robustness. To achieve high-precision online identification and prediction of lithium-ion battery SOC under complex working conditions, the model-based estimation method is more suitable for engineering applications and effective.

The performance of lithium-ion batteries model directly determines the prediction accuracy of SOC (Chen L. et al., 2018). Commonly used lithium-ion battery models include: the mechanism model (Zheng, 2018), neural network model (Wang et al., 2020), and equivalent circuit model (ECM) (Sung and Shin, 2015). Among them, the mechanism model, also known as the electrochemical model, is based on the porous electrode theory and the concentrated solution theory, and it describes the charge and discharge behavior of lithium-ion batteries by quantifying the internal electrochemical reaction kinetics, mass transfer, heat transfer, and other microscopic reactions (Gambhire et al., 2014). The electrochemical model can capture the dynamic behavior of lithium-ion batteries and has high prediction accuracy. However, the establishment of a model usually requires dozens of parameters. Not only is the model complex and the amount of calculation is large, but the majority of the parameters can only be determined through in-situ technical measurement. The modeling task is complex, resulting in a significant reduction in engineering feasibility (Jannesari et al., 2011; Xu et al., 2021; Gao et al., 2022; Liu, 2020).

The neural network model is independent of the internal chemical reaction of lithium-ion batteries. The external characteristic parameters of the battery, such as current, voltage, and temperature, are directly used as network input in the black-box modeling method to train the network structure until the network output error is reduced to an acceptable level or meets other termination conditions (Huang et al., 2014). The neural network model is efficient as it can distribute, store, and process data information in parallel. However, since the model requires a considerable amount of training to obtain the relationship between input and output, the model’s accuracy requires a large quantity and quality of training data, and it has prominent problems such as poor generalization ability and insufficient model stability (Chen et al., 2018b; Li and Xiao, 2022).

The ECM is composed of some simple circuit components such as ideal voltage source, resistance, and parallel coupling resistance-capacitance. At present, mature models widely used include the Rint model, RC model, Thevenin model, PNGV model, and GNL model (Jia et al., 2011). Compared with the mechanism model, the ECM can also simulate the dynamic characteristics of the battery. The model parameters are less, and the parameter identification is easy to implement, which is one of the commonly used models in the BMS (Waag et al., 2013; Fotouhi et al., 2016; Sun, 2021). Compared with the neural network model, the ECM does not rely on a large amount of experimental data, which balances the model accuracy and real-time calculation, and opens the door to online SOC estimation (Sun, 2021). However, the equivalent circuit (EC) used in the ECM cannot correspond to the internal structure of the battery. The electrochemical reaction in-side the battery is difficult to display and reflect precisely (Bute et al., 2018). The key problem of SOC estimation accuracy caused by the ECM needs to be solved (Ouyang et al., 2014).

In summary, to fully exploit the benefits of various models while addressing their flaws, hybrid models have emerged as a powerful tool and a research hotspot in contemporary modeling research. Many relevant scholars have explored and constructed a battery lumped model with certain internal mechanism explanation ability and external characteristic representation ability. The model offers high computational efficiency while improving the accuracy of battery SOC representation. Tan et al. (2010) established the lumped model of solid oxide fuel cells based on ohmic loss, active polarization loss, and concentration polarization loss, and deduced the mathematical function relationship of single-cell voltage, gas partial pressure, and current. They also analyzed the feasibility and reliability of the lumped model. In order to further explored the adaptability of the lumped model, Nejad et al. (2016) systematically expounded on the ECM structure of 10 lumped parameters including the RC model, and performed online identification of model parameters and states based on dual Extended Kalman Filter (dual-EKF) algorithm. Lithium-ion batteries with two different electrode chemical characteristics, lithium-ion iron phosphate (LiFePO4) and lithium nickel manganese cobalt oxide (LiNMC) were used to verify the universality of each model structure in the temperature range of 5°C–45°C. In addition, each model structure’s dynamic performance in SOC and SOP joint estimation was discussed. Though the accuracy of the lumped ECM below zero and the performance of SOC estimation had not been thoroughly investigated. In order to achieved the convenient and wide application of the lumped model in all-weather BMS and achieved high SOC estimation accuracy, Seo et al. (2021) introduced an innovative lumped battery model to estimate SOC at different ambient temperatures while analyzing the error caused by the lumped ECM. Based on the change in battery characteristics, SOC can be accurately estimated in a wide temperature range (−10°C–30°C) with a long sampling period. To further improved the prediction efficiency of the lumped model, Ekström et al. (2018) used circuit components based on generalized particle diffusion replace the traditional RC components for concentration polarization prediction. They studied three lumped models (RC model, model, and K model) that all contain linear ohmic resistance, nonlinear charge transfer resistance, and diffusion impedance, and defined them as the lumped semi-empirical model. This model described the diffusion process in lithium-ion batteries with fewer model fitting parameters, which considerably improves computational efficiency. Compared with the model without diffusion, all diffusion models had improved the voltage prediction ability. The prediction ability and applicability of the lumped semi-empirical battery model with diffusion impedance were analyzed based on the load data of dynamic cycle experiment. However, the influence factors such as dynamic conditions, DOD, and battery aging in actual scenarios are not comprehensively considered. The applicability of the lumped semi-empirical battery model needs to be further analyzed, and the engineering application of SOC estimation (Xu et al., 2019) needs to be further analyzed.

Based on this, this paper develops a battery performance prediction framework using a lumped semi-empirical model, incorporating three critical factors: state-of-health (SOH), depth of discharge (DOD), and operational load. And we further propose an SOC estimation methodology that leverages the model’s framework, analyzing three distinct aging states (unaged, mildly aged, and seriously aged) and comparing offline versus online parameter identification approaches. On this premise, aiming at the poor prediction ability of the model under a low SOC state, a segmented training prediction method is proposed, which considerably enhances the accuracy of the estimation results while reducing the calculation load. Finally, by comparing four different SOC estimation methods, a comprehensive evaluation of the performance of the proposed SOC estimation method was conducted, confirming its superiority. The rest of this paper is organized as follows. Section 2 briefly describes the mathematical theory and construction process of the lumped semi-empirical model. In Section 3, the lithium-ion battery experiment and model parameter estimation are carried out to obtain model input data. Section 4 analyzes the characteristics of the model according to the root mean square error and mean absolute percentage error between the actual load voltage and the predicted value of the model. Section 5 compares the SOC estimation ability of offline and online identification methods based on the lumped semi-empirical model. In addition, the segmented training idea is adopted for SOC pre-diction of lithium-ion batteries with low initial SOC, and the superiority of the proposed method was demonstrated through validation against other SOC estimation algorithms. Finally, in Section 6, some conclusions are drawn.

2 The lumped semi-empirical model of LIB

2.1 Model theory analysis

While a lithium-ion battery is charged and discharged, internal losses such as ohmic loss, activation loss, and concentration loss take place. Ekström et al. (2018) established a lumped semi-empirical model and described the loss inside the battery by defining the battery load voltage E_batt, E_batt is calculated by Equation 1.

$E_{batt}=E_{ocv}\left(SOC\right)+{\eta }_{ohm}+{\eta }_{act}+{\eta }_{conc}(1)$

Where η_ohm is ohmic overpotential, η_act is activation overpotential, η_conc is concentration overpotential. $E_{ocv}\left(SOC\right)$ is the open circuit voltage (OCV) of the battery, which has a functional relationship with the SOC of the battery. The relationship curve between OCV and SOC can be obtained through HPPC test in engineering. The size of SOC depends on the charge and discharge of the battery, which can be expressed by Equation 2.

$\frac{dSOC}{dt}=\frac{I_{batt}}{Q_{batt}}(2)$

Where Q_batt is battery capacity, I_batt is battery load current.

Ohmic overpotential which is used to characterize the ohmic loss is caused by the resistance of the electrolyte when the current passes through the lithium-ion battery (Ni et al., 2015). Referring to the first-order ECM, it can be expressed by Equation 3.

${\eta }_{ohm}=R_{ohm}{I}_{batt}(3)$

Where R_ohm is ohmic resistance.

Activation overpotential is the loss induced by the charge transfer process in the battery, which represents the overpotential required for electrochemical reaction. It can be expressed as follows through the Butler-Volmer equation (Gebregergis et al., 2009), which is used to characterize the activation loss, it is calculated by Equation 4.

${\eta }_{act}=\frac{2RT}{F}\arcsin h\left(\frac{I_{batt}}{2I_0}\right)(4)$

Where R is the gas molar constant (8.31J/(molk)); T is the working temperature; F is Faraday’s constant (96,485 C/mol); I₀ is exchange current.

Concentration overpotential which is used to characterize the concentration loss is caused by the mass transfer resistance of battery reactants and products as they pass through the porous electrode. The RC model, or the particle diffusion model based on idealized particle diffusion behavior, can be used to model the concentration overpotential in the lumped semi-empirical model. Following are descriptions of the two modeling methods.

(1) Concentration overpotential representation method based on the RC model

The RC model is modeled by the parallel-coupled resistance-capacitance (RC). The change in the concentration overpotential of a lithium-ion battery is described using the partial differential Equation 5.

${\tau }_c\frac{d{\eta }_{conc}}{dt}+{\eta }_{conc}=R_c{I}_{batt}(5)$

Applicable Where R_c is the resistance in RC parallel circuit; τ_c is the diffusion time constant of RC lumped model, τ_c = R_cC.

(2) Concentration overpotential representation method based on the particle diffusion model

The particle diffusion model is used to simulate the movement of lithium ions in a single electrode, relying on the idealized diffusion behavior of particles. This model can be considered a lumped model derived from a single particle approach defined by partial differential Equation 6. Using particle diffusion, the Fick diffusion of the dimensionless SOC variable under a unit concentration gradient is calculated by applying the spherical gradient operator along the X-axis (where the X-axis represents the particle radius direction and the origin is the particle center) with a length of 1 in unit time.

$\tau \frac{\mathrm{\partial }SOC}{\mathrm{\partial }t}+\nabla \left(-\nabla SOC\right)=0(6)$

Where τ is the diffusion time constant of the particle diffusion model and the inverse of the diffusion coefficient (about the function of battery concentration and temperature). When X = 0, the $\nabla SOC$ of the particle center is 0, X = 1 represents the particle surface, the $\nabla SOC$ can be obtained by the current, capacity and τ calculation of lithium battery, as shown in Equation 7:

$-\nabla SOC=\frac{\tau I_{batt}}{Q_{batt}d}(7)$

Where d is the dimension number of the particle, being either 1 for Cartesian, 2 for cylindrical or 3 for spherical coordinates, respectively. This paper selects spherical coordinates, d = 3.

The surface charge state SOC_surface is defined at the particle surface (X = 1). The average charge state SOC_average is defined by integrating over the particle volume, as shown in Equation 8:

$SO{C}_{average}=d{\displaystyle \underset{0}{\overset{1}{\int }}}SOC{X}^{d-1}dX=3{\displaystyle \underset{0}{\overset{1}{\int }}}SOC{X}^{2}dX(8)$

The total set voltage loss associated with the concentration overpotential is defined by Equation 9:

${\eta }_{conc}=E_{OCV}\left(SO{C}_{surface}\right)-E_{OCV}\left(SO{C}_{average}\right)(9)$

2.2 Construction process of model

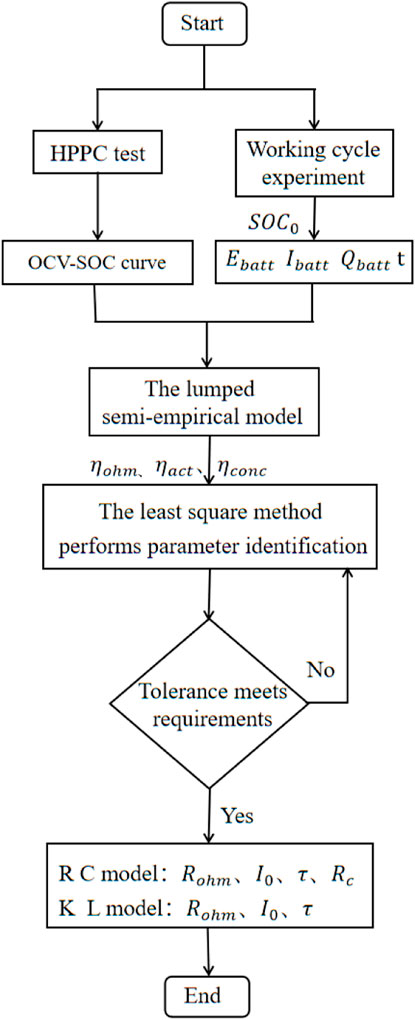
According to the above modeling procedures, the lumped semi-empirical model can be divided into the lumped semi-empirical model based on RC form (hereinafter referred to as the RC lumped model) and the lumped semi-empirical model based on particle diffusion (hereinafter referred to as the KL lumped model). Among them, the model parameters of the RC lumped model include R_ohm, I₀, τ_c, R_c, and the model parameters of the KL lumped model include R_ohm, I₀, τ. The identification of the above parameters and the acquisition of the lithium-ion battery model are the basis for the subsequent SOC estimation of lithium-ion batteries. To this end, the process of the lumped semi-empirical modeling is given as shown in Figure 1. Firstly, the HPPC test is performed to identify the characteristic parameters of the battery, such as the OCV-SOC curve. Secondly, the initial SOC (SOC₀) of lithium-ion battery is set to carry out the cycle discharge experiment under working condition, and the state parameters such as Q_batt, E_batt, I_batt and discharge time t are obtained. These data are used as model input, and the least square method is used to perform model parameter identification. Finally, the internal loss parameters of lithium-ion batteries are calculated using two lumped semi-empirical models.

Figure 1

Figure 1. The process of lumped semi-empirical modeling.

It can be found from the above process that the battery model is affected by input variables such as Q_batt, I_batt, t, SOC₀ and OCV-SOC curve, which are related to aging state and DOD. HPPC testing of various aging states and cycle tests of various depths of discharge are detailed in this paper. The parameter identification and performance analysis of the lumped semi-empirical model of lithium-ion battery are carried out. The DOD is the ratio of a lithium-ion battery’s discharge amount to its nominal capacity. The greater the value, the higher the discharge degree is. The DOD is closely related to the battery voltage and current, and it affects the battery life and performance. To study the prediction accuracy of the model for the subsequent performance of the battery under different DOD, the initial SOC (SOC₀) is used to characterize the battery state under different depths of discharge, and SOC₀ = 1-DOD. The aging state is measured by the SOH parameter of the lithium-ion battery. The lower the value is, the more serious the battery aging state is, and it is mainly reflected by a drop in the usable capacity of the lithium-ion battery and an increase in the internal resistance. In this paper, the SOH is defined by the capacity decline of the lithium-ion battery, which can be expressed by Equation 10:

$SOH=\frac{C_n}{C_o}\times 100\%(10)$

Where C₀ is the nominal capacity of lithium-ion battery in the initial state, and C_n is the maximum available capacity of lithium-ion battery after n cycles.

3 LIB experiment and parameter identification

3.1 Cycle experiment of LIB

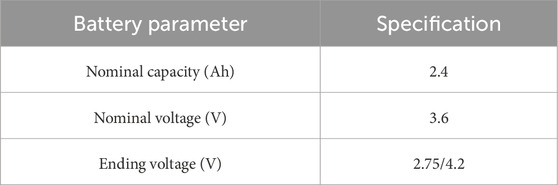
A 18,650 ternary lithium-ion battery was selected for the battery experiment, and its basic performance parameters are shown in Table 1.

Table 1

Table 1. Basic parameters of ternary lithium-ion battery.

In this study, all experiments were performed on a computer with a 12th Gen Intel(R) Core(TM) i5-12500 3.00 GHz and a 64-bit OS.

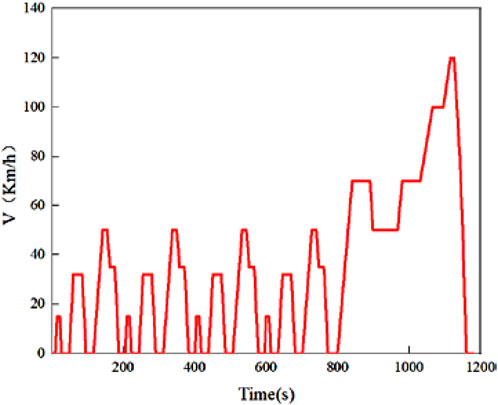
According to the two-stage charging and discharging cycle. The constant current and constant voltage (CC-CV) charging method was used in the charging stage. The NEDC driving condition was used in the discharge stage, as shown in Figure 2, which is composed of four urban cycles and one suburban cycle (Karavalakis et al., 2009; Liu et al., 2022). The charge and discharge test data were captured every second using the BTS client. The charge and discharge experiment steps are given in Table 2. For experiments, two groups of lithium-ion batteries with SOH of 100% and 95% were selected. Under normal temperature conditions, different initial SOC(SOC₀) values were obtained by applying different DOD. Then the discharge experiments under NEDC conditions were carried out respectively. The load current (I_batt), load voltage (E_batt) and discharge time t of lithium-ion battery were collected and recorded as input data of the lumped semi-empirical model.

Figure 2

Figure 2. Driving conditions of NEDC.

Table 2

Table 2. Charging and discharging experiment scheme of lithium-ion battery.

3.2 HPPC test

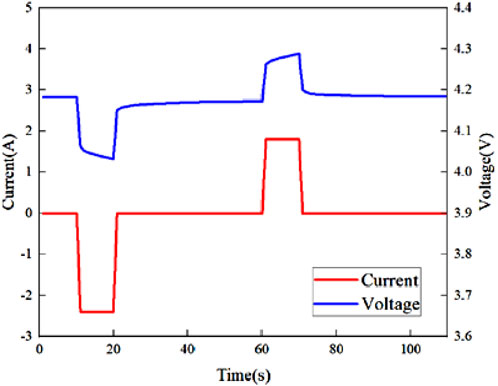
To obtain the relationship curve between OCV and SOC required for model training, the HPPC test scheme was developed according to the Freedom CAR test manual (Doughty and Crafts, 2006). In the range of 0%–100% SOC, the test battery was charged and discharged once every 10% SOC. The pulse current and voltage curve are shown in Figure 3. The specific experiment procedure was set as follows:

(1) The batteries were charged with a constant current at a constant voltage;

(2) The batteries were rested for 1 h to maintain the stability of the active material in the battery;

(3) The batteries were applied 1C discharge pulse current for 10 s, and rested for 40 s;

(4) The batteries were applied 0.75C charging pulse current for 10 s, and the batteries rested for 40 s;

(5) The batteries were discharged with CC (1C and 2.4A) until the SOC was decreased by 10% (this process takes about 6 min), and rested for 1 h;

(6) Steps (3)–(5) were repeated until SOC was reduced to 0%.

Figure 3

Figure 3. Pulse current and voltage profile of lithium-ion battery HPPC test.

3.3 Model parameter identification

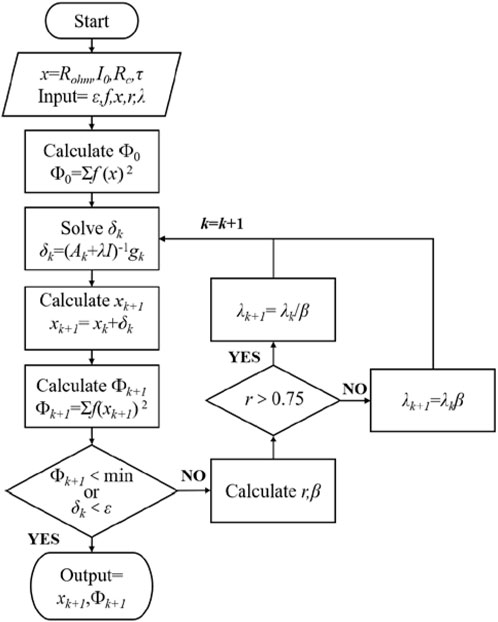
The input data required for battery model training was collected in real-time through the above NEDC cycle experiment and HPPC test, and then the model parameters were identified using the least square method to construct the lumped semi-empirical model of the ternary lithium-ion battery. Whether applied to linear or nonlinear systems, the least square method can improve statistical qualities without requiring additional mathematical statistics knowledge (Zhang et al., 2018). L-M algorithm also known as Damped Least Squares (DLS) (Fang et al., 2024) was widely used as a classical method for solving nonlinear equations and least-squares problems (Budil et al., 1996; Fan, 2013; Chen, 2016; Fan, 2012). In this paper, it is used for model training to estimate the battery model parameters in RC form and particle diffusion form. Figure 4 shows the flowchart of the DLS algorithm.

Figure 4

Figure 4. The flowchart of the DLS algorithm.

Based on the experimental data of the NEDC cycle experiment, the L-M algorithm was used to identify the model parameters, which the relevant parameters of the RC lumped model and KL lumped model can be dynamically calculated. Based on the optimal identification results of the parameters of the two types of lumped semi-empirical models, the training model was used to predict the load voltage. The prediction accuracy and robustness of the two types of lumped semi-empirical models were evaluated by analyzing the error between the predicted load voltage and the actual load voltage. Furthermore, the feasibility of the lumped semi-empirical model was verified, which provides a good theoretical basis for the subsequent online estimation of OCV and SOC.

4 Model predictive capability analysis

According to the parameter identification results of the above battery model, the parameter identification results were verified by the experimental data obtained from the NEDC test under two states of health and different depths of discharge, and the feasibility of the analysis model was verified. The performance of the model was evaluated by the root mean square error (RMSE) and mean absolute percentage error (MAPE) between the actual load voltage and the predicted value of the model. The calculation formulas of the RMSE and MAPE of this model are given in Equations 11, 12:

$RMSE=\sqrt{\frac{1}{N}\sum _{i=1}^n{\left(\stackrel{\wedge }{U_i}-U_i\right)}^2}(11)$

$MAPE=\frac{100\%}{n}{\displaystyle \sum _{i=1}^n}\left|\frac{\stackrel{\wedge }{U_i}-U_i}{U_i}\right|(12)$

Where $\stackrel{\wedge }{U_i}$ is the predicted voltage value of the i test point, $U_i$ is the test voltage value of the i test point.

Based on the NEDC cycle load data with different SOH and DOD, the characteristics of the model were analyzed. The test data and the final parameter identification results of the model were input into the RC model and the KL model, respectively. The comparison curves of the actual load voltage and the predicted voltage obtained are shown in Figures 5–9. As shown in Figures 5–7, it can be revealed that the overall trend of the predicted voltage of the two models is consistent with the experimental voltage, and the numerical agreement is favorable, under the same SOH and DOD in the range of 0%–50%. The maximum absolute error is around 25 mV, while the maximum prediction deviation is only 0.6%. The results suggest that the prediction accuracy of the two kinds of lumped semi-empirical models is higher.

Figure 5

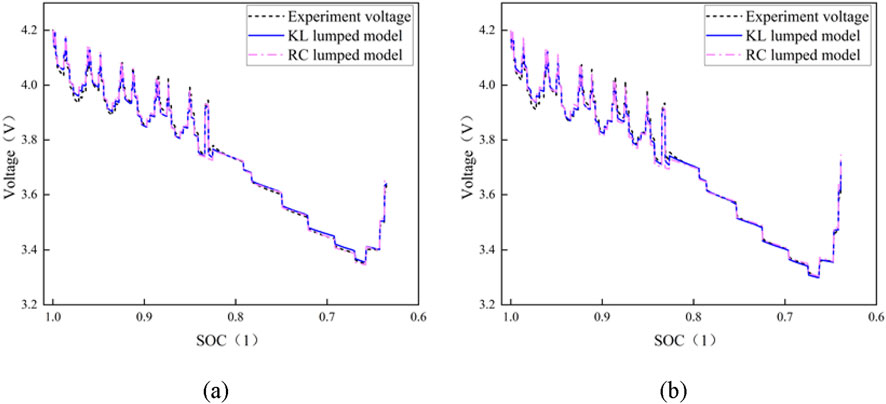
Figure 5. Predictive voltage and test voltage of RC and KL model when DOD = 0%. (a) Voltage curve comparison at SOH = 1; (b) Voltage curve comparison at SOH = 95%.

Figure 6

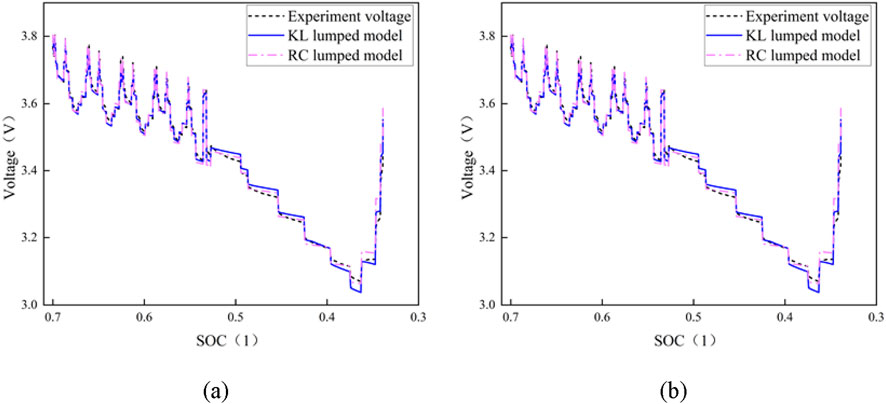
Figure 6. Predictive voltage and test voltage of RC and KL model when DOD = 30%. (a) Voltage curve comparison at SOH = 1; (b) Voltage curve comparison at SOH = 95%.

Figure 7

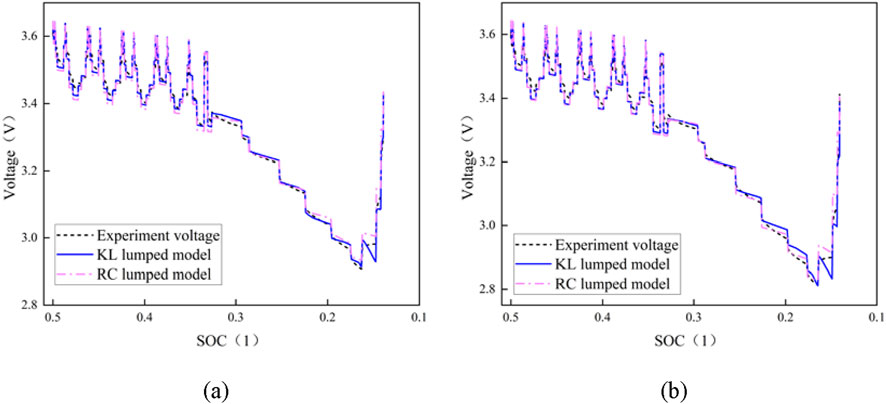
Figure 7. Predictive voltage and test voltage of RC and KL model when DOD = 50%. (a) Voltage curve comparison at SOH = 1; (b) Voltage curve comparison at SOH = 95%.

Figure 8

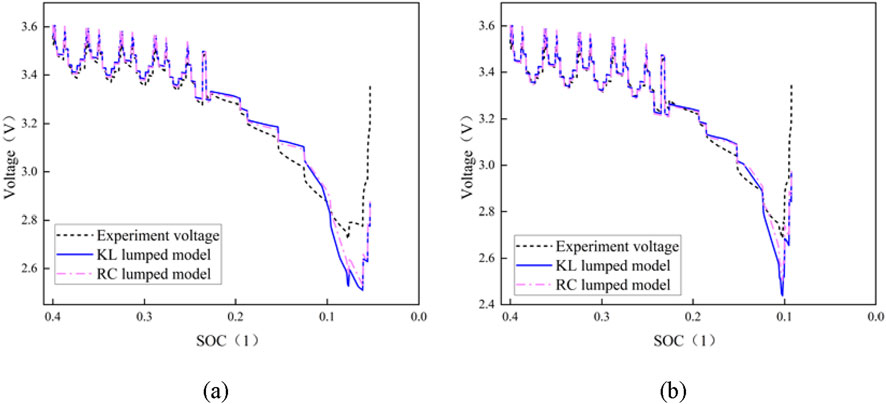
Figure 8. Predictive voltage and test voltage of RC and KL model when DOD = 60%. (a) Voltage curve comparison at SOH = 1; (b) Voltage curve comparison at SOH = 95%.

Figure 9

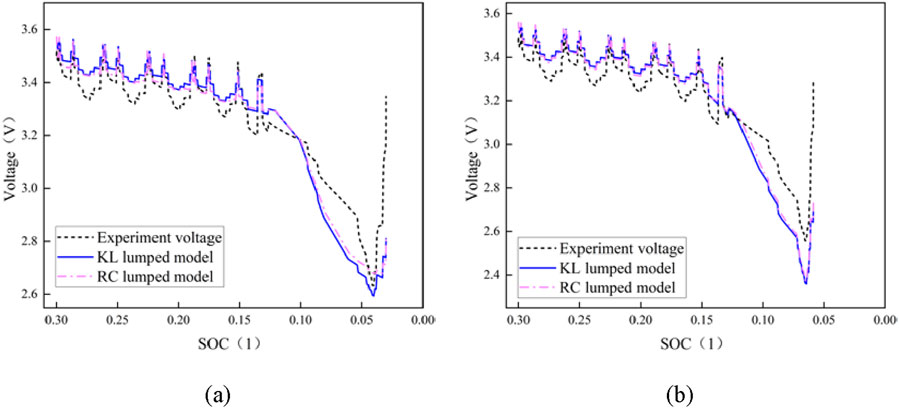
Figure 9. Predictive voltage and test voltage of RC and KL model when DOD = 70%. (a) Voltage curve comparison at SOH = 1; (b) Voltage curve comparison at SOH = 95%.

The comparison between the predicted voltage and the test voltage of the two lumped semi-empirical models when the DOD = 60% is shown in Figure 8. As shown in the figure, the overall trend of the two models is satisfactory and the numerical consistency is fair. However, there is a large error in the prediction voltage at the end of the cycle in the suburbs of NEDC. The SOH = 1 model predicted a significant fluctuation in the voltage curve, with a maximum prediction error of 492 mV.

The comparison between the predicted voltage and the test voltage of two lumped semi-empirical models when DOD = 70% is shown in Figure 9. The graph reveals that the overall trend of the prediction of the two models is unsatisfactory when DOD = 70% and the initial SOC is low. The model predicts a violent overall fluctuation of the voltage curve when the SOH = 1. The predicted voltage is feebly consistent with the test voltage under NEDC conditions, and the maximum prediction error is around 576 mV.

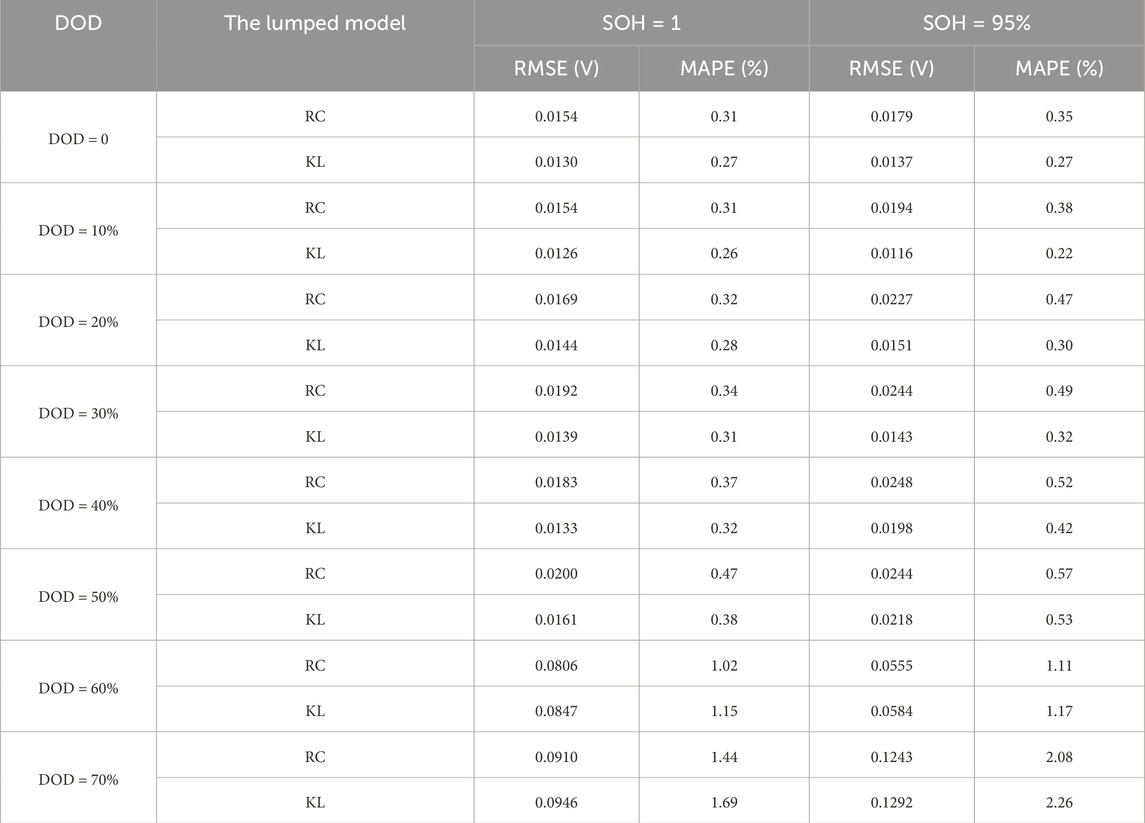
To analyze the performance of the two lumped semi-empirical models more intuitively, the RMSE and MAPE values of the two models under different aging conditions and different depths of discharge are presented in Table 3.

Table 3

Table 3. Model prediction error values under different DOD.

According to the RMSE and MAPE values in Table 3, it can be seen that:

(1) The RMSE values of the two models are less than 0.13 V when the lithium-ion battery varied at different depths of discharge, and the MAPE values are all less than 3%. The prediction accuracy results are excellent, with high voltage prediction accuracy.

(2) The KL lumped model performs well with high prediction accuracy when the DOD of a lithium-ion battery in the same SOH fluctuated between 0% and 50%. The least difference in RMSE value is 24 mV, and the minimum difference in MAPE value is roughly 0.03% when compared to the RC lumped model. When the DOD varied from 60% to 70%, the performance of the RC lumped model is better and the prediction accuracy is higher. Compared with KL lumped model, the minimum difference of RMSE is 41 mV and the minimum difference of MAPE is 0.06%.

(3) Nevertheless, in Figures 4–8, as the DOD of the model increased, there is a significant difference between the predicted voltage of the model and the actual load voltage, and the prediction error value of the model also gradually increases. In addition, the error value is greater in the stage of dramatic change of load current and the end of discharge in NEDC working conditions. Due to the instability of chemical substances in the lithium-ion battery at this time, the identification parameters are unable to meet the low SOC variation range, resulting in a large inaccuracy in model prediction. Deep discharge of lithium-ion batteries will not be performed in order to avoid excessive discharge in practical applications. As a result, the lumped semi-empirical model offers a higher predictive ability for NEDC operating conditions based on achieving the SOC required for actual battery work.

5 SOC estimation of LIB based on the lumped semi-empirical model

Lithium-ion battery SOC is a critical evaluation index and one of the core components of BMS. Accurate SOC estimation can not only improve the efficiency of lithium-ion battery utilization, but also improve the performance of new energy vehicles. The state of charge of a lithium-ion battery can be defined from a variety of perspectives, including power and energy. More uniform is the SOC defined by the United States Advanced Battery Consortium (USABC) in the ‘Electric Vehicle Battery Experiment Manual’ from the point of view of power (Plett, 2019; Laboratory, 1996), that is, the ratio of the remaining power consumption of the battery at a certain discharge rate to the rated power under the same conditions. The corresponding calculation formula is given in Equation 13:

$SOC=\frac{Q_r}{Q_0}\times 100\%(13)$

Where Q_r is the remaining available electricity of the battery after a certain discharge rate discharge, Q₀ is the nominal capacity of the battery given by the battery manufacturer, namely, the rated capacity of the battery. This SOC concept, however, cannot be applied properly to lithium-ion batteries for long-term use (Liu et al., 2019). The available capacity of the battery steadily diminishes as the battery charge-discharge cycle increases under actual operating conditions. Reference (Wang et al., 2013) proposed a more accurate SOC definition, which can be expressed by Equation 14:

$SOC=\frac{Q_r}{Q_T}\times 100\%(14)$

Where Q_T is the constant current discharge lithium-ion battery discharge real-time capacity.

However, current experimental equipment and data acquisition devices cannot generate an accurate SOC value, and certain methods can only be used to estimate the data value. The lumped semi-empirical model provides a better overall prediction effect, according to the analysis above. Therefore, SOC can be predicted based on load voltage and current data and identified model parameters. The procedure is shown in Figure 10.

Figure 10

Figure 10. SOC estimation flow chart of lumped semi-empirical model.

As shown in the SOC estimation method procedure in Figure 10, the parameter identification is affected by the load training data set and the OCV-SOC curve. The load training data set and the OCV-SOC curve are connected to the battery’s aging state. Hence, this paper conducts experiments on the batteries in three states: unaging, mild aging, and serious aging, further explores the influence of battery aging factors on SOC estimation, and studies the high-precision SOC estimation method.

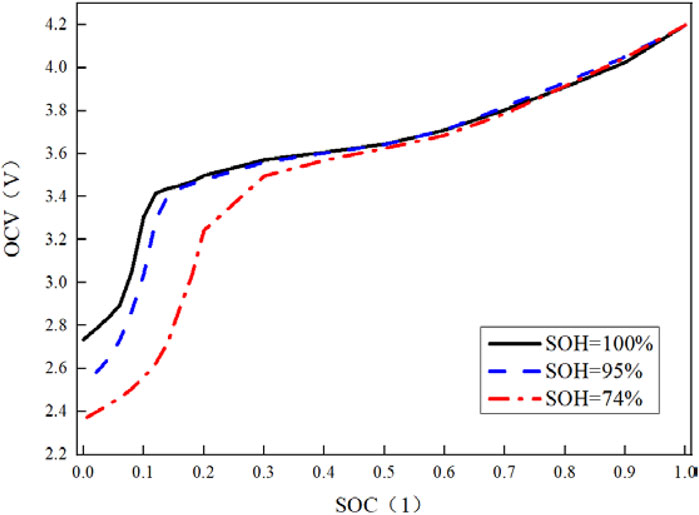
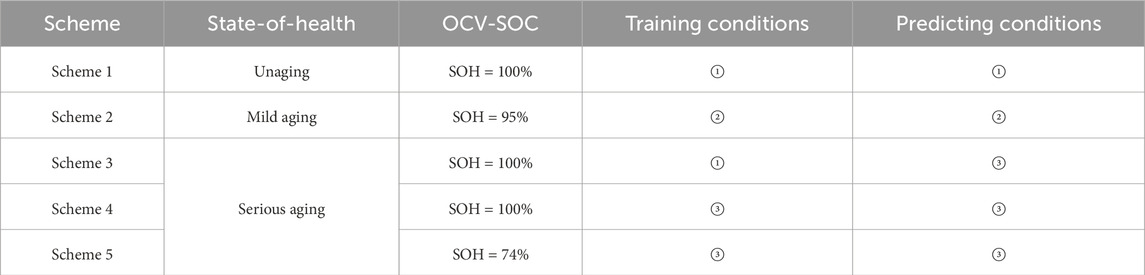
End of life (EOL) given that the battery capacity decays to 80% or 70% of its original capacity (Tang et al., 2019). The battery with SOH = 74% is selected to reflect the serious aging state, and the batteries with SOH = 100% and SOH = 95% are selected to reflect the unaging and mild aging state of the battery. HPPC test and NEDC discharge experiment were carried out for lithium-ion batteries in the above three states (each discharge experiment included two NEDC cycles). Based on the HPPC test, the OCV-SOC curve of different states of health is shown in Figure 11. The graph reveals that the relationship curves of the three states of health are relatively close under the medium and high SOC (about 0.4–1), and the deviation of the three relationship curves is greater under the low SOC (about 0–0.4). The lower the SOH is, the smaller the OCV value is under the same SOC. Apart from that, to facilitate the description of the NEDC cycle test of different healthy batteries, the NEDC cycle test at SOH = 100% is recorded as condition 1, the NEDC cycle test at SOH = 95% is recorded as condition 2, the NEDC cycle test at SOH = 74% is recorded as condition 3, and SOC prediction is carried out for the batteries in three states.

Figure 11

Figure 11. OCV-SOC curves of different states of health.

In the procedure of lithium-ion battery SOC prediction, it is necessary to identify the parameters of the lumped semi-empirical model. At present, the commonly used lithium-ion battery model parameter identification methods are mainly divided into two types: offline identification and online identification. Offline parameter identification mainly uses the experimental data collected after the battery cycle test and obtains the relevant parameters of the battery model through the optimization algorithms such as the genetic algorithm (Zhu et al., 2019) and particle swarm optimization algorithm (Chen and Li, 2021). In the SOC prediction, it is not necessary to adaptively adjust the parameters according to the real-time data, and the prediction efficiency is serviceable. By collecting voltage, current, and other data during the working cycle, the online parameter identification updates the parameters in the model in real-time, resulting in state variables that are close to the real state of the battery at any given time. The SOC value of the lithium-ion battery can be effectively predicted by using online identification to update the parameters (Tong et al., 2015; Tang et al., 2022).

Consequently, this paper investigates the SOC prediction method using both offline and online identifying methods. The load data set of the initial state of the lithium-ion battery and the OCV-SOC curve are selected for training the model based on the offline identification method to predict the SOC value of the aging battery in real-time during the offline identification process. To study SOC prediction methods of different aging states in detail, this paper proposes two different model training schemes. The first training scheme selects the real-time load data of the lithium-ion battery and the real-time OCV-SOC curve data to identify the parameters of the lumped semi-empirical model online and predict the SOC value of the real state of the battery. Considering the impracticality of the HPPC test in the actual use process, the OCV-SOC curve is generally not adjusted after the battery was set out from the factory, the second training scheme selects the OCV-SOC curve of the unaged state, and uses the load data of the original working condition and the real-time working condition to train, respectively. The offline and online models of the battery are constructed to predict the SOC value of the lithium-ion battery in the actual state. The specific research scheme is shown in Table 4.

Table 4

Table 4. SOC estimation scheme of lumped semi-empirical model.

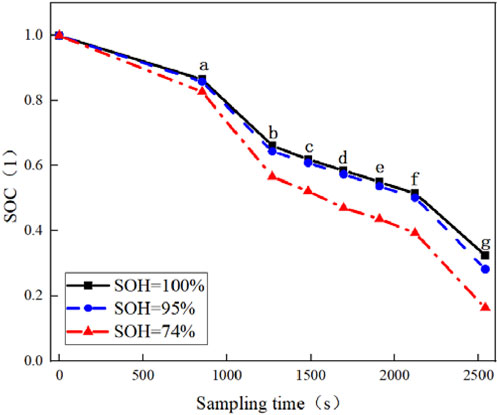
Multiple sampling points are chosen to analyze the SOC estimate performance in the time dimension to evaluate the model prediction ability of the entire NEDC cycle process. The first sampling point is the end time of the four urban cycles of the first NEDC cycle (marked as a), and the second sampling point is the end time of the first NEDC cycle (marked as b); To further analyze the SOC estimation accuracy of a low state of charge, for the second NEDC cycle, four urban cycle ending times are selected as the sampling points (marked as c, d, e, f), and the second NEDC cycle ending time is denoted as the sampling point g.

Based on the accurate definition of SOC in the actual working condition, combined with the discharge experimental data of the NEDC working condition, the experimental SOC value (SOC_E) of the lithium-ion battery is calculated as the real SOC result. Compared with the predicted SOC value (SOC_P) by the lumped semi-empirical model, the relative error (RE) of the two is calculated by Equation 15, as shown in Figure 13.

$RE=\left|\frac{SO{C}_E-SO{C}_P}{SO{C}_E}\right|(15)$

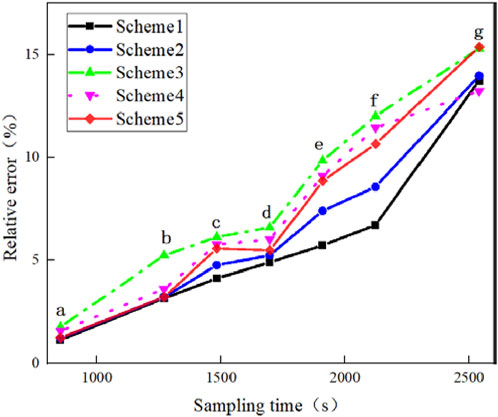
From Figures 12, 13:

(1) During the experiment, from full to low state of charge, the SOC of the three types of batteries decline. The more serious the battery’s aging state is, the more visible the decreasing trend is. With the decrease of SOC and the DOD of the battery increases, the relative error of SOC prediction increases gradually. The worse the SOH of the battery is, the greater the overall prediction error is.

(2) At sampling points a, b, c and d, the SOC prediction results of the five schemes are in terrific agreement with the experimental results, and the prediction error is comparatively small. Among them, for 100% and 95% of SOH batteries, the relative error values of the four sampling points are kept within 5%; for 74% of SOH batteries, the relative error values of the four sampling points are kept within 7%. In the middle and high charge intervals during this sampling stage of the battery, the SOC declined from 100% to nearly 50%, showing that the prediction approach based on the lumped semi-empirical model has better SOC prediction accuracy.

(3) At the sampling points e, f, and g, the SOC prediction results of the five schemes are in weak agreement with the experimental results, and the prediction error is larger. For 100% and 95% healthy batteries, the relative error of SOC prediction at times e and f is within 9%, and the relative error at g has reached 13.96%. For 74% healthy battery, the SOC prediction error at times e and f is within 12%, and the relative error at g has reached 15.38%. In this sampling stage, the SOC of 100% and 95% healthy state batteries have decreased from 50% to 35%, and the SOC of 74% healthy state batteries has decreased from 42% to 12%. The battery has a high DOD and a low charge state and the lumped semi-empirical model’s SOC prediction error is higher.

Figure 12

Figure 12. Real SOC curves of different SOH lithium-ion batteries.

Figure 13

Figure 13. Relative error of SOC estimation at each sampling point.

According to the battery reaction mechanism, the chemical instability of the battery increases, and the internal loss of the battery increases primarily when the battery DOD was high. As shown from Figures 4–8 the calculation results of the lumped semi-empirical model fluctuate greatly and the prediction error is relatively large in the low-charge interval, indicating that the model identification parameters had restricted accuracy for the characterization of the low SOC of the battery, which led to a significant increase in the prediction error of the battery SOC under the low state of charge. Therefore, the unified model parameter identification results are used to define the battery lumped semi-empirical model. Although it can better reflect the overall performance of the battery, the SOC prediction accuracy at different times is constrained due to the limited local representation ability.

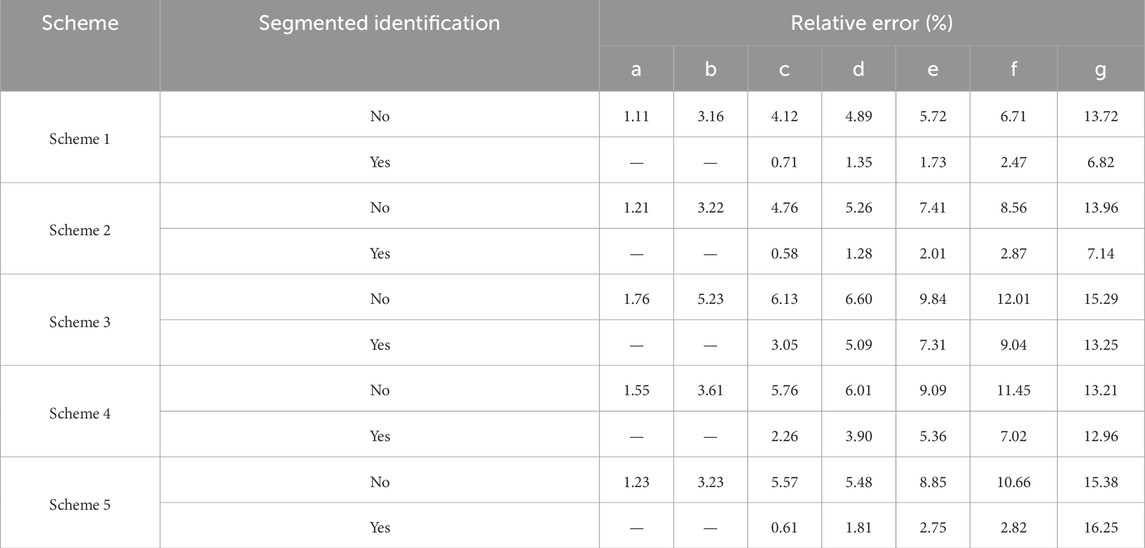
This paper utilizes the idea of segmented training and offers a SOC prediction method based on segmented identification to increase local SOC prediction accuracy, particularly low state of charge prediction accuracy. Namely, the data set of the battery is partitioned according to the SOC. In different charge intervals, the corresponding load data are used for training to obtain the battery model parameters suitable for the current charge interval, then the SOC of the corresponding charge interval is predicted. Considering that point c is approximately corresponding to the 60% SOC, the SOC prediction error before the point is little and the prediction error after the point is large, the sampling point c is selected as the segmentation point of the model SOC prediction. Therefore, the data after point c are trained and predicted. The calculation results before and after the improvement of the SOC prediction method are shown in Table 5.

Table 5

Table 5. The calculation results of the SOC prediction method.

It can be found from the relative error value in Table 5 that:

(1) After segmented training and prediction, the SOC prediction error values of each scheme are significantly reduced. After segmented training, the SOC estimation accuracy for 100% and 95% of SOH batteries is significantly improved. With improved prediction accuracy, the smallest estimation error is less than 1%, and the maximum estimation error is less than 8%. For 74% of the SOH battery, the SOC prediction accuracy has also been significantly improved after segmented training, especially in Scheme 5. It demonstrates that segmented training can improve the accuracy and robustness of SOC prediction while also being well-adapted to the online identification model.

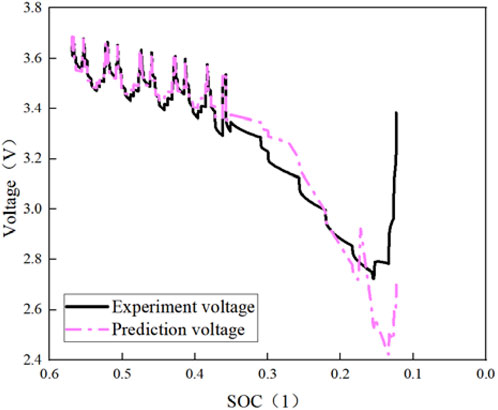
(2) Although the prediction method based on segmented identification effectively improves the SOC prediction accuracy, the prediction error at the sampling point g is still large, especially for 74% of the SOH battery. The relative prediction error is more than 10%. At this time, the actual SOC of the battery is about 12%, which is in the deep state of discharge. The electrochemical reaction fluctuates extremely, causing the model prediction performance to be unstable, and the aging state of the battery further aggravates the problem. As shown in Figure 14, there is a significant difference between the predicted voltage of the model and the actual voltage near the g point, indicating that the characterization accuracy of the lumped semi-empirical model is inadequate at that moment, which leads to a higher SOC prediction error.

(3) It should be noted that to improve the battery life, according to the calculations and operation experience, the battery works in the middle and low DOD range for a long time in practical work. Corresponding to this experiment, the best working range of the battery is before the d sampling point. In this interval, the prediction error of each method is greatly improved by segment identification. For 100% and 95% of SOH batteries, the maximum prediction error is only 1.35%. For 74% of the SOH battery, method 3 has the largest prediction error, which is controlled within 5.09%; method 5 has the smallest prediction error, which is controlled within 1.81%. It demonstrates that the lumped semi-empirical model based on segmented identification is suitable for unaged, mildly aged, and severely aged batteries, and that it has excellent accuracy and robustness in SOC prediction, meeting the engineering needs.

(4) For 74% of SOH battery, SOC estimation accuracy of schemes 3, 4, and 5 increases in turn. It shows that compared with offline identification, the SOC prediction method based on online identification had better accuracy, fewer identification parameters of lumped semi-empirical model, and higher efficiency of online identification. Based on the real-time OCV-SOC curve and load data for online identification, the obtained lumped semi-empirical model reflects the real-time state of the battery more accurately, which is conducive to the improvement of SOC prediction accuracy. However, considering that the real-time OCV-SOC curve of the battery is difficult to obtain in the actual working process, although scheme 5 has the highest accuracy, it is not conducive to engineering application. In contrast, although the prediction accuracy of scheme 4 is slightly lower than that of scheme 5, it is not necessary to obtain the OCV-SOC curve in real-time. Online identification based on real-time load data can receive more accurate SOC prediction results, which is more suitable for engineering applications.

Figure 14

Figure 14. Segmented training model predictive voltage.

To comprehensively evaluate the performance of the SOC estimation method proposed in this paper, four different SOC estimation methods were used for verification. Unaged batteries and real-time OCV-SOC curve data were selected for online parameter identification of the lumped semi-empirical model. To simplify the description of the various SOC estimation methods, the method based on the RC lumped model and the OCV-SOC curve is designated as RC-SOC. Similarly, the methods based on the KL lumped model and the first-order ECM for SOC estimation are designated as KL-SOC and ECM-SOC, respectively. The method based on the RC lumped model and EKF is designated as RC-EKF. True SOC values were calculated using the ampere-hour integration method. Table 6 provides a comparison of the error and performance of different SOC estimation methods.

Table 6

Table 6. Comparison of errors and performance of different SOC estimation methods.

According to Table 6:

(1) The RC-SOC and KL-SOC methods proposed in this paper, compared to the ECM-SOC method, in estimation accuracy: RMSE is reduced by 48.02% and 33.17%, and MAPE is reduced by 40.42% and 33.53%, respectively. In terms of computational burden: execution time increases by 0.06 s and 0.01 s, while memory usage increases by 4 KB and 13KB, respectively. This may be because the ECM-SOC method uses a first-order ECM model, which only considers ohmic polarization and concentration polarization during model construction, without accounting for activation polarization.

(2) The RC-EKF-based method demonstrates the highest accuracy, with the RMSE value improving by 49.52% at least compared to the other three methods. However, the accuracy improvement is due to the introduction of the Kalman filtering algorithm, which reduces errors through iterative optimization. Due to the integration of Kalman filtering, execution time and memory usage increase significantly, resulting in the highest computational burden. In contrast, the method proposed in this paper maintains practical accuracy while avoiding the additional consumption associated with filtering algorithms.

6 Conclusion

In this paper, the lumped semi-empirical model is used to study the SOC prediction method for lithium-ion batteries under complex conditions. Considering the three influencing factors of SOH, DOD, and working load, the NEDC experiment of ternary lithium-ion batteries under different states of health and depths of discharge is carried out, and the universality and robustness of the lumped semi-empirical model are analyzed. On this basis, a SOC prediction method based on a lumped semi-empirical model is proposed, and the proposed method’s accuracy and applicability are demonstrated using unaging, mild aging, and serious aging batteries as application objects. At the same time, aiming at the problem of large SOC prediction error in a low state of charge, the proposed method is improved by using the segmented identification method. The main conclusions are as follows:

(1) The two lumped semi-empirical models are applicable to the NEDC cycle of ternary lithium-ion batteries under different states of health and depths of discharge. Not only are the model parameters smaller, but the online identification efficiency is also higher, making it more suitable for engineering applications. Relatively speaking, for lithium-ion batteries with different states of health, the model based on particle diffusion has better prediction ability and fewer required parameters at lower DOD. When the DOD was above 60%, the model based on RC form has better prediction ability.

(2) The SOC prediction method based on the lumped semi-empirical model has better SOC estimation accuracy in the medium and high state of charge of the battery. Among them, the online identification based on real-time OCV-SOC curve and load data has the highest SOC prediction accuracy. Based on the initial OCV-SOC curve and real-time load data, more accurate SOC prediction results can also be obtained. Considering that the OCV-SOC curve is not easy to obtain in the actual working process, the second method has stronger engineering applicability.

(3) The improved SOC prediction method based on segmented identification can significantly improve the SOC prediction accuracy of each sampling point. This approach provides higher calculation accuracy for unaged and mildly aged batteries at high, medium, and low charge states. For seriously aged batteries, the prediction accuracy of this method is better under high and medium states of charge, but it still has to be improved under a low state of charge. Since the operation range of the battery is usually in the middle and low DOD, the proposed method still has high engineering applicability.

(4) Verification was performed using various SOC estimation methods. The results indicate that the proposed method not only requires less computational power compared to filtering methods but also achieves higher accuracy than traditional lightweight methods, thereby striking an optimal balance between “accuracy and efficiency.”

This paper focuses on various influencing factors in the actual working conditions, analyzes the characteristics of the lumped semi-empirical model, and studies the SOC prediction method on this basis, which provides a feasible path for the state estimation of lithium-ion batteries under complex working conditions. However, the segmentation identification research is insufficient. Artificial segmentation is currently primarily based on experience. Adaptive segmentation identification and prediction based on machine learning will be tested in the future. Simultaneously, the accuracy of battery SOC prediction under a low state of charge will be continually investigated. Furthermore, future research will focus on investigating the effects of extreme temperatures and calendar-cycle coupled aging, as well as assessing the practical applicability of the proposed method in actual BMS.

Data availability statement

The original contributions presented in this study are included in the article, and further inquiries can be directed to the corresponding author.

Author contributions

ML: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by National Major Science and Technology Project on Aero-Engine and Gas Turbine, grant number J2019-V0009-0103.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

BMS, Battery management system; CC-CV, Constant current and constant voltage; DOD, Depth of discharge; du-al-EKF, Dual Extended Kalman Filter; DLS, Damped Least Squares; EC, Equivalent circuit; EOL, End of life; ECM, Equivalent circuit model; HPPC, Hybrid pulse power characterization; LIBs, Lithium-ion batteries; MAPE, Mean absolute percentage error; NEDC, New European driving cycle; OCV, Open circuit voltage; RC, Resistance-capacitance; RMSE, Root mean square error; RE, Relative error; SOC, State-of-charge; SOH, State-of-health; SOP, State-of-power; SOF, State-of-function; USABC, United States Advanced Battery Consortium.

References

Bizeray, A. M., Duncan, S. R., and Howey, D. A. (2015). Li-Ion battery state estimation using a pseudo two-dimensional electrochemical model-based extended kalman filter with temperature and degradation effects. ECS Meet. Abstr., 85. doi:10.1149/ma2015-01/1/85

CrossRef Full Text | Google Scholar

Budil, D. E., Sanghyuk, L., Saxena, S., and Freed, J. H. (1996). Nonlinear-least-squares analysis of slow-motion EPR spectra in one and two dimensions using a modified levenberg-marquardt algorithm. J. Magnetic Reson. Ser. A 120, 155–189. doi:10.1006/jmra.1996.0113

CrossRef Full Text | Google Scholar

Buteau, S., Dahn, D. C., and Dahn, J. R. (2018). Explicit conversion between different equivalent circuit models for electrochemical impedance analysis of lithium-ion cells. J. Electrochem. Soc. 165, A228–A234. doi:10.1149/2.0841802jes

CrossRef Full Text | Google Scholar

Chen, L. (2016). A high-order modified levenberg-marquardt method for systems of nonlinear equations with fourth-order convergence. Appl. Math. Comput. 285, 79–93. doi:10.1016/j.amc.2016.03.031

CrossRef Full Text | Google Scholar

Chen, C., and Li, C. (2021). Process synthesis and design problems based on a global particle swarm optimization algorithm. IEEE Access 9, 7723–7731. doi:10.1109/ACCESS.2021.3049175

CrossRef Full Text | Google Scholar

Chen, L., Lü, Z., Lin, W., Li, J., and Pan, H. (2018a). A new state-of-health estimation method for lithium-ion batteries through the intrinsic relationship between ohmic internal resistance and capacity. Meas. J. Int. Meas. Con-federation. 116, 586–595. doi:10.1016/j.measurement.2017.11.016

CrossRef Full Text | Google Scholar

Chen, J., Ouyang, Q., Xu, C., and Su, H. (2018b). Neural network-based state of charge observer design for lithium-ion batteries. IEEE Trans. Control Syst. Technol. 26, 313–320. doi:10.1109/TCST.2017.2664726

CrossRef Full Text | Google Scholar

Doughty, D. H., and Crafts, C. C. (2006). FreedomCAR: electrical energy storage system abuse test manual for electric and hybrid electric vehicle applications (No. SAND2005-3123). Albuquerque, NM, and Livermore, CA: Sandia National Laboratories (SNL). doi:10.2172/889934

CrossRef Full Text | Google Scholar

Ekström, H., Fridholm, B., and Lindbergh, G. (2018). Comparison of lumped diffusion models for voltage prediction of a lithium-ion battery cell during dynamic loads. J. Power Sources. 402, 296–300. doi:10.1016/j.jpowsour.2018.09.020

CrossRef Full Text | Google Scholar

Fan, J. (2012). The modified levenberg-marquardt method for nonlinear equations with cubic convergence. Math. Comput. 81, 447–466. doi:10.1090/s0025-5718-2011-02496-8

CrossRef Full Text | Google Scholar

Fan, J. (2013). Accelerating the modified levenberg-marquardt method for nonlinear equations. Math. Comput. 83, 1173–1187. doi:10.1090/s0025-5718-2013-02752-4

CrossRef Full Text | Google Scholar

Fang, P., Zhang, A., Wang, D., Sui, X., and Yin, L. (2024). Lumped model of Li-ion battery considering hysteresis effect. J. Energy Storage 86, 111185. doi:10.1016/j.est.2024.111185

CrossRef Full Text | Google Scholar

Fotouhi, A., Auger, D. J., Propp, K., Longo, S., and Wild, M. (2016). A review on electric vehicle battery modelling: from lithium-ion toward lithium-sulphur. Renew. Sust. Energy Rev. 56, 1008–1021. doi:10.1016/j.rser.2015.12.009

CrossRef Full Text | Google Scholar

Gambhire, P., Hariharan, K. S., Khandelwal, A., Kolake, S. M., Yeo, T., and Doo, S. (2014). A physics based reduced order aging model for lithium-ion cells with phase change. J. Power Sources. 270, 281–291. doi:10.1016/j.jpowsour.2014.07.127

CrossRef Full Text | Google Scholar

Gao, Y., Liu, K., Zhu, C., Zhang, X., and Zhang, D. (2022). Co-Estimation of state-of-charge and State-of- health for lithium-ion batteries using an enhanced electrochemical model. IEEE Trans. Ind. Electron. 69, 2684–2696. doi:10.1109/TIE.2021.3066946

CrossRef Full Text | Google Scholar

Ge, M. F., Liu, Y., Jiang, X., and Liu, J. (2021). A review on state of health estimations and remaining useful life prognostics of lithium-ion batteries. Meas. J. Int. Meas. Confed. 174, 109057. doi:10.1016/j.measurement.2021.109057

CrossRef Full Text | Google Scholar

Gebregergis, A., Pillay, P., Bhattacharyya, D., and Rengaswemy, R. (2009). Solid oxide fuel cell modeling. IEEE Trans. Ind. Electron. 56, 139–148. doi:10.1109/TIE.2008.2009516

CrossRef Full Text | Google Scholar

Gong, D., Gao, Y., and Kou, Y. (2021). Parameter and state of charge estimation simultaneously for lithium-ion battery based on improved open circuit voltage estimation method. Energy Technol. 9. doi:10.1002/ente.202100235

CrossRef Full Text | Google Scholar

Hannan, M. A., Lipu, M. S. H., Hussain, A., and Mohamed, A. (2017). A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: challenges and recommendations. Renew. Sust. Energy Rev. 78, 834–854. doi:10.1016/j.rser.2017.05.001

CrossRef Full Text | Google Scholar

He, Y., Wu, J., Xie, G., Hong, X., and Zhang, Y. (2021). Data-driven relative position detection technology for high-speed maglev train. J. Int. Meas. Confed. 180, 109468. doi:10.1016/j.measurement.2021.109468

CrossRef Full Text | Google Scholar

Huang, M. H., Yan, Y. G., and Zhu, L. M. (2014). SOC estimation of lithium iron phosphate battery based on improved BP neural network. Journal of Wuhan University of Technology (Information & Management Engineering), 36, 790–793. doi:10.3963/j.issn.2095-3852.2014.06.014

CrossRef Full Text | Google Scholar

Jannesari, H., Emami, M. D., and Ziegler, C. (2011). Effect of electrolyte transport properties and variations in the morphological parameters on the variation of side reaction rate across the anode electrode and the aging of lithium ion batteries. J. Power Sources. 196, 9654–9664. doi:10.1016/j.jpowsour.2011.07.026

CrossRef Full Text | Google Scholar

Jia, Y. J., Da Xie, Y. J. G., Ai, Q., Jin, Z. J., and Gu, J. (2011). Classification and characteristics of equivalent circuit models for EV’s battery. Power&Energy 32 (6), 516–521.

Google Scholar

Karavalakis, G., Alvanou, F., Stournas, S., and Bakeas, E. (2009). Regulated and unregulated emissions of a light duty vehicle operated on diesel/palm-based methyl ester blends over NEDC and a non-legislated driving cycle. Fuel 88, 1078–1085. doi:10.1016/j.fuel.2008.11.003

CrossRef Full Text | Google Scholar

Laboratory, I. N. E. (1996). USABC electric vehicle battery test procedures manual. Revision 2, Office of Scientific and Technical Information Technical Reports.

Google Scholar

Li, J., and Xiao, H. (2022). Review on modeling of lithium-ion battery. Energy Storage Sci. Technol. 11, 697–703. doi:10.19799/j.cnki.2095-4239.2021.0450

CrossRef Full Text | Google Scholar

Li-ping, S., Shun-li, W., Zhan-feng, L., Shi-jun, F., and Cheng-cheng, X. (2014). Airborne battery SOC estimate method study basedon dis-Charge test method. doi:10.13234/j.issn.2095-28

CrossRef Full Text | Google Scholar

Liu, J. (2020). Accelerated life test and model study of lithium cobalt battery. Southwest University of Science and Technology. doi:10.27415/d.cnki.gxngc.2020.000400

CrossRef Full Text | Google Scholar

Liu, M., He, M., Qiao, S., Liu, B., Cao, Z., and Wang, R. (2019). A high-order state-of-charge estimation model by cubature particle filter. J. Int. Meas. Confed. 146, 35–42. doi:10.1016/j.measurement.2019.05.040

CrossRef Full Text | Google Scholar

Liu, Z., Liu, S., and Zheng, T. (2022). The influence of NEDC and CATC type approval test procedure on the E-range of battery electric vehicles. Energy Rep. 8, 36–42. doi:10.1016/j.egyr.2021.11.004

CrossRef Full Text | Google Scholar

Luo, Y., Qi, P., Huang, H., Wang, J., Wang, Y., and Li, P. (2020). Study on battery SOC estimation by ampere-hour integral method with capacity correction. Automotive Eng. 42 (5), 681–687. doi:10.19562/j.chinasae.qcgc.2020.05.017

CrossRef Full Text | Google Scholar

Nejad, S., Gladwin, D. T., and Stone, D. A. (2016). A systematic review of lumped-parameter equivalent circuit models for real-time estimation of lithium-ion battery states. J. Power Sources. 316, 183–196. doi:10.1016/j.jpowsour.2016.03.042

CrossRef Full Text | Google Scholar

Ni, M., Leung, M. K. H., and Leung, D. Y. C. (2015). Electrochemistry modeling of proton exchange membrane (PEM) water electrolysis for hydrogen production.

Google Scholar

Ouyang, M., Liu, G., Lu, L., Li, J., and Han, X. (2014). Enhancing the estimation accuracy in low state-of-charge area: a novel onboard battery model through surface state of charge determination. J. Power Sources. 270, 221–237. doi:10.1016/j.jpowsour.2014.07.090

CrossRef Full Text | Google Scholar

Plett, G. L. (2019). Review and some perspectives on different methods to estimate state of charge of lithium-ion batteries. J. Autom. Safety Energy 10 (3), 249. doi:10.3969/j.issn.1674-8484.2019.03.001

CrossRef Full Text | Google Scholar

Ren, L., Sun, Y., Wang, H., and Zhang, L. (2018). Prediction of bearing remaining useful life with deep convolution neural network. IEEE Access 6, 13041–13049. doi:10.1109/ACCESS.2018.2804930

CrossRef Full Text | Google Scholar

Seo, M., Song, Y., Kim, J., Paek, S. W., Kim, G. H., and Kim, S. W. (2021). Innovative lumped-battery model for state of charge estimation of lith-ium-ion batteries under various ambient temperatures. Energy 226, 120301. doi:10.1016/j.energy.2021.120301

CrossRef Full Text | Google Scholar

Sun, D. (2021). Research on SOC and capacity estimation methods of power lithium-ion battery. Zhejiang University. doi:10.27461/d.cnki.gzjdx.2021.000455

CrossRef Full Text | Google Scholar

Sung, W., and Shin, C. B. (2015). Electrochemical model of a lithium-ion battery implemented into an automotive battery management system. Comput. Chem. Eng. 76, 87–97. doi:10.1016/j.compchemeng.2015.02.007

CrossRef Full Text | Google Scholar

Tan, X.-Q., Wu, Z.-Q., Ye, Z., Hao, Z., and Li, J.-J. (2010). Solid oxide fuel cell lumped modeling and simulation. 30. doi:10.13334/j.0258-8013.pcsee.2010.17.017

CrossRef Full Text | Google Scholar

Tang, S., Wang, F., Sun, X., Xu, X., Yu, C., and Si, X.(2022). Unbiased parameters estimation and mis-specification analysis of wiener pro-cess-based degradation model with random effects. Appl. Math. Model. 109, 134–160. doi:10.1016/j.apm.2022.03.039

CrossRef Full Text | Google Scholar

Tang, X., Wang, Y., Yao, K., He, Z., and Gao, F. (2019). Model migration based battery power capability evaluation considering uncertainties of temperature and aging. J. Power Sources. 440, 227141. doi:10.1016/j.jpowsour.2019.227141

CrossRef Full Text | Google Scholar

Tong, S., Klein, M. P., and Park, J. W. (2015). Online optimization of battery open circuit voltage for improved state-of-charge and state-of-health estimation. J. Power Sources. 293, 416–428. doi:10.1016/j.jpowsour.2015.03.157

CrossRef Full Text | Google Scholar

Verbrugge, M. W. (2008). Adaptive characterization and modeling of electrochemical energy storage devices for hybrid electric vehicle applications. 1–108. doi:10.1007/978-0-387-49582-8_8

CrossRef Full Text | Google Scholar

Waag, W., Käbitz, S., and Sauer, D. U. (2013). Application-specific parameterization of reduced order equivalent circuit battery models for improved accuracy at dynamic load. Meas. J. Int. Meas. Confed. 46, 4085–4093. doi:10.1016/j.measurement.2013.07.025

CrossRef Full Text | Google Scholar

Wang, H., Liu, Y., Fu, H., and Li, G. (2013). Estimation of state of charge of batteries for electric vehicles. Int. J. Control Autom. 6 (2), 185–194. Available online at: https://www.earticle.net/Article/A207647.

Google Scholar

Wang, P., Fan, J., Ou, Y., Li, Z., Wang, Y., Deng, B., et al. (2020). A comparative study of machine learning based modeling methods for lithium-ion battery. IOP Conf. Ser. Earth Environ. Sci. 546, 052045. doi:10.1088/1755-1315/546/5/052045

CrossRef Full Text | Google Scholar

Wang, S., Verbrugge, M., Wang, J. S., and Liu, P. (2012). Power prediction from a battery state estimator that incorporates diffusion resistance. J. Power Sources. 214, 399–406. doi:10.1016/j.jpowsour.2012.04.070

CrossRef Full Text | Google Scholar

Wei, J., Dong, G., and Chen, Z. (2018). Remaining useful life prediction and state of health diagnosis for lithium-ion batteries using particle filter and support vector regression. IEEE Trans. Ind. Electron. 65, 5634–5643. doi:10.1109/TIE.2017.2782224

CrossRef Full Text | Google Scholar

Xu, X., Tang, S., Yu, C., Xie, J., Han, X., and Ouyang, M. (2021). Remaining useful life prediction of lithium-ion batteries based on wiener process under time-varying temperature condition. Reliab. Eng. Syst. Saf. 214, 107675. doi:10.1016/j.ress.2021.107675

CrossRef Full Text | Google Scholar

Xu, X., Yu, C., Tang, S., Sun, X., Si, X., and Wu, L.(2019). Remaining useful life prediction of lithium-ion batteries based on wiener processes with considering the relaxation effect. Energies 12, 1685. doi:10.3390/en12091685

CrossRef Full Text | Google Scholar

Zhang, C., Allafi, W., Dinh, Q., Ascencio, P., and Marco, J. (2018). Online estimation of battery equivalent circuit model parameters and state of charge using decoupled least squares technique. Energy 142, 678–688. doi:10.1016/j.energy.2017.10.043

CrossRef Full Text | Google Scholar

Zheng, J. (2018). Research on electrochemical performance and optimization of lithium-ion batteries based on the mechanism model. Harbin: Harbin Institute of Technology.

Google Scholar

Zhu, Q., Xu, M., Liu, W., and Zheng, M. (2019). A state of charge estimation method for lithium-ion batteries based on fractional order adaptive extended kalman filter. Energy 187, 115880. doi:10.1016/j.energy.2019.115880

CrossRef Full Text | Google Scholar