Research on parameter identification of high-head hydropower MMC-HVDC system based on Sobol sensitivity analysis and adaptive cuckoo search algorithm

With the increasing complexity of high-head hydropower systems and the rapid development of flexible DC transmission technology, accurate electromagnetic transient (EMT) modeling of hydropower flexible DC systems is essential. To address the challenge of parameter acquisition, this manuscript proposes a method based on Sobol sensitivity analysis and an adaptive cuckoo search (ACS) algorithm for parameter identification. First, an EMT model is constructed, and Sobol sensitivity analysis is used to evaluate parameter influence. Key parameters with high sensitivity indices are selected for further optimization. Finally, the ACS algorithm identifies these parameters with high accuracy. The case study results show that ACS outperforms both standard cuckoo search and particle swarm optimization (PSO) algorithms in terms of convergence speed and identification accuracy. Simulation results confirm the validity of the identified parameters across various operating conditions, demonstrating the method’s effectiveness and generalizability.

1 Introduction

With the continuous growth of global energy demand and the tightening of environmental protection regulations, hydropower—characterized by its clean, renewable, and sustainable nature—has increasingly become a vital component of strategic infrastructure in modern power systems (Bladh, 2012). To enhance energy utilization efficiency and optimize the configuration of the AC power grid, hydropower transmission via modular multilevel converter-based high-voltage direct current (MMC-HVDC) systems has gained considerable attention. In addition, with the continuous expansion of hydropower development capacity, numerous high-head and large-capacity hydropower units have been commissioned, posing new challenges to the reliable operation of hydropower transmission systems. To accurately describe the dynamic characteristics of high-head hydropower transmission via MMC-HVDC systems, an electromagnetic transient (EMT) simulation model is required rather than a simplified phasor-domain model. Phasor-domain models, although computationally efficient and suitable for long-term electromechanical studies, neglect high-frequency switching harmonics, fast control dynamics, and electromagnetic interactions that are prominent in MMC-based HVDC systems—particularly during fault transients and rapid control actions. The EMT model, by resolving sub-millisecond time steps, captures detailed converter switching behavior, control-loop dynamics, and the coupling between electrical and mechanical subsystems, which are critical for accurately assessing transient stability and dynamic performance under severe disturbances. Although EMT simulations incur substantially higher computational costs compared to phasor-domain models, the computational burden in this study is mitigated through Sobol sensitivity analysis for parameter space reduction and the use of an Adaptive Cuckoo Search (ACS) algorithm optimized for faster convergence. As a dominant part of the EMT model, the parameters in the model have a significant impact on the accuracy of the simulated response (Barros et al., 2003). Consequently, conducting high-precision identification of these parameters is not only theoretically significant for constructing accurate hydro-mechanical-electrical coupled models, but also of substantial practical value in enabling frequency regulation and peak shaving (Alvarez, 2020), fault prediction (Quintana and Van Cutsem, 1988), and stability analysis (Zarco and Exposito, 2000).

The main technical bottlenecks in parameter identification stem from the following complex characteristics: The foremost challenge lies in the inherently multi-physical coupling of unit dynamics, wherein dynamic responses are governed by the interplay among hydraulic, mechanical, and electrical domains (Zarco and Exposito, 2000), compounded by variations in operating conditions and coordinated control strategies (Rakpenthai et al., 2012). In high-head hydropower systems, such coupling is further complicated by phenomena like the water hammer effect in long penstocks, where rapid load changes induce pressure waves that interact with both the turbine and the electrical control system. These factors introduce significant uncertainty into model-based inverse parameter estimation. Furthermore, the control systems of hydropower units exhibit strong nonlinearity and hysteresis (Guo et al., 2014), for example, the nonlinear dead zones and rate-dependent hysteresis in turbine-governor servomotors, making traditional frequency-domain-based linear system identification approaches inadequate for capturing the unit’s dynamic stiffness matrix, thereby compromising identification fidelity (Rakpenthai et al., 2012; Petra et al., 2017). In addition, random disturbances in operational environments—such as non-stationary hydrological inputs and stochastic power grid load fluctuations—result in multi-source, non-stationary noise contamination of measured data (Zeng and Teng, 2011), greatly reducing the signal-to-noise ratio of input–output data pairs. A particularly critical challenge is the time-varying drift of system parameters, which poses a serious threat to model robustness (Milojević et al., 2018). Studies suggest the need for time-varying parameter identification frameworks with dynamic tracking capabilities (Mukherjee et al., 2020). By integrating online adaptive algorithms, continuous rolling updates to model parameters can be achieved, thereby enhancing identification accuracy over the entire lifecycle of the unit (Regulski et al., 2015). Addressing these issues necessitates the development of high-performance parameter identification methodologies.

To this end, researchers have explored a range of algorithms for parameter identification in hydro-turbine generator units, achieving notable progress. The majority of these approaches focus on improving global search capabilities, yet their time and space complexity remain largely unexplored.

For instance, an improved particle swarm optimization (PSO) algorithm introduced in Fang et al. (2011) leverages adaptive learning factors to enhance global search capability, significantly improving the tuning of PID controllers. However, the time complexity of this algorithm remains high, which limits its scalability for large systems. Another study (Liu et al., 2010) combined PSO with the uniform design method to optimize turbine governor parameters, demonstrating superior performance in complex systems. This approach has proven effective in improving parameter accuracy but struggles with higher computational demands, especially in systems with a large number of parameters.

Recent hybrid optimization strategies attempt to address these limitations. The hybrid moth-flame-PSO (HMFPSO) approach in Shaikh et al. (2023) integrates exploration-exploitation balancing mechanisms, achieving faster convergence in transmission line parameter estimation. While effective for mid-scale systems, its O(N²) complexity and sensitivity to control parameters hinder deployment in real-time large-grid scenarios. Similarly, grey wolf optimization (GWO) in Shaikh et al. (2021) reduces parameter dependencies but exhibits premature convergence when handling non-convex landscapes in three-phase power system.

Genetic Algorithms (GAs), as well-established global optimizers, have also found wide application in this domain. The method proposed in Gao et al. (2009), based on an enhanced GA incorporating chaotic mutation, achieved improved global search capability and was successfully applied to fluid transient process modeling. However, the time complexity for this method is O(N^2), which may limit its real-time application in large-scale systems. Similarly (Jiang et al., 2006), highlighted the GA’s effectiveness in PID parameter optimization, particularly in enhancing system stability and responsiveness. For multimodal optimization problems in hydro units, the Bacterial Foraging Optimization Algorithm (BFOA)—an algorithm inspired by bacterial foraging behavior—has demonstrated strong performance. In Kou et al. (2010), BFOA was used to identify turbine governor parameters, showing high robustness in handling complex scenarios, but its performance deteriorates when applied to large-scale systems due to its exponential time complexity.

Recently, Gravitational Search Algorithms (GSA) and their improved variants (IGSA) have emerged as efficient solutions for parameter identification. IGSA, as proposed in Chen et al. (2014a), integrates PSO’s velocity update mechanism with chaotic mutation, resulting in accelerated convergence and improved global search. The time complexity of IGSA is O(N log N), similar to PSO, yet it has shown faster convergence in practice. To address system uncertainties (Chen et al., 2017), proposed three novel identification approaches using distinct parameter observers based on system stability theorems, as well as an Ant Lion Optimizer (ALO)-based method. In this work, the ALO-based method demonstrated superior accuracy compared to PSO and GA-based methods, with the added benefit of reducing computational time, making it more efficient in real-time applications.

In turbine control system modeling (Zhang et al., 2018), presented a hybrid approach combining white-box mapping with a radial basis function (RBF) neural network. This method, particularly effective under data-scarce conditions, minimized reliance on large-scale testing, demonstrating practical viability. Finally (Chen et al., 2014b), focused on designing fractional-order PID controllers for turbine governor systems and employed a chaotic NSGA-II algorithm to optimize controller parameters. Results showed that fractional-order PID controllers outperformed traditional PID controllers in terms of control precision and response time, although the optimization process exhibits O(MN²) complexity, primarily dominated by its non-dominated sorting mechanism.

Collectively, these studies reveal three persistent challenges: (1) the complexity-accuracy trade-off in population-based algorithms, (2) poor generalization of hybrid strategies across varying power system topologies, and (3) limited theoretical guarantees for convergence in non-convex landscapes. This work addresses these gaps through a computationally constrained co-evolutionary framework, systematically optimizing time complexity while maintaining solution robustness for large-scale hydro-turbine systems. To address this critical gap, this work systematically reviews and analyzes existing PI algorithms for hydro-turbine units, focusing on identifying their inherent computational complexities and scalability limitations. We then propose a novel parameter identification method that integrates Sobol sensitivity analysis and an Adaptive Cuckoo Search (ACS) algorithm. The Sobol sensitivity analysis is used to calculate the sensitivity index of candidate parameters, from which dominant parameters with high sensitivity are selected for identification. Subsequently, ACS is employed to identify these dominant parameters efficiently. Finally, the accuracy of the proposed method is validated through a case study conducted on the CloudPSS simulation platform, demonstrating its effectiveness in reducing computational burden while maintaining high accuracy for high-head hydropower MMC-HVDC EMT model identification.

The remainder of the manuscript is presented in five sections. In Section 2, the EMT model of high-head hydropower transmission MMC-HVDC system is constructed. Section 3 introduces the screening method of dominant parameters according to the Sobol sensitivity analysis. The traditional CSA method and the ACS method are dis-cussed in Section 4. In Section 5, a simulation case is conducted. Section 6 concludes the manuscript.

2 Modeling of high-head hydropower MMC-HVDC system

2.1 System structure of large-capacity high-head hydropower units

As shown in Figure 1, large-capacity, high-head hydropower units integrated with an MMC-HVDC transmission system comprise a hydraulic turbine power generation system and a subsequent MMC-HVDC system. The hydro-turbine governing system, as a critical subsystem of the hydropower unit, is a typical closed-loop control system that mitigates the impact of internal and external disturbances on controlled variables while maintaining high control precision. This governing system can be further subdivided into three main components: the governor, the hydraulic servo system, and the unit-penstock system.

Figure 1

Figure 1. Large-capacity high-head hydropower units with MMC-HVDC transmission system.

2.1.1 Governor model

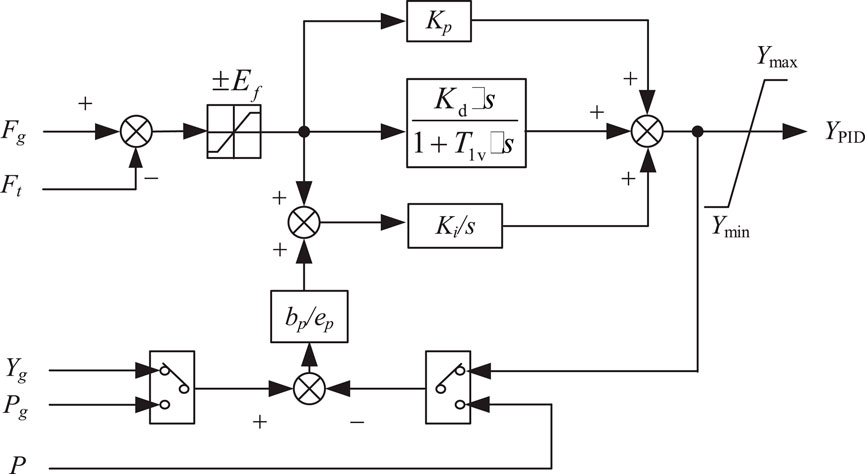
According to different control requirements, the governor has three operation modes under grid-connected conditions: frequency regulation, gate opening regulation, and power regulation. Frequency regulation is applied in no-load and isolated grid operation. Power regulation converts power deviation into flow setting through proportional-integral calculation to adjust turbine output power. Gate opening regulation is generally used in grid-connected operation. In high-head hydropower MMC-HVDC systems, gate opening regulation is prioritized because grid frequency stability is primarily maintained by the large interconnected AC system, allowing the hydro unit to focus on precise flow and torque control for optimal efficiency and rapid response during transient events. This mode also provides a more direct and measurable control input for parameter identification, reducing the influence of external grid frequency fluctuations and simplifying the modeling process. The turbine model established in this manuscript mainly focuses on gate opening regulation mode. While this choice enhances the accuracy and robustness of the identified parameters under typical grid-connected conditions, it should be noted that the model’s direct applicability to scenarios dominated by frequency or power regulation may require additional tuning of control loops to account for different feedback signals and operating objectives. The following figure shows the PID governor model of high-head turbine. In Figure 2, K_p is the proportional gain, K_i is the integral gain, and K_d is the derivative gain, T_1v is the differential time constant, E_f is the artificial frequency dead zone, b_p/e_p is the permanent slip coefficient, Y_PID is the regulator output, Y_max, Y_min is the regulator output limiting, F_t is the machine frequency, F_g is the frequency given, Y_g is the opening given, P_g is the power given, P is the unit power.

Figure 2

Figure 2. Overall block diagram of governor.

2.1.2 Hydraulic servo system model

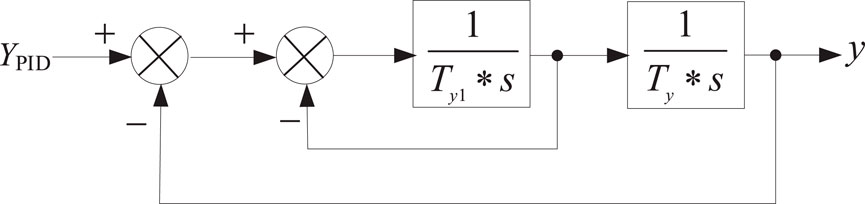
The hydraulic servo system converts electrical signals into mechanical displacement signals with operational force to drive the water guide mechanism. This adjusts the guide vanes’ opening (to increase or decrease water flow) by controlling the water passage. It typically employs a two-stage amplification configuration: the pilot valve-auxiliary servomotor assembly (first-stage amplification) and the main distributor valve-main servomotor assembly (second-stage amplification). When considering these two components as an integrated system, a typical auxiliary servomotor-type structure is generally adopted. The standard hydraulic servo system incorporating both stages can be represented by the model shown in Figure 3.

Figure 3

Figure 3. Overall block diagram of hydraulic servo system.

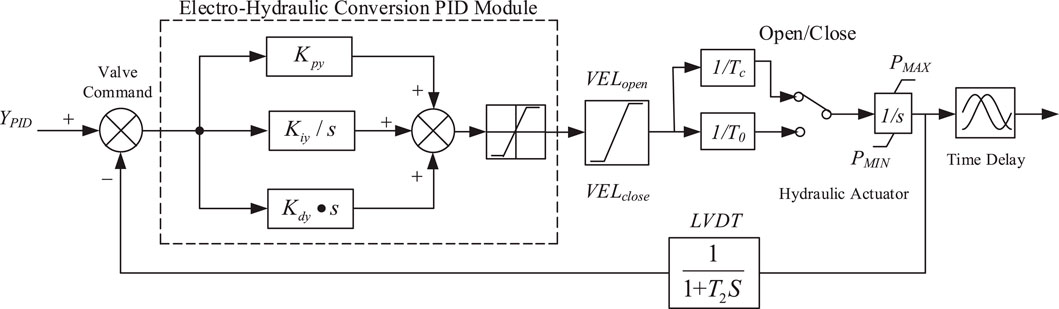
To prevent water hammer effects, both the opening and closing speeds of the servomotor are subject to certain limitations, and the opening and closing rates are typically not identical. Additionally, for simulation modeling purposes, a first-order integral amplification component is sufficient to characterize the servomotor’s operational behaviour. Therefore, the servo system can be represented by the model illustrated in Figure 4. In Figure 4, K_py, K_iy and K_dy represent proportional gain, integral gain and differential gain, respectively. VEL_open and VEL_close are the maximum opening speed and the maximum closing speed of the hydraulic servo motor, respectively. T_c and T₀ represent the closing time constant of the hydraulic actuator and the opening time constant of the hydraulic actuator, respectively. P_max and P_min are the maximum output power of prime mover and the minimum output power of prime mover, respectively. T₂ is the power delay time.

Figure 4

Figure 4. Block diagram of nonlinear hydraulic servo system.

2.1.3 Turbine-penstock system analytical model

It should be noted that an exact analytical model of hydraulic turbines is currently unavailable. This is primarily due to the highly nonlinear and multi-physics nature of turbine–waterway interactions, where hydraulic transients, turbulence, cavitation, and flow–structure coupling are difficult to capture in closed-form equations. The governing equations of fluid motion (Navier–Stokes equations) can be solved numerically via computational fluid dynamics (CFD), and in recent years, data-driven models based on machine learning have emerged as alternatives for capturing turbine behavior from operational data. However, both CFD and data-driven models present limitations for this study: CFD requires significant computational resources, making it impractical for iterative parameter identification in electromagnetic transient simulations, while purely data-driven approaches may lack physical interpretability and generalizability to off-design operating points. Under specific conditions, the dynamic behaviour of hydraulic turbines can be described by the following functional relationship, as shown in Equation 1.

$\left\{\begin{array}{l}{m}_t=f\left(y,\omega ,h\right)\\ q=g\left(y,\omega ,h\right)\end{array}\right.(1)$

Including opening y, flow q, head h, torque m, speed w and other variables, the turbine and diversion system can be modeled as a nonlinear function, where the opening serves as the input and the torque as the output.

The turbine is approximated as the output of the valve, and the nonlinear model of the turbine is given through the analytical expression. The establishment of this model is usually based on the following assumptions:

1. Flow rate is proportional to the guide vane opening and the square root of the net head, as given in Equation 2:

$q=k_{1}y\sqrt{h}(2)$

2. Turbine output power is proportional to the product of head and flow rate, as expressed in Equation 3:

$P=k_{2}qh(3)$

Expressing these equations in per-unit values:

$q=y\sqrt{h}(4)$

$P=qh(5)$

The relations in (2)–(5) are valid under steady or quasi-steady operating conditions near the rated point, where rapid transients, cavitation, and strong nonlinearities are minimal. These simplifications reduce model fidelity for extreme off-design or highly transient events but significantly improve computational efficiency, which is critical for large-scale EMT simulations and iterative parameter identification. The trade-off is a small loss in local accuracy in exchange for faster simulation and easier integration into system-level models. Equations 4 and 5, combined with the flow-head relationship for the penstock system, form a simplified nonlinear analytical model. The flow-head transfer function can be written as:

$G_d\left(s\right)=\frac{h\left(s\right)}{q\left(s\right)}(6)$

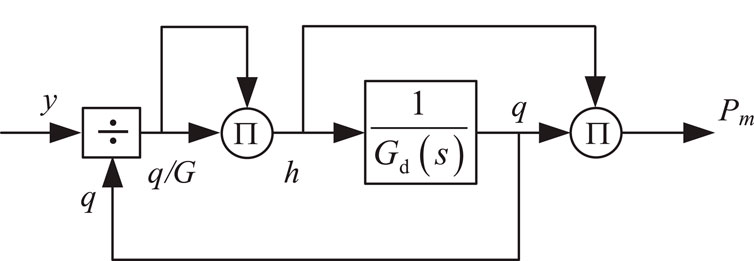
The simplified nonlinear analytical turbine-penstock system block diagram is shown in Figure 5 below:

Figure 5

Figure 5. Simplified nonlinear unit water diversion system block diagram.

The model described above does not need the model synthesis curve, but it is derived based on two assumptions of the hydraulic turbine, and the accuracy is slightly poor, but the model is relatively simple and suitable for power system simulation applications. A common analysis method for power system analysis is to linearize the system to investigate its small signal characteristics. The linearized model of the unit water diversion system in the turbine and its governing system can be obtained by linearizing the nonlinear model at the rated operating point. Equations 4–6 are linearized to obtain Equation 7:

$\left\{\begin{array}{l}\Delta q=\Delta y+\frac{1}{2}\Delta h\\ \Delta P=\Delta q+\Delta h\\ \Delta h=G_d\left(s\right)\Delta q\end{array}\right.(7)$

After simplifying and rearranging the above three equations, the result can be expressed as:

$\frac{\Delta P}{\Delta y}=\frac{1+G_d\left(s\right)}{1-0.5G_d\left(s\right)}(8)$

Since the research object of this paper is high-head Francis turbine and the diversion pipe is long, the traditional rigid water hammer model cannot accurately express its working characteristics. Therefore, this paper selects the elastic water hammer model to model its water diversion system, and ignores the influence of surge shaft and draft tube as:

$G_d\left(s\right)=-T_w\frac{\frac{T_r^2{s}^3}{24}+s}{\frac{T_r^2}{8}{s}^2+1}(9)$

where, T_r is the pipeline reflection time (s), also referred to as the elastic water hammer time constant. It represents the round-trip travel time of a pressure wave between the turbine and the upstream surge boundary, and is determined by the penstock length and the wave propagation velocity in water. Typical values range from approximately 0.5 s–3 s in high-head hydropower stations. T_w ​ is the water hammer time constant (s) of the hydraulic turbine, characterizing the inertia effects of the water column in the runner–penstock system. Its magnitude is influenced by turbine design parameters and hydraulic conditions, and usually falls in a similar range. In this study, both T_r and T_w are calculated theoretically from design parameters such as penstock length, cross-sectional area, and water wave speed, and are cross-checked with plant design specifications to ensure consistency.

By introducing Equation 9 into Equation 8, the transfer function model of the high-head turbine unit diversion system can be obtained, as shown in Equation 10:

$\frac{\Delta P}{\Delta y}=\frac{\frac{T_r^2}{8}{s}^2+1-T_W\left(\frac{T_r^2{s}^3}{24}+s\right)}{\frac{T_r^2}{4}{s}^2+2+T_W\left(\frac{T_r^2{s}^3}{24}+s\right)}(10)$

At this stage, the speed control system model of high-head hydropower units has been developed.

2.2 Modeling of MMC-HVDC system

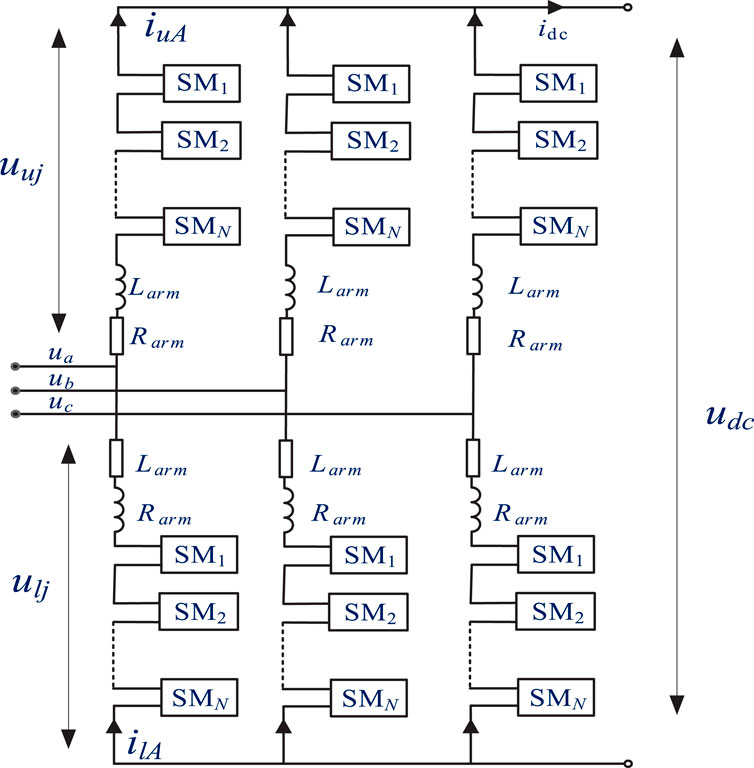
MMC-HVDC systems are capable of integrating and transmitting large-scale renewable energy and are therefore widely adopted in modern power systems. The main topology of MMC is shown in Figure 6. It includes six bridge arms. Each bridge arm contains N sub modules and the corresponding bridge arm resistance R_arm and bridge arm inductance L_arm. In Figure 6, u_dc and i_dc represent DC voltage and DC current, respectively. Z_gdc represents DC grid load impedance, and Z_gac represents AC grid impedance.

Figure 6

Figure 6. Basic structure of MMC.

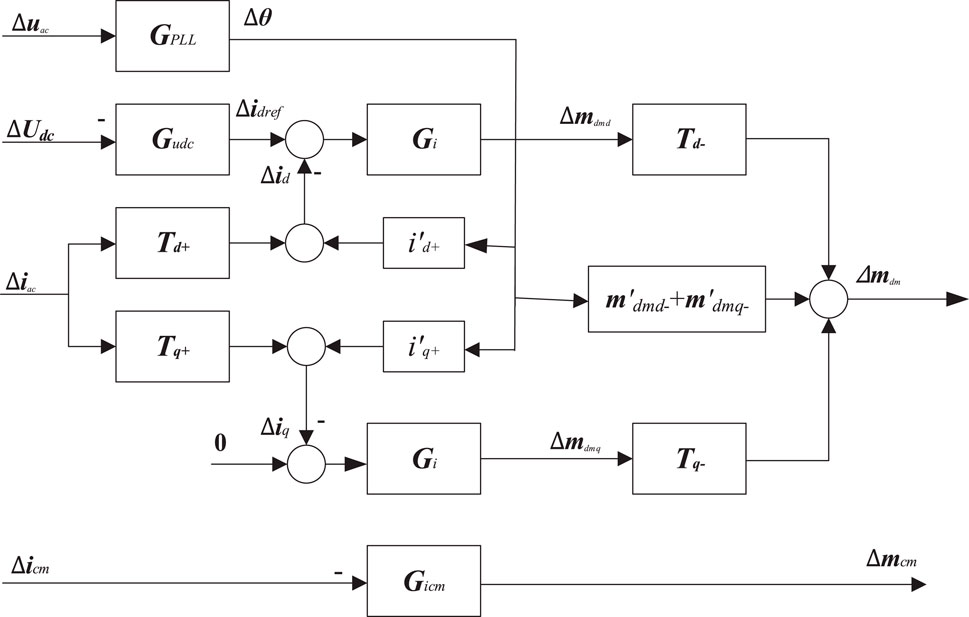
In practical projects, MMC operates in a closed-loop mode, and its modulation signal is generated by the control system. Therefore, this section further derives the mathematical model of the MMC integrated with the control system, building on the previous work. The MMC control system mainly includes phase-locked loop, constant voltage/power outer loop control, current inner loop control and circulating current suppression. The outer loop control is divided into constant DC voltage control and constant power control, corresponding to the rectifier station and inverter station of MMC.

To facilitate modeling and analysis, the harmonic state-space (HSS) model of the MMC control system, which is linear and time-invariant, is presented in Figure 7.

Figure 7

Figure 7. Block diagram of the overall HSS model of MMC controllers.

2.2.1 PLL model

In Figure 7, the phase-locked loop (PLL) synchronizes the phase of the output three-phase AC voltage with that of the AC grid, and the relationship is given in Equations 11–13:

$\Delta \theta \left(\omega \right)=G_{\text{PLL}}\left(\omega \right)\Delta u_{\text{ac}}(11)$

$\Delta u_{\text{ac}}=\Delta u_{\text{gac}}-Z_{\text{gac}}\Delta i_{\text{ac}}(12)$

$G_{\text{PLL}}\left(\omega \right)=\frac{-j\left[K_{\text{pPLL}}+K_{\text{iPLL}}/\left(j\omega \right)\right]}{j{\omega }_{\mathrm{p}}+V_1{e}^{j\phi }\left[K_{\text{pPLL}}+{K_{\mathrm{i}}}_{\text{PLL}}/\left(j\omega \right)\right]}(13)$

where G_PLL is the closed-loop transfer function of the PLL, K_pPLL and K_iPLL are the proportional and integral parameters of the internal PI control of the PLL.

2.2.2 Voltage outer loop and current inner loop control model

In the constant-voltage outer loop, the following relation holds, as given in Equation 14:

$\Delta m_{\text{dm}}=-G_{\mathrm{I}}\Delta i_{\mathrm{q}}-\left(G_{\text{udc}}\Delta u_{\text{dc}}+\Delta i_{\mathrm{d}}\right)G_{\mathrm{I}}(14)$

where G_udc(ω) and G_I(ω) is defined in Equations 15, 16:

$G_{\text{udc}}\left(\omega \right)=K_{\text{pudc}}+K_{\text{iudc}}/\left(j\omega \right)(15)$

$G_{\mathrm{I}}\left(\omega \right)=K_{\text{pI}}+K_{\text{iI}}/\left(j\omega \right)(16)$

As before, G_udc is the voltage outer loop transfer function. K_pudc and K_iudc are the proportional and integral link parameters of the constant voltage outer loop controller, respectively. K_pI and K_iI are the proportional and integral link parameters of the inner loop current controller, respectively.

2.2.3 Circulating current control modeling

During MMC operation, inter-phase circulating currents are generated, which in-crease operational losses. Therefore, a circulating current control loop must be implemented. This control can be achieved via PI or PR controllers, whose output is the common-mode modulation wave mcm. The relationship is given by Equation 17:

$\Delta m_{\text{cm}}=-G_{\text{icm}}\Delta i_{\text{cm}}(17)$

where G_cir is the transfer function of the PI controller for circulating current suppression. It can be expressed as Equation 18:

$G_{\text{cir}}\left(\omega \right)=K_{\text{picm}}+K_{\text{iicm}}/\left(j\omega \right)(18)$

3 Dominant parameter selection method based on Sobol sensitivity analysis

There are a large number of parameters in the established hydropower MMC-HVDC system model. They have different impacts on the dynamic response of the system. If the comprehensive parameter identification is directly carried out, it is easy to lead to the problems of complex identification process, large amount of calculation and poor convergence of identification results. Therefore, it is necessary to select the dominant parameters based on the sensitivity analysis before the parameter identification, which can significantly improve the efficiency and accuracy of identification.

As a well-known sensitivity analysis method, the Sobol global sensitivity analysis is adopted in this manuscript to determine the dominant parameters. It is a variance-based decomposition technique, quantifies the influence of individual parameters and their interactions on system dynamics by orthogonally decomposing the out-put variance of a computational model. Compared with alternative global sensitivity methods such as the Morris method or the Fourier Amplitude Sensitivity Test (FAST), Sobol analysis offers higher accuracy in quantifying both first-order effects and higher-order interaction effects. This capability is particularly critical in the context of high-head hydropower MMC-HVDC EMT models, where strong multi-physical coupling (e.g., between hydraulic transients, mechanical inertia, and converter control loops) can lead to significant parameter interaction effects that simpler screening methods may overlook. Although Sobol analysis typically incurs higher computational costs than Morris or FAST, this study mitigates the computational burden by first constraining the candidate parameter set to those with potential physical significance, and then applying parallelized simulations within the CloudPSS environment to accelerate the variance decomposition process. This work applies this methodology to dominant parameter identification in power system EMT models, where the impedance response Y = f(X) is modeled as a function of a d-dimensional uncertain parameter vector X=(x₁,x₂, … ,x_d)∈Φ_d, with Φ_d denoting the parameter domain.

According to Sobol’s decomposition theorem, when f(X) satisfies square-integrability, the model output can be uniquely expressed as shown in Equation 19.

$Y=f_0+{\displaystyle \sum _{i=1}^d}{f}_i\left(x_i\right)+{\displaystyle \sum _{1\le i<j\le d}}{f}_{ij}\left(x_i,x_j\right)+\cdots +f_{1,2,\dots ,d}\left(x_1,x_2,\dots ,x_d\right)(19)$

where f₀ represents the constant term, f_i(x_i) captures the independent effect of x_i, and f_ij(x_i,x_j) quantifies pairwise interactions. These components satisfy the orthogonality condition given in Equation 20.

${\int }_{\mathrm{\Phi }}{f}_{i_1,\dots ,i_s}\left(x_{i_1},\dots ,x_{i_s}\right)d{x}_k=0,\forall k\in i_1,\dots ,i_s(20)$

The total variance decomposition is given in Equation 21.

$\text{Var}\left(Y\right)={\displaystyle \sum _{i=1}^d}{V}_i+{\displaystyle \sum _{1\le i<j\le d}}{V}_{ij}+\cdots +V_{1,2,\dots ,d}(21)$

where $V_i=\text{Var}\left[\mathbb{E}\left(Y|x_i\right)\right]$ denotes the first-order contribution of x_i, and $V_{ij}=\text{Var}\left[\mathbb{E}\left(Y|x_i,x_j\right)\right]-V_i-V_j$ characterizes pairwise interactions, and higher-order terms account for multi-parameter synergies.

The first-order Sobol index S_i and total Sobol index S_Ti are defined in Equation 22:

$S_i=\frac{V_i}{\text{Var}\left(Y\right)},S_{T_i}=\frac{{\mathbb{E}}_{x_{-i}}\left[{\text{Var}}_{x_i}\left(Y|x_{-i}\right)\right]}{\text{Var}\left(Y\right)}(22)$

where S_i represents the individual influence of x_i and S_Ti incorporates all higher-order interactions involving x_i (Spall, 2003).

For numerical implementation, an enhanced Monte Carlo sampling scheme is adopted:

1. Generate an N×2d sample matrix, splitting it into submatrices A (first d columns) and B (last d columns).

2. Construct hybrid matrices $A_i^B$ by replacing the i-th column of A with the corresponding column in B.

3. The sensitivity indices are computed via Equation 23.

$\widehat{S}i\approx \frac{\frac{1}{N}\sum j=1^{N}f{\left(B\right)}_j\left[f{\left(A_i^B\right)}_j-f{\left(A\right)}_j\right]}{\text{Var}\left(Y\right)}(23)$

This algorithm achieves unbiased estimation of parameter sensitivity through N model evaluations, demonstrating particular efficacy for high-dimensional nonlinear systems like power system EMT models. In this manuscript, the X denotes the parameters requiring identification within the hydropower MMC-HVDC system, primarily the PI controller settings; Y corresponds to the active and reactive power observed during a phase-to-phase short circuit. Based on the Sobol index analysis, parameters associated with larger S_Ti values are selected as dominant and subsequently identified using the proposed parameter identification method.

4 Adaptive cuckoo search algorithm for parameter identification

4.1 Cuckoo search algorithm

The Cuckoo search algorithm (CSA) is a nature-inspired metaheuristic optimization method that mimics the brood parasitism behavior of certain cuckoo species. Utilizing Levy flight as its global stochastic search mechanism, CSA demonstrates superior optimization performance compared to genetic algorithms and particle swarm optimization in terms of convergence precision and exploration efficiency. Therefore, the CSA is well-suited for high-dimensional optimization problems.

The algorithm operates under three idealized biological principles:

1. Uniparous Reproduction: Each cuckoo lays one egg in a randomly selected host nest.

2. Elitist Preservation: Only nests with the highest fitness values are retained for subsequent generations.

3. Probabilistic Replacement: Hosts detect and abandon alien eggs with probability p_a∈[0,1], triggering nest replacement.

The position update mechanism for host nests is given by Equation 24.

$x_i^{\left(k+1\right)}=x_i^{\left(k\right)}+\alpha \otimes \text{Levy}\left(\beta \right)(24)$

where α > 0 controls the step size, ⊗ denotes element-wise multiplication, and Levy(β) represents the stochastic search path governed by the stability index β∈(0,2].

The Levy flight step $s_i^{\left(k\right)}$ is calculated using Equation 25.

$s_i^{\left(k\right)}=0.01·\frac{u}{{\left|v\right|}^{1/\beta }}\left(x_i^{\left(k\right)}-x_{\text{opt}}\right)(25)$

where $u\sim \mathcal{N}\left(0,{\sigma }_u^2\right)$ and $v\sim \mathcal{N}\left(0,1\right)$, with the scale parameter ${\sigma }_u$ defined in Equation 26.

${\sigma }_u={\left[\frac{\sin \left(\pi \beta /2\right)·\mathrm{\Gamma }\left(1+\beta \right)}{2^{\left(\beta -1\right)/2}·\beta ·\mathrm{\Gamma }\left(\frac{1+\beta }{2}\right)}\right]}^{1/\beta }(26)$

Here, Γ(⋅) denotes the gamma function.

If an egg is detected by the host, the nest position can be updated through Equation 27.

$x_i^{\left(k+1\right)}\leftarrow x_i^{\left(k\right)}+r·s_i^{\left(k\right)},r\sim \mathcal{U}\left(0,1\right)(27)$

where r is a uniformly distributed random number.

The adaptive step-length mechanism introduces dynamic exploration via Equation 28.

$r^{\prime }=\text{rand}·\left(x_{i\in \left[1,n\right]}-x_{j\in \left[1,n\right]}\right)(28)$

Then, the updated position is obtained from Equation 29.

$x^{\prime }=\left\{\begin{array}{ll}{x}_i+r^{\prime }& \text{if}{P}_a>p_a\\ x_i& \text{otherwise}\end{array}\right.(29)$

4.2 Adaptive cuckoo search algorithm

The traditional CSA shows advantages in solving the normal optimization problems, but it is insufficient for direct application in parameter identification of the hydropower MMC-HVDC system EMT model. Due to the model’s strong nonlinearity and parameter coupling, the CSA often suffers from slow convergence, local optima entrapment, and limited identification accuracy. Therefore, this manuscript pro-poses an adaptive CSA for the parameter identification of the selected dominant parameters in Section 3. The improvements include the following three aspects.

4.2.1 Tent chaotic mapping strategy

The diversity of initial populations critically influences the global search capability and convergence efficiency of optimization algorithms. Empirical studies demonstrate that uniformly distributed initial populations significantly enhance convergence speed and solution accuracy compared to traditional random initialization methods. However, the conventional CSA often suffers from population clustering and dimensional correlation during initialization due to its pseudo-random sampling strategy, which may reduce search efficiency. To address this limitation, this manuscript intro-duces a chaotic mapping strategy with ergodicity and stochasticity for population initialization.

Chaotic mapping generates pseudo-random sequences through deterministic equations, effectively mitigating dimensional correlation issues inherent in conventional random number generators. Among various chaotic maps, the Tent mapping offers distinct advantages, including superior uniformity in sequence distribution compared to the Logistic mapping, reduced sensitivity to initial values, avoidance of iteration failures observed in some other mappings, and high computational efficiency, making it well-suited for high-dimensional optimization problems.

The mathematical formulation of the Tent chaotic mapping is defined in Equation 30:

$y_{u+1}=\left\{\begin{array}{ll}\frac{10}{7}{y}_u,& y_u<0.7\\ \frac{10}{3}{y}_u\left(1-y_u\right),& \text{otherwise}\end{array}\right.(30)$

The population initialization process based on this mapping proceeds as follows:

1. Generate a d-dimensional initial vector y₀ = [y₀₁,y₀₂, … ,y_0d], where y_0i∉{0,0.5,1} to avoid fixed points.

2. Iterate the chaotic sequence {y₁,y₂, … ,y_T}for T cycles using Equation 30.

3. Map the chaotic sequence to the solution space in Equation 31:

$x_i=x_{\min }+y_u·\left(x_{\max }-x_{\min }\right)(31)$

where x_min and x_max represent the minimum and maximum limits of the optimization variables, respectively. This strategy produces an initial population with uniform spatial distribution, effectively avoiding dimensional coupling issues common in traditional methods.

4.2.2 Introducing improvement strategies for factor α and p

To accelerate the convergence and improve the solution accuracy of the CSA, this paper introduces dynamic adaptation mechanisms for two critical parameters: the step-size control factor α₀ and the discovery probability p_a.

CSA algorithm employs fixed values for α₀ and pa, which often lead to premature convergence or excessive computational overhead. To address this limitation, this manuscript proposes linearly decaying formulations that adaptively adjust these parameters throughout iterations. The step-size control factor α₀ is governed by Equation 32.

${\alpha }_0^{\left(k\right)}=\left({\alpha }_{0\_\mathit{max}}-{\alpha }_{0\_\mathit{min}}\right)\left(1-\frac{k}{k_{\mathit{max}}}\right)+{\alpha }_{0\_\mathit{min}}(32)$

where α_{0_max} and α_{0_min} denote the maximum and minimum step-size boundaries, k represents the current iteration number, and k_max is the maximum iteration count. This linear decay strategy ensures gradual transition from large steps to small steps which enabling precise local refinement near optimal regions.

Simultaneously, the discovery probability pa follows a similar adaptation rule given in Equation 33.

$p_a^{\left(k\right)}=\left(p_{a\_\mathit{max}}-p_{a\_\mathit{min}}\right)\left(1-\frac{k}{k_{\mathit{max}}}\right)+p_{a\_\mathit{min}}(33)$

where p_{a_max} and p_{a_min} define the upper and lower bounds for nest replacement probability. The coupled evolution of α₀ and p_a creates synergistic optimization dynamics for higher values in initial phases promote exploration of new solutions, while reduced values in later stages intensify exploitation of promising regions.

4.2.3 Introducing boundary conditions

Conventional boundary treatment in CSA forces out-of-bounds solutions to remain at the search space boundaries. While this prevents infinite search space expansion, it significantly slows convergence as boundary-trapped individuals require excessive iterations to approach optimal regions. To address this limitation, a boundary reset strategy is proposed to leverage current search information for accelerating convergence.

The improved boundary handling mechanism relocates out-of-bounds individuals to random positions between the current best solution and violated boundaries. This is mathematically expressed in Equation 34.

$x_i^{t+1}=\left\{\begin{array}{cc}C·x_{\text{best}}^t+\left(1-C\right)·ub,& x_i^t>ub\\ D·x_{\text{best}}^t+\left(1-D\right)·lb,& x_i^t<lb\end{array}\right.(34)$

where C, D∈[0,1] are uniform random numbers, $x_{best}^t$ denotes the best solution of current iteration, ub and lb represent upper and lower bounds, respectively.

This approach provides two critical advantages over traditional methods: the proposed scheme can accelerate convergence by redirecting individuals to inherit directional information from $x_{best}^t$ reducing the required convergence steps in benchmark testing; In addition, the proposed scheme can enhance exploration by introducing controlled diversity near the boundary with random coefficients C and D, pre-venting population stagnation.

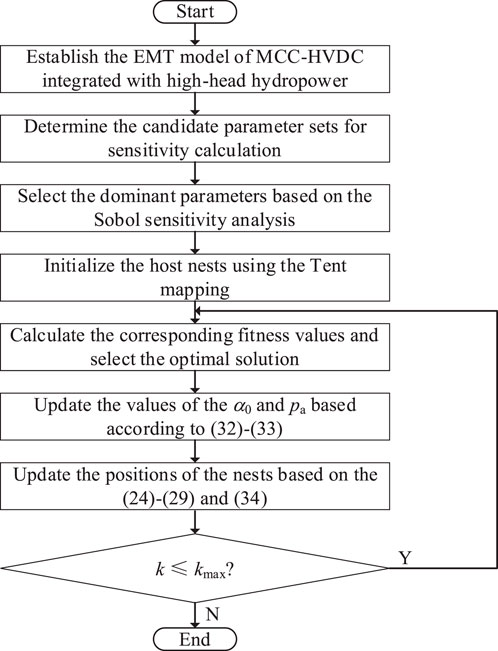
The overall procedure for parameter identification employed in this study is illustrated in Figure 8. First, the electromagnetic transient (EMT) model of the high-head hydropower MMC-HVDC system is developed to serve as the foundation for subsequent sensitivity analysis and parameter estimation. Candidate parameters are then selected, and their Sobol indices are computed using the Sobol sensitivity analysis method. Based on the sensitivity results, the dominant parameters are determined. The Adaptive Cuckoo Search (ACS) algorithm is subsequently applied to estimate the values of these dominant parameters. The integration of tent mapping and adaptive parameter updates further enhances the algorithm’s global search capability and convergence performance. After the maximum number of iterations is reached, the nest position corresponding to the optimal fitness value is taken as the final identified parameter set.

Figure 8

Figure 8. Structure block diagram of constant DC voltage control system.

5 Experimental results and discussion

5.1 Simulation-based validation results

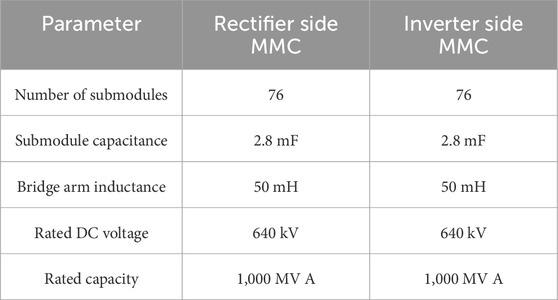
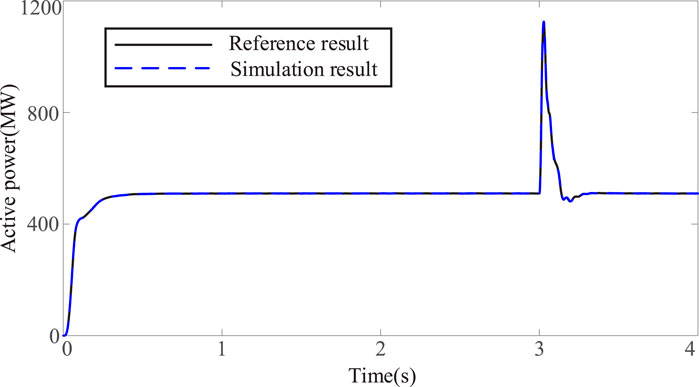
To validate the effectiveness of the proposed approach for identifying dominant system parameters, a high-head hydropower MMC-HVDC model was developed using the CloudPSS simulation platform, with its structure and control strategies outlined previously. All simulations were conducted on a desktop computer equipped with 32 GB RAM and a 2.10 GHz Intel Core i7-12700 processor. The simulation parameters of the MMC are listed in Table 1. In practical applications, the MMC-HVDC system may encounter operational faults, during which the control systems function to maintain system stability. Thus, parameter identification under fault conditions holds greater practical significance. In the simulation scenario, a phase-to-phase short-circuit fault lasting 0.1 s was introduced at t = 3s on the rectifier side of the MMC.

Table 1

Table 1. The parameters of the MMC in the simulation.

In the parameter identification process based on the ACS algorithm, each nest represents the value vector of the dominant parameter set. The corresponding fitness function calculation formula is given in Equation 35.

$F=\sqrt{\frac{1}{K}{\left(P_{ref}-P\right)}^2}+\sqrt{\frac{1}{K}{\left(Q_{ref}-Q\right)}^2}(35)$

where K denotes the number of sampling points. P_ref and Q_ref represent the reference values of active and reactive power, respectively, on the rectifier side during the time interval from 3 s to 3.5 s, while P and Q correspond to the simulated active and reactive power outputs.

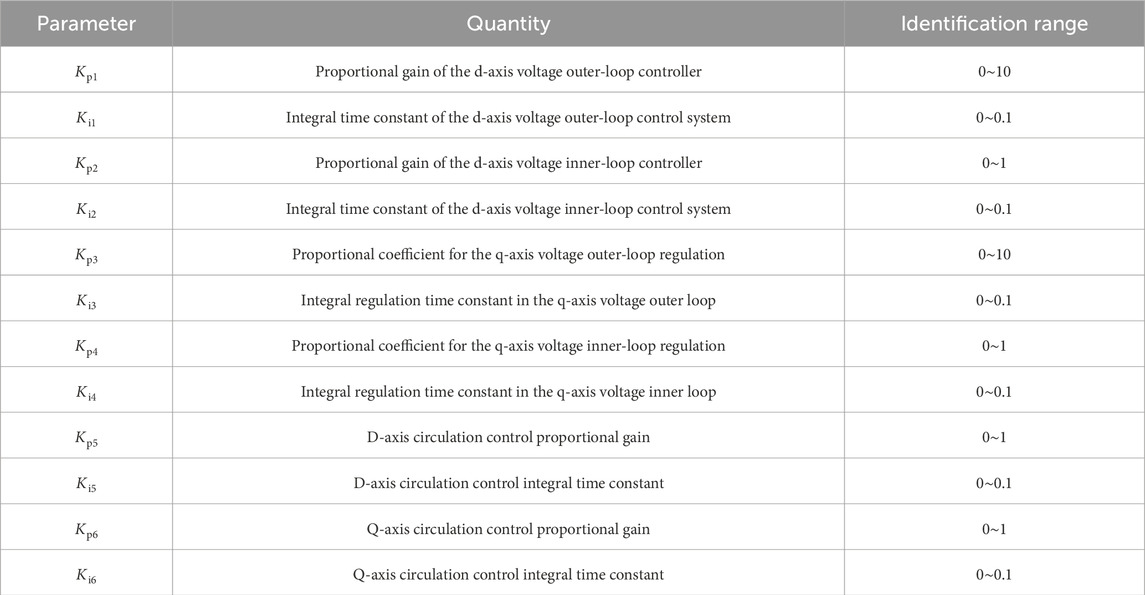
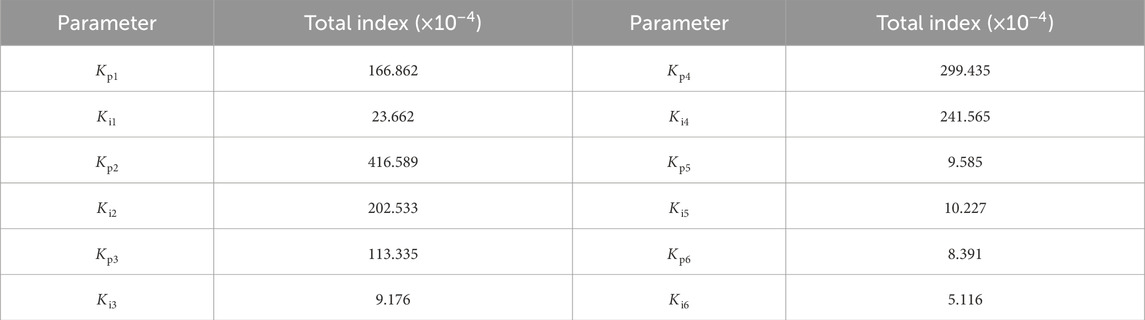
First, Sobol sensitivity analysis was conducted to determine the most influential parameters. Parameters within the MMC-HVDC control systems were selected as candidate sets based on their influence on system performance. The corresponding identification ranges for these candidates are provided in Table 2. Following the sensitivity analysis method detailed in Section 3, the total Sobol indices for these parameters were computed and are summarized in Table 3. It can be seen that K_p1, K_p2, K_i2, K_p3, K_p4 and K_i4 have higher sensitivity indexes compared with other parameters. Therefore, these six parameters are selected as the dominant parameters for the following identification.

Table 2

Table 2. The identification ranges of the candidate parameters in MMC-HVDC.

Table 3

Table 3. The sensitivity indexes of the candidate parameters.

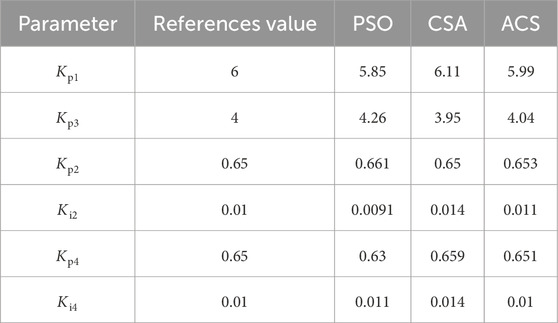
Following the sensitivity analysis, the dominant parameters were identified using the proposed approach. The identification ranges for these six parameters remained consistent with those specified in Table 2. The population size was set to 30, which represents a balanced choice between exploration capability and computational efficiency. Preliminary trials with different population sizes (e.g., 20, 40, and 50) indicated that increasing the size beyond 30 yielded only marginal improvements in identification accuracy while significantly increasing computation time, whereas smaller sizes occasionally led to premature convergence. Therefore, 30 was adopted as a suitable compromise for this study. To further evaluate the effectiveness of the proposed method, CSA, PSO, and ACS algorithms were employed for the identification task. The final identification outcomes obtained by each algorithm are summarized in Table 4. It is evident that the ACS method yields the smallest error, clearly demonstrating its superior accuracy in parameter identification.

Table 4

Table 4. The parameter identification results of the three optimization algorithms.

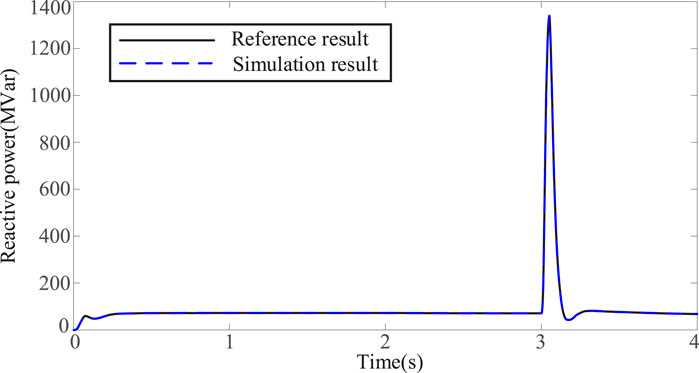
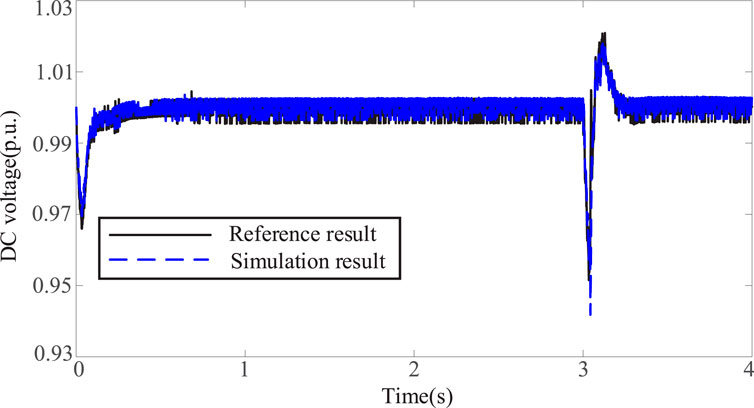
To verify the accuracy of the identification results shown in Table 4, simulations were conducted using both the reference parameters and the parameters identified by the proposed method. The corresponding simulation results are presented in Figures 9–11. As observed, the outputs derived from the identified parameters exhibit close agreement with the reference results, demonstrating the effectiveness of the ACS algorithm in model parameter identification.

Figure 9

Figure 9. Comparison of rectifier active power under reference and identified parameters.

Figure 10

Figure 10. Rectifier reactive power responses based on reference and identified parameters.

Figure 11

Figure 11. DC voltage profiles obtained using the reference and identified parameters.

Additionally, to assess the generalization capability of the identified parameters, further simulations were performed under single-phase and three-phase short-circuit conditions. The results, presented in Figure 12, show high consistency between the identified and reference responses, underscoring the robustness and reliability of the proposed parameter identification approach across diverse fault conditions.

Figure 12

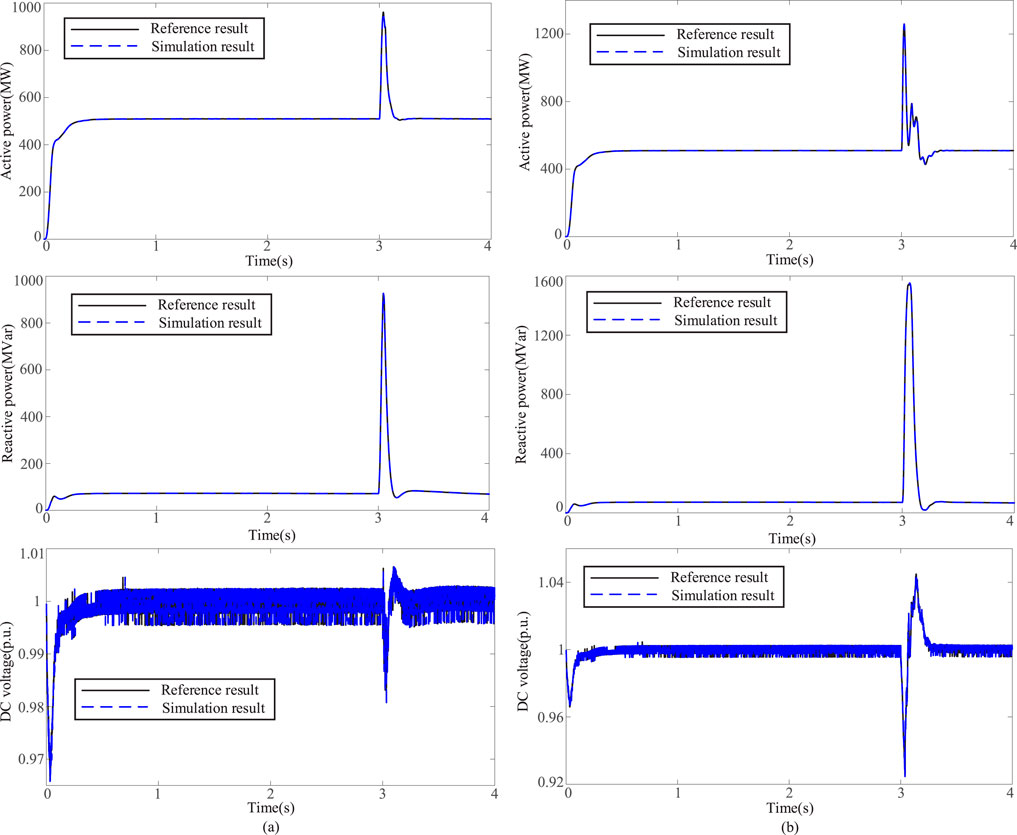
Figure 12. The simulation results obtained with the reference and identified parameters. (a) Single-phase short circuit; (b) three-phase short circuit.

5.2 Limitations

While the proposed Sobol–ACS method has shown superior performance in accurately identifying the six dominant parameters of the high-head hydropower MMC-HVDC EMT model, several aspects warrant further investigation to fully establish its broader applicability. In this study, the case analysis was conducted on a parameter set of moderate size, which is representative of many practical engineering scenarios. Nevertheless, some large-scale power system models or highly detailed component representations may involve significantly more parameters, potentially numbering in the dozens or hundreds. Although the Sobol sensitivity analysis effectively reduces dimensionality by isolating dominant parameters, the computational cost of the sensitivity evaluation itself increases with the size of the candidate set. Similarly, the ACS algorithm’s performance in very high-dimensional search spaces (e.g., beyond 20 parameters) should be examined more rigorously, as increased dimensionality can influence convergence speed and identification accuracy.

The current validation focused on a specific EMT model with operational and structural characteristics typical of high-head hydropower MMC-HVDC systems. While this provides a strong proof of concept, additional testing under different optimization landscapes would help confirm the robustness of the method. For example, evaluating its performance on problems with stronger non-convexity, lower signal-to-noise ratios, or more intricate parameter couplings could yield further insights. Extending the Sobol–ACS framework to other component models—such as synchronous generators with saturation effects, composite load models, or wide-area measurement system calibration—may also provide a broader assessment of its adaptability. These potential directions do not diminish the method’s demonstrated strengths but instead highlight opportunities for future research to further enhance its scope and applicability.

6 Conclusion

A parameter identification method for a high-head hydropower flexible DC transmission system, based on Sobol sensitivity analysis and an adaptive cuckoo search algorithm, is presented in this manuscript. Our theoretical framework and simulation studies demonstrate that the proposed method can effectively achieve accurate parameter identification for the system model. The simulation indicates that the introduced approach can obtain the better optimization results when compared with other optimization algorithms. Moreover, the simulation results verify that the identified parameters remain accurate under different operational conditions. The proposed method enables precise modeling of the high-head hydropower flexible DC system, ensuring that simulation outcomes faithfully reflect the behavior of the actual physical system. This contributes to improved stability and reliability in flexible DC grid-connected hydropower operations. Future research will focus on extending the proposed approach to larger-scale systems and more complex parameter sets, assessing its performance in higher-dimensional search spaces and under diverse optimization landscapes. This may include applying the method to different power system component models, incorporating distributed or parallel computing strategies to enhance efficiency, and evaluating its robustness in scenarios with stronger non-convexity or lower signal-to-noise ratios. Additionally, further investigation into real-time stability analysis methods based on the identified parameters, especially under fluctuating hydraulic conditions, would provide added value to the robustness of system operation.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

LJ: Conceptualization, Formal Analysis, Funding acquisition, Methodology, Project administration, Supervision, Validation, Writing – original draft, Writing – review and editing. WX: Data curation, Funding acquisition, Methodology, Project administration, Resources, Software, Supervision, Validation, Writing – review and editing. ZH: Data curation, Investigation, Software, Visualization, Writing – original draft.

Funding

The authors declare that this study received funding from China Southern Power Grid Co. Ltd. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

Authors LJ, WX, and ZH were employed by China Southern Power Grid Co., Ltd.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alvarez, G. E. (2020). Operation of pumped storage hydropower plants through optimization for power systems. Energy 202, 117797. doi:10.1016/j.energy.2020.117797

CrossRef Full Text | Google Scholar

Barros, M. T., Tsai, F. T., Yang, S. L., Lopes, J. E., and Yeh, W. W. (2003). Optimization of large-scale hydropower system operations. J. Water Resour. Plan. Manag. 129 (3), 178–188. doi:10.1061/(asce)0733-9496(2003)129:3(178)

CrossRef Full Text | Google Scholar

Bladh, J. (2012). Hydropower generator and power system interaction. Doctoral dissertation. Acta Univ. Ups. Available online at: https://www.diva-portal.org/smash/record.jsf?pid=diva2%3A558758&dswid=1582.

Google Scholar

Chen, Z., Yuan, X., Tian, H., and Ji, B. (2014a). Improved gravitational search algorithm for parameter identification of water turbine regulation system. Energy Convers. Manag. 78, 306–315. doi:10.1016/j.enconman.2013.10.060

CrossRef Full Text | Google Scholar

Chen, Z., Yuan, X., Ji, B., Wang, P., and Tian, H. (2014b). Design of a fractional order PID controller for hydraulic turbine regulating system using chaotic non-dominated sorting genetic algorithm II. Energy Convers. Manag. 84, 390–404. doi:10.1016/j.enconman.2014.04.052

CrossRef Full Text | Google Scholar

Chen, Z., Yuan, X., Yuan, Y., Iu, H. H. C., and Fernando, T. (2017). Parameter identification of integrated model of hydraulic turbine regulating system with uncertainties using three different approaches. IEEE Trans. Power Syst. 32 (5), 3482–3491. doi:10.1109/TPWRS.2016.2639293

CrossRef Full Text | Google Scholar

Fang, H., Chen, L., and Shen, Z. (2011). Application of an improved PSO algorithm to optimal tuning of PID gains for water turbine governor. Energy Convers. Manag. 52 (4), 1763–1770. doi:10.1016/j.enconman.2010.11.005

CrossRef Full Text | Google Scholar

Gao, L., Dai, Y., and Xia, J. (2009). “Parameter identification of hydro generation system with fluid transients based on improved genetic algorithm,” in Fifth international conference on natural computation (ICNC), 398–402.

Google Scholar

Guo, S., Norris, S., and Bialek, J. (2014). Adaptive parameter estimation of power system dynamic model using modal information. IEEE Trans. Power Syst. 29 (6), 2854–2861. doi:10.1109/TPWRS.2014.2316916

CrossRef Full Text | Google Scholar

Jiang, C., Ma, Y., and Wang, C. (2006). PID controller parameters optimization of hydro turbine governing systems using deterministic–chaotic-mutation evolutionary programming (DCMEP). Energy Convers. Manag. 47 (9), 1222–1230. doi:10.1016/j.enconman.2005.07.009

CrossRef Full Text | Google Scholar

Kou, P., Zhou, J., Li, C., He, Y., and He, H. (2010). “Identification of hydraulic turbine governor system parameters based on bacterial foraging optimization algorithm,” in Sixth international conference on natural computation (ICNC), 3339–3343.

Google Scholar

Liu, C., Liu, N., Sun, X., and Cui, J. (2010). “The research and application on parameter identification of hydraulic turbine regulating system based on particle swarm optimization and uniform design,” in Proceedings of international conference on computer science and information technology (ICCSIT) (Chengdu, China), 605–608.

Google Scholar

Milojević, V., Čalija, S., Rietveld, G., Ačanski, M. V., and Colangelo, D. (2018). Utilization of PMU measurements for three-phase line parameter estimation in power systems. IEEE Trans. Instrum. Meas. 67 (10), 2453–2462. doi:10.1109/TIM.2018.2843098

CrossRef Full Text | Google Scholar

Mukherjee, N., Chattopadhyaya, A., Chattopadhyay, S., and Sengupta, S. (2020). Discrete-wavelet-transform and stockwell-transform-based statistical parameters estimation for fault analysis in grid-connected wind power system. IEEE Syst. J. 14 (3), 4320–4328. doi:10.1109/JSYST.2020.2984132

CrossRef Full Text | Google Scholar

Ortega, R., Bobtsov, A., Pyrkin, A., and Aranovskiy, S. (2015). A parameter estimation approach to state observation of nonlinear systems. Syst. Control Lett. 85, 84–94. doi:10.1016/j.sysconle.2015.09.008

CrossRef Full Text | Google Scholar

Petra, N., Petra, C. G., Zhang, Z., Constantinescu, E. M., and Anitescu, M. (2017). A Bayesian approach for parameter estimation with uncertainty for dynamic power systems. IEEE Trans. Power Syst. 32 (4), 2735–2743. doi:10.1109/TPWRS.2016.2625277

CrossRef Full Text | Google Scholar

Quintana, V. H., and Van Cutsem, T. H. (1988). Power system network parameter estimation. Optim. Control Appl. Methods 9 (3), 303–323. doi:10.1002/oca.4660090307

CrossRef Full Text | Google Scholar

Rakpenthai, C., Uatrongjit, S., and Premrudeepreechacharn, S. (2012). State estimation of power system considering network parameter uncertainty based on parametric interval linear systems. IEEE Trans. Power Syst. 27 (1), 305–313. doi:10.1109/TPWRS.2011.2162859

CrossRef Full Text | Google Scholar

Regulski, P., Vilchis-Rodriguez, D. S., Djurović, S., and Terzija, V. (2015). Estimation of composite load model parameters using an improved particle swarm optimization method. IEEE Trans. Power Deliv. 30 (2), 553–560. doi:10.1109/TPWRD.2014.2301219

CrossRef Full Text | Google Scholar

Shaikh, M. S., Kumar, S., Kumar, S., Niazi, K. A. K., and Babu, R. (2021). Application of grey wolf optimization algorithm in parameter calculation of transmission lines. IET Sci. Meas. Technol. 15 (3), 311–322. doi:10.1049/smt2.12023

CrossRef Full Text | Google Scholar

Shaikh, M. S., Raj, S., Babu, R., Kumar, S., and Sagrolikar, K. (2023). A hybrid moth–flame algorithm with particle swarm optimization with application in power transmission and distribution. Decis. Anal. J. 6, 100182. doi:10.1016/j.dajour.2023.100182

CrossRef Full Text | Google Scholar

Spall, J. C. (2003). Estimation via Markov Chain Monte Carlo. IEEE Control Syst. Mag. 23 (2), 34–45. doi:10.1109/MCS.2003.1188770

CrossRef Full Text | Google Scholar

Zarco, P., and Exposito, A. G. (2000). Power system parameter estimation: a survey. IEEE Trans. Power Syst. 15 (1), 216–222. doi:10.1109/59.852124

CrossRef Full Text | Google Scholar

Zeng, B., and Teng, Z. (2011). Parameter estimation of power system signals based on cosine self-convolution window with desirable side-lobe behaviors. IEEE Trans. Power Deliv. 26 (1), 250–257. doi:10.1109/TPWRD.2010.2083701

CrossRef Full Text | Google Scholar

Zhang, Y., Zhou, J., Xu, Y., and Zheng, Y. (2018). “Parameter identification of hydraulic turbine governing system using white-box mapping model and RBF neural network,” in 2018 eighth international conference on instrumentation and measurement, computer, communication and control (IMCCC) (Harbin, China), 111–114.

Google Scholar