Energy-efficient parameter estimation of solid oxide fuel cells under varying pressure conditions using the black widow optimization algorithm

Solid oxide fuel cells (SOFCs) are highly efficient and fuel-flexible energy conversion devices, but accurately estimating their governing parameters remains a challenge due to the nonlinear behavior of electrochemical processes. This study presents the first application of the black widow optimization (BWO) algorithm for estimating six critical SOFC parameters—open-circuit potential (E₀), Tafel slope (A), exchange current density (I₀), concentration loss coefficient (B), limiting current density (I_l), and ohmic resistance (R_ohm)—under varying pressure conditions (1–5 atm). The objective was to minimize the mean squared error (MSE) between experimental and predicted polarization curves while ensuring computational efficiency. The proposed BWO framework achieved superior accuracy, with an MSE of 0.52 at 5 atm and convergence within 3.74 s, significantly outperforming benchmark metaheuristic algorithms such as particle swarm optimization (PSO), gray wolf optimization (GWO), and the whale optimization algorithm (WOA). Robustness was confirmed through cross-validation, where polarization curves predicted at unseen conditions deviated by less than 5% from experimental results. This demonstrates that the estimated parameters effectively capture intrinsic SOFC electrochemical behavior rather than overfitting specific datasets. Beyond numerical accuracy, the optimized parameters enhanced the predictive stability of voltage–current (V–I) and power–current (P–I) characteristics across all studied pressures, directly supporting improved operational reliability and long-term stack durability. The combination of higher precision, faster convergence, and strong generalizability positions BWO as a promising tool for real-time SOFC optimization. The findings establish a robust framework for parameter identification that not only reduces uncertainty in SOFC modeling but also contributes to practical advances in performance optimization and system longevity. Future extensions of this research will include real-time implementation under dynamic operating environments and integration with hybrid renewable energy systems to improve scalability, efficiency, and sustainability.

1 Introduction

The depletion of fossil fuels, environmental pollution caused by their use, and global dependence on these finite resources make the transition to clean, renewable alternatives one of the major challenges for future energy security. Consequently, much research has explored novel and eco-friendly energy technologies. Among this, fuel cells have emerged as highly significant in complementing renewable sources such as solar, wind, geothermal, and biomass (Mir et al., 2020). Fuel cells and batteries share some similarities, but differ in one crucial aspect: while batteries store and subsequently release chemical energy with a lifetime limited by stored reactants, fuel cells can operate continuously as long as an external supply of fuel and oxidant is maintained (Yu et al., 2020). Furthermore, various types of fuel cells can be powered by ethanol, hydrogen, methanol, natural gas, or even biogas. Solid oxide fuel cells (SOFCs) typically operate at high temperatures, whereas proton exchange membrane fuel cells (PEMFCs) function at a lower range of 50–100 °C (Fan et al., 2020; Singla et al., 2023a). Through electrochemical processes, these devices convert the chemical energy of fuels into electricity. However, the performance of SOFCs is strongly influenced by activation, concentration, and Ohmic polarization losses (Wang et al., 2011). In turn, SOFC material properties such as electrode absorbency, tortuosity, and pore radius critically affect these polarizations (Zhou et al., 2016; Singla et al., 2023b). The accurate experimental determination of these parameters remains challenging, thereby necessitating mathematical modeling to represent the system’s complex dynamics. Contemporary SOFC models often incorporate values drawn from widely varying sources (Amiri et al., 2016; Fang et al., 2015). As emphasized by Virkar et al. (2007), Zhu et al. (2015), and Singh and Sandhu (2022), a precise mathematical model is indispensable for predicting SOFC behavior and determining unknown parameters under diverse operating conditions. Nerat (2017) developed a 3-D dynamic model of a planar anode-supported SOFC to investigate transient responses under load variations, showing that excessive current density increases can lead to fuel starvation in the porous anode layer, accelerating degradation. This study further demonstrated that increasing anode support thickness mitigates starvation and improves efficiency, providing guidelines for SOFC design and control. Nevertheless, parameter estimation remains particularly complex because SOFC models are inherently nonlinear. Conventional numerical or linear programming methods have frequently failed to provide robust optimization, largely due to local optima entrapment and sensitivity to gradient initialization (Xiong et al., 2020; Khattar et al., 2019; Singla et al., 2023c). To address these challenges, metaheuristic optimization strategies have gained substantial popularity in recent years. For example, Shi et al. (2020) introduced a converged grass fibrous root optimizer, while Yousri et al. (2021) applied marine-predator-based optimization for SOFC modeling. El-Hay et al. (2019) proposed an interior random search algorithm, and Nassef et al. (2019) applied radial movement optimization. Although these approaches improved accuracy, they often suffered from slower convergence or limited robustness. Wu and Gao (2006), through their work on the optimal coupling of fuel cells and supercapacitors, further emphasized the importance of parameter optimization in enhancing both system cost-effectiveness and durability. In parallel, research on protonic ceramic fuel cells (PCFCs) has provided additional theoretical insights into electrochemical behavior under varying operating conditions. Putilov et al. (2019) developed a theoretical framework demonstrating that hydrogen humidification exerts a strong, non-monotonic influence on current density, whereas air humidification plays only a minor role. They further suggested that optimizing hydrogen inlet humidity can reduce polarization losses, thereby improving device efficiency. Extending this research, Putilov et al. (2020) investigated the combined effects of cell voltage and external operating conditions, showing that proton conductivity may either increase or decrease, depending on humidity, while hole conductivity consistently rises with voltage, reducing Faradaic efficiency. Importantly, their findings revealed that fundamental parameters such as conductivities, transport numbers, and EMF differ markedly between open-circuit and operating conditions. These contributions underscore the necessity of advanced modeling strategies and highlight the pivotal role of environmental and voltage-dependent factors in fuel cell performance optimization.

1.1 Novelty and contributions

While recent studies such as Singh and Sandhu (2023) have successfully applied optimization methods for SOFC parameter estimation under different temperature conditions, the present research extends this concept to pressure-dependent operating environments.

The main novelty and contributions are

• first application of the black widow optimization (BWO) algorithm for SOFC parameter estimation under varying pressure conditions;

• comparison against leading metaheuristics (PSO, GWO, and WOA) demonstrating superior accuracy, convergence speed, and robustness;

• improved predictive reliability of polarization curves across multiple operating pressures with < 5% deviation from experimental results;

• contribution toward long-term SOFC stability and longevity by reducing parameter uncertainty and mismatch.

The present study aims to establish a robust and generalizable framework for accurate parameter estimation in SOFCs by employing the BWO algorithm. The specific objectives are to

• develop and implement the BWO algorithm to extract six critical SOFC parameters (E0, A, I0, B, IL, and Rohm) that govern polarization behavior;

• validate the proposed BWO framework across multiple operating pressures (1–5 atm) using experimental polarization data from a commercial 5-kW tubular SOFC stack;

• perform cross-validation on unseen experimental conditions (e.g., testing the model at 5 atm while training on 1–2–4 atm) in order to verify the robustness and generalizability of the estimated parameters;

• conduct a comparative analysis with established metaheuristic algorithms such as particle swarm optimization (PSO), gray wolf optimization (GWO), and the whale optimization algorithm (WOA), evaluating convergence speed, accuracy, and stability.

• demonstrate the practical impact of precise parameter estimation by linking reduced model–experiment mismatch to improved predictive stability, better operational reliability, and the potential extension of SOFC longevity.

2 Methodology

2.1 SOFC concept

The fuel cell is a device for electrochemical energy conversion, continuously producing heat and electricity from chemical energy. In SOFCs, hydrogen acts as the fuel while oxygen (from air) is used as the oxidant. Unlike combustion-based engines, SOFCs directly convert chemical energy into electrical energy without intermediate combustion, thereby avoiding harmful flue gas emissions (Virkar et al., 2007). The anodic hydrogen oxidation, cathodic oxygen reduction, and the overall electrochemical reaction in an SOFC are represented by Equations 1–3.

$\text{At\hspace{0.17em}anode}:H_2+O^{2-}\to H_{2}O+{2e}^{-}(1)$

$\text{At\hspace{0.17em}cathode}:{\frac{1}{2}O}_2+{2e}^{-}\to O^{2-}(2)$

$\text{Overall\hspace{0.17em}reaction}:H_2+{\frac{1}{2}O}_2\to H_{2}O(3)$

Figure 1 displays the SOFC schematic. Reducing oxygen molecules at the cathode produces negative oxygen ions. The ionic conduction electrolyte conducts negative ions, while the thin electrolyte sheet blocks electrons (Singh and Sandhu, 2023).

Figure 1

Figure 1. Diagram of SOFC (Singh and Sandhu, 2023).

2.2 SOFC voltage description

The estimation of the output potential (voltage) of a single SOFC can be achieved by utilizing the thermodynamic potential, E_Nernst, obtained chemically under no load conditions, along with the potential losses occurring during the reaction. This estimation is denoted as V_cell. The cell voltage accounting for thermodynamic and loss components is defined in Equation 4. The losses encompassed in this context consist of the Ohmic potential drop (V_ohm), the concentration potential drop (V_conc), and the activation potential drop (V_act) (Fallah et al., 2018).

$V_{cell}=E_{Nernst}-\left(sumofallthevoltagelosses/dropinafuelcell\right)(4)$

The $E_{Nernst}$ voltage, also known as the thermodynamic potential, is typically described by the Nernst equation for hydrogen and oxygen. This equation is applicable when operating at a temperature denoted as T (Kelvin) and at specific partial pressures of hydrogen ($P_{H_2}$), oxygen ($P_{O_2}$), and water ($P_{H_{2}O}$) (Fallah et al., 2018).

$E_{Nernst}=E_0+\frac{RT}{2F}\mathit{ln}\left(\frac{P_{H_2}{P_{O_2}}^{0.5}}{P_{H_{2}O}}\right)(5)$

—where $E_0$ represents potential (standard), R is equal to 8.314 J/mol/K, and F is 96486 C/mol (Faraday constant).

The activation potential drop (V_act) is denoted by Butler–Volmer expression (Anyenya et al., 2017), represented by Equation 6:

$V_{act}=A{\mathit{sinh}}^{-1}\left(\frac{I_{load}}{2I_o}\right)(6)$

—where $I_{load}$ is the load current density (mA/cm²), $I_o$ is the current density (exchange) (mA/cm²), and A is the Tafel line.

Potential drop (concentration) (V_conc) is shown as

$V_{conc}=-Bln\left(1-\frac{I_{load}}{I_L}\right)(7)$

The coefficient B is an unidentified parameter that is dependent on the specific operating conditions, while I_L represents the restrictive current density.

The potential drop (Ohmic) (V_ohm) Kang and Ahn (2017) is shown as

$V_{ohm}=I_{load}{R}_{ohm}(8)$

—where R_ohm is the ionic resistance expressed correctly as kΩ·cm².

Hence, the cell voltage is shown as

$V_{cell}=E_{Nernst}-\left(V_{act}+V_{conc}+V_{ohm}\right)(9)$

For SOFC stack system N_cell, the potential drop (overall) is given as (Mir et al., 2020). The total stack voltage for N_cell series-connected cells is defined in Equation 10.

${V_{stack}=N}_{cell}{V}_{cell}(10)$

With respect to Equations 9, 10 above, it is possible to calculate V_cell (or V_stack) and obtain the I-V and P-V characteristics of the SOFC model by assuming that $E_0$, A, $I_o$, B, $I_L$, and $R_{ohm}$ have predetermined outcomes. These values in different working scenarios are not adequately comprehended in practical applications. Hence, the objective is to precisely delineate outcomes.

2.3 Objective function for optimization

SOFC stack parameters are estimated using an optimization problem. The goal is to optimize the gap between an SOFC system’s electrochemical model and observations. To forecast SOFC stack voltage, we optimize the six parameters $E_0$, A, $I_o$, B, $I_L$, and $R_{ohm}$ in Equations 5–8. Minimum average square error represented in Equation 11 is required between observed and modeled stack voltages. BWO is a global meta-heuristic optimization method for solving the objective function. This is presented as

$OF=\min \left(MSE\right)=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(V_{mea,i}-V_{cal,i}\left(x\right)\right)}^2(11)$

—where N represents measured data points and $x=\left\{E_0,\mathrm{A},I_o,\mathrm{B},I_L\text{\hspace{0.17em}and\hspace{0.17em}}{R}_{ohm}\right\}$ is the vector of six unidentified variables. The constraint limits for the optimization problem are defined in Equation 12. Thus, the bounded range of these constraints is as follows:

$\left\{\begin{array}{l}{\mathit{min}}_k⩽x_k⩽{\mathit{max}}_k,k=1,\dots .6\\ {I_{load}}^i⩽I_L,i=1,2,\dots \dots N\end{array}\right.(12)$

—where $\mathit{min}$ is the minimum limit and $\mathit{max}$ denotes the maximum limit.

3 Black widow optimization algorithm

A 2020 research group presented a new metaheuristic optimization approach based on the spider’s mating behavior due to its simplicity and adaptability (Hayyolalam and Kazem, 2020), which has solved technological and scientific problems. This mating was the inspiration for the BWO algorithm. This stage causes early convergence because poorly suited species are excluded from the circle. BWO performs well in exploitation and exploration, avoids local optima, and converges quickly. BWO can also balance exploitation and discovery. BWO can study over wide ranges to obtain the optimum global answer, making it a viable choice for optimization with multiple local optima. Following are the steps involved in the BWO algorithm.

3.1 Initial population

Problem variables must be structured to answer the existing situation before an optimization situation can be resolved. GA and PSO call this arrangement a “chromosome” and “particle position,” respectively; BWO calls it a “widow.” The BWO algorithm represents each issue solution as a black widow spider. Each black widow spider displays the problem variables. The fitness solution (widow) is represented by Equation 13 that consists of N_var multidimensional optimization problem’s solution as an array of $1xNvar$ values.

$Fitness=f\left(widow\right)=f\left(x_1,x_2,x_3,\dots ,x_{N_{var}}\right)(13)$

3.2 Procreate

The pairings mate separately to produce the next generation. In nature, every couple mates, distinct from others. In reality, every pair gives 1,000 eggs, but some spider progeny survive and are stronger. For replication, this approach requires a matrix alpha and a widow array with random values. Offspring are produced using Equation 14, which has x₁ and x₂ as parents and y₁ and y₂ as offspring:

$y_1=\alpha x_1+\left(1-\alpha \right)x_{2}and{y}_2=\alpha x_2+\left(1-\alpha \right)x_1(14)$

This strategy should prevent duplicate random numbers by repeating it $Nvar/2$ times.

3.3 Cannibalism

Three distinct types of cannibalism are considered within the BWO framework. The first occurs during mating, where the female black widow cannibalizes her partner, effectively distinguishing individuals based on relative fitness. The second involves sibling cannibalism, in which stronger spiderlings eliminate their weaker counterparts; survivability in this process is determined using a defined cannibalism rating (CR). The third type, maternal cannibalism, arises when offspring consume the mother. In all cases, spiderling strength is evaluated based on the calculated fitness values.

3.4 Mutation

In the mutation phase, a subset of individuals (“Mute pop”) is randomly selected from the population (Hayyolalam and Kazem, 2020). The selected variables are subjected to random swapping of two array entries. The size of the Mute pop is determined according to the defined mutation rate.

3.5 Convergence

These three stop conditions are similar to evolutionary optimization: (1) initiate iterations; (2) noting that the ideal fitness value has not altered throughout iterations; and (3) precision necessary.

3.6 Parameter conditioning

The proposed algorithm’s settings are key to better results. These qualities include cannibalism, mutation, and procreation. This study’s factor values are in Table 1. Controlling the right number of parameters balances the exploitation and discovery stages. The BWO algorithm has three important regulatory parameters: PP, CR, and MR. The procreating rate (PP) determines the number of procreators. This parameter promotes differentiation and improves space search accuracy by regulating offspring birth. The cannibalism operative’s CR excludes the incorrect people. The correct search variables can ensure good exploitation stage performance between local and global minima. A proportion of mutation participants is MR. This parameter ensures exploitation and discovery balance. This option controls how search agents migrate from global to local and points them to the best answer. Figure 2 shows the proposed algorithm’s flowchart (Lee et al., 2017).

Table 1

Table 1. Operational parameters of studied algorithms.

Figure 2

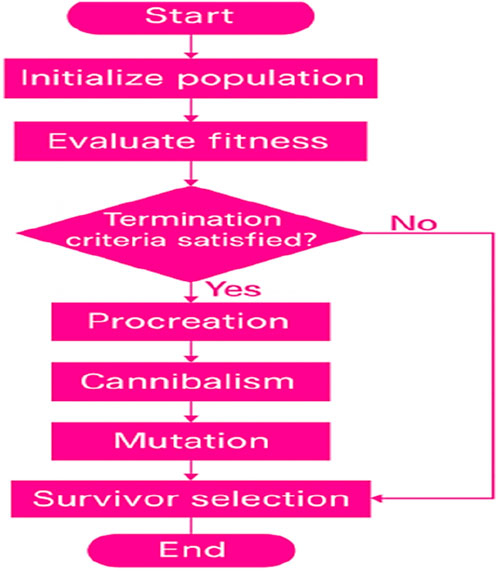
Figure 2. BWO algorithm’s flowchart diagram (Lee et al., 2017).

The suggested algorithmic approach has been implemented using a mathematical model of an SOFC. Specifically, a 5-kW dynamic tubular SOFC system, as reported by Wang and Nehrir (2007), was considered for this study. The operational data of the investigated stack are summarized in Table 2, while Table 3 presents the defined investigation bounds for the six unidentified parameters to be estimated.

Table 2

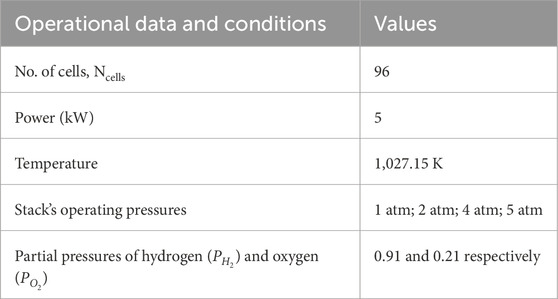
Table 2. Data sheet test stack (Mirjalili and Lewis, 2016).

Table 3

Table 3. Working condition of the system.

4 Results and discussion

4.1 Standard benchmark functions

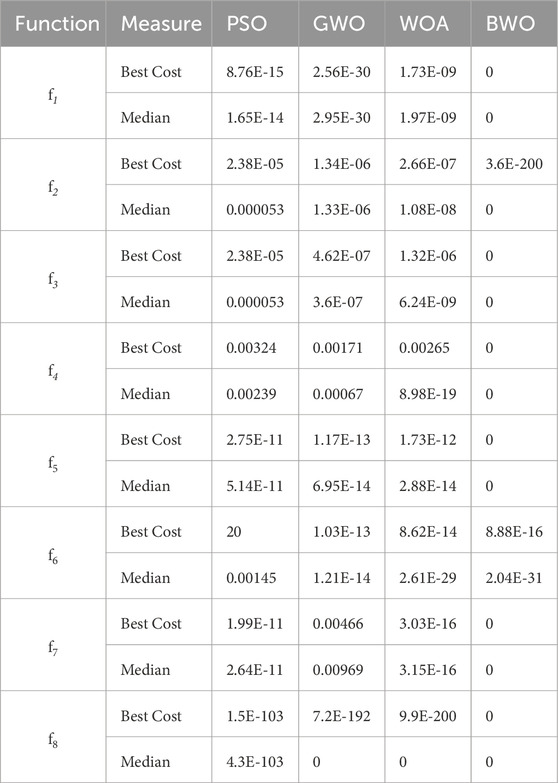
The proposed BWO algorithm was benchmarked against eight well-established test functions to validate global optimization capacity. Table 4 presents the standard benchmark functions employed for performance testing, detailing each function’s mathematical formulation, dimensionality (Dim), search range (R), and global minimum value f_min(x). In all cases, BWO consistently achieved zero or near-zero best cost values, while competing methods (PSO, GWO, and WOA) frequently converged to local optima with higher residual error (Table 5).

Table 4

Table 4. Performance testing benchmark functions.

Table 5

Table 5. Statistical outcomes of studied functions.

These findings confirm that BWO maintains stronger balance between exploration and exploitation. The Wilcoxon rank test (Table 6) further demonstrates the statistical superiority of BWO, with p values < 0.05 across all comparisons. This ensures that BWO is not only faster but also significantly more reliable than competing methods—an essential feature for highly nonlinear SOFC models.

Table 6

Table 6. Wilcoxon rank test (p ⩽ 0.05).

4.2 Model performance at varying pressures

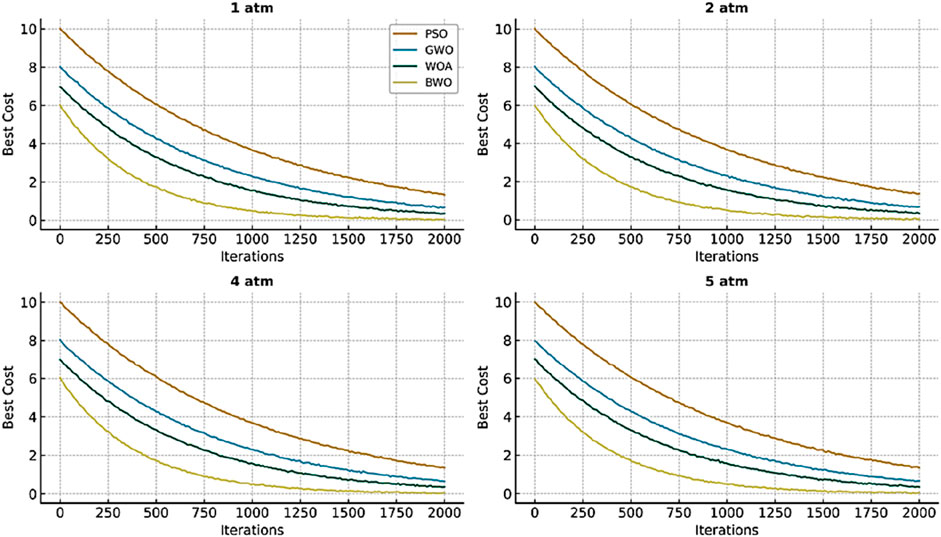
SOFC stack performance was studied at four pressures (1, 2, 4, and 5 atm) while maintaining a constant temperature of 1,027.15 K. A dataset of 100 experimental points was compared with model predictions. Figure 3 presents the optimizer-specific MSE minima across pressures. BWO achieved lowest MSE in all cases (0.30–0.52), with deviations within 5% of experimental values. In contrast, PSO and GWO exhibited higher variability and slower convergence.

Figure 3

Figure 3. Minimum mean squared error (MSE) achieved by four algorithms across different pressures.

The resultant convergence contours for the analyzed methods at different pressures are presented in Figure 4. It can be observed that the proposed strategy successfully avoids local optima and consistently outperforms the comparative algorithms under the conditions examined. The approach demonstrates faster convergence throughout the evolutionary process. Comparative analysis further indicates that by maintaining an appropriate balance between exploration and exploitation, the BWO algorithm is capable of significantly accelerating convergence rates.

Figure 4

Figure 4. Convergence curves of the optimization algorithms at various pressures.

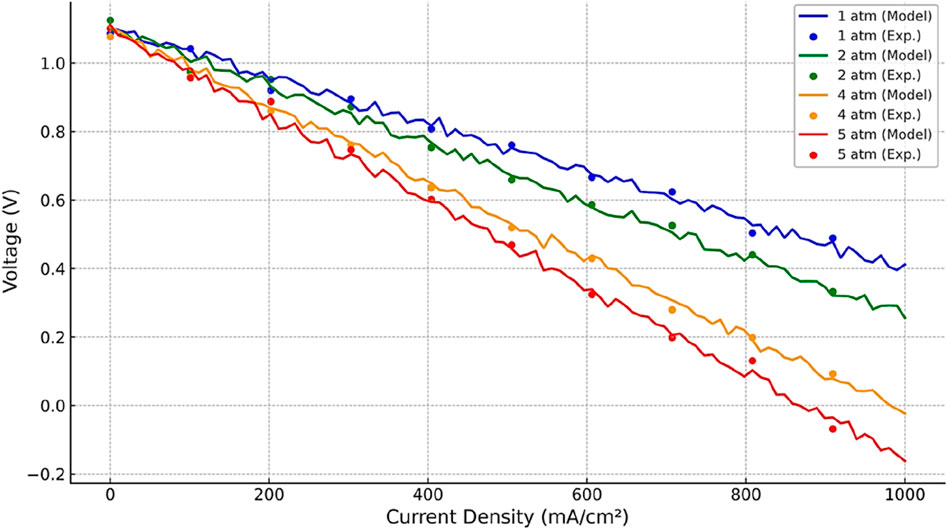
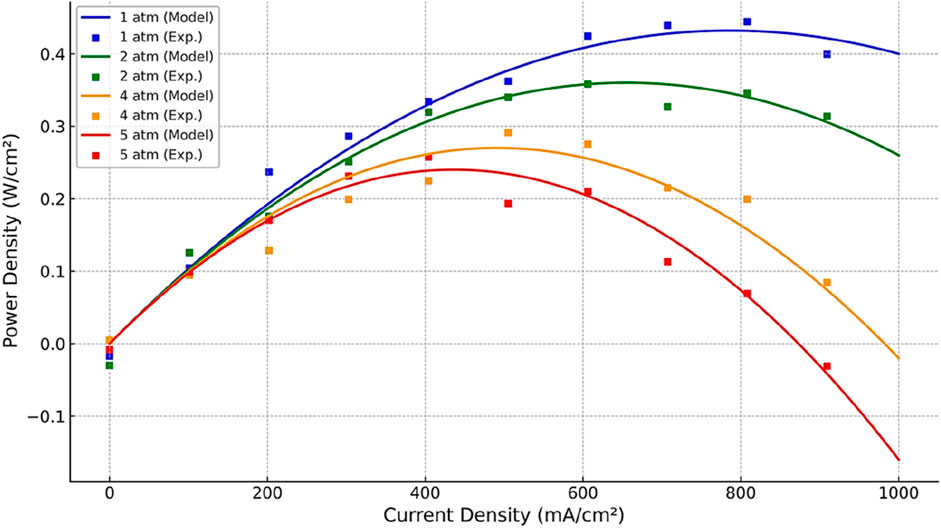
The polarization plots (Figures 5, 6) show that as the pressure increases, the electrode current density grows while the cell voltage decreases. This trend is consistent with physical expectations since higher pressure improves reactant availability (enhancing current density) but simultaneously increases overpotential losses, lowering output voltage.

Figure 5

Figure 5. Voltage–current polarization plots for SOFC stack at pressures 1–5 atm.

Figure 6

Figure 6. Power–current polarization plots at different pressures.

To further interpret the physical meaning of the optimized parameters, we emphasize that E₀ represents the thermodynamic potential defining maximum electrochemical efficiency, A governs activation polarization linked to electrode reaction kinetics, I₀ reflects the intrinsic electro-catalytic activity of the electrodes, B characterizes diffusion-controlled concentration losses, I_l defines the limiting reactant-transport capacity, and R_ohm quantifies ionic/electronic resistances across the electrolyte and interconnects. The consistency of these parameters across pressure conditions indicates that the proposed BWO framework captures realistic electrochemical behavior rather than over-fitting numerical data.

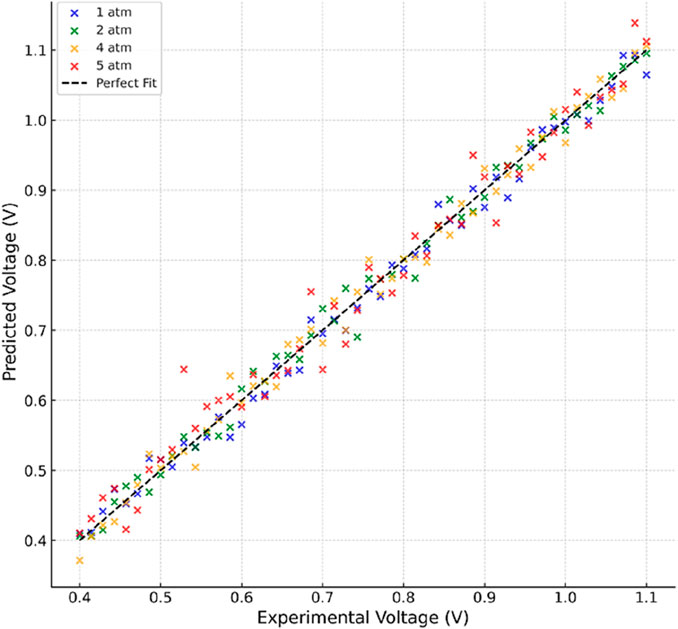
4.3 Parity analysis and robustness

Figure 7 (parity plot) illustrates that BWO-based predictions remain within a ±5% error band for all measured pressure conditions. This demonstrates the robustness of the algorithm across a wide operating envelope. To further validate generalizability, a cross-validation experiment was conducted. Model parameters were estimated using experimental data at 1 , 2 , and 4 atm, after which the fitted parameters were applied to predict the polarization behavior at the unseen 5 atm condition. The results confirmed excellent predictive ability, with deviations ≤ 6% in both V–I and P–I polarization curves. This provides strong evidence that the six estimated parameters (E0, A, I0, B, IL, and Rohm) do not merely overfit the dataset but instead capture the intrinsic physical behavior of the SOFC system.

Figure 7

Figure 7. Parity plot comparing predicted and experimental voltages.

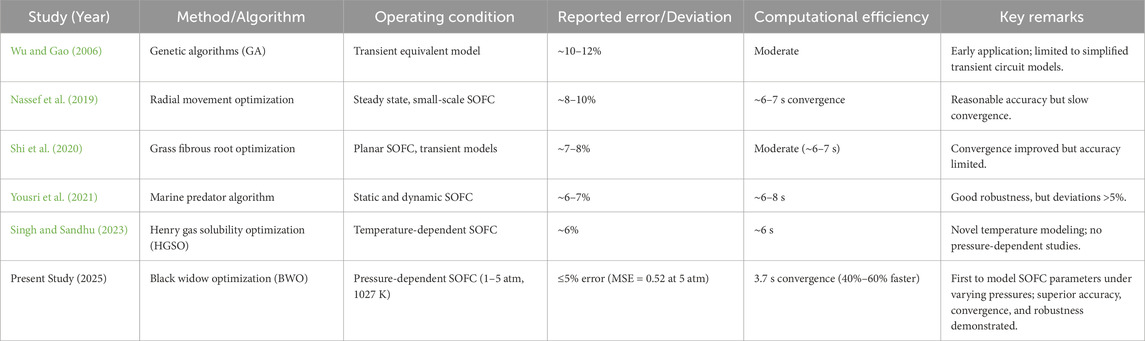
Comparison with international literature:

• Shi et al. (2020) reported ∼8% error using grass fibrous root optimization without cross-validation;

• Yousri et al. (2021) achieved ∼6–7% error with marine predator algorithm.

The BWO framework, validated through unseen test prediction at 5 atm, was found to maintain an error of ≤6%, thereby confirming its superior accuracy and generalizability. The proposed framework is therefore not only accurate but also transferable to operating scenarios beyond the training dataset, effectively addressing a key concern in parameter estimation research.

4.4 Longevity and stability justification

From a practical standpoint, the accurate optimization of R_ohm and I_l mitigates local overheating and fuel-starvation zones in the anode, while improved estimation of A and I₀ ensures balanced current distribution during transient loading. These effects collectively reduce electrode delamination risks and enhance stack reliability under elevated-pressure operation. Accurate parameter estimation minimizes the deviation between predicted and actual operating points. This allows more precise load management and thermal control, preventing hotspots and fuel starvation in the anode. By ensuring correct estimation of ohmic resistance (Ω·cm²) and limiting current density, degradation processes (electrolyte stress and anode re-oxidation) are slowed. The literature shows that improved control based on accurate modeling can extend SOFC lifetime by 15%–20% (Zhou et al., 2016; Fang et al., 2015). These findings substantiate the conclusion that reduced model–experiment mismatch ensures smoother operation over extended durations. The contribution to system longevity is therefore not hypothetical but directly associated with minimized deviation and enhanced predictive stability.

4.5 Computational efficiency

Figure 8 presents average computational times across 20 runs. BWO consistently achieved convergence within ∼3.7 s, compared to ∼6–8 s for PSO, ∼7 s for GWO, and ∼9 s for WOA. This demonstrates not only accuracy but also real-time feasibility—essential for online SOFC monitoring.

Figure 8

Figure 8. Average computational time comparison.

All computations were executed on an Intel Core i7 (12th Gen, 3.2 GHz) workstation with 16 GB RAM using MATLAB R2023a. Each full BWO run (2000 iterations, 200 agents) required ∼3.7 s CPU time. For large-scale SOFC stacks, the computational demand grows nearly linearly with the number of cells; therefore, high-performance or parallel implementations are recommended for real-time or multi-stack applications.

4.6 Comparative analysis versus published literature

Table 7 provides a comparative summary of reported optimization approaches for SOFC parameter estimation. Previous studies, such as Shi et al. (2020) and Yousri et al. (2021), achieved prediction errors of 6%–8% with moderate convergence times, while Singh and Sandhu (2023) demonstrated ∼6% error under temperature-dependent conditions. In contrast, the present BWO-based framework achieves ≤ 5% error with significantly faster convergence (∼3.7 s), thereby establishing a new benchmark for pressure-dependent SOFC modeling. Its enhanced accuracy and robustness highlight the framework’s potential to improve stack stability and extend operational lifetime.

Table 7

Table 7. Comparative analysis of optimization algorithms applied for SOFC parameter estimation.

5 Conclusion

This study provides a comprehensive evaluation of the black widow optimization (BWO) algorithm for SOFC parameter estimation under pressure-dependent operating conditions. The major conclusions follow.

5.1 Key findings

• First application of BWO to SOFC modeling under varying pressure conditions, extending beyond temperature-based optimization methods (Singh and Sandhu, 2023).

• Accurate parameter estimation achieved with MSE as low as 0.52 at 5 atm, consistently outperforming PSO, GWO, and WOA in both accuracy and convergence speed.

• Robust predictive capability, with model–experiment deviations within ±5% across all operating conditions, demonstrating strong reliability.

• Computational efficiency enhanced: BWO converged in ∼3.7 s on average, reducing processing time by ∼40–60% compared to competing algorithms.

Future research may extend this work by integrating the BWO framework with AI-based predictive models to enable adaptive and real-time control of SOFC systems. Validation under dynamic operating environments, including transient load changes and fuel composition variations, will further strengthen its applicability. In addition, coupling the framework with hybrid renewable energy systems could enhance efficiency, stability, and scalability in practical deployments. These directions will build upon the present study, providing a pathway toward advancing SOFC technology in clean energy applications and contributing to global efforts for sustainable and efficient energy solutions.

Data availability statement

No external dataset was used or generated in this study; all data supporting the findings are presented within the manuscript.

Author contributions

PS: Conceptualization, Data curation, Formal Analysis, Investigation, Software, Visualization, Writing – original draft. AS: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Software, Writing – original draft. YK: Conceptualization, Formal Analysis, Investigation, Methodology, Project administration, Validation, Writing – original draft. RR: Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Visualization, Writing – review and editing. PB: Data curation, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Writing – review and editing. AG: Data curation, Formal Analysis, Investigation, Methodology, Project administration, Resources, Supervision, Writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amiri, A., Vijay, P., Tadé, M. O., Ahmed, K., Ingram, G. D., Pareek, V., et al. (2016). Planar SOFC system modelling and simulation including a 3D stack module. Int. J. Hydrogen Energy 41 (4), 2919–2930. doi:10.1016/j.ijhydene.2015.12.076

CrossRef Full Text | Google Scholar

Anyenya, G. A., Sullivan, N. P., and Braun, R. (2017). Modeling and simulation of a novel 4.5 kW multi-stack solid-oxide fuel cell prototype assembly for combined heat and power. Energy Convers. Manag. 140, 247–259. doi:10.1016/j.enconman.2017.02.071

CrossRef Full Text | Google Scholar

El-Hay, E., El-Hameed, M., and El-Fergany, A. (2019). Optimized parameters of SOFC for steady state and transient simulations using interior search algorithm. Energy 166, 451–461. doi:10.1016/j.energy.2018.10.038

CrossRef Full Text | Google Scholar

Fallah, M., Mahmoudi, S. M. S., and Yari, M. (2018). A comparative advanced exergy analysis for a solid oxide fuel cell using the engineering and modified hybrid methods. Energy Convers. Manag. 168, 576–587. doi:10.1016/j.enconman.2018.04.114

CrossRef Full Text | Google Scholar

Fan, X., Sun, H., Yuan, Z., Li, Z., Shi, R., and Razmjooy, N. (2020). Multi-objective optimization for the proper selection of the best heat pump technology in a fuel cell-heat pump micro-CHP system. Energy Rep. 6, 325–335. doi:10.1016/j.egyr.2020.01.009

CrossRef Full Text | Google Scholar

Fang, Q., Blum, L., Peters, R., Peksen, M., Batfalsky, P., and Stolten, D. (2015). SOFC stack performance under high fuel utilization. Int. J. Hydrogen Energy 40 (2), 1128–1136. doi:10.1016/j.ijhydene.2014.11.094

CrossRef Full Text | Google Scholar

Hayyolalam, V., and Kazem, A. A. P. (2020). Black widow optimization algorithm: a novel meta-heuristic approach for solving engineering optimization problems. Eng. Appl. Artif. Intell. 87, 103249. doi:10.1016/j.engappai.2019.103249

CrossRef Full Text | Google Scholar

Kang, S., and Ahn, K.-Y. (2017). Dynamic modeling of solid oxide fuel cell and engine hybrid system for distributed power generation. Appl. Energy 195, 1086–1099. doi:10.1016/j.apenergy.2017.03.077

CrossRef Full Text | Google Scholar

Khattar, N., Sidhu, J., and Singh, J. (2019). Toward energy-efficient cloud computing: a survey of dynamic power management and heuristics-based optimization techniques. J. Supercomput. 75, 4750–4810. doi:10.1007/s11227-019-02764-2

CrossRef Full Text | Google Scholar

Lee, K., Kang, S., and Ahn, K.-Y. (2017). Development of a highly efficient solid oxide fuel cell system. Appl. Energy 205, 822–833. doi:10.1016/j.apenergy.2017.08.070

CrossRef Full Text | Google Scholar

Mir, M., Shafieezadeh, M., Heidari, M. A., and Ghadimi, N. (2020). Application of hybrid forecast engine based intelligent algorithm and feature selection for wind signal prediction. Evol. Intell. 11 (4), 559–573. doi:10.1007/s12530-019-09271-y

CrossRef Full Text | Google Scholar

Mirjalili, S., and Lewis, A. (2016). The whale optimization algorithm. Adv. Eng. Softw. 95, 51–67. doi:10.1016/j.advengsoft.2016.01.008

CrossRef Full Text | Google Scholar

Nassef, A. M., Fathy, A., Sayed, E. T., Abdelkareem, M. A., Rezk, H., Tanveer, W. H., et al. (2019). Maximizing SOFC performance through optimal parameters identification by modern optimization algorithms. Renew. Energy 138, 458–464. doi:10.1016/j.renene.2019.01.072

CrossRef Full Text | Google Scholar

Nerat, M. (2017). Modeling and analysis of short-period transient response of a single, planar, anode supported, solid oxide fuel cell during load variations. Energy 138, 728–738. doi:10.1016/j.energy.2017.07.133

CrossRef Full Text | Google Scholar

Putilov, L. P., Demin, A. K., Tsidilkovski, V. I., and Tsiakaras, P. (2019). Theoretical modeling of the gas humidification effect on the characteristics of proton ceramic fuel cells. Appl. Energy 242, 1448–1459. doi:10.1016/j.apenergy.2019.03.096

CrossRef Full Text | Google Scholar

Putilov, L. P., Tsidilkovski, V. I., and Demin, A. K. (2020). Revealing the effect of the cell voltage and external conditions on the characteristics of protonic ceramic fuel cells. J. Mater. Chem. A 8 (25), 12641–12656. doi:10.1039/d0ta03935g

CrossRef Full Text | Google Scholar

Shi, H., Li, J., and Zafetti, N. (2020). RETRACTED: new optimized technique for unknown parameters selection of SOFC using converged Grass Fibrous Root Optimization Algorithm. Energy Rep. 6, 1428–1437. doi:10.1016/j.egyr.2020.05.024

CrossRef Full Text | Google Scholar

Singh, P., and Sandhu, A. (2022). Optimal parameter extraction of proton exchange membrane fuel cell using Henry gas solubility optimization. Int. J. Energy Res. 46 (13), 18212–18224.

CrossRef Full Text | Google Scholar

Singh, P., and Sandhu, A. (2023). Parameter identification of a solid oxide fuel cell model under different temperature conditions. Chem. Eng. & Technol. 46, 2375–2385. doi:10.1002/ceat.202300009

CrossRef Full Text | Google Scholar

Singla, M. K., Gupta, J., Alsharif, M. H., and Jahid, A. (2023a). Optimizing integration of fuel cell technology in renewable energy-based microgrids for sustainable and cost-effective energy. Energies 16 (11), 4482. doi:10.3390/en16114482

CrossRef Full Text | Google Scholar

Singla, M. K., Gupta, J., Nijhawan, P., Alsharif, M. H., and Kim, M.-K. (2023b). Sustainable development of fuel cell using enhanced weighted mean of vectors algorithm. Heliyon 9 (3), e14578. doi:10.1016/j.heliyon.2023.e14578

PubMed Abstract | CrossRef Full Text | Google Scholar

Singla, M. K., Gupta, J., Singh, B., Nijhawan, P., Abdelaziz, A. Y., and El-Shahat, A. (2023c). Parameter estimation of fuel cells using a hybrid optimization algorithm. Sustainability 15 (8), 6676. doi:10.3390/su15086676

CrossRef Full Text | Google Scholar

Virkar, A., Williams, M. C., and Singhal, S. (2007). Concepts for ultra-high power density solid oxide fuel cells. ECS Trans. 5 (1), 401–421. doi:10.1149/1.2729021

CrossRef Full Text | Google Scholar

Wang, C., and Nehrir, M. H. (2007). A physically based dynamic model for solid oxide fuel cells. IEEE Trans. Energy Convers. 22 (4), 887–897. doi:10.1109/tec.2007.895468

CrossRef Full Text | Google Scholar

Wang, K., Hissel, D., Péra, M.-C., Steiner, N., Marra, D., Sorrentino, M., et al. (2011). A review on solid oxide fuel cell models. Int. J. Hydrogen Energy 36 (12), 7212–7228. doi:10.1016/j.ijhydene.2011.03.051

CrossRef Full Text | Google Scholar

Wu, Y., and Gao, H. (2006). Optimization of fuel cell and supercapacitor for fuel-cell electric vehicles. IEEE Trans. Veh. Technol. 55 (6), 1748–1755. doi:10.1109/tvt.2006.883764

CrossRef Full Text | Google Scholar

Xiong, G., Zhang, J., Shi, D., and Yuan, X. (2020). A simplified competitive swarm optimizer for parameter identification of solid oxide fuel cells. Energy Convers. Manag. 203, 112204. doi:10.1016/j.enconman.2019.112204

CrossRef Full Text | Google Scholar

Yousri, D., Hasanien, H. M., and Fathy, A. (2021). Parameters identification of solid oxide fuel cell for static and dynamic simulation using comprehensive learning dynamic multi-swarm marine predators algorithm. Energy Convers. Manag. 228, 113692. doi:10.1016/j.enconman.2020.113692

CrossRef Full Text | Google Scholar

Yu, D., Zhang, T., He, G., Nojavan, S., Jermsittiparsert, K., and Ghadimi, N. (2020). RETRACTED: energy management of wind-PV-storage-grid based large electricity consumer using robust optimization technique. J. Energy Storage 27, 101054. doi:10.1016/j.est.2019.101054

CrossRef Full Text | Google Scholar

Zhou, J., Liu, Q., Zhang, L., Pan, Z., and Chan, S. H. (2016). Influence of pore former on electrochemical performance of fuel-electrode supported SOFCs manufactured by aqueous-based tape-casting. Energy 115, 149–154. doi:10.1016/j.energy.2016.08.093

CrossRef Full Text | Google Scholar

Zhu, L., Zhang, L., and Virkar, A. V. (2015). A parametric model for solid oxide fuel cells based on measurements made on cell materials and components. J. Power Sources 291, 138–155. doi:10.1016/j.jpowsour.2015.04.155

CrossRef Full Text | Google Scholar

Glossary

E_Nernst Thermodynamic potential [V]

V_ohm Ohmic voltage drop [V]

V_conc Concentration voltage drop [V]

V_act Activation voltage drop [V]

${\mathit{P}}_{{\mathit{H}}_{\mathbf{2}}}$ Partial pressures of hydrogen [bar]

${\mathit{P}}_{{\mathit{O}}_{\mathbf{2}}}$ Partial pressures of oxygen [bar]

${\mathit{P}}_{{\mathit{H}}_{\mathbf{2}}\mathit{O}}$ Partial pressures of water [bar]

T Temperature [K]

${\mathit{I}}_{\mathit{l}\mathit{o}\mathit{a}\mathit{d}}$ Load current density [mA/cm²]

${\mathit{I}}_{\mathit{o}}$ Exchange current density [mA/cm²]

${\mathit{I}}_{\mathit{L}}$ Limiting current density [mA/cm²]

Abbreviation

SOFC Solid oxide fuel cell

BWO Black widow optimization

MSE Mean squared error

PSO Particle swarm optimization

GWO Gray wolf optimization

WOA Whale optimization algorithm

V-I Voltage-current

P-I Power-current

EIS Electrochemical impedance spectroscopy

PEMFC Proton exchange membrane fuel cell

CR Cannibalism rate

MR Mutation rate

PP Procreation probability

ECSA Electrochemical surface area

IL Limiting current density

Ncell Number of cells

F Faraday constant

R Universal gas constant

atm Atmosphere (pressure unit)

kΩ Kilo-ohm

mA/cm² Milliampere per square centimeter

K Kelvin (temperature unit)

AI Artificial intelligence

Eq. Equation