Renewable energy consumption optimization allocation strategy for a regional microgrid based on a shared energy storage mechanism

With the continuous maturation of the sharing economy model, the shared energy storage station service model emerges as a promising user-side energy storage application. This article proposes a bilayer optimal configuration method for regional microgrid systems, leveraging shared energy storage station services. First, this article introduces and analyzes the new model’s operation mechanism and profit model (the financial framework that outlines how the shared energy storage station service generates revenue and manages costs to achieve profitability), emphasizing its role in energy sharing governance to enhance economic and operational efficiency within the microgrid system. Second, this service model was applied to a combined cooling, heating, and power regional microgrid system. Aiming at the multiple goals of the lowest operating cost of the energy storage station and the best economic operation of the regional microgrid, a bilayer optimization model was established. The outer model aims to solve the configuration problem of energy storage stations, while the inner model is responsible for optimizing the economic consumption rate (the efficiency with which energy is utilized within the regional microgrids, considering the costs of its generation, storage, and distribution) and the operation of regional microgrids. Based on the Karush–Kuhn–Tucker (KKT) condition of the inner layer optimization model, the inner layer model is transformed into the constraint conditions of the outer layer model, and the Big-M method is adopted to linearize the nonlinear problems in the model. Finally, the rationality and effectiveness of the proposed bilayer optimization model were verified through a case analysis of three typical scenarios. The research results show that after configuring shared energy storage, the operating cost of the regional microgrid system decreases by 15.12%, the new energy consumption rate increases to 97.44%, and the shared energy storage service provider can recover the investment cost within 4.62 years. This indicates that the proposed method for constructing a bilayer optimization configuration can effectively consider the economic consumption of new energy and significantly improve the economic operation of shared energy storage stations and regional microgrids.

1 Introduction

With the continuous growth of global energy demand and the increasingly serious environmental problems, energy storage technology, as a crucial means to achieve sustainable energy development, has garnered widespread attention (Wang, 2023; Hashemizadeh et al., 2024). In recent years, the rapid development of energy storage technology and the emergence of the sharing economy model have presented new opportunities for user-side energy storage applications (Yang et al., 2024; Umar et al., 2025). An emerging form of energy storage application, the shared energy storage station service model can effectively reduce the initial investment cost for users, improve the utilization rate of energy storage systems, and show broad application prospects (Zheng et al., 2025).

However, current regional microgrid systems face numerous challenges in terms of energy storage configuration and operational optimization (Xia et al., 2024). Traditional energy storage configuration methods often overlook the economic and flexibility benefits of energy storage systems, making it challenging to meet the diverse energy demands and complex operating environments of regional microgrids (Shi et al., 2025). Therefore, studying an optimization configuration method for regional microgrids based on shared energy storage services has significant theoretical significance and practical application value (Song et al., 2025).

The optimization of shared energy storage systems in microgrids has been a focal point of research, with various optimization techniques proposed to address different operational objectives. Existing studies can be broadly categorized into three main themes: shared mechanism design, optimization algorithms, and evaluation metrics and control strategies. Below, we provide a detailed analysis and comparison of the techniques used in each category (Ng et al., 2024; Krishankumar et al., 2024).

The main aspects of designing shared energy storage mechanisms include game-theoretic approaches and decentralized frameworks. For the former, Wang Z. et al. (2024) propose a multi-strategy sharing model that combines capacity sharing and energy property trading. This approach effectively balances cost and demand, providing a comprehensive solution for energy storage sharing, although it is computationally intensive due to the use of an evolutionary game model. In contrast, He et al. (2025) introduce a dynamic on-demand renting framework for sharing energy storage capacity. The advantage of this approach is its adaptability to changing demand, but it is sensitive to the accuracy of demand forecasts. For the latter, He et al. (2024) propose a partially decentralized P2P transaction framework for shared energy storage, aiming to increase the utilization of demand-side resources and provide a robust framework for practical applications. However, it requires significant coordination among participants. Yan and Chen (2023) present an equilibrium model that captures the interactions between charging stations, shared energy storage, and the distribution network. However, implementing it in real-world scenarios may be challenging due to the complexity of interactions.

Existing research in the energy storage mechanism optimization configuration algorithm primarily falls into two categories: combinatorial auction mechanisms and two-stage optimization models. Faramarzi et al. (2025) present a computable combinatorial mechanism for energy storage sharing, including a novel auction-solving algorithm. Although it is efficient and accurate, it will be limited in handling highly complex scenarios with numerous participants. Hou et al. (2024) propose a two-stage scheduling optimization model for optimal scheduling in a smart community. However, the two-stage optimization process overlooked the issue of real-time energy consumption. He et al. (2024) further enhance optimization by proposing a two-stage trading optimization strategy, which not only considers supply and demand equilibrium but also incorporates safety, stability, and efficiency. It requires significant computational resources and coordination among multiple stakeholders. Wa et al. (2023) present an enhanced version of the multi-objective grasshopper optimization algorithm, which incorporates advanced features such as Sobol sequence initialization, adaptive social force, cosine parameter, and Levy flight mechanism. Despite the enhanced capabilities of the method, a notable drawback lies in its potentially higher computational demand.

In the control strategy for microgrid energy storage systems, Lin et al. (2024) propose a bi-objective model predictive control-weighted moving average strategy for the operational control of hybrid energy storage systems (HESS), which is sensitive to parameter settings and requires accurate forecasts of wind power generation. Jia et al. (2024) address the challenges of load forecasting accuracy by proposing a short-term load forecasting method using a spatiotemporal graph convolutional neural network. However, it needs significant computational resources and high-quality data for training. Li et al. (2024) propose a decentralized power sharing and stabilization method for HESSs using active disturbance rejection control, which effectively addresses the challenges of managing renewable energy fluctuations and maintaining stability in microgrids. However, there is a potential for higher costs due to the use of specialized components. Taye and Choudhury (2024) propose an adaptive filter-based method as an innovative control strategy for DC microgrid operation, aiming to ensure stable and smooth performance while addressing safety and degradation concerns of the storage devices. Real-time calculations are needed to manage the charging and discharging of the HESS components dynamically.

The technologies discussed in the above-mentioned literature examine the application in various microgrid implementations across different countries, signaling a growing generalization in the research on shared energy storage mechanisms. Advancements in renewable energy technologies have sparked interest in energy storage solutions to ensure grid stability and facilitate the integration of renewable energy. Shared energy storage systems offer benefits like reduced peak demand, increased renewable energy utilization, and improved grid reliability (Chen et al., 2024). A review of international case studies, including a European project that reduced peak demand by 20% and increased renewable energy utilization by 15% (Faria et al., 2025) and an American project that reduced grid congestion by 25% and improved reliability, demonstrates the potential of shared energy storage to improve grid stability and promote renewable energy integration (Barbosa et al., 2017). Additionally, a Chinese project achieved a 30% reduction in energy costs for participating microgrid users, further illustrating the global significance of shared energy storage systems (Li et al., 2023). Our research aims to contribute to the understanding of the role of shared energy storage in shaping sustainable energy systems worldwide, offering insights for its development and implementation in diverse contexts.

Although existing research has made progress in energy storage technology and shared energy storage models, combining the shared energy storage service model with the optimal configuration of regional microgrid systems remains an urgent problem. Most existing research focuses on single-objective optimization, lacking a coordinated approach to the dual objectives of energy storage configuration and system operation. Therefore, there is a need for a bilayer optimization model that can simultaneously consider energy storage configuration and system operation optimization to enhance the economy and efficiency of shared energy storage services and regional microgrid system operation.

Due to the limitations of existing research, this article proposes a bilayer optimal configuration method for regional microgrid systems that utilize shared energy storage services. The main contributions and innovation points can be summarized as follows:

Business model for regional microgrids with shared energy storage stations: Against the backdrop of new energy consumption, this article constructs a business model for shared energy storage services in a multiregional micro-energy network system and conducts an in-depth analysis of its profit principle. By integrating the concept of energy sharing governance, we aim to provide a framework that not only optimizes the economic benefits of shared energy storage but also promotes a more sustainable and efficient approach to energy management within microgrid systems.

Energy storage configuration method considering new energy consumption: This article examines the impact of new energy consumption on the configuration of shared energy storage stations and proposes a capacity and power configuration method for shared energy storage that accounts for reasonable power curtailment.

Bi-layer optimization configuration method: This article constructs a bilayer optimization model. The outer layer model is responsible for solving the configuration problem of energy storage stations, while the inner layer model optimizes the economic consumption rate and the operation of regional microgrids.

Multi-scenario microgrid case analysis: Through the case analysis of three typical scenarios, the rationality and effectiveness of the proposed bilayer optimization model for regional microgrids with shared energy storage stations have been verified.

The structure of the remaining part of this article is organized as follows: Section 2 provides a detailed description of the definition, operation mechanism, and profit model of the shared energy storage station service model and constructs an energy consumption model. Section 3 presents a shared energy storage configuration strategy that takes economic consumption into account, analyzes the impact of new energy consumption on energy storage configuration, and determines a reasonable power curtailment rate. Section 4 constructs a bi-layer optimization model. Section 5 elaborates in detail the solution methods of the model, including the application of Karush–Kuhn–Tucker (KKT) conditions and the linearization processing of the Big-M method. Section 6 verifies the rationality and effectiveness of the proposed method through typical scenario examples. Section 7 summarizes the research results.

2 Energy consumption model based on the shared energy storage mechanism

Shared energy storage is a commercial application model that integrates traditional energy storage technology with the sharing economy model. Energy storage stations are invested in and constructed by shared energy storage station service providers, and energy storage services are provided to users at a certain price. This mode enables users to utilize energy storage systems without incurring high investment, while leveraging the flexibility of the sharing economy to ensure the efficient utilization of energy storage systems, thereby achieving rapid cost recovery of shared energy storage stations.

The regional microgrid users analyzed in this article are the combined cooling, heating, and power regional microgrids, which incorporate various forms of power flow and can meet diverse energy needs, including cooling, heating, and electricity consumption (Huylo et al., 2025; Verdugo et al., 2025). The internal equipment of a regional microgrid includes distributed wind turbines, PVs, gas turbines (GTs), boilers, heat exchangers, refrigeration units, etc. The microgrid achieves coordinated operation of multiple energy sources and efficient energy management through an intelligent control system. Additionally, regional microgrids can enhance system efficiency and reliability by optimizing operational strategies, thereby providing users with stable and economical combined cooling, heating, and power services. The shared energy storage station optimization configuration strategy studied in this article is analyzed based on a combined cooling, heating, and power type regional microgrid system. A typical combined cooling, heating, and power type regional microgrid topology structure participating in the energy storage station service is shown in Figure 1.

Figure 1

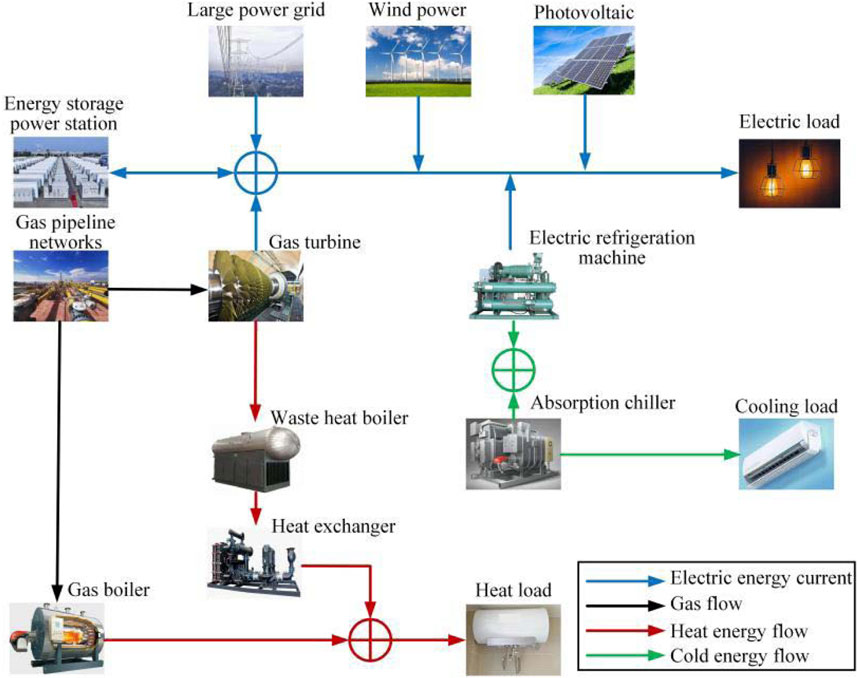
Figure 1. The regional microgrid structure of the combined cooling, heating, and power type participating in the energy storage station.

The connection between the shared energy storage station and the regional microgrid is shown in Figure 2. The shared energy storage station consists of energy storage batteries, power station scheduling modules, inverter modules, and support platform systems. Among them, the energy storage battery is responsible for the storage and release of energy, the inverter module is used to achieve the conversion of AC and DC electrical energy, and the power station scheduling module is responsible for real-time response to user electricity demand, managing the charging and discharging behavior of the energy storage station, and providing energy metering services. The support platform system provides data support and management functions for the operation of the entire power station. In Figure 2, P_sel and P_pur, respectively, represent the power of selling and purchasing electricity from the n-regional microgrid to the energy storage station; P_cha and P_dis are the charging and discharging power of energy storage stations, respectively.

Figure 2

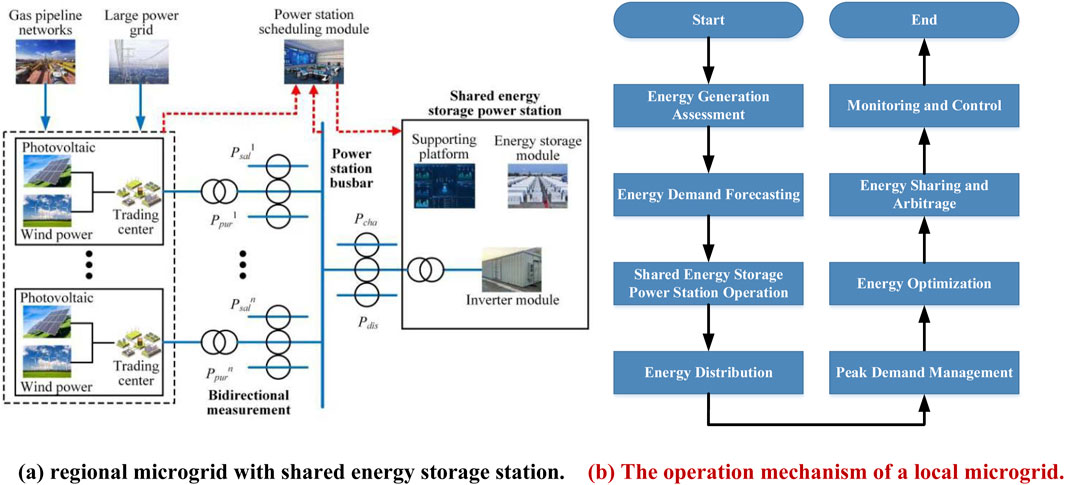
Figure 2. Schematic diagram of a regional microgrid shared energy storage station. (a) A regional microgrid with a shared energy storage station. (b) The operation mechanism of a local microgrid.

In Figure 2a, the power station scheduling module is the core of the entire system, which can dynamically adjust the charging and discharging strategies of the energy storage station based on the user’s electricity demand, grid electricity price, state of charge (SOC) of the energy storage station, and the operating status of the regional microgrid. For example, during periods of low electricity consumption, the scheduling module will prioritize absorbing excess electrical energy (P_sel) from the regional microgrid and storing it in energy storage batteries. During peak hours of electricity consumption, the stored energy will be released (P_cha) to meet the electricity demand (P_pur) of the regional microgrid. Additionally, the scheduling module can optimize the energy flow between the energy storage station and the regional microgrid using intelligent algorithms, thereby increasing the overall system efficiency. The flowchart in Figure 2B provides a visual representation of the operational steps and decision-making process for the shared energy storage power station within a regional microgrid, highlighting key considerations such as energy generation assessment, demand forecasting, and optimization strategies.

As shown in Figure 2, the shared energy storage station acts as a central hub for energy management within the regional microgrid. Excess energy generated by PV panels and wind turbines during peak production times is stored in the energy storage system. When energy demand exceeds supply or during times of low renewable energy generation, the stored energy is released to meet the microgrid’s needs. This process helps balance the supply and demand of energy, reducing reliance on fossil fuels and increasing the utilization of renewable energy sources. Additionally, the model incorporates load shifting mechanisms, where energy is stored during off-peak hours and used during peak demand periods. This helps to flatten the load curve and reduce peak demand, leading to cost savings and increased system reliability. The model facilitates energy arbitrage by exploiting price differences in the energy market. The shared energy storage station can purchase energy from the grid during low-price periods and sell it back during high-price periods, generating additional revenue for the microgrid system.

Compared to traditional energy storage stations, the buses of shared energy storage stations are directly connected to regional microgrid users, enabling bidirectional energy exchange through the power station’s buses. This connection method not only enables flexible transfer of electrical energy at the spatial level in multiregional microgrid systems but also fully utilizes the complementarity between each regional microgrid, improving the energy utilization efficiency of the entire system. For example, when the power generation of a regional microgrid exceeds its demand, the excess electricity can be transmitted to other regional microgrids through the power station bus, thereby avoiding energy waste.

In terms of energy measurement and service fees, shared energy storage stations accurately measure the charging and discharging energy as well as the energy exchanged between regional microgrids, and charge corresponding service fees. Specifically, the charging and discharging power of energy storage stations (P_cha and P_dis) and the power exchanged between regional microgrids (P_sel and P_pur) will be included in the metering system. It is worth noting that although the power exchanged between regional microgrids (P_sel and P_pur) does not directly flow through the energy storage battery, it is still regarded as the process of charging and discharging energy storage stations in terms of metering. This measurement method ensures unified management of all energy flows in energy storage stations and provides a basis for calculating service fees.

The service fees of shared energy storage stations include the following three parts:

The cost of purchasing electricity from regional microgrids, that is, the fee paid by energy storage power stations when absorbing electricity (P_abs) from regional microgrids; Selling electricity fees to regional microgrids, which refers to the fees charged by energy storage stations when releasing electricity (P_rel) to regional microgrids; Additional service fees include maintenance costs, management costs, and fees for optimizing operational strategies of energy storage power plants.

The calculation of these costs is dynamically determined by the power station scheduling module based on parameters such as grid electricity prices, regional microgrid electricity consumption status, and the SOC of the energy storage power station to ensure the economic benefits of the energy storage power station and the efficient operation of the system.

Through this shared energy storage model, not only can the initial investment cost of users be reduced, but the flexibility of the sharing economy can also be fully utilized to achieve efficient utilization and rapid cost recovery of the energy storage system. At the same time, this mode can also improve the energy utilization efficiency and reliability of regional microgrid systems, providing users with more stable and economical combined cooling, heating, and power services.

3 Principles for power configuration of shared energy storage stations

When energy storage power stations serve multi-regional microgrid systems, it is necessary to configure their power capacity to fully utilize the technical characteristics of energy storage systems and leverage the advantages of shared energy storage business models. The construction of shared energy storage stations in user-intensive areas requires considering interconnection with multi-regional microgrid systems during site selection, thereby fully utilizing cluster effects and the complementarity of user loads simultaneously. Compared to users separately configuring energy storage, the cost is lower, and the energy utilization rate is higher.

As shown in Figure 3, this article makes decision configurations for the power capacity of energy storage based on the bilayer optimization technology and at the same time optimizes and analyzes the operation mode of users under shared energy storage services. The decision making on the configuration capacity and power of shared energy storage stations must be comprehensively considered based on the predicted output values of wind power and PV power in the region, as well as the estimated loads of various users, to obtain the optimal energy storage capacity and power under the annual operating cost target of the energy storage power station. At the same time, it is necessary to address optimization operation problems, such as energy exchange between the multi-regional microgrid system and the energy storage power station under a shared energy storage service.

Figure 3

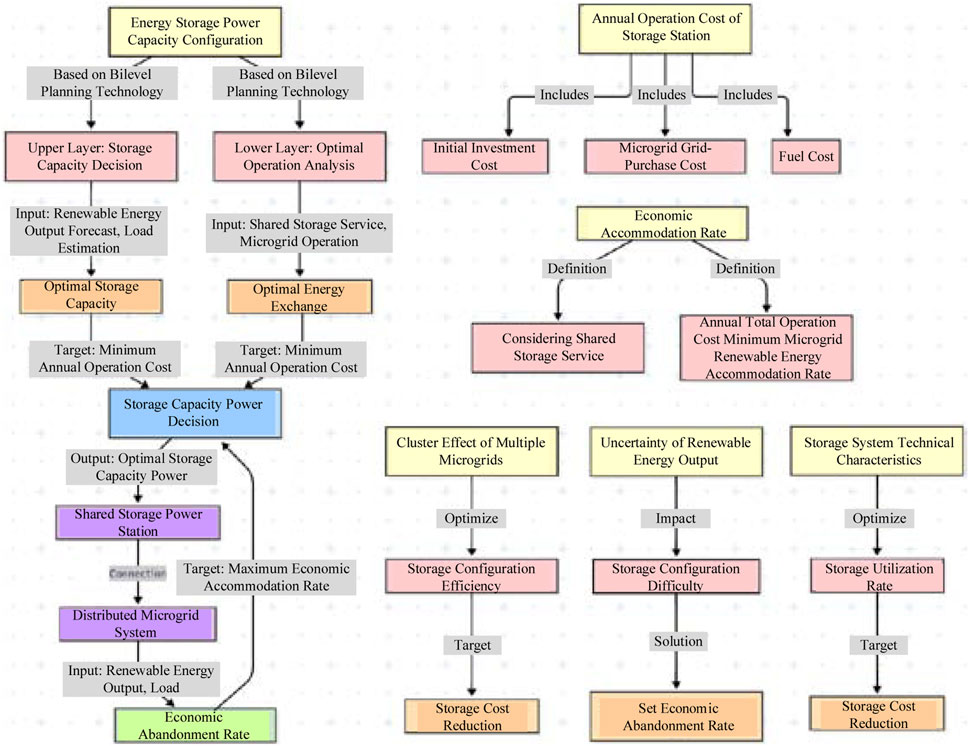
Figure 3. Schematic diagram of capacity and power configuration principles for shared energy storage stations.

Given the substantial uncertainty of the output of new energy, it is not easy to ensure the complete consumption of new energy in the actual operation of power stations. Under the condition of considering the complete consumption of new energy, the configuration of energy storage has little guiding significance for the actual operation of power stations. To fully leverage the role of energy storage systems in absorbing new energy and guide users to consume the output of wind and solar power sources economically, it is not advisable to unthinkingly configure energy storage power stations with the goal of complete consumption of new energy. Under the premise of ensuring that most of the new energy is consumed, a specific economic power curtailment rate can be set, allowing distributed new energy power sources to be reasonably curtailed within a specific range. The economic consumption rate is defined as the annual comprehensive consumption rate of new energy in a regional microgrid that minimizes the total annual operating cost of the power station-regional microgrid system after considering shared energy storage services. The annual operating cost of the power station-regional microgrid includes the annual value of the initial investment cost of the power station converted to the investment cost of each year based on the design service life, as well as the cost of purchasing electricity from the grid and the cost of purchasing fuel for the regional microgrid.

Remark 1. The proposed model is designed to optimize economic benefits and promote sustainable energy management within regional microgrid systems, incorporating advanced optimization techniques that consider the dynamic interplay between energy generation, storage, and consumption. One key innovation is the integration of energy sharing governance principles, which ensures that the shared energy storage station operates in a manner that maximizes economic benefits while promoting sustainable energy practices. This approach contrasts with traditional models, which often lack a comprehensive framework for energy sharing governance.

4 Optimize the configuration of the bilayer optimization modeling

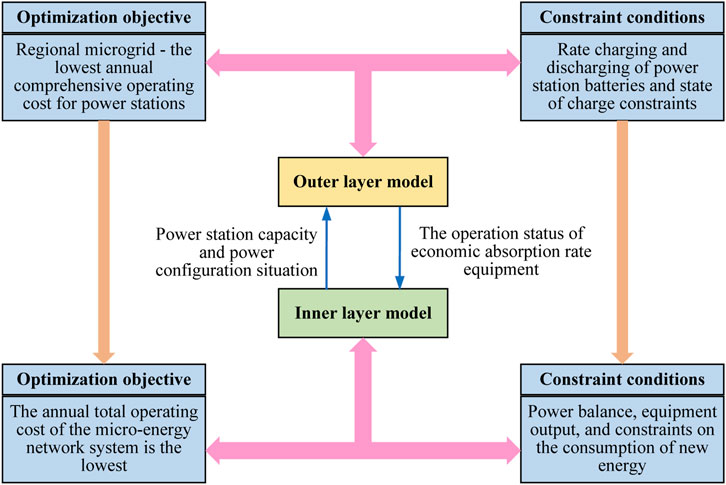
Bilevel optimization is a method that involves two levels of optimization problems, with two optimization objectives: the outer layer and the inner layer. The problem structure is shown in Figure 4. The bilayer problems are coupled, and the decision results influence each other. Under the condition that decisions are made first in the outer layer, the optimal value of the inner layer problem can be sought (Zhao et al., 2022).

Figure 4

Figure 4. Schematic diagram of the double-layer optimization model configuration.

The proposed algorithm utilizes an outer model to determine the optimal consumption rate of new energy and solve the configuration problem of shared energy storage stations. The inner model, based on the outer model, uses the consumption rate and energy storage power station configuration scheme decided by the outer model to solve the optimal operation problem of the regional microgrid.

Through this bi-level optimization method, coordinated optimization can be achieved between the outer and inner layers, thereby increasing the overall system’s efficiency and economy.

4.1 Outer layer model

The outer model is used to address the issues of economic consumption rates and shared energy storage station configurations. The optimization objective is to minimize the comprehensive cost of the shared energy storage station-regional microgrid system. The decision variables are the economic consumption rate of new energy and the power capacity of the shared energy storage station.

4.1.1 Optimize the objective function

The total cost of a shared energy storage station-regional microgrid system consists of three parts: the investment cost of the shared energy storage station, the cost of purchasing electricity from the grid for the regional microgrid, and the cost of purchasing fuel for the regional microgrid. The objective of the outer layer optimization is to minimize the comprehensive cost of the shared energy storage station-regional microgrid system. The objective function of optimization can be expressed as Equation 1 below:

$\min C=C_{\text{inv}}+C_{\text{grid}}+C_{\text{flue}}(1)$

where C_inv is the equal annual value of the investment cost of the shared energy storage station; C_grid is the annual cost of electricity purchased by the regional microgrid from the power grid; C_flue is the annual cost of fuel purchased for the regional microgrid.

4.1.1.1 Investment cost of shared energy storage stations

The investment in shared energy storage stations includes the annual value of the one-time investment for power station construction and the fixed investment cost for maintenance each year. When calculating the investment cost of shared energy storage stations, the time value of funds should be taken into account. Therefore, the annual value of the investment cost can be expressed as Equation 2 below:

$C_{\text{inv}}=\frac{r{\left(1+r\right)}^{\gamma }}{{\left(1+r\right)}^{\gamma }-1}\left({\delta }_{\mathrm{P}}{P}_{\text{ess}}+{\delta }_{\mathrm{E}}{E}_{\text{ess}}\right)+{\delta }_{\mathrm{M}}{P}_{\text{ess}}(2)$

where r represents the annual interest rate of funds; γ represents the life cycle of the device; δ_P represents the single-bit power investment cost; δ_E represents the investment cost per unit capacity; δ_M represents the maintenance cost of single-bit power; P_ess and E_ess are the rated charge and discharge power and rated capacity of the shared energy storage station, respectively.

4.1.1.2 The cost of purchasing electricity from the power grid

The cost for a regional microgrid to purchase electricity from the large power grid as Equation 3 below:

$\left\{\begin{array}{l}{C}_{\text{grid}}^{M,N}={\mathit{\delta }}_0{\left({\mathit{P}}_{\text{grid}}^{M,N}\right)}^{\mathrm{T}}\\ C_{\text{grid}}={\displaystyle \sum _{M=1}^n}{\displaystyle \sum _{N=1}^m}{C}_{\text{grid}}^{M,N}\end{array}\right.(3)$

where C_grid^M,N represents the cost of purchasing electricity from the grid for the Nth regional microgrid on the Mth typical day; δ₀ represents the unit electricity price matrix of the power grid for each dispatching period; P_grid^M,N is the power consumption matrix of the Nth regional microgrid in each scheduling period on the Mth typical day; m and n represent the typical number of days and the number of regional microgrids, respectively.

4.1.1.3 The cost of purchasing fuel

The cost of purchasing fuel for a regional microgrid as Equation 4 below:

$\left\{\begin{array}{l}{C}_{\text{flue}}^{M,N}={\mathit{c}}_0\left(\frac{{\mathit{P}}_{\text{GT}}^{M,N}}{{\eta }_{\text{GT}}{Q}_0}+\frac{{\mathit{Q}}_{\text{GB}}^{M,N}}{{\eta }_{\text{GB}}{Q}_0}\right)\\ C_{\text{flue}}={\displaystyle \sum _{M=1}^n}{\displaystyle \sum _{N=1}^m}{C}_{\text{flue}}^{M,N}\end{array}\right.(4)$

where C_flue^M,N represents the cost of purchasing fuel for the Nth regional microgrid on the Mth typical day; c0 is the matrix of natural gas cost per unit volume; P_GT^M,N, Q_GB^M,N represents the power matrix of the GT and gas boiler of the Nth regional microgrid during each dispatching period on the Mth typical day; η_GT and η_GB represent the efficiencies of GTs and gas boilers, respectively; Q₀ represents the calorific value of the gas.

4.1.2 Constraint conditions

The constraints of the outer model are considered from several aspects, including the energy ratio of the shared energy storage station, the charging and discharging constraints, and the SOC of the energy storage battery.

4.1.2.1 Energy ratio constraints

There is an energy ratio constraint between the capacity of energy storage batteries and their rated power, which is expressed explicitly as Equation 5 below:

$E_{\text{ess}}=\beta P_{\text{ess}}(5)$

where β represents the energy rate of the energy storage battery.

4.1.2.2 Charge and discharge constraints

During the same dispatching period, the charging and discharging status of the power station is determined by the total energy demand after energy exchange is completed at the power station busbar of each regional microgrid user. At the same time, the shared energy storage station is restricted from charging and discharging simultaneously during the same dispatching period. The constraint as Equation 6 below:

$\left\{\begin{array}{l}{\displaystyle \sum _{M=1}^m}\left(P_{\text{ess},\mathrm{s}}^{M,N}\left(t\right)-P_{\text{ess},\mathrm{b}}^{M,N}\left(t\right)\right)=P_{\text{abs}}^M\left(t\right)-P_{\text{rel}}^M\left(t\right)\\ 0\le P_{\text{abs}}^M\left(t\right)\le U_{\text{abs}}^M\left(t\right)P_{\text{ess}}\\ 0\le P_{\text{rel}}^M\left(t\right)\le U_{\text{rel}}^M\left(t\right)P_{\text{ess}}\end{array}\right.(6)$

where P_ess,s^M,N(t) and P_ess,b^M,N(t) represent the power of the Nth regional microgrid in selling electricity to and purchasing electricity from the energy storage power station during the Mth typical day t dispatch period, respectively; P_abs(t) and P_ral(t) are, respectively, the charging and discharging powers of the energy storage power station during the t dispatch period on the Mth typical day; U_abs^M(t) and U_rel^M(t) are the charging and discharging marking positions of the energy storage power station during the typical day t dispatch period of the Mth typical day, respectively

Remark 2. Above, (6) enshrines the charge and discharge constraints, reflecting the regulatory influence on the energy storage system. This ensures operational compliance with energy market policies, aligning the power station’s charging and discharging activities with the aggregated energy demand of microgrid users, while respecting the regulatory ban on simultaneous charging and discharging (Lin et al., 2025).

4.1.2.3 Energy storage batteries SOC constraints

The SOC constraints for energy storage batteries as Equation 7 below:

$\left\{\begin{array}{l}{E}_{\text{ess}}^M\left(t\right)=E_{\text{ess}}^M\left(t-1\right)+{\eta }_{\text{abs}}{P}_{\text{abs}}^M\left(t\right)-\frac{1}{{\eta }_{\text{rel}}}{P}_{\text{rel}}^M\left(t\right)\\ k_{\min }{E}_{\text{ess}}\le E_{\text{ess}}^M\left(t\right)\le k_{\max }{E}_{\text{ess}}\\ U_{\text{abs}}^M\left(t\right)+U_{\text{rel}}^M\left(t\right)\le 1\end{array}\right.(7)$

where E_ess^M(t) represents the SOC of the energy storage battery during the typical day t dispatch period on the Mth typical day; η_abs and η_rel represent the charging and discharging efficiency of the power station, respectively; P_abs^M(t) and P_rel^M(t) represent the charging power and discharging power of the energy storage power station during the typical day t dispatch period on the Mth typical day; k_min and k_max are respectively the lower and upper limits of the SOC of the power station.

Remark 3. Above, (7) sets the SOC constraint for energy storage batteries, adhering to battery management guidelines prescribed by energy authorities. Maintaining the SOC within a safe range prevents deep discharge and overcharging, ensuring battery longevity and economic performance, and highlights the model’s regulatory compliance (Bae and Kim, 2025).

4.2 Inner layer model

The inner model is used to solve the economic operation problem of the regional microgrid. The optimization objective is to minimize the annual operating cost of the regional microgrid. The decision variables include the operational status of each device within the regional microgrid, the regional microgrid’s situation regarding electricity purchases from the power grid, the power exchange situation between the regional microgrid and the shared energy storage station, and the economic consumption rate of new energy. The energy requirements of the regional microgrid can be met while minimizing its operating costs by optimizing these decision variables. This optimization method can not only enhance the economic efficiency of regional microgrids but also improve the utilization efficiency of new energy and promote the realization of sustainable development goals.

4.2.1 Optimize the objective function

The optimization objective of the inner model is to minimize the annual operating cost of the regional microgrid, which can be expressed as Equation 8 below:

$\min C_{\text{MG}}=C_{\text{grid}}+C_{\text{flue}}-C_{\text{ess},\mathrm{s}}+C_{\text{ess},\mathrm{b}}+C_{\text{serve}}(8)$

where C_ess,s represents the annual revenue from electricity sales by the regional microgrid to shared energy storage; C_ess,b represents the annual cost for the regional microgrid to purchase electricity from a shared energy storage station; C_serve is the annual cost of service fees for regional microgrids to shared energy storage stations.

4.2.1.1 Regional microgrid sales revenue to shared energy storage stations

The electricity sales revenue from the regional microgrid to the shared energy storage station can be described as Equation 9 below:

$\left\{\begin{array}{l}{C}_{\text{ess},\mathrm{s}}^{M,N}={\mathit{\delta }}_{\mathrm{s}}{\left({\mathit{P}}_{\text{ess},\mathrm{s}}^{M,N}\right)}^{\mathrm{T}}\\ C_{\text{ess},\mathrm{s}}={\displaystyle \sum _{M=1}^n}{\displaystyle \sum _{N=1}^m}{C}_{\text{ess},\mathrm{s}}^{M,N}\end{array}\right.(9)$

where C_ess,s^M,N represents the electricity sales revenue of the Nth microgrid at the Mth typical daily energy storage power station; δ_s represents the unit electricity price matrix for selling electricity to energy storage power stations during each dispatching period; P_ess,s^M,N represents the power matrix of the Nth microgrid selling electricity to the energy storage power station during each dispatching period on the Mth typical day.

4.2.1.2 Regional microgrid purchases cost from shared energy storage stations

The electricity purchase cost of a regional microgrid from a shared energy storage station can be described as Equation 10 below:

$\left\{\begin{array}{l}{C}_{\text{ess},\mathrm{b}}^{M,N}={\mathit{\delta }}_{\mathrm{b}}{\left({\mathit{P}}_{\text{ess},\mathrm{b}}^{M,N}\right)}^{\mathrm{T}}\\ C_{\text{ess},\mathrm{b}}={\displaystyle \sum _{M=1}^n}{\displaystyle \sum _{N=1}^m}{C}_{\text{ess},\mathrm{b}}^{M,N}\end{array}\right.(10)$

where C_essb^M,N represents the electricity purchase cost of the Nth regional microgrid from the energy storage power station on the Mth typical day; δ_b represents the electricity price matrix per unit of electricity purchased from energy storage power stations during each dispatching period; P_essb^M,N represents the power matrix of the Nth regional microgrid purchased from the energy storage power station during each dispatching period on the Mth typical day.

4.2.1.3 Regional microgrids pay costs to shared energy storage stations

The service cost paid by the regional microgrid to the shared energy storage station can be described as Equation 11 below:

$\left\{\begin{array}{l}{C}_{\text{serve}}^{M,N}={\mathit{\delta }}_{\mathrm{s}}{\left({\mathit{P}}_{\text{ess},\mathrm{s}}^{M,N}+{\mathit{P}}_{\text{ess},\mathrm{b}}^{M,N}\right)}^{\mathrm{T}}\\ C_{\text{serve}}={\displaystyle \sum _{M=1}^n}{\displaystyle \sum _{N=1}^m}{C}_{\text{serve}}^{M,N}\end{array}\right.(11)$

where C_serve^M,N represents the service fee paid by the Nth regional microgrid to the energy storage power station on the Mth typical day.

4.2.2 Constraint conditions

The constraint conditions of the inner model include several aspects, such as the regional microgrid power supply system constraint, the regional microgrid cooling/heating system constraint, the regional microgrid new energy consumption constraint, and the boiler waste heat balance constraint.

4.2.2.1 Constraints of the regional microgrid power supply system

The internal power of the regional microgrid must meet the balance of power generation and consumption, and the constraint conditions are shown in Equation 12 below:

${\mathit{P}}_{\text{GT}}^{M,N}+{\mathit{P}}_{\text{WD}}^{M,N}+{\mathit{P}}_{\text{PV}}^{M,N}+{\mathit{P}}_{\text{grid}}^{M,N}+{\mathit{P}}_{\text{ess},\mathrm{b}}^{M,N}={\mathit{P}}_{\text{ess},\mathrm{s}}^{M,N}+{\mathit{P}}_{\text{EC}}^{M,N}+{\mathit{P}}_{\text{LD}}^{M,N}(12)$

where P_PV^M,N, P_WD^M,N and N represent the PV and wind power output power matrices of the Nth regional microgrid at different dispatching periods on the Mth typical day, respectively; P_EC^M,N, and P_LD^M,N, respectively, represent the power consumption of the electric refrigeration machine and the power matrix of the electric load of the Nth microgrid at different dispatching periods on the Mth typical day.

Regional microgrids can exchange energy with shared energy storage stations, and they cannot charge and discharge simultaneously during the same dispatching period. The energy exchange constraint is shown as Equation 13:

$\left\{\begin{array}{l}0\le P_{\text{ess},\mathrm{s}}^{M,N}\left(t\right)\le U_{\text{ess},\mathrm{s}}^{M,N}\left(t\right)·P_{\text{ess},\max }\\ 0\le P_{\text{ess},\mathrm{b}}^{M,N}\left(t\right)\le U_{\text{ess},\mathrm{b}}^{M,N}\left(t\right)·P_{\text{ess},\max }\\ U_{\text{ess},\mathrm{s}}^{M,N}\left(t\right)+U_{\text{ess},\mathrm{b}}^{M,N}\left(t\right)\le 1\end{array}\right.(13)$

where P_ess,max represents the maximum exchange power between the microgrid and the shared energy storage station; P_ess,s^M,N(t) and P_ess,b^M,N(t) are, respectively, the power sold to the power station and the power purchased from the power station by the Nth regional microgrid during the dispatching period t on the Mth typical day; U_ess,s^M,N(t), U_ess,b^M,N(t) are respectively the charge and discharge identification bits of the Nth regional microgrid during the t scheduling period on the Mth typical day.

The output of electrical equipment within a microgrid and the power purchased by the regional microgrid from the large power grid must meet certain limitations. The constraint conditions as Equation 14 below:

$\left\{\begin{array}{l}{P}_{\text{GT},\min }\le P_{\text{GT}}^{M,N}\left(t\right)\le P_{\text{GT},\max }\\ P_{\text{EC},\min }\le P_{\text{EC}}^{M,N}\left(t\right)\le P_{\text{EC},\max }\\ 0\le P_{\text{grid}}^{M,N}\left(t\right)\le P_{\text{grid},\max }\end{array}\right.(14)$

where P_GT,max, P_GT,min are, respectively, the upper and lower limits of the power generation capacity of the GT; P_EC,max, P_EC,min respectively represent the upper and lower limits of the power consumption of the electric refrigeration machine; P_grid,max represents the maximum power that the regional microgrid can purchase from the power grid; P_GT^M,N(t), P_EC^M,N(t) are, respectively, the output power of the GT and the power consumption of the electric refrigeration machine of the Nth regional microgrid during the t dispatch period on the Mth typical day; P_grid^M,N(t) represents the power purchased by the Nth regional microgrid from the power grid during the t dispatch period on the Mth typical day.

4.2.2.2 Constraints of regional microgrid cooling and heating systems

The regional microgrid cooling and heating system must achieve a balance between cooling and heating power, as well as a balance of waste heat. The constraint conditions are shown in Equation 15:

$\left\{\begin{array}{l}\frac{{\mathit{P}}_{\text{HX}}^{M,N}}{{\eta }_{\text{HX}}}+\frac{{\mathit{Q}}_{\text{AC}}^{M,N}}{{\eta }_{\text{AC}}}={\mathit{P}}_{\text{GT}}^{M,N}{\gamma }_{\text{GT}}{\eta }_{\text{WH}}\\ {\mathit{Q}}_{\text{GB}}^{M,N}+{\mathit{P}}_{\text{HX}}^{M,N}={\mathit{P}}_{\text{heat}}^{M,N}\\ {\mathit{P}}_{\text{EC}}^{M,N}{\eta }_{\text{EC}}+{\mathit{Q}}_{\text{AC}}^{M,N}={\mathit{P}}_{\text{cool}}^{M,N}\end{array}\right.(15)$

where P_HX^M,N and Q_AC^M,N are, respectively, the thermal power matrix of the heat exchanger and the refrigeration power matrix of the absorption chiller of the Nth regional microgrid on the Mth typical day; P_heat^M,N and P_cool^M,N are, respectively, the heat load and cold power matrices of the Nth regional microgrid on the Mth typical day; η_HX, η_AC, η_WH, and η_EC are, respectively, the efficiency of the heat exchanger, the energy efficiency ratio of the absorption chiller, and the efficiency ratio of the waste heat boiler to the energy efficiency ratio of the chiller; γ_GT represents the thermoelectric ratio of the GT.

The constraint conditions determined by (15) ensure the balance of cooling and heating power, as well as the balance of waste heat, within the regional microgrid’s cooling and heating systems. They consider the efficiencies of the heat exchanger, absorption chiller, waste heat boiler, and energy conversion to optimize system performance, aligning the power outputs with the waste heat from the gas turbine and the heat and cooling demands.

The output of the cooling and heating system equipment within the regional microgrid must meet certain limits, and the constraint conditions are shown in Equation 16:

$\left\{\begin{array}{l}{P}_{\text{HX},\min }\le P_{\text{HX}}^{M,N}\left(t\right)\le P_{\text{HX},\max }\\ Q_{\text{AC},\min }\le Q_{\text{AC}}^{M,N}\left(t\right)\le Q_{\text{AC},\max }\\ Q_{\text{GB},\min }\le Q_{\text{GB}}^{M,N}\left(t\right)\le Q_{\text{GB},\max }\end{array}\right.(16)$

where P_HX,max, P_HX,min are the upper and lower limits of the heat exchanger power, respectively; Q_AC,max and Q_AC,min are respectively the upper and lower limits of the power of the absorption chiller; Q_GB,min, Q_GB,min, respectively, represent the upper and lower limits of the power efficiency of the gas boiler; P_HX^M,N(t), Q_AC^M,N(t) and Q_GB^M,N(t) are, respectively, the power of the heat exchanger, the power of the absorption chiller, and the power of the gas boiler of the Nth regional microgrid during the t dispatch period on the Mth typical day.

The constraint conditions determined in (16) set operational limits for the cooling and heating equipment, defining the minimum and maximum power outputs during each dispatch period. They prevent overloading or underutilization, maintaining the efficiency and reliability of the systems and ensuring the overall stability and performance of the regional microgrid.

4.2.2.3 Constraints of regional microgrid new energy consumption

The constraint conditions for the consumption of new energy in regional microgrids can be described as shown in Equation 17 below:

$\left\{\begin{array}{l}{\displaystyle \sum _{M=1}^n}{\displaystyle \sum _{N=1}^m}{\displaystyle \sum _{t=1}^{t_0}}\left(P_{\text{PV}}^{M,N}\left(t\right)+P_{\text{WD}}^{M,N}\left(t\right)\right)=\alpha {\displaystyle \sum _{M=1}^n}{\displaystyle \sum _{N=1}^m}{\displaystyle \sum _{t=1}^{t_0}}\left(P_{\text{PV}0}^{M,N}\left(t\right)+P_{\text{WD}0}^{M,N}\left(t\right)\right)\\ 0\le P_{\text{WD}}^{M,N}\le P_{\text{WD}0}^{M,N}\\ 0\le P_{\text{PV}}^{M,N}\le P_{\text{PV}0}^{M,N}\end{array}\right.(17)$

where P_PV^M,N(t) and P_WD^M,N(t) are, respectively, the output power of PV and wind power of the Nth regional microgrid during the dispatching period t on the Mth typical day; P_PV0^M,N(t) and P_WD0^M,N(t), respectively, represent the maximum available PV and wind power resources of the Nth regional microgrid during the t dispatch period on the Mth typical day; α represents the annual comprehensive consumption rate of new energy in the regional microgrid; t₀ represents the number of scheduling periods per typical day.

4.2.2.4 Constraints on the charging and discharging power of energy storage stations

The power constraints for the purchase and sale of electricity between regional microgrids and energy storage power stations as Equation 18 below:

$\left\{\begin{array}{l}0\le P_{\text{ess},\mathrm{s},w,i}\left(t\right)\le P_{\text{ess},\text{mg}}^{\max }·U_{\text{sale},w,i}\left(t\right):u_{7,i,t,w}^{\min },u_{7,i,t,w}^{\max }\\ 0\le P_{\text{ess},\mathrm{b},w,i}\left(t\right)\le P_{\text{ess},\text{mg}}^{\max }·U_{\text{buy},w,i}\left(t\right):u_{8,i,t,w}^{\min },u_{8,i,t,w}^{\max }\\ U_{\text{buy},w,i}\left(t\right)+U_{\text{sale},w,i}\left(t\right)\le 1:u_{9,i,t,w}^{\max }\end{array}\right.(18)$

where P_{ess, mg}^max represents the maximum interaction power between the microgrid and the energy storage power station; U_buy,w,i(t) and U_sale,w,i(t) represent the power purchase and sale status bits between the ith regional microgrid and the energy storage power station on each typical day; λ_1,i,t,w, λ_2,i,t,w, λ_3,i,t,w, λ_4,i,t,w, and λ_5,i,t,w are equality constraints corresponding to the Lagrange multiplier; u_1,i,t,w^min, u_1,i,t,w^max, u_2,i,t,w^min, u_2,i,t,w^max, u_3,i,t,w^min, u_3,i,t,w^max, u_4,i,t,w^min, u_4,i,t,w^max, u_5,i,t,w^min, u_5,i,t,w^max, u_6,i,t,w^min, u_6,i,t,w^max, u_7,i,t,w^min, u_7,i,t,w^max, u_8,i,t,w^min, u_8,i,t,w^max, u_9,i,t,w^min, and u_9,i,t,w^max are the Lagrange multipliers corresponding to the inequality constraints.

Remark 4. The bi-level optimization model described in Section 4 can be designed with a high degree of flexibility, allowing for its application across a variety of energy systems. The model’s modular structure and adaptable constraints enable it to be tailored to different scenarios, including hydrogen energy storage, district heating, and electric vehicle energy storage applications. By expanding the structure in Figure 4 to the flexible design, the bilevel optimization model can be effectively utilized in diverse energy management contexts, addressing the unique challenges and requirements of each system.

Remark 5. The modeling approach aims to strike a balance between complexity and practicality, focusing on precision sufficient for a bilevel optimization framework in regional microgrids that utilizes shared energy storage. This article recognizes the benefits of more detailed models but emphasizes the need for simplifications due to computational constraints. Assumptions such as fixed charging/discharging efficiencies and deterministic forecasts are used to streamline the optimization process. These simplifications enable efficient analysis of various scenarios and configurations. The model’s limitations are acknowledged and discussed in the Supplementary Material, ensuring transparency and aiding stakeholders’ decision making.

5 Solving process of the designed bilayer model

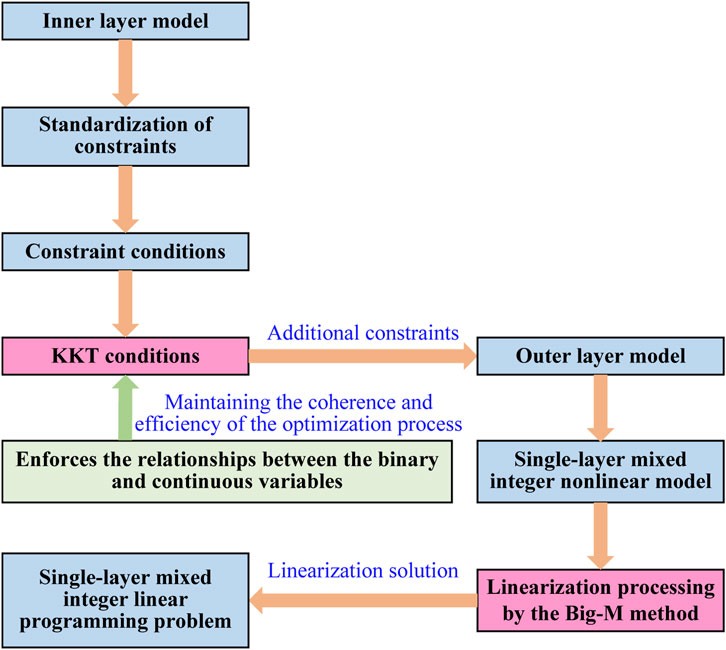
There are nonlinear constraints in the bilevel optimization model constructed in this article, and the bi-layer models are coupled with each other, making it difficult to solve directly. The KKT method can be used to transform and solve it. This method, under the premise of convex continuous differentiability of the inner layer model, can convert the inner layer model into additional constraints of the outer layer model by utilizing the complementary relaxation conditions of the inner layer model, thereby forming a single-layer model. The optimization objective of the transformed model only includes the original outer layer model optimization objective, while the original inner layer model optimization objective and constraint conditions exist in the form of constraints (Wang and Febri, 2024; Wang T. et al., 2024). The transformation and solution process of the bi-level optimization model is shown in Figure 5. The inner layer model is transformed into additional constraints of the outer layer model, forming a single-layer mixed integer linear optimization model. Then, the nonlinear terms in the transformed single-layer nonlinear model are linearized using the Big-M method to form a single-layer mixed integer linear optimization problem (Luo et al., 2021). Subsequently, the solver CPLEX12.8 can be used to solve it.

Figure 5

Figure 5. Schematic diagram of the transformation and solution process for bi-level optimization.

The specific model solution process corresponding to Figure 5 follows.

5.1 Standardization of the inner layer model

To construct the Lagrange function, it is necessary to convert the inner model equations and inequality constraints into the following Equation 19 forms,

$\left\{\begin{array}{l}{g}_i\left(P_i,Q_i\right)=0\\ h_j\left(P_j,Q_j,U_j\right)\le 0\end{array}\right.(19)$

where g_i and h_j represent equality constraints and inequality constraints, respectively; P_i and Q_i represent the variations of electric power and cold and hot power in the equation constraint conditions, respectively; P_j, Q_j, and U_j represent the electric power, cold and hot power, and identification bit variable in the inequality constraint, respectively.

Then, the Lagrange function is constructed in the following form as Equation 20:

$L\left(P_n,Q_n,U_n,{\lambda }_i,{\mu }_j\right)=C_{MG}+{\displaystyle \sum _{i=1}^x}{\lambda }_i{g}_i\left(P_i,Q_i\right)+{\displaystyle \sum _{j=1}^y}{\mu }_j{h}_j\left(P_j,Q_j,U_j\right)(20)$

where λ_i and μ_j are Lagrange multipliers for equality constraints and inequality constraints, respectively; x and y represent the number of constraints of equality and inequality, respectively. Among them, the Lagrange multiplier is a decision variable. To ensure the equation holds, its dimension should match that of the variable in the constraint conditions.

5.2 The inner layer model transformation

For the constructed Lagrange function, partial derivatives are taken for each decision variable. By combining the Lagrange function with the KKT conditions of the inner model, the inner model can be transformed into additional constraints for the outer model, as shown in Equation 21 below:

$\left\{\begin{array}{l}{\displaystyle \sum _{i=1}^x}{\lambda }_i{\nabla }_k{g}_i\left(P_i,Q_i\right)+{\displaystyle \sum _{j=1}^y}{\mu }_j{\nabla }_k{h}_j\left(P_j,Q_j,U_j\right)=0,k=P_i,Q_i,P_j,Q_j,U_j\\ g_i\left(P_i,Q_i\right)=0\\ h_j\left(P_j,Q_j,U_j\right)\le 0\\ {\mu }_j\ge 0\\ {\mu }_j{h}_j\left(P_j,Q_j,U_j\right)=0\end{array}\right.(21)$

where k represents the complete set of all decision variables under the constraints of equality and inequality. It should be noted that after the Lagrange function in the formula is partially differentiated with respect to all decision variables, the number of additional conditions obtained is the same as that of the decision variables.

Remark 6. In the lower-level optimization problem, the presence of binary buy/sell variables necessitates the application of the KKT conditions to transform the problem into a form suitable for integration into the outer-level model. This transformation is crucial for maintaining the coherence and efficiency of the overall optimization process. To address the potential non-convexity or discontinuity introduced by the binary variables, we have employed relaxation techniques and the Big-M method to linearize the model. The relaxation techniques involve replacing the binary variables with continuous variables, allowing for optimization using linear programming solvers. The Big-M method enforces the logical relationships between the binary and continuous variables, ensuring consistency with the original problem’s constraints. This approach maintains the integrity of the optimization problem while making it solvable using linear programming techniques. The relaxation techniques provide a lower bound on the original problem’s solution, and the Big-M method ensures consistency between the relaxed problem’s solution and the original problem’s constraints, resulting in a valid and reliable solution to the optimization problem. This approach optimizes the shared energy storage power station’s configuration and operation within the regional microgrid system, maximizing renewable energy utilization and improving economic and operational efficiency.

5.3 Model linearization

The transformed single-layer model is a mixed integer nonlinear optimization problem. Among them, the inequality constraints in (6) and the nonlinear constraints in the multiplication of decision variables in (21) require a linearization transformation. The Big-M method can be used to transform the above conditions.

The inequality constraints of (6) are transformed as following Equation 22:

$\left\{\begin{array}{l}0\le P_{\text{abs}}^M\left(t\right)\le P_{\text{ess}}\\ 0\le P_{\text{abs}}^M\left(t\right)\le U_{\text{abs}}^M\left(t\right)·M\\ 0\le P_{\text{relea}}^M\left(t\right)\le P_{\text{ess}}\\ 0\le P_{\text{relea}}^M\left(t\right)\le U_{\text{relea}}^M\left(t\right)·M\end{array}\right.(22)$

where M is a sufficiently large integer.

The linearization of the multiplication of decision variables in (21) is shown as following Equation 23:

$\left\{\begin{array}{l}0\le {\mu }_j\le M·u_j\\ 0\le h_j\le M·\left(1-u_j\right)\end{array}\right.(23)$

where u_j is a Boolean variable. It should be noted that to ensure the non-equation holds true, the Boolean dimension should match the dimension of the variable in the original constraint condition.

6 Analysis of calculation examples

A calculation example is set up to analyze the configuration of the shared energy storage station. The calculation example sets up three regional microgrid systems, namely, MG1, MG2, and MG3. Each microgrid user is directly connected to the shared energy storage station, while the microgrid users are not connected to each other. A year is divided into four typical days by season, and 24 dispatching periods are taken for each typical day, with each dispatching period lasting for 1 h. The typical days were selected using a clustering analysis based on historical weather and energy demand data. From each cluster, the day with the most representative characteristics was identified, which was then designated as the typical day for each season (Ma et al., 2024).

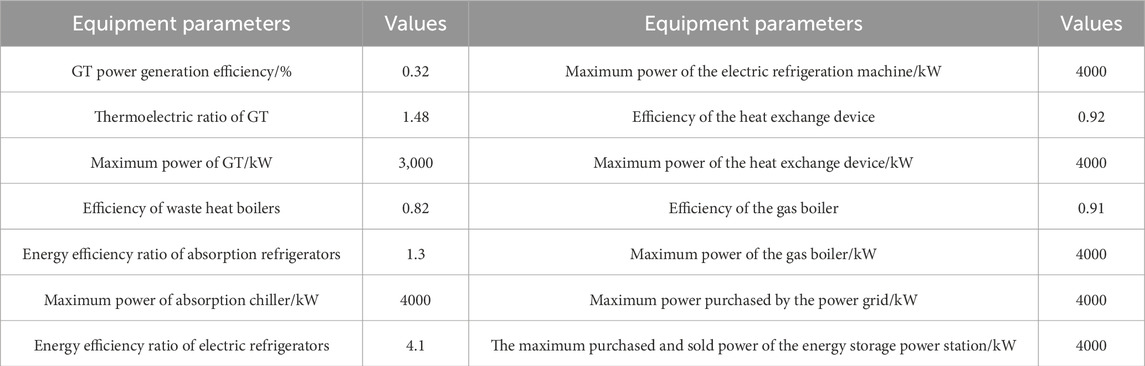
Among the regional systems, MG1 is a multi-power microgrid, MG2 is a general microgrid without wind power, and MG3 is a low-power microgrid. The number of days corresponding to each typical day is 91, and the dispatching time for each typical day is 24 h (Zhao et al., 2024). The relevant parameters of the equipment are shown in Table 1 below. Detailed data of MG1, MG2, and MG3 are listed in detail in the Supplementary Material.

Table 1

Table 1. Parameters of regional microgrid equipment.

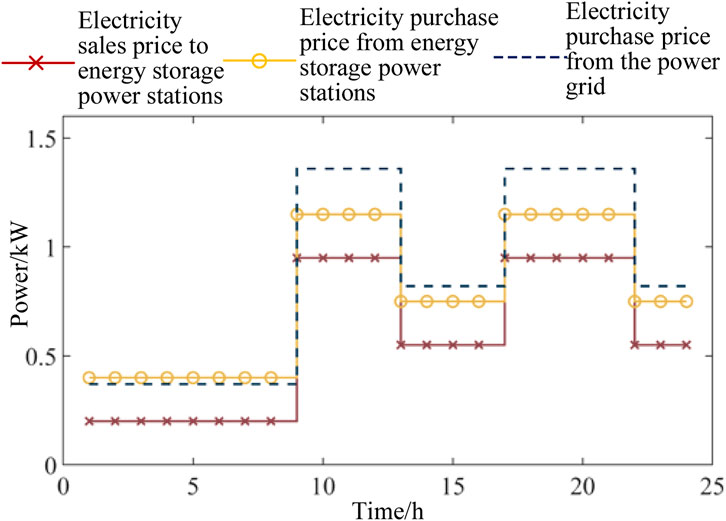
Taking the natural gas price of 2.3 yuan/m³ in Heilongjiang Province, China, as the reference, the grid purchase electricity price adopts the time-of-use electricity price for ordinary industrial users under 1 kV in Heilongjiang Province. The purchase and sale of electricity prices between the regional microgrid and the energy storage power station are shown in Figure 6. The unit price for regional microgrid payment of energy storage power station service fees is 0.06 yuan/(kW·h). The charging and discharging efficiency of the energy storage power station is assumed to be 0.96. The operating range of stored energy is taken as 0.12 to 0.91, and the initial stored energy is taken as 0.2. The capacity cost of the energy storage power station is based on the average winning bid price of lithium iron phosphate batteries in a certain energy storage project, which is 1,895 yuan/(kW·h), the power cost is 990 yuan/kW, the operation and maintenance cost is 74 yuan/(year·kW), and the life cycle of the energy storage power station is 10 years. Other algorithm parameters can be found in the open-source program in the Supplementary Material. In addition, the natural gas selling price and the transaction price of the shared energy storage system set here in this article are both based on the actual prices in the case area. The discussion on the model optimization performance caused by the fluctuation of price parameters is further supplemented in the Supplementary Material.

Figure 6

Figure 6. Schematic diagram of the transformation and solution process for bi-level optimization.

The typical calculation case scenarios in this article are set as follows:

1. Scenario 1: The combined cooling, heating, and power regional microgrid system does not have energy storage and operates independently. Any excess electricity is directly discarded, and electricity is purchased from the power grid to meet any insufficiencies.

2. Scenario 2: Configuring energy storage devices for a combined cooling, heating, and power regional microgrid system, considering the economic absorption of the regional microgrid and the energy storage power station, parameters such as the charging and discharging efficiency of the electrical energy storage are the same as those of the shared energy storage station.

3. Scenario 3: The combined cooling, heating, and power regional microgrid system participates in the shared energy storage station service, using the energy storage charging and discharging service of the energy storage power station, without considering additional economic consumption.

In the calculation example, the parameters of the regional microgrid equipment are known quantities. In Scenario 2, the bi-layer optimization method described in Section 4 is employed to address the configuration issues of energy storage power stations and optimize the operation of regional microgrids. Scenario 1 does not consider energy storage services. The optimization objective is to minimize the operating cost of the regional microgrid, and the constraints are similar to those of the inner layer model. The solution model of Scenario 3 is similar to that of Scenario 2, but it does not consider the constraint of renewable energy consumption in regional microgrids.

6.1 Scenario 1: analysis of regional microgrids without shared energy storage stations

Here, an analysis based on the regional microgrid data presents the power prediction analysis results of MG1, MG2, and MG3 on typical days of the four seasons in Figures 7–9, respectively. In the figures, a positive power represents the power provided by the power sources inside and outside the regional microgrid, while a negative power represents the power consumed by all the electrical loads within the regional microgrid. The maximum output of wind power and PV power represents the maximum available wind and solar energy during that period.

Figure 7

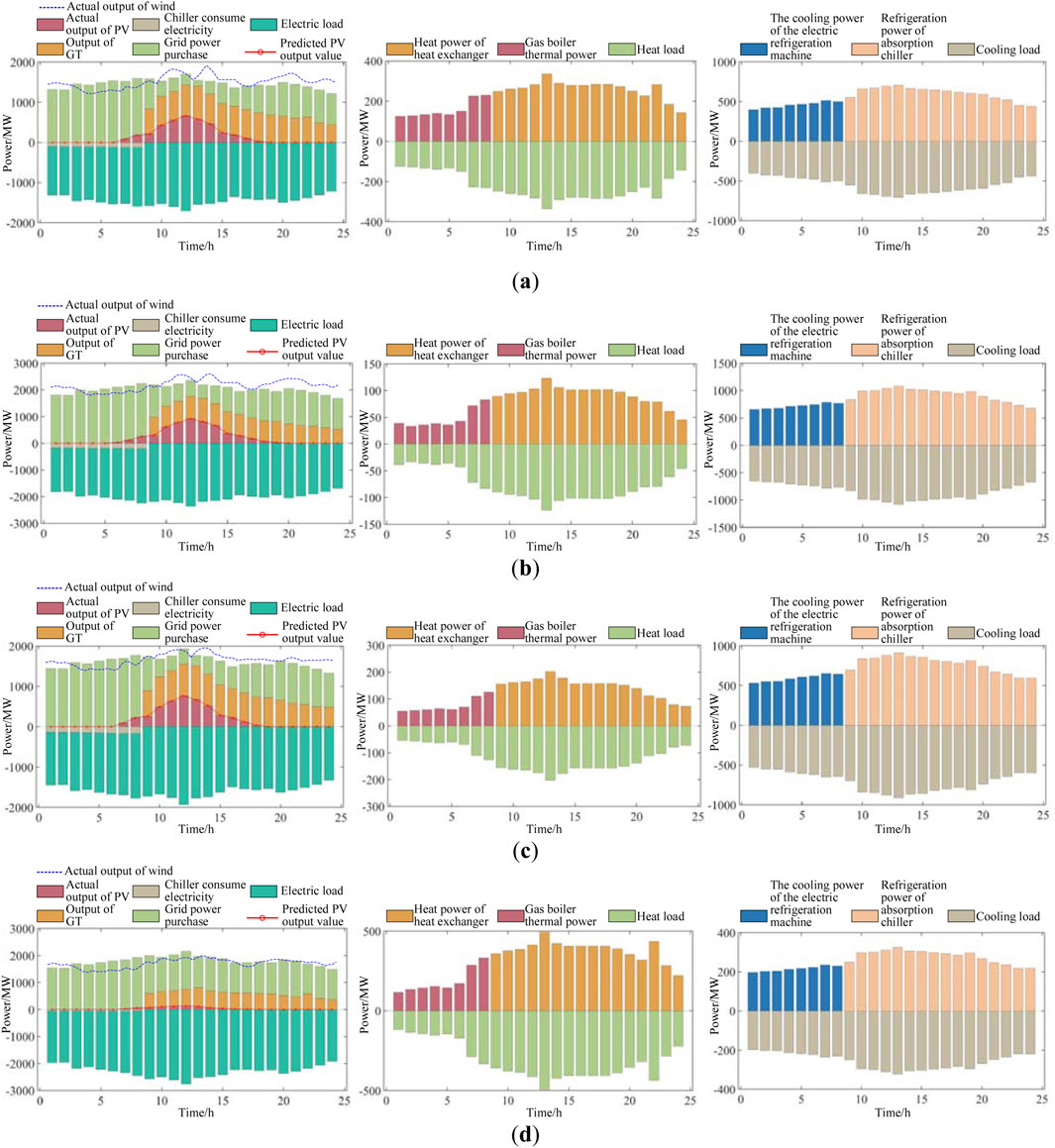
Figure 7. The cold, heat, and electric load power and the predicted generation power curve of PV and wind power of MG1 under Scenario 1: (a) spring forecast; (b) summer forecast; (c) autumn forecast; (d) winter forecast.

Figure 8

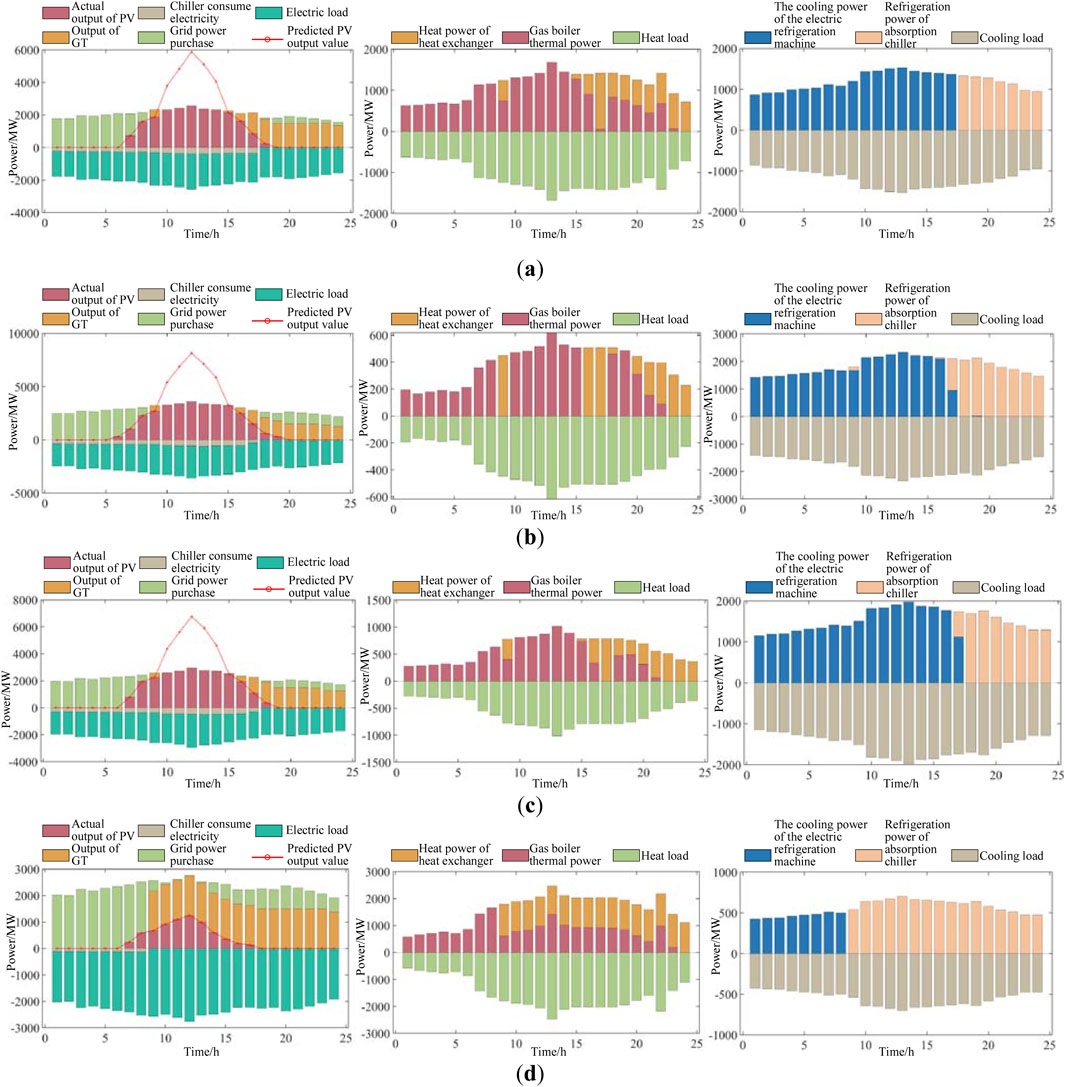
Figure 8. The cold, heat, and electric load power and the predicted generation power curve of PV and wind power of MG2 under Scenario 1: (a) spring forecast; (b) summer forecast; (c) autumn forecast; (d) winter forecast.

Figure 9

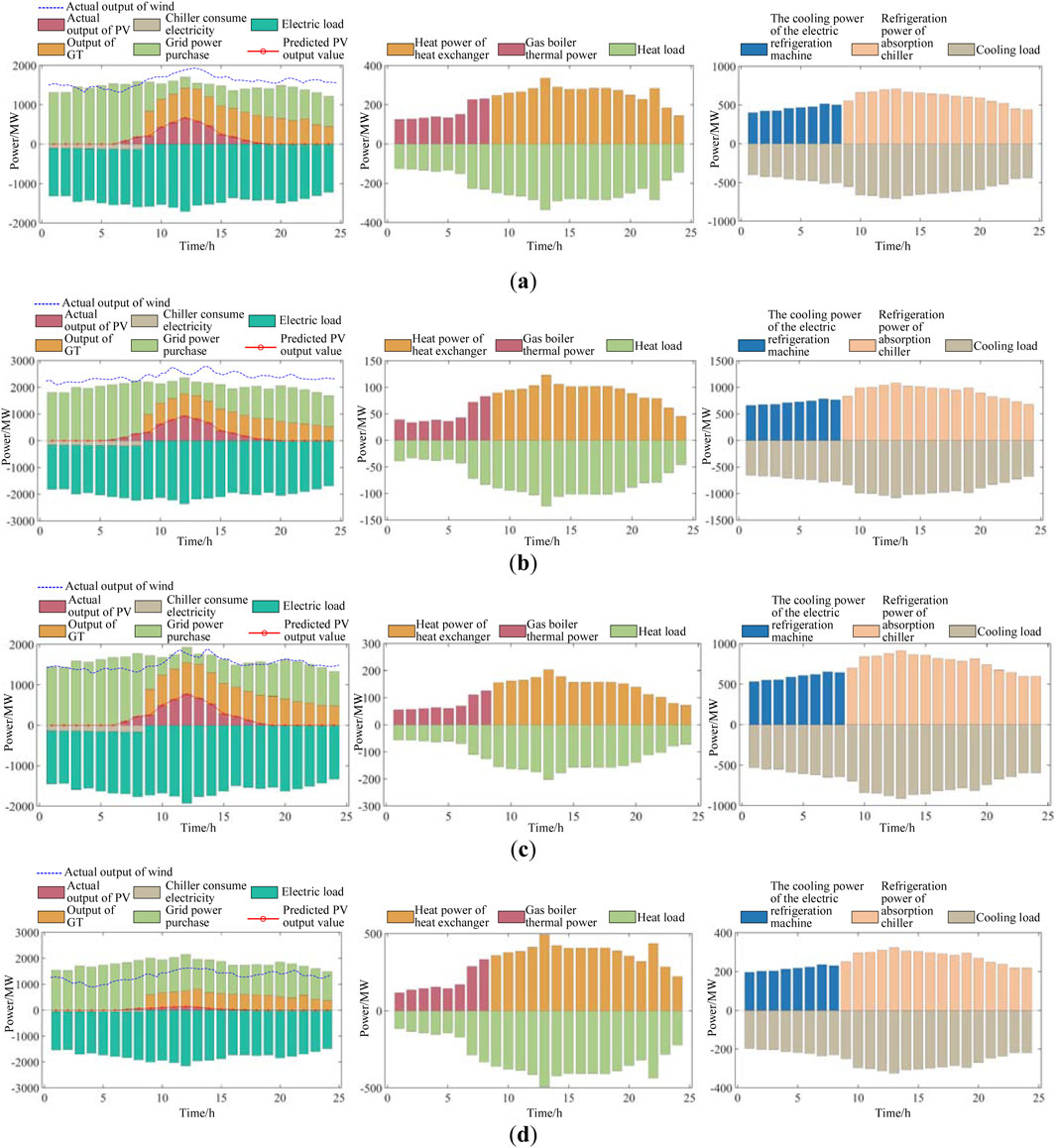
Figure 9. The cold, heat, and electric load power and the predicted generation power curve of PV and wind power of MG3 under Scenario 1: (a) spring forecast; (b) summer forecast; (c) autumn forecast; (d) winter forecast.

In Figure 7, the predicted energy value of the PV processing of MG1 without a shared energy storage device is generally lower, and the actual output power of the PV is also lower. The output power of the GT is higher, the thermal power of the gas boiler is lower, and the cooling power of the absorption chiller and the cooling power of the electric chiller are higher.

In Figure 8, the predicted energy value of the PV processing of MG2 without the configuration of shared energy storage devices is generally higher, while the actual output power of the PV is lower, the output power of the GT is lower, the thermal power of the gas boiler is higher, the cooling power of the electric chiller is higher, and the cooling power of the absorption chiller is lower.

In Figure 9, the predicted energy value of the PV processing of MG3 without shared energy storage devices is generally lower, and the actual output power of the PV is also lower. The overall output of the GT is higher, the thermal power of the gas boiler is lower, the cooling power of the electric chiller is lower, and the cooling power of the absorption chiller is higher.

Under the condition of Scenario 1, the operation mode of the regional microgrid was solved. The natural consumption rate of new energy was 66.47%, and the consumption situation of new energy was not ideal. Taking a typical day in spring as an example for analysis, the power balance of the three regional microgrids is shown in Figures 7a, 8a, 9a. On typical spring days, only MG3 can ensure the full consumption of new energy, while both MG1 and MG2 have varying degrees of power curtailment. The situation of power curtailment is relatively serious for 10–15 h. Among them, MG2 must purchase electricity from the power grid or use GTs to supplement when the PV output is insufficient, and power curtailment will occur when the PV output is excessive. There is an imbalance in the time distribution between the load and the power source. MG3 can fully consume its new energy, but it still needs to purchase a large amount of electricity from the power grid. This highlights the importance of the proposed strategy, which aims to address these inefficiencies and improve the overall performance of the regional microgrid system by optimizing the use of renewable energy sources through a shared energy storage mechanism, thereby increasing the consumption rate of new energy and reducing reliance on traditional power sources.

Remark 7. To ensure accurate metering of the exchanged energy within our shared energy storage power station service model, the algorithm incorporates specific parameters that track energy transactions between the shared storage and the regional microgrid users. These parameters are designed to capture the energy flow in real-time, providing a clear and transparent record of the energy exchanged between the shared storage and the microgrid users. The metering process is integrated into the algorithm’s structure, ensuring that all energy transactions are accounted for and that the economic analysis reflects the actual energy exchanges taking place within the microgrid system. By embedding these metering capabilities into the algorithm itself, we aim to enhance the transparency and reliability of our economic analysis, offering valuable insights for stakeholders seeking to implement shared energy storage solutions within regional microgrid systems.

6.2 Scenario 2: analysis of regional microgrids with economic absorption and shared energy storage stations

Here, a shared energy storage station is configured for the regional microgrid, and further analysis is conducted in combination with the energy consumption model of the local microgrid. The power prediction analysis results of MG1, MG2, and MG3 on typical days in the four seasons are respectively presented in Figures 10–12.

Figure 10

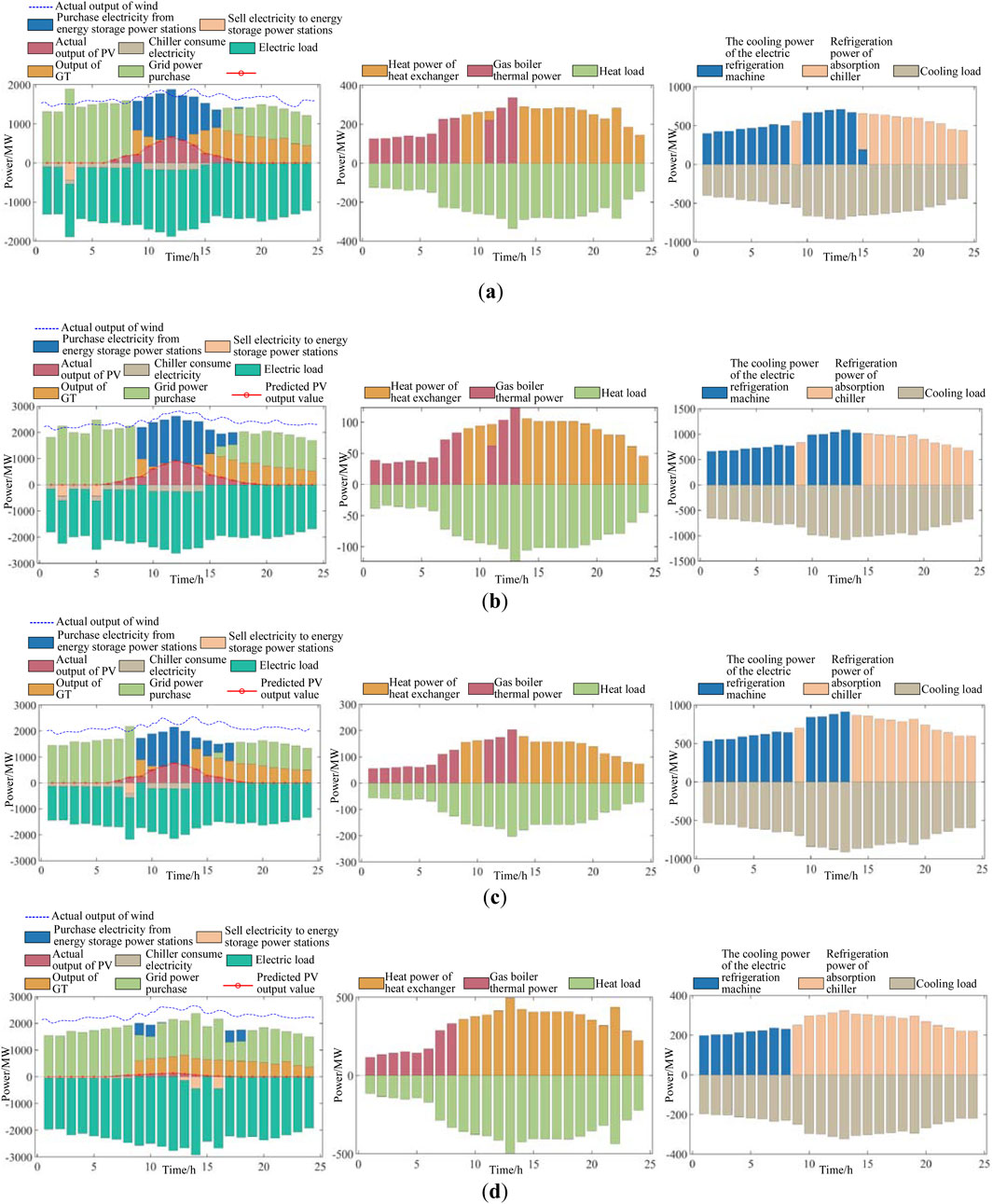
Figure 10. The cold, heat, and electric load power and the predicted generation power curve of PV and wind power of MG1 under Scenario 2: (a) spring forecast; (b) summer forecast; (c) autumn forecast; (d) winter forecast.

Figure 11

Figure 11. The cold, heat, and electric load power and the predicted generation power curve of PV and wind power of MG2 under Scenario 2: (a) spring forecast; (b) summer forecast; (c) autumn forecast; (d) winter forecast.

Figure 12

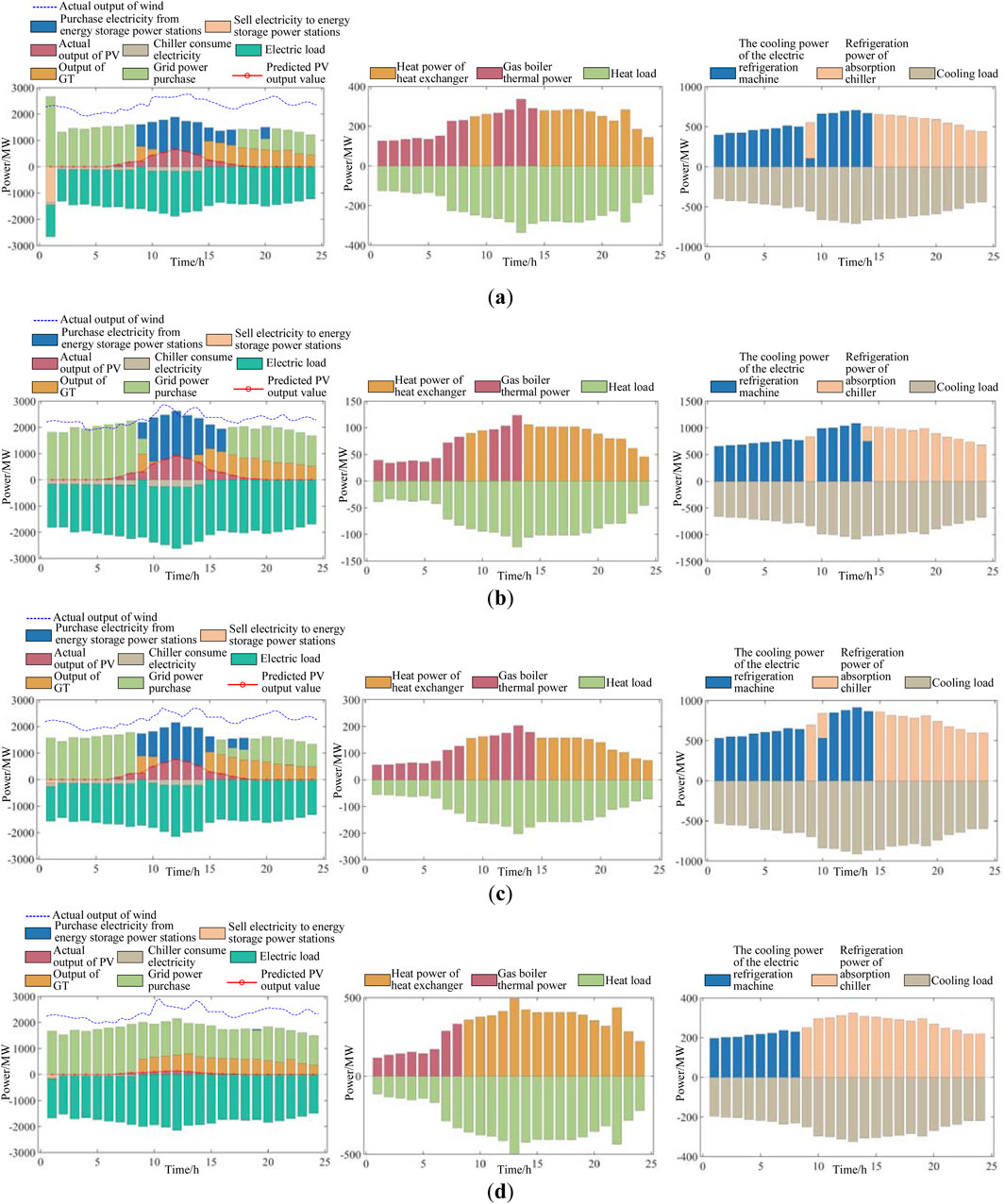
Figure 12. The cold, heat, and electric load power and the predicted generation power curve of PV and wind power of MG3 under Scenario 2: (a) spring forecast; (b) summer forecast; (c) autumn forecast; (d) winter forecast.

In Figure 10, when configuring the shared energy storage device, the predicted energy value of the PV processing of MG1 is generally low, and the actual output power of the PV is also low. The electricity purchased from the energy storage power station is high, while the electricity sold to the energy storage power station is very low. The thermal power of the gas boiler is low, the output of GTs is high, the cooling power of the absorption chiller is high, and the cooling power of the electric chiller is low.

In Figure 11, after configuring the shared energy storage device, the predicted energy value of the PV processing of MG2 is generally high, and the corresponding actual output power of the PV is also high. However, the electricity purchased from the energy storage power station is low, and the electricity sold to the energy storage power station is high. The thermal power of the gas boiler and the output power of the GT are both high, and the cooling power of the absorption chiller and the cooling power of the electric chiller are both high.

In Figure 12, after configuring the shared energy storage device, the predicted energy value of the PV processing of MG3 is generally low, and the actual output power of the PV is also low. Meanwhile, the electricity purchased from the energy storage power station is high, the electricity sold to the energy storage power station is low, the thermal power of the gas boiler is low, and the output of the GT is high. Additionally, the cooling power of the absorption chiller and the electric chiller is relatively high.

In Scenario 2, the regional microgrid is configured with shared energy storage services under the premise of considering economic consumption. The optimized shared energy storage station configuration power was 1,442.6 kW, and the configuration capacity was 3,837.4 kW h. The optimized economic consumption rate was 97.44%, and the cost recovery period was 4.62 years. These results underscore the critical role of the proposed strategy in significantly improving the efficiency and economic benefits of the regional microgrid. The optimized configuration of shared energy storage power stations maximizes the utilization of renewable energy. It ensures a swift return on investment, underscoring the importance of this strategy for sustainable and economically viable microgrid infrastructure. The costs of regional microgrids and the annual revenue of shared energy storage stations in Scenario 1 and Scenario 2 are shown in Table 2.

Table 2

Table 2. The economic benefits of the systems in Scenario 1 and Scenario 2.

Table 2 illustrates the economic impact of incorporating a shared energy storage station in Scenario 2 compared to Scenario 1. The shared energy storage model reduces the microgrid’s total annual operating cost by 377.2 ten thousand yuan, with the shared energy storage station generating a revenue of 255.81 ten thousand yuan. This results in a net system integrated operation cost of 1884.23 ten thousand yuan, demonstrating the financial benefits of shared energy storage. Additionally, the new energy consumption rate increases from 66.47% to 97.44%, indicating a significant boost in renewable energy utilization.

After considering the economic consumption and configuration of shared energy storage station services, the typical daily power balances of the regional microgrid in spring are shown in Figures 10–12. The consumption rate of new energy has increased from 66.47% under natural conditions to 97.44%. The annual total operating cost of regional microgrids has decreased by 15.12%, shared energy storage stations have achieved profitability, and the comprehensive operating cost of the regional microgrid power station system has dropped by 25.32% compared with that of regional microgrids without energy storage configuration.

By comparing the power balance diagrams of the regional microgrid before and after configuring energy storage, it can be seen that the consumption of new energy in the regional microgrid has improved after configuring energy storage. When the load of MG1 is relatively low, it sells the excess electricity to the shared energy storage station, and there are only a few periods of power curtailment. MG2 and MG3 purchase electricity from energy storage power stations when the energy is insufficient, achieving the transfer of energy in time and space, which has a certain improvement on the uncertainty and uncontrollability of the output of new energy.

Figure 13 presents the charging and discharging power dynamics and the SOC of the shared energy storage station on a typical spring day, showcasing the bi-level optimization model’s impact on the microgrid’s energy management. The power station operates with a net negative annual operating cost, indicating profitability, which is a direct result of the model’s strategic configuration and operational planning. During specific time intervals, the power station’s net charging and discharging power is zero in the periods of 0–1 h, 2–10 h, 11–12 h, 14–15 h, 19–20 h, and 22–23 h, allowing regional microgrids to exchange power through the shared busbar, demonstrating the model’s effectiveness in coordinating energy flows across spatial dimensions. During other periods, the power station actively charges and discharges, engaging in energy transfer on a temporal scale, reflecting the lower-level optimization model’s ability to fine-tune the power station’s operational strategy to match fluctuating energy demands. The model’s adaptability and responsiveness to real-time energy needs are evident in its seamless transition between charging and discharging modes, while maintaining a balanced SOC.

Figure 13

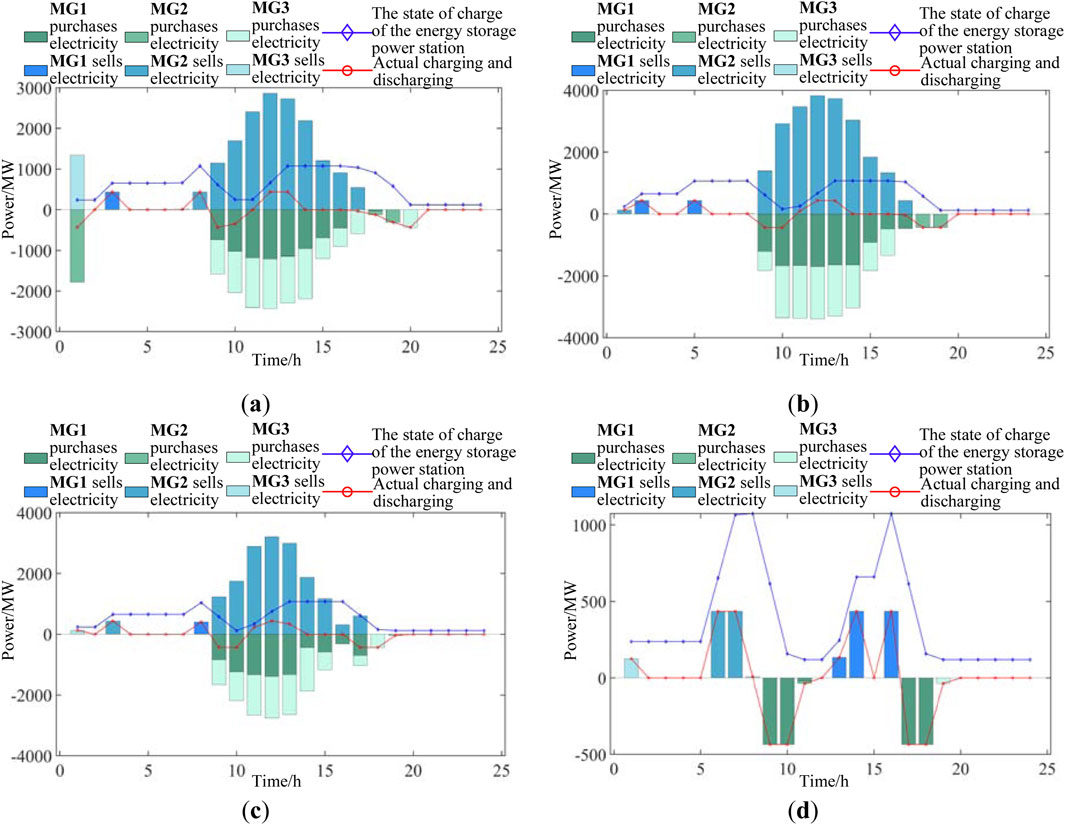
Figure 13. Electricity transaction data prediction between regional microgrids and shared energy storage stations under Scenario 2: (a) spring forecast, (b) summer forecast, (c) autumn forecast, and (d) winter forecast.

Remark 8. To elaborate on the practical implications for microgrid operators, policymakers, and investors, the following provides a more in-depth analysis based on the findings presented in Figures 10, 11, 12.

Microgrid operators: Operators can use Figures 10, 11, 12 to understand how shared energy storage enhances their microgrid’s power balance and increases renewable energy consumption from 66.47% to 97.44%. This rise indicates the model’s effectiveness in integrating renewable energy. Operators can utilize these insights to inform future energy storage investments and enhance energy management for increased renewable integration.

Policymakers: Policymakers can reference the figures to see the benefits of shared energy storage, including a 15.12% decrease in the annual total operating cost of regional microgrids and the profitability of the shared energy storage station. These findings can inform policies that encourage the deployment of energy storage, leading to a more sustainable energy infrastructure.

Investors: Investors can analyze the figures to assess the financial viability of shared energy storage projects. The 25.32% operating cost reduction and profitability of the shared energy storage station provide evidence of the investment potential. This information can help investors make informed decisions, supporting the growth of the renewable energy sector.

6.3 Scenario 3: analysis of regional microgrids with shared energy storage stations without economic absorption

In this scenario, a shared energy storage station is configured for regional microgrids without considering the energy consumption of the regional microgrid for analysis. The power prediction and analysis results of MG1 to MG3 on typical days of the four seasons are presented in Figures 14–16 below.

In Figure 14, after configuring the shared energy storage device, the predicted energy value of the PV processing of MG1 is generally high, and the actual output power of the PV is also high. The electricity purchased from the energy storage power station is low, and the electricity sold to the energy storage power station is high. The thermal power of the gas boiler and the output power of the GT are both high, and the cooling power of the absorption chiller and the cooling power of the electric chiller are also high.

Figure 14

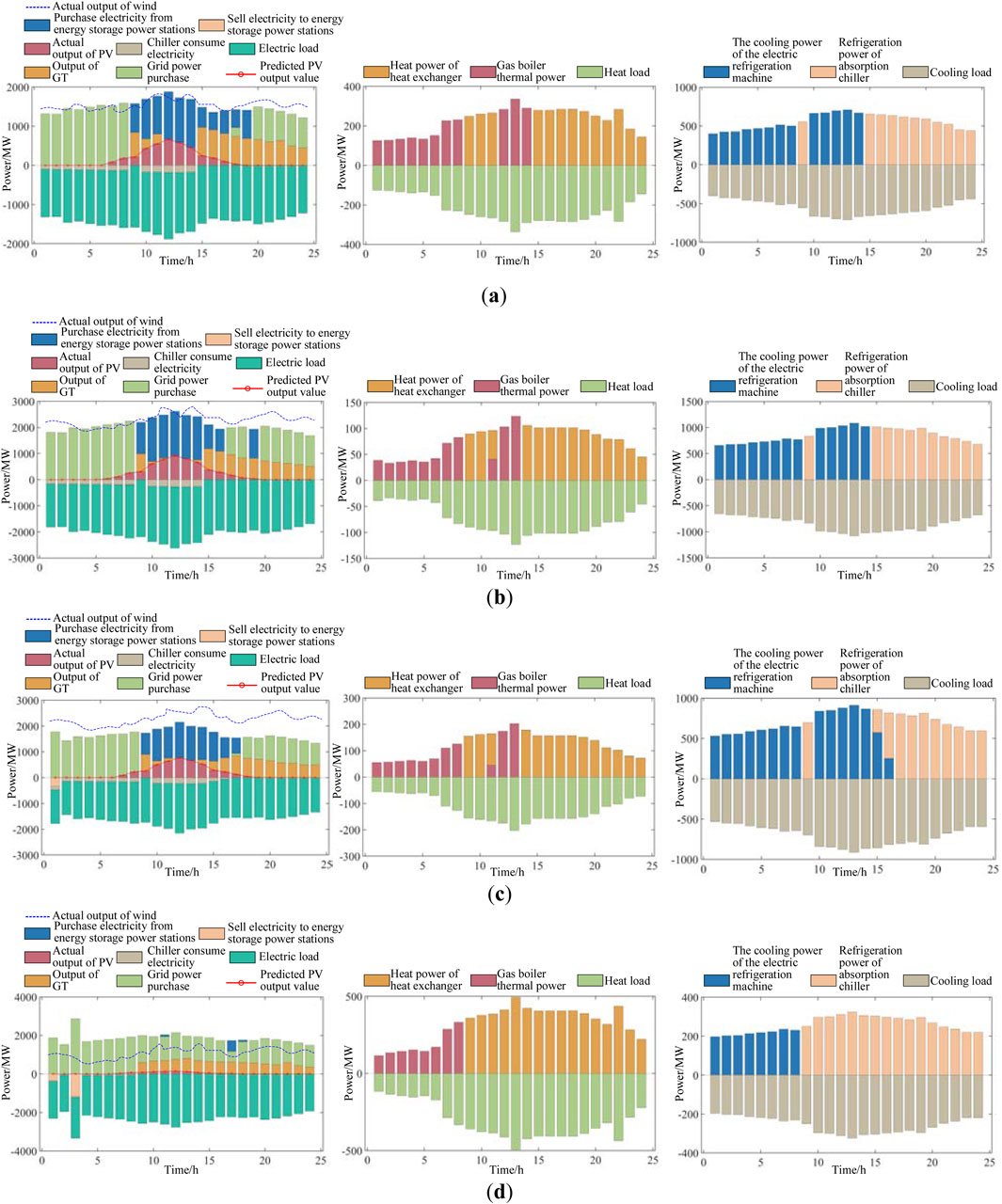
Figure 14. The cold, heat, and electric load power and the predicted generation power curve of PV and wind power of MG1 under Scenario 3: (a) spring forecast, (b) summer forecast, (c) autumn forecast, and (d) winter forecast.

In Figure 15, after configuring the shared energy storage device, the predicted energy value of the PV processing of MG2 and the actual output power of the PV are both relatively high. The electricity purchased from the energy storage power station is relatively low, and the electricity sold to the energy storage power station is relatively high. The thermal power of the gas boiler and the output power of the GT are both relatively high, and the cooling power of the absorption chiller and the cooling power of the electric chiller are also relatively high.

Figure 15

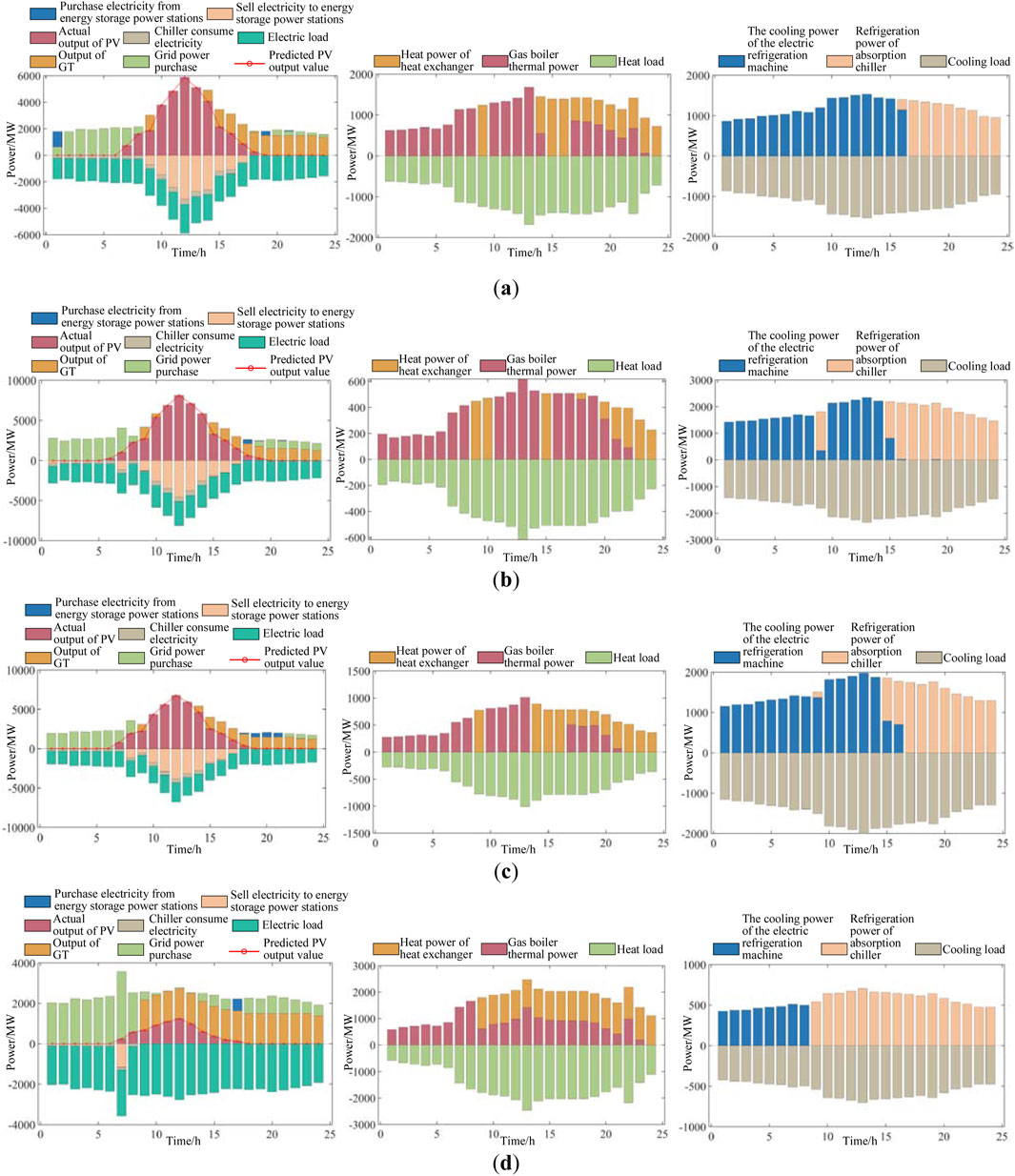
Figure 15. The cold, heat, and electric load power and the predicted generation power curve of PV and wind power of MG2 under Scenario 3: (a) spring forecast, (b) summer forecast, (c) autumn forecast, and (d) winter forecast.

In Figure 16, after configuring the shared energy storage device, both the predicted energy value of the PV processing of MG3 and the actual output power of the PV are relatively low. The electricity purchased from the energy storage power station is relatively high, the electricity sold to the energy storage power station is relatively low, the thermal power of the gas boiler is relatively high, the output of the GT is relatively low, and the cooling power of the absorption chiller and the electric chiller is also relatively high.

Figure 16

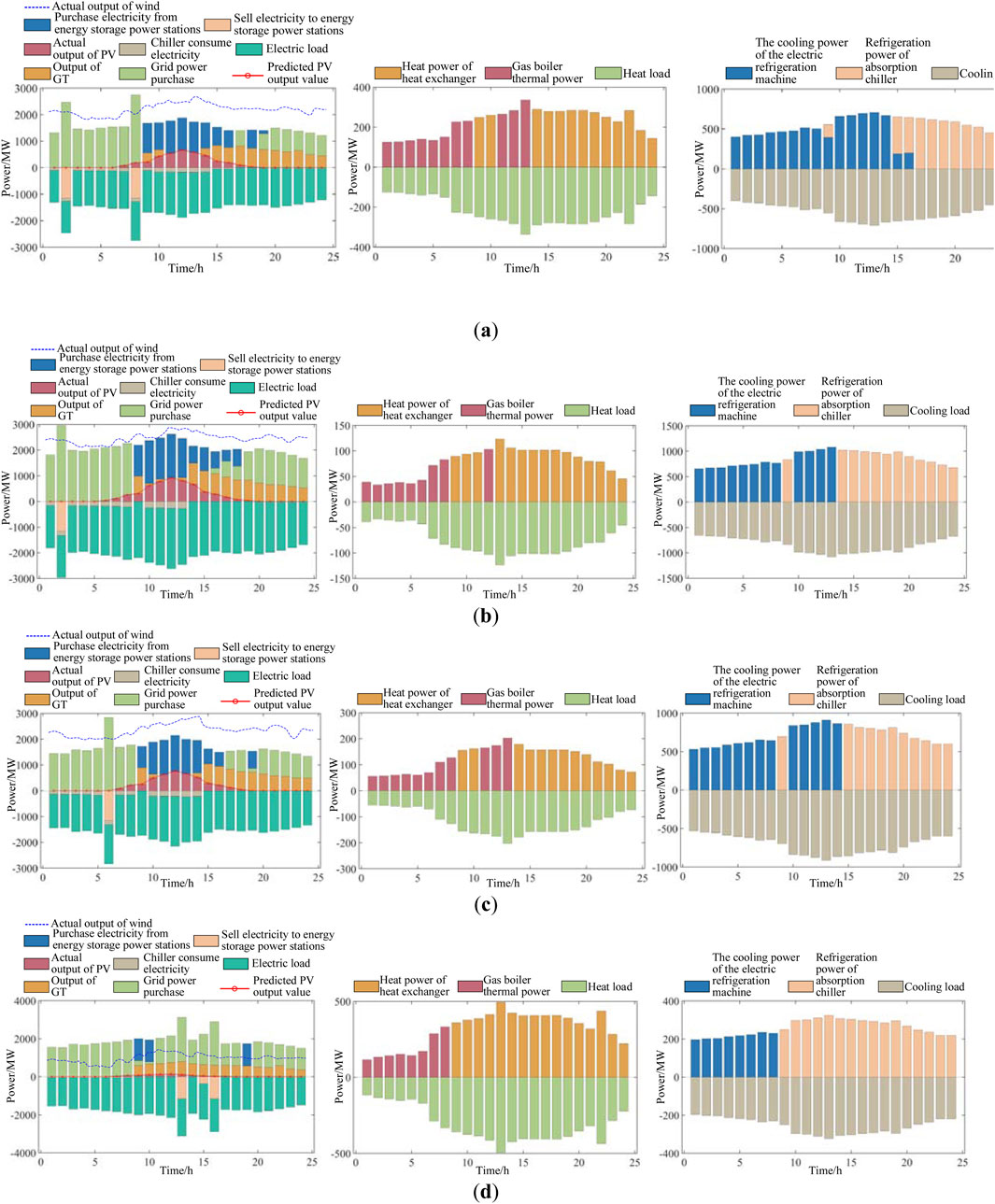
Figure 16. The cold, heat, and electric load power and the predicted generation power curve of PV and wind power of MG3 under Scenario 3: (a) spring forecast, (b) summer forecast, (c) autumn forecast, and (d) winter forecast.

Figure 17 shows the variation of the operating costs of regional microgrids and shared energy storage stations with the consumption rate. It can be seen from the profit change curve that as the consumption rate decreases, the cost of shared energy storage stations shows a decreasing trend, while the cost of regional microgrids increases with the decline in the consumption rate. The overall combined cost of the first two decreases and then increases with the decline in the consumption rate. In this example, the economically optimal consumption rate of the energy storage shared power station-regional microgrid system is 97.44%. When the consumption rate approaches 100%, the annual operating cost of shared energy storage stations increases significantly, turning from a profit to a loss. When the consumption rate reaches 100%, the cost of the power station rises to a positive value, and it is impossible to achieve profitability.

Figure 17

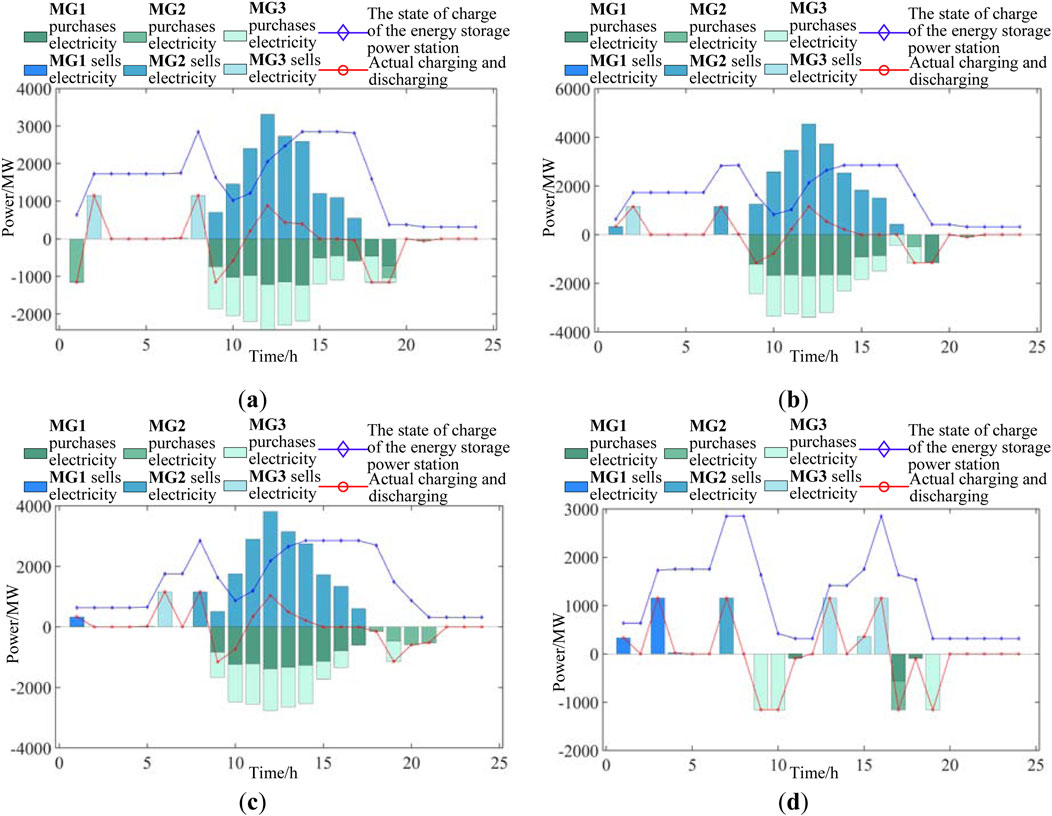
Figure 17. Electricity transaction data prediction between regional microgrids and shared energy storage stations under Scenario 3: (a) spring forecast, (b) summer forecast, (c) autumn forecast, and (d) winter forecast.

Table 3 shows the configuration of the shared energy storage station in Scenario 2 and Scenario 3. After taking economic consumption into account, the configured capacity of the power station decreased by 86.2% compared to the situation without considering economic consumption. Moreover, the shared energy storage station service provider of the power station can achieve profitability. However, in Scenario 3, without considering economic consumption, the power station service provider makes a loss during the operation cycle of the power station and cannot achieve profitability.

Table 3

Table 3. The shared energy storage configuration of Scenario 2 and Scenario 3.

Table 3 compares the shared energy storage configurations for Scenario 2 and Scenario 3. Scenario 2, with a power station configuration capacity of 3,835.2 kW h and configuration power of 1439.2 kW, achieves a profitable operation with a configuration cost of 872.23 ten thousand yuan and an annual operating cost of −253.69 ten thousand yuan. Scenario 3, with a larger configuration, has a higher configuration cost and a lower annual operating cost. This comparison highlights the importance of an optimal configuration for achieving economic viability and operational efficiency. The profitability of the shared energy storage model in Scenario 2 underscores its potential for practical application in regional microgrid systems.

The SOC and power balance curves of the power station on a typical winter day, as depicted in Figures 13d, 17d, reveal the nuanced operational strategies resulting from the bi-level optimization model. Scenario 3 demonstrates a peak charging power significantly higher than Scenario 2, with multiple charging power peaks representing the full consumption of new energy. This approach, while maximizing new energy utilization, leads to a lower overall utilization rate of the energy storage capacity, with resources being utilized primarily during a few periods. Additionally, to maintain a daily charge and discharge balance, the regional microgrid is forced to purchase electricity from the energy storage power station during off-peak hours, potentially reducing the system’s overall economic benefits. These observations underscore the importance of striking a balance between new energy consumption and the efficient use of energy storage resources, as well as the need to refine the model to optimize both economic benefits and technical performance. This ensures that the shared energy storage station operates at peak efficiency while providing cost-effective energy services to the regional microgrid.

Remark 9. In Scenario 3, the shared energy storage power station is configured without considering the economic absorption of the regional microgrid, focusing on maximizing storage capacity. This leads to a significant increase in capacity (approximately 7×) but also to reduced profitability due to higher initial investment and potentially suboptimal operational efficiency. To provide a more detailed understanding of the operational dynamics in Scenario 3, we have included a comprehensive analysis of state of charge (SOC), charge/discharge patterns, and congestion profiles within the Supplementary Material. The source code accompanying the manuscript allows readers to replicate and visualize these profiles, ensuring transparency and accessibility to the underlying data. The results underscore the importance of aligning shared energy storage with the microgrid’s energy consumption patterns to optimize economic performance and operational efficiency.

The above results show that the selection of the new energy consumption target for regional microgrids has a significant impact on the configuration cost of shared energy storage stations. Considering economic consumption can maintain a high new energy consumption rate while significantly reducing the configuration cost of shared energy storage stations and the operating cost of regional microgrids, making the annual comprehensive operating cost of the power station-regional microgrid system lower than the cost when the regional microgrid operates independently, promoting the full utilization of renewable energy.

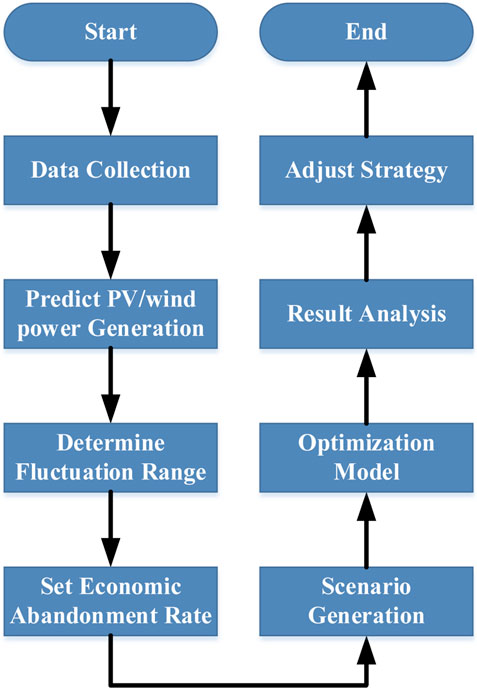
Remark 10. In Scenarios 1, 2, and 3, it can be recognized that the inherent variability of PV and wind power output is influenced by natural characteristics such as weather conditions and time of day. To address this variability and its impact on grid stability and energy management, a shared energy storage system is proposed as a key component of the microgrid. This storage solution improves the reliability of the power supply and optimizes the use of renewable energy resources. The process for managing renewable energy uncertainty, as depicted in the flowchart in Figure 18, involves several steps, including data collection, PV/wind generation prediction, determination of fluctuation ranges, setting of economic abandonment rates, scenario generation, optimization modeling, result analysis, and strategy adjustment. This structured approach is designed to improve the resilience and economic viability of the microgrid system, providing a framework for managing PV and wind power variability and sustainably integrating renewable energy resources.

Figure 18

Figure 18. Renewable energy uncertainty management and optimization flowchart.

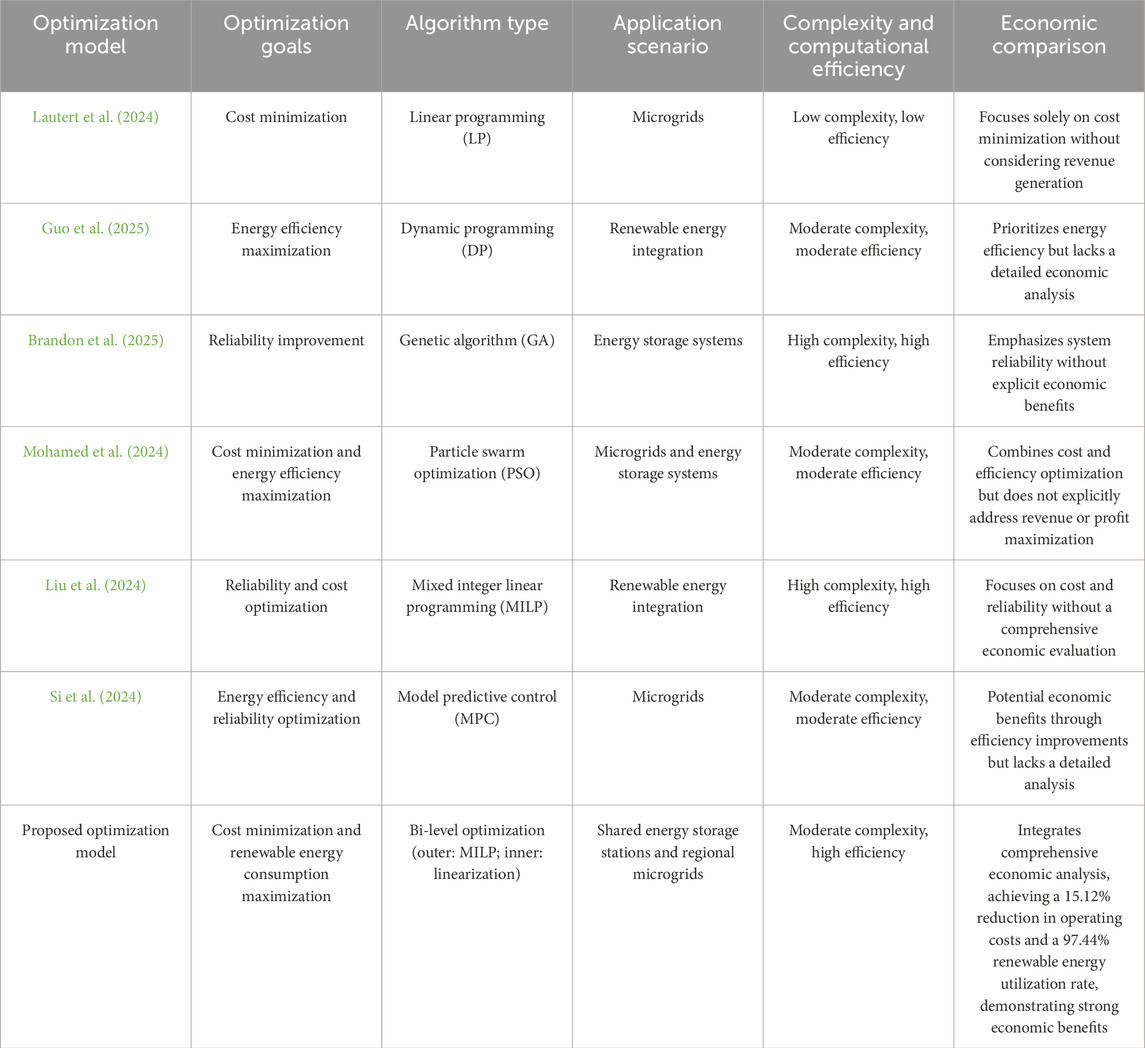
6.4 Comparison between the proposed method and the existing methods

To further validate the effectiveness and superiority of the proposed bi-level optimization method, we compare it with typical existing optimization methods in the field of energy storage and microgrid systems, as shown in Table 4 below. This comparison highlights the unique advantages of the bi-level optimization method in terms of optimization goals, algorithm types, application scenarios, computational efficiency, and economic comparison.

Table 4

Table 4. Comparison table of optimization methods.

Observing from Table 4, it can be easily seen that the proposed bi-level optimization method demonstrates significant advantages over existing approaches in terms of optimization goals, algorithm efficiency, and economic benefits. By incorporating both cost minimization and renewable energy consumption maximization, our method provides a more holistic solution to the challenges of shared energy storage systems and regional microgrids. The integration of comprehensive economic analysis has achieved a 15.12% reduction in operating costs and a 97.44% renewable energy utilization rate, underscoring our commitment to sustainable and economically viable energy practices. This comparison validates the effectiveness and innovation of our proposed method, making it a valuable contribution to the field of energy storage and microgrid optimization.

7 Conclusion

This article focuses on the combined cooling, heating, and power regional microgrid system, introducing a shared energy storage station service model. We propose a bi-layer optimization configuration method based on a bi-layer optimization model, which incorporates the concept of energy sharing governance to increase the economic and operational efficiency of the microgrid system. Among them, the outer model solves the problem of power station configuration, while the inner model solves the problems of economic consumption rate and the optimal operation of micro-energy networks. Based on the KKT conditions, the outer layer model is transformed into the constraint conditions of the inner-level model, and the Big-M linearization method is adopted to convert the nonlinear model into a mixed integer linear optimization problem. By analyzing and calculating the overall configuration of energy storage in three scenarios, the annual operating cost of the combined cooling, heating, and power regional microgrid system, the consumption rate of renewable energy, and the annual revenue of the shared energy storage station were verified. This analysis confirmed the economy and effectiveness of the proposed model. The conclusions drawn from the case study analysis are as follows:

The combined cooling, heating, and power regional microgrid system participates in the shared energy storage station service. By paying service fees to the energy storage power station operator in exchange for the charging and discharging services of energy storage, it can significantly reduce the annual operating cost of users, increase the regional microgrid’s new energy consumption rate to over 97%, and lower the annual operating cost of the regional microgrid by approximately 15.12%, demonstrating the model’s effectiveness in promoting renewable energy utilization. These findings highlight the model’s potential to improve both the financial viability and sustainability of microgrid systems, thereby contributing to the global transition toward renewable energy and sustainable energy practices.

Compared with the complete consumption of new energy, considering economic consumption can reduce the configured capacity of shared energy storage stations by 86.2%, significantly improving the economic benefits of shared energy storage stations, enabling shared energy storage station service providers to turn losses into profits and recover costs within 4.62 years.

The proposed bi-level optimization model algorithm is suitable for solving multi-objective optimization problems. It can effectively identify the power capacity configuration scheme that minimizes the operating cost of the shared energy storage station-regional microgrid integrated system, and solve the corresponding new energy consumption target.

In future work, we plan to explore additional visualization techniques to provide a more detailed and comprehensive description of the algorithm’s performance, enhancing the understanding and applicability of our proposed bi-level optimization model for shared energy storage stations in regional microgrids. We will highlight the universality of the proposed bi-level optimization mode and explore its application in other energy systems, such as hydrogen energy storage, district heating, and electric vehicle energy storage applications. The verification of the sensitivity analysis of key model variables and the application of the algorithm to electricity prices in different regions will also be included.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

HM: Conceptualization, Investigation, Validation, Writing – original draft, Writing – review and editing, Funding acquisition, Methodology, Project administration, Resources, Supervision. WZ: Conceptualization, Investigation, Validation, Writing – original draft, Writing – review and editing, Data curation, Formal Analysis, Software, Visualization. ZL: Formal Analysis, Supervision, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by the 2024 Special Fund for Science and Technology Innovation Strategy of Guangdong Province (Science and Technology Innovation Cultivation of College Students, grant number pdjh 2024a706) and the 2025 Climbing Plan of Guangdong Province (grant number pdjh 2025bk420, Student author: Ziqing Luo).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2025.1686684/full#supplementary-material

References

Bae, J., and Kim, Y. (2025). Validation of liquid-immersed battery energy storage system for fire safety and heat management. Energies 18, 1983. doi:10.3390/en18081983

CrossRef Full Text | Google Scholar

Barbosa, L. D. S. N. S., Bogdanov, D., Vainikkaand, P., and Breyer, C. (2017). Hydro, wind and solar power as a base for a 100% renewable energy supply for south and Central America. Plos One 12, e0173820. doi:10.1371/journal.pone.0173820

PubMed Abstract | CrossRef Full Text | Google Scholar

Brandon, C. C., Luis, F. G. N., Oscar, D. M., Rubén, I. B., and Javier, M. (2025). A multi-objective optimization approach based on the Non-Dominated Sorting Genetic Algorithm II for power coordination in battery energy storage systems for DC distribution network applications. J. Energy Storage 113, 115430. doi:10.1016/j.est.2025.115430

CrossRef Full Text | Google Scholar

Chen, L., Tang, W., Wang, Z., Zhang, L., and Xie, F. (2024). Low-carbon oriented planning of shared photovoltaics and energy storage systems in distribution networks via carbon emission flow tracing. Int. J. Electr. Power and Energy Syst. 160, 110126. doi:10.1016/j.ijepes.2024.110126

CrossRef Full Text | Google Scholar

Faramarzi, H., Ghaffarzadeh, N., and Shahnia, F. (2025). A new stochastic multi-objective model for the optimal management of a PV/wind integrated energy system with demand response, P2G, and energy storage devices. Front. Energy Res. 13, 1537703. doi:10.3389/fenrg.2025.1537703

CrossRef Full Text | Google Scholar

Faria, J. P. D., Pombo, J. A. N., Mariano, S. J. P. S., and Calado, M. R. A. (2025). Plug-and-play framework for assessment of renewable energy community strategies. IEEE Access 13, 29811–29829. doi:10.1109/access.2025.3539533

CrossRef Full Text | Google Scholar

Guo, Y., Wang, Q., Tang, Y., and Peng, X. (2025). Numerical modeling and optimization of the operational variables for a coaxial dual-piston compressor applied in hydrogen storage. Int. J. Green Energy 22, 1932–1946. doi:10.1080/15435075.2024.2446993

CrossRef Full Text | Google Scholar

Hashemizadeh, A., Liu, W., and Abadi, F. Z. B. (2024). Assessing the viability of sustainable nuclear energy development in belt and road initiative countries. Energy Sustain. Dev. 81, 101519. doi:10.1016/j.esd.2024.101519

CrossRef Full Text | Google Scholar

He, Y., Wu, H., Wu, A. Y., Li, P., and Ding, M. (2024). Optimized shared energy storage in a peer-to-peer energy trading market: Two-stage strategic model regards bargaining and evolutionary game theory. Renew. Energy 224, 120190. doi:10.1016/j.renene.2024.120190

CrossRef Full Text | Google Scholar

He, Y., Xiao, J., Wang, Y., Liu, Z., and He, S. (2025). Subjective-uncertainty-oriented dynamic renting framework for energy storage sharing. Appl. Energy 378, 124765. doi:10.1016/j.apenergy.2024.124765

CrossRef Full Text | Google Scholar

Hou, L., Tong, X., Chen, H., Fan, L., Liu, T., Liu, W., et al. (2024). Optimized scheduling of smart community energy systems considering demand response and shared energy storage. Energy 295, 131066. doi:10.1016/j.energy.2024.131066

CrossRef Full Text | Google Scholar

Huylo, M., Taheri, S., and Novoselac, A. (2025). Integration of renewable energy generation and storage systems for emissions reduction in an islanded campus microgrid. Build. Environ. 274, 112736. doi:10.1016/j.buildenv.2025.112736

CrossRef Full Text | Google Scholar

Jia, H. J., Wang, X., Jin, X., Cheng, L., Mu, Y., Yu, X., et al. (2024). Optimal pricing of integrated community energy system for building prosumers with P2P multi-energy trading. Appl. Energy 365, 123259. doi:10.1016/j.apenergy.2024.123259

CrossRef Full Text | Google Scholar

Krishankumar, R., Ecer, F., Kaya, S. K., and Pedrycz, W. (2024). Hydrogen energy storage technology selection through a cutting-edge probabilistic linguistic decision framework. Renew. Energy Focus 51, 100642. doi:10.1016/j.ref.2024.100642

CrossRef Full Text | Google Scholar

Lautert, R. R., Cambambi, C. A. C., Ortiz, M. D., Wolter, M., and Canha, L. N. (2024). Optimal power dispatch in microgrids using mixed-integer linear programming. AT-Automatisierungstechnik 72, 1030–1040. doi:10.1515/auto-2024-0094

CrossRef Full Text | Google Scholar

Li, Y., Li, H., Miao, R., Qi, H., and Zhang, Y. (2023). Energy-Environment-Economy (3E) analysis of the performance of introducing photovoltaic and energy storage systems into residential buildings: a case study in shenzhen, China. Sustainability 15, 9007. doi:10.3390/su15119007

CrossRef Full Text | Google Scholar

Li, Z., Wang, B., Xian, L., Zhang, M., and Xu, Q. (2024). Decentralized active disturbance rejection control for hybrid energy storage system in DC microgrid. IEEE Trans. Industrial Electron. 71, 14232–14243. doi:10.1109/tie.2024.3363772

CrossRef Full Text | Google Scholar

Lin, L., Cao, Y., Kong, X., Lin, Y., Jia, Y., and Zhang, Z. (2024). Hybrid energy storage system control and capacity allocation considering battery state of charge self-recovery and capacity attenuation in wind farm. J. Energy Storage 75, 109693. doi:10.1016/j.est.2023.109693

CrossRef Full Text | Google Scholar

Lin, X., Zheng, Y., Xiang, Z., and Wang, B. (2025). Optimal market-based battery energy storage system capacity sizing: considering strategic behavior of collusions in the electricity day-ahead market. J. Energy Storage 120, 116309. doi:10.1016/j.est.2025.116309

CrossRef Full Text | Google Scholar

Liu, J., Wunsch, D. C., Wang, S., and Bo, R. (2024). Multi-parametric analysis for mixed integer linear programming: an application to transmission upgrade and congestion management. Sustain. Energy, Grids Netw. 40, 101563. doi:10.1016/j.segan.2024.101563

CrossRef Full Text | Google Scholar

Luo, S., Chen, C., Qiu, W., Ma, J., Yang, L., and Lin, Z. (2021). Bi-layer optimal planning of rural distribution network based on KKT condition and Big-M method. Energy Rep. 7, 637–644. doi:10.1016/j.egyr.2021.09.206

CrossRef Full Text | Google Scholar

Ma, H., Zhang, W., and Wang, A. (2024). A two-phase robust comprehensive optimal scheduling strategy for regional distribution network based on multiple scenarios. Front. Energy Res. 12, 1496302. doi:10.3389/fenrg.2024.1496302

CrossRef Full Text | Google Scholar

Mohamed, M. A. E., Mahmoud, A. M., Saied, E. M. M., and Hadi, H. A. (2024). Hybrid cheetah particle swarm optimization based optimal hierarchical control of multiple microgrids. Sci. Rep. 14, 9313. doi:10.1038/s41598-024-59287-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Ng, J. Y., Tan, W. S., Chan, P. Y., and Elias, A. (2024). Multi-objective optimisation of buoyancy energy storage technology using transit search algorithm. Renew. Energy 225, 120342. doi:10.1016/j.renene.2024.120342

CrossRef Full Text | Google Scholar

Shi, Z., Wu, H., Xiao, T., Huang, X., Shao, L., Ma, Z., et al. (2025). Planning and energy self-supply strategy for distributed photovoltaic microgrids on highways considering regional layout constraints. Processes 13, 1377. doi:10.3390/pr13051377

CrossRef Full Text | Google Scholar

Si, X., Duan, J., and Fan, S. (2024). Design of an adaptive frequency control for flywheel energy storage system based on model predictive control to suppress frequency fluctuations in microgrids. Electr. Power Syst. Res. 235, 110900. doi:10.1016/j.epsr.2024.110900

CrossRef Full Text | Google Scholar

Song, X., Wu, H., Zhang, H., Guo, G., Zhang, Z., and Peña-Mora, F. (2025). Can retail electricity pricing promote microgrid operators to leverage shared energy storage services among internal aggregators? Energy 314, 134160. doi:10.1016/j.energy.2024.134160

CrossRef Full Text | Google Scholar

Taye, B. A., and Choudhury, N. B. D. (2024). A new control method of hybrid energy storage system for DC microgrid application. Energy Storage 6, e564. doi:10.1002/est2.564

CrossRef Full Text | Google Scholar

Umar, A., Jha, S. K., Kumar, D., Ghose, T., and Samantaray, S. R. (2025). Blockchain-driven demand side management in P2P energy markets for islanded microgrid systems. Front. Energy Res. 12, 1450988. doi:10.3389/fenrg.2024.1450988

CrossRef Full Text | Google Scholar

Verdugo, P., Cañizares, C., and Pirnia, M. (2025). Modeling and energy management of hangar thermo-electrical microgrid for electric plane charging considering multiple zones and resources. Appl. Energy 379, 124951. doi:10.1016/j.apenergy.2024.124951

CrossRef Full Text | Google Scholar

Wang, X., Zhang, X., Qin, B., and Guo, L. (2023). Improved multi-objective grasshopper optimization algorithm and application in capacity configuration of urban rail hybrid energy storage systems. J. Energy Storage 72, 108363. doi:10.1016/j.est.2023.108363

CrossRef Full Text | Google Scholar

Wang, W. (2023). The role of blockchain technology in advancing sustainable energy with security settlement: enhancing security and efficiency in China’s security market. Front. Energy Res. 11, 1271752. doi:10.3389/fenrg.2023.1271752

CrossRef Full Text | Google Scholar

Wang, K., and Febri, N. (2024). The vending machine deployment and shelf display problem: a bi-layer optimization approach. Transp. Res. Part E Logist. Transp. Rev. 187, 103581. doi:10.1016/j.tre.2024.103581

CrossRef Full Text | Google Scholar

Wang, Z., Chen, L., Li, X., and Mei, S. (2024a). A two-stage optimization approach-based energy storage sharing strategy selection for limited rational users. J. Energy Storage 93, 112098. doi:10.1016/j.est.2024.112098

CrossRef Full Text | Google Scholar

Wang, T., Huo, T., and Li, H. (2024b). Bi-layer planning of integrated energy system by incorporating power-to-gas and ground source heat pump for curtailed wind power and economic cost reduction. Energies 17, 1447. doi:10.3390/en17061447

CrossRef Full Text | Google Scholar

Xia, Q., Wang, Y., Zou, Y., Yan, Z., Zhou, N., Chi, Y., et al. (2024). Regional-privacy-preserving operation of networked microgrids: Edge-cloud cooperative learning with differentiated policies. Appl. Energy 370, 123611. doi:10.1016/j.apenergy.2024.123611

CrossRef Full Text | Google Scholar

Yan, D., and Chen, Y. (2023). Distributed coordination of charging stations with shared energy storage in a distribution network. IEEE Trans. Smart Grid 14, 4666–4682. doi:10.1109/tsg.2023.3260096

CrossRef Full Text | Google Scholar

Yang, H., Chen, Q., Liu, Y., Ma, Y., and Zhang, D. (2024). Demand response strategy of user-side energy storage system and its application to reliability improvement. J. Energy Storage 92, 112150. doi:10.1016/j.est.2024.112150

CrossRef Full Text | Google Scholar

Zhao, C., Zhou, Y., Hao, Y., and Zhang, G. (2022). A bi-layer decomposition algorithm for many-objective optimization problems. Appl. Intell. 52, 15122–15142. doi:10.1007/s10489-021-03135-2

CrossRef Full Text | Google Scholar

Zhao, M., He, Y., Tian, Y., Sun, K., Jiao, L., and Wang, H. (2024). Capacity optimization of wind-solar-storage multi-power microgrid based on two-layer model and an improved snake optimization algorithm. Electronics 13, 4315. doi:10.3390/electronics13214315

CrossRef Full Text | Google Scholar

Zheng, X., Ju, C., Yang, G., and Chu, J. (2025). Multi-agent modeling for energy storage charging station scheduling strategies in the electricity market: a cooperative learning approach. J. Energy Storage 106, 114226. doi:10.1016/j.est.2024.114226

CrossRef Full Text | Google Scholar