The Influence of Vibration on Friction: A Contact-Mechanical Perspective

A unified model for active control of static and sliding friction by normal, tangential, and transverse oscillations is discussed, building on a series of past publications. The model in question is quasi-static, uses Amontons friction and takes into account contact stiffness in both normal and tangential directions. This makes the model fully macroscopic, which stands in contrast to Prandtl-Tomlinson-derived microscopic models that seem to be the currently preferred explanation for the influence of vibration on friction. While many technical details and numerical simulations based on our model have already appeared in a series of publications, here we attempt to give a high-level overview and discuss the main properties of friction under oscillation as generally as possible, while making a minimum of assumptions.

1. Introduction

The fact that vibration can be used to significantly reduce the force of friction has been known since at least the 1950s (Fridman and Levesque, 1959). Since then, the effect has been studied extensively and exploited in many practical applications. Classical examples are to be found in wire drawing (Murakawa and Jin, 2001; Siegert and Ulmer, 2001), press forming (Eaves et al., 1975; Ashida and Aoyama, 2007), cutting (Thoe et al., 1998; Eggers et al., 2004), and other machining processes. Also well-known is the use of vibration for stabilization of system dynamics, e.g., suppression of brake squeal (Müller and Ostermeyer, 2007) and cornering noise (Heckl and Huang, 2000).

There are also a number of advanced applications that move beyond simple reduction of sliding or static friction, and involve vibration-driven directed transport or exact positioning (Popov, 2017). The most famous example of this are traveling wave motors (Schmidt et al., 1996; Storck et al., 2002), which are used to adjust focus in camera lenses, among many other applications. Similar principles are employed in high-precision linear actuators and positioning systems (Socoliuc et al., 2006), vibrational conveyors (Gaberson, 1971, 1972), and other types stick-slip drives.

The above examples are only a small sample of technical applications at the intersection of friction and vibration. Correspondingly, there is a large body of existing research in this field (see e.g., Pohlman and Lehfeldt, 1966; Godfrey, 1967; Storck et al., 2002; Chowdhury and Helali, 2008). Most of it is practical in nature, even though several well-known theoretical models have been proposed as well (De Wit et al., 1995). However, it is the contention of the author that an important factor is missing from currently popular models: the compliance of the contact and its interaction with the applied oscillation. The currently prevailing tendency is to ascribe the reduction of friction by vibration mostly to processes at the micro-scale (Popov et al., 2010). However, here we will argue that the primary (but not necessarily exclusive) mechanism is to be found on the macro-scale, in ordinary contact mechanics. It should be noted that this does not automatically invalidate previous work. In fact, it seems likely that a truly accurate model will be multiscale, combining both macroscopic dynamics and microscopic processes.

The primary advantage of our model is its simplicity. It relies only on macroscopic contact mechanics and introduces no new physics. In fact, it is likely to be the simplest possible model that is rich enough to describe almost the full range of behaviors exhibited by friction under the influence of external vibration. For this reason, the present paper can be seen as an exercise in minimalism, attempting to cover as much phenomenological ground as possible with a minimum of assumptions and variables.

1.1. Contributions

This work draws heavily on results recently published in a series of papers with participation of the present author (Mao et al., 2017; Popov et al., 2017; Benad et al., 2018a,b; Popov and Li, 2018). While there is substantial overlap with these papers, the present work is organized differently, seeking to present a “big picture” view without getting bogged down in details. Several results have been generalized from previous publications, while the discussion of the influence of oscillation waveforms has, to the best knowledge of the author, not previously appeared in the literature.

2. Static Friction

To warm up, we consider static friction. This case is much simpler than the sliding case and leads to some satisfyingly general results. The system under consideration consists of a body resting on a plane (Figure 1). The body is pressed into the plane with a force F_z and pulled sideways with a force F_x. The coefficient of friction between the body and the plane is assumed to be constant and equal to μ₀. The body remains at rest while

$\begin{array}{ll}|F_x|<{\mu }_0{F}_z& (1)\end{array}$

where μ₀F_z is the critical force at which the body just begins to slide. The static coefficient of friction is defined as the ratio of this critical force to the normal load. In the absence of oscillation, it is equal to μ₀:

$\begin{array}{ll}{\mu }_s={\mu }_0& (2)\end{array}$

FIGURE 1

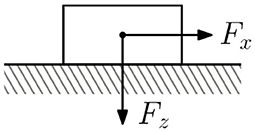
Figure 1. Static friction model. The intrinsic coefficient of friction in the contact is μ₀. The y-axis points out of the plane.

Things get slightly more interesting when we add an oscillatory force component. If the force oscillation acts normal to the plane, we denote it by A_zg(t), where A_z is the amplitude. The stick condition in that case needs to be amended to:

$\begin{array}{ll}|F_x|<{\mu }_0{\left(F_z+A_{z}g(t)\right)}^{+}& (3)\end{array}$

The (..)⁺ notation denotes the ramp function, which clips negative values to zero. It is necessary because the normal force does not turn negative when contact is lost.

It is easy to see that the critical force is reduced relative to the non-oscillatory case, since the above inequality must hold at all times, including the times when the normal force drops below its mean value F_z. In other words, static friction is limited by the minimum of normal force encountered during the oscillation. For the coefficient of static friction under normal oscillation we thus obtain:

$\begin{array}{ll}{\mu }_{s,z}={\mu }_0{(1-A_z/F_z)}^{+}& (4)\end{array}$

In a similar fashion, we can add an oscillatory component A_xg(t) that is aligned with the tangential force F_x. This results in the stick condition

$\begin{array}{ll}|F_x+A_{x}g(t)|<{\mu }_0{F}_z& (5)\end{array}$

Note that this inequality is only satisfiable when A_x < μ₀F_z. Otherwise the body starts to slide in place and the contact loses its ability to statically sustain a lateral force. Thus, μ_s can be expressed as:

$\begin{array}{ll}{\mu }_{s,x}={({\mu }_0-A_x/F_z)}^{+}& (6)\end{array}$

Notice the slight difference between this result and Equation (4). In particular, note that a tangential oscillation will reduce μ_s by a larger amount than a normal oscillation of the same amplitude if μ₀ < 1, and by a smaller amount otherwise.

Transverse oscillations are also able to reduce static friction. This case is qualitatively similar to that of tangential oscillation, with the difference that we need to use the vector norm of the in-plane forces instead of adding them directly:

$\begin{array}{ll}{F}_x^2+{\left(A_{y}g(t)\right)}^2<{({\mu }_0{F}_z)}^2& (7)\end{array}$

Once again, stick is impossible if A_y ≥ μ₀F_z, and for the static coefficient of friction we obtain:

$\begin{array}{ll}{\mu }_{s,y}=\sqrt{{\left({\mu }_0^2-A_y^2/F_z^2\right)}^{+}}& (8)\end{array}$

One particularly useful thing about these results is that they are quite general, and in particular independent of contact geometry, frequency of oscillation, and the shape of the oscillation waveform.

2.1. Static Friction Under Superimposed Oscillation

Things become considerably less transparent when we consider simultaneous oscillation in multiple directions. The stick condition itself does not change much, and in the most general case can be expressed as:

$\begin{array}{ll}{\left(F_x+A_x{g}_x(t)\right)}^2+{\left(A_y{g}_y(t)\right)}^2<{\mu }_0^2{\left(F_z+A_z{g}_z(t)\right)}^2& (9)\end{array}$

Unfortunately, actually finding the maximal F_x that still satisfies this inequality at all times quickly becomes unwieldy, leading to a large number of case distinctions—if a closed-form solution is possible at all. In addition, when the compliance of the contact is taken into account, the static coefficient of friction may become negative, in the sense that a constant force needs to be applied to prevent the contact from sliding. This effect is what frictional drives and actuators are based on. For an analysis of this case the reader is referred to Popov and Li (2018). In this paper, however, we ignore superimposed oscillation.

3. Sliding Friction Under Normal Oscillation

The key feature of the model that we use to describe dynamic friction is that the compliance of the contact is taken into account. In the initial formulation, the contact is modeled as a single Hookean spring that has an associated normal stiffness k_z and a lateral stiffness k_x (Figure 2). This is a reasonable approximation of a flat-ended cylinder in contact with a plane. The model can also be extended to cover arbitrary curved contacts with the help of the Method of Dimensionality Reduction (Popov and Heß, 2016). However, for a general analysis, a single spring is quite sufficient.

FIGURE 2

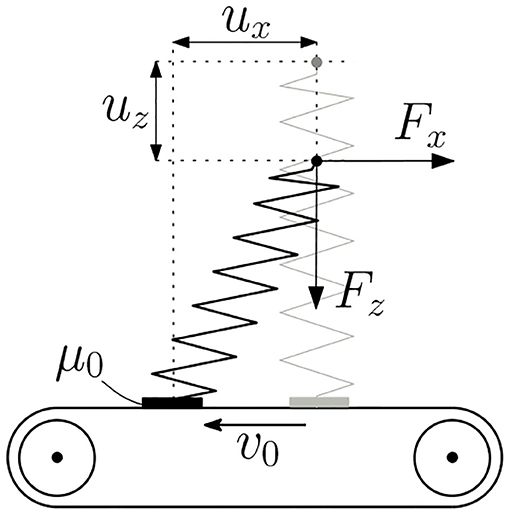
Figure 2. A single massless spring, which serves as a minimal model of a sliding frictional contact. The sliding velocity is constant, while the vertical coordinate oscillates. Amontons friction with the constant coefficient of friction μ₀ is assumed in the contact point.

The model considered here is displacement-controlled and quasi-static. A force-controlled and/or inertial model can be formulated within the same framework, which, however, leads to certain complications (e.g., resonances) that are outside the focus of the present paper. For an analysis of such a model, the reader is referred to Mao et al. (2017).

The kinematics of the model is as follows: The contact spring is pulled over a flat plane with a constant velocity v₀, although for convenience we consider the spring to be stationary, while the substrate slides underneath it. The normal displacement u_z of the spring is measured relative to the state of unstressed first contact with the substrate. u_z(t) represents the externally applied oscillation and is thus given explicitly. The lateral displacement u_x, on the other hand, depends on the current state of the system and is the only unknown variable.

We assume that Amontons' law of friction (with a constant coefficient of friction μ₀ that is the same for both static and sliding friction) holds in the contact point. In general, this may be an unrealistic assumption. However, the use of a constant coefficient of friction not only simplifies calculations, but also eliminates all possible micro-scale influences from the model. Since one of the primary aims of this paper is to advertise the feasibility of a purely macroscopic theory of friction under oscillation, making μ₀ constant is actually a prerequisite.

The effective coefficient of friction $\bar{\mu }$, which is to be determined in the sequel, is defined as the average tangential force exerted by the spring divided by the average normal force:

$\begin{array}{ll}\bar{\mu }=\frac{\langle F_x(t)\rangle }{\langle F_z(t)\rangle }& (10)\end{array}$

where 〈..〉 denotes averaging over one period of oscillation.

Previous publications on the topic assumed that the imposed normal oscillation is harmonic, so as to simplify analysis. However, this turned out to be an unnecessary restriction, so here we will work with a general periodic function that is parameterized as follows:

$\begin{array}{ll}{u}_z(t)={\overline{u}}_z+A_{z}w(ft)& (11)\end{array}$

Here $\overline{u}$_z is the mean indentation, A_z is the amplitude and f the frequency of the oscillation. w(φ) is a dimensionless function describing the “shape” of the oscillation, with φ = ft. The waveform w is normalized such that it is zero-mean, with a period of 1 and a minimum value of −1. Note however, that the maximum of w is left unconstrained.

3.1. Pure Sliding

While the behavior of a frictional couple under oscillation has its complexities in general, there are two extreme cases that lend themselves to easy and precise analysis: One of them, static friction, was already discussed above. The second, pure sliding, is briefly discussed here. The most important thing about pure sliding is that oscillations do not influence the coefficient of friction in that mode. This can be easily seen from the fact that the instantaneous tangential force is uniquely defined during slip (F_x = μ₀F_z), from which the effective coefficient of friction is immediately obtained:

$\begin{array}{ll}{\bar{\mu }}_{\text{slip}}=\frac{\langle F_x(t)\rangle }{\langle F_z(t)\rangle }=\frac{\langle {\mu }_0{F}_z(t)\rangle }{\langle F_z(t)\rangle }={\mu }_0& (12)\end{array}$

Irrespective of how complex the dependence F_z(t) may be, it always cancels out—by linearity of sliding friction. While this result may seem unimpressive by itself, it establishes an important “boundary condition” for the more general case of friction with stick-slip. Also, as in the static case, the coefficient of friction in pure slip has the important property of not being dependent on contact geometry and oscillation parameters. The result ${\bar{\mu }}_{\mathrm{\text{slip}}}={\mu }_0$ is also valid for tangential and combined normal/tangential oscillations. It can also be shown to be valid in the inertial case (Mao et al., 2017). However, transverse oscillations do not, strictly speaking, have this limiting case, although the deviation becomes negligible at high velocities. This will be discussed in more detail later.

3.2. Stick-Slip

Two extreme points have now been established: pure stick (static friction) and pure slip (plateau). Reason suggests that there is also something in between. It would be physically implausible for the coefficient of friction under oscillation to “snap” from near zero back to μ₀ due to arbitrarily slow sliding. And this is in fact not observed experimentally: At a given amplitude and frequency, the static coefficient of friction is lowest, and then smoothly increases with the sliding velocity until reaching a plateau of sorts. Fortunately, the transition region can also be described in our model. Unsurprisingly, it is dominated by stick-slip.

Let us now consider this phenomenon in more detail. During sliding, we have F_x = μ₀F_z, which can also be written as k_xu_x(t) = μ₀k_zu_z(t). Substituting u_z from Equation (11) and rearranging gives us the lateral displacement and velocity of the contact point:

$\begin{array}{ll}{u}_x(t)={\mu }_0\frac{k_z}{k_x}\left({\overline{u}}_z+A_{z}w(ft)\right)& (13)\end{array}$

$\begin{array}{ll}{\dot{u}}_x(t)={\mu }_0\frac{k_z}{k_x}{A}_{z}f{w}^{\prime }(ft)& (14)\end{array}$

A transition from slip to stick happens when the relative motion between the substrate and the contact point vanishes, i.e., when ${\dot{u}}_x(t)=v_0$. From this condition, the point of stick onset can be determined:

$\begin{array}{ll}{\phi }_1=f{t}_1={(w^{\prime })}^{-1}\left(\frac{k_x{v}_0}{{\mu }_0{k}_z{A}_{z}f}\right)& (15)\end{array}$

It becomes obvious that φ₁ is a function of a single compound variable, which combines all parameters of the system, except $\overline{u}$_z. To simplify further calculations, we introduce some dimensionless variables, α (corresponding to amplitude), β (corresponding to velocity), and φ (phase):

$\begin{array}{ll}\alpha =\frac{A_z}{{\overline{u}}_z}& (16)\end{array}$

$\begin{array}{ll}\beta =\frac{k_x{v}_0}{{\mu }_0{k}_z{A}_{z}f}& (17)\end{array}$

$\begin{array}{ll}\phi =ft& (18)\end{array}$

Using these variables, the static coefficient of friction (Equation 4) can be expressed as ${\mu }_{s,x}={\mu }_0{(1-\alpha )}^{+}$, while Equation (15) can be written as

$\begin{array}{ll}{\phi }_1={(w^{\prime })}^{-1}(\beta )& (19)\end{array}$

Noting that β is a positive quantity and assuming that w is differentiable (but not necessarily invertible—there can be multiple stick events), it can be seen that the above equation has solutions if

$\begin{array}{ll}\beta <{\displaystyle \underset{\phi }{max}}{w}^{\prime }(\phi )={\beta }_c& (20)\end{array}$

where β_c denotes the critical value that separates the stick-slip region from the continuous sliding region. A harmonic oscillation, for example, has β_c = 2π, while a right-leaning sawtooth function has β_c = 2, which is in fact the smallest possible value. The larger β_c, the more effective the waveform is at reducing friction at high velocities, but more on that later.

Once stick is initiated, the contact point is dragged along by the substrate with velocity v₀, so that the tangential displacement and force increase linearly with time:

$\begin{array}{ll}{F}_{\text{stick}}(t)={\mu }_0{F}_z(t_1)+k_x{v}_0(t-t_1)& (21)\end{array}$

This continues while the condition for static friction holds:

$\begin{array}{ll}{F}_{\text{stick}}(t)<{\mu }_0{F}_z(t)& (22)\end{array}$

Trivial as it is, this inequality lies at the core of reduction of friction in our model. It serves as the sole source of nonlinearity that allows the system to break free of the trivial solution exemplified by Equation (12). With pure slip, the spring force is always equal to μ₀F_z(t), while in stick-slip it is sometimes lower, which leads to lower average force and coefficient of friction (see also Figure 3). Another way of looking at it is that the contact point stands still when the normal force is highest, and covers more distance when the normal load diminishes. This leads to lower energy dissipation over the same distance. The whole process is somewhat similar to walking, where one leg carries the load without dissipation, while the other is lifted and advanced to the next position. Something analogous happens in our model, only there is just one “leg” and it is not necessarily lifted all the way.

FIGURE 3

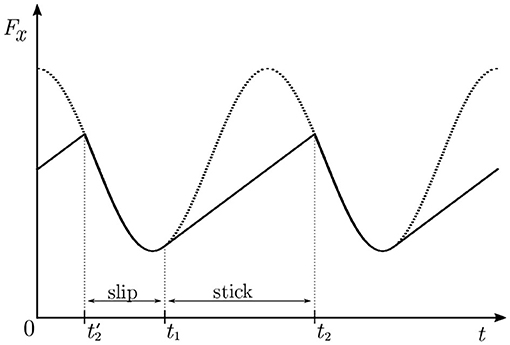
Figure 3. Stick and slip under the influence of a harmonic oscillation. The dotted line represents the tangential force as it would be in pure slip [F_slip = μ₀F_z(t)]. The solid line is the actual tangential force in the presence of stick-slip. The stick phases are the straight segments, e.g., between t₁ and t₂, while slip phases are the sinusoidal segments, e.g., between $t_2^{\prime }$ and t₁, repeating periodically. Note that F_x ≤ F_slip everywhere, which is the origin of friction reduction in our model.

The stick phase ends at time t₂ when the condition F_stick(t₂) = μ₀F_z(t₂) is met. Expanding this condition yields

$\begin{array}{ll}{\mu }_0{k}_z{u}_z(t_1)+k_x{v}_0(t_2-t_1)={\mu }_0{k}_z{u}_z(t_2)& (23)\end{array}$

or, more conveniently,

$\begin{array}{ll}\frac{v_0{k}_x}{{\mu }_0{k}_z}(t_2-t_1)=u_z(t_2)-u_z(t_1)& (24)\end{array}$

Substituting u_z and t = φ/f, this can be rewritten as:

$\begin{array}{ll}\beta ({\phi }_2-{\phi }_1)=w({\phi }_2)-w({\phi }_1)& (25)\end{array}$

Once again $\overline{u}$_z cancels out, leaving us with a function of only β. Unfortunately, the equation is implicit and cannot be solved symbolically for φ₂ except in the simplest cases (sawtooth, square wave, etc). In the case of a harmonic oscillation, for example, Equation (25) takes the form (cosx = a + bx), which does not have a closed-form solution in terms of standard functions. Numerical solution is required in most cases.

3.3. Effective Coefficient of Friction

We define the “macroscopic” or “effective” force of friction simply as the tangential force averaged over one period T = 1/f:

$\begin{array}{ll}\langle F_x\rangle =\frac{1}{T}{\displaystyle {\int }_0^T}{F}_x(t)\text{d}t& (26)\end{array}$

However, it will become clear in a moment that it is more convenient to consider the difference or reduction of the force of friction relative to the state of continuous sliding:

$\begin{array}{ll}\Delta F_x=\langle F_{\text{slip}}\rangle -\langle F_x\rangle =\frac{1}{T}{\displaystyle {\int }_0^T}(F_{\text{slip}}(t)-F_x(t))\text{d}t& (27)\end{array}$

Since F_x only differs from F_slip during the stick phase, we can tighten the integration bounds:

$\begin{array}{ll}\Delta F_x=\frac{1}{T}{\displaystyle {\int }_{t_1}^{t_2}}({\mu }_0{F}_z(t)-F_{\text{stick}}(t))\text{d}t& (28)\end{array}$

This form is convenient for numerical solution. However, some additional properties can gleaned by expanding F_stick and u_z(t) and making the substitution dt = Tdφ:

$\begin{array}{l}\Delta F_x=\frac{1}{T}{\displaystyle {\int }_{t_1}^{t_2}}\left({\mu }_0{F}_z(t)-{\mu }_0{F}_z(t_1)-k_x{v}_0(t-t_1)\right)\text{d}t\\ =\frac{1}{T}{\displaystyle {\int }_{t_1}^{t_2}}{\mu }_0{k}_z({\overline{u}}_z+A_{z}w(ft)-{\overline{u}}_z-A_{z}w(f{t}_1)\\ -\frac{k_x{v}_0}{{\mu }_0{k}_z}(t-t_1))\text{d}t\\ ={\mu }_0{k}_z{A}_z{\displaystyle {\int }_{{\phi }_1}^{{\phi }_2}}\left(w(\phi )-w({\phi }_1)-\beta (\phi -{\phi }_1)\right)\text{d}\phi & (29)\end{array}$

It becomes apparent that the expression for ΔF_x can be split into the dimensional factor μ₀k_zA_z and a dimensionless function Ψ_w of a single variable:

$\begin{array}{ll}\Delta F_x={\mu }_0{k}_z{A}_z{\text{Ψ}}_w(\beta )& (30)\end{array}$

where

$\begin{array}{ll}{\text{Ψ}}_w(\beta )={\displaystyle {\int }_{{\phi }_1}^{{\phi }_2}}\left(w(\phi )-w({\phi }_1)-\beta (\phi -{\phi }_1)\right)\text{d}\phi & (31)\end{array}$

We refrain from integrating this expression, since a closed-form solution is precluded by the lack of an explicit formula for φ₂. We merely draw attention to the fact that ΔF_x is invariant with respect to mean indentation. The same is not true for the coefficient of friction:

$\begin{array}{ll}\bar{\mu }=\frac{\langle {\mu }_0{F}_z\rangle -\Delta F_x}{\langle F_z\rangle }={\mu }_0-\frac{\Delta F_x}{k_z{\overline{u}}_z}& (32)\end{array}$

However, the dependence on $\overline{u}$_z is incidental, merely reflecting the fact that ΔF_x is subtracted from different baselines of friction force. Using our dimensionless variables, the above can also be written in the following compact form:

$\begin{array}{ll}\bar{\mu }={\mu }_0\left(1-\alpha {\text{Ψ}}_w(\beta )\right)& (33)\end{array}$

Further, it can be shown that Ψ_w is a fairly well-behaved function that has unit range and is monotonously decreasing and convex for all waveforms and any number of stick events per cycle of oscillation. However, space considerations prevent us from including a formal proof of these properties.

3.4. Oscillation Waveforms

The functional dependence (33) presented in the previous section permits an interesting observation: the overall strength of the friction reduction effect is primarily governed by the amplitude of the oscillation and not by the frequency. In principle, the effective coefficient of friction can be reduced to very low values, but that requires a force amplitude that is comparable to the mean normal force. Thus, the technique is not very useful for reducing friction in highly loaded contacts, e.g., rail-car or truck wheels.

Furthermore, a higher frequency cannot be used to compensate for small amplitude. However, frequency is still an important parameter, since it determines the “velocity-resistance” of the effect: As has been pointed out before, the largest reduction is always seen in the static case, and becomes lower with increasing sliding velocity. The frequency determines the scaling of this decline, and a strong reduction can be achieved even at high sliding velocities if the frequency of the applied oscillation is high enough. However, frequency is not the only factor that determines this “velocity-resistance.” The waveform of the oscillation is also quite important, which is why we briefly discuss it here.

By far the most important property of a waveform w is the maximal positive value of its first derivative, or β_c. A right-leaning sawtooth function, for example, has β_c = 2; a harmonic oscillation has β_c = 2π, which is slightly better; however, a left-leaning sawtooth function has β_c = ∞, which is ideal. An infinite value of β_c implies that the oscillation will provide some measure of friction reduction at arbitrarily high velocities. While this is not really possible in practice, the general rule for waveform selection is nevertheless that the load should increase as fast as possible and then relax slowly. Thus, approximations of left-leaning sawtooth or the square wave are preferable to smooth and symmetric functions like the harmonic oscillation. Naturally, this recommendation is subordinate to practical technological constraints. For example, a high-amplitude harmonic oscillation could be generated by exciting a natural vibrational mode of the system, while a square wave would likely require more sophisticated equipment.

We conclude this section by giving Ψ_w for a few common waveforms explicitly. For both sawtooth variants and the square wave Ψ_w can be calculated in closed form. However, for most oscillations, including sinusoidal ones, this is not possible. Nonetheless, the function can easily be computed numerically for arbitrary waveforms, and so we include two empirical approximations for the harmonic oscillation, which were first obtained in Popov et al. (2017). The first approximation is slightly more accurate.

$\begin{array}{ll}{\text{Ψ}}_{\text{str}}(\beta )=1-\frac{\beta }{2}& (34)\end{array}$

$\begin{array}{ll}{\text{Ψ}}_{\text{stl}}(\beta )=\frac{2}{2+\beta }& (35)\end{array}$

$\begin{array}{ll}{\Psi }_{\text{sqr}}(\beta )=\{\begin{array}{ll}1-\beta /8,\hfill & \text{for }\beta <4\hfill \\ 2/\beta ,\hfill & \text{for }\beta >4\hfill \end{array}& (36)\end{array}$

$\begin{array}{ll}{\text{Ψ}}_{sin}(\beta )\approx \frac{3}{4}{(1-\beta /{\beta }_c)}^2+\frac{1}{4}{(1-\beta /{\beta }_c)}^4& (37)\end{array}$

$\begin{array}{ll}\approx {(1-\beta /{\beta }_c)}^{2.4}& (38)\end{array}$

For a visual comparison, the dependence of the coefficient of friction on β is plotted in Figure 4 for all four of the above waveforms. To keep things simple, only the case of maximal friction reduction is shown α = 1, in which case Equation (33) reduces to $\bar{\mu }={\mu }_0\left[1-{\text{Ψ}}_w(\beta )\right]$. This is why all curves show zero static friction. For other values of α the shapes of the curves would remain the same, but they would start at nonzero values of μ_s and would be scaled accordingly.

FIGURE 4

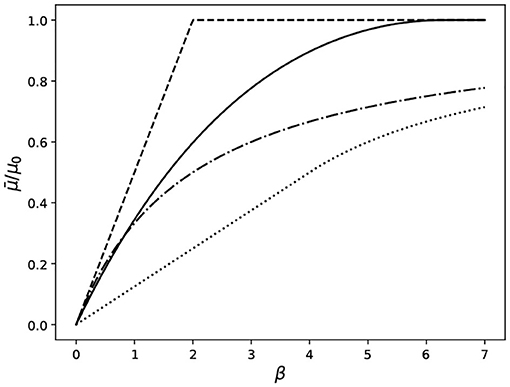
Figure 4. Coefficient of friction under normal vibration with different waveforms, computed using Equation (33) and the individual influence factors Equations (34)–(37). Note that for all curves α = 1, which corresponds to maximal friction reduction. Legend: dashed line—right-leaning sawtooth function (Equation 34); solid line—harmonic oscillation (Equation 37); dash-dotted line—left-leaning sawtooth function (Equation 35); dotted line—square wave (Equation 36).

As a final remark, we note that there is a unique optimal waveform with regards to reduction of friction. It is given by the periodic extension of δ(φ) − 1, where δ is the Dirac delta function. This “impulse wave” is −1 everywhere, except for very short positive spikes (impulses) that occur with a period of 1 and each integrate to 1, so that the average of the function is zero. With this degenerate waveform, the system slides most of the time, with only an infinitesimal stick phase at each spike, which implies that Ψ is very close to 1 for all β:

$\begin{array}{ll}{\text{Ψ}}_{\text{imp}}(\beta )\to 1& (39)\end{array}$

Thus, we conclude that friction can be reduced, in principle, to an arbitrary degree even at high sliding velocities, by effectively hopping over the surface. In practice, this approach will be limited by plastic deformation, radiation of elastic waves and the sheer difficulty of generating such an oscillation.

4. Tangential and Transverse Oscillations

Most of this paper was devoted to reduction of friction by normal oscillations. This focus is explained partly by the fact that the normal case is easiest to analyze, and partly because normal oscillations are generally the most efficient way to reduce friction, out of the three possible directions. Nevertheless, both tangential (in the direction of sliding) and transverse (in-plane, but orthogonal to sliding) vibration can reduce friction. For detailed analysis of the tangential case the reader is referred to Popov and Li (2018) and for the transverse case to Benad et al. (2018a). Here we only present some highlights and point out the major differences between normal oscillations and the other two modes.

In the tangential oscillation case the normal indentation is kept constant while an oscillatory component is added to the base of the spring. Sliding friction under such conditions can proceed in three modes: (I) pure sliding, in which the effective coefficient of friction is equal to μ₀, as argued previously. (II) simple stick-slip, which occurs for obvious reasons when the velocity amplitude is greater than the mean sliding velocity ($A_{x}f{w}^{\prime }(ft)>v_0$). (III) multiple stick-slip, which occurs when the velocity amplitude is much larger than v₀, so that the contact point slides back-and-forth in each cycle, going through two stick and slip phases each.

The most important difference between friction reduction by normal and tangential oscillations is that normal oscillations actually reduce the total dissipated energy through a walking-like mechanism, while tangential oscillations do not. The author is not aware of a good analogy to visualize the mechanism in the tangential case. But it is clear that, since the normal load (and therefore the force of sliding friction) is constant, the dissipated energy is simply friction force times distance (in mode II). Although the effective coefficient of friction (i.e., average spring force) may be lowered, the missing energy must be supplied by the oscillator. In mode III, when the amplitude is large enough to cause in-place sliding, the total sliding distance actually increases, and the total energy expenditure becomes larger than without oscillations, even though the effective coefficient of friction will still appear lower than μ₀.

Friction reduction by transverse oscillation always operates in something like mode III of tangential oscillation: it causes additional sliding in the direction orthogonal to the main sliding motion, thereby increasing the total path and therefore energy expenditure. However, the apparent coefficient of friction is reduced, because the magnitude of the local friction force is still limited to μ₀F_z, but now shared between the force components parallel and orthogonal to the main sliding direction. Thus, transverse oscillations are effectively “stealing” the friction vector from the slider, but at considerable expense of energy by the oscillator. This also accounts for the fact, mentioned previously, that the system never formally reaches the “invariant plateau” (${\bar{\mu }}_{\mathrm{\text{slip}}}={\mu }_0$) even at high sliding velocities, because the projection of the local friction force onto the sliding direction is always less than its total magnitude, so long as the transverse amplitude is non-zero. However, for sufficiently large sliding velocities this difference becomes very small, so for all practical purposes the plateau exists in the transverse case as well.

To summarize, normal oscillations are most effective at reducing dynamic friction and should be used in preference to the other directions. Not only do they actually reduce the total dissipated energy, but normal oscillations also act at right angles (by definition) to the sliding motion. Thus, they technically do not require energy to keep going. Of course, this is never quite the case in practice, but by exciting a resonant frequency the power needed to drive the oscillator can usually be made quite small. Compared to that, tangential oscillation requires a powerful oscillator (except in the static case), while transverse oscillation is even more energetically expensive, and also less effective overall. There are cases, however, where energy expenditure is not a primary concern (e.g., stabilization of system dynamics) and normal oscillations cannot be easily applied due to technological constraints. In such cases, tangential and even transverse oscillations are viable alternatives.

5. Conclusion

The present paper summarizes and generalizes a series of recent works that aim to establish a simple macroscopic contact model as a viable explanation for active control of friction by externally applied vibration. Despite its apparent simplicity, the model not only captures the full range of experimentally observed effects, but is also very flexible, being able to adapt to static and dynamic friction, oscillations in normal, tangential and transverse directions, contacts of curved bodies, etc. Apart from straight-forward reduction-of-friction settings, the model can also be applied to the study of frictional drives and actuators under complicated loading scenarios. A similar approach was also highly successful in modeling positioning systems without using any modified friction laws such as the elastoplastic model (see e.g., Teidelt et al., 2012; Grzemba et al., 2014; Teidelt, 2015).

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

MP conceived and conducted the research and prepared the manuscript.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was supported in part by the Tomsk State University competitiveness improvement programme, which the author gratefully acknowledges.

References

Ashida, Y., and Aoyama, H. (2007). Press forming using ultrasonic vibration. J. Mater. Process. Technol. 187, 118–122. doi: 10.1016/j.jmatprotec.2006.11.174

CrossRef Full Text | Google Scholar

Benad, J., Nakano, K., Popov, V. L., and Popov, M. (2018a). Active control of friction by transverse oscillations. Friction 7, 1–12. doi: 10.1007/s40544-018-0202-1

CrossRef Full Text | Google Scholar

Benad, J., Popov, M., Nakano, K., and Popov, V. L. (2018b). Stiff and soft active control of friction by vibrations and their energy efficiency. Forsch. Ingenieurw. 82, 331–339. doi: 10.1007/s10010-018-0281-1

CrossRef Full Text | Google Scholar

Chowdhury, M. A., and Helali, M. (2008). The effect of amplitude of vibration on the coefficient of friction for different materials. Tribol. Int. 41, 307–314. doi: 10.1016/j.triboint.2007.08.005

CrossRef Full Text | Google Scholar

De Wit, C. C., Olsson, H., Astrom, K. J., and Lischinsky, P. (1995). A new model for control of systems with friction. IEEE Trans. Autom. Control 40, 419–425. doi: 10.1109/9.376053

CrossRef Full Text | Google Scholar

Eaves, A., Smith, A., Waterhouse, W., and Sansome, D. (1975). Review of the application of ultrasonic vibrations to deforming metals. Ultrasonics 13, 162–170. doi: 10.1016/0041-624X(75)90085-2

CrossRef Full Text | Google Scholar

Eggers, G., Klein, J., Blank, J., and Hassfeld, S. (2004). Piezosurgery^®: an ultrasound device for cutting bone and its use and limitations in maxillofacial surgery. Br. J. Oral Maxillof. Surg. 42, 451–453. doi: 10.1016/j.bjoms.2004.04.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Fridman, H. D., and Levesque, P. (1959). Reduction of static friction by sonic vibrations. J. Appl. Phys. 30, 1572–1575. doi: 10.1063/1.1735002

CrossRef Full Text | Google Scholar

Gaberson, H. A. (1971). Particle motion on oscillating conveyors: the equations of motion and the rules for predicting motion form transitions. J. Eng. Ind.. 94, 50–56. doi: 10.1115/1.3428154

CrossRef Full Text | Google Scholar

Gaberson, H. A. (1972). Particle motion on oscillating conveyors-part 2. practical solutions to the equations of motion and the extension of the theory to beds of granular material. J. Eng. Ind. 94, 57–63. doi: 10.1115/1.3428155

CrossRef Full Text | Google Scholar

Godfrey, D. (1967). Vibration reduces metal to metal contact and causes an apparent reduction in friction. ASLE Trans. 10, 183–192. doi: 10.1080/05698196708972178

CrossRef Full Text | Google Scholar

Grzemba, B., Pohrt, R., Teidelt, E., and Popov, V. L. (2014). Maximum micro-slip in tangential contact of randomly rough self-affine surfaces. Wear 309, 256–258. doi: 10.1016/j.wear.2013.11.050

CrossRef Full Text | Google Scholar

Heckl, M. A., and Huang, X. (2000). Curve squeal of train wheels, part 3: active control. J. Sound Vibrat. 229, 709–735. doi: 10.1006/jsvi.1999.2512

CrossRef Full Text | Google Scholar

Mao, X., Popov, V. L., Starcevic, J., and Popov, M. (2017). Reduction of friction by normal oscillations. ii. in-plane system dynamics. Friction 5, 194–206. doi: 10.1007/s40544-017-0146-x

CrossRef Full Text | Google Scholar

Müller, M., and Ostermeyer, G. (2007). Cellular automata method for macroscopic surface and friction dynamics in brake systems. Tribol. Int. 40, 942–952. doi: 10.1016/j.triboint.2006.02.045

CrossRef Full Text | Google Scholar

Murakawa, M., and Jin, M. (2001). The utility of radially and ultrasonically vibrated dies in the wire drawing process. J. Mater. Process. Technol. 113, 81–86. doi: 10.1016/S0924-0136(01)00635-5

CrossRef Full Text | Google Scholar

Pohlman, R., and Lehfeldt, E. (1966). Influence of ultrasonic vibration on metallic friction. Ultrasonics 4, 178–185. doi: 10.1016/0041-624X(66)90244-7

CrossRef Full Text | Google Scholar

Popov, M., and Li, Q. (2018). Multimode active control of friction, dynamic ratchets and actuators. Phys. Mesomech. 21, 24–31. doi: 10.1134/S1029959918010046

CrossRef Full Text | Google Scholar

Popov, M., Popov, V. L., and Popov, N. V. (2017). Reduction of friction by normal oscillations. I. influence of contact stiffness. Friction 5, 45–55. doi: 10.1007/s40544-016-0136-4

CrossRef Full Text | Google Scholar

Popov, V. L. (2017). Oscillation-based methods for actuation and manipulation of nano-objects. AIP Conf. Proc. 1882:020056. doi: 10.1063/1.5001635

CrossRef Full Text | Google Scholar

Popov, V. L., and Heß, M. (2016). Method of Dimensionality Reduction in Contact Mechanics and Friction. Berlin: Springer. doi: 10.1007/978-3-642-53876-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Popov, V. L., Starcevic, J., and Filippov, A. (2010). Influence of ultrasonic in-plane oscillations on static and sliding friction and intrinsic length scale of dry friction processes. Tribol. Lett. 39, 25–30. doi: 10.1007/s11249-009-9531-6

CrossRef Full Text | Google Scholar

Schmidt, J. P., Hagedorn, P., and Bingqi, M. (1996). A note on the contact problem in an ultrasonic travelling wave motor. Int. J. Nonlin. Mech. 31, 915–924. doi: 10.1016/S0020-7462(96)00112-6

CrossRef Full Text | Google Scholar

Siegert, K., and Ulmer, J. (2001). Superimposing ultrasonic waves on the dies in tube and wire drawing. J. Eng. Mater. Technol. 123, 517–523. doi: 10.1115/1.1397779

CrossRef Full Text | Google Scholar

Socoliuc, A., Gnecco, E., Maier, S., Pfeiffer, O., Baratoff, A., Bennewitz, R., and Meyer, E. (2006). Atomic-scale control of friction by actuation of nanometer-sized contacts. Science 313, 207–210. doi: 10.1126/science.1125874

PubMed Abstract | CrossRef Full Text | Google Scholar

Storck, H., Littmann, W., Wallaschek, J., and Mracek, M. (2002). The effect of friction reduction in presence of ultrasonic vibrations and its relevance to travelling wave ultrasonic motors. Ultrasonics 40, 379–383. doi: 10.1016/S0041-624X(02)00126-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Teidelt, E. (2015). Oscillating contacts: friction induced motion and control of friction (Ph.D. thesis). TU Berlin, Berlin, Germany.

Google Scholar

Teidelt, E., Willert, E., Filippov, A., and Popov, V. L. (2012). Modeling of the dynamic contact in stick-slip microdrives using the method of reduction of dimensionality. Phys. Mesomech. 15, 287–292. doi: 10.1134/S1029959912030071

CrossRef Full Text | Google Scholar

Thoe, T., Aspinwall, D., and Wise, M. (1998). Review on ultrasonic machining. Int. J. Mach. Tools Manuf. 38, 239–255. doi: 10.1016/S0890-6955(97)00036-9

CrossRef Full Text | Google Scholar