A neo-cooperation search based evolutionary algorithm for multi-objective electric rope shovel production scheduling

In the manufacturing process of electric rope shovels, an extensive array of components need to be processed. Each component is subject to a distinct sequence of operations, with the number of operations varying by part. Moreover, each of these operations needs to be processed on specific machines within specific processing durations. Therefore, the electric rope shovel production scheduling problem turns out to be challenging for general optimizers, requiring to find the optimal operation sequence, make trade-offs between multiple conflicting objectives, and satisfy a series of strict constraints. To address this production scheduling problem, this paper proposes a neo-cooperation search based evolutionary algorithm. The proposed algorithm suggests a novel encoding scheme to represent a solution (i.e., the sequence of operations of multiple components) with a real decision vector and allocates computational resources to two cooperating populations for global search and local search, respectively. The proposed algorithm can effectively balance between exploration and exploitation, and is shown to outperform state-of-the-art evolutionary algorithms in the experiments.

1 Introduction

As a key piece of heavy engineering machinery, electric rope shovels are widely used in mining, construction, and infrastructure sectors, primarily for handling and excavating earth, rock, and ore materials (Topno et al., 2021; Wang et al., 2021). With the rapid development of the global mining and construction industries, the demand for electric rope shovels has gradually increased, particularly in large open-pit mines and major construction projects, where their work efficiency and production capacity are crucial. Consequently, the design and production of electric rope shovels have become increasingly complex and precise, involving the manufacture and assembly of numerous components. These components typically include core components such as buckets, boom assembly, upper mechanisms, and propel system, each requiring precision processing and assembly through multiple stages (Wei et al., 2011; Chen et al., 2021).

During the production process of electric rope shovels, the number of processes and the technology paths required vary due to the different structures and functions of each component. The machining process for each component may involve several operations, such as cutting, milling, drilling, welding, and heat treatment, and in each operation, different machines can often be chosen for processing (Wu et al., 2024; Babaei Khorzoughi and Hall, 2016). This constitutes a typical multi-operation, multi-machine scheduling problem. Unlike traditional assembly line production, the processing technology for electric rope shovel components exhibits significant flexibility and parallelism. Therefore, determining a reasonable processing sequence for each component with the most suitable machines for processing has become one of the core issues in production scheduling (Lei and Cai, 2020).

The optimization problems involved in the production of electric rope shovels can be modeled as single-objective (Rahimi et al., 2023; Wang P. et al., 2023) or multi-objective optimization problems (Shao et al., 2024a; Tian et al., 2024b). For single-objective optimization, the goal is to find a solution that minimizes or maximizes a certain function under certain constraints (Brest et al., 2017; Tong et al., 2021; Shao et al., 2025). The optimal solution of a single-objective problem refers to the solution that minimizes the objective function among all solutions that satisfy the constraints. However, since the number of objectives involved in the above optimization scenarios is usually more than one, there is no single optimal solution, and it is more reasonable to be modeled as a multi-objective optimization problem for processing (Tang et al., 2023; Wang Z. et al., 2023). This way, the optimization goal is to find a set of solutions that constitute the Pareto optimal solutions. Continuous optimization and combinatorial optimization are two important branches of multi-objective optimization problems (Tian et al., 2022; Tian et al., 2023), and in this study, the research object is the sequence optimization problems belonging to combinatorial optimization problems with complex search spaces.

Sequence optimization problems (Guo et al., 2006; Voutchkov et al., 2005) play a crucial role in various fields, aiming to find the optimal arrangement order within given constraints to maximize or minimize one or more objective functions. For instance, in the field of production manufacturing, job scheduling (Hamscher et al., 2000; Jamil et al., 2020) is a critical task that involves determining the sequence of operations in the production process to maximize productivity and minimize costs. By optimizing the order of jobs, idle time on the production line can be reduced, equipment utilization can be improved, and production efficiency can be optimized. Sequence optimization algorithms (Yang et al., 2021; Kim and Durlofsky, 2021) can help manufacturing companies better plan their production processes, enhance productivity, reduce costs, and improve market competitiveness.

The traveling salesman problem (Saller et al., 2023; Gutiérrez-Aguirre and Contreras-Bolton, 2024) is another typical case of sequence optimization problems. In the transportation sector, route planning for travel is an important problem. This problem refers to a scenario where a salesman needs to visit multiple cities, with each city visited only once, and the objective is to find the shortest route that minimizes the total distance traveled. By optimizing the order of cities to be visited, the distance traveled by the salesman can be effectively reduced, resulting in time and cost savings (Mosayebi et al., 2021; Zhang et al., 2021). This is particularly significant for logistics and courier industries as it can improve delivery efficiency, reduce transportation costs, and enhance customer satisfaction. In the field of bioinformatics, sequence optimization problems also exist. Genome sequence analysis (Nakagawa and Fujita, 2018; Xiao et al., 2024) involves studying and analyzing the genome sequences of organisms to reveal relationships between genes and discover new genes. By optimizing the arrangement order of gene sequences, a better understanding of the interrelationships between genes can be achieved, providing important foundations for disease treatment, gene editing, and other related areas.

Compared with general sequence optimization problems mentioned above, the sequence optimization problems involved in electric rope shovel production are completely different. In particular, the production of electric rope shovel is faced with the need for multi-objective optimization, and the production process usually involves multiple conflicting objective functions, such as: minimizing the total production duration, minimizing machine idle time, balancing workload and improving resource utilization. These objectives are mutually restricted and cannot be met by a simple optimization method at the same time. Therefore, the performance of traditional optimization methods is limited in solving such complex scheduling problems. In addition, in the production of electric rope shovel, the dependencies between sequence elements are more complex and the data sets involved are diverse, which also poses challenges to the existing multi-objective evolutionary algorithms. Intuitively, the production scheduling not only needs to determine the processing sequence of each component, but also to decide which machine to use for each process. Due to different components processing requirements and machine performance differences, scheduling schemes directly affect production efficiency, processing costs and equipment utilization.

In order to better solve the sequence optimization problems involved in electric rope shovel production, this paper models them as a constrained multi-objective sequence optimization problem, called production scheduling sequence optimization problems (PSSOPs), where a novel encoding scheme is suggested to represent a solution (i.e., the sequence of operations of multiple components) with a single real decision vector. Correspondingly, we propose an evolutionary algorithm for solving PSSOPs. This paper makes the following key contributions:

1. An evolutionary algorithm based on a neo-cooperation search is proposed, known as NCSEA, which allocates computational resources to two collaboratively optimized populations for global search and local search, respectively, effectively balancing exploration and exploitation. Specifically, one population focuses on the processing of all optimization objectives produced by the shovel, one population only selects the optimal solution of a specific objective for search, and the two populations can adaptively balance the search granularity of the two populations due to the co-evolution scheme. Additionally, deep reinforcement learning is used to learn the optimal mutation granularity for the two populations.

2. Based on the demand data for electric shovel production scheduling, we developed a test suite containing six test problems of varying difficulty levels. To validate the practical performance of the proposed NCSEA in solving the sequencing optimization problem in electric rope shovel production scheduling, we compared it with six state-of-the-art constrained multi-objective evolutionary algorithms. The experimental results show that NCSEA outperforms the compared constrained multi-objective evolutionary algorithms in most test instances and demonstrates stable performance across test problems of different difficulty levels.

This article is organized as follows. The second section provides a brief overview of existing sequence optimization algorithms. The third section details the proposed optimization model and algorithm. The fourth section reports the experimental results of a set of test problems with different characteristics. Finally, the fifth section summarizes the paper.

2 Related work

2.1 General form of sequence optimization

In general, a constrained multi-objective sequence optimization problem involves at least two objectives (Xiang et al., 2020; Wu and Shao, 2024; Shao et al., 2024b; Tian et al., 2024a) and one constraint, which is mathematically formulated as

$\begin{array}{cc}\hfill \text{Minimize\hspace{0.17em}}& f\left(\mathbf{x}\right)=\left(f_1\left(\mathbf{x}\right),f_2\left(\mathbf{x}\right),\dots ,f_m\left(\mathbf{x}\right)\right)\hfill \\ \hfill \text{Subject\hspace{0.17em}to\hspace{0.17em}}& \mathbf{x}=\left(x_1,x_2,\dots ,x_d\right)\in \mathrm{\Omega }\hfill \\ \hfill & g_i\left(\mathbf{x}\right)\le 0,i=1,\dots ,q\hfill \end{array},(1)$

where $\mathbf{x}=(x_1,x_2,\dots ,x_d)$ represents a $d$-dimensional decision variable, $\mathrm{\Omega }$ represents the decision space (i.e., all permutations of $1,\dots ,d$), $f(\mathbf{x})$ denotes its objective vector, $m$ is the dimension of the objective space, and $g_i(\mathbf{x})$ denotes $q$ inequality constraints. If feasible solutions $\mathbf{x}$ and $\mathbf{y}$ satisfy $f_i(\mathbf{x})\le f_i(\mathbf{y})$ for every $i\in 1,\dots ,m$ and $f_i(\mathbf{x})<f_i(\mathbf{y})$ for at least one $j\in 1,\dots ,m$, then $\mathbf{x}$ is said to dominate $\mathbf{y}$. The objective in solving Equation 1 is to discover a diversified set of feasible Pareto optimal solutions (Xiong et al., 2024) that are not dominated by any solutions in the decision space $\mathrm{\Omega }$ (Shao et al., 2023b; Zhang et al., 2024; Jia et al., 2023).

2.2 Existing evolutionary algorithms for sequence optimization

To find multiple feasible and Pareto optimal solutions for constrained multi-objective sequence optimization problems, a number of evolutionary algorithms have been developed in the last decades. In Zhang et al. (2005), the study investigates the multi-job batch flow problem in a two-stage hybrid flow shop. To tackle this NP-hard problem, the authors develop two heuristic methods, both of which involve sorting the jobs first and then applying a strategy of batch flow processing to each job. These two heuristic methods differ in the way they sort the jobs. The first heuristic treats each job as a whole entity. The second heuristic method views the system as a pure flow shop with machine aggregation at the first stage. It uses the summary files of each job from the single job batch flow results as the time requirements for the artificial pure flow shop. When solving the batch flow problem for each job in the sequence, both heuristic methods allocate a balanced number of sub-batches to the machines in the first stage and determine the size of the sub-batches. The results indicate that the aggregated machine heuristic algorithm performs significantly better. The aggregated machine algorithm shows good solution quality, with an average relative distance from the lower bound of only 6.85%. Therefore, it produces high-quality solutions and significantly improves upon the performance of traditional algorithms in this domain.

In qing Li et al. (2020), the authors introduce a heuristic Multi-Objective Evolutionary Algorithm based on Decomposition (MOEA/D) specifically tailored to tackle the complex hybrid flow shop batch scheduling problem. The algorithm makes several significant contributions to optimization in this domain. Firstly, a novel crossover operator is introduced to effectively handle scenarios where parent solutions exhibit varying sub-batch vectors. Secondly, a right-shift heuristic algorithm is proposed, taking into consideration both the problem structure and objective features to enhance the overall performance of the algorithm. Additionally, a population initialization heuristic algorithm is developed, which efficiently allocates each solution to the closest reference vector. Furthermore, a mutation heuristic algorithm is presented, incorporating considerations for sub-block arrangements to enhance the exploitation capabilities of the algorithm. Through rigorous experimentation and testing, the efficacy and efficiency of the proposed algorithm are empirically validated, demonstrating its effectiveness in solving the hybrid flow shop batch scheduling problem.

In Zhang et al. (2022), the study investigates a multi-objective mixed-model assembly line scheduling problem, with the aim of minimizing the maximum completion time and the total number of batches considering setup and transportation operations. A multi-objective mixed integer programming model was established, and a solver was used to evaluate the trade-off between the two objectives. To address this problem, an automatic algorithm design is introduced in the proposed framework to conceptualize an automated multi-objective evolutionary algorithm. This is the first study to use automatic algorithm design to solve a multi-objective mixed-model assembly line scheduling problem. Considering the characteristics of the problem and the algorithm framework, the authors designed configurable settings for numerical parameters and categorical parameters, as well as operators. Subsequently, an automated MOEA was constructed using an iterative racing procedure. Experimental validation of the performance of the proposed algorithm shows its efficiency and effectiveness.

In Duan et al. (2021), to capture the characteristics of real-world vehicle routing applications, the author developed a robust mutlti-objective vehicle routing problem with time windows (RMO-VRPTW), which includes two conflicting objectives: minimizing the number of vehicles and total distance. Additionally, a new form of uncertainty is introduced to capture disruptive features from practical applications. To address RMO-VRPTW, a robust optimization approach was developed, incorporating advanced encoding and decoding methods, robustness measures, and local search strategies. Initially, the deterministic problem space features were thoroughly explored to guide robust optimization. Furthermore, to further explore the search space, two local search strategies were proposed. One adjusts customer priorities based on associated time windows, while the other directly manipulates routes by removing customers from routes with fewer customers and inserting them into routes with stronger robustness.

To solve large-scale car sequence problems, a novel mutation-based multi-objective evolutionary algorithm called MOEA-PGX is proposed in Shao et al. (2023a). The core idea of the MOEA-PGX algorithm lies in extracting heuristic information from the population and constructing a probability matrix based on this information. During the optimization process, this probability matrix is utilized to heuristically repair infeasible solutions while retaining the advantageous genes from the parent solutions. This heuristic repair strategy enhances the quality and feasibility of solutions. To represent solutions, the MOEA-PGX algorithm converts them into permutation groups. By employing permutation-based crossover and mutation operations, high-quality characteristics are maintained when generating offspring solutions. This representation method captures the structural features of sequencing problems better, leading to the generation of superior solutions. Compared to existing algorithms, MOEA-PGX demonstrates faster convergence speed and a lower probability of getting trapped in local optima, making it an effective approach for solving large-scale car sequence problems.

2.3 Motivation of this work

Although the optimization algorithms mentioned above have achieved remarkable performance in various sequential optimization problems, the production scheduling sequence optimization in electric rope shovel production often presents unique challenges (Dong et al., 2024; Xie et al., 2024). Specifically, these algorithms typically rely on designing algorithms based on the characteristics of the problem’s dataset, which are not directly applicable to the optimization scenarios in electric rope shovel production. On the other hand, the sequence of operations in electric rope shovel production is not simply a permutation of $1,\dots ,d$, since multiple components have multiple operations. Additionally, the processing of components in electric rope shovel production often involves specific time requirements, adding strict constraints to the optimization. To address these issues, we propose a cooperative evolutionary algorithm to efficiently solve PSSOPs, the details of which are elaborated in the next section.

3 The proposed model and algorithm

3.1 The proposed optimization model

Let the set of components (e.g., boom assembly, bucket, etc.) to process be denoted as $J=\{J_1,J_2,\dots ,J_n\}$, where each component $J_i$ follows a predefined sequence of operations (e.g., cutting, welding, drilling, painting, etc.) $O_{i1},O_{i2},\dots ,O_{i{u}_i}$, and $O_{ij}$ denotes the $j$-th operation of component $J_i$. Given multiple machines $W=\{W_1,W_2,\dots ,W_M\}$, the processing time of operation $O_{ij}$ on machine $W_k$ is given by $T_{\mathit{ijk}}$ if the operation can be conducted on $W_k$. For a solution (i.e., the sequence of all operations of all components), the idle waiting time between operations $O_{i(j-1)}$ and $O_{ij}$ for component $J_i$ is $E{T}_{\mathit{ijk}}$, and thus the completion time of component $J_i$, denoted by $C_i$, is the total sum of the processing and waiting times of all its operations:

$C_i={\displaystyle \sum _{j=1}^{u_i}}\left(T_{\mathit{ijk}}+E{T}_{\mathit{ijk}}\right).(2)$

As for the proposed production scheduling sequence optimization problems (PSSOPs), the core goal is to minimize the maximum completion time across all components, which represents the overall production cycle. This can be formulated as the first objective function:

$f_1=\underset{i=1,\dots ,n}{\max }{C}_i,(3)$

which ensures that the completion time of the most time-consuming component is minimized, reflecting an optimized production cycle.

While each component should be completed within a specific time window, the second objective function aims to reduce penalties incurred from early or late deliveries. More specifically, if a component is finished earlier than its due time $d_{i1}$, an early completion penalty $E_i$ is introduced. Similarly, if a component is completed later than its late due time $d_{i2}$, a tardiness penalty $T_i$ is incurred. These penalties are defined as

$\begin{array}{c}\hfill E_i=\max \left(0,d_{i1}-C_i\right)\\ \hfill T_i=\max \left(0,C_i-d_{i2}\right)\end{array},(4)$

and the second objective function can be expressed as

$f_2={\displaystyle \sum _{i=1}^n}\left(\alpha E_i+\beta T_i\right).(5)$

Here, $\alpha$ and $\beta$ represent the respective weights for early and late penalties, allowing flexibility in balancing the costs of deviation from the scheduled due dates. The setting of these two parameters primarily reflects the different preferences for early and late penalties. Depending on changes in the production environment, these parameters can be adjusted to different combinations. In addition, due to strict time management, the second objective has to be less than a user-given constraint value for all solutions to make sense, so this is a typical constrained multi-objective optimization problem.

As a consequence, the complete definition of PSSOPs is as follows, where $SC$ represents a user-specified parameter for defining the constraint:

$\begin{array}{cc}\hfill \min & f_1=\underset{i\in S}{\max }{C}_i\hfill \\ \hfill \min & f_2={\displaystyle \sum _{i=1}^n}\left(\alpha E_i+\beta T_i\right)\hfill \\ \hfill \text{subject\hspace{0.17em}to}& f_2<SC\hfill \end{array}.(6)$

In this optimization model, each solution determines the value of $C_i$ for all components. Since a solution should contain the sequence of multiple operations of multiple components, it has to be represented by a complex vector like $O_{11},O_{31},O_{32},O_{21},\dots$. To facilitate the optimization of PSSOPs using various algorithms, we suggest a simple and flexible encoding scheme, representing each solution with a real vector that can be optimized using most constrained multi-objective evolutionary algorithms. As illustrated in Figure 1, we demonstrate a processing task involving three components: Component 1 has three operation, Component 2 has three operations, and Component 3 has four operations. The example solution is a real-coded vector (0.10,0.42,0.58,0.15,0.29,0.81,0.23,0.36,0.77,0.93), where each dimension corresponds to an ordered operation. To obtain the sequence of all operations, the solution is decoded by sorting all its real elements in an ascending order. Then, the resulting permutation (1,4,7,5,8,2,3,9,6,10) is converted into a sequence of operations, where elements 1,2,3 correspond to the three operations of Component 1, elements 4,5,6 correspond to the three operations of Component 2, and elements 7,8,9,10 correspond to the four operations of Component 3. Note that the rank of all operations of a component is predefined and cannot be modified, hence the elements corresponding to a component do not need to be associated with specific operations. Lastly, to calculate the completion time $C_i$, the operations are conducted one by one on specific machines, and they should be waited if other operations are being conducted on the same machine.

Figure 1

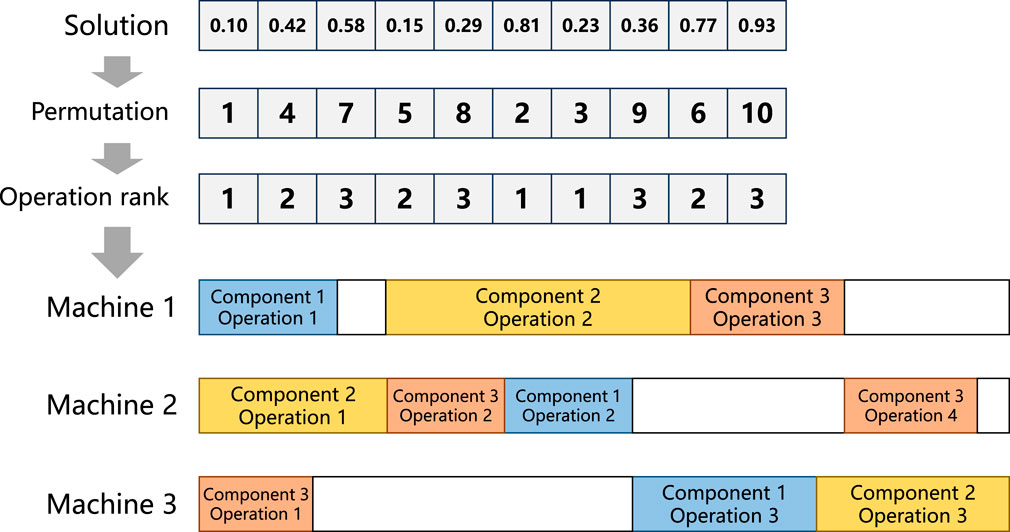
Figure 1. Illustration of the proposed encoding scheme, which represents the sequence of operations of multiple components using a real vector.

With the above encoding scheme, the proposed PSSOPs turn out to be continuous constrained multi-objective optimization problems, which can be handled by many constrained multi-objective evolutionary algorithms in theory. However, the conflicting objectives and strict constraints challenge many existing algorithms in finding feasible Pareto optimal solutions, especially when the landscape is still highly discretized due to the conversions from real vectors to discrete sequences. Therefore, an effective evolutionary algorithm is tailored for solving PSSOPs, the details of which are presented in the next subsection.

3.2 The proposed neo-cooperation search based evolutionary algorithm

The procedure of the proposed neo-cooperation search based evolutionary algorithm (NCSEA) is illustrated in Algorithm 1, which begins with the initialization of neural network and two populations, $Population1$ and $Population2$, both of which are created randomly (Lines 1, 3 and 4). The Neural network $Net$ are used to learn the optimal variation granularity $action$. The proposed algorithm also sets the initial count of consumed evaluations, $FE$, equal to the size of the populations (Line 6). Once the populations are established, the proposed algorithm enters a loop that continues until the maximum number of evaluations, $F{E}_{\mathit{max}}$, is reached. Within this loop, the proposed algorithm randomly selects $N$ parents from $Population1$ and randomly selects $N$ parents from $Population2$ (Lines 8 and 9). This selection process is used for maintaining a good performance gene pool, which enhances the algorithm’s ability to explore various solutions. After selecting the parents, the proposed algorithm generates $N$ offspring solutions from each set of parents (Lines 12 and 13). These offspring solutions represent new potential solutions that will be introduced to the populations. Since the optimization model of the proposed PSSOP introduces a novel encoding scheme representing solutions with real vectors, the real variation operators used in many evolutionary algorithms can be adopted, where the simulated binary crossover and polynomial mutation are adopted in the proposed NCSEA. Given two parent solutions ${\mathbf{x}}^1$ and ${\mathbf{x}}^2$, two offspring solutions ${\mathbf{o}}^1$ and ${\mathbf{o}}^2$ are generated by simulated binary crossover (Deb and Agrawal, 1995) and polynomial mutation (Deb and Goyal, 1996). Following the generation of offspring solutions, the proposed algorithm updates both $Population1$ and $Population2$ by combining each current population with all the newly created offspring solutions (Lines 12 and 13). This combination is designed to foster diversity and improve the quality of solutions.

Algorithm 1

Algorithm 1. Main procedure of NCSEA.

The next step, i.e., environmental selection, involves retaining $N$ solutions from $Population1$ and retaining $N$ solutions from $Population2$ (Lines 14 and 15), where the strategies are different for retaining solutions from the two populations. $Population1$ undergoes a selection process known as environmental selection, where $N$ solutions are chosen based on their performance according to non-dominated sorting and crowding distances, on the basis of constrained Pareto dominance relations. More specifically, the constraint violation of a solution $\mathbf{x}$ is calculated by

$CV\left(\mathbf{x}\right)=\max \left\{0,f_2\left(\mathbf{x}\right)-SC\right\},(7)$

so that a smaller $CV(\mathbf{x})$ indicates a smaller constraint violation, and $\mathbf{x}$ is feasible if and only if $CV(\mathbf{x})=0$. Then, a solution $\mathbf{x}$ is said to be better than (i.e., constrained dominate) another solution $\mathbf{y}$ if and only if

$CV\left(\mathbf{x}\right)<CV\left(\mathbf{y}\right),(8)$

or

$\left\{\begin{array}{c}CV\left(\mathbf{x}\right)=CV\left(\mathbf{y}\right)\hfill \\ f_1\left(\mathbf{x}\right)\le f_1\left(\mathbf{y}\right)\text{\hspace{0.17em}and\hspace{0.17em}}{f}_2\left(\mathbf{x}\right)\le f_2\left(\mathbf{y}\right)\hfill \\ f_1\left(\mathbf{x}\right)\ne f_1\left(\mathbf{y}\right)\text{\hspace{0.17em}or\hspace{0.17em}}{f}_2\left(\mathbf{x}\right)\ne f_2\left(\mathbf{y}\right)\hfill \end{array}\right.,(9)$

On the other hand, $Population2$ is truncated based on only the second objective, the minimization of which is also beneficial for the satisfaction of the constraint. More specifically, the $N$ solutions with smaller $f_2$ values are retained in $Population2$. That is, a solution $\mathbf{x}$ is said to be better than (i.e., constrained dominate) another solution $\mathbf{y}$ if and only if

$f_2\left(\mathbf{x}\right)<f_2\left(\mathbf{y}\right).(10)$

At the end of each loop, the proposed algorithm updates the agent as illustrated in Algorithm 2 (Line 17). The optimal mutation granularity $action$ of the next iteration is predicted by Algorithm 3 (Line 18). The evaluation count, $FE$, is updated to reflect the number of evaluations consumed during that iteration (Lnie 19). This ensures that the algorithm stays within the specified limits of function evaluations. Finally, once the loop completes and the maximum evaluation count is reached, the proposed algorithm returns the final population $Population1$ (Line 20), which contains the most promising solutions discovered throughout the process. It is worth noting that since the second objective involves constraints, the main purpose of the second population is to handle the second objective by ensuring that the constraints are satisfied. This structured approach allows NCSEA to efficiently explore and exploit the solution space, ultimately leading to high-quality outcomes.

Algorithm 2

Algorithm 2. $TrainingDQN(Net,M).$

Algorithm 3

Algorithm 3. $AdaptiveMutation(Net,M).$

3.3 Adaptive mutation

To further improve the algorithm’s exploration ability, reinforcement learning is employed to determine the optimal mutation granularity as illustrated in Algorithm 2 and Algorithm 3. Specifically, five mutation granularities—$\frac{1}{d}$, $\frac{1}{2d}$, $\frac{3}{2d}$, $\frac{4}{2d}$ and $\frac{1}{5d}$ (where $d$ represents the decision variable dimension)–are used as candidate strategies to effectively balance exploration and exploitation. The population state is defined by convergence, diversity, and feasibility metrics. Convergence is evaluated by the population’s average performance on each objective function, indicating how close solutions are to the Pareto optimal front. For each objective function $f_i(\mathbf{x})$, the convergence is calculated as follows:

$con={\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{\mathbf{x}\in \mathcal{P}}}{f}_i\left(\mathbf{x}\right),(11)$

where $f_i(\mathbf{x})$ represents the value of the $i$-th objective function, and $m$ is the number of objective functions. Diversity captures the population’s spread across each objective function, which is calculated using:

$div={\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{\mathbf{x}\in \mathcal{P}}}{\left(f_i\left(\mathbf{x}\right)-ob{j}_i\right)}^2,(12)$

where $ob{j}_i$ is the average value of the $i$-th objective function. While feasibility measures the degree to which the population satisfies problem constraints; a value of 0 denotes complete feasibility, while higher values suggest constraint violations. Feasibility is defined as:

$fea={\displaystyle \sum _{\mathbf{x}\in \mathcal{P}}}CV\left(\mathbf{x}\right),(13)$

where $CV(\mathbf{x})$ denotes the constraint violation of solution $\mathbf{x}$.

Together, these elements—convergence, diversity, and feasibility—form the population state $s_t$, encapsulating key attributes that allow the reinforcement learning agent to suggest the ideal mutation granularity. The hypervolume (HV) metric serves as the reward signal $r_t$ to assess resource allocation effectiveness, measuring convergence and diversity by evaluating the solution set’s enclosed volume. Each training entry comprises the current state, action, obtained reward, and the new state. To be specific, the states is a three-dimensional vector. The reward and action are a scalar, respectively. These data are generated at each iteration and sequentially inserted into the experience memory pool. This experience pool continuously enhances the agent’s decision-making capabilities. The agent is update rule according to:

$Q\left(s,a;\theta \right)\leftarrow Q\left(s,a;\theta \right)+\alpha \left(y-Q\left(s,a;\theta \right)\right)(14)$

where $\alpha$ is the learning rate, $\theta$ are the network parameters, and the target $y$ is defined as:

$y=r+\gamma \underset{a^{\prime }}{\max }Q\left(s^{\prime },a^{\prime };{\theta }^{-}\right)(15)$

Here, $r$ is the reward received after action $a$, $s^{\prime }$ is the next state, and ${\theta }^{-}$ represents the parameters of the target network. The DQN network architecture comprises an input layer with 4 nodes, two hidden layers, and an output layer. The input layer receives a 4-dimensional state vector as input. This is followed by the first hidden layer, which contains 10 nodes with a nonlinear activation function (i.e., ReLU) to enhance learning. The second hidden layer also processes information in preparation for the output layer, which has a single node that provides the Q-value for a particular action-state pair. This configuration enables the network to learn an effective mapping from states to action values in a compact, efficient structure. Based on the established mapping relationship, the reinforcement learning agent can recommend the optimal mutation granularity for the current population during the iteration process, i.e., determining the parameters for polynomial mutation that are suitable for the current population, thereby guiding the generation of offspring.

3.4 Discussions

From the above description, it can be seen that the proposed algorithm considers all the optimization objectives and constraint through the first population, while the second population focuses solely on the second objective. For the second population, since it only selects solutions that perform significantly on the second objective to generate offspring solutions, it is more likely to excel in the second objective. Moreover, if only the second population is used, the entire population will struggle to address the first objective, which is why the first population focuses on all the optimization objectives and constraint. It is worth noting that the offspring solutions generated by both populations are shared, allowing the second population to adaptively adjust its search for the second objective using the offspring solutions generated by the first population.

The coevolution mechanism of the proposed NCSEA is different from existing co-evolutionary algorithms for constrained multi-objective optimization. To be specific, most existing algorithms evolve a main population considering all objectives and constraints of the problem, and evolve one or more auxiliary populations eliminating part or all of the constraints. Such coevolution mechanism can help the main population to jump over local feasible regions, but is not effective enough for the proposed PSSOPs with highly discretized landscapes that are difficult to converge. On the contrary, the proposed NCSEA suggests a problem-dependent coevolution mechanism considering part of the objectives in an auxiliary population, which exhibits significantly better performance than existing algorithms as evidenced by the experimental results given in the next section.

4 Empirical studies

4.1 Settings of problems and algorithms

Six datasets with different conditions for electric rope shovel production are involved in the experiments, where there are a total of 14 components, each of which requires 3 to 6 operations to complete on one of eight machines within specific processing durations. For instance, in the production of electric rope shovels, the processing of the boom assembly requires five operations, including cutting, welding, drilling, heat treatment, and painting, to ensure strength and precision. The processing of the bucket requires six operations, including steel plate cutting, forming, welding, heat treatment, surface treatment, and wear-resistant coating, to enhance durability and abrasion resistance. The processing of the stick involves four operations, including cutting, welding, drilling, and painting, to ensure a precise fit with other components. As a result, the experiments involve six test instances denoted as PSSOP1–PSSOP6, each having 62 operations with different processing times and time windows. Specifically, each operation in PSSOP1 and PSSOP2 has a longer operation time, each operation in PSSOP3 and PSSOP4 involves more machines, and the time windows in PSSOP5 and PSSOP6 are more restricted. Due to these differing characteristics, these PSSOPs pose challenges for CMOEAs. Besides, the parameters $\alpha$ and $\beta$ for early and late penalties are set to 0.8 and 0.2, respectively, which can prefer handling of early penalties. The size of the experience pool is set to 1 000 to ensure there is enough space to store the experiences.

The proposed algorithm in this study is compared with six state-of-the-art constrained multi-objective evolutionary algorithms: TriP (Ming et al., 2022), EMCMO (Qiao et al., 2022), CMOQLMT (Ming et al., 2023), CMOSMA (He et al., 2022), DP-PPS (Ming et al., 2022), and C3M (Sun et al., 2022). For fair comparisons, compared algorithms follow the parameter settings in their original papers and all of them use simulated binary crossover and polynomial mutation to generate real-coded offspring solutions for PSSOPs, where the parameter $\eta$ is set to 20 and the mutation probability $prob$ is set to $1/d$ ($d$ is the number of decision variables). Each algorithm uses a population size of 100 and undergoes 10,000 function evaluations, resulting in each optimization process lasting tens of minutes for each test instance. At the same time, the function evaluation setting is large enough to detect the performance of each comparison algorithm and the proposed algorithm. As the Pareto fronts of the optimization problem are unknown, the hypervolume (HV) indicator is employed to evaluate the quality of each solution set. To ensure result reliability, 30 independent runs are conducted for each algorithm on every test instance, followed by a Wilcoxon rank sum test. Detailed experimental evidence is provided in the subsequent subsection to showcase the superior performance of the proposed algorithm.

4.2 Comparative experiments

The optimization results of the proposed algorithm and four comparative algorithms on PSSOP1–PSSOP6 are presented in Table 1. It can be observed that the proposed algorithm performs the best on all the six test instances, which means that the proposed algorithm significantly outperforms TriP, EMCMO, CMOQLMT, CMOSMA, DP-PPS, and C3M on PSSOPs. Moreover, Figure 2 displays the convergence curves of their HV values on PSSOP1–PSSOP6. The plots indicate that the proposed algorithm converges faster than the compared algorithms TriP, EMCMO, CMOQLMT, CMOSMA, DP-PPS, and C3M. It is worth noting that even with only 6,000 function evaluations, the population generated by the proposed algorithm can compete with those generated byTriP, EMCMO, CMOQLMT, CMOSMA, DP-PPS, and C3M, which have undergone 10,000 function evaluations on these test instances. To provide a more intuitive demonstration of the optimization results, Figure 3 shows the objective values of the final populations on PSSOP2 and PSSOP5. It can be observed that the proposed algorithm gains solutions dominating the solutions obtained by TriP, EMCMO, CMOQLMT, CMOSMA, DP-PPS, and C3M, further confirming the superiority of the proposed algorithm. It is worth noting that the proposed algorithm significantly outperforms the comparison algorithms in both optimization objectives. This indicates that the sequence solution found by the proposed algorithm can not only produce the corresponding parts within the specified time period, but also accelerate the entire production process, offering advantages in improving production efficiency and reducing costs.

Table 1

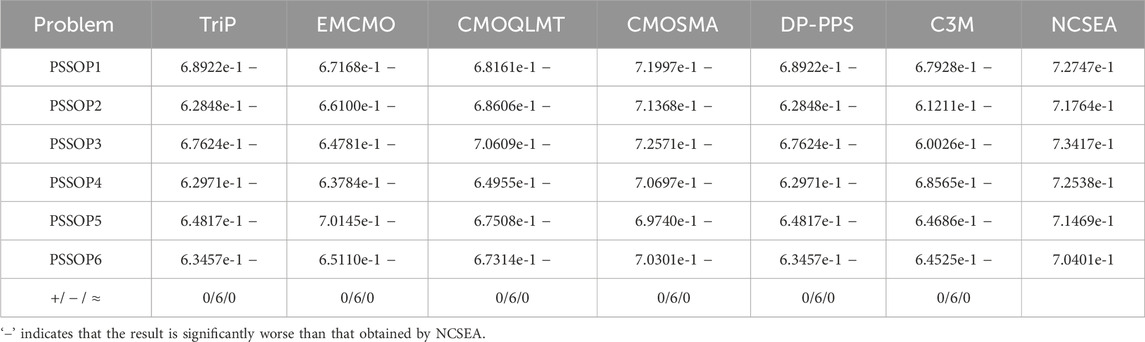
Table 1. Mean of HV values obtained by TriP, EMCMO, CMOQLMT, CMOSMA, DP-PPS, C3M, and the proposed NCSEA on PSSOP1–PSSOP6.

Figure 2

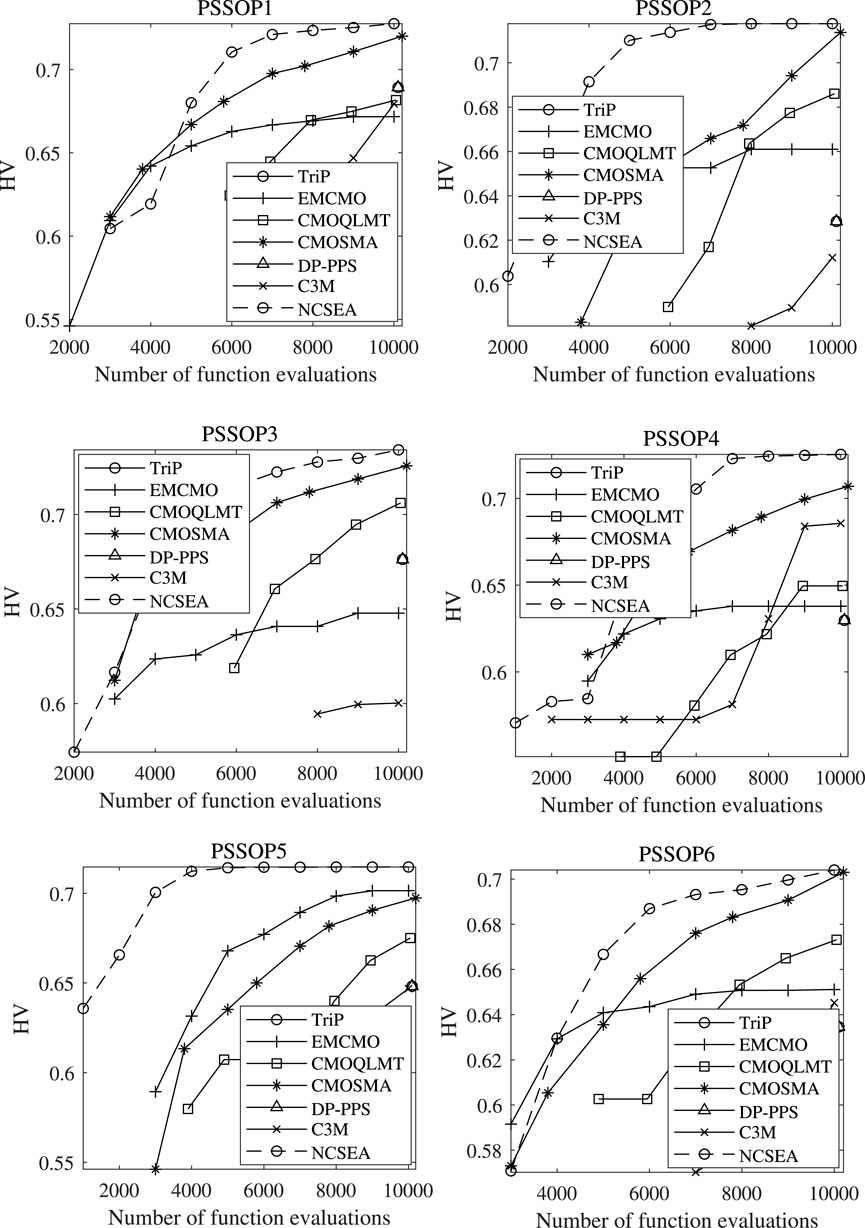
Figure 2. Convergence profiles obtained by TriP, EMCMO, CMOQLMT, CMOSMA, DP-PPS, C3M, and the proposed NCSEA on PSSOP1–PSSOP6.

Figure 3

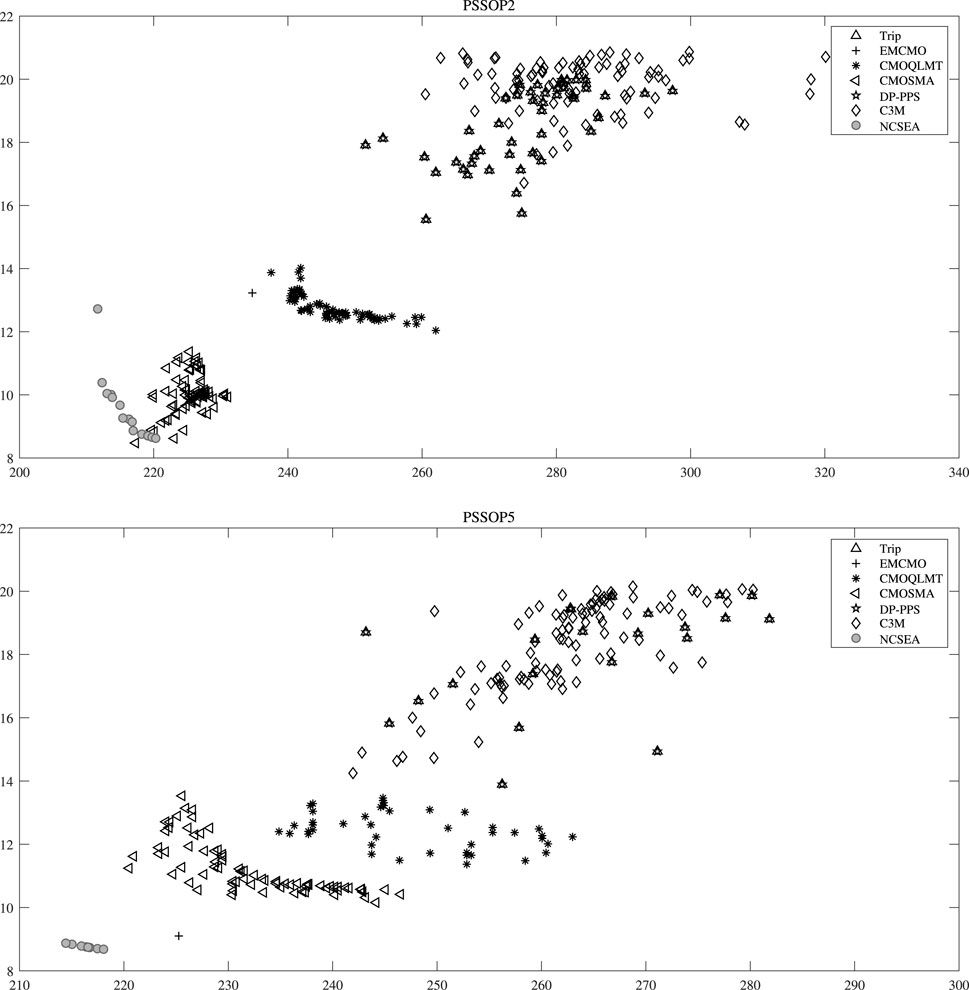
Figure 3. Populations with the median HV obtained by TriP, EMCMO, CMOQLMT, CMOSMA, DP-PPS, C3M and the proposed NCSEA on PSSOP2 and PSSOP5.

4.3 Ablation studies

To further validate the effectiveness of the proposed collaborative search method, NCSEA was compared with its variants that use a single search scheme, thereby completely eliminating the impact of other strategy differences. Table 2 lists the comparison results of NCSEA and its two variants, where NCSEA1 uses only population1, i.e., it only performs global search, and NCSEA2 uses only population2, i.e., it only performs local search. Clearly, the proposed NCSEA still demonstrates the best overall performance and is competitive with the different variants of NCSEA.

Table 2

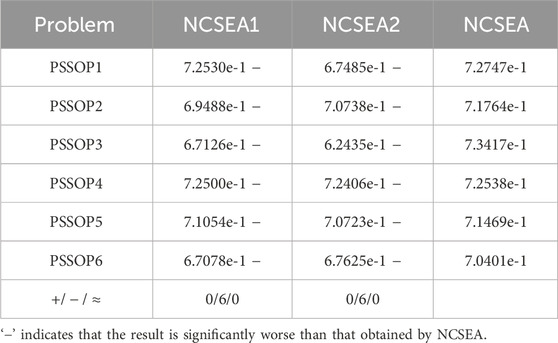
Table 2. Mean of HV values obtained by NCSEA1, NCSEA2, and NCSEA on PSSOP1–PSSOP6, where NCSEA1 only performs global search, and NCSEA2 only performs local search, and NCSEA is the original algorithm.

4.4 Computational efficiency

Furthermore, a comprehensive assessment of the computational efficiency of the seven compared algorithms is presented. As depicted in Table 3, an in-depth breakdown of the average runtime across TriP, EMCMO, CMOQLMT, CMOSMA, DP-PPS, C3M, and the proposed NCSEA is provided. Upon meticulous data analysis, it becomes evident that the proposed algorithm demonstrates competitive computational efficiency when compared with other algorithms. This observation underscores the robust computational efficiency of NCSEA, a purpose-built algorithm tailored to efficiently address optimization challenges brought by electric rope shovel production scheduling. Consequently, the NCSEA presented in this study emerges as a highly efficient algorithm for PSSOPs.

Table 3

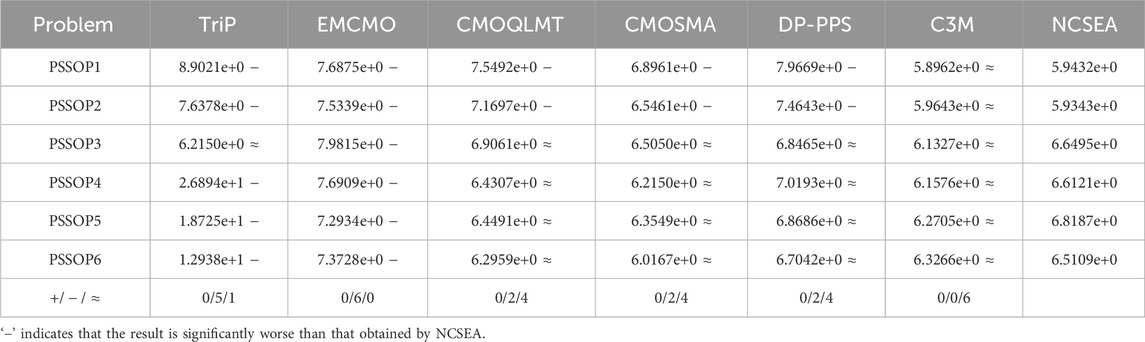
Table 3. Mean runtime obtained by TriP, EMCMO, CMOQLMT, CMOSMA, DP-PPS, C3M, and the proposed NCSEA on PSSOP1–PSSOP6.

5 Conclusion

To effectively address the scheduling optimization problem in electric rope shovel production, we have proposed an evolutionary algorithm based on a neo-cooperation search mechanism. The proposed algorithm allocates computational resources to two collaboratively optimized populations for global and local searches, effectively balancing exploration and exploitation. Experimental results have demonstrated that the proposed algorithm has significant advantages in practical applications. In future research, our goal is to further incorporate various heuristic information to better solve large-scale PSSOPs, thereby enhancing the algorithm’s applicability in real-world scenarios. Additionally, considering that reinforcement learning methods have been widely applied to sequence optimization problems, we plan to explore deep reinforcement learning to adaptively generate high-quality solution sets without the requirement of iterative search procedures.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

JZ: Conceptualization, Writing–original draft. HY: Conceptualization, Writing–original draft. YW: Validation, Writing–original draft. RG: Validation, Writing–original draft. SS: Writing–original draft, Writing–review and editing, Conceptualization, Supervision.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Babaei Khorzoughi, M., and Hall, R. (2016). A study of digging productivity of an electric rope shovel for different operators. Minerals 6, 48. doi:10.3390/min6020048

CrossRef Full Text | Google Scholar

Brest, J., Maučec, M. S., and Bošković, B. (2017). “Single objective real-parameter optimization: algorithm jso,” in 2017 IEEE congress on evolutionary computation (CEC) (IEEE), 1311–1318.

CrossRef Full Text | Google Scholar

Chen, Z., Xue, D., Wang, G., Cui, D., Fang, Y., and Wang, S. (2021). Simulation and optimization of the tracked chassis performance of electric shovel based on dem-mbd. Powder Technol. 390, 428–441. doi:10.1016/j.powtec.2021.05.085

CrossRef Full Text | Google Scholar

Deb, K., Agrawal, R. B., et al. (1995). Simulated binary crossover for continuous search space. Complex Syst. 9, 115–148.

Google Scholar

Deb, K., Goyal, M., et al. (1996). A combined genetic adaptive search (geneas) for engineering design. Comput. Sci. Inf. 26, 30–45.

Google Scholar

Dong, Z., Shao, S., and Tian, Y. (2024). “A sequence fine-tuning strategy based evolutionary algorithm for solving project scheduling problems,” in 2024 6th international conference on data-driven optimization of complex systems (DOCS) (IEEE), 170–177.

CrossRef Full Text | Google Scholar

Duan, J., He, Z., and Yen, G. G. (2021). Robust multiobjective optimization for vehicle routing problem with time windows. IEEE Trans. Cybern. 52, 8300–8314. doi:10.1109/tcyb.2021.3049635

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, Y., Mileham, A. R., Owen, G. W., and Li, W. (2006). Operation sequencing optimization using a particle swarm optimization approach. Proc. Institution Mech. Eng. Part B J. Eng. Manuf. 220, 1945–1958. doi:10.1243/09544054jem647

CrossRef Full Text | Google Scholar

Gutiérrez-Aguirre, P., and Contreras-Bolton, C. (2024). A multioperator genetic algorithm for the traveling salesman problem with job-times. Expert Syst. Appl. 240, 122472. doi:10.1016/j.eswa.2023.122472

CrossRef Full Text | Google Scholar

Hamscher, V., Schwiegelshohn, U., Streit, A., and Yahyapour, R. (2000). “Evaluation of job-scheduling strategies for grid computing,” in Grid computing —grid 2000: first IEEE/ACM international workshop Bangalore, India, december 17, 2000 proceedings 1 (Springer), 191–202.

Google Scholar

He, C., Li, M., Zhang, C., Chen, H., Zhong, P., Li, Z., et al. (2022). A self-organizing map approach for constrained multi-objective optimization problems. Complex and Intelligent Syst. 8, 5355–5375. doi:10.1007/s40747-022-00761-2

CrossRef Full Text | Google Scholar

Jamil, B., Shojafar, M., Ahmed, I., Ullah, A., Munir, K., and Ijaz, H. (2020). A job scheduling algorithm for delay and performance optimization in fog computing. Concurrency Comput. Pract. Exp. 32, e5581. doi:10.1002/cpe.5581

CrossRef Full Text | Google Scholar

Jia, W., Lin, Y., Ding, J., Qin, G., Shao, S., and Tian, Y. (2023). “Optimization of large-scale distribution center location selection in fresh produce transportation,” in International conference on bio-inspired computing: theories and applications (Springer), 256–270.

Google Scholar

Kim, Y. D., and Durlofsky, L. J. (2021). A recurrent neural network–based proxy model for well-control optimization with nonlinear output constraints. SPE J. 26, 1837–1857. doi:10.2118/203980-pa

CrossRef Full Text | Google Scholar

Lei, D., and Cai, J. (2020). Multi-population meta-heuristics for production scheduling: a survey. Swarm Evol. Comput. 58, 100739. doi:10.1016/j.swevo.2020.100739

CrossRef Full Text | Google Scholar

Li, J. Q., rui Tao, X., xian Jia, B., yan Han, Y., Liu, C., Duan, P., et al. (2020). Efficient multi-objective algorithm for the lot-streaming hybrid flowshop with variable sub-lots. Swarm Evol. Comput. 52, 100600. doi:10.1016/j.swevo.2019.100600

CrossRef Full Text | Google Scholar

Ming, F., Gong, W., and Gao, L. (2023). Adaptive auxiliary task selection for multitasking-assisted constrained multi-objective optimization [feature]. IEEE Comput. Intell. Mag. 18, 18–30. doi:10.1109/mci.2023.3245719

CrossRef Full Text | Google Scholar

Ming, F., Gong, W., Wang, L., and Lu, C. (2022). A tri-population based co-evolutionary framework for constrained multi-objective optimization problems. Swarm Evol. Comput. 70, 101055. doi:10.1016/j.swevo.2022.101055

CrossRef Full Text | Google Scholar

Mosayebi, M., Sodhi, M., and Wettergren, T. A. (2021). The traveling salesman problem with job-times (tspj). Comput. and Operations Res. 129, 105226. doi:10.1016/j.cor.2021.105226

CrossRef Full Text | Google Scholar

Nakagawa, H., and Fujita, M. (2018). Whole genome sequencing analysis for cancer genomics and precision medicine. Cancer Sci. 109, 513–522. doi:10.1111/cas.13505

PubMed Abstract | CrossRef Full Text | Google Scholar

Qiao, K., Yu, K., Qu, B., Liang, J., Song, H., and Yue, C. (2022). An evolutionary multitasking optimization framework for constrained multiobjective optimization problems. IEEE Trans. Evol. Comput. 26, 263–277. doi:10.1109/tevc.2022.3145582

CrossRef Full Text | Google Scholar

Rahimi, I., Gandomi, A. H., Chen, F., and Mezura-Montes, E. (2023). A review on constraint handling techniques for population-based algorithms: from single-objective to multi-objective optimization. Archives Comput. Methods Eng. 30, 2181–2209. doi:10.1007/s11831-022-09859-9

CrossRef Full Text | Google Scholar

Saller, S., Koehler, J., and Karrenbauer, A. (2023). A systematic review of approximability results for traveling salesman problems leveraging the tsp-t3co definition scheme. arXiv preprint arXiv:2311.00604

Google Scholar

Shao, S., Tian, Y., Wang, L., Yang, S., Zhang, P., and Zhang, X. (2023a). “A permutation group-based evolutionary algorithm for car sequencing problems in assembly lines,” in 2023 5th international conference on data-driven optimization of complex systems (DOCS) (IEEE), 1–8.

CrossRef Full Text | Google Scholar

Shao, S., Tian, Y., Zhang, L., Tan, K. C., and Zhang, X. (2024a). An evolutionary algorithm for solving large-scale robust multi-objective optimization problems. IEEE Trans. Evol. Comput., 1. doi:10.1109/tevc.2024.3435006

CrossRef Full Text | Google Scholar

Shao, S., Tian, Y., and Zhang, X. (2023b). “A non-uniform clustering based evolutionary algorithm for solving large-scale sparse multi-objective optimization problems,” in International conference on bio-inspired computing: theories and applications (Springer), 103–116.

Google Scholar

Shao, S., Tian, Y., and Zhang, X. (2024b). Deep reinforcement learning assisted automated guiding vector selection for large-scale sparse multi-objective optimization. Swarm Evol. Comput. 88, 101606. doi:10.1016/j.swevo.2024.101606

CrossRef Full Text | Google Scholar

Shao, S., Tian, Y., and Zhang, Y. (2025). Deep reinforcement learning assisted surrogate model management for expensive constrained multi-objective optimization. Swarm Evol. Comput. 92, 101817. doi:10.1016/j.swevo.2024.101817

CrossRef Full Text | Google Scholar

Sun, R., Zou, J., Liu, Y., Yang, S., and Zheng, J. (2022). A multistage algorithm for solving multiobjective optimization problems with multiconstraints. IEEE Trans. Evol. Comput. 27, 1207–1219. doi:10.1109/tevc.2022.3224600

CrossRef Full Text | Google Scholar

Tang, Y., Wang, Y., Wu, D., Chen, M., Pang, L., Sun, J., et al. (2023). Exploring temperature-resilient recycled aggregate concrete with waste rubber: an experimental and multi-objective optimization analysis. Rev. Adv. Mater. Sci. 62, 20230347. doi:10.1515/rams-2023-0347

CrossRef Full Text | Google Scholar

Tian, Y., Chen, H., Ma, H., Zhang, X., Tan, K. C., and Jin, Y. (2022). Integrating conjugate gradients into evolutionary algorithms for large-scale continuous multi-objective optimization. IEEE/CAA J. Automatica Sinica 9, 1801–1817. doi:10.1109/jas.2022.105875

CrossRef Full Text | Google Scholar

Tian, Y., Shao, S., Xie, G., and Zhang, X. (2024a). A multi-granularity clustering based evolutionary algorithm for large-scale sparse multi-objective optimization. Swarm Evol. Comput. 84, 101453. doi:10.1016/j.swevo.2023.101453

CrossRef Full Text | Google Scholar

Tian, Y., Si, L., Zhang, X., Tan, K. C., and Jin, Y. (2023). Local model-based Pareto front estimation for multiobjective optimization. IEEE Trans. Syst. Man, Cybern. Syst. 53, 623–634. doi:10.1109/tsmc.2022.3186546

CrossRef Full Text | Google Scholar

Tian, Y., Yao, L., Shao, S., Zhang, Y., and Zhang, X. (2024b). “Deep reinforcement learning based adaptive environmental selection for evolutionary multi-objective optimization,” in 2024 IEEE congress on evolutionary computation (CEC) (IEEE), 1–8.

CrossRef Full Text | Google Scholar

Tong, H., Huang, C., Minku, L. L., and Yao, X. (2021). Surrogate models in evolutionary single-objective optimization: a new taxonomy and experimental study. Inf. Sci. 562, 414–437. doi:10.1016/j.ins.2021.03.002

CrossRef Full Text | Google Scholar

Topno, S. A., Sahoo, L. K., and Umre, B. (2021). Energy efficiency assessment of electric shovel operating in opencast mine. Energy 230, 120703. doi:10.1016/j.energy.2021.120703

CrossRef Full Text | Google Scholar

Voutchkov, I., Keane, A., Bhaskar, A., and Olsen, T. M. (2005). Weld sequence optimization: the use of surrogate models for solving sequential combinatorial problems. Comput. methods Appl. Mech. Eng. 194, 3535–3551. doi:10.1016/j.cma.2005.02.003

CrossRef Full Text | Google Scholar

Wang, P., Feng, Y., Chen, Z., and Dai, Y. (2023a). Study of a hull form optimization system based on a Gaussian process regression algorithm and an adaptive sampling strategy, part i: single-objective optimization. Ocean. Eng. 279, 114502. doi:10.1016/j.oceaneng.2023.114502

CrossRef Full Text | Google Scholar

Wang, X., Song, X., and Sun, W. (2021). Surrogate based trajectory planning method for an unmanned electric shovel. Mech. Mach. Theory 158, 104230. doi:10.1016/j.mechmachtheory.2020.104230

CrossRef Full Text | Google Scholar

Wang, Z., Pei, Y., and Li, J. (2023b). A survey on search strategy of evolutionary multi-objective optimization algorithms. Appl. Sci. 13, 4643. doi:10.3390/app13074643

CrossRef Full Text | Google Scholar

Wei, B., Gao, F., Chen, J., He, J., Wu, S., and Song, Q. (2011). Mechanics performance of three-degree-of-freedom excavating mechanism of an electric shovel. Proc. Institution Mech. Eng. Part C J. Mech. Eng. Sci. 225, 1443–1457. doi:10.1177/2041298310395451

CrossRef Full Text | Google Scholar

Wu, J., Zhao, J., Wang, X., and Lin, B. (2024). Multidisciplinary collaborative design optimization of electric shovel working devices. Machines 12, 520. doi:10.3390/machines12080520

CrossRef Full Text | Google Scholar

Wu, P., and Shao, S. (2024). “A time window sequence-based evolutionary algorithm for solving large-scale daily task planning problems,” in 2024 IEEE congress on evolutionary computation (CEC) (IEEE), 1–8.

CrossRef Full Text | Google Scholar

Xiang, X., Tian, Y., Xiao, J., and Zhang, X. (2020). A clustering-based surrogate-assisted multiobjective evolutionary algorithm for shelter location problem under uncertainty of road networks. IEEE Trans. Industrial Inf. 16, 7544–7555. doi:10.1109/tii.2019.2962137

CrossRef Full Text | Google Scholar

Xiao, Z., Yang, A., Liu, Z., Ren, M., Cheng, L., Liu, D., et al. (2024). Comprehensive genome sequence analysis of ralstonia solanacearum gd-2, a phylotype i sequevar 15 strain collected from a tobacco bacterial phytopathogen. Front. Microbiol. 15, 1335081. doi:10.3389/fmicb.2024.1335081

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, G., Shao, S., and Tian, Y. (2024). “A two-stage repair strategy based evolutionary algorithm for solving resource-constrained project scheduling problems,” in 2024 6th international conference on data-driven optimization of complex systems (DOCS) (IEEE), 142–149.

CrossRef Full Text | Google Scholar

Xiong, J., Liu, G., Gao, Z., Zhou, C., Hu, P., and Bao, Q. (2024). A many-objective evolutionary algorithm based on learning assessment and mapping guidance of historical superior information. J. Comput. Des. Eng., qwae022.

Google Scholar

Yang, X., Hua, G., Hu, L., Cheng, T., and Huang, A. (2021). Joint optimization of order sequencing and rack scheduling in the robotic mobile fulfilment system. Comput. and Operations Res. 135, 105467. doi:10.1016/j.cor.2021.105467

CrossRef Full Text | Google Scholar

Zhang, B., Pan, Q.-k., Meng, L.-l., Lu, C., Mou, J.-h., and Li, J.-q. (2022). An automatic multi-objective evolutionary algorithm for the hybrid flowshop scheduling problem with consistent sublots. Knowledge-Based Syst. 238, 107819. doi:10.1016/j.knosys.2021.107819

CrossRef Full Text | Google Scholar

Zhang, W., Liu, J., Liu, J., Liu, Y., and Tan, S. (2024). A dual distance dominance based evolutionary algorithm with selection-replacement operator for many-objective optimization. Expert Syst. Appl. 237, 121244. doi:10.1016/j.eswa.2023.121244

CrossRef Full Text | Google Scholar

Zhang, W., Yin, C., Liu, J., and Linn, R. J. (2005). Multi-job lot streaming to minimize the mean completion time in m-1 hybrid flowshops. Int. J. Prod. Econ. 96, 189–200. doi:10.1016/j.ijpe.2004.04.005

CrossRef Full Text | Google Scholar

Zhang, Z., Liu, H., Zhou, M., and Wang, J. (2021). Solving dynamic traveling salesman problems with deep reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 34, 2119–2132. doi:10.1109/tnnls.2021.3105905

PubMed Abstract | CrossRef Full Text | Google Scholar