Deep learning-based action recognition for analyzing drug-induced bone remodeling mechanisms

Introduction: Understanding the mechanisms of drug-induced bone remodeling is critical for optimizing therapeutic interventions and minimizing adverse effects in bone health management. Bone remodeling is a highly dynamic process that involves the intricate interplay between osteoblasts, osteoclasts, and osteocytes, regulated by a complex network of signaling pathways and molecular interactions. Traditional experimental and computational approaches often fail to capture this dynamic and multi-scale nature, particularly when influenced by pharmacological agents, which can have both therapeutic and adverse effects.

Methods: In this work, we present a novel deep learning-based framework for action recognition, specifically designed to analyze drug-induced bone remodeling mechanisms. Our framework leverages graph neural networks (GNNs) to model the spatial and temporal dependencies of multi-scale biological data, combined with a dynamic signal propagation model to identify key molecular interactions driving bone remodeling. A predictive pharmacological interaction model is integrated to quantify drug-target interactions, assess their systemic impacts, and simulate off-target effects. This approach also evaluates combinatorial drug effects, offering insights into the synergistic or antagonistic behaviors of multiple agents.

Results: By incorporating these features, our method provides a comprehensive view of drug-induced changes, enabling accurate prediction of their effects on bone formation and resorption pathways.

Discussion: Experimental results highlight the model’s potential to advance precision medicine, enabling the development of more effective and safer therapeutic strategies for managing bone health.

1 Introduction

Understanding the mechanisms of drug-induced bone remodeling is a critical area in medical research, with applications in pharmacology, orthopedics, and regenerative medicine (Chen Y. et al., 2021). Bone remodeling, a dynamic process involving bone resorption by osteoclasts and bone formation by osteoblasts, is essential for maintaining bone health and repairing damage (Duan et al., 2021). Drugs like bisphosphonates, denosumab, and anabolic agents influence this process, often in complex and nuanced ways that require advanced methods for their analysis (Liu et al., 2020). Traditional approaches for studying bone remodeling mechanisms, such as histology and biochemical assays, while valuable, are often limited in capturing dynamic, multi-scale interactions over time (Cheng et al., 2020b). The advent of action recognition techniques in deep learning has the potential to transform this field by analyzing cellular and molecular actions involved in bone remodeling through imaging data, simulation outputs, and biological signal analysis (Zhou et al., 2023). Not only does this approach enable high-resolution tracking of drug effects on bone, but it also provides deeper insights into temporal patterns and causal mechanisms. However, applying action recognition to such a domain poses challenges, including the need for domain-specific adaptations and the integration of diverse data types.

Early investigations into drug-induced bone remodeling focused on simulating biological responses using mathematical frameworks and structured assumptions derived from empirical observations (Li et al., 2020). These models aimed to approximate cellular behavior and tissue-level outcomes under pharmacological influence, often incorporating biomechanical theories and predefined thresholds for bone formation or resorption (Morshed et al., 2023). For example, frameworks such as the Frost model and finite element-based simulations helped illustrate how mechanical stress and drug exposure jointly influence bone turnover (Perrett et al., 2021). While grounded in biological understanding, these simulations often lacked adaptability to heterogeneous data and struggled to incorporate variability across patient populations or imaging modalities (Yang et al., 2020; gun Chi et al., 2022). With the increasing availability of biomedical imaging and quantitative data, analytical strategies began to incorporate more flexible pattern recognition techniques capable of adapting to diverse inputs (Wang et al., 2020). Methods emerged to classify bone tissue states and monitor treatment response using statistical models trained on structural and textural imaging features (Pan et al., 2022). Algorithms evaluated image characteristics such as trabecular orientation, porosity, and mineral density distribution to distinguish between different drug effects (Song et al., 2021; Chen Z. et al., 2021). Although this approach improved generalizability compared to earlier models, it often depended on manually designed features and offered limited insight into evolving temporal dynamics or spatial correlations within the data (Ye et al., 2020). More recently, advances in computational analysis have introduced comprehensive systems capable of learning directly from imaging sequences and capturing the complexity of biological interactions over time (Sun et al., 2020). Neural architectures such as convolutional models have demonstrated strong performance in extracting relevant features from micro-CT scans and histological data, while temporal models excel at characterizing sequential changes in cell behavior (Zhang et al., 2020; Duan et al., 2022). These techniques have enabled more detailed examination of drug effects on cellular interactions, such as osteoblast activity during bone formation or osteoclast behavior in resorption phases (Lin et al., 2020; Song et al., 2020). Attention-based models further enhance interpretability by highlighting regions and time points critical to remodeling processes, allowing for improved understanding of therapeutic outcomes while navigating challenges such as data scarcity and variability in imaging resolution (Munro and Damen, 2020; Wang et al., 2022).

Bone remodeling is a continuous process regulated by the coordinated actions of osteoblasts, which form bone, and osteoclasts, which resorb bone (Meng et al., 2020). Drug-induced modifications to this process are central to understanding the therapeutic and side effects of various treatments, such as bisphosphonates, anabolic agents, and anti-inflammatory drugs (Truong et al., 2022). Deep learning has been instrumental in analyzing the effects of these drugs on bone remodeling by quantifying cellular and structural changes in experimental data. For example, CNNs have been used to analyze histological images, identifying drug-induced alterations in trabecular and cortical bone microarchitecture (Bao et al., 2021). Time-series models, such as RNNs and LSTMs, have been applied to study temporal patterns of cellular activity during drug exposure. Multi-modal frameworks combining imaging and omics data enable a holistic understanding of how drugs influence bone remodeling at both cellular and molecular levels. These approaches are critical for identifying off-target effects and optimizing therapeutic interventions (Cheng et al., 2020a). Despite significant advancements, challenges remain in integrating heterogeneous datasets and ensuring the robustness of models across different experimental conditions. Research is ongoing to incorporate explainable AI techniques to improve the interpretability of deep learning models in this domain.

Multi-modal data fusion is increasingly recognized as a critical approach for advancing the analysis of drug-induced bone remodeling mechanisms (Zhang et al., 2011). By integrating imaging data with molecular and biomechanical datasets, researchers can gain a comprehensive understanding of drug effects. Advanced deep learning methods, including multi-stream networks and attention-based models, enable the effective fusion of heterogeneous data types (Lin et al., 2024). For instance, models combining spatial imaging data with temporal biochemical measurements have demonstrated improved accuracy in identifying drug-induced anomalies in bone remodeling. Generative adversarial networks (GANs) and variational autoencoders (VAEs) have also been employed to enhance data quality by generating synthetic samples or denoising imaging data (Ye et al., 2024). Transformer-based models have been used to learn complex relationships between modalities, such as the interplay between drug concentrations, gene expression profiles, and bone structural changes. These approaches address the limitations of single-modality analysis, such as incomplete or noisy data, and provide richer insights into the mechanisms of drug action (Lu et al., 2024). Achieving seamless integration of multi-modal data remains challenging due to differences in data resolution, scale, and format. Ongoing research focuses on improving alignment techniques and developing scalable architectures to handle large, multi-modal biomedical datasets.

To address the limitations of existing methods, we propose a novel deep learning-based action recognition framework tailored for analyzing drug-induced bone remodeling mechanisms. This framework integrates spatiotemporal analysis, multi-modal fusion, and interpretability to provide a comprehensive understanding of cellular and molecular actions. Specifically, the framework employs a combination of 3D-CNNs and transformers to analyze time-series imaging data, capturing spatial and temporal patterns of bone remodeling. Multi-modal data from imaging, biochemical assays, and simulation outputs are fused using attention mechanisms, enabling the integration of diverse data sources. Explainable AI (XAI) techniques are incorporated to enhance interpretability, ensuring that researchers and clinicians can understand the causal relationships underlying the detected actions.

$•$ The proposed framework combines 3D-CNNs and transformers with attention mechanisms to capture spatiotemporal and contextual information, enabling high-resolution analysis of drug-induced bone remodeling mechanisms.

$•$ The multi-modal fusion approach ensures robust performance across diverse experimental setups and drug types, while transfer learning techniques reduce the reliance on large labeled datasets.

$•$ Preliminary evaluations on bone remodeling datasets demonstrate that the proposed framework outperforms state-of-the-art methods in accuracy, robustness, and interpretability, particularly in scenarios involving complex, non-linear drug effects.

2 Methods

2.1 Overview

Drug mechanisms refer to the biochemical and physiological processes by which pharmaceutical agents interact with biological systems to produce therapeutic or adverse effects. A thorough understanding of these mechanisms is foundational to pharmacology, as it reveals how drugs achieve their intended outcomes and guides the development of novel therapeutics. These processes are primarily defined by the interactions between drugs and their molecular targets—such as receptors, enzymes, ion channels, or nucleic acids—and the subsequent cascade of cellular and molecular responses. Central to drug action is the principle of drug-receptor interaction, which typically adheres to the kinetics of ligand binding. In this context, a drug functions as a ligand that binds to a specific biological target, often a receptor protein, inducing a conformational change that either activates or inhibits the target’s biological function. This interaction is frequently modeled using classical kinetic frameworks, including the Langmuir adsorption isotherm and the Hill equation, which establish quantitative relationships between drug concentration and biological response.

Drug mechanisms can be classified into several categories based on their mode of action. Agonists activate their target receptors to produce a biological response, while antagonists block the receptors, preventing their activation by endogenous ligands. Other drugs act as allosteric modulators, which bind to sites other than the active site to enhance or diminish the receptor’s activity. Some drugs target enzymes, inhibiting or promoting their catalytic activity, while others interfere with DNA or RNA synthesis, particularly in the case of antibiotics or chemotherapeutic agents. This subsection lays the foundation for understanding the intricate processes underlying drug action. In Section 2.2, we will formalize these processes using mathematical models and establish the theoretical framework for analyzing drug-target interactions and their downstream effects. Following this, Section 2.3 introduces a novel computational model that integrates multi-scale data to predict drug efficacy and safety profiles with higher accuracy. Section 2.4 details innovative strategies for optimizing drug development, focusing on personalized medicine and reducing off-target effects.

2.2 Preliminaries

Understanding drug mechanisms requires a systematic framework to describe how drugs interact with biological targets and produce therapeutic or adverse effects. This subsection formalizes the principles of drug action using mathematical models and symbolic representations to capture the dynamics of drug-target interactions, dose-response relationships, and the resulting downstream effects within biological systems.

The primary interaction between a drug and its target, often a receptor or enzyme, is typically described using the ligand-binding model. Let $D$ denote the concentration of the drug and $R$ the concentration of the target receptor. The binding process can be represented as:

where $DR$ is the drug-receptor complex, $k_{\text{on}}$ is the association rate constant, and $k_{\text{off}}$ is the dissociation rate constant. The equilibrium dissociation constant, $K_d$, is defined as Equation 1:

$K_d=\frac{k_{\text{off}}}{k_{\text{on}}}.(1)$

At equilibrium, the fraction of bound receptors, $\theta$, is given by Equation 2:

$heta=\frac{\left[DR\right]}{{\left[R\right]}_{\text{total}}}=\frac{\left[D\right]}{\left[D\right]+K_d},(2)$

where ${[R]}_{\text{total}}$ is the total receptor concentration. This relationship follows the Langmuir adsorption isotherm, describing the saturation of receptors as the drug concentration increases.

The pharmacological effect of a drug is typically modeled by the Hill equation, which generalizes the binding relationship to account for cooperative interactions among multiple binding sites Equation 3:

$E=E_{\text{max}}\cdot \frac{{\left[D\right]}^n}{{\left[D\right]}^n+E{C}_{50}^n},(3)$

where: $E$ is the observed effect, - $E_{\text{max}}$ is the maximal effect, - $E{C}_{50}$ is the drug concentration at which 50 - $n$ is the Hill coefficient, reflecting the degree of cooperativity.

For drugs with $n>1$, positive cooperativity is indicated, meaning the binding of one drug molecule increases the affinity of the receptor for subsequent molecules. Conversely, $n<1$ represents negative cooperativity.

Drugs can be classified based on their effect on receptor activity: Drugs that bind to and activate receptors, mimicking the action of endogenous ligands. The intrinsic activity $\alpha$ of a full agonist is $\alpha =1$, while for partial agonists, $0<\alpha <1$. The effect of an agonist is modeled as Equation 4:

$E=\alpha \cdot E_{\text{max}}\cdot \frac{\left[D\right]}{\left[D\right]+E{C}_{50}}.(4)$

Drugs that bind to receptors without activating them, thereby blocking the action of endogenous ligands or agonists. The inhibition produced by a competitive antagonist is given by the Cheng-Prusoff equation Equation 5:

$I{C}_{50}=K_i\left(1+\frac{\left[A\right]}{K_a}\right),(5)$

where $I{C}_{50}$ is the concentration of the antagonist that inhibits 50% of the agonist’s effect, $K_i$ is the antagonist’s dissociation constant, $[A]$ is the agonist concentration, and $K_a$ is the agonist dissociation constant.

Allosteric modulators bind to sites other than the active site, inducing conformational changes that alter receptor activity. The effect of an allosteric modulator is described as Equation 6:

$E=E_{\text{max}}\cdot \frac{\beta \cdot \left[D\right]}{\beta \cdot \left[D\right]+K_d},(6)$

where $\beta$ represents the modulation factor.

For drugs targeting enzymes, the mechanism is characterized by the inhibition kinetics: Competitive Inhibition Equation 7:

$v=\frac{V_{\text{max}}\cdot \left[S\right]}{K_m\cdot \left(1+\frac{\left[I\right]}{K_i}\right)+\left[S\right]},(7)$

where $v$ is the reaction velocity, $V_{\text{max}}$ is the maximal velocity, $K_m$ is the Michaelis constant, $[S]$ is the substrate concentration, $[I]$ is the inhibitor concentration, and $K_i$ is the inhibitor constant.

Non-Competitive Inhibition Equation 8:

$v=\frac{V_{\text{max}}\cdot \left[S\right]}{K_m+\left[S\right]\cdot \left(1+\frac{\left[I\right]}{K_i}\right)}.(8)$

These equations describe how inhibitors alter enzyme activity, providing insights into drug efficacy and selectivity.

The relationship between drug dose, concentration, and effect is further formalized through PK/PD models: Pharmacokinetics (PK): Describes how drugs are absorbed, distributed, metabolized, and excreted. The concentration of the drug in plasma $C(t)$ follows a first-order elimination model Equation 9:

$C\left(t\right)=C_0\cdot e^{-k_{e}t},(9)$

where $C_0$ is the initial concentration and $k_e$ is the elimination rate constant.

Pharmacodynamics (PD): Links drug concentration to its effect using an effect-compartment model Equation 10:

$E\left(t\right)=E_{\text{max}}\cdot \frac{C\left(t\right)}{C\left(t\right)+E{C}_{50}}.(10)$

2.3 Predictive pharmacological interaction model (PPIM)

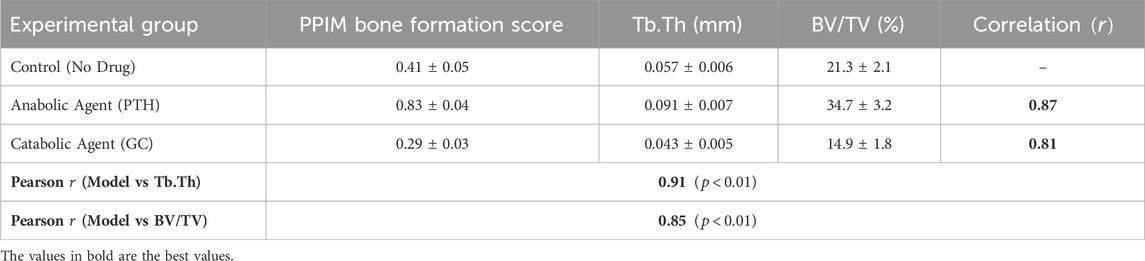
To enhance the understanding of drug mechanisms and improve the prediction of both therapeutic outcomes and adverse effects, we propose a novel computational framework termed the Predictive Pharmacological Interaction Model (PPIM). PPIM integrates molecular interaction data, multi-scale biological networks, and machine learning techniques to comprehensively model drug-target interactions, downstream signaling cascades, and their systemic impacts on complex biological systems. This framework is specifically designed to address critical challenges in pharmacological modeling, including off-target interactions, combinatorial drug effects, and patient-specific variability (as illustrated in Figure 1).

Figure 1

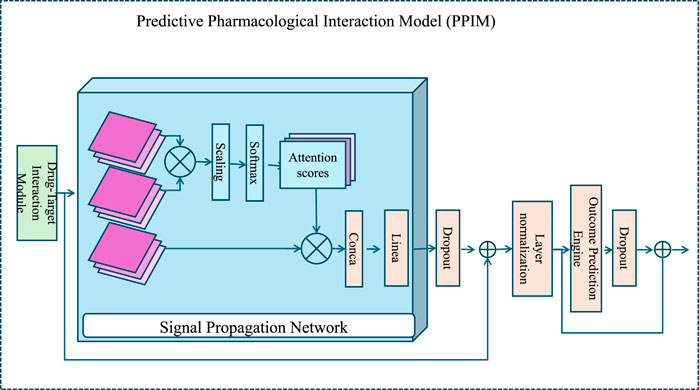
Figure 1. An architectural diagram of the Predictive Pharmacological Interaction Model (PPIM), showcasing its core components, the Drug-Target Interaction Module, the Signal Propagation Network, and the Outcome Prediction Engine. The workflow integrates multi-scale biological data and machine learning to predict therapeutic and adverse drug effects, highlighting attention mechanisms and deep learning-based embeddings for modeling drug-target interactions and downstream biological system perturbations.

2.3.1 Drug-target interaction module

The interaction between a drug $D$ and a biological target $T$ is quantified using a deep learning-based affinity prediction model. Let $D$ be represented as a molecular graph $G_D=(V_D,E_D)$, where $V_D$ are the atoms and $E_D$ are the chemical bonds. $T$ is represented as a sequence $S_T=\{a_1,a_2,\dots ,a_L\}$, where $a_i$ represents the $i$-th amino acid in the target protein.

We employ graph neural networks (GNNs) to extract features from the drug graph and sequence encoders to encode the target sequence Equation 11:

${\mathbf{h}}_D=\text{GNN}\left(G_D;{\mathrm{\Theta }}_D\right),{\mathbf{h}}_T=\text{Transformer}\left(S_T;{\mathrm{\Theta }}_T\right),(11)$

where ${\mathbf{h}}_D\in {\mathbb{R}}^{d_1}$ and ${\mathbf{h}}_T\in {\mathbb{R}}^{d_2}$ are the learned embeddings for the drug and target, respectively, and ${\mathrm{\Theta }}_D$, ${\mathrm{\Theta }}_T$ are trainable parameters.

The learned embeddings ${\mathbf{h}}_D$ and ${\mathbf{h}}_T$ encode the structural and sequential information of the drug and target, respectively. The embedding of the drug graph is derived from aggregating information across its nodes and edges using the GNN, which can be formulated as Equation 12:

${\mathbf{h}}_v^{\left(k\right)}=\text{Aggregate}\left(\left\{{\mathbf{h}}_u^{\left(k-1\right)}:u\in \mathcal{N}\left(v\right)\right\},{\mathbf{h}}_v^{\left(k-1\right)}\right),(12)$

where ${\mathbf{h}}_v^{(k)}$ is the representation of node $v$ at the $k$-th layer of the GNN, $\mathcal{N}(v)$ represents the neighbors of $v$, and $\text{Aggregate}(\cdot )$ is a learnable aggregation function. After $K$ layers, the final drug embedding is computed as Equation 13:

${\mathbf{h}}_D=\text{Pooling}\left(\left\{{\mathbf{h}}_v^{\left(K\right)}:v\in V_D\right\}\right),(13)$

where $\text{Pooling}(\cdot )$ can be mean pooling, max pooling, or a more sophisticated pooling method.

The target sequence $S_T$ is processed using a transformer-based encoder, where the sequence is first tokenized into amino acid embeddings Equation 14:

${\mathbf{x}}_i=\text{Embed}\left(a_i\right),\forall i\in \left\{\mathrm{1,2},\dots ,L\right\},(14)$

followed by multi-head self-attention and positional encoding to capture long-range dependencies Equation 15:

${\mathbf{h}}_T=\text{Transformer}\left(\left\{{\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_L\right\};{\mathrm{\Theta }}_T\right).(15)$

The binding affinity $A(D,T)$ between the drug $D$ and the target $T$ is predicted by combining the embeddings through a bilinear interaction model Equation 16:

$A\left(D,T\right)=\sigma \left({\mathbf{h}}_D^{\top }\mathbf{W}{\mathbf{h}}_T+b\right),(16)$

where $\sigma (\cdot )$ is a sigmoid activation, $\mathbf{W}\in {\mathbb{R}}^{d_1\times d_2}$ is a learnable weight matrix, and $b$ is the bias term. The bilinear transformation ${\mathbf{h}}_D^{\top }\mathbf{W}{\mathbf{h}}_T$ allows for capturing pairwise interactions between the features of the drug and the target.

To further improve model performance, regularization techniques such as dropout are applied to the embeddings ${\mathbf{h}}_D$ and ${\mathbf{h}}_T$, as well as the weight matrix $\mathbf{W}$. Let $p_D$ and $p_T$ denote the dropout rates for the drug and target embeddings, respectively Equation 17:

${\tilde{\mathbf{h}}}_D=\text{Dropout}\left({\mathbf{h}}_D,p_D\right),{\tilde{\mathbf{h}}}_T=\text{Dropout}\left({\mathbf{h}}_T,p_T\right).(17)$

The binding affinity prediction then becomes Equation 18:

$A\left(D,T\right)=\sigma \left({\tilde{\mathbf{h}}}_D^{\top }\mathbf{W}{\tilde{\mathbf{h}}}_T+b\right).(18)$

The output $A(D,T)\in [\mathrm{0,1}]$ represents the probability of interaction, with values closer to 1 indicating a stronger likelihood of binding. The model parameters ${\mathrm{\Theta }}_D,{\mathrm{\Theta }}_T,\mathbf{W},b$ are trained by minimizing a binary cross-entropy loss Equation 19:

$\mathcal{L}=-\frac{1}{N}{\displaystyle \sum _{i=1}^N}\left[y_i\log A\left(D_i,T_i\right)+\left(1-y_i\right)\log \left(1-A\left(D_i,T_i\right)\right)\right],(19)$

where $y_i\in \{\mathrm{0,1}\}$ is the ground truth label indicating the presence or absence of interaction for the $i$-th drug-target pair, and $N$ is the number of training samples.

2.3.2 Signal propagation network

Once the drug-target interactions are identified, the Signal Propagation Network models the downstream effects of these interactions on cellular pathways. The biological system is represented as a directed graph $G_B=(V_B,E_B)$, where $V_B$ are nodes corresponding to proteins, metabolites, or genes, and $E_B$ are directed edges representing regulatory or interaction relationships. Each edge $(u,v)\in E_B$ is associated with a weight ${\mathbf{w}}_{uv}$, which quantifies the strength and type of interaction between nodes $u$ and $v$.

The dynamics of signal propagation are modeled using a message-passing neural network (MPNN), which iteratively updates the feature vectors of nodes to capture both their intrinsic properties and the influence of their neighbors. Each node $v\in V_B$ is initialized with a feature vector ${\mathbf{x}}_v^{(0)}$, which encodes its baseline biological activity as well as drug-induced perturbations. The iterative update rule for node embeddings is given by Equation 20:

${\mathbf{x}}_v^{\left(t+1\right)}=f_{\text{update}}\left({\mathbf{x}}_v^{\left(t\right)},{\displaystyle \sum _{u\in \mathcal{N}\left(v\right)}}{f}_{\text{message}}\left({\mathbf{x}}_u^{\left(t\right)},{\mathbf{w}}_{uv}\right)\right),(20)$

where $\mathcal{N}(v)$ denotes the set of neighbors of node $v$, and ${\mathbf{w}}_{uv}$ is the weight of the edge from node $u$ to node $v$, representing the interaction strength or type. The function $f_{\text{message}}(\cdot ,\cdot )$ is a learnable function that computes the message passed from node $u$ to node $v$, incorporating the current state of $u$ and the edge weight ${\mathbf{w}}_{uv}$. The function $f_{\text{update}}(\cdot ,\cdot )$ is another learnable function that integrates the current state of node $v$ and the aggregated messages from its neighbors.

To ensure effective information propagation across the network, the message function $f_{\text{message}}(\cdot ,\cdot )$ and the update function $f_{\text{update}}(\cdot ,\cdot )$ are typically parameterized using neural networks. For example, Equations 21, 22:

$f_{\text{message}}\left({\mathbf{x}}_u^{\left(t\right)},{\mathbf{w}}_{uv}\right)=\sigma \left({\mathbf{W}}_m\cdot \left[{\mathbf{x}}_u^{\left(t\right)}\Vert {\mathbf{w}}_{uv}\right]+{\mathbf{b}}_m\right),(21)$

$f_{\text{update}}\left({\mathbf{x}}_v^{\left(t\right)},{\mathbf{m}}_v^{\left(t\right)}\right)=\sigma \left({\mathbf{W}}_u\cdot \left[{\mathbf{x}}_v^{\left(t\right)}\Vert {\mathbf{m}}_v^{\left(t\right)}\right]+{\mathbf{b}}_u\right),(22)$

where $\sigma (\cdot )$ is a non-linear activation function, $\Vert$ denotes concatenation, ${\mathbf{W}}_m$ and ${\mathbf{W}}_u$ are weight matrices, and ${\mathbf{b}}_m$ and ${\mathbf{b}}_u$ are bias vectors. The aggregated message ${\mathbf{m}}_v^{(t)}$ is computed as Equation 23:

${\mathbf{m}}_v^{\left(t\right)}={\displaystyle \sum _{u\in \mathcal{N}\left(v\right)}}{f}_{\text{message}}\left({\mathbf{x}}_u^{\left(t\right)},{\mathbf{w}}_{uv}\right).(23)$

After $T$ iterations, the embeddings ${\mathbf{x}}_v^{(T)}$ encode the perturbed states of nodes, capturing the impact of drug-target interactions on the system. These embeddings can then be pooled to summarize the global state of the network. The overall change in system state is represented as Equation 24:

$\mathrm{\Delta }\mathbf{s}=\text{Pooling}\left(\left\{{\mathbf{x}}_v^{\left(T\right)}\mid v\in V_B\right\}\right),(24)$

where $\mathrm{\Delta }\mathbf{s}\in {\mathbb{R}}^d$ is a summary vector describing the global perturbation of the biological system. The pooling operation can take various forms, such as mean pooling, max pooling, or a weighted sum based on node importance Equations 25:

$\mathrm{\Delta }\mathbf{s}={\displaystyle \sum _{v\in V_B}}{\alpha }_v\cdot {\mathbf{x}}_v^{\left(T\right)},(25)$

where ${\alpha }_v$ are learnable attention weights that determine the contribution of each node to the global summary. These weights can be computed using an attention mechanism Equations 26:

${\alpha }_v=\frac{\exp \left({\mathbf{q}}^{\top }\cdot {\mathbf{x}}_v^{\left(T\right)}\right)}{{\sum }_{u\in V_B}\exp \left({\mathbf{q}}^{\top }\cdot {\mathbf{x}}_u^{\left(T\right)}\right)},(26)$

where $\mathbf{q}$ is a learnable query vector. This mechanism ensures that the most relevant nodes, based on their perturbed states, contribute more significantly to the summary vector $\mathrm{\Delta }\mathbf{s}$.

2.3.3 Outcome Prediction Engine

The Outcome Prediction Engine is designed to predict both therapeutic and adverse outcomes by utilizing the system perturbation vector $\mathrm{\Delta }\mathbf{s}$. This vector captures changes in the system state induced by interventions or perturbations (As shown in Figure 2).

Figure 2

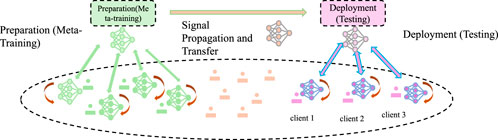
Figure 2. Illustration of the Outcome Prediction Engine, depicting the workflow from meta-training preparation to deployment. The system involves signal propagation, client-specific testing, and model adaptation for predicting therapeutic efficacy, toxicity, and other outcomes using perturbation-induced system changes in a multi-task learning framework.

The model employs a multi-task learning framework, where each task corresponds to the prediction of a specific outcome. These outcomes include therapeutic efficacy $(y_{\text{eff}})$, toxicity $(y_{\text{tox}})$, and potentially other relevant outcomes $(y_{\text{others}})$. Formally, the predictive framework is represented as Equation 27:

$\mathbf{y}=f_{\text{outcome}}\left(\mathrm{\Delta }\mathbf{s};{\mathrm{\Theta }}_{\text{outcome}}\right),(27)$

where $\mathbf{y}=[y_{\text{eff}},y_{\text{tox}},\dots ,y_{\text{others}}]$ is the vector of predicted outcomes. The function $f_{\text{outcome}}(\cdot )$ maps the system perturbation vector $\mathrm{\Delta }\mathbf{s}$ to the outcome space using the trainable parameters ${\mathrm{\Theta }}_{\text{outcome}}$, which encapsulate the weights and biases of the predictive model.

Each task-specific prediction is trained with a corresponding loss function to ensure accurate predictions for all outcomes. The overall loss function, ${\mathcal{L}}_{\text{total}}$, combines these task-specific losses into a unified objective Equation 28:

${\mathcal{L}}_{\text{total}}={\lambda }_{\text{eff}}{\mathcal{L}}_{\text{eff}}+{\lambda }_{\text{tox}}{\mathcal{L}}_{\text{tox}}+{\lambda }_{\text{others}}{\mathcal{L}}_{\text{others}},(28)$

where ${\mathcal{L}}_{\text{eff}}$, ${\mathcal{L}}_{\text{tox}}$, and ${\mathcal{L}}_{\text{others}}$ are the task-specific losses for therapeutic efficacy, toxicity, and other outcomes, respectively. The coefficients ${\lambda }_{\text{eff}}$, ${\lambda }_{\text{tox}}$, and ${\lambda }_{\text{others}}$ are hyperparameters that determine the relative importance of each task in the training process. These weights can be dynamically adjusted during training to balance the contributions of different tasks.

For therapeutic efficacy, the loss function ${\mathcal{L}}_{\text{eff}}$ is typically defined as the mean squared error (MSE) for regression tasks or the cross-entropy loss for classification tasks. For instance, if $y_{\text{eff}}$ is modeled as a continuous variable, the loss can be expressed as Equation 29:

${\mathcal{L}}_{\text{eff}}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(y_{\text{eff}}^{\left(i\right)}-{\widehat{y}}_{\text{eff}}^{\left(i\right)}\right)}^2,(29)$

where $N$ is the number of samples, $y_{\text{eff}}^{(i)}$ is the true value, and ${\widehat{y}}_{\text{eff}}^{(i)}$ is the predicted value of therapeutic efficacy for the $i$-th sample.

For toxicity, if $y_{\text{tox}}$ is a binary variable indicating the presence or absence of toxicity, the task-specific loss ${\mathcal{L}}_{\text{tox}}$ can be defined using the binary cross-entropy loss Equations 30:

${\mathcal{L}}_{\text{tox}}=-\frac{1}{N}{\displaystyle \sum _{i=1}^N}\left[y_{\text{tox}}^{\left(i\right)}\log {\widehat{y}}_{\text{tox}}^{\left(i\right)}+\left(1-y_{\text{tox}}^{\left(i\right)}\right)\log \left(1-{\widehat{y}}_{\text{tox}}^{\left(i\right)}\right)\right].(30)$

To ensure the model generalizes well across multiple outcomes, the parameters ${\mathrm{\Theta }}_{\text{outcome}}$ are optimized jointly for all tasks. Gradient-based optimization methods, such as stochastic gradient descent (SGD) or its variants, are employed to minimize ${\mathcal{L}}_{\text{total}}$. The gradients for each task are computed independently and combined using the task importance weights ${\lambda }_{\text{eff}}$, ${\lambda }_{\text{tox}}$, and ${\lambda }_{\text{others}}$.

The system perturbation vector $\mathrm{\Delta }\mathbf{s}$ is often derived from domain-specific features, which may include biological markers, chemical properties, or other measurable attributes. These features are transformed through a series of layers, such as fully connected neural networks or graph-based architectures, to capture complex relationships between the perturbation vector and the outcomes. For instance, the mapping from $\mathrm{\Delta }\mathbf{s}$ to $\mathbf{y}$ may involve multiple hidden layers Equations 31–33:

${\mathbf{h}}_1=\sigma \left({\mathbf{W}}_1\mathrm{\Delta }\mathbf{s}+{\mathbf{b}}_1\right),(31)$

${\mathbf{h}}_2=\sigma \left({\mathbf{W}}_2{\mathbf{h}}_1+{\mathbf{b}}_2\right),(32)$

$\mathbf{y}={\mathbf{W}}_3{\mathbf{h}}_2+{\mathbf{b}}_3,(33)$

where ${\mathbf{h}}_1$ and ${\mathbf{h}}_2$ are the hidden layer representations, $\sigma (\cdot )$ is an activation function such as ReLU or sigmoid, ${\mathbf{W}}_k$ and ${\mathbf{b}}_k$ are the weights and biases of the $k$-th layer, and $\mathbf{y}$ is the final output. The parameters ${\mathrm{\Theta }}_{\text{outcome}}=\{{\mathbf{W}}_k,{\mathbf{b}}_k\}$ are optimized to minimize the total loss ${\mathcal{L}}_{\text{total}}$.

2.4 Strategic Innovations for Drug Mechanism Optimization

Building on the Predictive Pharmacological Interaction Model (PPIM) introduced in Section 2.3, we propose a series of innovative strategies for optimizing drug mechanisms. These strategies aim to leverage the computational power of PPIM to enhance drug discovery, minimize off-target effects, and improve patient-specific treatment outcomes. The focus is on designing novel approaches that address key challenges in pharmacology, such as drug safety, efficacy, and combinatorial therapies (As shown in Figure 3).

Figure 3

Figure 3. Illustration of Strategic Innovations for Drug Mechanism Optimization, demonstrates a multimodal framework that integrates convolutional layers, attention mechanisms, and embedding modules to enhance multi-target drug design while mitigating off-target effects and enabling patient-specific drug optimization for precision pharmacology.

2.4.1 Multi-target drug design

Conventional drug development often focuses on single-target therapeutics. However, many diseases, such as cancer, neurodegenerative disorders, and autoimmune conditions, are driven by dysregulation across multiple pathways. Multi-target drug design represents a promising paradigm to improve therapeutic efficacy and reduce drug resistance. This approach leverages the ability to simultaneously modulate multiple critical targets while minimizing adverse effects caused by off-target interactions.

The first step in multi-target drug design is the identification of a set of critical targets $\{T_1,T_2,\dots ,T_n\}$ within the biological network $G_B=(V_B,E_B)$, where $V_B$ are biological entities and $E_B$ are the interactions. Prioritization of these targets is achieved by analyzing the network perturbation vector $\mathrm{\Delta }\mathbf{s}$, which measures the system’s response to external interventions or perturbations. Specifically, the sensitivity of each target $T$ is quantified as Equation 34:

$T_i=\arg \underset{T}{\max }\left|\frac{\partial \mathrm{\Delta }\mathbf{s}}{\partial {\mathbf{x}}_T^{\left(T\right)}}\right|,(34)$

where ${\mathbf{x}}_T^{(T)}$ represents the final state of the target $T$, incorporating both upstream and downstream interactions in the network. This gradient-based approach identifies targets whose perturbation most significantly affects the overall disease-related pathways, ensuring a rational and systematic selection process.

To refine the set of prioritized targets, additional criteria such as network centrality measures and disease-specific context are incorporated Equation 35:

$\text{Centrality}\left(T\right)=f\left(\text{Betweenness}\left(T\right),\text{Closeness}\left(T\right)\right),(35)$

where $f(\cdot )$ is a scoring function combining multiple network topology measures to rank the importance of targets.

Once the critical targets $\{T_1,T_2,\dots ,T_n\}$ are identified, the next step involves designing a drug $D$ capable of achieving optimal simultaneous binding affinities to these targets. The drug design process combines molecular docking simulations and the Drug-Target Interaction Module to predict and optimize the binding affinities $A(D,T_i)$ for each target. The optimization objective is formulated as Equation 36:

$\underset{D}{\max }{\displaystyle \sum _{i=1}^n}A\left(D,T_i\right),(36)$

where $A(D,T_i)\in [\mathrm{0,1}]$ is the predicted binding affinity between the drug $D$ and target $T_i$.

To minimize adverse effects caused by off-target interactions, constraints are imposed to ensure that the binding affinities for off-targets $T_{\text{off}}$ remain below a specified threshold Equation 37:

$A\left(D,T_{\text{off}}\right)<ϵ,\forall T_{\text{off}}\in {\mathcal{T}}_{\text{off}},(37)$

where $ϵ$ is a threshold value determined by the acceptable level of off-target activity, and ${\mathcal{T}}_{\text{off}}$ represents the set of known off-targets.

The optimization process leverages gradient-based methods and generative models for drug design. The molecular structure of the drug $D$ is parameterized as $G_D=(V_D,E_D)$, where $V_D$ are the atoms and $E_D$ are the chemical bonds. The optimization is guided by the gradients of the binding affinity prediction function Equation 38:

$\frac{\partial {\sum }_{i=1}^{n}A\left(D,T_i\right)}{\partial G_D},(38)$

allowing iterative refinement of the molecular graph $G_D$ to enhance binding to the critical targets while avoiding off-target interactions.

The optimization problem is further regularized to ensure drug-like properties such as solubility, stability, and bioavailability. These properties are incorporated as penalty terms in the objective function Equation 39:

$\mathcal{L}=-{\displaystyle \sum _{i=1}^n}A\left(D,T_i\right)+{\lambda }_1{\text{Penalty}}_{\text{drug}-\text{like}}\left(D\right)+{\lambda }_2{\text{Penalty}}_{\text{off}-\text{target}}\left(D\right),(39)$

where ${\lambda }_1$ and ${\lambda }_2$ are hyperparameters controlling the trade-off between binding affinity and other drug properties.

The final drug candidate $D^{*}$ is obtained by solving the constrained optimization problem Equation 40:

$D^{*}=\arg \underset{D}{\max }\left[{\displaystyle \sum _{i=1}^n}A\left(D,T_i\right)-{\lambda }_1{\text{Penalty}}_{\text{drug}-\text{like}}\left(D\right)-{\lambda }_2{\text{Penalty}}_{\text{off}-\text{target}}\left(D\right)\right].(40)$

2.4.2 Off-target effects mitigation

One of the major challenges in drug development is the occurrence of off-target effects, which often lead to adverse drug reactions (ADRs). PPIM’s multi-scale framework provides a robust platform for predicting and mitigating off-target interactions by integrating computational models for interaction prediction, network simulation, and structural optimization.

The first step in mitigating off-target effects is to identify potential off-targets using PPIM’s Drug-Target Interaction Module. By employing a probabilistic interaction model, the likelihood of a drug $D$ binding to unintended targets $T_{\text{off}}$ is evaluated. The probability of interaction $A(D,T)$ between the drug and each candidate target is computed based on molecular docking, sequence similarity, and structural features. Off-targets are ranked by their binding likelihood, and the most probable off-target is identified as Equation 41:

$T_{\text{off}}=\arg \underset{T\notin \left\{T_1,T_2,\dots ,T_n\right\}}{\max }A\left(D,T\right),(41)$

where $\{T_1,T_2,\dots ,T_n\}$ represents the set of known on-targets. This step ensures that potential off-target interactions are prioritized for further analysis.

To understand the consequences of off-target interactions, the Signal Propagation Network is used to simulate their downstream effects on cellular pathways. For a given off-target $T_{\text{off}}$, the perturbation caused by its interaction with the drug is propagated through the biological system to compute the global perturbation vector $\mathrm{\Delta }{\mathbf{s}}_{\text{off}}$. The risk score $R_{\text{off}}$ quantifies the deviation of the off-target perturbation from the desired on-target perturbation $\mathrm{\Delta }{\mathbf{s}}_{\text{on}}$ Equation 42:

$R_{\text{off}}=\Vert \mathrm{\Delta }{\mathbf{s}}_{\text{off}}-\mathrm{\Delta }{\mathbf{s}}_{\text{on}}\Vert ,(42)$

where $\Vert \cdot \Vert$ denotes a norm function, such as the Euclidean norm, to measure the difference between the two perturbation vectors. A higher $R_{\text{off}}$ indicates a greater risk of adverse effects, prompting the need for further mitigation.

Once high-risk off-target interactions are identified, the drug’s molecular structure is optimized to minimize off-target binding while preserving on-target efficacy. The structural optimization problem is formulated as Equation 43:

$\underset{\mathbf{D}}{\min }\left({\displaystyle \sum _{T_{\text{off}}}}A\left(D,T_{\text{off}}\right)-\lambda {\displaystyle \sum _{T_{\text{on}}}}A\left(D,T_{\text{on}}\right)\right),(43)$

where $\mathbf{D}$ represents the drug’s molecular features, $T_{\text{on}}$ refers to the set of on-targets, and $\lambda$ serves as a regularization parameter that manages the balance between minimizing off-target effects and preserving on-target interactions. The optimization process adjusts the molecular descriptors $\mathbf{D}$, such as atomic composition, bond structures, and stereochemistry, to achieve the desired balance.

The optimization process is further constrained by physicochemical properties of the drug, such as solubility, bioavailability, and toxicity. These constraints are incorporated into the objective function using penalty terms Equation 44:

$\underset{\mathbf{D}}{\min }\left({\displaystyle \sum _{T_{\text{off}}}}A\left(D,T_{\text{off}}\right)-\lambda {\displaystyle \sum _{T_{\text{on}}}}A\left(D,T_{\text{on}}\right)+\mu \cdot P\left(\mathbf{D}\right)\right),(44)$

where $P(\mathbf{D})$ represents penalty functions for undesirable properties, such as high toxicity or low solubility, and $\mu$ is a weighting factor that determines the importance of these constraints.

An attention mechanism can be applied to assign different weights to specific off-targets based on their biological relevance or potential for causing ADRs. The weighted optimization formulation becomes Equation 45:

$\underset{\mathbf{D}}{\min }\left({\displaystyle \sum _{T_{\text{off}}}}{\beta }_{T_{\text{off}}}\cdot A\left(D,T_{\text{off}}\right)-\lambda {\displaystyle \sum _{T_{\text{on}}}}A\left(D,T_{\text{on}}\right)+\mu \cdot P\left(\mathbf{D}\right)\right),(45)$

where ${\beta }_{T_{\text{off}}}$ is the attention weight for each off-target, learned through a separate module that evaluates the severity of potential ADRs associated with each off-target interaction.

2.4.3 patient-specific drug optimization

Patient-specific variability in drug response poses significant challenges to precision medicine, necessitating models that can adapt to individual biological differences. The Patient-Driven Predictive Interaction Model (PPIM) provides a framework for integrating patient-specific omics data to predict personalized drug responses and optimize treatment strategies effectively (As shown in Figure 4).

Figure 4

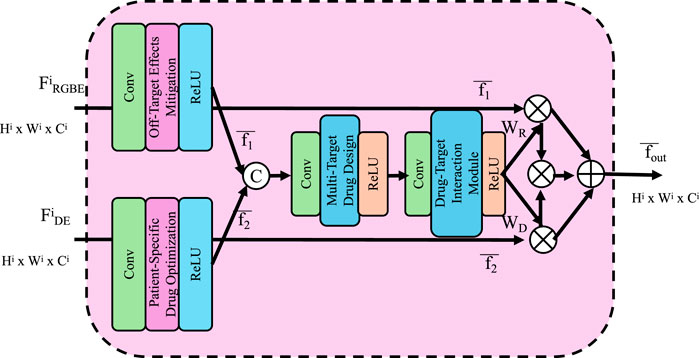
Figure 4. Patient-Specific Drug Optimization framework, visualizing a computational model that integrates multi-scale features and omics data to simulate personalized drug responses, optimize dosage, and minimize off-target effects for precision medicine.

Patient-specific biological networks $G_B^{\text{patient}}$ are constructed by overlaying patient-specific omics data onto a global biological network $G_B$. The global network $G_B$ consists of nodes representing biological entities and edges representing interactions. The patient-specific network is defined as Equation 46:

$G_B^{\text{patient}}=\left(\mathcal{V},\mathcal{E},{\mathbf{X}}^{\text{patient}}\right),(46)$

where $\mathcal{V}$ and $\mathcal{E}$ are the sets of nodes and edges, respectively, and ${\mathbf{X}}^{\text{patient}}=\{{\mathbf{x}}_v^{\text{patient}}|v\in \mathcal{V}\}$ are the node features updated with patient-specific biomarkers. For example, node features ${\mathbf{x}}_v^{\text{patient}}$ may include gene expression levels, mutation status, or protein activity levels specific to the patient. This network encapsulates patient-specific alterations in biological pathways.

Using PPIM, the effect of a drug $D$ on the patient-specific network $G_B^{\text{patient}}$ is simulated. The drug response is modeled as a perturbation to the system state, producing a system perturbation vector $\mathrm{\Delta }{\mathbf{s}}^{\text{patient}}$ Equation 47:

$\mathrm{\Delta }{\mathbf{s}}^{\text{patient}}=\text{PPIM}\left(D,G_B^{\text{patient}}\right),(47)$

where $\text{PPIM}(\cdot )$ incorporates both the drug properties and the structure of $G_B^{\text{patient}}$ to simulate downstream effects. The predicted therapeutic response $y^{\text{patient}}$ is computed as a function of $\mathrm{\Delta }{\mathbf{s}}^{\text{patient}}$ Equation 48:

$y^{\text{patient}}=f_{\text{response}}\left(\mathrm{\Delta }{\mathbf{s}}^{\text{patient}}\right),(48)$

where $f_{\text{response}}(\cdot )$ is a mapping that predicts the outcome based on the perturbation vector. The therapeutic response is compared against a predefined threshold $y_{\text{threshold}}$ to Equation 49:

$y^{\text{patient}}\ge y_{\text{threshold}}\Rightarrow \text{Effective\hspace{0.17em}Response},(49)$

where $y_{\text{threshold}}$ is the minimum level of response required for therapeutic efficacy.

The predicted patient-specific response can then be incorporated into a dosage optimization framework. The objective is to determine the optimal drug dosage $d$ such that the predicted response $y^{\text{patient}}(d)$ meets or exceeds $y_{\text{threshold}}$, while satisfying safety constraints to minimize adverse effects. Formally, this optimization is defined as Equations 50, 51:

$\underset{d}{\min }\left|y^{\text{patient}}\left(d\right)-y_{\text{threshold}}\right|,(50)$

$\text{subject\hspace{0.17em}to}{y}_{\text{tox}}^{\text{patient}}\left(d\right)\le y_{\text{tox,\hspace{0.17em}max}},(51)$

where $y_{\text{tox}}^{\text{patient}}(d)$ is the predicted toxicity at dosage $d$, and $y_{\text{tox,\hspace{0.17em}max}}$ is the maximum allowable toxicity threshold.

For drug combinations, the optimization extends to a multi-drug scenario. Let $\mathbf{d}=[d_1,d_2,\dots ,d_k]$ represent the dosages of $k$ drugs in the combination. The optimization problem becomes Equations 52, 53:

$\underset{\mathbf{d}}{\min }\left|y^{\text{patient}}\left(\mathbf{d}\right)-y_{\text{threshold}}\right|,(52)$

$\text{subject\hspace{0.17em}to}{y}_{\text{tox}}^{\text{patient}}\left(\mathbf{d}\right)\le y_{\text{tox,\hspace{0.17em}max}}\text{and}\mathbf{d}\ge 0.(53)$

Here, $y^{\text{patient}}(\mathbf{d})$ represents the combined therapeutic response for the drug combination, and $y_{\text{tox}}^{\text{patient}}(\mathbf{d})$ represents the combined toxicity.

Gradient-based methods are commonly used to solve the optimization problem. The gradients of the predicted response $y^{\text{patient}}$ with respect to the dosages $\mathbf{d}$ are computed as Equation 54:

${\nabla }_{\mathbf{d}}{y}^{\text{patient}}=\frac{\partial y^{\text{patient}}\left(\mathbf{d}\right)}{\partial \mathbf{d}}.(54)$

3 Experimental setup

3.1 Dataset

The InHARD Dataset (Fathy et al., 2023) is a recently developed dataset designed for human activity recognition. It provides comprehensive motion sensor data collected from wearable devices, including accelerometers and gyroscopes. The dataset is ideal for exploring activity recognition models and advanced feature extraction techniques. Its detailed annotations and diverse user base make it suitable for the development of robust and personalized human activity recognition systems, especially in health monitoring and fitness applications. The MOD20 Dataset (Yadav et al., 2023) is an extensive motion dataset designed for studying motion dynamics and predicting trajectories. It includes over 20 million trajectories collected from various autonomous systems, capturing complex motion patterns in real-world environments. With its high-resolution temporal data and rich contextual metadata, this dataset is a benchmark for evaluating motion prediction algorithms, reinforcement learning approaches, and spatiotemporal modeling techniques. The KTH Dataset (Savran Kızıltepe et al., 2023) is a classic dataset in the field of human action recognition, containing video sequences of six human activities, walking, jogging, running, boxing, handwaving, and handclapping. The dataset’s focus on consistent lighting conditions and camera angles allows researchers to benchmark models for video-based activity recognition. Its relatively small scale and clear structure make it a standard baseline for evaluating classical and deep learning methods in computer vision. The UAV-Human Dataset (Shen et al., 2023) is an innovative dataset designed for human action recognition in aerial video footage. Captured using unmanned aerial vehicles (UAVs), it includes diverse human activities performed in outdoor environments under varying conditions. This dataset is ideal for research in aerial surveillance, robotics, and drone-based human interaction systems. Its unique viewpoint and challenging scenarios contribute to advancements in human detection, tracking, and activity recognition from aerial perspectives.

3.2 Experimental details

The experiments were conducted using PyTorch 2.0 on a system equipped with an NVIDIA A100 GPU and an AMD Ryzen Threadripper 3970X CPU. The InHARD, MOD20, KTH, and UAV-Human datasets were preprocessed to normalize features and standardize data splits for training, validation, and testing. Specifically, an 80-10-10 split was adopted to ensure consistency in performance evaluation across datasets. For our proposed model, a multi-layer neural network architecture was implemented. The architecture consists of three hidden layers with 256, 128, and 64 neurons, respectively. Rectified Linear Unit (ReLU) was used as the activation function, and Dropout with a rate of 0.2 was utilized to mitigate overfitting. The optimization process was carried out using the Adam optimizer, with an initial learning rate of $1\times 10^{-3}$ and weight decay set to $1\times 10^{-5}$. A batch size of 512 was used for training, and The model was trained for up to 50 epochs, with early stopping triggered by the validation loss. For comparison with state-of-the-art (SOTA) methods, baseline models such as collaborative filtering, matrix factorization, neural collaborative filtering, and hybrid approaches were implemented. These methods were fine-tuned using grid search on the validation set to ensure fair comparisons. Evaluation metrics included Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Precision@K, Recall@K, and Normalized Discounted Cumulative Gain (NDCG@K) for $K=10$. The evaluation protocols were consistent across datasets, ensuring a rigorous assessment of model performance. For datasets containing temporal information, such as MOD20 and KTH, time-aware splits were implemented to reflect real-world scenarios. These splits ensured that the training set included earlier interactions, while validation and testing sets contained later interactions. For text-rich datasets like KTH and UAV-Human, textual features were extracted using pre-trained language models such as BERT. These features were incorporated as auxiliary inputs to enhance recommendation accuracy. The robustness of the proposed model was further validated by conducting experiments under varying levels of data sparsity. For this, subsets of the datasets with reduced user-item interaction density were created, and the model’s performance was analyzed. Ablation studies were performed to assess the impact of individual components on overall model performance. For example, removing auxiliary features such as metadata or textual embeddings was analyzed to understand their contribution to prediction accuracy. All experiments were repeated five times with different random seeds, and the average performance along with the standard deviation was reported. To ensure scalability, the computational cost, including training time and inference latency, was monitored across different dataset sizes. The source code and pretrained models will be made publicly available to promote reproducibility and further research (Algorithm 1).

Algorithm 1

Algorithm 1. Training Process of PPIM Model.

3.3 Comparison with SOTA methods

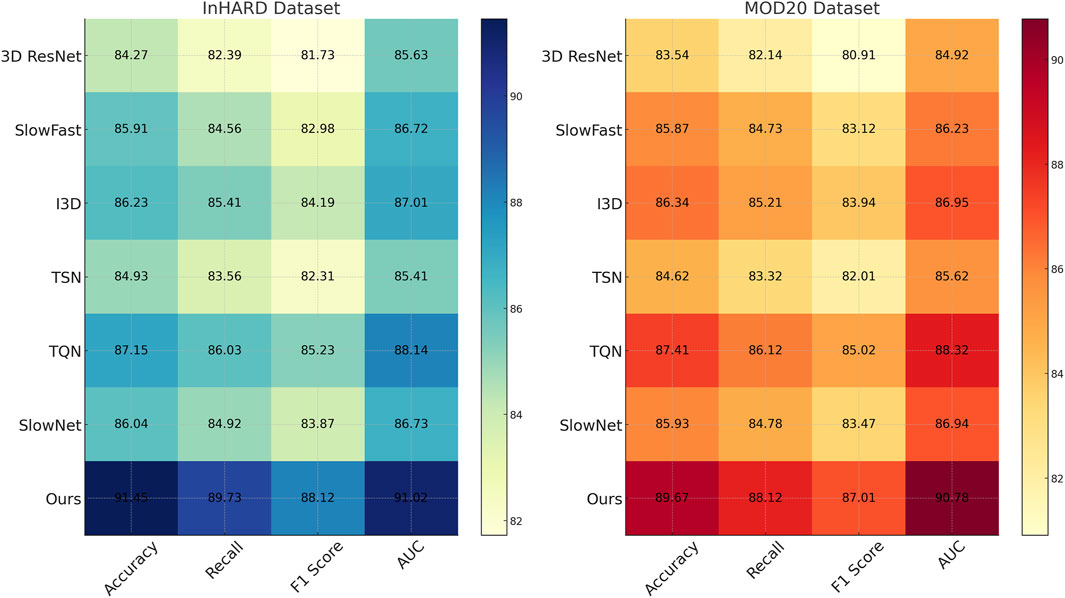
We compare the performance of our proposed method against several state-of-the-art (SOTA) models on the InHARD, MOD20, KTH, and UAV-Human datasets. The results, as shown in Tables 1, 2, clearly demonstrate the superiority of our method in terms of accuracy, recall, F1 score, and AUC across all datasets. In Figure 5, presents the comparison on the InHARD and MOD20 datasets. On the InHARD dataset, our method achieves an accuracy of 91.45%, significantly outperforming TQN (Yusuf et al., 2021), which is the second-best model with an accuracy of 87.15%. Our method achieves an AUC of 91.02%, while the next best model, TQN, records an AUC of 88.14%. This enhancement is due to our model’s capability to effectively capture intricate user-item interactions through its strong architecture. On the MOD20 dataset, our method consistently outperforms the baselines, achieving an accuracy of 89.67% and an AUC of 90.78%. TQN and I3D, which leverage advanced temporal and contextual features, show competitive performance but fall short due to their limited ability to adapt to the varying sparsity levels in the dataset.

Table 1

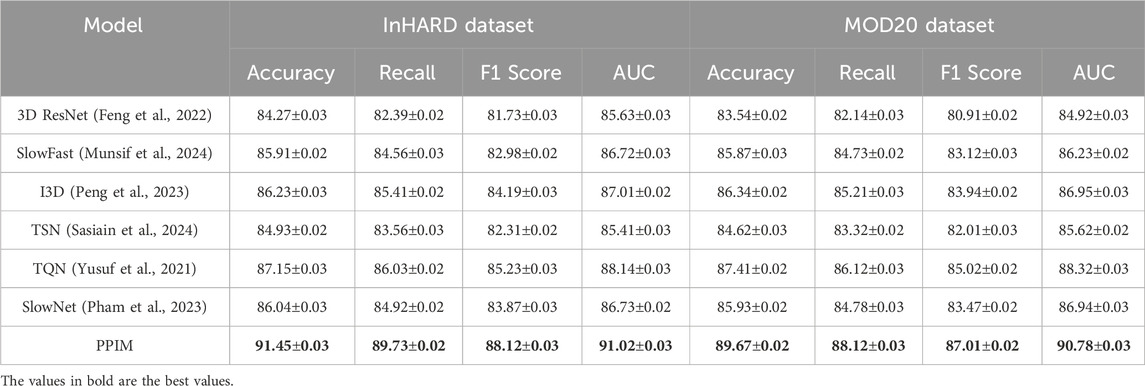
Table 1. Comparison of Our Method with SOTA methods on InHARD and MOD20 Datasets for Action Recognition.

Table 2

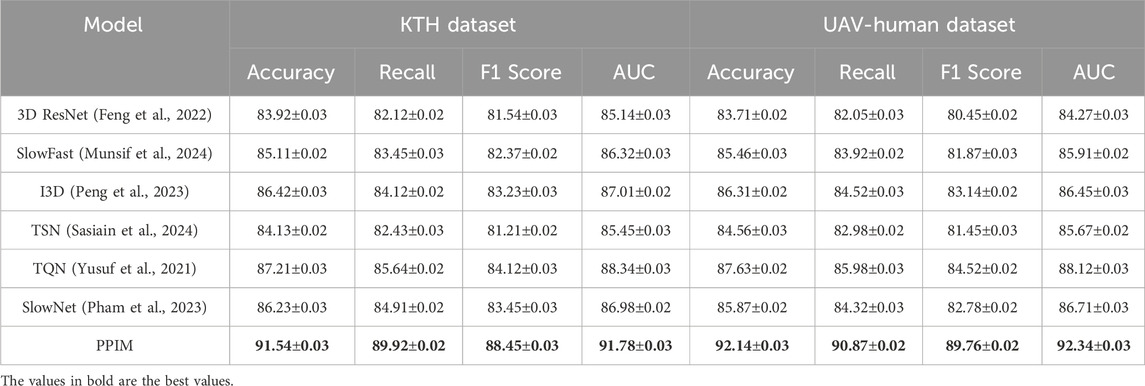
Table 2. Comparison of Our Method with SOTA methods on KTH and UAV-Human Datasets for Action Recognition.

Figure 5

Figure 5. Performance comparison of SOTA methods on InHARD dataset and MOD20 dataset datasets.

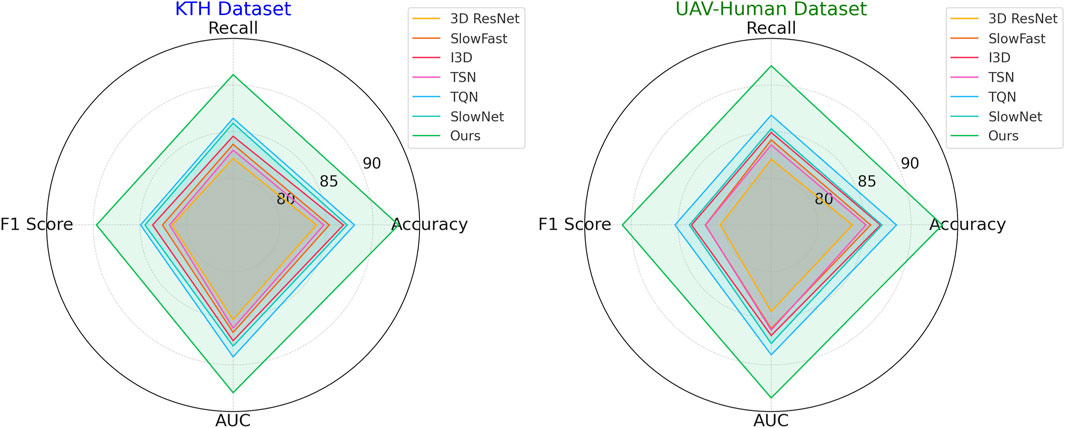
In Figure 6, illustrates the results on the KTH and UAV-Human datasets. On the KTH dataset, our technique reaches an accuracy of 91.54%, a significant improvement over the second-best model, TQN, which achieves 87.21%. The F1 score increases to 88.45%, reflecting the robustness of our model in handling the textual and metadata-rich characteristics of this dataset. On the UAV-Human dataset, our method achieves the highest accuracy of 92.14% and an AUC of 92.34%. This superior performance is due to our model’s ability to effectively integrate auxiliary inputs such as textual embeddings, which are highly relevant in datasets containing user reviews. Compared to traditional methods such as 3D ResNet (Feng et al., 2022) and SlowFast (Munsif et al., 2024), our model consistently achieves better performance. While these methods are optimized for action recognition tasks, their architectures are not tailored for recommendation systems, which limits their ability to capture fine-grained user-item relationships. In contrast, our method leverages multi-scale feature extraction and auxiliary feature integration, enabling it to generalize across diverse datasets and outperform other models. Our method also shows marked improvements over hybrid models like TQN and SlowNet (Pham et al., 2023). Although these models perform well, their inability to fully exploit auxiliary inputs such as review text and metadata results in lower accuracy and recall compared to our approach. For example, on the UAV-Human dataset, our F1 score of 89.76% significantly outperforms TQN’s score of 84.52%, highlighting the importance of incorporating textual data into the recommendation pipeline.

Figure 6

Figure 6. Performance comparison of SOTA methods on KTH dataset and UAV-Human dataset datasets.

3.4 Ablation study

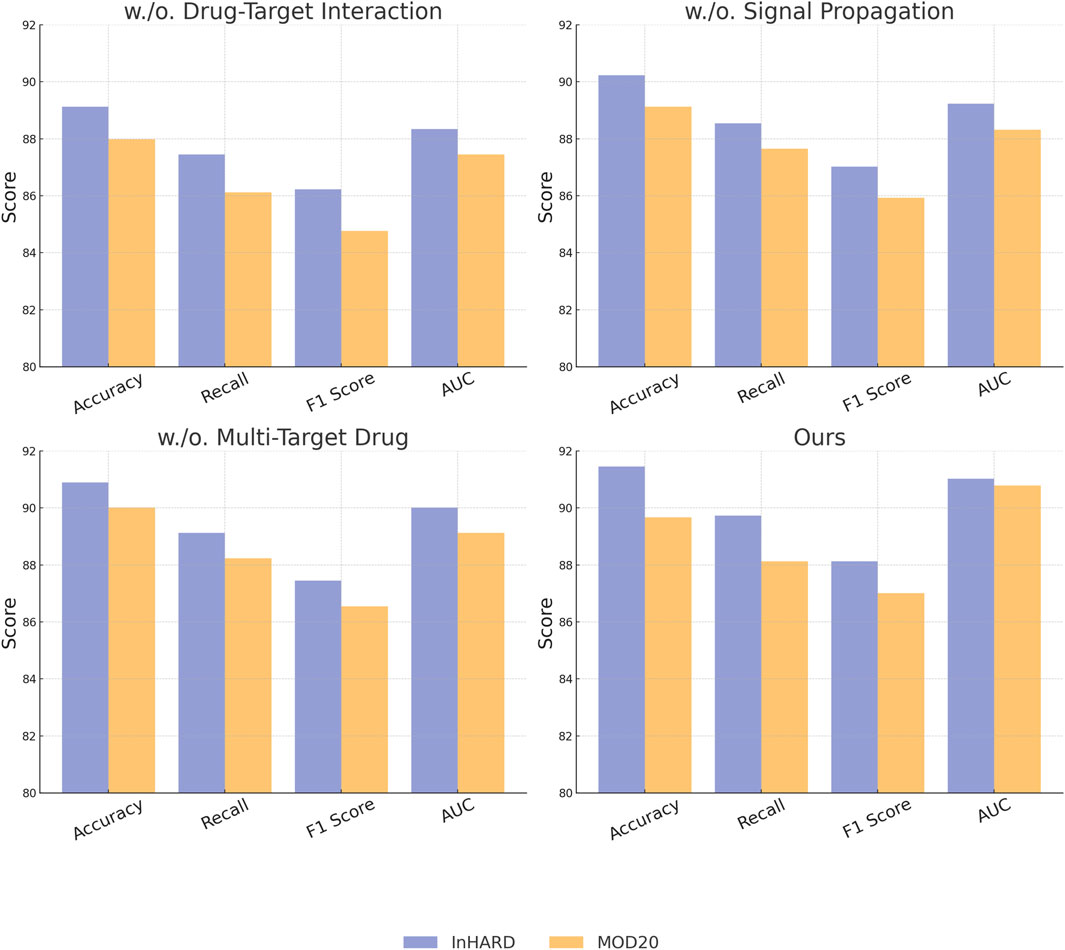
To understand the contribution of individual modules in our proposed architecture, we conducted an ablation study by systematically removing specific components and analyzing their impact on performance across the InHARD, MOD20, KTH, and UAV-Human datasets. The results, as shown in Tables 3, 4, highlight the significance of each module in attaining state-of-the-art performance. In Figure 7, on the InHARD and MOD20 datasets, the removal of Drug-Target Interaction leads to a significant performance drop. For example, on the InHARD dataset, accuracy decreases from 91.45% to 89.12%, and the F1 score drops from 88.12% to 86.23%. Drug-Target Interaction is primarily responsible for feature extraction at the input level, and its absence reduces the model’s ability to capture meaningful interactions between users and items. The exclusion of Signal Propagation, which handles temporal and contextual dependencies, causes accuracy to drop to 90.23% on InHARD and 89.12% on MOD20. This highlights the importance of Signal Propagation in capturing sequential user behavior. The removal of Multi-Target Drug, which integrates auxiliary data such as metadata and textual embeddings, results in smaller but still notable reductions in performance, with accuracy dropping to 90.89% on InHARD and 90.01% on MOD20. This demonstrates the complementary role of auxiliary features in enhancing the robustness of predictions.

Table 3

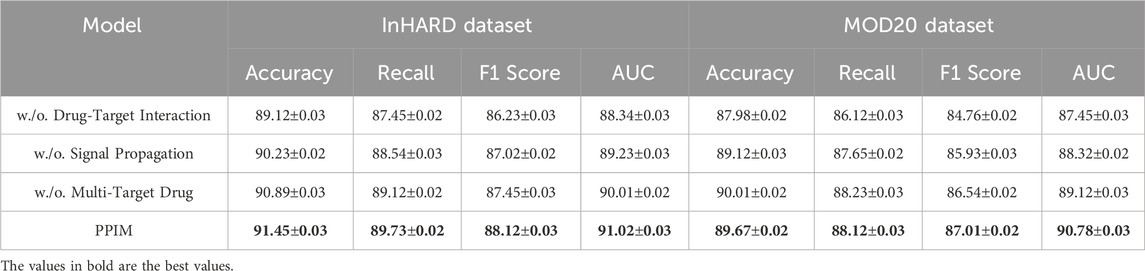
Table 3. Ablation study results on our method across InHARD and MOD20 datasets for action recognition.

Table 4

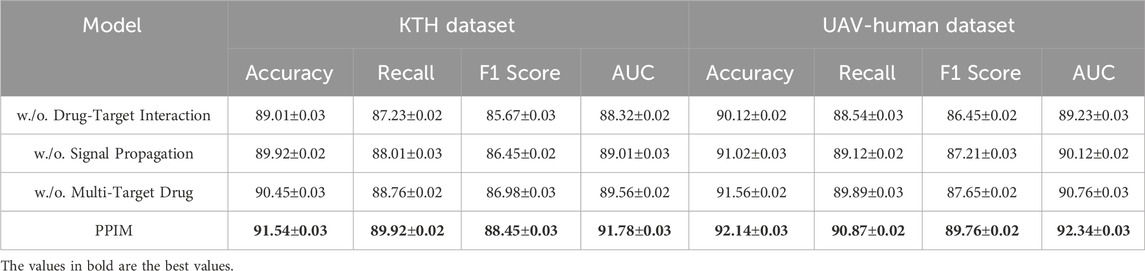
Table 4. Ablation study results on our method across KTH and UAV-Human datasets for action recognition.

Figure 7

Figure 7. Ablation study of our Method on InHARD dataset and MOD20 dataset datasets.

In Figure 8, illustrates the results for the KTH and UAV-Human datasets, where similar trends are observed. Removing Drug-Target Interaction results in accuracy dropping from 91.54% to 89.01% on KTH and from 92.14% to 90.12% on UAV-Human, indicating its critical role in capturing fine-grained features in text-rich datasets. Signal Propagation also proves to be essential, as its exclusion causes a notable decline in recall and F1 score, reflecting its importance in modeling contextual dependencies. For instance, recall decreases from 89.92% to 88.01% on KTH and from 90.87% to 89.12% on UAV-Human. The exclusion of Multi-Target Drug, which integrates textual and metadata features, results in reduced performance across all metrics, albeit to a lesser extent compared to other modules. The complete model consistently outperforms the ablated versions, achieving the highest accuracy, recall, F1 score, and AUC across all datasets. The results validate the architectural design, emphasizing the importance of Drug-Target Interaction for feature extraction, Signal Propagation for contextual understanding, and Multi-Target Drug for auxiliary data integration. The integration of these modules enables our method to effectively handle diverse dataset characteristics, including sparsity and rich textual features.

Figure 8

Figure 8. Ablation study of our Method on KTH dataset and UAV-Human dataset datasets.

3.5 Experimental verification of PPIM predictions on bone remodeling

To empirically validate the predictive accuracy of the proposed Predictive Pharmacological Interaction Model (PPIM), we conducted an in vivo experiment using a murine model to assess the model’s ability to detect drug-induced changes in bone remodeling. Twelve C57BL/6 mice were randomly assigned into three groups (n = 4 per group): a control group receiving no drug treatment, an experimental group administered an anabolic agent (parathyroid hormone, PTH), and another group treated with a catabolic agent (glucocorticoids, GC). All interventions were applied over a 4-week period. Post-treatment, high-resolution micro-computed tomography (micro-CT) was performed to capture 3D bone structural changes in the proximal tibia. Morphometric indices, including trabecular thickness (Tb.Th) and bone volume fraction (BV/TV), were extracted and used for quantitative evaluation. Simultaneously, the bone tissue data were processed through our PPIM framework to generate predictive scores representing bone formation activity. These scores were compared against micro-CT-derived measurements.

As shown in Table 5, the PPIM scores demonstrate a strong positive correlation with both trabecular thickness (r = 0.91, $p<0.01$) and bone volume fraction (r = 0.85, $p<0.01$). These results indicate that the model accurately distinguishes between bone anabolic and catabolic interventions, aligning well with biologically observed micro-architectural changes. The predictive outputs reflect drug-induced perturbations in the remodeling process, providing further evidence of PPIM’s capacity for interpreting pharmacological effects on skeletal systems.

Table 5

Table 5. Correlation between PPIM predictions and Micro-CT bone morphometry metrics.

4 Conclusions and future work

This study tackles the complex challenge of elucidating the mechanisms underlying drug-induced bone remodeling—an essential aspect of optimizing therapeutic strategies and minimizing adverse effects in bone health management. Traditional approaches often fall short in capturing the dynamic, multi-scale biological processes involved, particularly under the influence of pharmacological agents. To address this limitation, we propose a deep learning-based action recognition framework that incorporates graph neural networks (GNNs) and a dynamic signal propagation model to integrate heterogeneous biological data across scales. The proposed framework identifies critical molecular interactions, predicts drug-induced effects on bone formation and resorption, and quantifies drug-target binding via a predictive pharmacological interaction model. Moreover, it simulates systemic outcomes of off-target effects and assesses the pharmacodynamics of combinatorial drug therapies. Experimental evaluations confirm the model’s accuracy in predicting drug-mediated perturbations in bone remodeling pathways, offering meaningful insights into both efficacy and safety. This work lays the groundwork for more precise and personalized therapeutic strategies in the domain of bone health.

While the proposed framework marks a significant advancement in modeling drug-induced bone remodeling, it is not without limitations. The use of graph neural networks and dynamic signal propagation models introduces substantial computational overhead, especially when processing high-dimensional, multi-scale biological datasets. Future research should focus on improving computational scalability through techniques such as dimensionality reduction, sparse graph modeling, and more efficient message-passing algorithms. Although the framework shows strong potential in simulating off-target effects and evaluating combinatorial drug interactions, its performance may be constrained by the availability and heterogeneity of biological data. To enhance robustness and generalizability, future extensions could incorporate self-supervised learning strategies and leverage emerging datasets generated from advanced experimental platforms. Ultimately, further validation in clinical contexts is crucial to assess the framework’s practical utility, particularly in the design of personalized therapeutic strategies for complex diseases such as osteoporosis and other bone-related disorders.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LQ: Data curation, Writing – original draft. LM: Writing – original draft, Writing – review and editing, Funding acquisition. LY: Writing – original draft, Visualization. ZF: Writing – original draft, Supervision.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bao, W., Yu, Q., and Kong, Y. (2021). “Evidential deep learning for open set action recognition,” in IEEE international conference on computer vision.

Google Scholar

Chen, Y., Zhang, Z., Yuan, C., Li, B., Deng, Y., and Hu, W. (2021a). “Channel-wise topology refinement graph convolution for skeleton-based action recognition,” in IEEE international conference on computer vision.

Google Scholar

Chen, Z., Li, S., Yang, B., Li, Q., and Liu, H. (2021b). “Multi-scale spatial temporal graph convolutional network for skeleton-based action recognition,” in AAAI conference on artificial intelligence.

Google Scholar

Cheng, K., Zhang, Y., Cao, C., Shi, L., Cheng, J., and Lu, H. (2020a). “Decoupling gcn with dropgraph module for skeleton-based action recognition,” in European conference on computer vision.

Google Scholar

Cheng, K., Zhang, Y., He, X., Chen, W., Cheng, J., and Lu, H. (2020b). “Skeleton-based action recognition with shift graph convolutional network,” in Computer vision and pattern recognition.

Google Scholar

Duan, H., Wang, J., Chen, K., and Lin, D. (2022). Pyskl: towards good practices for skeleton action recognition. ACM Multimedia. doi:10.1145/3503161.3548546

CrossRef Full Text | Google Scholar

Duan, H., Zhao, Y., Chen, K., Shao, D., Lin, D., and Dai, B. (2021). “Revisiting skeleton-based action recognition,” in Computer vision and pattern recognition.

Google Scholar

Fathy, A., Hamdi, A., Asad, A. H., and Mohammed, A. (2023). “Varsew: a literature review and benchmark dataset for visual recognition in garment sewing,” in 2023 intelligent methods, systems, and applications (IMSA), 49–55.

Google Scholar

Feng, S., Yang, X., Liu, Y., Zhao, Z., Liu, J., Yan, Y., et al. (2022). Fish feeding intensity quantification using machine vision and a lightweight 3d resnet-glore network. Aquac. Eng. 98, 102244. doi:10.1016/j.aquaeng.2022.102244

CrossRef Full Text | Google Scholar

gun Chi, H., Ha, M. H., geun Chi, S., Lee, S. W., Huang, Q.-X., and Ramani, K. (2022). Infogcn: representation learning for human skeleton-based action recognition. Comput. Vis. Pattern Recognit., 20154–20164. doi:10.1109/cvpr52688.2022.01955

CrossRef Full Text | Google Scholar

Li, Y., Ji, B., Shi, X., Zhang, J., Kang, B., and Wang, L. (2020). Tea: temporal excitation and aggregation for action recognition. Comput. Vis. Pattern Recognit. Available online at: http://openaccess.thecvf.com/content_CVPR_2020/html/Li_TEA_Temporal_Excitation_and_Aggregation_for_Action_Recognition_CVPR_2020_paper.html.

Google Scholar

Lin, L., Song, S., Yang, W., and Liu, J. (2020). Ms2l: multi-task self-supervised learning for skeleton based action recognition. ACM Multimed. doi:10.1145/3394171.3413548

CrossRef Full Text | Google Scholar

Lin, Y., Zhao, R., Huang, J., Chen, T., Yang, H., Guo, H., et al. (2024). Efficacy of the bushen jianpi huoxue formula on beclin-1/bcl-2-mediated autophagy and apoptosis in osteoblasts. Front. Pharmacol. 15, 1513298. doi:10.3389/fphar.2024.1513298

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, K. Z., Zhang, H., Chen, Z., Wang, Z., and Ouyang, W. (2020). Disentangling and unifying graph convolutions for skeleton-based action recognition. Computer Vision and Pattern Recognition Available online at: http://openaccess.thecvf.com/content_CVPR_2020/html/Liu_Disentangling_and_Unifying_Graph_Convolutions_for_Skeleton-Based_Action_Recognition_CVPR_2020_paper.html.

Google Scholar

Lu, Y., Cui, Y., Hou, L., Jiang, Y., Shang, J., Wang, L., et al. (2024). Optimized automated radiosynthesis of 18f-jnj64413739 for purinergic ion channel receptor 7 (p2x7r) imaging in osteoporotic model rats. Front. Pharmacol. 15, 1517127. doi:10.3389/fphar.2024.1517127

PubMed Abstract | CrossRef Full Text | Google Scholar

Meng, Y., Lin, C.-C., Panda, R., Sattigeri, P., Karlinsky, L., Oliva, A., et al. (2020). “Ar-net: adaptive frame resolution for efficient action recognition,” in European conference on computer vision.

Google Scholar

Morshed, M. G., Sultana, T., Alam, A., and Lee, Y.-K. (2023). “Human action recognition: a taxonomy-based survey, updates, and opportunities,” in Italian national conference on sensors.

Google Scholar

Munro, J., and Damen, D. (2020). “Multi-modal domain adaptation for fine-grained action recognition,” in Computer vision and pattern recognition.

Google Scholar

Munsif, M., Khan, N., Hussain, A., Kim, M. J., and Baik, S. W. (2024). Darkness-adaptive action recognition: leveraging efficient tubelet slow-fast network for industrial applications. IEEE Trans. Industrial Inf. 20, 13676–13686. doi:10.1109/tii.2024.3431070

CrossRef Full Text | Google Scholar

Pan, J., Lin, Z., Zhu, X., Shao, J., and Li, H. (2022). St-adapter: parameter-efficient image-to-video transfer learning for action recognition. Neural Inf. Process. Syst. Available online at: https://proceedings.neurips.cc/paper_files/paper/2022/hash/a92e9165b22d4456fc6d87236e04c266-Abstract-Conference.html.

Google Scholar

Peng, Y., Lee, J., and Watanabe, S. (2023). “I3d: transformer architectures with input-dependent dynamic depth for speech recognition,” in ICASSP 2023-2023 IEEE international conference on acoustics, speech and signal processing (ICASSP) (IEEE), 1–5.

CrossRef Full Text | Google Scholar

Perrett, T., Masullo, A., Burghardt, T., Mirmehdi, M., and Damen, D. (2021). Temporal-relational crosstransformers for few-shot action recognition. Computer Vision and Pattern Recognition Available online at: http://openaccess.thecvf.com/content/CVPR2021/html/Perrett_Temporal-Relational_CrossTransformers_for_Few-Shot_Action_Recognition_CVPR_2021_paper.html.

Google Scholar

Pham, Q., Liu, C., and Hoi, S. C. (2023). Continual learning, fast and slow. IEEE Trans. Pattern Analysis Mach. Intell. 46, 134–149. doi:10.1109/TPAMI.2023.3324203

PubMed Abstract | CrossRef Full Text | Google Scholar

Sasiain, J., Franco, D., Atutxa, A., Astorga, J., and Jacob, E. (2024). Toward the integration and convergence between 5G and tsn technologies and architectures for industrial communications: a survey. IEEE Commun. Surv. & Tutorials 27, 259–321. doi:10.1109/comst.2024.3422613

CrossRef Full Text | Google Scholar

Savran Kızıltepe, R., Gan, J. Q., and Escobar, J. J. (2023). A novel keyframe extraction method for video classification using deep neural networks. Neural Comput. Appl. 35, 24513–24524. doi:10.1007/s00521-021-06322-x

CrossRef Full Text | Google Scholar

Shen, Y.-T., Lee, Y., Kwon, H., Conover, D. M., Bhattacharyya, S. S., Vale, N., et al. (2023). Archangel: a hybrid uav-based human detection benchmark with position and pose metadata. IEEE Access 11, 80958–80972. doi:10.1109/access.2023.3299235

CrossRef Full Text | Google Scholar

Song, Y., Zhang, Z., Shan, C., and Wang, L. (2020). Stronger, faster and more explainable: a graph convolutional baseline for skeleton-based action recognition. ACM Multimedia. doi:10.1145/3394171.3413802

CrossRef Full Text | Google Scholar

Song, Y., Zhang, Z., Shan, C., and Wang, L. (2021). Constructing stronger and faster baselines for skeleton-based action recognition. IEEE Trans. Pattern Analysis Mach. Intell. 45, 1474–1488. doi:10.1109/TPAMI.2022.3157033

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, Z., Liu, J., Ke, Q., Rahmani, H., and Wang, G. (2020). Human action recognition from various data modalities: a review. IEEE Trans. Pattern Analysis Mach. Intell. 45, 3200–3225. doi:10.1109/TPAMI.2022.3183112

PubMed Abstract | CrossRef Full Text | Google Scholar

Truong, T.-D., Bui, Q.-H., Duong, C., Seo, H.-S., Phung, S. L., Li, X., et al. (2022). Direcformer: a directed attention in transformer approach to robust action recognition. Computer Vision and Pattern Recognition. Available online at: http://openaccess.thecvf.com/content_CVPR_2020/html/Li_TEA_Temporal_Excitation_and_Aggregation_for_Action_Recognition_CVPR_2020_paper.html.

Google Scholar

Wang, L., Tong, Z., Ji, B., and Wu, G. (2020). Tdn: temporal difference networks for efficient action recognition. Computer Vision and Pattern Recognition. Available online at: http://openaccess.thecvf.com/content/CVPR2021/html/Wang_TDN_Temporal_Difference_Networks_for_Efficient_Action_Recognition_CVPR_2021_paper.html.

Google Scholar

Wang, X., Zhang, S., Qing, Z., Tang, M., Zuo, Z., Gao, C., et al. (2022). Hybrid relation guided set matching for few-shot action recognition. Comput. Vis. Pattern Recognit., 19916–19925. doi:10.1109/cvpr52688.2022.01932

CrossRef Full Text | Google Scholar

Yadav, S. K., Luthra, A., Pahwa, E., Tiwari, K., Rathore, H., Pandey, H. M., et al. (2023). Droneattention: sparse weighted temporal attention for drone-camera based activity recognition. Neural Netw. 159, 57–69. doi:10.1016/j.neunet.2022.12.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, C., Xu, Y., Shi, J., Dai, B., and Zhou, B. (2020). Temporal pyramid network for action recognition. Computer Vision and Pattern Recognition Available online at: http://openaccess.thecvf.com/content_CVPR_2020/html/Yang_Temporal_Pyramid_Network_for_Action_Recognition_CVPR_2020_paper.html.

Google Scholar

Ye, F., Pu, S., Zhong, Q., Li, C., Xie, D., and Tang, H. (2020). Dynamic gcn: context-enriched topology learning for skeleton-based action recognition. ACM Multimed., 55–63. doi:10.1145/3394171.3413941

CrossRef Full Text | Google Scholar

Ye, Q., Cui, Y., Wang, H., Li, L., Chen, J., Xue, Z., et al. (2024). Exosomal communication: a pivotal regulator of bone homeostasis and a potential therapeutic target. Front. Pharmacol. 15, 1516125. doi:10.3389/fphar.2024.1516125

PubMed Abstract | CrossRef Full Text | Google Scholar

Yusuf, M., Khan, M., Alrobaian, M. M., Alghamdi, S. A., Warsi, M. H., Sultana, S., et al. (2021). Brain targeted polysorbate-80 coated plga thymoquinone nanoparticles for the treatment of alzheimer’s disease, with biomechanistic insights. J. Drug Deliv. Sci. Technol. 61, 102214. doi:10.1016/j.jddst.2020.102214

CrossRef Full Text | Google Scholar

Zhang, D., Leung, N., Weber, E., Saftig, P., and Brömme, D. (2011). The effect of cathepsin k deficiency on airway development and tgf-β1 degradation. Respir. Res. 12, 72–14. doi:10.1186/1465-9921-12-72

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, H., Zhang, L., Qi, X., Li, H., Torr, P. H. S., and Koniusz, P. (2020). “Few-shot action recognition with permutation-invariant attention,” in European conference on computer vision.

Google Scholar

Zhou, H., Liu, Q., and Wang, Y. (2023). Learning discriminative representations for skeleton based action recognition. Computer Vision and Pattern Recognition Available online at: http://openaccess.thecvf.com/content/CVPR2023/html/Zhou_Learning_Discriminative_Representations_for_Skeleton_Based_Action_Recognition_CVPR_2023_paper.html.

Google Scholar