- 1Air Force Institute of Technology, Wright-Patterson Air Force Base, Denton, OH, United States
- 2Center for Nonlinear Sciences and Department of Physics, University of North Texas, Denton, TX, United States
We study the propagation of a quantum field composed of a few photons interacting with a three-level
1 Introduction
Electromagnetic radiation consists of photons that propagate in an empty space with the speed of light. The speed of propagation can be different when the radiation beam propagates through a medium. The index of refraction has been introduced to take into account the interaction between the radiation and the medium, and the behavior of the radiation beam is determined by the index of refraction of the medium.
Optical devices like lenses and prisms enable the manipulation of classical and quantum optical beams [see, for example, work by Leonhardt (1997)]. If the optical beam contains only a few photons, the quantum state of the radiation becomes crucial. It raises the question of whether the index of refraction remains a useful concept for single-photon physics or whether it can be applied as successfully as it has been for classical optical beams [see, for example, work by Rostovtsev et al. (2023)].
In our paper, we have used the quantum photon states using the Gaussian envelopes because they are widely used in optics and combine mathematical elegance with physical practicality, providing stable, smooth, and efficient solutions for pulse generation, propagation, and manipulation. In addition, many laser systems naturally produce pulses with Gaussian envelopes, as they arise from the fundamental mode of many optical cavities (e.g.,
For simplicity, we consider only a one-dimension model that could be applied if we deal with a focused Gaussian beam or the radiation in a waveguide. For example, in the work by Zheng et al. (2013), a novel scheme for quantum computation is proposed using propagating photons in a one-dimensional waveguide interacting with matter qubits. Our approach is similar in that we consider one three-level
The three-level atoms driven by coherent fields, as has been shown by Fleischhauer et al. (2005) and Fleischhauer and Lukin (2000), have demonstrated various coherence effects such as the electromagnetically induced transparency (Harris, 1997) that was even demonstrated for a single atom in free space in work by Slodička et al. (2010). The important feature is the control field that can strongly modify the atomic response, as well as trap and manipulate photon states in the atomic ensembles, as shown by Lukin (2003). The process of absorption and emission is related to the phase change of the quantum fields [see, for example, work by Pollnau (2018). The strong coupling between single atoms and photons leads to the nonlinear
As is also well known, multiple qubits can be encoded per photon, and the information-carrying capacity of a single photon can be vastly expanded by exploiting its multiple degrees of freedom: spatial, temporal, and polarization [as shown by Kok and Lovett (2014) and Seitz and Theuwissen (2011)]. For example, the two-qubit single-photon quantum operations have been realized in work by Schumacher (1995), and an experimental demonstration of three-qubit single-photon, linear, deterministic quantum gates that exploit photon polarization and the two-dimensional spatial-parity-symmetry of the transverse single-photon field shown by Nielsen and Chuang (2010). Long-distance quantum communications have been demonstrated by Aspelmeyer et al. (2003). It brings us to the conclusion that the propagation of single photons in different quantum states is important, for example, when studying the stability of quantum states carrying the quantum information for quantum communications. But even more, it is interesting to see whether it is possible, for example, to develop various devices to manipulate a beam of a few photons in particular quantum states to filter quantum states and/or control their propagation. One example is a plane of single atoms that can “work” as a thin lens to manipulate and control the propagation of a single photon; that is, focusing a single photon by an array of atoms allows one to localize a single photon closer to the detector to enhance detection rate. If we can control atomic states, the focusing can be controlled, too.
Our investigations involved the simulation of a quantum field consisting of a wave packet of one multimode photon or two photons interacting with a three-level Lambda-type atomic system (see Figure 1). The incident photons (in state
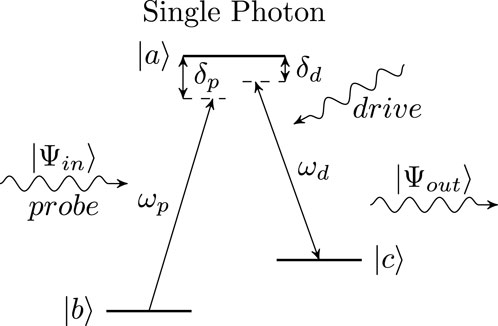
Figure 1. Energy levels of an atom are shown. A single incident photon (
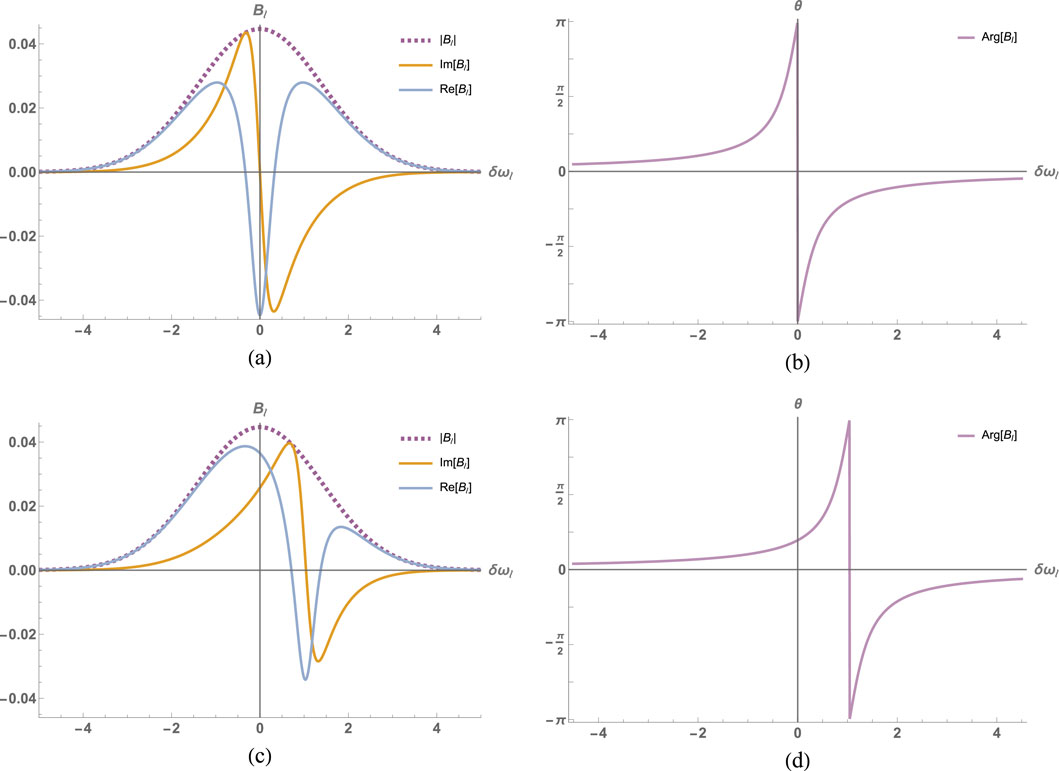
Figure 2. The real, imaginary parts of the probability amplitudes
In the paper, we demonstrate the phase shift produced by a single atom for a single photon that can be detected by using the Mach–Zehnder interferometer. This approach allows us to show that it is possible to introduce the index of refraction for a single photon that can “work” for a broad range of applications of quantum fields: quantum information, quantum computation, imaging, and improving microscopy and long-distance quantum communication.
2 Methods
To take into account the propagation effects, let us consider a simple model consisting of a Lambda-type three-level atom interacting with a pulse of electromagnetic field. A clear picture of the propagation of a few photons can be obtained by employing a mode function [see the book by Kok and Lovett (2014)]. We use a wave packet for a Gaussian envelope consisting of a few photons as follows:
where
where
Then, the field operator can be written as Equation 3:
where summation over all
The state vector describing the three-level
The Hamiltonian of the atom interacting with the quantum field
where
The interaction Hamiltonians with the quantum field and the classical fields
where
Then, all A, B, and C coefficients in Equation 4 satisfy the coupled equations.
The simulations of the set of the above equations (Equations 9–15) are presented in Figures 2–5 and reveal a variety of regimes. These include scenarios in the absence of a driving field and under the influence of the driving field. The results clearly demonstrate that introducing a driving field provides an efficient mechanism for controlling the interaction with quantum fields consisting of one- and two-photon states.
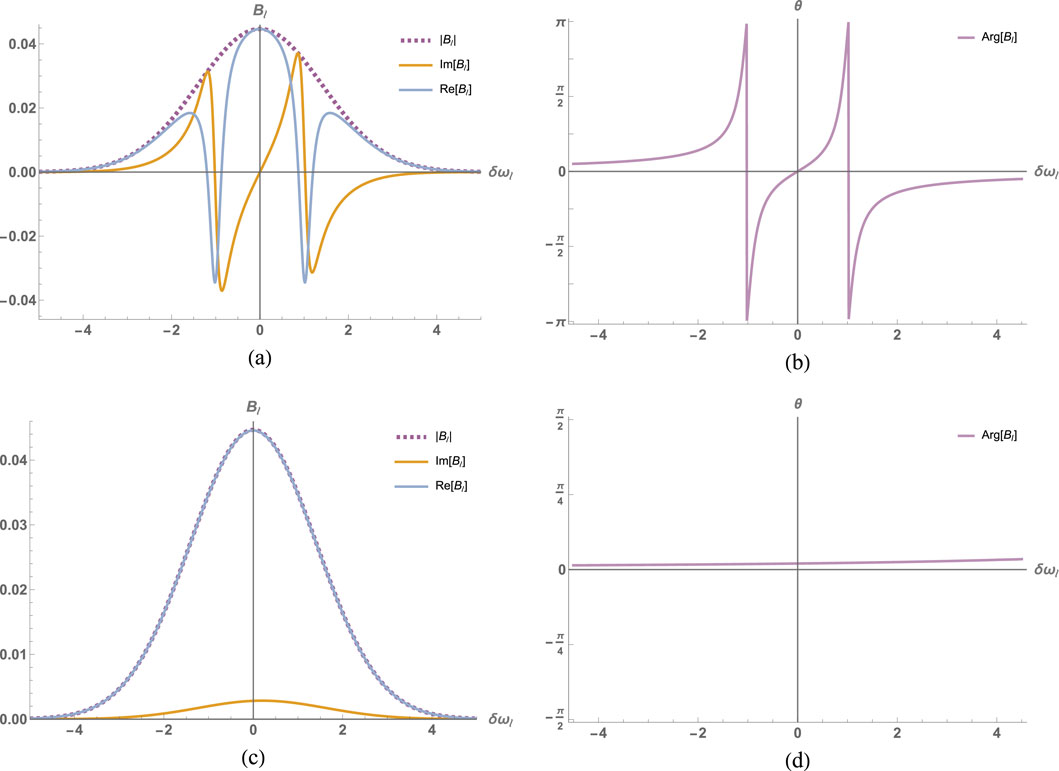
Figure 3. The real, imaginary parts of the probability amplitudes
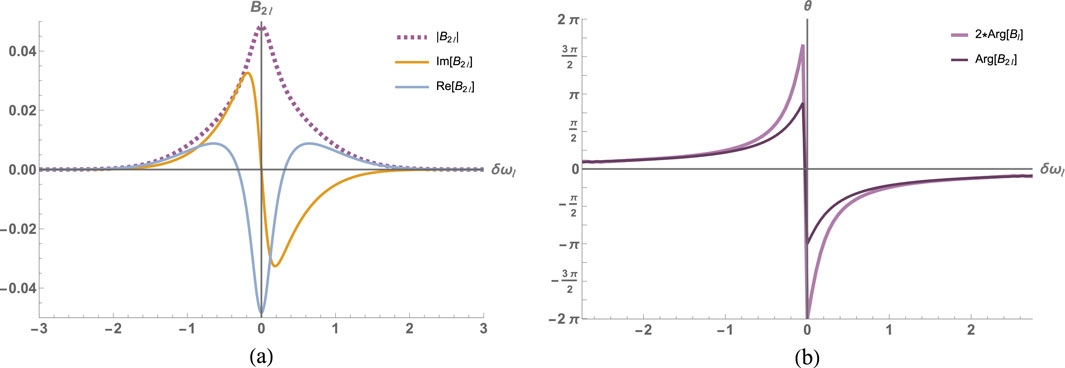
Figure 4. (a) The real, imaginary, and absolute value parts of the probability amplitudes
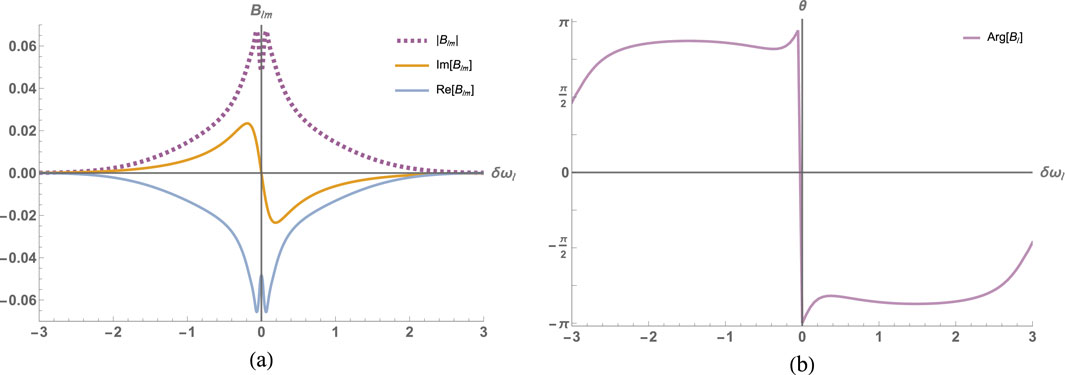
Figure 5. (a) The real, imaginary, and absolute value parts of the probability amplitudes
Specifically, the driving field enables precise tuning of the system’s dynamics, allowing for enhanced manipulation of quantum states and greater flexibility in achieving desired outcomes. This level of control is critical for applications in quantum information processing and quantum optics, where the ability to manage photon interactions plays a key role in developing advanced technologies such as quantum sensors and single-photon sources. The simulations underscore the importance of driving fields in optimizing system performance and exploring new regimes of light–matter interaction.
2.1 Resonant interaction
At resonance,
Equations 9–15 describe the interaction of the system with a quantum field and also describe the relaxation of the system prepared in the excited state. These absorption and excitation processes are closely related [see work by Pollnau (2018)].
Let us first consider the relaxation that occurs when the initial condition is
Consider
and plugging back in Equation 16, we obtain Equation 19, the following well-known procedure [see, for example, work by Scully and Zubairy (1997)]:
where
Now let us consider the atom in the ground state,
Then, for the amplitude of the atom in the excited state, we can write Equation 22:
Substituting Equation 22 into Equation 21 yields Equations 23 and 24:
where
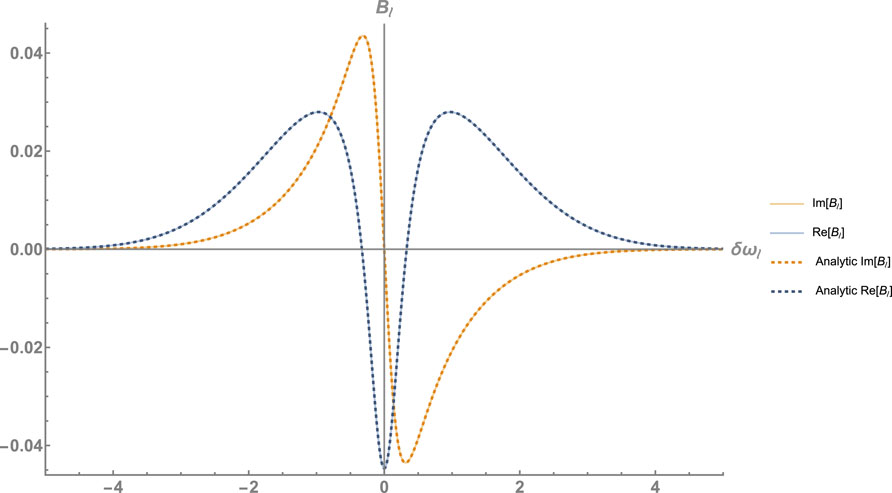
Figure 6. The real and imaginary parts of
2.2 Mode function
For large detuning, when
and substituting it into Equation 17:
We can see indeed that all one-photon modes acquired the same phase given by Equation 27, as was also confirmed by our simulations and shown in Figure 3. The linear combination of the vacuum modes can be viewed as a photon with creation/annihilation operators defined as Equation 28:
where
Then, using the assumption that all modes acquire the same phase,
and
We can write for the case of a quantum field consisting of one and two photons, the state vector of the system can be written as Equation 34:
where the
where
Under the conditions (when the probe is far detuned), the entire envelope of the photon acquires the same phase; that is, the mode function approximation works very well, as one can see in Figures 6, 4B. The important results here are also that the phase acquired by the two-photon state given by Equation 42
is exactly twice larger than the phase acquired for the one-photon state (this can be seen in Figure 4B, where the phase of the
2.3 Mach–Zehnder interferometer
A natural way to experimentally observe the dispersion of a single photon produced by a single atom is to use the Mach–Zehnder (MZ) interferometer shown in Figure 7. A photon has two paths for propagation; if the path is identical, the photon goes in one direction with probability 1 and probability 0 at the second port of the interferometer. Meanwhile, if one path contains a single atom, it changes phases of modes and breaks the symmetry of the balanced interferometer. This results in changes in the probabilities that the photon appears at different ports of the MZ interferometer. Detecting these probabilities allows one to obtain the dispersion of the single photon during propagation through the corresponding arm of the interferometer.
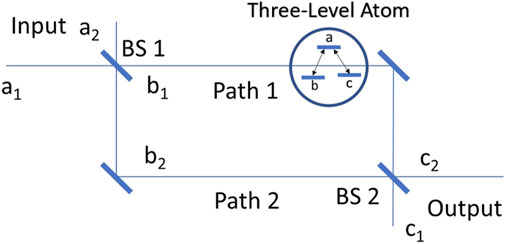
Figure 7. The Mach–Zehnder interferometer. The input
The fields
where
and
Let us consider an input photon state to be a one-photon state
Now, we can consider the MZ interferometer, which contains two beam splitters and two arms. For each beam splitter, we must calculate the output fields using Equation 44,
Then, the second beam splitter is taken into account by Equation 46:
For the output state, we finally obtain Equation 47:
where
In a balanced Mach–Zehnder interferometer with no obstruction in either arm, the photon wave packet can exit one of the ports with nearly 100% certainty. However, introducing an atom into one arm of the interferometer drastically alters the phase of the wave packet near the resonant transition frequency, as illustrated in Figure 2. When the central-photon frequency is detuned far from resonance, the interaction results in only a slight modification to the probability amplitude of the wave packet. This effect corresponds to an approximately uniform phase shift across all plane-wave modes within the packet, consistent with the mode function representation.
We can examine how the presence of the atom in the interferometer would affect the probability by which port (C1 or C2) the wave packet exits from the MZ interferometer. In the simulation, the balanced interferometer is constructed so that with no atom present, the photon will exist through the C1 port with probability 1. In Figure 8, we introduce the atom without a driving field, and, as a result, the probability that the wave packet leaves through the C1 port decreases. The phase of the photon wave packet is strongly modified because of the resonant interaction. As the photon is detuned from the atomic transition frequency, the phase shift is reduced. The probability that the photon will exit through the C1 port tends to 1, just as in the case where there is no atom present.
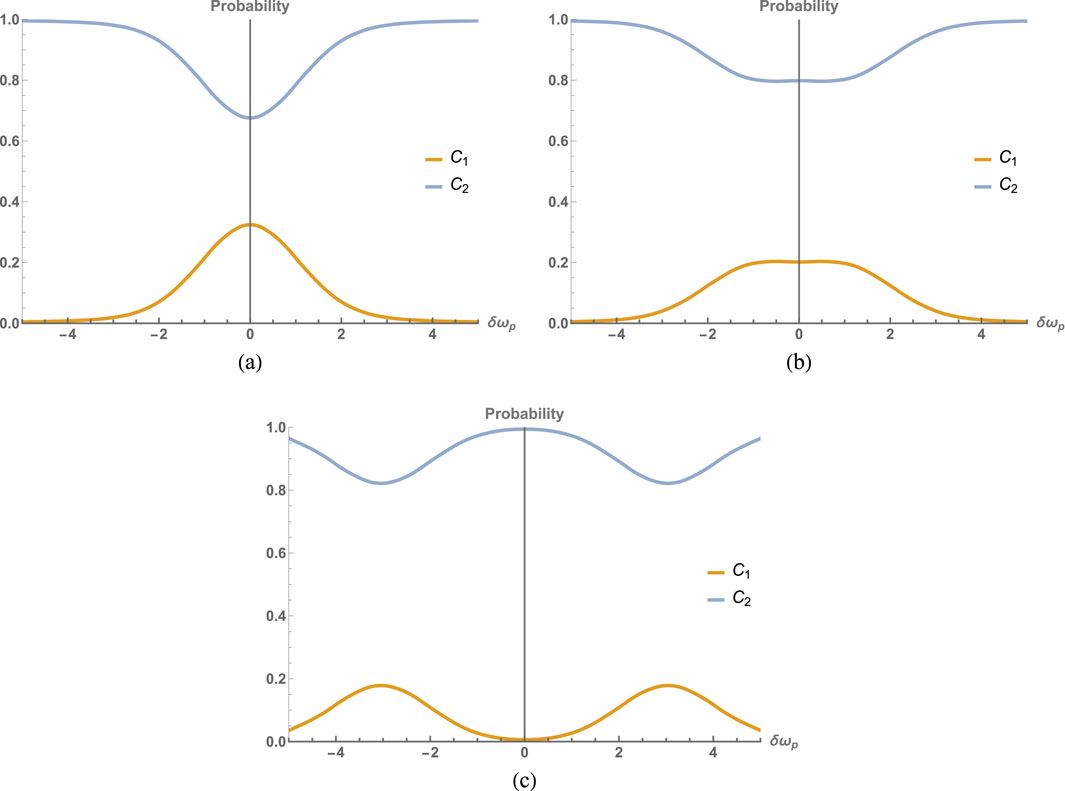
Figure 8. (a) Probability that the photon will exit a given port as a function of detuning from atomic transition
Now, we introduce a drive to the atom to see its effects on the probability of the photon. Figure 8A shows a drive
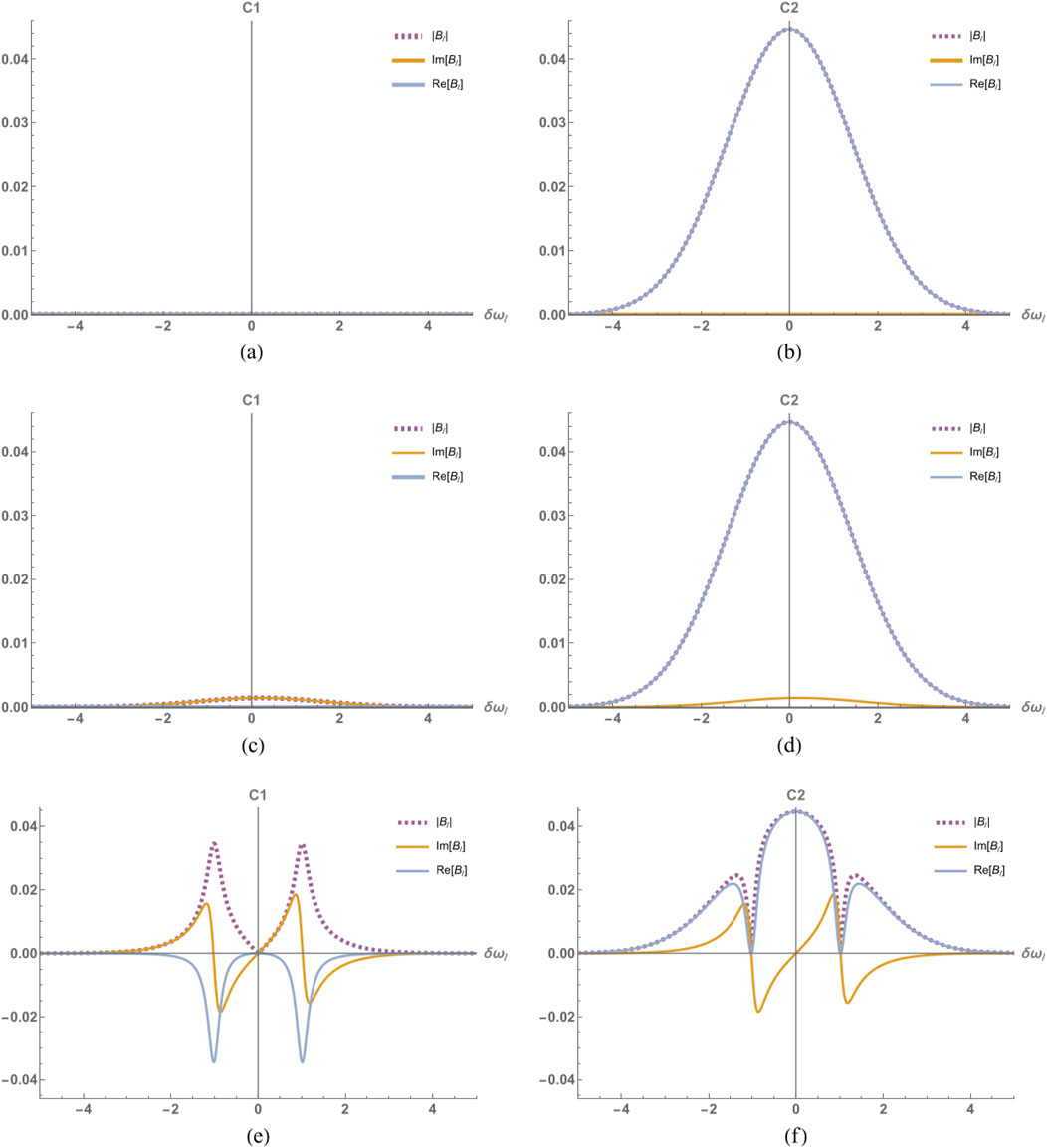
Figure 9. Balanced MZ interferometer with no atom present. The probability amplitude of
We note here that comparing the obtained results for a single atom with a few photons with the classical index of refraction given by the Maxwell equations can provide valuable insights into their behavior and interactions.
From the effective Hamiltonian given by Equation 41, assuming for a weak field that the population stays in the ground state, the atomic operator
Then, using the adiabatic approximation valid for the large detuning
where we can see that the phase factor, which appears above, coincides with the index of refraction that can be obtained from Maxwell equations for the classical field [see, for example, the book by Scully and Zubairy (1997)]. Indeed, according to Equation 50, the phase shift is given by
where
and
which is exactly the index of refraction for the weak classical field [see, for example, the book Scully and Zubairy (1997)]. For our consideration,
Then, the “collective” dipole moment is given by
Possible applications of the obtained results can be related to controlling the output of the MZ interferometer. In particular, with a three-level atom present in one arm of the interferometer, one can use the driving field in conjunction with a path delay phase shift to achieve a variety of desirable effects. In a simple case, the driving field can be used to toggle the MZ interferometer between a balanced configuration and a desired output so long as the photon wave packet’s central frequency is close to the resonant transition frequency. If the initial photon states are unknown, one could, in principle, drive the atom to act as a filter for particular photon states. Given a known initial photon state, one could use the atom as a veritable splitter to control which port the photon would leave with adjustable probability. Given that the incident photon was in some entangled state, the atom could be used as a scheme to perform some interaction-free measurements.
Thus, we can see that our study is focused on the dynamics of a single photon interacting with a three-level atom. We investigated various aspects related to the propagation of this photon and highlighted the significance of phase and group velocities in the context of long-distance quantum communications.
Understanding the behavior of a single photon is of great importance in quantum communication systems, where information is encoded and transmitted using quantum states. By examining the interaction between a single photon and a two-level atom, we gained insights into how the photon’s properties are influenced and modified during its propagation.
By studying the dispersion of the single-photon propagation, we have deepened our understanding of the fundamental properties that govern quantum communications. These findings contribute to the development of more efficient and reliable quantum communication systems, which are crucial to the advancement of technologies such as quantum cryptography, quantum teleportation, and quantum computing.
3 Conclusion
In conclusion, we have demonstrated that the mode function can be effectively utilized in scenarios involving large detunings, highlighting its versatility and relevance in quantum systems with non-resonant interactions. Through our analysis, several useful approximations of the density matrix solution have been derived, offering valuable insights into the dynamics of such systems.
Furthermore, we have shown that the one- and two-photon resonance modes undergo significant phase shifts, which are crucial for understanding and manipulating quantum coherence and interference effects. These findings pave the way for more precise control in applications such as quantum information processing, nonlinear optics, and spectroscopy. The ability to predict and manage these phase shifts could enable the design of novel quantum devices and experiments, pushing the boundaries of what is achievable in the field of quantum optics and quantum mechanics. In particular, we describe the system of generating correlated photons.
We provide a detailed description of the system designed for generating correlated photons, emphasizing its underlying principles, mechanisms, and potential applications. The system leverages quantum coherence and nonlinearity to create photon pairs with strong temporal and spectral correlations, which are essential for various applications in quantum technologies.
By carefully controlling the interaction of optical fields with the medium, we demonstrate how the system can produce photons that are entangled or exhibit strong quantum correlations. These correlated photons play a pivotal role in advancing quantum communication protocols, such as quantum key distribution, and are fundamental resources for quantum computing and quantum sensing.
Additionally, the approach offers a platform to explore the fundamental properties of quantum light, such as photon statistics, coherence, and interference, thus contributing to a broader understanding of quantum mechanics. This system not only highlights the feasibility of generating correlated photons but also provides a foundation for the development of scalable and efficient quantum light sources for practical implementations.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.
Author contributions
JE: investigation, methodology, validation, writing – original draft, and writing – review and editing. AP: conceptualization, investigation, methodology, project administration, supervision, writing – original draft, and writing – review and editing. YR: conceptualization, formal analysis, investigation, methodology, project administration, validation, writing – original draft, and writing – review and editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. AP is thankful the Directed Energy Joint Transition Office (JDETO) for the support. This paper has been cleared for public release, clearance number 88ABW-2024-1017.
Acknowledgments
We thank Girish Agarwal, Konstantin Dorfman, Billie Deluca, Keith A. Wyman, Michael Pak, David E. Weeks, and Barnabas (Moochan) Kim for fruitful discussions, comments, and suggestions. JE and YR are grateful for the support of the 2023–2024 AFOSR Summer Faculty Fellowship Programs at AFIT. AP is thankful for the AFOSR grant.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Gen AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aspelmeyer, M., Jennewein, T., Pfennigbauer, M., Leeb, W., and Zeilinger, A. (2003). Long-distance quantum communication with entangled photons using satellites. IEEE J. Sel. Top. Quantum Electron. 9, 1541–1551. doi:10.1109/.jstqe.2003.820918
Dicke, R. H. (1954). Coherence in spontaneous radiation processes. Phys. Rev. 93, 99–110. doi:10.1103/PhysRev.93.99
Fleischhauer, M., Imamoglu, A., and Marangos, J. (2005). Electromagnetically induced transparency: optics in coherent media. Rev. Mod. Phys. 77, 633–673. doi:10.1103/revmodphys.77.633
Fleischhauer, M., and Lukin, M. D. (2000). Dark-state polaritons in electromagnetically induced transparency. Phys. Rev. Lett. 84, 5094–5097. doi:10.1103/PhysRevLett.84.5094
Harris, S. E. (1997). Electromagnetically induced transparency. Phys. Today 50, 36–42. doi:10.1063/1.881806
Junge, C., O’Shea, D., Volz, J., and Rauschenbeutel, A. (2013). Strong coupling between single atoms and nontransversal photons. Phys. Rev. Lett. 110, 213604. doi:10.1103/PhysRevLett.110.213604
Kok, P., and Lovett, B. W. (2014). Optical quantum information processing. Cambridge: Cambridge University Press.
Leonhardt, U. (1997). Measuring the quantum state of light. Cambridge, UK: Cambridge University Press.
Lukin, M. D. (2003). Colloquium: trapping and manipulating photon states in atomic ensembles. Rev. Mod. Phys. 75, 457–472. doi:10.1103/RevModPhys.75.457
Nielsen, M. A., and Chuang, I. L. (2010). Quantum computation and quantum information. Cambridge: Cambridge University Press.
Pollnau, M. (2018). Phase aspect in photon emission and absorption. Optica 5, 465–474. doi:10.1364/optica.5.000465
Rostovtsev, Y., Emerick, J., and Patnaik, A. (2023). The refractive index of a single atom experienced by a single photon. Results Opt. 13, 100568. doi:10.1016/j.rio.2023.100568
P. Seitz, and A. J. P. Theuwissen (2011). Single-photon imaging (Heidelberg: Springer-Verlag Berlin).
Slodička, L., Hétet, G., Gerber, S., Hennrich, M., and Blatt, R. (2010). Electromagnetically induced transparency from a single atom in free space. Phys. Rev. Lett. 105, 153604. doi:10.1103/physrevlett.105.153604
Utsugi, T., Goban, A., Tokunaga, Y., Goto, H., and Aoki, T. (2022). Gaussian-wave-packet model for single-photon generation based on cavity quantum electrodynamics under adiabatic and nonadiabatic conditions. Phys. Rev. A 106, 023712. doi:10.1103/physreva.106.023712
Volz, J., Scheucher, M., Junge, C., and Rauschenbeutel, A. (2014). Nonlinear π phase shift for single fibre-guided photons interacting with a single resonator-enhanced atom. Nat. Photonics 8, 965–970. doi:10.1038/nphoton.2014.253
Walther, H., Varcoe, B. T., Englert, B.-G., and Becker, T. (2006a). Cavity quantum electrodynamics. Rep. Prog. Phys. 69, 1325–1382. doi:10.1088/0034-4885/69/5/r02
Walther, H., Varcoe, B. T. H., Englert, B.-G., and Becker, T. (2006b). Cavity quantum electrodynamics. Rep. Prog. Phys. 69, 1325–1382. doi:10.1088/0034-4885/69/5/R02
Keywords: photons, quantum fields, quantum optics, three-level atoms, interference, Mach–Zehnder interferometer
Citation: Emerick J, Patnaik AK and Rostovtsev Y (2025) The refractive index of a single three-level atom experienced by a single photon. Front. Quantum Sci. Technol. 4:1546480. doi: 10.3389/frqst.2025.1546480
Received: 16 December 2024; Accepted: 27 March 2025;
Published: 29 April 2025.
Edited by:
Chunlei Qu, Stevens Institute of Technology, United StatesReviewed by:
Aneesh Ramaswamy, Stevens Institute of Technology, United StatesJabir Chathanathil, United States Army Research Laboratory, United States
Copyright © 2025 Emerick, Patnaik and Rostovtsev. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yuri Rostovtsev, cm9zdEB1bnQuZWR1
 Jacob Emerick
Jacob Emerick Anil K. Patnaik
Anil K. Patnaik Yuri Rostovtsev
Yuri Rostovtsev