Dynamics of the ideal quantum measurement of a spin-1 with a Curie–Weiss magnet

Quantum measurement is a dynamical process involving an apparatus coupled to a test system. The ideal measurement of the $z$-component of a spin-$\frac{1}{2}$ $(s_z=\pm \frac{1}{2})$ has been modeled by the Curie–Weiss model for quantum measurement. Recently, the model was generalized to higher spins, and its thermodynamics were solved. Here, the dynamics are considered. To this end, the dynamics for the spin-$\frac{1}{2}$ case are cast in general notation. The dynamics of the measurement of the $z$-component of a spin-1 $(s_z=0,\pm 1)$ are solved in detail and evaluated numerically. The energy costs of the measurement, which are macroscopic, are evaluated. The generalization to higher spin is straightforward.

1 Introduction

This year, we celebrate the centennial of the formulation of quantum theory; see Capellmann (2017) for the prehistory. After the “Zur Quantummechanik” by Born and Jordan (1925), the Dreimänner Arbeit by Born et al. (1926) on the matrix mechanics was soon followed by Schrödinger's (1926) formulation of wave mechanics, inspired by the insights of De Broglie (1924). The predictive power of the theory was expressed by Born's (1926) rule. For a compilation of historical contributions, see Wheeler and Zurek (2014).

The interpretation of quantum mechanics has been discussed throughout the century since then. The Copenhagen interpretation— with the Born rule and the collapse postulate—emerged as the most reasonable. Many attempts to deepen understanding begin with these postulates. However, they are merely shortcuts for what happens in a laboratory. With our collaborators Armen Allahverdyan and Roger Balian, we have taken the viewpoint of starting from the uninterpreted quantum formalism and applied it to the dynamics of an idealized measurement. The elements of this approach that have already been solved do not need to be interpreted; interpretation is needed to put the results in a proper, global context. As discussed below, this effort has led to a specified version of the statistical interpretation of quantum mechanics, popularized by Ballentine (1970).

The present study deals with the dynamics of an ideal quantum measurement. It is based on the Curie–Weiss model for measuring the $z$-component of a spin $\frac{1}{2}$, introduced by Allahverdyan et al. (2003a). After reviewing various models for quantum measurement, it was considered in great detail by Allahverdyan et al. (2013). The apparatus consists of a mean-field type magnet having $N\gg 1$ spins $\frac{1}{2}$ coupled to a harmonic oscillator bath. The magnet starts in a metastable, long-lived, paramagnetic state, which is separated by free energy barriers from the stable states with upward or downward magnetization. It is in a “ready” state for use in a measurement.

When employed as an apparatus, the magnetization acts as a pointer for the outcome. The coupling to the tested spin causes a quick transition to one of the stable states, thereby registering the measurement. For this to succeed, the coupling must be large enough to overcome the free energy barrier. While the final state of the magnet is described by thermodynamics, much detail is contained in the dynamical evolution toward this state.

In an ideal measurement, the Born rule appears due to the non-disturbance of the measured operator. It provides probabilities for the pointer, that is, for the final magnetization to be upward or downward. The state of the microscopic spin is correlated with it and inferred from the pointer indication.

Understanding the dynamics also provides a natural route toward the interpretation of quantum mechanics. Indeed, when assuming the quantum formalism, the task is to work out its predictions, and only then to interpret the results. This leads to viewing the wave function, or, more generally, the density matrix, as a state of best knowledge and the “collapse of the wave function” or “disappearance of cat states” as an update of knowledge after the selection of the runs with identical outcomes, compatible with the quantum formalism. Notably, quantum theory is not a theory of Nature based on an ontology; rather, it is an abstract construct to explain its probabilistic features.

The “measurement problem,” that is, describing the individual experiments that occur in a laboratory, is, in our view, still the most outstanding challenge of modern science. Many attempts have been made to solve it by making adaptations or small alterations to quantum mechanics or by interpreting it differently. We hold the opinion that this entire enterprise is in vain; one should start completely from scratch to “derive quantum mechanics,” that is to say, establish the origin of quantum behavior in Nature¹.

Various formalisms of quantum mechanics were reviewed by David (2015). The insight that quantum mechanics is only meaningful in a laboratory context, stressed in particular by Bohr, is central to the approaches of Auffeves and Grangier (2016) and Auffeves and Grangier (2020), it leads to new insights regarding the Heisenberg cut between quantum and classical (Van Den Bossche and Grangier, 2023). One century of interpretation of the Born rule, including the modern one, was overviewed by Neumaier (2025).

1.1 The Curie–Weiss model for quantum measurement

A macroscopic material consists of atoms, which are quantum particles. The starting point for their dynamics lies in quantum statistical mechanics. For a measurement, the apparatus must be macroscopic and have a macroscopic pointer so that the outcome of the measurement can be read off or processed automatically. Hereto, an operator formalism is required, with dynamics set by the Liouville–von Neumann equation, the generalization of the Schrödinger equation to mixed states.

Progress on solvable models for quantum measurement has been made in recent decades when we, together with A. Allahverdyan and R. Balian introduced and solved the so-called Curie–Weiss model for quantum measurement (Allahverdyan A. E. et al., 2003) in our “ABN” collaboration. Here, the classical Curie–Weiss model of a magnet is taken in its quantum version and applied to the measurement of a quantum spin $\frac{1}{2}$. Various further aspects were presented in Allahverdyan A. E. et al. (2003), Allahverdyan et al. (2005a), Allahverdyan et al. (2005b), Allahverdyan et al. (2007), and Allahverdyan et al. (2006). They were reviewed and greatly expanded in Allahverdyan et al. (2013). Lecture notes were presented by Nieuwenhuizen et al. (2014). A straightforward interpretation for a class of these measurement models was provided by Allahverdyan et al. (2017); it is a specified version of the statistical interpretation made popular by Ballentine (1970).

Simultaneous measurement of two noncommuting quantum variables was worked out (Perarnau-Llobet and Nieuwenhuizen, 2017a), as well as an application to Einstein-Podolsky-Rosen type of measurements (Perarnau-Llobet and Nieuwenhuizen, 2017b). A numerical test on a simplified version of the Curie–Weiss model reproduced nearly all of its properties (Donker et al., 2018).

Our ensuing insights, which are suitable for teachers of quantum theory (at the high school, bachelor’s, or master’s levels), are presented in Allahverdyan et al. (2024) and summarized in a feature article (Allahverdyan et al., 2025).

1.2 Higher-spin Curie–Weiss models

The mentioned Curie–Weiss model was recently generalized by us to measure a spin $l>\frac{1}{2}$ (Nieuwenhuizen, 2022). This study will be termed “Models” henceforth. For spin $l$, the state of the magnet is described by $2l$ order parameters. To assure an unbiased measurement, the Hamiltonian of the apparatus and the interaction Hamiltonian with the tested system have $Z_{2l+1}$ symmetry. The statics were solved for spin-1, $\frac{3}{2}$, 2, and $\frac{5}{2}$.

Here, the dynamics are worked out for spin-1, laying the groundwork for higher-spin dynamics. In the spin $\frac{1}{2}$ Curie–Weiss model, it was found that Schrödinger cat terms disappear through two mechanisms: dephasing of the magnet, possibly followed by decoherence due to the thermal bath. Similar behavior is now investigated for spin-1.

The setup of the article is as follows. In Section 2, we recall the formulation of the Curie–Weiss model for general spin-$l$ and discuss aspects of its physical implementation for spin $\frac{1}{2}$ and spin-1. In Section 3, we revisit the spin-$\frac{1}{2}$ case and cast its dynamics in a general form. In Section 4, we analyze the dynamics of the spin-1 situation. We close with a summary in Section 5.

2 Higher-spin Curie–Weiss Hamiltonian models

We start by recalling some properties of higher-spin models that we introduced in “Models” (Nieuwenhuizen, 2022). The statics were considered there; here, we define and study the dynamics, recalling parts of the spin $\frac{1}{2}$ case. We often refer to the review by Allahverdyan et al. (2013) to be termed “Opus.”

In the following, we denote quantum operators by a hat, specifically $\widehat{\mathbf{s}}$ and ${\widehat{s}}_z$ for the measured spin and ${\widehat{\sigma }}^{(i)}$ and ${\widehat{\sigma }}_z^{(i)}$ for the spins of the apparatus. For simplicity of notation, we follow Models and denote the eigenvalues without a hat, notably those of ${\widehat{s}}_z$ by $s$ and the ones of ${\widehat{\sigma }}_z^{(i)}$ by ${\sigma }_i$. Sums over $i$ lead to the operators ${\widehat{m}}_k$ and their scalar values $m_k$ for $k=\mathrm{1,2},\dots ,2l$. Switching between these operators and their eigenvalues is straightforward.

The strategy is to measure the $z$-component of a quantum spin-$l$ with $(l=\frac{1}{2},1,\frac{3}{2},\cdots )$. The eigenvalues $s$ of the operator ${\widehat{s}}_z$ lie in the spectrum²

$s\in {\text{spec}}_l=\left\{-l,-l+1,\dots ,l-1,l\right\}.(2.1)$

The measurement will be performed by employing an apparatus with $N\gg 1$ vector spins-$l$ having operators ${\widehat{\sigma }}^{(i)}$, $i=1,\dots ,N$. They have components ${\widehat{\sigma }}_a^{(i)}$ $(a=x,y,z)$, with eigenvalues ${\sigma }_a^{(i)}\in {\text{spec}}_l$. These operators are mutually coupled in the Hamiltonian of M. For each $i=1,\cdots N$, and for each ${\widehat{\sigma }}_a^{(i)}$, $a=x,y,z$, they are also coupled to a thermal harmonic oscillator bath; for the case $l=\frac{1}{2}$, this was worked out by Allahverdyan et al. (2003a), Allahverdyan et al. (2003b), and Allahverdyan et al. (2013). The generalization of such a bath for arbitrary spin-$l$ is straightforward and will be applied to the spin-1 model.

2.1 Spin–spin Hamiltonian of the magnet

A quantum measurement is often assumed to be “instantaneous.” In our idealized modeling, it will take a finite time, but the tested spin will not evolve in the meantime. In other words, the spin itself is “sitting still” and waiting to be measured. Neither should it evolve during the “fast” measurement. This is realized when its Hamiltonian ${\widehat{H}}_{\text{S}}$ commutes with ${\widehat{s}}_z$; we consider the simplest case: ${\widehat{H}}_{\text{S}}=0$.

In order to have an unbiased apparatus, the Hamiltonian of the magnet should have degenerate minima and maximal symmetry. To construct such a functional, we consider, in the eigenvalue presentation, the form

$C_2={\nu }^2{\displaystyle \sum _{i,j=1}^N}\cos \frac{2\pi \left({\sigma }_i-{\sigma }_j\right)}{2l+1},\nu \equiv \frac{1}{N},(2.2)$

which is maximal in ferromagnetic states ${\sigma }_i={\sigma }_1$ $(i=2,\dots ,N)$. In general, these interactions do not seem realistic, but here, the cosine rule allows expressing this as spin–spin interactions,

$C_2={\text{co}}_l^2+{\mathrm{s}\mathrm{i}}_l^2,(2.3)$

which is bilinear in the single-spin sums

${\text{co}}_l=\frac{1}{N}{\displaystyle \sum _{i=1}^N}\cos \frac{2\pi {\sigma }_i}{2l+1}, {\mathrm{s}\mathrm{i}}_l=\frac{1}{N}{\displaystyle \sum _{i=1}^N}\sin \frac{2\pi {\sigma }_i}{2l+1}.(2.4)$

The discrete values of the spin projections allow expressing these terms in the $2l$ spin moments,

$m_k=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\sigma }_i^k,\left(k=1,\dots ,2l\right),(2.5)$

while $m_0\equiv 1$. For $l=\frac{1}{2}$, the values $s=\pm \frac{1}{2}$ imply

$\cos \pi s=0,\sin \pi s=2s.(2.6)$

Applying this for $s\to {\sigma }_i$ and summing over $i$ yields

${\text{co}}_{\frac{1}{2}}=0,{\mathrm{s}\mathrm{i}}_{\frac{1}{2}}=2m_1,m_1=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\sigma }_i.(2.7)$

In the case $l=1$, one has $s=0,\pm 1$. The rule

$\cos \frac{2\pi s}{3}=1-\frac{3}{2}{s}^2,\sin \frac{2\pi s}{3}=\frac{\sqrt{3}}{2}s,(2.8)$

leads to $s\to {\sigma }_i$ and summing over $i$ leads to

${\text{co}}_1=1-\frac{3}{2}{m}_2,{\mathrm{s}\mathrm{i}}_1=\frac{\sqrt{3}}{2}{m}_1,(2.9)$

Here, $m_2$ ranges from 0 to 1 with steps of $\nu \equiv 1/N$, while $m_1$ ranges from $-m_2$ to $m_2$ with steps of $2\nu$. At finite $N$, one can label the discrete $m_{\mathrm{1,2}}$ as

$\begin{array}{ccc}\hfill & \hfill & m_1=\left(2n_1-n_2\right)\nu ,m_2=n_2\nu ,\hfill \\ \hfill & \hfill & \left(0\le n_2\le N,0\le n_1\le n_2\right).\hfill \end{array}(2.10)$

The results for $s=\frac{3}{2}$, 2, and $\frac{5}{2}$ are given in Models.

Let out of the $N$ spins ${\sigma }_i$, a number $N_{\sigma }={\sum }_i{\delta }_{{\sigma }_i,\sigma }$ take the value $\sigma \in {\text{spec}}_l$ and let $x_{\sigma }=N_{\sigma }/N$ be their fraction. The sum rule ${\sum }_{\sigma }{N}_{\sigma }=N$ implies $m_0\equiv {\sum }_{\sigma }{x}_{\sigma }=1$. The moments read

$m_k={\displaystyle \sum _{\sigma =-l}^l}{x}_{\sigma }{\sigma }^k,k=1,\dots ,2l,(2.11)$

Inversion of these relations determines the $x_{\sigma }$ as linear combinations of the $m_k$. For $l=\frac{1}{2}$, one has

$m_1=\frac{1}{2}{x}_{\frac{1}{2}}-\frac{1}{2}{x}_{-\frac{1}{2}},x_{\pm \frac{1}{2}}=\frac{1}{2}\pm m_1.(2.12)$

For spin-1 $(l=1)$, one has

$m_1=-x_{-1}+x_1,m_2=x_{-1}+x_1.(2.13)$

With $x_{-1}+x_0+x_1=1$, their inversion reads

$x_0=1-m_2,x_{\pm 1}=\frac{m_2\pm m_1}{2}.(2.14)$

In a quantum approach, one goes to operators and sets $s\to {\widehat{s}}_z$, ${\sigma }_i\to {\widehat{\sigma }}_z^{(i)}$, and $m_k\to {\widehat{m}}_k$. For the Hamiltonian ${\widehat{H}}_{\text{M}}=N\widehat{H}$, we follow Allahverdyan et al. (2003a) and Allahverdyan et al. (2003b) and adopt the spin–spin and four–spin interactions:

${\widehat{H}}_{\text{M}}=N\widehat{H},\widehat{H}=-\frac{1}{2}{J}_2{\widehat{C}}_2-\frac{1}{4}{J}_4{\widehat{C}}_2^2.(2.15)$

Multispin interaction terms like $-\frac{1}{6}{J}_6{\widehat{C}}_2^3-\frac{1}{8}{J}_8{\widehat{C}}_2^4$ can be added without changing the overall picture.

2.2 The interaction Hamiltonian

The coupling between the tested spin S and the magnet M is chosen similar to Equation 2.2,

${\widehat{H}}_{\text{SA}}=N\widehat{I}, \widehat{I}=\frac{g}{N}{\displaystyle \sum _{i=1}^N}\cos \frac{2\pi \left({\widehat{s}}_z{\widehat{\sigma }}_z^{(i)}\right)}{2l+1},(2.16)$

where $g$ is the coupling constant. It takes the values

$\begin{array}{ll}\hfill I_s\left(\left\{{\sigma }_i\right\}\right)& =-\frac{g}{N}{\displaystyle \sum _{i=1}^N}\left(\cos \frac{2\pi s}{2l+1}\cos \frac{2\pi {\sigma }_i}{2l+1}\right.\hfill \\ \hfill & \left.+\sin \frac{2\pi s}{2l+1}\sin \frac{2\pi {\sigma }_i}{2l+1}\right),\hfill \end{array}(2.17)$

This can be expressed as a linear combination of the moments $m_1$, $\cdots$, $m_{2l}$. For $l=\frac{1}{2}$, one has

$I_s\left(m_1\right)=-4gs{m}_1,(2.18)$

and for $l=1$, denoting $\mathbf{\text{m}}=(m_1,m_2)$,

$I_s\left(\mathbf{\text{m}}\right)=-g\left[\left(1-\frac{3}{2}{s}^2\right)\left(1-\frac{3}{2}{m}_2\right)+\frac{3}{4}s{m}_1\right].(2.19)$

The total spin Hamiltonian,

$\widehat{H}={\widehat{H}}_{\text{M}}+{\widehat{H}}_{\text{SA}}={\widehat{H}}_{\text{M}}-N\widehat{I},(2.20)$

has $Z_{2l+1}$ symmetry: on the diagonal basis, a shift $s\to s+\bar{s}$ with $\bar{s}=\mathrm{1,2},\dots ,2l+1$ can be accompanied by a shift ${\sigma }_i\to {\sigma }_i+\bar{s}$ for all $i$. This is evident in the cosine expressions and implies a somewhat hidden invariance in the formulation in terms of the moments $m_k$, as discussed in Models.

2.3 Coupling to a harmonic oscillator bath

For a general spin $l$, the magnet–bath coupling is taken as the spin–boson coupling of Opus Equation 3.10,

${\widehat{H}}_{\text{MB}}\equiv \sqrt{\gamma }{\displaystyle \sum _{i=1}^N}{\sum }_{a=x,y,z}{\widehat{\sigma }}_a^{(i)}{\widehat{B}}_a^{(i)},(2.21)$

with $\gamma \ll 1$, where the bath operators read

${\widehat{B}}_a^{(i)}={\sum }_k\sqrt{c_k}\left({\widehat{b}}_{k,a}^{(i)}+{\widehat{b}}_{k,a}^{†\left(n\right)}\right),(2.22)$

for each $i,a$, there is a large set of oscillators labeled by $k$, having a common coupling parameter $c_k$. These bosons have the Hamiltonian

${\widehat{H}}_{\text{B}}={\displaystyle \sum _{i=1}^N}\sum _{a=x,y,z}\sum _k\hslash {\omega }_k{\widehat{b}}_{k,a}^{{†}^{(i)}}{\widehat{b}}_{k,a}^{(i)},(2.23)$

with the ${\omega }_k$ also identical for all $n,a$. The autocorrelation function of $B$ defines a bath kernel $K$, which is identical for all $i,a$,

$\begin{array}{ccc}\hfill & {\mathrm{t}\mathrm{r}}_{\text{B}}\left[{\widehat{R}}_{\text{B}}\left(0\right){\widehat{B}}_a^{(i)}\left(t\right){\widehat{B}}_b^{\left(j\right)}\left(t^{\prime }\right)\right]={\delta }_{i,j}{\delta }_{a,b}K\left(t-t^{\prime }\right),\hfill & \hfill \\ \hfill & {\widehat{B}}_a^{(i)}\left(t\right)\equiv e^{i{\widehat{H}}_{\text{B}}t}{\widehat{B}}_a^{(i)}{e}^{-i{\widehat{H}}_{\text{B}}t}.\hfill & \hfill \end{array}(2.24)$

Writing $c_k=c({\omega }_k)$, this leads to

$\begin{array}{ccc}\hfill K\left(t\right)& \hfill & ={\sum }_{k}c\left({\omega }_k\right)\left(\frac{e^{i{\omega }_{k}t}}{e^{\beta {\omega }_k}-1}+\frac{e^{-i{\omega }_{k}t}}{1-e^{-\beta {\omega }_k}}\right)\hfill \\ \hfill & \equiv \hfill & \frac{1}{2\pi }{\int }_{-\infty }^{+\infty }\mathrm{d}\omega e^{i\omega t}\tilde{K}\left(\omega \right).\hfill \end{array}(2.25)$

The kernel $\tilde{K}(\omega )$ can be read off and expressed in the spectral density ${\rho }_c(\omega )={\sum }_{k}c({\omega }_k)\delta (\omega -{\omega }_k)$,

$\tilde{K}\left(\omega \right)=\frac{2\pi }{|\omega |}{\rho }_c\left(\left|\omega \right|\right)\frac{\omega }{e^{\beta \omega }-1}.(2.26)$

We adopt an Ohmic spectrum with a Debye cutoff,

$\tilde{K}\left(\omega \right)=\frac{e^{-\left|\omega \right|/\mathrm{\Gamma }}}{4}\frac{\omega }{e^{\omega /T}-1},(2.27)$

where $T=1/\beta$ is the temperature of the phonon bath, and $\mathrm{\Gamma }$ the typical cutoff frequency. In Opus, we also consider a Lorentzian (power law) cutoff, for which the statics allows analytic results.

With the couplings in Equations 2.21, 2.22, and 2.23 independent of $a$, ${\widehat{H}}_{\text{MB}}$ is statistically invariant under $Z_{2l+1}$. Combined with the invariance of ${\widehat{H}}_{\text{M}}$ and ${\widehat{H}}_{\text{SA}}$, this ensures an unbiased measurement.

2.4 Evolution of the density matrix

The evolution of the density matrix of the total system is given by the Liouville–von Neumann equation. On the eigenbasis of ${\widehat{s}}_z$, its elements ${\widehat{R}}_{s\bar{s}}$ evolve independently as given in Equation 4.8 of Opus; this involves the apparatus spins and the bath. The procedure of Opus for spin $l=\frac{1}{2}$ appears to hold for general spin-$l$ operators.

Let us consider the time evolution of ${\widehat{R}}_{s\bar{s}}$ as given in Equation 4.8 of Opus (we now denote $i\to s$, $j\to \bar{s}$), where the action of the harmonic oscillator bath has been expressed in the bath kernel $K(t)$ and which involves commutators of ${\widehat{R}}_{s\bar{s}}$ with the spin operators ${\widehat{\sigma }}_a^{(i)}$, $a=x,y,z$; $i=1,\dots ,N$.

Formally, the initial state (Equation 5.4) is a constant function of the ${\widehat{\sigma }}_z^{(i)}$. In addition, ${\dot{R}}_{s\bar{s}}(t_{\text{i}})$ is a function of them, so it is consistent to assume that, at all $t$, ${\widehat{R}}_{s\bar{s}}$ only depends on the ${\widehat{\sigma }}_z^{(i)}$. As a result, the $a=z$ terms of Equation 4.8 in Opus have vanishing commutators for any spin $l$. Left with the $x,y$ commutators, we define (using the index $n$ rather than $i$ to label the ${\widehat{\sigma }}_{x,y}$)

${\widehat{\sigma }}_{\pm }^{(n)}={\widehat{\sigma }}_x^{(n)}\pm i{\widehat{\sigma }}_y^{(n)}.(2.28)$

Because ${\sum }_{ax,y}{\widehat{\sigma }}_a^{(n)}\widehat{O}{\widehat{\sigma }}_a^{(n)}=\frac{1}{2}{\sum }_{\alpha =\pm 1}{\widehat{\sigma }}_{\alpha }^{(n)}\widehat{O}{\widehat{\sigma }}_{-\alpha }^{(n)}$ for any operator $\widehat{O}$, Equation 4.8 in Opus takes the form

$\begin{array}{ccc}\hfill & \hfill & \frac{\mathrm{d}{\widehat{R}}_{s\bar{s}}\left(t\right)}{\mathrm{d}t}=-i{\widehat{H}}_s{\widehat{R}}_{s\bar{s}}\left(t\right)+i{\widehat{R}}_{s\bar{s}}\left(t\right){\widehat{H}}_{\bar{s}}\hfill \\ \hfill & \hfill & +\frac{\gamma }{2}\sum _{\alpha ,\beta =\pm 1}{\displaystyle \sum _{n=1}^N}{\int }_0^t\text{d}uK\left(\beta u\right){\widehat{C}}_{s\bar{s},\beta }^{\left(\alpha ,n\right)}\left(u\right),\hfill \end{array}(2.29)$

where

$\begin{array}{ccc}\hfill & \hfill & {\widehat{C}}_{s\bar{s},+}^{\left(\alpha ,n\right)}\left(u\right)=\left[e^{-iu{\widehat{H}}_s}{\widehat{\sigma }}_{-\alpha }^{(n)}{e}^{iu{\widehat{H}}_s}{\widehat{R}}_{s\bar{s}}\left(t\right),{\widehat{\sigma }}_{\alpha }^{(n)}\right],\hfill \\ \hfill & \hfill & {\widehat{C}}_{s\bar{s},-}^{\left(\alpha ,n\right)}\left(u\right)=\left[{\widehat{\sigma }}_{-\alpha }^{(n)},{\widehat{R}}_{s\bar{s}}\left(t\right)e^{-iu{\widehat{H}}_{\bar{s}}}{\widehat{\sigma }}_{\alpha }^{(n)}{e}^{iu{\widehat{H}}_{\bar{s}}}\right],\hfill \end{array}(2.30)$

are commutators involving the Hamiltonian of M coupled to S in state $s$, without the bath, viz.

${\widehat{H}}_s={\widehat{H}}_{\text{M}}+{\widehat{H}}_{\text{SA}}^s=NH\left({\widehat{m}}_1\right)+N{I}_s\left({\widehat{m}}_1\right).(2.31)$

The action of the bath is expressed in the kernel $K(\pm u)$, with the smallness of $\gamma$ allowing truncation at its first order. Equations 2.29, 2.30 are valid for general spin $l=\frac{1}{2},1,\frac{3}{2},\cdots$.

Most importantly, the ${\widehat{R}}_{s\tilde{s}}$ are decoupled in the separate $s,\bar{s}$ sectors, a property of ideal measurement but absent in general. Examples of these non-idealities are a spin S having nontrivial dynamics during the measurement and a biased measurement, in which the Hamiltonian of the magnet and/or the bath depends on the state of S.

2.5 Physical implementation of the model

The spin-$\frac{1}{2}$ Curie–Weiss model for quantum measurement (Allahverdyan A. et al., 2003) was initially conceived as a tool to understand the dominant physical aspects of idealized quantum measurements. It has served this purpose well. Let us look here at possible realizations of the model.

Curie–Weiss models are mean-field types of spin models. Their distance-independent couplings apply to a small magnetic grain. The grain need not be very large. From studies of spin glasses and cluster glasses, it is known that “fat spins,” clusters of hundreds or thousands of coherent spins, are easily detectable (Mydosh, 1993).

The Ising nature of the couplings refers to fairly anisotropic spin–spin interactions. For spin $\frac{1}{2}$, Equation 2.15 expresses the pair and quartet couplings between the $z$-components of the spins. Multispin interactions are a natural result of the overlap of electronic orbits; here, they are approximated as not decaying with the distance between the spins in the grain. How reasonable this approximation is must be considered in each separate application. The main feature of our modeling, a first-order phase transition in the magnet, suggests that it represents a large class of short-range systems. This is underlined by the model’s support of the Copenhagen postulates of collapse and Born probabilities.

These features also hold for the spin-1 Curie–Weiss model. However, on top of this, Equation 2.8 produces the combination ${\widehat{\mathrm{\Sigma }}}_i\equiv {\widehat{\sigma }}_z^{(i)2}-2/3$, which takes the values $1/3$ for the “out-of-plane” cases ${\sigma }_i=\pm 1$ and $-2/3$ for the “in-plane” case ${\sigma }_i=0$. Separate-spin terms of the form ${\sum }_{i}D{\widehat{\sigma }}_z^{(i)2}$ are well known, stemming from crystal fields. For the apparatus, the ${\text{co}}_1^2$ term of Equation 2.3 relates to the interaction ${\sum }_{ij}{\widehat{\mathrm{\Sigma }}}_i{\widehat{\mathrm{\Sigma }}}_j$ between the ${\widehat{\mathrm{\Sigma }}}_i$, so it involves both the aforementioned $D$-term and also the terms ${\widehat{\sigma }}_z^{(i)2}{\widehat{\sigma }}_z^{(j)2}$. How to implement these crystal-field-type spin–spin interactions in practice is an open question.

Concerning numerical implementations, Donker et al. (2018)’s approximation of the Curie–Weiss model can be generalized to higher spin.

3 The spin $\frac{1}{2}$ case revisited

3.1 Elements of the statics

We set the stage by considering the spin-$\frac{1}{2}$ situation, the original Curie–Weiss model for quantum measurement in slightly adapted notation³. The spin operators are ${\widehat{\sigma }}_{x,y,z}$, with ${\widehat{\sigma }}_z=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}(\frac{1}{2},-\frac{1}{2})$. It holds that $[{\widehat{\sigma }}_a,{\widehat{\sigma }}_b]=i{\epsilon }_{\mathit{abc}}{\widehat{\sigma }}_c$ and ${\widehat{\sigma }}_x^2+{\widehat{\sigma }}_y^2+{\widehat{\sigma }}_z^2=\frac{3}{4}{\widehat{\sigma }}_0$ with ${\widehat{\sigma }}_0=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}(\mathrm{1,1})$.

The magnet has $N$ these spins ${\widehat{\sigma }}_{x,y,z}^{(i)}$, $i=\mathrm{1,2},\dots ,N$. They have magnetization operator

${\widehat{M}}_1=N{\widehat{m}}_1,{\widehat{m}}_1=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\widehat{\sigma }}_z^{(i)},(3.1)$

taking eigenvalues $-\frac{1}{2}\le m_1\le \frac{1}{2}$. In the paramagnetic state, $m_1=0$. The Hamiltonian is taken as pair and quartet interactions,

${\widehat{H}}_{\text{M}}=N\widehat{H},\widehat{H}=-2J_2{\widehat{m}}_1^2-4J_4{\widehat{m}}_1^4.(3.2)$

With ${\widehat{x}}_{\sigma }={\widehat{N}}_{\sigma }/N$, it holds that

${\widehat{m}}_1=\frac{1}{2}{\widehat{x}}_{1/2}-\frac{1}{2}{\widehat{x}}_{-1/2},{\widehat{x}}_{\pm 1/2}=\frac{1}{2}\widehat{I}\pm {\widehat{m}}_1.(3.3)$

The spins have eigenvalues ${\sigma }_i=\pm \frac{1}{2}$, so that ${\widehat{m}}_1$ has eigenvalues $m_1=\nu {\sum }_i{\sigma }_1$ ranging from $-\frac{1}{2}$ to $\frac{1}{2}$ with steps of $\nu$.

3.2 The interaction Hamiltonian

To use the magnet coupled to its bath as an apparatus for a quantum measurement, a system–apparatus (SA) coupling is needed. According to Equation 2.18, it is chosen as a spin–spin coupling,

${\widehat{H}}_{\text{SA}}=-4g{\displaystyle \sum _{i=1}^N}\widehat{s}{\widehat{\sigma }}_z^{(i)}=-4gN\widehat{s}{\widehat{m}}_1,(3.4)$

and takes the values $H_{\text{SA}}^s(m_1)=-4gsN{m}_1$. The full Hamiltonian of S + A in the sector $s$ thus reads

${\widehat{H}}_s=-2J_{2}N{\widehat{m}}_1^2-4J_{4}N{\widehat{m}}_1^4-4gsN{\widehat{m}}_1.(3.5)$

The eigenvalues of ${\widehat{s}}_z$ are $s=\pm \frac{1}{2}$ and those of ${\widehat{\sigma }}_z^{(i)}$ are ${\sigma }_i=\pm \frac{1}{2}$, so that ${\widehat{m}}_1$ has the eigenvalues $\nu {\sum }_{i=1}^N{\sigma }_i$. The degeneracy of a state with magnetization $m_1$ is

$G_N=\frac{N!}{N_{-\frac{1}{2}}!N_{\frac{1}{2}}!}=\frac{N!}{\left(N{x}_{-\frac{1}{2}}\right)!\left(N{x}_{\frac{1}{2}}\right)!},(3.6)$

and entropy $S_N=\log G_N$. At large $N$, we get the standard result for the entropy $S_N=NS$ with

$S=\frac{1-2m_1}{2}\log \frac{1-2m_1}{2}-\frac{1+2m_1}{2}\log \frac{1+2m_1}{2}.(3.7)$

Combining Equation 3.5 and Equation 3.6, the free energy in the $s$-sector reads

$\begin{array}{ccc}\hfill & \hfill & F_s\left(m_1\right)=-2J_{2}N{m}_1^2-4J_{4}N{m}_1^4\hfill \\ \hfill & \hfill & -4gsN{m}_1-T\log G_N\left(m_1\right),\hfill \end{array}(3.8)$

which yields, for large $N$,

$\frac{F_s}{N}=-2J_2{m}_1^2-4J_4{m}_1^4-4gs{m}_1-TS\left(m_1\right).(3.9)$

3.3 Dynamics of the spin $\frac{1}{2}$ model

At the initial time $t_{\text{i}}$ of the measurement, the state of the tested system, S, here $\widehat{\mathbf{s}}$, a spin-$\frac{1}{2}$ operator, is described by its $2\times 2$ density matrix $\widehat{r}(t_{\text{i}})$ with elements $r_{s\bar{s}}(t_{\text{i}})$ for $s,\bar{s}=\pm \frac{1}{2}$. The magnet M has $N\gg 1$ quantum spins-$\frac{1}{2}$ ${\widehat{\sigma }}^{(i)}$ $(i=1,\dots ,N)$. In each $s,\bar{s}$ sector, S + M lie in the state ${\widehat{R}}_{s\bar{s}}(t)={\widehat{R}}_{\bar{s}s}^{†}(t)$, which is an operator that can be represented by a $2^N\times 2^N$ matrix. At $t_{\text{i}}$, M is assumed to lie in the paramagnetic state wherein the spins are fully disordered and uncorrelated. Multiplying by the respective element of $\widehat{r}(t_{\text{i}})$ leads to the elements of the initial density matrix of S + M

${\widehat{R}}_{s\bar{s}}\left(t_{\text{i}}\right)=r_{s\bar{s}}\left(t_{\text{i}}\right)\frac{{\widehat{\sigma }}_0^{(1)}}{2}\otimes \frac{{\widehat{\sigma }}_0^{(2)}}{2}\otimes \cdots \otimes \frac{{\widehat{\sigma }}_0^{(N)}}{2}.(4.1)$

3.4 Truncation for spin $\frac{1}{2}$

The dynamics of the off-diagonal elements (cat terms) were worked out in Opus. In the relevant short-time domain, the spin–spin couplings are ineffective; therefore, it suffices to study independent spins coupled by the interaction Hamiltonian and the bath. These elements vanish dynamically, truncating the density matrix $\widehat{R}$ to a form diagonal on the eigenbasis of ${\widehat{s}}_z$. There is no reason to repeat that here; for spin-1, this will be worked out in Section 4.1.

3.5 Registration for spin $\frac{1}{2}$

Registration of the measurement is described by the evolution of the diagonal elements of the density matrix of the full system. For the situation of higher spin, it is instructive to reconsider and slightly reformulate the spin $\frac{1}{2}$ situation.

For $\bar{s}=s$, the Hamiltonian terms drop out of Equation 2.29; hence, the dynamics are a relaxation set by

$\begin{array}{ccc}\hfill & \hfill & \frac{\mathrm{d}{\widehat{R}}_{ss}\left(t\right)}{\mathrm{d}t}=\frac{\gamma }{2}\sum _{\alpha ,\beta =\pm 1}{\displaystyle \sum _{n=1}^N}{\int }_0^t\text{d}uK\left(\beta u\right){\widehat{C}}_{ss,\beta }^{\left(\alpha ,n\right)}\left(u\right).\hfill \\ \hfill & \hfill & \hfill \end{array}(4.2)$

For $l=\frac{1}{2}$, the spin operators ${\widehat{\sigma }}_{x,y,z}$ anticommute; hence, for any function $f$ of the ${\widehat{\sigma }}_z^{(i)}$, it holds that

$\begin{array}{ccc}\hfill {\widehat{\sigma }}_{\alpha }^{(n)}f\left(\left\{{\widehat{\sigma }}_z^{(i)}\right\}\right)& =\hfill & \widehat{f}\left(\left\{{\left(-1\right)}^{{\delta }_{i,n}}{\widehat{\sigma }}_z^{(i)}\right\}\right){\widehat{\sigma }}_{\alpha }^{(n)}\hfill \\ \hfill & \equiv \hfill & f^{(n)}\left(\left\{{\widehat{\sigma }}_z^{(i)}\right\}\right){\widehat{\sigma }}_{\alpha }^{(n)}.\hfill \end{array}(4.3)$

This brings the ${\widehat{\sigma }}_{\alpha }^{(n)}$ and ${\widehat{\sigma }}_{-\alpha }^{(n)}$ next to each other, which allows to eliminate them using the sum ${\sum }_{\alpha =\pm 1}{\widehat{\sigma }}_{\alpha }^{(n)}{\widehat{\sigma }}_{-\alpha }^{(n)}={\widehat{\sigma }}_0^{(n)}$. With only functions of the ${\widehat{\sigma }}_z^{(i)}$ $(i=1,\dots ,N)$ remaining, we can go to their diagonal bases to work with scalar functions of their eigenvalues ${\sigma }_i=\pm \frac{1}{2}$ (see also Opus, Section 4.4). This expresses Equation 2.30 as

$\begin{array}{ccc}\hfill & \hfill & C_{s\bar{s},+}^{(n)}\left(u\right)\equiv \sum _{\alpha =\pm 1}{C}_{s\bar{s},+}^{\alpha n}\left(u\right)\hfill \\ \hfill & \hfill & =e^{-iu{H}_s}{e}^{iu{H}_s^{(n)}}{R}_{s\bar{s}}^{(n)}\left(t\right)-e^{-iu{H}_s^{(n)}}{e}^{iu{H}_s}{R}_{s\bar{s}}\left(t\right),\hfill \\ \hfill & \hfill & C_{s\bar{s},-}^{(n)}\left(u\right)\equiv \sum _{\alpha =\pm 1}{C}_{s\bar{s},-}^{\alpha n}\left(u\right)\hfill \\ \hfill & \hfill & =R_{s\bar{s}}^{(n)}\left(t\right)e^{-iu{H}_{\bar{s}}^{(n)}}{e}^{iu{H}_{\bar{s}}}-R_{s\bar{s}}\left(t\right)e^{-iu{H}_{\bar{s}}}{e}^{iu{H}_{\bar{s}}^{(n)}},\hfill \end{array}(4.4)$

where for any function $f(\{{\sigma }_i\})$, $f^{(n)}$ has the sign of ${\sigma }_n$ reversed,

$f^{(n)}\left(\left\{{\sigma }_i\right\}\right)=f\left(\left\{{\left(-1\right)}^{{\delta }_{i,n}}{\sigma }_i\right\}\right).(4.5)$

We employed the obvious rules ${(fg)}^{(n)}=f^{(n)}{g}^{(n)}$ and ${[f(g)]}^{(n)}=f(g^{(n)})$. The terms in Equation 4.4, being scalars, yield the relation $C_{s\bar{s},-}^{(n)}(u)=C_{s\bar{s},+}^{(n)}(-u)$, which allows combining the integrals of Equations 2.29 and 2.30 as a single one from $u=-t$ to $t$. Because $\gamma \ll 1$, the typical scale of $t$, the registration time $1/\gamma T$ is much larger than the bath equilibration time $1/T$. Hence, we may now take the integral over the entire real axis to arrive at the Fourier-transformed kernel $\bar{K}(\omega )$ at specific frequencies.

The next step is to reduce the $2^N\times 2^N$ matrix problem to a problem of $N+1$ variables by considering $R_{ss}(\{{\sigma }_i\})=R_{ss}(m_1)$ to be functions of the order parameter $m_1=\nu \sum {\sigma }_i$. This is formally true at $t_{\text{i}}$ and valid for ${\dot{R}}_{s\bar{s}}(t_{\text{i}})$; hence, it remains valid over time. Denoting $P_s(m_1)$ as the probability that $R_{ss}(\{{\sigma }_i\})/r_{ss}(t_{\text{i}})$ involves $m_1=\nu {\sum }_i{\sigma }_i$, it picks up the degeneracy number $G_N$ in Equation 3.6 of realizations $\{{\sigma }_i\}$ with the same $m_1$,

$P_s\left(m_1\right)=G_N\left(m_1\right)\frac{R_{ss}\left(m_1\right)}{r_{ss}\left(t_{\text{i}}\right)}.(4.6)$

To obtain the evolution of ${\dot{P}}_s$, we multiply Equation 4.2 by $G_N(m_1)/r_{ss}(t_{\text{i}})$. At given $m_1$, one has $m_1^{(n)}=m_1-2\nu {\sigma }_n$, so we can split the terms with ${\sigma }_n=\frac{1}{2}$ (and $-\frac{1}{2}$) and perform the sum over $n$. The fraction of terms that flips an up spin ${\sigma }_n=\frac{1}{2}$ is $x_{\frac{1}{2}}(m_1)$, which multiplies $P(m_1-\nu )$; flipping a down spin ${\sigma }_n=-\frac{1}{2}$ happens with probability $x_{-\frac{1}{2}}(m_1)$, which multiplies $P(m_1+\nu )$. Due to Equation 4.6, these $P$s involve the ratios

$\begin{array}{ccc}\hfill & \hfill & \frac{G_N\left(m_1\right)}{G_N\left(m_1-\nu \right)}=\frac{x_{-\frac{1}{2}}\left(m_1-\nu \right)}{x_{\frac{1}{2}}\left(m_1\right)},\hfill \\ \hfill & \hfill & \frac{G_N\left(m_1\right)}{G_N\left(m_1+\nu \right)}=\frac{x_{\frac{1}{2}}\left(m_1+\nu \right)}{x_{-\frac{1}{2}}\left(m_1\right)},\hfill \end{array}(4.7)$

which has the effect of eliminating the $x_{\pm \frac{1}{2}}(m_1)$. Introducing the operators $E_{\pm }$ and ${\mathrm{\Delta }}_{\pm }=E_{\pm }-1$ by

$\begin{array}{ccc}\hfill & \hfill & E_{\pm }f\left(m_1\right)=f\left(m_1\pm \nu \right),\hfill \\ \hfill & \hfill & {\mathrm{\Delta }}_{\pm }f\left(m_1\right)=f\left(m_1\pm \nu \right)-f\left(m_1\right),\hfill \end{array}(4.8)$

the evolution of $P_s$ gets condensed as

$\begin{array}{ccc}\hfill & \hfill & {\dot{P}}_s\left(m_1\right)=\frac{\gamma N}{2}\hfill \\ \hfill & \hfill & \sum _{\alpha =\pm 1}{\mathrm{\Delta }}_{\alpha }\left\{x_{\frac{1}{2}\alpha }\left(m_1\right)\tilde{K}\left[{\mathrm{\Omega }}_{s\alpha }\left(m_1\right)\right]P_s\left(m_1\right)\right\}.\hfill \end{array}(4.9)$

where

${\mathrm{\Omega }}_{s\pm }\left(m_1\right)={\mathrm{\Delta }}_{\mp }{H}_s=H_s\left(m_1\mp \nu \right){-H}_s\left(m_1\right).(4.10)$

This is now a problem for $N+1$ functions $P(m_1;t)$ subject to the normalization ${\sum }_{m_1}P(m_1;t)=1$.

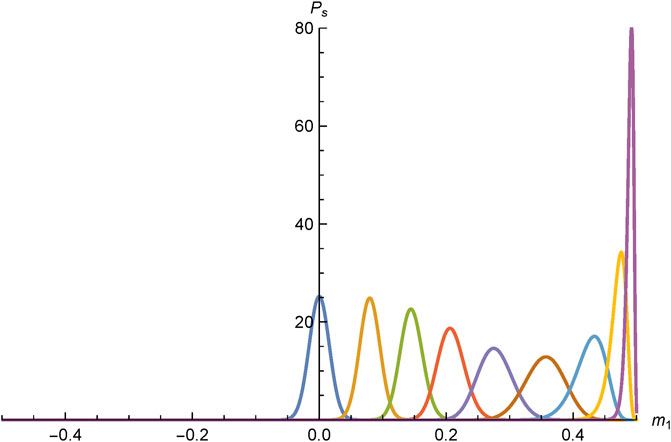
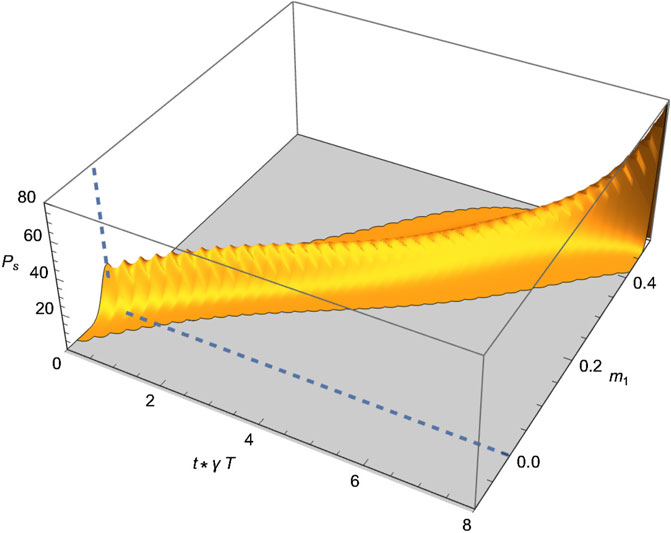
In Figure 1, the distribution of the magnetization $m_1$ is depicted at various times. In Figure 2, this evolution is represented in a $3d$ plot.

Figure 1

Figure 1. Evolution of the magnetization distribution $P_s(m_1;t)$ for $s=+\frac{1}{2}$ at times $\mathrm{0,1},\dots ,8$ in units of $1/\gamma T$. The paramagnetic state at $t=0$ is peaked around $m_1=0$; the coupling between S and A moves the peak toward $m_1=+\frac{1}{2}$. In doing so, it first broadens and later narrows significantly.

Figure 2

Figure 2. The case of Figure 1 plotted in $3d$ at intervals $\mathrm{\Delta }t=0.2/\gamma T$.

3.6 $H$-theorem and relaxation to equilibrium

The dynamical entropy of the distribution $P_s(m_1;t)=G_N(m_1)R_{ss}(\{{\sigma }_i\};t)/r_{ss}(t_{\text{i}})$ is defined as

$\begin{array}{ccc}\hfill S_s\left(t\right)& \hfill & =-\mathrm{T}\mathrm{r}\frac{{\widehat{R}}_{ss}\left(t\right)}{r_{ss}\left(t_{\text{i}}\right)}\log \frac{{\widehat{R}}_{ss}\left(t\right)}{r_{ss}\left(t_{\text{i}}\right)}\hfill \\ \hfill & \hfill & =-\sum _{m_1}{P}_s\left(m_1;t\right)\log \frac{P_s\left(m_1;t\right)}{G_N\left(m_1\right)}.\hfill \end{array}(4.11)$

As in Opus, we introduce a dynamical free energy:

$\begin{array}{ccc}\hfill & \hfill & F_{\text{dyn}}^s\left(t\right)=U_s\left(t\right)-T{S}_s\left(t\right)\hfill \\ \hfill & \hfill & =\sum _{m_1}{P}_s\left(m_1;t\right)\left[H_s\left(m_1\right)+T\log \frac{P_s\left(m_1;t\right)}{G_N\left(m_1\right)}\right],\hfill \end{array}(4.12)$

which adds the $P_s\log P_s$ term to the average of the free energy functional $F_N(m_1)=H_s(m_1)-T{S}_N(m_1)$. With $\beta =1/T$, Equation 5.36 yields.

${\dot{F}}_{\text{dyn}}^s=T\sum _{m_1}{\dot{P}}_s\left(m_1\right)\log \frac{P_s\left(m_1\right)e^{\beta H_s\left(m_1\right)}}{G_N\left(m_1\right)}$

$=\frac{\gamma NT}{2}\sum _{\alpha =\pm 1}\sum _{m_1}{\mathrm{\Delta }}_{\alpha }\left[x_{\frac{1}{2}\alpha }\tilde{K}\left({\mathrm{\Omega }}_{s\alpha }\right)P_s\right]\log \frac{P_s{e}^{\beta H_s}}{G_N}.$

For general functions $f_{\mathrm{1,2}}(m_1)$ and $\alpha =\pm 1$, partial summation yields

$\begin{array}{ccc}\hfill & \hfill & \sum _{m_1}\left({\mathrm{\Delta }}_{\alpha }{f}_1\right)f_2=\sum _{m_1}{f}_1\left({\mathrm{\Delta }}_{-\alpha }{f}_2\right)=\hfill \\ \hfill & \hfill & \sum _{m_1}{E}_{\alpha }\left[f_1\left({\mathrm{\Delta }}_{-\alpha }{f}_2\right)\right]=-\sum _{m_1}\left(E_{\alpha }{f}_1\right)\left({\mathrm{\Delta }}_{\alpha }{f}_2\right).\hfill \end{array}(4.13)$

provided that the boundary terms $f_{\mathrm{1,2}}(m_{\pm }^{\nu })$ at $m_{\pm }^{\nu }=\pm (1+\nu )$ vanish. As discussed, this holds for $P_s$ but also for the logarithm in Equation 4.13 because we may insert a factor $(1-{\delta }_{m_1,m^{\nu }}-{\delta }_{m_1,-m^{\nu }})$ that makes this explicit. For $\alpha =+1$, we now use the last expression, and for $\alpha =-1$, we use the second one, which yields, also using Equation 4.10 and the property $\tilde{K}(-\omega )=\tilde{K}(\omega )e^{\beta \omega }$ satisfied in (Equations 2.26, 2.27), the result

$\begin{array}{ccc}\hfill & \hfill & {\dot{F}}_{\text{dyn}}^s=-\gamma NT{\sum }_{m_1}\tilde{K}\left({\mathrm{\Delta }}_{+}{H}_s\right)\times \hfill \\ \hfill & \hfill & \left\{e^{{\mathrm{\Delta }}_{+}\beta H_s}\left(E_{+}{x}_{\frac{1}{2}}\right)\left(E_{+}{P}_s\right)x_{-\frac{1}{2}}{P}_s\right\}{\mathrm{\Delta }}_{+}\log \frac{P_s{e}^{\beta H_s}}{G_N}.\hfill \end{array}(4.14)$

The various $x$–factors are such that a term $G_N(m_1)x_{-\frac{1}{2}}$ can be factored out to yield

$\begin{array}{ccc}\hfill & \hfill & {\dot{F}}_{\text{dyn}}^s=-\gamma NT{\sum }_{m_1}{\sum }_{\beta =\pm 1}{G}_N{x}_{-\frac{1}{2}}\tilde{K}\left({\mathrm{\Delta }}_{+}{H}_s\right)\hfill \\ \hfill & \hfill & \times \left\{e^{{\mathrm{\Delta }}_{+}\beta H_s}\left(E_{+}\frac{P_s}{G_N}\right)\frac{P_s}{G_N}\right\}{\mathrm{\Delta }}_{+}\log \frac{P_s{e}^{\beta H_s}}{G_N}.\hfill \end{array}(4.15)$

With ${\mathrm{\Delta }}_{+}{H}_s=E_{+}{H}_s-H_s$, $G_N=\exp (S_N)$ and $F_s(m_1)=H_s(m_1)-T{S}_N(m_1)$, this can finally be expressed as

$\begin{array}{ccc}\hfill & \hfill & {\dot{F}}_{\text{dyn}}^s\left(t\right)=-\gamma NT{\sum }_{m_1}{x}_{-\frac{1}{2}}\tilde{K}\left({\mathrm{\Delta }}_{+}{H}_s\right)e^{-\beta F_s}\hfill \\ \hfill & \hfill & \times \left({\mathrm{\Delta }}_{+}\frac{P_s}{e^{-\beta F_s}}\right)\left({\mathrm{\Delta }}_{+}\log \frac{P_s}{e^{-\beta F_s}}\right).\hfill \end{array}(4.16)$

The last factors have the form $(x^{\prime }-x)\log (x^{\prime }/x)$, which is nonnegative, so that $F_{\text{dyn}}^s$ is a decreasing function of time. Dynamic equilibrium occurs when these factors vanish, which happens when the magnet has reached the thermodynamic equilibrium set by the Gibbs state $P_s=e^{-\beta F_s}/Z_s$ and ${\widehat{R}}_{ss}=e^{-\beta {\widehat{H}}_s}/Z_s$, with $Z_s={\sum }_{m_1}\exp (-\beta F_s)={\sum }_{m_1}{G}_N(m_1)\exp (-\beta H_s)=\mathrm{T}\mathrm{r}\exp (-\beta {\widehat{H}}_s)$, as usual. The dynamical free energy (Equation 4.12) indeed ends up at the thermodynamic one,

$F_{\text{dyn}}^s\left(\infty \right)=-T\log Z_s=F_s\left(g\right).(4.17)$

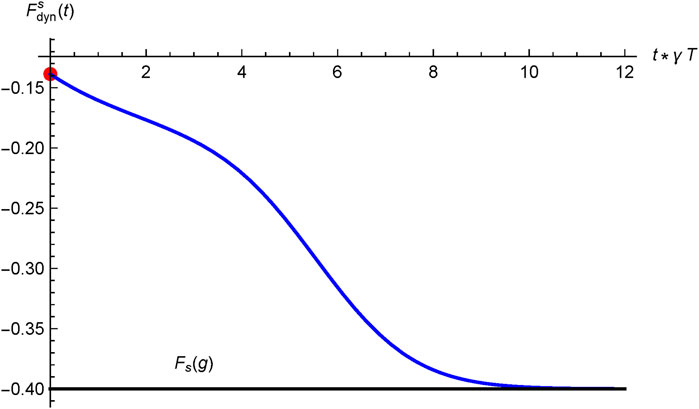
This constitutes an example of the apparatus going dynamically to its lowest thermodynamic state and the pointer state indicating the measurement outcome $s=\pm \frac{1}{2}$. The temporal evolution from $F_{\mathit{\text{dyn}}}(0)$ to $F_s(g)$ is depicted in Figure 3.

Figure 3

Figure 3. Evolution of the dynamical free energy $F_{\text{dyn}}^s(t)$, identical in both sectors $s=\pm \frac{1}{2}$, after coupling the apparatus to a spin-$\frac{1}{2}$ at time $t=0$. Its approach to the Gibbs state with $F_s(g)$ (bottom line), exponential in $t$, expresses the registration of the measurement.

3.7 Decoupling the apparatus

Near the end of the measurement, at a suitable time $t_{\text{dc}}$, the apparatus is decoupled from the system, by setting $g=0$; in doing so, an energy $U_{\text{dc}}=-{\sum }_{m_1}{P}_s(m_1;t_{\text{dc}})H_{\text{SA}}(m_1)$ must be supplied to the magnet, which will then relax further its nearby minimum of the $g=0$ situation, to provide a stable pointer indication with a macroscopic order parameter $M_1=N{m}_1$ that can be read off.

4 Dynamics of the spin-1 model

We now focus on the spin-1 case, in which the tested system, S, is $\widehat{\mathbf{s}}$, a spin-1 operator with ${\widehat{s}}_z$ having eigenvalues $s_z=-\mathrm{1,0,1}$. Our magnet M has $N\gg 1$ quantum spins-1 ${\widehat{\sigma }}^{(i)}$ $(i=1,\dots ,N)$. According to Equation 2.5, one now deals with two order parameters,

${\widehat{m}}_1=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\widehat{\sigma }}_i,{\widehat{m}}_2=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\widehat{\sigma }}_i^2.(5.1)$

While ${\widehat{m}}_1$ is the usual magnetization in the $z$-direction, ${\widehat{m}}_2$ is a spin-anisotropy order parameter that discriminates the sectors with eigenvalues ${\sigma }_i=\pm 1$ from the sector with eigenvalues ${\sigma }_i=0$.

The quantity ${\widehat{C}}_2$, the operator-form of Equation 2.2, is our starting point for a permutation-invariant Hamiltonian that ensures unbiased measurement. Expanding the cosine, employing Equation 2.8 for each spin ${\widehat{\sigma }}_i$, and summing over $i$ yields a polynomial in the moments ${\widehat{m}}_{\mathrm{1,2}}$,

${\widehat{C}}_2={\left(1-\frac{3}{2}{\widehat{m}}_2\right)}^2+\frac{3}{4}{\widehat{m}}_1^2.(5.2)$

For the Hamiltonian, we take as in Equation 3.2

${\widehat{H}}_N=N\widehat{H},\widehat{H}=-\frac{1}{2}{J}_2{\widehat{C}}_2-\frac{1}{4}{J}_4{\widehat{C}}_2^2.(5.3)$

It can be understood as containing the single-spin term ${\widehat{m}}_2$, the pair couplings ${\widehat{m}}_1^2=1/N^2{\sum }_{ij}{\widehat{\sigma }}_i{\widehat{\sigma }}_j$ and ${\widehat{m}}_2^2=1/N^2{\sum }_{ij}{\widehat{\sigma }}_i^2{\widehat{\sigma }}_j^2$, the triplet couplings ${\widehat{m}}_1^2{\widehat{m}}_2$ and the quartet couplings ${\widehat{m}}_1^4$, ${\widehat{m}}_1^2{\widehat{m}}_2^2$, and ${\widehat{m}}_2^4$. However, note its different conception in Section 2.5.

At the initial time $t_{\text{i}}$ of the measurement, its state is described by its $3\times 3$ density matrix $\widehat{r}(t_{\text{i}})$ with elements $r_{s\bar{s}}(t_{\text{i}})$ for $s,\bar{s}=-\mathrm{1,0,1}$.

In each $s,\bar{s}$ sector, M lies in its state ${\widehat{R}}_{s\bar{s}}(t)={\widehat{R}}_{\bar{s}s}^{†}(t)$, which is an operator that can be represented by a $3^N\times 3^N$ matrix. This exponential problem gets transformed into a polynomial one, a step that is exact for the considered mean-field-type Hamiltonian.

At $t_{\text{i}}$, M is assumed to lie in a paramagnetic state, wherein the spins are fully disordered and uncorrelated. For each spin, its state is thus ${\widehat{\sigma }}_0^{(i)}/3$ where ${\widehat{\sigma }}_0^{(i)}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}(\mathrm{1,1,1})$. Multiplying by the respective element of $\widehat{r}(t_{\text{i}})$ leads to the elements of the initial density matrix of S + M in the $s,\bar{s}=0,\pm 1$ sector,

${\widehat{R}}_{s\bar{s}}\left(t_{\text{i}}\right)=r_{s\bar{s}}\left(t_{\text{i}}\right)\frac{{\widehat{\sigma }}_0^{(1)}}{3}\otimes \frac{{\widehat{\sigma }}_0^{(2)}}{3}\cdots \otimes \frac{{\widehat{\sigma }}_0^{(N)}}{3}.(5.4)$

For general angular momentum, the commutation relations $[{\widehat{L}}_a,{\widehat{L}}_b]=i{\epsilon }_{\mathit{abc}}{\widehat{L}}_c$ and ${\widehat{L}}_x^2+{\widehat{L}}_y^2+{\widehat{L}}_z^2=l(ł+1)\widehat{I}$ carry over to general spin

$\left[{\widehat{\sigma }}_a,{\widehat{\sigma }}_b\right]=i{\epsilon }_{\mathit{abc}}{\widehat{\sigma }}_c,{\widehat{\sigma }}_x^2+{\widehat{\sigma }}_y^2+{\widehat{\sigma }}_z^2=l\left(l+1\right){\widehat{\sigma }}_0,(5.5)$

While we considered $l=\frac{1}{2}$ in Section 3, we now focus on $l=1$.

We proceed as for spin $\frac{1}{2}$. The $a=z$ commutator in Equation 2.29 does again not contribute. We introduce ${\widehat{\sigma }}_{\alpha }={\widehat{\sigma }}_x+i\alpha {\widehat{\sigma }}_y$ for $\alpha =\pm 1$. From Equation 5.5, it follows for general $l$ that

$\begin{array}{ccc}\hfill & \hfill & {\widehat{\sigma }}_{\alpha }{\widehat{\sigma }}_{-\alpha }=l\left(l+1\right){\widehat{\sigma }}_0+\alpha {\widehat{\sigma }}_z-{\widehat{\sigma }}_z^2\hfill \\ \hfill & \hfill & {\left({\widehat{\sigma }}_{\alpha }{\widehat{\sigma }}_{-\alpha }\right)}_{\sigma {\sigma }^{\prime }}=\left(l+1-\alpha \sigma \right)\left(l+\alpha \sigma \right){\delta }_{\sigma {\sigma }^{\prime }}.\hfill \end{array}(5.6)$

In the present case $l=1$, this has nontrivial values

${\left({\widehat{\sigma }}_{\alpha }{\widehat{\sigma }}_{-\alpha }\right)}_{\sigma \sigma }=2{\delta }_{\sigma ,\alpha }+2{\delta }_{\sigma ,0},\left(\sigma =0,\pm 1\right),(5.7)$

with Equation 5.6 implying that the $\sigma =-\alpha$ term indeed drops out. The SO(3) generators

$\begin{array}{ccc}\hfill & \hfill & {\widehat{\sigma }}_x=\frac{1}{\sqrt{2}}\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right),{\widehat{\sigma }}_y=\frac{1}{\sqrt{2}}\left(\begin{array}{ccc}\hfill 0\hfill & \hfill -i\hfill & \hfill 0\hfill \\ \hfill i\hfill & \hfill 0\hfill & \hfill -i\hfill \\ \hfill 0\hfill & \hfill i\hfill & \hfill 0\hfill \end{array}\right),\hfill \\ \hfill & \hfill & \hfill \\ \hfill & \hfill & {\widehat{\sigma }}_z=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill \end{array}\right),\hfill \end{array}(5.8)$

allow verifying these relations. Each of the ${\widehat{\sigma }}^{(i)}$ $(i=1,\dots ,N)$ has such a presentation. In Equation 2.30, the interchange of the ${\widehat{\sigma }}_{\alpha }^{(i)}$ with the ${\widehat{\sigma }}_z^{(n)}$ will be needed. For $i\ne n$, they commute, while for $i=n$,

$\begin{array}{ccc}\hfill & \hfill & {\widehat{\sigma }}_{\alpha }^{\left(n\right)}{\widehat{\sigma }}_z^{\left(n\right)k}={\left({\widehat{\sigma }}_z^{(n)}-\alpha {\widehat{\sigma }}_0^{(n)}\right)}^k{\widehat{\sigma }}_{\alpha }^{\left(n\right)},\hfill \\ \hfill & \hfill & {\widehat{\sigma }}_z^{(n)k}{\widehat{\sigma }}_{\alpha }^{\left(n\right)}={\widehat{\sigma }}_{\alpha }^{\left(n\right)}{\left({\widehat{\sigma }}_z^{(n)}+\alpha {\widehat{\sigma }}_0^{(n)}\right)}^k.\hfill \end{array}(5.9)$

Valid for $k=1$, induction yields this for higher $k$. For functions of the $\{{\widehat{\sigma }}_z^{(i)}\}$, $(i=1,\dots ,N)$, that can be expanded in a power series, it follows that

$\begin{array}{ccc}\hfill & \hfill & {\widehat{\sigma }}_{\alpha }^{\left(n\right)}f\left(\left\{{\widehat{\sigma }}_z^{(i)}\right\}\right)\equiv f^{\left(n,\alpha \right)}\left(\left\{{\widehat{\sigma }}_z^{(i)}\right\}\right){\widehat{\sigma }}_{\alpha }^{\left(n\right)},\hfill \\ \hfill & \hfill & f^{\left(n,\alpha \right)}\left(\left\{{\widehat{\sigma }}_z^{(i)}\right\}\right)=f\left(\left\{{\widehat{\sigma }}_z^{(i)}-{\delta }_{i,n}\alpha {\widehat{\sigma }}_0^{(n)}\right\}\right).\hfill \end{array}(5.10)$

Now the ${\widehat{\sigma }}_{\pm }$ can be eliminated using Equation 5.6, which leaves functions of only the ${\widehat{\sigma }}_z^{(i)}$, with the shifts in their arguments arising as the cost for this. As before, we can assume that ${\widehat{R}}_{s\bar{s}}(t)=R_{s\bar{s}}(\{{\widehat{\sigma }}_z^{(i)}\},t)$, where $R_{s\bar{s}}(\{{\sigma }_i\},t)$ is a scalar function of the eigenvalues ${\sigma }_i=0,\pm 1$ of the ${\widehat{\sigma }}_z^{(i)}$. Valid at $t_{\text{i}}$, this holds for $(\text{d}{\widehat{R}}_{s\tilde{s}}/\text{d}t)(t_{\text{i}})$, so it remains valid in time. Hence, it is possible to go from the matrix equations to scalar equations. With the equality in Equation 5.6 applied for spin $n$, we end up with the scalar expressions

$\begin{array}{ccc}\hfill & \hfill & C_{s\bar{s},+}^{(n,\alpha )}\left(u\right)=\left({\delta }_{{\sigma }_n,-\alpha }+{\delta }_{{\sigma }_n,0}\right)e^{-iu{H}_s}{e}^{iu{H}_s^{(n,\alpha )}}{R}_{s\bar{s}}^{(n,\alpha )}\left(t\right)\hfill \\ \hfill & \hfill & -\left({\delta }_{{\sigma }_n,\alpha }+{\delta }_{{\sigma }_n,0}\right)e^{-iu{H}_s^{(n,-\alpha )}}{e}^{iu{H}_s}{R}_{s\bar{s}}\left(t\right),\hfill \\ \hfill & \hfill & C_{s\bar{s},-}^{(n,\alpha )}\left(u\right)=C_{s\bar{s},+}^{(n,\alpha )}\left(-u\right),\hfill \end{array}(5.11)$

where for any function $R_{s\bar{s}}$ expandable in powers of the ${\sigma }_i=0,\pm 1$ $(i=1,\dots ,N)$, it holds that

$R_{s\bar{s}}^{(n,\alpha )}=R_{s\bar{s}}\left(\left\{{\sigma }_i\to {\sigma }_i+\alpha {\delta }_{i,n}\right\}\right),(5.12)$

Now that all terms are scalar functions of the ${\widehat{\sigma }}_z^{(i)}$, it is seen that $C_{s\bar{s},-}^{(n,\alpha )}(u)=C_{s\bar{s},+}^{(n,\alpha )}(-u;H_s\to H_{\bar{s}})$. We no longer need to track the operator structure and can work with scalar functions of the eigenvalues.

4.1 Off-diagonal sector: truncation of Schrödinger cat terms

In the spin $\frac{1}{2}$ Curie–Weiss model, it was found that the Schrödinger cat terms disappear by two mechanisms: dephasing of the magnet, possibly followed by decoherence due to the thermal bath. Similar behavior is now investigated for spin-1.

4.1.1 Initial regime: dephasing

Truncation of the density matrix (disappearance of the cat states) is a collective effect that takes place within an initial time window, in which the magnet stays in the paramagnetic phase, so that the mutual spin couplings $J_{\mathrm{2,4}}$ and the coupling to the bath can be neglected. The spins of M act individually by their coupling to the tested spin S and do not get correlated yet. In the sector where the eigenvalue of the operator ${\widehat{s}}_z$ is $s$, the Hamiltonian of the magnet is

$\begin{array}{ccc}\hfill & \hfill & {\widehat{H}}_{\text{SA}}=\sum _n{\widehat{H}}_{\text{SA}}^{sn},\hfill \\ \hfill & \hfill & {\widehat{H}}_{\text{SA}}^{sn}=-g\left[\left(1-\frac{3}{2}{s}^2\right)\left({\widehat{\sigma }}_0^{(n)}-\frac{3}{2}{\widehat{\sigma }}_z^{(n)2}\right)+\frac{3}{4}s{\widehat{\sigma }}_z^{(n)}\right].\hfill \end{array}(5.13)$

At a given $s$, this is a trace-free diagonal matrix with elements $\frac{1}{2}g$ (twice) and $-g$,

$\begin{array}{ccc}\hfill & \hfill & {\left(H_{\text{SA}}^{sn}\right)}_{\sigma \tilde{\sigma }}=\frac{g}{2}{\delta }_{\sigma ,\tilde{\sigma }}\left(1-3{\delta }_{\sigma ,s}\right),\hfill \\ \hfill & \hfill & {\delta }_{\sigma ,s}=\frac{1}{3}+\left(\frac{2}{3}-s^2\right)\left(1-\frac{3}{2}{\sigma }^2\right)+\frac{1}{2}s\sigma ,\hfill \end{array}(5.14)$

for $(s,\sigma ,\tilde{\sigma }=0,\pm 1)$. In this approximation, the $3^N\times 3^N$ density matrix of the magnet in each sector $s\bar{s}$ maintains the product structure (Equation 5.4) of uncorrelated spins at $t=t_{\text{i}}$,

${\widehat{R}}_{s\bar{s}}\left(t\right)=r_{s\bar{s}}\left(t_{\text{i}}\right){\widehat{\rho }}_{s\bar{s}}^{(1)}\left(t\right)\cdots \otimes {\widehat{\rho }}_{s\bar{s}}^{\left(2\right)}\left(t\right)\cdots \otimes {\widehat{\rho }}_{s\bar{s}}^{(N)}\left(t\right),(5.15)$

where, setting $t_{\text{i}}=0$, for each $n$,

$\begin{array}{ccc}\hfill & \hfill & {\widehat{\rho }}_{s\bar{s}}^{(n)}\left(t\right)=e^{-it{\widehat{H}}_{\text{SA}}^{s,n}}\frac{{\widehat{\sigma }}_0^{(n)}}{3}{e}^{it{\widehat{H}}_{\text{SA}}^{\bar{s},n}}={\left({\widehat{\rho }}_{\bar{s}s}^{(n)}\left(t\right)\right)}^{†},\hfill \\ \hfill & \hfill & {\left({\rho }_{s\bar{s}}^{(n)}\left(t\right)\right)}_{\sigma \tilde{\sigma }}=\frac{1}{3}{\delta }_{\sigma ,\tilde{\sigma }}\exp \left[\frac{3}{2}igt\left({\delta }_{\sigma ,s}-{\delta }_{\sigma ,\bar{s}}\right)\right].\hfill \end{array}(5.16)$

Diagonal elements $s=\bar{s}$ thus essentially do not evolve in this short-time window. The off-diagonal ones imply for $s\ne \bar{s}$

$r_{s\bar{s}}\left(t\right)={\mathrm{T}\mathrm{r}}_{\text{M}}{\widehat{R}}_{s\bar{s}}\left(t\right)=r_{s\bar{s}}\left(0\right){\left(\frac{1}{3}+\frac{2}{3}\cos \frac{3}{2}gt\right)}^N.(5.17)$

For small $t$, this decays as $r_{s\bar{s}}(0)\exp (-t^2/{\tau }_{\text{dph}}^2)$ with the dephasing time ${\tau }_{\text{dph}}=2/g\sqrt{3N}$, very short for large $N$. The undesired recurrences at $t_n=4\pi n/3g$, where the cosine equals 1 again, can be suppressed by assuming that the $g\to g_n=\bar{g}+\delta g_n$ values in Equation 5.16 have a small spread $\delta g_n$ (see Opus, Section 6.1.1). If the thermal oscillator bath has proper parameters, it will cause decoherence, as seen next.

4.1.2 Second step: decoherence

To include the bath in Equation 5.16, we now make the generalized Ansatz:

$\begin{array}{ccc}\hfill & \hfill & {\left({\widehat{\rho }}_{s\bar{s}}^{(n)}\left(t\right)\right)}_{\sigma \tilde{\sigma }}={\delta }_{\sigma ,\tilde{\sigma }}\frac{1}{3}\exp \left[-B_{\sigma }\left(t\right)\right]\times \hfill \\ \hfill & \hfill & \exp \left[-it{H}_{\text{SA}}^{\left(s,n\right)}\left(\sigma \right)+it{H}_{\text{SA}}^{\left(\bar{s},n\right)}\left(\sigma \right)\right].\hfill \end{array}(5.18)$

In the commutators (Equation 5.11), $H_s$ now reduces to the $H_{\text{SA}}^{s,n}$ of Equation 5.14, and the terms are identical for all $n$. We can neglect $B\sim \gamma$ in the exponents of Equation 2.29 and find, putting $-\alpha \to \alpha$ in the minus terms,

$\begin{array}{ccc}\hfill & \hfill & {\dot{B}}_{\sigma }=\frac{\gamma }{2}{\sum }_{\alpha }\left\{\left[K_{t>}\left({\mathrm{\Delta }}_{\alpha }^{\sigma }{H}_s\right)+K_{t<}\left({\mathrm{\Delta }}_{\alpha }^{\sigma }{H}_{\bar{s}}\right)\right]\right.\hfill \\ \hfill & \hfill & -\left.\left[K_{t>}\left({-\mathrm{\Delta }}_{\alpha }^{\sigma }{H}_s\right)+K_{t<}\left({-\mathrm{\Delta }}_{\alpha }^{\sigma }{H}_{\bar{s}}\right)\right]e_{s\bar{s}}^{\alpha \sigma }\left(t\right)\right\},\hfill \end{array}(5.19)$

with

$\begin{array}{ccc}\hfill & \hfill & K_{t>}\left(\omega \right)={\int }_0^t\text{d}uK\left(u\right)e^{-i\omega u},\hfill \\ \hfill & \hfill & K_{t<}\left(\omega \right)={\int }_{-t}^0\text{d}uK\left(u\right)e^{-i\omega u}.\hfill \end{array}(5.20)$

Here, $K_{t>}(\omega )=K_{t>}^{*}(\omega )$ because the kernel $\tilde{K}(\omega )$ is real valued; see the example in Equation 2.27, and

$\begin{array}{ccc}\hfill & \hfill & {\mathrm{\Delta }}_{\alpha }^{\sigma }{H}_s=H_s\left(\sigma +\alpha \right)-H_s\left(\sigma \right)\hfill \\ \hfill & \hfill & =\frac{3g}{2}\left[\left(1-\frac{3}{2}{s}^2\right)\left(1+2\alpha \sigma \right)-\frac{1}{2}s\alpha \right],\hfill \end{array}(5.21)$

with a similar expression for ${\mathrm{\Delta }}_{\alpha }^{\sigma }{H}_{\bar{s}}$, and finally

$e_{s\bar{s}}^{\alpha \sigma }\left(t\right)=\exp \left[-it\left({\mathrm{\Delta }}_{\alpha }^{\sigma }{H}_s-{\mathrm{\Delta }}_{\alpha }^{\sigma }{H}_{\bar{s}}\right)\right].(5.22)$

For $\bar{s}=s$, one has $e_{s\bar{s}}^{\alpha \sigma }(t)=1$. For $t\gg 1/2\pi T$, one gets, using $\tilde{K}(-\omega )=e^{\beta \omega }\tilde{K}(\omega )$,

$\begin{array}{lll}\hfill & \hfill & \hfill {\dot{B}}_{\sigma }=\frac{\gamma }{2}{\sum }_{\alpha }\tilde{K}\left({\mathrm{\Delta }}_{\alpha }^{\sigma }{H}_s\right)-\tilde{K}\left(-{\mathrm{\Delta }}_{\alpha }^{\sigma }{H}_s\right)\\ \hfill & \hfill & \hfill =\frac{\gamma }{2}{\sum }_{\alpha }\left({\mathrm{\Delta }}_{\alpha }^{\sigma }{H}_s\right)e^{-|{\mathrm{\Delta }}_{\alpha }^{\sigma }{H}_s|/\mathrm{\Gamma }}\sim \frac{\gamma }{N},\end{array}(5.23)$

because $H_s\sim N$, ${\mathrm{\Delta }}_{\alpha }^{\sigma }{H}_s\sim N^0$, and ${\sum }_{\alpha }{\mathrm{\Delta }}_{\alpha }^{\sigma }{H}_s\sim 1/N$. Therefore, for $s=\bar{s}$, this confirms that hardly any dynamics take place in this time window. In the next subsection, we show that they occur on a longer time scale ${\tau }_{\text{reg}}=1/\gamma T$.

For off-diagonal elements $\bar{s}\ne s$, it is seen that $e_{s\bar{s}}^{\alpha \sigma }(t)$ has terms $e^{\pm 3igt/2}$ and $e^{\pm 3igt}$, so that

$\begin{array}{ccc}\hfill & \hfill & e_{s\bar{s}}^{\alpha \sigma }\left(t\right)=\sum _{j=-2,-\mathrm{1,1,2}}{c}_j{e}^{3ijgt/2},\hfill \\ \hfill & \hfill & {\int }_0^t\text{d}u{e}_{s\bar{s}}^{\alpha }\left(\sigma ;u\right)=\sum _{j=-2,-\mathrm{1,1,2}}{c}_j\frac{e^{3ijgt/2}-1}{3ijg/2}.\hfill \end{array}(5.24)$

The exponentials are equal to unity, making $E_{s\bar{s}}^{\alpha }=1$, at the times $t_n=4\pi n/3g$, $n=\mathrm{1,2},\cdots$, encountered below Equation 5.17, when appearing in the dephasing process, and thus also as times where ${\dot{B}}_{\sigma }(t)=0$. To suppress recurrences like in the dephasing, we again set in each $n$-term $g\to g_n=\bar{g}+\delta g_n$ with small Gaussian distributed $\delta g_n$. For times well exceeding the coherence time $1/2\pi T$ of the bath, the $K_{t>}$ and $K_{t<}$ reach their finite limits, so that we have

$\begin{array}{ccc}\hfill & \hfill & {\int }_0^t\text{d}{t}^{\prime }{K}_{t^{\prime }>}\left(\omega \right)E_{s\bar{s}}^{\alpha }\left(\sigma ;t^{\prime }\right)\hfill \\ \hfill & \hfill & ={\int }_0^t\text{d}{t}^{\prime }\left[K_{t^{\prime }>}\left(\omega \right)-K_{\infty >}\left(\omega \right)\right]E_{s\bar{s}}^{\alpha }\left(\sigma ;t^{\prime }\right)\hfill \\ \hfill & \hfill & +K_{\infty >}\left(\omega \right){\int }_0^t\text{d}u{E}_{s\bar{s}}^{\alpha \sigma }\left(u\right),\hfill \end{array}(5.25)$

The first part is small, and the second is given in Equation 5.24. After canceling out its exponents by the $\delta g_n$, an imaginary part remains. Hence, for $t\gg 1/2\pi T$, the $E_{s\bar{s}}^{\alpha \sigma }$ terms can be neglected in $\mathfrak{R}B$. We keep

$\begin{array}{ccc}\hfill & \hfill & \mathfrak{R}{B}_{\sigma }\left(t\right)\approx \mathfrak{R}{\dot{B}}_{\sigma }\times t,\hfill \\ \hfill & \hfill & \mathfrak{R}{\dot{B}}_{\sigma }\approx \frac{\gamma }{2}{\sum }_{\alpha }\left[\tilde{K}\left({\mathrm{\Delta }}_{\alpha }^{\sigma }{H}_s\right)+\tilde{K}\left({\mathrm{\Delta }}_{\alpha }^{\sigma }{H}_{\bar{s}}\right)\right],\hfill \end{array}(5.26)$

which is positive, so that $|\exp (-N{B}_{\sigma })|=\exp (-N\mathfrak{R}{B}_{\sigma })$ with $N\mathfrak{R}{B}_{\sigma }\sim \gamma Ngt$ leads for large enough values of $N$ to a decoherence of the off-diagonal elements $r_{s\bar{s}}(t)$ of the density matrix at the characteristic decoherence time $t_{\mathit{dec}}=1/\gamma gN$ and $\gamma Ng{\tau }_{\text{reg}}\sim Ng/T$.

Decoherence is a combined effect of the $N$ apparatus spins; despite it, the individual elements of ${\widehat{R}}_{s\bar{s}}$ hardly decay in this time window, behaving as $\exp (-\gamma gt)=\exp (-t/N{t}_{\mathit{dec}})\approx 1$.

4.2 Registration dynamics for spin-1

In Section 3, a difference equation was derived for the distribution of the magnetization of the magnet for any number $N$ of spins-$\frac{1}{2}$. Our aim here is to derive an analogous equation for the spin-1 case.

In the paramagnet, one has the form $R_{ss}(\{{\sigma }_i\})=r_{ss}(t_{\text{i}})/3^N$. Let $P_s(\mathbf{\text{m}})$ with $\mathbf{\text{m}}=(m_1,m_2)$ be the probability for a state of the magnet M characterized by the moments $m_{\mathrm{1,2}}$. It gathers the value $R_{ss}(\mathbf{\text{m}})/r_{ss}(t_{\text{i}})$ for all sequences $\{{\sigma }_i\}$ compatible with $m_{\mathrm{1,2}}$, the number of which is the degeneracy factor $G_N=\exp S_N$,

$\begin{array}{ccc}\hfill & \hfill & P_s\left(\mathbf{\text{m}};t\right)=G_N\left(\mathbf{\text{m}}\right)\frac{R_{ss}\left(\mathbf{\text{m}};t\right)}{r_{ss}\left(t_{\text{i}}\right)},\hfill \\ \hfill & \hfill & G_N\left(\mathbf{\text{m}}\right)=\frac{N!}{\left(N_{-1}\right)!\left(N_0\right)!\left(N_1\right)!},N_{\sigma }=x_{\sigma }N,\hfill \end{array}(5.27)$

with the $x_{\pm 1}=\frac{1}{2}(m_2\pm m_1)$ and $x_0=1-m_2$ from Equation 2.14. The normalizations are

$\begin{array}{ccc}\hfill & \hfill & {\displaystyle \sum _{{\sigma }^{(1)}=-1}^1}\cdots {\displaystyle \sum _{{\sigma }^{(N)}=-1}^1}{R}_{ss}\left(\left\{{\sigma }^{(i)}\right\};t\right)=r_{ss}\left(t_{\text{i}}\right),\hfill \\ \hfill & \hfill & {\displaystyle \sum _{m_2=0}^1}{\displaystyle \sum _{m_1=-m_2}^{m_2}}{P}_s\left(m_1,m_2;t\right)=1.\hfill \end{array}(5.28)$

Due to the relations described by Equations 2.13 and 2.14 between the spin moments $m_{0,\pm 1}$ and the spin fractions $x_{0,\pm 1}$, the shifts in $m_{\mathrm{1,2}}$ induce the shifts $N_{\sigma }^{\prime }=N_{\sigma }+\delta N_{\sigma }$ and $x_{\sigma }^{\prime }=x_{\sigma }+\nu \delta N_{\sigma }$, with

$\delta N_{\pm 1}=\frac{1\pm \alpha }{2}+\alpha {\sigma }_n, \delta N_0=-1-2\alpha {\sigma }_n,(5.29)$

which are integers, as they should be. The degeneracies for ${\sigma }_n=-\alpha ,0,\alpha$ lead to the respective factors

$\begin{array}{ccc}\hfill & \hfill & \frac{G_N}{{\left(G_N\right)}^{\prime }}=\frac{N_{-1}^{\prime }!N_0^{\prime }!N_1^{\prime }!}{N_{-1}!N_0!N_1!}=\frac{x_0+\nu }{x_{-\alpha }}{\delta }_{{\sigma }_n,-\alpha }\hfill \\ \hfill & \hfill & +\frac{x_{\alpha }+\nu }{x_0}{\delta }_{{\sigma }_n,0}+\frac{\left(x_{-1}+\nu \right)\left(x_1+\nu \right)+\left(x_{\alpha }+2\nu \right)}{x_0\left(x_0-\nu \right)\left(x_0-2\nu \right)}{\delta }_{{\sigma }_n,\alpha },\hfill \end{array}(5.30)$

where $N_{\sigma }=N{x}_{\sigma }$ is used. The complicated last term is fortunately not needed, while the denominators of the first two will factor out.

Going to the functions $P_s$ of the moments $m_{\mathrm{1,2}}$, we proceed as for the spin $\frac{1}{2}$ situation. The $C_{\pm }$ terms of Equation 5.11 can again be combined and performing the $u$-integrals in Equation 4.2 leads for $t\gg 1/T$ to the kernel $\tilde{K}(\omega )$ at the frequencies

${\mathrm{\Omega }}_{\alpha }^{\beta }\left(\mathbf{\text{m}}\right)=H_s\left(m_1\alpha -\nu ,m_2-\beta \nu \right)-H_s\left(\mathbf{\text{m}}\right),(5.31)$

for $\alpha ,\beta =\pm 1$. Multiplying Equation 4.2 by $G_N$ and summing over $\alpha$, there results an evolution equation for the distribution $P_s$ at each discrete value of $m_{\mathrm{1,2}}$,

$\begin{array}{lll}\hfill & \hfill & {\dot{P}}_s\left(m_1,m_2;t\right)=\gamma N\sum _{\alpha =\pm 1}\hfill \\ \hfill & \hfill & \hfill \left\{\left(x_0+\nu \right)\tilde{K}\left(-{\mathrm{\Omega }}_{s,-\alpha }^{+}\right)P_{s\alpha }^{-}\left(m_1,m_2;t\right)\right.\\ \hfill & \hfill & \hfill +\left(x_{\alpha }+\nu \right)\tilde{K}\left(-{\mathrm{\Omega }}_{s,-\alpha }^{-}\right)P_{s\alpha }^{+}\left(m_1,m_2;t\right)\\ \hfill & \hfill & \hfill \left.-\left[x_{\alpha }\tilde{K}\left({\mathrm{\Omega }}_{s\alpha }^{+}\right)+x_0\tilde{K}\left({\mathrm{\Omega }}_{s\alpha }^{-}\right)\right]P_s\left(m_1,m_2;t\right)\right\}.\end{array}(5.32)$

Let us condense notation and introduce the shift operators $E_{\alpha }^{\beta }$ and ${\mathrm{\Delta }}_{\alpha }^{\beta }=E_{\alpha }^{\beta }-1$ by their action

$\begin{array}{ccc}\hfill & \hfill & E_{\alpha }^{\beta }f\left(\mathbf{\text{m}}\right)=f\left(m_1+\alpha \nu ,m_2+\beta \nu \right),\hfill \\ \hfill & \hfill & {\mathrm{\Delta }}_{\alpha }^{\beta }f\left(\mathbf{\text{m}}\right)=f\left(m_1+\alpha \nu ,m_2+\beta \nu \right)-f\left(\mathbf{\text{m}}\right).\hfill \end{array}(5.33)$

on any $f(\mathbf{\text{m}})$. They have the properties

$\begin{array}{ccc}\hfill & \hfill & E_{\alpha }^{\beta }{\mathrm{\Delta }}_{-\alpha }^{-\beta }=-{\mathrm{\Delta }}_{\alpha }^{\beta },{\mathrm{\Omega }}_{s\alpha }^{\beta }={\mathrm{\Delta }}_{-\alpha }^{-\beta }{H}_s,\hfill \\ \hfill & \hfill & E_{\alpha }^{\beta }{\mathrm{\Omega }}_{s\alpha }^{\beta }=-{\mathrm{\Delta }}_{\alpha }^{\beta }{H}_s=-{\mathrm{\Omega }}_{s,-\alpha }^{-\beta }.\hfill \\ \hfill & \hfill & E_{\alpha }^{\beta }{x}_{\alpha }=x_{\alpha }+\frac{1+\beta }{2}\nu ,E_{\alpha }^{\beta }{x}_0=x_0-\beta \nu .\hfill \end{array}(5.34)$

Hence, Equation 5.32 can be expressed as

$\begin{array}{ccc}\hfill & \hfill & {\dot{P}}_s\left(m_1,m_2;t\right)=\gamma N\sum _{\alpha =\pm 1}\hfill \\ \hfill & \hfill & \left({\mathrm{\Delta }}_{\alpha }^{+}\left[x_{\alpha }\tilde{K}\left({\mathrm{\Omega }}_{s\alpha }^{+}\right)P_s\right]+{\mathrm{\Delta }}_{\alpha }^{-}\left[x_0\tilde{K}\left({\mathrm{\Omega }}_{s\alpha }^{-}\right)P_s\right]\right),\hfill \end{array}(5.35)$

which has a remarkable analogy to Equation 4.9 and Equation 4.16 of Opus for the spin-$\frac{1}{2}$ case. By denoting $x_{\alpha }^{+}=x_{\alpha }$ above and $x_{\alpha }^{-}=x_0$, this is condensed further,

${\dot{P}}_s\left(m_1,m_2;t\right)=\gamma N\sum _{\alpha ,\beta =\pm 1}{\mathrm{\Delta }}_{\alpha }^{\beta }\left[x_{\alpha }^{\beta }\tilde{K}\left({\mathrm{\Omega }}_{s\alpha }^{\beta }\right)P_s\right].(5.36)$

4.3 $H$-theorem and relaxation to equilibrium

We now exhibit a $H$ theorem that assures the relaxation of the magnet towards its Gibbs equilibrium state and, thus, a successful measurement. The dynamical entropy of the distribution $P_s(\mathbf{\text{m}};t)=G_N(\mathbf{\text{m}})R_{ss}(\{{\sigma }_i\})/r_{ss}(t_{\text{i}})$ is defined as

$\begin{array}{ccc}\hfill S_s\left(t\right)& =\hfill & -\mathrm{T}\mathrm{r}\frac{{\widehat{R}}_{ss}\left(t\right)}{r_{ss}\left(t_{\text{i}}\right)}\log \frac{{\widehat{R}}_{ss}\left(t\right)}{r_{ss}\left(t_{\text{i}}\right)}\hfill \\ \hfill & =\hfill & -\sum _{\mathbf{\text{m}}}{P}_s\left(\mathbf{\text{m}};t\right)\log \frac{P_s\left(\mathbf{\text{m}};t\right)}{G_N\left(\mathbf{\text{m}}\right)}.\hfill \end{array}(5.37)$

Following Opus and Equation 4.12 above, we consider the dynamical free energy

$\begin{array}{ccc}\hfill & \hfill & F_{\text{dyn}}^s\left(t\right)=U_s\left(t\right)-T{S}_s\left(t\right)\hfill \\ \hfill & =\hfill & \sum _{\mathbf{\text{m}}}{P}_s\left(\mathbf{\text{m}};t\right)\left[H_s\left(\mathbf{\text{m}}\right)+T\log \frac{P_s\left(\mathbf{\text{m}};t\right)}{G_N\left(\mathbf{\text{m}}\right)}\right].\hfill \end{array}(5.38)$

It appears to depend on $s$. The simultaneous change $s\to -s$, $m_1\to -m_1$ implies that $F_{\text{dyn}}^1(t)=F_{\text{dyn}}^{-1}(t)$ at all $t$, as happened for $s=\pm \frac{1}{2}$ in the spin $\frac{1}{2}$ case, but the $F_{\text{dyn}}^{\pm 1}(t)$ differ from $F_{\text{dyn}}^0(t)$, except in the thermal situations at $t=0$ and $t\to \infty$.

With $\beta =1/T$, not to be confused with the index $\beta =\pm 1$, Equation 5.36 yields

$\begin{array}{ccc}\hfill & \hfill & {\dot{F}}_{\text{dyn}}^s=T\sum _{\mathbf{\text{m}}}{\dot{P}}_s\left(\mathbf{\text{m}}\right)\log \frac{P_s\left(\mathbf{\text{m}}\right)e^{\beta H_s\left(\mathbf{\text{m}}\right)}}{G_N\left(\mathbf{\text{m}}\right)}\hfill \\ \hfill & \hfill & =\gamma NT{\sum }_{\alpha ,\beta =\pm 1}{\sum }_{\mathbf{\text{m}}}{\mathrm{\Delta }}_{\alpha }^{\beta }\left[x_{\alpha }^{\beta }\tilde{K}\left({\mathrm{\Omega }}_{s\alpha }^{\beta }\right)P_s\right]\log \frac{P_s{e}^{\beta H_s}}{G_N}.\hfill \end{array}(5.39)$

For general functions $f_{\mathrm{1,2}}(\mathbf{\text{m}})$ with vanishing boundary terms, partial summation yields

$\begin{array}{ccc}\hfill & \hfill & \sum _{\mathbf{\text{m}}}\left({\mathrm{\Delta }}_{\alpha }^{\beta }{f}_1\right)f_2=\sum _{\mathbf{\text{m}}}{f}_1\left({\mathrm{\Delta }}_{-\alpha }^{-\beta }{f}_2\right)\hfill \\ \hfill & \hfill & =\sum _{\mathbf{\text{m}}}{E}_{\alpha }^{\beta }\left[f_1\left({\mathrm{\Delta }}_{-\alpha }^{-\beta }{f}_2\right)\right]=-\sum _{\mathbf{\text{m}}}\left(E_{\alpha }^{\beta }{f}_1\right)\left({\mathrm{\Delta }}_{\alpha }^{\beta }{f}_2\right).\hfill \end{array}(5.40)$

For $\alpha =+1$, we use the last expression, and for $\alpha =-1$, we use the second one, while taking $\beta \to -\beta$, and also using Equation 5.34 and the property $\tilde{K}(-\omega )=\tilde{K}(\omega )e^{\beta \omega }$ satisfied generally in Equation 2.26, which yields the result

$\begin{array}{ccc}\hfill & \hfill & {\dot{F}}_{\text{dyn}}^s=-\gamma NT\sum _{\mathbf{\text{m}}}\sum _{\beta =\pm 1}\tilde{K}\left({\mathrm{\Delta }}_{+}^{\beta }{H}_s\right)\hfill \\ \hfill & \hfill & \times \left\{e^{{\mathrm{\Delta }}_{+}^{\beta }\beta H_s}\left(E_{+}^{\beta }{x}_{+}^{\beta }\right)\left(E_{+}^{\beta }{P}_s\right)-x_{-1}^{-\beta }{P}_s\right\}{\mathrm{\Delta }}_{+}^{\beta }\log \frac{P_s{e}^{\beta H_s}}{G_N}.\hfill \end{array}(5.41)$

The various parts are such that a term $G_N(\mathbf{\text{m}})x_{-1}^{-\beta }$ can be factored out, to express this as

$\begin{array}{ccc}\hfill & \hfill & {\dot{F}}_{\text{dyn}}^s=\gamma NT\sum _{\mathbf{\text{m}}}\sum _{\beta =\pm 1}{G}_N{x}_{-1}^{-\beta }\tilde{K}\left({\mathrm{\Delta }}_{+}^{\beta }{H}_s\right)\hfill \\ \hfill & \hfill & \times \left\{e^{{\mathrm{\Delta }}_{+}^{\beta }\beta H_s}\left[E_{+}^{\beta }\left(\frac{P_s}{G_N}\right)\right]-\frac{P_s}{G_N}\right\}{\mathrm{\Delta }}_{+}^{\beta }\log \frac{P_s{e}^{\beta H_s}}{G_N}.\hfill \end{array}(5.42)$

With ${\mathrm{\Delta }}_{+}^{\beta }{H}_s=E_{+}^{\beta }{H}_s-H_s$, $G_N=\exp (S_N)$, and $F_s(\mathbf{\text{m}})=H_s(\mathbf{\text{m}})-T{S}_N(\mathbf{\text{m}})$, this is equal to

$\begin{array}{ccc}\hfill & \hfill & {\dot{F}}_{\text{dyn}}^s\left(t\right)=-\gamma NT\sum _{\mathbf{\text{m}}}\sum _{\beta =\pm 1}{x}_{-1}^{-\beta }\tilde{K}\left({\mathrm{\Delta }}_{+}^{\beta }{H}_s\right)e^{-\beta F_s}\hfill \\ \hfill & \hfill & \times \left({\mathrm{\Delta }}_{+}^{\beta }\frac{P_s}{e^{-\beta F_s}}\right)\left({\mathrm{\Delta }}_{+}^{\beta }\log \frac{P_s}{e^{-\beta F_s}}\right).\hfill \end{array}(5.43)$

The last factors have the form $(x^{\prime }-x)\log (x^{\prime }/x)$, which is nonnegative, implying that $F_{\text{dyn}}^s$ is a decreasing function of time. Dynamic equilibrium occurs when these factors vanish, which happens when the magnet has reached thermodynamic equilibrium, that is, the Gibbs state $P_s=e^{-\beta F_s}/Z_s$ and ${\widehat{R}}_{ss}=e^{-\beta {\widehat{H}}_s}/Z_s$, with $Z_s={\sum }_{\mathbf{\text{m}}}\exp (-\beta F_s)={\sum }_{\mathbf{\text{m}}}{G}_N(\mathbf{\text{m}})\exp (-\beta H_s)=\mathrm{T}\mathrm{r}\exp (-\beta {\widehat{H}}_s)$, as usual. The dynamical free energy (Equation 5.38) then ends up at the thermodynamic free energy,

$F_{\text{dyn}}^s\left(\infty \right)=-T\log Z_s,(5.44)$

which actually does not depend on $s$ due to the invariance map of the static state, reflecting that the measurement is unbiased. This constitutes an explicit example of the apparatus going dynamically to its lowest thermodynamic state, the pointer state registering the measurement outcome.

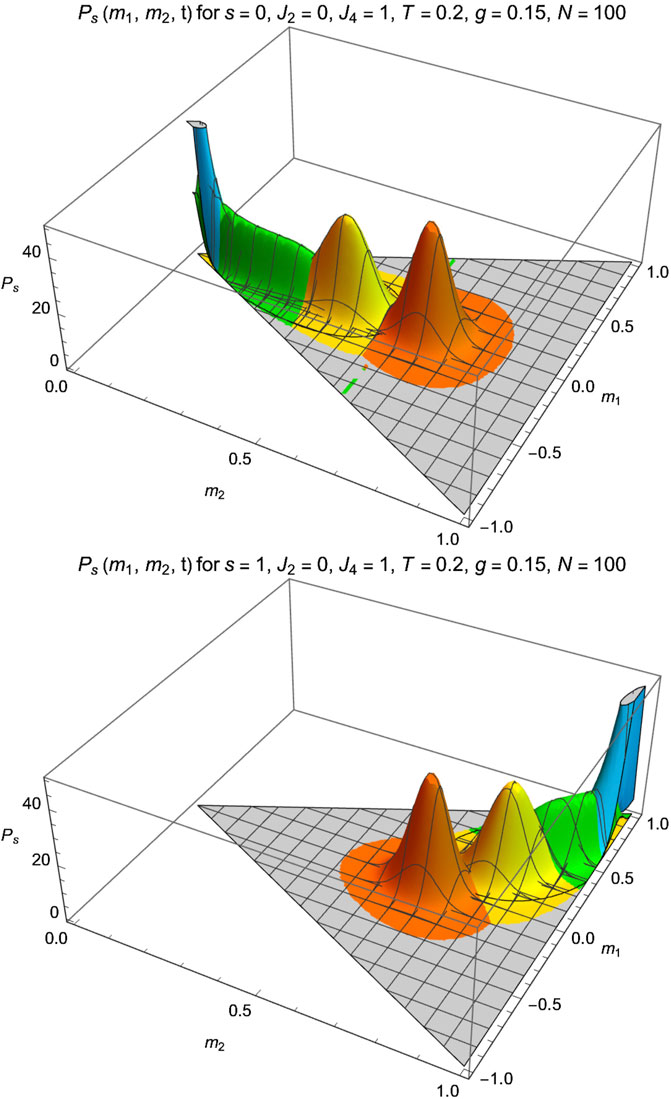
Although the statics are identical for $s=0,\pm 1$, this does not hold for the dynamics. While it is similar for $s=\pm 1$ (to change the sign of $s=\pm 1$, also change the sign of $m_1$), this deviates from the $s=0$ dynamics. For $s=0$, all ${\mathrm{\Omega }}_{\alpha }^{\beta }(\mathbf{\text{m}})$ are finite, but for $s=\pm 1$, there are cases where ${\mathrm{\Omega }}_{\alpha }^{\beta }(\mathbf{\text{m}})$ vanishes, which leads to a slower dynamics; see Figure 5.

4.4 Numerical analysis

The initial spin-1 Hamiltonian leads to a $3^N\times 3^N$ matrix problem, which is numerically hard. For the considered mean-field-type model, the formulation in terms of the order parameters $m_{\mathrm{1,2}}$ is exact; it lowers the dimensionality considerably. The variable $m_2=(1/N){\sum }_{i=1}^N{\sigma }_i^2$ can take $N+1$ values between 0 and 1. The value of $M_2=N{m}_2$ indicates that $N-M_2$ of the ${\sigma }_i$ take the value 0, while the other $M_2$ of the ${\sigma }_i$ are $\pm 1$. Given this number, $m_1=(1/N){\sum }_{i=1}^N{\sigma }_i$ can take $M_2+1$ values between $-m_2$ and $m_2$. Accounting for conservation of total probability, this leads to $N(N+3)/2$ dynamical variables, a polynomial problem.

(Concerning higher spin: For spin $\frac{3}{2}$, one separates terms with $s_i=\pm \frac{3}{2}$ from those with $s_i=\pm \frac{1}{2}$; for spin-2, one selects terms with $s_i=0$, $\pm 1$, or $\pm 2$, etc.)

Equation 5.32 can be solved numerically as a set of linear differential equations. Programming it is straightforward; the vanishing of boundary terms and conservation of the total probability must be verified as a check on the code.

The magnet starts in the paramagnetic initial state

$\begin{array}{ccc}\hfill & \hfill & P_s\left(\mathbf{\text{m}};0\right)=\frac{1}{3^N}{G}_N\left(\mathbf{\text{m}}\right)\hfill \\ \hfill & \hfill & \approx \frac{3^{3/2}}{2\pi N}\exp \left\{-N\left[\frac{3}{4}{m}_1^2+{\left(\frac{3}{2}{m}_2-1\right)}^2\right]\right\}.\hfill \end{array}(5.45)$

The sum of $P_s$ over $m_{\mathrm{1,2}}$ equals unity and, with the mesh $\mathrm{\Delta }{m}_1\mathrm{\Delta }{m}_2=2{\nu }^2$, so does its integral.

The dynamics (Equation 5.32) can be solved numerically, and the results are presented in upcoming figures. We consider the parameters, with $g$ large enough,

$\begin{array}{ccc}\hfill & \hfill & N=100,J_2=0,J_4=1,g=0.15,T=0.2,\mathrm{\Gamma }=10.\hfill \end{array}(5.46)$

We plot in Figures 4A,B snapshots of $P_s/(2{\nu }^2)$ at four times, for $s=0$ and $s=1$. The case $s=-1$ follows from the case $s=1$ by setting $m_1\to -m_1$.

Figure 4

Figure 4. Snapshots of the distribution $P_s$ of the magnetization moments $m_{\mathrm{1,2}}$ for registration of the spin-1 measurement. Upper: $P_s\ge 10^{-3}$ data in the $s=0$ sector at times $t=(\mathrm{0,1,2,3})\times 2/\gamma T$ from right to left. Lower: the $s=1$ sector at $t=(\mathrm{0,1,2,3})\times 5/\gamma T$ from left to right; it evolves more slowly. The parameters are listed in Equation 5.46.

Figure 5 shows the evolution of the dynamical free energy $F_{\text{dyn}}^s(t)$.

Figure 5

Figure 5. The spin-1 dynamical free energy $F_{\text{dyn}}^s$ of Equation 5.38 relaxes from its $t=0$ value to its thermodynamic value. $F_s(g)$ of Equation 5.44, thereby registering the measurement. Parameters are as in Figures 4A,B, and time is expressed in units of $1/\gamma T$. The relaxation for $s=\pm 1$ is slower than for $s=0$ due to the occurrence of zero frequencies. The initial “shoulders” describe the initial broadenings in Figures 4A,B.

4.5 Decoupling of the apparatus

Near the end of the measurement, the interaction between the system and the apparatus is cut off by setting $g=0$; in doing so, at decoupling time $t_{\text{dc}}$, Equation 5.13 expresses that an amount of energy

$\begin{array}{ccc}\hfill & \hfill & U_{\text{dc}}=-\sum _{\mathbf{\text{m}}}{P}_s\left(\mathbf{\text{m}};t_{\text{dc}}\right)H_{\text{SA}}\left(\mathbf{\text{m}}\right)=+gN\times \hfill \\ \hfill & \hfill & \sum _{\mathbf{\text{m}}}{P}_s\left(\mathbf{\text{m}};t_{\text{dc}}\right)\left[\left(1-\frac{3}{2}{s}^2\right)\left(1-\frac{3}{2}{m}_2\right)+\frac{3}{4}s{m}_1\right],\hfill \end{array}(5.47)$

must be supplied to the magnet, leaving it with the post-decoupling free energy

$F_{\text{dc}}=\sum _{\mathbf{\text{m}}}{P}_s\left(\mathbf{\text{m}};t_{\text{dc}}\right)\left(H_{\text{M}}-T\log G_N\right).(5.48)$

This post-decoupling state is not an equilibrium state; the magnet will now relax to the nearby minimum of the $g=0$ case. There follows a relaxation driven by bath, with the magnet evolving under the $g=0$ Hamiltonian $H_{\text{M}}(\mathbf{\text{m}})$ to its Gibbs state $P_{\text{G}}(\mathbf{\text{m}})=G_N\exp [-H_{\text{M}}(\mathbf{\text{m}})/T]/Z_{\text{G}}$, with free energy $F_G={\sum }_{\mathbf{\text{m}}}{P}_G(\mathbf{\text{m}})[H_{\text{M}}(\mathbf{\text{m}})-T{S}_N(\mathbf{\text{m}})]$.

When the decoupling time $t_{\text{dc}}$ is large enough, the magnet M lies in its Gibbs state at coupling $g$, $P_s(t_{\text{dc}})\sim \exp [-\beta H_s(\mathbf{\text{m}})]$. Due to the invariance of the $g=0$ situation, the approach to it is identical for starting in any of the sectors $s=0,\pm 1$.

To compare with the dynamics that end up in one of the minima, one must restrict the Gibbs state, which has three degenerate minima, to the nearby minimum. This is achieved numerically even at moderate $N$ by discarding $\exp (-\beta H_s)$ well away from the peak of $P_s(t_{\text{dc}})$, also in $Z_{\text{G}}$. For $s=0$, it suffices to keep $\exp (-\beta H_s)$ for $m_2<\frac{1}{3}$; for $s=\pm 1$ by doing that for $m_{1}s>\frac{1}{3}$.

The change of the state is also seen in $⟨m_2⟩(t)={\sum }_{\mathbf{\text{m}}}{m}_2{P}_s(\mathbf{\text{m}};t)$. Let us consider the sector $s=0$, where $⟨m_1⟩=0$ at all $t$. Here, the coupling $H_{\text{SA}}=gN(\frac{3}{2}{m}_2-1)$ has the tendency to suppress $m_2$, so after decoupling, $m_2$ will relax to a larger value. For $N\to \infty$, we get from the Gibbs states at $g$ and at $g=0$, respectively,

$\langle m_2\left(0\right)\rangle =3.6310^{-4},\langle m_2\left(\infty \right)\rangle =11.510^{-4}.(5.49)$

The full-time behavior for $N=100$ and couplings as in Equation 5.46 is presented in Figure 6, with the finite-$N$ values increasing from $⟨m_2(0)⟩=9.97510^{-4}$ to $⟨m_2(\infty )⟩={12.6910}^{-4}$.

Figure 6

Figure 6. After decoupling the apparatus from the system, the magnet relaxes to its nearby $g=0$ equilibrium. If this happens at a time $t_{\text{dc}}$ where finite-$g$ equilibrium has been reached, this goes identical in the sectors $s=0,\pm 1$. The dynamical free energy is plotted with parameters as in Figures 4, 5, relaxing from its decoupled value (indicated by the dot) to its $g=0$ thermodynamic limit $F$ (lower line). Compared to Figure 5, this macroscopic energy cost is a permille effect.

The relaxation in the sectors $s=\pm 1$ follows immediately from this. The map (Equation 5.50) yields. The maps (4.11) and (4.13) of Models lead to

$\begin{array}{ccc}\hfill & \hfill & {⟨m_1⟩}_{s=\pm 1}=\pm \left(1-\frac{3}{2}{⟨m_2⟩}_{s=0}\right),\hfill \\ \hfill & \hfill & {⟨m_2⟩}_{s=\pm 1}=1-\frac{1}{2}{⟨m_2⟩}_{s=0}.\hfill \end{array}(5.50)$

4.6 Energy cost of quantum measurement

The Copenhagen postulates obscure one of the facts of life in a laboratory: a firm cost for the energy needed to keep the setup running. In this work, we consider two intrinsic costs. In the previous subsection, we established the cost of decoupling the apparatus from the system. Here, we consider resetting the magnet for another run. It must be set from its stable state back to its metastable state. Being related to the magnet, both costs are macroscopic.

Our initial state, the paramagnet (pm), has zero magnetic energy and maximal entropy

$F_{\text{pm}}=-NT\log 3,(5.51)$

The energy needed to reset the Gibbs state of the magnet to the paramagnetic one is

$\begin{array}{cccc}\hfill & \hfill & U_{\text{reset}}=F_{\text{pm}}-F_G=\hfill & -{\sum }_{\mathbf{\text{m}}}{P}_G\left(\mathbf{\text{m}}\right)\left[H_{\text{M}}-T\log \left(G_N/3^N\right)\right].\hfill \end{array}(5.52)$

It is evidently macroscopic. The condition that $U_{\text{reset}}$ is positive was identified in Opus and in Models as the condition that the initial paramagnetic state is metastable but not stable.

5 Conclusion

This article dealt with the dynamics of an ideal quantum measurement of the $z$-component of a spin-1. The statics for this task were worked out recently in our “Models” article (Nieuwenhuizen, 2022); it generalized to any spin $l>\frac{1}{2}$ the Curie–Weiss model to measure a spin $\frac{1}{2}$; the latter was considered in great detail in “Opus” (Allahverdyan et al., 2013). Here, we first reformulated the dynamics of the known case for spin $\frac{1}{2}$ and worked out some further properties. The resulting formalism is suitable as a basis for models to measure any higher spin.

The dynamics of measurement in the spin-1 case were analyzed in detail. Off-diagonal elements of the density matrix (“cat states”) were shown to decay very fast (“truncation of the density matrix”) due to dephasing, possibly followed by decoherence.

The evolution of the diagonal elements of the density matrix was expressed as coupled first-order differential equations for the distribution of two magnetization-type-order parameters, $m_{\mathrm{1,2}}$. The approach to a Gibbs equilibrium was certified by demonstrating a $H$-theorem. The resulting scheme was found to be numerically a polynomial problem. These are easily solved with the present power of laptops for an apparatus consisting of a few hundred spins. The evolution of the probability density was evaluated, and the $H$-theorem was verified. The macroscopic energy costs for decoupling the apparatus from the spin and for resetting it from its stable state to its metastable state for use in the next run of the measurement were quantified.

For general spin $l$, this method simplified the numerically hard problem of dimension ${(2l+1)}^{2N}-1$ by a polynomial problem of order $N^{2l}$ for its $2l$-order parameters. For more complicated models of the apparatus, it will likewise pay off to focus on the order parameter of the dynamical phase transition of the pointer that achieves the registration of the measurement. The fact that the phase transition in the magnet is of first order underlines that our mean-field-type models, although of mathematical convenience, are not essential for the fundamental description of quantum measurements.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

TN: writing – original draft and writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹An analogy is offered by the dark matter problem in cosmology. Abandoning particle dark matter, we view dark “matter” as a form of energy and assume new properties of vacuum energy. This provides a description of black holes with a core rather than a singularity (Nieuwenhuizen, 2023), aspects of dark matter throughout the history and future of the Universe (Nieuwenhuizen, 2024a), and the giant dark matter clouds around isolated galaxies (Nieuwenhuizen, 2024b), explaining the “indefinite flattening” of their rotation curves (Mistele et al., 2024). Remarkably, this approach is a generalization of the classical Lorentz–Poincaré electron—a charged, non-spinning spherical shell filled with vacuum energy (Nieuwenhuizen, 2025).

²To simplify the notation, we replace the standard notation for spins with $s\to l$ and $s_z\to s$. For an angular momentum $L^2=l(l+1)$, the model also applies to the measurement of ${\widehat{L}}_z$ with eigenvalues $m\to s$. We employ units $\hslash =k=1$.

³For the connection with the parameters in Opus, see ref 1.

References

Allahverdyan, A., Balian, R., and Nieuwenhuizen, T. M. (2003a). The quantum measurement process: an exactly solvable model. Atti della Fondazione Giorgio Ronchi, 719. Available online at: https://arxiv.org/abs/cond-mat/0309188.

Google Scholar

Allahverdyan, A. E., Balian, R., and Nieuwenhuizen, T. M. (2003b). Curie-Weiss model of the quantum measurement process. EPL Europhys. Lett. 61, 452–458. doi:10.1209/epl/i2003-00150-y

CrossRef Full Text | Google Scholar

Allahverdyan, A. E., Balian, R., and Nieuwenhuizen, T. M. (2005a). The quantum measurement process in an exactly solvable model. AIP Conf. Proc. 750, 26–34. doi:10.1063/1.1874554

CrossRef Full Text | Google Scholar

Allahverdyan, A. E., Balian, R., and Nieuwenhuizen, T. M. (2005b). Dynamics of a quantum measurement. Phys. E Low-dimensional Syst. Nanostructures 29, 261–271. doi:10.1016/j.physe.2005.05.023

CrossRef Full Text | Google Scholar

Allahverdyan, A. E., Balian, R., and Nieuwenhuizen, T. M. (2006). Phase transitions and quantum measurements. AIP Conf. Proc. 810, 47–58. doi:10.1063/1.2158710

CrossRef Full Text | Google Scholar

Allahverdyan, A. E., Balian, R., and Nieuwenhuizen, T. M. (2007). “The quantum measurement process: lessons from an exactly solvable model,” in Beyond the quantum (World Scientific), 53–65.

Google Scholar

Allahverdyan, A. E., Balian, R., and Nieuwenhuizen, T. M. (2013). Understanding quantum measurement from the solution of dynamical models. Phys. Rep. 525, 1–166. doi:10.1016/j.physrep.2012.11.001

CrossRef Full Text | Google Scholar

Allahverdyan, A. E., Balian, R., and Nieuwenhuizen, T. M. (2017). A sub-ensemble theory of ideal quantum measurement processes. Ann. Phys. 376, 324–352. doi:10.1016/j.aop.2016.11.001

CrossRef Full Text | Google Scholar

Allahverdyan, A. E., Balian, R., and Nieuwenhuizen, T. M. (2024). Teaching ideal quantum measurement, from dynamics to interpretation. Comptes Rendus. Phys. 25, 251–287. doi:10.5802/crphys.180

CrossRef Full Text | Google Scholar

Allahverdyan, A. E., Balian, R., and Nieuwenhuizen, T. M. (2025). Interpretation of quantum mechanics from the dynamics of ideal measurement. Europhys. News, appear 56, 23–25. doi:10.1051/epn/2025210

CrossRef Full Text | Google Scholar

Auffèves, A., and Grangier, P. (2016). Contexts, systems and modalities: a new ontology for quantum mechanics. Found. Phys. 46, 121–137. doi:10.1007/s10701-015-9952-z

CrossRef Full Text | Google Scholar

Auffèves, A., and Grangier, P. (2020). Deriving born’s rule from an inference to the best explanation. Found. Phys. 50, 1781–1793. doi:10.1007/s10701-020-00326-8

CrossRef Full Text | Google Scholar

Ballentine, L. E. (1970). The statistical interpretation of quantum mechanics. Rev. Mod. Phys. 42, 358–381. doi:10.1103/revmodphys.42.358

CrossRef Full Text | Google Scholar

Born, M. (1926). Zur Quantenmechanik der Stoßvorgänge. Z. für Phys. 38, 803–827. doi:10.1007/bf01397184

CrossRef Full Text | Google Scholar

Born, M., Heisenberg, W., and Jordan, P. (1926). Zur quantenmechanik. II. Z. für Phys. 35, 557–615. doi:10.1007/bf01379806

CrossRef Full Text | Google Scholar

Born, M., and Jordan, P. (1925). Zur quantenmechanik. Z. für Phys. 34, 858–888. doi:10.1007/bf01328531

CrossRef Full Text | Google Scholar

Capellmann, H. (2017). “The quantum theory of Born, Heisenberg, and Jordan,” in The development of elementary quantum theory (Cham: Springer International Publishing), 23–39. Available online at: https://link.springer.com/content/pdf/10.1007/978-3-319-10539-0.pdf.

CrossRef Full Text | Google Scholar

David, F. (2015). The formalisms of quantum mechanics. Lect. notes Phys. 893, 42–43. doi:10.1007/978-3-319-10539-0

CrossRef Full Text | Google Scholar

De Broglie, L. (1924). Recherches sur la théorie des quanta. Paris: Migration-université en cours d’affectation. PhD thesis.

Google Scholar

Donker, H., De Raedt, H., and Katsnelson, M. (2018). Quantum dynamics of a small symmetry breaking measurement device. Ann. Phys. 396, 137–146. doi:10.1016/j.aop.2018.07.010

CrossRef Full Text | Google Scholar

Mistele, T., McGaugh, S., Lelli, F., Schombert, J., and Li, P. (2024). Indefinitely flat circular velocities and the baryonic tully–Fisher relation from weak lensing. Astrophysical J. Lett. 969, L3. doi:10.3847/2041-8213/ad54b0

CrossRef Full Text | Google Scholar

Mydosh, J. A. (1993). Spin glasses: an experimental introduction. London: CRC Press. doi:10.1201/9781482295191

CrossRef Full Text | Google Scholar

Neumaier, A. (2025). The Born rule–100 years ago and today. arXiv Prepr. arXiv:2502.08545 27, 415. doi:10.3390/e27040415

PubMed Abstract | CrossRef Full Text | Google Scholar

Nieuwenhuizen, T. (2022). Models for quantum measurement of particles with higher spin. Entropy Basel, Switz. 24, 1746. doi:10.3390/e24121746

PubMed Abstract | CrossRef Full Text | Google Scholar

Nieuwenhuizen, T. M. (2023). Exact solutions for black holes with a smooth quantum core. arXiv Prepr. arXiv:2302.14653.

Google Scholar

Nieuwenhuizen, T. M. (2024a). Solution of the dark matter riddle within standard model physics: from black holes, galaxies and clusters to cosmology. Front. Astronomy Space Sci. 11, 1413816. doi:10.3389/fspas.2024.1413816

CrossRef Full Text | Google Scholar

Nieuwenhuizen, T. M. (2024b). Indefinitely flat rotation curves from Mpc sized charged cocoons. Europhys. Lett. 148, 49002. doi:10.1209/0295-5075/ad895f

CrossRef Full Text | Google Scholar

Nieuwenhuizen, T. M. (2025). How the vacuum rescues the Lorentz electron and imposes its Newton and geodesic motion, and the equivalence principle, to appear Eur. J. Phys.

Google Scholar

Nieuwenhuizen, T. M., Perarnau-Llobet, M., and Balian, R. (2014). Lectures on dynamical models for quantum measurements. Int. J. Mod. Phys. B 28, 1430014. doi:10.1142/s021797921430014x

CrossRef Full Text | Google Scholar

Perarnau-Llobet, M., and Nieuwenhuizen, T. M. (2017a). Simultaneous measurement of two noncommuting quantum variables: solution of a dynamical model, Physical Review A 95 (5), 052129.

CrossRef Full Text | Google Scholar

Perarnau-Llobet, M., and Nieuwenhuizen, T. M. (2017b). Dynamics of quantum measurements employing two Curie--Weiss apparatuses, Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 375 (2106), 20160386.

PubMed Abstract | CrossRef Full Text | Google Scholar

Schrödinger, E. (1926). An undulatory theory of the mechanics of atoms and molecules. Phys. Rev. 28, 1049–1070. doi:10.1103/physrev.28.1049

CrossRef Full Text | Google Scholar

Van Den Bossche, M., and Grangier, P. (2023). Contextual unification of classical and quantum physics. Found. Phys. 53, 45. doi:10.1007/s10701-023-00678-x

CrossRef Full Text | Google Scholar

Wheeler, J. A., and Zurek, W. H. (2014). Quantum theory and measurement, 15. Princeton University Press.

Google Scholar