Modeling Biowaste Biorefineries: A Review

The biorefining of biowaste is an upcoming novel strategy, but is mostly still in its conceptual phase. Biowaste biorefineries would allow (rural) communities to convert their biowaste into value-added biofuels, biochemical compounds, and fertilizers. Several different types of biowaste biorefineries have already been developed, but little to none of these designs are already commercially exploited. Their further development and commercial implementation is hampered by the high investment costs and risks, little trusts in its novel technologies, expected yields and profits, and operating reliability. Modeling these integrated processes, together with their supply chains, would allow for optimizing the considered biorefinery designs and coincidently speeding up the R&D-process. The optimized biorefinery designs and supply chains would additionally embed an increased amount of trust in potential investors in terms of the economic sustainability of the considered novel processes. Therefore, in this publication, a summary of existing biorefinery models is presented, together with supply chain network models. The discussed biorefinery models are categorized according to the conversion platform they use, being thermochemical, biological, or hybrid ones. Furthermore, the overall inherent advantages and disadvantages of all conversion platforms are summarized and a scope of further research needs is presented.

1. Introduction

Major cities in Europe have recently been flooded several times with an ever increasing number of climate protesters. These climate protests and marches have been partially triggered by the 2018 United Nations Climate Report (IPCC, 2018). The report clearly states that immediate and grand actions are required if the increase in global temperature should be limited to the still manageable scenario of +1.5°C. In general, the public support for a more sustainable production and energy industry has drastically increased since the first effects of climate change are becoming more prevalent and visible. Fossil resources are becoming more controversial and are to be replaced with bio-resources in the future. However, in order to fully exploit the potential of these bio-resources, and additionally safeguarding arable land for food production, the use of waste streams as feed stocks for the production of energy and chemical compounds will have to be intensified. Just like fossil resources are converted into energy and chemical compounds in a refinery, bio-resources are converted in useful compounds in a biorefinery (Naik et al., 2010).

First generation biorefineries use general crops as feedstock (Cherubini et al., 2009). Most noticeable are rapeseeds and corn. This generation of biorefineries is already economically exploited but its use of general crops as feedstock raises ethical questions. The production of these crops takes up arable land, which can no longer be used for food. Additionally, while the growing of crops for energy is more profitable for farmers than the production of food, the diversity of crops is heavily reduced. Mono-crop farmlands and -areas are more prone for crop diseases and plagues, jeopardizing the energy supply, the food supply, and livelihood of farmers (Mohr and Raman, 2013).

The acknowledgment of the shortcomings of the first generation biorefineries led to the development of second generation biorefineries which use residual and waste streams as feedstock. These streams include lignocellulosic materials, green fertilizers and other farm residues (e.g., corn stover), kitchen waste, industrial waste, and forestry wastes (Cherubini et al., 2009; Naik et al., 2010; Mohr and Raman, 2013). These so-called biowaste biorefineries will be the main focus of this review. The economical exploitation of this type of biorefineries is still limited, mainly because of the inherent fluctuations in the feedstock supply, and therefore also in the expected yield. Waste streams are subjected to seasonal fluctuations in size and/or composition and are often difficult to preserve. To obtain an economically viable biorefinery, these fluctuations need to be taken into account in the designing phase. To speed up the designing (and eventually implementation) of biowaste biorefineries, whilst taking the multitude of possible feedstocks into account, rigorous models are needed (Wang et al., 2015). The main goal of this contribution is to give the reader an overview of already existing models, as well as assessing their properties and extent. An upcoming third generation of biorefineries are the marine biorefineries which use algae as feedstock. This type of biorefineries, together with algae technology, is still in its early development stages and will therefore not be taken into account in this contribution. The interested reader is referred to Laurens et al. (2017) and Cesario et al. (2018).

The sustainability of the biowaste biorefinery is additionally heavily affected by the management of the supply chain network. Policy makers and designers must also decide where to locate the biorefinery plant and, based on which feedstocks are abundantly available in the vicinity of the plant, the supply chain network, and used biorefining processes will change. To stress the importance of a convenient and smart supply chain network, a supply chain network model is included and briefly discussed.

The structure of this review is as follows: section 2 introduces the overall biorefining concept to give the reader a general overview of existing technologies and practices. The selected biowaste biorefinery models are presented in sections 3–5, based on which conversion platforms they use. This contribution will mainly focus on the presentation of process models which can be translated into algebraic and differential equations. Only in section 5, flowsheet models are considered. In section 6, a supply chain network model is presented. The presented models of sections 3–6 are discussed in section 7. Finally, in sections 8, 9, the overall conclusions and scopes for further research are presented, respectively.

2. Biorefining Concept

A biorefinery is the renewable equivalent of a fossil-based (petroleum) refinery. A variety of chemical components are produced starting from a biomass feedstock stream. Biorefineries can be subdivided in different categories based on four characteristics: (i) the used platforms or key intermediate products and processes, (ii) the targeted products (production of energy or components), (iii) the used feedstock, and (iv) the used processes (Cherubini et al., 2009). This contribution will categorize the discussed biorefinery models based on which conversion platform is used. There has been opted for this alternative while the other listed categorization techniques often display overlap, rendering it difficult to present a clear-cut overview of available models.

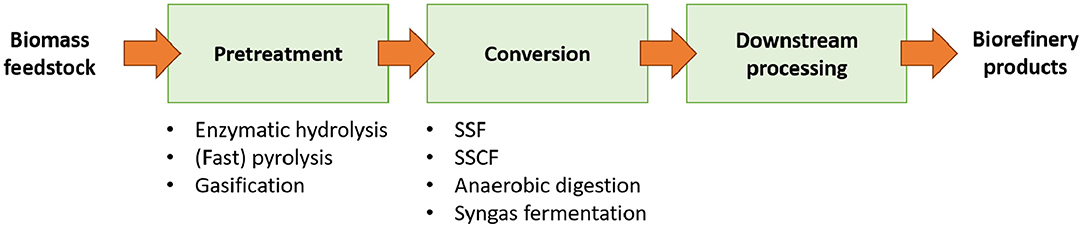
The general public still mostly associates biorefineries with the production of (liquid) biofuels. However, the production of platform chemicals via biorefining processes is deemed to be more sustainable than the production of biofuels (Mohr and Raman, 2013; Isikgor and Becer, 2015). Platform chemicals are not a final product on themselves but are used in subsequent processes to produce plastics, fibers, additives, etc. (Cherubini et al., 2009). Figure 1 represents the general layout of biorefinery plant (Cherubini et al., 2009). A biomass feedstock is, successively, submitted to pretreatment, conversion, and downstream processing steps. Depending on the selected feedstock and processes, different products are obtained. The pretreatment step is one of the most important steps in the entire process while both the efficiency of the conversion and downstream processing steps depend on it. The overall goal of the pretreatment is reducing the crystallinity of the raw feedstock and making the C5-, C6-sugars, and other structural components more accessible for the conversion steps. The fraction of biomass that is eventually not converted in one of the targeted products has to be separated from the product stream and decreases the process' carbon efficiency. Commonly used pretreatment steps include ammonia conditioning, (diluted) acid pretreatments, mechanic pretreatments (milling, i.a.), and steam reforming/explosion (Cherubini et al., 2009).

FIGURE 1

Figure 1. General biorefinery flowsheet, positioning the discussed models.

2.1. Conversion Platforms

Conversion platforms can be subdivided in three major categories (Cherubini et al., 2009): biochemical or biological, thermochemical, and hybrid conversion platforms. Biochemical and biological conversion platforms convert the pretreated biomass stream in the desired products with the use of micro-organisms, enzymatic, and fermentation processes, while thermochemical conversion platforms use general chemical processes. Recently developed hybrid conversion platforms combine the strengths of both previous options and are often characterized by a thermochemical pretreatment step and a biological conversion step (Michailos, 2018; Michailos et al., 2019).

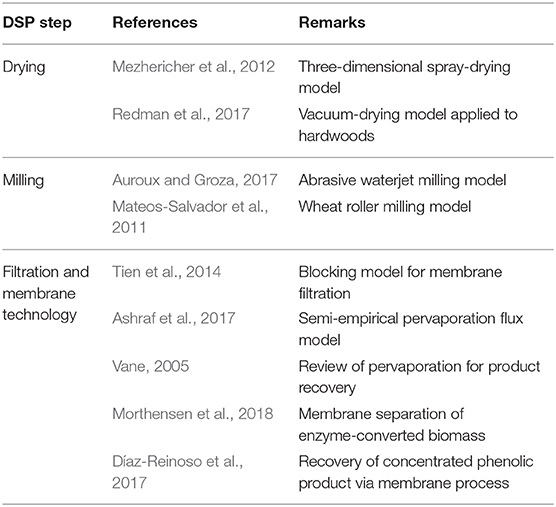
The targeted products have to eventually be separated from each other, by-products, and/or the fermentation media using columns and/or evaporation units. The efficiency and energy requirements of the downstream processing (DSP) steps heavily depend on the efficiency of all the previous steps. Remaining solids in the process stream can be removed via filtrations, centrifuges, and membrane technology. Crystallization, drying, and milling units can be added to the downstream processing train if the product has to be delivered in a certain form. The main focus of this contribution however will be on the pretreatment and conversion steps. The DSP steps are already extensively investigated and treated in literature. Table 1 lists several interesting sources on the commonly used DSP steps for the interested reader.

TABLE 1

Table 1. Further reading on DSP steps.

2.2. Feedstocks

2.2.1. Lignocellulosic Biomass

Lignocellulosic biorefineries are the most commonly investigated biorefinery type (regardless of what conversion platform they use), mainly due to the abundant occurrence of its feedstock (Piccolo and Bezzo, 2009). The main components of lignocellulosic biomass are lignin (L), hemicellulose (HC), and cellulose (C) (see Figure 2). The ratio of these main components will differ based on the source. Table 2 gives an overview of the composition of several lignocellulosic materials (Qian, 2014; Isikgor and Becer, 2015).

FIGURE 2

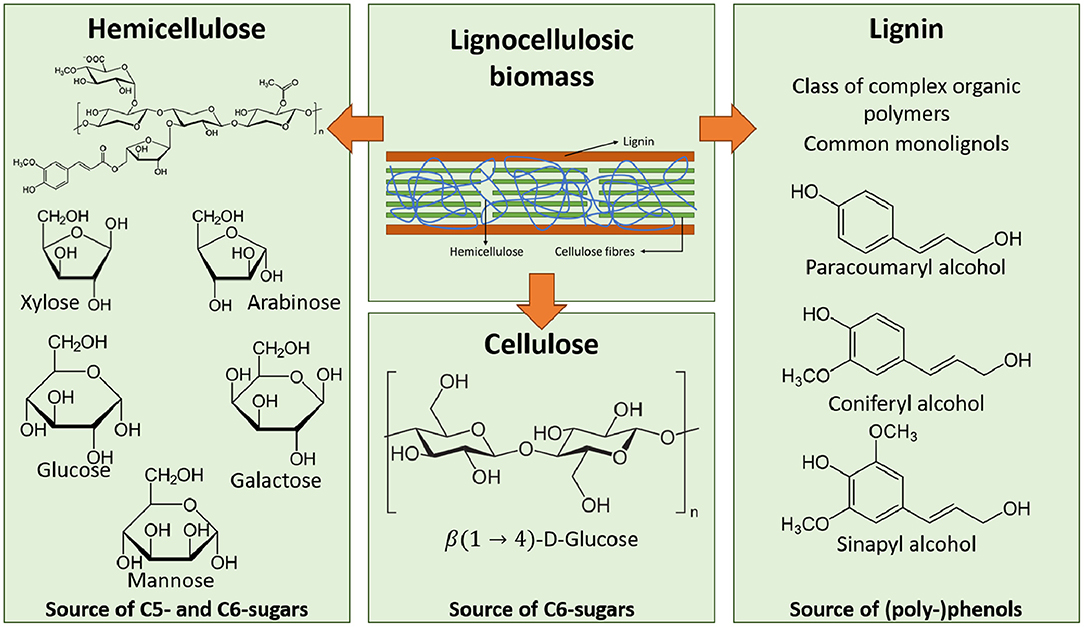
Figure 2. Composition of lignocellulosic biomass (Isikgor and Becer, 2015).

TABLE 2

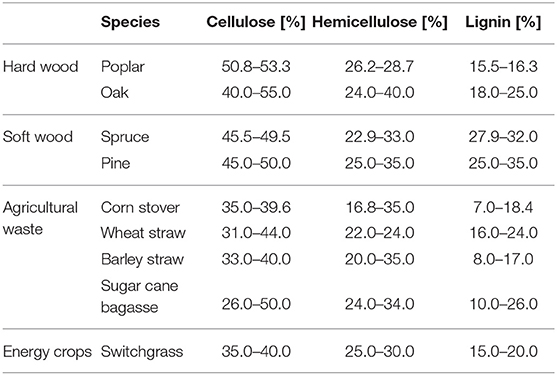
Table 2. Composition of different lignocellulosic biomass species (Carroll and Sommerville, 2009; Qian, 2014; Biswas et al., 2015; Isikgor and Becer, 2015).

Cellulose is made up of linked cellobiose (CB) chains, or linked β(1 → 4)-D-glucose (G) units (see Figure 2). It is the primary component of the cell walls of plants and is the most abundantly available organic carbon source on the planet (Isikgor and Becer, 2015). While cellulose is made up of linked glucose-units, it is a source of fermentable C6-sugars. Hemicellulose on the other hand is made up of both C6- and C5-sugars (see Figure 2). It acts as glue in the cell wall, interlinking cellulose fibers with each other and with lignin. The predominant structure of hemicellulose additionally differs between soft and hard wood. While soft wood hemicellulose is mostly made up of glucomannans, hard wood hemicellulose predominantly consists out of xylans (HX). The occurring C5-sugars in hemicellulose are xylose (X) an arabinose, and the occurring C6-sugars are mannose, glucose, and galactose. Lignin (L) is a polyphenolic polymer and is the third main component of lignocellulosic biomass. Its high polyphenolic content makes it the ideal natural source of aromatic compounds and (poly-)phenols. The three main reoccurring monolignons are paracoumaryl alcohol, coniferyl alcohol, and sinapyl alcohol (see Figure 2) (Carroll and Sommerville, 2009; Qian, 2014; Isikgor and Becer, 2015).

2.2.2. Green Biomass

Green biomass streams consists of living, herbaceous, and wet biomass like grasses and clover (Bedoic et al., 2019). Grasses can be sourced from, i.a., pasture lands, roadside cuttings, and (private) gardens and parks. Clover is a so-called cover crop and green manure. The soil is protected from erosion and run-off by the root system of the clovers during, what otherwise would be, fallow periods. Clovers are additionally part of the Leguminosae family which are characterized by containing the symbiotic Rhizobia bacteria in their root nodules. Rhizobia are capable of fixating atmospheric nitrogen, and thus fertilizing the soil. Harvested grasses and clovers can be used as fodder but a large fraction remains underused (Kamm et al., 2016; Bedoic et al., 2019).

2.2.3. Biowaste

The interest in waste biorefineries has steadily increased over the past decade. This type of biorefineries have a double advantage while, next to their biorefining capacities, they also act as waste processors. Biomass waste can be obtained from several different sources and industries. The main sources are agricultural waste streams (food), industry waste streams, and urban municipal waste. Most components of the agricultural waste streams can, however, also be subdivided into either lignocellulosic (e.g., corn stover) or green biomass (e.g., clovers and other grasses and herbaceous plants). The food industry is another major source of biomass waste streams: spent grains and filter cakes from breweries, bagasse and molasses from the sugar industry, etc. The final customers of the produced foods and agricultural products, i.e., urban municipalities, are on their turn also major producers of biomass waste streams. The composition of this waste is the most diverse one of all the feedstocks that are discussed in research. Fluctuations in feedstock size and composition are two major challenges that any waste-based, or even any, biorefinery must tackle. The efficiency of the biorefinery supply chain and overall logistic network plays a crucial role in guaranteeing the success of these biorefineries (Fava et al., 2015; Vea et al., 2018).

3. Biochemical and Biological Conversion Platforms

As mentioned in section 2.1, biorefineries using a biochemical or biological conversion platform employ enzymes and microorganisms to convert biomass into valuable products and energy. Generally, the overall structure of the biomass is broken down via enzymatic hydrolysis and the obtained hydrolysate stream is subsequently fermented using (genetically modified) microorganisms. Enzymatic reactions are characterized by an extremely high product selectivity, making this conversion platform the ideal platform to produce very specific products. Additionally, the used fermentation processes display high similarities to other, established, bioproduction processes. A multitude of techniques are therefore already available and the overall processes themselves have already been studied extensively (Michailos et al., 2019).

However, the particular biomass feedstocks (most commonly lignocellulosic biomass) have proven to introduce problems and challenges in the context of the otherwise straightforward biological conversion platform. The dense crystalline structure of lignocellulosic biomass makes it difficult for enzymes to penetrate and access the glycosidic bonds they are meant to hydrolyse. The yield of fermentable sugars in the hydrolysate streams can be so insufficient that the overall process is no longer profitable. It is therefore of crucial importance that the dense biomass feedstock is accordingly pretreated, allowing the enzymes to penetrate the structure more easily.

3.1. Enzymatic Hydrolysis

The enzymatic hydrolysis of lignocellulosic biomass is a highly specific process, rendering fermentable C5- and C6-sugars, oligomers, and polymers. The hydrolysis process is catalyzed by cellulase enzymes which decompose the cellulosic material in its structural compounds. The lignin fraction of the lignocellulosic material, however, is not decomposed or hydrolysed and remains as a solid in the hydrolysate. This inability of processing a major fraction, and thus carbon source, of the lignocellulosic feedstock is one of the major disadvantages of this technique (Sun and Cheng, 2002; Michailos et al., 2019).

Kadam et al. (2004) introduced a validated kinetic model of the enzymatic hydrolysis of lignocellulosic biomass, but only considers the hydrolysis of cellulose to cellobiose and glucose. It was experimentally validated by, amongst others, Hodge et al. (2008), Sin et al. (2010). The modeled reaction scheme is presented in Figure 3. Prunescu and Sin (2013) extended the model of Kadam et al. (2004) and added the enzymatic decomposition of xylan (the main component of hemicellulose) into acetic acid and xylose. The model of Kadam et al. (2004) already considered the inhibition of the cellulose decomposition reactions by xylose but did not consider its formation. Prunescu and Sin (2013) additionally takes the inhibitory effect of furfural (F) into account on the decomposition reactions of cellulose. Furfural can be formed in pretreatment processes preceding the enzymatic hydrolysis step. Especially acidic conditioning steps are prone of forming furfural (Jönsson and Martín, 2016).

FIGURE 3

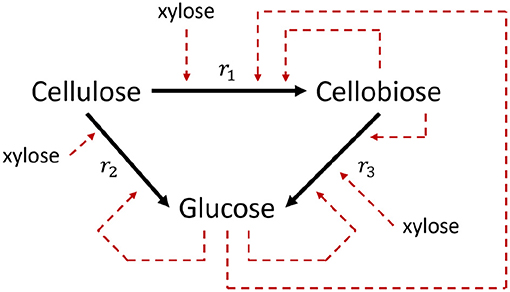
Figure 3. Modeled reaction scheme of the enzymatic hydrolysis of cellulose. Dashed lines indicated inhibition reactions (Kadam et al., 2004).

Figure 4 represents the general enzymatic reaction scheme that is modeled by both Kadam et al. (2004) and Prunescu and Sin (2013). The inhibitory effect of glucose, cellobiose, xylose, and furfural on the hydrolysis of cellulose is considered to be competitive. This implies that the inhibitors bind on the active site of the enzyme and thus compete with the substrate for this spot. Competitive inhibition is reversible and is deemed to be mechanistically more realistic than the irreversible noncompetitive inhibition (Kadam et al., 2004). Product is formed after the substrate adsorbs to the active site of the enzyme (E) and the enzyme-substrate complex (ES) is formed. This adsorption is reversible and is modeled via a Langmuir isotherm (see Equation 1). The formation and desorption of product (P) is considered to be irreversible. The reactions with cellulose as substrate are assumed to be first-order reactions and occur on the cellulose surface (see Equation 2). The formation of glucose from cellobiose occurs in the liquid reactor medium and is assumed to follow Michaelis-Menten kinetics (see Equation 3) (Kadam et al., 2004; Prunescu and Sin, 2013).

$\begin{array}{ll}\left[EC\right]=\frac{E{C}_{max}{K}_{EC,ad}\left[E_F\right]\left[C\right]}{1+K_{EC,ad}\left[E_F\right]}& (1)\end{array}$

with EC the enzyme-cellulose complex, EC_max the maximum mass of enzyme that can adsorb on one mass unit of cellulose, and [E_F] the concentration of free enzymes.

$\begin{array}{ll}{r}_i=\frac{k_i{\eta }_i\left(T,pH\right)\left({\displaystyle {\sum }_{j=1}^i}\left[E_{i}C\right]\right)}{1+\frac{\left[CB\right]}{K_{I,i}^{CB}}+\frac{\left[X\right]}{K_{I,i}^X}+\frac{\left[G\right]}{K_{I,i}^G}+\frac{\left[F\right]}{K_{I,i}^F}}i=1,2& (2)\end{array}$

$\begin{array}{ll}{r}_3=\frac{k_3\left[E_{3,F}\right]\left[CB\right]{\eta }_3(T,pH)}{1+\frac{\left[X\right]}{K_{I,3}^X}+\frac{\left[G\right]}{K_{I,3}^G}+\frac{\left[F\right]}{K_{I,3}^F}+\left[CB\right]}& (3)\end{array}$

The xylan to xylose reaction rate r₄ is modeled similarly to the cellulose to cellobiose and glucose reaction rates (Prunescu and Sin, 2013):

$\begin{array}{ll}{r}_4=\frac{k_4\left[E_{4}HX\right]\left[HX\right]{\eta }_4(T,pH)}{1+\frac{\left[CB\right]}{K_{I,4}^{CB}}+\frac{\left[X\right]}{K_{I,4}^X}+\frac{\left[G\right]}{K_{I,4}^G}+\frac{\left[F\right]}{K_{I,4}^F}}& (4)\end{array}$

with k_i the specific reaction rate constant of the i-th reaction, η_i(T, pH) the influence factor of T and pH on the i-th reaction, and $K_{I,i}^a$ the inhibitory constant of component a on the i-th reaction. The mass balances of cellulose, cellobiose, and glucose are given by (Kadam et al., 2004):

$\begin{array}{ll}\frac{d\left[C\right]}{dt}=-r_1-r_2& (5)\end{array}$

$\begin{array}{ll}\frac{d\left[CB\right]}{dt}=1.056r_1-r_3& (6)\end{array}$

$\begin{array}{ll}\frac{d\left[G\right]}{dt}=1.111r_1+1.053r_3& (7)\end{array}$

Flores-Sánchez et al. (2013) successfully adapted their model-based optimal experimental design framework to estimate the values of the kinetic parameters of the proposed enzymatic hydrolysis model in Equations (1) to (4). While enzymes display a (narrow) optimal temperature range, the reactor temperature T was found to have a major affect on the reaction rates and other kinetic parameters. Prunescu and Sin (2013) included this influence, together with the pH influence in the η_i(T, pH) factor. Flores-Sánchez et al. (2013) also included this influence by dynamically designing an optimal experimental design framework. By doing so, they include the inherent non-linearity of the reaction system, allowing for the attainment of good estimations for the kinetic parameters. The models presented by Kadam et al. (2004) and Prunescu and Sin (2013) have been implemented in several case studies. Amongst others are the kinetic modeling of the enzymatic hydrolysis of pretreated sugarcane straw, as presented by Angarita et al. (2015), and the model-based optimization of a large-scale bioethanol plant, presented by Prunescu et al. (2017).

FIGURE 4

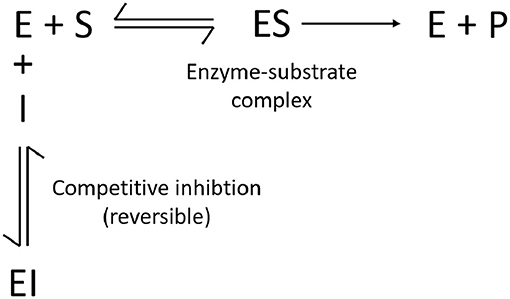
Figure 4. General enzymatic reaction scheme with competitive inhibition (E = enzyme, I = inhibitor, S = substrate, P = product).

More recently, Liang et al. (2019) developed a long-term Holtzapple-Caram-Humphrey-1 (HCH-1) model for the enzymatic hydrolysis of cellulose (C) by adapting the original HCH-1 model developed by Holtzapple et al. (1984). The original model only accounted for the initial reaction rates, making it invalid for long-term predictions, while the hydrolysis products have an influence on the reaction rates. The modified HCH-1 accounts for this influence on the cellulose conversion rate and enzyme stability over longer periods. Its main features are its use of the product binding constant β and the quantification of the number of active sites that are covered by enzymes (E) with the parameter ε (Holtzapple et al., 1984; Liang et al., 2019). The modified long-term HCH-1 model is given by Equation (8):

$\begin{array}{ll}\frac{d\left[G\right]}{dt}=\frac{\kappa \left[C\right]\left[E\right]i}{\alpha +\varphi \left[C\right]+ϵ\left[E\right]}& (8)\end{array}$

with

$\begin{array}{ll}i=\frac{1}{1+\beta \left[G\right]}& (9)\end{array}$

$\begin{array}{ll}\varphi =\frac{\left[C\right]-\alpha -\epsilon \left[E\right]+\sqrt{{\left(\left[C\right]-\alpha -\epsilon \left[E\right]\right)}^2+4\alpha \left[C\right]}}{2\left[C\right]}& (10)\end{array}$

$\begin{array}{ll}\alpha =\frac{a_1\left[G\right]}{\left[E\right](1+exp(-a_{2}x+a_3))}& (11)\end{array}$

$\begin{array}{ll}\frac{-d\left[E\right]}{dt}=k_1\left[E\right]-k_2(\left[E_0\right]-\left[E\right])\left[E_0\right]& (12)\end{array}$

$\begin{array}{ll}\kappa =\frac{k_3}{{(1+x^{k_4})}^{k_5}}+k_6& (13)\end{array}$

with κ the kinetic constant of the lumped enzyme, k_i, i = 1, …, 6, a_j, j = 1, …, 3, ϵ, and β are the 11 model parameters. x is the cellulose conversion. The estimation of the model parameters is described in Liang et al. (2019) but is not included in this contribution.

While the models developed by Kadam et al. (2004) and extended by Prunescu and Sin (2013) use a combination of both adsorption mechanisms and Michaelis-Menten kinetics, the HCH-1 model is purely based on adsorption mechanics. It additionally assumes non-competitive inhibition of the enzyme activity by the obtained hydrolysis products, in comparison with the competitive inhibition as used in the Kadam et al. (2004) model. The modified HCH-1 model further distinguishes itself from the original model by considering a lumped enzyme mixture (κ is the kinetic constant of the lumped enzyme), making it more closely aligned with reality (Liang et al., 2019).

3.2. Simultaneous Saccharification and Fermentation

All enzymatic hydrolysis models presented in section 3.1 strongly focus on the inhibitory effect of the hydrolysis products on the enzyme activity. This is one of the major disadvantages of the enzymatic hydrolysis process. To circumvent this, the produced sugars are immediately fermented after their formation. The hydrolysis (or saccharification) and fermentation process occur simultaneously in the same vessel. The reasoning of the simultaneous saccharification and fermentation (SSF) process is based on the Le Chatelier's principle, which states that a system in equilibrium will shift to a new equilibrium if a change in the system occurs, in order to neutralize the imposed change. Thus, if the product of the hydrolysis process is removed, new product will be formed, pushing the hydrolysis to the product side of the equation. SSF processes, however, are very complex and their performance is highly dependent on the operating conditions and used feedstock (Shadbahr et al., 2017; Singh et al., 2018).

Early mathematical models of the SSF process were developed by Philippidis et al. (1992, 1993). In its essence, the proposed SSF model is a coupling of the enzymatic hydrolysis of cellulose and the fermentation of glucose to ethanol by microorganisms. More recent contributions are made by Shadbahr et al. (2017), Sakimoto et al. (2017), and Singh et al. (2018). While Shadbahr et al. (2017) consider the SSF of cellulose, Singh et al. (2018) consider the SSF of starch. The latter model can therefore be applied to model SSF processes of starchy biowaste, like kitchen waste and agricultural residues containing a, relatively, little amount of lignocellulose. Hou and Bao (2018) modeled the SSF of cellulose to citric acid but this model will not be discussed in this contribution.

The kinetic SSF model of Shadbahr et al. (2017) is a modification of the mathematical SSF models presented by Philippidis et al. (1992, 1993) and Pettersson et al. (2002). The enzymatic hydrolysis step of cellulose by cellulases is modeled as the degradation of cellulose to cellobiose. The amount of glucose that is formed by the exo- and endo-glucanases is considered to be negligible. Cellobiose is eventually converted to glucose by β−glucosidase (see Figure 5). The formed glucose is subsequently fermented to ethanol (Et) and is used for biomass (B) accumulation. Shadbahr et al. (2017) additionally consider the fermentation of mannose to ethanol (and biomass) while this C6-sugar is common in softwood and other lignocellulosic material.

FIGURE 5

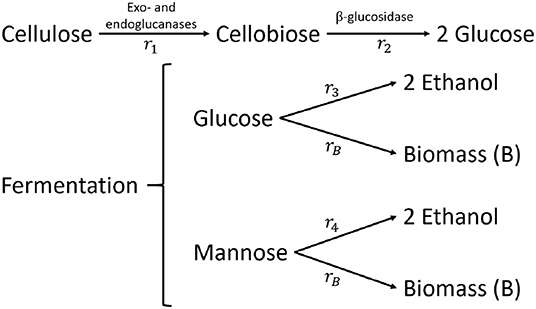
Figure 5. Reaction flowsheet of the SSF of cellulose to ethanol and biomass (Philippidis et al., 1992; Shadbahr et al., 2017).

The conversion rate r₁ of cellulose to cellobiose by the exo- and endo-glucanases is given by (Prunescu and Sin, 2013; Sakimoto et al., 2017; Shadbahr et al., 2017):

$\begin{array}{ll}{r}_1=\frac{\kappa \left[C\right]exp\left(-\lambda t\right)}{1+\left[CB\right]/K_{I,1}^{CB}+\left[G\right]/K_{I,1}^G}\left(\frac{K_{I,1}^{Et}}{K_{I,1}^{Et}+\left[Et\right]}\right)& (14)\end{array}$

with κ the lumped specific rate constant of the exo- and endoglucanases, and λ the rate of cellulose surface decrease due to enzymatic activity. $K_I^{Et}$ is the inhibition constant of the cellulases by ethanol. Bezerra and Dias (2005) however found that the inhibitory effect of ethanol on the enzymatic hydrolysis of cellulose is very limited. The conversion rate r₂ of cellobiose to glucose by β−glucosidase is given by (Prunescu and Sin, 2013; Shadbahr et al., 2017):

$\begin{array}{ll}{r}_2=\frac{k_2\left[Et\right]\left[CB\right]}{K_{S,E}\left(1+\left[G\right]/K_{I,2}^G\right)+\left[CB\right]}\left(1-K_{EL,ad}\left[L\right]\right)& (15)\end{array}$

While the lignin-fraction of the lignocellulosic biomass is not metabolized, its inhibitory effect on the enzymatic reactions must also be accounted for. β−glucosidase is prone to adsorb to lignin (L), resulting in a loss of free enzymes and thus enzymatic activity (Philippidis et al., 1992; Shadbahr et al., 2017). K_{EL, ad} is the specific adsorption rate constant of the adsorption of β-glucosidase enzyme to lignin. K_{S, E} is the cellobiose saturation constant for β-glucosidase. Michaelis-Menten kinetics are assumed for the enzymatic processes and the adsorption of the enzymes to the cellulose is modeled according to the Langmuir isotherm (see Equation 1).

The volumetric consumption rates r₃ and r₄ by the microorganism of glucose and mannose, respectively, are given by (Philippidis et al., 1992; Sakimoto et al., 2017; Shadbahr et al., 2017):

$\begin{array}{ll}{r}_3=\frac{\left[G\right]}{\left[G\right]+\left[M\right]}\left(\frac{r_B}{Y_{B,G}}+m_s\left[B\right]\right)& (16)\end{array}$

$\begin{array}{ll}{r}_4=\frac{\left[M\right]}{\left[G\right]+\left[M\right]}\left(\frac{r_B}{Y_{B,M}}+m_s\left[B\right]\right)& (17)\end{array}$

with r_B the volumetric rate of biomass production and Y_BG the yield coefficient of biomass from metabolizing glucose. r_B is given by (Philippidis et al., 1992; Shadbahr et al., 2017):

$\begin{array}{ll}{r}_B={\mu }_m\left[B\right]\left(\frac{\left[G\right]+\left[M\right]}{K_G+\left[G\right]+\left[M\right]}\right)\left(\frac{K_{I,B}^{Et}}{K_{I,B}^{Et}+\left[Et\right]}\right)& (18)\end{array}$

with μ_m the maximum specific growth rate of the used microorganism and $K_{I,B}^{Et}$ the inhibitory effect of ethanol on (the growth of) the microorganism. The mass balances of the considered system components are given by (Philippidis et al., 1992; Prunescu and Sin, 2013; Shadbahr et al., 2017):

$\begin{array}{ll}\frac{d\left[C\right]}{dt}=-r_1& (19)\end{array}$

$\begin{array}{ll}\frac{d\left[CB\right]}{dt}=1.056r_1-r_2& (20)\end{array}$

$\begin{array}{ll}\frac{d\left[G\right]}{dt}=1.053r_2-r_3& (21)\end{array}$

$\begin{array}{ll}\frac{d\left[M\right]}{dt}=-r_4& (22)\end{array}$

$\begin{array}{ll}\frac{d\left[B\right]}{dt}=r_B& (23)\end{array}$

$\begin{array}{ll}\frac{d\left[Et\right]}{dt}=0.511(r_3+r_4)& (24)\end{array}$

The SSF model presented by Singh et al. (2018) considers the degradation of starch into glucose with the use of amylase. The formed glucose is subsequently fermented into ethanol and CO₂ with the use of Saccharomyces cerevisiae. The enzymatic saccharification of starch (St) into glucose (G) was modeled with Michaelis-Menten kinetics (Singh et al., 2018):

$\begin{array}{ll}{r}_S=V_{max}\frac{\left[St\right]}{K_{MM,S}+\left[St\right]}& (25)\end{array}$

with r_S the rate of glucose formation from starch, V_max the maximum rate of glucose formation, and K_MM,S the Michaelis-Menten constant for the considered enzymatic reaction. The mass balance of glucose in the system is given by (Singh et al., 2018):

$\begin{array}{ll}\frac{d\left[G\right]}{dt}=r_S-r_u& (26)\end{array}$

with r_u the uptake rate of glucose by S. cerevisiae. The magnitude of r_u is defined by the amount of glucose that is used for ethanol production, the accumulation of biomass, and cell maintenance. The specific growth rate μ of S. cerevisiae is modeled according to Monod kinetics and is defined by (Singh et al., 2018):

$\begin{array}{ll}\mu ={\mu }_m\frac{\left[G\right]}{K_S+\left[G\right]}& (27)\end{array}$

with μ_m the maximum specific growth rate of S. cerevisiae and K_S the saturation constant. Accordingly (Singh et al., 2018):

$\begin{array}{ll}\frac{d\left[B\right]}{dt}=\mu \left[B\right]={\mu }_m\frac{\left[G\right]}{K_S+\left[G\right]}\left[B\right]& (28)\end{array}$

The mass balances of the system's key components are defined by (Singh et al., 2018):

$\begin{array}{ll}\frac{d\left[St\right]}{dt}=-r_S=-V_{max}\frac{\left[St\right]}{K_{MM}+\left[St\right]}& (29)\end{array}$

$\begin{array}{ll}\frac{d\left[B\right]}{dt}={\mu }_m\frac{\left[G\right]}{K_s+\left[G\right]}\left[B\right]& (30)\end{array}$

$\begin{array}{ll}\frac{d\left[Et\right]}{dt}=q_m\frac{\left[G\right]}{K_s+\left[G\right]}\left[B\right]& (31)\end{array}$

$\begin{array}{l}\frac{d\left[G\right]}{dt}=1.11r_S-r_u=1.11V_{max}\frac{\left[St\right]}{K_{MM}+\left[St\right]}\\ -\left(\frac{1}{Y_{P,St}}\frac{d\left[Et\right]}{dt}+\frac{1}{Y_{B,St}}\frac{d\left[B\right]}{dt}+m_S\left[B\right]\right)& (32)\end{array}$

Per 1.11 unit of hydrolysed cellulose, 1 unit of glucose is formed. Y_{P, St}, Y_{B, St} are the product and biomass yield coefficients, linking the observed production and growth rates to the substrate uptake rate. m_S is a similar coefficient, linking the consumption of substrate to the rate of cell maintenance. The proposed model was validated for the SSF of algal starch (i.e., starch produced by algae) and was able to accurately predicted the considered key system components (Singh et al., 2018).

Note that while Philippidis et al. (1992) and Shadbahr et al. (2017) did consider the inhibitory effect of glucose on the microbial growth rate, Singh et al. (2018) did not, by assuming that the glucose accumulation in the reactor medium is negligible. They additionally did not consider product inhibition by the produced ethanol, assuming that the produced amount is equally negligible. The model proposed by Singh et al. (2018) can however by easily converted to match the outlay of the more detailed SSF model proposed by Shadbahr et al. (2017) by adding the appropriate inhibitory factors.

Both presented models mainly focus on the hydrolysis of cellulose and the fermentation of glucose, or other C6-sugars. However, as indicated by the SSF model developed by Prunescu and Sin (2013), C5-sugars are also present in the system. In an SSF process, these C5-sugars, like xylose, are not metabolized during the fermentation step. The full potential of the hydrolysate stream is thus not fully exploited. To circumvent this deficiency, the simultaneous saccharification and co-fermentation process was introduced.

3.3. Simultaneous Saccharification and Co-fermentation

The main goal of a simultaneous saccharification and co-fermentation (SSCF) process is the simultaneous, or co-fermentation, of both C5- and C6-sugars. Most microorganisms, however, either metabolize either C5- or C6-sugars, or display a very distinct preference for one of the two. Advances in the genetic modification of microorganisms, however, has allowed for the development of microorganism strains that are capable of processing both C5- and C6-sugars, without displaying a preference for one of the two. Morales-Rodriguez et al. (2011), for instance, consider the modified Escherichia coli ATCC-55124 strain in their SSCF model, while Krishnan et al. (1999) consider the modified S. cerevisiae 1400(pLNH33) strain. Chen et al. (2018) on the other hand modeled a co-fermentation process based on the co-culture of several genetically modified S. cerevisiae strains, each one specialized in metabolizing one particular type of substrate.

The SSCF model as proposed by Morales-Rodriguez et al. (2011) is a combination of the enzymatic hydrolysis of cellulose as presented by Kadam et al. (2004) and the co-fermentation model as presented by Krishnan et al. (1999). While the enzymatic hydrolysis of cellulose has already been extensively discussed in the previous sections (see sections 3.1 and 3.2), this part of the model will not be discussed in the context of SSCF processes. The enzymatic hydrolysis process of hemicellulose with the use of xylanases was extensively analyzed and modeled by Dutta and Chakraborty (2015). This enzymatic process is, just like the enzymatic hydrolysis of cellulose, a two-phase process during which the insoluble solid, being (hemi-)cellulose, is decomposed into smaller components that immediately dissolve in the reactor medium. Dutta and Chakraborty (2015) model the adsorption of the enzymes from the liquid phase on the solid phase according to the Langmuir isotherm (see Equation 1).

Chen et al. (2018) modeled the subsequent co-fermentation of cellobiose and xylose via a mixed culture of recombinant S. cerevisiae species. The proposed model assumes that the fermentation process follows Monod kinetics. The model includes substrate competition and the inhibitory effect of both substrates and products on the growth of the recombinant S. cerevisiae. The model considers two simultaneously grown S. cerevisiae strains, EJ2 and SR8, that metabolize cellobiose and xylose, respectively. For the EJ2-strain, it was found that the initial cellobiose concentration has a major impact on the ethanol production by the recombinant S. cerevisiae strain. Therefore, a S₀ factor was included in the expression for the ethanol production growth rate ν, rendering the following (semi-empirical) correlation (Chen et al., 2018):

$\begin{array}{ll}\nu =exp\left(0.011\left[S_0\right]\right)\frac{{\nu }_m\left[S\right]}{K_M+\left[S\right]+{\left[S\right]}^2/K_I}\left(1-{\left(\frac{\left[Et\right]}{\left[E{t}_m\right]}\right)}^{\gamma }\right)& (33)\end{array}$

with [S₀] the initial cellobiose concentration, K_M the Monod constant, K_I the inhibition constant, ν_m the maximum ethanol production rate, [S] the current glucose and xylose concentration, [Et] the ethanol concentration, [Et_m] the lethal ethanol concentration (above which the cells cease to grow), and γ a constant linking ν and [Et].

Chen et al. (2018) noticed that the SR8 strain was unable to uptake xylose when it was only in a small concentration present in the medium. Additionally, when xylose levels were low and xylose consumption had ceased, the consumption of ethanol by the SR8 strain became prevalent. Both phenomena caused the experimentally acquired data to differ from the predictions made by the model. To rectify the discrepancy, the ethanol consumption was accounted for in the model via curve fitting and the introduction of two additional fermentation constants b₁ and b₂. The inhibitory effect of xylose was neglected, as its effect was much smaller as that of the produced ethanol. The modified kinetic model of the substrate consumption is given by the following correlation (Chen et al., 2018):

$\begin{array}{ll}-\frac{d\left[S\right]}{dt}=\frac{1}{b_1{Y}_{Et,S}}\frac{d\left[Et\right]}{dt}+\frac{1}{b_2{Y}_{B,S}}\frac{d\left[B\right]}{dt}+m_s& (34)\end{array}$

with Y_Et,S the product yield constant, Y_B,S the cell mass yield constant, [B] the cell concentration, and m_s the maintenance coefficient.

Another co-fermentation model was developed by Sreemahadevan et al. (2018) and considers the co-culture of S. cerevisiae and Scheffersomyces stipitis instead. The growth kinetics were also derived from the Monod equation, which was altered accordingly to account for product and substrate inhibitory effects. The model proposed by Sreemahadevan et al. (2018) displays high similarities with the model proposed by Chen et al. (2018) and is therefore not further discussed.

3.4. Anaerobic Digestion

The anaerobic digestion of waste water treatment sludge, and (solid) biowaste is being applied more and more often. The main products obtained from an anaerobic digestion process are biogas, compost, and fertilizers (Pastor-Poquet et al., 2018). The most commonly used process model is the IWA Anaerobic Digestion Model No 1 (ADM1), compiled by Batstone et al. (2002). Both biochemical and physico-chemical processes are considered. The anaerobic digester is modeled as a CSTR with a fixed volume (F_out = F_in) (see Figure 6). In the context of biochemical reactions, only the biodegradable substrate COD (Chemical Oxygen Demand) input is considered. All intracellular reaction are modeled via Monod-kinetics. The physico-chemical reactions in the liquid phase can be mathematically formulated both using algebraic or differential equations. If it is opted for the latter option, the model is more prone to become stiffer due to the large number of differential equations. The ADM1 as presented by Batstone et al. (2002) considers 24 components, 19 reactions, and the time unit is days (d). The mass balance of a component i, in the liquid phase, is defined by:

$\begin{array}{ll}\frac{d{S}_{l,i}}{dt}=\frac{F_{in}{S}_{in,i}}{V_l}-\frac{F_{out}{S}_{out,i}}{V_l}+{\displaystyle \sum _{j=1}^{19}}{\rho }_j{\nu }_{i,j}& (35)\end{array}$

with ρ_j kinetic rate coefficients and ν_{i, j} the biochemical rate coefficient of process j for the formation of component i.

FIGURE 6

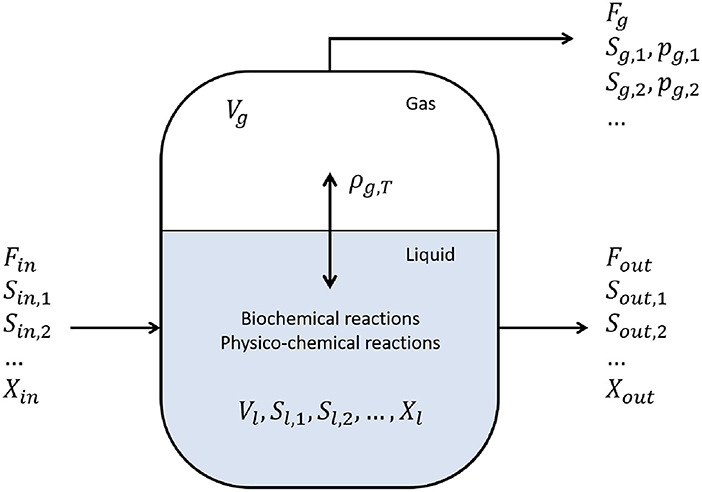
Figure 6. Anaerobic digestion reaction system. With F_i the flow [m³ · d⁻¹], S_i the concentration of a dissolved component i in the liquid phase, and X_i the concentration of a particle i in the liquid phase, both in [kg COD · m⁻³], p_i the pressure of component i [bar], V_i the volume of component i [m³], and ρ_{j, T} the rate of reaction j at temperature T (Batstone et al., 2002).

The ADM1 as presented by Batstone et al. (2002) has already been applied (and adapted) to a multitude of processes. Biernacki et al. (2013) applied the ADM1-model to the anaerobic digestion of grass, maize, silage, and industrial glycerine. Arnell et al. (2016) modeled the co-digestion of multiple feedstock by including co-digestion in the ADM1-model. A hydrogen-production model was developed by Ntaikou et al. (2010) based on the ADM1-model, while Zhao et al. (2019) adapted the ADM1-model for the production of bio-methane from food waste. The structural and practical identifiability of the ADM1-model was assessed by Nimmegeers et al. (2017). While structural identifiability refers to whether or not the model's structure allows for the unique estimation of the underlying model parameters, practical identifiability refers to the problem of finding accurate parameter estimates considering the (practical) limitations of the model input and measuring conditions. Several more examples of the application, adaptation, and extension of the ADM1-model are available in literature, but are not included in this review for the sake of clarity. The interested reader is referred to, i.a., García-Diéguez et al. (2013) and Song et al. (2018).

4. Thermochemical Conversion Platforms

One of the major disadvantages of the previously discussed biochemical conversion platforms are their inability to process the lignin fraction of (lignocellulosic) biomass. The lignin fraction even displayed an inhibitory effect on the conversion of cellulose and hemicellulose. Removing lignin from the feedstock prior to its conversion is costly and additionally inherently results in an unwanted loss of carbon (Li et al., 2018). Biorefineries which employ a thermochemical conversion platform decompose the entire biomass feedstock in its basic structural elements or components, which are subsequently converted to the desired products via tubular flow reactors and catalytic synthesis (Baliban et al., 2013; Michailos et al., 2017). This results in a more efficient usage of the biomass feedstock in comparison to the biochemical conversion platforms.

Two main thermochemical conversion techniques will be discussed in this section, with a focus on two thermochemical pretreatment steps: fast pyrolysis and gasification. Both techniques are based on the breakdown of the biomass with the use of added heat. The different process conditions of pyrolysis and gasification processes result in the formation of different intermediate products. A (fast) pyrolysis process transforms the biomass, in the absence of oxygen, into non-condensable gases (like CO, CO₂, and H₂), tar or bio-oil, and biochar or solid carbon. (Fast) pyrolysis processes occur at relatively low temperatures (between 300 and 600 °C) and are characterized by a high liquid fuel yield, i.e., bio-oil (Anca-Couce and Scharler, 2017; Goyal and Pepiot, 2017). Bio-oil is considered to be a suitable replacement for fossil fuels and displays many advantageous properties, like its ease of storing and transportation (Cai et al., 2018). Gasification processes are in their essence pyrolysis processes, but occur at higher temperatures (800–1,200 °C) and mostly in the presence of oxygen (Goyal and Pepiot, 2017; Jin et al., 2017). Because of the higher process temperatures, the yield of gaseous products is higher than in the case of pyrolysis processes. The produced syngas mainly consists of H₂, CO, CO₂, and CH₄.

4.1. Fast Pyrolysis

During a pyrolysis process, the biomass feedstock is depolymerized in the absence of oxygen. The pyrolysis of (lignocellulosic) biomass is a heterogeneous endothermic reaction, with increasing reaction rate with temperature (Papari and Hawboldt, 2015; Dhyani and Bhaskar, 2018). Four types of pyrolysis processes can be distinguished: (i) Fast pyrolysis, (ii) Slow pyrolysis, (iii) Intermediate pyrolysis, and (iv) hydropyrolysis. The first three processes occur in an inert nitrogen environment, while the latter occurs in a reductive hydrogen environment. The adjectives fast, slow, and intermediate relate to the heating rate used during the process. The faster the heating rate of the biomass is, the more liquid bio-oil is produced. Slower heating rates enable the occurrence of more unwanted secondary reactions and the formation of non-condensable compounds from the primary pyrolysis products (Dhyani and Bhaskar, 2018). Fast pyrolysis processes are characterized by high heating rates, as the biomass is rapidly heated to high temperatures. While this pyrolysis process type yields the most bio-oil, it will be the main focus of this section.

Commonly used pyrolysis reactors include fixed-, bubbling, and boiling bed reactors (Isahak et al., 2012; Dhyani and Bhaskar, 2018). These reactor types have already been extensively analyzed and modeled in the context of the pyrolysis of coal. Due to the high resemblance of coal and lignocellulosic biomass, early (lignocellulosic) biomass models are unsurprisingly heavily influenced by and based on the already available coal pyrolysis models. For instance, Michailos et al. (2017) modeled and compared the fast pyrolysis of bagasse followed by hydroprocessing, and the gasification of bagasse followed by Fischer-Tropsch synthesis. Both processes have already been previously successfully applied for the production of liquid fuels from coal.

Other earlier model contributions include the mathematical models of the fast pyrolysis of a single wood particle by Rabinovich et al. (2009) and the fast pyrolysis of biomass in circulating fluidized bed reactors by Van de Velden et al. (2008). Anca-Couce et al. (2013) introduced a multi-scale model of the pyrolysis of biomass in a fixed-bed reactor. Lerkkasemsan and Achenie (2014) introduced a fuzzy modeling framework and applied it to the pyrolysis of biomass.

The fast pyrolysis model proposed by Rabinovich et al. (2009) consists of three submodels: (i) A kinetic model of the pyrolysis of the different components [cellulose (C), hemicellulose (HC), and lignin (L)] of the biomass, (ii) A thermal model for the heating of one biomass particle in the boiling bed reactor, and (iii) A model of the biomass particle motion in the free reactor space. The diameter of the biomass particle is assumed to be smaller than 1 mm because the goal of the biomass pyrolysis is the production of liquid bio-oil. Therefore, the heating rate of the biomass should be high. Figure 7 represents the reaction flowsheet considered by Rabinovich et al. (2009). The kinetic parameters k_i are assumed to obey Arrhenius law:

$\begin{array}{ll}{k}_i=A_{i}exp\left(\frac{-E_{a,i}}{RT}\right)& (36)\end{array}$

with A_i the pre-exponential factor, E_{a, i} the activation energy of the i-th reaction, and R the universal gas constant. k₁–k₄ are separately determined for each biomass component. Nunes (2015) and Wang et al. (2017) extended the Arrhenius law to the fast pyrolysis of lignocellulosic biomass via the introduction the biomass conversion magnitude α, which is also a function of the reactor temperature T (Nunes, 2015; Wang et al., 2017):

$\begin{array}{ll}\frac{d\alpha }{dt}=k(T)f(\alpha )& (37)\end{array}$

$\begin{array}{ll}=Aexp\left(\frac{-E_a}{RT}\right)f\left(\alpha \right)& (38)\end{array}$

with k(T) the reaction rate, according to the Arrhenius law as presented in Equation (36). Equation (37) is valid for an isothermal reaction. In the case of a non-isothermal reaction with a linear heating rate dT/dt = β, Equation (37) is replaced by (Nunes, 2015; Wang et al., 2017):

$\begin{array}{ll}\frac{d\alpha }{dT}=\frac{d\alpha }{dt}\frac{dt}{dT}=\frac{1}{\beta }Aexp\left(\frac{-E_a}{RT}\right)f\left(\alpha \right)& (39)\end{array}$

f(α) models the biomass pyrolysis reaction. The most commonly used model is the first-order reaction model (Cai et al., 2013; Wang et al., 2017): f(α) = (1−α)ⁿ (with n = 1). The thermogravimetric analyses performed by Van de Velden et al. (2008) confirm this assumption. The reaction flowsheet as modeled by Van de Velden et al. (2008) is represented in Figure 8. The mass balances of the biomass (BM), non-condensable gases (G), bio-oil (BO), and char (C) are given by (Van de Velden et al., 2008):

$\begin{array}{ll}\frac{d{m}_{BM}(t)}{dt}=-(k_1+k_2+k_3)m_{BM}(t)=-k{m}_{BM}(t)& (40)\end{array}$

$\begin{array}{ll}\frac{d{m}_G(t)}{dt}=k_1{m}_{BM}(t)+k_4{m}_{BO}(t)& (41)\end{array}$

$\begin{array}{ll}\frac{d{m}_{BO}(t)}{dt}=k_2{m}_{BM}(t)-k_4{m}_{BO}(t)& (42)\end{array}$

$\begin{array}{ll}\frac{d{m}_C(t)}{dt}=k_3{m}_{BM}(t)& (43)\end{array}$

More recent contributions in the field of (fast) pyrolysis modeling include the Aspen Plus model for the pyrolysis of municipal green waste by Kabir et al. (2015), the kinetic model of the fast pyrolysis of bagasse in a fluidized bed reactor by Michailos (2018), and the mathematical model of the bio-oil production via the fast pyrolysis of bagasse in a circulating fluidized bed reactor by Treedet et al. (2017). Ciesielski et al. (2018) presented a multi-scale model of the catalytic fast pyrolysis of biomass. The considered process scales by Ciesielski et al. (2018) range from the atomistic scale to the reactor scale. Other contributions include Matta et al. (2017) and Ranzi et al. (2017a,b). Several comprehensive review papers have already been published on the subject biomass pyrolysis. The interested reader is referred to Isahak et al. (2012), Sharma et al. (2015), Papari and Hawboldt (2015), and Dhyani and Bhaskar (2018). Additionally, SriBala et al. (2019) recently presented a review on the state of the art in measuring fast pyrolysis kinetics. This comprehensive review is especially useful in the context of further extending the already available pyrolysis model collection, and validating existing models with experimental data.

FIGURE 7

Figure 7. Reaction flowsheet of the biomass pyrolysis process (adapted from Rabinovich et al., 2009).

FIGURE 8

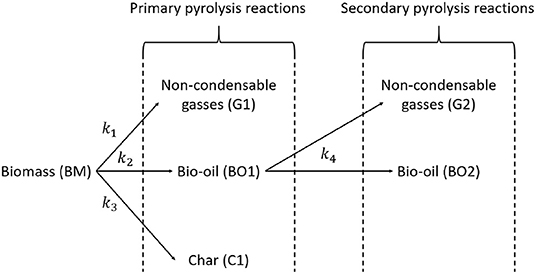
Figure 8. Reaction flowsheet of the biomass pyrolysis process (adapted from Van de Velden et al., 2008).

4.2. Gasification

Gasification processes are thermochemical conversion processes that occur at higher temperatures (800–1,200°C) than pyrolysis processes and in the presence of oxygen. The main product obtained during gasification processes is syngas, mainly consisting of H₂, CO, CO₂, CH₄, and other lightweight hydrocarbons. Syngas can be directly used as a gaseous fuel, but can also be transformed into other products, like alcohols and acids, using (bio-)chemical processes (Goyal and Pepiot, 2017; Hejazi et al., 2017a).

While the gasification process is in its essence a rigorous pyrolysis process, both processes display a high level of resemblance. The developed kinetic models describing the gasification of biomass are therefore often very, to entirely, similar to those describing the (fast) pyrolysis of the same biomass feedstock. The kinetic biomass gasification model developed by Hejazi et al. (2017a), for instance, considers a two-step gasification mechanism which is very similar to the reaction flowsheet displayed in Figure 8. The second step in the gasification process as modeled by Hejazi et al. (2017a) converts the bio-oil fraction entirely into non-condensable gases. This so-called thermal bio-oil cracking during the secondary pyrolysis reactions is one of the main differences between pyrolysis and gasification processes. The stoichiometry of the bio-oil (BO) cracking process is given by (Hejazi et al., 2017a):

$\begin{array}{ll}\text{BO}\to {\lambda }_{CO}CO+{\lambda }_{C{O}_2}C{O}_2+{\lambda }_{H_2}{H}_2+{\lambda }_{C{H}_4}C{H}_4+{\lambda }_{BO}BO& (44)\end{array}$

with λ_i the corresponding stoichiometric coefficients. The operating conditions, like residence time in the reactor and temperature, have an influence on the stoichiometric coefficients. Depending on these operating conditions, the remaining bio-oil fraction can fluctuate between 22 and 0% (Hejazi et al., 2017a). The cracking process is modeled as a first-order process, following the Arrhenius law. The primary reactions, which convert the biomass stream into char, non-condensable gases, and bio-oil, are also modeled as first-order reaction (Van de Velden et al., 2008; Hejazi et al., 2017a). The model presented by Hejazi et al. (2017a) considers a dual fluidized bed reactor and is compared and validated based on the experimental results obtained from a pilot set-up (Hejazi et al., 2017b).

Other contributions include the kinetic-compartmental model for the gasification of potassium-containing cellulose (Egedy et al., 2018), the compact kinetic biomass gasification model (Goyal and Pepiot, 2017), and the multi-scale model of biomass gasification in a steam-air blown bubbling fluidized bed reactor (Bates et al., 2017). Due to their high resemblance to the already discussed kinetic models in section 4.1, these models will not be further discussed.

5. Hybrid Conversion Platforms

The main disadvantage of biochemical degradation and conversion processes is their inability to process the lignin fraction of the biomass feedstock. This inherently results in a loss of carbon and thus an inefficient feedstock usage. Purely thermochemical conversion processes, on the other hand, are characterized by their low product selectivity and thus relatively low yields. Hybrid biorefineries employ both previously introduced bioconversion platforms, i.e., biological and thermochemical conversion platforms, simultaneously. By using a thermochemical degradation step (like pyrolysis or gasification), followed by a biochemical conversion step, the usage of the biomass feedstock, and the production of the desired products, is significantly increased. These characteristics make the two-platform biorefinery perhaps the most integrated design (Pardo-Planas et al., 2017; Michailos et al., 2019).

Pardo-Planas et al. (2017) presented an Aspen Plus model of the production of ethanol and acetic acid with the use of syngas fermentation. The considered biomass feedstock is switchgrass (see Table 2). The process flowsheet is represented in Figure 9. The modeled process consists of a gasification unit, a fermentation unit, and a downstream processing unit. The model for the gasification unit was based on an Auger gasifier (see Isahak et al., 2012; Jahirul et al., 2012; Sharma et al., 2015; Dhyani and Bhaskar, 2018). Auger gasifiers have distinguished drying, pyrolysis, and combustion zones. This allows for a tight control of how much feedstock carbon is converted into char. The fermentation module was modeled in Aspen Plus with the use of a stoichiometric reactor. The reactor operates at ambient pressure and 37°C. Acetogenic bacteria, like Clostridium ljungdahlii, Clostridium carboxidivorans, Alkalibaculum bacchi, were present in the reactor and catalyzed the following reactions (Pardo-Planas et al., 2017):

$\begin{array}{ll}4CO+2H_{2}O\to C{H}_{3}COOH+2C{O}_2& (45)\end{array}$

$\begin{array}{ll}2C{O}_2+4H_2\to C{H}_{3}COOH+2H_{2}O& (46)\end{array}$

$\begin{array}{ll}6CO+3H_{2}O\to C_2{H}_{5}OH+4C{O}_2& (47)\end{array}$

$\begin{array}{ll}2C{O}_2+6H_2\to C_2{H}_{5}OH+3H_{2}O& (48)\end{array}$

Michailos et al. (2019) developed another Aspen Plus model of a syngas fermentation process, but modeled the gasifier as a circulating fluidized bed reactor and used a CSTR reactor for the fermentation process. The considered acetogenic bacterium was C. ljungdahlii, which converts, respectively, 70 and 50% of the CO and H₂ present in the syngas to ethanol (see Equations 45–48).

FIGURE 9

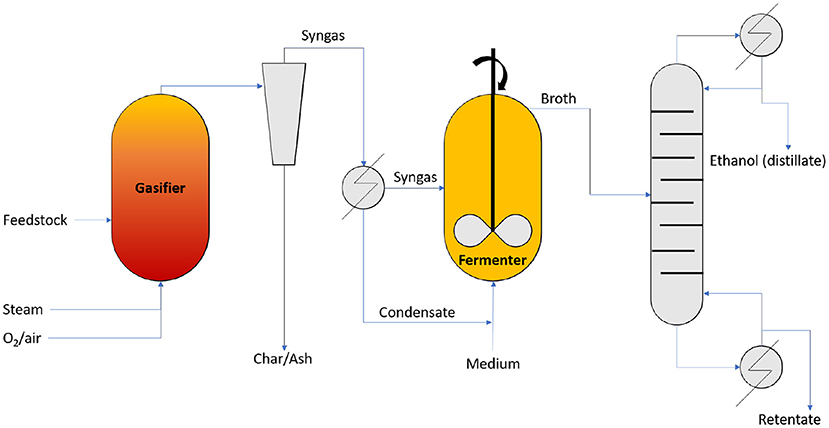
Figure 9. Syngas fermentation process flowsheet (adapted from Pardo-Planas et al., 2017).

6. Supply Chain Network Models

In order to accurately predict the economic feasibility of any biorefinery design, comprehensive process models do not suffice. The sustainability and economic feasibility of the supply of the required feedstock to the biorefinery is additionally of crucial essence when designing and operating a biorefinery. Several biorefinery supply chain models have already been published. The most recent ones include, amongst others, the contributions of Wang et al. (2015), Cambero et al. (2016), Martinkus et al. (2018), and Jonkman et al. (2019).

Jonkman et al. (2019), for instance, presented a decision support tool for the sustainable design of a biorefinery supply chain network, taking local actors and their individual objectives into account. Jonkman et al. (2019) additionally states that previous biomass supply chain design did not take the competition in cultivation between different types of feedstocks into account, but rather the competition in usage (or the other way around). Both options are however simultaneously available to the farmers producing the biomass feedstocks and must therefore be taken into account. Thus, a competition exists between what is most beneficial for the biomass producers and the biorefinery itself. When designing a biorefinery, it is therefore of crucial importance that possible future suppliers are persuaded to produce the biomass the biorefinery requires by assuring that this scenario would also be the most beneficial one for them. The biomass supply chain modeling approach as presented by Jonkman et al. (2019) is based on allocating the benefits of the biorefinery supply chain as fairly as possible over all actors, based on collaborative game theory. Jonkman et al. (2019) applied their developed modeling framework and decision support tool to the supply chain design of biorefinery using sugars beets as feedstock, located in the Netherlands.

Wang et al. (2015) on the other hand provided a mathematical model for the growth of energy crops. For the sake of simplicity, Wang et al. (2015) does not consider temperature, fertilizers, and water as potential limiting factors. The potential growth rate of energy crops (EC) is then defined by (Wang et al., 2015):

$\begin{array}{ll}{G}_{EC}=ϵ\varphi f_{PR}(1-exp(-k-LAI))HI& (49)\end{array}$

with G_EC the energy crop growth index, ϵ the crop radiation utilization factor, ϕ the solar radiation, f_PR the amount of radiation that is used in photosynthetic processes, k the leaf canopy extinction coefficient, LAI the leaf area index, and HI the harvest index (Wang et al., 2015).

Another possibility of estimating the expected annually biomass harvest, is to incorporate Geographic Information Systems (GIS) into the strategic planning and supply chain developing process. Schröder et al. (2019) presented an integrated strategic planning model which takes the configuration, scaling, and siting of a multi-product lignocellulosic biorefinery simultaneously into account. A combined evolutionary strategy/Non-Linear-Programming (NLP) algorithm is presented which is used to generate a set of optimal feasible solutions for the siting, configuration, and scale of the biorefinery plant. The return on investment (ROI) is used as the optimization objective:

$\begin{array}{ll}maxROI=\frac{profit}{investment}=\frac{rev-ic-oc-\mathrm{irc}}{inv}& (50)\end{array}$

The revenue rev is dependent on the capacity of the facility, and thus the amount of product that can be produced, the types of products that are produced, and their market sales prices. ic represents the cost of the biomass purchase and the transportation costs from a supply point to the biorefinery facility. Generally, a fixed average transportation cost is used per amount of biomass transported and distance traveled. The distance between a supply point and the biorefinery facility is calculated using the Minkowski distance. The operating costs oc are dependent on the amount of energy that is used (and produced) by the plant, and the materials that are used during the production process. Investment related costs irc are, maintenance, insurance, and overhead costs. They represent a certain percentage of the total investment cost inv. Finally, the investment cost inv is scaled from a standardized investment cost for 1 ton of biomass. The facility size and capacity needed for 1 ton biomass is scaled up to the required facility size with the use of an up-scaling coefficient which takes the so-called economy of scale into account (Schröder et al., 2019).

7. Discussion

Of the biological conversion platforms, anaerobic digestion processes are a well-known and -exploited technology but its development varies across the European countries. Germany, Switzerland, Czech Republic, Luxembourg, and Austria are at the forefront of the exploitation of anaerobic digestion process (or biogas plants), with 136–48 biogas plants per 1 million inhabitants (EBA, 2018). The economic application of other biological conversion platform processes are in most cases still confined to pilot-scale set-ups. Thermochemical techniques, however, are already applied in commercial-scale biorefinery plants. This application gap is also visible in the availability of comprehensive process models. While the models presented in section 3 are highly based on assumptions, and ideal Michaelis-Menten and Monod kinetics, the models presented in section 4 are more accurate, based on experimental data, and a relatively thorough process knowledge. Additionally, in the context of the thermochemical conversion of biomass, it was possible to adapt the already available gasification and pyrolysis models for coal to suit the biomass feedstock, due to its high similarity. The already available (Computational Fluid Dynamics) gasification and pyrolysis reactor models only benefit the accelerated commercial exploitation of gasification and pyrolysis processes. These models, amongst others, allow for accurate temperature control in the reactors. The few disadvantages of the thermochemical conversion platform include the low product selectivity of the subsequent conversion processes (not discussed in this contribution) and the relatively high energy consumption.

Although the biological conversion platform uses familiar fermentation-based conversion processes and displays exceptionally high product selectivity in comparison to the catalytic driven conventional conversion processes used in purely thermochemical conversion platforms, its economic exploitation is still hampered by its multiple disadvantages. Its inability to process the lignin fraction of the feedstock introduces a significant inherent feedstock usage inefficiency and the lack of comprehensive mechanistic knowledge and data on the occurring processes, delays the development of extensive process models. The absence of thorough predictive models puts possible investors off due to the unavailability of return on investment assurance. The additional high initial investment cost does not contribute to the already reticent behavior of investors.

The hybrid conversion platform seems to be the perfect combination of both platforms, but is still in its initial development phase. Hybrid conversion platform models are still limited and are often restricted to only Aspen Plus simulations. The commercial exploitation of the hybrid conversion platform, or any other one, can only benefit from increased modeling efforts and the collection and communication of experimental data, obtained from pilot set-ups. Comprehensive process models with a high predictive ability will only aid in increasing the confidence of investors in these processes, and thus the further expansion and application of biorefinery processes.

The modeling of biorefinery supply chain networks is steadily gaining interest (Martinkus et al., 2018; Sharma et al., 2018). Due to general concerns regarding the overall sustainability of using single food crops as biorefinery feedstocks, research focusses have gradually shifted toward the use of biowaste streams as biorefinery feedstocks (see section 2.2). Biowaste streams, in comparison to the uniform single food crop feedstocks, are unsystematic and flexible by nature. Therefore, it is essential that biorefinery exploiters are able to predict the availability of a biowaste feedstock and its overall composition. Predicting both of these aspects is very challenging since they are dependent on a multitude of factors. Climate, harvest time, seasonality, geographical location, and competing buyers for the biowaste in question have a major influence on the availability and/or composition of a certain feedstock. Additionally, if the economic viability of a biorefinery is considered within its local setting, logistics and the (already) available infrastructure will play a key role. Coupling supply chain models with conversion models is, however, challenging. This is often mainly due to discrepancies in supply chain models outputs and the required conversion model inputs, and significantly different time scales. Conversion models require fairly detailed feedstock composition input, mostly in terms of (hemi-)cellulose and lignin content, while supply chain network models are often limited to only predicting the tonnages of a more general feedstock (e.g., pruning waste) that can be expected during a certain time period. These so-called general feedstocks mostly consist of a mixture of several similar species which are not necessarily similar in composition. For instance, the amount of pruning waste sourced from the trees in a certain area could be estimated based on GIS-information but this feedstock will not distinguish between different tree species. Table 2, however, clearly indicates the differences in composition of several tree species. Other issues that arise when coupling supply chain network models with conversion models, are due to the significantly different time scales of both model-types. While supply chain network models can consider time spans up to a year (and possibly more), most conversion models consider time spans from less than a few hours up to a few hundred hours (with anaerobic digestion processes as an exception, sometimes reaching residence times up to 100 days) (Batstone et al., 2002; Pastor-Poquet et al., 2018). Coupling a supply chain model with conversion models could be beneficial for strategic planning purposes like designing the process layout and scale of a to-be-built biorefinery and/or planning process cycles in an operational biorefinery.

Coupling issues are not only limited to supply chain models and conversion models. The mutual coupling of different conversion models can also give rise to similar issues. When coupling any conversion models, it is essential that the aspects mentioned above, i.e., time scale and discrepancies in model outputs and inputs, are considered. The main issues that may arise when coupling two conversion models will most likely be the result of the latter. For instance, furfural (F) is a common by-product of the dilute acid pretreatment of a biomass feedstock. This pretreatment step can, e.g., precede an enzymatic hydrolysis process or an SSF process. The inhibitory effect of furfural on the enzymatic hydrolysis is considered in the enzymatic hydrolysis model, as proposed by Kadam et al. (2004) and Prunescu and Sin (2013). However, its inhibitory effect is not considered in the SSF model, as proposed by Shadbahr et al. (2017) and Singh et al. (2018), nevertheless the SSF process also encompasses an enzymatic hydrolysis process. Thus, if a conversion model describing a dilute acid pretreatment process (not included in this contribution) would be coupled with the presented SSF-model (as proposed by Shadbahr et al., 2017; Singh et al., 2018), the lack of the incorporation of the inhibitory effect of furfural in the latter, should be addressed accordingly. Moreover, while most of these models are only validated for a few distinct feedstocks, the identification and validation of the kinetic model parameters for other feedstocks may be lacking or insufficient. In these cases, there will be a need of sufficient experimental data to identify and/or validate the required kinetic parameters.

8. Conclusion

The general support for a more sustainable process industry has never been this high yet, but the considered processes are leaping behind. Biorefinery processes convert a biomass feedstock into liquid fuels and chemical compounds, effectively replacing fossil fuels. The commercial exploitation of any biorefinery type however is still very limited. The lack of thorough process knowledge and the accompanying return on investment uncertainty causes many investors to withhold. The development and use of process models to predict the (economic) output of the considered biorefinery process can aid in guiding investors and policy makers toward investing more in biorefinery plants.

This contribution gives an overview of the available biorefinery models, subdivided according to the used conversion platform (thermochemical, biological, or hybrid). Biological (or biochemical) conversion platforms use enzymes and microorganisms to convert a biomass feedstock to liquid fuels and chemical compounds. These processes display a high product selectivity and are similar to other already commonly used and available bioproduction processes. The commercial application of the biological conversion platform is however still very limited, due to the lack of mechanistic knowledge of the enzymatic and microorganism's activity and the shortage of experimental data. The conversion platform's inability to process the lignin fraction of the biomass (which even has an inhibitory effect on the (hemi-)cellulose conversion processes) causes the carbon efficiency of these processes to be relatively low. Available models are relatively limited and often assume ideal reaction kinetics like Michaelis-Menten and Monod kinetics.

Thermochemical conversion processes are based on the degradation of the biomass feedstock with the use of thermal energy. The obtained products depend on the severity of the thermal degradation process and range from char, bio-oil, and non-condensable gasses to syngas (mainly consisting of H₂, CO, CO₂, and CH₄). The degradation products are subsequently converted into the desired biorefinery products using conventional catalytic conversion processes, like Fischer-Tropsch synthesis, hydroprocessing, etc. Thermochemical conversion processes are able to utilize the entire biomass feedstock, but the conversion processes display a limited product selectivity. The used process models are often based on the fossil process analogs, using coal as a feedstock. Due to the high structural and functional similarities between coal and lignocellulosic biomass, the already existing gasification and pyrolysis models for coal could easily be extended to a lignocellulosic feedstock.

Hybrid conversion processes use thermal energy to degrade the entire biomass feedstock, but subsequently use fermentation processes to convert the obtained syngas into liquid fuels and chemical compounds. The hybrid conversion platform is a promising conversion platform, displaying a high carbon efficiency coupled with a high product selectivity. The available models for this type of conversion platform are however still limited.

Finally, a supply chain model was presented, stressing the importance of including the bigger picture when planning the design of an economically sustainable biorefinery. A solid feedstock supply is of key essence and the objectives of (local) biorefinery actors should not be overlooked.

9. Further Research

While the pyrolysis or gasification of biomass is highly similar to the thermochemical treatment of coal, a significantly large amount of accurate mathematical and kinetic models is already available for the thermochemical conversion platform. Existing models considering coal were easily adapted to a biomass feedstock, quickly rendering a wide range of (basic) biomass gasification and pyrolysis models. Contributors considering the biological conversion of (lignocellulosic) biomass, however, did not have the luxury of already possessing a relatively large amount of basic models. Additionally, the mechanistic knowledge of the microorganisms and enzymes catalyzing the biological and biochemical degradation and conversion processes is still too limited.

While the main knowledge gap is in regard to the biological conversion platform, future research should mainly focus on these processes. The increased acquirement of experimental data and mechanistic knowledge is of key importance if the biological processes modeling efforts are to be intensified. Additionally, further expanding and elaborating the hybrid conversion concept is deemed to be beneficial for the short- and long-term commercial exploitation of sustainable biorefinery processes.

Finally, the lack of integrated biorefinery models is one of the most striking gaps in this contribution. All presented mathematical and kinetic process models are limited to only one process step. The models presented in the section regarding the hybrid conversion platforms are quoted to be the most integrated design modeled thus far. The feedstock usage efficiency of this conversion platform is indeed the most efficient one in comparison with the other two conversion platforms, but an integrated biorefinery also consider the continued processing of the biorefinery waste streams and the produced (by-)products. Intensified modeling efforts in the context of integrated biorefinery design is therefore considered to be highly desirable.

Author Contributions

VD, MP, and JV: conceptualization, resources, writing, review and editing. VD: investigation and literature review, writing, original draft preparation, and visualization. JV: supervision and funding acquisition. MP and JV: project administration.

Funding

This work was supported by the ERA-NET FACCE-SurPlus FLEXIBI Project, co-funded by VLAIO project HBC.2017.0176. VD was supported by FWO-SB Grant 1SC0920N.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Anca-Couce, A., and Scharler, R. (2017). Modelling heat of reaction in biomass pyrolysis with detailed reaction schemes. Fuel 206, 572–579. doi: 10.1016/j.fuel.2017.06.011

CrossRef Full Text | Google Scholar

Anca-Couce, A., Zobel, N., and Jakobsen, H. A. (2013). Multi-scale modeling of fixed-bed thermo-chemical processes of biomass with the representative particle model: application to pyrolysis. Fuel 103, 773–782. doi: 10.1016/j.fuel.2012.05.063

CrossRef Full Text | Google Scholar

Angarita, J., Souza, R., Cruz, A., Biscaia, E., and Secchi, A. (2015). Kinetic modeling for enzymatic hydrolysis of pretreated sugarcane straw. Biochem. Eng. J. 104, 10–19. doi: 10.1016/j.bej.2015.05.021

CrossRef Full Text | Google Scholar

Arnell, M., Astals, S., Åmand, L., Batstone, D. J., Jensen, P. D., and Jeppsson, U. (2016). Modelling anaerobic co-digestion in Benchmark Simulation Model No. 2: parameter estimation, substrate characterisation and plant-wide integration. Water Res. 98, 138–146. doi: 10.1016/j.watres.2016.03.070

PubMed Abstract | CrossRef Full Text | Google Scholar

Ashraf, M. T., Schmidt, J. E., Kujawa, J., Kujawski, W., and Arafat, H. A. (2017). One-dimensional modeling of pervaporation systems using a semi-empirical flux model. Separ. Purif. Technol. 174, 502–512. doi: 10.1016/j.seppur.2016.10.043

CrossRef Full Text | Google Scholar

Auroux, D., and Groza, V. (2017). Optimal parameters identification and sensitivity study for abrasive waterjet milling model. Inverse Probl. Sci. Eng. 25, 1560–1576. doi: 10.1080/17415977.2016.1273916

CrossRef Full Text | Google Scholar

Baliban, R. C., Elia, J. A., Floudas, C. A., Gurau, B., Weingarten, M. B., and Klotz, S. D. (2013). Hardwood biomass to gasoline, diesel, and jet fuel: 1. Process synthesis and global optimization of a thermochemical refinery. Energy Fuels 27, 4302–4324. doi: 10.1021/ef302003f

CrossRef Full Text | Google Scholar

Bates, R. B., Ghoniem, A. F., Jablonski, W. S., Carpenter, D. L., Altantzis, C., Garg, A., et al. (2017). Steam-air blown bubbling fluidized bed biomass gasification (BFBBG): multi-scale models and experimental validation. AIChE J. 63, 1543–1565. doi: 10.1002/aic.15666

CrossRef Full Text | Google Scholar

Batstone, D. J., Keller, J., Angelidaki, I., Kalyuzhnyi, S. V., Pavlostathis, S. G., Rozzi, A., et al. (2002). The IWA anaerobic digestion model No 1 (ADM1). Water Sci. Technol. 45, 65–73. doi: 10.2166/wst.2002.0292

PubMed Abstract | CrossRef Full Text | Google Scholar

Bedoic, R., Čuček, L., Ćosić, B., Krajnc, D., Smoljanić, G., Kravanja, Z., et al. (2019). Green biomass to biogas - A study on anaerobic digestion of residue grass. J. Clean. Product. 213, 700–709. doi: 10.1016/j.jclepro.2018.12.224

CrossRef Full Text | Google Scholar

Bezerra, R. M., and Dias, A. A. (2005). Enzymatic kinetic of cellulose hydrolysis. Appl. Biochem. Biotechnol. 126, 49–59. doi: 10.1007/s12010-005-0005-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Biernacki, P., Steinigeweg, S., Borchert, A., and Uhlenhut, F. (2013). Application of Anaerobic Digestion Model No. 1 for describing anaerobic digestion of grass, maize, green weed silage, and industrial glycerine. Bioresour. Technol. 127, 188–194. doi: 10.1016/j.biortech.2012.09.128

PubMed Abstract | CrossRef Full Text | Google Scholar

Biswas, R., Uellendahl, H., and Ahring, B. (2015). Wet explosion: a universal and efficient pretreatment process for lignocellulosic biorefineries. BioEnergy Res. 8, 1101–1116. doi: 10.1007/s12155-015-9590-5

CrossRef Full Text | Google Scholar

Cai, J., Wu, W., Liu, R., and Huber, G. W. (2013). A distributed activation energy model for the pyrolysis of lignocellulosic biomass. Green Chem. 15, 1331–1340. doi: 10.1016/j.rser.2014.04.052

CrossRef Full Text | Google Scholar

Cai, W., Liu, R., He, Y., Chai, M., and Cai, J. (2018). Bio-oil production from fast pyrolysis of rice husk in a commercial-scale plant with a downdraft circulating fluidized bed reactor. Fuel Process. Technol. 171, 308–317. doi: 10.1016/j.fuproc.2017.12.001

CrossRef Full Text | Google Scholar

Cambero, C., Sowlati, T., and Pavel, M. (2016). Economic and life cycle environmental optimization of forest-based biorefinery supply chains for bioenergy and biofuel production. Chem. Eng. Res. Design 107, 218–235. doi: 10.1016/j.cherd.2015.10.040

CrossRef Full Text | Google Scholar

Carroll, A., and Sommerville, C. (2009). Cellulosic biofuels. Annu. Rev. Plant Biol. 60, 165–182. doi: 10.1146/annurev.arplant.043008.092125

PubMed Abstract | CrossRef Full Text | Google Scholar

Cesário, M. T., da Fonseca, M. M. R., Marques, M. M., and de Almeida, M. C. M. D. (2018). Marine algal carbohydrates as carbon sources for the production of biochemicals and biomaterials. Biotechnol. Adv. 36, 798–817. doi: 10.1016/j.biotechadv.2018.02.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y., Wu, Y., Zhu, B., Zhang, G., and Wei, N. (2018). Co-fermentation of cellobiose and xylose by mixed culture of recombinant Saccharomyces cerevisiae and kinetic modeling. PLoS ONE 13:e199104. doi: 10.1371/journal.pone.0199104

PubMed Abstract | CrossRef Full Text | Google Scholar

Cherubini, F., Jungmeier, G., Wellisch, M., Willke, T., Skiadas, I., Ree, R. V., et al. (2009). Toward a common classification approach for biorefinery systems. Biofuels Bioprod. Biorefin. 3, 534–546. doi: 10.1002/bbb.172

CrossRef Full Text | Google Scholar

Ciesielski, P. N., Pecha, M. B., Bharadwaj, V. S., Mukarakate, C., Leong, G. J., Kappes, B., et al. (2018). Advancing catalytic fast pyrolysis through integrated multiscale modeling and experimentation: challenges, progress, and perspectives. Wiley Interdisc. Rev. 7:e297. doi: 10.1002/wene.297

CrossRef Full Text | Google Scholar

Dhyani, V., and Bhaskar, T. (2018). A comprehensive review on the pyrolysis of lignocellulosic biomass. Renew. Energy 129, 695–716. doi: 10.1016/j.renene.2017.04.035

CrossRef Full Text | Google Scholar

Díaz-Reinoso, B., Moure, A., González, J., and Domínguez, H. (2017). A membrane process for the recovery of a concentrated phenolic product from white vinasses. Chem. Eng. J. 327, 210–217. doi: 10.1016/j.cej.2017.06.088

CrossRef Full Text | Google Scholar

Dutta, S. K., and Chakraborty, S. (2015). Kinetic analysis of two-phase enzymatic hydrolysis of hemicellulose of xylan type. Bioresour. Technol. 198, 642–650. doi: 10.1016/j.biortech.2015.09.066

PubMed Abstract | CrossRef Full Text | Google Scholar

EBA (2018). Statistical Report of the European Biogas Association 2018.

Egedy, A., Gyurik, L., Varga, T., Zou, J., Miskolczi, N., and Yang, H. (2018). Kinetic-compartmental modelling of potassium-containing cellulose feedstock gasification. Front. Chem. Sci. Eng. 12, 708–717. doi: 10.1007/s11705-018-1767-y

CrossRef Full Text | Google Scholar

Fava, F., Totaro, G., Diels, L., Reis, M., Duarte, J., Carioca, O. B., et al. (2015). Biowaste biorefinery in Europe: opportunities and research & development needs. New Biotechnol. 32, 100–108. doi: 10.1016/j.nbt.2013.11.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Flores-Sánchez, A., Flores-Tlacuahuac, A., and Pedraza-Segura, L. L. (2013). Model-based experimental design to estimate kinetic parameters of the enzymatic hydrolysis of lignocellulose. Indust. Eng. Chem. Res. 52, 4834–4850. doi: 10.1021/ie400039m

CrossRef Full Text | Google Scholar

García-Diéguez, C., Bernard, O., and Roca, E. (2013). Reducing the Anaerobic Digestion Model No. 1 for its application to an industrial wastewater treatment plant treating winery effluent wastewater. Bioresour. Technol. 132, 244–253. doi: 10.1016/j.biortech.2012.12.166

PubMed Abstract | CrossRef Full Text | Google Scholar

Goyal, H., and Pepiot, P. (2017). A compact kinetic model for biomass pyrolysis at gasification conditions. Energy Fuels 31, 12120–12132. doi: 10.1021/acs.energyfuels.7b01634

CrossRef Full Text | Google Scholar

Hejazi, B., Grace, J. R., Bi, X., and Mahecha-Botero, A. (2017a). Kinetic model of steam gasification of biomass in a bubbling fluidized bed reactor. Energy Fuels 31, 1702–1711. doi: 10.1021/acs.energyfuels.6b03161

CrossRef Full Text | Google Scholar

Hejazi, B., Grace, J. R., Bi, X., and Mahecha-Botero, A. (2017b). Kinetic model of steam gasification of biomass in a dual fluidized bed reactor: comparison with pilot-plant experimental results. Energy Fuels 31, 12141–12155. doi: 10.1021/acs.energyfuels.7b01833

CrossRef Full Text | Google Scholar

Hodge, D. B., Karim, M. N., Schell, D. J., and McMillan, J. D. (2008). Model-based fed-batch for high-solids enzymatic cellulose hydrolysis. Appl. Biochem. Biotechnol. 152:88. doi: 10.1007/s12010-008-8217-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Holtzapple, M. T., Caram, H. S., and Humphrey, A. E. (1984). The HCH-1 model of enzymatic cellulose hydrolysis. Biotechnol. Bioeng. 26, 775–780. doi: 10.1002/bit.260260723

PubMed Abstract | CrossRef Full Text | Google Scholar

Hou, W., and Bao, J. (2018). Simultaneous saccharification and aerobic fermentation of high titer cellulosic citric acid by filamentous fungus Aspergillus niger. Bioresour. Technol. 253, 72–78. doi: 10.1016/j.biortech.2018.01.011

PubMed Abstract | CrossRef Full Text | Google Scholar

IPCC (2018). Global Warming of 1.5 Degrees Celsius. An IPCC Special Report on the Impacts of Global Warming of 1.5 Degrees Celsius Above Pre-industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty. In Press.

Google Scholar

Isahak, W. N. R. W., Hisham, M. W., Yarmo, M. A., and Yun Hin, T. (2012). A review on bio-oil production from biomass by using pyrolysis method. Renew. Sustain. Energy Rev. 16, 5910–5923. doi: 10.1016/j.rser.2012.05.039

CrossRef Full Text | Google Scholar

Isikgor, F., and Becer, C. (2015). Lignocellulosic biomass: a sustainable platform for production of bio-based chemicals and polymers. Polym. Chem. 6, 4497–4559. doi: 10.1039/C5PY00263J

CrossRef Full Text | Google Scholar

Jahirul, M. I., Rasul, M. G., Chowdhury, A. A., and Ashwath, N. (2012). Biofuels production through biomass pyrolysis -a technological review. Energies 5, 4952–5001. doi: 10.3390/en5124952

CrossRef Full Text | Google Scholar

Jin, C.-L., Wu, Z.-M., Wang, S.-W., Cai, Z.-Q., Chen, T., Farahani, M. R., et al. (2017). Economic assessment of biomass gasification and pyrolysis: a review. Energy Sour. Part B 12, 1030–1035. doi: 10.1080/15567249.2017.1358309

CrossRef Full Text | Google Scholar

Jonkman, J., Kanellopoulos, A., and Bloemhof, J. M. (2019). Designing an eco-efficient biomass-based supply chain using a multi-actor optimisation model. J. Clean. Product. 210, 1065–1075. doi: 10.1016/j.jclepro.2018.10.351

CrossRef Full Text | Google Scholar

Jönsson, L. J., and Martín, C. (2016). Pretreatment of lignocellulose: formation of inhibitory by-products and strategies for minimizing their effects. Bioresour. Technol. 199, 103–112. doi: 10.1016/j.biortech.2015.10.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Kabir, M. J., Chowdhury, A. A., and Rasul, M. G. (2015). Pyrolysis of municipal green waste: a modelling, simulation and experimental analysis. Energies 8, 7522–7541. doi: 10.3390/en8087522

CrossRef Full Text | Google Scholar

Kadam, K. L., Rydholm, E. C., and McMillan, J. D. (2004). Development and validation of a kinetic model for enzymatic saccharification of lignocellulosic biomass. Biotechnol. Prog. 20, 698–705. doi: 10.1021/bp034316x

PubMed Abstract | CrossRef Full Text | Google Scholar

Kamm, B., Schönicke, P., and Hille, C. (2016). Green biorefinery - industrialimplementation. Food Chem. 197, 1341–1345. doi: 10.1016/j.foodchem.2015.11.088

PubMed Abstract | CrossRef Full Text | Google Scholar

Krishnan, M. S., Ho, N. W. Y., and Tsao, G. T. (1999). Fermentation kinetics of ethanol production from glucose and xylose by recombinant Saccharomyces 1400(pLNH33). Appl. Biochem. Biotechnol. 78, 373–388.

Google Scholar

Laurens, L. M. L., Markham, J., Templeton, D. W., Christensen, E. D., Van Wychen, S., Vadelius, E. W., et al. (2017). Development of algae biorefinery concepts for biofuels and bioproducts; a perspective on process-compatible products and their impact on cost-reduction. Energy Environ. Sci. 10, 1716–1738. doi: 10.1385/ABAB:78:1-3:373

CrossRef Full Text | Google Scholar

Lerkkasemsan, N., and Achenie, L. E. (2014). Pyrolysis of biomass - fuzzy modeling. Renew. Energy 66, 747–758. doi: 10.1016/j.renene.2014.01.014

CrossRef Full Text | Google Scholar

Li, J., Zhang, M., Li, J., and Wang, D. (2018). Corn stover pretreatment by metal oxides for improving lignin removal and reducing sugar degradation and water usage. Bioresour. Technol. 263, 232–241. doi: 10.1016/j.biortech.2018.05.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, C., Gu, C., Raftery, J., Karim, M. N., and Holtzapple, M. (2019). Development of modified HCH-1 kinetic model for long-term enzymatic cellulose hydrolysis and comparison with literature models. Biotechnol. Biofuels 12:34. doi: 10.1186/s13068-019-1371-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Martinkus, N., Latta, G., Brandt, K., and Wolcott, M. (2018). A multi-criteria decision analysis approach to facility siting in a wood-based depot-and-biorefinery supply chain model. Front. Energy Res. 6:124. doi: 10.3389/fenrg.2018.00124

CrossRef Full Text | Google Scholar

Mateos-Salvador, F., Sadhukhan, J., and Campbell, G. M. (2011). The normalised Kumaraswamy breakage function: a simple model for wheat roller milling. Powder Technol. 208, 144–157. doi: 10.1016/j.powtec.2010.12.013

CrossRef Full Text | Google Scholar

Matta, J., Bronson, B., Gogolek, P. E., Mazerolle, D., Thibault, J., and Mehrani, P. (2017). Comparison of multi-component kinetic relations on bubbling fluidized-bed woody biomass fast pyrolysis reactor model performance. Fuel 210, 625–638. doi: 10.1016/j.fuel.2017.08.092

CrossRef Full Text | Google Scholar

Mezhericher, M., Levy, A., and Borde, I. (2012). Three-dimensional spray-drying model based on comprehensive formulation of drying kinetics. Drying Technol. 30, 1256–1273. doi: 10.1080/07373937.2012.686136

CrossRef Full Text | Google Scholar

Michailos, S. (2018). Kinetic modelling and dynamic sensitivity analysis of a fast pyrolysis fluidised bed reactor for bagasse exploitation. Biofuels 1–10. doi: 10.1080/17597269.2018.1461522

CrossRef Full Text | Google Scholar

Michailos, S., Parker, D., and Webb, C. (2017). Comparative analysis of synthetic natural gas versus hydrogen production from bagasse. Chem. Eng. Technol. 40, 546–554. doi: 10.1002/ceat.201600424

CrossRef Full Text | Google Scholar

Michailos, S., Parker, D., and Webb, C. (2019). Design, sustainability analysis and multiobjective optimisation of ethanol production via syngas fermentation. Waste Biomass Valoriz. 10, 865–876. doi: 10.1007/s12649-017-0151-3

CrossRef Full Text | Google Scholar

Mohr, A., and Raman, S. (2013). Lessons from first generation biofuels and implications for the sustainability appraisal of second generation biofuels. Energy Policy 63, 114–122. doi: 10.1016/j.enpol.2013.08.033

PubMed Abstract | CrossRef Full Text | Google Scholar

Morales-Rodriguez, R., Gernaey, K. V., Meyer, A. S., and Sin, G. (2011). A mathematical model for simultaneous saccharification and co-fermentation (SSCF) of C6 and C5 sugars. Chinese J. Chem. Eng. 19, 185–191. doi: 10.1016/S1004-9541(11)60152-3

CrossRef Full Text | Google Scholar

Morthensen, S. T., Zeuner, B., Meyer, A. S., Jørgensen, H., and Pinelo, M. (2018). Membrane separation of enzyme-converted biomass compounds: recovery of xylose and production of gluconic acid as a value-added product. Separ. Purif. Technol. 194, 73–80. doi: 10.1016/j.seppur.2017.11.031

CrossRef Full Text | Google Scholar

Naik, S., Goud, V. V., Rout, P. K., and Dalai, A. K. (2010). Production of first and second generation biofuels: a comprehensive review. Renew. Sustain. Energy Rev. 14, 578–597. doi: 10.1016/j.rser.2009.10.003

CrossRef Full Text | Google Scholar

Nimmegeers, P., Lauwers, J., Telen, D., Logist, F., and Impe, J. V. (2017). Identifiability of large-scale non-linear dynamic network models applied to the ADM1-case study. Math. Biosci. 288, 21–34. doi: 10.1016/j.mbs.2017.02.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Ntaikou, I., Gavala, H., and Lyberatos, G. (2010). Application of a modified Anaerobic Digestion Model 1 version for fermentative hydrogen production from sweet sorghum extract by Ruminococcus albus. Int. J. Hydrog. Energy 35, 3423–3432. doi: 10.1016/j.ijhydene.2010.01.118

CrossRef Full Text | Google Scholar

Nunes, A. S. (2015). Thermochemical conversion of lignocellulosic biomass into biofuels with aspen plus simulation. (Master's thesis). Universidade de Coimbra, Coimbra, Portugal.

Papari, S., and Hawboldt, K. (2015). A review on the pyrolysis of woody biomass to bio-oil: focus on kinetic models. Renew. Sustain. Energy Rev. 52, 1580–1595. doi: 10.1016/j.rser.2015.07.191

CrossRef Full Text | Google Scholar

Pardo-Planas, O., Atiyeh, H. K., Phillips, J. R., Aichele, C. P., and Mohammad, S. (2017). Process simulation of ethanol production from biomass gasification and syngas fermentation. Bioresour. Technol. 245, 925–932. doi: 10.1016/j.biortech.2017.08.193

PubMed Abstract | CrossRef Full Text | Google Scholar

Pastor-Poquet, V., Papirio, S., Steyer, J.-P., Trably, E., Escudié, R., and Esposito, G. (2018). High-solids anaerobic digestion model for homogenized reactors. Water Res. 142, 501–511. doi: 10.1016/j.watres.2018.06.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Pettersson, P. O., Eklund, R., and Zacchi, G. (2002). Modeling Simultaneous Saccharification and Fermentation of Softwood. Totowa, NJ: Humana Press.

PubMed Abstract | Google Scholar

Philippidis, G. P., Smith, T. K., and Wyman, C. E. (1993). Study of the enzymatic hydrolysis of cellulose for production of fuel ethanol by the simultaneous saccharification and fermentation process. Biotechnol. Bioeng. 41, 846–853. doi: 10.1002/bit.260410903

PubMed Abstract | CrossRef Full Text | Google Scholar

Philippidis, G. P., Spindler, D. D., and Wyman, C. E. (1992). Mathematical modeling of cellulose conversion to ethanol by the simultaneous saccharification and fermentation process. Appl. Biochem. Biotechnol. 34:543. doi: 10.1007/BF02920577

CrossRef Full Text | Google Scholar

Piccolo, C., and Bezzo, F. (2009). A techno-economic comparison between two technologies for bioethanol production from lignocellulose. Biomass Bioenergy 33, 478–491. doi: 10.1016/j.biombioe.2008.08.008

CrossRef Full Text | Google Scholar

Prunescu, R., Blanke, M., Jakobsen, J., and Sin, G. (2017). Model-based plantwide optimization of large scale lignocellulosic bioethanol plants. Biochem. Eng. J. 124, 13–25. doi: 10.1016/j.bej.2017.04.008

CrossRef Full Text | Google Scholar

Prunescu, R. M., and Sin, G. (2013). Dynamic modeling and validation of a lignocellulosic enzymatic hydrolysis process - a demonstration scale study. Bioresour. Technol. 150, 393–403. doi: 10.1016/j.biortech.2013.10.029

PubMed Abstract | CrossRef Full Text | Google Scholar

Qian, E. W. (2014). “Chapter 7: Pretreatment and saccharification of lignocellulosic biomass,” in Research Approaches to Sustainable Biomass Systems, eds S. Tojo and T. Hirasawa (Boston, MA: Academic Press), 181–204.

Rabinovich, O. S., Korban, V. V., Palćhenok, G. I., and Khorolśkaya, O. P. (2009). Modeling of fast pyrolysis of a single biomass particle in an inert boiling bed. J. Eng. Phys. Thermophys. 82:611. doi: 10.1007/s10891-009-0244-3

CrossRef Full Text | Google Scholar

Ranzi, E., Debiagi, P. E. A., and Frassoldati, A. (2017a). Mathematical modeling of fast biomass pyrolysis and bio-oil formation. Note I: Kinetic mechanism of biomass pyrolysis. ACS Sustain. Chem. Eng. 5, 2867–2881. doi: 10.1021/acssuschemeng.6b03096

CrossRef Full Text | Google Scholar

Ranzi, E., Debiagi, P. E. A., and Frassoldati, A. (2017b). Mathematical modeling of fast biomass pyrolysis and bio-oil formation. Note II: Secondary gas-phase reactions and bio-oil formation. ACS Sustain. Chem. Eng. 5, 2882–2896. doi: 10.1021/acssuschemeng.6b03098

CrossRef Full Text | Google Scholar

Redman, A. L., Bailleres, H., Perré, P., Carr, E., and Turner, I. (2017). A relevant and robust vacuum-drying model applied to hardwoods. Wood Sci. Technol. 51, 701–719. doi: 10.1007/s00226-017-0908-7

CrossRef Full Text | Google Scholar

Sakimoto, K., Kanna, M., and Matsumura, Y. (2017). Kinetic model of cellulose degradation using simultaneous saccharification and fermentation. Biomass Bioenerg. 99, 116–121. doi: 10.1016/j.biombioe.2017.02.016

CrossRef Full Text | Google Scholar

Schröder, T., Lauven, L.P., Sowlati, T., and Geldermann, J. (2019). Strategic planning of a multi-product wood-biorefinery production system. J. Clean. Prod. 211, 1502–1516. doi: 10.1016/j.jclepro.2018.12.004

CrossRef Full Text | Google Scholar

Shadbahr, J., Khan, F., and Zhang, Y. (2017). Kinetic modeling and dynamic analysis of simultaneous saccharification and fermentation of cellulose to bioethanol. Energy Convers. Manage. 141, 236–243. doi: 10.1016/j.enconman.2016.08.025

CrossRef Full Text | Google Scholar

Sharma, A., Pareek, V., and Zhang, D. (2015). Biomass pyrolysis–A review of modelling, process parameters and catalytic studies. Renew. Sustain. Energy Rev. 50, 1081–1096. doi: 10.1016/j.rser.2015.04.193

CrossRef Full Text | Google Scholar

Sharma, B., Clark, R., Hilliard, M. R., and Webb, E. G. (2018). Simulation modeling for reliable biomass supply chain design under operational disruptions. Front. Energy Res. 6:100. doi: 10.3389/fenrg.2018.00100

CrossRef Full Text | Google Scholar

Sin, G., Meyer, A. S., and Gernaey, K. V. (2010). Assessing reliability of cellulose hydrolysis models to support biofuel process design—Identifiability and uncertainty analysis. Comput. Chem. Eng. 34, 1385–1392. doi: 10.1016/j.compchemeng.2010.02.012

CrossRef Full Text | Google Scholar

Singh, S., Chakravarty, I., Pandey, K. D., and Kundu, S. (2018). Development of a process model for simultaneous saccharification and fermentation (SSF) of algal starch to third-generation bioethanol. Biofuels 1–9. doi: 10.1080/17597269.2018.1426162

CrossRef Full Text | Google Scholar

Song, Y.-C., Kim, M., Shon, H., Jegatheesan, V., and Kim, S. (2018). Modeling methane production in anaerobic forward osmosis bioreactor using a modified anaerobic digestion model No. 1. Bioresour. Technol. 264, 211–218. doi: 10.1016/j.biortech.2018.04.125

PubMed Abstract | CrossRef Full Text | Google Scholar

Sreemahadevan, S., Singh, V., Roychoudhury, P. K., and Ahammad, S. Z. (2018). Mathematical modeling, simulation and validation for co-fermentation of glucose and xylose by Saccharomyces cerevisiae and Scheffersomyces stipitis. Biomass Bioenerg. 110, 17–24. doi: 10.1016/j.biombioe.2018.01.008

CrossRef Full Text | Google Scholar

SriBala, G., Carstensen, H.-H., Van Geem, K. M., and Marin, G. B. (2019). Measuring biomass fast pyrolysis kinetics: state of the art. Wiley Interdisc. Rev. 8:e326. doi: 10.1002/wene.326

CrossRef Full Text | Google Scholar

Sun, Y., and Cheng, J. (2002). Hydrolysis of lignocellulosic materials for ethanol production: a review. Bioresour. Technol. 83, 1–11. doi: 10.1016/s0960-8524(01)00212-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Tien, C., Ramarao, B., and Yasarla, R. (2014). A blocking model of membrane filtration. Chem. Eng. Sci. 111, 421–431. doi: 10.1016/j.ces.2014.01.022

CrossRef Full Text | Google Scholar

Treedet, W., Taechajedcadarungsri, S., and Suntivarakorn, R. (2017). Fast pyrolysis of sugarcane bagasse in circulating fluidized bed reactor - part B: modelling of bio-oil production. Energ. Proc. 138, 806–810. doi: 10.1016/j.egypro.2017.10.073

CrossRef Full Text | Google Scholar

Van de Velden, M., Baeyens, J., and Boukis, I. (2008). Modeling CFB biomass pyrolysis reactors. Biomass Bioenerg. 32, 128–139. doi: 10.1016/j.biombioe.2007.08.001

CrossRef Full Text | Google Scholar

Vane, L. M. (2005). A review of pervaporation for product recovery from biomass fermentation processes. J. Chem. Technol. Biotechnol. 80, 603–629. doi: 10.1002/jctb.1265

CrossRef Full Text | Google Scholar

Vea, E. B., Romeo, D., and Thomsen, M. (2018). Biowaste valorisation in a future circular bioeconomy. Proc. CIRP 69, 591–596. doi: 10.1016/j.procir.2017.11.062

CrossRef Full Text | Google Scholar

Wang, L., Agyemang, S. A., Amini, H., and Shahbazi, A. (2015). Mathematical modeling of production and biorefinery of energy crops. Renew. Sustain. Energy Rev. 43, 530–544. doi: 10.1016/j.rser.2014.11.008

CrossRef Full Text | Google Scholar

Wang, S., Dai, G., Yang, H., and Luo, Z. (2017). Lignocellulosic biomass pyrolysis mechanism: a state-of-the-art review. Prog. Energy Combust. Sci. 62, 33–86. doi: 10.1016/j.pecs.2017.05.004

CrossRef Full Text | Google Scholar

Zhao, X., Li, L., Wu, D., Xiao, T., Ma, Y., and Peng, X. (2019). Modified Anaerobic Digestion Model No. 1 for modeling methane production from food waste in batch and semi-continuous anaerobic digestions. Bioresour. Technol. 271, 109–117. doi: 10.1016/j.biortech.2018.09.091

PubMed Abstract | CrossRef Full Text | Google Scholar

Nomenclature