Optimizing winner determination for sustainability and timeliness in fresh agricultural product logistics service procurement auctions: insights from a fourth-party logistics perspective

With the rapid development of e-commerce in the field of fresh agricultural products and the growing prominence of environmental issues, delivery timeliness and low-carbon concepts are critical considerations in the development of cold chain logistics. From the perspective of fourth-party logistics (4PL), this paper studies the logistics services procurement auction problem of fresh agricultural product logistics considering timeliness and sustainability under demand uncertainty, aiming to achieve efficient and sustainable development of fresh agricultural product transportation through collaborative cooperation among third-party logistics (3PL). To address this problem, a two-stage stochastic model for winner determination with timeliness and sustainability under uncertain demand in fresh agricultural products logistics service procurement auction. The first stage determines the winning 3PLs, while the second stage determines the transportation volume of the 3PLs based on the decision results in the first stage. Through the sample average approximation (SAA) technology, the proposed two-stage stochastic programming is approximated as a mixed-integer linear programming model. Since winner determination problem is NP-hard, the increasing number of decision variables and demand scenarios poses challenges to the problem. Based on Latin hypercube sampling approach, this paper reconstructs the traditional SAA algorithm framework, and combines the dual decomposition and Lagrangian relaxation algorithm to develop a sampling-based approximate algorithm to solve the proposed model. The effectiveness of the proposed model and algorithm is demonstrated through a real case from a logistics enterprise in Shenzhen, China, revealing the complex coupling relationship between carbon caps, time window sizes, and decision outcomes, thereby providing insights for 4PL management practices in fresh agricultural product transportation.

1 Introduction

Recently, the rapid rise of e-commerce globally profoundly changed the traditional retail pattern (Lu et al., 2025a). In the fresh agricultural products (FAP) sector, transaction volume has increased by more than 50% in the past five years and will continue to expand in the future. This trend not only drives a surge in consumption of FAP, but also poses unprecedented challenges to the cold chain logistics system. Due to their perishable nature and seasonal supply constraints, FAP significantly increase consumer demand for diversity and immediacy. Immediacy is one of the essential performance indicators that cannot be ignored in agricultural product e-commerce logistics. Transportation delays not only lead to economic losses, but may also cause food safety issues, which in turn affects consumer trust and brand reputation. According to data from the China Food Industry Association, economic losses resulting from vegetable and fruit wastage have surpassed 100 billion yuan (Luo et al., 2022; Chen et al., 2024). Lukasse et al. (2023) also pointed out that about one-third of global food losses occur. Meanwhile, global attention to sustainable development is increasing. Cold chain transportation is one of the main transportation methods for FAP. It not only consumes a lot of energy, but also produces significant carbon emissions. Compared to regular supply logistics, FAP supply logistics requires significantly more fuel consumption to sustain the low-temperature environment within refrigerated vehicles (Kim et al., 2016; Bai et al., 2022). According to the International Energy Agency, global CO₂ emissions from industrial production and energy combustion increased by 12.7 billion tons from 2000 to 2023. ¹ Among them, the transportation sector contributes ~30% of global carbon emissions (Bi et al., 2025).

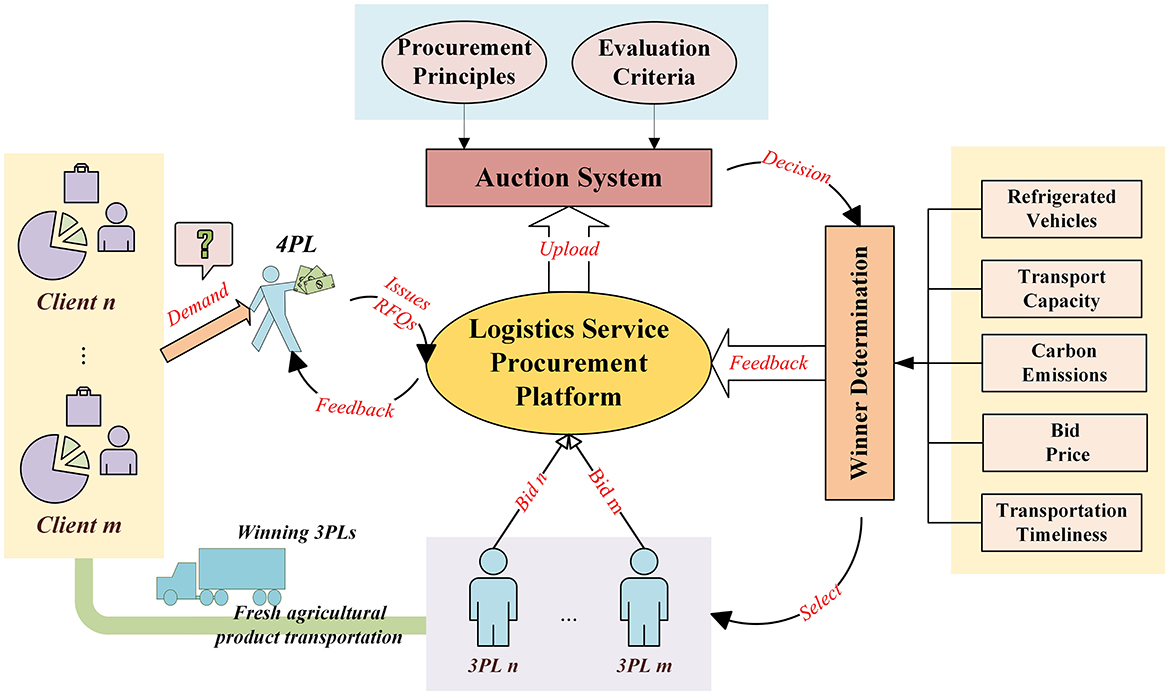
With Lean operations as the main criterion, managers can improve the cooperation profitability by selecting low-cost suppliers and carriers (Fu et al., 2025). The recent rapid development of third-party logistics (3PL) provides strong support for cold chain transportation of FAP, which can effectively enhance customer satisfaction and transportation efficiency of FAP (Göl and Çatay, 2007; Singh et al., 2018). The direct delivery model of 3PL can ensure “continuous transportation chain” for FAP by simplifying the transportation process. However, it is difficult for a single 3PL to realize resource integration, resulting in high cold chain transportation costs. In addition, enterprises rely on a single 3PL, which makes it difficult to achieve efficient resource allocation and response capabilities in the face of complex demand fluctuations and rapidly changing market conditions. The proposal and development of fourth-party logistics (4PL) provide new opportunities for the transformation of cold chain logistics. As a supply chain integrator, the 4PL can integrate the capabilities of multiple 3PLs, technologies, and logistics resources, improve supply chain efficiency and achieve efficient resource allocation. Unilever Southern Africa pointed out that 4PL can help enterprises integrate logistics resources to improve economic benefits and reduce carbon emissions (Tao et al., 2017). Eva reduces transportation-related carbon footprints by optimizing routes and consolidating freight.² As the largest 4PL platform in China, Cainiao Group improves comprehensive green logistics solutions by collaborating with multiple 3PLs. Accordingly, this paper investigates the logistics service procurement (LSP) for FAP from the 4PL perspective, with the objective of reducing transportation costs and enhancing transportation efficiency through the integration of cold chain transportation tasks and logistics resources. A key challenge in LSP for FAP lies in selecting the most suitable 3PL among the many available to effectively fulfill cold chain transportation requirements. Auction is one of the most effective ways to achieve resource procurement. Common auction mechanisms include sequential auction mechanism, parallel auction mechanism, and combinatorial auction mechanism, among which combinatorial auction allows bidders to bid as packages in a single transaction (Sandholm, 2002; Wu and Hao, 2015). Based on the combinatorial auction mechanism, the application of the combinatorial reverse auction (CRA) mechanism can further enhance procurement efficiency and customer satisfaction. Consequently, this paper, based on the CRA platform, aims to further optimize the utilization efficiency of cold chain logistics resources and procurement auctions for fresh produce enterprise to address a LSP auction problem. Specifically, the 4PL, acting as the auctioneer, publishes logistics demand through the auction platform, whereas the 3PLs, serving as bidders, submit detailed information such as transportation capacity, environmental performance of refrigerated vehicles, bid prices, and expected delivery timelines. The platform employs the auction system to determine the winning 3PLs and allocates cold chain transportation tasks to the selected providers based on predefined requirements—a process known as the winner determination (WD) problem, as shown in Figure 1.

Figure 1

Figure 1. The process of logistics service procurement auction for fresh agricultural product.

To address the LSP auction problem for FAP, this study investigates the WD problem within a CRA framework, incorporating timeliness and sustainability considerations under demand uncertainty from a 4PL perspective. A key challenge is how to ensure the timeliness and sustainability of FAP transportation with the introduction of multiple tasks and multiple 3PLs. To this end, the study incorporates constraints related to time windows for 3PL transportation and carbon cap regulations. In response to this issue, a two-stage stochastic programming (TS-SP) model is proposed to minimize total costs under demand uncertainty. The first-stage decision determines the winning 3PLs, while the second-stage decision determines their respective shipping volumes. By applying the sample average approximation (SAA) method, the TS-SP problem is approximated as a mixed-integer linear programming (MILP) model. Since WD problem is an NP-hard problem, the computational complexity increases significantly with the number of decision variables (Parkes et al., 2001). This paper reconstructs the SAA algorithm framework based on Latin hypercube sampling (LHS), integrates dual decomposition and Lagrangian relaxation (DDLR) algorithm, and develops a sampling-based approximate algorithm to solve the proposed model. A real case from Shenzhen, China is presented to evaluate the effectiveness of the proposed model and algorithm. The case analysis results reveal the complex coupling relationship between carbon caps, time window sizes, and unit outsourcing costs, thereby providing valuable management insights for 4PLs.

The main contributions of this study can be summarized as follows:

• From the 4PL perspective, this paper presents a LSP auction problem for FAP considering timeliness and sustainability under demand uncertainty, with an emphasis on how multiple tasks and multiple 3PLs affect transportation timeliness and sustainability.

• With the objective of minimizing the total cost, a TS-SP model is developed and approximated as a MILP model using the SAA method.

• The traditional SAA algorithm framework is reconstructed using LHS, chi-square test and DDLR algorithm, thereby a sample-based approximation algorithm is developed, which provides a means to obtain the lower and upper bounds of the optimal solution.

• The validity of the developed model and algorithm is demonstrated by investigation a real case from Shenzhen, China, which reveals the complex coupling relationship between carbon cap, time window size and unit outsourcing costs, providing management insights for 4PLs.

The structure of the paper is as follows. In Section 2, review the related prior works to support the research innovation of this paper. In Section 3, the relevant model is developed, and a brief overview of the research problem is presented. In Section 4, a sample-based approximation algorithm is developed. Section 5 analyzes a real case to demonstrate the performance of the algorithm and the effectiveness of the model, and provides some management insights for managers. In Section 6, a brief summary is given.

2 Literature review

This paper studies the WD problem in the LSP auction problem for FAP with a focus on sustainability and timeliness under demand uncertainty, from a 4PL perspective. Research on the WD problem in transportation service procurement (TSP) and on supply chains for FAP are closely related to the topic of this study. Accordingly, this section reviews prior studies from these two perspectives.

2.1 Winner determination in transportation service procurement

WD problem is one of the most effective means to achieve TSP. Currently, many scholars conduct research on the WD within the TSP. Based on the nature of demand, existing studies can be divided into WD under deterministic and uncertain environments.

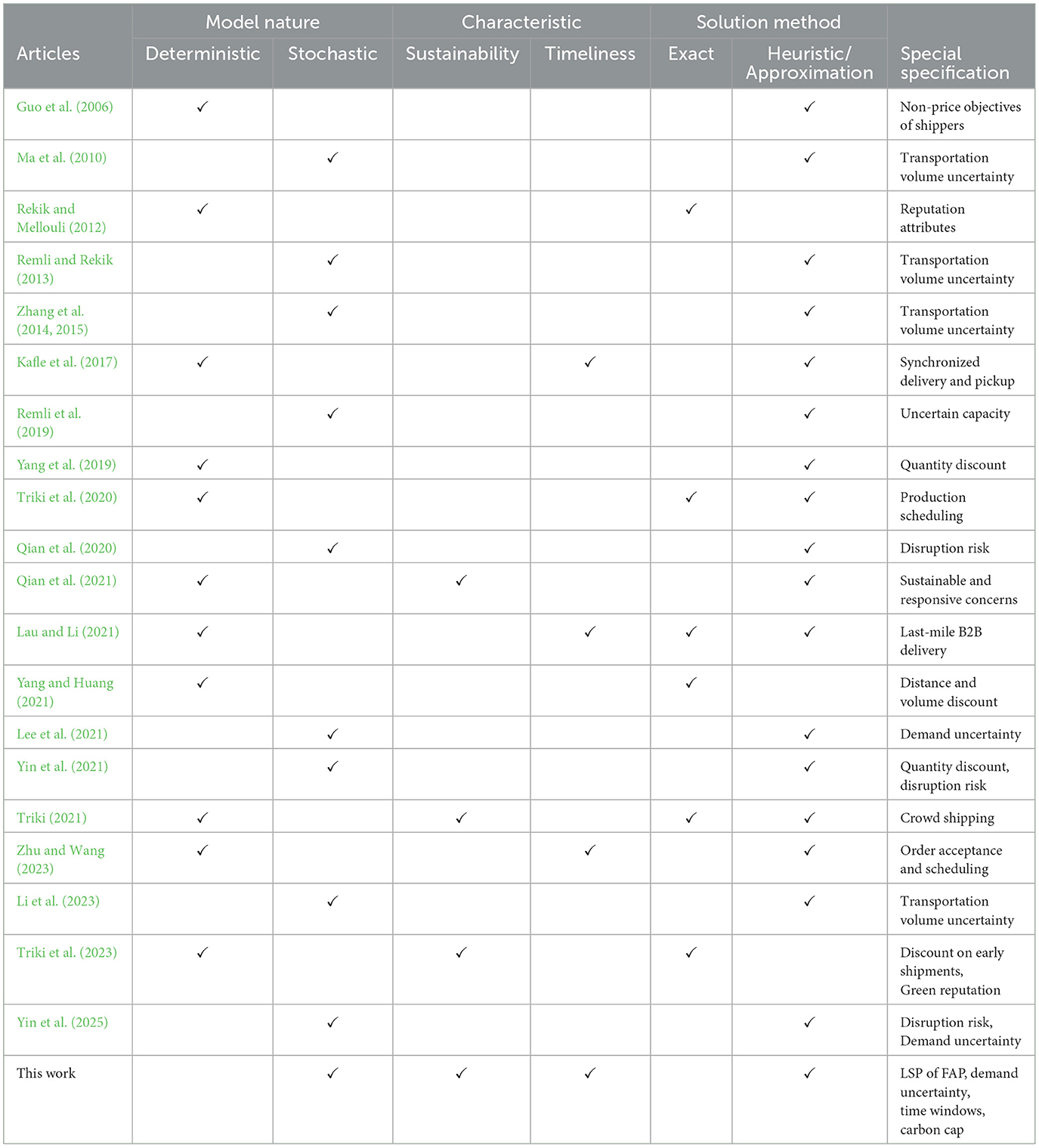
In the study of demand deterministic environments, many scholars propose valuable research viewpoints and practical applications related to associated issues, making significant contributions to the development of WD problem. Reviewing early relevant literature, Caplice and Sheffi (2003) proposed a MILP model for WD that assigns lanes to designated carriers. Subsequently, Sheffi (2004) found that applying a combinatorial auction mechanism to TSP could reduce management costs for businesses. Guo et al. (2006) focused on incorporating non-price objectives of shippers and the transfer point costs of carriers. They introduced minimum and maximum allocation constraints for carriers to establish an integer programming model. Rekik and Mellouli (2012) established a WD model based on bid prices and reputation attributes. Their findings demonstrated that focusing on carrier reputation could effectively reduce transportation costs. Yang et al. (2019) developed a MILP model that focuses on shipment volume discounts, utilizing an iterative algorithm to help shippers make better decisions. Yang and Huang (2021) concentrated on discounts related to transportation distance and volume, proposing a mixed-integer non-convex programming model. They employed a superior encoding formulation to avoid imbalances in the pruning tree during solving, as well as to reduce big-M constraints to accelerate solution time. Additionally, many scholars combine WD with other issues. For instance, Triki (2021) addressed the selection of temporary drivers as a WD problem while focusing on the vehicle routing, effectively reducing transportation and outsourced driver costs. Under the subsidized routes, Kinene et al. (2022) first established an airline bid preparation model and then utilized WD to obtain reasonable solutions based on predefined evaluation criteria. Triki et al. (2020) was the first to combine production scheduling with WD, creating a MILP that incorporates delivery time constraints. In the matching problem for shippers and carriers in last-mile B2B delivery, Lau and Li (2021) included time window constraints in their proposed MILP model, solving small-scale problems using branch-and-cut methods and large-scale instances with an adaptive large neighborhood search approach. In a crowdsourced urban package delivery system, Kafle et al. (2017) decomposed the overall problem into WD and a synchronized delivery and pickup problem with time windows, iteratively solving both problems using a Tabu search method. Zhu and Wang (2023) described WD as a profit-maximizing order acceptance and scheduling problem with time window constraints on identical parallel machines, developing a algorithm based on Lagrangian relaxation techniques to solve it. The above studies mainly focus on the WD under deterministic demand environments, with insufficient exploration of uncertainty.

Without loss of generality, there are usually many uncertain events in the actual practice of TSP, such as customer demand uncertainty and transportation capacity uncertainty, which can easily lead to serious economic losses to the logistics and transportation system. Therefore, considering uncertain events can improve the efficiency of logistics services and enhance the decision-making efficiency of solving solutions. Considering transportation volume uncertainty, Ma et al. (2010) used commercial solving software to address a TS-SP model based on combinatorial auctions. Zhang et al. (2014) proposed a sampling-based TS-SP model and used a Monte Carlo sampling (MCS) approximation algorithm to solve it. Subsequently, Zhang et al. (2015) developed a tractable two-stage robust optimization (TS-RO) model and used a data-driven method to describe multifaceted uncertainty sets. Remli and Rekik (2013) studied a TS-RO model and solved it using a constraint generation (CG) algorithm. In their earlier model, Remli et al. (2019) considered transportation capacity uncertainty and enhanced the convergence speed of the CG algorithm through multiple improvement strategies. Qian et al. (2020) presented a disruption risk mitigation strategy in their proposed TS-SP model and effectively addressed a large number of complex scenarios using scenario reduction techniques. Yin et al. (2021) investigated the impact of changes in quantity discounts on decision outcomes under disruption risk. Subsequently, Qian et al. (2021) investigated a WD problem that considers sustainability and responsiveness under disruption risk, employing a scoring method to evaluate the sustainable attributes of 3PL to ensure the sustainable development of TSP. By integrating the schedules of different shipping carriers, Lee et al. (2021) utilized a CG algorithm to solve a TS-RO problem that considers non-probabilistic demand uncertainty, thereby aiding shippers in making better decisions. Based on multi-attribute decision-making methods, Qian et al. (2023b) created a TS-SP model that incorporates outsourcing options under demand uncertainty, selecting a superior 3PL by evaluating their sustainability and flexibility. Subsequently, in the context of quantity discounts and demand uncertainty, Qian et al. (2023a) transformed a TS-SP model into an equivalent deterministic MILP problem using SAA and linearization techniques. Under the uncertainty of transportation volume, Li et al. (2023) proposed a TS-RO model introducing basic risk index and procurement budget, and converted it into a MILP problem through linear decision rules and dual theory. Yin et al. (2025) explored a WD problem under the double uncertainty of disruption risk and demand. The aforementioned literature mainly focuses on the management of transportation volume uncertainty and disruption risk uncertainty, whereas limited research has been conducted on carbon emission management and time window constraints under demand uncertainty.

2.2 Green supply chain for fresh agricultural products

FAP is an essential food in people's daily lives, and many scholars have conducted research on the FAP supply chain (Agustina et al., 2014; Sun et al., 2022; Tan et al., 2023; Zhang et al., 2020; Shi et al., 2025; Anand and Barua, 2022; Wang et al., 2023). As consumers and governments increasingly focus on the development of a low-carbon economy, environmental factors become an important concern in the FAPSC (Yadav et al., 2022).

As Parashar et al. (2020) points out, reducing carbon footprints is a pressing global issue. Validi et al. (2014) proposed a optimization model that minimizes total costs while reducing CO₂ emissions during transportation. Bortolini et al. (2016) constructed a distribution planner that considers carbon footprint, execution costs, and delivery time objectives and solves the optimization problem of FAP distribution networks. Guo et al. (2017) proposed a reverse and forward logistics network and path planning model for FAP e-commerce enterprises with a focus on low carbon. In the design of imported FAP green cold chain network, Fang et al. (2018) developed a multi-objective model with balancing total cost and carbon emissions as competing objectives. In the sustainable hub location-vehicle scheduling problem, Musavi and Bozorgi-Amiri (2017) focus on optimizing the total carbon emissions of vehicles and transportation costs. Yakavenka et al. (2020) focused on sustainable supply chain network design and proposed a MILP model with cost and emission minimization. Pratap et al. (2022) studied the carbon footprint, time window constraints, and production capacity. They created a logistics route planning model to minimize carbon emissions. Wu et al. (2023) studied the green vehicle routing problem for delivery FAP and developed a k-means clustering optimization algorithm to solve it. In the design of green forward and reverse supply chain networks, Fathollahzadeh et al. (2024) studied a TS-SP model with the objectives of minimizing carbon emissions and maximizing profits. Based on the framework of Objectives, Goals, Strategies, Measures, Lu and Yu (2024) developed a multi-objective model for partner selection considering carbon emissions. This model seeks to reduce carbon emissions, enhance the quality of FAP, and maximize profits. Govindan et al. (2014) considered carbon emission cost decisions in their proposed multi-objective model, introducing a location-routing problem with time windows. Zulvia et al. (2020) studied a green vehicle routing model that optimized carbon emissions and customer satisfaction while considering time window constraints and the impact of working hours during peak and off-peak periods. Chen et al. (2020) focused on the environmental factors of carbon emissions in a vehicle routing problem with time windows. Chen et al. (2019) proposed a route optimization model for cold chain distribution that incorporates quality deterioration costs and carbon emissions. The research on FAP supply chain management primarily focuses on issues such as network design, route optimization, and facility location, with in-depth studies on time windows and carbon regulations. However, research on using the WD problem to solve the LSP for FAP is not common.

2.3 Research gaps

The above literature review is summarized in Table 1, from which several research gaps can be identified. First, although stochastic WD problems have been investigated by scholars, most focus on transportation volume uncertainty and disruption risk, with relatively limited attention given to demand uncertainty. Second, research that simultaneously considers sustainability and timeliness in decision-making remains limited, with most existing studies addressing only one of these aspects. Third, while there have been studies on cold chain logistics for FAP, few scholars have integrated the WDP into the LSP auction problem for FAP.

Table 1

Table 1. Summary of literature related to WD problem in TSP.

In this regard, based on the CRA mechanism and the 4PL perspective, this paper investigates the LSP auction problem for FAP under demand uncertainty, focusing on the timeliness and sustainability. Furthermore, a WD problem with time window constraints and a carbon cap strategy is proposed. To solve the complex TS-SP model with coupling characteristics, this paper reconstructs the traditional SAA algorithm framework using LHS, the chi-square test and DDLR algorithms. A real case from Shenzhen, China is applied to demonstrate the applicability of the proposed model and the algorithm, and to reveal the complex coupling between carbon caps, time window sizes and unit outsourcing costs, which provides managerial insights for 4PLs.

3 Problem description and model

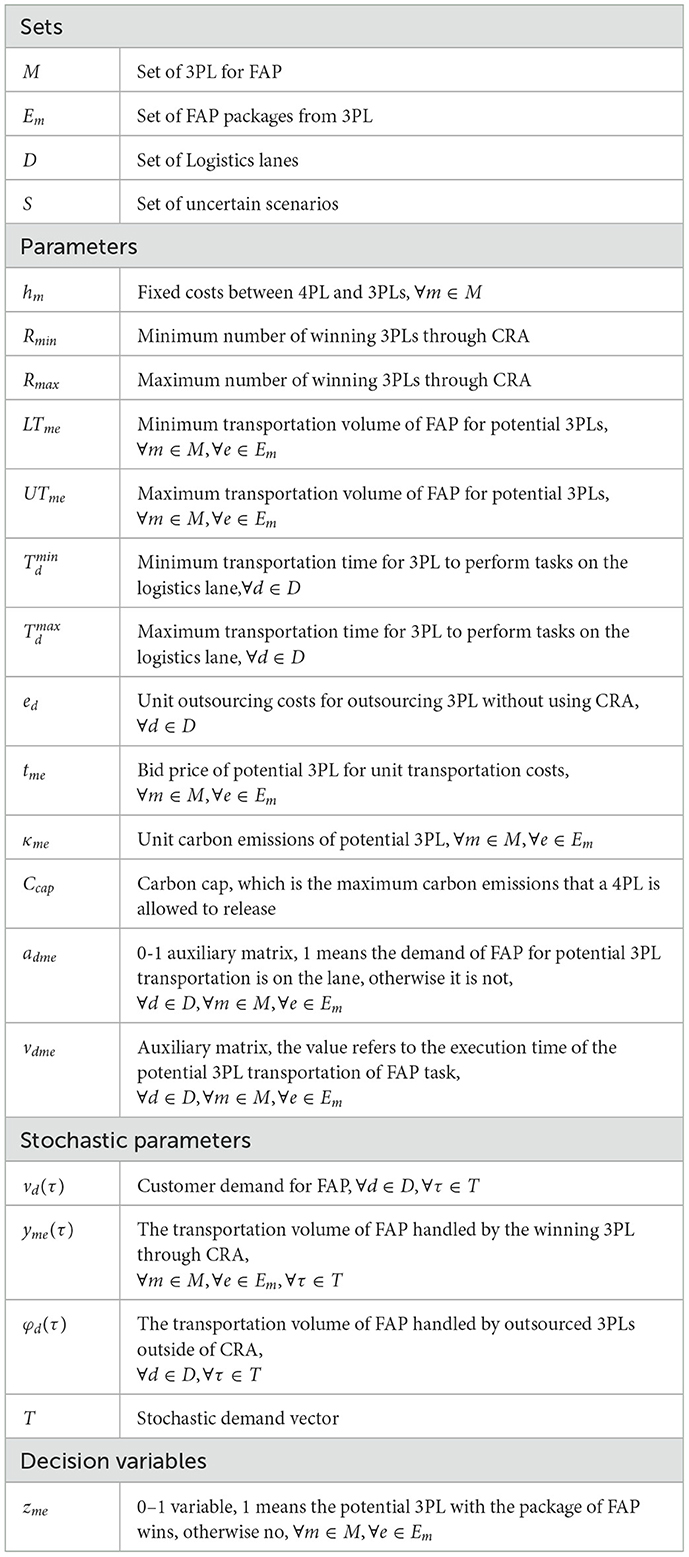
This paper assumes that the logistics tasks of fresh produce as lanes, with their origins and destinations represented as nodes. Lu et al. (2025b) pointed out that “scenarios” can be applied to the domains of food safety and produce transportation. Therefore, demand uncertainty is represented by a set of scenarios in this study. Additionally, each bidding package submitted by 3PLs includes a bid price to aid the platform in selecting potential logistics service providers and is subject to constraints defined by R_min and R_max, which specify the minimum and maximum number of 3PLs that can be selected. When a 3PL is selected to undertake logistics tasks, it must pay a fixed cost h_m to the platform, which covers platform usage fees, refrigerated vehicle maintenance, and driver rental, among other operational costs. In addition to introducing a time window constraint ($T_d^{min}$, $T_d^{max}$) to regulate the timeliness of winning 3PLs, a carbon emission factor is also assigned to each bidding 3PL to support 4PLs in managing carbon emissions. A carbon cap C_cap is defined to represent the maximum volume of carbon emissions that a company is permitted to release. If demand cannot be fulfilled by the winning 3PLs, temporarily outsourced 3PLs (those not involved in the auction) may be used to ensure customer satisfaction. The usage cost e_d of these temporary providers can be varied in response to market fluctuations or special conditions. Notably, the carbon emissions of these providers are not included in the enterprise's carbon management. To address this issue, a two-stage WD model is proposed under demand uncertainty, incorporating time window constraints and a carbon cap strategy, with the objective of minimizing total cost. For ease of understanding, a description of the sets, parameters, and decision variables involved in the model is provided in Table 2.

Table 2

Table 2. Notations and descriptions of the model.

(P1): The first stage problem

$\begin{array}{l}min{\displaystyle \sum _{m\in M}}{\displaystyle \sum _{e\in E_m}}{h}_m{z}_{me}+E_{\tau }\left[f(z,y,\phi ,\tau )\right]\\ \text{s.t.}\\ {\displaystyle \sum _{e\in E_m}}{z}_{me}\le 1,\forall m\in M& (1)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{m\in M}}{\displaystyle \sum _{e\in E_m}}{z}_{me}\le R_{max}& (2)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{m\in M}}{\displaystyle \sum _{e\in E_m}}{z}_{me}\ge R_{min}& (3)\end{array}$

$\begin{array}{l}{T}_d^{min}\le (1-a_{dme})T_d^{min}+a_{dme}((1-z_{me})T_d^{min}+z_{me}{\nu }_{dme}),\\ \forall d\in D,\forall m\in M,\forall e\in E_m& (4)\end{array}$

$\begin{array}{l}{T}_d^{max}\ge (1-a_{dme})T_d^{min}+a_{dme}((1-z_{me})T_d^{min}+z_{me}{\nu }_{dme}),\\ \forall d\in D,\forall m\in M,\forall e\in E_m& (5)\end{array}$

$\begin{array}{ll}{z}_{me}\in \left\{0,1\right\},\forall m\in M,\forall e\in E_m& (6)\end{array}$

The second stage problem

$\begin{array}{l}\begin{array}{c}f(z,y,\phi ,\tau )={\displaystyle \sum _{m\in M}}{\displaystyle \sum _{e\in E_m}}{y}_{me}(\tau )t_{me}+{\displaystyle \sum _{d\in D}}{e}_d{\phi }_d(\tau )\end{array}\\ \text{s.t.}\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{m\in M}}{\displaystyle \sum _{e\in E_m}}{a}_{dme}{y}_{me}(\tau )+{\phi }_d(\tau )=v_d(\tau ),\forall d\in D,\forall \tau \in T& (7)\end{array}$

$\begin{array}{ll}{z}_{me}L{T}_{me}\le y_{me}(\tau ),\forall m\in M,\forall e\in E_m,\forall \tau \in T& (8)\end{array}$

$\begin{array}{ll}{z}_{me}U{T}_{me}\ge y_{me}(\tau ),\forall m\in M,\forall e\in E_m,\forall \tau \in T& (9)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{m\in M}}{\displaystyle \sum _{e\in E_m}}{y}_{me}(\tau ){\kappa }_{me}\le C_{cap},\forall \tau \in T& (10)\end{array}$

$\begin{array}{ll}G{z}_{me}\ge y_{me}(\tau ),\forall m\in M,\forall e\in E_m,\forall \tau \in T& (11)\end{array}$

$\begin{array}{ll}{y}_{me}(\tau )\ge 0,\forall m\in M,\forall e\in E_m,\forall \tau \in T& (12)\end{array}$

$\begin{array}{ll}{\phi }_d(\tau )\ge 0,\forall d\in D,\forall \tau \in T& (13)\end{array}$

Based on the notation and problem description, the LSP auction problem for FAP presented in this paper can be structured as a two-stage model (P1), with an objective function that represents the minimization of the total cost, and includes fixed costs and expected operating costs. In particular, the expected operating cost mainly involves the transportation cost of the winning 3PLs and the outsourcing cost incurred by the temporarily outsourced 3PLs. The specific meanings of the constraints are as follows. Equation 1 ensures that the winning 3PL can be selected for at most one FAP task package. Equations 2, 3 guarantee the maximum and minimum number of winning 3PLs. Equations 4, 5 guarantee the shortest and longest transportation times for the winning 3PLs transporting FAP. Equation 6 represents the constraints for the 0–1 integer decision variables. Equation 7 ensures that both the winning 3PL and the outsourced 3PL can complete the transportation tasks for FAP issued by the 4PL. Equations 8, 9 ensure the minimum and maximum shipment volumes for the 3PL selected through CRA. Equation 10 represents that the total carbon emissions of all winning 3PLs do not exceed the allocated carbon cap. In Equation 11, G is a sufficiently large number to ensure that there are sufficient selected 3PLs to accomplish the task of transportation of FAP. Equations 12–13 denote the non-negativity constraints.

(P2)

$\begin{array}{l}\begin{array}{c}min{\displaystyle \sum _{m\in M}}{\displaystyle \sum _{e\in E_m}}{h}_m{z}_{me}+\frac{1}{N}{\displaystyle \sum _{w=1}^N}\left[{\displaystyle \sum _{m\in M}}{\displaystyle \sum _{e\in E_m}}{y}_{mew}{t}_{me}+{\displaystyle \sum _{d\in D}}{e}_d{\phi }_{dw}\right]\end{array}\\ \text{s.t.}\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{e\in E_m}}{z}_{me}\le 1,\forall m\in M& (14)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{m\in M}}{\displaystyle \sum _{e\in E_m}}{z}_{me}\le R_{max}& (15)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{m\in M}}{\displaystyle \sum _{e\in E_m}}{z}_{me}\ge R_{min}& (16)\end{array}$

$\begin{array}{l}{T}_d^{min}\le (1-a_{dme})T_d^{min}+a_{dme}((1-z_{me})T_d^{min}+z_{me}{\nu }_{dme}),\end{array}$

$\begin{array}{ll}\forall d\in D,\forall m\in M,\forall e\in E_m& (17)\end{array}$

$\begin{array}{l}{T}_d^{max}\ge (1-a_{dme})T_d^{min}+a_{dme}((1-z_{me})T_d^{min}+z_{me}{\nu }_{dme}),\end{array}$

$\begin{array}{ll}\forall d\in D,\forall m\in M,\forall e\in E_m& (18)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{m\in M}}{\displaystyle \sum _{e\in E_m}}{a}_{dme}{y}_{mew}+{\phi }_{dw}=v_{dw},\forall d\in D,\forall w\in S& (19)\end{array}$

$\begin{array}{ll}{z}_{me}L{T}_{me}\le y_{mew},\forall m\in M,\forall e\in E_m,\forall w\in S& (20)\end{array}$

$\begin{array}{ll}{z}_{me}U{T}_{me}\ge y_{mew},\forall m\in M,\forall e\in E_m,\forall w\in S& (21)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{m\in M}}{\displaystyle \sum _{e\in E_m}}{y}_{mew}{\kappa }_{me}\le C_{cap},\forall w\in S& (22)\end{array}$

$\begin{array}{ll}G{z}_{me}\ge y_{mew},\forall m\in M,\forall e\in E_m,\forall w\in S& (23)\end{array}$

$\begin{array}{ll}{y}_{mew}\ge 0,\forall m\in M,\forall e\in E_m,\forall w\in S& (24)\end{array}$

$\begin{array}{ll}{\phi }_{dw}\ge 0,\forall d\in D,\forall w\in S& (25)\end{array}$

$\begin{array}{ll}{z}_{me}\in \left\{0,1\right\},\forall m\in M,\forall e\in E_m& (26)\end{array}$

Due to the difficulty in obtaining the probability density function of f(z, y, φ, τ), the aforementioned TS-SP model cannot be directly reformulated as a deterministic model. According to Yin et al. (2024), the SAA method proposed by Kleywegt et al. (2002) effectively transforms stochastic programming models into deterministic equivalents. By using N discrete samples to replace the continuous distribution, the stochastic model can be approximated as a MILP model, denoted as P2.

Notably, P2 is a MILP problem, which can be directly solved using commercial optimization software such as CPLEX. However, as the number of scenarios increases, the computational complexity of solving the problem increases significantly. Therefore, in the next section, an approximate algorithm is proposed to obtain the lower and upper bounds of the model based on the DDLR and SAA methods.

4 A sampling-based approximate algorithm

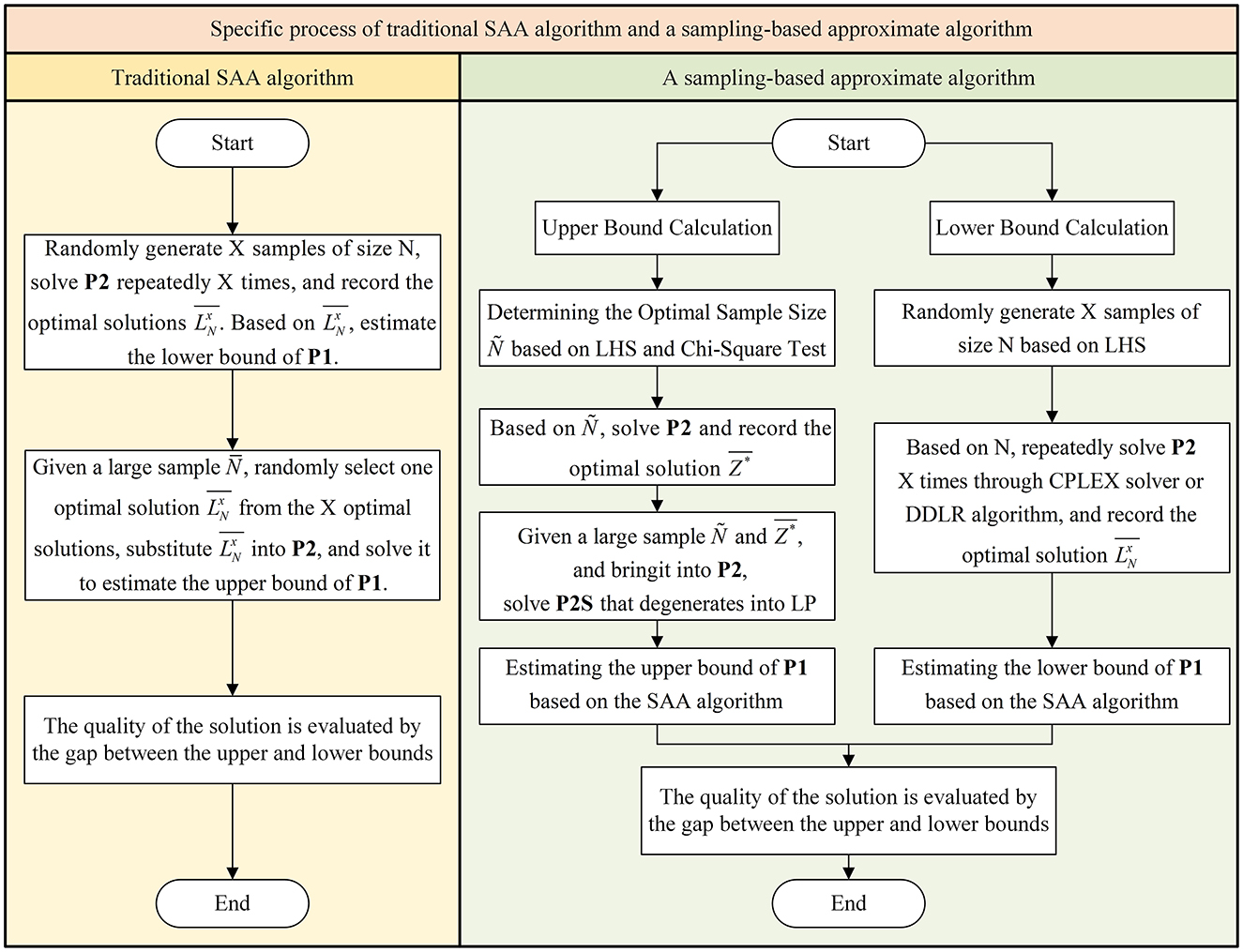
In this section, the LHS method is applied to improve the solution framework of the traditional SAA algorithm, while embedding the DDLR algorithm to improve the efficiency of model solving. The first problem to be solved in the SAA method is how to obtain samples. Although the traditional SAA method using MCS method can identify suitable parameters to improve the performance of the algorithm, it requires substantial computational resources (Fu et al., 2024). According to Yin et al. (2024), the LHS method can achieve the same or even better results than the MCS method with only 1/5 of the sample size. Another problem is how to determine the number of samples. Traditional SAA methods typically set the sample size randomly and determine the optimal sample size through extensive numerical testing. However, the randomness of the sample size reduces the efficiency of the SAA algorithms and increases the instability of the solution quality. In this paper, the chi-square test is applied to replace the repeated tests to determine the optimal sample number N to improve the efficiency of obtaining the upper bound of the optimal solution of the problem model, and a detailed comparison between the traditional SAA algorithm and the proposed approximate solution algorithm is shown in Figure 2.

Figure 2

Figure 2. Specific details and processes of different algorithms.

Specifically, Section 4.1, an algorithm for determining a upper bound is provided, Section 4.2, an algorithm for determining a lower bound is provided, and Section 4.3 provides a formula for determining the gap.

4.1 Upper bound determination

First, LHS is used to obtain sample data, and the optimal sample size Ñ is determined based on the P-value and the chi-square value in the chi-square test. Then, problem P2 is solved based on the sample size Ñ, and the corresponding optimal solution ${\bar{\text{Z}}}^{*}$ is recorded. Given $\bar{N}$, $\bar{N}\gg Ñ$, substitute ${\bar{\text{Z}}}^{*}$ and Ñ back into problem P2, and P2 can be reduced to the following linear programming (LP) problem:

$L_{\overline{N}}\left({\overline{Z}}^{*}\right)=h{\overline{Z}}^{*}+\frac{1}{\overline{N}}{\displaystyle \sum _{w=1}^{\overline{N}}\left[{\displaystyle \sum _{m\in M}{\displaystyle \sum _{e\in E_m}{y}_{mew}{t}_{me}}}+{\displaystyle \sum _{d\in D}{e}_d{\phi }_{dw}}\right]}$

Here, $\text{h}{\bar{\text{Z}}}^{*}$ is a fixed constant, so the above LP can be further decomposed into Ñ subproblems to enhance computational efficiency. The w-th subproblem is expressed as follows:

(P2S)

$L{S}_w\left({\overline{Z}}^{*}\right)={\displaystyle \sum _{m\in M}{\displaystyle \sum _{e\in E_m}{y}_{mew}{t}_{me}}}+{\displaystyle \sum _{d\in D}{e}_d{\phi }_{dw}}$

Then, $L_{\overline{N}}\left({\overline{Z}}^{*}\right)=h{\overline{Z}}^{*}+\frac{1}{\overline{N}}{\displaystyle \sum _{w=1}^{\overline{N}}L{S}_w\left({\overline{Z}}^{*}\right)}$ is an unbiased estimator of an upper bound for P1. Let $S_{Ñ}^2(\overline{{\text{Z}}^{*}})$ denote the variance of $L_{Ñ}(\overline{{\text{Z}}^{*}})$, and its corresponding sample variance can be calculated using the formula provided below.

$\begin{array}{ll}{\sigma }_{\bar{N}}^2=\frac{1}{\bar{N}}{S}_{\bar{N}}^2({\bar{\text{Z}}}^{*})& (27)\end{array}$

4.2 Lower bound determination

Generate X samples of size N, and based on the sample N, solve problem P2 repeatedly X times, recording the corresponding objective function values ${\bar{L}}_N^x,x=1,2,\dots ,X$. The sample variance and mean can be calculated using the following formulas.

$\begin{array}{ll}{\widehat{L}}_{N,X}=\frac{1}{X}{\displaystyle \sum _{x=1}^X}{\overline{L}}_N^x& (28)\end{array}$

$\begin{array}{ll}{\widehat{\sigma }}_{{\overline{L}}_{N,X}}^2=\frac{1}{X(X-1)}{\displaystyle \sum _{x=1}^X}{({\overline{L}}_N^x-{\widehat{L}}_{N,X})}^2& (29)\end{array}$

${\widehat{L}}_{N,X}$ is a point estimate of a lower bound for P1. Since P2 is an MILP problem, we can solve P2 using commercial software such as CPLEX. However, as the number of constraints and decision variables increases, the computational efficiency will decrease. According to the work by Yin et al. (2024), we can improve computational efficiency by using the DDLR algorithm with an improved step size.

The main idea of Lagrangian relaxation and dual decomposition methods is to decompose P2 into N independent subproblems. Let ${Ẑ}_w^T,w=1,2,\cdots ,N$ represent the decision variables of the subproblems after decomposition. The unexpected constraints must be added to the model so that the decomposed problem is equivalent to the original problem, which is as follows:

(P3)

$\begin{array}{l}\min \frac{1}{N}{\displaystyle \sum _{w=1}^N[{\displaystyle \sum _{m\in M}{\displaystyle \sum _{e\in E_m}{h}_m{z}_{mew}}}+{\displaystyle \sum _{m\in M}{\displaystyle \sum _{e\in E_m}{y}_{mew}{t}_{me}}}}\\ +{\displaystyle \sum _{d\in D}{e}_d{\phi }_{dw}}]\\ \text{s.t.}\\ {\widehat{Z}}_w^T={\widehat{Z}}_{w+1}^T,w=1,2,\dots ,N-1\\ \text{ Constraints:\hspace{1em}}(14)-(26)& (30)\end{array}$

According to the work by Yin et al. (2024), we can infer that Equation 30 can be expressed in the following form.

$\begin{array}{ll}{\displaystyle \sum _{w=1}^N}{\text{P}}_w{({\widehat{\text{Z}}}_w^T)}^T=0& (31)\end{array}$

Where P_w is an auxiliary matrix composed of the identity matrix and zero matrix, and its specific form can be found in the work by Yin et al. (2024). Let λ denote the Lagrange multipliers, then the Lagrangian relaxation of problem P3 is formulated as follows:

(LR)

$\begin{array}{l}LR(\lambda )=\min \frac{1}{N}{\displaystyle \sum _{w=1}^N[{\displaystyle \sum _{m\in M}{\displaystyle \sum _{e\in E_m}{h}_m{z}_{mew}}}+{\displaystyle \sum _{m\in M}{\displaystyle \sum _{e\in E_m}{y}_{mew}{t}_{me}}}}\\ +{\displaystyle \sum _{d\in D}{e}_d{\phi }_{dw}}]+{\lambda }^T{\displaystyle \sum _{w=1}^N{P}_w}{({\widehat{\text{Z}}}_w^T)}^T\end{array}$

LR(λ) can be decomposed into multiple independent subproblems, and its specific form given by the following formula.

(LRQ)

$\begin{array}{l}L{R}_w(\lambda )=\min \frac{1}{N}[{\displaystyle \sum _{m\in M}{\displaystyle \sum _{e\in E_m}{h}_m{z}_{mew}}}+{\displaystyle \sum _{m\in M}{\displaystyle \sum _{e\in E_m}{y}_{mew}{t}_{me}}}\\ +{\displaystyle \sum _{d\in D}{e}_d{\phi }_{dw}}]+{\lambda }^T{P}_w{({\widehat{\text{Z}}}_w^T)}^T\end{array}$

The corresponding Lagrangian dual problem can be expressed as.

(LDP)

$\begin{array}{l}LDP(\lambda )={\displaystyle \underset{\lambda }{max}}LR(\lambda )\end{array}$

Since the Lagrangian dual problem is a concave, non-differentiable, and unconstrained optimization problem, the subgradient algorithm can be employed to solve it effectively. However, the convergence speed is related to the size of the step size. If the step size is small, then the convergence is very slow, whereas if it is too large, then convergence may not be observed. Thus, determining an appropriate step size for the subgradient is a critical issue that warrants further study. The process of the subgradient algorithm is shown in the following steps.

step 1. Given an initial Lagrange multiplier λ¹, set the iteration step k = 1.

step 2. After calculating the formula for LRQ with λ^k and recording the corresponding subgradient $\sum _{w=1}^N{\text{P}}_w{{({({\widehat{\text{Z}}}_w^T)}^{*})}_k}^T$, the value of LR(λ^k) is then calculated, and the optimal objective function value in the LDP is updated.

step 3. The Lagrangian multiplier is updated using the following formula.

$\begin{array}{ll}{\lambda }^{k+1}={\lambda }^k+{\text{s}}^k{\displaystyle \sum _{w=1}^N}{\text{P}}_w{{({({\widehat{\text{Z}}}_w^T)}^{*})}_k}^T& (32)\end{array}$

where ${\mathrm{\text{s}}}^k={\alpha }^k\frac{{\beta }^k-(LR({\lambda }^k))}{{||\sum _{w=1}^N{\text{P}}_w{{({({\widehat{\text{Z}}}_w^T)}^{*})}_k}^T||}^2}$, α^k = κ(k), β^k = (1+κ′(k))σ^*. Here, σ^* is the current optimal objective function value, and κ(k) and κ′(k) are linear monotonically decreasing functions about k. If σ^* remains unchanged for three iterations, set α^k+1 = ηα^k to ensure the convergence of the algorithm, where 0 < η < 1.

step 4. The termination condition of the algorithm is set as follows.

$\begin{array}{ll}\left|\frac{LR({\lambda }^{k+1})-LR({\lambda }^k)}{LR({\lambda }^k)}\right|\le \epsilon & (33)\end{array}$

where ε is the maximum tolerance. If this condition is satisfied, the algorithm terminates; otherwise, the Lagrange multiplier is updated, and the objective function value is recalculated.

4.3 Gap calculation for upper and lower bounds

To illustrate the quality of the solution obtained using a sample-based approximation algorithm, in this section we propose the following calculation formula to solve the gap between the upper and lower bounds:

$\begin{array}{ll}gap({\bar{\text{Z}}}^{*})=L_{\bar{N}}({\bar{\text{Z}}}^{*})-{\widehat{L}}_{N,X}& (34)\end{array}$

$\begin{array}{ll}{\sigma }_{gap}^2={\widehat{\sigma }}_{{\bar{L}}_{N,X}}^2+{\sigma }_{\bar{N}}^2& (35)\end{array}$

For the optimal gap at the 1−α confidence level, it can be calculated as follows:

$\begin{array}{ll}{L}_{\bar{N}}({\bar{\text{Z}}}^{*})-{\widehat{L}}_{N,X}\pm x_{\alpha }\sqrt{{\widehat{\sigma }}_{{\bar{L}}_{N,X}}^2+{\sigma }_{\bar{N}}^2}& (36)\end{array}$

where $x_{\alpha }={\Lambda }^{-1}(1-\alpha )$, and Λ(x) is the cumulative distribution function of standard normal distribution.

5 A real case study

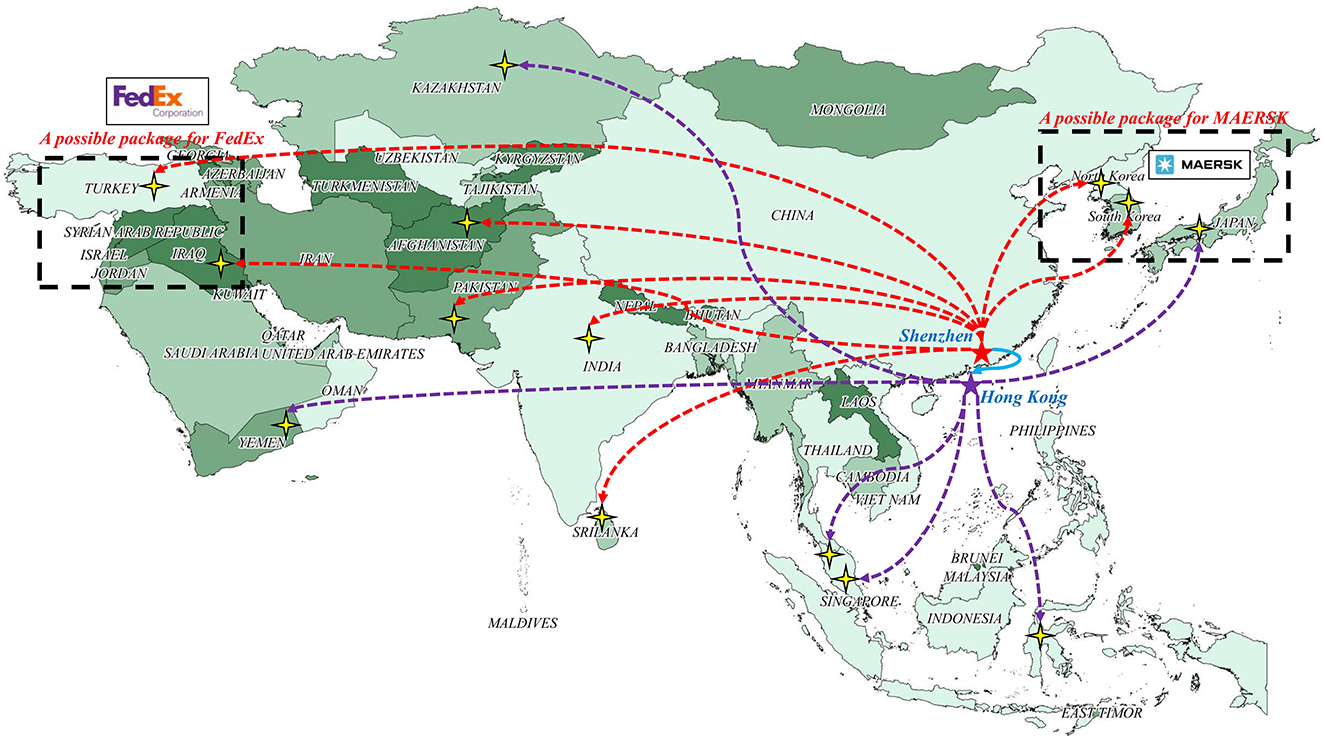
A real case of a 4PL corporation located in Shenzhen, China is provided to analyze the feasibility of the model and the effectiveness of the algorithm. As shown in Figure 3, the case assigns 29 transportation lane tasks to 42 3PL companies (MAERE, DHL, FedEx, etc.). Specifically, there are six bi-directional transportation routes from Hong Kong, 16 bi-directional transportation routes from Shenzhen, and one uni-directional transportation route from Shenzhen to Hong Kong. Demand from neighboring regions can be bundled as one package, for example, the logistics demand from Turkey and Iran is bundled as one package and may be transported by FedEx Logistics. In addition, the values of parameters such as package quantity, price, and capacity are obtained from Qian et al. (2021), and the ICAO Carbon Emissions Calculator³ is utilized to obtain the values of carbon emissions per unit.

Figure 3

Figure 3. Transportation lane tasks in a real case.

In this section, based on the data from the real case study, we conducted several sets of comparative experiments. In Section 5.1, a chi-square test is performed on the sampling results based on both LHS and MCS methods. Section 5.2 offers a comparative analysis between the proposed algorithm and the CPLEX commercial solver to validate the effectiveness of the proposed approach. Section 5.3 conducts sensitivity analysis on key parameters and provides management insights for 4PL.

5.1 Comparison of LHS and MCS methods

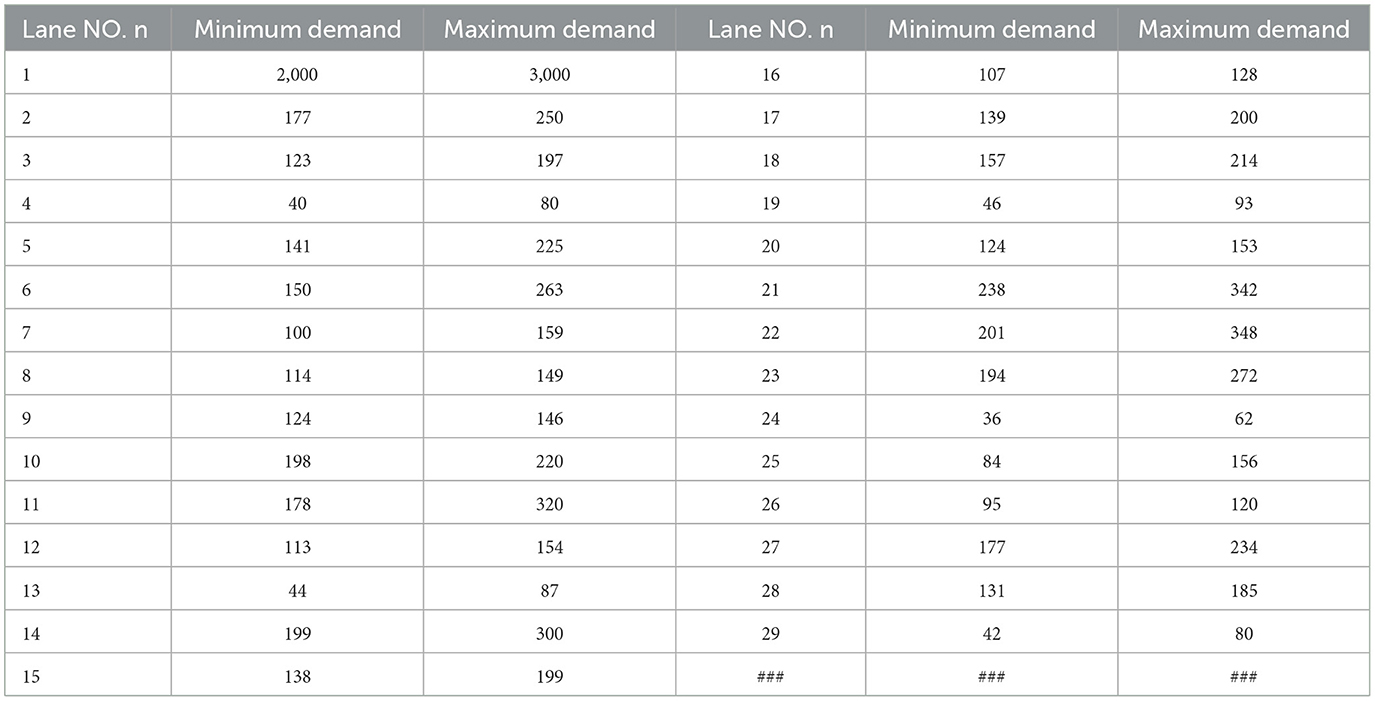
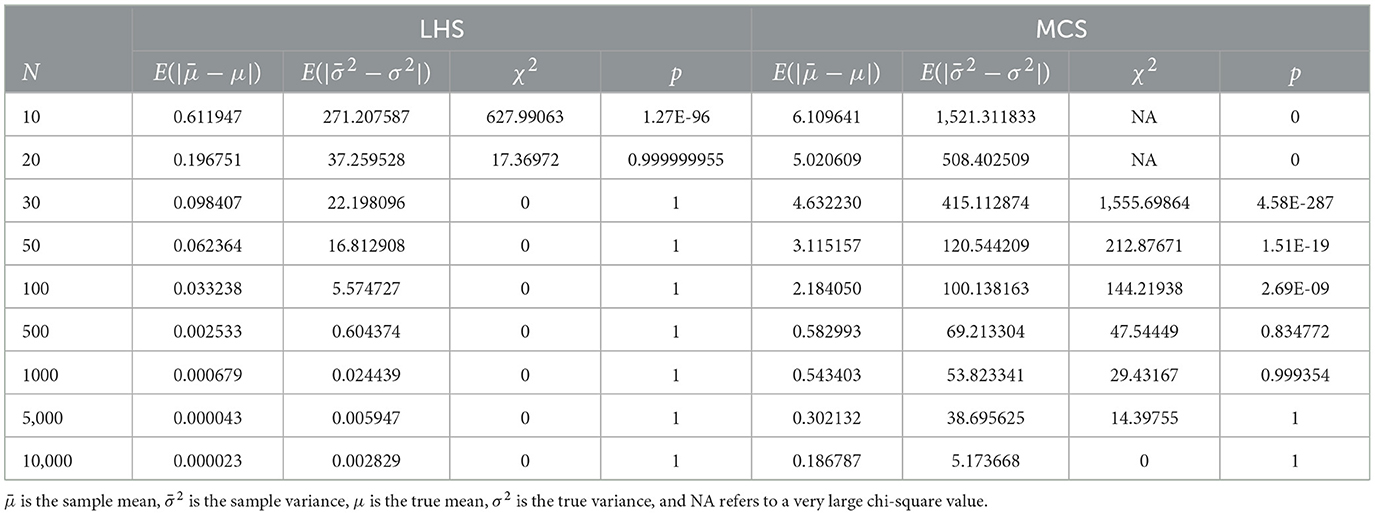
The chi-square test technique is used to determine the optimal sample size by counting the degree of deviation between the actual observed values and the theoretically inferred values of the sample, and using this to determine the optimal sample size Ñ. The actual demand data for each lane are provided in Table 3. To further demonstrate the difference between utilizing the LHS technique and the MCS technique, the comparison of the chi-square test results by multidimensional sampling of demand with different sample sizes N is shown in Table 4.

Table 3

Table 3. Details of demand in a real case.

Table 4

Table 4. Chi-square test results.

From Table 4, as the sample size increases N increases, $E(|{\bar{\sigma }}^2-{\sigma }^2|)$ and $E(|\bar{\mu }-\mu |)$ of LHS method and MCS method are decreasing and the chi-square value is decreasing to 0 and the p-value is increasing to 1. However, the chi-square test based on MCS does not have any significant difference between the samples only when the sample size N is 10,000, on the contrary, there is no significant difference between the samples already when the sample size is N = 30 based on LHS. Therefore, we found that LHS sampling can significantly reduce the sample size and thus increase the computational efficiency. Based on this information, the LHS technique is utilized to sample the demand where Ñ is 30 and N is set to 20.

5.2 Algorithm performance analysis

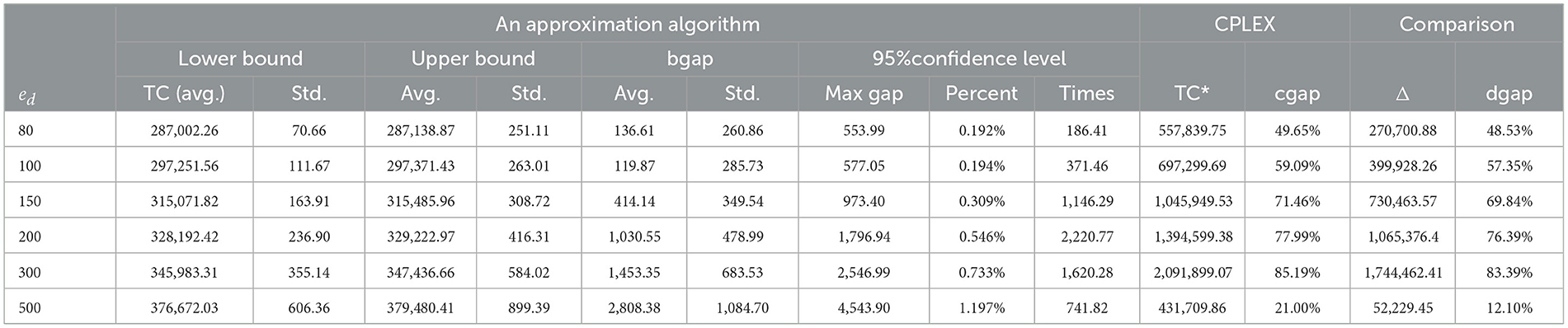
The CPLEX, as an exact solver, can be used in algorithmic comparisons to demonstrate the validity of the developed algorithms and models (Zhang et al., 2024). The comparison results between the proposed approximation algorithm and CPLEX for different unit outsourcing costs e_d are presented in this subsection. All test data run on a computer with a 2.5 GHz CPU and 16GB of memory, with the tests set to stop after 2 h of running on the CPLEX solver. The detailed algorithm comparison results are shown in Table 5. Here, bgap refers to the difference between the upper and lower bounds. avg. represents the average value, TC refers to the total cost, and std. represents the standard deviation. The * symbol indicates the solution provided by CPLEX when the runtime reaches 2 h. cgap refers to the gap value provided by CPLEX. Δ denotes the difference between the sampling-based approximate algorithm and the upper bound obtained by CPLEX solver. dgap represents the percentage difference between the upper bound obtained by CPLEX and the algorithm.

Table 5

Table 5. Results of algorithm comparison.

From Table 5, we observe the following results. The maximum gap and percentage obtained using the proposed approximation algorithm are tolerable, and the algorithm's solution time is shorter than that of directly using CPLEX. When CPLEX runs for 2 h, the difference between the objective value provided by the commercial solver itself and the upper bound obtained using a sample-based approximation algorithm is large, and the gap is intolerable. Since the objective function value is obtained in an acceptable time and the obtained gap between the upper and lower bounds is < 2%, solving the model using the proposed approximation algorithm can assist managers to provide a more accurate solution in a short period of time, which can further help the organization to achieve sustainability and timeliness.

5.3 Sensitivity analysis

In this section, to analyze the impact of changes in key parameters on the results, we design the following experiments. Section 5.3.1 examines the impact of carbon cap variations on the results, and Section 5.3.2 explores the impact of time window changes on decision results.

5.3.1 Analysis of carbon cap

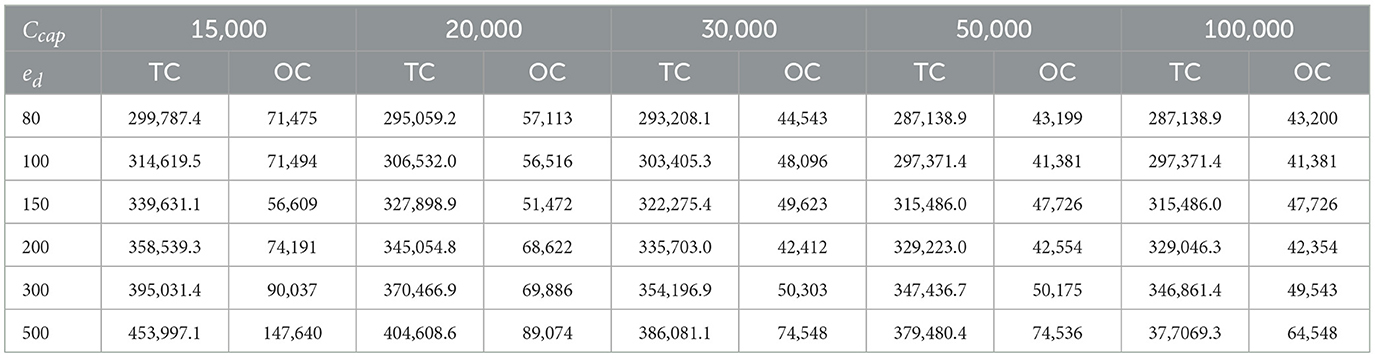
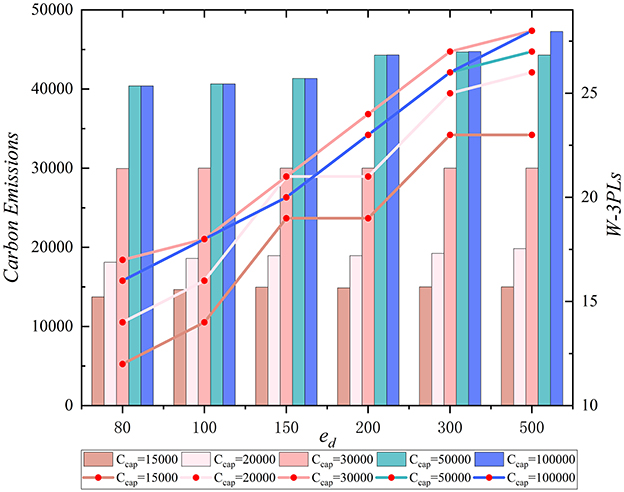
A perturbation analysis is conducted on the carbon emission constraint in the model in this subsection. Carbon cap C_cap ∈ {15, 000, 20, 000, 30, 000, 50, 000, 100, 000}, unit outsourcing cost e_d ∈ {80, 100, 150, 200, 300, 500}, and time window TW = 48. The impact of changes in the carbon cap on cost is detailed in Table 6, and the variation in the number of selected 3PLs and carbon emissions is shown in Figure 4. Here, TC refers to the total cost, OC refers to the outsourcing cost, and W-3PLs refers to the number of 3PLs selected through CRA.

Table 6

Table 6. Impact of carbon cap on costs.

Figure 4

Figure 4. Changes in the number and carbon emissions of selected 3PLs under different C_cap.

From Table 6, the following observations can be made. On one hand, as the unit outsourcing cost increases, the total cost under different carbon caps also increases, while the changes in outsourcing costs are irregular. Combining with Figure 4, it can be observed that as the unit outsourcing cost increases, the number of selected 3PLs increases under different carbon caps, while the carbon emissions remain almost unchanged. From this, several reasons for the irregularity of outsourcing cost changes can be deduced: First, there are differences in the transportation capacity and unit carbon emissions of the 3PLs participating in the bidding. Some of the selected 3PLs have weaker transportation capabilities, which results in a significant number of unfinished tasks being assigned to temporarily outsourced 3PLs, leading to higher outsourcing costs. Second, the variation in unit outsourcing costs. Although the selected 3PLs have strong transportation capabilities and can assign very few unfinished tasks to temporarily outsourced 3PLs, the higher unit outsourcing costs mean that managers need to spend more to cover these expenses. Based on the above situation, it can be concluded that when outsourcing costs are low, managers should focus on increasing the number of participating 3PLs in the bidding process to enhance competition among them, which in turn improves transportation efficiency and reduces expenditure. As unit outsourcing costs increase, 4PL managers not only need to expand the competitiveness of the 3PLs but also need to appropriately increase the carbon cap to select more 3PLs with higher carbon emissions.

On the other hand, as the carbon cap increases, both the total cost and outsourcing costs decrease to varying degrees under the same unit outsourcing cost. As shown in Figure 4, with the increase in carbon cap, the number of selected 3PLs and the carbon emissions both increase. It is noteworthy that under different unit outsourcing costs, the number of selected 3PLs at C_cap = 50,000 is fewer than at C_cap = 30,000, but the carbon emissions are higher, while at C_cap = 100,000, the number of selected 3PLs is almost the same as at C_cap = 50,000, and the carbon emissions do not show significant changes. The reason lies in that when the carbon cap is small, such as C_cap ∈ {15, 000, 20, 000, 30, 000}, the carbon emissions are very close to the carbon cap, leading the 4PL to prefer selecting 3PLs with lower unit carbon emissions for transportation, without considering the transportation capabilities of the selected 3PLs. However, when the carbon cap is large, such as C_cap ∈ {50, 000, 100, 000}, each selected 3PL can generate a larger amount of transportation-related carbon emissions, and high-emission 3PLs will replace low-emission ones. For FAP procurement, higher carbon emissions mean better guarantees for the long-term preservation and quality of FAP. However, for transporting different types of FAP, simply purchasing carbon caps can reduce total cost expenditure, but it is also crucial to consider the transaction costs of purchasing carbon caps and the environmental impact of carbon emissions. Therefore, setting the carbon cap can help managers enhance their environmental awareness when selecting low-carbon and highly capable logistics suppliers. When the carbon cap is low, managers should first focus on using 3PLs with low unit outsourcing costs and appropriately increase the carbon cap to reduce total and outsourcing costs. Secondly, they should optimize the transportation capabilities of the 3PLs in the bidding process to increase the number of selected 3PLs. As the carbon cap increases, managers should reduce the use of 3PLs with high unit outsourcing costs to minimize carbon emissions and total costs.

5.3.2 Analysis of time window

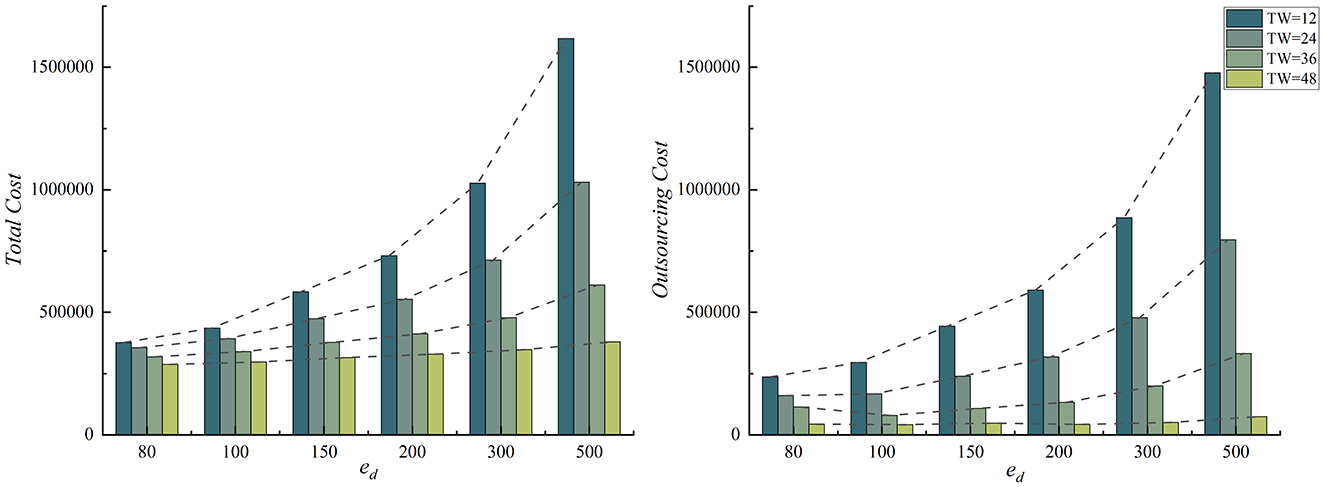
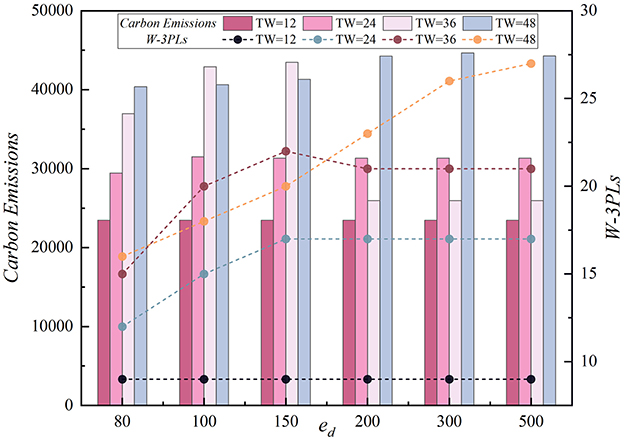
This section discusses the impact of changes in the time window on cost. Set Carbon Cap C_cap = 50,000, unit outsourcing costs e_d ∈ {80, 100, 150, 200, 300, 500}, and the time window TW ∈ {12, 24, 36, 48}. The impact of the time window on cost is shown in Figure 5. The changes in the number of selected 3PLs and carbon emissions are shown in Figure 6.

Figure 5

Figure 5. Impact of different time windows on costs.

Figure 6

Figure 6. Number and carbon emissions of selected 3PLs under different time windows.

From Figure 5, we can draw the following conclusions. The outsourcing cost and total cost decrease as the time window width increases. Under different time window widths, both the outsourcing cost and overall cost increase as the unit outsourcing cost rises; however, the rate of increase slows as the time window expands. Specifically, as shown in Figure 6, when the time window is very short, such as TW = 12, the unit outsourcing cost has little impact on the number of selected 3PLs and carbon emissions. This is because, for FAP, reducing transportation time is crucial, and only a few potential 3PLs can complete transportation tasks within a short period. The remaining logistics tasks must be outsourced to 3PLs, causing the total cost and outsourcing costs to increase sharply with rising unit outsourcing costs. Therefore, when the time window is short, the manager should increase the number of potential 3PLs to enhance competition among them, thereby improving the execution efficiency of the selected 3PLs for FAP.

As the time window width increases, some 3PLs with moderate transportation capacity are selected, leading to a reduction in the overall cost. However, when the time window width increases, the changes in carbon emissions and the number of selected 3PLs are irregular as the unit outsourcing cost increase. For example, when TW = 36, the carbon emissions under high unit outsourcing costs are lower than under low unit outsourcing costs, while the number of selected 3PLs remains unchanged under high unit outsourcing costs. The irregularity in the changes is primarily due to the excessively large transportation time window. In the case of low unit outsourcing costs, the large time window causes a wide variation in the transportation capacities of the selected 3PLs, leading to task assignments to outsourced 3PLs. Under high unit outsourcing costs, the number of selected 3PLs with weak transportation capacity decreases, resulting in a downward trend in W-3PLs, which in turn reduces overall transportation carbon emissions.

Therefore, the manager should first set different time windows based on the types of FAP to minimize the total cost. Second, when the time window is large and unit outsourcing costs are low, the manager should appropriately increase the carbon cap and the number of competing 3PLs. Third, when the time window is large and unit outsourcing costs are high, the manager should reduce the carbon cap and moderately increase the time window width to increase the number of selected 3PLs, thereby improving the transportation efficiency of FAP.

5.3.3 Management insights

Through the sensitivity analysis on key parameters in the real case, the following insights can be derived. First, when unit outsourcing costs are low, managers should eliminate 3PLs with weak transportation capacity and reduce the purchase of carbon caps. As unit outsourcing costs increase, total costs and outsourcing expenses also rise. When unit outsourcing costs are high, managers should increase the number of bidding 3PLs and the carbon cap.

Second, when the carbon cap is low, managers need to increase the number of potential 3PLs and reduce focus on 3PLs with high unit outsourcing costs. As the carbon cap increases, total costs and outsourcing expenses decrease. When the carbon cap is large, managers should increase attention to 3PLs with low unit outsourcing costs and moderately reduce the carbon cap based on the results of the model.

Third, when the time window width is small, managers should reduce the use of high unit outsourcing costs and increase the number of potential 3PLs to improve competition among them. As the time window increases, total costs and outsourcing expenses decrease. When the time window is large, under low unit outsourcing costs, managers should appropriately increase the carbon cap and the number of competing 3PLs. When unit outsourcing costs are high, managers should reduce the carbon cap and moderately increase the time window width to increase the number of selected 3PLs.

6 Conclusion

This paper, from the perspective of 4PL, studies the LSP auction problem for FAP under uncertain demand, considering both timeliness and sustainability. The aim is to achieve efficient and sustainable transportation of FAP through collaborative cooperation among 3PLs. Time windows and carbon emission constraints are incorporated into the study to ensure the timeliness and sustainability of FAP transportation. To address the challenges brought by demand uncertainty, a TS-SP model for WD problem with timeliness and sustainability under uncertain demand in LSP auction is proposed. To handle demand uncertainty, the SAA method is employed to transform the original model into an equivalent MILP model. The traditional SAA algorithm framework is reconstructed using the LHS method, and a sampling-based approximation algorithm is developed in combination with the DDLR algorithm to solve the model. Subsequently, a real case of a logistics company from Shenzhen, China, demonstrates that the gap derived from the sampling-based approximation algorithm is tolerable, and a high-quality optimal solution is obtained within a short time. The results of parameter sensitivity analysis show that expanding the quantity of potential 3PLs may improve the transportation efficiency of FAP, and increasing the number of 3PLs with strong transportation capabilities participating in the bidding may reduce the total cost. Additionally, the use of carbon caps can significantly impact the operational costs of the fresh agricultural product procurement system. Therefore, the algorithm proposed can effectively solve the proposed WD model and help enhance the green strategic goals and transportation efficiency of FAP logistics companies.

In the future, further research can focus on the following areas. First, this paper only focuses on the carbon cap mechanism. An interesting direction for future studies would be to consider both the carbon cap and carbon tax mechanisms. Second, this paper addresses demand uncertainty, but quantity discounts are also common in practice. Combining demand uncertainty with quantity discounts presents a feasible research direction.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YZ: Conceptualization, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. MY: Conceptualization, Formal analysis, Funding acquisition, Methodology, Resources, Software, Writing – original draft, Writing – review & editing. QL: Data curation, Formal analysis, Project administration, Resources, Writing – review & editing. XQ: Investigation, Project administration, Resources, Supervision, Writing – review & editing. DJ: Investigation, Project administration, Resources, Visualization, Writing – review & editing. XL: Investigation, Project administration, Resources, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the Natural Science Foundation of Liaoning Province under Grant 2024-BS-227; the Foundation of the Educational Department of Liaoning Province under Grant No. JYTQN2023345; the Social Science Foundation of Liaoning Province under Grant L24CGL031; the Foundation of the Educational Department of Liaoning Province under Grant No. JYTMS20231434; the Innovation Team Project of the Educational Department of Liaoning Province under Grant LJ222410148036; the Foundation of Talent Scientific Research Fund of LNPU Grant No. 2023XJJL-004; and the Foundation of National Local Joint Engineering Laboratory for Optimization of Petrochemical Process Operation and Energy saving Technology under Grant No. LJ232410148002.

Acknowledgments

The authors would like to thank the editor and reviewers for their constructive comments and encouragement, which greatly improved the quality of the paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fsufs.2025.1585053/full#supplementary-material

Footnotes

1. ^https://www.iea.org/data-and-statistics/charts/total-increase-in-energy-related-co2-emissions-1900-2023

2. ^https://eva.guru/blog/amazon-3pl-logistics/

3. ^https://www.icao.int/environmental-protection/Carbonoffset/Pages/default.aspx

References

Agustina, D., Lee, C., and Piplani, R. (2014). Vehicle scheduling and routing at a cross docking center for food supply chains. Int. J. Prod. Econ. 152, 29–41. doi: 10.1016/j.ijpe.2014.01.002

Crossref Full Text | Google Scholar

Anand, S., and Barua, M. (2022). Modeling the key factors leading to post-harvest loss and waste of fruits and vegetables in the agri-fresh produce supply chain. Comput. Electron. Agr. 198:106936. doi: 10.1016/j.compag.2022.106936

Crossref Full Text | Google Scholar

Bai, Q., Yin, X., Lim, M. K., and Dong, C. (2022). Low-carbon VRP for cold chain logistics considering real-time traffic conditions in the road network. Ind. Manage. Data. Syst. 122, 521–543. doi: 10.1108/IMDS-06-2020-0345

Crossref Full Text | Google Scholar

Bi, H., Gu, Y., Lu, F., and Mahreen, S. (2025). Site selection of electric vehicle charging station expansion based on Gis-Fahp-Mabac. J. Clean. Prod. 507:145557. doi: 10.1016/j.jclepro.2025.145557

Crossref Full Text | Google Scholar

Bortolini, M., Faccio, M., Ferrari, E., Gamberi, M., and Pilati, F. (2016). Fresh food sustainable distribution: cost, delivery time and carbon footprint three-objective optimization. J. FooD. Eng. 174, 56–67. doi: 10.1016/j.jfoodeng.2015.11.014

Crossref Full Text | Google Scholar

Caplice, C., and Sheffi, Y. (2003). Optimization-based procurement for transportation services. J. Bus. Logist. 24, 109–128. doi: 10.1002/j.2158-1592.2003.tb00048.x

Crossref Full Text | Google Scholar

Chen, J., Dan, B., and Shi, J. (2020). A variable neighborhood search approach for the multi-compartment vehicle routing problem with time windows considering carbon emission. J. Clean. Prod. 277:123932. doi: 10.1016/j.jclepro.2020.123932

Crossref Full Text | Google Scholar

Chen, J., Gui, P., Ding, T., Na, S., and Zhou, Y. (2019). Optimization of transportation routing problem for fresh food by improved ant colony algorithm based on tabu search. Sustainability 11:6584. doi: 10.3390/su11236584

Crossref Full Text | Google Scholar

Chen, X., Wang, C., Jia, D., and Bai, Y. (2024). Multi-period pricing and order decisions for fresh produce with option contracts. Ann. Oper. Res. 335, 79–110. doi: 10.1007/s10479-023-05515-y

Crossref Full Text | Google Scholar

Fang, Y., Jiang, Y., Sun, L., and Han, X. (2018). Design of green cold chain networks for imported fresh agri-products in belt and road development. Sustainability 10:1572. doi: 10.3390/su10051572

Crossref Full Text | Google Scholar

Fathollahzadeh, K., Saeedi, M., Khalili-Fard, A., Rabbani, M., and Aghsami, A. (2024). Multi-objective optimization for a green forward-reverse meat supply chain network design under uncertainty: utilizing waste and by-products. Comput. Ind. Eng. 197, 110578. doi: 10.1016/j.cie.2024.110578

Crossref Full Text | Google Scholar

Fu, Y., Gao, K., Wang, L., Huang, M., Liang, Y.-C., Dong, H., et al. (2025). Scheduling stochastic distributed flexible job shops using an multi-objective evolutionary algorithm with simulation evaluation. Int. J. Prod. Res. 63, 86–103. doi: 10.1080/00207543.2024.2356628

Crossref Full Text | Google Scholar

Fu, Y., Wang, Y., Gao, K., and Huang, M. (2024). Review on ensemble meta-heuristics and reinforcement learning for manufacturing scheduling problems. Comput. Electr. Eng. 120:109780. doi: 10.1016/j.compeleceng.2024.109780

Crossref Full Text | Google Scholar

Göl, H., and Çatay, B. (2007). Third-party logistics provider selection: insights from a turkish automotive company. Supply. Chain. Manag. 12, 379–384. doi: 10.1108/13598540710826290

Crossref Full Text | Google Scholar

Govindan, K., Jafarian, A., Khodaverdi, R., and Devika, K. (2014). Two-echelon multiple-vehicle location-routing problem with time windows for optimization of sustainable supply chain network of perishable food. Int. J. Prod. Econ. 152, 9–28. doi: 10.1016/j.ijpe.2013.12.028

Crossref Full Text | Google Scholar

Guo, J., Wang, X., Fan, S., and Gen, M. (2017). Forward and reverse logistics network and route planning under the environment of low-carbon emissions: a case study of shanghai fresh food e-commerce enterprises. Comput. Ind. Eng. 106, 351–360. doi: 10.1016/j.cie.2017.02.002

Crossref Full Text | Google Scholar

Guo, Y., Lim, A., Rodrigues, B., and Zhu, Y. (2006). Carrier assignment models in transportation procurement. J. Oper. Res. Soc. 57, 1472–1481. doi: 10.1057/palgrave.jors.2602131

Crossref Full Text | Google Scholar

Kafle, N., Zou, B., and Lin, J. (2017). Design and modeling of a crowdsource-enabled system for urban parcel relay and delivery. Transport. Res. B-Meth. 99, 62–82. doi: 10.1016/j.trb.2016.12.022

Crossref Full Text | Google Scholar

Kim, K., Kim, H., Kim, S.-K., and Jung, J.-Y. (2016). i-rm: an intelligent risk management framework for context-aware ubiquitous cold chain logistics. Expert. Syst. Appl. 46, 463–473. doi: 10.1016/j.eswa.2015.11.005

Crossref Full Text | Google Scholar

Kinene, A., Granberg, T. A., Birolini, S., Adler, N., Polishchuk, V., Skoglund, J.-M., et al. (2022). An auction framework for assessing the tendering of subsidised routes in air transportation. Transport. Res. A-Pol. 159, 320–337. doi: 10.1016/j.tra.2022.03.002

Crossref Full Text | Google Scholar

Kleywegt, A. J., and Shapiro, A. Homem-de Mello, T. (2002). The sample average approximation method for stochastic discrete optimization. SIAM. J. Optimiz. 12, 479–502. doi: 10.1137/S1052623499363220

Crossref Full Text | Google Scholar

Lau, H. C., and Li, B. (2021). Solving the winner determination problem for online b2b transportation matching platforms. Transport. Res. E-Log. 150:102324. doi: 10.1016/j.tre.2021.102324

Crossref Full Text | Google Scholar

Lee, C.-Y., Shu, S., and Xu, Z. (2021). Optimal global liner service procurement by utilizing liner service schedules. Prod. Oper. Manag. 30, 703–714. doi: 10.1111/poms.13311

Crossref Full Text | Google Scholar

Li, N., Zhang, Y., Tiwari, S., and Kou, G. (2023). Winner determination problem with purchase budget for transportation procurement under uncertain shipment volume. Transport. Res. E-Log. 176:103182. doi: 10.1016/j.tre.2023.103182

Crossref Full Text | Google Scholar

Lu, F., Du, Z., Wang, Z., Wang, L., and Wang, S. (2025a). Towards enhancing the crowdsourcing door-to-door delivery: an effective model in beijing. J. Ind. Manag. Optim. 21, 2371–2395. doi: 10.3934/jimo.2024175

Crossref Full Text | Google Scholar

Lu, F., Meng, F., and Bi, H. (2025b). Scenario deduction of explosion accident based on fuzzy dynamic bayesian network. J. Loss. Prev. Process. Ind. 96:105613. doi: 10.1016/j.jlp.2025.105613

Crossref Full Text | Google Scholar

Lu, Z., and Yu, J. (2024). An ogsm-based multi-objective optimization model for partner selection in fresh produce supply chain considering carbon emissions. Comput. Ind. Eng. 194:110402. doi: 10.1016/j.cie.2024.110402

Crossref Full Text | Google Scholar

Lukasse, L., Schouten, R., Castelein, R., Lawton, R., Paillart, M., Guo, X., et al. (2023). Perspectives on the evolution of reefer containers for transporting fresh produce. Trends Food. Sci. Tech. 140:104147. doi: 10.1016/j.tifs.2023.104147

Crossref Full Text | Google Scholar

Luo, M., Zhou, G., and Xu, H. (2022). Retracted article: three-tier supply chain on temperature control for fresh agricultural products using new differential game model under two decision-making situations. Oper. Manage. Res. 15, 1028–1047. doi: 10.1007/s12063-021-00244-6

Crossref Full Text | Google Scholar

Ma, Z., Kwon, R. H., and Lee, C.-G. (2010). A stochastic programming winner determination model for truckload procurement under shipment uncertainty. Transport. Res. E-Log. 46, 49–60. doi: 10.1016/j.tre.2009.02.002

Crossref Full Text | Google Scholar

Musavi, M., and Bozorgi-Amiri, A. (2017). A multi-objective sustainable hub location-scheduling problem for perishable food supply chain. Comput. Ind. Eng. 113, 766–778. doi: 10.1016/j.cie.2017.07.039

Crossref Full Text | Google Scholar

Parashar, S., Sood, G., and Agrawal, N. (2020). Modelling the enablers of food supply chain for reduction in carbon footprint. J. Clean. Prod. 275:122932. doi: 10.1016/j.jclepro.2020.122932

Crossref Full Text | Google Scholar

Parkes, D. C., Kalagnanam, J. R., and Eso, M. (2001). “Achieving budget-balance with vickrey-based payment schemes in exchanges,” in 17th International Joint Conference on Artificial Intelligence, 1161–1168. Available online at: https://dash.harvard.edu/entities/publication/73120378-8d5f-6bd4-e053-0100007fdf3b

Google Scholar

Pratap, S., Jauhar, S. K., Paul, S. K., and Zhou, F. (2022). Stochastic optimization approach for green routing and planning in perishable food production. J. Clean. Prod. 333:130063. doi: 10.1016/j.jclepro.2021.130063

Crossref Full Text | Google Scholar

Qian, X., Chan, F. T., Yin, M., Zhang, Q., Huang, M., Fu, X., et al. (2020). A two-stage stochastic winner determination model integrating a hybrid mitigation strategy for transportation service procurement auctions. Comput. Ind. Eng. 149:106703. doi: 10.1016/j.cie.2020.106703

Crossref Full Text | Google Scholar

Qian, X., Yin, M., Chan, F. T., and Yue, K. (2023a). Winner determination with sustainable-flexible considerations under demand uncertainty in transportation service procurement auctions. Netw. Spat. Econ. 23, 953–984. doi: 10.1007/s11067-023-09599-8

Crossref Full Text | Google Scholar

Qian, X., Yin, M., Chan, F. T., Zhang, J., and Huang, M. (2021). Sustainable-responsive winner determination for transportation service procurement auctions under accidental disruptions. J. Clean. Prod. 320:128833. doi: 10.1016/j.jclepro.2021.128833

Crossref Full Text | Google Scholar

Qian, X., Yin, M., Li, X., and Zhang, Q. (2023b). Two-stage stochastic nonlinear winner determination for logistics service procurement auctions under quantity discounts. J. Ind. Manag. Optim. 19, 1–18. doi: 10.3934/jimo.2022252

Crossref Full Text | Google Scholar

Rekik, M., and Mellouli, S. (2012). Reputation-based winner determination problem for combinatorial transportation procurement auctions. J. Oper. Res. Soc. 63, 1400–1409. doi: 10.1057/jors.2011.108

Crossref Full Text | Google Scholar

Remli, N., Amrouss, A., El Hallaoui, I., and Rekik, M. (2019). A robust optimization approach for the winner determination problem with uncertainty on shipment volumes and carriers' capacity. Transport. Res. B-Meth. 123, 127–148. doi: 10.1016/j.trb.2019.03.017

Crossref Full Text | Google Scholar

Remli, N., and Rekik, M. (2013). A robust winner determination problem for combinatorial transportation auctions under uncertain shipment volumes. Transp. Res. Part C: Emerg. Technol. 35, 204–217. doi: 10.1016/j.trc.2013.07.006

Crossref Full Text | Google Scholar

Sandholm, T. (2002). Algorithm for optimal winner determination in combinatorial auctions. Artif. Intell. 135, 1–54. doi: 10.1016/S0004-3702(01)00159-X

Crossref Full Text | Google Scholar

Sheffi, Y. (2004). Combinatorial auctions in the procurement of transportation services. Interfaces 34, 245–252. doi: 10.1287/inte.1040.0075

PubMed Abstract | Crossref Full Text | Google Scholar

Shi, H., Ma, J., Liu, Q., Li, J., Jiang, X., Li, P., et al. (2025). Model-free output feedback optimal tracking control for two-dimensional batch processes. Eng. Appl. Artif. Intel. 143:109989. doi: 10.1016/j.engappai.2024.109989

Crossref Full Text | Google Scholar

Singh, R. K., Gunasekaran, A., and Kumar, P. (2018). Third party logistics (3pl) selection for cold chain management: a fuzzy ahp and fuzzy topsis approach. Ann. Oper. Res. 267, 531–553. doi: 10.1007/s10479-017-2591-3

Crossref Full Text | Google Scholar

Sun, J., Jiang, T., Song, Y., Guo, H., and Zhang, Y. (2022). Research on the optimization of fresh agricultural products trade distribution path based on genetic algorithm. Agriculture 12:1669. doi: 10.3390/agriculture12101669

Crossref Full Text | Google Scholar

Tan, C., Zeng, Y., Ip, W., and Wu, C.-H. (2023). B2c or o2o? the strategic implications for the fresh produce supply chain based on blockchain technology. Comput. Ind. Eng. 183:109499. doi: 10.1016/j.cie.2023.109499

Crossref Full Text | Google Scholar

Tao, Y., Chew, E. P., Lee, L. H., and Shi, Y. (2017). A column generation approach for the route planning problem in fourth party logistics. J. Oper. Res. Soc. 68, 165–181. doi: 10.1057/s41274-016-0024-3

Crossref Full Text | Google Scholar

Triki, C. (2021). Using combinatorial auctions for the procurement of occasional drivers in the freight transportation: a case-study. J. Clean. Prod. 304:127057. doi: 10.1016/j.jclepro.2021.127057

Crossref Full Text | Google Scholar

Triki, C., Hasan, M. R., and Elomri, A. (2023). Solving the winner determination problem with discounted bids in transportation auctions. Ann. Oper. Res. 1–24. doi: 10.1007/s10479-023-05457-5

Crossref Full Text | Google Scholar

Triki, C., Piya, S., and Fu, L.-L. (2020). Integrating production scheduling and transportation procurement through combinatorial auctions. Networks 76, 147–163. doi: 10.1002/net.21967

Crossref Full Text | Google Scholar

Validi, S., Bhattacharya, A., and Byrne, P. (2014). A case analysis of a sustainable food supply chain distribution system—a multi-objective approach. Int. J. Prod. Econ. 152, 71–87. doi: 10.1016/j.ijpe.2014.02.003

Crossref Full Text | Google Scholar

Wang, Y., Deng, X., Lu, Q., Nicolescu, C. M., Guan, M., Kang, A., et al. (2023). Numerical analysis and service quality evaluation of the fresh agricultural produce supply chain platform. Appl. Sci-Basel. 13:713. doi: 10.3390/app13020713

Crossref Full Text | Google Scholar

Wu, D., Yan, R., Jin, H., and Cai, F. (2023). An adaptive nutcracker optimization approach for distribution of fresh agricultural products with dynamic demands. Agriculture 13:1430. doi: 10.3390/agriculture13071430

Crossref Full Text | Google Scholar

Wu, Q., and Hao, J.-K. (2015). Solving the winner determination problem via a weighted maximum clique heuristic. Expert. Syst. Appl. 42, 355–365. doi: 10.1016/j.eswa.2014.07.027

Crossref Full Text | Google Scholar

Yadav, V. S., Singh, A., Gunasekaran, A., Raut, R. D., and Narkhede, B. E. (2022). A systematic literature review of the agro-food supply chain: challenges, network design, and performance measurement perspectives. Sustain. Prod. Consump. 29, 685–704. doi: 10.1016/j.spc.2021.11.019

Crossref Full Text | Google Scholar

Yakavenka, V., Mallidis, I., Vlachos, D., Iakovou, E., and Eleni, Z. (2020). Development of a multi-objective model for the design of sustainable supply chains: the case of perishable food products. Ann. Oper. Res. 294, 593–621. doi: 10.1007/s10479-019-03434-5

Crossref Full Text | Google Scholar

Yang, F., and Huang, Y.-H. (2021). An optimization approach for winner determination problem considering transportation cost discounts. J. Glob. Optim. 80, 711–728. doi: 10.1007/s10898-021-01035-w

Crossref Full Text | Google Scholar

Yang, F., Huang, Y.-H., and Li, J. (2019). Alternative solution algorithm for winner determination problem with quantity discount of transportation service procurement. Physica. A. 535:122286. doi: 10.1016/j.physa.2019.122286

Crossref Full Text | Google Scholar

Yin, M., Huang, M., Wang, D., Fang, S.-C., Qian, X., Wang, X., et al. (2024). Multi-period fourth-party logistics network design with the temporary outsourcing service under demand uncertainty. Comput. Oper. Res. 164:106564. doi: 10.1016/j.cor.2024.106564

Crossref Full Text | Google Scholar

Yin, M., Qian, X., Huang, M., and Zhang, Q. (2021). Winner determination for logistics service procurement auctions under disruption risks and quantity discounts. Eng. Appl. Artif. Intel. 105:104424. doi: 10.1016/j.engappai.2021.104424

PubMed Abstract | Crossref Full Text | Google Scholar

Yin, M., Wang, H., Liu, Q., Qian, X., Zhang, H., Lang, X., et al. (2025). A sampling-based winner determination model and algorithm for logistics service procurement auctions under double uncertainty. Sci. Rep. 15:12054. doi: 10.1038/s41598-025-94748-x

PubMed Abstract | Crossref Full Text | Google Scholar

Zhang, B., Ding, H., Li, H., Wang, W., and Yao, T. (2014). A sampling-based stochastic winner determination model for truckload service procurement. Netw. Spat. Econ. 14, 159–181. doi: 10.1007/s11067-013-9214-6

Crossref Full Text | Google Scholar

Zhang, B., Yao, T., Friesz, T. L., and Sun, Y. (2015). A tractable two-stage robust winner determination model for truckload service procurement via combinatorial auctions. Transport. Res. B-Meth. 78, 16–31. doi: 10.1016/j.trb.2015.03.019

Crossref Full Text | Google Scholar

Zhang, H., Xu, H., and Pu, X. (2020). Comparisons of pre-sale strategies for a fresh agri-product supply chain with service effort. Agriculture 10:324. doi: 10.3390/agriculture10080324

Crossref Full Text | Google Scholar

Zhang, Z., Fu, Y., Gao, K., Pan, Q., and Huang, M. (2024). A learning-driven multi-objective cooperative artificial bee colony algorithm for distributed flexible job shop scheduling problems with preventive maintenance and transportation operations. Comput. Ind. Eng. 196:110484. doi: 10.1016/j.cie.2024.110484

Crossref Full Text | Google Scholar

Zhu, Q., and Wang, X. (2023). An auction mechanism for capacity allocation in identical parallel machines with time window constraints. Eur. J. Ind. Eng. 17, 833–855. doi: 10.1504/EJIE.2023.134700

PubMed Abstract | Crossref Full Text | Google Scholar

Zulvia, F. E., Kuo, R.-J., and Nugroho, D. Y. (2020). A many-objective gradient evolution algorithm for solving a green vehicle routing problem with time windows and time dependency for perishable products. J. Clean. Prod. 242:118428. doi: 10.1016/j.jclepro.2019.118428

Crossref Full Text | Google Scholar