- 1Department of Statistics, Columbia University, New York, NY, United States
- 2Department of Mathematics, University of Arizona, Tucson, AZ, United States
In this paper, we develop asymptotic theories for a class of latent variable models for large-scale multi-relational networks. In particular, we establish consistency results and asymptotic error bounds for the (penalized) maximum likelihood estimators when the size of the network tends to infinity. The basic technique is to develop a non-asymptotic error bound for the maximum likelihood estimators through large deviations analysis of random fields. We also show that these estimators are nearly optimal in terms of minimax risk.
1. Introduction
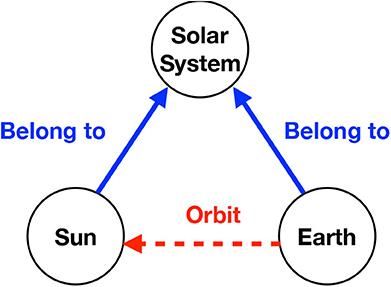
A multi-relational network (MRN) describes multiple relations among a set of entities simultaneously. Our work on MRNs is mainly motivated by its applications to knowledge bases that are repositories of information. Examples of knowledge bases include WordNet [1], Unified Medical Language System [2], and Google Knowledge Graph (https://developers.google.com/knowledge-graph). They have been used as the information source in many natural language processing tasks, such as word-sense disambiguation and machine translation [3–5]. A knowledge base often includes knowledge on a large number of real-world objects or concepts. When a knowledge base is characterized by MRN, the objects and concepts correspond to nodes, and knowledge types are relations. Figure 1 provides an excerpt from an MRN in which “Earth,” “Sun,” and “solar system” are three nodes. The knowledge about the orbiting patterns of celestial objects forms a relation “orbit,” and the knowledge on classification of the objects forms another relation “belong to” in the MRN.
An important task of network analysis is to recover the unobserved network based on data. In this paper, we consider a latent variable model for MRNs. The presence of an edge from node i to node j of relation type k is a Bernoulli random variable Yijk with success probability Mijk. Each node is associated with a vector, θ, called the embedding of the node. The probability Mijk is modeled as a function f of the embeddings, θi and θj, and a relation-specific parameter vector wk. This is a natural generalization of the latent space model for single-relational networks [6]. Recently, it has been successfully applied to knowledge base analysis [7–14]. Various forms of f are proposed, such as distance models [7], bilinear models [12–14], and neural networks [15]. Computational algorithms are proposed to improve link prediction for knowledge bases [16, 17]. The statistical properties of the embedding-based MRN models have not been rigorously studied. It remains unknown whether and to what extent the underlying distribution of MRN can be recovered, especially when there are a large number of nodes and relations.
The results in this paper fill in the void by studying the error bounds and asymptotic behaviors of the estimators for Mijk's for a general class of models. This is a challenging problem due to the following facts. Traditional statistical inference of latent variable models often requires a (proper or improper) prior distribution for θi. In such settings, one works with the marginalized likelihood with θi integrated out. For the analysis of MRN, the sample size and the latent dimensions are often so large that the above-mentioned inference approaches are computationally infeasible. For instance, a small-scale MRN could have a sample size as large as a few million, and the dimension of the embeddings is as large as several hundred. Therefore, in practice, the prior distribution is often dropped, and the latent variables θi's are considered as additional parameters and estimated via maximizing the likelihood or penalized likelihood functions. The parameter space is thus substantially enlarged due to the addition of θi's whose dimension is proportionate to the number of entities. As a result, in the asymptotic analysis, we face a double-asymptotic regime of both the sample size and the parameter dimension.
In this paper, we develop results for the (penalized) maximum likelihood estimator of such models and show that under regularity conditions the estimator is consistent. In particular, we overcome the difficulty induced by the double-asymptotic regime via non-asymptotic bounds for the error probabilities. Then, we show that the distribution of MRN can be consistently estimated in terms of average Kullback-Leibler (KL) divergence even when the latent dimension increases slowly as the sample size tends to infinity. A probability error bound is also provided together with the upper bound for the risk (expected KL divergence). We further study the lower bound and show the near-optimality of the estimator in terms of minimax risk. Besides the average KL divergence, similar results can be established for other criteria, such as link prediction accuracy.
The outline of the remaining sections is as follows. In section 2, we provide the model specification and formulate the problem. Our main results are presented in section 3. Finite sample performance is examined in section 4 through simulated and real data examples. Concluding remarks are included in section 5.
2. Problem Setup
2.1. Notation
Let | · | be the cardinality of a set and × be the Cartesian product. Set {1, …, N} is denoted by [N]. The sign function sgn(x) is defined to be 1 for x ≥ 0 and 0 otherwise. The logistic function is denoted by σ(x) = ex/(1 + ex). Let 1A be the indicator function on event A. We use U[a, b] to denote the uniform distribution on [a, b] and Ber(p) to denote the Bernoulli distribution with probability p. The KL divergence between Ber(p) and Ber(q) is written as . We use || · || to denote the Euclidean norm for vectors and the Frobenius norm for matrices.
For two real positive sequences {an} and {bn}, we write an = O(bn) if lim supn→∞ an/bn < ∞. Similarly, we write an = Ω(bn) if lim supn→∞ bn/an < ∞ and an = o(bn) if . We denote an ≲ bn if lim supn→∞ an/bn ≤ 1. When {an} and {bn} are negative sequences, an ≲ bn means liminfn→∞ an/bn ≥ 1. In some places, we use bn ≳ an as an interchangeable notation of an ≲ bn. Finally, if , we write an ~ bn.
2.2. Model
Consider an MRN with N entities and K relations. Given i, j ∈ [N] and k ∈ [K], the triple λ = (i, j, k) corresponds to the edge from entity i to entity j of relation k. Let Λ = [N] × [N] × [K] denote the set of all edges. We assume in this paper that an edge can be either present or absent in a network and use Yλ ∈ {0, 1} to indicate the presence of edge λ. In some scenarios, the status of an edge may have more than two types. Our analysis can be generalized to accommodate these cases.
We associate each entity i with a vector θi of dimension dE and each relation k with a vector wk of dimension dR. Let be a compact domain where the embeddings θ1, …, θN live. We call the entity space. Similarly, we define a compact relation space for the relation-specific parameters w1, …, wK. Let x = (θ1, …, θN, w1, …, wK) be a vector in the product space Θ = N × K. The parameters associated with edge λ = (i, j, k) is then xλ = (θi, θj, wk). We assume that given x, elements in {Yλ ∣ λ ∈ Λ} are independent with each other and that the log odds of Yλ = 1 is
Here ϕ is defined on 2 × , and ϕ(xλ) is often called the score of edge λ.
We will use Y to represent the N × N × K tensor formed by {Yλ ∣ λ ∈ Λ} and M(x) to represent the corresponding probability tensor {P(Yλ = 1 ∣ x) ∣ λ ∈ Λ}. Our model is given by
where x* stands for the true value of x and Yλ's are independent. In the above model, the probability of the presence of an edge is entirely determined by the embeddings of the corresponding entities and the relation-specific parameters. This imposes a low-dimensional latent structure on the probability tensor M* = M(x*).
We specify our model using a generic function ϕ. It includes various existing models as special cases. Below are two examples of ϕ.
1. Distance model [7].
where , bk ∈ ℝ and wk = (ak, bk). In the distance model, relation k from node i to node j is more likely to exist if θi shifted by ak is closer to θj under the Euclidean norm.
2. Bilinear model [9].
where and diag(wk) is a diagonal matrix with wk as the diagonal elements. Model (5) is a special case of the more general model , where is a matrix parameterized by . Trouillon et al. [12], Nickel et al. [13], and Liu et al. [14] explored different ways of constructing wk.
Very often, only a small portion of the network is observed [18]. We assume that each edge in the MRN is observed independently with probability γ and that the observation of an edge is independent of Y. Let ⊂ Λ be the set of observed edges. Then the elements in are independent draws from Λ. For convenience, we use n to represent the expected number of observed edges, namely, n = E[||] = γ|Λ| = γN2K. Our goal is to recover the underlying probability tensor M* based on the observed edges {Yλ ∣ λ ∈ }.
REMARK 1. Ideally, if there exists x* such that for all λ ∈ Λ, then Y can be recovered with no error under x*. This is, however, a rare case in practice, especially for large-scale MRN. A relaxed assumption is that Y can be recovered with some low dimensional x* and noise {ϵλ} such that
By introducing the noise term, we formulate the deterministic MRN as a random graph. The model described in (2) is an equivalent but simpler form of (6).
2.3. Estimation
According to (2), the log-likelihood function of our model is
We omit the terms in (7) since γ is not the parameter of interest. To obtain an estimator of M*, we take the following steps.
1. Obtain the maximum likelihood estimator (MLE) of x*,
2. Use the plug-in estimator
as an estimator of M*.
In (8), the estimator is a maximizer over the compact parameter space Θ = N × K. The dimension of Θ is
which grows linearly in the number of entities N and the number of relations K.
2.4. Evaluation Criteria
We consider the following criteria to measure the error of the above-mentioned estimator. They will be used in both the main results and numerical studies.
1. Average KL divergence of the predictive distribution from the true distribution
2. Mean squared error of the predicted scores
3. Link prediction error
where and .
REMARK 2. The latent attributes of entities and relations are often not identifiable, so the MLE is not unique. For instance, in (4), the values of ϕ and M(x) remain the same if we replace θi and ak, respectively by Γθi + t and Γak, where t is an arbitrary vector in and Γ is an orthonormal matrix. Therefore, we consider the mean squared error of scores, which are identifiable.
3. Main Results
We first provide results of the MLE in terms of KL divergence between the estimated and the true model. Specifically, we investigate the tail probability and the expected loss . In section 3.1, we discuss upper bounds for the two quantities. The lower bounds are provided in section 3.2. In section 3.3, we extend the results to penalized maximum likelihood estimators (pMLE) and other loss functions. All proofs are included in the Supplementary Materials.
3.1. Upper Bounds
We first present an upper bound for the tail probability in Lemma 1. The result depends on the tensor size, the number of observed edges, the functional form of ϕ, and the geometry of parameter space Θ. The lemma explicitly quantifies the impact of these element on the error probability. It is key to the subsequent analyses. Lemma 2 gives a non-asymptotic upper bound for the expected loss (risk). We then establish the consistency of and the asymptotic error bounds in Theorem 1.
We will make the following assumptions throughout this section.
ASSUMPTION 1. x* ∈ Θ = N × K, where and are Euclidean balls of radius U.
ASSUMPTION 2. The function ϕ is Lipschitz continuous under the Euclidean norm,
where α is a Lipschitz constant.
Assumption 1 is imposed for technical convenience. The results can be easily extended to general compact parameter spaces. Let . Without loss of generality, we assume that C ≥ 2.
LEMMA 1. Consider defined in (9) and the average KL divergence L in (10). Under Assumptions 1 and 2, for every t > 0, β > 0 and 0 < s < nt,
where m = NdE + KdR is the dimension of Θ, n = γN2K is the expected number of observations, and .
In the proof of Lemma 1, we use Bennett's inequality to develop a uniform bound that does not depend on the true parameters. It is sufficient for the current analysis. If the readers need sharper bounds, they can read through the proof and replace the Bennett's bound by the usual large deviation rate function which provides a sharp exponential bound that depends on the true parameters. We don't pursue this direction in this paper.
Lemma 2 below gives an upper bound of risk , which follows from Lemma 1.
LEMMA 2. Consider defined in (9) and loss function L in (10). Let C1 = 18C, and C3 = 2 max {C1, C2}. If Assumptions 1 and 2 hold and , then
We are interested in the asymptotic behavior of the tail probability in two scenarios: (i) t is a fixed constant and (ii) t decays to zero as the number of entities N tends to infinity. The following theorem gives an asymptotic upper bound for the tail probability and the risk.
THEOREM 1. Consider defined in (9) and the loss function L in (10). Let the number of entities N → ∞ and C, K, U, dE, dR, α, and γ be fixed constants. If Assumptions 1 and 2 hold, we have the following asymptotic inequalities.
When t is a fixed constant,
When ,
Furthermore,
The consistency of is implied by (16) and the rate of convergence is if t is a fixed constant. The rate decreases to Ω(N log N) for the choice of t producing (17). It is also implied by (17) that with high probability. We show in the next section that this upper bound is reasonably sharp.
The condition that K, U, dE, dR, and α are fixed constants can be relaxed. For instance, we can let U, dE, dR, and α go to infinity slowly at the rate O(log N) and K at the rate O(N). We can let γ go to zero provided that .
3.2. Lower Bounds
We show in Theorem 2 that the order of the minimax risk is , which implies the near optimality of in (9) and the upper bound in Theorem 1. To begin with, we introduce the following definition and assumption.
DEFINITION 1. For u = (θ, θ′, w) ∈ 2 × , the r-neighborhood of u is
Similarly, for , the r-neighborhood of x is
ASSUMPTION 3. There exists and r, κ > 0 such that and
THEOREM 2. Let . Under Assumptions 2 and 3, if , then for any estimator , there exists x* ∈ Θ such that
where . Consequently, the minimax risk
3.3. Extensions
3.3.1. Reguralization
In this section, we extend our asymptotic results in Theorem 1 to regularized estimators. In practice, regularization is often considered to prevent overfitting. We consider a regularization similar to elastic net [19]
where || · ||1 stands for L1 norm and ρ1, ρ2 ≥ 0 are regularization parameters. The pMLE is
Note that the MLE in (8) is a special case of the pMLE above with ρ1 = ρ2 = 0. Since is shrunk toward 0, without loss of generality, we assume that and are centered at 0. We generalize Theorem 1 to pMLE in the following theorem.
THEOREM 3. Consider the estimator given by (23) and (9) and the loss function L in (10). Let the number of entities N → ∞ and C, K, U, dE, dR, α, γ be absolute constants. If Assumptions 1 and 2 hold and ρ1 + ρ2 = o(log N), then asymptotic inequalities (16), (17), and (18) in Theorem 1 hold.
3.3.2. Other Loss Functions
We present some results for the mean squared error loss MSEϕ defined in (11) and the link prediction error defined in (12). Corollaries 1 and 2 give upper and lower bounds for MSEϕ, and Corollary 3 gives an upper bound for under an additional assumption.
COROLLARY 1. Under the setting of Theorem 3 with the loss function replaced by MSEϕ, we have the following asymptotic results.
If t is a fixed constant,
If ,
Furthermore,
COROLLARY 2. Under the setting of Theorem 2 with the loss function replaced by MSEϕ, we have
and
ASSUMPTION 4. There exists ε > 0 such that for every λ ∈ Λ.
COROLLARY 3. Under the setting of Theorem 3 with the loss function replaced by and Assumption 4 added, we have the following asymptotic results.
If t is a fixed constant,
If ,
Furthermore,
3.3.3. Sparse Representations
We are interested in sparse entity embeddings and relation parameters. Let || · ||0 be the number of non-zero elements of a vector and τ be a pre-specified sparsity level of x (i.e., the proportion of non-zero elements). Let mτ = mτ be the upper bound of non-zero parameters, that is, . Consider the following estimator
The estimator defined above maximizes the L0-penalized log-likelihood.
THEOREM 4. Consider defined in (32) and (9) and the loss function L in (10). Let the number of entities N → ∞ and τ, C, K, U, dE, dR, α be absolute constants. Under Assumptions 1 and 2, the following asymptotic inequalities hold.
If t is a fixed constant,
If ,
Furthermore,
We omit the results for other loss functions as well as the lower bounds since they can be analogously obtained.
4. Numerical Examples
In this section, we demonstrate the finite sample performance of through simulated and real data examples. Throughout the numerical experiments, AdaGrad algorithm [20] is used to compute in (8) or (23). It is a first-order optimization method that combines stochastic gradient descent (SGD) [21] with adaptive step sizes for finding the local optima. Since the objective function in (8) is non-convex, a global maximizer is not guaranteed. Our objective function usually has many global maximizers, but, empirically, we found the algorithm works well on MRN recovery and the recovery performance is insensitive to the choice of the starting point of SGD. Computationally, SGD is also more appealing to handle large-scale MRNs than those more expensive global optimization methods.
4.1. Simulated Examples
In the simulated examples, we fix K = 20, d = 20 and consider various choices of N ranging from 100 to 10,000 to investigate the estimation performance as N grows. The function ϕ we consider is a combination of the distance model (4) and the bilinear model (5),
where and wk = (ak, bk). We independently generate the elements of , , and from normal distributions N(0, 1), N(0, 1), and N(0, 0.25), respectively, where N(μ, σ2) denotes the normal distribution with mean μ and variance σ2. To guarantee that the parameters are from a compact set, the normal distributions are truncated to the interval [−20, 20]. Given the latent attributes, each Yijk is generated from the Bernoulli distribution with success probability . The observation probability γ takes value from {0.005, 0.01, 0.02}. For each combination of γ and N, 100 independent datasets are generated. For each dataset, we compute and in (8) and (9) with AdaGrad algorithm and then calculate defined in (10) as well as the link prediction error defined in (12). The two types of losses are averaged over the 100 datasets for each combination of N and γ to approximate the theoretical risks and . These quantities are plotted against N in log scale in Figure 2. As the figure shows, in general, both risks decrease as N increases. When N is small, n/m is not large enough to satisfy the condition n/m ≥ C2 + e in Lemma 2 and the expected KL risk increases at the beginning. After N gets sufficiently large, the trend agrees with our asymptotic analysis.
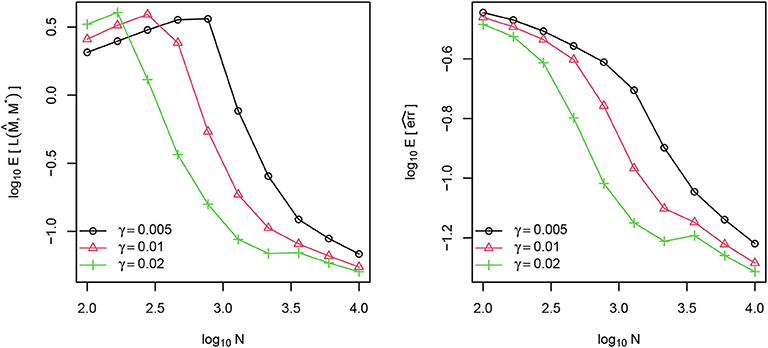
Figure 2. Average Kullback-Leibler divergence (left) and average link prediction error (right) of for different choices of N and γ.
4.2. Real Data Example: Knowledge Base Completion
WordNet [1] is a large lexical knowledge base for English. It has been used in word sense disambiguation, text classification, question answering, and many other tasks in natural language processing [3, 5]. The basic components of WordNet are groups of words. Each group, called a synset, describes a distinct concept. In WordNet, synsets are linked by conceptual-semantic and lexical relations, such as super-subordinate relation and antonym. We model WordNet as an MRN with the synsets as entities and the links between synsets as relations.
Following Bordes et al. [7], we use a subset of WordNet for analysis. The dataset contains 40,943 synsets and 18 types of relations. A triple (i, j, k) is called valid if relation k from entity i to entity j exists, i.e., Yijk = 1. All the other triples are called invalid triples. Among more than 3.0 × 1010 possible triples in WordNet, only 151,442 triples are valid. We assume that 141,442 valid triples and the same proportion of invalid triples are observed. The goal of our analysis is to recover the unobserved part of the knowledge base. We adopt the ranking procedure, which is commonly used in knowledge graph embedding literature, to evaluate link predictions. Given a valid triple λ = (i, j, k), we rank estimated scores for all the invalid triples inside in descending order and call the rank of as the head rank of λ, denoted by Hλ. Similarly, we can define the tail rank Tλ and the relation rank Rλ by ranking among the estimated scores of invalid triples in Λij· and Λi·k, respectively. For a set V of valid triples, the prediction performance can be evaluated by rank-based criteria, mean rank (MR), mean reciprocal rank (MRR), and hits at q (Hits@q), which are defined as
and
The subscripts E and R represent the criteria for predicting entities and relations, respectively. Models with higher MRRs, Hits@q's or lower MRs are more preferable. In addition, MRR is more robust to outliers than MR.
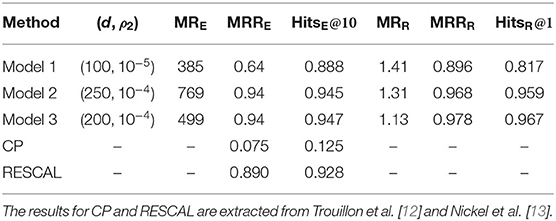
The three models described in (4), (5), and (36) are considered in our data analysis and we refer to them as Model 1, 2, and 3, respectively. For each model, the latent dimension d takes value from {50, 100, 150, 200, 250}. Due to the high dimensionality of the parameter space, L2 penalized MLE is used to obtain the estimated latent attributes , with tuning parameters ρ1 = 0 and ρ2 chosen from {0, 10−2, 10−3, 10−4, 10−5} in (22). Since information criteria based dimension and tuning parameter selection is computationally intensive for dataset of this scale, we set aside 5,000 of the unobserved valid triples as a validation set and select the d and ρ2 that produce the smallest MRRE on this validation set. The model with the selected d and ρ2 is then evaluated on the test set consisting of the rest 5,000 unobserved valid triples.
The computed evaluation criteria on the test set are listed in Table 1. The table also includes the selected d and ρ2 for each of the three score models. Models 2 and 3 generate similar performance. The MRRs for the two models are very close to 1, and the Hits@q's are higher than 90%, suggesting that the two models can identify the valid triples very well. Although Model 1 is inferior to the other two models in terms of most of the criteria, it outperforms them in MRE. The results imply that Model 2 and Model 3 could perform extremely bad for a few triples.
In addition to Models 1–3, we also display the performance of the Canonical Polyadic (CP) decomposition [22] and a tensor factorization approach, RESCAL [23]. Their MRRE and HitsE@10 results on the WordNet dataset are extracted from Trouillon et al. [12] and Nickel et al. [13], respectively. Both methods, especially CP, are outperformed by Model 3.
5. Concluding Remarks
In this article, we focused on the recovery of large-scale MRNs with a small portion of observations. We studied a generalized latent space model where entities and relations are associated with latent attribute vectors and conducted statistical analysis on the error of recovery. MLEs and pMLEs over a compact space are considered to estimate the latent attributes and the edge probabilities. We established non-asymptotic upper bounds for estimation error in terms of tail probability and risk, based on which we then studied the asymptotic properties when the size of MRN and latent dimension go to infinity simultaneously. A matching lower bound up to a log factor is also provided.
We kept ϕ generic for theoretical development. The choice of ϕ is usually problem-specific in practice. How to develop a data-driven method for selecting an appropriate ϕ is an interesting problem to investigate in future works.
Besides the latent space models, sparsity [24] or clustering assumptions [25] have been used to impose low-dimensional structures in single-relational networks. An MRN can be seen as a combination of several heterogeneous single-relational networks. The distribution of edges may vary dramatically across relations. Therefore, it is challenging to impose appropriate sparsity or cluster structures on MRNs. More empirical and theoretical studies are needed to quantify the impact of heterogeneous relations and to incorporate the information for recovering MRNs.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
ZW provided the theoretical proofs. ZW and XT conducted the simulation and real data analysis. All authors contributed to manuscript writing and revision.
Funding
This work was supported by National Science Foundation grants SES-1826540 and IIS-1633360.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2020.540225/full#supplementary-material
References
1. Miller GA. WordNet: a lexical database for English. Commun ACM. (1995) 38:39–41. doi: 10.1145/219717.219748
2. McCray AT. An upper-level ontology for the biomedical domain. Compar Funct Genomics. (2003) 4:80–4. doi: 10.1002/cfg.255
3. Gabrilovich E, Markovitch S. Wikipedia-based semantic interpretation for natural language processing. J Artif Intell Res. (2009) 34:443–98. doi: 10.1613/jair.2669
4. Scott S, Matwin S. Feature engineering for text classification. In: ICML Vol. 99 Bled (1999). p. 379–88.
5. Ferrucci D, Brown E, Chu-Carroll J, Fan J, Gondek D, Kalyanpur AA, et al. Building Watson: an overview of the DeepQA project. AI Mag. (2010) 31:59–79. doi: 10.1609/aimag.v31i3.2303
6. Hoff PD, Raftery AE, Handcock MS. Latent space approaches to social network analysis. J Am Stat Assoc. (2002) 97:1090–8. doi: 10.1198/016214502388618906
7. Bordes A, Usunier N, Garcia-Duran A, Weston J, Yakhnenko O. Translating embeddings for modeling multi-relational data. In: Burges CJC, Bottou L, Welling M, Ghahramani Z, Weinberger KQ, editors. Advances in Neural Information Processing Systems 26. Curran Associates, Inc. (2013). p. 2787–95. Available online at: http://papers.nips.cc/paper/5071-translating-embeddings-for-modeling-multi-relational-data.pdf
8. Wang Z, Zhang J, Feng J, Chen Z. Knowledge graph embedding by translating on hyperplanes. In: AAAI. Québec City, QC (2014). p. 1112–9.
9. Yang B, Yih SWt, He X, Gao J, Deng L. Embedding entities and relations for learning and inference in knowledge bases. In: Proceedings of the International Conference on Learning Representations. San Diego, CA (2015).
10. Lin Y, Liu Z, Sun M, Liu Y, Zhu X. Learning entity and relation embeddings for knowledge graph completion. In: AAAI. Austin, TX (2015). p. 2181–7.
11. Garcia-Duran A, Bordes A, Usunier N, Grandvalet Y. Combining two and three-way embedding models for link prediction in knowledge bases. J Artif Intell Res. (2016) 55:715–42. doi: 10.1613/jair.5013
12. Trouillon T, Welbl J, Riedel S, Gaussier É, Bouchard G. Complex embeddings for simple link prediction. In: International Conference on Machine Learning. (2016). p. 2071–80.
13. Nickel M, Rosasco L, Poggio TA. Holographic embeddings of knowledge graphs. In: AAAI. Phoenix, AZ (2016). p. 1955–61.
14. Liu H, Wu Y, Yang Y. Analogical inference for multi-relational embeddings. In: Proceedings of the 34th International Conference on Machine Learning. Vol. 70. Sydney, NSW (2017). p. 2168–78.
15. Socher R, Chen D, Manning CD, Ng A. Reasoning with neural tensor networks for knowledge base completion. In: Burges CJC, Bottou L, Welling M, Ghahramani Z, Weinberger KQ, editors. Advances in Neural Information Processing Systems. Lake Tahoe, NV: Curran Associates, Inc. (2013) p. 926–34.
16. Kotnis B, Nastase V. Analysis of the impact of negative sampling on link prediction in knowledge graphs. arXiv. (2017) 170806816.
17. Kanojia V, Maeda H, Togashi R, Fujita S. Enhancing knowledge graph embedding with probabilistic negative sampling. In: Proceedings of the 26th International Conference on World Wide Web Companion. Perth, WA (2017) p. 801–2. doi: 10.1145/3041021.3054238
18. Min B, Grishman R, Wan L, Wang C, Gondek D. Distant supervision for relation extraction with an incomplete knowledge base. In: HLT-NAACL. Atlanta, GA (2013). p. 777–82.
19. Zou H, Hastie T. Regularization and variable selection via the elastic net. J R Stat Soc B. (2005) 67:301–20. doi: 10.1111/j.1467-9868.2005.00503.x
20. Duchi J, Hazan E, Singer Y. Adaptive subgradient methods for online learning and stochastic optimization. J Mach Learn Res. (2011) 12:2121–59. doi: 10.5555/1953048.2021068
21. Robbins H, Monro S. A stochastic approximation method. Ann Math Stat. (1951) 22:400–7. doi: 10.1214/aoms/1177729586
22. Hitchcock FL. The expression of a tensor or a polyadic as a sum of products. J Math Phys. (1927) 6:164–89. doi: 10.1002/sapm192761164
23. Nickel M, Tresp V, Kriegel HP. A three-way model for collective learning on multi-relational data. In: Proceedings of the 28th International Conference on International Conference on Machine Learning. ICML'11. Madison, WI: Omnipress (2011). p. 809–16.
24. Tran N, Abramenko O, Jung A. On the sample complexity of graphical model selection from non-stationary samples. IEEE Trans Signal Process. (2020) 68:17–32. doi: 10.1109/TSP.2019.2956687
Keywords: multi-relational network, knowledge graph completion, tail probability, risk, asymptotic analysis, non-asymptotic analysis, maximum likelihood estimation
Citation: Wang Z, Tang X and Liu J (2020) Statistical Analysis of Multi-Relational Network Recovery. Front. Appl. Math. Stat. 6:540225. doi: 10.3389/fams.2020.540225
Received: 04 March 2020; Accepted: 31 August 2020;
Published: 19 October 2020.
Edited by:
Yajun Mei, Georgia Institute of Technology, United StatesCopyright © 2020 Wang, Tang and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xueying Tang, eHl0YW5nQG1hdGguYXJpem9uYS5lZHU=
 Zhi Wang
Zhi Wang Xueying Tang
Xueying Tang Jingchen Liu1
Jingchen Liu1