Robust Weighted Averaging Accounts for Recruitment Into Collective Motion in Human Crowds

Introduction

Much like schools of herring and murmurations of starlings, groups of humans exhibit collective motion, whether a group of friends walking together down a sidewalk or large crowds in a shopping plaza or a mass protest. It is generally believed that such patterns of collective motion emerge via similar processes of self-organization, where local interactions between individuals give rise to patterns of global behavior [1, 2]. An understanding of these local interactions has two aspects: first, identifying the rules of engagement that govern how an individual responds to a neighbor, and second, characterizing the neighborhood of interaction over which these rules operate and how neighbor influences are combined.

Despite the similarity of collective motion across many species, this behavior has been treated separately in humans and other animals. For flocks, schools, and herds, the main approach has been the attraction-repulsion-alignment framework [3–6], in which three local interaction rules or hypothetical forces apply over different ranges: 1) repulsion from near neighbors to avoid collisions, 2) alignment with the velocities of intermediate neighbors to generate common motion, and 3) attraction to far neighbors to maintain group cohesion. The influences of multiple neighbors are combined by averaging over the neighborhood. Pedestrian models, in contrast, have mainly focused on collision avoidance based on repulsion and attraction forces [7–9], although they can also generate collective motion under certain boundary conditions [10, 11]. We focus instead on the alignment of velocity direction or heading, which is sufficient to generate collective motion [12, 13].

Cucker and Smale [14] showed numerically that a weighted average of neighbor velocities, with weights that decay gradually with distance, yields emergent collective motion. This result demonstrated that distance-weighted averaging over a spatial neighborhood offers a potential mechanism of self-organization: a self-limiting positive feedback that recruits an increasing number of individuals into collective motion until all individuals are aligned. Rio, Dachner and Warren [15] empirically identified a similar “soft metric” neighborhood of interaction in human crowds, in which neighbor influence decays exponentially to zero at a distance of 4–5 m.

Rio, et al. [15] modeled this soft metric neighborhood using a weighted-averaging model. Because people have a ∼180° horizontal field of view and tend to face in the walking direction [16], the neighborhood is a semi-circular region with an eccentricity of −90° to +90° about the current heading direction, and neighbor influence is largely unidirectional. When following a crowd, a pedestrian steers by reducing the mean difference between their current heading direction (${\varphi }_p$) and the heading direction of each neighbor (${\varphi }_i$), weighted by distance. Specifically, pedestrian p’s angular acceleration (change in heading direction) is proportional to the weighted average of the heading deviations of each neighbor,

${\ddot{\varphi }}_p=-\frac{k}{n}{\displaystyle \sum }_{i=1}^n{w}_{i}sin\left({\varphi }_i-{\varphi }_p\right)(1)$

$w_i=\frac{a}{{\text{e}}^{\omega d_i}+a}(2)$

where n is the number of neighbors within a 5 m radius and a 180° field of view, and k = 3.15 is the stiffness or gain, fit to data on pedestrian following [17]. The weight of each neighbor (w_i) decreases exponentially with distance (d_i), where ω = 1.3 is the decay rate and a = 9.2 is a scaling constant, fit to motion-capture data on real crowds [15]. Thus, neighbors that are closer to the pedestrian or have larger heading deviations (up to ±90°) exert a greater influence, such that the pedestrian turns to align with the weighted mean heading in the neighborhood. An analogous equation for linear acceleration controls a pedestrian’s walking speed [15]. In terms of the system’s dynamics, the proximity and average deviation of neighbors determine the strength of attraction to the mean heading in the neighborhood, and hence the turning rate and the relaxation time of the alignment response. It is interesting to note that Eq. 1 is a version of the Kuramoto model of synchronization in systems of phase-coupled oscillators [18, 19] with second-order dynamics, which converges to a small cluster of phases analogous to a small distribution of heading directions.

This weighted-averaging model closely simulates individual trajectories in human experiments with virtual and real crowds [15], and generates robust collective motion in multi-agent simulations [20]. So far, however, only groups of aligned virtual humans with small heading differences (10°) have been tested experimentally [15]. Here we investigate whether weighted averaging is sufficient to recruit pedestrians into collective motion in a wider range of crowd scenarios. Clearly, people can perform a variety of locomotor behaviors under intentional constraints, such as walking to a goal, following another pedestrian, and so on [21]. Thus, although collective motion can arise spontaneously, we study its formation under the intention to walk with a crowd.

To probe the limits of weighted averaging in humans, we performed three experiments in which the participant was asked to walk with a virtual crowd, allowing us to manipulate the motions of virtual humans (neighbors). Using virtual–as opposed to real–crowds enables precise experimental control, while still yielding meaningful insight into real-world behavior, as tests of virtual reality as a method have demonstrated [22, 23]. In each experiment, we perturbed the heading (walking) direction of neighbors in the crowd and measured the participant’s heading response, the time series of their heading direction. In Experiment 1 (Noisy Neighbors), the heading directions of neighbors were randomized about the mean direction of the crowd, with a range up to 90°. The model closely predicts the human data, indicating that weighted averaging is highly robust. In Experiment 2 (Splitting Crowd), the virtual crowd diverged into two groups, with an angle up to 40° between them, and the proportion of the crowd in the each group was varied. Surprisingly, participants head between the two groups, just as predicted by the weighted averaging model. In Experiment 3 (Coherent Subgroup), the coherence of a perturbed subgroup was manipulated (heading Standard Deviation (SD) from 0° to 20°) within a noisy crowd (heading range 180°), and the proportion of the crowd in the subgroup was varied. Once again, heading responses were predicted by weighted averaging.

In each case, we find that participants align their heading with the weighted mean of the neighborhood, consistent with Rio, et al’s [15] model. Moreover, as a larger proportion of neighbors turns, the mean heading deviation increases, and the strength of attraction to the neighborhood mean increases. Weighted averaging in humans is thus highly robust to crowd noise and diverging groups. The results show that individuals are not attracted to more coherent neighbors, but to the mean heading in their neighborhood. A common heading direction thus propagates across neighborhoods, providing a positive feedback that recruits more individuals into emerging collective motion.

General Method

Participants

Participants (10 in Experiment 1, 12 in Experiment 2, 12 in Experiment 3) were recruited at Brown University, had normal or corrected-to-normal vision, reported no motor impairments, and had not participated in any other virtual crowd experiments. Informed consent was obtained from all participants, who were compensated for their time. The research protocol was approved by Brown University’s Institutional Review Board, in accordance with the principles expressed in the Declaration of Helsinki.

Equipment

Experiments were conducted in the Virtual Environment Navigation Lab (VENLab) at Brown University. Participants walked freely in a 12 × 14 m tracking area, while viewing a virtual environment in a stereoscopic head mounted display (HMD). The HMD’s inter-ocular distance was adjusted for each participant. In Experiments 1 and 2, the HMD was an Oculus Rift CV1 (Irvine CA; 94°H x 93°V field of view, 1,080 x 1,200 pixels per eye, 90 Hz refresh rate); stereoscopic displays were generated on a Dell XPS workstation and transmitted wirelessly to the HMD using two HDTV transmitters at a frame rate of 30–60 fps. Head position and orientation were recorded with an IS-900 inertial/ultrasonic tracking system (Intersense, Billerica, MA) at a sampling rate of 60 Hz, with a total latency of 50–67 ms. In Experiment 3, the HMD was a Samsung Odyssey (Seoul, S. Korea; 101°H x 105 V field of view, 1440 H × 1600 V pixels per eye, 90 Hz refresh rate), and stereoscopic displays were generated on a backpack computer (MSi VR-One, New Taipei City, Taiwan) at a frame rate of 45–90 fps. Head position and orientation were recorded with the Odyssey’s inside-out tracking system, consisting of two cameras and an inertial measurement unit (90 Hz sampling rate, downsampled to 45 Hz), with a total latency of about 11 ms.

Displays

The virtual environment was created in Vizard (Worldviz, Santa Barbara, CA) and consisted of a ground plane with a grayscale granite texture and a blue sky. A green start pole and a red orienting pole (radius 0.2 m, height 3 m) appeared 12.73 m apart. The crowd consisted of animated virtual humans (WorldViz Complete Characters) with 36 unique appearances, equal numbers of men and women, and diverse races and ethnicities. In Experiment 1, 24 of the appearances were randomly chosen and used for all trials. In Experiments 2 and 3, more than 36 virtual humans were presented, so some appearances were duplicated. Each of the human models was animated with a walking gait with randomly varied phase.

Procedure

Participants were instructed to “walk with the crowd” and to “treat the virtual humans as though they were real people.” Two practice trials were used to familiarize participants with walking in the virtual environment, followed by a series of test trials. On each trial, the participant walked to the start pole and turned to face the orienting pole. After 2 s, the poles disappeared and the virtual crowd appeared; 1 s later, the virtual crowd began walking and a verbal command (“Begin”) was played through headphones. The display continued until the participant either walked for 10.4 s or came within 1.5 m of the room walls, whereupon the end of the trial was signaled by a verbal command (“End”). A new start pole then appeared, and the next trial began. Trials were presented in a randomized order unique to each participant.

Data Processing and Analysis

For each trial, the time series of head position in the horizontal (X–Y) plane was filtered using a forward and backward fourth-order low-pass Butterworth filter to reduce oscillations due to the step cycle and occasional tracker error. Time series of heading direction and walking speed were then computed from the filtered position data. A 0.6 Hz cut-off was used when filtering the data for computing heading to reduce lateral oscillations on each stride, while a 1.0 Hz cutoff was used for computing speed to reduce anterior–posterior oscillations on each step. The first and last second of the time series were then truncated to eliminate “edge effects” due to filtering. Because the virtual crowd turned right (+angles) or left (- angles) on an equal number of trials (where 0° is straight ahead), the data were left/right collapsed by multiplying the heading angle on left turn trials by −1.

To investigate possible effects of practice or fatigue, we performed a Pearson correlation between trial number and the mean final heading of all participants. In all three experiments, there was a near zero correlation between trial number and final heading. We thus combined trials regardless of order when computing the mean heading in each condition.

A mean time series was calculated for each participant in each experimental condition (see Design) by computing the mean value of heading at each time step. This averaging further reduced the noise due to gait oscillations, as well as any random variation between trials. The final heading on each trial was calculated as the average heading during the last 2 s of the time series, and the mean final heading was computed for each participant in each condition. To account for variation between trials within a condition, the variable error in final heading was calculated for each subject (the within-subject standard deviation (SD) of final heading).

The heading data were statistically analyzed using linear mixed effects (LME) regression (Matlab fitlme function, MathWorks, Natick, MA), with fixed effects corresponding to the experimental factors and their interactions, and a maximal random effects structure with a unique intercept for every participant, to account for between-subject differences. The main effects and interactions were tested by comparing statistical models in a step-down procedure that removes the tested term from the full model, using likelihood ratio chi-squared tests. The final model included only the statistically significant effects.

Simulation Procedure

Simulations of the weighted averaging model (Eqs 1, 2) with fixed parameter values were performed using the Runge-Kutta method (Matlab ode45 function). For each trial, the participant’s initial position and heading were taken as the initial conditions, and the positions and velocities of virtual humans on that trial were treated as input. Because we only manipulated heading, the model’s speed was determined by the time series of the participant’s speed on that trial. The output was a time series of simulated heading for every trial in the experiment. To compare the simulations with the human data, we calculated the root mean squared error (RMSE) between the mean data time series for each participant in each condition and the corresponding mean simulated time series for each participant in each condition. We chose to calculate the error on mean time series, rather than individual trials, to reduce error due to gait oscillations, for we were not attempting to model gait. We used Bayes Factors to evaluate the strength of evidence for competing hypotheses.

Experiment 1: Noisy Neighbors

Experiment 1 tested the effect of adding noise into the heading directions of the virtual humans in a crowd. It is well known that, when viewing moving dots in the frontal plane (on a screen), the visual system integrates stochastic local motions to perceive the direction of coherent global motion, with a range of dot directions up to 90° [24]. Here we ask whether this holds for an observer embedded in a moving crowd, when viewing local motions in depth, in the horizontal plane.

The heading direction of each neighbor was selected from a uniform distribution with a mean of either ±10° or ±20° (left or right) and a range that varied from 0° (aligned) to 90° (±45° about the mean) (see schematic in Figure 1A). If participants average the headings of neighbors in the neighborhood, their mean final heading should be close to the crowd mean. In addition, the model predicts that the variable error in a participant’s heading response across trials should increase with the amount of crowd “noise.” This prediction stems from the fact that the neighborhood average depends on distance and heading deviation of neighbors, which vary from trial to trial. If participants ignore neighbors with large heading deviations, we would expect the human variability to stop increasing at a critical noise level. We tested these hypotheses by measuring the participant’s heading response as a function of crowd noise, and comparing the results to model simulations of the stimuli.

FIGURE 1

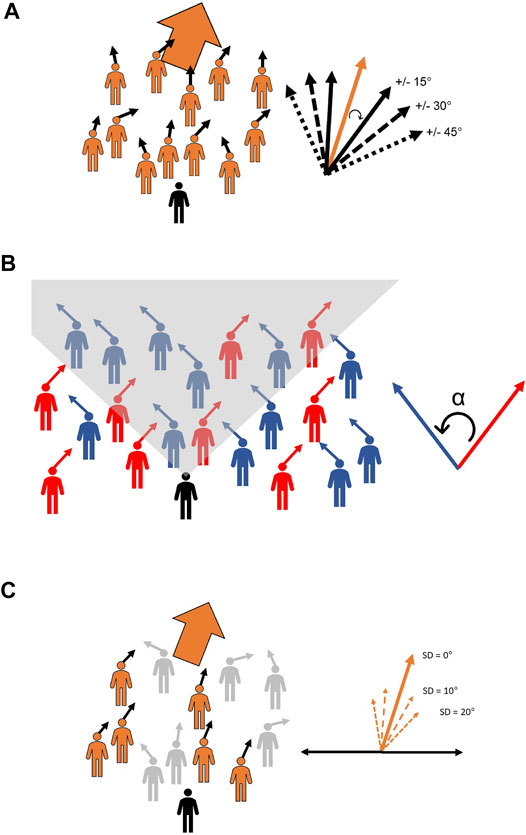
FIGURE 1. Schematics of experimental designs. (A) Experiment one, Noisy Neighbors: The participant (black figure) was immersed in a crowd of virtual humans (orange figures, n = 24) that had “noisy” heading directions (small black arrows) about the crowd mean (large orange arrow, 10° or 20° left or right). Individual headings were randomly selected from a uniform distribution centered on the crowd mean (orange vector on right), with a range of 0°, +/- 15°, +/-30°, or ± 45° (set of black vectors on right). (B) Experiment two, Splitting Crowd: The participant (black figure) was immersed in a virtual crowd (n = 48) that split into two groups, each turning by the same angle to the left (blue figures) and to the right (red figures). We manipulated the angular difference between the heading of the two groups (α = 10°, 20°, 30° or 40°) and the proportion of the crowd in the majority group (50, 66 or 84%). The two groups formed continuously crossing streams and did not spatially separate. If the participant rotated their head, members of both groups appeared in the field of view (gray shading) in an approximately constant proportion. (C) Experiment three, Coherent Subgroup: The participant (black figure) was immersed in a crowd of virtual humans (n = 48) with very noisy heading directions sampled from a uniform distribution (range ±90°, centered on 0° heading). A subgroup of the crowd (orange figures and arrows) turned left or right with a mean heading of 20° (large orange arrow), and their coherence was manipulated (heading SD = 0°, 10°, 20°), while the rest of the crowd continued walking in the same directions (gray figures and arrows). The proportion of the crowd in the subgroup (0, 25, 50, 75, or 100%) was also varied.

Displays

Twenty-four virtual humans were initially positioned at equal intervals on each of six concentric arcs (four neighbors on each arc) with the participant at the center. The arcs had radii of 2.5–7.5 m (1 m apart) and an eccentricity of -88° to +88° (176° total) about the participant’s initial heading direction. These initial positions were jittered in depth and eccentricity on every trial; the amount of jitter was randomly selected from a Gaussian distribution in polar coordinates (radius Δr: SD = 0.5 m; eccentricity Δθ: SD = 5°).

At the beginning of each trial, the virtual humans appeared facing the orientation pole, with their backs to the participant; after 1 s they began walking straight ahead (0° heading), accelerating from a stand-still (0 m/s) to a speed of 1.15 m/s over a period of 3 s. One second later, the headings of the entire crowd were perturbed. Each virtual human was randomly assigned a heading sampled from a uniform distribution with a mean of ±10° or ±20° (left or right), and a range of ±0° (aligned), ±15°, ±30°, or ±45° about the mean. These headings were re-sampled for each trial and each participant, providing unique stimuli for every participant.

Design

Mean turn angle (10°, 20°, collapsed left/right) was crossed with noise range (±0°, ±15°, ±30°, ±45°) to yield eight experimental conditions. There were 12 repetitions per condition (half left and half right turns), for a total of 96 trials per participant.

Results

Final Heading

The participants’ mean final heading in each condition appears in Figure 2A. It is clear that the mean response in the 10° turn condition (mean heading M = 9.04°, cyan curve) and the 20° turn condition (M = 20.30°, dark blue curve) are close to their respective crowd turn angles, and constant across noise conditions. Thus, participants closely match the crowd’s mean heading in both aligned (0°) and very noisy crowds (up to ±45°), consistent with spatial averaging.

FIGURE 2

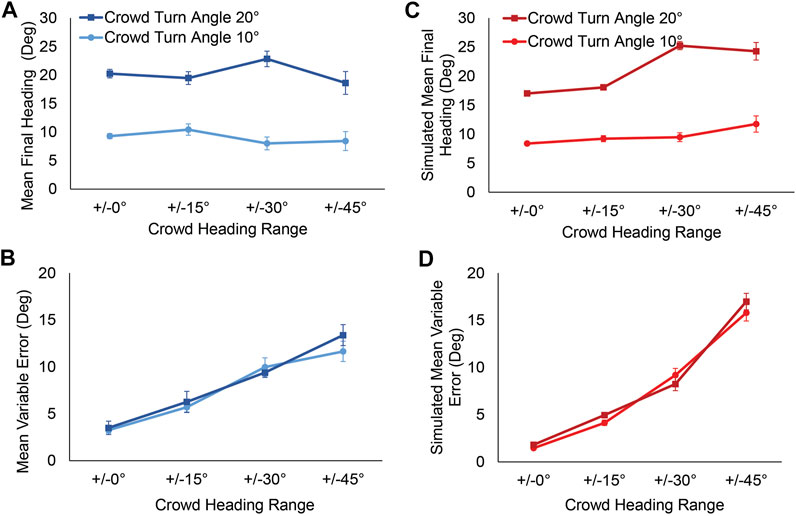
FIGURE 2. Results of Experiment 1. (A) Mean final heading as a function of crowd noise (heading range in the virtual crowd), for human participants. Curves represent the crowd’s mean turn angle. (B) Mean variable error in final heading across trials as a function of crowd noise, for the participants. (C) Model simulations of mean final heading and (D) mean variable error, corresponding to the human data in panels A and B. For both human and model, final heading increases with crowd turn angle, whereas variable error increases with crowd noise. Error bars represent the standard error of the mean (±SEM).

An LME regression was used to analyze final heading, with fixed effects of crowd turn angle, crowd noise, and their interaction, and participants as random effects. The results (Supplementary Table SM1A) demonstrate that only the crowd’s turn angle significantly contributed to the variability in final heading [χ2 (1) = 33.50, p < 0.001]. The level of crowd noise was not significant, either as a main effect or an interaction with turn angle [χ2 (2) = 0.86, p = 0.650]. The regression analysis allows us to estimate that for every degree increase in the crowd turn angle, there is a corresponding 1.11° (±0.08 SE) increase in the participants’ final heading response. This pattern of results indicates that participants are attracted to the crowd’s mean heading, regardless of the amount of crowd noise.

Variable Error

The mean variable error in each condition appears in Figure 2B, and was analyzed in a similar LME regression. The results (Supplementary Table SM1B) show that only the crowd noise contributes to variability in the variable error [χ2 (1) = 31.09, p < 0.001], while neither the turn angle nor the interaction between turn angle and crowd noise do so [χ2 (2) = 1.43, p = 0.490]. For every degree increase in the range of crowd noise (from 0° to 90°), the regression analysis estimates a corresponding 0.11° (±0.01 SE) increase in the variable error. Thus, the variable error in a participant’s final heading increases with crowd noise due to larger trial-to-trial variation in neighbor headings, as predicted by weighted averaging over the neighborhood.

Heading Over Time

The mean time series of heading in each condition appears in Figure 3. The strength of attraction to the neighborhood mean is reflected in the turning rate (rate of change in heading over time), where a steeper slope indicates a stronger attractor. According to the weighted averaging model (Eqs 1, 2), a larger turn angle (solid vs. dashed curves in Figure 3) should be more attractive because it creates a larger difference between the participant’s current heading and the neighborhood mean. Somewhat counter-intuitively, attractor strength should be unaffected by increased heading noise that is symmetric about the crowd mean (colored curves in Figure 3), because this does not alter the neighborhood mean or the heading difference with the participant.

FIGURE 3

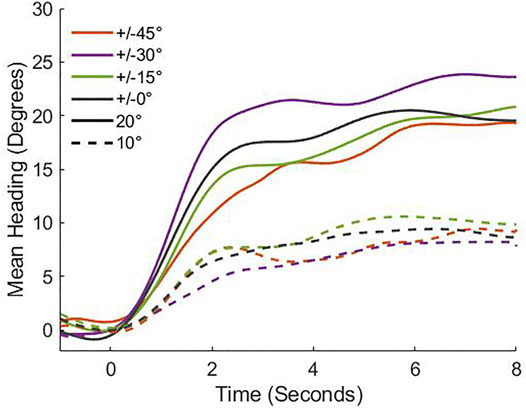
FIGURE 3. Mean time series of heading for participants in Experiment 1. Dashed curves represent crowd turns of 10°, solid curves represent 20° turns; color denotes the crowd noise level (heading range). The data are aligned so the heading perturbation occurs as t = 0. Slopes indicate the attractiveness of the mean heading in the participant’s neighborhood.

To compare attractor strength in different conditions, we analyzed the time series of heading using an LME regression with fixed effects of crowd turn angle, crowd noise, time, the interactions with time, and participants as random effects (see final model in Supplementary Table SM1C). The results show that both the crowd turn angle [χ2 (1) = 15.50, p < 0.001] and time [χ2 (1) = 58.93, p < 0.001] had significant effects on mean heading. More importantly, so did their interaction (χ2 (1) = 37.42, p < 0.001), indicating that the time series had steeper slopes in the 20° than the 10° turn condition (see Figure 3). On the other hand, there was no effect of crowd noise, the interaction between time and crowd noise, the interaction between crowd noise and crowd turn angle, or the three way interaction between noise, turn angle, and time (χ2 (4) = 1.50, p = 0.824). This pattern of results is expected by weighted averaging.

Simulations of Exp. 1

To test the predictions of the weighted-average model (Eqs 1, 2), every experimental trial was simulated using the model with a 90° field of view (see General Methods for details). The RMSE between the mean heading time series for the model and each participant in each condition was computed. This resulted in a mean RMSE of 4.06° (±0.70° SD) for the experiment. This value can be compared with the performance of a null model that does not respond to the stimuli and simply moves straight ahead on each trial, providing an estimate of the floor for any model. The RMSE between the null model and the human data was 12.81° (±1.65° SD), more than twice the error of the weighted-average model (BF₁₀ > 100). The weighted-average model thus generates a steering trajectory over time that is quite close to the human data.

Final Heading

The model’s mean final heading in each noise condition appears in Figure 2C. Like the human data in Figure 2A, the simulation curves are fairly flat and hover around the crowd mean. In the 20° turn condition, the model slightly undershoots the crowd mean at lower levels of noise and slightly overshoots at higher levels. Nevertheless, the overall pattern is similar to human subjects.

Variable Error

The mean variable error in final heading for model simulations is plotted as a function of crowd noise in Figure 2D. Again, note the similarity with the corresponding human data in Figure 2B–in both graphs, the response variability increases monotonically with crowd noise.

A model that computes the weighted average of neighbor headings thus predicts the observed increase in variable error as crowd noise increases. This finding strongly implies that the human response variability across trials is a direct result of averaging. On each trial, variation in the distances and headings of virtual neighbors produces a slightly different mean heading in the participant’s neighborhood. With increasing crowd noise, the trial-to-trial variation in neighbor headings increases, yielding larger fluctuations in the neighborhood mean. Thus, the increase in variable error is a simple consequence of averaging noisy neighbors.

Taken together, the similarities between model predictions and human behavior provide strong evidence that participant heading responses are based on weighted averaging over the neighborhood, consistent with model (Eqs 1, 2).

Discussion

The results of Experiment 1 show that even with the noisiest neighbors, the participants’ mean heading was still clustered around the mean heading of the crowd. This finding indicates that participants average the headings in their neighborhood when walking with a crowd. On the other hand, variable error in heading increased in proportion to crowd noise, due to heading fluctuations in the neighborhood from trial to trial. An analysis of the time series of heading found that the attractor strength of the crowd mean increased with turn angle but was unaffected by symmetric crowd noise. This result reveals that a pedestrian who deviates from the crowd will be recruited to align with the crowd mean, regardless of the level of noise; if all pedestrians obey this rule, the crowd will become progressively aligned. All of these findings are predicted by Rio, et al.’s [15] weighted averaging model, as demonstrated by the simulations. Weighted averaging in humans is thus highly robust to noise in crowd headings, and acts as a recruitment mechanism into collective motion.

Experiment 2: Splitting Crowd

If a crowd splits into two groups, will a pedestrian follow one group or walk in the average direction of the two groups? Previous studies have found that participants average all neighbors in a virtual crowd when the heading difference between two groups is 10° [15]. In Experiment 2, we investigate whether robust averaging extends to larger heading differences between groups. Rio, et al’s [15]. model predicts that participants will continue to walk in the mean direction even with large angular differences between groups.

In the present experiment we manipulated the angular difference between the heading directions of two completely aligned groups (α = 10–40°) and the proportion of the crowd in the majority group (50, 67 or 84%). On each trial, the virtual crowd began walking straight ahead, and then two groups turned by the same angle (α/2) left and right, and continued walking (see schematic in Figure 1B). The groups appeared as two spatially overlapping, continuously crossing streams, with new neighbors coming into view as others went out of view.

If participants average over their neighborhood, their final heading should align with the mean of the crowd–that is, they should walk between the two groups. Note that the crowd mean shifts from straight ahead (0°) toward the majority group as it increases in size, which should also lead the participant to turn at a faster rate due to the larger discrepancy from the neighborhood mean. Alternatively, if participants follow one group, then their final heading should align with that group. As the angular difference α between groups increases, we would expect to observe a transition from averaging to following if the limits of weighted averaging are reached. In that case, if participants are more attracted to the majority, their final heading should align with the larger group.

Displays

To create a display with two continuously crossing groups, the crowd consisted of 48 virtual humans initially positioned on six concentric 182° arcs, with radii of 1.6–6.6 m (at 1 m intervals), with eight virtual humans evenly spaced on each arc. Thus, many virtual humans were outside the 94° horizontal field of view of the HMD. These initial positions were then jittered by sampling from a uniform distribution in polar coordinates (radius Δr: SD = 0.15 m; eccentricity Δθ: range = −15°–15°) on every trial. The neighbors that were perturbed to the right were selected randomly in depth, but evenly distributed in eccentricity, such that no matter where the participant looked there was representation from each turn group. By default, the remainder of the crowd turned in the opposite direction such that the members of each group were spatially dispersed throughout the entire crowd. Consequently there were two continuous streams of neighbors crossing at the specified angle in the field of view.

On each trial, the virtual humans appeared with their backs to the participant. After 2 s they began walking straight ahead (0°), accelerating from a stand-still to a speed of 1.15 m/s over a period of 2 s. After a random interval (1.8–2.8 s from the start of walking), a percentage of the crowd (50, 66 or 84%) turned to the right by 5°, 10°, 15° or 20°, and the rest turned an equal angle to the left (or vice versa).

Design

Four angular differences (α = 10°, 20°, 30° or 40°) were crossed with three proportions (50, 66 or 84%) in the majority, yielding 12 conditions. The proportions were left/right counter-balanced, but subsequently collapsed for analysis and normalized with the majority turning to the right. There were eight repetitions in each condition, for a total of 96 trials in a single 1-h session.

Results

Histograms of mean final heading for each condition appear in Figure 4; the white arrows on the horizontal axis indicate the crowd mean in that condition. Note that the crowd mean (white arrows) and the center of the distribution shift together to the right as the proportion in the majority group increases (within each row); this shift is amplified by the angular difference between groups (within each column). This allows us to infer that participants generally walked in the mean heading direction of the crowd in all conditions, even with the largest angular difference between groups, consistent with the weighted averaging prediction. The spread of the distribution, increases with angular difference (within each column), however, but does not appear to depend on the size of the majority (within each row). We consider these results in turn.

FIGURE 4

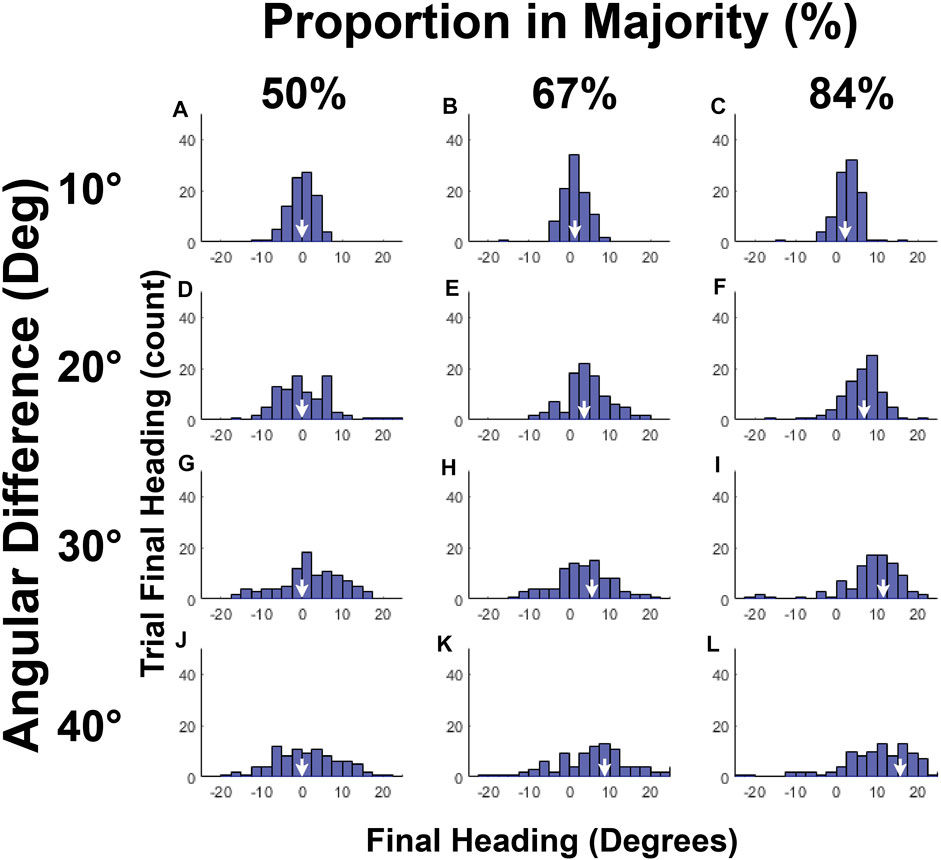
FIGURE 4. Histograms of final heading for each condition in Experiment 2. (A-L) Panels represent the frequency of final heading (2.5° intervals) for all trials in that condition, where positive heading values are in direction of the majority group. Columns represent the proportion of the crowd in the majority group, rows represent the angular heading difference between the two groups. White arrows indicate the overall mean heading of the entire crowd in the corresponding condition, which shifts rightward as the proportion in the majority grows and as the angular difference increases. Data cluster around the crowd mean in each condition.

Final Heading

The mean final heading in each condition appears in Figure 5A, which clearly illustrates its dependence on the heading difference between groups (horizontal axis) and the percentage of neighbors in the majority (curves). With 50% of the crowd in each group, the mean heading is close to zero, for participants split the difference between them. But with majorities of 67 and 84%, mean final heading is biased toward the majority and increases with the angular difference.

FIGURE 5

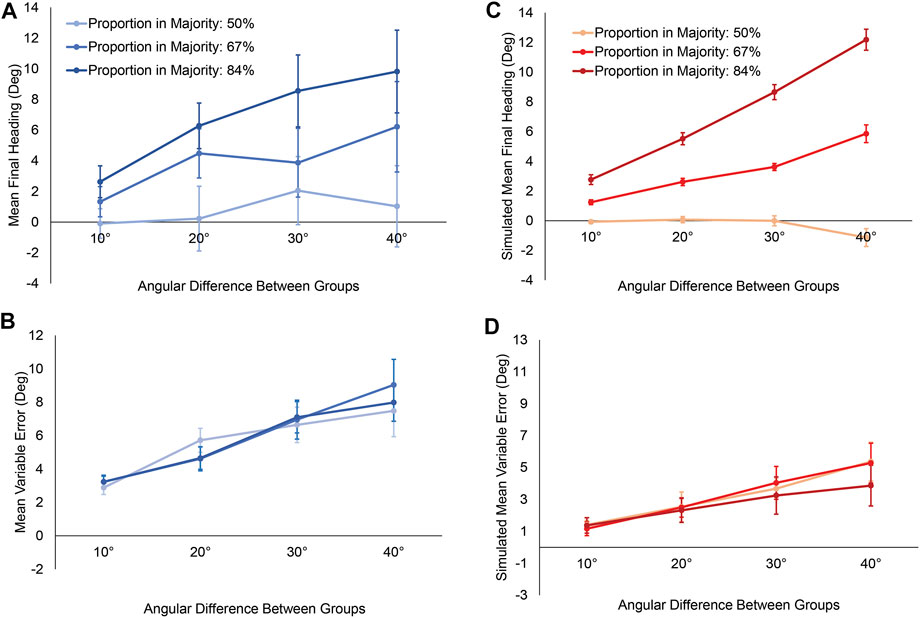
FIGURE 5. Results of Experiment 2. (A) Mean final heading and (B) mean variable error as a function of the angular difference between groups, where positive heading values are in the direction of the majority group. Curves represent the proportion of the crowd in the majority. Panels A and B summarize the data in the histograms of Figure 4. (C) Model simulations of mean final heading and (D) mean variable error corresponding to the human data in panels A and B. For human and model, final heading increases with both the proportion in the majority and the angular difference, whereas the variable error only increases with angular difference. Error bars represent the standard error of the mean (±SEM).

We analyzed final heading using an LME regression with fixed effects of the angular difference (α), percentage in the majority, and their interaction, and participants as random effects (see final model in Supplementary Table SM2A). Chi-squared likelihood ratio tests reveal a significant effect of angular difference [χ2 (1) = 59.71, p < 0.001], a significant effect of percentage [χ2 (1) = 133.81, p < 0.001], as well as a significant interaction between them [χ2 (1) = 16.81, p < 0.001]. The regression results allow us to estimate that going from a majority of 50–84% accounts for a ∼5.8° increase in final heading, going from an angular difference of 10°–40° accounts for a ∼4.4° increase in final heading, and their interaction accounts for an additional ∼5.3° increase in final heading. Thus, overall, mean final heading shifts both with an increase in angular difference and an increase in the size of the majority, as well as their interaction.

To determine whether heading responses were more aligned with the mean of the crowd or the mean of the majority group, we used simple linear regression. When the participants’ mean final heading in each condition is regressed onto the crowd’s mean heading (Figure 6A) there is a strong linear relationship (R² = 0.94) with a steep slope (0.714). In contrast, when mean final heading is regressed on the mean heading of the majority group (Figure 6B), there is a much weaker relationship (R² = 0.65) and a shallow slope (0.35). These results clearly indicate that participants average the headings of all neighbors, not just the majority group, as predicted by the weighted averaging model. The fact that the slope is less than 1 is likely due to the fact that trials with large perturbations often ended before the participant finished turning and heading stabilized (e.g., time series in Figures 7C,D). A Bayes Factor confirmed that the human final heading was closer to the crowd’s mean heading (C) than the majority group’s heading (G), BF_CG > 100, providing decisive evidence for the former hypothesis.

FIGURE 6

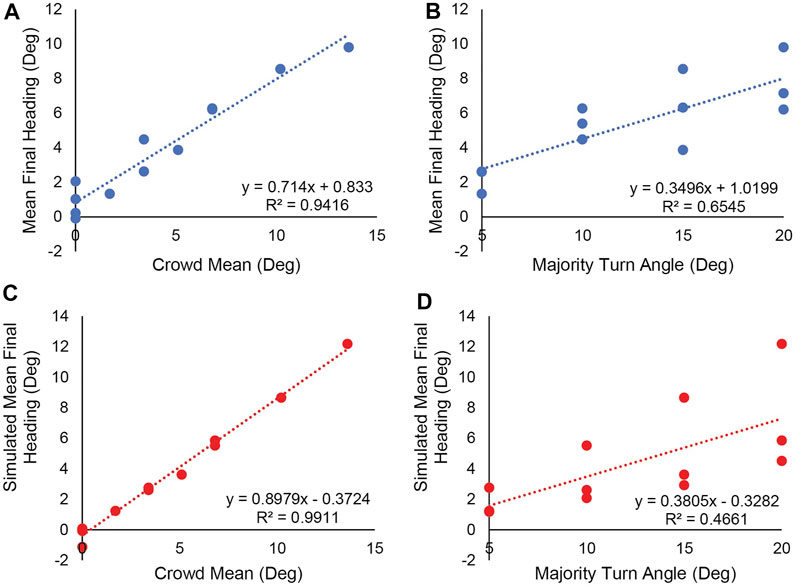
FIGURE 6. Did participants follow the majority or the crowd average in Experiment 2? Linear regression of mean final heading on (A) the mean heading of the crowd or (B) the heading of the majority subgroup in each condition. (C,D) Corresponding linear regressions for simulations of the weighted-averaging model. Regression slopes and correlations (R²) on each panel indicate that final heading is much closer to the crowd mean than the majority for both humans and model.

FIGURE 7

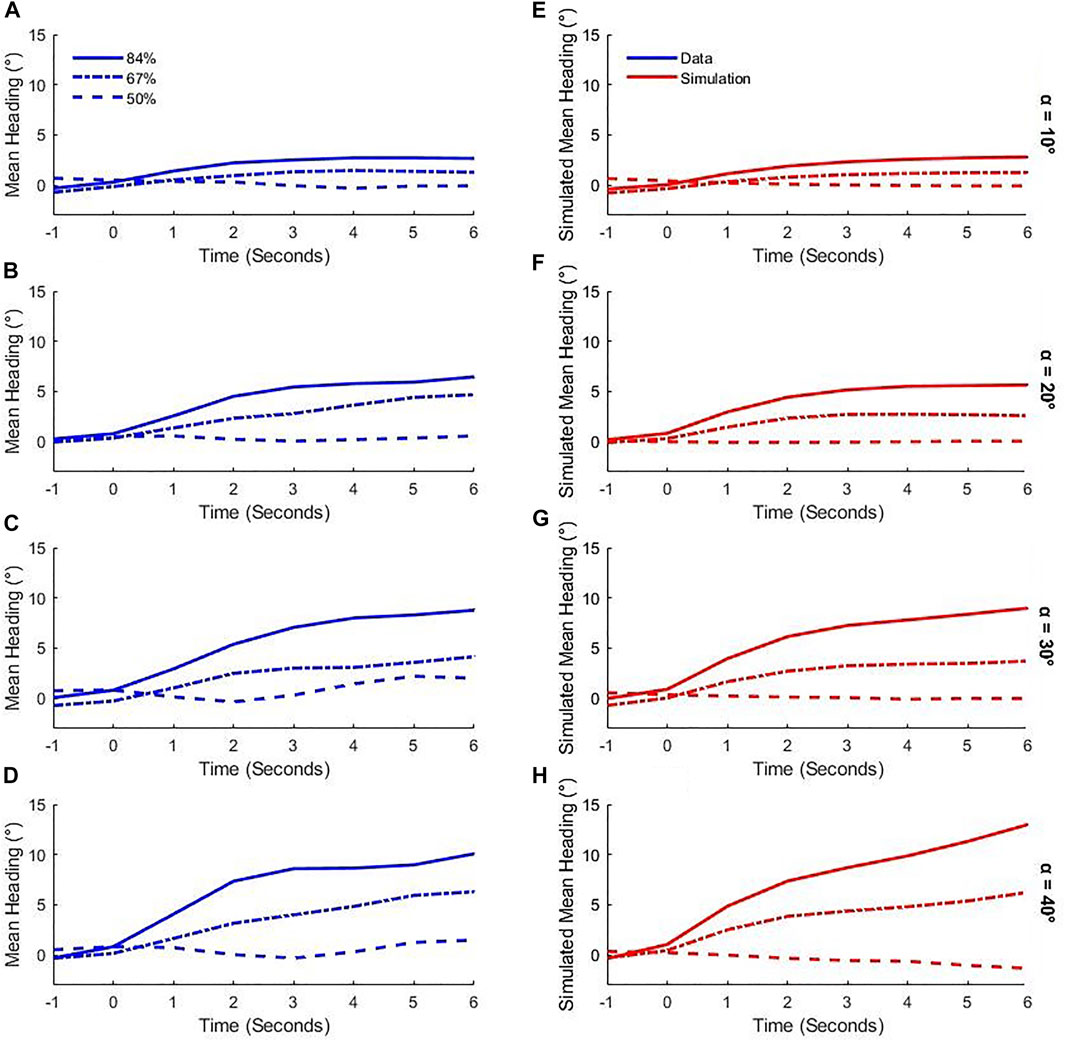
FIGURE 7. Mean time series of heading for each condition in Experiment 2. (A-D) Human heading over time at each angular difference, α = 10°, 20°, 30°, and 40°, respectively. Curves represent the percentage of the crowd in the majority group (solid = 84%, dash-dot = 67%, dashes = 50%). (E-H) Model simulations of heading over time in the corresponding conditions. Slopes indicate the attractiveness of the mean heading in the neighborhood, which increases with both independent variables for the model and human participants. The weighted averaging model thus predicts the increase in attraction strength with the deviation of the neighborhood mean from the participant’s initial heading.

Variable Error

The mean variable error in final heading appears in Figure 5B. A participant’s variability increases with the angular difference between groups (horizontal axis), but not with the proportion in the majority (curves). This effect occurs because the trial-to-trial variation in neighbor headings increased with the heading difference between groups, whereas the proportion of neighbors in each group merely shifted the mean heading in the neighborhood, and is consistent with weighted averaging over the neighborhood.

A similar mixed effects linear regression was used to analyze variable error in heading (final model in Supplementary Table SM2B). Chi-squared likelihood ratio tests reveal a significant effect of angular difference [χ2 (1) = 75.32, p < 0.001], but no effect of majority size [χ2 (1) = 0.02, p = 0.90], nor an interaction between them [χ2 (1) = 0.23, p = 0.63]. The regression results allow us to estimate that going from an angular difference of 10°–40° accounts for a 5.12° increase in the variable error.

Heading Over Time

The mean time series of heading in each condition appear in Figure 7 (blue curves), where Panels A to D correspond to the angular difference between groups (10° to 40°, respectively). According to the weighted averaging model, attraction strength, and hence the rate of change in heading, should increase with the difference between the crowd mean and the participant’s initial heading (0°). Consistent with this expectation, the slope of the time series appears to increase with both the size of the majority (curves) and the angular difference between groups (panels)–with the exception of the 50% condition, which predicts a heading near 0°.

Heading over time was analyzed using an LME regression with fixed effects of angular difference, percentage in the majority, time, and their interactions, and participants as random effects (final model in Supplementary Table SM2C). The results show that time [χ2 (1) = 22.29, p < 0.001], the interaction of angular difference and time [χ2 (1) = 15.68, p < 0.001], the interaction of percentage and time [χ2 (1) = 27.09, p < 0.001], and the three-way interaction [χ2 (1) = 10.32, p = 0.001] have significant effects on heading. The two-way interactions indicate that the turning rate (slope) increases with both the percentage in the majority and the angular difference between groups; the three-way interaction indicates an additional effect of the combined factors on turning rate. This analysis confirms that the attraction strength of the crowd mean increased with its deviation from the participant’s initial heading.

Simulations of Exp. 2

To compare the data with predictions of the weighted-averaging model (Eqs 1, 2), all experimental trials were simulated using a 90° field of view similar to the Oculus Rift HMD (see General Methods for details). Histograms of the simulated final heading in each condition appear in Figure 8. Visual comparison with the histograms of the human data (Figure 4) reveals similar unimodal distributions centered around the overall crowd mean (white arrows), although they are less variable that the human data (The lower variability is attributable to the fact that the model does not simulate gait oscillations and tracker error). The impression is supported by graphs of the model’s mean final heading (Figure 5C) and the mean variable error (Figure 5D) in each condition, which are quite similar to the corresponding plots of the human data (Figures 5A,B).

FIGURE 8

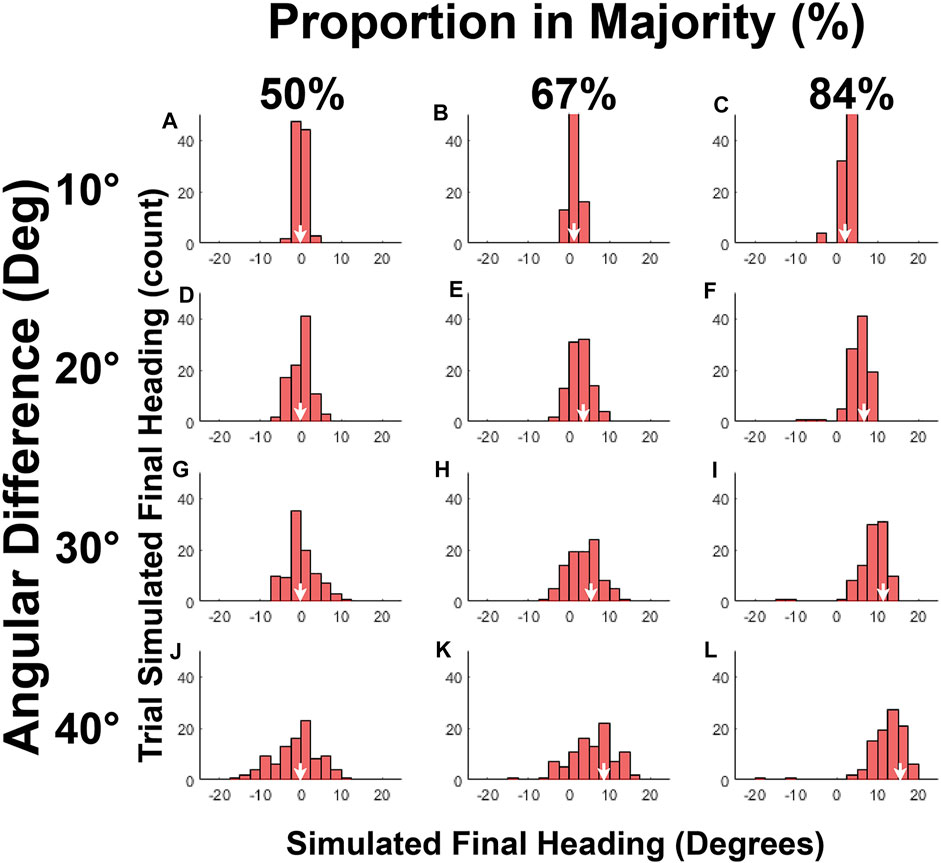
FIGURE 8. Histograms of final heading for model simulations of Experiment 2. (A-L) Panels represent the frequency of final heading (2.5° intervals) for all simulated trials in each condition, same layout as Figure 4. Although the spread of the model histograms is narrower that the human histograms, the clustering about the crowd mean in each condition (white arrows) is quite similar.

To measure the model’s performance we calculated the RMSE between the time series of heading for the model and the participant on every trial. The mean RMSE for Experiment 2 (excluding the 50% condition) was 4.35° (±1.55° SD), which is better than the RMSE for the null “do nothing” model of 6.12° (±1.65° SD). A Bayes Factor comparing them provides decisive evidence that the weighted averaging model outperforms the null model (BF₁₀ > 100). Mean heading time series for the model in each condition appear in Figures 7E–H, revealing their similarity to the human mean time series (Figures 7A–D). The comparable pattern of slopes confirms that the increase in attraction strength as the crowd mean deviates from the agent’s initial heading follows from the dynamics of weighted averaging.

We also used simple linear regressions to compare the weighted averaging model’s alignment with the crowd mean and with the majority group. When the model’s mean final heading in each condition is regressed on the crowd mean (Figure 6C) there is a strong linear relationship (R² > 0.99) with a steep slope (0.898). In contrast, when mean final heading is regressed on the majority group’s heading (Figure 6D) there is a much weaker relationship (R² = 0.47) and a shallow slope (0.38). The similarity with the human regressions (Figures 6A,B) confirms that participants averaged the headings in their neighborhood, as predicted by the weighted averaging model, rather than following the majority group.

Discussion

The results of Experiment 2 reveal that when a crowd splits into two continuously crossing groups heading to the left and right, participants align with the mean heading in all conditions, even with a large angular difference of 40°. As the size of the majority group increases, the final heading shifts along with the crowd mean. Human averaging is thus highly robust not only to noise but to diverging groups in a crowd. The data are quite close to the model predictions, evidence that humans rely on a weighted average of headings in their neighborhood.

To test whether weighted averaging generalized to groups that separated in space, we repeated the experiment with a virtual crowd consisting of eight or 16 virtual humans that diverged into two visibly separate groups (see Supplementary Material). The spatial separation of the two groups increased through the trial, so up to half of the neighbors had moved out of the field of view by the end of a trial. Nevertheless, the results were the same: The participants’ mean final heading was more closely aligned with the crowd mean than the majority group, as were model simulations of the stimuli. Thus, even with visibly separate groups, participants followed the crowd mean, consistent with robust weighted averaging.

It is important to note that in our splitting crowd experiments, only the virtual humans appeared in the display. In many real-world situations, two subgroups might be moving toward two visible goals, such as marked exits. An explicit choice between two alternatives would add competing attractors to the crowd dynamics. For example, Kinateder and Warren [25] studied an emergency evacuation scenario in which a virtual crowd split into two subgroups that walked to two visible exits. In this situation the authors did not observe weighted averaging, but rather a tradeoff between following the majority and going to the uncrowded exit, which depended on both the size of the crowd and the width of the exit. In a subsequent article, we plan to report a model of choice behavior in which nonlinear competition between alternatives is added to the weighted averaging model. The present findings highlight the robust nature of averaging in the absence of explicit alternatives.

Experiment 3: Coherent Subgroup

Experiments 1 and 2 demonstrated that participants align with a crowd by spatially averaging over both “noisy neighbors” and diverging groups. This alignment behavior is well characterized by the weighted averaging model (Eqs 1, 2). In Experiment 3, we investigate whether weighted averaging extends to a coherent subgroup within a noisy crowd. According to the perceptual grouping principle of “common fate” [26], elements that move together in the frontal plane tend to be perceived as a group. Similarly, if a subgroup of neighbors in a noisy crowd moves in a common direction in depth, they might be perceived as a unit and attract a pedestrian to align with them. On the other hand, there is also evidence that it is difficult to identify a coherently moving group of elements amid incoherent element motions [27].

In the present experiment, the participant was immersed in a noisy crowd whose members walked in random directions within a range of 180° (±90° centered on the participant’s heading). After a few seconds, a subgroup of neighbors that were interspersed in the crowd turned with a mean angle of ±20° (right or left) (see schematic in Figure 1C). The coherence of the subgroup was manipulated by selecting their individual headings from a Gaussian distribution with an SD of 0° (aligned), 10°, or 20° about the mean. In addition, the proportion of the crowd in the subgroup was varied (0, 25, 50, 75, or 100%), shifting the mean heading of the entire crowd from 0° to 20°.

If participants are attracted to align with a coherent subgroup, their final heading should match the subgroup’s mean heading (20°), and the attraction strength should increase with the subgroup’s coherence. On the other hand, according to the weighted-averaging model participants should align with the crowd mean in all conditions. The model thus predicts that final heading will gradually shift from 0° to 20° as the subgroup proportion increases from 0 to 100%, whereas attraction strength will be unaffected by subgroup coherence. The model also predicts that variable error will decrease as the subgroup proportion increases, because this reduces the overall noise in the crowd; for the same reason, variable error may also decrease slightly as the subgroup becomes more coherent. The pattern of results once again supports robust weighted averaging.

Displays

The virtual crowd consisted of 48 virtual humans. Each virtual human was initially positioned in polar coordinates with a radius ranging from 1.6 to 6.6 m (1 m apart) in depth, and a theta ranging from 91° to −91° (26° apart) in eccentricity. Their positions were then jittered by sampling from a uniform distribution in polar coordinates (Δr: SD = 0.15 m; Δθ: range = −16°–16°) on every trial.

On each trial, the virtual humans appeared facing in directions randomly selected from a uniform distribution with a range of ±90°, centered on the participant’s initial heading (0°), and accelerated from a stand-still (0 m/s) to a speed of 1.15 m/s over a period of 3 s. After a random interval (2.5–3.5 s from the start of walking), a subgroup of virtual humans (0, 25, 50, 75, or 100% of the crowd), evenly spaced in eccentricity and depth, was perturbed: each turned and walked in a new heading direction selected from a Gaussian distribution with a mean of ±20° (positive values to the right), and an SD of 0°, 10°, or 20° (subgroup coherence).

Design

The factors of subgroup proportion (0, 25, 50, 75, 100%) and subgroup coherence (SD = 0°, 10°, or 20°) were crossed, yielding 15 experimental conditions. There were eight repetitions per condition (half left and half right turns), for a total of 120 trials in a 1-h session.

Results

Final Heading

Mean final heading in each condition appears in Figure 9A. If participants align with the coherent subgroup, mean final heading should be close to 20° in all conditions (except the 0% condition, which predicts no response). However, final heading gradually shifted with the percentage of the crowd in the subgroup, consistent with weighted averaging. There appears to be no systematic relationship between final heading and crowd coherence (curves).

FIGURE 9

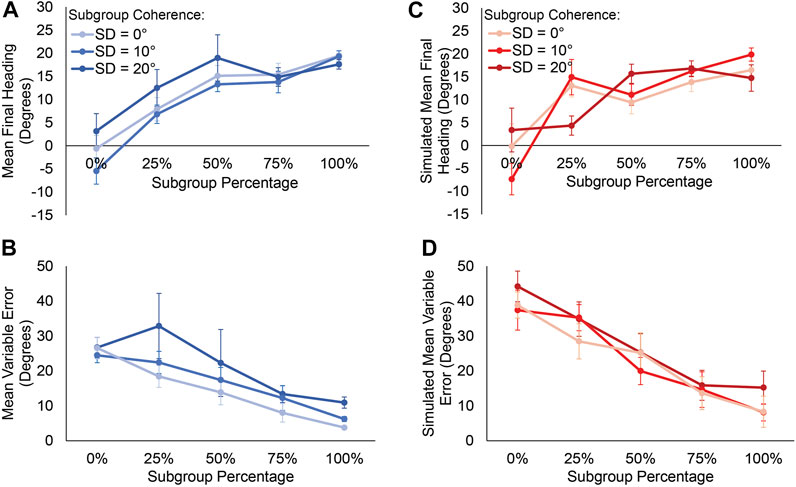
FIGURE 9. Results of Experiment 3. (A) Mean final heading and (B) mean variable error as a function of the proportion of the crowd in the subgroup, for participants. Curves represent the coherence of headings in subgroup (C) Model simulations of mean final heading and (D) mean variable error corresponding to the data in panels A and B. See text for comparisons. Error bars represent the standard error of the mean (±SEM).

Final heading was analyzed using an LME regression with fixed effects of subgroup percentage, subgroup coherence, and their interaction, and participants as random effects (see final model in Supplementary Table SM3A). The analysis reveals that only the subgroup percentage had a significant effect on final heading (χ2 (1) = 24.18, p < 0.001), with no effect of subgroup coherence or interaction (χ2 (2) = 1.58, p = 0.457). The regression estimate indicates that for every percent increase in the subgroup size, there was 0.19° (±0.02 SE) increase in final heading.

Bayes Factors were calculated to assess whether the human mean final heading was closer to the subgroup mean (20°) or the crowd mean in the neighborhood (as measured by the weighted-averaging model), for conditions in which these predictions differ (25, 50, 75% in the subgroup). The results indicated that the human data were closer to the crowd mean (C) than the subgroup mean (G) in the 25% subgroup condition (BF_CG = 67.7), very strong evidence favoring the crowd mean. The data did not distinguish the two hypotheses in the 50% (BF_CG = 1.02) or 75% (BF_CG = 1.01) conditions, however, as the predicted difference became smaller and the maximum heading response was reached (about 18.79°). These results indicate that participants aligned with the crowd mean in their neighborhood, which was meaningfully different from the subgroup mean in the 25% condition.

Variable Error

The mean variable error in final heading (Figure 9B) decreases with the subgroup percentage, and also appears to decrease with as the subgroup becomes more coherent (curves).

A similar LME regression was used to analyze variable error in final heading (the final model appears in Supplementary Table SM3B). Chi-squared likelihood ratio tests revealed significant effects of both subgroup percentage (χ2 (1) = 23.30, p < 0.001) and subgroup coherence (χ2 (1) = 4.48, p = 0.035), with no interaction (χ2 (1) = 0.010, p = 0.752). The statistical model indicates that for every point increase in the subset percentage, there was a 0.21° (±0.03 SE) decrease in a participant’s variable error. It also reveals that for every degree of increase in the subgroup’s SD (i.e., decrease in coherence), there was a corresponding 0.36° (±0.13 SE) increase in a participant’s variable error.

Both of these effects can be attributed to the total noise in the virtual crowd, much as observed in Experiment 1. First, as the percentage of virtual humans in the coherent subgroup goes up, the number of random headings in the rest of the crowd goes down; there is thus less heading variation in the neighborhood from trial to trial, so the variability in the participant’s response is reduced. Second, as the coherence of the subgroup goes up, the total heading variation in the crowd decreases slightly–enough to reduce the participant’s variable error. Thus, both effects are expected from a weighted-average neighborhood. We compare the predictions of the model in the following simulations.

Heading Over Time

The mean time series of heading in each condition appear in Figure 10. Turning rate (slope) tends to increase with subgroup percentage (curves). An LME regression analysis reveals a significant effect of time (χ2 (1) = 57.70, p < 0.001), and a significant interaction of the subgroup percentage and time (χ2 (1) = 12.33, p < 0.001). There was no effect of subgroup coherence, the interaction of coherence and time, the interaction between subgroup coherence and subgroup percentage, or the three-way interaction between time, subgroup percentage, and subgroup coherence (χ2 (4) = 4.08, p = 0.396) (see Supplementary Table SM3C for final statistical model). This finding indicates that a larger subgroup was more attractive not because it was more coherent, but because it increased the deviation of the crowd’s mean from the participant’s current heading.

FIGURE 10

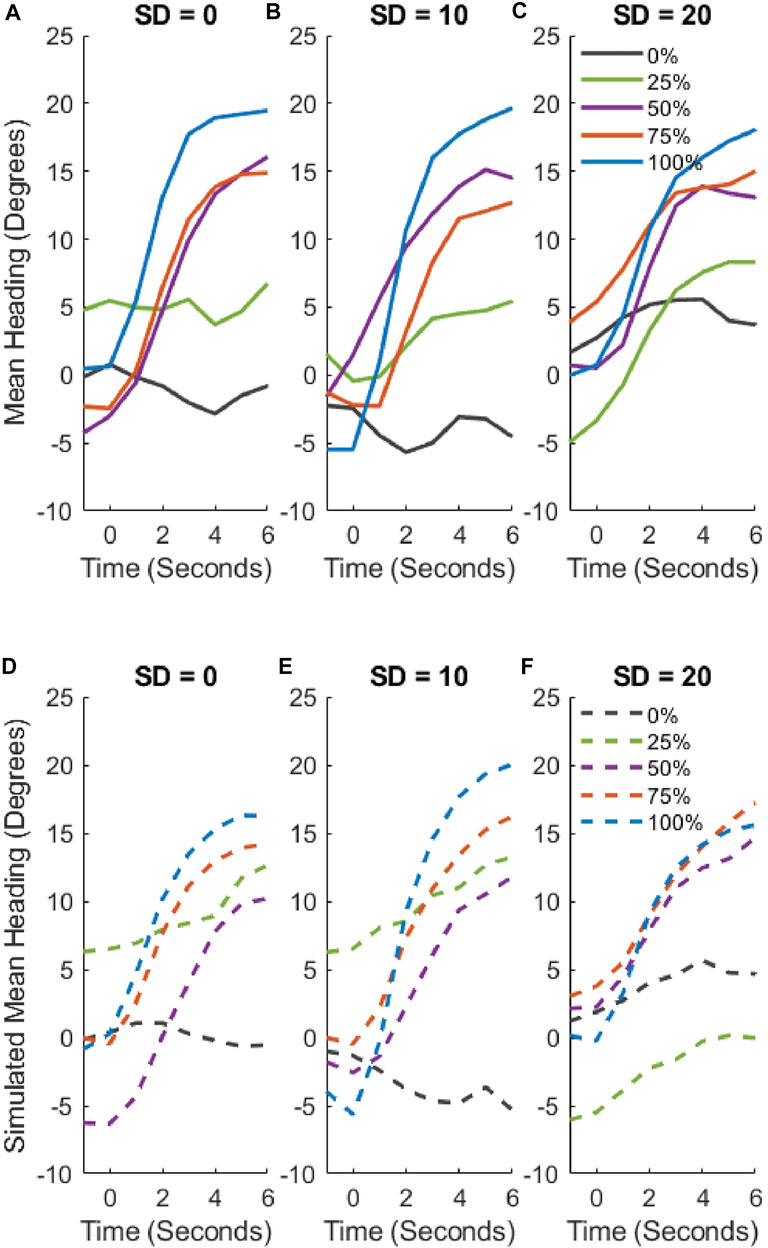
FIGURE 10. Mean time series of heading for each condition in Experiment 3. (A–C) Human heading over time in each coherence condition (SD = 0°, 10°, 20°, respectively). Curves represent the proportion of the crowd in the subgroup. (D–F) Model simulations of heading over time in the corresponding conditions. Slopes indicate the attractiveness of the mean heading in the neighborhood, and are highly similar for humans and model: they increase with subgroup proportion, but not with subgroup coherence.

Simulations of Exp. 3

To compare the results with the weighted-averaging predictions, the experimental trials were simulated as before, using a 110° horizontal field of view similar to the Odyssey HMD. The average RMSE between the mean time series for each participant in each condition and the corresponding mean simulated time series was 9.24° (±4.23° SD). For purposes of comparison, this value is better than the RMSE of 11.73° (±2.41° SD) for the null model that moves straight ahead (BF₁₀ > 100), but worse than the weighted-average model for the noisy neighbors in Experiment 1 (mean RMSE = 4.19°). This suggests that participants in the present experiment may not have been averaging all headings in the neighborhood.

To investigate the source of this discrepancy, we broke down the mean RMSE by condition (see Supplementary Figure S7). The mean RMSE decreases linearly as a function of subgroup proportion, as overall crowd noise decreases. Thus, the discrepancy between the model and human data is greatest in the 0 and 25% conditions, when most of the crowd has random headings in a 180° range, and lowest in the 75 and 100% conditions, when most of the crowd has headings within a narrow range (SD = 0° to 20°). This pattern implies that participants may be ignoring neighbors with highly discrepant headings (>45°) that are greater than those in Experiment 1 (<45°).

Final Heading

The model’s final heading in each condition appears in Figure 9C. Note the similarity with the human data in Figure 9A: in both cases, the final heading monotonically shifts toward the subgroup mean (20°) as the subgroup percentage grows. Thus, the mean model output predicts the mean human heading quite well, consistent with weighted averaging.

Variable Error

The model’s mean variable error in final heading in each condition appears in Figure 9D. The graph is similar to the corresponding human variable error (Figure 9B): response variability decreases monotonically with the subgroup percentage, consistent with averaging a less noisy crowd (cf. Experiment 1, Figure 2B). There are, however, two notable differences.

First, the model variable error is markedly higher than the human error in the 0 and 25% subgroup conditions. This confirms that participants are ignoring highly discrepant neighbors. Compare the present variable error (Figures 9C,D, 0% condition) with that in Experiment 1 (Figures 2B,D, ±45° condition): the model’s variable error is much greater in the present experiment with crowd noise of ±90° (about 40°) than in Experiment 1 with crowd noise of ±40° (about 13°)–but the human variable error is the same in the two experiments (about 12°). This comparison reveals that, whereas the model averages all headings, participants ignore large heading differences (>45°), thus reducing human variable error.

Second, the model variable error shows no consistent ordering by subgroup coherence (Figure 9D, curves), whereas there was a significant effect of coherence on human variable error (Figure 9B). We suspect that, because participants ignored highly discrepant headings, they were sensitive to the slight reduction in overall crowd noise produced by a more coherent subgroup. In contrast, because the model is strongly influenced by discrepant headings, this slight reduction in noise had little effect on its variable error.

In sum, the patterns of RMSE and variable error indicate that participants ignore neighbors with highly discrepant headings (>45°). This leads humans to be less influenced by extreme crowd noise than predicted by the weighted-averaging model.

Discussion

Experiment 3 tested the hypothesis that participants would be attracted to align with a coherent subgroup in a noisy crowd, and that this attraction would increase with subgroup coherence. In contrast, the results were consistent with robust weighted averaging: mean final heading gradually shifted together with the crowd mean as the percentage in the subgroup increased from 0 to 100%. Moreover, the strength of attraction did not increase with the subgroup’s coherence, but with the deviation of the crowd’s mean heading from the participant’s current heading. These results support the weighted averaging model.

In addition, the pattern of errors clearly indicates that humans ignore highly discrepant headings that differ from the participant’s current heading by > 45°. In other words, human weighted averaging only extends over heading differences of 0˚-45°, suggesting a modest revision to the model.

The results of this experiment reveal an essential property of the mechanism of recruitment. One might expect that a pedestrian would be more attracted to a group of neighbors as their coherence (degree of alignment) increased, consistent with the principle of common fate. This response would amplify the alignment in the crowd and recruit more individuals into collective motion. In contrast, however, we find that a subgroup is not attractive due to its coherence, but due to its effect on the mean heading deviation in an individual’s neighborhood. We consider the implications of this finding in the concluding section.

Conclusion

In three experiments, we asked participants to walk with a virtual crowd in several scenarios. Experiment 1 added noise in the heading directions of crowd members (range up to 90°), and found that participants aligned with the crowd mean in all conditions. Experiment 2 presented two diverging groups (angular difference up 40°) and varied their proportions, and again found that participants aligned with the crowd’s mean heading rather than following one group. In Experiment 3, a coherent subgroup in a noisy crowd (range 180°) was perturbed, and participants once again aligned with the mean heading of the crowd rather than the subgroup. Taken together, these results show that weighted averaging in humans is highly robust: pedestrians align with the mean heading direction in their neighborhood, just as predicted by Rio, et al’s [15] soft metric model (Eqs 1, 2). However, the results indicate that weighted averaging is limited to heading differences of 0°-45°, and humans ignore highly discrepant neighbors (>45°).

Weighted averaging within a spatial neighborhood thus provides a mechanism of self-organization: a positive feedback that recruits an increasing number of individuals into collective motion. But how, exactly, is this positive feedback to be understood? First, consider the phenomenon from the perspective of an individual pedestrian. It would seem intuitive that an individual is more strongly attracted to align with neighbors that are more coherent (aligned with each other); in this way, the individual would increase the attractiveness of the emerging collective. But this type of positive “coherence” feedback does not follow from Eqs 1, 2 and is empirically disconfirmed by Experiments 1 and 3: neighbors that are more coherent (aligned) do not in fact increase the attractiveness of their mean heading. Rather, as predicted by Eqs 1, 2, attraction strength increases with the deviation of the neighborhood mean from the individual’s current heading (Figure 3, 7, 10).

Now consider the phenomenon from the perspective of the collective. When a few neighbors move in a similar heading direction, they shift the mean heading in adjacent neighborhoods toward that direction. The adjacent neighbors are attracted to their new neighborhood mean–with a strength that increases with their current deviation from the mean–which in turn contributes to a common heading direction in more neighborhoods, in a self-reinforcing cascade. This common heading thus propagates through the crowd, yielding emergent collective motion. This type of positive “heading” feedback is a result of weighted averaging over a soft metric neighborhood, and follows from Eqs 1, 2.

In sum, the present experimental evidence and model simulations indicate that robust weighted averaging provides a mechanism of self-organization in human crowds, which acts to recruit individuals into emerging collective motion through a positive “heading” feedback.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://doi.org/10.26300/6wv7-r075.

Ethics Statement

The studies involving human participants were reviewed and approved by Brown University IRB #00000556. The patients/participants provided their written informed consent to participate in this study.

Author Contributions

TW and WW designed the research; TW performed the experiments, statistically analyzed the data, and simulated the results; TW wrote the first draft and WW revised and wrote sections of the manuscript. Both authors read and approved the submitted version.

Funding

This research was supported by the United States National Science Foundation, award numbers BCS-1431406 and BCS-1849446 to the second author, and by a Link Foundation Fellowship to the first author.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors thank Dr. Gregory Dachner and Dr. Brittany Baxter for their assistance with model simulation and statistical analysis.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2021.761445/full#supplementary-material

References

1. Couzin, ID, and Krause, J. Self-organization and Collective Behavior in Vertebrates. Adv Study Behav (2003) 32:1–75. doi:10.1016/s0065-3454(03)01001-5

CrossRef Full Text | Google Scholar

2. Sumpter, DJT. Collective Animal Behavior. Princeton, NJ: Princeton University Press (2010).

Google Scholar

3. Reynolds, CW. Flocks, Herds and Schools: A Distributed Behavioral Model. SIGGRAPH Comput Graph (1987) 21:25–34. doi:10.1145/37402.37406

CrossRef Full Text | Google Scholar

4. Couzin, ID, Krause, J, James, R, Ruxton, GD, and Franks, NR. Collective Memory and Spatial Sorting in Animal Groups. J Theor Biol (2002) 218:1–11. doi:10.1006/jtbi.2002.3065

CrossRef Full Text | Google Scholar

5. Grégoire, G, Chaté, H, and Tu, Y. Moving and Staying Together Without a Leader. Physica D: Nonlinear Phenomena (2003) 181(3-4):157–70. doi:10.1016/s0167-2789(03)00102-7

CrossRef Full Text | Google Scholar

6. Giardina, I. Collective Behavior in Animal Groups: Theoretical Models and Empirical Studies. HFSP J (2008) 2(4):205–19. doi:10.2976/1.2961038

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Helbing, D, and Molnár, P. Social Force Model for Pedestrian Dynamics. Phys Rev E (1995) 51:4282–6. doi:10.1103/physreve.51.4282

CrossRef Full Text | Google Scholar

8. Duives, DC, Daamen, W, and Hoogendoorn, SP. State-of-the-art Crowd Motion Simulation Models. Transportation Res C: Emerging Tech (2013) 37:193–209. doi:10.1016/j.trc.2013.02.005

CrossRef Full Text | Google Scholar

9. Moussaïd, M, Helbing, D, and Theraulaz, G. How Simple Rules Determine Pedestrian Behavior and Crowd Disasters. Proc Natl Acad Sci (2011) 108(17):6884–8. doi:10.1073/pnas.1016507108

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Helbing, D, Molnár, P, Farkas, IJ, and Bolay, K. Self-Organizing Pedestrian Movement. Environ Plann B Plann Des (2001) 28:361–83. doi:10.1068/b2697

CrossRef Full Text | Google Scholar

11. Moussaïd, M, Guillot, EG, Moreau, M, Fehrenbach, J, Chabiron, O, Lemercier, S, et al. Traffic Instabilities in Self-Organized Pedestrian Crowds. Plos Comput Biol (2012) 8(3):e1002442. doi:10.1371/journal.pcbi.1002442

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Vicsek, T, Czirók, A, Ben-Jacob, E, Cohen, I, and Shochet, O. Novel Type of Phase Transition in a System of Self-Driven Particles. Phys Rev Lett (1995) 75(6):1226–9. doi:10.1103/physrevlett.75.1226

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Czirók, A, Stanley, HE, and Vicsek, T. Spontaneously Ordered Motion of Self-Propelled Particles. J Phys A: Math Gen (1997) 30:1375–85. doi:10.1088/0305-4470/30/5/009

CrossRef Full Text | Google Scholar

14. Cucker, F, and Smale, S. Emergent Behavior in Flocks. IEEE Trans Automat Contr (2007) 52(5):852–62. doi:10.1109/tac.2007.895842

CrossRef Full Text | Google Scholar

15. Rio, KW, Dachner, GC, and Warren, WH. Local Interactions Underlying Collective Motion in Human Crowds. Proc R Soc B (2018) 285(1878):20180611. doi:10.1098/rspb.2018.0611

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Grasso, R, Prévost, P, Ivanenko, YP, and Berthoz, A. Eye-Head Coordination for the Steering of Locomotion in Humans: an Anticipatory Synergy. Neurosci Lett (1998) 253:115–8. doi:10.1016/s0304-3940(98)00625-9

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Dachner, GC, and Warren, WH. Behavioral Dynamics of Heading Alignment in Pedestrian Following. Transportation Res Proced (2014) 2:69–76. doi:10.1016/j.trpro.2014.09.010

CrossRef Full Text | Google Scholar

18. Dörfler, F, and Bullo, F. On the Critical Coupling for Kuramoto Oscillators. SIAM J Appl Dyn Syst (2011) 10:1070–99. doi:10.1137/10081530x

CrossRef Full Text | Google Scholar

19. Strogatz, SH. From Kuramoto to Crawford: Exploring the Onset of Synchronization in Populations of Coupled Oscillators. Physica D: Nonlinear Phenomena (2000) 143:1–20. doi:10.1016/s0167-2789(00)00094-4

CrossRef Full Text | Google Scholar

20. Warren, WH, and Dachner, GC. Comparing Simple-Radius and Doughnut Models of Collective Crowd Motion. J Vis (2018) 18(10):1038. doi:10.1167/18.10.1036

CrossRef Full Text | Google Scholar

21. Warren, WH, and Fajen, BR. Behavioral Dynamics of Visually-Guided Locomotion. In: A Fuchs, and V Jirsa, editors. Coordination: Neural, Behavioral, and Social Dynamics. Heidelberg: Springer (2008). p. 45–75.

Google Scholar

22. Kinateder, M, Wirth, TD, and Warren, WH. Crowd Dynamics in Virtual Reality. Crowd Dyn (2018) 1:15–36. doi:10.1007/978-3-030-05129-7_2

CrossRef Full Text | Google Scholar

23. Kinateder, M, and Warren, WH. Social Influence on Evacuation Behavior in Real and Virtual Environments. Front Robotics AI (2016) 3:43. doi:10.3389/frobt.2016.00043

CrossRef Full Text | Google Scholar

24. Williams, DW, and Sekuler, R. Coherent Global Motion Percepts From Stochastic Local Motions. Vis Res (1984) 24(1):55–62. doi:10.3389/frobt.2016.00043

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Kinateder, M, and Warren, WH. Exit Choice During Evacuation Is Influenced by Both the Size and Proportion of the Egressing Crowd. Physica A: Stat Mech its Appl (2021) 569:125746. doi:10.1016/j.physa.2021.125746

CrossRef Full Text | Google Scholar

26. Wagemans, J, Elder, JH, Kubovy, M, Palmer, SE, Peterson, MA, Singh, M, et al. A century of Gestalt Psychology in Visual Perception: I. Perceptual Grouping and Figure-Ground Organization. Psychol Bull (2012) 138(6):1172–217. doi:10.1037/a0029333

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Levinthal, BR, and Franconeri, SL. Common-fate Grouping as Feature Selection. Psychol Sci (2011) 22(9):1132–7. doi:10.1177/0956797611418346

PubMed Abstract | CrossRef Full Text | Google Scholar