A short review of our current understanding of the development of ring faults during collapse caldera formation

Geyer, Adelina; Martí, Joan

doi:10.3389/feart.2014.00022

REVIEW article

Front. Earth Sci., 26 September 2014

Sec. Volcanology

Volume 2 - 2014 | https://doi.org/10.3389/feart.2014.00022

A short review of our current understanding of the development of ring faults during collapse caldera formation

$\r\nAdelina Geyer*$ Adelina Geyer^*

Joan Martí

Geophysical and Geochemical Modelling of Geohazard Processes and Subsurface Resources, Group of Volcanology, SIMGEO (UB-CSIC), Institute of Earth Sciences Jaume Almera, ICTJA-CSIC, Barcelona, Spain

The term collapse caldera refers to those volcanic depressions resulting from the sinking of the chamber roof due to the rapid withdrawal of magma during the course of an eruption. During the last three decades, collapse caldera dynamics has been the focus of attention of numerous, theoretical, numerical, and experimental studies. Nonetheless, even if there is a tendency to go for a general and comprehensive caldera dynamics model, some key aspects remain unclear, controversial or completely unsolved. This is the case of ring fault nucleation points and propagation and dip direction. Since direct information on calderas' deeper structure comes mainly from partially eroded calderas or few witnessed collapses, ring faults layout at depth remains still uncertain. This has generated a strong debate over the detailed internal fault and fracture configuration of a caldera collapse and, in more detail, how ring faults initiate and propagate. We offer here a very short description of the main results obtained by those analog and theoretical/mathematical models applied to the study of collapse caldera formation. We place special attention on those observations related to the nucleation and propagation of the collapse-controlling ring faults. This summary is relevant to understand the current state-of-the-art of this topic and it should be taken under consideration in future works dealing with collapse caldera dynamics.

Introduction: Collapse Calderas and Ring-Faults

The term collapse caldera refers to those volcanic depressions resulting from the sinking of the chamber roof into the magmatic reservoir due to the rapid withdrawal of magma during the course of an eruption. This definition includes all kind of calderas, regardless magma composition, tectonic setting (regional and local), shape, size, and amount of subsidence. During the last three decades, collapse caldera dynamics have been the focus of numerous field (e.g., Lipman, 1997; Moore and Kokelaar, 1997, 1998), theoretical (e.g., Scandone, 1990), numerical (e.g., Gudmundsson, 1988; Burov and Guillou-Frottier, 1999; Folch and Martí, 2004; Hardy, 2008; Holohan et al., 2011), and experimental (e.g., Komuro et al., 1984; Komuro, 1987; Martí et al., 1994; Acocella et al., 2000; Roche et al., 2000; Geyer et al., 2006) studies. Nonetheless, even if there is a tendency to go for a general and comprehensive caldera dynamic model, some key aspects remain unclear, controversial, or completely unsolved.

Traditionally, two main caldera-collapse trigger mechanisms have been presented (Martí et al., 2009): (i) overpressure within the magma chamber initiating fractures in the roof (e.g., Gudmundsson, 1988, 1998; Gray and Monaghan, 2004; Gudmundsson, 2007; Gregg et al., 2012), or (ii) underpressure inside the magma chamber following an eruption (e.g., Roche et al., 2000; Folch and Martí, 2004; Geyer et al., 2006; Holohan et al., 2011). This latter trigger mechanism, despite being one the most appealing models to understand caldera-forming events, has been refuted on several occasions (e.g., Gudmundsson, 1998; Gudmundsson and Nilsen, 2006). Some of the arguments against the overpressure model include inconsistency between the volume of erupted material and the collapse itself, apparent contradictory dip direction of the resulting ring-faults compared to field data, etc. From the list of arguments against this model (see Gudmundsson and Nilsen, 2006), probably the most relevant one is the fact that, in the case of underpressure conditions inside the magma chamber, the conduit should close and the eruption will cease before reaching the required underpressure for caldera collapse. Numerical models published by Pinel and Jaupart (2005) demonstrate that a topographic load of sufficient size modifies the stress field in a manner that prevents feeder dykes to get shut by the confining pressure, allowing caldera collapse to occur during chamber deflation. To deepen into this discussion is beyond the scope of this paper. However, it is certainly an additional aspect to consider in future works together with the recent investigations concerning the elastic energy release during caldera-forming events (Gudmundsson, 2014). In addition to the over- and underpressure model, some authors consider also the possibility of an external overload (ash-flow units) leading to the breakage of the roof cover from above (e.g., Burov and Guillou-Frottier, 1999; Guillou-Frottier et al., 2000).

Despite the diverse opinions concerning the causes leading to a caldera collapse, it is broadly accepted that the main structure of these volcanic depressions consists of a set of concentric faults limiting a block of roof (Figure 1A). The structure of the latter may vary from coherent (e.g., Silali caldera; Mahood, 1984) to chaotic or fragmented (e.g., Somma Vesuvius calderas; Cioni et al., 1999). The concentric faults, also called ring faults, are defined as those structures through which roof subsidence takes place during the course of the caldera-forming episode. In theoretical rock mechanics terms, ring faults can be described as either dip-slip (normal or reverse) faults or as mixed-mode (extension and shear) propagating structures if there is magma flowing through them, i.e., dyke emplacement (Gudmundsson, 2007). Complementarily, later field observations, as well as analog and numerical experimental results, have demonstrated that oblique-slip faulting (dip- and strike-slip combined) may also occur during caldera collapses (Holohan et al., 2008, 2013).

FIGURE 1

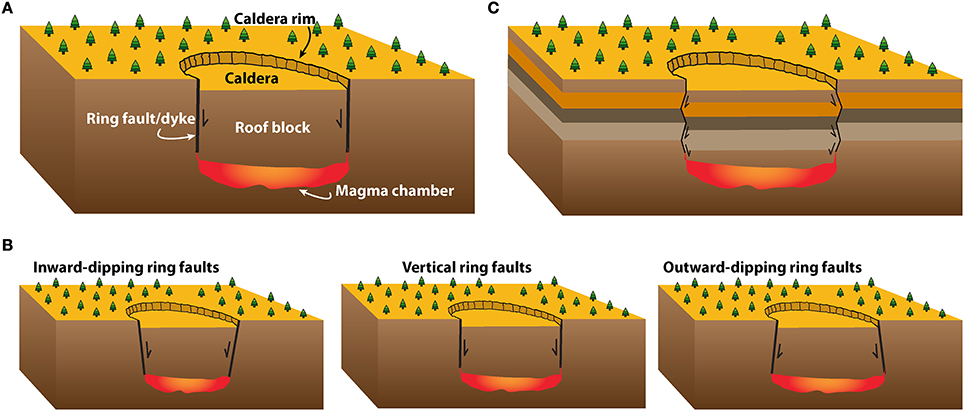
Figure 1. (A) Sketch of a circular collapse caldera. (B) Sketch of the different dip direction options for the outer normal ring faults. (C) Sudden changes in mechanical properties between layers in the host rock may favor outward- or inward-dipping ring fault segments in some layers but vertical in others (Modified from Gudmundsson, 2007).

Since direct information on calderas' deeper structure comes mainly from partially eroded calderas (e.g., Scafell, Branney and Kokelaar, 1994; Kokelaar et al., 2007; Glencoe, Moore and Kokelaar, 1997, 1998; Troll et al., 2000) or few witnessed and/or monitored collapses (e.g., Miyakejima, Geshi et al., 2002; Geshi, 2009; Piton de la Fournaise, Michon et al., 2007a,b; Michon and Saint-Ange, 2008; Rabaul, Mori and McKee, 1987; Sierra Negra, Jónsson et al., 2005; Jónsson, 2009), the layout of ring faults at depth remains still unclear. This has generated a strong debate over the complete internal fault and fracture configuration of a caldera collapse, and in more detail, how ring faults initiate and propagate.

Regarding ring fault initiation, from a theoretical point of view, two end-members can be distinguished: (i) at surface and propagating to deeper levels until impinging on the magma chamber or other structures, or (ii) from the magma chamber and propagating upwards until reaching the surface. Besides, ring faults have been variously described as normal inward-dipping, reverse outward-dipping or vertical, with existing field and geophysical evidences for any of the dip options and propagation directions (Acocella, 2007; Burchardt and Walter, 2010) (Figure 1B). Gudmundsson (2007) pointed out that, as shear fractures, ring faults make certain angles with the directions (trajectories) of the principal stresses and thus, their dip may vary from one layer to the next (Figure 1C). Also, from experimental studies, we know that formation of calderas imply the generation of several sets of concentric faults that combine to facilitate caldera collapse (e.g., Martí et al., 1994; Roche et al., 2000; Geyer et al., 2006; Acocella, 2007).

The nucleation spot (at surface or at depth) and dip direction (inward-, outward-dipping, or vertical) of ring faults have been differently described by analog and numerical models but with hardly any considerations about the direct implications and consequences. Certainly, the dip and propagation directions of ring faults have been demonstrated to be important parameters controlling the size of the resultant collapsed structure and its relationship to that of the underlying magma reservoir (e.g., Roche et al., 2000; Acocella, 2007; Martí et al., 2009), syn-collapse eruption locations (e.g., Geshi and Oikawa, 2008), magma chamber, and vent dynamics (e.g., Folch and Martí, 2009), and the distribution of post-caldera volcanism (e.g., Walker, 1984; Geyer and Martí, 2008), geothermal activity (e.g., Goeff and Gardner, 1994; Goff et al., 2000), and ore deposits (e.g., Guillou-Frottier et al., 2000; Stix et al., 2003).

We offer here a short description of the main results obtained by those analog and theoretical/mathematical models applied to the study of collapse caldera formation. We place special attention on those observations related to the nucleation and propagation of the collapse-controlling ring faults. For further detail, the reader is referred to the recent review by Acocella (2007), and the works by Gudmundsson (2007) and Martí et al. (2008), as well as the original papers cited here. We believe that the present summary is relevant to understand the current state-of-the-art of this topic and it should be taken under consideration in future works dealing with collapse caldera dynamics.

Studying Ring-Fault Formation: Insights from Analog and Numerical Results

Regardless of the nature of the experiments, analog, or numerical, it is possible to distinguish two main model groups depending on whether they consider the collapse to originate due to over- or underpressure inside the magma chamber. Strictly speaking, no analog experiments model caldera collapse due to magma chamber overpressure, only those depressions generated during periods of pre-collapse tumescence or pluton emplacement (Acocella, 2007) (Figure 2A). Since the resultant collapsed roof does not perturb the magma chamber in any sense, the developed depressions cannot be referred to as volcanic calderas. Therefore, most analog experiments on caldera collapse simulate situations in which magma chamber decompresses to achieve the condition to drive caldera subsidence. Very few experiments have considered the effect of inflation previous to deflation on the caldera collapse mechanisms (e.g., Martí et al., 1994; Acocella et al., 2000; Walter and Troll, 2001; Troll et al., 2002).

FIGURE 2

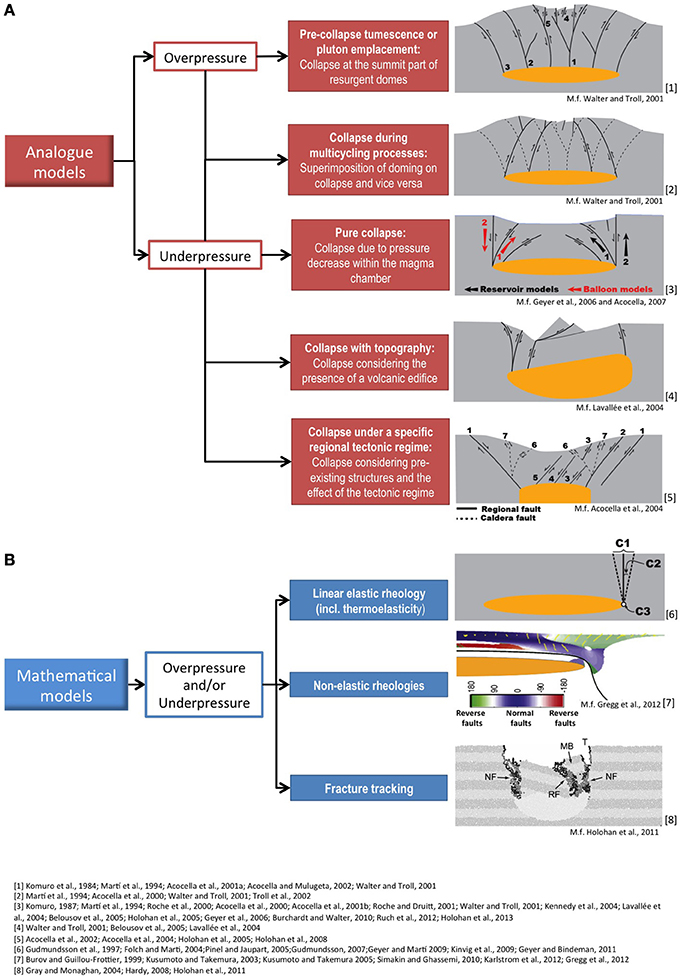
Figure 2. Summary of the different types of analog (A) and numerical (B) experiments carried out during the last decades focused to understand collapse caldera dynamics. M.f., Modified from Acocella et al. (2001a), Acocella and Mulugeta (2002).

Thus, from the analog experiments, we can differentiate two main groups: those that contemplate inflation of the magma chamber previous to its decompression and those that directly assume decompression (Figure 2A). Within analog models it is also possible to find those considering the effect of regional stress field or pre-existing structures (e.g., Acocella et al., 2004; Holohan et al., 2005, 2008) and of the presence of topography (e.g., Walter and Troll, 2001; Lavallée et al., 2004; Belousov et al., 2005) (Figure 2A). Finally, there are also some experiments studying the collapse dynamics during multiple cycles of tumescence and collapse (e.g., Martí et al., 1994; Acocella et al., 2000; Walter and Troll, 2001; Troll et al., 2002) (Figure 2A).

Briefly, in all analog experiments complete collapse consistently gives two sets of ring structures (Figure 2A) (Acocella, 2007): inner outward dipping reverse ring faults and, after a certain subsidence, outer inward dipping to subvertical normal ring fault. Acocella (2007) indicated that the amount of faults mainly depends on whether the reservoir is flat or domed. In the first case, the nucleation of a single pair (reverse + normal) of ring faults is enhanced. In the second, strain may accumulate also at the points of maximum curvature of the reservoir, generating additional ring faults (Acocella, 2007). Other subsidence-related secondary structures include, for example, concentric tensile fractures and fissures, minor concentric normal (outward- or inward-dipping) faults, etc. (e.g., Roche et al., 2000; Geyer et al., 2006; Holohan et al., 2013).

Among all analog models simulating a pure collapse process (with no regional stress field, topography, or external surface load), there seems to be a consistency in the dip and propagation direction of the internal outward-dipping reverse faults, which would nucleate at the magma chamber borders and propagate upwards (Burchardt and Walter, 2010) (Figure 3A, 1 and 2). However, this is not the case of the outer normal ring faults, for which these experiments present inconsistent results regarding dip and propagation directions (Table 1). Table 1 is a complemented and modified version of the one provided by Burchardt and Walter (2010). Although quite comprehensive, their table presented some debatable data such as the description of the normal fault propagation for Martí et al. (1994) and Hardy (2008). These disagreements may be probably related to fact that all generated structures during the collapse are interpreted as normal faults.

FIGURE 3

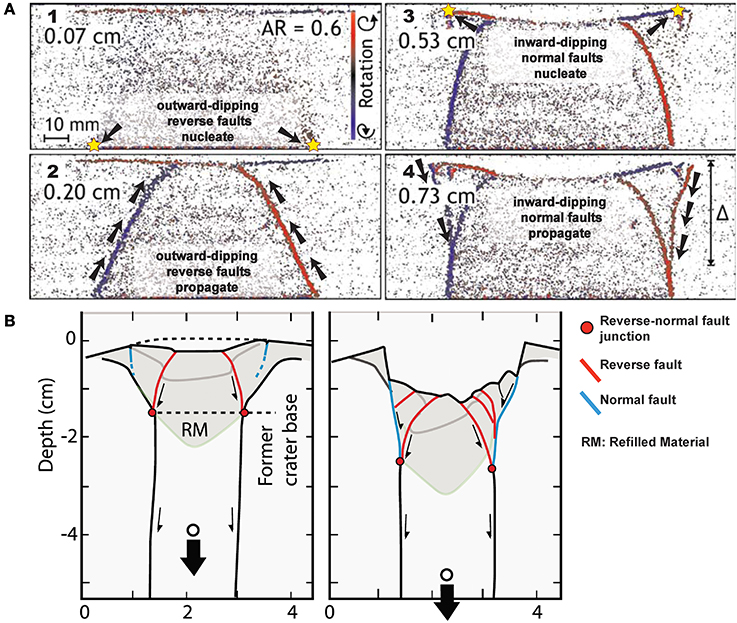
Figure 3. (A) Sequence of pictures of 2D_15-110 experiment by Burchardt and Walter (2010) with a magma chamber depth/width ratio of 0.6. The collapse starts with the nucleation at depth of the outward dipping reverse faults (1), which propagate upwards as subsidence continues (2). Inward dipping normal faults nucleate at surface (3) and then propagate downward and link with the reverse faults at depth Δ = 4.39 cm (4). Subsidence in cm and rotation of individual particles relative to their previous position are also indicated (Modified from Burchardt and Walter, 2010). Stars indicate nucleation points of faults. (B) Sketch of the CAL12B experiment by Ruch et al. (2012) (Modified from Ruch et al., 2012).

TABLE 1

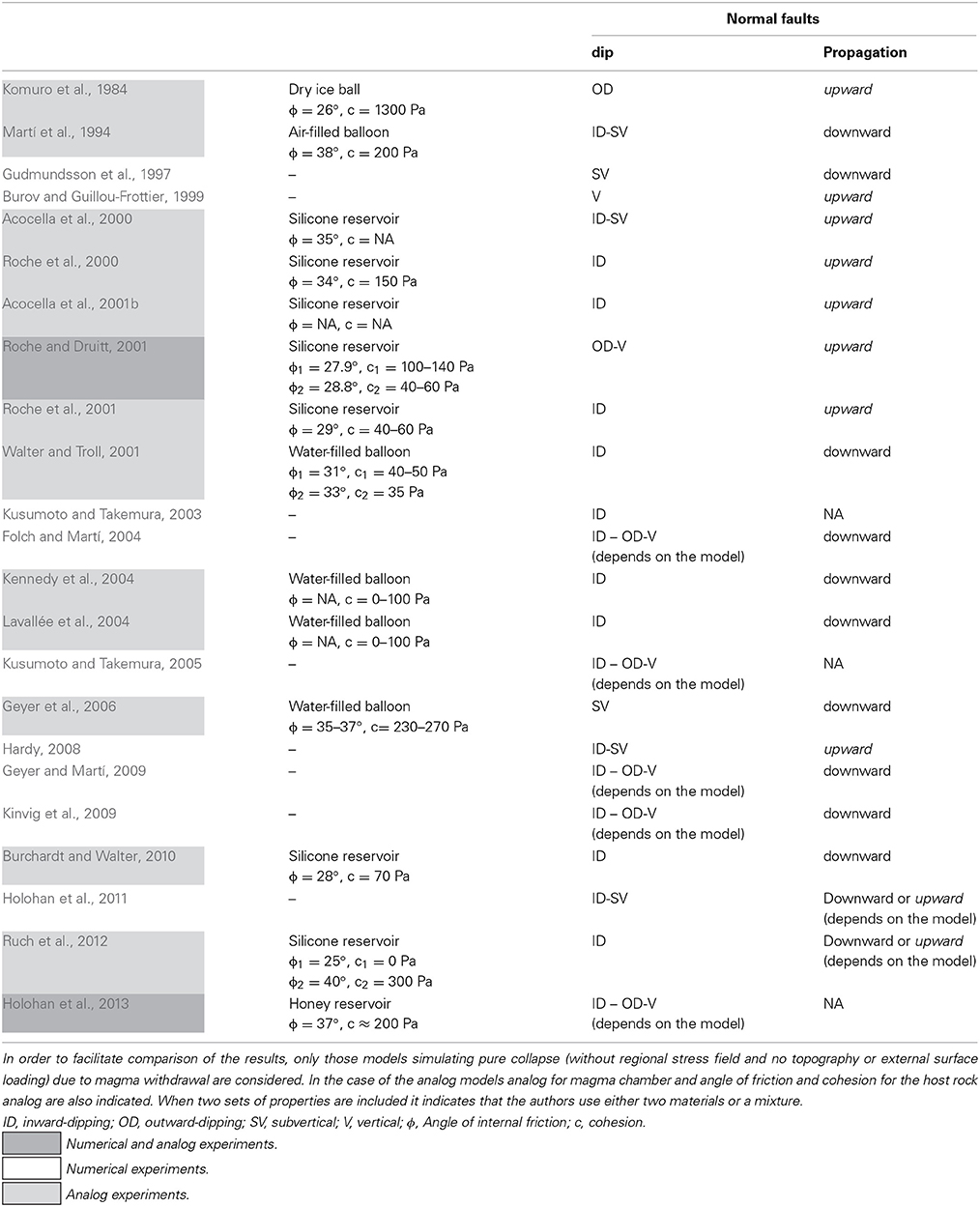
Table 1. Summary of those experimental (analog and numerical) works focused on understanding collapse caldera dynamics and internal structure.

One may be tempted to think that this inconsistency between the different analog models results is related to the specific experimental set-up and analog materials applied, i.e., to the mechanical properties of the host rock analog material or the chosen magma chamber analog, which can be a water- or air-filled balloon (Walter and Troll, 2001; Troll et al., 2002; Kennedy et al., 2004; Lavallée et al., 2004; Belousov et al., 2005; Holohan et al., 2005; Geyer et al., 2006), a silicone putty or honey reservoir (Acocella et al., 2000, 2001b, 2004; Holohan et al., 2008, 2013; Burchardt and Walter, 2010; Ruch et al., 2012), or others (Komuro et al., 1984; Komuro, 1987). Indeed, there seems to be a consensus among the results when distinguishing between silicone reservoir and balloon experiments. Thus, in those models with a silicone reservoir as magma chamber analog, the outer normal faults tend to nucleate at the reservoir margins and propagate upwards, whereas in the case of those experiments using a water- or air-filled balloon, these faults seem to nucleate at surface and propagate downwards (Figure 2A). Nonetheless, the results by Burchardt and Walter (2010) and Ruch et al. (2012) show contrary behaviors (Table 1). In the first case, the authors observe, even using a silicone reservoir, how the outer normal faults initiate at surface and propagate downwards connecting with the reverse faults at depth (Figure 3A, 3 and 4). Similar results are obtained by Ruch et al. (2012), with the only difference that their inward dipping normal faults nucleate instead at very shallow levels and propagate upwards until reaching the surface. Contrarily, for those experiments reproducing a caldera sequence after refilling a previous collapsed structure, normal faults start at surface (as open fractures) and propagate downward along the boundary between the former crater and the refilled material (Figure 3B) (Ruch et al., 2012). These authors propose that variations in the dip angles for the faults (specially the reverse ones) are related to changes in the applied material cohesion, the roof aspect ratio (i.e., magma chamber depth/width ratio) and the presence of pre-existing fractures.

Thus, variations seen in the analog model results may be due to a combination of the selected set-up for the magma chamber analog, if this is representing a flat or a domed reservoir (Acocella, 2007), the material properties (grain-size, cohesion, angle of internal friction, density) of the chosen host rock analog, the roof aspect ratio and other variables such as pre-existing fractures, etc. To which extent each of these parameters influences dip and propagation direction of the inner reverse and outer normal faults is a question that remains open and needs a more careful analysis.

The main restriction of analog models is that available materials and the accuracy of the method itself do not allow simulating other processes: (a) the real relationship between the mechanical properties of the different existing depositional units conforming the host rock, (b) the thermal gradient implicit in the crust and the magma chamber related thermal effects, and (c) the injection of magma into the generated fractures. Concerning the thermal effects, as already pointed out by Holohan et al. (2005) and Acocella (2007), the crust immediately around the magma chamber is subjected to very high temperatures, which could locally induce ductile behavior. By contrast, in the current analog models, all the crust is considered to behave in a brittle manner. Holohan et al. (2005) argued that local strain rates involved in magma chamber inflation and deflation are typically very high and would favor brittle deformation. Nonetheless, currently, it is not possible to assess via analog experiments whether the existence of a thermal profile, the contrasting rock properties between layers or the injection of magma into the generated fractures would influence or not the results obtained in terms of ring fault nucleation, orientation and propagation.

A further constrain of analog experiments is that, until now, it is impossible to model the injection and flow of magma through the generated ring faults. On the one hand, those experimental set-ups using balloons (filled either with water or air) as magma chamber analogs will never capable to do so. On the other, honey or silicone putties are too viscous to intrude the faults and fractures generated during the experimental collapse and if so, properly scaling of the intrusion velocity, as well as other time-dependent variables may certainly be a challenging task.

Despite these restrictions, it has been repeatedly mentioned in the literature that existing analog models tend to accurately reproduce the collapse of basaltic calderas (e.g., Acocella, 2007; Burchardt and Walter, 2010; Holohan et al., 2013). These may be commonly related to quite homogeneous volcanic edifices without important contrasting mechanical properties between layers (Gudmundsson, 2009) and in most occasions, magma withdrawal takes place through lateral eruptions with consequently, hardly or no magma flowing through the generated subsidence controlling faults (e.g., Miyakejima, Geshi et al., 2002; Geshi, 2009; Piton de la Fournaise, Michon et al., 2007a,b; Michon and Saint-Ange, 2008). Thus, it seems that in these cases of passive foundering of the caldera block, analog models may be a good approximation of the processes occurring in nature. So, analog experiments have been successfully applied to provide full comprehension of the kinematics and timing of ring fault evolution in recently formed collapse calderas such as Miyakejima (Geshi et al., 2002; Geshi, 2009) or Dolomieu caldera at the summit of Piton de la Fournaise volcano (Michon et al., 2007a,b; Michon and Saint-Ange, 2008). Experimental results obtained have helped explaining and understanding field observations, geophysical and monitoring data recorded during these recent collapse events, as well as their geometry and structural relationships (e.g., Acocella, 2007; Burchardt and Walter, 2010; Holohan et al., 2013). Moreover, analog models have also been applied to understand the origin and evolution of some well-known (not necessarily basaltic in composition) nested calderas (e.g., Latera and Tavua calderas, Acocella et al., 2001b; Las Cañadas caldera, Martí and Gudmundsson, 2000) and the influence of active tectonic settings on the final collapse structure and geometry (e.g., Long Valley, Acocella et al., 2004; Taupo, Holohan et al., 2005). However, an important aspect still remains unclear, how do analog models manage to explain the genesis, evolution and structure of silicic calderas? Even if some aspects such as the geometry of some nested calderas may be partially explained through analog experiments, to study silicic calderas it is necessary to deal with the following aspects: (i) they occur in really heterogeneous and long-lived volcanic edifices (i.e., presenting pre-existing structures), (ii) they are normally linked to a complex pre-caldera evolution of the associated magma chamber, which may involve important processes of thermal heating of the host rock, and (iii) ring faults act commonly as eruptive vents during the caldera-forming eruption (i.e., magma flows through the ring faults) (Folch and Martí, 2009). Considering these observations and the abovementioned intrinsic restrictions, it is clear that in order to investigate trough analog models the silicic calderas, some limitations of the experimental set-ups have to be overcome.

Several theoretical/mathematical models have been developed in the last decades, in an attempt to go a step further on the understanding on collapse calderas dynamics and to deal with the restrictions of analog experiments. Ideally, modeling of collapse calderas formation should consider those physical processes occurring inside and outside the magma reservoir. Nevertheless, our understanding of this “fluid-structure” interaction (i.e., coupling between rock mechanics and fluid dynamics) is far from complete. For simplification, models tend to deal with only a part of the problem (chamber or surrounding rocks) at a time, i.e., to focus on one domain and incorporate simplistically the effect of the other (Martí et al., 2008). In this sense, theoretical models on collapse calderas formation can be classified in two main groups: (i) models based on thermodynamics and fluid mechanics that aim to quantify processes occurring inside the chamber prior to and during collapse, i.e., the evolution of pressure within the magma reservoir (e.g., Martí et al., 2000; Folch and Martí, 2009); and (ii) models based on solid mechanics, exploring processes occurring in the host rock, i.e., formation of fractures and faults (e.g., Gudmundsson, 1998; Burov and Guillou-Frottier, 1999; Holohan et al., 2011). For the present work, our interest mainly focuses on this last group.

Concerning the models based on solid mechanics, it is possible to distinguish three subgroups (Figure 2B). The first one, the most extended in terms of number of published works, assumes elasticity (and/or thermoelasticity) to account for the host rock rheology and an empty “over- or under-pressurized” cavity representing the “inflating” or “deflating” magma chamber (Figure 2B). This set of models studies the stress distribution around the magmatic reservoir and the roof rock in order to estimate the position where ring faults could nucleate due to the verification of specific critical conditions explain below (Gudmundsson, 2007 and references therein). A subsequent group of models predicts fault location using non-elastic rheologies (e.g., Burov and Guillou-Frottier, 1999; Guillou-Frottier et al., 2000; Kusumoto and Takemura, 2003, 2005; Simakin and Ghassemi, 2010; Gregg et al., 2012; Karlstrom et al., 2012) and finally, the third group comprises discontinuum-based numerical approaches focus on “tracking” the exact position of the faults as, for example, the smoothed particle hydrodynamics (SPH) method (Gray and Monaghan, 2004) or the discrete (Hardy, 2008) or distinct element method (Holohan et al., 2011).

Most of the models dedicated on studying the stress distribution around the magma chamber and the roof rock assuming elastic or thermoelastic rheology for the host rock (except those by Holohan et al., 2013), are based on the premise that, from a theoretical point of view, ring faults, as shear fractures, cannot form or slip unless the stress field satisfies three conditions simultaneously (Gudmundsson et al., 1997; Gudmundsson, 1998; Folch and Martí, 2004) (Figure 4): (C1) The minimum value of compressive stress (σ₃), i.e., the maximum tension, must occur at the Earth's surface, (C2) The maximum value of shear stress (σ₁ − σ₃) must occur at the lateral margins of the magma chamber, and (C3) The maximum tension (minimum σ₃) at surface, must peak approximately above the lateral ends of the magma chamber. These conditions allow ring faults to initiate at surface by tension and then propagate to greater depths changing into shear fractures or normal-faults toward the boundary of the magma chamber (Gudmundsson, 2007). The nucleation point is assumed to occur at surface by tension since the authors undertake that the initiation of the ring faults at depth would lead to dike injection. Additionally, Folch and Martí (2004) assumed C3 condition to be verified if the angle α (Figure 4) is in the range or lower than 10–15°, i.e., when the absolute minimum value of σ₃ peaks at the Earth's surface at a certain radial distance approximately equal to the horizontal extension of the chamber plus minus h_max (Figure 4).

FIGURE 4

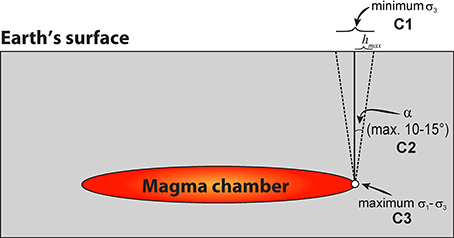
Figure 4. As discussed in the text, the formation of subvertical normal ring-faults is encouraged if critical conditions [C1] to [C3] are simultaneously satisfied; that is when [C1] the absolute minimum of σ₃ is at the surface, [C2] the maximum shear stress concentrates at the margins of the magma chamber, and [C3] the maximum tension (minimum σ₃) at surface, must peak approximately above the lateral ends of the magma chamber.

There exist a considerable amount of research works based on stress field computations assuming linear elasticity. They have analyzed distinct collapse scenarios defined by different loading conditions (e.g., magma chamber overpressure or underpressure, regional tectonic stresses, topographic loading/unloading) (e.g., Acocella et al., 2002; Folch and Martí, 2004; Pinel and Jaupart, 2005; Gudmundsson, 2007; Geyer and Martí, 2009; Geyer and Bindeman, 2011; Holohan et al., 2013), geometrical configurations of the magmatic system (magma chamber shape/depth relationship) (e.g., Gudmundsson et al., 1997; Folch and Martí, 2004), mechanical properties of the surrounding media (e.g., Gudmundsson, 2007; Geyer and Martí, 2009; Kinvig et al., 2009) and the existence of faults or other structures (e.g., Simakin and Ghassemi, 2010). All these models study the effect of the abovementioned factors in the resultant stress field and evaluate if the latter favors or not ring fault generation. The main inconvenient is that most of these models do not provide information about the outward- or inward-dipping style of the ring faults (Table 1). They just assume that within the α = 10°–15° range, the normal faults may be subvertical to steeply outward- or inward-dipping. Also, it is important to remark that elastic models are only able to detect the location of the first fractures that may appear due to deformation. However, they are not capable of tracking all appearing structures. Therefore, they do not provide much information concerning the internal structure of caldera collapses.

Important distinction has to be made to the recent work by Holohan et al. (2013), which comprises, to the authors' knowledge, the first numerical models in 3D studying the stress field distribution around a magma chamber that may lead to the initiation of a caldera collapse assuming an underpressurized reservoir. Even if their continuum-based approach without plasticity is unable to directly simulate fracture development, it offers a first-order prediction of fracturing in the initial stages of a brittle deformation process. The authors estimate the locations, orientations, and modes of potential fractures by comparing the calculated stresses to an appropriate failure criterion (Holohan et al., 2013). For the first time and thanks to the use of a 3D geometry, these authors have been able to reproduced the existence of the oblique-faulting during caldera collapse processes as already observed in natural examples (e.g., Miyakejima and Dolomieu, Holohan et al., 2013). Definitely, their models represent a first step toward outlining the 3D nature of faulting in roofs above magma chambers.

As mentioned, a further group of numerical models have addressed the problem applying other rheologies such as viscoelasticity assuming a linear Maxwell model (e.g., Simakin and Ghassemi, 2010; Gregg et al., 2012). Probably, the most relevant results of all models comprised in this subgroup are those recently obtained by Gregg et al. (2012). These authors investigate, using temperature-dependent viscoelastic rheologies, how caldera collapses may be initiated depending on their roof aspect ratio and size (i.e., volume), either directly due to deflation of the magma chamber because the rapid withdrawal of magma during the course of an eruption or by breaking of the magma chamber roof due to overpressure inside the magma chamber. In summary, small reservoirs (<10² km³) would lead to more frequent and small eruptions, which would eventually lead to a caldera collapse due to magma chamber deflation. In the case of medium-sized magma chambers (10²–10⁴ km³), the temperature-dependence of the viscoelastic host rock inhibits failure at the magma chamber boundary and hence dyke formation. This conclusion is agreement with previous results by Jellinek and de Paolo (2003), who proposed that prolonged heating of country rocks produces a shell of viscoelastic material that may undergo viscous creep on the timescale of chamber pressurization, relaxing away deviatoric stresses in the country rocks responsible for fracture and dyke generation. Finally, for larger magma chambers (>10⁴ km³), modest pressure increases within the magma reservoir result in significant pre-eruption uplift. The latter generates through-going faults within the crust, which may trigger an eruption by rupturing the magma chamber margin. Related to this last point, it is also worth mentioning here the numerical results obtained by Caricchi et al. (2014), which indicate that large volcanic eruptions are triggered by an increase in magma buoyancy as opposed to a rise in overpressure directly provoked by, for example, magma recharge.

Similarly to the analog models results, the roof aspect ratio seems to be a primary parameter controlling the mechanical failure of the roof. Gregg et al. (2012) indicated that for high roof aspect ratios (>2) eruption is likely triggered from the magma chamber boundary since the roof block is sufficiently thick and remains stable up to large applied overpressures. By contrast, large volume and low aspect ratio systems are most likely triggered due to fault propagation in the overlying roof.

Regarding the models tracking fault propagation (Gray and Monaghan, 2004; Hardy, 2008; Holohan et al., 2011). Holohan et al. (2011), probably offers the most sophisticated one, where results obtained clearly demonstrate that the shape of the reservoir and the material properties play an important role in the resultant structures (Figure 5). This would explain the existing differences between the various analog models related to the diverse magma chamber and host rock analog materials and set-ups. The authors state that because faults represent discontinuities, their development is difficult or impossible to accurately simulate in continuum-based methods as applied in all the different models in the previous subgroups. The latter, as mentioned before, are typically valid only until the point of fracture, so they can only estimate (from calculated stress patterns and via certain failure criteria assumptions) the geometry and mode of initial faults. The study by Holohan et al. (2011) complements and improves the one by Hardy (2008) since they are able to test the effects of a range of strengths and elastic properties typical of natural rock masses and use a more realistic definition of the magma reservoir and their depletion due to magma chamber withdrawal.

FIGURE 5

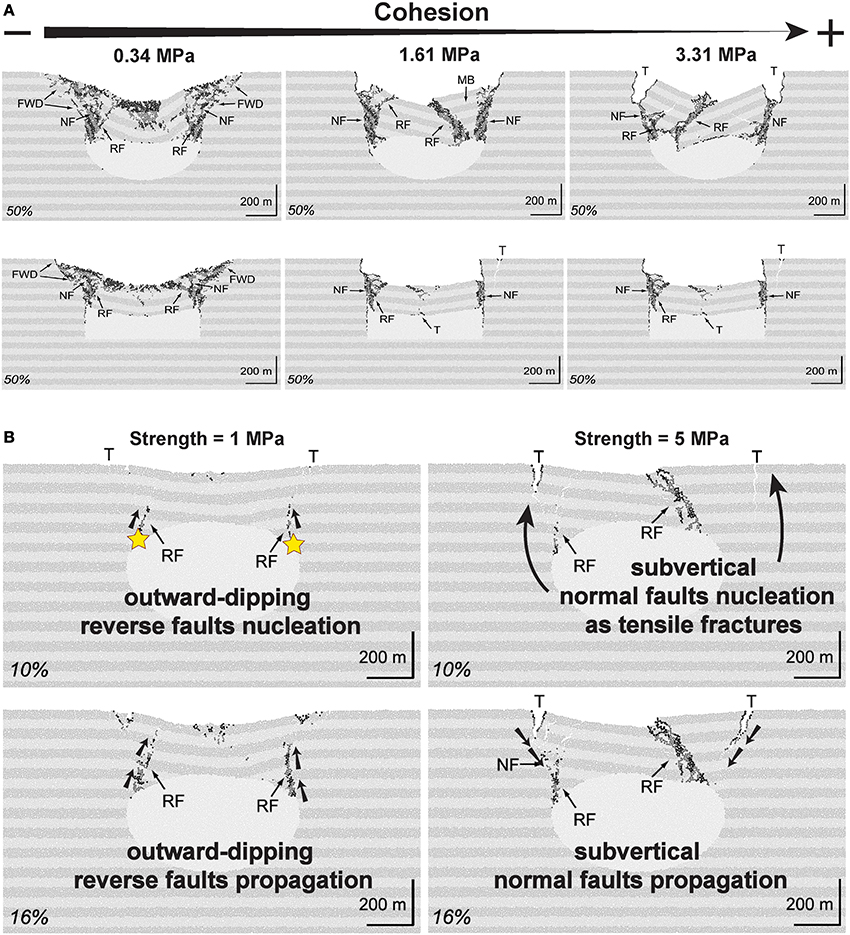
Figure 5. (A) Snap-shots of the reservoir roof collapses for both an elliptical domed-roofed and a rectangular flat-roofed reservoir and for different host rock strengths. (B) Snap-shots of the reservoir roof collapses for a roof aspect ratio of 0.27. Young's modulus is ~1 GPa; Poisson's ratio is ~0.25. Horizontal layering (only superficial) is only for visualization purposes and does not imply any changes in the material properties. Shaded particles indicate strain localization. The proportion (in percentage) of withdrawn reservoir material is also included. T, tensile cracks or fissures; RF, reverse fault; NF, normal fault; MB, marginal bench; FWD, footwall detachment surfaces (normal faults at lower angle than initial marginal normal fault and cutting through the latter's footwall). Stars indicate nucleation points of faults (Modified from Holohan et al., 2011).

Results obtained by Holohan et al. (2011) indicate that the main structural features occurring during the simulated caldera collapse are principally influenced by the geometry of the reservoir, the roof aspect ratio and the bulk properties of the discrete elements conforming the host rock computational domain. These bulk properties, expressed in particle Young's modulus and bond strength, can be translated into real rock mass properties given as Young's modulus, unconfined compressive and tensile strength and cohesion. Thus, the resultant collapse dynamics appears to be controlled by a trade-off between the abovementioned parameters (Figure 5). For example, for a given Young's modulus, the switch of subsidence style from single central block to multiple central blocks is governed mainly by the roof's strength and aspect ratio. Thus, for example, less cohesive but with high Young's modulus models retain the single central block style to higher roof aspect ratio values. By contrast, multiple central block failure style is favored when the roof is of intermediate- high thickness, of medium-high strength, and of low E. Additionally, according to Holohan et al. (2011), regardless of roof geometry or material properties, inward inclined normal faults typically form in the later stages of subsidence. These steeply dipping normal faults accommodate part of the roof's vertical displacement and the horizontal extension component induced by the central shortening of the roof.

Even if the results by Gregg et al. (2012) or Holohan et al. (2011, 2013) provide new and important insights into caldera systems, several additional factors remain unstudied mainly because the intrinsic restrictions of the numerical models. Particularly important is the lack of coupled models that are able to investigate simultaneously the processes occurring inside the magma chamber and in the overlying roof block. Significant limitations may arise also when trying to simulate the effect of regional tectonic stresses and pre-existing faults, or the flow of magma through the newly formed collapse structures once these have reached (or nucleate at) the reservoir boundary. Furthermore, from the methodological point of view, there is a need to evaluate the advantages and drawbacks of both possible numerical approaches: discontinuum- or continuum-based. In the first case, similarly to analog models, it is possible to directly simulate fracture development and pattern. By contrast, a continuum-based approach is only able to provide a first-order prediction of fracturing in the preliminary stages of a brittle deformation (Holohan et al., 2013).

Some Considerations and Future Works

From the summary above, and as already indicated by Acocella (2007), is clear that there are similarities and discrepancies when comparing the existing analog and numerical results. In both cases, results obtained are conditioned to the imposed boundary and initial conditions (or experimental set-up), as well as the mechanical and thermal properties of both host rock (analog) and magma chamber (analog). Acocella (2007) state that whereas some numerical results are in agreement with the underpressure analog experiments (e.g., Kusumoto and Takemura, 2003, 2005) others may be in partial or total disagreement (e.g., Gudmundsson et al., 1997; Gray and Monaghan, 2004). The author infers that the main discrepancies, specially on the normal faults, may be due to some conditions imposed in the models such as simulating the magma chamber using a cavity, the elastic rheology for the host rock or the use of sill-like geometries. So, there is no apparent consensus between the analog and the numerical results (Table 1). Different methodologies, i.e., boundary and initial conditions as well as the selected type of reservoir and host rock, mechanical properties, heterogeneities, etc. may play a fundamental role in the results obtained.

As explained before, basaltic calderas are apparently the most similar, structurally and cinematically, to some exiting numerical and analog results. Indeed, as explained by Holohan et al. (2011), different subsidence styles at Fernandina, Dolomieu, and Miyakejima are compatible to various levels with those produced in their models. The dissimilarities between all three collapses can be related to distinctive combinations of the magma chamber roof aspect ratio and mechanical properties of the rock (Holohan et al., 2011). However, a different situation is to be expected for silicic calderas. In these cases, some aspects such as the potential size of the underlying reservoir, the possible heterogeneities of the magma chamber roof (the latter translated as different mechanical properties) or the fact that the caldera-forming eruptions tend to take place along the ring faults (i.e., magma flows through the generated collapse structures) may lead to considerable differences in their collapse dynamics. Thus, the first question to be answered here is if the structures described in the analog and discontinuum-based models are, or not, capable of transporting magma.

According to Burchardt and Walter (2010) magma transport within upward-propagating ring faults is possible from the initial stages of subsidence. However, magma transport along the initial ring faults may become constrained due to their closure. At the contrary, the downward-propagating outer ring faults can only act as magma feeders if they link to the magma bearing reverse faults at depth or they reach the magma chamber. Therefore, the temporal variability of the ring faults during subsidence implies that the location of conduits is also temporally variable (c.f. Burchardt and Walter, 2010). Nonetheless, if the outer normal faults nucleate at the magma chamber margins as indicated by some analog models (Table 1), they would be potentially able to transport magma to the surface.

However, if there is magma injection into the reverse faults (or eventually into the normal faults) at the very beginning of the caldera collapse, how does it affect the whole collapse dynamics? Is the collapse expected to develop similarly to the analog models results? On the one hand, the development of a dyke intrusion leads to rapid decompression in the magma chamber, which may prevent further propagation of the dyke tip (Cañón-Tapia and Merle, 2006). Nevertheless, the larger the chamber volume with respect to the dyke scale volume is, the more negligible a withdrawal of magma is in terms of variations in magma flow rate and reservoir overpressure (cf. Traversa et al., 2010). Additionally, according to the works by Gregg et al. (2012) and Jellinek and de Paolo (2003), the prolonged heating of the rocks around the magma chamber would prevent fracture initiation from it. Nevertheless, according to the current analog experiments and some numerical results (Hardy, 2008; Holohan et al., 2011), this is the theoretical nucleation point of the inner reverse faults.

A further partially unsolved topic is whether the outer normal ring faults are outward- or inward-dipping. It is starting to become quite clear that their dip direction is strongly controlled by the mechanical properties of the host rock (Gudmundsson, 2007; Holohan et al., 2011), which would explain why the different experimental set-ups in terms of cohesion, angle of internal friction, grain-size, etc. of the host rock analog, would show distinctive results (Table 1). Concerning the nucleation point, no apparent correlation exists between the experimental set-up (including both magma chamber and host rock analog) and the results obtained.

Thus, although much has been done so far, some crucial aspects of collapse calderas still remain unclear. Here we have presented how the different analog models tend to show diverse behaviors related to normal fault propagation and nucleation. It may be plausible that the obtained differences are related to the mechanical properties of the applied host rock analog material, and that the controlling parameters and the cause–effect relationship are not clear at first sight. Other factors such as the selected magma chamber analog, its geometry (flat or domed), the roof aspect ratio or pre-existing fractures, also lead to variations in the analog results. Further investigations and a more meticulous analysis may be needed around this topic. In order to figure out the extent to which the material properties or the experimental set-up control the collapse dynamics and final structure, a parametric and detailed study should be carried out similar to the one performed numerically by Holohan et al. (2011). Authors and research groups defending analog experiments over numerical ones, should clearly understand that the limitations of the first may prevent understanding the whole caldera collapse process since thermal effects and magma injection do not seem to be aspects ease to handle. Analog models have been demonstrated to be fundamental to understand the three-dimensional geometry and evolution of collapse calderas, as shown by the remarkable correspondences between existing analog model results and natural calderas (e.g., Acocella, 2007; Holohan et al., 2013). Despite the great amount of results already provided by the existing analog experiments, further research is needed in this direction specially to develop experimental set-ups that may overcome the restrictions of current ones. Therefore, much effort is required to be able to simulate, for example, mechanical heterogeneities within the host rock analog or thermal effects due to the magma chamber reservoir. However, it is obvious that until now, analog experiments have been a much more convenient tool to visualize fracture propagation and structures than most numerical models.

Indeed, much more numerical work is needed to merge the advances done by Gregg et al. (2012) and Holohan et al. (2011). Combining the Gregg et al. (2012) model with the methodology of Holohan et al. (2011), i.e., discontinuum-based models with thermal effects, is still a model to be developed under the framework of collapse caldera studies. Additionally, there is still a step missing, coupling host rock deformation with the fluid dynamics, i.e., simulating the dynamic inside the magma chamber once the roof starts to disrupt the reservoir and also the influence of magma injection through the fractures and faults generated during the collapse. Thus, future works should put an effort in overcoming the restrictions presented above for the analog models or the numerical approximations, which day by day allow more complex multiphysics interaction. See for example how numerical models on collapse calderas have considerably improve since the review by Acocella (2007). The new fracture tracking models allow the perfect reproduction of some analog results (Hardy, 2008) in terms of fracture patter and propagation and also to figure out which key parameters no reproducible with the analog models may play an important role.

In summary, all the models, analog, and mathematical, that exist today on the formation and dynamics of collapse calderas, provide good insights on such processes, particularly if we take into account their complexity. However, when comparing these models together we observe that there may be significant differences offering contrasting results, which in turn, complicate adopting a position in favor of one or another. Maybe the best agreement is found between analog models and basaltic calderas where collapse seems to follow passively the lateral withdrawal of the magma chamber. However, we are still far from really understanding the mechanics of explosive silicic calderas. The current impossibly of simulating both experimentally and mathematically such complex eruptions prevent the provision of precise answers to the pending questions. Also, the scarcity of good natural examples where field relationships informing on the formation of ring faults and ring dikes can be observed imposes a significant restriction on the study of the formation of such caldera systems. Natural examples offer a photo-finish of some parts of the structure but hardly provide insights of their dynamics, which restrict the potential conclusions we can extract from their study and may occasionally lead to their over interpretation. In addition to these restrictions, it is worth mentioning that the rheological behavior of the host rock during caldera collapse is still not well constrained. All the theoretical studies we have reviewed in this paper refer to the pre-caldera behavior, including how magma chambers form, grow and fracture, this having proposed to occur under many different rheologies (elastic, thermoelastic, plastic). These processes occur over time lengths of thousands to hundreds of thousands of years, which imply very slow strain rates. However, caldera collapse may occur in a few hours or few days, thus changing completely the strain rate and, consequently, the behavior of the host rock. How this will affect the dynamics of the ring faults, in particular when magma flows through them, is not known although it constitutes one of the main problems. Therefore, future studies on the formation of collapse caldera structures through mathematical and analog modeling should aim at finding a successful solution to couple solid mechanics (host rock) and fluid dynamics (magma), considering the different time scales involved in the whole process, and taking advantage of the information provided from deeply eroded calderas and from the products of younger calderas, as well as from fossil magma chambers and their host rocks.

As a final remark, due to their distinct advantages and limitations, analog, and numerical models have resulted to be complementary tools when studying collapse calderas. Whereas the first have allowed visualizing and studying in a qualitative or semi-quantitative way the process, numerical results permit quantifying it and the development of parametric studies. Therefore, future improvements in each of the individual methodologies will have consequently a positive feedback on the other and in any case, both will progress with new incoming field, geophysical, monitoring, and remote sensing data.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Adelina Geyer is grateful for her Juan de la Cierva post-doctoral grant (JCI-2010-06092) and her Ramón y Cajal contract (RYC-2012-11024). We thank the Associated Editor Agust Gudmundsson and two anonymous reviewers for their comments that help to improve an earlier version of the manuscript.

References

Acocella, V. (2007). Understanding caldera structure and development: an overview of analogue models compared to natural calderas. Earth Sci. Rev. 85, 125–160. doi: 10.1016/j.earscirev.2007.08.004