- 1Department of Earth Science and Engineering, Imperial College London, London, UK
- 2Research School of Earth Sciences, The Australian National University, Canberra, ACT, Australia
Using erratics associated with large flood events, this paper assesses whether their viscous remanent magnetisation (VRM) can be used to date the flood events. We tested this method using flood erratics from three large events: (1) the Late Pleistocene Bonneville mega-flood in Idaho, USA, (~14–18 ka), (2) the 1918 A.D. Mt. Katla, Iceland, eruption and associated jökulhaup (meltwater flood) at Mýrdalssandur, and (3) the Markarfljót jökulhaup due to an earlier eruption of Mt. Katla (~2.5 ka). We measured 236 specimens, 66 of which yielded clear identifiable and measurable viscous magnetisation signals from erratics with clustered VRM directions. From the VRM unblocking temperatures, age estimates were made. The age estimate for the most recent event (Mýrdalssandur) worked well, with a median estimated age of 80 years (with individual erratic estimates distributed between 61–105 years) compared to the known age of 91 years. The ages of the other two events were over-estimated. The estimates for Markarfljót [15 ka (7–33 ka)] were based on the results of just one erratic. For the Bonneville flood the estimates were too old, however, this locality had the largest uncertainty in the ambient temperature used in the age determination; the VRM acquired is strongly dependent on the ambient temperature, the older the event the greater the uncertainty. Southern Idaho currently has hot summers, with average summer maximum temperatures of ~31°C, but a mean annual temperature of only ~ 9°C. It is suggested that the VRM dating method works best for recent events (<2–3 ka) where the ambient temperature history can be constrained.
Introduction
If a magnetic-mineral bearing rock is moved or re-oriented, the magnetisation of the smaller magnetic grains slowly re-aligns to the direction of the ambient magnetic field direction due to thermal fluctuations. This secondary magnetisation is termed viscous remanent magnetisation (VRM), and is logarithmically time dependent (Dunlop, 1973, 1983). This time-dependency of the intensity of the VRM, has been applied successfully to the dating of archeological events (e.g., Heller and Markert, 1973; Borradaile, 1996, 2003; Borradaile et al., 1999), however, this same method has not been used in widely in geological studies (i.e., Borradaile, 1998; Sato et al., 2014).
The VRM dating method can be used to date any geological event that results in a significant and sudden movement/rotation of a rock, with no significant subsequent movement. One such scenario are large erratics moved during a flood, i.e., if the VRM acquired by flood erratics can be isolated it is possible to date the flood event (Figure 1). Another is rock-slides and cliff slumps, e.g., Borradaile (1998) used VRM dating to examine cliff-slumps on the east coast of England. The advantage of this approach over other potential methods is that the VRM is an intrinsic property of the rock and is not dependent on features like snow coverage, e.g., annual exposure rates for cosmogenic dating, nor it is dependent on the presence of any other material, e.g., organic material in the case of radiocarbon dating.
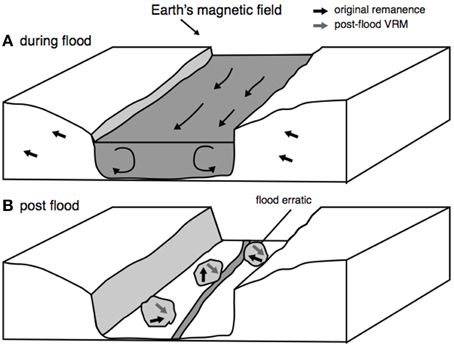
Figure 1. A schematic of VRM acquisition. (A) Before the flood, the bedrock records an original remanence, e.g., a thermoremanence for a basaltic lava, aligned with an ancient magnetic field direction (this could be reversed as depicted). During the flood the bedrock is eroded from canyon walls and boulders are transported downstream. (B) Post-flood erratics deposited on the flood plain remain in situ and acquire a younger VRM parallel to the Earth's magnetic field; the original magnetisation vectors are left randomly orientated.
This paper presents a preliminary investigation into the use of VRM dating to determine the age of geologic events. We tested this method on two independently dated floods: (1) the Late Pleistocene Bonneville mega-flood in Idaho, USA, (~14–18 ka), and (2) the 1918 AD Mt. Katla, in South-West Iceland, eruption and associated jökulhaup (meltwater flood) at Mýrdalssandur. We also applied this method to another Mt. Katla jökulhaup; the poorly constrained Markarfljót flood.
Theory of VRM Dating
The magnetisation in very small magnetic particles is uniform, and such particles are termed single-domain (SD), as the grains become larger in size the magnetisation splits up into regions of uniformity (domains) divided by very thin domain walls. These particles are termed multidomain (MD). The threshold size between SD and MD magnetic structures depends on mineralogy, grain shape etc. (Muxworthy and Williams, 2006a); however, for magnetite the threshold size is of the order 100 nm. Generally speaking, small SD grains contribute significantly to VRM, whereas MD grains do not (Williams and Muxworthy, 2006).
The theory of VRM dating is based on the thermoviscous model of Néel (1949) for magnetically ideal SD particles with uniaxial anisotropy. For an individual particle the relaxation of its magnetic moment over a given energy barrier ΔE:
where τ is the characteristic time for thermal activation, τ−10 is the atomic attempt frequency, kB Boltzmann's constant and T the absolute temperature. For ideal SD particles in small external magnetic fields, like those of the Earth, whose magnetic anisotropy is controlled by a shape anisotropy, ΔE is given by μ0NMS(T)2v/2, where v the volume of the particle, μ0 the permeability of free space, MS(T) the temperature dependent spontaneous magnetization and N the shape demagnetizing factor (Nagata, 1961).
The characteristic relaxation time τ is effectively the duration, t, of the time-frame of interest, e.g., will barriers be overcome on geological timescales or the duration of a laboratory experiment etc. Using this definition of τ, it is possible to rearrange Equation (1) to define the blocking volume (vb), which is the critical volume of a crystal that has an equal probability of remaining fixed (blocked) for a given time t:
Thus, the critical blocking volume is a function of both temperature and time, i.e., a particle can become blocked at different combinations of time and temperature. For SD grains, for a geological VRM acquired in a time tA and temperature TA, then for a particular grain volume we can remove this VRM in a laboratory time tL and temperature TL using the following relationship (Pullaiah et al., 1975):
For dating purposes, time tA is the VRM age, i.e., the event age to be estimated. Re-arranging Equation (3) to solve for tA and using the standard relationship; MS(T) ∝ (1-T/TC)1/2 (Jiles, 1991), where TC is the Curie temperature of a given mineral, gives:
In Equation (4) the parameters tL, TL and TC can be measured in the laboratory, τ0 is of the order 10−9 s (Moskowitz et al., 1997) and TA can be estimated, allowing for tA to be determined.
Some investigations of VRM (e.g., Kent, 1985; Smith and Verosub, 1994) have also assessed the VRM theory of Walton (1980) and Middleton and Schmidt (1982), which attempts to modify Equation (4) slightly to account for the effect of grain-size distributions. It is has been found that this model appears to work better than Equation (4) for long timescales, i.e, >>1 Myrs, but for shorter timescales, i.e., thousands of years, Equation (4) appears to be more applicable (Smith and Verosub, 1994).
VRM dating has been applied, albeit infrequently, to archeological investigations to yield construction ages (Heller and Markert, 1973; Borradaile and Almqvist, 2006), although not always through the direct application of Equation (4) due to the potential sources of uncertainty in this equation. For example, when determining the building dates of Roman and Medieval structures Borradaile and colleagues (Borradaile, 1996; Borradaile and Brann, 1997; Borradaile et al., 1999; Maher et al., 2000; Borradaile and Almqvist, 2006) constructed calibration curves from age-constrained buildings of the same material, allowing the relative age estimation of previously undated masonry. In this study, we consider geological events and thus such constrained calibrations are infeasible. Instead, we apply Equation (4) directly to the determination of VRM age, thereby estimating absolute, independent ages. There have been only two previous VRM-dating studies of geological processes (Borradaile, 1998; Sato et al., 2014).
Geological Sampling
Ten millimeter core samples were collected using an electric drill during fieldtrips to the USA and Iceland in the summer of 2009.
The Lake Bonneville Flood
The Bonneville flood is one of the largest known geological flood events (Jarrett and Malde, 1987). It occurred when Lake Bonneville, in what is now Utah, USA, breached causing a catastrophic flood. The flood event was first identified (Malde, 1968) by the scabland topography and spectacular erosional and depositional geomorphic features in the Snake River Plain and the Snake River canyon further downstream. Discharge predictions yield flood durations of several weeks up to ~1 year for its 1110 km flow length (Jarrett and Malde, 1987); effectively a geologically instantaneous event. Large basaltic erratics derived from localized outcrops are littered along the Snake River canyon. Many of these erratics are several cubic meters in size, and are unlikely to have been significantly eroded or moved since they were deposited (Malde, 1968).
Using radiocarbon, U-series and aminostratigraphy dating, Oviatt et al. (1992, 1994) predicted ages between 15 and 14.5 kyr for the flood event. These studies provide the most comprehensive and best age estimate. A later palaeomagnetic investigation by Liddicoat and Coe (1997) used palaeosecular variation measurements to estimate the transgressive period of Lake Bonneville as ~18 kyr with a span of 1000–3000 years, therefore inferring ages up to the flood event.
Three-hundred orientated cores from 45 different erratics were collected (Table 1). At locality one (B samples) erratics were ~1 m3 in size and at locality two (H samples) 1–3 m3.
Katla Jökulhlaups
Iceland's second most active volcano, sub-glacial Katla, erupts frequently releasing catastrophic meltwater floods (jökulhlaups) (Duller et al., 2008). The caldera can be divided into three drainage sectors: Ko, So and En, that drain onto Mýrdalssandur, Sólheimasandur and Markarfljót plains (Eliasson et al., 2006). Historical records show most floods have followed along route Ko, a few have followed the So route, whereas there are only geological records of jökulhlaups from the En sector (Eliasson et al., 2006). Recurrence times are estimated as ~58 years for Ko-type jökulhlaups and 500–800 years for En-type (Smith et al., 2002).
Orientated cores (137) from 12 basaltic erratics (size range was 0.5–1 m3) associated with the jökulhlaup on the 12th of October 1918 were collected from the Mýrdalssandur flood plain. This was the last large Ko route jökulhlaup. On the same fieldtrip, oriented cores from three basaltic erratics (size range was ~2 m3) associated with an En sector flood that formed the Markarfljót canyon were collected. Estimates for the age of the Markarfljót event suggest that its age is ~2500 years (Tómmason, 2002), however, this estimate is poorly constrained (pers. comm. Kate Smith).
Experimental Methods
To avoid magnetic contamination, on collecting and orienting the samples in the field, the 10 mm cores were immediately placed in mu-metal boxes for transportation back to the Palaeomagnetic Laboratory at Imperial College London. The cores were cut and temporarily stored in a dynamic Helmholtz cage with a magnetic field <100 nT. All the measurements were conducted within 8 months of collection.
To determine the age of a VRM, it is necessary to measure tL, TL, and TC (Equation 4). On heating the sample, the temperature at which the VRM demagnetizes (unblocks) is TL. TL was determined by continuous thermal demagnetisation with an Orion three-component low-field (<100 nT) vibrating sample magnetometer (VSM). Most samples were continually thermally demagnetised up to 250°C; this took approximately 10 min per sample. A small number of randomly selected samples were heated to 650°C. During these heating experiments tL was measured to be 2.5 ± 0.2 s. To estimate the Curie temperature (TC) of the remanence carrying minerals, the samples were initially demagnetised using an alternating field (AF) to erase the effect of remanence, and a low-field DC (0.5 mT) susceptibility measured as a function of temperature.
To better characterize the VRM acquisition recording process and dating fidelity of the samples, two further experiments were conducted: First, magnetic hysteresis parameters of nine unheated samples were measured using a high-field vibrating sample magnetometer. The parameters HC (coercive force), HCR (remanent coercive force), MRS (saturation remanence) and MS (saturation magnetisation) were determined and plotted on a domain state “Day” plot (Day et al., 1977). Second, we measured directly the viscosity acquisition response of 13 samples, by first AF demagnetising the samples, followed by measurement of VRM acquisition in a field of 100 A/m (~126 μT) for 10 min.
Results
Thermal Demagnetisation of NRM
To determine the critical unblocking temperature TL (Equation 4), the thermal demagnetisation data were plotted on orthogonal projection plots, and inflection points identified (Figure 2). Generally, most samples contained only two components: the characteristic remanent magnetisation (ChRM) and a secondary component associated with VRM (Figure 2). As all the samples were basaltic lavas, ChRM was very likely to be a thermoremanent magnetisation in origin. Where the inflection points could not be clearly identified, because either the VRM and the ChRM were closely aligned or the VRM was poorly defined, the data were rejected. For example, Bonneville sample BQ5 has a sharp inflection providing a discrete, accurate TL selection with minimal error, while Mýrdalssandur sample YJ3 had a less distinct inflection point increasing uncertainty in TL selection (Figure 2). Bonneville sample H39 (Figure 2C) is an example where no clear VRM was identified; such samples were not used for age estimation. If the inflection covered a range of temperatures, probably reflecting the grain-size distribution, the higher temperature was designated as TL(Figure 2A).
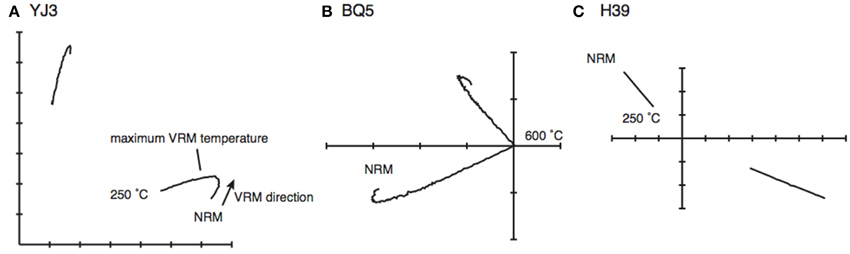
Figure 2. Orthogonal plots (Zijderveld plots) of continuous thermal demagnetisation for specimens.(A) YJ3 (Mýrdalssandur), (B) BQ5 (Bonneville), and (C) H39 (Bonneville). In (A) the identification of the VRM is highlighted, with the maximum VRM temperature (TL) identified. The data is measured every degree, therefore only lines are shown, not individual data points.
In total 236 specimens from 34 erratics were analyzed. Nine of the erratics showed no evidence for a VRM. After removing unquantifiable cases, only 117 estimates were made. Generally, the TL estimates for the Bonneville samples were between ~150–210°C, from Mýrdalssandur ~ 60–130°C, and ~90–120°C for Markarfljót (Supplementary Material Table S1).
To confirm that the VRM had been correctly identified, the direction of the VRM was constrained using principal component analysis (Kirschvink, 1980). Individual VRM vectors for each erratic were plotted onto stereographic projections and the mean direction determined (Figure 3). The VRM should be approximately aligned with the current day magnetic field direction, or at least in the northern hemisphere. There will be some scatter in the VRM directions for two reasons: (1) the VRM signal is normally a minor secondary component and is subject to noise, and (2) secular variation of the geomagnetic field, means that the VRM is recording a direction that is changing significantly on the timescales of interest for the Bonneville and Markarfljót flood events. Older VRMs will be more affected by secular variation effects.
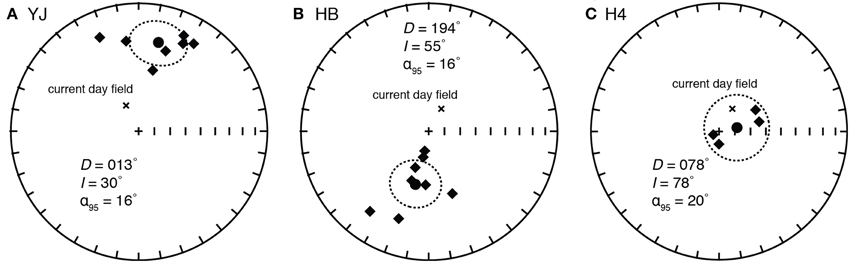
Figure 3. Equal area projection plots for erratics. (A) YJ (Mýrdalssandur), (B) HB (Bonneville) and (C) H4 (Bonneville). Stereographic projections for erratics MB, BQ, YJ, and HB. All the points are solid filled squares, indicating they plot on the lower hemisphere. Mean directions are plotted (solid circles) and quoted, as are the α95 values. For reference, the current day field is also highlighted (cross); this is for 2009 when the samples were collected.
Some erratics, e.g., YJ and HB have clustered VRM directions (Figure 3), with north orientated components. Some erratics have poorly clustered VRM directions, or the mean direction was not in the correct hemisphere. The data from such erratics were rejected from further analysis. After directional analysis, a further 51 specimens were rejected, leaving 66 specimens for dating analysis (Section Age Estimations): 29 specimens (six erratics) from Bonneville, 28 specimens (four erratics) from Mýrdalssandur, and nine specimens from one erratic from Markarfljót (Supplementary Material Table S1).
High-temperature Thermomagnetic Analysis
Curie temperatures (technically maximum unblocking temperatures) were determined using the double derivative method of Tauxe (1998) (Table 1). Most, but not all, heating curves (Figure 4) for the Bonneville specimens had a single high-temperature TC, e.g., HA3, whereas the Icelandic samples, e.g., YK3 and YJ4, displayed a gradual decay in their thermomagnetic curves, suggesting a broad range of unblocking spectra and mineralogies, making it difficult to accurately constrain TC. As a general rule the Icelandic specimens had lower Curie temperatures (≤500°C) than Bonneville specimens (≤500°C) (Supplementary Material Table S1).
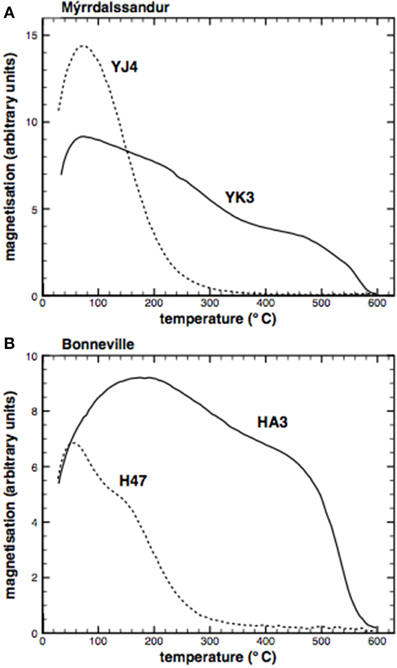
Figure 4. Representative thermomagnetic curves for samples from (A) Mýrdalssandur, and (B) Bonneville. The samples were first alternating field (AF) demagnetised in a peak field of 200 mT, and heated in a field of 0.5 mT; the thermomagnetic curves are DC susceptibility curves.
Magnetic Hysteresis
The magnetic hysteresis data is summarized on a “Day” plot in Figure 5. Most specimens plot within the pseudo-single-domain (PSD) grain region, with one sample plotting slightly to the left. There is no distinct grouping between samples that were accepted for dating analysis in Section Thermal Demagnetisation of NRM, and those that were rejected.
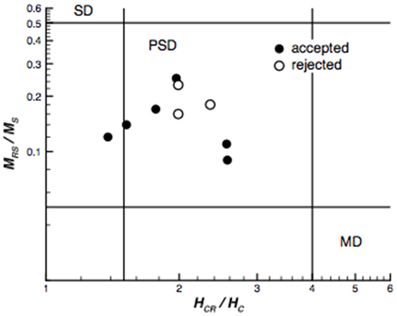
Figure 5. A “Day” plot (Day et al., 1977) of the ratio of HCR/HC vs. MRS/MR for accepted samples. Whether a sample was accepted or rejected from the final dating calculation is highlighted. The standard SD, PSD, and MD fields are drawn.
Viscosity Measurements
The rate of acquisition of viscous magnetisation, i.e., the viscosity acquisition parameter SA was determined and quantified using the first-order approximation (Street and Woolley, 1949):
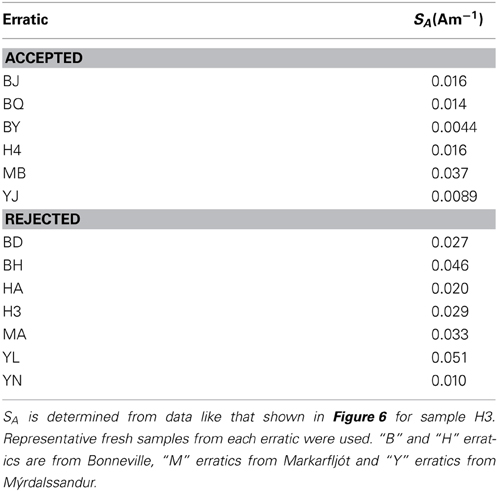
where M is the magnetisation. Generally the samples displayed a logarithmic dependency (Figure 6) over the measurement time (~10 min) in agreement with previous studies (Muxworthy and Williams, 2006b). The samples displayed a range of estimates for SA, as quantified in Table 1. Generally, samples that were accepted for VRM dating (Table 1), had lower SA values. The means of the accepted and rejected samples were 0.016 and 0.030 Am−1, respectively.
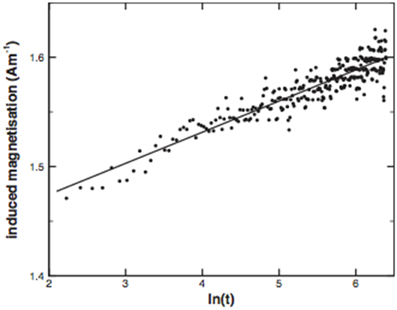
Figure 6. Magnetisation versus time for a representative sample from erratic H3 (H35). The samples were AF demagnetised in peak fields of 200 mT, and then the magnetisation was measured as a function of time in an applied field of 126 μT. The viscosity acquisition parameter SA (Equation 5) is determined directly from such plots.
Discussion
After analysis of the NRM data, 66 specimens out of 236 were deemed to be suitable for reliable estimates of TL, having clear inflection points and “well-behaved” VRM directions (Figures 2, 3 and Supplementary Material Table S1).
Age Estimations
To make age estimations we apply Equation (4). All the parameters in Equation (4) were directly measured with the exception of the ambient temperature (TA) and τ0. We have determined the ages using the mean annual temperatures for TA for Mýrdalssandur, Markarfljót and Bonneville (Supplementary Material Table S1), where the temperature ~5.5°C for Mýrdalssandur was taken from the 1961–2013 record [available from the Icelandic Meteorological Office (http://en.vedur.is/)] for nearby Vík í Mýrda. For Markarfljót a mean annual temperature of ~3.5°C was used, based on temperature records from Básar á Goðoalandi relative to Sámsstaðoir and Vík í Mýrda. For Bonneville the mean annual temperature (~9°C) from the 1961–1990 record from Twin Falls, Idaho, was used (www.usclimatedata.com).
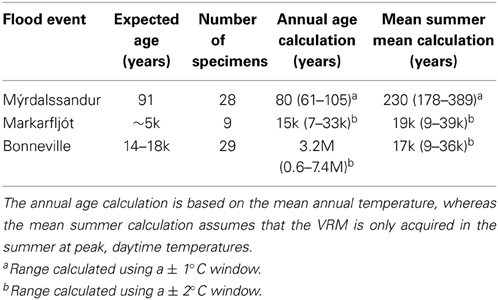
Each specimen yields a different tA (Supplementary Material Table S1). It is immediately clear that the distribution of age estimates is not normally distributed; therefore we take the median to determine three representative VRM ages. Although there are several sources of error in the parameter estimates (see Section Uncertainties in input parameters for further analysis), to investigate the sensitivity of tA on TA, we plot tA as function of TA for median ages from Bonneville, Mýrdalssandur and Markarfljót (Figure 7). We have plotted two curves: (1) a mean annual temperature curve (24 h for 365 days), and (2) a mean summer maximum temperature curve. In the later calculation it is assumed that most of the VRM is acquired mostly at higher temperatures, and tA is determined using VRM acquisition of only 6 h per day for 60 days of summer. To estimate the error on tA we use a ± 1.0°C temperature window for the recent Mýrdalssandur flood, and for the older Bonneville and Markarfljót floods a ± 2.0°C window (Table 2). The ± 2.0°C window is a little arbitrary and should be seen as a guide rather than absolute measure of the error.
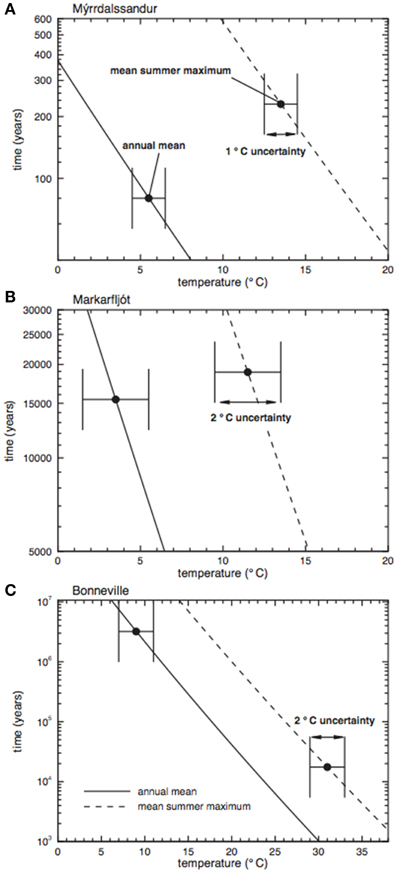
Figure 7. VRM age estimates (tA) as a function of the ambient temperature TA for median ages from: (A) Mýrdalssandur, (B) Markarfljót and (C) Bonneville. On each diagram, two curves are plotted: (1) a annual mean temperature curve (24 h for 365 days), and (2) a mean summer maximum temperature curve. In the latter calculation it is assumed that the VRM is acquired mostly at higher temperatures, and tA is determined using VRM acquisition of only 6 h per day for 60 days a year. To estimate the ages we use annual mean and mean summer maximum temperatures of: (A) 5.5 and 13.5°C, (B) 3.5 and 11.5°C, and (C) 9 and 31°C. To estimate the error on tA we use a ± 1.0°C temperature window for the recent Mýrdalssandur flood, and for the older Bonneville and Markarfljót floods a ± 2.0°C window.
The age estimate (80 years) for the median Mýrdalssandur erratic is within 11 years of the known age of 91 years, and ± 1°C uncertainty in the mean annual temperature yields a range estimate of 61–105 years. The median estimate for the Markarfljót flood (~15 ka) is older than the published value (~2500 years, Tómmason, 2002), however, this is poorly constrained and is very likely younger or concurrent with the Younger Dryas, i.e., ≤12 ka. The Bonneville flood estimate (~3.2 Ma) for the mean annual temperature is very old, however, the summer maximum temperature estimate is close to the expected value.
Possible Reasons for Failure
Potential errors in the age calculations can arise from a number of sources: (1) theoretical assumptions about the intrinsic magnetic properties of a specimen, (2) uncertainties in the input parameters into Equation (4), in particular in the ambient temperature TA and τ0, (3) variations in the geomagnetic field, and (4) sample handling. There was no obvious correlation between the time from collection to measurement, and rejection.
Domain state, mineralogy and viscous acquisition
The VRM dating method is based on the assumption that the magnetic remanence is carried by assemblages of non-interacting SD particles, dominated by uniaxial anisotropy imparted with a thermoremanence. The samples in this study display hysteresis properties typical for basalt, i.e., distributions of PSD particles (Figure 4). There is no real trend between the specimens accepted or rejected for VRM determination, based on their hysteresis properties; perhaps, the accepted specimens are slightly more SD-like? However, hysteresis is an in-field measurement allowing for large MD particles, which are not thought to contribute significantly to VRM acquisition (Dunlop, 1983), to dominate, i.e., the SD particles, which contribute most to the VRM signal, might be masked. If MD particles are more abundant, then it might be expected that given the difference between blocking and unblocking temperatures for MD particles, that the MD contribution to VRM might lead to an overestimate for tL. No such relationship was noticed in this study; however, this feature is likely to be quite subtle and easily dominated by other effects.
The viscosity acquisition parameter SA (Equation 5) of the accepted erratics was roughly half that of the rejected erratics (Table 1). While the variation may be due to variation in magnetic mineral concentration, it suggests that erratics that are more efficient at acquiring a VRM component are less reliable. This initially seems counter intuitive; however, it may be because grains with high SA values are more susceptible to short term paleosecular variation and are likely to acquire a contamination VRM signal subsequent to collection.
The theory used to determine the VRM date (Equation 4) is based on a magnetic thermal activation model. There are also non-magnetic effects, which can alter the magnetisation, e.g., disaccommodation (Moskowitz, 1985; Muxworthy and Williams, 2006b), which can lead to VRM acquisition behavior that is not explained by Equation (4) (Lowrie and Kent, 1978; Tivey and Johnson, 1984); it will likely lead to an overestimate of tA. Such processes would be expected to have greater effects on older VRMs.
Ideally samples should be chosen which show no evidence of chemical alteration (oxidation); then the signal associated with the VRM should be thermal in origin.
Uncertainties in input parameters
The age estimate tA is sensitive to uncertainties in the input parameters in Equation (4), and is most likely the cause of the data scatter (Supplementary Material, Table S1). To assess these uncertainties we examine the partial derivatives of the five variables in Equation (4) in Table 3. It is clear that the biggest uncertainty comes from the uncertainty in τ0, with uncertainties in TA and TL roughly equally important, whilst the uncertainties in the measured parameters TC and tL are less significant. For the Mýrdalssandur flood event, TA is relatively well constrained from meteorological data from a nearby weather station; the calculation in Table 3 uses an error of 5 K, but it is likely much smaller than this, i.e., ~1–2 K. For the other two events, which are significantly older, we have made estimates for TA based on recent temperature records; clearly, age estimates for older events will have greater uncertainties in TA; 5 K is possibly an underestimate of the error in the mean temperature. The age estimates based on mean annual temperatures are clearly too old for Bonneville, and slightly too old for Markarfljót (Table 2). Because Equation (4) is very sensitive to temperature, i.e., a few hours at a higher temperature has a greater effect than many hours at a lower temperature, we have also calculated tA based on mean summer maximum temperatures. For Markarfljót, the age estimate is similar to that for the mean annual temperature; for Bonneville the age estimate from the average summer maximum temperature is much lower and within the expected range. This difference in behavior is most likely due to the very large variation in mean temperatures in mid-latitude continental regions, in contrast, in maritime regions the temperature variation is significantly less, i.e., there is less variation and uncertainty in TA. The temperatures used in the estimation of tA are air temperatures; rock surfaces exposed to the sun can reach much higher temperatures, i.e., the temperatures used in this study might be too low or too high depending on average exposure to sunlight. The error in TL, may not have been as large as quoted in Table 3, and depends on the shape of the inflection in the orthogonal projection plots (Figure 2): Care should be taken in identifying TL.
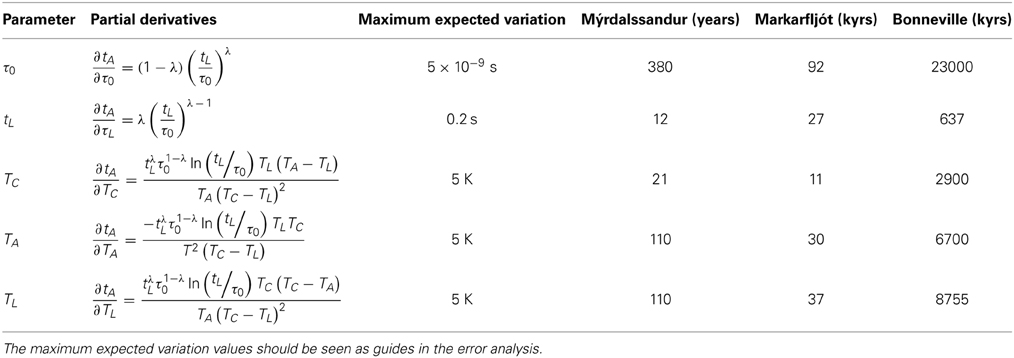
Table 3. Estimation of the effect of errors/approximations for the parameters in Equation (4) on Equation (4) through analysis of partial derivatives.
Variations in the VRM directions
Several erratics had low-temperature magnetisations components that were south seeking; erratics displaying such behavior were not used in the age estimations. There are two possible causes of this behavior: (1) A remanence other than a VRM associated with the flood event had been measured, i.e., the VRM signal had been contaminated since collection (to reduce this effect the samples were placed directly in mu-metal boxes in the field). (2) The erratic had moved since the flood event, however, this must have happened relatively recently for the associated flood-event VRM not to be overprinted by a new north-seeking VRM direction. For erratics with mixed north- and south-seeking directions, the first scenario is more likely, and for erratics with only south seeking VRM directions, the second mechanism is more likely. Secular variation of the geomagnetic field will cause a variation in the inclination and declination that the VRM records, however, the variation is not large enough to cause a VRM to become south-seeking. It should also be noted that the directions of some VRM were poorly constrained, as the some VRMs demagnetisation data, e.g., Figure 2, were essentially curves rather than a straight line, making it difficult to determine an accurate VRM direction.
Comparisons with Previous Studies
Both previous VRM-dating studies of geological processes (Borradaile, 1998; Sato et al., 2014), relied on step-wise thermal demagnetisation rather than continuous thermal demagnetization as used in this study; this means that: (1) the temperature step sizes were larger purely for practical reasons, and (2) the heating rates are not identical, i.e., static versus continuous heating. Borradaile (1998) used a calibrated system based on archeological masonary to date rock slumps <1000 years in age; he primarily used the protocol to put events into chronological sequence. Sato et al. (2014) examined two large paleotsunami erratics. They used the same equation as us to determine the age of erratics, i.e., Equation (4). However, they did not conduct detailed error analysis, and essentially only used the VRM-dating technique to put events in chronological sequence.
On comparison, in this study we have conducted a significantly more extensive study by sampling many erratics, we have employed a more detailed temperature analysis of VRM demagnetisation through continuous demagnetisation and have conducted more rigorous error analysis. We believe that this study is a significant advancement on previous studies.
We also considered the VRM theory of Walton (1980) and Middleton and Schmidt (1982), which requires the same input data as Equation (4), though it is slightly modified. When we applied this approach to our data, all the ages for the erratics were less than a year. We therefore believe that Equation (4) is more appropriate.
Future Improvements
This work is a preliminary study. We suggest a number of improvements for future studies:
• To better constrain TA, collect cores from rock surfaces that are predominately in shadow or partially buried.
• Measure thermomagnetic curves for all the specimens or at one least per erratic, and use these thermomagnetic curves as input in the estimation calculation rather than using single Curie temperature estimations for each erratic.
• Determine τ0 for a range of specimens, and assess whether it is necessary to determine τ0 for each specimen/erratic.
• Determine the optimal heating rate for tL.
• To reduce VRM decay rate and remove acquisition of new VRMs in the laboratory, store samples in mu-metal boxes in a refrigerator.
• Use of more detailed climate records for older events.
Conclusions
We have tested a VRM dating method on erratics associated with three flood events: (1) Mýrdalssandur (1918 AD), Markarfljót (~5 ka) and Bonneville (14–18 ka). We measured 236 specimens from 34 erratics, and based on various selection criteria only 66 were used in the final calculations (Supplementary Material Table S1). In summary the dating method is partially successful; inconsistency in age estimates increases dramatically for the older flood events. The results for the most recent event, worked reasonably well with an estimated age of 80 years (61–105 years) compared to the expected answer of 91 years. The ages of the other two events were over-estimated (Table 2). The estimates for Markarfljót were based on the results of just one erratic, whilst the uncertainty in the ambient temperature used in the age determination (Equation 4) was very large for Bonneville. From this it is concluded that the technique will work best for erratics associated with recent events, i.e., <2–3 ka, in locations that have constrained temperature histories. To further improve estimates, estimating τ0 on a specimen/erratic/material level may be necessary.
Cosmogenic exposure analysis, arguably the most important technique for dating erratics (Phillips et al., 2006) is also dependent on rock type, variations in exposure, and changes in the geomagnetic field. 36Cl dating can measure surface exposure time of young volcanic rocks and geomorphic features in the age range of 103–106 years (Phillips et al., 1986). Estimates for the youngest Mýrdalssandur flood on the scale of 102 years proved successful and therefore the VRM technique may be a more appropriate tool for dating recent erratics than cosmogenic dating.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was funded by a Royal Society grant to Adrian R. Muxworthy. We thank Karin Strohecker for assistance during the fieldwork in Iceland.
References
Borradaile, G. J. (1996). An 1800-year archeological experiment in remagnetization. Geophys. Res. Lett. 23, 1585–1588. doi: 10.1029/96GL01575
Borradaile, G. J. (1998). Rock magnetic constraints on long-term cliff-slump rates and coastal erosion. Géotechnique 48, 271–279. doi: 10.1680/geot.1998.48.2.271
Borradaile, G. J. (2003). Viscous magnetization, archaeology and Bayesian statistics of small samples from Israel and England. Geophys. Res. Lett. 30:1528 doi: 10.1029/2003GL016977
Borradaile, G. J., and Almqvist, B. S. (2006). Installation age of limestone masonry determined from its viscous remagnetization. Geoarchaeology 21, 29–60. doi: 10.1002/gea.20088
Borradaile, G. J., and Brann, M. (1997). Remagnetization dating of roman and mediaeval masonry. J. Archaeol. Sci. 24, 813–824. doi: 10.1006/jasc.1996.0162
Borradaile, G. J., Cameron, C., and Stewart, J. D. (1999). Magnetization dating at a medieval monastery (Tupholme, Lincolnshire). Archaeometry 41, 175–183. doi: 10.1111/j.1475-4754.1999.tb00859.x
Day, R., Fuller, M. D., and Schmidt, V. A. (1977). Hysteresis properties of titanomagnetites: grain-size and compositional dependence. Phys. Earth Planet. Inter. 13, 260–267. doi: 10.1016/0031-9201(77)90108-X
Duller, R. A., Mountney, N. P., Russell, A. J., and Cassidy, N. C. (2008). Architectural analysis of a volcaniclastic jokulhlaup deposit, southern Iceland: sedimentary evidence for supercritical flow. Sedimentology 55, 939–964. doi: 10.1111/j.1365-3091.2007.00931.x
Dunlop, D. J. (1973). Theory of magnetic viscosity of lunar and terrestrial rocks. Rev. Geophys. Space Phys. 11, 855–901. doi: 10.1029/RG011i004p00855
Dunlop, D. J. (1983). Viscous magnetization of 0.04-100 μm magnetites. Geophys. J. R. Astron. Soc. 74, 667–687.
Eliasson, J., Larsen, G., Gudmundsson, M. T., and Sigmundsson, F. (2006). Probabilistic model for eruptions and associated flood events in the Katla caldera, Iceland. Comput. Geosci. 10, 179–200. doi: 10.1007/s10596-005-9018-y
Heller, F., and Markert, H. (1973). The age of viscous remanent magnetization of Hadrian's Wall (northern England). Geophys. J. 31, 395–406. doi: 10.1111/j.1365-246X.1973.tb06510.x
Jarrett, R. D., and Malde, H. E. (1987). Paleodischarge of the late pleistocene bonneville flood, snake river, Idaho, computed from new evidence. Geol. Soc. Am. Bull. 99, 127–134.
Kent, D. V. (1985). Thermoviscous remagnetization in some Appalachian limestones. Geophys. Res. Lett 12, 805–808. doi: 10.1029/GL012i012p00805
Kirschvink, J. L. (1980). The least-squares line and plane and the analysis of paleomagnetic data. Geophys. J. R. Astron. Soc. 62, 699–718. doi: 10.1111/j.1365-246X.1980.tb02601.x
Liddicoat, J. C., and Coe, R. S. (1997). Paleomagnetic investigation of Lake Lahontan sediments and its application for dating pluvial events in the northwestern Great Basin. Q. Res. 47, 45–53. doi: 10.1006/qres.1996.1867
Lowrie, W., and Kent, D. V. (1978). Characteristics of VRM in Oceanic Basalts. J. Geophys. 44, 297–315.
Maher, L., Boarradaile, G., Stewart, J. D., and O'connor, M. (2000). The romanesque frieze at Lincoln Cathedral (England) - primary or secondary insertion? magnetic considerations. Archaeometry 42, 225–236. doi: 10.1111/j.1475-4754.2000.tb00878.x
Malde, H. E. (1968). The Catastrophic Late Pleistocene Bonneville Flood in the Snake River Plain, Idaho. Geol. Surv. Prof. Pap. 596, 1–69.
Middleton, M. F., and Schmidt, P. W. (1982). Paleothermometry of the Sydney basin. J. Geophys. Res. 87, 5351–5359. doi: 10.1029/JB087iB07p05351
Moskowitz, B. M. (1985). Magnetic viscosity, diffusion after-effect and disaccommodation in natural and synthetic samples. Geophys. J. R. Astron. Soc. 82, 143–161. doi: 10.1111/j.1365-246X.1985.tb05133.x
Moskowitz, B. M., Frankel, R. B., Walton, S. A., Dickson, D., Wong, K. K. W., Douglas, T., et al. (1997). Determination of the pre-exponential frequency factor for superparamagnetic maghemite particles in magnetoferritin. J. Geophys. Res. 102, 22671–22680.
Muxworthy, A. R., and Williams, W. (2006a). Critical single-domain/multidomain grain sizes in non-interacting and interacting elongated magnetite particles: implications for magnetosomes. J. Geophys. Res. 111:B12S12. doi: 10.1029/2006JB004588
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Muxworthy, A. R., and Williams, W. (2006b). Low-temperature viscous magnetization of multidomain magnetite: evidence for disaccommodation contribution. J. Magn. Magn. Mater. 307, 113–119. doi: 10.1016/j.jmmm.2006.03.052
Néel, L. (1949). Influence des fluctuations thermiques sur l'aimantation de grains ferromagnétiques très fins. Comp. Ren. Heb. Séan. Acad. Sci. 228, 664–666.
Oviatt, C. G., Currey, D. R., and Sack, D. (1992). Radiocarbon chronology of Lake Bonneville, Eastern Great Basin, USA. Palaeogeogr. Palaeoclimatol. Palaeoecol. 99, 225–241. doi: 10.1016/0031-0182(92)90017-Y
Oviatt, C. G., McCoy, W. D., and Nash, W. P. (1994). Sequence stratigraphy of lacustrine deposits: a quaternary example from the Bonneville basin. Geol. Soc. Am. Bull. 106, 133–144.
Phillips, F. M., Leavy, B. D., Jannik, N. O., Elmore, D., and Kubik, P. (1986). The accumulation of cosmogenic chlorine-36 in rocks: a method for surface exposure dating. Science 231, 41–43. doi: 10.1126/science.231.4733.41
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Phillips, W. M., Hall, A. M., Mottram, R., Fifield, L. K., and Sugden, D. E. (2006). Cosmogenic 10Be and 26Al exposure ages of tors and erratics, cairngorm mountains, Scotland: timescales for the development of a classic landscape of selective linear glacial erosion. Geomorphology 73, 222–245. doi: 10.1016/j.geomorph.2005.06.009
Pullaiah, G., Irving, E., Buchan, K. L., and Dunlop, D. J. (1975). Magnetization changes caused by burial and uplift. Earth Planet. Sci. Lett. 28, 133–143. doi: 10.1016/0012-821X(75)90221-6
Sato, T., Nakamura, N., Goto, K., Kumagai, Y., Nagahama, H., and Minoura, K. (2014). Paleomagnetism reveals the emplacement age of tsunamigenic coral boulders on Ishigaki Island, Japan. Geology. 42, 603–606. doi: 10.1130/G35366.1
Smith, K. T., Dugmore, A. J., Larsen, G., Vilmundardottir, E. G., and Haraldsson, H. (2002). “New evidence for Holocene jökulhlaup routes west of Mýrdalsjökull,” in The 25 Nordic Geological Winter Meeting Abstracts, ed S. S. Jonsson (Reykjavík: University of Iceland), 106.
Smith, R. T., and Verosub, K. L. (1994). Thermoviscous remanent magnetism of columbia river basalt blocks in the cascade landslide. Geophys. Res. Lett. 21, 2661–2664. doi: 10.1029/94GL02669
Street, R., and Woolley, J. C. (1949). A study of magnetic viscosity. Proc. Phys. Soc. Lond. A 62, 562–572. doi: 10.1088/0370-1298/62/9/303
Tivey, M. A., and Johnson, H. P. (1984). The characterization of viscous remanent magnetization in large and small magnetite particles. J. Geophys. Res. 89, 543–552. doi: 10.1029/JB089iB01p00543
Tómmason, H. (2002). “Catastrophic floods in Iceland” in The Extremes of Extremes: Extraordinary Floods Vol. 271, eds A. Snorrason, H. P. Finnsdóttir and M. E. Moss (Wallingford: IAHS International Commission on Water Resources Systems), 121–126.
Walton, D. (1980). Time-temperature relations in the magnetisation of assemblies of single domain grains. Nature 286, 245–247. doi: 10.1038/286245a0
Keywords: viscous remanent magnetisation, dating, flood erratic, cataclysmic event, rock magnetism
Citation: Muxworthy AR, Williams J and Heslop D (2015) Testing the use of viscous remanent magnetisation to date flood events. Front. Earth Sci. 3:1. doi: 10.3389/feart.2015.00001
Received: 24 November 2014; Paper pending published: 12 December 2014;
Accepted: 07 January 2015; Published online: 23 January 2015.
Edited by:
Eric Font, University of Lisbon, PortugalReviewed by:
Greig A. Paterson, Chinese Academy of Sciences, ChinaAnn Marie Hirt, Swiss Institute of Technology Zürich, Switzerland
Copyright © 2015 Muxworthy, Williams and Heslop. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Adrian R. Muxworthy, Department of Earth Science and Engineering, Imperial College London, South Kensington Campus, London, SW7 2AZ, UK e-mail:YWRyaWFuLm11eHdvcnRoeUBpbXBlcmlhbC5hYy51aw==
 Adrian R. Muxworthy
Adrian R. Muxworthy Jason Williams
Jason Williams David Heslop
David Heslop