- 1Hydrology and Natural Hazards, Department of Forecasting Systems, Regional Agency for Environmental Protection of Piemonte, Turin, Italy
- 2Department of Environment, Land and Infrastructure (DIATI), Politecnico di Torino, Turin, Italy
A method to predict the most probable flow rheology in Alpine debris flows is presented. The methods classifies outcropping rock masses in catchments on the basis of the type of resulting unconsolidated deposits. The grain size distribution of the debris material and the depositional style of past debris flow events are related to the dominant flow processes: viscoplastic and frictional/collisional. Three catchments in the upper Susa Valley (Western Alps), characterized by different lithologies, were selected for numerical analysis carried out with a Cellular Automata code with viscoplastic and frictional/collisional rheologies. The obtained numerical results are in good agreement with in site evidences in terms of depositional patterns, confirming the possibility of choosing the rheology of the debris flow based on the source material within the catchment.
Introduction
Debris flows are rapid to very rapid flows of sediment water mixtures, with high solid concentration (Jakob and Hungr, 2005). As these natural phenomena are among the most dangerous and destructive events, the definition of runout scenarios for risk assessment has received wide interest in recent decades.
During rainstorm events catchments can be subject to debris flows along their channels. At this scale a quick and simple procedure of runout assessment can be useful for hazard mitigation.
The estimation of runout is generally performed by numerical modeling. To this end, the identification of the rheology of the mixture is required in order to choose the most appropriate constitutive law to be used in debris flow simulations. The behavior of debris flows can depend on several factors, but a key parameter is the grain size distribution of the debris material. In particular the presence of fine sediments (clay, clayey silt) affects substantially both the type of flow and the deposition pattern. Very roughly debris flow behavior can be subdivided into two basic main types (Coussot and Meunier, 1996): viscoplastic (high fine content material) and frictional/collisional (coarse material with low fine content).
As the debris material, in mountain catchments, is the result of rock rupture and weathering, a classification of outcropping rock masses based on the type of resulting unconsolidated deposits can give useful information on the grain size and consequently on the expected flow behavior.
In this way, a correct debris flow hazard evaluation in mountainous areas depended on proper identification of the dominant sedimentary processes (Blair and McPherson, 1994; Bonnet-Staub, 1998; Lin et al., 2000; Moscariello et al., 2002; Bardou et al., 2003; Wilford et al., 2004), inferred both from modern deposits and sedimentary records (facies characteristics and distribution). This approach was refined and tested by Tiranti et al. (2008) in some catchments of the Western Italian Alps, characterized by a great variability in terms of geomorphology and geology. Tiranti et al. (2008) evidenced that the different depositional styles, related to the dominant flow process of debris flows, could be directly related to the type of source material within the catchments. In particular three classes of source material are identified and related to the rheology of the mixture, on the basis of clay content (Tiranti et al., 2008, 2014).
The method here proposed couples the sedimentological characterization of catchment source deposits and related torrential processes with numerical simulations of debris flow deposition patterns. The method consists of a simple procedure for the definition of debris flow deposition scenarios based on the features of the catchments. In particular by the knowledge of the rock forming the catchment it is possible to estimate the amount of fine material in the bulk, to identify the most probable rheological behavior of the mixture and finally to adopt the appropriate constitutive law to be implemented in simulations. To this end, three catchments in the upper Susa Valley (Western Alps) have been selected and characterized. The catchments are then classified according to the findings of Tiranti et al. (2014) and the expected type of flow behavior is finally defined.
The simulations were performed with a Cellular Automaton code (Segre and Deangeli, 1995; Deangeli, 2008; Deangeli et al., 2013, 2015) using two different rheological laws: Bingham model and Bagnold model. The results of the numerical runs were compared with the characteristic depositional style observed in each catchment.
Catchment Lithology and Related Deposits
North-western alpine catchments were classified by Tiranti et al. (2014) into three main classes of catchment lithology through the Clay Weathering Index (CWI) which indicates the propensity of lithofacies to weather into clay or other fine minerals with clay-like rheology behavior (e.g., other phyllosilicate groups): Excellent Clay-Maker (ECM) catchments are mainly formed by rocks having a very high propensity to weather into clay or clay-like minerals (e.g., thinning-foliated and phyllosilicates-rich metamorphic rocks); Good Clay-Maker (GCM) catchments are mainly formed by rocks having a good propensity to weather into clayey silt and clay (e.g., massive carbonate rocks); Bad Clay-Maker (BCM) catchments are mainly formed by rocks having a bad propensity to weather into clay or clay-like minerals (e.g., massive crystalline rocks). The characterization of rocks and derived shallow deposits is useful for the identification and evaluation of potential source areas. What is evident is a different amount of unconsolidated material production, both in terms of abundance and grain-size, depending on the catchment lithologies. The unconsolidated material in the catchment area affects the depositional style of debris flows and is directly linked to the rheology. Depositional styles are easily identifiable for each catchment class through direct field observations in channel beds and in alluvial fan areas.
ECM catchments generate abundant unconsolidated material with high clay/clay-like component (Figure 1) and provide for large landslide deposits. The unconsolidated material consists of shallow deposits characterized by a clast- or matrix-supported texture, with grain-size varying from fine-grained to coarse-grained deposits or unsorted deposits. These types of deposit can change their rheological properties with the water content and are more susceptible to the mobilization with rainfall of moderate intensity. ECM levee deposits are characterized by narrow, steep shapes with strongly transversal asymmetry; they have a frontal boulder followed by gradually smaller-size clasts (Figure 2A). Lobe deposits are also found abundant and they show a teardrop shape and the clasts drawing a semicircle in toe area, with the major axes of the clasts arranged tangentially to the semicircle (Figure 2B). This secondary deposit corresponds to debris flow surges or local flows of low energy. The lobes are often associated with levees as secondary deposits due to a late stage of deposition. These lobes are deposited on the external lateral sides of levees and their longitudinal axis forms an angle of approximately 30° with the longitudinal axis of the levees. ECM clasts forming levees and lobes are characterized by low sphericity and angular shape. The clasts structure shows a very high imbrications angle (often vertical) with the major axis of clasts parallel to the transport direction (Figure 2C). These deposits are characterized by poor sorted, clast-supported texture and abundant fine-grained matrix (Figure 2C). The matrix in the shallow portions of deposits is often winnowed by liquid-tail of debris flow events.

Figure 1. An example of unconsolidated material generated by ECM catchments (from Rio Frejus, Bardonecchia, Turin, Italy).

Figure 2. (A) ECM levee deposit; (B) ECM lobe deposit; (C) Cross section of ECM debris flow deposit (from Rio Frejus, Bardonecchia, Turin, Italy).
GCM catchments generate large quantities of unconsolidated material characterized by clast- or matrix-supported texture, and unsorted from fine to coarse-grained material (Figure 3) with significant quantities of clayey silt fraction. These deposits change their rheological behavior in presence of water and are susceptible to the mobilization with rainfall of moderate-high intensity. On the contrary, the debris directly generated from outcropped bedrock (talus deposits) are characterized by open-work or partially open-work textures susceptible to the mobilization with high-very high rainfall intensity. GCM debris flow deposits consist mainly of levee deposits characterized by wide and flat shape and symmetrical in transversal section. Typically these deposits show a front boulder gradually followed by clasts of smaller size. The clasts are also characterized by a high-angle of imbrications, with the major axis of clasts parallel to the transport direction, as for ECM levees. The clasts forming levees and lobe are characterized by high sphericity and angular shape (Figure 4). The lobe deposits are also profuse, especially in central and distal areas of the alluvial fan, and correspond to deposition in low energy conditions. Commonly the levee and lobe deposits texture could be apparently confused with an open-work texture if the observation is limited to the shallow portion of the deposit. This is due to leaching effect of the liquid-tail that characterizes the final stages of a debris flow event.

Figure 3. An example of unconsolidated material generated by GCM catchments (from Rio Comba Crosa, Cesana, Turin, Italy).
BCM catchments generate smaller amounts of unconsolidated material, than the other two catchment types. Most unconsolidated material consists of talus deposit formed by large boulders (Figure 5). These catchments are also poor producers of clay/clay-like sediments. The unconsolidated material consists mainly of coarse debris deposits with open-work or partially open-work texture (e.g., talus deposits, rock fall deposits, debris in the incised channel) that are mobilized only with very high water discharge (e.g., associated with a Glacial Lake Outburst Flood or very intense or extreme rainfall events). The deposits are always characterized by a well-sorted clast-supported texture. BCM debris flows do not exhibit levee deposits, but the so called levee-like boulder train deposits. These deposits consist of an array of low-angle overlapping blocks with the major axis normal to the transport direction. In addition, these deposits are typically matrix-free (Figure 6).

Figure 5. An example of unconsolidated material generated by BCM catchments (from Rio Secco, Salbertrand, Turin, Italy).
However, the levee-like boulder train deposits are not the most common depositional style for BCM debris flows. In fact, it is more common to find large matrix-free fan-lobe deposits. As opposed to the lobe deposits for ECM and GCM catchments, BCM fan-lobe deposits do not necessarily indicate a debris flow surge of lower energy than the processes responsible for deposition of the boulder trains. The clasts forming boulder trains and fan-lobes are characterized by an intermediate sphericity and angular shape.
The observations and analysis reported in the previous paragraphs allow the definition of the following distinctive alluvial fans characteristics that are also driven by the catchment type:
ECM alluvial fans are much smaller than the feeding catchments (on average fan area/catchment area ratio of 5%) and are characterized by moderate slope and an irregular geometry. Natural, unaltered alluvial fans oftentimes have a higher number of asymmetrical-steep levees than lobes. These are regularly distributed from apex to toe, near the main channel. The longitudinal cross-section of these alluvial fans show a regular slope (Figure 7A). The high amount of fine particles is responsible of the small, starved-shape fans. Thick debris flow deposits were observed along and near the main channel at the high and intermediate sections of ECM catchments.
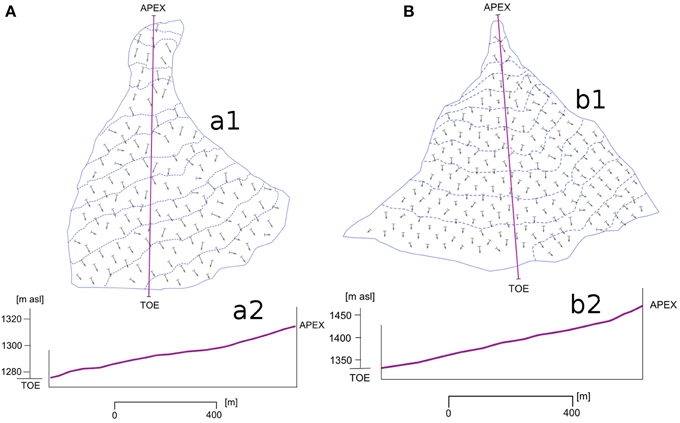
Figure 7. (A) ECM alluvial fan geometry (e.g., Rio Frejus, Bardonecchia, Turin, Italy). (a1) Steeper fan slopes are shown by longer arrows. Fan slope is irregular, with little difference from apex to toe. The longitudinal cross-section of ECM fans (a2) are characterized by slopes slightly higher than the GCM fans and by a regular profile. (B) GCM fan geometry (e.g., Rio Fosse, Bardonecchia, Turin, Italy). (b1) Steeper fan slopes are shown by longer arrows. The longitudinal cross-section of GCM fans (b2) are characterized by a regular, gentle slope from apex to toe.
GCM alluvial fans are definitely impressive compared to the feeding catchments (on average, fan area/catchment area ratio of 20%) and are characterized by regular geometry and gentle slope (Figure 7B). Natural, unaltered alluvial fans have lobes in central and distal areas, and, symmetrical broad-flat levees near to the apex. The transition from levee-rich to lobe-rich areas is underlined by a gradual decrease of the fan slope from apex to toe.
BCM catchments show relatively small, lobe-shaped alluvial fans (fan area/catchment area ratio of 5%), with high slopes particularly at the apex of the fan (Figure 8A). A distinct change of the grain size distribution of the deposited material is evident between the apex of the fan and the central and distal area of the fan. The larger boulders are concentrated at the apex of the fan as fan-lobes and subordinated levee-like boulder trains. From apex to toe, the boulders decrease while the heterogeneity of debris size increases in correspondence to more or less evident morphologic scarps along the fans slope. The sand-silt matrix abundance grows from apex to toe of alluvial fan, it is common to observe a sandy toe with occasional blocks. If the BCM alluvial fans are dominated by prevalent sheet-flooding processes (as hyperconcentrated flows) and show lobe-shaped alluvial fans with more gentle slope than the debris flow dominated alluvial fans. The debris size distribution and the slope gradient are regular (Figure 8B). In this sub-type of BCM fans, boulders are more rare than in the previous type and debris size is very heterogeneous, even if cobbles and pebbles dominate.
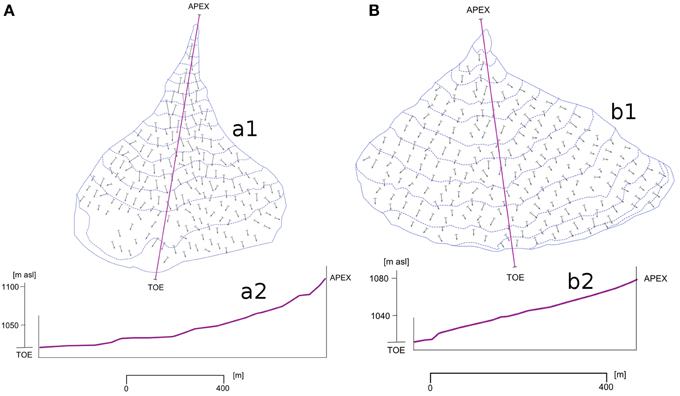
Figure 8. (A) BCM fan geometry (e.g., Rio Secco, Salbertrand, Turin, Italy). (a1) Steeper fan slopes are shown by longer arrows. Fan slope is irregular with higher gradient at the apex zone of alluvial fan. The longitudinal cross-section of BCM fan (a2) are characterized by slopes significantly higher than the ECM and GCM fans, showing a sharp change in gradient that corresponds to changes in size of the deposited material. (B) BCM fan geometry, deposited by sheet-flooding processes (e.g., Rio Geronda, Salbertrand, Turin, Italy). (b1) Steeper fan slopes are shown by the longer arrows. Fan slope is regular and characterized by a longitudinal profile (b2) with more gentle slope than the BCM alluvial fans dominated by debris flow processes.
Selection of the Test Catchments
Three catchments have been selected in the upper Susa Valley, characterized and classified according to the previous indications.
ECM test—catchment: the Rio Gautier (Rio Frejus)
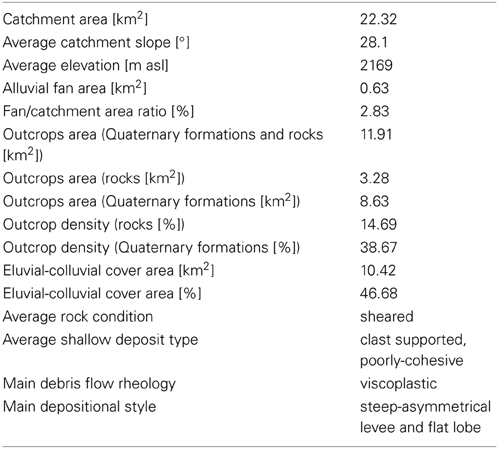
The Rio Frejus catchment (Table 1) is about 22 km2 and on its alluvial fan stands the Bardonecchia town (Turin, Italy). The Frejus catchment is mostly composed by calc-schistes and characterized by a high density of active landslides (about 50% of the catchment surface) which sometimes involve the whole slopes (deep-seated gravitational slope deformations) (Figure 9A). The high frequency of mass transport phenomena is due to the abundance of debris along stream channels.
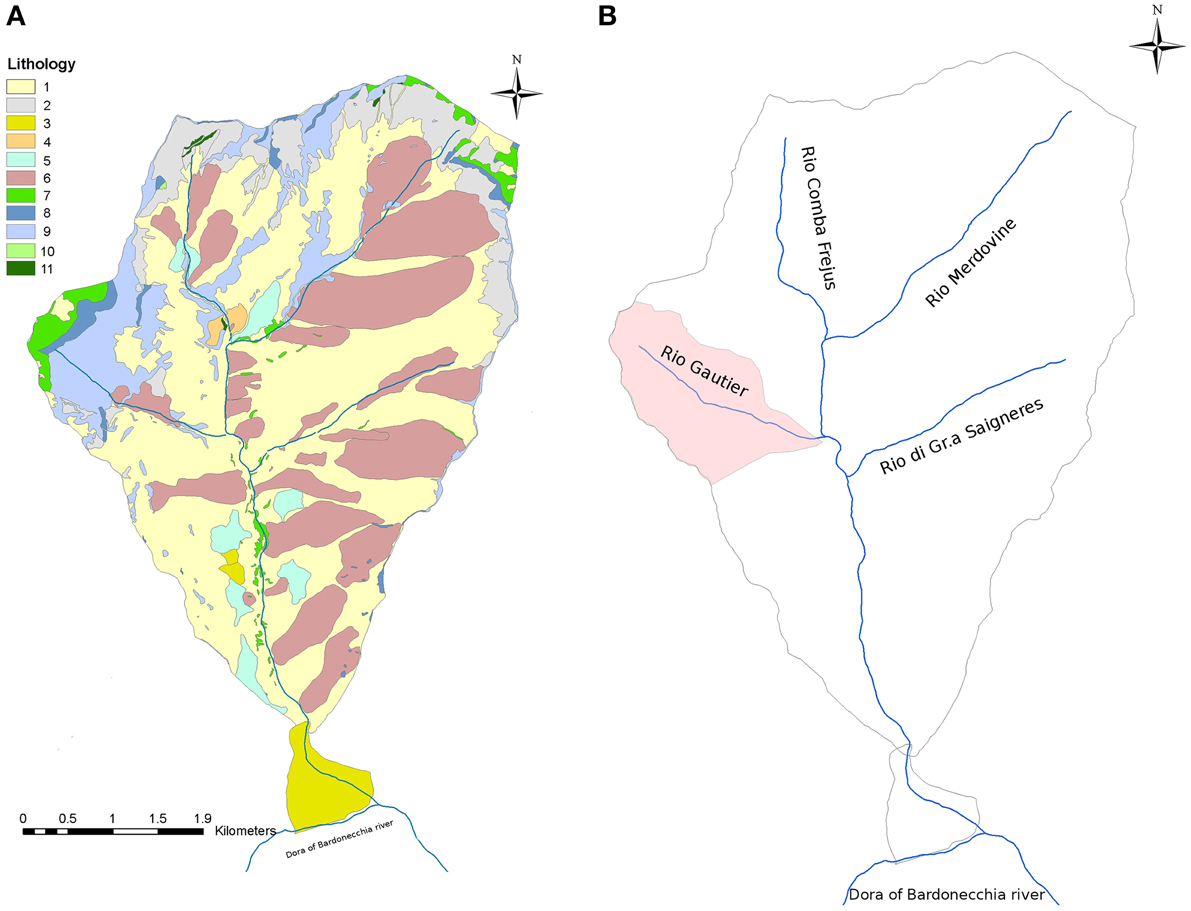
Figure 9. (A) Geological sketch map of the Rio Frejus catchment: (1) colluvial cover, (2) talus deposit, (3) alluvial fan deposit, (4) diamicton deposit, (5) glacial deposit, (6) landslide deposit, (7) calc-schist, (8) black shale, (9) marble and phyllite, (10) quartzite, (11) serpentinite. The percentages of outcrops: 74.2% shallow deposits, 27.28% schists, 0.22% serpentinites, and 0.03% quartzites. (B) The Rio Gautier catchment (in red).
The main features of Rio Frejus are reported in Table 1.
The Rio Frejus catchment, stretching in a N-S direction is articulated in various sub-catchments. The main sub-catchments are: Rio Merdovine, Rio Comba del Frejus, Rio Gautier and Rio Gr.a Saigneres (Figure 9B).
Debris flow triggering analysis of the last century (21 reported events between 1989 and 2009), highlights different frequencies for different types of processes observed on the alluvial fan: debris flows with high fine content (with an average occurrence of more than 1 year) and hyperconcentrated flows (with an average occurrence of less than 1 year).
In all the Rio Frejus catchment, extensive source areas from which debris flows could originate were observed. In particular, the catchment between the Rio Merdovine and the Rio Gautier catchments presents large accumulations of unconsolidated material at the base of cliffs. The latter are characterized by a high degree of fracturing and alteration. These deposits are deeply incised by numerous gullies and represent important sources of erodible clayey material.
Along less steep slopes there are modest quantities of eluvial-colluvial cover (usually < 2 m) where extensive shallow landslides and widespread rill erosion phenomena can be observed. The landslides also include slow slope movements, such as earth-debris slumps, where the sliding surface is found mostly in correspondence to the colluvial cover-bedrock contact. Moreover, there are large quantities of well-preserved debris flow deposits on the main channel bed of Rio Frejus.
In this work, the Rio Gautier was identified as the main source area, because historically it is the catchment where the highest number of debris flows have occurred (Figure 9B) (Bosco et al., 2007).
GCM test-catchment: the Rio Fosse
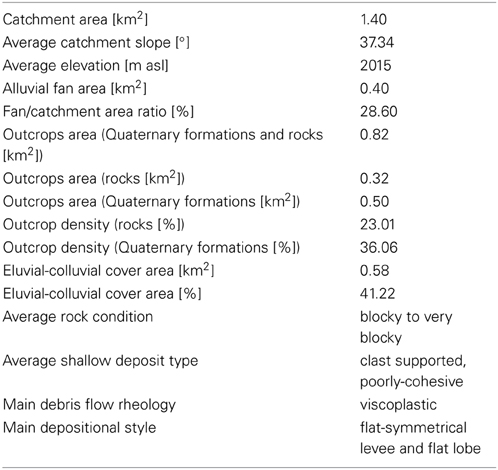
The Rio Fosse is a small catchment with an area of about 1.40 km2 characterized by a catchment lithology mainly formed by dolostones and limestones, and subordinate calc-schists (Figure 10) It is located near town of Bardonecchia (Turin, Italy).
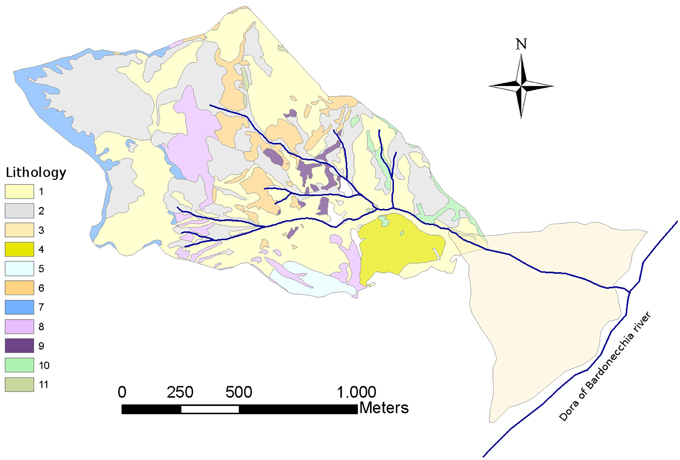
Figure 10. Geological sketch map of the Rio Fosse catchment. (1) Colluvial cover, (2) talus deposit, (3) alluvial fan deposit, (4) landslide deposit, (5) glacial deposit, (6) karst carbonate breccia (“pseudocarniole” Alberto et al., 2008), (7) limestone, (8) dolostone, (9) gypsum, (10) calc-schist, (11) carbonate schist. The percentages of outcrops: 50% shallow deposits, 37% carbonate rocks, 7% calc-schists, and 6% gypsum.
Viscoplastic debris flows (identified from the deposits on the fan) are the dominant processes along the Rio Fosse main incised channel and they are the main processes forming the large alluvial fan.
The main features of Rio Fosse are reported in Table 2.
The triggering areas were identified as two secondary gullies at the catchment head where debris deposits were observed. These main source areas are characterized by a high production of unconsolidated material and very steep slopes composed of dolomitic limestones and secondary outcrops of gypsum and carbonate breccias. Generally, the debris flows occurring at the Rio Fosse, are triggered if the runoff is able to mobilize the coarser sediments covering the surface of the bed-sediment layer. The surface layer in channel bed is somehow armored through the presence of winnowed partially open-work deposit that cover a clast-supported deposits formed by blocks and boulders in a matrix formed by gravel, sand and clayey-silt. The mobilization of coarse sediments of shallow layers produces debris flows and the entrainment of underlying matrix-rich deposits is responsible of the viscoplastic behavior of debris flows.
The historical records of this catchment showed 25 debris flow events characterized by a low-moderate magnitude since 1868. However, only the data between 1947 and 1973 constitute a continuous historical dataset. The Second World War occurred just before this time-interval and many risk mitigation structures were constructed after 1973. Moreover, the main target-object (the “Camping mari e monti”) was removed in 1985.
BCM test—catchment: the Rio Secco
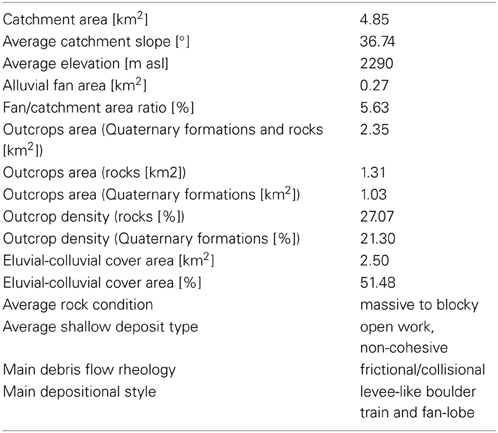
Rio Secco is located near the Salbertrand village (Turin, Italy) and has a catchment area of about 4.85 km2. It is characterized by a lithology mainly formed by gneisses and massive mica-schists, and very subordinate dolostones and calc-schists (Figure 11).

Figure 11. Geological sketch map of the Rio Secco catchment. (1) Colluvial cover, (2) talus deposit, (3) diamicton deposit, (4) karst carbonate breccia, (5) glacial deposit, (6) alluvial fan deposit, (7) calc-schist, (8) dolostone, (9) gypsum, (10) marble, (11) quartzite and carbonate breccia, (12) massive quartzite and quartzite meta-conglomerate, (13) mica-schist, (14) amphibolite, (15) mica-schist and paragneiss, (16) orthogneiss. The percentages of outcrops: 44.02% shallow deposits, 39.4% massive crystalline rocks, 13.2% carbonates, 3.2% schists, and 0.5% gypsum.
The frictional/collisional debris flows are the dominant processes along the main channel of the Rio Secco and forming its alluvial fan. The main depositional style is well-preserved by levee-like boulder train and fan-lobe deposits.
The main features of Rio Secco are reported in Table 3.
The source areas are characterized by abundant talus deposits distributed at the catchment head. The main source areas have large deposits of very coarse material, with open work structure that resists on very steep slopes.
The mobilization of coarse sediments is possible only with very extreme rainfall events. In fact, the historical records of this catchment showed only eight debris flow events occurred between 1728 and 2000.
Materials and Methods
The aim of this study is the definition of a procedure for selecting the most probable dominant flow process for debris flows in catchments on the basis of the dominant lithology. The knowledge of type of flow process aids the choice of the constitutive law that can be implemented in analytical or numerical simulations required for the determination of debris flow runout. This procedure should be intended as a comprehensive tool for risk mitigation for small catchments or large catchments containing several sub-catchments periodically affected by channelized debris flows. The results should be considered as possible scenarios. This methodology has been tested in the three catchments described above.
Simulation of Depositional Patterns
Debris flow deposition patterns in the selected catchments have been simulated by a 3D numerical code based on Cellular Automata Method. The numerical code was originally created to analyze debris flows in the inertial regime (Segre and Deangeli, 1995), according to the solution of Takahashi (1978, 1991), based on the dilatant fluid (Bagnold, 1954) constitutive law. A detailed description of the mathematical algorithms implemented in the code is reported in the papers of Segre and Deangeli (1995) and Deangeli (2008). This numerical tool was successfully applied to analyze flume experiments (Deangeli, 2008) and the evolutive behavior of actual granular flows, occurred in different settings and contexts (Deangeli and Grasso, 1996; Deangeli and Giani, 1998). The original code has been improved and modified by the implementation of a viscoplastic algorithm by Deangeli et al. (2013).
The numerical code was set up to analyze debris flows in a 3D field over a rigid substratum. The linear momentum conservation equation and the mass balance are imposed together with the constitutive law. The combination and integration of the previous equations supplies the velocity of the debris flow. The average velocity is used for the calculation of the flow rate in the model. The solid-liquid mixture is considered as a single phase fluid. The site is discretized in elementary cells of finite size. The state of each cell in then defined, according to the geometric and rheological features of the debris material. The system evolves in discrete timesteps, based on the Courant criterion. The simulations starts from the original configuration of the debris material deposited on the channel bed and/or on the adjacent slopes. The debris material is then saturated and the quantities necessary for a given rheology are then calculated. At each time step, for every cell of the system, a flow rheology-dependent initiation rule is verified. If a cell satisfies the initiation condition, a flow rate proportional to the timestep is calculated and stored. The system is simultaneously updated, according to the flow rates of each cell, at the end of the time step. The elementary flows from one cell to another cell are uniform flows. Deposition and remobilization of the debris material can occur at each time step, according to the evolution of the system. The simulation ends when no cell can receive or supply a rate of solid liquid mixture.
A key issue to be considered in debris flow modeling is whether the actual flow behavior can be regarded as a viscoplastic flow or a frictional/collisional flow.
The debris flow behavior depends on many factors and the coexistence, for a given event, of different regimes during the propagation phase has been observed (Iverson, 2003). The evolving behavior of granular flows has been observed also in flume experiments under controlled conditions (Deangeli, 2008).
As noted by Hungr (1995, 2002) it is necessary to choose an equivalent fluid whose rheological properties supply a bulk behavior of the flow similar to the supposed bulk behavior of the actual flow. Consequently the properties of the equivalent fluid do not necessary correspond to those of the actual flowing material. The properties of this fluid cannot be measured directly and must be evaluated by back analysis of past events by matching some field data: deposition pattern, flow velocity. However, this does not provide evidence that the constitutive equation is appropriate (Ancey, 2007).
The volumes of past events can be estimated by field surveys, but there is always the doubt concerning the entrainment and/or the deposition of material along the debris flow path. These two processes, entrainment and deposition, strongly influence the overall phenomenon. As observed by Rickenmann et al. (2006), in practical applications such problems are by-passed by running the numerical simulations with various reasonable scenarios for volume and other parameters. However, the rheological parameters resulting from the process of back analysis are sometimes dependent on the magnitude of the event.
The previous considerations have steered some aspects related to the debris flow modeling in the three selected catchments:
1. The phenomenon is simulated from the initiation through the propagation along the channel to the deposition. This approach allowed the investigation of the deposition along the path, that was mainly observed in ECM catchments.
2. Unlike other more classic approaches proposed and applied in the same alpine context (Bertolo and Bottino, 2008; Pirulli and Marco, 2010), the model does not attempt to reproduce a specific past debris flow event and its actual deposition areas, but it considers a reasonable volume for the investigated site based on the distribution and density of sediment source areas and an admissible deposition pattern compatible with the alluvial fan geometry and the depositional style characterizing the considered catchment. The aim of the simulations is to match the predominant observed depositional style on the alluvial fan and the channel bed. In this way, the model can be applied in absence of a detailed report (actual magnitude, invasion areas, etc.) of a debris flow event used as calibration test.
3. Very simple constitutive laws are used for the numerical simulations, in order to reduce the number of unknowns that cannot be realistically assessed with field surveys.
The numerical simulations of debris flows in the three selected catchments have been carried out according to the rheological behavior resulting from the classification proposed in the previous paragraphs:
1. The Rio Gautier catchment is characterized by a high amount of fine sediments, therefore the numerical runs have been performed with a viscoplastic constitutive law.
2. The Rio Fosse catchment is characterized by a medium/high amount of fine sediments. The depositional patterns observed in site indicate a viscoplastic behavior, influenced by the presence of granular material. Therefore, the numerical runs have been carried out with both the constitutive laws: frictional/collisional and viscoplastic.
3. The Rio Secco catchment is strongly characterized by the presence of coarse granular material. The numerical runs have been performed with a frictional/collisional constitutive law.
DTM used for the numerical simulations is composed by square cells of 10*10 m. Inaccuracy of the topography data affects the numerical simulations, resulting in preferential flow paths and deposition patterns that have not any confirmation with on site investigations (Deangeli et al., 2015). The inconsistency of such a type of errors can therefore be detected with the comparison between simulations results and in site evidences.
The Constitutive Laws and the Rheological Parameters
For viscoplastic debris flows the simple Bingham law has been implemented in the Cellular Automata code (Deangeli et al., 2013):
where τy is the yield stress and μ is the viscosity of the mixture.
In viscoplastic fluid models the most important variation of the final results is related to the yield strength of the material that affects movement and stopping of the flow. At first a lower bound of yield stress and viscosity can be defined, on the basis of laboratory measurements reported in the literature (O'Brien and Julien, 1988). However, in the studied cases the coarse debris was not negligible if compared with the bulk grain size distribution of the material: this coarse fraction contributes to the yield strength by means of frictional contacts (Rodine and Johnson, 1976; Iverson, 1997a,b, 2003; Coussot et al., 1998).
In order to consider the properties of the bulk material, debris flow deposition is assumed to occur when the basal shear stress no longer exceeds the shear strength (Sosio et al., 2007). According to Johnson (1970) and Johnson and Rodine (1984), and assuming a Coulomb viscous model for the material, the thickness of the deposited material observed in site has been used for the assessment of the shear strength of the debris flow. This approach assumes that the yield strength is approximately equal to the mean basal shear stress at the time of deposition:
where h is the thickness of lobes with width-to-depth ratios >10 (Whipple, 1997), γ is the unit weight of the fluid matrix and θ is the bed slope at which the motion stops. The viscosity is estimated from the maximum debris flow velocity (Sharp and Nobles, 1953; Fink et al., 1981; Johnson and Rodine, 1984):
where Q is the flow discharge, Rc is the channel radius and dm is the radius of the rigid plug above a critical flow depth:
The procedure reported above suffers from the uncertainties related to the estimate of the involved variables. However, it is necessary to find an engineering solution to the problem related to the rheological parameters required for the numerical simulations of scenarios.
The solution adopted in the present study is based on a preliminary calculation of the rheological parameters, according to Equations (2), (3) and (4), by the introduction of the most frequent observed values of the variables for each catchment. These preliminary values of the rheological parameters are in agreement with those reported in the literature (Sosio et al., 2007).
Afterwards different independent random seeds were used to assign a relatively small deviation around the calculated value of each rheological parameter.
For frictional/collisional debris flows the Bagnold grain inertial constitutive law was implemented by Segre and Deangeli (1995):
Where: a is an empirical constant, ϕ is the friction angle of the debris (according to the Takahashi solution), ρ s is the density of the solid particle; λ is the linear concentration of the mixture and d is the grain diameter.
The debris flow velocity is calculated according to the solution proposed by Takahashi (1978, 1991). The debris flow initiation rule is based on the scheme of an infinite slope subject to seepage parallel to the slope:
Where ρ is the density of the solid-liquid mixture and ρf is the density of the interstitial fluid.
Results of the Simulations and Discussion
The results of the numerical runs are reported in terms of area of deposition of debris flow events. In particular the position, the shape and the thickness of the deposit of debris flows, potentially occurring in each catchment, are compared with in situ evidences. Several simulations for each case are performed with different values of the rheological parameters in order to obtain the best fit with in situ data (in all the figures the contour of the alluvial fan is reported in red).
The Rio Gautier (Rio Frejus)
Since the Rio Gautier has been classified as ECM catchment, the viscoplastic law has been adopted. The initial rheological parameters, calculated according to Equations (2), (3) and (4), are τ = 1400 Pa and μ = 80 Pa*s, by assuming a solid concentration equal c = 0.4. In this case the frictional resistance of the debris material is strongly reduced by the high content in fines. This is reflected in the relatively low value of the obtained yield strength. The interstitial fluid used in the simulations is water (ρf = 1000 kg/m3).
The result of the numerical run correspondent to the calculated values is reported in Figure 12. This figure shows that the process of deposition occurs on both the channel bed (close to 45% of total volume, or higher) and fan, in agreement with in site observations.
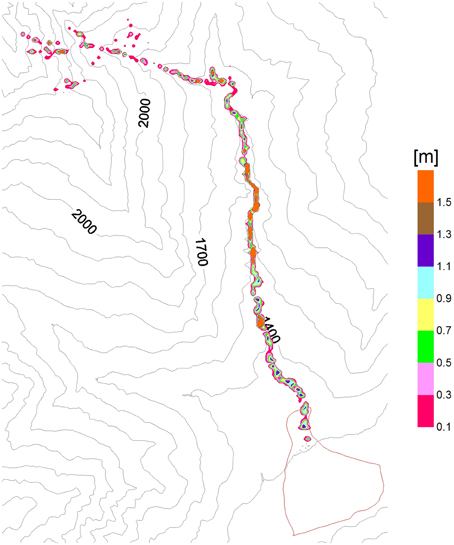
Figure 12. Rio Gautier (Rio Frejus) debris flow simulation: viscoplastic rheology (τ = 1400 Pa; μ = 80 Pa*s; C = 0.4).
Deposition style sensitivity to yield strength and viscosity has been investigated. The results of numerical simulations performed with an increased yield strength τ = 2000 Pa and with the calculated value of viscosity does not substantially change the scenario of deposition. Conversely when the numerical runs are performed with a large increase of the rheological parameters (τ = 3000 Pa and μ = 115 Pa*s) the deposition occurs exclusively on the channel bed.
The Rio Fosse
The numerical simulations of debris flows in the Rio Fosse have been performed with two different rheological laws, frictional/collisional and viscoplastic, being this catchment type (GCM) intermediate between the other two types (ECM and BCM).
Numerical runs performed with the frictional/collisional constitutive law considered the variation of the friction angle (15, 25, 30, and 35°), the density of the interstitial fluid (water ρf = 1000 kg/m3 and muddy water ρf = 1200 kg/m3) and the solid concentration (c = 0.4 and c = 0.5).
The results of the run performed with a friction angle equal to 15° appear to be poorly consistent with the depositional style of the catchment. In this case the spread of the material is characterized by a very thin and too extended deposit.
Figures 13A–D report the results of some numerical simulation characterized by water as interstitial fluid. The case correspondent to a friction angle equal to 35° (Figure 13A) is characterized by strong deposition along the channel (close to 30% of total volume) and at the apex of the alluvial fan. Results more consistent with in situ evidences are obtained with lower friction angles (25 and 30°) or with a lower solid concentration (c = 0.4) as reported in Figures 13B–D, respectively. Although the effect of a decrease in solid concentration supplies depositional styles similar to those obtained with a reduced frictional angles (25 and 30°) however the value of the friction angle for the best fit resulted equal to 35°. This value is maybe too high for the solid concentration of the mixture (c = 0.4).
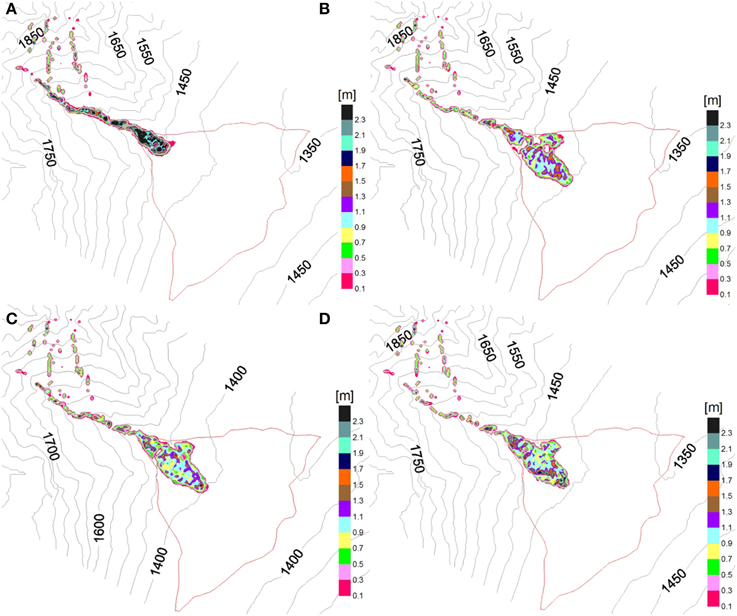
Figure 13. Rio Fosse debris flow simulation. (A) Frictional/collisional rheology (= 35°; C = 0.5; ρf = 1000 kg/m3); (B) Frictional/collisional rheology (= 25°; C = 0.5; ρf = 1000 kg/m3); (C) Frictional/collisional rheology (= 30°; C = 0.5; ρf = 1000 kg/m3); (D) Frictional/collisional rheology (= 35°; C = 0.4; ρf = 1000 kg/m3).
Figure 14A reports the numerical results for a frictional/collisional rheology when the interstitial fluid is muddy water. This type of analysis considers the finer part of the material as a component of the fluid phase. The best fit is obtained with a friction angle equal to 35° and a solid concentration equal to 0.5. The figure indicates that the effect of an increase in fluid density produces an increase of the area involved in the deposition process. Wholly this result appears more consistent than the previous ones in terms of thickness of the deposited material.
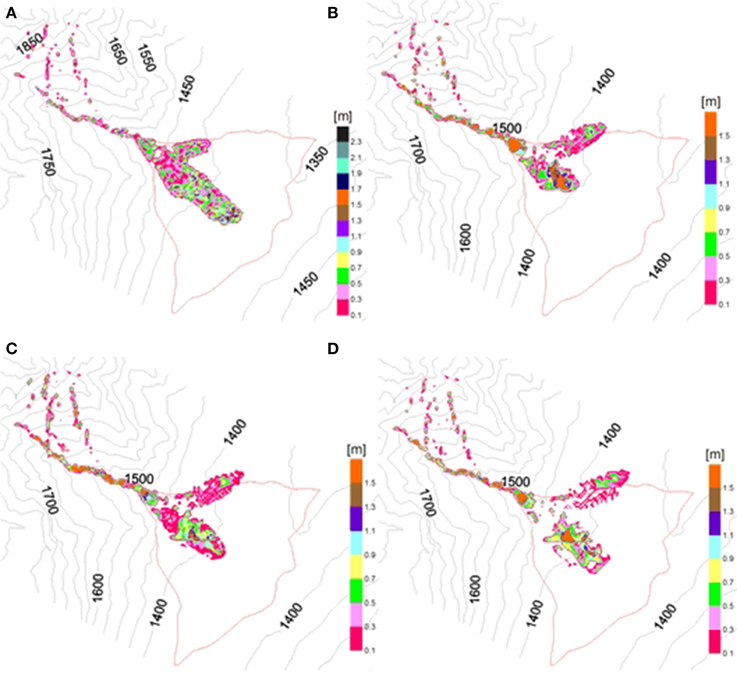
Figure 14. Rio Fosse debris flow simulation. (A) Frictional/collisional rheology (= 35°; C = 0.5; ρf = 1200 kg/m3) (B) Viscoplastic rheology (τ = 4460 Pa; μ = 200 Pa s; C = 0.5); (C) Viscoplastic rheology (τ = 4000 Pa; μ = 190 Pa s; C = 0.5); (D) Viscoplastic rheology (τ = 3100 Pa; μ = 190 Pa s; C = 0.5).
The use of the viscoplastic law needs the calculation of the rheological parameters with Equations (2), (3), and (4). The resulting values are τ = 4460 Pa and μ = 200 Pa*s. In this case the depositional pattern obtained in the numerical simulation (Figure 14B) is in good agreement with in situ observations, although a relative high amount of material is deposited on the channel bed. A small reduction of the yield strength τ = 4000 Pa and viscosity μ = 190 Pa*s reduces the amount of deposited material on the apex of the fan and results in a more flat style of deposition, in agreement with in site observations (Figure 14C).
A further reduction in yield strength (τ = 3100 Pa) leads to a depositional pattern less consistent with the observations (Figure 14D), indicating that the value of the yield strength suitable for this catchment is probably just slightly lower than the value calculated with Equation (2), according to Figure 14C.
For the numerical simulations performed with the viscoplastic law the deposition of the material on the left side is out the boundary of the alluvial fan. This result is consistent with in situ evidences for this type of catchments.
All the results of the numerical runs indicate that for this type of catchments the coarse fraction of the debris cannot be disregarded because strongly contributes to the (shear) strength by means of frictional contacts. This is reflected in the “high” values of the yield strength (τ = 4000 Pa) if the viscoplastic rheology is implemented. On the other hand the relatively high presence of clayey material strongly influences the behavior of the mixture. In fact the values of the friction angle should range from 25 to 30° if the frictional/collisional rheology is adopted. This range of friction angles could appear low if one consider the strong presence of very coarse debris, typical of this type of catchments.
The Rio Secco
According to the classification of the catchments in the Western Alps, Rio Secco belongs to BCM type. The numerical simulations of debris flows have been carried out with the frictional/collisional rheology.
As the debris mantling is characterized by very coarse material, the friction angle used in the numerical runs ranges from 35 to 40°. The interstitial fluid used in the simulations is water (ρf = 1000 kg/m3).
Figure 15 reports the results obtained with a friction angle equal to 38°. The depositional style is characterized by steep slopes of the deposit and scarce deposition along the channel bed (close to 15% of total volume). Despite the considerably high volume of debris material involved in the process the area affected by the deposition is quite small and corresponds to the alluvial fan apex, but the thickness of deposit is relevant, as it can be observed in site. The position of deposited materials (on the left side of the apex) is caused by a very high concentration of mega boulders in the apex zone.
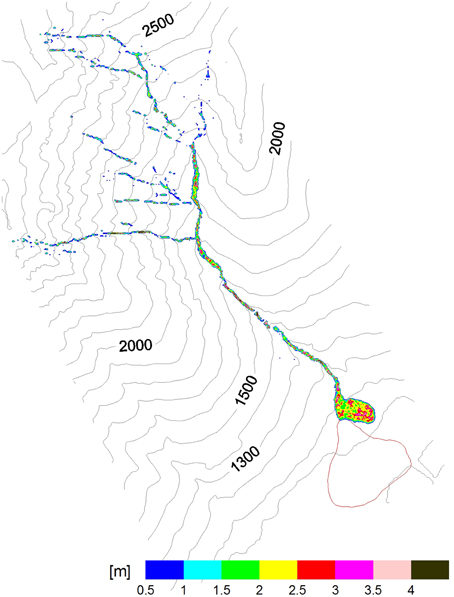
Figure 15. Rio Secco debris flow simulation: frictional/collisional rheology (= 38°; C = 0.5; ρf = 1000 kg/m3).
Globally the depositional pattern is in agreement with in site observations, indicating that the frictional/collisional rheology is appropriate for this type of catchments.
Discussion
The results of the simulations for the site with ECM material show a good agreement with in site observations. In fact deposition occurs on both the channel bed and fan as expected in such a type of catchments. Although the constitutive law implemented for the analysis is very simple, however the use of a viscoplastic rheology in ECM catchments seems to capture the macroscopic features of real events. Furthermore, for this specific case, considering the volume involved in all the analysis, the more consistent results are those obtained with the calculated values of the rheological parameters, according to Equations (2), (3), and (4). However, this outcome needs to be confirmed by other simulations performed in different ECM catchments.
For the GCM catchment, which is characterized by an intermediate type of material, both the frictional/collisional and the viscoplastic constitutive laws have been used. The simulations performed with the frictional/collisional law evidenced that the best fit is obtained with friction angles relatively high (25–30°), confirming the importance of the coarse material in flow behavior and in deposition style. In this context some simulations have been carried out by considering an increased density of the fluid phase. This approach produced the best result with a friction angle = 35°, which is a consistent value, because it just refers to the coarser part of the debris material. The depositional pattern obtained with this approach seems to be more in agreement with in site data than that obtained with the previous analysis. The rheological parameters obtained with Equations (2), (3), and (4) for the viscoplastic analysis are definitively higher than those calculated for ECM catchment. The results of simulations performed with the calculated parameters and those performed with reduced parameters indicate that probably the yield strength for the best fit is just slightly lower than the calculated value. The yield strength obtained with Equation (2) has been compared with a frictional yield strength, in order to obtain an equivalent friction angle. This equivalent friction angle resulted equal to 28°, which is an intermediate value of the range 25–30° obtained for the best fit in the frictional/collisional analysis. The depositional style obtained with the viscoplastic rheology seem to reproduce the observed phenomena, in terms of thickness and area of the debris material. In conclusions for catchments belonging to GCM type, the presence of both fine and coarse material cannot be disregarded. According to the numerical results, in this type of catchments, the best results are obtained with the viscoplastic rheology although in this case, deposition occurs also on the channel bed. The parameters of the rheological law calculated with Equations (2), (3), and (4) should be reduced for obtaining the best fit.
The numerical runs in the BCM catchments have been performed exclusively with the frictional/collisional law. According to in situ observations the investigated range of friction angles is quite high (35–40°). The best fit has been obtained with = 38°. This angle is 10° lower than that equivalent friction angle back analyzed for the GCM catchment, showing that the frictional collisional law is appropriate for BCM catchments. The modeled depositional style is in agreement with in site observations and is characterized by scarce volume of deposited material along the channel bed. In all the simulations the area of deposition on the fan is quite small but the thickness of deposits is very high and deviated with respect to the alluvial fan delimitation (red line). This fact can be related to the presence of big boulders in the apex zone and to the consequent topography inaccuracy, being the grid 10 x 10 m.
Conclusions
A classification of debris flow source areas in the Western Alps based on the catchment lithology has been presented. The classification is based on the features of the outcropping rock masses that originates unconsolidated material with different grain size distribution. The outcomes of the catchment classification have identified in the Western Alps three distinct classes of derived source material: Excellent Clay Maker, Good Clay Maker, and Bad Clay Maker.
The grain size of the material affects its propensity to be mobilized during rainfall events. The fine content influences the behavior of the water solid mixture and the depositional style of debris flows. Therefore, the type of lithology of the catchments may directly help for the choice of the constitutive law to be implemented in numerical simulations for the definition of debris flow deposition scenarios.
The methodology has been applied to three catchments located in the Western Alps, exhibiting different features according to the geological model.
Debris flow simulations have been performed with a 3D numerical code based on Cellular Automata Method. The results of the numerical simulations have proved the reliability of the geological model for the three investigated catchments.
Although the behavior of debris flows is very complex and may vary along the path and a fixed constitutive law is not capable to capture all the processes occurring during the evolution of the phenomenon, however the results of the numerical runs are in good agreement with in site observations. In particular the numerical results are compatible with the architecture and the morphological features of the alluvial fans of the three investigated catchments. Finally the proposed methodology seems to be a simple but effective tool for the set up of debris flow scenarios devoted to the hazard mitigation.
Conflict of Interest Statement
The Associate Editor Markus Stoffel declares that, despite having collaborated with the author Davide Tiranti, the review process was handled objectively. The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Alberto, W., Giardino, M., Martinotti, G., and Tiranti, D. (2008). Geomorphological hazards related to deep dissolution phenomena in the Western Italian Alps: distribution, assessment and interaction with human activities. Eng. Geol. 99, 147–159. doi: 10.1016/j.enggeo.2007.11.016
Ancey, C. (2007). Plasticity and geophysical flows: a review. J. Nonnewton. Fluid Mech. 142, 4–35. doi: 10.1016/j.jnnfm.2006.05.005
Bagnold, R. A. (1954). Experiments on a gravity-free dispersion of large solid spheres in a Newtonian fluid under shear. Proc. R. Soc. Lond. A 225, 49–63.
Bardou, E., Ancey, C., Bonnard, C., and Vulliet, L. (2003). “Classification of debris flow deposits for hazard assessment in alpine areas,” in Debris Flow Hazard Mitigation: Mechanics, Prediction and Assessment. Proceedings of the Third International Conference on Debris-Flow, eds D. Rickenmann and C. L. Chen (Davos; Rotterdam: Millpress), 1.
Bertolo, P., and Bottino, G. (2008). Debris-flow event in the Frangerello Stream-Susa Valley (Italy)—calibration of numerical models for the back analysis of the 16 October, 2000 rainstorm. Landslides 5, 19–30. doi: 10.1007/s10346-007-0099-7
Blair, T. C., and McPherson, J. G. (1994). Alluvial fans and their natural distinction from rivers based on morphology, hydraulic processes, sedimentary processes, and facies assemblages. J. Sediment Res. A 64, 450–489.
Bonnet-Staub, I. (1998). Définition d'une typologie des dépôts de laves torrentielles et identification de critères granulométriques et géotechniques concernant les zones sources. Bull. Eng. Geol. Environ. 57, 359–367.
Bosco, F., Gandini, D., Giudici, I., Marco, F., Paro, L., Tararbra, M., et al. (2007). “The mass movement of the Rio Frejus (Bardonecchia, NW Italian Alps) on August 6th, 2004,” in Evaluation and Prevention of Natural Risks, Vol. 470, eds S. Campus, S. Barbero, S. Bovo, and F. Forlati (London: Taylor and Francis Group NL/Balkema), 409–447.
Coussot, P., Laigle, D., Arattano, M., Deganutti, A., and Marchi, L. (1998). Direct determination of rheological characteristics of debris flow. J. Hydr. Eng. 124, 865–868.
Coussot, P., and Meunier, M. (1996). Recognition, classification and mechanical description of debris flows. Earth Sci. Rev. 40, 209–227.
Deangeli, C. (2008). Laboratory granular flows generated by slope failures. Rock Mech. Rock Eng. 41, 199–217. doi: 10.1007/s00603-007-0131-1
Deangeli, C., and Giani, G. P. (1998). “Physical and numerical models to rehabilitate a waste disposal site,” in Proceedings of the 8th International Congress IAEG (Vancouver; Rotterdam: Balkema), 1813–1818.
Deangeli, C., and Grasso, P. (1996). “The evolutive mechanism of debris flows: analysis and protection works,” in Proceedings of the 7th International Symposium on Landslides (Trondheim; Rotterdam: Balkema), 1183–1188.
Deangeli, C., Paltrinieri, E., and Tiranti, D. (2013). “Debris flow analysis: from lithological classification of the basin to deposition,” in Landslide Science and Practice, Vol. 3, Spatial Analysis and Modeling, Chap. 2: Rapid Landslide Runout Analysis, eds C. Margottini, P. Canuti, and K. Sassa (Berlin; Heidelberg: Springer-Verlag), 301–307, 440.
Deangeli, C., Tiranti, D., Marco, F., and Volpato, M. (2015). “Comparison of Debris flow depositional scenarios using different DTMs,” in Engineering Geology for Society and Territory, Vol. 2, eds G. Lollino, D. Giordan, G. B. Crosta, J. Corominas, R. Azzam, J. Wasowski, and N. Sciarra (Springer International Publishing), 1667–1671. doi: 10.1007/978-3-319-09057-3_296
Fink, J. H., Malin, M. C., D'Alli, R. E., and Greeley, R. (1981). Rheological properties of mudflows associated with the Spring 1980 eruptions of Mount St. Helens volcano, Washington. Geophys. Res. Lett. 8, 43–46.
Hungr, O. (1995). A model for the runout analysis of rapid flow slides, debris flows and avalanches. Can. Geotechnical J. 32, 610–623. doi: 10.1139/t95-063
Hungr, O. (2002). “Analytical models for slides and flows,” in Proceedings of the International Symposium on Landslide Risk Mitigation and Protection of Cultural and Natural Heritage, ed K. Sassa (Kyoto: Kyoto University), 559–586.
Iverson, R. M. (1997b). “Hydraulic modelling of unsteady debris flow surges with solid–fluid interactions,” in First International Conference on Debris-Flow Hazard Mitigation: Mechanics, Prediction and Assessment, ed C. L. Chen (New York, NY: American Society of Civil Engineers), 550–560.
Iverson, R. M. (2003). “The debris flow rheology myth,” in Third International Conference on Debris-Flow Hazard Mitigation: Mechanics, Prediction and Assessment, eds D. Rickenmann and C. L. Chen (New York, NY: American Society of Civil Engineers) 303–314.
Jakob, M., and Hungr, O. (2005). Debris-Flow Hazards and Related Phenomena. Heidelberg: Springer-Verlag/Chichester: Praxis Publishing Ltd.
Johnson, A. M. (1970). “Debris flows,” in Physical Processes in Geology (San Francisco, CA: Freeman, Cooper), 433–534.
Johnson, A. M., and Rodine, J. D. (1984). “Debris flow,” in Slope Instability, eds D. Brunsden and D. B. Prior (Chichester: Wiley), 257–361.
Lin, C. W., Wu, M. C., and Shieh, C. L. (2000). “Influence of geology on debris-flows: examples from Hsin-Yi, Nantou County, Taiwan,” in Debris Flow Hazard Mitigation: Mechanics, Prediction and Assessment. Proceedings of the Second International Conference on Debris-Flow, eds G. F. Wieczorek and N. D. Naeser (Taiwan: Balkema), 169–176.
Moscariello, A., Marchi, L., Maraga, F., and Mortara, G. (2002). “Alluvial fans in the Alps: sedimentary facies and processes,” in Flood and Megaflood Processes and Deposits: Recent and Ancient Examples, Vol. 32, eds I. P. Martini, V. R. Baker, and G. Garzón (Oxford, UK: Blackwell Publishing Ltd.), 141–166. doi: 10.1002/9781444304299.ch9
O'Brien, J. S., and Julien, P. Y. (1988). Laboratory analysis of mudflow properties. J. Hydr. Eng. 110, 877–887.
Pirulli, M., and Marco, F. (2010). Description and numerical modelling of the October 2000 Nora debris flow, Northwestern Italian Alps. Can. Geotech. J. 47, 135–146. doi: 10.1139/T09-082
Rickenmann, D., Laigle, D., McArdell, B. W., and Hubl, J. (2006). Comparison of 2D debris-flow simulation models with field events. Comput. Geosci. 10, 241–264. doi: 10.1007/s10596-005-9021-3
Rodine, J. D., and Johnson, A. M. (1976). The ability of debris, heavily freighted with coarse clastic material to flow of gentle slope. Sedimentology 23, 213–234.
Segre, E., and Deangeli, C. (1995). Cellular Automaton for realistic modelling of landslides. Nonlinear Process. Geophys. 2, 1–15.
Sharp, R. P., and Nobles, L. H. (1953). Mudflow of 1941 at Wrightwood, southern California. Geol. Soc. Am. Bull. 64, 547–560.
Sosio, R., Crosta, G. B., and Frattini, P. (2007). Field observations, rheological testing and numerical modelling of a debris flow event. Earth Surf. Process. Landforms 32, 290–306. doi: 10.1002/esp.1391
Tiranti, D., Bonetto, S., and Mandrone, G. (2008). Quantitative basin characterization to refine debris-flow triggering criteria and processes: an example from the Italian Western Alps. Landslides 5, 45–57. doi: 10.1007/s10346-007-0101-4
Tiranti, D., Cremonini, R., Marco, F., Gaeta, A. R., and Barbero, S. (2014). The DEFENSE (DEbris Flows triggEred by storms - Nowcasting SystEm): an early warning system for torrential processes by radar storm tracking using a Geographic Information System (GIS). Comput. Geosci. 70, 96–109. doi: 10.1016/j.cageo.2014.05.004
Whipple, K. X. (1997). Open-channel flow of Bingham fluids: applications in debris-flow research. J. Geol. 105, 243–257.
Keywords: torrential sedimentary processes, catchment lithology, flow rheology, cellular automata model, Western Alps
Citation: Tiranti D and Deangeli C (2015) Modeling of debris flow depositional patterns according to the catchment and sediment source area characteristics. Front. Earth Sci. 3:8. doi: 10.3389/feart.2015.00008
Received: 24 September 2014; Accepted: 15 February 2015;
Published online: 03 March 2015.
Edited by:
Markus Stoffel, University of Geneva, SwitzerlandReviewed by:
José Darrozes, Université de Toulouse, FranceAdrian Parker, Oxford Brookes University, UK
Copyright © 2015 Tiranti and Deangeli. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Davide Tiranti, Hydrology and Natural Hazards, Department of Forecasting Systems, Regional Agency for Environmental Protection of Piemonte, Via Pio VII n. 9, 10135 Turin, Italy e-mail:ZGF2aWRlLnRpcmFudGlAYXJwYS5waWVtb250ZS5pdA==
 Davide Tiranti
Davide Tiranti Chiara Deangeli
Chiara Deangeli