- 1Water Resources Section, Faculty of Civil Engineering and Geosciences, Delft University of Technology, Delft, Netherlands
- 2Geoscience and Remote Sensing Department, Faculty of Civil Engineering and Geosciences, Delft University of Technology, Delft, Netherlands
- 3Department of Inland Water Systems, Deltares, Delft, Netherlands
The hydrological decade on Predictions in Ungauged Basins (PUB) led to many new insights in model development, calibration strategies, data acquisition and uncertainty analysis. Due to a limited amount of published studies on genuinely ungauged basins, model validation and realism assessment of model outcome has not been discussed to a great extent. With this paper we aim to contribute to the discussion on how one can determine the value and validity of a hydrological model developed for an ungauged basin. As in many cases no local, or even regional, data are available, alternative methods should be applied. Using a PUB case study in a genuinely ungauged basin in southern Cambodia, we give several examples of how one can use different types of soft data to improve model design, calibrate and validate the model, and assess the realism of the model output. A rainfall-runoff model was coupled to an irrigation reservoir, allowing the use of additional and unconventional data. The model was mainly forced with remote sensing data, and local knowledge was used to constrain the parameters. Model realism assessment was done using data from surveys. This resulted in a successful reconstruction of the reservoir dynamics, and revealed the different hydrological characteristics of the two topographical classes. This paper does not present a generic approach that can be transferred to other ungauged catchments, but it aims to show how clever model design and alternative data acquisition can result in a valuable hydrological model for an ungauged catchment.
1. Introduction
In 2003 the International Association of Hydrological Sciences (IAHS) launched the Predictions in Ungauged Basins (PUB) initiative (2003–2013) (Sivapalan et al., 2003), to improve scientific understanding and estimation of hydrological behavior of ungauged catchments. The main reason behind this was because hydrologic behavior in ungauged basins is poorly understood (Sivapalan, 2003), while the majority of basins worldwide is effectively ungauged (Hrachowitz et al., 2013). Within these 10 years, the hydrological community developed a wide variety of new data acquisition techniques and approaches for hydrological modeling, to allow better estimations of model uncertainty and hydrological behavior in ungauged catchments. Although this resulted in a set of new tools and methods it remains difficult to put PUB into practice (Efstratiadis et al., 2014). We believe that this is strongly related to the fact that clear validation methods in PUB are still missing and are therefore omitted in many cases.
The lack of independent validation data does not only influence the validation process, but also blocks further model improvement, as there is no objective validation method to compare subsequent model versions. Unfortunately, this process does not get much attention, because many research papers present model development and validation rather as a linear process, while in reality it is an iterative process (Beven, 2011). Only few studies (e.g., Fenicia et al., 2008), present methods on how this iterative process can be described and formalized to improve our understanding of hydrological processes. Figure 1 gives an oversight of how we think the process of model development works in a classical and a PUB case. On the left the classical method is shown, which starts with an initial model development and enters an iterative process of model improvement based on certain validation criteria to find the optimal model structure. However, in PUB cases, validation data are often not available, which reduces the iterative process to a simple linear one (Figure 1, middle diagram), without a feedback mechanism. This means that in most cases we trust the tool or model we are using and accept the outcome of this tool as is. Sadly, this removes the important mechanism of error detection and model optimization. Additionally, this approach always leaves us with a lot of unanswered questions about model realism: Is this method also applicable in our study? What is the uncertainty and reliability of our results? And how can we compare the results from different methods?
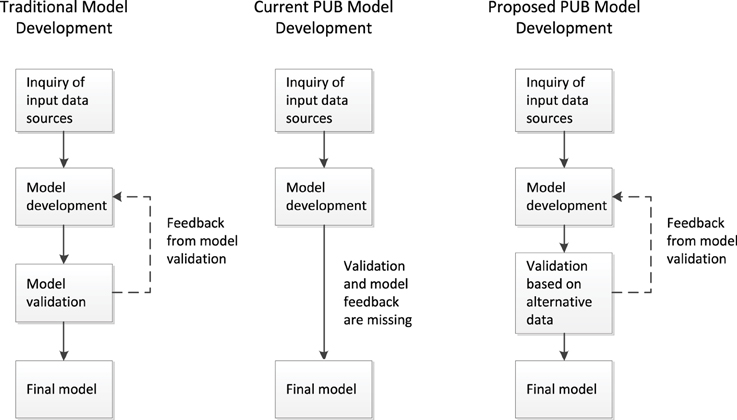
Figure 1. On the left a representation of the classical model development, in the middle the common practice in PUB cases, and on the right the proposed new approach for PUB cases. Due to the absence of a validation phase, the iterative model improvement is removed in most PUB cases, which makes the model much more sensitive for model errors and generally results in a sub-optimal model.
With this paper we aim to emphasize the fact that validation in PUB cases is of vital importance, because it enables the feedback mechanism in model development of PUB cases (Figure 1, right side) and reduces structural model uncertainty. Therefore, we have to find validation data, other than a priori defined data from gauging stations, which requires both creativity and in-depth knowledge of the local hydrology. Also, we have to accept that PUB models come with large model epistemic uncertainties. This means that estimation of the uncertainty in the model output becomes even more important to give adequate decision support. Our task is to adapt our model structure to the available data, and desired output, to minimize errors and uncertainties.
The setup of the paper is as follows: First a brief overview of the PUB heritage is given. Secondly, a case study in Cambodia is used as an illustration of PUB model development, calibration, and validation. Finally, our approach of model realism assessment in PUB is discussed.
2. PUB Heritage
The heritage of the PUB initiative consists of a large catalog, filled with tools that can be applied to any catchment, but particular in PUB cases. In this paragraph we do not aim to give a full oversight of the PUB heritage, but we will indicate the main methods for model improvement and uncertainty reduction. For a more elaborate and comprehensive overview of the PUB heritage see Hrachowitz et al. (2013). For this paper, we mainly used three types of papers that were published within the PUB framework: (1) new (remote sensing) data acquisition, (2) development of flexible, process based models, (3) and PUB case studies. We will briefly touch upon some examples from these categories that were (partially) used in our case study.
(1). By definition, ungauged basins have a significant lack of in situ hydrological data, such as precipitation, streamflow and evaporation time series. In search for methods to overcome this data gap, the PUB initiative helped to raise interest in the development of innovative in situ gauging techniques, as well as the use of remotely sensed earth observation data. Nowadays, precipitation (TRMM, Kummerow et al., 1998; GPM, Hou et al., 2014), evaporation and water stress (Bastiaanssen et al., 1998; van Emmerik et al., 2015), topography (DEM), large scale groundwater variation (GRACE, Mulder et al., 2015), reservoir dynamics (Eilander et al., 2014) and soil moisture (SMOS, Kerr et al., 2001; SMAP, Entekhabi et al., 2010; AMSR-E, Khan et al., 2012), among others, can be estimated on a global scale, with high temporal and spatial resolution. However, in most PUB cases these data are only used as model inputs, while hydrologists still rely on discharge measurements as a calibration and validation tool. This means that the iterative model development is still difficult, unless these new data are also used in the validation process.
(2). An important result of PUB was the development of flexible and process based modeling frameworks. During the PUB decade several flexible modeling approaches have been developed for comparison and testing (Beven, 2000; McDonnell, 2003; Savenije, 2009; Fenicia et al., 2011). For example, the FLEX modeling framework (Fenicia et al., 2008) is based on generic building blocks that can be combined to arrive at a tailor-made model, based governing hydrologic processes in a catchment. Savenije (2010) proposed the landscape driven FLEX-Topo modeling framework, which connects dominant land classes with governing hydrological processes. The advantage of this approach is that even in ungauged catchments dominant hydrologic processes can be identified and directly implemented in these models. Also, similarity of different catchments can be used to implement findings from gauged catchments into ungauged catchments (Gao et al., 2014a). These developments can therefore strongly improve the quality of the initial model setup.
(3). Over the years various PUB case studies have been presented, to test PUB tools, and assess their performance. However, in many cases gauged catchments were treated as ungauged catchments (e.g., Guo et al., 2012; Cibin et al., 2014), and the available streamflow data was used to conventionally assess the model performance. This is a very robust way to test PUB modeling strategies. However, if a catchment is truly ungauged, this is impossible, raising the question how well these tools would work in a really ungauged situation. This left the hydrological community with a wide range of methods that can improve the reliability of predictions in ungauged basins, but the lack of model validation methods in real case studies hinders a widespread use of these models. This is also expressed by Efstratiadis et al. (2014), who discussed model realism in truly ungauged case studies. They concluded that flood design and modeling in ungauged basins is more than “blind application of recipes,” and one should carefully assess to what extent modeling results can be trusted.
With this paper we would like to stress that many catchments in the world are genuinely ungauged, meaning that one will never be able to use data for classical model validation. The philosophy of PUB is that with the developed tools, one should be able to make a prediction of hydrological behavior in these areas too. The grand question in this case is how one will validate the model results? How can one assess the degree of realism of such a model? And to what extent can we trust model outcomes? Using a genuine PUB case study, performed in a truly ungauged basin, we would like to share our experiences on how one can determine the value of PUB tools using catchment specific validation methods.
3. A Cambodian PUB Case Study
3.1. Motivation
In Chamcar Bei (10.57°N, 104.38° E, see Figure 2A), southern Cambodia, a small scale irrigation system is operated by local farmers. Because of the current unreliability of the system's water supply, and possible expansion of the irrigated area, the local government wants to improve and optimize the system. In order to assess annual water availability for irrigation purposes, an estimation of the annual water balance dynamics is required. For this purpose, a hydrological model was developed. As mentioned in the introduction, defining the purpose of a modeling exercise is a key factor to determine what PUB tools can be applied. If for example the purpose of a model is to estimate river flooding, a model time scale of (sub)daily might be required. In our case, we determined that our model needed to give acceptable results on a monthly to yearly time scale.
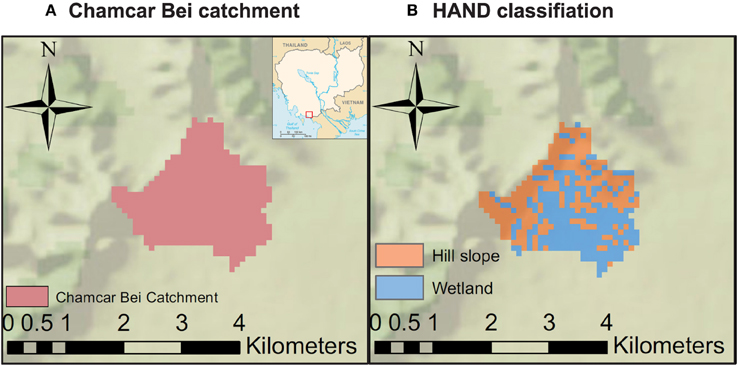
Figure 2. (A) Location of Chamcar Bei catchment, (B) classification of catchment into wetland and hillslope areas, based on the Height Above the Nearest Drainage (HAND).
3.2. Data
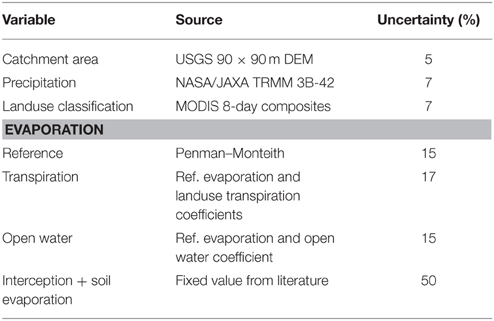
The catchment area was determined using freely available data from the USGS 90 × 90 m Digital Elevation Models. Daily precipitation was estimated using the TRMM 3B-42 product. Reference crop evaporation (hypothetical well-watered grass) was calculated based on the Penman–Monteith equation, using monthly averaged measurements from a nearby weather station and estimated radiation values (Monteith, 1965; Allen et al., 1998). This reference evaporation was then used to calculate transpiration and open water evaporation. Transpiration was calculated based on transpiration coefficients, derived from MODIS data and land use, multiplied by the reference evaporation. Open water evaporation was determined by multiplying the reference evaporation with 1.05, the suggested coefficient for sub-humid and tropical climates (Allen et al., 1998). Interception was also included as a source of evaporation, because it can account for a considerable proportion of total evaporation (Savenije, 2004). The interception was combined with soil evaporation and accounted for by subtracting 2 mm/d from the daily precipitation.
To determine the influence of data uncertainty on the model outcome, uncertainties of the different input data sets were determined. For some products, such as TRMM precipitation, this information is already given in the data itself, while others where based on literature or data analysis. To determine the error in the simulated runoff, standard error propagation theory was used. An overview of the data, the data sources, and the data uncertainty is presented in Table 1. In this study, uncertainty is defined as one standard deviation.
Additional data was obtained through a survey conducted among farmers in the Chamcar Bei catchment. In total 20 out of 120 farming families were interviewed. The interview questions were prepared using the methodology of Bolt and Fonseca (2001), to improve the reliability of information from interviews, e.g., by preventing suggesting questions. Through the surveys information on the annual crop calendar, irrigation practices, irrigation water requirement, annual patterns of river discharge, runoff mechanisms, and minimum and maximum reservoir levels was obtained.
3.3. Model Structure
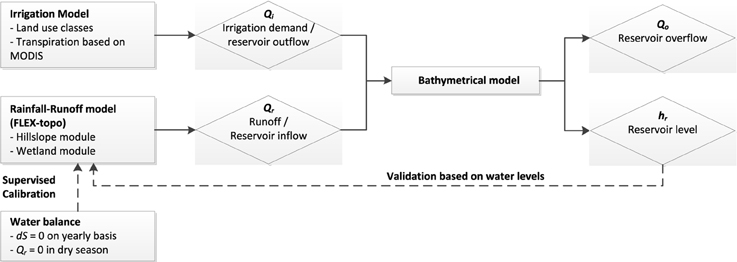
The model developed to estimate the water level of the irrigation reservoir is based on a simple water balance:
Where is the reservoir storage change, Qr the catchment runoff or reservoir inflow, Qi the irrigation demand or reservoir outflow, Qo reservoir spill overflow and Eo open water evaporation. To derive the different components of the reservoir water balance, we used the following modeling techniques: The inflow of the reservoir was modeled using a rainfall-runoff model. Based on the DEM, flow path simulations showed that all streamflow of the Chamcar Bei catchment flows into the reservoir. The irrigation demand, or reservoir outflow, was estimated using an irrigation demand model. Finally, a bathymetrical model of the reservoir was used to estimate the relation between reservoir volume and water level. We will briefly discuss the rainfall-runoff model and the implementation of irrigation demand and reservoir characteristics in the total model.
The Chamcar Bei catchment consists of two considerably different topography classes: a mountainous upper part and a lower laying wetland area. Therefore, we based our hydrological model on the flexible conceptual topography-driven modeling approach FLEX-Topo, as introduced by Savenije (2010). Landscape elements are linked to dominant rainfall-runoff mechanisms, which were used to derive several fairly simple conceptual models for different landscape classes. Landscape classification was based on the Height Above the Nearest Drainage (HAND), as proposed by Rennó et al. (2008), Nobre et al. (2011), and used by Gharari et al. (2011). Field visits showed that there is a clear distinction between sloped and forest terrain, and flat terrain with crops. Using photography and GPS, the area was classified in two zones. Using DEMs, an overlapping classification was made, dividing the catchment into hillslope (50%) and wetland (50%) classes (see Figure 2B).
The model setup of the hillslope and wetland classes are as follows: The hillslope model consists of a unsaturated zone and groundwater reservoir. The slow component of total discharge is driven by the deep ground reservoir, the fast component is driven by the unsaturated zone. In the wetland model the unsaturated zone and groundwater reservoir is lumped. Runoff is dominated by saturated overland flow, which is the fast component of this zone. Groundwater flow is a supporting, slow runoff mechanism. For a full description of the FLEX-Topo model see Savenije (2010). In our final model we slightly modified this setup by eliminating the capillary rise in the hillslope class, and coupling the powers of the beta functions. During initial runs, capillary rise appeared to have negligible influence on the model outcome and was therefore excluded to decrease the number of parameters. Visual inspection of the soil characteristics of the upper soil layers suggested that the upper soil layers in the hillslope and wetlands areas behave similarly. To decrease the number of parameters, it was therefore assumed that the power of the beta functions in both classes is equal. The model includes a total of six parameters: power of the beta function β, maximum hill slope soil moisture storage Sh, max, hill slope groundwater residence time Kh, groundwater recharge a, maximum wetland soil moisture storage Sw, max, and wetland groundwater residence time Kw. Initially, the model was forced by precipitation and Penman–Monteith reference evaporation.
The irrigation demand of the Chamcar Bei irrigation system was determined by calculating the transpiration of each individual land class. Using MODIS 8-day composites, land classes were defined based on vegetation types. Irrigation need was determined by calculating the crop evaporation (Penman–Monteith combined with FAO crop factors), multiplied by estimated water conveyance efficiency. Based on FAO standards (Brouwer et al., 1989), earthen loam canals (as found in Chamcar Bei) have a conveyance efficiency of 0.75.
A bathymetrical model of the irrigation reservoir was made, based on reservoir profile measurements conducted during a fieldwork campaign. This allowed modeling of the reservoir volume and water depth. The main reservoir inflow was based on modeled streamflow from the rainfall-runoff model, which was adjusted with the rainfall and open water evaporation at the reservoir. The outflow from the reservoir was generally based on the calculated irrigation demand, but when the reservoir was full, all additional inflow was assumed to be spilled. A conceptualization of the model approach is shown is Figure 3.
3.4. Calibration and Validation
As no measured ground data was available for calibration, we used a set of alternative constraints or objective functions to limit the parameter space and decrease parameter uncertainty. In this process we selected all models which satisfied the different constraints. Finally, the best performing model was selected and used to evaluate the influence of the uncertainties in the input parameters on the model outcome. The advantage of this method is that improbable parameter sets are removed, but at the risk that the “real” best parameter set might have been excluded as well. This paper does therefore not focus on finding the best parameter set for this case, but rather aims to present an approach on how one validates and assess the realism of a selected good parameter set. The number of parameters was intentionally decreased to minimize equifinality (Savenije, 2001). Previous work has shown that including expert knowledge results in a better approximation of the feasible parameter space (Seibert and McDonnell, 2002; Gao et al., 2014a,b; Gharari et al., 2014a,b; Hrachowitz et al., 2014). For this study, we used the following constraints:
• First, the total annual discharge modeled with the rainfall-runoff model Qrr against the total annual discharge derived from the annual water balance Qwb (see Figure 3), using the Nash-Sutcliffe efficiency (NSE) (Nash and Sutcliffe, 1970). The annual water balance was estimated, based on the total yearly streamflow, which was derived from TRMM precipitation, evaporation for all separate land classes, and the assumption that there was no annual storage carry-over. Parameters were selected using Monte Carlo simulations. Initially, 10,000 runs were done using the complete parameter space, see Table 2. Parameters β, Kh, a, and Kw are values between 0 and 1, and therefore the whole range was initally used. For the hillslope and wetland maximum storage Sh, max and Sw, max the initial space of 0–1000 was selected. The maximum value of 1000 was considered unreasonably large. The parameter space was confined by eliminating all model outcomes with an NSE lower than 0.8. This threshold is quite arbitrary, but was used to narrow down to select about 10 % of the model runs with the best performance.
• Second, the the model was constrained by including the actual evaporation estimates, derived from MODIS and reference evaporation. Based on land use classification, actual evaporation estimates were estimated and imposed for every land use class.
• Water storage capacity: The maximum storage capacity of the unsaturated zone in the hillslope and wetland areas, Sh, max and Sw, h, were approximated using the Mass Curve Technique (MCT). Water storage capacity in most hydrological models reflects the root zone storage capacity. Recently, Gao et al. (2014b) has shown that the MCT, based on effective precipitation (precipitation minus interception), average annual plant water demand, and water demand in dry seasons, can be used to accurately predict the root zone storage capacity. Sh, max and Sw, h were defined separately for the hillslope and wetland areas, based on mean annual and mean dry season plant water demands derived from 3 years of MODIS NDVI data for both areas. In the hillslope areas (mainly trees) it was assumed that the water storage capacity was optimized for a 10 year return period. For the wetland areas (mainly crops), a 3 year return period was used.
• Last, for the discharge it was assumed that (1) streamflow only occurred during the rainy reason (April–September), and (2) total streamflow in the dry season should reach 0 mm/month. Both constraints were based on results from the interviews with the farmers.
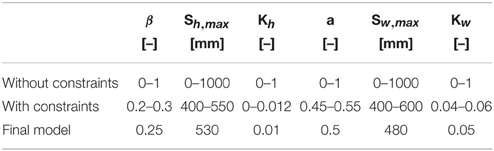
Table 2. Parameters distributions before calibration, after calibration and after imposing constraints.
These four constrains resulted in a new parameter space from which again 10.000 runs were done. From these runs the final optimal solution was selected based on the NSE value. Note that the parameter space after application of the constrains does not represent an uncertainty band, but are merely meant to show how one can reduce the parameter space of the model by applying some simple constraints. The uncertainty of input parameters was also not used in the calibration phase, but evaluated afterwards by running an ensemble of the optimal model with varying input values.
3.5. Modeling Results
Figure 4A presents simulated discharge, computed using parameter values from the unconfined (gray) and confined (red) parameter space. After calibration both the parametric uncertainty in the model output was significantly reduced (Table 2). The simulated discharges were then used to run the reservoir model (Figure 4B), and it can be seen that calibration resulted in a much smaller bandwidth of possible model outcomes.
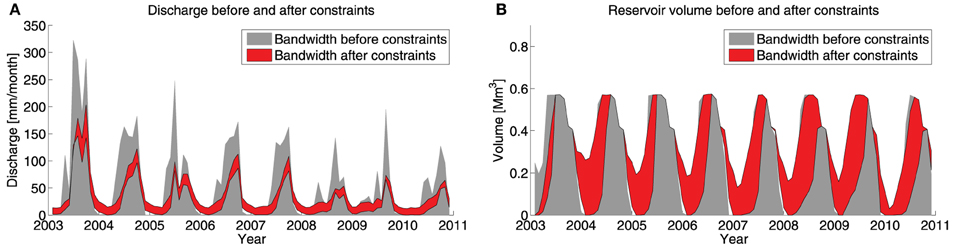
Figure 4. (A) Bandwidth of simulated discharge for the whole parameter space (gray) and the confined parameter space after applying constraints (red), and (B) bandwidth of the reservoir volume for the whole parameter space (gray) and the confined parameter space after applying constraints (red).
Also, interesting and effective constraints for the maximum water storage capacity in the unsaturated zone, Sw, max and Sh, max, were found by using the MCT. Figures 5A,B present the MCT for the wetland and hillslope areas, respectively. Using MODIS NDVI, different plant water demands for the hillslope (50% forest, 50% plantation) and wetland (70% crops, 30% bushes) were estimated. As found by Gao et al. (2014b), the root zone capacity is connected to the vegetation type. In general, the root zone is adapted to the plant water deficit (plant water demand minus effective precipitation). Different vegetation types are optimized for different drought return periods. For example, trees can adapt to droughts with a much higher return period (10–20 years) than crops (3–5 years). It can be seen that the wetlands have a lower mean plant water demand during the dry periods, and hence a lower water storage capacity. The wetlands are mainly used to grow crops, which have root zones that are adapted to droughts of a lower return period. The vegetation in the hillslope areas mainly consists of trees. The root systems of trees, compared to crops, are generally optimized for droughts with longer return periods. Trees have more developed roots systems that, if necessary, can reach deeper and access more water. In this case, this resulted in a higher root zone water storage capacity in the hillslope area.
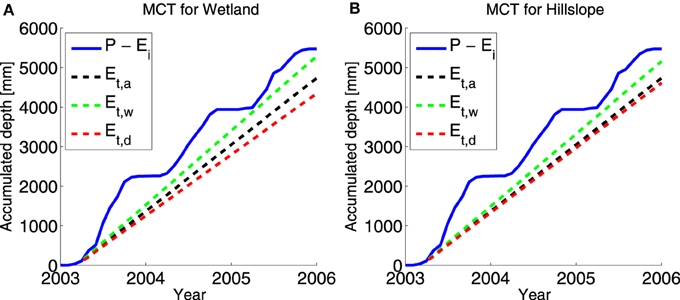
Figure 5. Mass curve technique (MCT) results showing effective precipitation (precipitation P minus interception Ei (blue), mean annual plant water demand Et, a (black), mean plant water demand in the wet season Ew, a (green), and mean plant water demand in the dry season Ed, a (red), for the (A) wetland areas, and (B) hillslope areas.
Constraining the discharge to reach 0 mm/month in the dry season was another effective filter to define the subspace of the best parameter sets. This was well-defined (see Table 2). Simulated discharge using the optimal parameter set is shown in Figure 6A. As can be seen it fulfills the constraint that discharge should approach 0 during the dry season. For this parameter set, an ensemble run of precipitation, potential and actual evaporation including uncertainty (see Table 1), was used to determine the uncertainty bands of the model outcome (gray). It can be seen that the uncertainty is the highest during the high flows. This is due to the combined error of the forcing data and model structure. Figure 6B presents the reservoir volume, using the simulated discharge. As the outlet of the reservoir was located 1.5 m above the lowest point in the reservoir, some of the reservoir volume can be considered as dead storage (black dashed line in Figure 6B). Every year the reservoir reaches a peak storage at the end of the rainy season, due to discharge and precipitation. During the dry season the reservoir empties again, to match the irrigation demand. The annual pattern is generally similar in every year between 2003 and 2010. However, in 2010 the reservoir volume was below the dead storage, meaning it was dry.
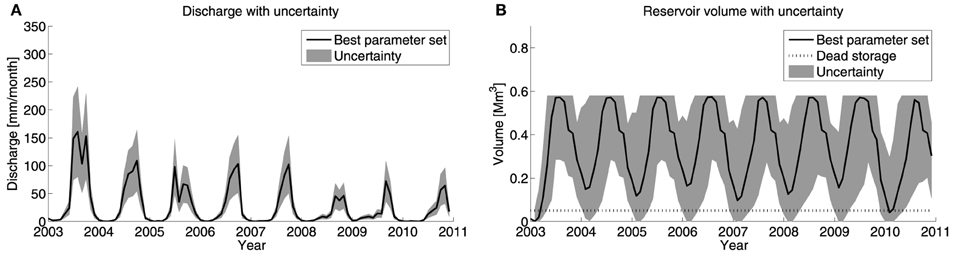
Figure 6. (A) Simulated discharge using the best parameter set, including uncertainty bands, and (B) reservoir volume using best parameter set, including uncertainty bands. The uncertainty bands are based on input data uncertainty.
For the model validation, we used data obtained through a survey among twenty farmers in the Chamcar Bei catchment. These surveys yielded qualitative information about the state of the reservoir and variation in the water levels in the unsaturated zone. The most important new expert knowledge was about the volume of the reservoir over time. Although the reservoir empties during the dry season, according to the interviews it only ran dry once in the period from 2003 to 2011, during the dry season of 2010. Recall Figure 6B, in which it can be seen that indeed only in 2010 the reservoir volume is empty. We acknowledge that this is very limited data to validate the performance, but it does serve the purpose of the model. The model was developed to improve the irrigation system, and modeling the behavior of the reservoir is crucial, especially during extremes. Using the imposed constraints, the model was able to reproduce this.
3.6. Model Realism Assessment
In the last couple of years many studies have been published about predicting discharge in ungauged basins. However, only little attention has been given to developing methods to validate the model output, and assess the realism of the applied model. Recently, some studies discussed ways to check quality of simulated discharge in ungauged basins (e.g., Skaugen et al., 2015; Wan and Konyha, 2015). Simulated discharge or flow indices were compared to data from (surrounding) gauged catchments. However, in many cases it is very likely that catchments surrounding ungauged catchments, are ungauged as well.
Using our Cambodian case study, we discuss several examples of how one can assess the realism of the model outcome, without using knowledge of other catchments. For the validation of a PUB model, one can do three things: (1) no validation, as no data is available, (2) gather conventional data, such as streamflow, or (3) find unconventional and additional data sources. Gathering conventional data requires investment of time and resources, and only after a considerable length of time one has sufficient data to validate a model. In many situations, the only feasible option is the third: finding alternative data. In the last years, many hydrologists have explored the possibilities of using soft data for model calibration (Winsemius et al., 2009). Recently, Gao et al. (2014a) defined four types of soft data: (1) explicit knowledge of hydrological processes, (2) expert knowledge on parameter values, (3) understanding relative magnitude of specific parameters of your model, and (4) using auxiliary (unconventional) data sources.
A targeted fieldwork campaign to obtain soft data can be of great help to develop and validate your PUB model (Seibert and McDonnell, 2013). For the calibration and quality assessment of our model, soft data from all four categories were collected during a short, but intensive fieldwork campaign from February to April 2012. First, an inquiry was made of the governing runoff processes. This was done through surveys among the local population, and observations during and after precipitation events. Based on this inquiry, it was decided to conceptualize the Chamcar Bei catchment as a combination of wetland and hillslope areas. Second, the topographical classification of the catchment into wetland and hillslope zones using DEMs was validated during the fieldwork campaign. Third, alternative auxiliary data was obtained through surveys to validate the water volume in the reservoir. Using the knowledge of the local population, we learned that the reservoir ran dry in 2010. This was used in the validation and evaluation of our model. Last, we tried to understand and quantify the relative magnitude of the variation of the unsaturated reservoirs, by using a MCT to define the required maximum water storage capacity for the wetland and hillslope areas.
With this PUB case study we do not aim to provide a standard recipe for model validation and quality assessment in ungauged basins. Our goal is to emphasize that “much can be accomplished with clever targeted fieldwork” (Seibert and McDonnell, 2013). If conventional model calibration and validation is not possible, targeted field visits can significantly improve conceptualization of the modeled catchment, as well as validate the model outcome. For every catchment it should be inquired individually which data sources can be used. In our Cambodian case study we used the (1) presence of a reservoir, (2) the memory of the catchment inhabitants, and (3) field observations, which might not be available in other ungauged catchments. We aim to show that creative model development and innovative use of soft data might give insight in the performance of a hydrological model, and reduce epistemic model uncertainty in a genuinely ungauged basin.
4. Discussion
The presented case study illustrates how one can cope with validation and model realism in a real PUB case study. This showed that both knowledge of the basin (soft data), and a creative and flexible modeling approach can improve model results and understanding of the hydrological processes behind it. For example, without visiting the basin, it would not have become clear that the main land use classes are coupled with hydrological zones in the basin. Furthermore, the irrigation and water distribution system gave significant insight in the magnitude and temporal variation of the water fluxes. Although our case study follow the design scheme of a conventional hydrological modeling exercise, we believe that we were able to capture the main hydrological features and signatures in the Chamcar Bei catchment. We implemented some creative solutions to improve our model design, constrain the parameter space, validate the outcome, and assess the model realism. It was very helpful to couple the rainfall-runoff model to the irrigation reservoir. This allowed us to use knowledge of the local population about the reservoir levels to validate our model. This is an example of how creative model might be very helpful in basins without (conventional) data. We also showed that by applying constraints based on knowledge about the catchment, the parameter space can be decreased significantly. We stress that this does not mean that the uncertainty of the parameters necessarily decreases, since we only used only one objective function. Our goal was to narrow down the parameter space, find a best parameter set, and evaluate the model outcome using that set. We believe that given the limited data and approaches available, we succeeded. Especially given the goal of the modeling exercise, which was to estimate the annual water availability.
The case study also showed that, although a lot of the results from many developed PUB tools are promising, they still come with large uncertainties. For example, the used rainfall estimates are only given for grid cells of 0.25 degrees, while the rainfall pattern in our region is likely influenced by local topography. The same and other problems hold for evaporation estimates. In our final model we used a rather simple approach using MODIS data and reference evaporation, but we also checked different evaporation products, like MOD16 Mu et al. (2007) or CMRSET Guerschman et al. (2009). However, due to cloud cover, pixel size and heterogeneity within the studied catchment results where not satisfying. Fortunately, recent developments show that the data quality of these PUB tools is improving rapidly due to better quality and higher resolution of remote sensing data. For example, a 30 m DEM from SRTM for our area came available in 2015, while our study is still based on a 90 m DEM. Finally, although many hydrologists agree that confining the parameter space can lead to better model results (Seibert and McDonnell, 2002; Gao et al., 2014a; Gharari et al., 2014a,b; Hrachowitz et al., 2014), it is difficult to do so because parameter values cannot easily be deducted. For example, soil properties are linked to parameters of the unsaturated zone, but the exact relationship is not known or not measurable. Also, parameters for fast runoff and groundwater flow can be deducted from streamflow measurements, but these data are not available in many PUB cases.
The direct usability and practical importance of these additional validation data illustrate that use of standard PUB tools above is not sufficient, but should be combined with additional knowledge or data from the basin. This means that at least some data or information should be gathered locally and integrated in the model to reduce uncertainty in model setup, model parameters and finally model results. Herewith we echo (Seibert and McDonnell, 2013), who said that clever and targeted fieldwork (in ungauged basins) contributes to accomplish good modeling results. The direct consequence is that the success of a case study is more dependent on the creativity and understanding of the hydrologist. According to Savenije (2009), hydrological modeling requires art, which “lies in the ability to reconstruct the architecture of a largely unknown system from a few observable signatures that characterize its behavior.” When modeling an ungauged basins, even fewer signatures can be observed. However, we would like to emphasize that even with few observations, one might be able to reconstruct and model the hydrological behavior of a system. With fewer observations available, the importance of uncertainties becomes more important if one wants to assess the quality of the model output. Decisions on whether to use different data sources in a PUB case study becomes strongly dependent on uncertainties and error propagation, because traditional validation techniques are unavailable. Therefore, reliable estimates of uncertainty become even more important in these cases and should be included in model development.
This does not mean that, due to the uniqueness and low likelihood of transferability of every case study, developed methods should not be documented. Case studies that focus on validation and assessment of realism do not present the standard recipes as given in many PUB methods. However, we believe that one of the strengths of PUB is the idea and, evaluation of creative and flexible modeling approaches. Meanwhile, these case studies show exactly how the gap between PUB theory and practice can be closed by integration of PUB tools with additional, locally obtained, validation data. This means that we have to switch from following prescribed hydrological methods to a more creative process of model development, validation and realism assessment in PUB cases.
Such a modeling approach does not only restrict itself to development of hydrological models for ungauged basins. Within the framework of the current IAHS Hydrological Decade on “Panta Rhei” (Montanari et al., 2013), the emerging science of socio-hydrology brings similar challenges. As hydrologists try to include anthropogenic processes in rainfall-runoff models, the need for alternative data and expert knowledge is increasing. Recent socio-hydrologic modeling studies (e.g., Dermody et al., 2014; Elshafei et al., 2014; van Emmerik et al., 2014; Liu et al., 2015) have showed that by using new types of data, and by using expert (historical) knowledge about a catchment, observed reality can be mimicked well. We hope that this approach will be adopted by modelers within the PUB and “Panta Rhei” frameworks, and beyond.
5. Conclusions
This study aims to stress that more efforts should be made to develop tools to validate and assess the realism of hydrological models for ungauged basins. With a case study from a truly ungauged basin, we give examples of how a targeted, short term fieldwork campaign focused on obtained soft data can result in an acceptable model design. More importantly, we demonstrate the value of soft data in validating and quality control the model output.
By coupling the hydrological rainfall-runoff model to the irrigated reservoir, we were able to use additional data for model improvement, constraining parameters, and validating the model outcome. We defined a best parameter, which resulted in an acceptable model outcome. Furthermore, the model was able to capture the case of an empty reservoir in 2010. This would not have been possible without the use of soft data.
The modeling was able to capture some key features of the hydrological behavior in the Chamcar Bei catchment. We acknowledge that the magnitude of the terms of the water balance are still uncertain. However, we strongly believe we were able to mimic the general annual fluctuations. For the goal of this model, estimating annual water availability, this is sufficient.
If one is to model streamflow in an ungauged basin, one should also design a plan for the validation of the model output. We emphasize that future studies should focus on exploring the use of alternative data sources for this. The availability and usability of soft data is very site specific. In our case study we relied on anthropogenic factors, such as an irrigation reservoir and the memory of the local population. In many, especially pristine, catchments, other types of data should be used. Hydrological modeling asks for creativity, especially in ungauged basins. Using specific knowledge of the basin is key for model development, and design of a validation strategy.
Models in PUB cases should be based on the purpose of the model, the availability of data, and the possibilities of acquiring auxiliary (soft) data for validation. In the presented case study, a relatively course temporal resolution was sufficient to meet the goal of the model. If the model was to serve another purpose (e.g., daily peak streamflow prediction), the current model structure might not have been sufficient. No standard recipe can be designed for modeling ungauged basins. At best, hydrologists can learn from approaches used in site specific case studies, and be creative in designing their own approach.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank everyone from Bridges Across Borders Cambodia (BABC) in Chamcar Bei for their support during the fieldwork campaign. We are grateful to Martina Groenemeijer who contributed significantly to obtaining survey data in Chamcar Bei. We also want to thank Dr. Markus Hrachowitz for his valuable suggestions to improve this paper. Finally, we want to thank the two reviewers who helped to significantly improve this paper.
References
Allen, R. G., Pereira, L. S., Raes, D., and Smith, M. (1998). Crop Evapotranspiration-guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56, Vol. 300. Rome: FAO.
Bastiaanssen, W., Menenti, M., Feddes, R., and Holtslag, A. (1998). A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. J. Hydrol. 212, 198–212. doi: 10.1016/S0022-1694(98)00253-4
Beven, K. J. (2000). Uniqueness of place and process representations in hydrological modelling. Hydrol. Earth Syst. Sci. Discuss. 4, 203–213. doi: 10.5194/hess-4-203-2000
Bolt, E., and Fonseca, C. (2001). Keep it Working: A Field Manual to Support Community Management of Rural Water Supplies. Delft: IRC. IRC Technical Paper Series 36.
Brouwer, C., Prins, K., and Heibloem, M. (1989). Irrigation Water Management: Irrigation Scheduling, Vol. 4. Rome: FAO.
Cibin, R., Athira, P., Sudheer, K., and Chaubey, I. (2014). Application of distributed hydrological models for predictions in ungauged basins: a method to quantify predictive uncertainty. Hydrol. Process. 28, 2033–2045. doi: 10.1002/hyp.9721
Dermody, B., Van Beek, R., Meeks, E., Klein Goldewijk, K., Scheidel, W., Van Der Velde, Y., et al. (2014). A virtual water network of the roman world. Hydrol. Earth Syst. Sci. 18, 5025–5040. doi: 10.5194/hess-18-5025-2014
Efstratiadis, A., Koussis, A. D., Koutsoyiannis, D., and Mamassis, N. (2014). Flood design recipes vs. reality: can predictions for ungauged basins be trusted? Nat. Hazards Earth Syst. Sci. 14, 1417–1428. doi: 10.5194/nhess-14-1417-2014
Eilander, D., Annor, F. O., Iannini, L., and van de Giesen, N. (2014). Remotely sensed monitoring of small reservoir dynamics: a Bayesian approach. Remote Sens. 6, 1191–1210. doi: 10.3390/rs6021191
Elshafei, Y., Sivapalan, M., Tonts, M., and Hipsey, M. (2014). A prototype framework for models of socio-hydrology: identification of key feedback loops and parameterisation approach. Hydrol. Earth Syst. Sci. 18, 2141–2166. doi: 10.5194/hess-18-2141-2014
Entekhabi, D., Njoku, E. G., O'Neill, P. E., Kellogg, K. H., Crow, W. T., Edelstein, W. N., et al. (2010). The soil moisture active passive (SMAP) mission. Proc. IEEE 98, 704–716. doi: 10.1109/JPROC.2010.2043918
Fenicia, F., Kavetski, D., and Savenije, H. H. G. (2011). Elements of a flexible approach for conceptual hydrological modeling: 1. Motivation and theoretical development. Water Resour. Res. 47:W11510. doi: 10.1029/2010wr010174
Fenicia, F., Savenije, H. H. G., Matgen, P., and Pfister, L. (2008). Understanding catchment behavior through stepwise model concept improvement. Water Resour. Res. 44:W01402. doi: 10.1029/2006WR005563
Gao, H., Hrachowitz, M., Fenicia, F., Gharari, S., and Savenije, H. H. G. (2014a). Testing the realism of a topography-driven model (FLEX-Topo) in the nested catchments of the Upper Heihe, China. Hydrol. Earth Syst. Sci. 18, 1895–1915. doi: 10.5194/hess-18-1895-2014
Gao, H., Hrachowitz, M., Schymanski, S., Fenicia, F., Sriwongsitanon, N., and Savenije, H. (2014b). Climate controls how ecosystems size the root zone storage capacity at catchment scale. Geophys. Res. Lett. 41, 7916–7923. doi: 10.1002/2014GL061668
Gharari, S., Hrachowitz, M., Fenicia, F., Gao, H., and Savenije, H. (2014a). Using expert knowledge to increase realism in environmental system models can dramatically reduce the need for calibration. Hydrol. Earth Syst. Sci. 18, 4839–4859. doi: 10.5194/hess-18-4839-2014
Gharari, S., Hrachowitz, M., Fenicia, F., and Savenije, H. H. G. (2011). Hydrological landscape classification: investigating the performance of HAND based landscape classifications in a central European meso-scale catchment. Hydrol. Earth Syst. Sci. 15, 3275–3291. doi: 10.5194/hess-17-149-2013
Gharari, S., Shafiei, M., Hrachowitz, M., Kumar, R., Fenicia, F., Gupta, H. V., et al. (2014b). A constraint-based search algorithm for parameter identification of environmental models. Hydrol. Earth Syst. Sci. 18, 4861–4870. doi: 10.5194/hess-18-4861-2014
Guerschman, J. P., Dijk, A. I. J. M. V., Mattersdorf, G., Beringer, J., Hutley, L. B., Leuning, R., et al. (2009). Scaling of potential evapotranspiration with {MODIS} data reproduces flux observations and catchment water balance observations across Australia. J. Hydrol. 369, 107–119. doi: 10.1016/j.jhydrol.2009.02.013
Guo, Y., Yang, Z., Qin, D., Chen, G., Gao, X., and Chen, C. (2012). Development and application of a distributed hydrological model for discharge predictions in un-gauged basins: case study in malian river basin. HKIE Trans. 19, 25–32. doi: 10.1080/1023697X.2012.10668994
Hou, A. Y., Kakar, R. K., Neeck, S., Azarbarzin, A. A., Kummerow, C. D., Kojima, M., et al. (2014). The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 95, 701–722. doi: 10.1175/BAMS-D-13-00164.1
Hrachowitz, M., Fovet, O., Ruiz, L., Euser, T., Gharari, S., Nijzink, R., et al. (2014). Process consistency in models: the importance of system signatures, expert knowledge, and process complexity. Water Resour. Res. 50, 7445–7469. doi: 10.1002/2014WR015484
Hrachowitz, M., Savenije, H., Blöschl, G., McDonnell, J., Sivapalan, M., Pomeroy, J., et al. (2013). A decade of predictions in ungauged basins (PUB) a review. Hydrol. Sci. J. 58, 1198–1255. doi: 10.1080/02626667.2013.803183
Kerr, Y. H., Waldteufel, P., Wigneron, J.-P., Martinuzzi, J., Font, J., and Berger, M. (2001). Soil moisture retrieval from space: the soil moisture and ocean salinity (SMOS) mission. Geosci. Remote Sens. IEEE Trans. 39, 1729–1735. doi: 10.1109/36.942551
Khan, S., Hong, Y., Vergara, H. J., Gourley, J. J., Brakenridge, G. R., De Groeve, T., et al. (2012). Microwave satellite data for hydrologic modeling in ungauged basins. Geosci. Remote Sens. Lett. IEEE 9, 663–667. doi: 10.1109/LGRS.2011.2177807
Kummerow, C., Barnes, W., Kozu, T., Shiue, J., and Simpson, J. (1998). The tropical rainfall measuring mission (TRMM) sensor package. J. Atmos. Oceanic Technol. 15, 809–817. doi: 10.1175/1520-0426(1998)015<0809:TTRMMT>2.0.CO;2
Liu, D., Tian, F., Lin, M., and Sivapalan, M. (2015). A conceptual socio-hydrological model of the co-evolution of humans and water: case study of the tarim river basin, western China. Hydrol. Earth Syst. Sci. 19, 1035–1054. doi: 10.5194/hess-19-1035-2015
McDonnell, J. J. (2003). Where does water go when it rains? Moving beyond the variable source area concept of rainfall-runoff response. Hydrol. Process. 17, 1869–1875. doi: 10.1002/hyp.5132
Montanari, A., Young, G., Savenije, H., Hughes, D., Wagener, T., Ren, L., et al. (2013). “Panta rhei–everything flows”: change in hydrology and society–the IAHS scientific decade 2013–2022. Hydrol. Sci. J. 58, 1256–1275. doi: 10.1080/02626667.2013.809088
Mu, Q., Heinsch, F. A., Zhao, M., and Running, S. W. (2007). Development of a global evapotranspiration algorithm based on {MODIS} and global meteorology data. Remote Sens. Environ. 111, 519–536. doi: 10.1016/j.rse.2007.04.015
Mulder, G., Olsthoorn, T., Al-Manmi, D., Schrama, E., and Smidt, E. (2015). Identifying water mass depletion in northern Iraq observed by GRACE. Hydrol. Earth Syst. Sci. 19, 1487–1500. doi: 10.5194/hess-19-1487-2015
Nash, J., and Sutcliffe, J. V. (1970). River flow forecasting through conceptual models part I–A discussion of principles. J. Hydrol. 10, 282–290. doi: 10.1016/0022-1694(70)90255-6
Nobre, A., Cuartas, L., Hodnett, M., Rennó, C., Rodrigues, G., Silveira, A., et al. (2011). Height above the nearest drainage–a hydrologically relevant new terrain model. J. Hydrol. 404, 13–29. doi: 10.1016/j.jhydrol.2011.03.051
Rennó, C. D., Nobre, A. D., Cuartas, L. A., Soares, J. V., Hodnett, M. G., Tomasella, J., et al. (2008). Hand, a new terrain descriptor using SRTM-DEM: mapping terra-firme rainforest environments in Amazonia. Remote Sens. Environ. 112, 3469–3481. doi: 10.1016/j.rse.2008.03.018
Savenije, H. (2009). HESS opinions “The art of hydrology”*. Hydrol. Earth Syst. Sci. 13, 157–161. doi: 10.5194/hess-13-157-2009
Savenije, H. (2010). HESS Opinions “Topography driven conceptual modelling (FLEX-Topo).” Hydrol. Earth Syst. Sci. 14, 2681–2692. doi: 10.5194/hess-14-2681-2010
Savenije, H. H. (2001). Equifinality, a blessing in disguise? Hydrol. Process. 15, 2835–2838. doi: 10.1002/hyp.494
Savenije, H. H. (2004). The importance of interception and why we should delete the term evapotranspiration from our vocabulary. Hydrol. Process. 18, 1507–1511. doi: 10.1002/hyp.5563
Seibert, J., and McDonnell, J. J. (2002). On the dialog between experimentalist and modeler in catchment hydrology: use of soft data for multicriteria model calibration. Water Resour. Res. 38:1241. doi: 10.1029/2001WR000978
Seibert, J. and McDonnell, J. (2013). Gauging the ungauged basin: relative value of soft and hard data. J. Hydrol. Eng. 20:A4014004. doi: 10.1061/(ASCE)HE.1943-5584.0000861
Sivapalan, M. (2003). Prediction in ungauged basins: a grand challenge for theoretical hydrology. Hydrol. Process. 17, 3163–3170. doi: 10.1002/hyp.5155
Sivapalan, M., Takeuchi, K., Franks, S., Gupta, V., Karambiri, H., Lakshmi, V., et al. (2003). IAHS decade on predictions in ungauged basins (PUB), 2003–2012: shaping an exciting future for the hydrological sciences. Hydrol. Sci. J. 48, 857–880. doi: 10.1623/hysj.48.6.857.51421
Skaugen, T., Peerebom, I. O., and Nilsson, A. (2015). Use of a parsimonious rainfall–run-off model for predicting hydrological response in ungauged basins. Hydrol. Process. 29, 1999–2013. doi: 10.1002/hyp.10315
van Emmerik, T., Li, Z., Sivapalan, M., Pande, S., Kandasamy, J., Savenije, H., et al. (2014). Socio-hydrologic modeling to understand and mediate the competition for water between agriculture development and environmental health: murrumbidgee river basin, Australia. Hydrol. Earth Syst. Sci. 18, 4239–4259. doi: 10.5194/hess-18-4239-2014
van Emmerik, T., Steele-Dunne, S. C., Judge, J., and van de Giesen, N. (2015). Impact of diurnal variation in vegetation water content on radar backscatter from maize during water stress. Geosci. Remote Sens. IEEE Trans. 53, 3855–3869. doi: 10.1109/TGRS.2014.2386142
Wan, Y., and Konyha, K. (2015). A simple hydrologic model for rapid prediction of runoff from ungauged coastal catchments. J. Hydrol. 528, 571–583. doi: 10.1016/j.jhydrol.2015.06.047
Keywords: PUB, case study, hydrology, model validation, model realism, Cambodia, soft data, reservoir
Citation: van Emmerik T, Mulder G, Eilander D, Piet M and Savenije H (2015) Predicting the ungauged basin: model validation and realism assessment. Front. Earth Sci. 3:62. doi: 10.3389/feart.2015.00062
Received: 20 July 2015; Accepted: 25 September 2015;
Published: 09 October 2015.
Edited by:
Wouter Buytaert, Imperial College London, UKReviewed by:
Alexander Maria Rogier Bakker, Pennsylvania State University, USAJoshua Larsen, University of Queensland, Australia
Copyright © 2015 van Emmerik, Mulder, Eilander, Piet and Savenije. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tim van Emmerik, dC5oLm0udmFuZW1tZXJpa0B0dWRlbGZ0Lm5s
 Tim van Emmerik
Tim van Emmerik Gert Mulder
Gert Mulder Dirk Eilander
Dirk Eilander Marijn Piet1
Marijn Piet1 Hubert Savenije
Hubert Savenije