- 1Earth System Science Interdisciplinary Center, University of Maryland, College Park, MD, USA
- 2Cryospheric Sciences Laboratory, NASA Goddard Space Flight Center, Greenbelt, MD, USA
- 3Mathematics and Geoscience, Penn State DuBois, DuBois, PA, USA
- 4Department of Geosciences, Pennsylvania State University, University Park, PA, USA
Stick-slip motion such as that observed at Whillans Ice Stream, West Antarctica, is one example of transient forcing significantly affecting longer-term ice-stream dynamics. We develop and present a two-dimensional map-plane viscoelastic model of perturbations to ice-stream dynamics suitable for simulating and analyzing stick-slip behavior. Model results suggest important roles in stick-slip motion for both the elastic and viscous components of ice rheology, confirming and extending inferences drawn from simple models and observations. Elastic behavior depends on the rate of applied stress, at times allowing significant velocity perturbations with little change in accumulated stress perturbation; in contrast, viscous behavior depends on total accumulated stress and can lead to changes in ice-stream thickness over many stick-slip cycles.
1. Introduction
Fast-flowing ice streams are the primary outlets through which ice drains from interior regions of ice sheets into oceans (Bentley, 1987); it follows that understanding ice-stream dynamics is critical for projections of global sea level (e.g., Bindschadler et al., 2013). Streaming flow is typically enabled by some combination of a weak till bed and high subglacial water pressure, with the complexity of the processes involved leading to widely varying theories of basal sliding, from linear-viscous (Alley et al., 1987) to plastic (Tulaczyk, 2006) till rheology. Under these conditions, ice motion is primarily by basal processes, with vertical shear concentrated in the till and negligible in the ice, making the dynamics comparable to those of an ice shelf and permitting a depth-integrated modeling approach (MacAyeal, 1989). Ice streams are thus sensitive to perturbations in basal drag, and when longitudinal stresses are considered, to perturbations in hydrostatic pressure at the ice front.
Transient perturbations over shorter timescales (seconds to hours) require consideration of the elastic properties of ice in addition to the nonlinearly viscous flow that dominates ice stream dynamics over longer periods. For example, some ice streams (e.g., Bindschadler and Rutford) are known to be sensitive to transient forcings such as ocean tides (e.g., Anandakrishnan et al., 2003; Gudmundsson, 2007), and their behavior has been successfully analyzed with viscoelastic models (e.g., Gudmundsson, 2011; Walker et al., 2012). This modeling is of interest beyond study of the transients themselves, as matching model output with observations can lead to inference of physical properties (in this case, the form of the basal sliding law) that cannot be obtained from standard inverse methods applied to time-averaged velocity observations (e.g., Joughin et al., 2004). In another example, Voytenko et al. (2015) apply the model of Walker et al. (2012) to observations of the velocity of the terminus of Helheim Glacier, Greenland by terrestrial radar interferometry to infer extremely weak ice in the floating portion.
One of the most complicated behaviors so far observed occurs on Whillans Ice Stream (WIS), which averages flow speeds over 300 m a−1 in its lower reaches (the Whillans Ice Plain, WIP) despite moving only in short bursts roughly twice per day. Bindschadler et al. (2003) observed that this stick-slip behavior consists of long periods (6–18 h) of little motion, followed by bursts (10–30 min) of motion at over 30 times the average speed of WIS triggered by ocean tides under the Ross Ice Shelf. Subsequent studies have revealed a rich range of phenomena. A large, central “sticky spot” is especially important in supporting stress between motion events, then triggering motion events and generating far-field seismic energy (e.g., Wiens et al., 2008; Walter et al., 2011; Winberry et al., 2011; Pratt et al., 2014). In addition, one sticky spot near the grounding zone contributes to triggering of some motion events, and other sticky spots near the grounding zone provide localized resistance and generate additional seismic energy following initiation of fast motion (Walter et al., 2011, 2015; Winberry et al., 2011, 2014; Pratt et al., 2014).
Physical models for the stick-slip behavior are still under development. The sticky spots tend to occupy local maxima in subglacial hydrologic potential, and thus are better drained than surrounding regions, helping explain their locations (Alley, 1993; Horgan et al., 2013; Winberry et al., 2014). Geological heterogeneity may contribute (Walter et al., 2011; Muto et al., 2013). At least some of the sticky spots near the grounding zone may be related to till compaction resulting from the inland extension of ice-shelf tidal flexure; feedbacks with ice flow help generate hydropotential highs in the regions where downward flexure from rising tide favors till compaction (Christianson et al., 2013; Walker et al., 2013; Walter et al., 2015). The widespread occurrence of basal freeze-on beneath the ice streams of the Ross Embayment (e.g., Christoffersen et al., 2010), and the likelihood of regelation of stationary ice into subglacial sediments (Iverson, 1993), suggest that fault healing strengthens the sticky spots between motion events (Zoet et al., 2013; Winberry et al., 2014). However, Walter et al. (2015) suggested that the basic features of WIP stick-slip can be reproduced without spatial or temporal variations in bed strength. The value of a modeling framework to test hypotheses is clear.
In this study, we develop a two-dimensional viscoelastic model of transient perturbations to steady ice-stream flow and apply the model to an idealization of the WIP. Our primary goal is model development and demonstration rather than reproducing the full complexity of the observed motion of the WIP. We focus on the effects of sticky-spot formation and release on ice-stream dynamics, leaving the underlying mechanics of subglacial till for future work. Through a series of experiments, we demonstrate the importance of both elastic and viscous ice behavior for the dynamics of a single stick-slip cycle and longer-term ice thickness trends, respectively, confirming the inferences of Winberry et al. (2014) about interactions of viscous and elastic processes.
2. Model
The derivation of our model essentially follows that of Walker et al. (2012) except in two dimensions (map plane) rather than one (flowline). We begin with the MacAyeal-Morland equations (MacAyeal, 1989) for depth-integrated flow of ice streams and/or ice shelves:
for ice surface elevation s, ice density ρ, and gravitational acceleration g. These equations assume all velocity arises below the ice (basal sliding or till deformation), so that the basal drag τb becomes a horizontal body force and ice velocity does not vary with depth; however, they retain longitudinal stresses, allowing instantaneous ice velocity response to changes in applied stress from e.g., ice-shelf buttressing or basal “sticky spots.” Here, we have written the equations in terms of the deviatoric stresses σij and have restored the inertial terms (using the velocity (u, v)) that generally are negligible. Scaling arguments and experience with this model and the Walker et al. (2012) model show that these terms are indeed negligible even on tidal timescales, but our interest in stick-slip motion motivates their inclusion. The basal drag τb depends on our choice of sliding law, and will be discussed further when the model is applied. (We note that our use of the “shelfy stream” force balance implicitly assumes that perturbations to τb will be small enough not to produce significant internal deformation of the ice, which is a reasonable assumption for the experiments we will present). If we express the stresses and velocities as the sum of steady and perturbation components (, u = ū + ũ, etc.) and differentiate with respect to time, we obtain
where the ice thickness h is taken as constant because we are interested in short timescales (seconds to hours).
In order to solve the perturbed Equations (3), (4), we must assume a rheology (flow law) for ice. The simplest viscoelastic rheology that displays both instantaneous elastic response and long-time viscous behavior is a Maxwell material. In one dimension, a Maxwell material can be conceptually modeled as an elastic spring and viscous dashpot in series, so that the same stress acts across both and the total strain is the sum of the strains in each element. For plane stress, the Maxwell rheology may be written in terms of the deviatoric stresses σij as (e.g., Turcotte and Schubert, 2002)
where are the strain rates, E is Young's modulus, η is viscosity, and ν is Poisson's ratio. We take η to be given by Glen's law and assume that it changes slowly enough to allow us to use the (possibly spatially varying) viscosity of the steady background state to calculate the perturbations. If we follow the usual practice and consider ice to be incompressible, ν = 0.5, the pressure p is eliminated from the rheology (Cuffey and Paterson, 2010). We can then solve for the stress rate components:
where we have used the definitions of strain rates in terms of velocity components.
The final perturbed momentum equations are then found by substituting (8)–(10) into (3), (4) to obtain
where advective terms resulting from the total time derivatives in (8)–(10) are negligible (cf. Reeh et al., 2003; Walker et al., 2012). Boundary conditions for these perturbed momentum equations may be essential (specified velocities) or natural [specified stress rates, using (3), (4) in the weak forms of (11), (12)]; for our rectangular domains, natural boundary conditions amount to zero longitudinal stress (rate) at transverse boundaries and zero shear stress (rate) at lateral boundaries. The system (8)–(12) is solved in MATLAB by fully implicit timestepping along with finite element spatial discretization using first-order triangular elements in the sparseFEM package (https://bitbucket.org/maurow/sparsefem).
3. Application
We use the model to investigate stick-slip behavior on an idealized domain similar to the Whillans Ice Plain. The domain is an L × L square, where L = 100 km for most runs, with ice thickness varying linearly from h = 812.1 m at x = 0 to h = 803.4 m at x = L. The background flow is taken to be in the positive x direction; we assume ū ~ 400 m a−1, although this figure is used only for comparison with the perturbation velocity and does not enter the model. We impose a sticky spot at the center of the domain (analogous to the “central sticky spot” at “Ice Rise A” on WIP, Winberry et al., 2011) by setting, with x and L in m,
where 0 ≤ F(t) ≤ 1 describes the growth and decay of the sticky spot and 8 kPa is its maximum strength. Note that the time-dependent part of τbx averaged over a 100 × 100 km domain with F(t) = 1 is slightly more than 120 Pa, roughly comparable to the 300–350 Pa average pressure drop estimated by Winberry et al. (2009) for stick-slip events on WIP. For simplicity, we would like to assume that the bed outside of the sticky spot is perfectly plastic (consistent with Bindschadler et al., 2003), so that ∂t τ bx = ∂t τ by = 0. However, in practice it is necessary (see below) to assume a slight departure from perfect plasticity, which we linearize as . Note that because this is a linearization of nearly plastic behavior, α2 is much smaller than the usual coefficient β2 for a linear sliding law (of order 104, vs. order 108–109).
3.1. Reference Experiment
In our reference experiment, the sticky spot strengthens linearly over 12 h and then releases over 10 min (consistent with Bindschadler et al., 2003). More formally, we have
in (13). Note that this piecewise linear definition makes the rates of applied stress from the sticky spot constant (in time) for both the strengthening and weakening phases. [In practice, we smooth this function slightly by taking F′(43200) = 0.] We apply natural (zero perturbation stress rate) boundary conditions at the upstream and downstream boundaries, and essential (zero perturbation velocity) boundary conditions at the lateral boundaries. The basal drag coefficient is α2 = 4.3 × 104 Pa s m−1. With E = 3 GPa and η = 1016 Pa s, the Maxwell relaxation time 2η∕E is roughly 77 days, so this experiment will be dominated by elastic behavior. The choice of E = 3 GPa rather than the laboratory value of 9 GPa (Schulson and Duval, 2009) is consistent with past modeling studies of large bodies of damaged glacier ice (e.g., Anandakrishnan and Alley, 1997); the values of η in this study lie within the range of effective viscosities typically encountered in viscous (Glen's law) modeling of ice flow (Cuffey and Paterson, 2010).
The onset of sticking can be seen to begin directly over the sticky spot before spreading rapidly across the domain in roughly 3 min, reaching an essentially steady state within 10 min. Within 5 s of stick onset, ice over the sticky spot has already slowed by 48 m a−1 relative to the background flow, despite stress perturbation components of only roughly 2 Pa or less (Figure 1). This is a consequence of elasticity, for which velocity depends only on the instantaneous rate of applied stress and not on the accumulated stress. Once the initial effects of inertia have been overcome, the velocity perturbation field remains the same throughout the strengthening phase due to the constant rate of applied basal stress, even as a considerable stress perturbation builds up. The along-mean-flow velocity perturbation reaches −382 m a−1, indicating that a sticky spot strengthening at this rate can essentially temporarily shut down the idealized ice stream. (This velocity perturbation is also comparable to the mean velocity of WIP). By the end of the strengthening phase, almost 20 kPa of along-mean-flow compressive stress and an equal amount of extensive stress have accumulated upstream and downstream, respectively, of the sticky spot, as well as over 12 kPa of shear stress across the sticky spot (Figure 2).
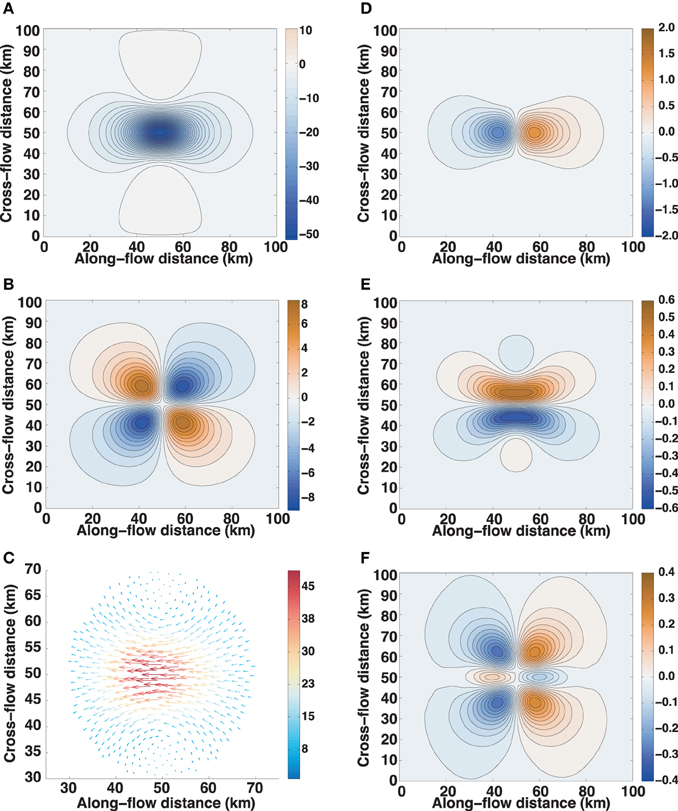
Figure 1. Perturbation at t = 5 s: (A) along-flow velocity; (B) cross-flow velocity; (C) vector velocity (colored by magnitude) within 20 km of sticky-spot center; (D) along-flow stress; (E) shear stress; (F) cross-flow stress. Velocities in m a−1, stresses in Pa. Mean velocity is from left to right in the positive along-flow direction.
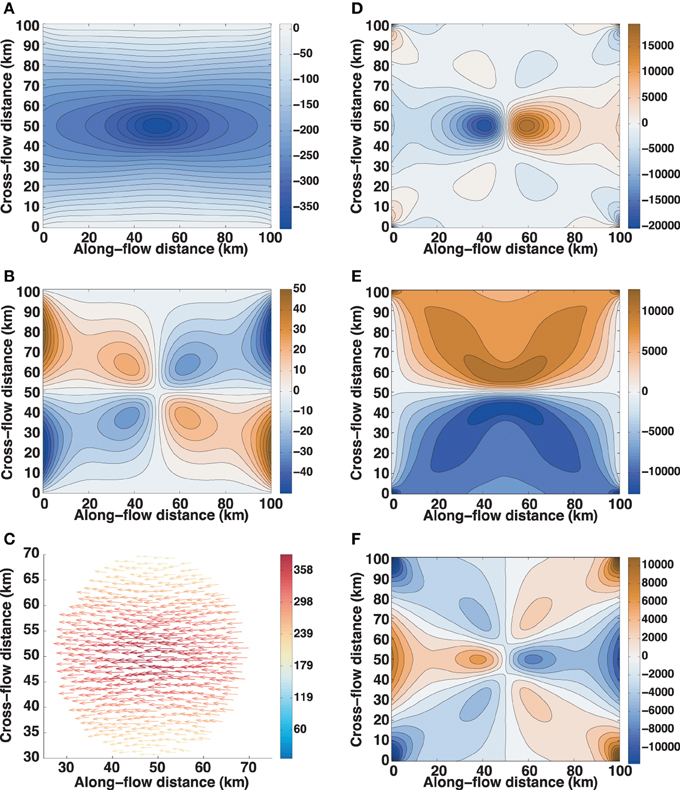
Figure 2. Perturbation at t = 12 h: (A) along-flow velocity; (B) cross-flow velocity; (C) vector velocity (colored by magnitude) within 20 km of sticky-spot center; (D) along-flow stress; (E) shear stress; (F) cross-flow stress. Velocities in m a−1, stresses in Pa. Mean velocity is from left to right in the positive along-flow direction.
The onset of slipping is essentially the same process in reverse, only with a much larger rate of applied stress because we assume failure of the sticky spot takes only 10 min following 12 h of strengthening. Slip begins directly over the weakening sticky spot and spreads rapidly; inertial effects are overcome and a steady velocity perturbation is reached after roughly 5 min. We note that the dependence of the elastic component of velocity on stress rate means that very high slipping velocities can be reached with release of only a fraction of the accumulated stress; the difference in, e.g., τxx between 5 s before and 5 s after slip onset is quite small, but the along-stream velocity perturbation is already over 3 km a−1 (Figure 3). Peak downstream velocities of ~ 74 m d−1 are close to the roughly 70 m d−1 observed on WIP for a slip event following a skipped slip (J. P. Winberry, pers. comm.), suggesting that this experiment is reasonable, but that the decrease in basal drag during a real WIP slip event is more gradual. By the end of slip (Figure 4), nearly all of the accumulated stress has been released (components ~ 1000 Pa or less); due to inertial effects, the remaining stress takes roughly another 5 min to dissipate (components ~ 30 Pa or less, and velocity components < 1 m a−1).
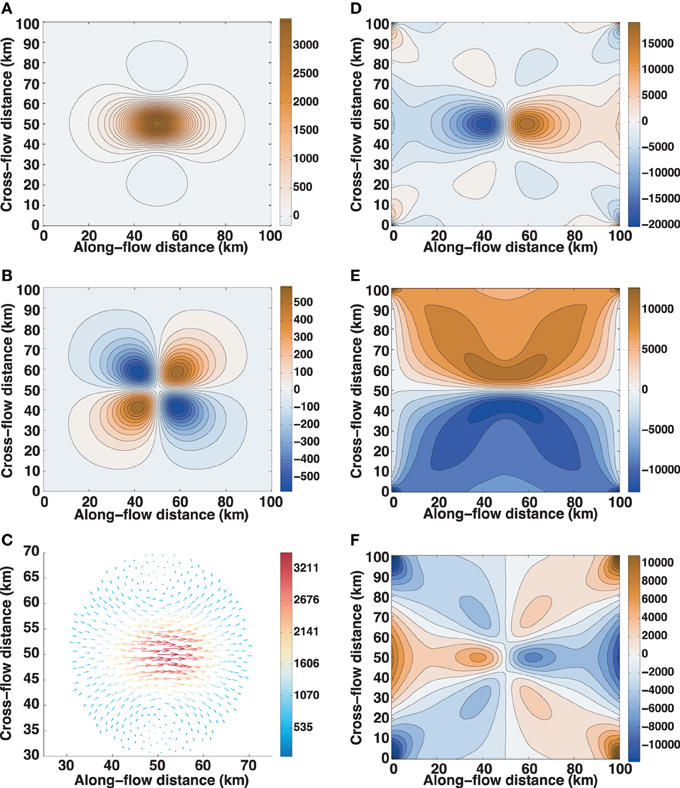
Figure 3. Perturbation at t = 12 h + 5 s: (A) along-flow velocity; (B) cross-flow velocity; (C) vector velocity (colored by magnitude) within 20 km of sticky-spot center; (D) along-flow stress; (E) shear stress; (F) cross-flow stress. Velocities in m a−1, stresses in Pa. Mean velocity is from left to right in the positive along-flow direction.
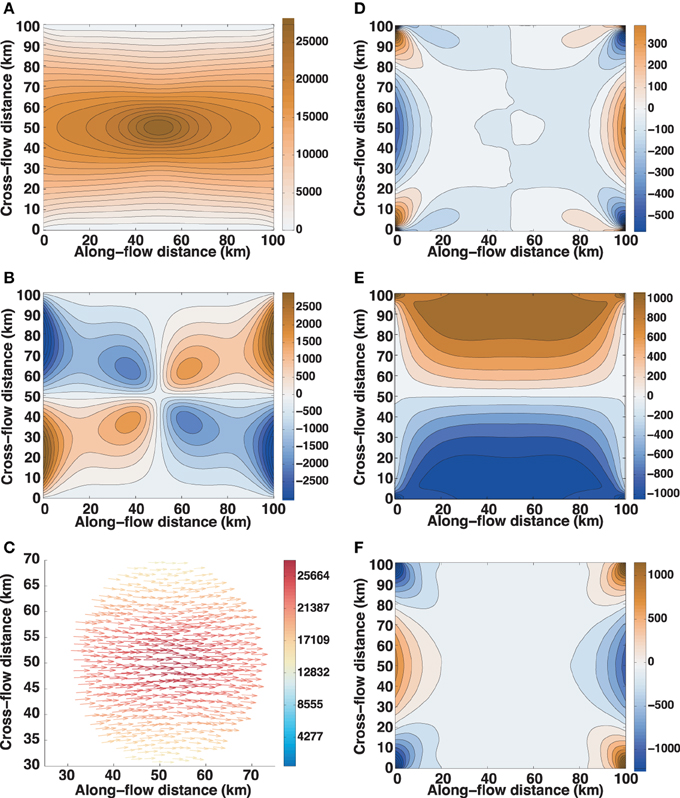
Figure 4. Perturbation at t = 12 h +10 min: (A) along-flow velocity; (B) cross-flow velocity; (C) vector velocity (colored by magnitude) within 20 km of sticky-spot center; (D) along-flow stress; (E) shear stress; (F) cross-flow stress. Velocities in m a−1, stresses in Pa. Mean velocity is from left to right in the positive along-flow direction.
3.2. Effects of Inertial Terms and Linearized Basal Drag
Having presented a typical experiment, we can now explain in greater detail the effects of the inertial and linearized basal drag terms. For clarity, we focus on the along-flow velocity perturbation ũ at the center of the sticky spot. If neither term is present, we have a perfectly plastic case in which the effects of forcing propagate instantaneously across the domain; given our piecewise forcing (13), ũ is given by a step function (Figure 5), which is not realistic. If the inertial term is present without linearized basal drag, our model Equations (11), (12) allow fast wave solutions that cause a “ringing” effect in which the solution oscillates about a mean, potentially with relatively large amplitude. While these fast wave solutions are mathematically correct and would be reasonable for a seismic event, oscillations of this sort have not been observed on time scales of interest for ice-stream stick-slip events (Winberry et al., 2009, 2011). We therefore apply linearized basal drag both to represent a small departure from perfect plasticity and to damp out these fast waves, choosing the smallest α2 that eliminates the oscillations. Because the basal drag term delays signal propagation (cf. Walker et al., 2014), the effect of adding the inertial term is rather small compared to the perfectly plastic case, resulting only in a small difference in timing.
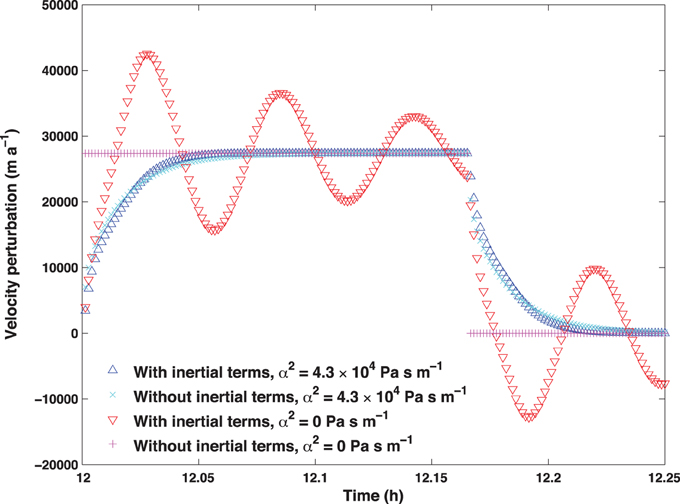
Figure 5. Along-flow velocity perturbation at center of domain (over sticky spot), showing effect of including/excluding inertial terms and/or linearized basal drag.
3.3. Effects of Boundary Conditions
In order to examine the effects of the lateral boundary conditions, we expand the domain to L = 200 km and run with the same forcing. The first noticeable effect of the larger domain is that the linearized drag needed to damp fast waves is cut in half (α2 = 2.1 × 104 Pa s m−1) due to the fast waves needing to travel twice as far before reflecting from the boundaries.
The onset of sticking is quite similar between the domains for roughly the first 30 s, before the perturbation has traveled far enough for shearing at the lateral boundaries to become significant. The time required for significant lateral shear to develop scales with the domain size, so that the time required for the disturbance to propagate across the domain and subsequently reach an essentially steady state doubles. However, the influence of the lateral walls decreases with distance, as expected, so the along-mean-flow velocity perturbation is of greater magnitude (−453 m a−1) than for the original domain. During the slipping phase, the weakening of lateral shear becomes more readily apparent, as the along-mean-flow velocity perturbation reaches over 32.6 km a−1, though the relative increase in magnitude is 19% in both cases.
3.4. Effects of Viscosity
The previous experiments examined cases for which elastic behavior is dominant; we now consider truly viscoelastic cases in which viscous behavior is significant. In particular, we consider the situation discussed by Winberry et al. (2009) in which healing of the bed produces a concave down strength profile. We model this using
in (13). In order to obtain reasonable elastic velocity perturbations, we use n = 1.5 and weaken the sticky spot to kPa. (Here, a reasonable perturbation is one in which the sticking phase slows, but does not reverse, the flow of the ice stream). We return to the L = 100 km domain for this experiment.
Based on the resulting profile of applied basal drag, we expect the elastic component of the perturbation (which depends on stress rate) to be largest at the onset of stick (or slip) and decrease thereafter, and the viscous component (which depends on accumulated stress) to increase over time. While the 10 min slip period is too brief for significant viscous effects to occur, the 12 h stick period allows this possibility. Using reasonable values of η, we can obtain behavior ranging from the purely elastic case to cases in which the viscous component dominates once the initially high stress rate diminishes after ~ 1 h (Figure 6). Interestingly, for η = 1 × 1014 Pa s (which gives a relaxation time of roughly 18 h) the increasing viscous component and decreasing elastic component offset to produce a very nearly steady along-flow velocity perturbation despite time-varying basal drag, a possibility suggested by Winberry et al. (2014).
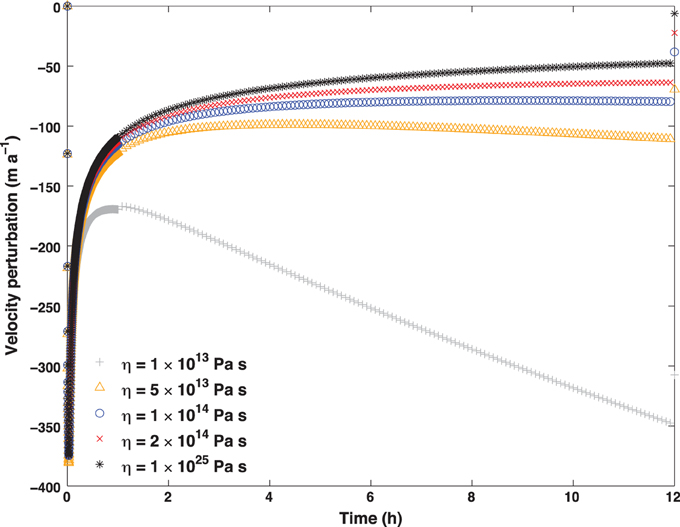
Figure 6. Along-flow velocity perturbation at center of domain (over sticky spot), showing effect of varying viscosity. Results for η≥1 × 1016 Pa s not shown due to overlap with the η = 1 × 1025 Pa s experiment, which is an artificially high value chosen to obtain purely elastic behavior.
Furthermore, the presence of a significant viscous component raises the possibility of stick-slip behavior affecting the long-term mean flow of the ice stream. For example, Winberry et al. (2014) observe a broad area thickening at ~ 0.3 m a−1 (from 2006–2010) upstream of WIP, which they attribute to viscous deformation between slips. Although our model assumes plane stress, the incompressibility condition
does imply a vertical velocity, and thus a thinning/thickening rate. The two-dimensional divergence ∂x ũ visc + ∂y ṽ visc of the viscous component (for the η = 1 × 1014 Pa s experiment) is easily calculated in the finite element framework provided by sparseFEM (Figure 7), and the vertical velocity found by integrating over depth. (Recall that for Maxwell rheology, the viscous component of a viscoelastic solution can be found by subtracting the elastic (η → ∞) solution). By averaging over a cycle, we see that, even though is small enough to support our assumption that h is constant over shorter timescales, the thinning/thickening resulting from the viscous component of stick-slip (up to 0.17 m a−1) can be significant over years to decades. If we consider the case of a “skipped” slip (Winberry et al., 2014) and increase the period between slips to 24 h, we obtain the same pattern of dh∕dt with magnitude increased roughly 70% (to a maximum of 0.29 m a−1, close to the observed rate noted above). Further analysis will require a model with an advective component to determine the interaction of this thickening with the mean flow, and is a subject for future research.
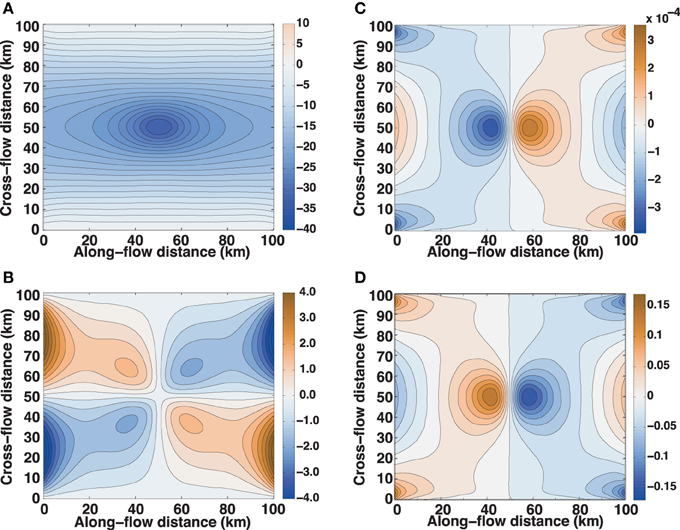
Figure 7. (A–C) Viscous components of (A) along-flow velocity perturbation (m a−1), (B) cross-flow velocity perturbation (m a−1), and (C) two-dimensional divergence of velocity perturbation (s−1), all at t = 12 h, for the η = 1014 Pa s experiment; (D) Time-averaged thickening rate (m a−1) resulting from viscous component of perturbation. Mean velocity is from left to right in the positive along-flow direction.
4. Discussion
We have long known that side drag is important in restraining well-lubricated ice streams (e.g., Raymond et al., 2001). This new work confirms that such boundary effects are important for elastic as well as viscous flow, with important elastic differences when we increased the domain size beyond 100 km. The magnitude of velocity perturbations produced by a sticky spot of a given strength during both stick and slip phases increases with distance from fixed boundaries, i.e., zero-velocity essential boundary conditions. We experimented with natural as well as essential lateral boundary conditions; not surprisingly, we found some dependence of results on the nature as well as the location of the lateral boundary. (These experiments are not shown because “removing” a side wall from our reference experiment by changing to a natural boundary condition results in unrealistic velocity perturbations much larger than those resulting from doubling the domain size). We also note that the boundary conditions we have used, while reasonable in theory, have not been confirmed by observations. The results here thus suggest that additional physical and modeling work on the elastic coupling of ice streams to their surroundings would be valuable.
This study has focused on the effects of sticky-spot formation and release on ice dynamics by imposing idealized profiles of basal drag. However, real stick-slip events on WIP are paced by oscillations of the ocean tides, with ruptures propagating to trigger secondary slip events. The present model can be forced by ocean tides as a natural (stress) boundary condition, with velocity and stress perturbations propagating inland. In order to produce more realistic simulations in future work, the remaining challenge is to develop a model of bed strength consistent with observations and to couple this with the existing ice-stream model. The current model thus provides a platform for further progress, as multiple bed models can be implemented and tested against observations.
Consistent with earlier studies (Winberry et al., 2014), the work here shows that viscous ice deformation in response to compression upglacier of the sticky spot and tension downglacier is not very important for WIS when it is slipping twice per day; however, over longer times, viscous deformation becomes notable. WIS is shifting toward one slip event per day (Winberry et al., 2014), with a pattern of skipped events that is influenced by the spring-neap tidal cycle, and other tidally influenced ice flow has been shown to respond to tidal components slower than diurnal (Gudmundsson, 2007). This interaction between viscous and elastic processes on ice streams means that viscoelastic ice-flow modeling offers advantages over models treating the different regimes separately.
5. Summary
We develop and present a two-dimensional viscoelastic model of stick-slip ice-stream motion that is somewhat more complex than earlier slider block models (e.g., Winberry et al., 2009, 2014). In situations where elastic ice behavior is dominant, the velocity perturbation depends strongly on the rate of applied basal stress, so that very high velocities can be reached early in the slipping process, with the release of only a small fraction of the accumulated stress. We note that this is consistent with the conclusion of Winberry et al. (2009) that increases in slip magnitude are caused by increases in accumulated stress, provided that the duration of slip events remains roughly constant. In situations where viscous ice behavior becomes important, the viscous component of the perturbation grows with total accumulated stress; we show that this growth can offset decreases in the elastic component of ice velocity when the sticky-spot strength profile is concave down. Perhaps more importantly, we demonstrate that the viscous components of repeated stick-slip cycles can gradually lead to thickening upstream and thinning downstream of the sticky spot. For parameters approximately representative of Whillans Ice Stream, the lateral boundaries affect stick-slip behavior even with an aspect ratio over 100:1, emphasizing the importance of characterizing these boundaries in field work and modeling. While work remains to be done regarding the mechanisms of sticky-spot growth and collapse, the model presented here does provide insight as to the importance of both components of viscoelastic ice rheology in stick-slip ice-stream dynamics.
Author Contributions
All authors contributed to the theory underlying this work. RW and BP were responsible for the mathematical development of the model. RW coded the numerical model and ran the experiments. RA proposed the experiments in Section 3.4. All authors participated in the writing of this manuscript and approved the final version.
Funding
This research was supported by NASA under grants NNX12AD03A (RW), NNX12AP50G (RW) and NNX15AH84G (BP), and by the NSF under grants AGS 13-38832 (RA, BP), PLR 14-43190 (BP, RW), and PLR 04-24589 (RA, BP) to the Center for Remote Sensing of Ice Sheets (CReSIS). Additional funding was provided to SN by NASA through its Cryospheric Sciences and Modeling Analysis and Prediction Programs.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Mauro Werder for sharing the sparseFEM MATLAB package, which he wrote with Christian Schoof and Ian Hewitt. We also thank the editor and reviewers for constructive comments that led to a greatly improved final manuscript.
References
Alley, R. B., Blankenship, D. D., Bentley, C. R., and Rooney, S. T. (1987). Till beneath Ice Stream B: 3. Till deformation – evidence and implications. J. Geophys. Res. 92, 8921–8929. doi: 10.1029/JB092iB09p08921
Anandakrishan, S., and Alley, R. B. (1997). Tidal forcing of basal seismicity of ice stream C, West Antarctica, observed far inland. J. Geophys. Res. 102, 15183–15196. doi: 10.1029/97JB01073
Anandakrishnan, S., Voigt, D. E., Alley, R. B., and King, M. A. (2003). Ice stream D flow speed is strongly modulated by the tide beneath the Ross Ice Shelf. Geophys. Res. Lett. 30, 1361. doi: 10.1029/2002GL016329
Bentley, C. R. (1987). Antarctic ice streams – a review. J. Geophys. Res. 92, 8843–8858. doi: 10.1029/JB092iB09p08843
Bindschadler, R. A., King, M. A., Alley, R. B., Anandakrishnan, S., and Padman, L. (2003). Tidally controlled stick-slip discharge of a west Antarctic ice stream. Science 301, 1087–1089. doi: 10.1126/science.1087231
Bindschadler, R. A., Nowicki, S. M. J., Abe-Ouchi, A., Aschwanden, A., Choi, H., Fastook, J., et al. (2013). Ice-sheet model sensitivities to environmental forcing and their use in projecting future sea level (the SeaRISE project). J. Glaciol. 59, 195–224. doi: 10.3189/2013jog12j125
Christianson, K., Parizek, B. R., Alley, R. B., Horgan, H. J., Jacobel, R. W., Anandakrishnan, S., et al. (2013). Ice sheet grounding zone stabilization due to till compaction. Geophys. Res. Lett. 40, 5406–5411. doi: 10.1002/2013GL057447
Christoffersen, P., Tulaczyk, S., and Behar, A. (2010). Basal ice sequences in Antarctic ice stream: exposure of past hydrologic conditions and a principal mode of sediment transfer. J. Geophys. Res. Earth Surf. 115:F03034. doi: 10.1029/2009JF001430
Gudmundsson, G. H. (2007). Tides and the flow of Rutford Ice Stream, West Antarctica. J. Geophys. Res. 112:F04007. doi: 10.1029/2006JF000731
Gudmundsson, G. H. (2011). Ice-stream response to ocean tides and the form of the basal sliding law. Cryosphere 5, 259–270. doi: 10.5194/tc-5-259-2011
Horgan, H. J., Alley, R. B., Christianson, K., Jacobel, R. W., Anandakrishnan, S., Muto, A., et al. (2013). Estuaries beneath ice sheets. Geology 41, 1159–1162. doi: 10.1130/G34654.1
Iverson, N. R. (1993). Regelation of ice through debris at glacier beds - implications for sediment transport. Geology 21, 559–562.
Joughin, I., MacAyeal, D. R., and Tulaczyk, S. (2004). Basal shear stress of the Ross ice streams from control method inversions. J. Geophys. Res. 109:B09405. doi: 10.1029/2003JB002960
MacAyeal, D. R. (1989). Large-scale ice flow over a viscous basal sediment: theory and application to Ice Stream B, Antarctica. J. Geophys. Res. 94, 4071–4087. doi: 10.1029/JB094iB04p04071
Muto, A., Christianson, K., Horgan, H. J., Anandakrishnan, S., and Alley, R. B. (2013). Bathymetry and geological structures beneath the Ross Ice Shelf at the mouth of Whillans Ice Stream, West Antarctica, modeled from ground-based gravity measurements. J. Geophys. Res. Solid Earth 118, 4535–4546. doi: 10.1002/jgrb.50315
Pratt, M. J., Winberry, J. P., Wiens, D. A., Anandakrishnan, S., and Alley, R. B. (2014). Seismic and geodetic evidence for grounding-line control of Whillans Ice Stream stickslip events. J. Geophys. Res. 119, 333–348. doi: 10.1002/2013JF002842
Raymond, C. F., Echelmeyer, K. A., Whillans, I. M., and Doake, C. S. M. (2001). “Ice stream shear margins,” in The West Antarctic Ice Sheet: Behavior and Environment, Antarctic Research Series, Vol. 77, eds R. B. Alley and R. A. Bindschadler (Washington, DC: American Geophysical Union), 137–155.
Reeh, N., Christensen, E. L., Mayer, C., and Olesen, O. B. (2003). Tidal bending of glaciers: a linear viscoelastic approach. Ann. Glaciol. 37, 83–89. doi: 10.3189/172756403781815663
Schulson, E. M., and Duval, P. (2009). Creep and Fracture of Ice. New York, NY: Cambridge University Press. doi: 10.1017/CBO9780511581397
Tulaczyk, S. (2006). Scale independence of till rheology. J. Glaciol. 52, 377–380. doi: 10.3189/172756506781828601
Turcotte, D. L., and Schubert, G. (2002). Geodynamics, 2nd Edn. New York, NY: Cambridge University Press. doi: 10.1017/CBO9780511807442
Voytenko, D., Stern, A., Holland, D. M., Dixon, T. H., Christianson, K., and Walker, R. T. (2015). Tidally driven ice speed variation at Helheim Glacier, Greenland, observed with terrestrial radar interferometry. J. Glaciol. 61, 301–308. doi: 10.3189/2015JoG14J173
Walker, R. T., Christianson, K., Parizek, B. R., Anandakrishnan, S., and Alley, R. B. (2012). A viscoelastic flowline model applied to tidal forcing of Bindschadler Ice Stream, West Antarctica. Earth Planet. Sci. Lett. 309, 128–132. doi: 10.1016/j.epsl.2011.12.019
Walker, R. T., Parizek, B. R., Alley, R. B., Anandakrishnan, S., Riverman, K. L., and Christianson, K. (2013). Ice-shelf flexure and subglacial pressure variations. Earth Planet. Sci. Lett. 361, 422–428. doi: 10.1016/j.epsl.2012.11.008
Walker, R. T., Parizek, B. R., Alley, R. B., Brunt, K. M., and Anandakrishnan, S. (2014). Ice-shelf flexure and tidal forcing of Bindschadler Ice Stream, West Antarctica. Earth Planet. Sci. Lett. 395, 184–193. doi: 10.1016/j.epsl.2014.03.049
Walter, J. I., Brodsky, E. E., Tulaczyk, S., Schwartz, S. Y., and Pettersson, R. (2011). Transient slip events from near-field seismic and geodetic data on a glacier fault, Whillans Ice Plain, West Antarctica. J. Geophys. Res. 116:F01021. doi: 10.1029/2010JF001754
Walter, J. I., Svetlizky, I., Fineberg, J., Brodsky, E. E., Tulaczyk, S., Barcheck, C. G., et al. (2015). Rupture speed dependence on initial stress profiles: insights from glacier and laboratory stick-slip. Earth Planet. Sci. Lett. 411, 112–120. doi: 10.1016/j.epsl.2014.11.025
Wiens, D. A., Anandakrishnan, S., Winberry, J. P., and King, M.A. (2008). Simultaneous teleseismic and geodetic observations of the stick slip motion of an Antarctic ice stream. Nature 453, 770–774. doi: 10.1038/nature06990
Winberry, J. P., Anandakrishnan, S., Alley, R. B., Bindschadler, R. A., and King, M. A. (2009). Basal mechanics of ice streams: insights from the stick-slip motion of Whillans Ice Stream, West Antarctica. J. Geophys. Res. 114:F01016. doi: 10.1029/2008JF001035
Winberry, J. P., Anandakrishnan, S., Wiens, D. A., Alley, R. B., and Christianson, K. (2011). Dynamics of stick-slip motion, Whillans Ice Stream, Antarctica. Earth Planet. Sci. Lett. 305, 283–289. doi: 10.1016/j.epsl.2011.02.052
Winberry, J. P., Anandakrishnan, S., Alley, R. B., Wiens, D. A., and Pratt, M.J. (2014). Tidal pacing, skipped slips and the slowdown of Whillans Ice Stream, Antarctica. J. Glaciol. 60, 283–289. doi: 10.3189/2014JoG14J038
Keywords: ice stream dynamics, stick-slip, viscoelasticity, ice rheology, Whillans ice stream, numerical ice sheet modeling
Citation: Walker RT, Parizek BR, Alley RB and Nowicki SMJ (2016) A Viscoelastic Model of Ice Stream Flow with Application to Stick-Slip Motion. Front. Earth Sci. 4:2. doi: 10.3389/feart.2016.00002
Received: 08 October 2015; Accepted: 07 January 2016;
Published: 26 January 2016.
Edited by:
Alun Hubbard, University of Tromso and Aberystwyth University, NorwayReviewed by:
Chris Borstad, The University Centre in Svalbard, NorwayRachel Joanne Carr, Newcastle University, UK
Jake Walter, University of Texas at Austin, USA
Copyright © 2016 Walker, Parizek, Alley and Nowicki. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ryan T. Walker, cnlhbi50LndhbGtlckBuYXNhLmdvdg==
 Ryan T. Walker
Ryan T. Walker Byron R. Parizek
Byron R. Parizek Richard B. Alley
Richard B. Alley Sophie M. J. Nowicki
Sophie M. J. Nowicki